Effects of surface and shear forces on nano-confined smectic-A liquid crystals studied by X-ray diffraction†
Masashi
Mizukami
 *a,
Noboru
Ohta
b,
Kazuhito
Tomita
a,
Takuya
Yanagimachi
c,
Yuuta
Shibuya
c,
Naoto
Yagi
b and
Kazue
Kurihara
*a,
Noboru
Ohta
b,
Kazuhito
Tomita
a,
Takuya
Yanagimachi
c,
Yuuta
Shibuya
c,
Naoto
Yagi
b and
Kazue
Kurihara
 *c
*c
aInstitute of Multidisciplinary Research for Advanced Materials, Tohoku University, Katahira 2-1-1, Aoba-ku, Sendai 980-8577, Japan. E-mail: masashi.mizukami.e7@tohoku.ac.jp
bJapan Synchrotron Radiation Research Institute/SPring-8, Sayo, Hyogo 679-5198, Japan
cNew Industry Creation Hatchery Center, Tohoku University, 2-1-1 Katahira, Aoba-ku, Sendai 980-8577, Japan. E-mail: kazue.kurihara.b7@tohoku.ac.jp
First published on 20th October 2020
Abstract
The orientational behavior of a smectic-A liquid crystal (4-cyano-4′-octylbiphenyl, 8CB) confined between mica surfaces as well as between silica surfaces with a nanometer scale thickness was investigated by synchrotron X-ray diffraction measurement. The crystallographic axes of two confining mica sheets were adjusted parallel to each other to induce the preferential orientation of 8CB molecules along their crystallographic axis. The silica surfaces, which were hydrophilic and amorphous and had nanometer level smoothness, were prepared on mica surfaces using a sputtering technique. The X-ray diffraction measurement revealed that the 8CB molecules, confined between mica surfaces (DHW = 1.7 nm) and between silica surfaces (DHW = ca. 2 nm), took a planar orientation (oriented its long axis parallel to the surface) and formed a lamellar structure. However, the in-plane orientation of the confined 8CB changed depending on the confining surfaces. The lamellar axis of the 8CB confined between mica surfaces uniaxially oriented most probably due to the preferential alignment of its long axis along the principal crystallographic a-axis of the mica. On the other hand, 8CB between the silica surfaces formed lamellar domains in which the lamellar axis of 8CB omnidirectionally oriented in-plane. The effect of the shear on the orientation of the nano-confined 8CB was also investigated. The lamellar axis, corresponding to the long axis of the 8CB molecules confined between the mica surfaces, rotated only ca. 3 degrees within the plane parallel to the surface by perpendicularly applying shear to the axis. The lamellar axis of the 8CB molecules between the silica surfaces showed no noticeable change by applying the shear. These results indicated that the effect of shear to align the 8CB molecules was significantly suppressed due to the confinement effect which significantly reduces the mobility of molecules as well as the alignment effect along the crystallographic axis in the case of mica. We also observed a change in the orientation of nano-confined 8CB after shear treatment at large D (= 3.3 μm).
1 Introduction
The properties of nano-confined liquids are known to be quite different from those of the bulk liquids due to the restriction of their motions and interactions with the solid surfaces based on studies by computer simulation1,2 as well as by various experiments3 including surface force measurement using surface force apparatus (SFA).4–12 It is also known that the structure and properties of confined liquids depend not only on the liquid itself but also on the surface properties.13–15 However, the molecular level characterization of nano-confined liquids is still limited due to the lack of appropriate techniques though it is imperative for understanding this complex phenomenon. Recently, nano-confined liquids have attracted increasing attention because it has been recognized that nano-confined liquids play a crucial role in developing technologies such as tribology,13–19 micro/nano-fluidics,20 and nano-molding.19 Therefore, the characterization and elucidation of confined liquids are becoming more important.Liquid crystals (LCs) belong to the class of typical liquids which have been investigated in a confined space, because the orientation behavior due to their anisotropic nature has been utilized for a wide variety of optical devices.21 Their nature is usually controlled by the surface properties. Prepared by rubbing and/or chemical modification and using the electric field, LCs are also known to exhibit excellent lubrication properties and have the potential to act as the active control of lubrication by an external field such as an electric field and shear.22 Therefore, it is important to understand the orientation behavior of LCs adjacent to the solid surfaces and in confined spaces, and the effects of the surface properties and the external fields on them.
One of the powerful tools to investigate the orientation of LC molecules confined between two surfaces is normal and shear force measurements using surface force apparatus (SFA). The experiments using SFA can characterize the orientation of LCs controlled by substrate surfaces by monitoring the viscous properties and the refractive index of LCs confined between surfaces. A planar orientation was reported for the nematic liquid crystals of 4-cyano-4′-pentylbiphenyl (5CB)23 and 4-cyano-4′-hexylbiphenyl (6CB),24 as well as for a smectic-A liquid crystal of 4-cyano-4′-octylbiphenyl (8CB)25,26 confined between mica surfaces. A homeotropic orientation was reported for 5CB, 6CB and 8CB confined between hydrophobized mica surfaces.23–25 The orientation of LCs can be controlled by changing the density of a mesogen polymer anchored to the surface, the mechanism of which has been studied using SFA.27 We have investigated the viscous properties of 6CB confined between mica surfaces as a function of the surface separation distance (D) using resonance shear measurement (RSM) developed by us,9,10 and found that the viscosity of the confined 6CB significantly increased at D < ca. 20 nm.9–11 The RSM study of the effect of an electric field on the orientation of 6CB confined between mica surfaces revealed that the orientation could not be controlled by the electric field at D < 12.5 ± 1.3 nm.28 The experiments using SFA can evaluate the average orientation from surface normal, and distinguish the planar or homeotropic orientation based on the measurement of normal forces, refractive index, and shear forces. However, the experiments using SFA cannot evaluate the in-plane (parallel to the surface) ordering.
In order to obtain more direct and detailed information about the structure and orientation of confined liquids, especially in-plane orientation, we have established the X-ray diffraction measurement of nano-confined liquids by using the high brilliance synchrotron X-ray beam in SPring-8.15,29 The first observation of the X-ray diffraction measurement of nanometer thick layers of 8CB between mica surfaces demonstrated that 8CB formed a planar uniaxial orientation with a very long structural relaxation time (ca. 60 min).29 More recently, we reported the X-ray diffraction study of nano-confined ionic liquids (ILs), which demonstrated the anion and cation organization in nano-spaces expected from a molecular dynamics simulation.13–15 The results for the smallest separation distance, ca. 2 nm, revealed the specific anion and cation arrangements on the silica surfaces, thus explaining the specific viscosities of the nano-confined ILs between silica surfaces.15 Previously, the X-ray diffraction measurement of 8CB confined between mica surfaces under shear was performed and the shear-induced orientation was observed. However, the measurements were performed only for large thicknesses of the 8CB > 390 nm.30–33
In this study, we employed the X-ray diffraction measurement for studying the orientation of a room-temperature smectic-A liquid crystal (4-cyano-4′-octylbiphenyl (8CB)) confined between mica surfaces as well as between hydrophilic silica surfaces. As we mentioned, it is known that the mica surface aligns the liquid crystal molecules along its crystallographic axis. On the other hand, the silica is amorphous and the alignment of the liquid crystal molecules along a specific direction cannot be expected. Thus, mica and silica surfaces were employed to investigate how the properties of the confining surfaces can affect the orientation and the structure of the liquid crystal. The in-plane orientation/alignment of nano-confined 8CB changed depending on the surface properties. The effect of shear on the orientation of 8CB confined between the surfaces was also investigated.
2 Experimental
2.1 Liquid crystal
The liquid crystal used in this study, 4-cyano-4′-octylbiphenyl (8CB), was purchased from Merck and used as received (Fig. 1). 8CB shows a smectic-A phase between 21.5 and 33.5 °C, a nematic phase between 33.5 and 40.5 °C, and an isotropic phase above 40.5 °C. It is known that 8CB forms dimers with a width and a length of ca. 1 nm and 3.14 nm, respectively.262.2 Preparation of mica and silica surfaces for X-ray scattering
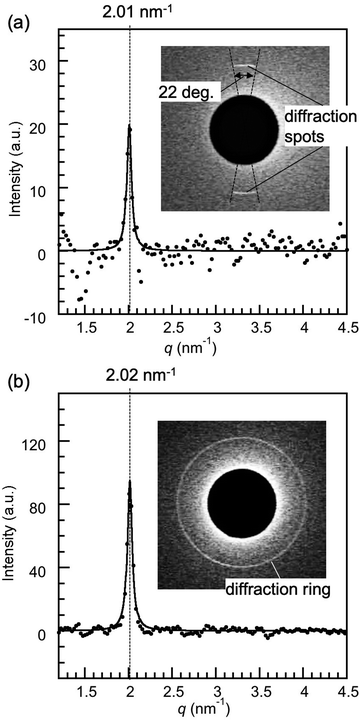
Fig. 2(a) shows a schematic illustration of the sample surfaces and confined liquid between them. As described in our previous reports,15,29 the muscovite mica sheets (thickness of 8–10 μm) used as the substrates were freshly cleaved, and then gold (ca. 15 nm) was evaporated onto the backside of the mica sheets. The gold layer was deposited to improve the contrast of the Newton's ring which was used for determining the contact position. A pair of mica sheets were then glued onto a pair of cylindrical disks made of the Super Invar (Nilaco Corp.) metal alloy (radius of curvature (R) of ca. 20 mm, with a concentric φ = 1 mm pinhole) using an ultraviolet curing resin (NOA61, Norand Product, Inc.) with the gold-covered side down on the disks. It was ensured that no resin spread into the X-ray beam path to reduce the background scattering. It is known that the mica surface has an effect to align the long axis of 8CB along its crystallographic axis a (principal refractive axis β) in a cleavage plane.26 Thus, the crystallographic axes of two confining mica sheets were adjusted parallel to each other to induce the preferential orientation of the 8CB molecules along their crystallographic axes. Before gluing the mica sheets on the cylindrical discs, the direction of the principal refractive axes of β and γ in a cleavage plane was confirmed using a pair of polarizers in a crossed nicol arrangement in order to know the direction of the crystallographic axes of a and b during the cleavage. The two mica sheets were then glued on the cylindrical discs ensuring that the crystallographic axes of the two mica sheets became parallel to each other when the discs were placed in a chamber in a crossed cylinder geometry. | ||
| Fig. 2 Schematic drawings of sample surfaces and confined liquid between them (a), and an apparatus for the X-ray diffraction measurement (b). | ||
For the X-ray scattering measurement of the confined 8CB between the hydrophilic silica surfaces, thin silica films were deposited on mica sheets after gluing them on the cylindrical disks. The silica layers with a thickness of ca. 90 nm were deposited on the mica substrates using an RF magnetron sputtering system (C-400-2C, Ulvac Riko, Inc.) at an RF power of 200 W following the procedure previously reported34 except for the heat treatment. The contact angle of water on the silica surfaces was 1.9 ± 0.9 deg., which confirmed the hydrophilic nature (high surface free energy) of the prepared silica surfaces. The root mean square (rms) and peak to valley (p–v) roughness of the prepared silica surfaces characterized by atomic force microscopy (SPA400-NanoNavi, Seiko Instruments, Inc.) images (scan area of 1 × 1 μm2) were 0.26 ± 0.03 nm and 2.79 ± 0.39 nm, respectively.
Both the mica and silica surfaces were covered by freshly cleaved thin mica sheets to avoid contamination until just before the XRD measurement at SPring-8.
2.3 X-Ray diffraction measurement of confined liquids
Fig. 2(b) shows a schematic illustration of the surface force apparatus (SFA) designed for the X-ray diffraction measurement of confined liquids at SPring8 (Hyogo, Japan) in the BL40B2 experimental hutch. The basic setting for the X-ray diffraction measurement was the same as that in our previous report.15,29 Briefly, half cylindrical disks, on which the mica sheets or silica sputtered mica sheets were glued, were mounted in an SFA chamber with a crossed cylinder geometry. The axis of one cylindrical disc was adjusted in the X-direction (χ = 0 degree) and that of the other disc was adjusted in the Y-direction (χ = 90 degree). The disk on the downstream side (against the incident X-ray beam) was connected to leaf springs, and was driven by a stepper motor stage (M-111.1DG, Physik Instruments Japan) and the piezo stage (P-752.11C, Physik Instruments Japan). A sodium vapor lamp irradiated the sample surfaces from the upstream side, and the generated Newton's ring was observed using a microscope to determine the contact position. To bring the contact position near the center of the pinhole, the position and the tilt of the upstream disk were adjusted by an X–Y stage (TASB-152, Sigma Koki) and a biaxial goniostage (GOH-15A10, Sigma Koki), respectively.The monochromatic X-ray beam (15 keV) was passed through a pinhole (diameter = 50 μm) located ca. 0.2 m from the sample. Using a radiochromic film (Gafchromic HD810, ISP Technologies, Inc.), the size and the in-plane (x–y plane) position of the X-ray beam were confirmed, and then the center of Newton's ring, i.e., the contact position, was adjusted to the position of the X-ray beam by moving the whole chamber using the motor driven x–y stage placed under the chamber.
The X-ray diffraction profiles were recorded using an imaging plate system (R-AXIS VII, Rigaku Co., Ltd) with a 0.3 × 0.3 m2 area, which was placed 0.29 m from the sample position. The scattering vector q = 2π/d = (4π/λ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) was calibrated from the lattice spacing (d = 5.838 nm; d is the repeat distance) of a silver behenate standard powder at room temperature,35 in which 2θ is the scattering angle and λ = 0.083 nm is the wavelength of the X-ray beam. The recorded diffraction pattern was circularly averaged (from angle χ = 0 to 360 degree) to obtain a radial intensity profile. The background X-ray diffraction patterns were measured with an exposure time of 600 s before injecting the 8CB between the surfaces. After injection of the 8CB (about 20 μL), the X-ray diffraction patterns were obtained at the hard wall thickness (DHW), i.e., the smallest surface separation distance in the presence of 8CB under compression. The typical DHW value for the confined 8CB was determined to be 1.7 nm using the fringes of equal chromatography (FECO) in a separate surface force measurement in our laboratory, which agreed with the previous value.29
θ) was calibrated from the lattice spacing (d = 5.838 nm; d is the repeat distance) of a silver behenate standard powder at room temperature,35 in which 2θ is the scattering angle and λ = 0.083 nm is the wavelength of the X-ray beam. The recorded diffraction pattern was circularly averaged (from angle χ = 0 to 360 degree) to obtain a radial intensity profile. The background X-ray diffraction patterns were measured with an exposure time of 600 s before injecting the 8CB between the surfaces. After injection of the 8CB (about 20 μL), the X-ray diffraction patterns were obtained at the hard wall thickness (DHW), i.e., the smallest surface separation distance in the presence of 8CB under compression. The typical DHW value for the confined 8CB was determined to be 1.7 nm using the fringes of equal chromatography (FECO) in a separate surface force measurement in our laboratory, which agreed with the previous value.29
The surface separation distance (D) (normal load (L)) remained constant during the exposure time using a feedback loop control. The laser interferometer deflection sensor (SI-F01, SI-F01U, SI-F1000V, Keyence) fixed to the disc holder of the upstream surface was used to monitor the distance (D′) between the sensor and the holder of the downstream surface. To keep D constant, D′ was kept constant by moving the downstream surface using the piezo stage. When the change in D′ was detected using a laser interferometry sensor, the piezo stage was driven to keep D′ constant through a PID controlled feedback program developed on the LabVIEW platform (National Instruments).
To investigate the effect of shear on the orientation of the confined 8CB, the upstream surface was perpendicularly oscillated to the long axis of the leaf spring connected to the downstream surface using a device designed for the X-ray diffraction measurement chamber. The upstream surface was connected to a four-sectored piezo tube and hung by a pair of vertical leaf springs. By applying sinusoidal voltages of the amplitude (Uin) and the resonance peak frequency (f) to the piezo tube, the upstream surface was oscillated. The amplitude of the input voltage (Uin) used was in the range of 1–100 V. The input voltage Uin of 1 V corresponded to a shear amplitude (Apeak) of ca. 14 nm at the hard wall thickness (DHW). The frequency (f) of the input voltage (Uin) was adjusted to the peak frequency (fpeak) of the resonance curve (Uout/Uinvs. ω (= 2πf)).
3 Results and discussion
3.1 XRD study of nano-confined 8CB: comparison of mica and silica
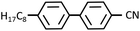
Fig. 3(a) shows the X-ray diffraction intensity profiles of 8CB confined between the mica surfaces, in which the crystallographic axes were adjusted parallel to each other, measured at the hard wall thickness DHW (= 1.7 nm). A sharp peak at q = 2.01 nm−1 (the corresponding spacing (d) = 3.13 nm) with a full width at half maximum (FWHM) of 0.064 nm−1 was observed. A d value of 3.11 nm well agreed with the reported lamellar spacing value of 8CB (3.173 nm)36 and our previous observation.29 This indicated that the 8CB molecules are completely oriented parallel to the mica surfaces (planar orientation) and formed an in-plane lamellar structure. As shown in the inset of Fig. 3(a), the diffraction image for a smaller angle region (q < ca. 2.5 nm−1) exhibited two circular arc spots with a center angle of ca. 22 degrees located at the centrosymmetric position (χ = 90 and 270 degrees). This indicated that the 8CB molecules confined between the mica surfaces are almost uniaxially (with an angle distribution of ca. 22 degree) oriented at least within the X-ray beam spot area (φ = 50 μm). This result was consistent with the report by Salmeron et al.,26 which detailed that the 8CB molecules on mica preferentially align its long axis along the crystallographic axis (a-axis) of mica. The intensity parameter (C) and the FWHM of the peak in Fig. 3(a) were calculated using the Lorentz function, and are summarized in Table 1 together with the peak positions.| Peak position, qpeak (nm−1) | FWHM, w (nm−1) | Intensity parameter, C | |
|---|---|---|---|
| 8CB confined between mica surfaces | 2.01 | 0.064 | 20 |
| 8CB confined between silica surfaces | 2.02 | 0.066 | 95 |
In order to study the influence of the surface properties of substrates confining 8CB, silica substrates were used to replace the mica. Fig. 3(b) shows the X-ray diffraction intensity profiles of 8CB confined between hydrophilic silica surfaces measured at DHW (= 1.7 nm). A sharp peak at q = 2.02 nm−1, which corresponded to the lamellar spacing (d = 3.11 nm), was observed similar to 8CB confined between the mica surfaces. The FWHM value for 8CB confined between the silica surfaces was 0.066 nm−1, which was also very similar to the value for 8CB confined between the mica (0.064 nm−1). These results indicated that 8CB molecules oriented parallel to the silica surfaces, which were hydrophilic and smooth (see the Experimental section), and formed an in-plane lamellar structure similar to those confined between the mica surfaces (planar orientation). However, the diffraction image (inset of Fig. 3(b)) showed a ring diffraction pattern, which was different from the centrosymmetric spots observed for mica surfaces. This indicated that the in-plane orientation of the 8CB molecules confined between the silica surfaces was omnidirectional, and many small lamellar domains with different in-plane orientations existed within the X-ray beam spot area (φ = 50 μm). This difference can be due to the different surface crystallinity, crystalline mica and amorphous silica, and/or the larger surface roughness of silica surface (rms roughness: 0.26 ± 0.03 nm) compared with that of atomically flat mica surface. Considering the normal distribution of the roughness of silica, the thickness distribution of confined 8CB was estimated to be from 0.6 nm (minimum) to 2.8 nm (maximum), corresponding to one to three layers of 8CB dimers, and about 70% of 8CB were within a thickness of 1.7 ± 0.3 nm (DHW ± rms roughness). Therefore, the measured molecular orientation should be an averaged value of these conditions, which we considered from the single domain size and the diffraction peak positions for two cases. The single domain sizes of 8CB confined between silica surfaces and between mica surfaces were compared. Here, the single domain sizes of confined 8CB were estimated from the FWHM's using the Scherrer's equation typically used for evaluating the size of the crystal domain (B = 0.94λ/(ΔθFWHM·cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), θ (rad): scattering angle, and ΔθFWHM (rad): full width at half maximum).37 The single domain size of 8CB confined between silica surfaces was estimated to be 179 nm, which was practically identical to the value for mica surfaces, 184 nm. This means that the roughness of the silica had no significant effect on the domain size of confined 8CB. The similar diffraction peak position for mica (q = 2.01 nm−1) and silica (q = 2.02 nm−1) also indicated that the surface roughness had no significant effect on the in-plane lamellar spacing of confined 8CB. These results indicate that the thickness distribution from one to three layers of 8CB dimer had less significant effects on the orientation of the confined 8CB between silica surfaces. Therefore, the primary cause of the omnidirectional domains of 8CB confined between silica surfaces should be the amorphous nature of the silica surfaces. The intensity parameter (C) and the FWHM of the peak in Fig. 3(b) were calculated using the Lorentz function, and are summarized in Table 1 together with the peak positions.
θ), θ (rad): scattering angle, and ΔθFWHM (rad): full width at half maximum).37 The single domain size of 8CB confined between silica surfaces was estimated to be 179 nm, which was practically identical to the value for mica surfaces, 184 nm. This means that the roughness of the silica had no significant effect on the domain size of confined 8CB. The similar diffraction peak position for mica (q = 2.01 nm−1) and silica (q = 2.02 nm−1) also indicated that the surface roughness had no significant effect on the in-plane lamellar spacing of confined 8CB. These results indicate that the thickness distribution from one to three layers of 8CB dimer had less significant effects on the orientation of the confined 8CB between silica surfaces. Therefore, the primary cause of the omnidirectional domains of 8CB confined between silica surfaces should be the amorphous nature of the silica surfaces. The intensity parameter (C) and the FWHM of the peak in Fig. 3(b) were calculated using the Lorentz function, and are summarized in Table 1 together with the peak positions.
3.2 XRD study of effect of shear on nano-confined 8CB
We have studied the effect of shear by perpendicularly applying the shear (Uin = 10 and 100 V) to the lamellar axis (long axis of 8CB). Fig. 4 compares the X-ray diffraction images of 8CB confined between the mica surfaces without the shear (a) and under shear (b and c). As already mentioned, the 8CB molecules were in almost uniaxial orientation without the shear. As shown in Fig. 4(b), the positions of the centrosymmetric two circular arc spots rotated ca. 3 degrees in the clockwise direction. This indicated that the lamellar axis of the nano-confined 8CB was only slightly rotated by applying the shear. In a previously reported XRD study on the effect of shear on the 8CB confined between mica surfaces with a surface separation distance (D) of 1 μm, 8CB molecules were well aligned along the shear direction.31 On the other hand, our measurement revealed that the effect of shear on the orientation was significantly suppressed when the 8CB molecules were confined in a nanometer level gap (DHW = 1.7 nm). It is known that 8CB forms dimers with a width of ca. 1 nm, and the hard wall thickness DHW = 1.7 nm corresponds to the two layers of the 8CB dimers. Therefore, at DHW = 1.7 nm, all the 8CB dimers directly interacted with the mica surfaces and aligned along the crystallographic axis of the mica.26 It is also known that the mobility of the molecules under nano-confinement could be significantly suppressed, cf., we have previously determined that the relaxation time of the nano-confined 8CB between the mica surfaces is long, ca. 60 min.29 These effects could be the reason for the suppression of the shear-induced alignment effect. Concerning the intensity of the diffraction, the brightness of the spots slightly decreased. This will be discussed later based on the diffraction profiles.As shown in Fig. 4(c), by applying shear of a higher amplitude (Uin = 100 V) perpendicular to the lamellar axis (long axis of 8CB), the positions of the centrosymmetric two circular arc spots remained the same as those under the shear of lower amplitude (Uin = 10 V). This means that the increase in the shear amplitude had no further shear aligning effect due to the opposing strong effects of alignment and nano-confinement by the mica surfaces. However, the brightness of the diffraction spots increased by applying higher shear.
The changes in the diffraction intensities induced by applying the shear (Uin = 10 and 100 V) are discussed based on the diffraction intensity profiles shown in Fig. 5. Fig. 5 shows the X-ray diffraction intensity profiles of 8CB confined between the mica surfaces obtained by integrating the scattering intensities in the diffraction images shown in Fig. 4. The peak position of the lamellar spacing obtained under shear (Uin = 10 and 100 V) was at q = 2.01 nm−1, and was completely the same as that obtained without shear. This indicated that no out-of-plane orientation was induced by applying the shear, and only a slight in-plane rotation of the orientation angle was induced as observed in Fig. 4(a) and (b). The intensity parameter (C) and the FWHM of the peaks in Fig. 5 are summarized in Table 2 together with the peak positions. The intensity parameter (C) decreased and the FWHM value increased by applying the shear of lower amplitude (Uin = 10 V). This indicated that the orientation of the 8CB became less ordered and the size of the domain decreased from 180 nm to 140 nm by applying the shear of lower amplitude. This could be ascribed to the aligning effect of the shear, which was perpendicular to the aligning effect along the crystallographic axis of the mica surfaces.
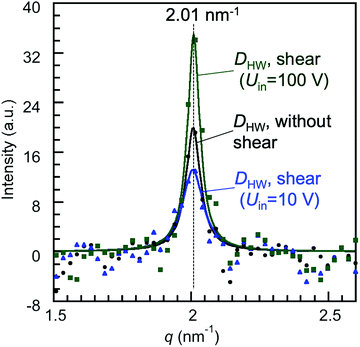 | ||
| Fig. 5 X-Ray diffraction intensity profiles of 8CB confined at DHW (= 1.7 nm) between the mica surfaces, in which the crystallographic axes were aligned parallel to each other, obtained by integrating the scattering intensities in the diffraction images shown in Fig. 4. The filled symbols are the obtained diffraction data, and the solid lines are the fitting curves of the Lorentz function (I(q) = Cw/(4(q − qpeak)2 + w2)). C is the intensity parameter, qpeak is the peak position, and w is the full width at half maximum (FWHM). | ||
| Peak position, qpeak (nm−1) | FWHM, w (nm−1) | Intensity parameter, C | |
|---|---|---|---|
| 8CB between mica without shear | 2.01 | 0.064 | 20 |
| 8CB between mica under shear (Uin = 10 V) | 2.01 | 0.09 | 13.2 |
| 8CB between mica under shear (Uin = 100 V) | 2.01 | 0.054 | 35 |
On the other hand, by applying the shear of higher amplitude (Uin = 100 V), the intensity parameter (C) increased and the FWHM value decreased (Table 2). The domain size estimated using Scherrer's equation increased to ca. 230 nm. These changes indicated that the order of the orientation was enhanced, and thus the domain size was increased by applying the shear of higher amplitude, resulting in the increase in the diffraction intensity. The orientation angle rotated only by three degrees under the shear possibly due to the balance of the two opposing aligning effects of the shear and the crystallographic axis of the mica surfaces. This may increase the mutual orientation of the 8CB molecules and then should have contributed to the increase in the diffraction intensity.
We then further investigated the effect of the surface properties. By applying the shear (Uin = 10 V, f = 96.5 Hz), the diffraction image showed no noticeable change (see ESI†). Fig. S1 (ESI†) shows the X-ray diffraction images of 8CB confined between the silica surfaces at DHW (= ca. 2 nm): (a) the data without shear (same as the inset of Fig. 3(b)), (b) under the shear (Uin = 10 V, f = 96.5 Hz). This indicated that the shear could not induce any noticeable changes on nano-confined 8CB between silica surfaces because of the suppression of molecular movement at the hard wall thickness.
3.3 XRD study of effect of shear on 8CB of micrometer thickness
We then further investigated the effect of the shear on 8CB with micrometer level thickness. Fig. 6 shows the X-ray diffraction images of 8CB confined between the mica surfaces measured at DHW (= 1.7 nm); Fig. 6(a) shows the data without shear, and (b) after applying the shear at a large surface separation distance (D = 3.3 μm, input voltage Uin = 50 V, and frequency f = 90.0 Hz) and returned to DHW (= 1.7 nm). As shown in Fig. 6(b), the two circular arc spots were significantly broadened and rotated ca. 40 degrees after applying the shear at D = 3.3 μm. This indicated that the orientation of 8CB was rotated by applying the shear at large D (= 3.3 μm) where the mobility of the 8CB was not suppressed. This result was consistent with a previously reported XRD study on the 8CB confined between mica surfaces at D = 1 μm.31 The change in the orientation at large D resulted in the broadened distribution of the in-plane orientation angle of nano-confined 8CB in the case of mica surfaces.Fig. 6(c) shows the data for silica surfaces without shear (same data as the inset of Fig. 3(b)), and (d) after applying the shear at a large surface separation distance (D = 3.3 μm, input voltage Uin = 50 V, and frequency f = 90.0 Hz) and returned to DHW (= ca. 2 nm). As shown in Fig. 6(d), the diffraction pattern disappeared after applying the shear at a large D (= 3.3 μm). This indicated that the orientation of the 8CB was significantly disordered, and the lamellar structure almost disappeared by applying the shear at a large D (= 3.3 μm) where the mobility of the 8CB was not suppressed. Possible changes in the ordering of 8CB were the out-of-plane rotation and the decrease in the domain size of 8CB because of the weaker aligning effects of silica surfaces compared with mica surfaces.
4 Conclusion
We employed synchrotron X-ray diffraction measurements to investigate the orientational behavior of a smectic-A liquid crystal (4-cyano-4′-octylbiphenyl, 8CB) of nanometer scale thickness confined between mica surfaces as well as between silica surfaces. The effects of the surface properties as well as the shear on the in-plane orientation of the nano-confined 8CB molecules were investigated.(1) A clear difference in the in-plane orientation of the 8CB confined between mica and silica surfaces was observed. The centrosymmetric two diffraction spots observed for the 8CB confined between the mica surfaces (DHW = 1.7 nm) demonstrated the uniaxial orientation of the lamellar axis of the 8CB most probably due to the preferential alignment of its long axis along the crystallographic axis (a-axis) of the mica. On the other hand, the ring diffraction pattern observed for the 8CB confined between the silica surfaces (DHW = ca. 2 nm) demonstrated the omnidirectional orientation of the lamellar axis of the 8CB in-plane.
(2) The centrosymmetric two diffraction spots for the nano-confined 8CB between the mica surfaces, which reflected the orientation of the lamellar axis of 8CB, were rotated only ca. 3 degrees within the plane parallel to the surface on application of the shear. The ring diffraction pattern, which represented the omnidirectional in-plane orientation of the lamellar axis of the nano-confined 8CB between the silica, showed almost no change on application of the shear. These results demonstrated for the first time that the effect of shear on the orientation of 8CB was significantly suppressed when the surface separation distance (D) was at the nm level regardless of the kind of surface.
(3) On the other hand, when the shear was applied to 8CB at a large D (= 3.3 μm), then returned to the DHW, the orientation of 8CB confined between mica surfaces was rotated and that for 8CB between silica surfaces disappeared. These results indicated that the 8CB was significantly disordered on application of the shear at a large D where the mobility of the 8CB was not suppressed.
The XRD measurement of the nano-confined liquid crystal (8CB) revealed that the in-plane orientations of the 8CB significantly depended on the properties of the confining surfaces (mica or silica). This was a clear demonstration of the significant effects of surface properties on the structure of the nano-confined liquids. These results should be important for the application of liquid crystals such as in optical devices and lubricants in which the effects of the surface properties are becoming more significant for finer and smaller devices.
As a future research, it could be interesting to perform the XRD measurement of nano-confined liquid crystals at various temperatures to investigate in detail the effects of confinement on the phase behavior of liquid crystals. Actually, we have reported that the viscosities of 6CB (4-cyano-4′-hexyl biphenyl) both in nematic and isotropic phases significantly increased and became almost identical under nano-confinement at D < 5 nm,38 indicating that the nematic–isotropic phase transition was suppressed by the confinement effect. The D dependence of XRD could be also interesting to obtain the structural information of the nano-confined liquid crystal which shows a drastic increase in the viscosity at D < ca. 20 nm.11,28
The combination of the X-ray diffraction measurement and surface force measurement (including shear force measurement) can be very useful for obtaining a new molecular level insight into nano-confined liquids. This method has great potential to advance the molecular level of understanding of confined liquids, which exhibit complex behavior, and can also provide useful information for the innovative design of materials such as lubricants, micro/nano-fluids, and nano-molding.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The synchrotron radiation experiments were performed at the BL40B2 in the SPring-8 with the approval of the SPring-8 Proposal Review Committee (proposal numbers 2015A1644, 2016B1056, 2017A1498, 2017A1861, 2017B1521, 2018A2069, 2019B2089). This study was supported by the “Research and Development of Next-Generation Filed” from the Ministry of Education, Culture, Sports, Science and Technology, Japan.References
- J. Gao, W. D. Luedtke and U. Landman, J. Chem. Phys., 1997, 106, 4309–4318 CrossRef CAS.
- H. Matsubara, F. Pichierri and K. Kurihara, Phys. Rev. Lett., 2012, 109, 197801 CrossRef.
- L. Benamsili, J.-P. Korb, G. Hamon, A. Louis-Joseph, B. Bouyssiere, H. Zhou and R. G. Bryant, Energy Fuels, 2014, 28, 1629 CrossRef CAS.
- R. G. Horn and J. N. Israelachvili, J. Chem. Phys., 1981, 75, 1400–1411 CrossRef CAS.
- J. N. Israelachvili, P. M. MacGuiggan and A. H. Homola, Science, 1988, 240, 189–191 CrossRef CAS.
- J. Peachey, J. V. Alsten and S. Granick, Rev. Sci. Instrum., 1991, 62, 463 CrossRef CAS.
- S. Granick, Science, 1991, 253, 1374–1379 CrossRef CAS.
- J. Klein and E. Kumacheva, Physica A, 1998, 249, 206–215 CrossRef CAS.
- C. Dushkin and K. Kurihara, Colloids Surf., A, 1997, 129–130, 131–139 CrossRef.
- C. Dushkin and K. Kurihara, Rev. Sci. Instrum., 1998, 69, 2095–2104 CrossRef CAS.
- M. Mizukami, K. Kusakabe and K. Kurihara, Prog. Colloid Polym. Sci., 2004, 128, 105–108 CAS.
- H. Sakuma, K. Otsuki and K. Kurihara, Phys. Rev. Lett., 2006, 96, 046104 CrossRef.
- F. F. Canova, H. Matsubara, M. Mizukami, K. Kurihara and A. L. Shluger, Phys. Chem. Chem. Phys., 2014, 16, 8247–8256 RSC.
- F. F. Canova, M. Mizukami, T. Imamura, K. Kurihara and A. L. Shluger, Phys. Chem. Chem. Phys., 2015, 17, 17661–17669 RSC.
- K. Tomita, M. Mizukami, S. Nakano, N. Ohta, N. Yagi and K. Kurihara, Phys. Chem. Chem. Phys., 2018, 20, 13714–13721 RSC.
- A. E. Somers, P. C. Howlett, D. R. MacFarlane and M. Forsyth, Lubricants, 2013, 1, 3–21 CrossRef.
- J. Watanabe, M. Mizukami and K. Kurihara, Tribol. Lett., 2014, 56, 501–508 CrossRef CAS.
- T. Kamijo, H. Arafune, T. Morinaga, S. Honnma, T. Sato, M. Hino, M. Mizukami and K. Kurihara, Langmuir, 2015, 31, 13265–13270 CrossRef CAS.
- M. Kasuya, K. Tomita, M. Hino, M. Mizukami, H. Mori, S. Kajita, T. Ohmori, A. Suzuki and K. Kurihara, Langmuir, 2017, 33, 3941–3948 CrossRef CAS.
- G. M. Whitesides, Nature, 2006, 442, 368–373 CrossRef CAS.
- Z. He, F. Gou, R. Chen, K. Yin, T. Zhan and S.-T. Wu, Crystals, 2019, 9, 292 CrossRef CAS.
- K. Nakano, Tribol. Lett., 2003, 14, 17–24 CrossRef CAS.
- R. G. Horn, J. N. Israelachvili and E. Perez, J. Phys., 1981, 42, 39–52 CrossRef CAS.
- J. Janik, R. Tadmor and J. Klein, Langmuir, 1997, 13, 4466–4473 CrossRef CAS.
- M. Ruths, S. Steinberg and J. N. Israelachvili, Langmuir, 1996, 12, 6637–6650 CrossRef CAS.
- A. Artsyukhovich, L. D. Broekman and M. Salmeron, Langmuir, 1999, 15, 2217–2223 CrossRef CAS.
- T. Yanagimachi, X. Li, P. F. Nealy and K. Kurihara, Adv. Colloid Interface Sci., 2019, 272, 101997 CrossRef CAS.
- S. Nakano, M. Mizukami and K. Kurihara, Soft Matter, 2014, 10, 2110–2115 RSC.
- S. Nakano, M. Mizukami, N. Ohta, N. Yagi, I. Hatta and K. Kurihara, Jpn. J. Appl. Phys., 2013, 52, 035002 CrossRef.
- S. H. J. Idziak, C. R. Safinya, R. S. Hill, K. E. Kraiser, M. Ruths, H. E. Warriner, S. Steinberg, K. S. Liang and J. N. Israelachvili, Science, 1994, 267, 1915 CrossRef.
- I. Koltover, S. H. J. Idziak, P. Davidson, Y. Li, C. R. Safinya, M. Ruths, S. Steinberg and J. N. Israelachvili, J. Phys. II, 1996, 6, 893–907 CrossRef CAS.
- S. H. J. Idziak, I. Koltover, J. N. Israelachvili and C. R. Safinya, Phys. Rev. Lett., 1996, 76, 1477–1480 CrossRef CAS.
- Y. Golan, A. Martin-Herranz, Y. Li, C. R. Safinya and J. Israelachvili, Phys. Rev. Lett., 2001, 86, 1263–1266 CrossRef CAS.
- H.-Y. Ren, M. Mizukami and K. Kurihara, Rev. Sci. Instrum., 2017, 88, 095198 Search PubMed.
- T. C. Huang, H. Toraya, T. N. Blanton and Y. Wu, J. Appl. Crystallogr., 1993, 26, 180 CrossRef CAS.
- C. R. Safinya, E. B. Sirota, R. F. Bruinsma, C. Jeppesen, R. J. Piano and L. J. Wenzel, Science, 1993, 261, 588–591 CrossRef CAS.
- B. E. Warren, X-Ray Diffraction, Dover, New York, 1990 Search PubMed.
- K. Mori, K. Kusakabe, H. Tamas and K. Kurihara, Trans. Mater. Res. Soc. Jpn., 2001, 26, 909–912 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp04266h |
| This journal is © the Owner Societies 2021 |