Tuning the transition barrier of H2 dissociation in the hydrogenation of CO2 to formic acid on Ti-doped Sn2O4 clusters†
Plaban J.
Sarma
 a,
Dikshita
Dowerah
a,
Nand K.
Gour
a,
Dikshita
Dowerah
a,
Nand K.
Gour
 a,
Andrew J.
Logsdail
a,
Andrew J.
Logsdail
 b,
C. Richard A.
Catlow
b,
C. Richard A.
Catlow
 bcd and
Ramesh Ch.
Deka
bcd and
Ramesh Ch.
Deka
 *a
*a
aDepartment of Chemical Sciences, Tezpur University, Tezpur, Assam, India. E-mail: ramesh@tezu.ernet.in
bCardiff Catalysis Institute, School of Chemistry, Cardiff University, Cardiff CF10 3AT, UK
cDepartment of Chemistry, University College London, 20 Gordon St., London WC1HOAJ, UK
dUK Catalysis Hub, Research Complex at Harwell, RAL, Oxford, OX11 0FA, UK
First published on 27th November 2020
Abstract
A density functional theory study has been performed to investigate cation-doped Sn2O4 clusters for selective catalytic reduction of CO2. We study the influence of Si and Ti dopants on the height of the H2 dissociation barrier for the doped systems, and then the subsequent mechanism for the conversion of CO2 into formic acid (FA) via a hydride pinning pathway. The lowest barrier height for H2 dissociation is observed across the ‘Ti–O’ bond of the Ti-doped Sn2O4 cluster, with a negatively charged hydride (Ti–H) formed during the heterolytic H2 dissociation, bringing selectivity towards the desired FA product. The formation of a formate intermediate is identified as the rate-determining step (RDS) for the whole pathway, but the barrier height is substantially reduced for the Ti-doped system when compared to the same steps on the undoped Sn2O4 cluster. The free energy of formate formation in the RDS is calculated to be negative, which reveals that the hydride transfer would occur spontaneously. Overall, our results show that the small-sized Ti-doped Sn2O4 clusters exhibit better catalytic activity than undoped clusters in the important process of reducing CO2 to FA when proceeding via the hydride pinning pathway.
Introduction
Combustion of fossil fuels is a major contributing factor to the increasing atmospheric concentration of CO2, which is regarded as one of the major anthropogenic contributors to global warming.1,2 To address the current “Climate Emergency”, mitigation of CO2 either by conversion or trapping is now essential. For this purpose, reduction of CO2 into commercially valuable chemicals such as formic acid (FA), methanol and longer-chained alcohols is highly advantageous.3–5 Furthermore, hydrogenation of CO2 to liquid phase HCOOH and CH3OH also addresses challenges associated with storage and transport of H2, with the low volumetric density of H2 in the gas phase considered prohibitive for its potential use as an energy vector; HCOOH is a non-toxic liquid at room temperature, making it easy to transport and allowing direct implementation in fuel cells.6 Currently, however, chemical reduction of CO2 to formic acid is limited by the availability of suitable catalysts to activate the thermodynamically stable C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, which has a bond energy of 5.52 eV (533 kJ mol−1).7 There are several reported methods of CO2 reduction, including catalytic hydrogenation, electrochemical reduction, photocatalysis and biological reduction; among these, electrochemical and photochemical reductions are promising for facilitating product selectivity, lower production costs and high catalytic efficiency.8–10
O bond, which has a bond energy of 5.52 eV (533 kJ mol−1).7 There are several reported methods of CO2 reduction, including catalytic hydrogenation, electrochemical reduction, photocatalysis and biological reduction; among these, electrochemical and photochemical reductions are promising for facilitating product selectivity, lower production costs and high catalytic efficiency.8–10
During the last decade, the study of Sn-based electrodes for electrochemical CO2 reduction has grown rapidly due to the higher overpotentials necessary for competing H2 evolution reactions, thus bringing selectivity to the reduction of CO2 to HCOOH.11–13 Like other non-noble metals, tin undergoes corrosion and degradation, but the oxide layer formed has been identified as highly catalytic towards the electrochemical reduction of CO2. The importance of the oxide layer was highlighted by Chen and Kanan, who reported that the catalytic activity of SnO2 depends on the oxide layer percentage, showing that the depth of the oxide layer was proportional to the reduction efficiency.14 Particle size also has an important effect on catalyst efficacy, with Xu et al. describing the significance of quantum confinement for SnO2 quantum dots (QDs) within the range of 0.5–2.5 nm, as illustrated for gas sensing properties towards ethanol; QDs show higher sensitivity than larger SnO2 nanowires.15 Liu et al. compared the electrocatalytic properties of SnO2 quantum wires (1.7 nm) with SnO2 nanoparticles (5.5 nm) for HCOOH formation and concluded that the quantum wires have exposed grain boundaries that enhance the current density, as well as faradaic efficiency, by over 80% for HCOOH formation.16 This also reveals the importance of small-sized clusters in the catalytic reduction of CO2 to HCOOH and it influences the overpotential of formic acid production.
In contrast to the catalytic application of pure SnO2 clusters, there is limited literature for the application of doped SnO2 clusters towards the hydrogenation of CO2 to HCOOH. H2 dissociation on doped metal oxide clusters and surfaces such as Al-doped ZnO, CeO2 and MgO has been reported, as well as on Ni clusters doped with Rh, Pt, Pd and Au metals.17,18 However, the mechanism of CO2 reduction using doped-SnO2 nanoparticles remains relatively unexplored. Saravanan et al. performed theoretical calculations of SnO2 surfaces to try and understand the consequences of transition metal doping,19 considering two types of dopants: Ti, V, Nb, Ta and Zr replacing the six coordinated Sn(IV) in a pristine crystal; and Cd, Co, Pb, Sb and Zn accompanied by a neighbouring O vacancy, i.e. at an Sn(II) site. The extrinsic dopants at the Sn(IV) site resulted in a material showing potential to reduce CO2 to HCOOH at lower overpotentials than pure SnO2, with Ti-doped SnO2 identified as the best catalyst. Such Ti-doped SnO2 nanoparticles are used currently as sensing materials for ethanol, and both Ti- and Si-doped SnO2 nanoparticles have been studied to understand the influence of the doping metal on the electrical conductivity.20–23
Previously, CO2 activation on the catalyst surface has been reported as occurring by the formation of a carbonate-like structure, followed by the transfer of a hydrogen atom to the carbon atom, producing formate and subsequently formic acid.14,23,24 Earlier studies show that H2 can dissociate heterolytically on ZnO clusters, which leads to the formation of a metal-hydride bond.17,25 Similarly, another study on SnO2 reported a hydride pinning pathway whereby heterolytic H2 dissociation leads to the formation of an Sn-hydride bond, and CO2 activation occurs during the (rate-determining) hydride transfer step; the observed outcome was total selectivity of HCOOH formation at an overpotential of 0.25 eV.26 In the present work, we consider whether dopants in a model dimeric Sn2O4 cluster modify the key steps in this favourable hydrogenation pathway of CO2 to HCOOH. Structures for the Sn2O4 clusters have been taken from previous studies26 and, for the newly considered doped system, we chose two dopants: Si, which is isovalent with Sn, with a stable +4 oxidation state as well as vacant 3d orbitals; and Ti, which has an atomic radius similar to Sn, vacant 3d electrons, and stability in the +4 oxidation state (though somewhat reducible). As both dopants are considered formally in +4 oxidation states, their introduction to the cluster does not require compensating oxygen vacancies.
Results and discussion
Structures of Si- and Ti-doped Sn2O4 clusters
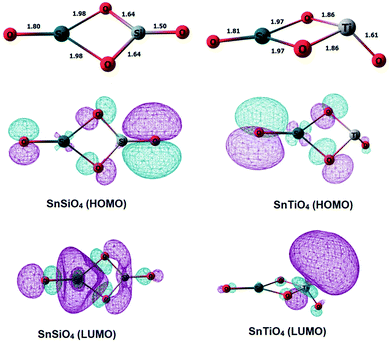
Si and Ti dopants replace a Sn atom in the small dimeric Sn2O4 cluster, and the structures were geometry-optimized using density functional theory (DFT) (Fig. 1). The structure of the SnSiO4 cluster is similar to that of the pure Sn2O4 cluster, maintaining a planar 2-dimensional configuration; in contrast, the SnTiO4 cluster is 3-dimensional, with the Ti-center taking a distorted Td shape surrounded by two bridging and one terminal oxygens. The shape of the TiO3 unit in the SnTiO4 cluster resembles the Ti-center of a pure Ti2O4 cluster.27The formation energy (Ef) of the doped clusters upon replacement of one Sn by the Si or Ti atom is calculated via the equation as follows:
| Ef = (ESnMO4 + ESnO2) − (ESn2O4 + EMO2), |
Natural bond orbital (NBO) calculations have been performed to interpret the bonding interactions of the metal dopants with the oxygen atoms in the clusters, and diagrams of the highest occupied molecular orbitals (HOMOs) and the lowest unoccupied molecular orbitals (LUMOs) are included accordingly in Fig. 1. The HOMOs of both of the doped clusters are concentrated on the lone pairs of oxygen, i.e. the non-bonding electrons. The LUMO of SnSiO4 has the π* character of an O–Si bond, and some character of the Sn-center, which provides us the evidence of having an O–Si π interaction resulting from the back donation of electron density from the oxygen lone pairs to the empty 3d orbitals of silicon. To verify the involvement of Si d orbitals in the bonding interactions, we have analyzed the percentage of individual atomic contributions towards the participating bonds in the SnSiO4 and SnTiO4 clusters (Table 1, column 4), along with the orbital contributions of the s, p and d orbitals (Table 1, column 5). Some occupancy of the Si d orbitals is observed in both the terminal and bridging Si–O bonds, along with the s and p orbitals, which reveals that the O–Si π bonding interaction includes the contributions from the Si d orbitals; however, for the SnTiO4 cluster, the percentage contribution of the d orbitals is much more than those of the s and p orbitals. These observations lead us to conclude that the more covalent-like Si interactions in the SnSiO4 cluster favourably stabilise the system when compared to those of the Ti-dopant in SnTiO4. The individual atomic contributions (column 4) of the participating bonds show that O contributes significantly to bonding compared to the Sn, Si and Ti atoms.
| Cluster | Bond type | Atom | Elemental contribution (%) | Angular contribution (%) |
|---|---|---|---|---|
| SnSiO4 | Bridging Si–O | Si | 12.65 | s (27.98) p (48.21) d (23.78) |
| O | 87.35 | s (33.69) p (65.90) | ||
| Terminal Si–O | Si | 19.53 | s (43.39) p (55.60) d (0.99) | |
| O | 80.47 | s (34.36) p (65.0%) | ||
| Bridging Sn–O | Sn | 12.82 | s (26.54) p (72.66) d (0.45) | |
| O | 87.18 | s (12.24) p (87.36) | ||
| Terminal Sn–O | Sn | 29.85 | s (46.92) p (52.58) d (0.33) | |
| O | 70.15 | s (6.94) p (92.93) | ||
| SnTiO4 | Bridging Ti–O | Ti | 12.86 | s (23.60) p (23.94) d (51.79) |
| O | 87.14 | s (29.51) p (70.39) | ||
| Terminal Ti–O | Ti | 20.57 | s (10.69) p (7.40) d (81.33) | |
| O | 79.43 | s (19.70) p (80.22) | ||
| Bridging Sn–O | Sn | 13.65 | s (27.35) p (71.28) d (0.89) | |
| O | 86.35 | s (9.23) p (90.65) | ||
| Terminal Sn–O | Sn | 28.95 | s (45.08) p (54.31) d (0.43) | |
| O | 71.05 | s (7.29) p (92.58) | ||
H2 dissociation on the SnMO4 clusters
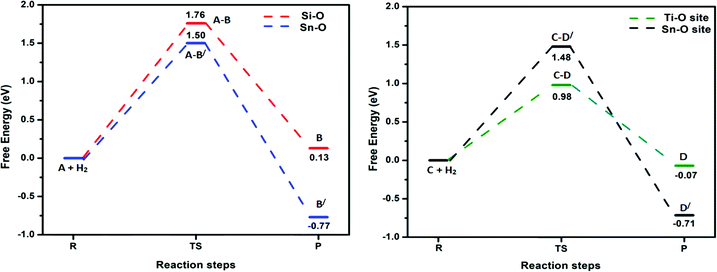
Previously, an undoped Sn2O4 cluster has been observed to dissociate H2 at Sn–O bridging sites, with the hydride pinning pathway leading to selective reduction of CO2 to HCOOH via a formate intermediate.26 Considering this observation, we calculated the transition states and barrier heights of H2 dissociation on all possible bridging sites in the doped cluster; the subsequent optimized minima and transition state geometries are shown in Fig. 2, and the reaction energy profiles in Fig. 3.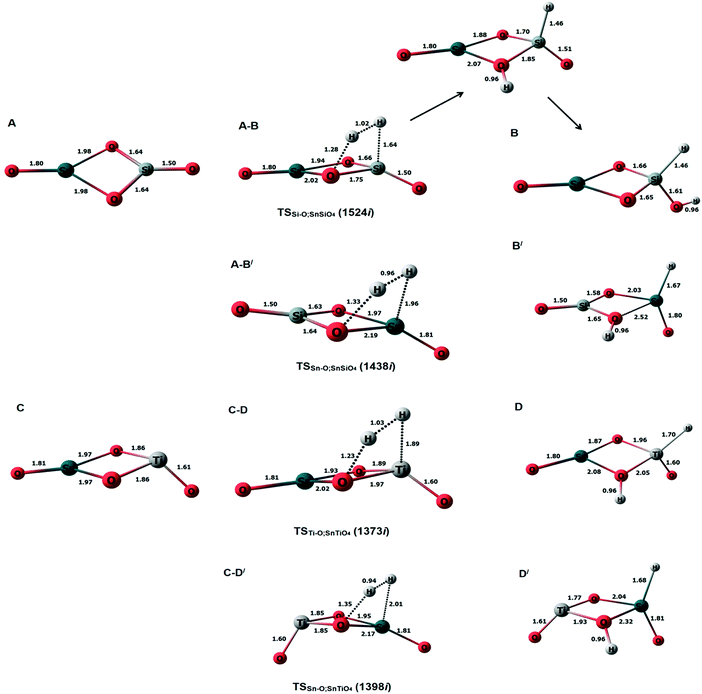 | ||
| Fig. 2 The optimized structures of doped clusters along with the transition states and H2 dissociated products. Top: SnSiO4; bottom: SnTiO4. | ||
For the SnSiO4 cluster, the activation energy for H2 dissociation is 1.76 eV (40.61 kcal mol−1) on a Si–O bond, which is 0.26 eV (5.99 kcal mol−1) higher than at the Sn–O bond [1.50 eV, 34.73 kcal mol−1]. The transition states corresponding to H2 dissociation on Si–O (A–B) and Sn–O (A–B′) sites (Fig. 2) are characterized by the presence of imaginary frequencies of 1524i cm−1 and 1438i cm−1, respectively. The dissociated products ‘B’ and ‘B′’, formed on the Si–O and Sn–O sites, respectively, are also shown in Fig. 2. Interestingly, despite dissociation occurring at the bridging position of the Si–O site for product B, as confirmed via the transition state (A–B) and IRC calculation (Fig. S1, ESI†), the product has a geometry based on the terminal Si–O bond. The convergence graph is shown in Fig. 4 for the reaction A → A–B → B. Fig. 4 indicates that, whilst the H2 dissociation transition state is at the bridging site, the product H is unstable at this bridging location and converts to a more stable terminal-positioned structure (Fig. 2, structure B). We attribute the formation of the terminal H to the Si–O dπ–pπ interaction observed for the bridging Si–O bond in the SnSiO4 cluster, which provides extra stability to the bridging Si–O bonds; the dπ–pπ interaction is less pronounced in the terminal Si–O bond, with the contribution of the Si d orbital reduced (0.99%, compared to 23.78% for the bridging bond). The H2 dissociation on the Sn–O site results in similar structural arrangement to H2 dissociation on the undoped Sn2O4 cluster investigated previously.26
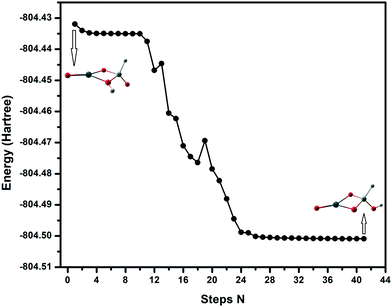 | ||
| Fig. 4 Structural convergence from H2 dissociation at the bridging ‘Si–O’ site to terminal ‘Si–O’ site. | ||
In contrast, the SnTiO4 cluster shows a smaller barrier on the Ti–O bridge (C–D) of 0.98 eV (22.62 kcal mol−1), with an imaginary frequency of 1373i cm−1. The barrier height is 0.50 eV (11.68 kcal mol−1) lower than that of the Sn–O bridge (C–D′), as shown in Fig. 3. The lower barrier over the Ti–O bridge can be explained via the orbital structures: The LUMO of the SnTiO4 cluster is located on the Ti-center and thus, when H2 dissociation takes place over the Ti–O bridge, it occurs via interaction with the LUMO; however, on the Sn–O bridge, H2 dissociation cannot take place through the Ti-centered LUMO, interacting instead with the LUMO+1 (Fig. S2, ESI†). Therefore, a higher orbital reorganization energy is required for H2 dissociation over the Sn–O bridge, which leads to a larger activation energy for the process. Notably, H2 dissociation on the Ti–O site has a lower activation energy than on the Sn–O site in doped and undoped Sn2O4 clusters (barrier height = 1.25 eV).26
To understand the strength of the M–H bond, and confirm whether the hydride ion has formed, we analyzed the Bader charge of the H2 dissociated products (B, B′, D and D′) in Table 2. A hydride is observed in all the models, as the hydrogen of newly formed M–H possesses a negative formal charge. The calculated percentages of orbital contributions of H and M in the M–H bond are shown in Table 3; in the bonding of Si–H, the contribution of the Si 3p orbital is the greatest (46.86%), whereas the Ti–H bond is formed most prominently of 3d orbitals (44.90%). In the latter case, the contribution of d is more than those of valence 4s and 4p orbitals, which contribute 25.81% and 29.12%, respectively, and as a consequence the Ti–H bond is weaker than the Si–H bond.
| Structure | Bond | Bond distances, Å | Bader charges, e |
|---|---|---|---|
| B | Si–H | 1.46 | Si = +3.15, H = −0.71 |
| O–H | 0.96 | O = −1.45, H = +0.70 | |
| B′ | Sn–H | 1.67 | Sn = +1.98, H = −0.25 |
| O–H | 0.96 | O = −1.53, H = +0.70 | |
| D | Ti–H | 1.60 | Ti = +2.17, H = −0.55 |
| O–H | 0.96 | O = −1.37, H = +0.68 | |
| D′ | Sn–H | 1.67 | Sn = +1.99, H = −0.27 |
| O–H | 0.96 | O = −1.36, H = +0.67 | |
| Cluster | Atom | Elemental contribution (%) | Angular contribution (%) |
|---|---|---|---|
| SnSiO4 | Si | 31.60 | s (30.85) p (46.86) d (22.21) |
| H | 68.40 | s (99.93) p (0.07) | |
| Sn | 37.57 | s (31.12) p (68.44) d (0.33) | |
| H | 62.43 | s (99.85) p (0.14) | |
| SnTiO4 | Ti | 36.88 | s (25.81) p (29.12) d (44.90) |
| H | 63.12 | s (99.85) p (0.14) | |
| Sn | 38.10 | s (42.59) p (56.78) d (0.56) | |
| H | 61.90 | s (99.86) p (0.14) | |
Mechanistic study via hydride pinning pathway
After dissociation of H2 on the doped Sn2O4 cluster, we extended our study to the hydrogenation of CO2via the hydride pinning pathway. As already discussed, the H2 dissociation barrier height is lower on SnTiO4 than that on SnSiO4, and hence CO2 reduction is considered only on the SnTiO4 cluster. The overall pathway follows a two-step catalytic mechanism:26(a) First, gas phase CO2 takes up the hydride from the catalytic site following the ‘Eley Rideal’ (ER) mechanism and binds with the Sn-center in the cluster.
(b) Second, the remaining hydrogen transfers to the co-adsorbed oxygen of HCOO by following the ‘Langmuir Hinshelwood’ (LH) mechanism, to form the product HCOOH.
The potential energy pathway for hydrogenation of CO2 on the SnTiO4 cluster is presented in Fig. 5. In the mechanism studied, the hydride pinning step is initiated by the product ‘D’ (Fig. 2) where the hydride is transferred from the Ti-site to the carbon of CO2 to form the formate (HCOO*) intermediate that further binds with the catalyst by one of the intermediate's oxygens. This hydride transfer step proceeds via the transition state TS1 (607i cm−1) to form the intermediate IM2 with an activation energy of 0.49 eV (11.49 kcal mol−1). The transition barrier of the hydride transfer step for the doped system is lower than for the undoped cluster [1.15 eV (26.51 kcal mol−1)],26 which is attributed to two factors: first, the weakness of the Ti–H bond relative to the Sn-H bond, which results in hydride transfer to the carbon being less energetically demanding; second, the Ti-centre in the doped SnTiO4 cluster retains its tetrahedral shape throughout i.e energy is not required for structure changes of SnTiO4, unlike for bare Sn2O4 where the Sn-centre changes its shape from tetrahedral to planar.26 In the transition state TS1, the Ti–H bond elongates from 1.60 Å to 1.78 Å, while the bond distances of the newly formed C–H and Sn–O bonds are 1.73 Å and 2.33 Å, respectively. After the formation of the HCOO* intermediate, the orientation spontaneously changes to IM2′ by flipping the –CHO group of HCOO* around the C–O(–Sn) bond, with a ΔG of −0.30 eV (−6.91 kcal mol−1), which then allows uptake of the second hydrogen from the cluster. In the optimized IM2′, we observe a new Sn⋯O interaction of 2.36 Å (along with the remaining Sn–O bond); the O is now nearer to the remaining H on the cluster, and this hydrogen then transfers from the cluster to form HCOOH. During the formation of HCOOH, IM2′ overcomes an activation barrier of 0.35 eV (8.17 kcal mol−1) via the transition state TS2 (920i cm−1), which is smaller than that of the pinning step (TS1) and so indicating that the reaction will proceed rapidly to the equilibrium once the HCOO* intermediate is formed. The HCOOH product leaves the catalytic cycle in the same step and hence the catalyst is recycled for the next H2 dissociation step.
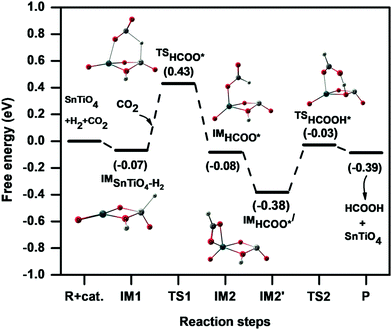 | ||
| Fig. 5 Potential energy diagram representing the hydrogenation of CO2 to HCOOH on the SnTiO4 cluster via the hydride pinning pathway. | ||
For the overall reaction, the hydride pinning step (TS1) is the rate-determining step (RDS) and hence the free energy difference between IM2′ and IM1 equates to the necessary overpotential for realising the hydrogenation process. This overpotential factor can be calculated from the computational hydrogen electrode (CHE) model given by Nørskov et al.,37 which is discussed in the computational methodology. In the outlined reaction mechanism, the difference in free energies is −0.31 eV, which reveals that the formation of HCOO* intermediate is calculated to be thermodynamically spontaneous. This spontaneity was not observed in the case of undoped Sn2O4, where the required overpotential of HCOO* formation is 0.25 eV.26
Comparing the present results with previous studies on the hydrogenation of CO2 to HCOOH on dimeric SnO2,26 we can propose the following:
(a) The H2 dissociation barrier height on the Ti-doped Sn2O4 is 0.98 eV, which is 0.54 eV lower than that on the undoped Sn2O4 (1.52 eV). The doped cluster is therefore a potentially more active catalyst due to the reduced kinetic H2 dissociation barrier.
(b) In the hydride transfer step, the barrier height for formate formation is 0.49 eV on the Ti-doped cluster, which is 0.66 eV greater than that on the undoped Sn2O4 (1.15 eV). The doped cluster therefore has potentially improved catalytic selectivity towards reduction of CO2 to HCOOH via the hydride pinning pathway.
(c) Lastly, the overpotential factor drops from 0.25 eV when considering the undoped Sn2O4 cluster to −0.31 eV for SnTiO4, correlating with the previous work reported by Saravanan et al.19 and illustrating that the reaction would proceed favourably.
Summary and conclusions
Titanium and silicon dopants have been considered on the Sn4+ centers of a pure Sn2O4 cluster, and subsequently tested in the context of CO2 hydrogenation. Negative formation energies for SnSiO4 and SnTiO4 reveal the replacement of Sn by Si or Ti to be energetically favourable. H2 dissociation barrier heights are calculated as favourable on all the bridging sites available on the clusters, with the lowest activation energy on the bridging Ti–O site of the SnTiO4 cluster. Our observations of the potential role for Si and Ti dopants indicates that metals providing π character in the M–O bond will be less suitable catalysts for CO2 reduction, while first and second row early transition metals (e.g. Ti, V, Nb and Zr), are good candidates as dopants in SnO2 clusters because π bonding is less common. Bader charge analysis of the metal–hydride (Ti–H) shows that one H on each cluster possesses a formal negative charge. The hydride is the key in the hydride-assisted pathways for CO2 reduction, triggering the total selectivity for the formation of HCOOH over CO at a lower overpotential. The SnTiO4 cluster has a reduced barrier relative to the pure Sn2O4 cluster in the rate-determining step (HCOO* formation), and also requires a lower overpotential for the formation of HCOOH, delivering product selectivity. Experimentally, small-sized bare SnO2 quantum dots are used for the conversion of CO2 to HCOOH at low overpotentials but the use of Ti-doped SnO2 particles is not yet reported; therefore, our results should be considered as a stimulus for further experimental investigation of HCOOH formation via the hydride pinning pathway.Methodology
Kohn–Sham density functional theory (DFT), as implemented in the Gaussian 09 software package,29 has been used to obtain the lowest energy structures and thermochemical properties involved in the mechanism of CO2 reduction. For geometry relaxation and frequency calculations, a range-separated hybrid non-separable meta-NGA, MN12-SX,30 is used; the accuracy of the MN12-SX density functional when predicting structures and energies has been extensively studied previously.26,31,32 A combination of density fitting triple-ξ def2TZVPP basis sets is used,33 as these minimise the basis set superposition error (BSSE) and give results close to the DFT basis set limit;34 the BSSE is <0.04 eV with the triple-ξ basis set, and energies reported in the manuscript include this correction.Frequency calculations are used to confirm the stability of the reactants (Rs), intermediates (IMs) and products (Ps) along the reaction pathway, and to verify the transition states (TSs) identified. The presence of one imaginary frequency, consistent with the eigenvector along with the reaction coordinate, confirms that the TS structure is a first-order saddle point, whereas only real vibrational frequencies are observed for the R, IM and P minima. Changes in the free energy of each reaction step (ΔG) and free energy of activation (ΔG‡) are calculated from the free energy differences between the final and initial states, assuming room temperature and atmospheric pressure (298 K, 1 atm). Formic acid is formed in the liquid phase at room temperature and therefore, as discussed elsewhere previously, a correction of −0.12 eV (taken from the NIST database) is included in our calculated energy of the FA product to account for the free energy difference between its liquid- and gas-phase forms.26,35 Bader charge analysis is performed on charge density distribution using the AIMALL software package.36
To interpret the overpotential factor associated with the formic acid formation, we have used the computational hydrogen electrode (CHE) model, which correlates the reaction free energy change with the electrochemical potential. We calculate the free energy change at the rate-determining step (RDS), determined as the hydride transfer step to form the HCOO* intermediate, where the CHE gas-phase hydrogen is at equilibrium with a proton and electron pair (H+ + e− → 1/2H2) at a potential of 0 V against the reversible hydrogen electrode (RHE) for all pH values, all temperatures and 1 atm of pressure.37
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are thankful to the Science & Engineering Research Board (SERB) (EMR/2016/003195), the Department of Science and Technology (DST) nanomission ([SR/NM/NS-1147/2016(G)]) and the Department of Biotechnology (DBT) project (BT/PR16182/NER/95/92/2015) New Delhi, India, and Tezpur University for the financial support. AJL acknowledges funding by the UKRI Future Leaders Fellowship program (MR/T018372/1). The authors gratefully acknowledge Dr Sanjeev P. Mahanta and Dr Dharitri Das of Tezpur University for their valuable suggestions while carrying out the work.References
- J. C. Fyfe, N. P. Gillet and F. W. Zwiers, Nat. Clim. Change, 2013, 3, 767–769 CrossRef.
- A. Stips, D. Macias, C. Coughlan, E. Garcia-Gorriz and X. S. Liang, Sci. Rep., 2016, 6, 21691–21699 CrossRef CAS PubMed.
- W. Li, H. Wang, X. Jiang, J. Zhu, Z. Liu, X. Guo and C. Song, RSC Adv., 2018, 8, 7651–7669 RSC.
- Q. Li, J. Fu, W. Zhu, Z. Chen, B. Shen, L. Wu, Z. Xi, T. Wang, G. Lu, J. Zhu and S. Sun, J. Am. Chem. Soc., 2017, 139, 4290–4293 CrossRef CAS PubMed.
- A. Álvarez, A. Bansode, A. Urakawa, A. V. Bavykina, T. A. Wezendonk, M. Makkee, J. Gascon and F. Kapteijn, Chem. Rev., 2017, 117, 9804–9838 CrossRef PubMed.
- A. K. Singh, S. Singh and A. Kumar, Catal. Sci., 2016, 6, 12–40 RSC.
- K. Ahmad and S. Upadhyayula, Environ. Prog. Sustainable Energy, 2019, 38, 98–111 CrossRef CAS.
- Z. Sun, T. Ma, H. Tao, Q. Fan and B. Han, Chem, 2017, 3, 560–587 CAS.
- F. Li, L. Chen, G. P. Knowles, D. R. MacFarlane and J. Zhang, Angew. Chem., Int. Ed., 2017, 56, 505–509 CrossRef CAS PubMed.
- J. Wu, Y. Huang, W. Ye and Y. Li, Adv. Sci., 2017, 4, 1–29 Search PubMed.
- J. Wu, F. G. Risalvato, S. Ma and X. D. Zhou, J. Mater. Chem. A, 2014, 2, 1647–1651 RSC.
- W. Deng, L. Zhang, L. Li, S. Chen, C. Hu, Z. J. Zhao, T. Wang and J. Gong, J. Am. Chem. Soc., 2019, 141, 2911–2915 CrossRef CAS PubMed.
- S. Zhang, P. Kang and T. J. Meyer, J. Am. Chem. Soc., 2014, 136, 1734–1737 CrossRef CAS PubMed.
- Y. Chen and M. W. Kanan, J. Am. Chem. Soc., 2012, 134, 1986–1989 CrossRef CAS PubMed.
- X. Xu, J. Zhuang and X. Wang, J. Am. Chem. Soc., 2008, 130, 12527–12535 CrossRef CAS PubMed.
- S. Liu, J. Xiao, X. F. Lu, J. Wang, X. Wang and X. W. Lou, Angew. Chem., Int. Ed., 2019, 58, 8499–8503 CrossRef CAS PubMed.
- T. W. Keal, P. Sherwood, G. Dutta, A. A. Sokol and C. R. A. Catlow, Proc. R. Soc. London, Ser. A, 2011, 467, 1900–1924 CAS.
- N. S. Venkataramanan, A. Suvitha, H. Mizuseki and Y. Kawazoe, Int. J. Quantum Chem., 2013, 113, 1940–1948 CrossRef CAS.
- K. Saravanan, Y. Basdogan, J. Dean and J. A. Keith, J. Mater. Chem. A, 2017, 5, 11756–11763 RSC.
- A. P. S. Isabel, C. H. Kao, R. K. Mahanty, Y. C. S. Wu, C. Y. Li, C. Y. Lin and C. F. Lin, Ceram. Int., 2017, 43, 10386–10391 CrossRef.
- J. Q. Wang, H. L. Kang and Y. Zhang, Mater. Res. Express, 2018, 5, 075902–075913 CrossRef.
- J. Jang, H. Yim and J. W. Choi, Thin Solid Films, 2018, 660, 606–612 CrossRef CAS.
- Q. Tang, Y. Lee, D. Y. Li, W. Choi, C. W. Liu, D. Lee and D. E. Jiang, J. Am. Chem. Soc., 2017, 139, 9728–9736 CrossRef CAS PubMed.
- C. W. Lee, N. H. Cho, K. D. Yang and K. T. Nam, ChemElectroChem, 2017, 4, 2130–2136 CrossRef CAS.
- S. A. French, A. A. Sokol, S. T. Bromley, C. R. A. Catlow, S. C. Rogers, F. King and P. Sherwood, Angew. Chem., Int. Ed., 2001, 40, 4437–4440 CrossRef CAS PubMed.
- P. J. Sarma, S. D. Baruah, A. J. Logsdail and R. C. Deka, ChemPhysChem, 2019, 20, 680–686 CrossRef CAS PubMed.
- O. Lamiel-Garcia, A. Cuko, M. Calatayud, F. Illas and S. T. Bromley, Nanoscale, 2017, 9, 1049–1058 RSC.
- F. Weinhold and R. West, Organometallics, 2011, 30, 5815–5824 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al., Gaussian09 Revision D.01, Gaussian Inc., Wallingford CT. 2010 Search PubMed.
- R. Peverati and D. G. Truhlar, Phys. Chem. Chem. Phys., 2012, 14, 16187–16191 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- J. Frau and D. Glossman-Mitnik, Theor. Chem. Acc., 2018, 137, 1–10 Search PubMed.
- S. Paranthaman, J. Moon, J. Kim, D. E. Kim and T. K. Kim, J. Phys. Chem. A, 2016, 120, 2128–2134 CrossRef CAS PubMed.
- H. Afeefy, J. Liebman and S. Stein, Neutral thermochemical data. in ed. P. Linstrom and W. Mallard, NIST Chemistry WebBook, NIST Standard Reference Database Number. 69 (National Institute of Standards and Technology), Gaithersburg MD, USA, 2010 Search PubMed.
- AIMAll (Version 17.11.14), Todd A. Keith, TK Gristmill Software, Overland Park KS, USA, 2017 (aim.tk gristmill.com) Search PubMed.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp04472e |
| This journal is © the Owner Societies 2021 |