Atomistic description of plasmonic generation in alloys and core shell nanoparticles
Lasse K.
Sørensen
 *a,
Anton D.
Utyushev
*a,
Anton D.
Utyushev
 bc,
Vadim I.
Zakomirnyi
bd and
Hans
Ågren
bc,
Vadim I.
Zakomirnyi
bd and
Hans
Ågren
 ab
ab
aDepartment of Physics and Astronomy, Uppsala University, Box 516, SE-751 20 Uppsala, Sweden. E-mail: lasse.kragh.soerensen@gmail.com
bSiberian Federal University, Krasnoyarsk, 660041, Russia
cSiberian State University of Science and Technology, 660014, Krasnoyarsk, Russia
dInstitute of Computational Modeling, Federal Research Center KSC SB RAS, Krasnoyarsk, 660036, Russia
First published on 26th November 2020
Abstract
Using the extended discrete interaction model we investigate the tunabilty of surface plasmon resonances in alloys and core–shell nanoparticles made from silver and gold in the small (1–15 nm) nanoscale regime where classical models based on the bulk dielectric constant may not apply. We show that the surface plasmon resonance of these alloys and core–shell particles to a large extent follow Vegard's law irrespective of the geometry of the nanoparticle. The evolution of the polarizability with size demonstrates a highly non-linear behaviour of the polarizability with the ratio of the constituents and geometry in alloys and core–shell nanoparticles, with the exception of the longitudinal surface plasmon resonance in nanorods and, partly, nanodisc alloys. We here show that the non-linear behaviour can be explained in terms of the difference in polarizability of the mixing constituents and local effects causing a quenching of the dipoles for geometries with a low aspect ratio. A thorough statistical investigation reveals that there is only a small dependence of the surface plasmon resonance on atomic arrangement and exact distribution in a nanoparticle and that the standard deviation decreases rapidly with the size of the nanoparticles. The physical ground for the random distribution algorithm for alloys in discrete interaction models is explained in detail and verified by a statistical analysis. For nanoparticles below 4 nm a sampling strategy is recommended.
1 Introduction
Like for plasmonic nanoparticles in general, there is a great deal of interest in bimetallic, or alloyed, small nanoparticles1,2 due to their potential applications in a number of technological areas, like bioimaging,3 biomedical plasmonic based sensors and devices,4 and in heterogeneous catalysis. For instance, the position of plasmon resonances can be adjusted over a wide range of wavelengths by varying the composition of the constituent metals, making bimetallic particles an interesting proposition for use in surface plasmon enhanced imaging. The recent advancement in their synthesis and characterization5,6 have thus opened up possibilities to produce such alloyed or bimetallic nanoparticles for particular purposes and applications. This goes especially for bimetallic particles formed by noble metal elements like platinum, gold, silver and copper. Like for the corresponding monometallic plasmonic particles there are requirements on their design with respect to crystallographic structure, shape and size and, for certain applications, surface functionalization. In addition to what is required for monometallic particles, there is also need to characterize the element composition and the internal elementary distribution of the particles and the homogeneity of the particle population. Furthermore, creating alloys or core–shell structures is really the only way to get a significant blue-shift in the surface plasmon resonance frequency since geometry alterations away from spherical always gives significant red-shift.As in other areas of nanothechnology the synthesis and characterization procedures can be greatly boosted by design strategies based on theoretical modelling.7,8 The bimetallic nature and the new parametric dimensions that appear for such particles with respect to the monometallic ones, pose special requests not easily met by traditional classical plasmonic models. This goes especially for “small” bimetallic nanoparticles for which the use of dielectric constants of bulk materials makes it impossible to take into account structural differentiation for the dielectric response, and, in particular, when the small particles are mixed with different elements and with large surface to volume ratios and thus when the mean free path of the conduction electrons need to be considered. Here approaches are called for that are more precisely can relate to the discrete atomic structure of the nanoparticles to the dielectric and plasmonic properties. Unfortunately pure quantum approaches are still only applicable for the very small particles, leaving a size region 1–15 nm unattainable by either classical and quantum theory. Discrete interaction models have the inherent capacity to deal with size effects down to the atomic level.
In a recent work we presented an extended discrete interaction model (ex-DIM) to simulate the geometric dependence of plasmons in the size range of 1–15 nm where the Clausius–Mossotti relation is replaced by a static atomic polarizability to obtain the frequency-dependent dielectric function.9 The static atomic polarizability was modeled as the sum of three size-dependent Lorentzian oscillators and, with Gaussian charge distributions and atomic radii that vary with the coordination number. The frequency-dependent Lorentzian oscillators depend on the plasmon length along the three Cartesian directions using the geometric concept of the plasmon length as defined in the work of Ringe et al.10 In this way we extended previous discrete interaction models to make possible description of the polarizability of nanoparticles with different size, shape and composition, and take account of the dependence of the polarizability of the surface topology or structure of the metallic nanoparticles. This extension of the DIM models serves as a necessary step in order to model bimetallic particles.
The purpose of the present work is to use the extended DIM model to explore the appearance of plasmonic excitation in small alloyed nanoparticles, taking alloys between gold and silver as example, and explore how their plasmonic and response properties evolve with respect to concentration of the two components, how size and shape of the full particles modify the properties, how these features can be related to the corresponding properties of the mono-metallic particles containing either element and to compare trends with experimental findings that now are available. This in particular for the breaking of Vegard's law due to simple geometric alterations as reported by Nishijima et al. for nanodiscs11 and for the non-linear behaviour of the polarizability seen for spherical nanoparticles.12–14
2 Theory and approximations
The modelling of alloys is not as straight forward as of the pure metal due to the unknown dielectric function which has only been measured for some ratios and a selected set of frequencies.15 Nevertheless, the modelling of alloys can be performed in numerous different ways out of which a few methods can be highlighted that recently have been applied to gold–silver alloys for larger systems. The dielectric function in the classical Drude–Lorentz model has received some attention since the assumption of a simple weighted linear combination of the constituents does not suffice as it is not physically realistic for alloys and, secondly, because experimental data for the dielectric function is of limited availability.12,15,16 Gold-silver alloys were also recently modelled by Skidanenko et al.,13 who applied the T-matrix approach by Waterman17 where the expansion coefficients of the incident field are connected over regular vector spherical harmonics, and by Borah et al.18 by solving Maxwell's equations using the finite element method. In a comparison Borah et al. showed that solving Maxwell's equations using the finite element method and fitting the dielectric function gave very similar results for both pure metals as well as alloys.182.1 ex-DIM
The extended Discrete Interaction Model (ex-DIM),9,19 is a further development of the DIM model20,21 where significant improvements in the description of the surface topology, geometric dependence and parameterization of the SPR(s) are introduced. The ex-DIM model has a special applicable edge for systems in the 1–15 nm size range, where quantum mechanical models cannot be applied due to the scaling of these methods, and where the concept of a bulk dielectric constant used in classical models breaks down. The 1–15 nm size range is, however, a very important region since this is the size region where the onset of the SPR(s) is seen and where the nanoparticles are still small enough to be used in bio-medical applications. Due to the inability of extrapolating data from quantum mechanical methods and classical methods into the 1–15 nm size range the ex-DIM must be parameterized directly from experimental data.9 We will in Section 3.1 briefly show how a new element easily can be parameterized for the ex-DIM and in Section 3.3 describe how alloys with a given initial distribution is implemented.The ex-DIM model is a discrete structure model where each atom is represented by a Gaussian charge distribution and endowed with a polarizability and a capacitance which govern the interatomic interaction. The Lagrangian is written in the usual form as the interaction energy E minus the charge equilibration constraint expressed via the Lagrangian multiplier λ:
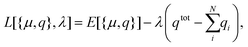 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μ,q}] in this way captures all different types of interactions involving fluctuating dipoles
μ,q}] in this way captures all different types of interactions involving fluctuating dipoles ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μ, charges q and an external field. Since it is the atomic interaction strength with size that is being parameterized, the ex-DIM is also very suited for alloys since it is only the interaction strength that differs between different atoms. The parameterized interaction from a metal can therefore be used also in alloys without having to introduce any additional terms. The ex-DIM model is described in greater detail in ref. 9.
μ, charges q and an external field. Since it is the atomic interaction strength with size that is being parameterized, the ex-DIM is also very suited for alloys since it is only the interaction strength that differs between different atoms. The parameterized interaction from a metal can therefore be used also in alloys without having to introduce any additional terms. The ex-DIM model is described in greater detail in ref. 9.
The surface topology is captured by a coordination number, as defined by Grimme,22 and is assigned to each atom. The coordination number fcn modifies the atomic polarizability through the scaling of the radius
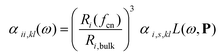 | (2) |
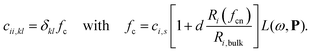 | (3) |
In Eqn (2) and (3), Ri,bulk is the bulk radius of the atom, Ri(fcn) the coordination number scaled radius,9 ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αi,s,kl the static atomic polarizability,23d = 0.1 a scaling factor and L(ω,P) a size-dependent Lorentzian. The polarizability and capacitance of alloys will in this way not only have a spacial dependence from the discrete structure from the interaction but also a small one from the modified surface atoms.
αi,s,kl the static atomic polarizability,23d = 0.1 a scaling factor and L(ω,P) a size-dependent Lorentzian. The polarizability and capacitance of alloys will in this way not only have a spacial dependence from the discrete structure from the interaction but also a small one from the modified surface atoms.
The geometric dependence of the SPR is determined by the size-dependent Lorentzian L(ω,P)
| L(ω,P) = N(Lx(ω,Px) + Ly(ω,Py) + Lz(ω,Pz)), | (4) |
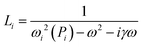 | (5) |
| ωi(Pi) = ωa(1 + A/Pi). | (6) |
In this way cluster size dependence and complicated geometrical shapes, with up to at least three SPRs, can be simulated for solid particles. Since the atomic radius for different atoms is slightly different the plasmon length Pi is not a constant even when the same discrete structure is used for alloys though the change is only in the difference between the atomic radii of the constituents. ωa and A are the only fitted parameters in the ex-DIM model.9
The isotropic polarizability is determined from the fluctuating charges, q, and dipoles, ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μ which are determined by inversion of the relay matrix.9,24–29 In this way all SPRs are presented together in the same spectrum.
μ which are determined by inversion of the relay matrix.9,24–29 In this way all SPRs are presented together in the same spectrum.
3 Geometry
A fundamental problem of the geometric models is the need for a discrete structure in the simulations. In molecular physics the geometry of known molecules is usually tabulated and can be read in directly or optimized. This, however, is not the case for metallic nanoparticles where neither the discrete structure or even the number of particles are known. Only the overall geometric shape of the cluster with dimension on the nm length scale with some error bars are known and these provide no information about the internal discrete structure. Geometry optimization is also not helpful since geometry optimization is NP-hard and therefore not feasible for clusters with thousands of atoms.30–32 We will therefore here briefly discuss the influence of discrete structure and a pragmatic yet accurate approach in which a geometry is easily generated for both pure metals and for alloys.3.1 Sensitivity to structure
From systematic investigations on small silver and gold nanoparticles it is evident that there is a clear trend in the evolution of the surface plasmon resonance with size at the nanometer scale.14,33–45 Yet for any given particle size all measured particles vary in both the discrete structure and particle number. Since the discrete structure differences do not lead to an extreme broadening of the plasmon peak for larger clusters the discrete structure differences instead show that having the exact discrete structure, like in molecular physics, is not of much importance for the SPR. This implies that having the same discrete lattice structure, for which the method has been optimized, should suffice for all sizes.For smaller structures the sensitivity to the discrete structure is expected to be larger which is also seen in the parameterization of gold in Fig. 1. This greater variation in the SPR is due to the greater percentage variation in the number of particles for a fixed plasmon length and that with fewer atoms comes an increasing sensitivity to the placement of the individual atoms in the discrete structure. For clusters with a plasmon length of 1.85 nm we, in this case, see the greatest variation in the surface plasmon resonance, from 2.45–2.67 eV, but we here also have the greatest percentage variation in the particle number since the number of atoms range from 141–249. For larger clusters we see a much smaller variation in the surface plasmon resonance. For example we see that particles with a plasmon length of 5.92 nm the surface plasmon resonance only varies from 2.41–2.42 eV and even though the particle number ranges from 6051 to 7011.
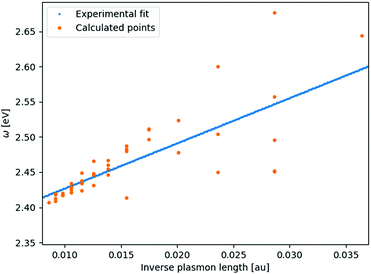 | ||
| Fig. 1 Linear fit of the experimental data14,41,42 compared with the recalculated clusters using the fitted parameters. The number of atoms in the clusters here vary from 135–7419 with sizes from 1.45–6.18 nm. | ||
For nano particles with a diameter below ≈4 nm, with significantly greater variance within a given plasmon length, it would be recommended to sample several different clusters with a size distribution given by the standard deviation from the experimental clusters. Since the computational time used in the calculations of nano particles with a diameter below ≈4 nm is low no significant increase in computational time is added by the sampling. For clusters above ≈4 nm not much is gained by sampling and a single structure can be used.
The parameterization of gold data taken from experiments of gold clusters in a watery solution in the 3.6–17.6 nm size region have been used.14,41,42 The parameterization was performed by fitting the experimental data to the inverse plasmon length and afterwards by finding an optimum frequency for a set of different clusters. From this procedure ωa and A of eqn (6) could be fitted in the same way that the silver parameters was obtained.9 We here find ωa = 0.0682549 and A = 6.43041 in atomic units. Furthermore for the static polarizability we use α = 36 a.u.23 and set the broadening γ = 0.0016 along with the surface and bulk radii of r1 = 1.74 and r2 = 1.56, respectively.
While ex-DIM is parameterized from spherical clusters within a 1–15 nm size range and a limited frequency interval it still remains valid in a much broader frequency range as shown by calculations on nanorods and nanocubes.9 The large frequency range of the ex-DIM model is possible because any red or blue shift due to geometric distortions from a sphere can be described by the interaction between the atoms in this model and no external data is required for this.9 The ex-DIM model is therefor not limited in the frequency range by the parameterization range unlike classical models which are limited by the experimental range for which the dielectric constant have been measured.
3.2 Geometry of alloy and core–shell clusters
Like for the pure metals the discrete structure of alloys is not possible to obtain from experiment and contains an added complication since the unit cells of the metals in the alloy will differ. The latter problem of not knowing the lattice parameters of the alloy can usually be overcome using the empirical law from Vegard| aA1−xBx = (1 − x)aA + xaB | (7) |
For core shell structures connecting the lattice of the core with the shell is not a simple problem for models using a discrete structure and there does not seem to be a simple way to connect two perfect lattices with different lattice parameters without having to distort these lattices at the boundaries. In order to overcome this we have optimized gold and silver using the same lattice constants which is only possible due to the very small difference in the lattice constants for these two metals. We see the usage of the same lattice constants as a pragmatic approach for this particular type of core–shell structures and not a general solution.
3.3 Alloy implementation
Since the exact placement of the constituents in an alloy cannot be predicted and differ from cluster to cluster we have chosen to represent this using a simple random selection of elements based on an initial probability distribution. This means that there will be both a random spacial distribution of elements along with a small variation in the ratio between the elements due to the randomized drawing of the elements. In this way no two clusters will be exactly alike in our sampling and a statistical analysis of the slightly expected broadening of the SPR for alloys can be analyzed in terms of the variation in the ratio and spacial distribution of the constituents and error bars for the alloys can be assessed. Two random distributions for a sphere and disc structure are shown in Fig. 2.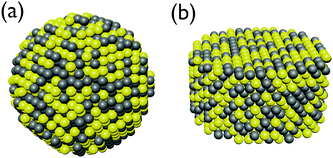 | ||
| Fig. 2 Schematic representation of alloy sphere (a) and disc (b) nanoparticles taken from a random distribution of Au (yellow) and Ag (grey) atoms. | ||
4 Results and discussion
Even though Vegard's law initially was formulated in order to estimate the lattice parameters of alloys it has often been extended to include all properties of alloys| PA1−xBx = (1 − x)PA + xPB | (8) |
We will first perform a statistical analysis to determine how the error varies with spacial and constituent distribution along with size of the cluster for a spherical alloy nanoparticle in order to get an estimation of the error bars when performing a single calculation.
4.1 Statistical analysis of the model
The aim of the statistical analysis is to examine the effect of randomly drawing elements and give estimations for error bars since it will not always be possible to make a full statistical analysis for every cluster. A secondary goal is to ensure that the model behaves as would be expected from a random drawing of a finite number of elements with a given probability and to analyse how large the error is for classical models when going towards smaller clusters along with how the standard deviation varies with the size of the cluster. From the fitting of Au in Fig. 1 we expect that the standard deviation of the SPR of an alloy would decrease with size since the importance of the individual placement of an atom would decrease and less sensitivity to variations in the actual distribution of the constituents should be seen. Secondly from a statistical perspective we expect that the standard deviation for alloys where one of the constituents is very dominating is lower than one where the distribution is more even.In Table 1 we present a statistical analysis for a set of clusters ranging from 249 to 6051 atoms or 1.85 to 5.79 nm in size with three different distributions in order to show both the size and distribution dependence of the standard deviation of the SPR and extinction cross section. Due to computational resources we reduce the number of sampling points with the size and width of the sample, though significant changes with increasing number of sampling points are not expected and all trends are easy to recognize. Due to the larger standard deviation in the SPR seen for smaller clusters the frequency range sampled in Table 1 is not the same though the interval between each frequency was constant and set at 0.0001 a.u. Since the CPU time set for each size, above 1553 atoms, is the same the number of samples for each distribution varies. We have in Table 1 added extra digits on both the standard deviation σ and the averages μ in order to better illustrate the trends.
| Distribution | Samples # | Ag | SPR [nm] | Extinction cross section [nm2 per atom] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Atoms | % Ag | % Au | μ | σ | Min | Max | μ | σ | Min | Max | μ | σ | Min | Max | |
| 249 | 90 | 10 | 9099 | 224 | 5 | 205 | 242 | 348.4 | 1.92 | 342.6 | 356.5 | 0.2486 | 0.0109 | 0.1914 | 0.2866 |
| 50 | 50 | 9099 | 124.4 | 7.9 | 96 | 157 | 392.9 | 7.85 | 368.9 | 424.6 | 0.1678 | 0.0091 | 0.1331 | 0.1994 | |
| 30 | 70 | 9099 | 74.7 | 7.2 | 49 | 101 | 431.9 | 10.3 | 402.5 | 460.2 | 0.1496 | 0.0064 | 0.1263 | 0.1773 | |
| 675 | 90 | 10 | 8810 | 607 | 8 | 578 | 639 | 350.8 | 11.2 | 332.4 | 367.1 | 0.2149 | 0.0075 | 0.1956 | 0.2368 |
| 50 | 50 | 9099 | 338 | 13 | 290 | 385 | 410.7 | 4.91 | 395.9 | 427.8 | 0.1542 | 0.0038 | 0.1408 | 0.1697 | |
| 30 | 70 | 9099 | 203 | 12 | 159 | 254 | 448.2 | 4.26 | 430.3 | 462.5 | 0.1416 | 0.0028 | 0.1305 | 0.1541 | |
| 1553 | 90 | 10 | 8134 | 1398 | 12 | 1355 | 1436 | 359.7 | 1.25 | 356.0 | 364.5 | 0.2405 | 0.0030 | 0.2288 | 0.2510 |
| 50 | 50 | 5564 | 777 | 20 | 709 | 852 | 412.3 | 2.99 | 405.0 | 421.9 | 0.1620 | 0.0028 | 0.1520 | 0.1725 | |
| 30 | 70 | 6194 | 465 | 18 | 403 | 535 | 450.6 | 2.79 | 440.2 | 459.2 | 0.1444 | 0.0019 | 0.1363 | 0.1511 | |
| 3367 | 90 | 10 | 2732 | 3030 | 17 | 2976 | 3090 | 367.3 | 0.96 | 363.6 | 370.4 | 0.2368 | 0.0020 | 0.2297 | 0.2436 |
| 50 | 50 | 1634 | 1684 | 28 | 1598 | 1784 | 423.1 | 1.71 | 417.2 | 429.0 | 0.1673 | 0.0018 | 0.1622 | 0.1723 | |
| 30 | 70 | 2621 | 1009 | 26 | 919 | 1121 | 457.5 | 1.60 | 452.0 | 462.6 | 0.1529 | 0.0011 | 0.1488 | 0.1567 | |
| 6051 | 90 | 10 | 1159 | 5446 | 23 | 5372 | 5515 | 370.6 | 0.49 | 369.0 | 372.2 | 0.2575 | 0.0017 | 0.2515 | 0.2624 |
| 50 | 50 | 746 | 3024 | 38 | 2900 | 3145 | 424.2 | 1.30 | 419.6 | 428.2 | 0.1719 | 0.0013 | 0.1682 | 0.1762 | |
| 30 | 70 | 809 | 1818 | 33 | 1710 | 1921 | 459.4 | 1.20 | 456.2 | 464.0 | 0.1546 | 0.0009 | 0.1516 | 0.1575 | |
As expected, we see that the standard deviation in the number of Ag atoms increases with both size and evenness in the distribution. For the SPR we also see, also as expected, from Fig. 1, that the standard deviation for the SPR decreases with size and increase with evenness in the distribution. At around 3000 atoms the standard deviation is below 2 nm and therefore below the accuracy which can be expected from any calculation. From an atomistic perspective we therefore also see that the classical way of treating an alloy without any resolution at the atomic level does not introduce any significant error for the SPR of larger systems calculated using classical methods.12,13,18,57,61 Furthermore, we see that with good size correction the classical methods for alloys can safely be extended to small systems down to 4–5 nm. For alloys where one of the constituents is dominating, above 90 percent, even smaller systems can be safely simulated. There is, however, one outlier in the data in Table 1 namely the 675 atoms cluster with distribution of 10% Au and 90% Ag where the standard deviation for the SPR is 11.2 nm whereas a standard deviation of around 1.5 nm would be expected from the trend. This outlier appears because many of the spectra for this 675 atom cluster shows a double peak, between which the maximum alternates, thereby causing a very broad distribution and hence large standard deviation. This double peak would not be visible in experimental spectra but only lead to additional broadening of the peak since the experimental spectra is made up of many clusters with slightly varying size and distribution of elements.
In order to analyse and illustrate the effect of the random distributing on a fixed number of constituents and the variation of the constituents due to the random drawing of them we have chosen to focus on the 1553 atom cluster with different distributions. The 1553 atoms cluster shows a clear difference in the standard deviation of both the number of Ag atoms and the SPR for the different distributions and a sufficient number of samples could easily be collected as seen in Table 1. In Fig. 3a–c the three different distributions from Table 1 of the 1553 atoms cluster is plotted.
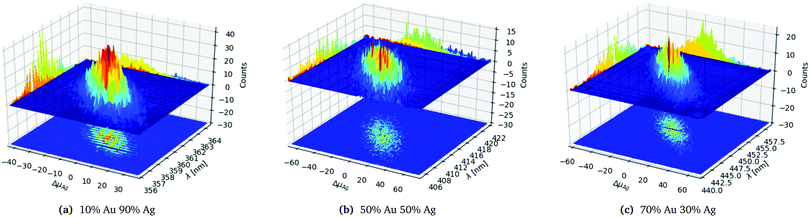 | ||
| Fig. 3 Statistics data for the 1553 atoms alloy cluster with a random distribution with different probability distributions as labelled below the figures. | ||
In Fig. 3a we clearly see that the SPR follows the change away from the average number of Ag atoms ΔμAg, with a red shift for a negative shift of ΔμAg and blue shift for a positive shift of ΔμAg as would be expected. For the clusters with the same number of constituents we also see that the spacial distribution of the atoms also matters though less than the variation in ΔμAg since we have an elliptical shaped peak as clearly seen in the projection on the counts axis.
Comparing the three distributions in Fig. 3a–c we clearly see that the 10% Au 90% Ag distribution in Fig. 3a is significantly more narrow and peaked both along ΔμAg and λ. This can also be seen from the projection onto the Counts axis where it is clear that the less even the distribution is the more clear and narrow the peak becomes. The significantly smaller standard deviation for the SPR of the 10% Au 90% Ag distribution compared to the 50% Au 50% Ag and 70% Au 70% Ag distributions is also clearly visible from the projection of the distribution onto the λ axis.
The extinction cross section per atom in Table 1 shows no real variance with size but only with distribution where the extinction cross section increases with the amount of Ag in the alloy. Though the difference in the extinction cross section between 70% Au 30% Ag and 50% Au 50% Ag distributions is significantly smaller than could be expected from Vegard's law. We will analyse this observation in more detail in Section 4.3 when we look at the evolution of the polarizability as a function of the constituents. We here also see the expected trend where the standard deviation decreases with size though it remain rather small throughout. We here note that since the broadening of the Lorentzians in eqn (4) is not fitted only the trend and not the absolute values of the extinction cross section is to be interpreted here for the ex-DIM model.
In the direct comparison with experiment not only the standard deviation for an alloy with a given number of atoms should be considered but also the deviation seen within a specific size since the variation there can be comparable as seen in Fig. 1. For alloys we again recommend to make a sampling for nano particles below ≈4 nm when comparing to experiment due to the slightly greater standard deviation for these small clusters. For larger nano particles sampling does not seem to be necessary since the sensitivity to atomic arrangement and number of particles diminishes very fast with size.
4.2 Surface plasmon resonance for alloys and core shells
Since Vegard's law assumes linearity a linear energy scale for the SPR should be used| λVegard(x, R) = (1 − x)λAu(R) + xλAg(R). | (9) |
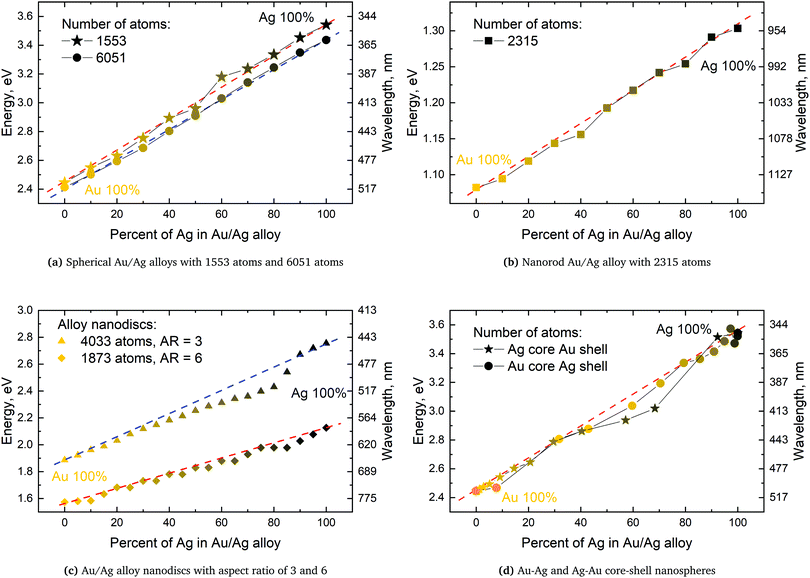
We will in the following use eV and not nm, even if nm is the prevalent choice of unit, since only the former of the two is a linear energy unit. We here examine if any non-linearity effects in the SPR can be induced by the geometric structure of the alloy clusters as observed experimentally by Nishijima et al. on nano discs.11 The experimentally observed very large red shift in the spectra was reproduced by these authors in theoretical predictions using FDTD where the plasma frequency ωp and relaxation time τ was extracted by inserting the experimental data into the Drude model.11 However, from a theoretical viewpoint using a plasma frequency which depends on the distribution of the constituents as derived from the extraction of experimental data does limit the theoretical predictions to a posteriori confirmation of the reproducibility of the results.
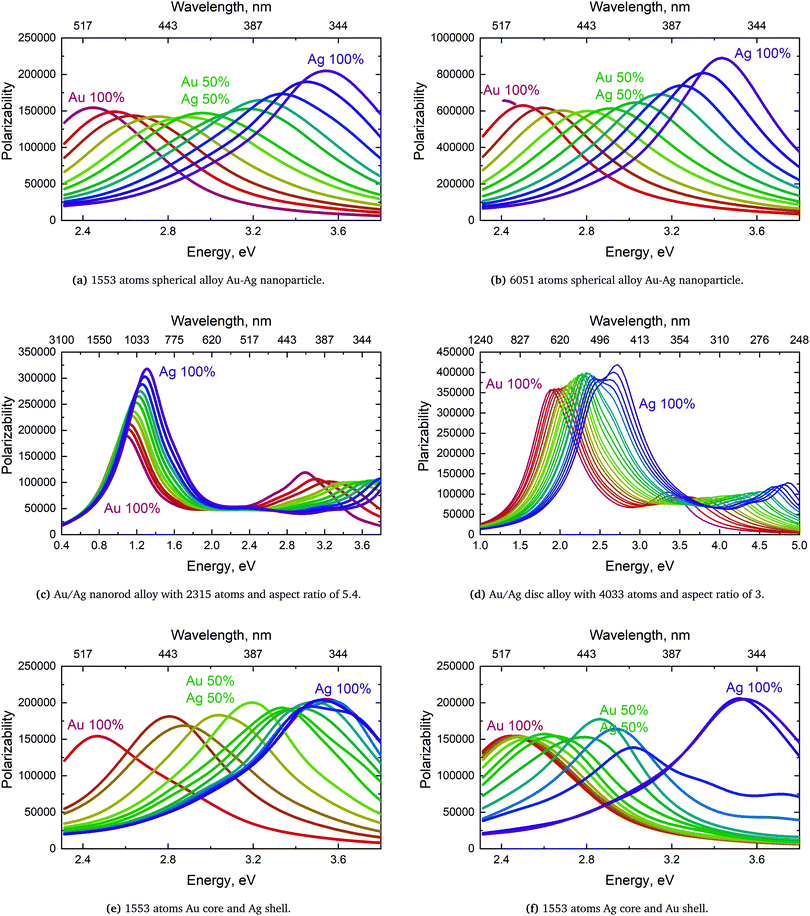
We will here examine two spherical clusters with different radii, a nanorod and two nano discs one with different relative dimensions and one similar to the ones used experimentally by Nishijima et al. though significantly smaller in size. Another possibility of mixing metals is by making core–shell structures. For the core–shell structures we will examine spheres where we show both Au core and Ag shells along with Ag core and Au shells in order to examine if there is significant difference in which metal is the core and the shell. Since the atoms in ex-DIM are discrete, the steps in the distribution of the metals for the core shell structures cannot be divided into equal steps as it can for alloys. Furthermore the use of spherical structures having a percentage wise large core will result in an atomically thin surface and the very large core structures should therefore be interpreted with care. In Appendix A we plot all spectra from which data have been extracted.
From Fig. 4a–c we show Vegard's law for the position of the SPR of alloys with different geometries and distributions. We have in Fig. 4a chosen a random alloy from those sampled in Section 4.1 and not the average one since all distributions and geometries have not been sampled. The same random choice goes for the nanorod and nanodisc alloys in Fig. 4b and c. One should therefore keep in mind the standard deviation along with the minimum and maximum for the SPR shown in Table 1 when interpreting these results. Comparing the 1553 and 6051 atom spherical clusters in Fig. 4a we see that changing the size of the sphere does induce any non-linearity nor does the change in geometry which can be seen by comparing all figures from Fig. 4a to c. This is in line with other experimental and theoretical works13,18,57 except that by Nishijima et al.11 In Fig. 4c there appears to be some systematic non-linearity in the position of the SPR for the nanodisc with 4033 atoms and lower aspect ratio. By analysing the spectra in Fig. 8d in Appendix A we see that the non-linearity comes from the appearance of a shoulder for the pure Ag cluster which turn into a double peak with 15% Au mixed in and finally the shoulder becomes the dominant peak with 20–25% Au in the alloy. This behaviour is not expected for all discs, as seen for the 1873 atoms disc in Fig. 4c, and the deviation seen up to 0.2 eV is much below the very significant red shift observed by Nishijima et al.11 As observed in Fig. 4c even if we vary and increase the aspect ratio up to the experimental aspect ratio we cannot reproduce the results from Nishijima et al.11 and it does not seem likely that this very large red shift can be reproduced elsewhere.
At the right hand side of Fig. 4a–c the nm scale is also shown. Since the energy range used is small the shift in the SPR on the nm scale will also be almost linear but not completely. This can explain some observed weak non-linear trends in the SPR since this will automatically appear if the nm energy scale and not the eV energy scale is used.
The core–shell structure with an Au core and Ag shell shown in Fig. 4d also follows Vegard's law while the Ag core Au shell core–shell structure shows a small dip of up to 0.2 eV when the number of atoms in the Ag core exceeds 50 and below 80 percent. In this region we, for this cluster, see a large broadening of the spectra as seen in Fig. 8f in Appendix A.
4.3 Polarizability for alloys and core shells
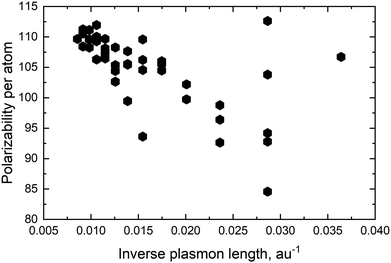
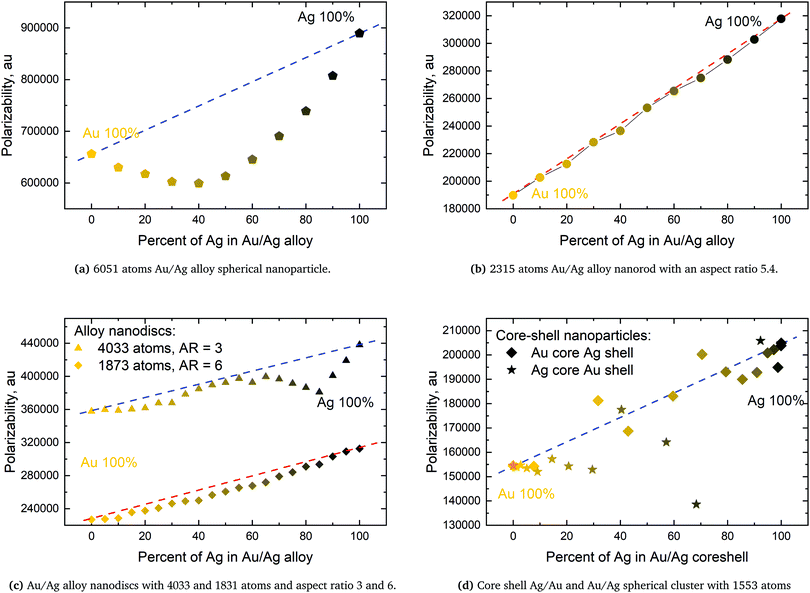
For pure metals the polarizability will decrease proportionally to the inverse plasmon length and, in the ex-DIM approach, with the current broadening factor, an asymptotic bulk limit of approximately 115 a.u. is obtained as seen for Au in Fig. 5. The total polarizability in spheres is therefore in general proportional to the static atomic polarizability and the inverse plasmon length.Since the SPR of all alloys and core–shell structures obeyed Vegard's law, except for a small deviation for the nanodisc alloys and the Ag core Au shell as seen in Fig. 4c and d, and seeing that the polarizability per atom is proportional to the static polarizability it could easily be assumed that the polarizability also would obey Vegard's law
| pVegard(x, R) = (1 − x)pAu(R) + xpAg(R), | (10) |
For the Au and Ag sphere alloys a very characteristic dip in the polarizability, as seen in Fig. 6a, is observed when adding Ag to an Au nanoparticle despite the fact that Ag has a higher static polarizability. As seen from Fig. 6a there is a minimum with 40 percent Ag in the alloy and the polarizability for 30 and 50 percent Ag is very close. The closeness for the polarizability with 30 and 50 percent Ag explains why the extinction cross section per atom in Table 1 for these distributions is very close and why the 90 percent Ag is significantly higher. For the spheres we see exactly the same trend as seen in other studies.13,18,56
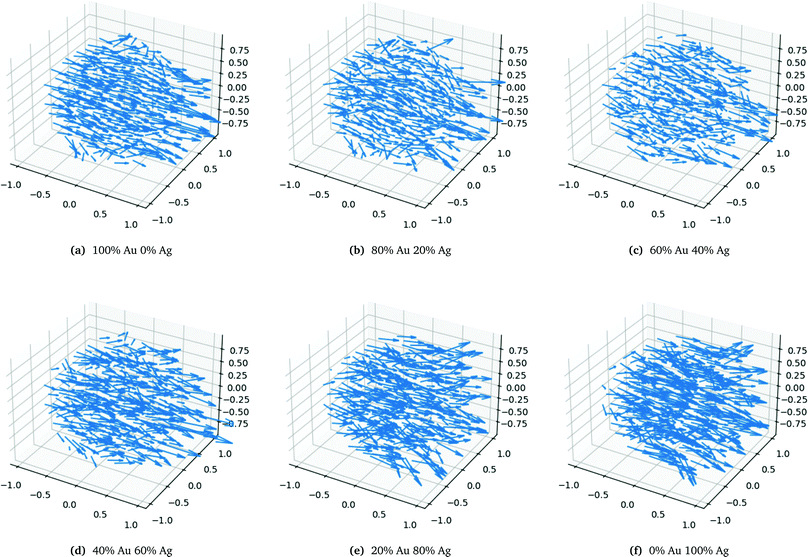
The very characteristic dip in the polarizability seen in Fig. 6a is seen for all spheres irrespective of size. The dip is caused by the quenching of the alignment and hence size of the dipoles when going from a homogeneous environment, thus from a pure or only slightly mixed clusters to a more heterogeneous environment as in alloys with a more equal mixing. By plotting the dipoles of the individual atoms for a cluster with only 369 atoms and a field with the polarization along the x-direction this misalignment and subsequent quenching can be visualized as seen in Fig. 7. Fig. 7a–f shows the dipoles from a random distribution with an initial probability distribution of the elements given below each figure. The dipoles in the pure Au cluster in Fig. 7a clearly shows a very good alignment with the largest dipoles on the right hand side of the cluster as expected with the applied field. Going from the pure Au cluster in Fig. 7a and gradually mixing in Ag into the Au cluster, as seen in Fig. 7b and c, it is clear that there is a quenching and increased misalignment of the dipoles due to the increased heterogeneity where the nearest neighbours do not all respond to the external field in the same way thereby causing the dipoles not to properly align and lose the cooperative effect of aligned dipoles. This effect is particularly clear in spheres since the number of atoms in the plane orthogonal to the polarizing field is significant in comparison to the length of the cluster along the field of polarization which will cause a greater chance of misalignment of the dipoles. Further increasing the amount of Ag as seen in Fig. 7d and e until the pure Ag cluster in Fig. 7f the alignment of the dipoles are again restored and become even greater due to the larger polarizability of Ag in comparison to Au.
For the rod alloy, shown in Fig. 6b, we observe a perfect linear correlation of the polarizability with the distribution for the longitudinal SPR. The longitudinal SPR of the rod alloy is the only alloy geometry that we have tested where the polarizability follows Vegard's law exactly and the only geometry where there is no loss in response to the external field in comparison to Vegard's law. The linear correlation and no broadening of the longitudinal SPR, as seen in Fig. 8c in Appendix A, is in line with the theoretical calculations from Bansal et al.57 The reason for the perfect linear correlation is the relative high aspect ratio of 5.4 where the number of atoms along the field of polarization is large in comparison to the number of atoms in the plane orthogonal to the polarizing field. This makes the cooperative effect of alignment of the dipole easier and significantly more dominant than the difference in polarization of the nearest neighbors.
The nanodisc alloy with 4033 atoms, seen in Fig. 6c, shows a very large dip in the maximum polarizability when having 10–30 percent Au in the alloy. The dip in the maximum polarizability is again related to the appearance of a shoulder and double peak as seen in Fig. 8d where the peak is significantly broader than for the rest of the nanodisc alloys. Broad or very close double peaks can occur for certain size, geometry and distribution in the ex-DIM model and will not show up in experiments unless the broad or double peaks are formed from a sizeable range and distribution in the experimental sample. For the smaller nanodisc with the larger aspect ratio this double peak is not seen and the polarizability only dips slightly below the prediction following Vegard's law just like for the larger nanodisc where the double peak is not present. Despite the slightly larger aspect ratio of the smaller nanodisc in comparison to the nanorod in Fig. 6b the nanodisc shows a small dip in the polarizability in comparison to Vegard's law. The reason for the small dip in the nanodisc is that the aspect ratio is only large in comparison to the thickness and not to the width and misalignment will increase the further away from the center where the nearest neighbour effect will be non-negligible.
The greater the difference in polarizability between the mixing species is the greater the quenching will be since the difference in the response to the external polarizing field of the nearest neighbors will increase and it will therefore become increasingly difficult to have a good alignment. The trends in the geometry shown for the sphere, rod and disc will still be the same but can be increased or decreased depending on the difference in the polarizability of the mixing species.
For the core–shell structures shown in Fig. 6d there is no obvious trend and larger variations from the small changes in the distribution is seen. The large dip is seen for the large Ag core and a thin Au shell where the number of atoms in the core is just below 70 percent. This is again caused by a large broadening of the spectra as seen in Fig. 8f in Appendix A. As the only one, that we have found, do the Au core Ag shell nanoparticles have a few sizes of core and shell where the polarizability is above that predicted by Vegard's law though nothing appears as systematic.
5 Discussion
We have in this work presented a way of creating accurate calculations on alloys using a discrete atomic structure model with good estimation of error bars. This was achieved by using a simple random number generator and distribution for the constituents in our extended discrete interaction model (ex-DIM) in the initial placement of atoms in the alloy. We lay out the physical reasoning of why it is appropriate to use a perfect lattice for all sizes of both pure metals and alloys which is backed up by a statistical analysis of the alloys from where error bars can be estimated. We see that the trend in the errors follows that expected trend from the fitting of the size dependence of Au clusters and a statistics where the standard deviation of the surface plasmon resonance (SPR) increases inversely with size and evenness of the constituents in the alloy.From the fitting of the Au nano clusters we observe that the sensitivity of the SPR to the number of atoms and their spatial arrangement decreases rapidly with size and is likewise observed for the standard deviation for the alloys. In order to create accurate predictions with small error bars we therefore find that for spherical clusters and alloys with a diameter below approximately 4 nm a sampling strategy where multiple clusters with varying number of atoms and a sampling of the spacial distribution of the constituents would be prudent. When comparing directly to experiments in this size range some small variation in the allocated plasmon length based on the standard deviation of the cluster size from the experiment would also be advised. Since the number of atoms in the spherical clusters with a diameter below 4 nm are small the numerical effort will not be a problem. For spherical clusters above approximately 4 nm only little would be gained from sampling a fixed number of atoms and one geometry can be employed without introducing large errors.
Much of the motivation for creating alloys or core–shell structures is given by the ability of also blue shifting the SPR and having a chemically less reactive surface while still having significant response to the impinging light. Another motivating fact was the experimental report by Nishijima et al.11 on the breaking of Vegard's law46,47 for the SPR simply from geometrical alterations. We have here examined three Au–Ag alloys with different geometrical structures namely spheres, a rod and a disc and have found no deviations from Vegard's law for the SPR, using a linear energy unit, that is not readily explained by the estimated error bars or from the emergence of a double peak. For spheres this is in line with other experimental and theoretical predictions for large clusters.13,18,56 For the discs we, just like Peña-Rodríguez et al.,12 were not able to reproduce the experimental findings by Nishijima et al.11 even if the atomic interaction in the ex-DIM should be able to simulate the polarization of the individual atoms. The idealized structure of alternating Ag and Au atoms giving a closed shell pair structure of Ag and Au envisioned by Nishijima et al. as an explanation of the large red shift of the SPR will of course never be seen by a random distribution and we have not observed any extremely red shifted outliers in our data. While the size of the discs differ the aspect ratio is the same and like Peña-Rodríguez et al.12 we doubt that the size effect will play any role. For spherical core–shell structures the Au core Ag shell also shows agreement with Vegard's law while the Ag core Au shell shows a red shift of up to 0.2 eV compared to that expected from Vegard's law for large Ag cores. Though these peaks for the large Ag cores showed much larger broadening, no systematic behaviour in the evolution of the SPR with variations of the size of the core could be observed.
While the position of the SPR, in all cases tested here, closely follows Vegard's law this was not the case for the maximum value of the polarizability which shows a great dependence on the geometry of the nanoparticle. For the alloys there was in general a slight broadening of the spectra leading to a lower maximum value of the polarizability. This showed up systematically for the spherical alloys where there was a minimum in the polarizability at around 40 percent Ag in the Au/Ag alloy irrespective of size. The nanorod was the only alloy which followed Vegard's law and the polarizability was not below that predicted by Vegard's law. For the nanodisc we, in the low aspect ratio case, saw a sudden dip in the polarizability due to having a double peak for alloys containing 75–90 percent Ag. Otherwise both nanodiscs almost followed Vegard's law. The dip below Vegard's law for the polarizability is due to the heterogeneous environment in the alloy in comparison to the homogeneous environment in the pure cluster. In the heterogeneous environment there is a quenching and increased misalignment of the dipoles due to the heterogeneity where the nearest neighbours do not all respond to the external field in the same way thereby causing the dipoles not to properly align and lose the cooperative effect of aligned dipoles. The polarizability for the core–shell structure showed a very unsystematic nature and it would therefore be hard to predict the polarizability for these. We therefore have not observed any enhancement in the polarizability which is above Vegard's law. We in this way show that the ex-DIM is capable of capturing the non-linear behaviour of the polarizability.
From an atomistic perspective we see that the classical methods of treating an alloy without any resolution at the atomic level does not introduce any significant error for the SPR of larger systems.15,16,18,55,61 Provided that the size correction for the dielectric function is good then there should thus be no problems for classical methods in simulating nanoparticle alloys down to the 4–5 nm size or even smaller depending on the distribution of elements since at these sizes we still see very small standard deviations in our calculations. However, the smaller the size, the more irregular the shape, the more complex the elementary composition, the more is an atomistically decomposed model, like here the applied ex-DIM model, called for.
Conflicts of interest
There are no conflicts of interest to declare.Appendix A: Complete curves for alloys and core–shell nanoparticles
We here show the complete curves for all alloys and core–shell nanoparticles. For the spherical alloys seen in Fig. 8b we see that the shape of the spectra is not altered by the mixing of Au and Ag and Vegard's law for the SPR is obeyed. The dip in the polarizability as discussed in Section 4.3 and plotted in Fig. 6a for both spheres is also visible in Fig. 8b. The fact that the width does change can be caused by the fact that the broadening factor used for Au and Ag is the same.For the nanorod alloy in Fig. 8c both the longitudinal and transverse SPRs are clearly visible. From Fig. 8c it is seen that Vegard's law is obeyed for both the SPR and polarizability for the longitudinal SPR. For the transverse only the SPR follows Vegard's law. The nanorod alloy is the only nanoparticle, we have found, where Vegard's law is obeyed for both the SPR and the polarizability and also the only nanoparticle alloy where the polarizability is not below Vegard's law.
The longitudinal and transverse SPRs are also visible for the nanodisc alloy in Fig. 8d. It is clearly seen that what appears to be some systematic deviation from Vegard's law in Fig. 4c is due to the appearance of a shoulder for the pure Ag cluster which turns into a double peak with 15% Au mixed in and finally the shoulder becomes the dominant peak with 20–25% Au in the alloy. The shoulder and double peak also explain the sharp drop in the maximum value for the polarizability in Fig. 6c. So while a small and systematic deviation from Vegard's law is observed here the deviation is far from that observed by Nishijima et al. where the red shift of the SPR for the alloy consisting of 50% Au and Ag is below the pure Au peak.11
For the core–shell spectra in Fig. 8f no real pattern emerges in the progression from pure Au to pure Ag clusters since both the maximum polarizability and the FWHM change rapidly. Due to the atomistic nature of the ex-DIM model, having smaller steps in some of the areas where there is a rapid change can be difficult.
Acknowledgements
H. Å., V. Z., A. U. acknowledges the support from the Ministry of Science and High Education of Russian Federation, project no. FSRZ-2020-0008. L. K. S. acknowledges the support of Carl Tryggers Stifetelse, project CTS 18-441. The simulations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at NSC under the project “Multiphysics Modeling of Molecular Materials”, SNIC 2019/2-41.References
- G. Sharma, A. Kumar, S. Sharma, M. Naushad, R. Prakash Dwivedi, Z. A. ALOthman and G. T. Mola, J. King Saud Univ., Sci., 2019, 31, 257–269 CrossRef.
- K. Loza, M. Heggen and M. Epple, Adv. Funct. Mater., 2020, 30, 1909260 CrossRef CAS.
- S. Sun, I. L. Rasskazov, P. S. Carney, T. Zhang and A. Moroz, J. Phys. Chem. C, 2020, 124, 13365–13373 CrossRef CAS.
- V. I. Zakomirnyi, I. L. Rasskazov, S. V. Karpov and S. P. Polyutov, J. Quant. Spectrosc. Radiat. Transfer, 2017, 187, 54–61 CrossRef CAS.
- Y. Wang, A. Kumar, T. Y. Wu and D. S. Weiss, Science, 2016, 352, 1562–1565 CrossRef CAS.
- A. Yasuhara, K. Kubo, S. Yanagimoto and T. Sannomiya, J. Phys. Chem. C, 2020, 124, 15481–15488 CrossRef CAS.
- I. L. Rasskazov, A. Moroz and P. S. Carney, J. Opt. Soc. Am. A, 2019, 36, 1591 CrossRef CAS.
- I. L. Rasskazov, P. S. Carney and A. Moroz, OSA Continuum, 2020, 3, 2290 Search PubMed.
- V. I. Zakomirnyi, Z. Rinkevicius, G. V. Baryshnikov, L. K. Sørensen and H. Ågren, J. Phys. Chem. C, 2019, 123, 28867–28880 CrossRef.
- E. Ringe, M. R. Langille, K. Sohn, J. Zhang, J. Huang, C. A. Mirkin, R. P. Van Duyne and L. D. Marks, J. Phys. Chem. Lett., 2012, 3, 1479–1483 CrossRef CAS.
- Y. Nishijima and S. Akiyama, Opt. Mater. Express, 2012, 2, 1226–1235 CrossRef CAS.
- O. P. N. Rodríguez, M. Caro, A. Rivera, J. Olivares, J. M. Perlado and A. Caro, Opt. Mater. Express, 2014, 4, 403–410 CrossRef.
- A. V. Skidanenko, L. A. Avakyan, E. A. Kozinkina and L. A. Bugaev, Phys. Solid State, 2018, 60, 2571–2578 CrossRef CAS.
- S. Link and M. A. El-Sayed, J. Phys. Chem. B, 1999, 103, 4212–4217 CrossRef CAS.
- D. Rioux, S. Valliéres, S. Besner, M. Philip, E. Mazur and M. Meunier, Adv. Opt. Mater., 2014, 2, 176–182 CrossRef.
- O. Peña-Rodríguez, J. Alloys Compd., 2017, 694, 857–863 CrossRef.
- P. C. Waterman, Proc. IEEE, 1965, 53, 805–812 Search PubMed.
- R. Borah and S. W. Verbruggen, J. Phys. Chem. C, 2020, 124, 12081–12094 CrossRef CAS.
- V. I. Zakomirnyi, I. L. Rasskazov, L. K. Sørensen, P. S. Carney, Z. Rinkevicius and H. Ågren, Phys. Chem. Chem. Phys., 2020, 22, 13467–13473 RSC.
- L. L. Jensen and L. Jensen, J. Phys. Chem. C, 2008, 112, 15697–15703 CrossRef CAS.
- L. L. Jensen and L. Jensen, J. Phys. Chem. C, 2009, 113, 15182–15190 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- P. Schwerdtfeger and J. K. Nagle, Mol. Phys., 2019, 117, 1200–1225 CrossRef CAS.
- R. R. Birge, J. Chem. Phys., 1980, 72, 5312–5319 CrossRef CAS.
- B. Thole, Chem. Phys., 1981, 59, 341–350 CrossRef CAS.
- L. Jensen, P.-O. Åstrand, K. O. Sylvester-Hvid and K. V. Mikkelsen, J. Phys. Chem. A, 2000, 104, 1563–1569 CrossRef CAS.
- L. Jensen, O. H. Schmidt, K. V. Mikkelsen and P.-O. Åstrand, J. Phys. Chem. B, 2000, 104, 10462–10466 CrossRef CAS.
- B. Shanker and J. Applequist, J. Chem. Phys., 1996, 104, 6109–6116 CrossRef CAS.
- M. L. Olson and K. R. Sundberg, J. Chem. Phys., 1978, 69, 5400–5404 CrossRef CAS.
- X. Shao, X. Liu and W. Cai, J. Chem. Theory Comput., 2005, 1, 762–768 CrossRef CAS.
- W. Huang, X. Lai and R. Xu, Chem. Phys. Lett., 2011, 507, 199–202 CrossRef CAS.
- T.-E. Fan, G.-F. Shao, Q.-S. Ji, J.-W. Zheng, T.-D. Liu and Y.-H. Wen, Comput. Phys. Commun., 2016, 208, 64–72 CrossRef CAS.
- W. Harbich, S. Fedrigo and J. Buttet, Z. Phys. D: At., Mol. Clusters, 1993, 26, 138–140 CrossRef CAS.
- S. Fedrigo, W. Harbich and J. Buttet, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 10706–10715 CrossRef CAS.
- J. A. Scholl, A. L. Koh and J. A. Dionne, Nature, 2012, 483, 421–427 CrossRef CAS.
- S. Raza, N. Stenger, S. Kadkhodazadeh, S. V. Fischer, N. Kostesha, A.-P. Jauho, A. Burrows, M. Wubs and N. A. Mortensen, Nanophotonics, 2013, 2, 131–138 CAS.
- N. Nilius, N. Ernst and H.-J. Freund, Phys. Rev. Lett., 2000, 84, 3994–3997 CrossRef CAS.
- K.-P. Charlé, L. König, S. Nepijko, I. Rabin and W. Schulze, Cryst. Res. Technol., 1998, 33, 1085–1096 CrossRef.
- T. Lünskens, P. Heister, M. Thämer, C. A. Walenta, A. Kartouzian and U. Heiz, Phys. Chem. Chem. Phys., 2015, 17, 17541–17544 RSC.
- A. Campos, N. Troc, E. Cottancin, M. Pellarin, H.-C. Weissker, J. Lermé, M. Kociak and M. Hillenkamp, Nat. Phys., 2019, 15, 275 Search PubMed.
- N. G. Bastús, J. Comenge and V. Puntes, Langmuir, 2011, 27, 11098–11105 CrossRef.
- J. Piella, N. G. Bastús and V. Puntes, Chem. Mater., 2016, 28, 1066–1075 CrossRef CAS.
- D. Paul and R. Biswas, IEEE Trans. Nanotechnol., 2018, 17, 596–602 CAS.
- P. N. Njoki, I.-I. S. Lim, D. Mott, H.-Y. Park, B. Khan, S. Mishra, R. Sujakumar, J. Luo and C.-J. Zhong, J. Phys. Chem. C, 2007, 111, 14664–14669 CrossRef CAS.
- S. Hong and X. Li, J. Nanomater., 2013, 2013, 790323 Search PubMed.
- L. Vegard, Z. Phys., 1921, 5, 17–26 CrossRef CAS.
- A. R. Denton and N. W. Ashcroft, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 3161–3164 CrossRef CAS.
- H. W. King, J. Mater. Sci., 1966, 1, 79–90 CrossRef CAS.
- H. Duan, J. Wang and B. Karihaloo, Theory of Elasticity at the Nanoscale, Elsevier, 2009, vol. 42, pp. 1–68 Search PubMed.
- S. Ristig, O. Prymak, K. Loza, M. Gocyla, W. Meyer-Zaika, M. Heggen, D. Raabe and M. Epple, J. Mater. Chem. B, 2015, 3, 4654–4662 RSC.
- S. Link, Z. L. Wang and M. A. El-Sayed, J. Phys. Chem. B, 1999, 103, 3529–3533 CrossRef CAS.
- H. Nishi, T. Torimoto and T. Tatsuma, Phys. Chem. Chem. Phys., 2015, 17, 4042–4046 RSC.
- K.-i. Okazaki, T. Kiyama, K. Hirahara, N. Tanaka, S. Kuwabata and T. Torimoto, Chem. Commun., 2008, 691–693 RSC.
- M. S. Shore, J. Wang, A. C. Johnston-Peck, A. L. Oldenburg and J. B. Tracy, Small, 2011, 7, 230–234 CrossRef CAS.
- R. Kuladeep, L. Jyothi, K. S. Alee, K. L. N. Deepak and D. N. Rao, Opt. Mater. Express, 2012, 2, 161–172 CrossRef CAS.
- A. N. Hidayah, D. Triyono, Y. Herbani, Isnaeni and M. M. Suliyanti, J. Phys.: Conf. Ser., 2019, 1245, 012064 CrossRef CAS.
- A. Bansal, J. S. Sekhon and S. Verma, J. Mod. Opt., 2015, 62, 1665–1673 CrossRef CAS.
- Y. Tian, G. Li, H. Zhang, L. Xu, A. Jiao, F. Chen and M. Chen, Opt. Express, 2018, 26, 23347–23358 CrossRef CAS.
- N. Zhang, S. Ning, K. Dai, Y. Zhang, Y. Wu, F. Yuan and F. Zhang, Opt. Mater. Express, 2020, 10, 1204–1214 CrossRef CAS.
- Y. Ni, C. Kan, L. He, X. Zhu, M. Jiang and D. Shi, Photonics Res., 2019, 7, 558–565 CrossRef CAS.
- D. Rioux, S. Vallières, S. Besner, P. Muñoz, E. Mazur and M. Meunier, Adv. Opt. Mater., 2014, 2, 176–182 CrossRef.
| This journal is © the Owner Societies 2021 |