Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Surface contacts strongly influence the elasticity and thermal conductivity of silica nanoparticle fibers†
Yu
Cang
ab,
Bohai
Liu‡
c,
Sudatta
Das‡
b,
Xiangfan
Xu
 c,
Jingli
Xie
d,
Xu
Deng
c,
Jingli
Xie
d,
Xu
Deng
 d and
George
Fytas
d and
George
Fytas
 *b
*b
aSchool of Aerospace Engineering and Applied Mechanics, Tongji University, 100 Zhangwu Road, 200092, Shanghai, China
bMax Planck Institute for Polymer Research, Ackermannweg 10, 55128, Mainz, Germany. E-mail: fytas@mpip-mainz.mpg.de
cCenter for Phononics and Thermal Energy Science, School of Physical Science and Engineering, Tongji University, Shanghai, 200092, China
dInstitute of Fundamental and Frontier Sciences, University of Electronic Science and Technology of China, Chengdu, 610054, China
First published on 10th December 2020
Abstract
Granular materials are often encountered in science and engineering disciplines, in which controlling the particle contacts is one of the critical issues for the design, engineering, and utilization of their desired properties. The achievable rapid fabrication of nanoparticles with tunable physical and chemical properties facilitates tailoring the macroscopic properties of particle assemblies through contacts at the nanoscale. Models have been developed to predict the mechanical properties of macroscopic granular materials; however, their predicted power in the case of nanoparticle assemblies is still uncertain. Here, we investigate the influence of nanocontacts on the elasticity and thermal conductivity of a granular fiber comprised of close-packed silica nanoparticles. A complete elastic moduli characterization was realized by non-contact and non-destructive Brillouin light spectroscopy, which also allowed resolving the stiffness of the constituent particles in situ. In the framework of effective medium models, the strong enhancement of the elastic moduli is attributed to the formation of adhesive nanocontacts with physical and/or chemical bondings. The nanoparticle contacts are also responsible for the increase in the fiber thermal conductivity that emphasizes the role of interface thermal resistance, which tends to be ignored in most porosity models. This insight into the fundamental understanding of structure–property relationships advances knowledge on the manipulation of granular systems at the nanoscale.
Introduction
In the last three decades, much research effort has focused on the synthesis of metallic and non-metallic nanoparticles (NPs) with controlled chemistry, size, shape, and composition driven by their intriguing quantized behavior like that of atoms.1 This enormous progress has boosted new research on the assembly of these NPs into hierarchical-architectured materials. Their unanticipated novel properties and consequently a plethora of applications have stimulated further research efforts in this large field of nanomaterials.2–4 More recently, free-standing assemblies have been fabricated to eliminate unwanted interactions with solder substrates leading to radiation damage or kinetically trapped non-equilibrium structures. Nanoparticle assemblies can find numerous applications in acoustic, optoelectronics, and thermoelectric devices.2,4–6 For the realization of these technological applications, an understanding of the phononic properties is of equal importance. The propagation of phonons not only yields the elasticity, which is important for stability, but also allows the characterization of the interparticle contacts, which enhance heat conduction and the rigidity of colloid-based structures. Coherent phonons can be either injected by an optical pump pulse in picosecond acoustic techniques5,7 or probed by spontaneous Brillouin light spectroscopy (BLS).8–10 The latter is a non-destructive technique that can resolve both propagated phonons with the wave vector and polarization resolution and localized phonons associated with the colloid elastic vibrations.11–13 The concurrent access to effective medium phonons and particle vibrations enables independent monitoring of the film and the constituent component elasticity.Among different colloidal NP assembly shapes, uniform macroscale colloidal fibers have been reported with wide application perspectives, such as the fabrication of microchannels14 and photonic devices,15 due to the excellent controllability of their morphology and periodicity. Recently, harnessing crack engineering, a unique strategy was developed to fabricate transparent centimeter-scale fibers without a template.16 The fiber dimensions could be controlled simply by tuning the physical parameters, such as solvent composition, suspension descending rate, and NP volume fraction, and its large-scale production has shown great promise in practical applications. For instance, the fibers can be utilized as a platform of Ag-coated nanostructured surfaces exhibiting considerably higher sensitivity for probing small molecules compared to a typical smooth silicon wafer in the surface-enhanced Raman scattering detection. To realize broad applications, exploring the fundamental properties and understanding their relationships with the structure is an important requisite. It was found that the mechanical stiffness of NP-assembled fibers could be reinforced by thermal annealing without significantly altering the nanostructure; however, the physics behind these strong enhancements was not discussed.16 Also other properties, such as thermal conductivity, which is important in practical applications, have not been examined either.
In this work, we address these questions by investigating the complete elasticities and thermal conductivity of free-standing fibers comprised of SiO2 NPs for different annealing durations combined with complementary continuum mechanical and heat transport analysis. To achieve this, we performed non-contact elastic characterizations on silica fibers and their constituent particles via Brillouin light spectroscopy (BLS). The experimental data were interpreted by effective medium models, thus enabling an assessment of the roles of the nanocontacts and the adhesion processes in different annealing times. Moreover, we measured the thermal conductivity of the silica fibers using a T-bridge method, in which the increase with annealing time was well represented by a contact radius-controlled heat conduction path.
Results and discussion
Preparation of the silica fibers
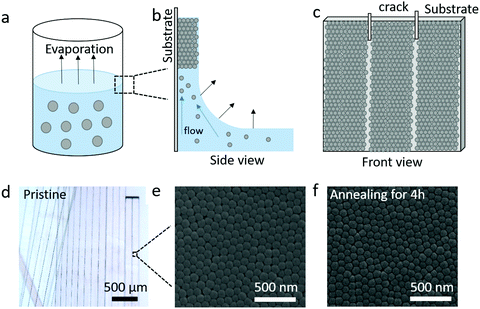
The silica (SiO2) fibers were prepared from the controlled crack formation, as illustrated in Fig. 1a–c.16 Here, as the solvent (water/ethanol) of SiO2 NPs (diameter d = 95 ± 7 nm) colloidal suspension evaporates between 323 and 363 K (Fig. 1a), their self-assembly into a wet colloidal film on the vial's wall (substrate) is driven by the capillary and Marangoni flows (Fig. 1b). Meanwhile, cracks are formed in the wet film and propagate vertically downwards. A centimeter-scale fiber consisting of self-assembled NPs is formed between two adjacent cracks as the evaporation process is completed, as shown in Fig. 1c. The shape of the pristine (without annealing) silica fibers and its nanostructure of the surface were determined here by optical (Fig. 1d) and scanning electron microscopy (SEM) (Fig. 1e). In order to further improve the mechanical stiffness, the pristine fibers were placed under thermal treatment at T = 1173 K for different annealing times (0.5, 2, and 4 h). The corresponding SEM images shown in Fig. 1f and Fig. S1 (ESI†) indicate that the nanostructures after annealing were almost identical to the pristine state. The samples coded as F-annealing time are listed in Table 1 along with structural and physical parameters of the fibers and the constituent NPs.| Sample code | Annealing durationa (hour) | Density of fibers, ρ (kg m−3) | Core–core distance, dc (nm) | Diameter of SiO2 NPs, d (nm) | Porosityb, p (%) | Refractive index, n | Density of SiO2 NPsc, ρNP (kg m−3) | Adhesion energyd, W (J m−2) |
|---|---|---|---|---|---|---|---|---|
| a Annealing at T = 1173 K. b Porosity p = ρ/ρNP. c Estimated from the density-dependent modulus in Fig. 3. d W is calculated eqn (3) assuming A = 16. | ||||||||
| F-0 | 0 | 1273 ± 107 | 89 ± 10 | 95 ± 7 | 0.33 | 1.32 | 1900 | 0.14 |
| F-05 | 0.5 | 1602 ± 119 | 85 ± 7 | 90 ± 4 | 0.26 | 1.34 | 2200 | 0.39 |
| F-2 | 2 | 1639 ± 77 | 80 ± 8 | 90 ± 4 | 0.24 | 1.33 | 2200 | 1.42 |
| F-4 | 4 | 1683 ± 156 | 77 ± 6 | 90 ± 4 | 0.22 | 1.34 | 2200 | 3.17 |
Complete elasticity of the silica fibers and their constituent nanoparticles
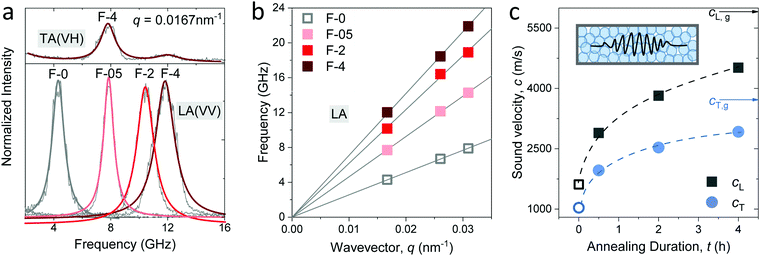
For a transparent sample, BLS measures the sound velocities of both longitudinal (LA) and transverse (TA) acoustic phonons at hypersonic frequency (GHz), and hence can uniquely determine the complete material elasticities if the sample density is known. The sound velocity of the LA phonon is detectable in a polarized (VV) BLS spectrum, where VV denotes vertical polarization of both the incident (ki) and scattered (ks) lights relative to the scattering plane (ki,ks). Fig. 2a exemplifies the VV BLS spectra (anti-Stokes side, grey lines) of the pristine and three annealed silica fibers recorded in the transmission scattering geometry at a phonon wavevector q = 0.0167 nm−1 and T = 294 K. At the transmission scattering geometry illustrated in Fig. S2 and Section 1.2 in ESI,† the phonon wavevector q is parallel to the film plane and its magnitude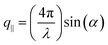 , with λ = 532 nm being the wavelength of the incident light, which is independent of the materials’ refractive index; i.e., q = 0.0167 nm−1 for an incident angle α = 45°. The VV BLS spectra for all fibers in Fig. 2a are well represented by single Lorentzian lineshapes (red lines) yielding the frequencies f of LA phonons at q = 0.0167 nm−1. The linear acoustic dispersions f(q) of LA phonons are shown in Fig. 2b, where q*s (>0.024 nm−1) directed normal to the film plane were achieved in the reflection and backscattering geometries (Fig. S2 and Section 1.2 in ESI†), respectively. The magnitude of this out-of-plane
, with λ = 532 nm being the wavelength of the incident light, which is independent of the materials’ refractive index; i.e., q = 0.0167 nm−1 for an incident angle α = 45°. The VV BLS spectra for all fibers in Fig. 2a are well represented by single Lorentzian lineshapes (red lines) yielding the frequencies f of LA phonons at q = 0.0167 nm−1. The linear acoustic dispersions f(q) of LA phonons are shown in Fig. 2b, where q*s (>0.024 nm−1) directed normal to the film plane were achieved in the reflection and backscattering geometries (Fig. S2 and Section 1.2 in ESI†), respectively. The magnitude of this out-of-plane 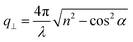 now depends on the fiber refractive index, n. Assuming elastic isotropy, f = cq/2π is linear throughout q's range yielding n = 1.33 ± 0.02 which is, within error, the same for all the samples. The corresponding longitudinal sound velocity cL(= 2πf/q) for different annealing durations is shown in Fig. 2c (black squares).
now depends on the fiber refractive index, n. Assuming elastic isotropy, f = cq/2π is linear throughout q's range yielding n = 1.33 ± 0.02 which is, within error, the same for all the samples. The corresponding longitudinal sound velocity cL(= 2πf/q) for different annealing durations is shown in Fig. 2c (black squares).
Access to the sound velocity of transverse acoustic (TA) phonon, cT, is necessary to calculate the shear and hence Young's modulus. This is feasible if the depolarized (VH) BLS spectra are sufficiently strong to be recorded; VH denotes the vertical and parallel polarizations of the incident and scattered lights relative to the (ki,ks) plane, respectively. The top panel in Fig. 2a displays the VH spectrum (grey line) of F-4 at q = 0.0167 nm−1 along with its representation (red line) by two Lorentzians. The low-frequency strong peak was assigned to the TA phonon, whereas the weaker peak at a higher frequency is the LA phonon in the VV spectrum due to the scrambling of the scattered light polarization. The transverse sound velocity cT (= 2πf/q) in the four fibers is shown in Fig. 2c (blue circles).
The sound velocities shown in Fig. 2c represent the effective medium values in the fibers consisting of randomly close-packed SiO2 NPs. Both cL and cT increased abruptly by about 85% from the pristine (F-0, open symbols) to the fiber annealed for a short time (F-05) and a reduced increase to about 50% with prolonged annealing to 4 h (F-4). Note that even for the longest annealed F-4 sample, both cL and cT remained ∼22% less than the corresponding values of typical amorphous glass (arrows in Fig. 2c). An increase in the effective medium sound velocities can, in principle, arise from denser packing (decreasing porosity), densification of the SiO2 NPs, and/or due to the increasing adhesion forces between NPs. The increase in the fiber density by 25% from F-0 to F-05 and only by 5% from F-05 to F-4 was clearly lower than the corresponding increase in the sound velocities, suggesting that packing alone cannot account for the higher sound velocities (hardening) of the fibers upon annealing. Prior to the discussion of the elastic moduli of the fibers and understanding the origin of its elastic enhancements, knowledge of the elastic properties of the constituent silica NPs is a prerequisite. Experimental access to the elasticity of NPs and their assembled structure simultaneously by BLS is, for the first time, reported in the granular materials.5,7,17,18
It is well established that NPs exhibit vibrations, in analogy to the electron motion in atoms. For non-interacting spheres, the resolved lowest-frequency mode by BLS can be assigned to the quadrupole (1,2) vibration, where 1 and 2 denote the radial and angular momentum, respectively.13,19 This is a resonance localized mode and hence f(1,2) is q-independent. For isolated NPs, the (1,2) mode should be a single symmetric peak at f(1,2) = A(νNP) cT,NP/d, where cT,NP denotes the transverse sound velocity of the NP with diameter d and A is a dimensionless constant depending on the NP's Poisson's ratio, νNP.19 Here, f(1,2) is much higher than the frequencies of the LA and TA phonons at the probed q's of BLS (Fig. 2c). Fig. 3a shows this high-frequency (1,2) mode in the VV BLS spectra (grey lines) of F-0 and F-4 recorded at the backscattering geometry. Due to the d−1 dependence, the size polydispersity leads to a broadening of the (1,2) peaks.20 The (1,2) mode of both F-0 and F-4 was not single and hence is represented (blue lines) by two Lorentzian lines (red lines) centered at the frequencies f1 and f2(>f1). The splitting of the (1,2) mode, resulting from interactions between two NPs,13,21 suggests the presence of surface contacts and adhesion between SiO2 NPs, which was much more pronounced for F-4. The effect of interaction can be accounted for by computing f(1,2) = 2f1 − f2 which is utilized to compute cT,NP (= f(1,2)d/A) using A = 0.84.22,23
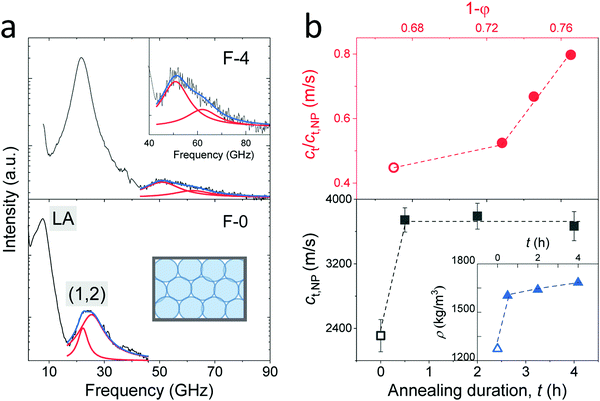 | ||
| Fig. 3 (a) Polarized BLS spectra of the F-0 (low panel) and F-4 (upper panel) fibers recorded at the backscattering geometry. The resolved modes are assigned to LA phonon for the fibers and quadrupole mode (1,2) for the SiO2 NPs as indicated in the plot. The (1,2) mode is represented (blue lines) by a double Lorentzian (red lines) shapes. A zoom-in of the vibration spectrum in F-4 is shown in the inset to the upper panel. (b) Low panel: The transverse sound velocity of SiO2 NPs (cT,NP) vs. annealing duration, t, where the density of the fibers (Table 1) is presented in the inset. Upper panel: Normalized transverse sound velocity of the fibers, cT/cT,NP, as a function of NP volume fraction, 1 − p, with p being the porosity (Table 1). For the pristine fibers, the physical quantities are denoted by empty symbols in (b). | ||
The computed transverse sound velocities of the SiO2 NPs, cT,NP, shown in the lower panel of Fig. 3b strongly increased (by 65%) with annealing from 0 to 0.5 h, but became virtually constant with prolonged annealing. For the pristine SiO2 NPs in F-0, cT,NP = 2310 ± 50 m s−1 was slightly lower than the cT,NP = 2390 m s−1 of the NPs with ρ = 1960 kg m−3.23 Since cT,NP mainly depends on the NPs’ density, we assigned ρ = 1900 kg m−3 to the pristine SiO2 NPs in F-0 based on the density-dependence of the modulus;23 whereby this density value is in good agreement with the literature values of Stöber silica NPs.24 For the SiO2 NPs in the three annealed fibers, the virtually constant cT,NP = 3720 ± 50 m s−1 reached the cT,bulk = 3740 m s−1 of bulk fused silica with the density ρ = 2200 kg m−3.23,25 The fiber density was found to display a similar behavior with annealing as depicted in the inset in the lower panel of Fig. 3b. Building on this data consistency, the upper panel of Fig. 3b depicts the variation of the normalized transverse sound velocity in the silica fiber, cT/cT,NP, with the particle volume fraction (1 − p). Interestingly, this ratio was not constant but a stronger increase was observed with the annealing duration, indicating a strengthening of the cohesive forces between SiO2 NPs, as will be discussed for the elasticity moduli next.
Access to both cT and cL in the silica fibers allows an estimation of their complete effective elastic moduli, including Young's (E), shear (G), and bulk (K) moduli. The G = ρcT2, E = 2G(1 + ν) and Poisson's ratio 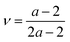 with
with 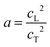 are shown in Fig. 4a. The trend of the fiber elasticities (E and G) with annealing was clearly distinct from the GNP of the constituent SiO2 NPs (Fig. 3b); whereby the former significantly increased with annealing time, whereas the latter was virtually constant. Hence additional effects should become important for the observed enhanced elasticity of the fibers in the annealing regime (0.5–4 h). For the Poisson's ratio of fiber ν, it dropped from 0.16 (F-0) to 0.08 in F-05 and then increased toward the bulk value (v = 0.17) with prolonging the annealing time.
are shown in Fig. 4a. The trend of the fiber elasticities (E and G) with annealing was clearly distinct from the GNP of the constituent SiO2 NPs (Fig. 3b); whereby the former significantly increased with annealing time, whereas the latter was virtually constant. Hence additional effects should become important for the observed enhanced elasticity of the fibers in the annealing regime (0.5–4 h). For the Poisson's ratio of fiber ν, it dropped from 0.16 (F-0) to 0.08 in F-05 and then increased toward the bulk value (v = 0.17) with prolonging the annealing time.
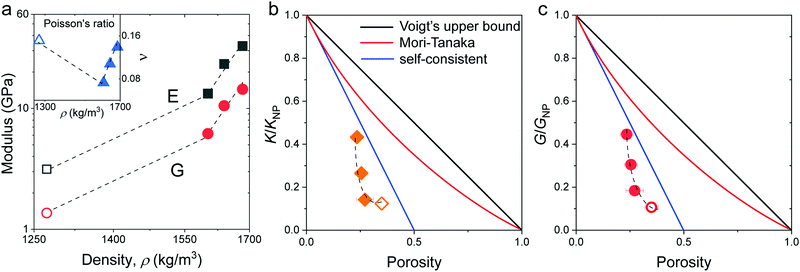 | ||
| Fig. 4 (a) Young's (E, black squares) and shear (G, red circles) moduli as a function of density for the four silica fibers. Inset: Poisson's ratio ν vs. fiber density. Normalized to that of the constituent SiO2 particles, K/KNP in (b) and G/GNP in (c), plotted as a function of the porosity. The color lines denote different model predictions: Voigt's upper bound (black), Mori-Tanaka (red), and self-consistent (green) models (Section 2.1 in ESI†). The dashed lines are guided to the eye. All open symbols refer to the pristine F-0. | ||
Surface contacts
To shed light on the origin of the elasticity enhancement, we employed different continuum mechanics models for the interpretation of the experimental moduli of the silica fibers. First, we utilized the representative elementary volume (REV) models proposed for porous materials with a random packing of NPs (Section 2.1 in ESI†). The simple linear mixing rule for the effective Young's modulus, E = (1 − p)ENP, (Voigt's upper bound) assumes a similar deformation of holes and NPs. Two additional approaches, Mori–Tanaka's26 and self-consistent approximation,27 take into account the shape and percolation of pores, yielding reliable predictions for some porous structures.28 However, all these REV models cannot quantitatively represent the experimental data shown in Fig. 4b and c, whereby the normalized moduli K/KNP and G/GNP of the fibers increase much stronger with porosity than the theoretical prediction made by different REV models. It should be noted that all REV models envisage the NPs as a homogenous matrix and ignore mutual interactions. The latter, however, have been found to play a decisive role in the effective properties, especially in the close packing structures as shown next.In the framework of effective medium theory, the effective elastic moduli of disordered granular systems with identical particles of diameter d can be related to the normal (kn) and tangential (ks) contact stiffness between NPs.29,30 Accordingly, kn and ks are given by
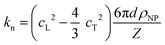 | (1a) |
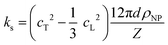 | (1b) |
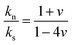 (eqn (1)) is controlled by the fiber Poisson's ratio v (Fig. 4a) and varied in the range of 1.5–3 (top panel of Fig. 5b). Note, the SiO2 NP's contact interactions impact the experimental sound velocities but are not explicitly presented in eqn (1).
(eqn (1)) is controlled by the fiber Poisson's ratio v (Fig. 4a) and varied in the range of 1.5–3 (top panel of Fig. 5b). Note, the SiO2 NP's contact interactions impact the experimental sound velocities but are not explicitly presented in eqn (1).
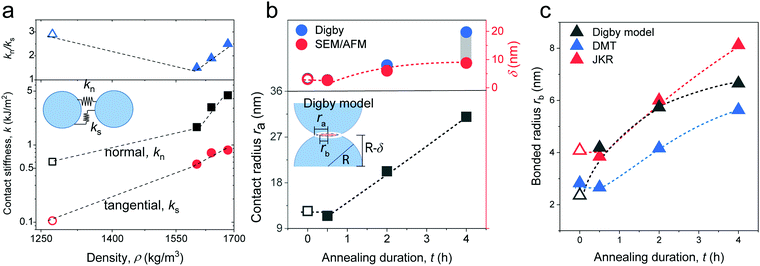 | ||
| Fig. 5 (a) Normal (kn) (black squares) and tangential (ks) (red circles) stiffness computed from (eqn (1)) as a function of density. The ratio kn/ks is shown in the upper panel along with a schematic illustration of kn and ks as the inset. (b) Contact radius ra (black squares) and indentation of a particle δ (blue circles) estimated from the Digby model and experimental δ (red circles) as a function of annealing duration. Inset: Schematic of the NP contact geometry in the Digby model. (c) Bonded radius rb computed from the Digby, JKR,42 and DMT46 models as a function of the annealing duration. All dashed lines are guides for the eye and open symbols refer to the pristine F-0. | ||
Several microstructural continuum models have quantitatively addressed the relation of the contact stiffness to the micro-deformation at the interface.29,32,33 Digby proposed a phenomenological description29 of kn and ks for smooth particles with the contact radius ra, and an initially bonded area of radius rb (see scheme in the inset to Fig. 5b) as a function of the constituent NP elasticity:
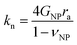 | (2a) |
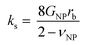 | (2b) |
Since cohesive forces can be introduced in the annealing process, we utilized the Digby model for a rationalization of the computed contact radii. Fig. 5b shows the variation of the contact radius, ra, estimated from eqn (1a) and (2a) for the silica fibers with the annealing time. For F-0, the value ra = 12 nm remained virtually unchanged after the initial annealing for 0.5 h and then largely increased to 31 nm as the annealing time was extended to 4 h. According to eqn (1a) and (2a), ra ∼ kn/GNP ∼ K/KNP and hence the similar K/KNP and ra values for F-0 and F-05 (Fig. 4b) implied that the enhanced KNP, due to a densification of the particles in F-05, could account for the increase in K. For longer annealing, the increase in ra could be ascribed to the adhesion processes, such as cementation and consolidation. This could be directly evidenced by the decrease in the mutual approach of two NPs’ centers, δ, schematically shown in Fig. 5b.
The parameter δ = (d − dc)/2 helps assess the role of NP adhesion on the increase of ra in F-2 and F-4. Experimentally, the intercore distance, dc, (Table 1) and the diameter of the constituent SiO2 NPs, d, were determined from the SEM images of the silica fibers and NP powders in Fig. S1 (ESI†), respectively. In the Digby model, 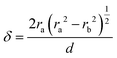 was related to the contact radius, ra, and bonded radius, rb, which were computed from eqn (2). Fig. 5b depicts the experimental and computed δ for the silica fibers. While the approximately similar δ in the pristine F-0 and F-05 excluded cementation, the augmented δ for F-2 was an indication of a cementation effect with prolonged annealing. The computed (blue symbols) δ values capture the experimental (red circles) values for the silica fibers in Fig. 5b (upper panel) except for F-4.
was related to the contact radius, ra, and bonded radius, rb, which were computed from eqn (2). Fig. 5b depicts the experimental and computed δ for the silica fibers. While the approximately similar δ in the pristine F-0 and F-05 excluded cementation, the augmented δ for F-2 was an indication of a cementation effect with prolonged annealing. The computed (blue symbols) δ values capture the experimental (red circles) values for the silica fibers in Fig. 5b (upper panel) except for F-4.
A subtle cementation increase could play a significant role in the growth of the contact grain radius, ra,ce, according to the equation, 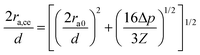 proposed by Dvokin et al.,35–38 where the porosity decrease Δp is a consequence of the cementation and ra0 is the initial contact radius (Δp = 0). This relation allows weighting the cementation effect on ra in F-2 and F-4 via the comparison between ra and ra,ce. Assuming a decrease Δp = 0.03(0.05) for F-2(F-4) relative to F-05 with ra0 = 12 nm, the computed ra,ce = 21.6 nm is comparable to ra (= 20.3 nm) in F-2, indicating the domination of cementation. For F-4, however, there is a discrepancy between ra,ce = 23 nm, and ra (= 31 nm) along with an overestimated δ by the Digby model. In light of the covalent bonds between SiO2 NPs at high temperature,39 the strong adhesive force of chemical bonding may be responsible for the high ra in F-4.
proposed by Dvokin et al.,35–38 where the porosity decrease Δp is a consequence of the cementation and ra0 is the initial contact radius (Δp = 0). This relation allows weighting the cementation effect on ra in F-2 and F-4 via the comparison between ra and ra,ce. Assuming a decrease Δp = 0.03(0.05) for F-2(F-4) relative to F-05 with ra0 = 12 nm, the computed ra,ce = 21.6 nm is comparable to ra (= 20.3 nm) in F-2, indicating the domination of cementation. For F-4, however, there is a discrepancy between ra,ce = 23 nm, and ra (= 31 nm) along with an overestimated δ by the Digby model. In light of the covalent bonds between SiO2 NPs at high temperature,39 the strong adhesive force of chemical bonding may be responsible for the high ra in F-4.
In the Digby model, the strong interparticle adhesion is expressed in terms of the bonded area with radius rb (eqn (2b)), which monotonically increased with the annealing time, as shown in Fig. 5c. The adhesion energy W, defining the work of detaching two interfaces, can be estimated from the fiber's Young's modulus, E, according to Kendall's relation:40–42
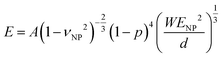 | (3) |
The adhesion energy W relates to the bonded radius rb, which has been taken into account in contact models such as the Derjaguin–Muller–Toporov (DMT)46 and Johnson–Kendall–Roberts (JKR) models:40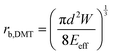 and
and 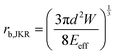 where
where 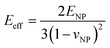 for identical contacted particles. The JKR model was proposed for soft and compliant particles with strong adhesion versus the DMT model, which is suggested for rigid systems with low adhesion: rb,JKR > rb,DMT for the same contacts. The bonded rb values from the DMT and JKR models for the four silica fibers are shown in Fig. 5c along with the rb values from Digby's model. For pristine F-0, rb = 2.4 nm is similar to rb,DMT (= 2.8 nm), whereas for F-05, rb = 4.2 nm conformed to rb,JKR (= 4.1 nm). This crossover of rb from hard DMT to soft JKR contacts could result from the softening of the annealed SiO2 NPs (at high temperature). For F-2, rb ≈ rb,JKR (= 6 nm) increased well above the value for F-05, mainly because of the newly formed covalent bonds between the NPs, which increased W (Table 1). The chemical nature of the binding molecules on connected nanoparticles plays a crucial role in the elasticities of colloidal films.7 As compared to the physical bonding (i.e., van der Waals forces), the much stronger chemical bonds (e.g., covalent and hydrogen bonding) have a greater impact with their increasing fraction with annealing time on the fiber elasticity (F-4). For F-4 with the largest adhesion energy W among the four silica fibers, a discrepancy between rb (= 6.6 nm) and rb,JKR (= 8.6 nm) was observed. We recall the overestimated particle normal displacement, δ, and the contact radius, ra, for the same sample F-4 (Fig. 5b), which revealed the failure of Digby's model to represent systems with a relatively large adhesion (e.g., F-4). In fact, ra includes the contribution from rb at a high W since K (∼kn ∼ ra), the elastic response of a material to uniform compression, is no longer insensitive to the stiffening caused by adhesion forces over a large area with radius rb.47
for identical contacted particles. The JKR model was proposed for soft and compliant particles with strong adhesion versus the DMT model, which is suggested for rigid systems with low adhesion: rb,JKR > rb,DMT for the same contacts. The bonded rb values from the DMT and JKR models for the four silica fibers are shown in Fig. 5c along with the rb values from Digby's model. For pristine F-0, rb = 2.4 nm is similar to rb,DMT (= 2.8 nm), whereas for F-05, rb = 4.2 nm conformed to rb,JKR (= 4.1 nm). This crossover of rb from hard DMT to soft JKR contacts could result from the softening of the annealed SiO2 NPs (at high temperature). For F-2, rb ≈ rb,JKR (= 6 nm) increased well above the value for F-05, mainly because of the newly formed covalent bonds between the NPs, which increased W (Table 1). The chemical nature of the binding molecules on connected nanoparticles plays a crucial role in the elasticities of colloidal films.7 As compared to the physical bonding (i.e., van der Waals forces), the much stronger chemical bonds (e.g., covalent and hydrogen bonding) have a greater impact with their increasing fraction with annealing time on the fiber elasticity (F-4). For F-4 with the largest adhesion energy W among the four silica fibers, a discrepancy between rb (= 6.6 nm) and rb,JKR (= 8.6 nm) was observed. We recall the overestimated particle normal displacement, δ, and the contact radius, ra, for the same sample F-4 (Fig. 5b), which revealed the failure of Digby's model to represent systems with a relatively large adhesion (e.g., F-4). In fact, ra includes the contribution from rb at a high W since K (∼kn ∼ ra), the elastic response of a material to uniform compression, is no longer insensitive to the stiffening caused by adhesion forces over a large area with radius rb.47
Summing up this section, an enhanced elasticity in the annealed fibers is favored by different processes, which include densification, cementation, and the formation of covalent bonds, and their relative contribution depends on the annealing time. The rapid densification process is responsible for the elastic enhancements in a short annealing time (F-05). On the other hand, the cementation and condensation reaction (covalent bonds) processes occur after long-time annealing, and these determined the elastic enhancement in F-2 and F-4. The cementation controlled the K in F-2, and K was further enhanced by the formation of covalent bonds in the case of F-4. A large elasticity usually accompanies a high thermal conductivity κ, which is important for materials applications.48 To gain insights into the thermal-elastic properties of fibers with distinct interfacial adhesion, we next examine κ at different annealing times.
Thermal conductivity
The thermal conductivity κ (red circles) of the silica fibers measured by the T-bridge method49–51 is shown in Fig. 6a as a function of the fiber density. The pristine F-0 (open red circle) had κ = 0.14 ± 0.06 W m−1 K−1, which is about one magnitude lower than the bulk value (= 1.4 W m−1 K−1) of fused silica. As the fiber density increased (porosity decreased) with annealing time, κ significantly increased and reached 1.24 ± 0.23 W m−1 K−1 in F-4. Effective medium models that are usually applied to represent the thermal conductivity of porous materials are based on approximations of coherent potential (CP) and porosity weight medium (PWDM),52–54 which take into account the effect of a pore's shape and/or size (Section 2.2 in ESI†). It should be noted that these effective medium models for thermal conductivity are typically empirical and quasi-physical. Based on the inset in Fig. 5a, both models could not represent the strong increase of κ with decreasing porosity. Notably, all these effective medium models ignored the interfacial thermal resistance, which is related to the fraction of the interparticle conduction path Cs.55 As the interfacial contacts were found to greatly impact the speed of sound in all four fibers (Section 2.3), the contribution of Cs to κ should be considered. For particles in contact, Cs = 2ra/d and the computed κ = CsκNP55 (black square) assuming a bulk κNP = 1.4 W m−1 K−1 for the SiO2 NPs, as shown in Fig. 6a. A good agreement between the computed and experimental κ values was observed for the three annealed fibers, corroborating the notion of a contact-induced enhancement of heat transport. For F-0, the interfacial contacts led to an overestimation of the κ probably due to the overestimated (by 120%) κNP (= κbulk) due to its more porous SiO2 NPs. In fact, for the pristine F-0, the SiO2 NPs were observed to be much softer as compared to the bulk silica (Fig. 3b). Note that the thermal conductivity depended on ra/d (∼Cs) and thereby its size dependence resembled that of the elastic modulus, E (eqn (3)).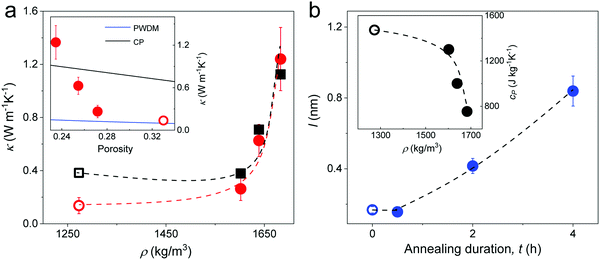 | ||
| Fig. 6 (a) Experimental (red circles) thermal conductivity κ, and computed κ = CsκNP (black squares) of silica fibers as a function of density. Inset: κ vs. porosity along with two effective medium approximations, CP and PWDM (Section 2.2 in ESI†). (b) The computed mean free path l in the fibers at different annealing time. Inset: Specific heat capacity obtained from DSC as a function of fiber density. All the dashed lines are guided to the eye and all open symbols refer to pristine F-0. | ||
According to the kinetic theory, thermal conductivity is related to the elasticity by 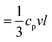 , where cp is the specific heat capacity, v = (cL + 2cT)/3 and is the average sound velocity, and l is the mean free path, respectively. The experimental cp, determined from differential scanning calorimetry (DSC) is shown in the inset of Fig. 6b, whereas the computed l values in the four fibers are shown in Fig. 6b. The somewhat counterintuitive decrease in cp in the three annealed fibers was attributed to the reduction of the surface dangling hydroxyl groups (OH) of the SiO2 NPs.56 The latter were transformed into covalent siloxane bonds due to the condensation reactions at high temperatures. Since the cp = 733 J kg−1 K−1 of F-4 reached the bulk value of silica (= 754 J kg−1 K−1), the OH groups should be completely consumed after 4 h annealing. The computed l qualitatively resembled the dependence of ra on the annealing time (Fig. 5b). For F-0 and F-05, l = 0.2 nm seemed to be insensitive to the densification of both the SiO2 NPs and fibers (Table 1). With enlarged contact grains and an enhanced adhesive force, the computed l was significantly increased to 0.4 nm (0.85 nm) for F-2 (F-4). Notably, for F-4, the phonon mean free path became very similar to the value l (= 0.8 nm) for bulk silica.57 Therefore, the interfacial properties dominated the thermal conductivity of the fibers κ prepared with a long annealing time (F-2 and F-4), while the bulk κNP of the SiO2 nanoparticles controlled the κ for the short annealing time (F-05).
, where cp is the specific heat capacity, v = (cL + 2cT)/3 and is the average sound velocity, and l is the mean free path, respectively. The experimental cp, determined from differential scanning calorimetry (DSC) is shown in the inset of Fig. 6b, whereas the computed l values in the four fibers are shown in Fig. 6b. The somewhat counterintuitive decrease in cp in the three annealed fibers was attributed to the reduction of the surface dangling hydroxyl groups (OH) of the SiO2 NPs.56 The latter were transformed into covalent siloxane bonds due to the condensation reactions at high temperatures. Since the cp = 733 J kg−1 K−1 of F-4 reached the bulk value of silica (= 754 J kg−1 K−1), the OH groups should be completely consumed after 4 h annealing. The computed l qualitatively resembled the dependence of ra on the annealing time (Fig. 5b). For F-0 and F-05, l = 0.2 nm seemed to be insensitive to the densification of both the SiO2 NPs and fibers (Table 1). With enlarged contact grains and an enhanced adhesive force, the computed l was significantly increased to 0.4 nm (0.85 nm) for F-2 (F-4). Notably, for F-4, the phonon mean free path became very similar to the value l (= 0.8 nm) for bulk silica.57 Therefore, the interfacial properties dominated the thermal conductivity of the fibers κ prepared with a long annealing time (F-2 and F-4), while the bulk κNP of the SiO2 nanoparticles controlled the κ for the short annealing time (F-05).
Conclusions
We utilized Brillouin light spectroscopy to obtain the full isotropic elasticities of disordered granular silica fibers fabricated via crack engineering, and the in situ the shear modulus of the constituent nanoparticles at different thermal annealing circles. The BLS study was complemented by thermal conductivity measurements of the same fibers. Our data analysis allowed identifying the contributions of the adhesion processes to both the elastic stiffness and thermal conductivity of silica fibers. Under the framework of the Digby, cemented, and DMT/JKR theoretical models, the contact radius was revealed to control the elastic enhancement. However, the underlined mechanisms affecting the size and impact of the contact radius depended on the annealing time. With a short annealing time (0.5 h), the contacts between the particles barely changed compared to the pristine fiber and the properties of the fibers relied on their constituent NPs. Tiny cementation occurred after prolonged annealing (2 h), leading to a significant increase in the contacts and a pronounced enhancement of the elasticity. However, at a relatively long annealing time (4 h), the cementation effect alone could not account for the sustained strong elasticity enhancement. Instead the adhesive force between the nanoparticles was strengthened by additional contributions from the emerging covalent bonds due to condensation reactions. Surface contact effects were manifested in the thermal conductivity of the same fibers through the interface thermal resistance. The relation between the contacts and heat transport was collaborated by the computed phonon mean free path, which exhibited a large increase as the number of contacts grew.Conflicts of interest
There are no conflicts to declare.Acknowledgements
B. L. thanks the financial support from the program of China Scholarships Council (No. 201906260224). G. F. acknowledge the financial support by ERC AdG SmartPhon (Grant No. 694977) and the support by the High-Level Foreign Expert Program of Tongji University. Y. C. acknowledge the financial support by Shanghai Pujiang Program (Grant No. 20PJ1413800). Open Access funding provided by the Max Planck Society.Notes and references
- M. A. Kastner, Phys. Today, 1993, 46, 24 CrossRef CAS.
- Y. Liu, B. Fan, Q. Shi, D. Dong, S. Gong, B. Zhu, R. Fu, S. H. Thang and W. Cheng, ACS Nano, 2019, 13, 6760–6769 CrossRef CAS.
- K. E. Mueggenburg, X.-M. Lin, R. H. Goldsmith and H. M. Jaeger, Nat. Mater., 2007, 6, 656–660 CrossRef CAS.
- Q. Shi and W. Cheng, Adv. Funct. Mater., 2020, 30, 1902301 CrossRef CAS.
- C. L. Poyser, T. Czerniuk, A. Akimov, B. T. Diroll, E. A. Gaulding, A. S. Salasyuk, A. J. Kent, D. R. Yakovlev, M. Bayer and C. B. Murray, ACS Nano, 2016, 10, 1163–1169 CrossRef CAS.
- D. V. Talapin, J.-S. Lee, M. V. Kovalenko and E. V. Shevchenko, Chem. Rev., 2010, 110, 389–458 CrossRef CAS.
- A. Ayouch, X. Dieudonné, G. Vaudel, H. Piombini, K. Vallé, V. Gusev, P. Belleville and P. Ruello, ACS Nano, 2012, 6, 10614–10621 CrossRef CAS.
- E. Alonso-Redondo, M. Schmitt, Z. Urbach, C. Hui, R. Sainidou, P. Rembert, K. Matyjaszewski, M. Bockstaller and G. Fytas, Nat. Commun., 2015, 6(1), 8309 CrossRef CAS.
- E. Alonso-Redondo, L. Belliard, K. Rolle, B. Graczykowski, W. Tremel, B. Djafari-Rouhani and G. Fytas, Sci. Rep., 2018, 8, 16986 CrossRef CAS.
- B. Graczykowski, N. Vogel, K. Bley, H.-J. R. Butt and G. Fytas, Nano Lett., 2020, 20, 1883–1889 CrossRef CAS.
- W. Cheng, J. Wang, U. Jonas, G. Fytas and N. Stefanou, Nat. Mater., 2006, 5, 830–836 CrossRef CAS.
- M. Mattarelli, M. Montagna, T. Still, D. Schneider and G. Fytas, Soft Matter, 2012, 8, 4235–4243 RSC.
- H. Kim, Y. Cang, E. Kang, B. Graczykowski, M. Secchi, M. Montagna, R. D. Priestley, E. M. Furst and G. Fytas, Nat. Commun., 2018, 9, 2918 CrossRef.
- B. Li, B. Jiang, W. Han, M. He, X. Li, W. Wang, S. W. Hong, M. Byun, S. Lin and Z. Lin, Angew. Chem., Int. Ed., 2017, 56, 4554–4559 CrossRef CAS.
- O. Dalstein, E. Gkaniatsou, C. Sicard, O. Sel, H. Perrot, C. Serre, C. Boissière and M. Faustini, Angew. Chem., Int. Ed., 2017, 129, 14199–14203 CrossRef.
- J. Xie, J. Guo, D. Wang, Y. Cang, W. Zhang, J. Zhou, B. Peng, Y. Li, J. Cui, L. Chen, G. Fytas and X. Deng, Adv. Mater. Interfaces, 2020, 2000222 CrossRef.
- L. Saviot, S. Le Gallet, F. Demoisson, L. David, G. Sudre, A. Girard, J. Margueritat and A. Mermet, J. Phys. Chem. C, 2017, 121, 2487–2494 CrossRef CAS.
- A. Girard, J. Ramade, J. Margueritat, D. Machon, L. Saviot, F. Demoisson and A. Mermet, Nanoscale, 2018, 10, 2154–2161 RSC.
- T. Still, M. Mattarelli, D. Kiefer, G. Fytas and M. Montagna, J. Phys. Chem. Lett., 2010, 1, 2440–2444 CrossRef CAS.
- W. Cheng, J. Wang, U. Jonas, W. Steffen, G. Fytas, R. Penciu and E. Economou, J. Chem. Phys., 2005, 123, 121104 CrossRef CAS.
- E. Kang, H. Kim, L. A. Gray, D. Christie, U. Jonas, B. Graczykowski, E. M. Furst, R. D. Priestley and G. Fytas, Macromolecules, 2018, 51, 8522–8529 CrossRef CAS.
- H. Lamb, Proc. R. Soc. London, Ser. A, 1917, 93, 114–128 Search PubMed.
- H. Lim, M. Kuok, S. Ng and Z. Wang, Appl. Phys. Lett., 2004, 84, 4182–4184 CrossRef CAS.
- N. C. Bell, C. Minelli, J. Tompkins, M. M. Stevens and A. G. Shard, Langmuir, 2012, 28, 10860–10872 CrossRef CAS.
- D. B. Fraser, J. Appl. Phys., 1968, 39, 5868–5878 CrossRef CAS.
- T. Mori and K. Tanaka, Acta Metall., 1973, 21, 571–574 CrossRef.
- R. Hill, J. Mech. Phys. Solids, 1965, 13, 213–222 CrossRef.
- A. Lesaine, D. Bonamy, G. Gauthier, C. L. Rountree and V. Lazarus, Soft Matter, 2018, 14, 3987–3997 RSC.
- P. Digby, J. Appl. Mech., 1981, 48, 803–808 CrossRef.
- K. W. Winkler, Geophys. Res. Lett., 1983, 10, 1073–1076 CrossRef.
- R. M. German, Powder Technol., 2014, 253, 368–376 CrossRef CAS.
- K. L. Johnson and K. L. Johnson, Contact Mechanics, Cambridge university press, 1987 Search PubMed.
- A. Norris and D. Johnson, J. Appl. Mech., 1997, 64, 39–49 CrossRef.
- V. Langlois and X. Jia, Powder Technol., 2011, 208, 509–514 CrossRef CAS.
- J. Dvorkin, A. Nur and H. Yin, Mech. Mater., 1994, 18, 351–366 CrossRef.
- J. Dvorkin, Mech. Mater., 1996, 23, 29–44 CrossRef.
- J. Dvorkin and D. Yale, Comput. Geotechn., 1997, 20, 287–302 CrossRef.
- V. Langlois and X. Jia, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 023206 CrossRef CAS.
- L. Zhang, M. D'Acunzi, M. Kappl, A. Imhof, A. van Blaaderen, H.-J. Butt, R. Graf and D. Vollmer, Phys. Chem. Chem. Phys., 2010, 12, 15392–15398 RSC.
- K. L. Johnson, K. Kendall and A. Roberts, Proc. R. Soc. London, Ser. A, 1971, 324, 301–313 CAS.
- K. Kendall, N. M. Alford and J. D. Birchall, Proc. R. Soc. London, Ser. A, 1987, 412, 269–283 CAS.
- K. Kendall, Molecular Adhesion and Its Applications: The Sticky Universe, Springer Science & Business Media, 2007 Search PubMed.
- T. Rouxel, J. Am. Ceram. Soc., 2007, 90, 3019–3039 CrossRef CAS.
- C. J. Brinker and G. W. Scherer, Sol–Gel Science: The Physics and Chemistry of Sol–Gel Processing, Academic press, 2013 Search PubMed.
- L. Zhuravlev, Langmuir, 1987, 3, 316–318 CrossRef CAS.
- B. V. Derjaguin, V. M. Muller and Y. P. Toporov, J. Colloid Interface Sci., 1975, 53, 314–326 CrossRef CAS.
- Y. Cang, Z. Wang, C. Bishop, L. Yu, M. Ediger and G. Fytas, Adv. Funct. Mater., 2020, 30, 2001481 CrossRef CAS.
- Z. Wang, K. Rolle, T. Schilling, P. Hummel, A. Philipp, B. A. Kopera, A. M. Lechner, M. Retsch, J. Breu and G. Fytas, Angew. Chem., Int. Ed., 2020, 132, 1302–1310 CrossRef.
- M. Fujii, X. Zhang, H. Xie, H. Ago, K. Takahashi, T. Ikuta, H. Abe and T. Shimizu, Phys. Rev. Lett., 2005, 95, 065502 CrossRef.
- W. Jang, W. Bao, L. Jing, C. Lau and C. Dames, Appl. Phys. Lett., 2013, 103, 133102 CrossRef.
- J. Kim, D.-J. Seo, H. Park, H. Kim, H.-J. Choi and W. Kim, Rev. Sci. Instrum., 2017, 88, 054902 CrossRef.
- B.-Y. Tsui, C.-C. Yang and K.-L. Fang, IEEE Trans. Electron Devices, 2004, 51, 20–27 CrossRef CAS.
- T. Coquil, E. K. Richman, N. J. Hutchinson, S. H. Tolbert and L. Pilon, J. Appl. Phys., 2009, 106, 034910 CrossRef.
- W. Zhu, G. Zheng, S. Cao and H. He, Sci. Rep., 2018, 8, 10537 CrossRef.
- M. Liu, L. Qiu, X. Zheng, J. Zhu and D. Tang, J. Appl. Phys., 2014, 116, 093503 CrossRef.
- M. Marszewski, D. Butts, E. Lan, Y. Yan, S. C. King, P. E. McNeil, T. Galy, B. Dunn, S. H. Tolbert and Y. Hu, Appl. Phys. Lett., 2018, 112, 201903 CrossRef.
- C. Kittel, Phys. Rev., 1949, 75, 972 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp05377e |
| ‡ B. L. and S. D. are equally contributed to this work. |
| This journal is © the Owner Societies 2021 |