Time-of-flight measurements of the low-energy scattering of CH₄ from Ir(111)

Abstract

We have measured high-resolution time-of-flight (TOF) spectra of methane scattered from an Ir(111) surface at an incident energy of 81 meV. The angular distributions of scattered CH₄ reveal the presence of a sharp and intense specular peak in addition to sharp features corresponding to rotationally inelastic diffraction (RID) peaks along the two main symmetry directions of Ir(111). TOF spectra have been recorded at several RID positions for the two high-symmetry directions. The data show that the scattering dynamics of CH₄ is more complex than the one reported for H₂/D₂, where energy losses in TOF correspond to the expected excitation/deexcitation RID energy transitions. For CH₄, this is the case only for RID peaks showing up far from the specular peak, whereas those appearing close to the specular position present different behaviors, depending on the incident direction. The results are compared with Ne scattering TOF data, which allows to assess the relevance of multiphonon scattering in the energy-exchange process. Finally, we report experimental evidence of selective adsorption resonances detected with CH₄ beams. This will allow characterizing the CH₄–metal surface physisorption well by measuring angular distributions with CH₄ beams.

---

The dissociative chemisorption of methane on transition-metal surfaces has been a target of surface science studies for decades due to its role as the rate-limiting step in the steam reforming reaction.^1,2 In addition to its great practical interest, this reaction became a benchmark system from a fundamental point of view, since it combines several features of chemically complex reaction systems while remaining tractable to state-of-the-art theoretical calculations.^3,4 In fact, current state-of-the-art calculations are able to describe the dissociative chemisorption of methane on metal surfaces including most of the 15 molecular degrees of freedom.^5–7 Developing an ab initio theory capable of predicting gas–surface interaction outcomes, which is necessary for finding suitable catalysts for technological applications as well as for providing insights into the mechanisms of surface reactions, requires experimental studies to assess its predictive power.⁸ Experimental studies of methane scattering from metal surfaces are technically challenging as the scattered intensities are usually low, comparable to background intensities from the residual gas in a UHV chamber, and methane does not have any suitable schemes for detection by Resonance-enhanced multiphoton ionization.⁸

The present study is the continuation of a line of work aimed at undestanding the low-energy scattering dynamics of CH₄ from metal surfaces. We have recently shown that, by choosing the appropriate experimental conditions, it is possible to observe diffraction of CH₄ molecular beams from a metal surafce.⁹ These results proved that quantum coherence is preserved, despite the small separation between rotational levels and the interaction with surface phonons. Furthermore, we showed that CH₄ with low incident energies still undergoes single scattering events when interacting with the Ir(111) surface despite the long interaction time and the much larger depth of the physisorption well. In the current work we address the issue of the energy-resolved scattering dynamics of CH₄.

When a molecule impinges on a surface it can either scatter elastically giving diffraction peaks in the angular distribution of the scattered beam or, under certain incident conditions, energy exchange can take place between internal degrees of freedom of the molecule resulting in Rotationally Inelastic Diffraction (RID) peaks. In this process, the incident molecules convert part of their translational energy into excitation of a rotational quantum level when colliding with the surface. RID peaks show up in the form of additional diffraction peaks in the angular distributions, and are usually observed with H₂ and D₂ beams.^10–13 Recently, sharp RID peaks have been observed in the scattering of CH₄ from Ni(111)¹⁴ and Ir(111).⁹ Here we present high-resolution energy-resolved data measured at RID positions for the scattering of CH₄ from Ir(111). In contrast to expectation, the data cannot be explained based solely on the energy loss corresponding to the RID excitation/deexcitation energy transfer. As we will show, the comparison with Ne diffraction data helps to disentangle the different contributions of pure multiphonon scattering from energy exchanges due to CH₄ rotational transitions. In addition, we report experimental evidence of selective adsorption resonances (SAR) detected with CH₄ beams. SAR are often observed with He and H₂/D₂ beams, and allow for a precise determination of bound-state energies in the particle-surface potential.^15,16 This opens up the possibility of characterizing experimentally the laterally averaged van der Waals well, an important piece of information to test the validity of current state-of-the-art calculations.

1 Experimental details

The experiments were performed with a high-resolution time-of-flight (TOF) spectrometer.¹⁷ This apparatus has been built in the group of J. P. Toennies in Göttingen, and was donated by the Max-Planck-Gesellschaft to our laboratory in 2004. In this system, the angle between incident and outgoing reflected beams is fixed, and angular distributions of scattered particles are measured by continuous rotation of the crystal. In this way, the incident angle Θ_i changes in time during data acquisition while the sum of incident and scattered beam angles (Θ_S = Θ_i + Θ_f) remains constant. After scattering with a fixed, recently calibrated, angle Θ_S = 108°, particles travel through three differentially pumped stages along the 1.7 m long time-of-flight drift tube before reaching the detector, where they are ionized by electron bombardment. The ions are selected by a home-made mass spectrometer using a fixed magnetic field and collected by a channeltron.

The pure CH₄ beam is formed by expanding the gas from a ∅30 μm nozzle operated at 7 bar. The beam energy can be varied between 60 meV and 200 meV by changing the nozzle temperature from 200 to 400 K. The corresponding energy spread varies from 28% to 35%. The incident beam energy was calibrated using a dedicated detector installed in the direct beam path.⁹ All measurements have been performed at a surface temperature T = 110 K, well above the desorption temperature of CH₄ from Ir(111). The beam's initial kinetic energy has been measured with a second detector aligned with the incident beam. This allowed verification of the relationship 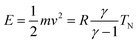, where m and v are the mass and average velocity of the beam particles, T_N is the nozzle temperature, R is the ideal gas constant and γ is the heat capacity ratio which equals 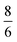for CH₄. We found that the actual beam energies are slightly smaller than the calculated values, as detailed in supplementary information of an earlier work.⁹ The rotational population of the CH₄ beam is expected to be close to the pure statistical weight for a given nozzle temperature.¹⁸ From measurements performed under similar expansion conditions, our CH₄ beam population can be estimated as 30% in J = 0, 50% in J = 1 and 20% in J = 2. Although small deviation from this distribution is expected, especially for room-temperature beams, which may contain fractions of J = 3 and J = 4 states.¹⁹

Clean Ir(111) surface was prepared in UHV by repeated cycles of ion sputtering and flash-annealing at ca. 1600 K. The azimuthal alignment of the sample was optimised by adsorbing oxygen, leading to intense helium diffraction peaks due to the high surface corrugation. Further details on sample preparation can be found elsewhere.²⁰

2 Results and discussion

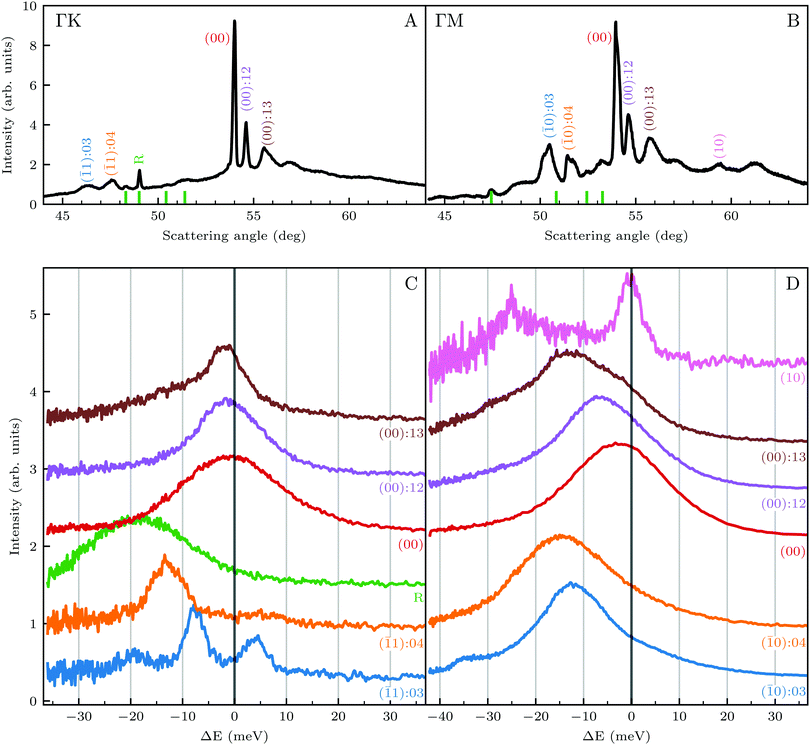
We reported in an earlier work⁹ high-resolution diffraction measurements from an Ir(111) surface along the high-symmetry direction of its unit cell. Fig. 1 shows diffraction spectra and TOF measurements of CH₄ scattered from Ir(111) along the two main high-symmetry directions, 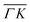in panels A and C and 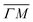in panels B and D. In the current measurements we used a less collimated incident beam than in our previous work (∅1.1 instead of 0.5 mm) as this increases the beam intensity by a factor of 4 and thus improves the signal-to-noise ratio in the TOF measurements, even though using a wider beam decreases the angular resolution of the diffraction measurement by increasing the width of the diffraction peaks.²¹ However, increasing the beam width was necessary since measuring the very low intensities of scattered CH₄ is quite difficult as its mass 16 u coincides with one of the H₂O fragments which constitutes the majority of the residual gas in the UHV chamber. The TOF spectra in Fig. 1 have been measured by integrating over 30–90 minutes.

Fig. 1 (Top) Angular diffraction measurement of CH₄ with incident energy of 81 meV along the two main high-symmetry directions of the Ir(111) unit cell. Labels indicate the locations of selected RID peaks, whereby their colors correspond to the TOF measurements shown in the lower panels. (Bottom) TOF measurements in energy exchange scale under the same experimental conditions at selected scattering angles indicated by labels of the same color in panels A and B.

Several RID peaks are observed in the angular distributions shown in Fig. 1A and B. The position of RID peaks within an angular distribution can be determined by combining the Bragg condition for surface diffraction with conservation of energy.¹³ The RID peaks are labeled as (mn): j_ij_f, whereby (mn) denotes the reciprocal lattice vector involved in the rotational transition, and j_i and j_f the initial and final rotational state of the CH₄ molecule, respectively. (00) is the specular peak and (10) is the first order elastic diffraction peak, which appears at 59.4°. The peak at a scattering angle 49, labeled ‘R’ in green in panel A could not be attributed to the angular position of any RID peak. Therefore, it is expected to result from satisfying the resonance condition of SAR. Similarly, additional green vertical lines in panels A and B indicate peaks that we previously assigned to RIDs in an earlier work,⁹ where we reported diffraction measurements of CH₄ from Ir(111) in the 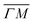direction. However, in the light of the new measurements presented here along the 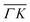direction we suspect that the appearance of these peak at positions of reasonable RIDs was just a coincidence, specifically the peaks that were labeled as (00):21 and (00):31 (in the previous work). 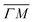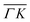The position of those peaks should be independent from the surface lattice constant, which means that they should appear in both and directions at the same angular positions, as is the case for instance for the (00):12 and (00):13 peaks. The fact that they do not appear in the 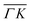direction, and instead two new peaks appear at different scattering angles (which do not correspond to any expected RID position) suggests that these are SAR peaks.

The TOF spectra in Fig. 1C and D where measured under the same experimental conditions used in the top panels. Labels and colors of the spectra correspond to those of the RIDs labeled in the angular diffraction spectra in the top panels. The width of the spectrum in the specular position (red curve) corresponds to the energy spread of the incident beam, ΔE/E_i = 28%. A first visual comparison of both set of TOF data reveals the strange behavior of CH₄ scattering, which is qualitatively very different from the one reported using H₂/D₂ beams. In effect, the energy exchange associated with a RID transition is expected to depend only on the associated excitation/deexcitation energy, and should be therefore independent from the azimuthal orientation of the sample. We see that this is the overall case for the orange and blue curves in Fig. 1C and D, whose maxima appear at negative energy losses of ca. 10–15 meV. However, the TOF spectra of the (00):12 and (00):13 peaks (violet and brown curves, respectively), show a broad distribution with a clear displacement of ca. 5–15 meV in the energy loss direction along 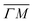but a distribution centered at ΔE = 0 meV along 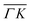. This simple analysis reveals that the expectation of measuring spectra similar in width to that at the specular condition but shifted in the energy loss direction by the value of the rotational transition energy is not fulfilled when monochromatic CH₄ beams are used. Moreover, these spectra, whose structure should be independent from the azimuthal orientation of the sample, look very different when measured along 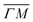or 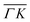. The TOF spectrum measured at the position of the first-order diffraction peak (10) yields a very sharp peak (pink curve). This is due to a energy selection effect produced by Bragg's condition. Once the incident and final angles are fixed, there is only one energy satisfying Bragg's condition; all other energies in the incident beam are filtered out. This is a fingerprint of a pure elastic diffraction peak. Finally, the TOF spectrum measured at a SAR position (green curve) is quite broad, comparable to the one measured at the specular position. This is the expected behavior, since the Bragg condition is not involved here and therefore, the energy distribution of the molecules scattered off after being trapped in the CH₄–Ir(111) potential reflects the energy distribution in the incident beam. Additional well resolved peaks are also observed, like the ones in Fig. 1C at +5 meV, −20 meV in (−11):03 and in Fig. 1D at −25 meV in (10), −30 meV in (00):13 and −35 meV in (−10):03. These peaks can be the result of single phonon creation/annihilation events.

A more detailed, quantitative analysis of the TOF data presented in Fig. 1C and D is summarized in Fig. 2 and Table 1. In this analysis we are concerned only with the most intense peak in each TOF spectrum. The maxima were identified (eyeballed) on the measured data in energy exchange scale,²² then the momentum exchange was calculated and plotted along with the corresponding scan curve. Scan curves are functions of the incident energy and scattering angles, hence they overlap for (00) peaks which are shown in blue. Scan curves for TOFs measured along 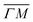and 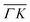are plotted in orange and green, respectively. The gray dashed lines indicate the energy levels of the corresponding rotational transitions, the values are stated in Table 1. Since the energy difference between the rotational levels 0 and 1 of CH₄ is only 1.3 meV, the angular position of the RIDs with initial energy 0 or 1 almost overlap for each final energy on the angular diffraction spectra, additionally, the energy spread of the incident beam makes it difficult to distinguish such a small energy difference in the TOF spectra. Therefore, we will consider measured ΔE values to be accepted if they fall within ±1 meV from their expected values. The two data points along 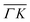(on green scan curves in Fig. 2) as well as the (1̄0):04 and (10) peaks measured in 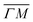(on orange scan curves) are considered to be sufficiently explained by the rotational transitions and the Bragg diffraction. On the other hand, the rest of the data measured along 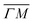are all shifted to almost double their expected values (blue shift of absolute values), whereas the (00):12 and (00):13 peaks measured in the 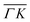direction have their maxima at almost half their expected values (red shift of absolute values). Clearly, these values cannot be explained by the expected mechanism of exchange between kinematic and rotational energies of incident CH₄ molecules.

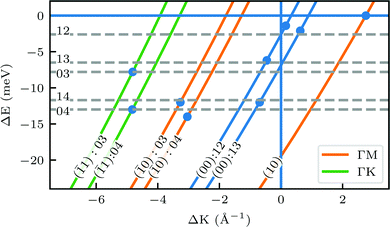Fig. 2 Maximum energy loss values from the TOF spectra plotted on their corresponding scan curves and compared to the rotational transition energies of CH₄ (gray dashed lines). Scan curve labels indicate the corresponding RID peak from Fig. 1A and B. Scan curves are plotted in orange, green and blue if they correspond to 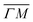, 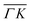or both directions, respectively.

Table 1 Expected and measured energy exchange values from TOF measurements of CH₄ on Ir(111) from the spectra shown in Fig. 1C and D and their dispersion in Fig. 2

Direction	RID transition	Expected ΔE (meV)	Measured ΔE (meV)
a Estimated from SAR, see text.
	(00):12	−2.6	−1.4
	(00):13	−6.5	−2.1
	(1̄1):03	−6.5/−7.8	−7.8
	(1̄1):04	−11.7/−13	−13
	R	23^a	−19
	(00):12	−2.6	−6.2
	(00):13	−6.5	−12
	(1̄0):03	−6.5/−7.8	−12
	(1̄0):04	−11.7/−13	−14
	(10)	0	0

---

In order to get a better understanding of the peaks observed in the TOF data, we compare in Fig. 3 TOF spectra measured at the specular peak position (blue curve, intensity scaled by × 0.5 for better visibility) with two RID peaks ((00):12 in orange and (00):13 in red) and one measurement taken at the background between these two RID peaks (in green). The latter's intensity and position are good indicators of the intensity and position of the multiphonon peak in the other spectra. The total intensity of these peaks, relative to the one at the specular position, is 32% and 24% for (00):12 and (00):13, respectively. This is in contrast with the intensities from the angular diffraction measurements, where the diffraction peak intensities are 48.3% and 80.8% of the specular peak for (00):12 and (00):13 RID peaks, respectively. The discrepancy in intensities between diffraction and TOF measurements is a result of the energy spread of the incident beam, which induces an angular spread in the scattered beam as a function of ΔK. In other words, the TOF data show information from a limited slice of the peaks that appear in the diffraction measurements. Note that, as can be seen in Fig. 3, the widths of TOF peaks in the RID positions are smaller than that at the specular condition, the latter does not exhibit energy selection similar to the other peaks since ΔK = 0. A simple comparison between the spectra in Fig. 3 shows that the multiphonon peak in the TOF spectra is responsible for the wide background and not the intense sharp peak.

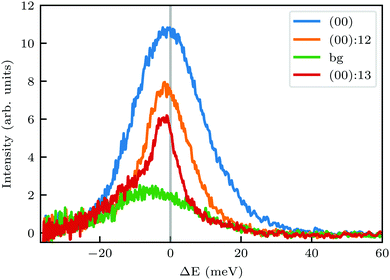Fig. 3 Intensity of TOF spectra at positions corresponding to specular (blue), RID (orange and red), or background (green) angular positions in the diffraction spectra shown in Fig. 1A. The green spectrum was measured at an intermediate position between the two RID spectra. Intensity of the spectrum at specular position (blue curve) was scaled by × 0.5.

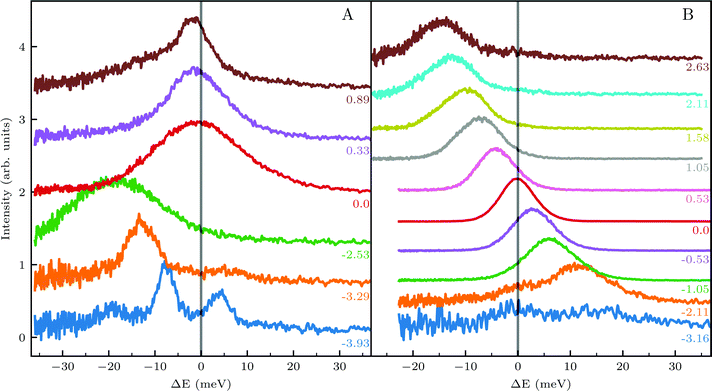
We further compared the TOF spectra of CH₄ scattering from Ir(111) with spectra of Ne scattering under similar conditions in Fig. 4. Panel A shows the same data from Fig. 1C where E_i = 81 meV and panel B shows Ne TOF spectra measured with E_i = 69 meV. Both set of data have been measured at the same surface temperature (T_S = 100 K) and azimuthal orientation (). This comparison is interesting because, being the mass of CH₄ nearly identical to that of Ne, at the same incident energy multiphonon scattering is expected to be comparable in both cases. The spectra from the specular peak are shown in red for both Ne and CH₄. The labels on the spectra indicate the value of ΔK, the elastic momentum exchange parallel to the surface, i.e. for ΔE = 0. The FWHM of the incident Ne beam energy is 7.9 meV. The Ne data show a typical classical behavior of the dispersion of a multiphonon peak, namely, energy gain when losing momentum and vice versa, together with increasing width of the peaks as the absolute value of ΔK increases. However, when the absolute values of ΔK are above 1.5 Å⁻¹ the dispersion of these peaks resembles that of a surface Rayleigh wave. In other words, for angles close to the specular condition, the Ne data show the same behavior of multiphonon interaction already observed in Ne scattering from a hot Ir(111) surface, which could be explained using a classical model.²³ This could be one of the reasons why in our TOF measurements of CH₄ scattering from Ir(111) we see well-defined sharp peaks with maxima at the positions expected for rotational transitions for peaks away from the specular position, whereas spectra from positions near the specular condition yielded quite different values. Especially, since it is obvious from the data that the inelastic background in the diffraction measurements is substantially high in the angular region near the specular condition. For instance, the TOF spectra at peaks (1̄0):04 and (1̄1):04 (orange) in Fig. 1 exhibit roughly the same energy loss in both directions and , ΔE = −13 and −14 meV, respectively. The difference in the widths of the peaks might be a consequence of the fact that the RID peaks appear at angular positions further from the specular condition in 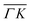than in 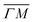, which reduces the intensity of the multiphonon peak and means larger angular dispersion in the scattering angle and thus better energy selection in the energy-resolved measurements.

Fig. 4 Comparison of TOF measurements of CH₄ (A) and Ne (B) scattered from the Ir(111) surface (T_S = 100 K) along with incident beam energies 81 meV and 69 meV, respectively. The labels indicate the value of the elastic momentum exchange parallel to the surface, ΔK, in Å⁻¹.

Nonetheless, the above explanation does not seem to give a satisfactory answer to other anomalies in our data, which have been obtained under conditions that favor coherent single event scattering, and cannot be explained with the same classical models used to explain TOF measurements of CH₄ scattering from Pt(111).^24–26 For instance, when comparing the (1̄0):03 and (1̄1):03 peaks (blue spectra in Fig. 1C and D), the TOF measurement along 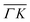yields a sharp peak at an energy loss value as expected from the RID transition (−7.8 meV). However, in the 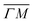direction the maximum of the measured TOF is shifted towards a much larger energy loss value (−12 meV). The multiphonon interaction might explain partially the width of the (1̄0):03 peak, but it cannot explain the additional shift in energy loss of ca. 4 meV. We propose below a mechanism which can explain how SARs can be responsible of the anomalies that cannot be explained otherwise.

We showed in an earlier work that CH₄ sees different surface corrugations when scattered form Ir(111) along the two main high symmetry directions.⁹ In fact, a comparison between the diffraction spectra in Fig. 1 along 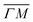and 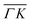already shows that the 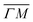direction appears more corrugated for CH₄ due to the presence of more pronounced diffraction peaks. Similarly, in a work on low energy CH₄ scattering from Pt(111), we measured different angular scattering spectra that, although did no show diffraction peaks, exhibited clear differences in the angular distributions measured along the two high-symmetry directions. Analyzing the data using the washboard model, we estimated a difference in corrugation of 0.03 Å, whereby the larger corrugation corresponds to the 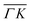direction of Pt(111).²⁷ Additionally, DFT calculations of the potential energy surface (PES) for CH₄–Ir(111) revealed that CH₄ samples quite different surface corrugations of the PES depending on the azimuthal orientation of the sample surface as well as the orientation of the impinging molecule.⁹ The differences of sampled corrugation amplitudes varies between 0.02–0.20 Å, depending on the orientation of the incoming CH₄ molecules. However, in our experimental setup we cannot select the initial state of the molecular orientation as has been done in other molecular beam studies, where it was shown that the alignment of an incident diatomic molecule strongly influences the angular distribution of the scattered molecules, the energy loss during the collision and the trapping probability.^8,28–31 In summary, the sampled surface corrugation, which plays a crucial role in RID, is affected by both the azimuthal and molecular orientations. Our measurements can address the former, however, our experimental setup does not allow us to address the latter.

Surface corrugation is of special importance, especially in highly corrugated surfaces, which were shown to produce pronounced SAR peaks in the diffraction spectra of molecular beams, similar to the peaks indicated with green lines in Fig. 1. The kinematic condition for resonance into a bound state with binding energy ε_n < 0 can be easily derived from the conservation of energy and parallel momentum, as 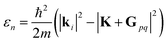, where m is the particle mass, and k_i is the wavevector of the incident beam, K, is the component of k_i parallel to the surface and G_pq is the surface reciprocal vector giving rise to the resonance.¹⁵ From this equation, using the value 2.715 Å for the lattice constant, we found that the peaks at 49 in and 47.5 in correspond to resonance energies 23 and 23.3 meV, respectively, assuming a coupling to the G₀₁ vector of the surface reciprocal lattice.

To explain the large energy loss value of the (1̄0):03 peak (blue spectrum in Fig. 1D), we draw the reader's attention to the SAR peak observed in a close vicinity of the (1̄0):03 peak, which is indicated by a green line in Fig. 1B. This peak is better resolved using a more collimated incident beam, as shown in Fig. 1 of ref. 9. 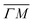We also note that the shapes and energy losses of the (00):12 and (00):13 peaks are very different in the and directions. It is also known that physisorption of molecules at surfaces exhibits azimuthal angle dependence, indicating that the conversion of parallel to normal momentum is very important along the ‘rough’ direction and limits the trapping probability.^8,32 We expect that a better understanding of the current TOF measurements can provide new insights about the interplay between the surface lattice structure and the CH₄–Ir(111) interaction potential, helping to improve our understanding of the under-barrier dissociation channels reported in other works.

Our results are quite surprising because the angle-resolved scattering spectra can be explained with simple kinematics, whereas the explanation of the energy-resolved spectra is not straightforward. In other words, we observe momentum conservation but cannot always explain the energy exchange, which might require including electronic degrees of freedom to be explained. We will not delve into details in the discussion of SARs as it requires a good description of the molecule-surface potential and its eigenstates, which in the case of CH₄ scattering from Ir(111) varies substantially depending on the orientation of the impinging molecule and the scattering location on the surface unit cell.⁹ Therefore, we cannot provide an unambiguous discussion of the SAR associated peaks without a proper ab initio theory that provides a correct description of the attractive part of the interaction potential of methane and Ir(111).

3 Conclusions

The diffraction measurements of CH₄ from Ir(111) exhibit RID peaks at positions that agree very well with theoretically calculated positions. However, the high-resolution time-of-flight spectra measured at an incident energy of 81 meV reveal that the scattering dynamics of CH₄ is more complex than the one usually observed with H₂/D₂ beams, where energy losses in TOF correspond to the expected excitation/deexcitation RID energy transitions. For CH₄, this is the case only for RID peaks showing up far from the specular peak, whereas those appearing close to the specular position present different behaviors, depending on the incident direction. In particular, the energy loss for the same RID transition depends strongly on the azimuthal orientation of the sample, which means that our current results cannot be explained by simple kinematics nor by a flat surface model. The role played by multiphonon scattering in the energy-exchange process has been estimated by measuring Ne scattering TOF data. To better understand the energy exchange mechanism it would be helpful to measure TOF spectra taken with well-defined incident molecular orientations. Finally, we observed features in the angular distributions which can be ascribed to SAR, and provided evidence that the proximity of a SAR angular position to a RID angular position yields an anomaly in the energy-resolved spectra.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge J. P. Toennies and the Max-Planck Gesellschaft for the donation of the scattering apparatus used in our experiments. This work has received funding from the Spanish Ministerio de Ciencia e Innovación under project PID2019-109525RB-I00, from the Comunidad de Madrid (project NanoMagCostCOST-CM, P2018/NMAT-4321) and the Spanish Ministerio de Ciencia, Innovación y Universidades (project SpOrQuMat). IMDEA Nanociencia thanks the support from the “Severo Ochoa” Programme for Centers of Excellence (MINECO, Grant SEV-2016-0686). R. M. and D. F. acknowledge financial support from the Spanish Ministry of Economy and Competitiveness, through the “María de Maeztu” Programme for Units of Excellence in R&D (CEX2018-000805-M).

References

1. J. H. Larsen and I. Chorkendorff, Surf. Sci. Rep., 1999, 35, 163–222.
2. L. Juurlink, D. Killelea and A. Utz, Prog. Surf. Sci., 2009, 84, 69–134.
3. R. Smith, D. Killelea, D. DelSesto and A. Utz, Science, 2004, 304, 992–995.
4. R. D. Beck, P. Maroni, D. C. Papageorgopoulos, T. T. Dang, M. P. Schmid and T. R. Rizzo, Science, 2003, 302, 98–100.
5. S. Nave and B. Jackson, J. Chem. Phys., 2009, 130, 054701.
6. S. Nave, A. K. Tiwari and B. Jackson, J. Phys. Chem. A, 2014, 118, 9615–9631.
7. X. Zhou, F. Nattino, Y. Zhang, J. Chen, G.-J. Kroes, H. Guo and B. Jiang, Phys. Chem. Chem. Phys., 2017, 19, 30540–30550.
8. G. B. Park, B. C. Krüger, D. Borodin, T. N. Kitsopoulos and A. M. Wodtke, Rep. Prog. Phys., 2019, 82, 096401.
9. A. Al Taleb, G. Anemone, L. Zhou, H. Guo and D. Farías, J. Phys. Chem. Lett., 2019, 10, 1574–1580.
10. K. B. Whaley, C.-f. Yu, C. S. Hogg, J. C. Light and S. J. Sibener, J. Chem. Phys., 1985, 83, 4235–4255.
11. R. Berndt, J. Toennies and C. Wöll, J. Chem. Phys., 1990, 92, 1468–1477.
12. L. C. Shackman and G. O. Sitz, J. Chem. Phys., 2005, 122, 114702.
13. D. Farías and R. Miranda, Thermal Energy Atomic and Molecular Beam Diffraction from Solid Surfaces, Springer Berlin Heidelberg, 2013, pp. 51–73.
14. A. Al Taleb and D. Farías, Phys. Chem. Chem. Phys., 2017, 19, 21267–21271.
15. D. Farías and K.-H. Rieder, Rep. Prog. Phys., 1998, 61, 1575.
16. M. F. Bertino and D. Farías, J. Phys.: Condens. Matter, 2002, 14, 6037.
17. D. Barredo, G. Laurent, P. Nieto, D. Farías and R. Miranda, J. Chem. Phys., 2010, 133, 124702.
18. E. B. Wilson, J. Chem. Phys., 1935, 3, 276–285.
19. L. B. F. Juurlink, R. R. Smith and A. L. Utz, Faraday Discuss., 2000, 117, 147–160.
20. A. Al Taleb, G. Anemone, J. Manson and D. Farías, 2D Mater., 2018, 5, 045002.
21. J. M. Moix, E. Pollak and W. Allison, J. Chem. Phys., 2011, 134, 024319.
22. G. Benedek and J. P. Toennies, Experimental Methods of HAS Surface Phonon Spectroscopy in Atomic Scale Dynamics at Surfaces: Theory and Experimental Studies with Helium Atom Scattering, Springer, Berlin, Heidelberg, 2018, vol. 63.
23. W. Hayes, A. Al Taleb, G. Anemone, J. Manson and D. Farías, Surf. Sci., 2018, 678, 20–24.
24. S. Yagyu, T. Hiraoka, Y. Kino and S. Yamamoto, Appl. Surf. Sci., 2000, 165, 217–223.
25. T. Kondo, T. Sasaki and S. Yamamoto, J. Chem. Phys., 2002, 116, 7673–7684.
26. I. Moroz and J. R. Manson, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 113405.
27. T. Kondo, A. Al Taleb, G. Anemone and D. Farías, J. Chem. Phys., 2018, 149, 084703.
28. M. Kurahashi, Prog. Surf. Sci., 2016, 91, 29–55.
29. O. Godsi, G. Corem, Y. Alkoby, J. T. Cantin, R. V. Krems, M. F. Somers, J. Meyer, G.-J. Kroes, T. Maniv and G. Alexandrowicz, Nat. Commun., 2017, 8, 15357.
30. M. Kurahashi and T. Kondo, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 99, 045439.
31. Y. Alkoby, H. Chadwick, O. Godsi, H. Labiad, M. Bergin, J. T. Cantin, I. Litvin, T. Maniv and G. Alexandrowicz, Nat. Commun., 2020, 11, 1–8.
32. J. A. Stinnett, M. C. McMaster, S. L. Schroeder and R. J. Madix, Surf. Sci., 1996, 365, 683–700.

---