Molecular insights on the dynamic stability of peptide nucleic acid functionalized carbon and boron nitride nanotubes†
Nabanita
Saikia
 *a,
Mohamed
Taha
*a,
Mohamed
Taha
 b and
Ravindra
Pandey
b and
Ravindra
Pandey
 *a
*a
aDepartment of Physics, Michigan Technological University, 1400 Townsend Drive, Houghton, Michigan 49931, USA. E-mail: nsaikia@mtu.edu; pandey@mtu.edu
bMaterials Science and Nanotechnology Department, Faculty of Postgraduate Studies for Advanced Sciences (PSAS), Beni–Suef University, Egypt
First published on 8th December 2020
Abstract
The strategic approaches to the design of self-assembled hybrids of biomolecular systems at the nanoscale such as deoxyribonucleic acid (DNA) with single-wall carbon nanotubes (CNTs) and their structural analog, boron nitride nanotubes (BNNTs), rely on understanding how biomolecules recognize and mediate intermolecular interactions with the nanomaterial's surface. In this paper, we consider peptide nucleic acid (PNA), which is a synthetic analog of DNA, and investigate its interaction with a zigzag CNT and BNNT of similar diameter. The results based on the molecular dynamics method find that PNA provides definitive contrasts in the adsorption on the tubular surface in aqueous solution: it prefers to wrap along the circumferential direction on a (11,0) CNT, whereas it binds along the axial direction adopting an extended configuration on a (11,0) BNNT. Moreover, gas-phase Monte Carlo simulations show a dependence of the nanotube diameter on the calculated adsorption energy, with BNNTs exhibiting higher adsorption energy compared to CNTs, and the largest-diameter (25,0) tubular configuration facilitates encapsulation of PNA rather than PNA being adsorbed on its sidewall. The results are expected to be of relevance in the design of novel PNA-based archetypal hybrid materials for nanoscale applications in health-related areas including biosensing.
1. Introduction
The integration of biological molecules with nanoscale materials including carbon nanotubes (CNTs) and boron nitride nanotubes (BNNTs) is presently being pursued in the design and development of the next generation of biosensors,1 nanocomposites with enhanced mechanical properties, and molecular electronic devices.2–4 Hybridizations of single-strand deoxyribonucleic acid (ssDNA) with CNTs and BNNTs exemplify one of such examples wherein the inherent electronic properties of the nanotubes along with the natural amphiphilic nature of ssDNA promote the conjugation of functionalized nanostructures, distinct in properties yet unique in applications.5,6 The complementary structure of ssDNA is stabilized by the van der Waals (vdW) interactions facilitated by π-stacking between the nucleobases7 and the hydrophilic (charged) phosphate backbone enhances the stability of the DNA/CNT hybrid in aqueous solution.8 Recent studies on the helical wrapping of ssDNA around CNTs are motivated by the inherent mobility to disperse CNTs, DNA sensing, and biomedical applications.9–11 DNA polynucleotides are also predicted to have strong interactions with BNNTs.12 For DNA/BNNT hybrids, polynucleotide and peptide wrapping improves the dispersion of BNNTs with a reduction in the bundling effect.13,14The emergent applications proffered by DNA nanotechnology have motivated our research interest in the synthetic analogs of DNA termed peptide nucleic acids (PNAs).15,16 PNA was originally designed for the specific recognition of DNA in a base complementary manner.17 In PNA, the chiral sugar–phosphate backbone is mimicked by N-(2-aminoethyl) glycine (aeg) polyamine, with the nucleobases attached via methyl carbonyl linkers (see Fig. 1).18 Similar to DNA, PNA can form duplexes through Watson–Crick base pairing and adopt a helical (P-type) structure with 18 bases per turn and has a diameter of 28 Å.19 Exciting new developments in the application of PNA for molecular recognition, gene expression, biosensing, and antisense hybridization are foreseen owing to the sequence-specific recognition of complementary DNA/RNA.20 The advantage of PNA over DNA is its resistance to changes in pH and ionic strength, greater mismatch sensitivity, and stability to degradation by proteases and nucleases.21 The lack of a charged backbone eliminates electrostatic repulsion during hybridization, thereby rendering high stability to PNA. Both PNA and ssDNA demonstrate similar dynamics in aqueous solution with the structural transition to a random coil-like aggregate, though the dynamics of PNA is independent of the salt concentration due to the lack of a charged backbone.22 It should be noted that the assimilation of PNA with nanomaterials is relatively less explored compared to the wide-scale applicability of the ssDNA counterparts.
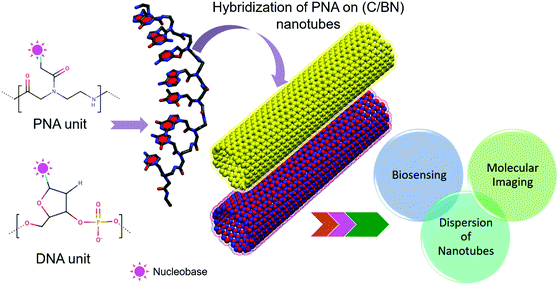 | ||
| Fig. 1 Schematic of the hybridization of PNA on a CNT (or BNNT) with potential applications in molecular imaging, biosensing, and chirality-dependent sorting of nanotubes. | ||
The first report on DNA-assisted separation and dispersion of CNTs published in 2003 opened up the prospect of CNT-based applications in biotechnology.5 This serves as the motivation for our present study, wherein we “attempt and realize” the integration of PNA with CNTs or BNNTs to propose emergent potential research avenues per DNA nanotechnology. We expect that our research findings will be of relevance in the design of novel PNA-based archetypal hybrid nanoscale materials and can be used to efficiently integrate PNA with nanomaterials for the principal research areas of biosensing, molecular imaging, and effective dispersion of nanotubes as illustrated in Fig. 1.23–25
2. Computational method
2.1. Model
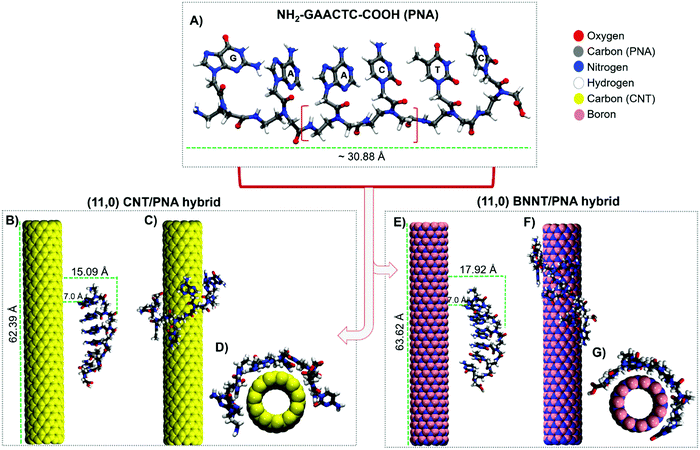
The achiral aeg backbone of PNA has been shown to adopt both right-handed and left-handed conformations.26 A model single-stranded 6-mer PNA (i.e. NH2–GAACTC–COOH) having a length of ∼30.9 Å and width of ∼10.6 Å was considered in our study, since the synthesis of a shorter PNA oligopeptide can be performed easily and a shorter PNA sequence provides a faster response in orientation at shorter timescales, thus facilitating high affinity and sequence selectivity.27 The force field parameters of PNA were adopted from a previous study by Weroński et al.28 The partial charges of PNA atoms are listed in the ESI,† Table S1. In the case of DNA, it was reported that short DNA strands have a greater ability to recognize and distinguish chiral (7,6) and (6,5) single-wall CNTs, resulting in a larger current response.29 Short strands of DNA of different sequence and/or composition have demonstrated the ability to form highly sequence-specific structures on different chiral CNTs and the structure effect leads to the difference in electrochemical behaviors. For DNA strands with adequate length, H-bonding facilitates DNA to wrap completely around the nanotube tubular surface and self-stitch, which would show no difference in structure. It is important to mention that similar to ssDNA, the nucleobase sequence and length of PNA would determine the dynamics of interaction and sequence-specific assembly on the nanotube sidewall, and thus the choice of nucleobase sequence model is important in simulations. DFT calculations on the binding energy of nucleic acids adenine (A), guanine (G), cytosine (C), and thymine (T) on a high-curvature zigzag (5,0) BNNT followed the order: G > A ≈ C ≈ T ≈ U and G > A > T > C ≈ U.30,31 The individual polarizability, governed by the dispersive forces, like vdW, of the nucleobases, determined the binding energy associated with the CNT. In general, the guanine nucleobase exhibited the strongest binding on both the CNT and BNNT.We considered a periodic model of a (11,0) zigzag CNT having a length of ∼62.4 Å and a diameter of ∼8.6 Å. The carbon atoms were modeled as uncharged Lennard-Jones (LJ) particles with sp2 carbon parameters (atom type CA) defined by the CHARMM27 force field.32 Our choice of considering a semiconducting zigzag (11,0) CNT was based on the aromaticity; metallic nanotubes are reported to be slightly less aromatic than the semiconducting counterparts and, in general, semiconducting nanotubes are analogous to [4n + 2]annulenes (aromatic by the Hückel rule), whereas metallic nanotubes are equivalent to [4n]annulenes (antiaromatic by the Hückel rule).33 A periodic model of a (11,0) zigzag BNNT having a length of ∼63.6 Å and a diameter of ∼8.7 Å was considered since it has comparable dimensions and chirality as a (11,0) CNT. The charges of boron and nitrogen atoms were assigned as +0.4 and −0.4 e, respectively, and the LJ parameters were adopted from previous reports.34,35 Periodic supercells with dimensions of (60.0 × 60.0 × 62.40) Å3 and (60.0 × 60.0 × 63.65) Å3 for the (11,0) CNT/PNA and (11,0) BNNT/PNA hybrids, respectively, were employed. The atomic positions of C (and B/N) atoms were fixed during the MD simulations. PNA was initially aligned parallel to the axis of the CNT and BNNT at a distance of ∼15.0 Å and ∼17.9 Å, respectively, with respect to the peptide backbone and tubular axis. Three independent MD simulations were performed with different starting conformations of PNA to check the reproducibility of our results on the preferred orientations of adsorption of PNA on the CNT and BNNT.
2.2. Molecular dynamics simulations
MD simulations were performed in an aqueous solution at room temperature in the NVT (constant mass, volume, and temperature) canonical ensemble, using the NAMD program.36 The temperature was maintained by employing Langevin dynamics with a damping coefficient of 1 ps−1. Each simulation included 2000 steps of energy minimization using the conjugate gradient algorithm and a production run of 50 ns, with an integration time step of 1.0 fs. The water molecules were modeled by the TIP3P potential,37 with constraints applied to bond lengths and angles using the SETTLE algorithm. The Particle Mesh Ewald method was applied to calculate the periodic electrostatic interactions with a long-range cutoff of 12.0 Å.38 The convergence of the simulation trajectory was confirmed using the root-mean-square deviation (RMSD) of the atomic positions of PNA in the CNT (or BNNT) hybrids (excluding the waters). The visualization of simulation snapshots along with the statistical analysis was carried out using the VMD 1.9.2. program.39The MD results were further analyzed in terms of the radius of gyration, radial distribution function, normalized center of mass (COM) distance, and the number of hydrophobic contacts (NHC) between the aromatic rings of the nucleobases and the nanotube for the CNT (BNNT)/PNA hybrids.
The radius of gyration (Rg) is defined as the root mean square distance of atoms or groups from their reference COM, and is given by:
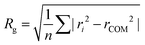 | (1) |
The Radial Distribution Function (RDF) or the pair correlation function, g(r), represents the probability to find an atom at a distance ‘r’ from a reference atom. For distances ≤ the atomic diameter, g(r) is zero, corresponding to the strong repulsive forces in the system. The first large peak in g(r) demonstrates the likeliness of two molecules residing at this separation, yielding the nearest-neighbor distance in the system. At long distances, g(r) approaches one, indicating an absence of long-range order in the system.40 In the present study, the RDF is used to determine the degree of water ordering at the interface of the complexes.
2.3. Monte Carlo (MC) simulations
The rationale behind integrating Monte Carlo (MC) simulations with MD is to investigate the interactions of PNA on different diameter zigzag CNTs and BNNTs and quantify the adsorption energies in the respective hybrids. Since MC calculations in explicit solvent are computationally expensive, we performed the simulations in the gas phase. The PNA, CNT, and BNNT structures were initially optimized using the Dreiding force field.41 The vdW forces were defined by the LJ potential and the electrostatic forces were described by atomic monopoles and a screened Coulombic term. The hydrogen bonding term was defined by an explicit LJ 12-10 potential. The optimization process was carried out with the Forcite module. The smart algorithm was used and the convergence energy, force, and displacement tolerances were 2 × 10−5 kcal mol−1, 1 × 10−3 kcal mol−1 Å−1, and 1 × 10−5 Å, respectively. The summation and truncation methods for the electrostatic, vdW, and hydrogen bond terms were atom-based and cubic spline, respectively. The cutoff distance, spline width, and buffer width for both electrostatic and vdW interactions were 18.5, 1.0, and 0.5 Å, respectively, while the parameters for the hydrogen bond term were 4.5, 0.5, and 0.5 Å, respectively. The MC simulations were based on the Metropolis method as implemented in the BIOVIA Materials Studio 2017 package (Accelrys Software Inc.). For the simulated annealing step, the maximum and final temperatures were considered to be 1.0 × 105 K and 100 K. The number of heating cycles was 10 and each cycle consisted of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps. In the MC simulations, the adsorption energy (Eads), in kcal mol−1, is calculated as follows:
000 steps. In the MC simulations, the adsorption energy (Eads), in kcal mol−1, is calculated as follows:| Eads = E(rigid adsorption energy) + E(deformation energy) | (2) |
3. Results and discussion
3.1. Self-assembly of PNA on a (11,0) CNT and (11,0) BNNT
Fig. 2A depicts a 6-mer PNA consisting of N-(2-aminoethyl)-glycine repeat units, with the nucleobases attached to the peptide backbone via methylene carbonyl groups. It has been reported that, in the presence of a solvent, PNA can aggregate and fold into globular structures stabilized by the intermolecular interactions between hydrophobic nucleobases.42,43 This leads to nonspecific adherence towards other biomolecules like a complementary DNA sequence and hinders the registry on surfaces. To benchmark our modeling elements, we initially performed a 50 ns MD simulation of the modeled 6-mer PNA oligopeptide in aqueous solution in the absence of the nanotube (Fig. S2A of the ESI†). PNA folds into an aggregated structure, mediated by the intermolecular π-stacking interactions between the bases (Fig. S2B of the ESI†). The excellent agreement in the observed conformational dynamics of PNA in aqueous solution with a previous report44 validates the reliability of the modeling elements employed in this work. Fig. 2B–D show the 50 ns snapshot of the CNT/PNA hybrid. We find that the adsorption of PNA on the CNT is quite spontaneous and the nucleobases interact with the nanotube surface within the first 500 ps. The conformational flexibility of PNA enables π-stacking of nucleobases followed by circumferential wrapping of the oligopeptide backbone around the nanotube sidewall. Likewise, the spontaneous helical wrapping of PNA on the BNNT leads to the formation of a stable self-assembled hybrid (Fig. 2E–G). PNA adopts an extended conformation on the BNNT, thereby maximizing the number of contacts and the contact area with the tubular surface (Fig. 2F and G). Although PNA forms stable contacts on both the CNT and BNNT, the nature of hybridization and assembly is quite distinctive: PNA wraps along the circumferential direction in the CNT, whereas it binds along the axial direction in the BNNT (Fig. 2C and F). As opposed to the CNT, the nucleobases show a higher degree of contact on the BNNT (Fig. 2D and G).To consider the effect of any bias in the nature of adsorption of PNA on the nanotube surface in our MD simulations, we performed additional simulations with different initial configurations of PNA such as (i) PNA rotated at ∼90° with respect to the tubular axis of the nanotube, and (ii) PNA placed at an initial distance of ∼20.0 Å from the tubular surface (Fig. S3–S6 of the ESI†). The MD simulations in both cases show that PNA prefers to adopt a compact circumferentially-wrapped conformation rather than an extended conformation on the CNT. On the other hand, selectivity for the axial orientation of PNA is demonstrated for the BNNT/PNA hybrid as shown in Fig. S4C and D, ESI,† for case (i) and Fig. S5C and D (ESI†) for case (ii). Thus, the preferred orientation of PNA on the CNT/BNNT as predicted by the MD simulations is not biased by the initial configurations of PNA interacting with the CNT and BNNT.
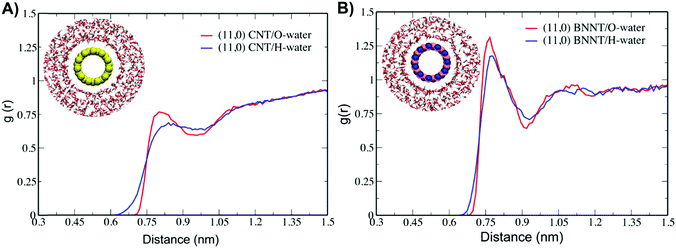
Fig. 3 shows the radial distribution function (RDF) between the center of mass (COM) of the CNT and BNNT and the oxygen (O) and hydrogen (H) atoms of water. The peak between the CNT and the O atoms of waters is centered at 0.79 nm with a shoulder at ∼1.11 nm, which corresponds to the first water hydration sphere around the CNT (Fig. 3A). Thereafter, the RDF gradually extends to bulk water with an increase in the radial distance. The RDF between the COM of the CNT and the H atoms of waters is centered at 0.84 nm with a shoulder at ∼1.12 nm. For the BNNT/PNA hybrid, a strong RDF peak between the COM of the BNNT and the O atoms of waters is centered at 0.74 nm with a broad distribution between 1.0 and 1.13 nm (Fig. 3B) which progressively extends to bulk water. The electronegative O atoms of waters are oriented at a shorter interaction distance with the BN-atoms of the BNNT compared to the carbon atoms of the CNT. The RDF of H atoms of waters is centered at 0.75 nm and extends to bulk water with an increase in the radial distance. The contributions to the water density profile from O and H atoms of waters around the CNT (BNNT) further support the observations from the RDF profile. For distances away from the vicinity of the nanotube, the combined mass density profile of H and O atoms extends to a bulk water density of 0.998 g cm−3 (ESI,† Fig. S7A and B). We find uniform first-layer water ordering around the nanotube sidewall, which is reflected in the pairwise RDF and the bulk water density is similar for both the complexes.
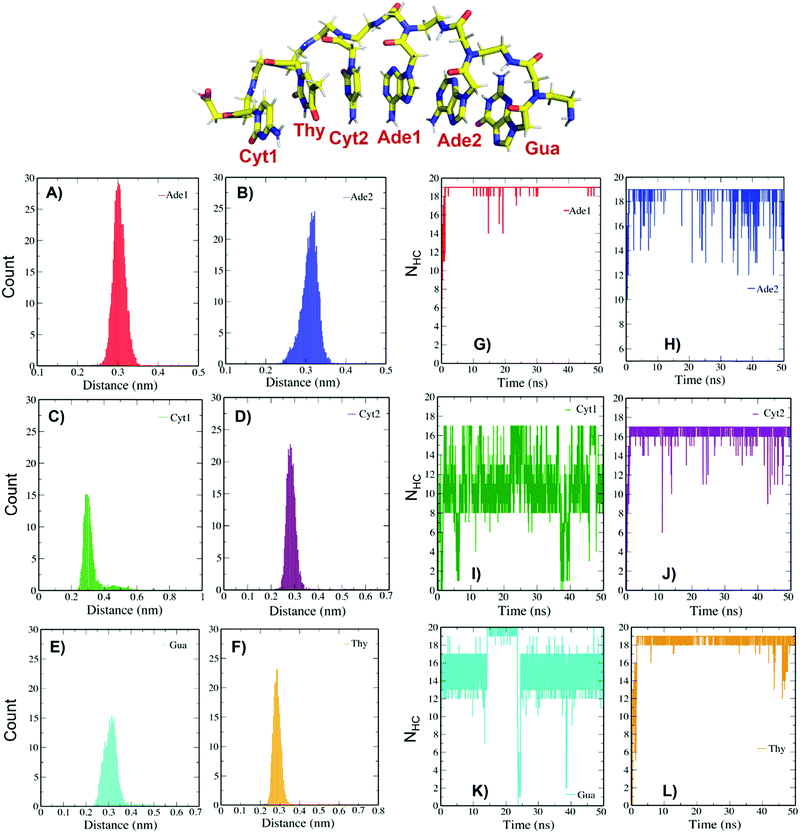
The number of hydrophobic contacts (NHC) between the aromatic rings of the nucleobases and the nanotube sidewall was further computed to ascertain the role of π–π stacking interactions in stabilizing the adsorption of PNA onto the nanotubes. Fig. 4 shows the histograms of the minimum distance and NHC between the constituent nucleobases and the tubular surface of the CNT and BNNT, respectively. The minimum distance of interaction between the PNA and CNT is calculated to be around 0.3 nm (Fig. 4A–F). The terminal cytosine (Cyt1) and guanine (Gua) bases present the highest fluctuations with lower hydrophobic contact and nucleobases adenine (Ade1), thymine (Thy), and Cyt2 make more hydrophobic contacts with the CNT sidewall (Fig. 4G–L). The minimum distance of interaction between PNA and the BNNT is calculated to be around 0.25 nm as shown in the ESI,† Fig. S10A–F. The terminal Cyt1 and Gua nucleobases have a slightly higher interaction distance above 0.25 nm (Fig. S10C and E of the ESI†). Except for the terminal Cyt1, the other nucleobases exhibit increased hydrophobic contacts with reduced nucleobase fluctuations on the BNNT sidewall (Fig. S10G–L of the ESI†). This supports the predicted distinctive trends in the preferential adsorption of PNA on the CNT and BNNT.
The contrast in the wrapping of PNA on the CNT and BNNT was further confirmed by the calculated contact area, which is calculated to be 4.9 and 5.1 nm2 in the CNT/PNA and BNNT/PNA hybrids, respectively (see the ESI,† Fig. S8). A previous study by Mudedla et al. reported a contact area of ∼6.3 nm2 for a polyalanine/(12,12) BNNT hybrid,45 which suggests agreement with our simulated results on PNA/(11,0) BNNT. To compare the preferential adsorption of PNA (circumferential vs. axial wrapping) onto the CNT and BNNT, we computed the 2D scatter plot of Rgvs. RMSD for the CNT/PNA and BNNT/PNA hybrids as shown in Fig. 5. For CNT/PNA, the configuration space is broadly characterized by two regions, region I with an RMSD of 0–1.15 Å and Rg of ∼17.3 Å, and region II with an RMSD of 1.0–1.5 Å and Rg of ∼18.5 Å. In contrast, the BNNT/PNA hybrid displays an almost linear increase in Rg with an increase in RMSD, which indeed corresponds to PNA adopting an extended conformation with the nucleobases aligned along the axial direction (Fig. 5, inset MD snapshot).
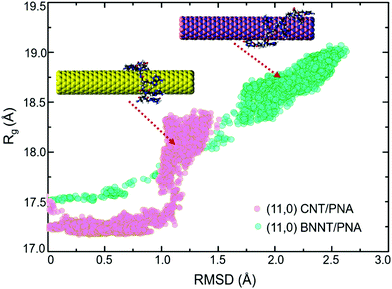 | ||
| Fig. 5 2D scatter plot of Rgvs. RMSD for the CNT/PNA and BNNT/PNA hybrids in aqueous solution. The inset snapshots depict the adsorption of PNA onto the CNT and BNNT. | ||
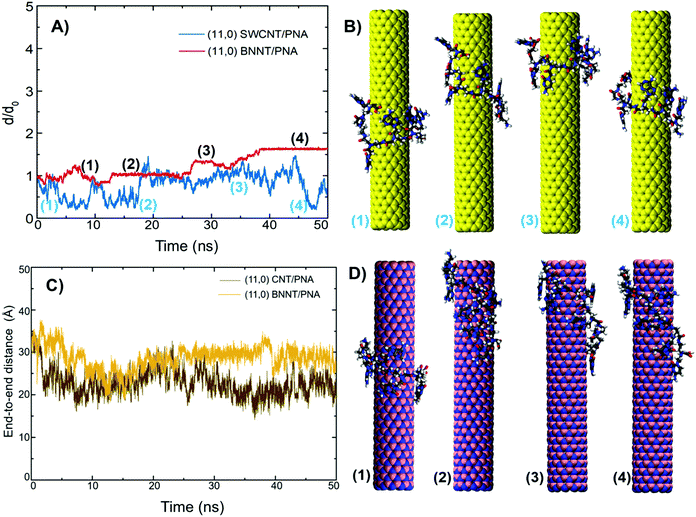
Further, to ascertain the overall stability of the CNT (BNNT)/PNA hybrids, we calculated the normalized COM–COM distance (d/d0) between the nanotube and PNA. Here d0 is the initial COM distance between PNA and the nanotube, and d is the COM distance at a given simulation time. The comparatively higher oscillations in CNT/PNA correspond to the lateral movement of PNA along the tubular axis. The increase in the normalized COM distance between 20 and 45 ns resembles the transient movement of PNA along the edge of a nanotube (labels 2 and 3 of Fig. 6A and B) followed by a decrease in the distance, wherein PNA traverses back towards the center (label 4 of Fig. 6B). On the other hand, the normalized COM distance for BNNT/PNA can be partitioned into four regions, labeled (1–4) in Fig. 6A. With an increase in the COM distance from the initial (label 1) to the 50 ns configuration (label 4), PNA adopts an extended configuration as shown in Fig. 6D. Beyond 38 ns, we do not find any major oscillations and the COM distance normalizes at ∼1.65, suggesting no occurrence of noticeable conformational changes in PNA interacting with the BNNT. Fig. 6C shows the variation in the computed end-to-end distance with the simulation time, suggesting that the conformational changes are associated with the dynamics of PNA wrapping on the tubular surfaces. The average end-to-end distance of PNA in the CNT/PNA system is calculated to be below 25.0 Å for the last 10 ns of the MD simulation. For BNNT/PNA, the extended conformation followed by axial wrapping of PNA is reflected by an increase in the average end-to-end distance at ∼30.0 Å.
3.2. Effect of the nanotube diameter and chirality on the adsorption of PNA
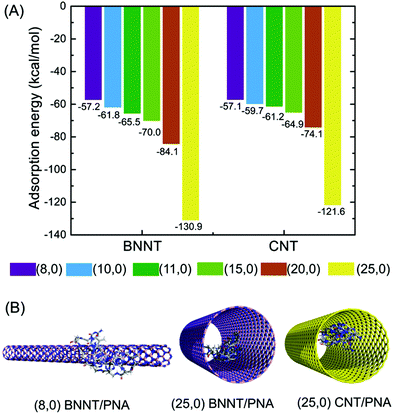
The chirality dependence of the CNT properties has been shown to be important in the dispersion of CNTs.46 A previous study by Zheng et al.8 showed that ssDNA can bind to CNTs in an aqueous environment and form stable hybrids where ssDNA prefers to helically wrap around the nanotube sidewall. This facilitates the dispersion and separation of nanotubes based on their chirality. A previous study showed that the lower surface curvature of a (7,7) BNNT (diameter of 9.60 Å) leads to a stronger interaction with nucleobases than a large diameter (5,0) BNNT (diameter of 4.16 Å).30 A similar trend in the effect of the surface curvature on the binding energy between a nucleobase and CNT was predicted.31Gas-phase MC simulations were employed to compare the trends in adsorption energy of PNA on the CNT and BNNT surface as a function of the nanotube diameter or curvature effect. Since MC algorithms are flexible and scalable, this technique can significantly reduce complex models to a set of basic events and interactions, thereby reasonably predicting the trends in the adsorption energy of the PNA–nanotube hybrids. We considered only zigzag nanotube models of varying diameter in this set of studies because of the limitation in proposing a general strategy in binding based on the nanotube chirality selectivity at a computational level. We, therefore, realize that developing a flexible approach for characterizing the effect of the PNA interaction strength with CNTs and BNNTs of varying diameter or curvature effects would be an improved approach to highlight the significance of the trends in intermolecular interactions. Since, for a given chirality, BNNTs and CNTs have an almost similar diameter, the trends in adsorption energy indicate BNNTs to have larger adsorption energy compared to the CNT counterparts and the adsorption energy increases with an increase in the nanotube diameter (Fig. 7A). The decrease in nanotube curvature with an increase in diameter leads to an increase in adsorption energy, which may be accounted for by enhanced vdW π-stacking interactions between the aromatic nucleobases of PNA and the nanotube sidewall and the curvature effect contributing to the enhanced interaction and self-assembly of PNA.
The (8,0) chirality nanotube has comparable adsorption energy towards PNA as shown in Fig. 7A. Interestingly, for the largest diameter (25,0) nanotube model considered, PNA prefers to be encapsulated within the nanotube rather than being adsorbed along the sidewall (Fig. 7B). This indicates that for the larger diameter nanotubes, encapsulation is the energetically favored mode of adsorption with a significant increase in adsorption energy. Although MC simulations in the gas phase are limited in providing definitive quantitative insights on the nature of adsorption or preferential selectivity in wrapping as predicted from all-atom MD simulations in aqueous solution, they do ascertain the diameter or curvature effect on the interaction strength in the PNA/nanotube hybrids.
A previous DFT study on the adsorption of adenine and thymine nucleobases on armchair (6,6) and zigzag (8,0) CNTs showed that the electronic properties of the nanotubes were not changed significantly upon adsorption and the main contribution to the noncovalent interaction was between the delocalized π-orbitals from the nucleobases and the nanotubes.47 A DFT study on the interaction of the pyrazinamide drug with (5,5) and (9,0) SWCNTs showed that for nanotubes with almost comparable diameters, noncovalent π-stacking interactions were stronger in the zigzag nanotubes compared to the armchair counterparts and subsequently the zigzag nanotubes exhibited higher interaction strength than the armchair counterparts.48 It was also reported that the adsorption of aromatic amino acids on armchair and zigzag SWCNTs using self-consistent charge density-functional tight-binding calculations showed that amino acid complexes in zigzag nanotubes were more stable than armchair CNTs due to their larger binding energy.49 A recent study on the effects of the chirality and diameter of CNTs on PW3 peptide adsorption indicated that the aromatic content and π–π stacking had a dominant role in the adsorption of the PW3 peptide on the nanotube surface and zigzag nanotubes might be a good option for future biomedical applications under physiological conditions.50 For nanotubes with almost comparable diameters but varying in chirality, the vdW energy was shown to be larger for chiral and zigzag nanotubes over armchair ones, which was attributed to the high aromatic content in the former.
4. Summary
In this work, atomistic simulations were employed to provide molecular-level understanding of the nature of the interaction, adsorption energy profile, and self-assembly of PNA onto CNTs and BNNTs. The results show that a 6-mer PNA oligopeptide folds into a random self-aggregated structure, stabilized by vdW π-stacking interactions. In presence of the CNT and BNNT, PNA provides definitive contrasts in the nature of assembly; PNA wraps along the circumferential direction of the CNT but adopts an extended configuration on the BNNT in aqueous solution. Quantitative parameters like the radius of gyration, center of mass distance, number of hydrophobic contacts, and radial distribution function support the observed trends in the preferential adsorption of PNA (circumferential vs. axial wrapping) onto CNTs and BNNTs.The gas-phase MC simulations confirm that PNA exhibits higher adsorption energy on the BNNT compared to the CNT counterpart and the diameter of the nanotube is an important determinant; e.g., for the (25,0) CNT and BNNT models, PNA prefers to be encapsulated rather than being adsorbed along the nanotube sidewall. The ability of PNA to mimic the structural characteristics of DNA represents the first unique approach to efficient surface hybridization and directing the formation of stable self-assembled hybrids at the solid–liquid interface. The results obtained from MD and MC simulations are expected to be of relevance in fabricating nanoscale devices based on novel PNA-based archetypal hybrid materials for biosensing and other health-related applications.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We thank Dr S. Höefinger and S. Gowtham for the helpful discussions. The superior high–performance computing cluster at Michigan Technological University was utilized in obtaining the results presented in the study.References
- C. Staii and A. T. Johnson, DNA-Decorated Carbon Nanotubes for Chemical Sensing, Nano Lett., 2005, 5, 1774–1778 CrossRef CAS PubMed.
- M. V. Karachevtsev, G. O. Gladchenko, A. M. Plokhotnichenko, V. S. Leontiev and V. A. Karachevtsev, Adsorption of Biopolymers on SWCNT: Ordered Poly(rC) and Disordered Poly(rI), J. Phys. Chem. B, 2013, 117, 2636–2644 CrossRef CAS PubMed.
- Y. Choi, I. S. Moody, P. C. Sims, S. R. Hunt, B. L. Corso, I. Perez, G. A. Weiss and P. G. Collins, Single–Molecule Lysozyme Dynamics Monitored by an Electronic Circuit, Science, 2012, 335, 319–324 CrossRef CAS PubMed.
- X. Zhong, S. Mukhopadhyay, S. Gowtham, R. Pandey and S. P. Karna, Applicability of Carbon and Boron Nitride Nanotubes as Biosensors: Effect of Biomolecular Adsorption on the Transport Properties of Carbon and Boron Nitride Nanotubes, Appl. Phys. Lett., 2013, 102, 133705 CrossRef.
- M. Zheng, A. Jagota, M. S. Strano, A. P. Santos, P. Barone, S. G. Chou, B. A. Diner, M. S. Dresselhaus, R. S. McLean and G. B. Onoa, et al., Structure–Based Carbon Nanotube Sorting by Sequence–Dependent DNA Assembly, Science, 2003, 302, 1545–1548 CrossRef CAS PubMed.
- Z. Gao, C. Zhi, Y. Bando, D. Golberg and T. Serizawa, Noncovalent Functionalization of Boron Nitride Nanotubes in Aqueous Media Opens Application Roads in Nanobiomedicine, Nanobiomed., 2014, 1, 7 CrossRef PubMed.
- S. Meng, W. L. Wang, P. Maragakis and E. Kaxiras, Determination of DNA–Base Orientation on Carbon Nanotubes through Directional Optical Absorbance, Nano Lett., 2007, 7, 2312–2316 CrossRef CAS PubMed.
- M. Zheng, A. Jagota, E. D. Semke, B. A. Diner, R. S. McLean, S. R. Lustig, R. E. Richardson and N. G. Tassi, DNA–Assisted Dispersion and Separation of Carbon Nanotubes, Nat. Mater., 2003, 2, 338–342 CrossRef CAS PubMed.
- H. Gao and Y. Kong, Simulation of DNA–Nanotube Interactions, Annu. Rev. Mater. Res., 2004, 34, 123–150 CrossRef CAS.
- C. Hu, Y. Zhang, G. Bao, Y. Zhang, M. Liu, Z. L. Wang and D. N. A. Functionalized, Single–Walled Carbon Nanotubes for Electrochemical Detection, J. Phys. Chem. B, 2005, 109, 20072–20076 CrossRef CAS PubMed.
- K. A. Williams, P. T. M. Veenhuizen, B. G. de la Torre, R. Eritja and C. Dekker, Nanotechnology: Carbon Nanotubes with DNA Recognition, Nature, 2002, 420, 761 CrossRef CAS PubMed.
- S. Mukhopadhyay, S. Gowtham, R. H. Scheicher, R. Pandey and S. P. Karna, Theoretical Study of Physisorption of Nucleobases on Boron Nitride Nanotubes: A New Class of Hybrid Nano–Biomaterials, Nanotechnology, 2010, 21, 165703 CrossRef PubMed.
- Z. Gao, C. Zhi, Y. Bando, D. Golberg and T. Serizawa, Isolation of Individual Boron Nitride Nanotubes via Peptide Wrapping, J. Am. Chem. Soc., 2010, 132, 4976–4977 CrossRef CAS PubMed.
- C. Zhi, Y. Bando, W. Wang, C. Tang, H. Kuwahara and D. Golberg, DNA–Mediated Assembly of Boron Nitride Nanotubes, Chem. – Asian J., 2007, 2, 1581–1585 CrossRef CAS PubMed.
- P. E. Nielsen, Peptide nucleic acid (PNA) From DNA Recognition to Antisense and DNA Structure, Biophys. Chem., 1997, 68, 103–108 CrossRef CAS PubMed.
- P. E. Nielsen and M. Egholm, An Introduction to Peptide Nucleic Acid, Curr. Issues Mol. Biol., 1999, 1, 89–104 CAS.
- P. E. Nielsen and M. Egholm, Peptide Nucleic Acids: Protocols and Applications, Horizon Scientific Press, Wymondham, UK, 1999 Search PubMed.
- V. V. Demidov, V. N. Potaman, M. D. Frank–Kamenetskii, M. Egholm, O. Buchard, S. H. Sönnichsen and P. E. Nielsen, Stability of Peptide Nucleic Acids in Human Serum and Cellular Extracts, Biochem. Pharmacol., 1994, 48, 1310–1313 CrossRef CAS PubMed.
- A. Paul, R. M. Watson, P. Lund, Y. Xing, K. Burke, Y. He, E. Borguet, C. Achim and D. H. Waldeck, Charge Transfer Through Single–Stranded Peptide Nucleic Acid Composed of Thymine Nucleotides, J. Phys. Chem. C, 2008, 112, 7233–7240 CrossRef CAS.
- J. C. Hanvey, N. C. Peffer, J. E. Bisi, S. A. Thomson, R. Cadilla, J. A. Josey, D. J. Ricca, C. F. Hassman, M. A. Bonham and K. G. Au, et al., Antisense and Antigene Properties of Peptide Nucleic Acids, Science, 1992, 258, 1481–1485 CrossRef CAS PubMed.
- R. Chakrabarti and A. M. Klibanov, Nanocrystals Modified with Peptide Nucleic Acids (PNAs) for Selective Self–Assembly and DNA Detection, J. Am. Chem. Soc., 2003, 125, 12531–12540 CrossRef CAS PubMed.
- S. Tomac, M. Sarkar, T. Ratilainen, P. Wittung, P. E. Nielsen, B. Norden and A. Gräslund, Ionic Effects on the Stability and Conformation of Peptide Nucleic Acid (PNA) Complexes, J. Am. Chem. Soc., 1996, 118, 5544–5552 CrossRef CAS.
- K. V. Singh, R. R. Pandey, X. Wang, R. Lake, C. S. Ozkan, K. Wang and M. Ozkan, Covalent Functionalization of Single Walled Carbon Nanotubes with Peptide Nucleic Acid: Nanocomponents for Molecular Level Electronics, Carbon, 2006, 44, 1730–1739 CrossRef CAS.
- D. Bonifazi, L.-E. Carloni, V. Corvaglia and A. Delforge, Peptide Nucleic Acids in Materials Science, Artif. DNA, 2012, 3, 112–122 CrossRef PubMed.
- K. Kerman, Y. Morita, Y. Takamura, E. Tamiya, K. Maehashi and K. Matsumoto, Peptide Nucleic Acid–Modified Carbon Nanotube Field–Effect Transistor for Ultra–Sensitive Real–Time Detection of DNA Hybridization, NanoBiotechnol., 2005, 1, 65–70 CrossRef CAS.
- M. Moccia, M. F. A. Adamo and M. Saviano, Insights on Chiral, Backbone Modified Peptide Nucleic Acids: Properties and Biological Activity, Artif. DNA, 2014, 5, e1107176 CrossRef PubMed.
- M. Li, T. Zengeya and E. Rozners, Short Peptide Nucleic Acids Bind Strongly to Homopurine Tract of Double Helical RNA at pH 5.5, J. Am. Chem. Soc., 2010, 132, 8676–8681 CrossRef CAS PubMed.
- P. Weroński, Y. Jiang and S. Rasmussenz, Molecular Dynamics Study of Small PNA Molecules in Lipid–Water System, Biophys. J., 2007, 92, 3081–3091 CrossRef PubMed.
- W. He, J. Dai, T. Li, Y. Bao, F. Yang, X. Zhang and H. Uyama, Novel Strategy for the Investigation on Chirality Selection of Single– Walled Carbon Nanotubes with DNA by Electrochemical Characterization, Anal. Chem., 2018, 90, 12810–12814 CrossRef CAS PubMed.
- S. Mukhopadhyay, S. Gowtham, R. H. Scheicher, R. Pandey and S. P. Karna, Theoretical study of physisorption of nucleobases on boron nitride nanotubes: a new class of hybrid nano–biomaterials, Nanotechnology, 2010, 21, 165703 CrossRef PubMed.
- S. Gowtham, R. H. Scheicher, R. Pandey, S. P. Karna and R. Ahuja, First-principles study of physisorption of nucleic acid bases on small-diameter carbon nanotubes, Nanotechnology, 2008, 19, 125701 CrossRef CAS PubMed.
- N. Foloppe and A. D. MacKerell Jr., All-Atom Empirical Force Field for Nucleic Acids: I. Parameter Optimization Based on Small Molecule and Condensed Phase Macromolecular Target Data, J. Comput. Chem., 2000, 21, 86–104 CrossRef CAS.
- E. Joselevich, Electronic Structure and Chemical Reactivity of Carbon Nanotubes: A Chemist's View, ChemPhysChem, 2004, 5, 619–624 CrossRef CAS PubMed.
- M. Thomas, M. Enciso and T. A. Hilder, Insertion Mechanism and Stability of Boron Nitride Nanotubes in Lipid Bilayers, J. Phys. Chem. B, 2015, 119, 4929–4936 CrossRef CAS PubMed.
- S. K. Mudedla, K. Balamurugan and V. Subramanian, Unravelling the Structural Changes in α-Helical Peptides on Interaction with Convex, Concave, and Planar Surfaces of Boron-Nitride-Based Nanomaterials, J. Phys. Chem. C, 2016, 120, 28246–28260 CrossRef CAS.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, Ch Chipot, R. D. Skeel, L. Kale and K. Schulten, Scalable Molecular Dynamics with NAMD, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- P. Mark and L. Nilsson, Structure and Dynamics of the TIP3P, SPC, and SPC/E Water Models at 298 K, J. Phys. Chem. A, 2001, 105, 9954–9960 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, Particle Mesh Ewald: An N-log(N) Method for Ewald Sums in Large Systems, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- N. Saikia and R. Pandey, Polarity–Induced Surface Recognition and Self–Assembly of Noncanonical DNA Nucleobases on Hexagonal Boron Nitride, J. Phys. Chem. C, 2018, 122, 3915–3925 CrossRef CAS.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, III, DREIDING: A generic forcefield, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- F. Totsingan, V. Jain and M. M. Green, Helix control in Polymers: Case of Peptide Nucleic Acids (PNAs), Artif. DNA, 2012, 3, 31–44 CrossRef PubMed.
- S. Sen and L. Nilsson, MD Simulations of Homomorphous PNA, DNA, and RNA Single Strands: Characterization and Comparison of Conformations and Dynamics, J. Am. Chem. Soc., 2001, 123, 7414–7422 CrossRef CAS PubMed.
- G. C. Shields, C. A. Laughton and M. Orozco, Molecular Dynamics Simulation of a PNA‚ DNA‚ PNA Triple Helix in Aqueous Solution, J. Am. Chem. Soc., 1998, 120, 5895–5904 CrossRef CAS.
- S. K. Mudedla, K. Balamurugan and V. Subramanian, Unravelling the Structural Changes in α-Helical Peptides on Interaction with Convex, Concave, and Planar Surfaces of Boron-Nitride-Based Nanomaterials, J. Phys. Chem. C, 2016, 120, 28246–28260 CrossRef CAS.
- M. C. Amirani and T. A. Tang, QM:MM model for the interaction of DNA nucleotides with carbon nanotubes, Phys. Chem. Chem. Phys., 2015, 17, 7564–7575 RSC.
- Y. V. Shtogun, L. M. Woods and G. I. Dovbeshko, Adsorption of Adenine and Thymine and Their Radicals on Single–Wall Carbon Nanotubes, J. Phys. Chem. C, 2007, 111, 18174–18181 CrossRef CAS.
- N. Saikia and R. C. Deka, A comparison of the effect of nanotube chirality and electronic properties on the π–π interaction of single–wall carbon nanotubes with pyrazinamide antitubercular drug, Int. J. Quantum Chem., 2013, 113, 1272–1284 CrossRef CAS.
- C. Wang, S. Li, R. Zhang and Z. Lin, Adsorption and properties of aromatic amino acids on single–walled carbon nanotubes, Nanoscale, 2012, 4, 1146–1153 RSC.
- L. Tohidifar and N. L. Hadipour, Tracing chirality, diameter dependence, and temperature-controlling of single-walled carbon nanotube non-covalent functionalization by biologically compatible peptide: insights from molecular dynamics simulations, J. Mol. Model., 2019, 25(274), 1–12 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Simulation snapshot at 50 ns of a 6-mer PNA (NH2–GAACTC–COOH) oligopeptide. Simulation snapshots of CNT/PNA and BNNT/PNA hybrids at different initial configurations of PNA. Contact area for CNT (BNNT)/PNA hybrids. RMSF of (11,0) CNT/PNA and (11,0) BNNT/PNA. Mass density profile of water in CNT (BNNT)/PNA hybrids. Histograms of the minimum interaction distance between the individual PNA nucleobases and BNNT sidewall and the number of hydrophobic contacts between the nucleobases and BNNT sidewall. See DOI: 10.1039/d0cp05759b |
| This journal is © the Owner Societies 2021 |