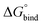Open Access Article
Open Access ArticleThermodynamic driving forces of guest confinement in a photoswitchable cage†
Selina
Juber
 a,
Sebastian
Wingbermühle
a,
Sebastian
Wingbermühle
 a,
Patrick
Nuernberger
a,
Patrick
Nuernberger
 b,
Guido H.
Clever
b,
Guido H.
Clever
 c and
Lars V.
Schäfer
c and
Lars V.
Schäfer
 *a
*a
aTheoretical Chemistry, Ruhr-University Bochum, D-44780 Bochum, Germany. E-mail: lars.schaefer@ruhr-uni-bochum.de; Tel: +49-234-3221582
bInstitut für Physikalische und Theoretische Chemie, Universität Regensburg, D-93040 Regensburg, Germany
cFaculty of Chemistry and Chemical Biology, TU Dortmund University, D-44227 Dortmund, Germany
First published on 22nd February 2021
Abstract
Photoswitchable cages that confine small guest molecules inside their cavities offer a way to control the binding/unbinding process through irradiation with light of different wavelengths. However, detailed characterization of the structural and thermodynamic consequences of photoswitching is very challenging to achieve by experiments alone. Thus, all-atom molecular dynamics (MD) simulations were carried out to gain insight into the relationship between the structure and binding affinity. Binding free energies of the B12F122− guest were obtained for all photochemically accessible forms of a photoswitchable dithienylethene (DTE) based coordination cage. The MD simulations show that successive photo-induced closure of the four individual DTE ligands that form the cage gradually decreases the binding affinity. Closure of the first ligand significantly lowers the unbinding barrier and the binding free energy, and therefore favours guest unbinding both kinetically and thermodynamically. The analysis of different enthalpy contributions to the free energy shows that binding is enthalpically unfavourable and thus is an entropy-driven process, in agreement with the experimental data. Separating the enthalpy into the contributions from electrostatic, van der Waals, and bonded interactions in the force field shows that the unfavourable binding enthalpy is due to the bonded interactions being more favourable in the dissociated state, suggesting the presence of structural strain in the bound complex. Thus, the simulations provide microscopic explanations for the experimental findings and provide a possible route towards the targeted design of switchable nanocontainers with modified binding properties.
1 Introduction
Enzymes possess the ability to significantly enhance the speed of chemical reactions, leading only to the specific product desired. In addition, they work under moderate conditions and can be regulated precisely. Combining these qualities in artificially synthesized systems is a goal in modern supramolecular chemistry. For this purpose, macromolecular assemblies are obtained through different routes. Besides classic organic synthesis, more modular approaches based on the self-assembly of macromolecules by coordination chemistry have been used to synthesize compounds that possess a cavity, in which other molecules can bind.1–4 These cavities are designed to create a specific micro-environment, which enables small molecule binding as well as targeted catalysis of chemical reactions.5,6 Such systems are referred to as host–guest systems. However, ideal shape complementarity does not always lead to high binding affinities, as was shown for some enzymes.7 This intricate relationship between the structure and function poses a challenge for designing such systems.8 A first step towards obtaining systems that have catalytic abilities similar to enzymes is designing molecular cage-like structures.9–11 Besides the capability to promote reactions within their nanoconfined interior,5,6,8,9,12–16 artificial hosts have also been equipped with switchable functionality17 to allow external control over their action, e.g., by regulating the substrate uptake and product release.18–21 One example of such a stimuli-responsive cage structure is the photochromic dithienylethene (DTE) cage designed by Clever and coworkers.22Fig. 1 shows this cage, which consists of four DTE ligands that coordinate with two palladium(II) ions in a square-planar fashion to create a molecule with a cavity enclosed by the four organic bridges to the sides and the metal ions at the top and bottom.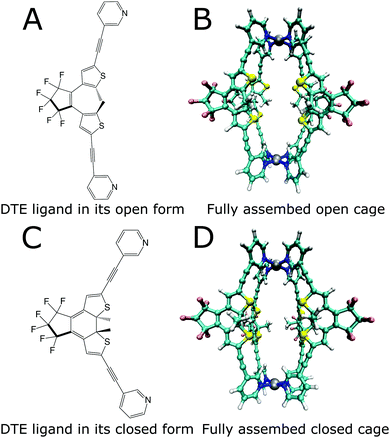 | ||
| Fig. 1 Lewis structures of the open (A) and closed (C) photoisomers of the DTE ligand and structures of the photoswitchable cage formed by the ligands (B and D). | ||
The DTE ligand, four of which form the cage, can exist in two different photoisomeric forms. In solution, two conformations of the open-ring form coexist in almost equal amounts, a parallel conformation where the heterocyclic rings are strongly twisted out of the plane of the cyclopentene, and an antiparallel conformation with one heterocyclic ring slightly tilted upwards and the other one downwards with respect to this plane and both methyl groups residing in close proximity. Only from the latter conformation is the photocyclization possible.23,24 Several approaches exist to increase the amount of the antiparallel form, e.g., by spatial confinement25,26 or by bridging constraints.27,28 Forming a cage puts a similar constraint on the open DTE ligands, and hence structures corresponding to the antiparallel conformation are prevalent, as is confirmed by the optimizations displayed in Fig. 1, thus facilitating photo-induced ring closure.
Irradiation of the more flexible open-ring form (Fig. 1a) with UV light in the spectral range around 365 nm yields the more rigid closed-ring photoisomer shown in Fig. 1c. This photoswitching process is reversible since irradiation of closed DTE with visible light around 600 nm leads again to the open DTE ligand.23 DTE derivatives have been investigated by advanced spectroscopy methods with femtosecond time resolution,24,27–38 disclosing many aspects of the photoswitching dynamics. Reversible switching is also possible for DTE ligands in cage systems as investigated here.22 Cages with all four ligands open and closed are shown in Fig. 1b and d, respectively.
The Clever group characterised the reversible binding of a B12F122− dianion to these cages. NMR titration experiments showed that this guest binds inside the open and also the closed form of the cage. The binding constants were determined by non-linear regression methods from NMR data22 and show that the open cage has a higher affinity towards the guest (Ka = 3.2 × 104 M−1) than the closed cage (Ka = 6.7 × 102 M−1).
NMR titration and isothermal titration calorimetry (ITC) experiments were performed to obtain further thermodynamic information on the guest binding.39 For the closed system, ΔHbind is 10 kJ mol−1 and ΔSbind is 95 J K−1 mol−1, as obtained from ITC, and the total free energy of binding is −19.0 kJ mol−1 at 298 K. The ITC experiments for the open cage yielded a ΔHbind of 6 kJ mol−1, ΔSbind of 110 J K−1 mol−1 and a ΔGbind of −26.6 kJ mol−1. The NMR titration experiment yielded slightly different values (which is not surprising because both methods monitor different sub-sets of processes associated with the combination of the host and guest solutions40). For the closed system, ΔHbind is 0.6 kJ mol−1, ΔSbind is 56 J K−1 mol−1 and ΔGbind is −15.9 kJ mol−1. For the open cage, NMR titration yielded a ΔHbind of 30 kJ mol−1, ΔSbind is 187 J K−1mol−1 and ΔGbind is −24.5 kJ mol−1 at 298 K.41 The binding free energies obtained with both methods thus show that the guest binding is favourable (i.e., is associated with a negative free energy change) for both systems, with the open cage binding the guest more favourably than the closed cage (by about 8 kJ mol−1). While the binding free energy values obtained from the two experimental methods (ITC and NMR) are in relatively good agreement with each other, the contributions from entropy and enthalpy differ significantly. However, both methods agree that the enthalpic contribution is unfavourable, and hence the binding process is driven by entropy. While providing important insight into the thermodynamics governing the host–guest binding, these data neither provide any atomic-level insight nor information on when the guest unbinding occurs during the stepwise photoswitching process from an all-open-ligand cage to an all-closed-ligand cage. Experimental data on a closely related host–guest system indicate early guest rejection during the step-wise closure of four DTE photoswitches.41
In the present study, molecular dynamics (MD) simulations in an explicit solvent were employed to obtain atomic level insight into the host–guest interactions underlying the observed thermodynamic signatures. For this purpose, a molecular mechanics force field was parametrized to accurately describe the structure of the coordination cage in classical MD simulations. The different, fully or partially switched photoisomeric forms of the cage are easily accessible to classical simulation on multi-nanosecond timescales. While upon excitation, DTE molecules may undergo intersystem crossing to a triplet state lasting for microseconds, the major pathways for photoswitching occur on ultrafast timescales.24,27–38 For the cage systems at thermodynamic equilibrium, this rapid photoswitching process does not determine the differences in the free energy of binding of the different photoisomeric forms of the cage towards the guest. Instead, it is the structural change of the cage as a consequence of photoswitching that leads to different binding thermodynamics, which involves molecular interactions and structural dynamics on timescales of nanoseconds and beyond. In the present work, free energy simulations were carried out to investigate the impact of switching of specific DTE ligands in the cage on the host–guest interactions under equilibrium conditions. This study thus focuses on the thermodynamic details of binding by reconstructing at the atomic level the dynamic binding/unbinding pathways for all possible cage photoisomers, and not separately considering stereoisomers.
2 Methods
2.1 Force field parametrization
An initial force field topology of the host was generated using CHIMERA (version 1.12),42 with initial parameters taken from the GAFF force field.43 The C2-symmetric DTE ligand, configurationally stable in its closed form, epimerizes in its open antiparallel form between P and M helical enantiomers, which leads to a total of six cage stereoisomers (PPPP, MMMM, PMMM, MPPP, PPMM, and PMPM). It is experimentally known that in solution, the open-form cage exists as a mixture of all six, but only the PPMM meso form was crystallized39 in complex with B12F122−, which was thus used to set up the calculations. The atomic partial charges for the isolated (single) DTE ligands (open and closed forms) were calculated using the AM1-BCC method.44 An additional atomic partial charge calculation step was necessary for the palladium centers. The different chemical environment due to the presence of palladium affects the atomic partial charges of the ligand atoms, especially of the nitrogen atoms that are bound to palladium. This additional charge calculation step was performed using the DFT functional B3LYP with a 6-31G* basis set for all but the palladium atoms, for which the Stuttgart–Dresden (SDD) pseudopotentials45 were used. A polarizable continuum (PCM) model46 for acetonitrile was used and the calculations were performed with GAUSSIAN 09. The Hirshfeld charges of the atoms were calculated. This charge calculation was performed for a single (isolated) ligand as well as for the whole cage. The atomic partial charges of symmetry-related atoms in the four DTE ligands in the cage were averaged. Then, the Hirshfeld charge difference Δq between these ligand atomic partial charges and the atomic partial charges of the isolated ligand was subtracted from the AM1-BCC charges calculated in the first step. In this way, the influence of the palladium centers on the partial charges is captured in Δq. The charge difference Δq was small for the distant ligand atoms and larger for the ligand atoms in proximity to the Pd centers. Table S1 and Fig. S1 (ESI†) show the resulting charges. Lennard-Jones (6,12) parameters were taken from the GAFF force field. For Pd, the Lennard-Jones (6,12) parameters from the study by Yoneya and coworkers47 were taken. For BF4− and B12F122−, the Lennard-Jones (6,12) parameters were taken from the study by de Andrade and coworkers,48 and Hirshfeld charges were calculated with B3LYP/6-31G*. For the Pd–N bonds, relaxed potential energy surface scans were performed by the PM6 semiempirical method. Single point energies of the geometry-optimized structures obtained from the PM6 bond scans were then obtained with B3LYP/6-31G*. The same procedure was followed for the N–Pd–N angle. The potential energy surfaces are shown in Fig. S2 and S3 (ESI†). For the Pd–N bond, a Morse potential was used to account for anharmonicities that have become important already at relatively small bond length deviations from the equilibrium value.To quantify the quality of the structural description, the root mean square deviation (RMSD) of the cage structure after geometry optimization with B3LYP/6-31G*, PM6, and the force field with respect to the X-ray crystal structure39 was calculated (Fig. S4, ESI†).
In addition to comparing the structures from quantum chemical and force field calculations, also the binding energies in vacuum were compared. The structures of the DTE cage, the B12F122− guest, and the host/guest complex were optimized in a vacuum with PM6 using GAUSSIAN 09. With the force field, the structures were optimized by conjugate gradient energy minimization until machine precision using GROMACS compiled in double precision; for these force field optimizations, no cutoffs were used for the nonbonded interactions. The binding energy was obtained as the difference between the bound system and the sum of the two separate molecules (Table S2, ESI†).
2.2 Free energy simulations
All simulations were carried out with GROMACS (version 2016.3)49 patched with PLUMED (version 2.3.3).50 To obtain potentials of mean force (PMFs), the umbrella sampling method51 was used. The simulations were set up in a 4.97 nm × 4.97 nm × 5.85 nm rectangular box. The cage was oriented such that the Pd–Pd axis was aligned along the x-axis. The B12F122− guest was placed inside the host cavity. The system was solvated with 1520 acetonitrile molecules and 2 BF4− anions were added to keep the overall charge of the simulation box neutral, which resulted in a system comprised of 9376 atoms in total. The acetonitrile force field parameters were taken from the study by Caleman and coworkers.52 The equations of motion were integrated with time steps of 0.5 fs. Periodic boundary conditions were used. The buffered Verlet neighbor list was used to evaluate the Lennard-Jones (6,12) interactions up to a distance cutoff of 1.0 nm. Long-range electrostatic interactions were treated with the smooth particle-mesh Ewald algorithm53 with a 1.0 nm distance to switch between real and reciprocal space and a 0.12 nm grid spacing. The temperature of the system was kept at 298 K with the velocity rescaling thermostat developed by Bussi and coworkers54 with a coupling time constant of 0.1 ps. For constant 1 bar pressure, isotropic pressure coupling with the Berendsen barostat was used, with a 2 ps coupling time constant and a compressibility of 4.5 × 10−5 bar−1.The GROMACS pull-code was used to generate starting structures for the umbrella sampling simulations, with the guest placed at different points along the reaction coordinate, which was chosen as the z-component of the vector connecting the centre of mass (COM) of the cage and the COM of the guest. The guest was pulled with a harmonic spring with a force constant of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 nm−2, moving away from the COM of the host with a constant velocity of 0.1 nm ns−1. This stiff spring was necessary to be able to extract structures in the vicinity of the barrier, where the curvature of the free energy landscape is high. To avoid the situation where the cage was pulled together with the guest, a harmonic position restraint (with force constant 10
000 kJ mol−1 nm−2, moving away from the COM of the host with a constant velocity of 0.1 nm ns−1. This stiff spring was necessary to be able to extract structures in the vicinity of the barrier, where the curvature of the free energy landscape is high. To avoid the situation where the cage was pulled together with the guest, a harmonic position restraint (with force constant 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 nm−2) acting on the COM of the two Pd atoms was applied, such that the cage could still rotate but not significantly translate.
000 kJ mol−1 nm−2) acting on the COM of the two Pd atoms was applied, such that the cage could still rotate but not significantly translate.
For the umbrella sampling simulations, snapshots were extracted from the above pulling simulations such that the z-component of the host–guest distance increases by about 0.05 nm between neighboring windows. In the vicinity of the barrier, additional windows were added to ensure the necessary overlap between the histograms in the umbrella sampling simulations. Therefore, the exact number of umbrella windows used varied between the individual systems, ranging between 42 and 50 windows. For each umbrella window, 50 ns of MD sampling was performed, with the same MD parameters as described above. The force constants of the umbrella potential were 1000 kJ mol−1 nm−2 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 nm−2 in the additional umbrella windows that were added to the barrier region to ensure the necessary overlap of the umbrella histograms. The total accumulated sampling time of the umbrella sampling simulations amounts to 23.1 μs. The potential of mean force (PMF) was obtained with the GROMACS tool gmx wham.55 The default tolerance of 10−6 was used as a convergence criterion for the PMF. The statistical error of the PMFs was estimated via Bayesian bootstrapping, as implemented in gmx wham. The PMFs with error bars are shown in Fig. S5 (ESI†).
000 kJ mol−1 nm−2 in the additional umbrella windows that were added to the barrier region to ensure the necessary overlap of the umbrella histograms. The total accumulated sampling time of the umbrella sampling simulations amounts to 23.1 μs. The potential of mean force (PMF) was obtained with the GROMACS tool gmx wham.55 The default tolerance of 10−6 was used as a convergence criterion for the PMF. The statistical error of the PMFs was estimated via Bayesian bootstrapping, as implemented in gmx wham. The PMFs with error bars are shown in Fig. S5 (ESI†).
To reduce the volume that the guest needs to sample in the unbound state, a flat-bottom restraining potential was applied that limits the motion of the guest in the xy-plane (i.e., orthogonal to the reaction coordinate),
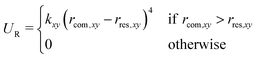 | (1) |
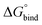 , was analytically corrected for (see below).
, was analytically corrected for (see below).
Furthermore, the symmetry of the system needs to be considered.56 The B12F122− guest is an icosahedral molecule and consequently many symmetry-equivalent binding orientations are possible. Likewise, the cage is also symmetric. One would need to equally sample all (symmetry-equivalent) mutual orientations in all umbrella windows, which might be no problem for the unbound state, but, due to the energy barriers associated with the reorientation of the guest inside the cage, it is hard to achieve within the simulation time for the bound state. This was resolved by restraining two angles between the host and guest to ensure that the guest samples have only one orientation relative to the host. These orientation restraints do not necessitate a correction to the PMF in the present case because all symmetry-equivalent orientations are equally likely at all points along the reaction coordinate and only one orientation is sampled in all umbrella windows, i.e., the orientation restraint leads to an entropic offset that is constant along the entire reaction coordinate. To fix the relative orientation of the guest with respect to the host, harmonic restraining potentials were applied on the two angles shown in Fig. S6 (ESI†), with the minimum of the restraining potential set at zero degrees and a force constant of 400 kJ mol−1 rad−2. The angles were measured with and without restraints in one umbrella window where the guest was bound inside the host cavity. This was done for the open and the closed cage. Fig. S7 (ESI†) shows that the angle restraints applied have the desired effect.
The free energy of binding was calculated by integrating over the PMF57,58 according to59,60
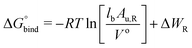 | (2) |
In eqn (2), R is the gas constant, T is the temperature, V0 = 1.661 nm3 is the standard state volume at c = 1 mol l−1, lb is the bound length, and ΔWR is the PMF depth defined as59
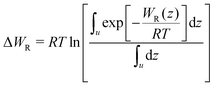 | (3) |
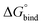 .58,59 The bound length is the Boltzmann-weighted length integrated over the bound region,
.58,59 The bound length is the Boltzmann-weighted length integrated over the bound region,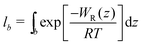 | (4) |
The area in the xy-plane available for the guest in the not fully bound state under the influence of the restraining potential is60
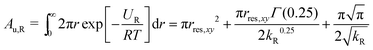 | (5) |
In addition to the calculation of the free energy of binding, the enthalpy of binding was calculated and the individual energetic contributions of the different components of the system were analysed. Internal energy differences, as obtained from the force field, are a good approximation for enthalpy differences because the pΔV term is negligible in condensed liquid phase systems at ambient pressure. For each umbrella window, the total potential energy (as obtained from the force field) was calculated and partitioned into bonded, electrostatic and Lennard-Jones contributions. Bonded contributions include bond, angle, and dihedral terms of the force field. Furthermore, the Lennard-Jones and electrostatic interaction energies of the individual parts of the system with each other were calculated, e.g., the interaction energy of the host with the guest, with the solvent, etc. As it is less straightforward to obtain the individual pairwise contributions to the interaction energies from the PME grid part,61 the nonbonded cutoff was set to 2.4 nm in the analysis of the interaction energies, including long-range contributions up to that distance. The total interaction energy calculated for the real space cutoff of 1.0 nm (used in the MD simulations) and for the cutoff of 2.4 nm with and without the long-range Coulomb interactions (from the PME grid) is shown in Fig. S8 (ESI†), showing that the long-range interactions are almost quantitatively included with the large 2.4 nm cutoff.
For each umbrella window, the energies were averaged over simulation time, such that the average energy in each window can be plotted over the reaction coordinate, thus giving insight into the energy changes along the reaction coordinate. The statistical errors were estimated by block-averaging over the time series of the total interaction energy.
The enthalpy of binding was calculated according to eqn (6).62
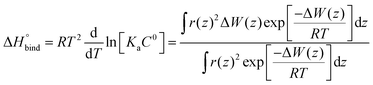 | (6) |
3 Results and discussion
3.1 Free energies
First, the capability of the force field to describe the structure of the DTE cage and the energetics of B12F122− binding was validated by comparing force field calculations to quantum chemical calculations at the DFT level. The results confirm that the force field derived in this work can provide a realistic description of the system (Fig. S4 and Table S2, ESI†) and can hence be used for obtaining atomic-level insights into the thermodynamic driving forces of host–guest binding at room temperature from free energy simulations. Fig. 2 shows the free energy profiles (potentials of mean force, PMFs) for B12F122− binding to all possible photoisomeric forms of the cage, i.e., 4 open ligands (4O), 3 open/1 closed ligands (3O1C), 2 open/2 closed ligands (2O2C), 1 open/3 closed ligands (1O3C), and 4 closed ligands (4C). For the 2O2C cage, both cis and trans forms were studied. In addition, for the cages consisting of two different ligand photoisomers (the flexible open and more rigid closed DTE forms), different guest unbinding pathways were considered. For example, for the 3O1C cage, guest unbinding either between two open ligands (coined “oo”) or between one closed and one open ligand (“co”) was investigated. An MD movie of the binding/unbinding process is provided in the ESI.†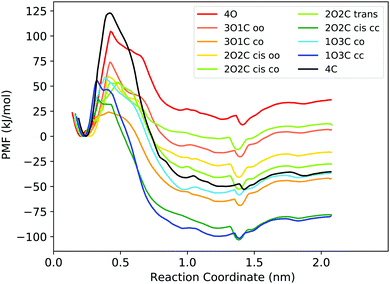 | ||
| Fig. 2 PMFs for binding of the B12F122− guest to the different photoisomeric forms of the cage. In the legend, the numbers before the O and C indicate the number of open and closed DTE ligands in the cage, respectively. The small letters indicate between which two ligands the guest unbinds from the cage. Fig. S5 (ESI†) shows the PMFs with statistical uncertainties estimated from bootstrapping, and the histograms are shown in Fig. S9 and S10 (ESI†). | ||
First, to compare the results from the simulations with the experimental values, the free energy of binding, 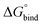 , was calculated for all photoisomers and all pathways by integrating the PMFs according to eqn (2). The results are summarized in Table 1 and plotted in Fig. 3.
, was calculated for all photoisomers and all pathways by integrating the PMFs according to eqn (2). The results are summarized in Table 1 and plotted in Fig. 3.
All free energies are negative and therefore binding is favourable for all systems. However, 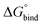 depends on the photoisomeric form of the ligands. The all-ligand-open cage (4O) has the most favourable free energy of binding, while the all-ligand-closed cage (4C) has the least favourable
depends on the photoisomeric form of the ligands. The all-ligand-open cage (4O) has the most favourable free energy of binding, while the all-ligand-closed cage (4C) has the least favourable 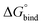 . The binding free energy of −28.1 kJ mol−1 for 4O can be compared to −26.6 kJ mol−1 in ITC and −24.5 kJ mol−1 in NMR. The closed host has a binding free energy of −11.9 kJ mol−1 in our simulations, which can be compared to −19.0 kJ mol−1 in ITC and −15.9 kJ mol−1 in NMR. The binding free energies obtained from the simulations are in good agreement with the experimental values. In particular, the experimental trend that the open cage binds the guest more favourably than the closed cage is captured in the simulations. Furthermore, different (un-)binding pathways for the same cage photoisomer (i.e., oo and co pathways) result in the same free energy of binding, even though the PMFs show different features (Fig. 2). This is reassuring because it confirms the PMF integration method used to obtain
. The binding free energy of −28.1 kJ mol−1 for 4O can be compared to −26.6 kJ mol−1 in ITC and −24.5 kJ mol−1 in NMR. The closed host has a binding free energy of −11.9 kJ mol−1 in our simulations, which can be compared to −19.0 kJ mol−1 in ITC and −15.9 kJ mol−1 in NMR. The binding free energies obtained from the simulations are in good agreement with the experimental values. In particular, the experimental trend that the open cage binds the guest more favourably than the closed cage is captured in the simulations. Furthermore, different (un-)binding pathways for the same cage photoisomer (i.e., oo and co pathways) result in the same free energy of binding, even though the PMFs show different features (Fig. 2). This is reassuring because it confirms the PMF integration method used to obtain  and also shows that the statistical uncertainties are small (see Fig. S5, ESI† for the PMFs with statistical errors estimated from bootstrapping).
and also shows that the statistical uncertainties are small (see Fig. S5, ESI† for the PMFs with statistical errors estimated from bootstrapping).
The binding free energy becomes less favourable with an increasing number of DTE ligands being switched from open to closed (Table 1 and Fig. 3). However, this step-wise loss in affinity is not linear. Starting from the 4O cage, the largest loss of affinity is already associated with switching the first ligand into its closed form (ΔΔGbind(3O1C–4O) = 8.3 kJ mol−1). Subsequent photoinduced closure of the remaining ligands only leads to much smaller binding free energy changes of about 2–3 kJ mol−1 per step (Table 1). This suggests that the guest can leave the cavity after the first ligand is switched to its closed form. This agrees with a recent report of a DTE-based host comparable to the one studied here performed by the Clever group.41 This cage contains a quinoline coordinating the palladium cations (instead of the pyridine in the cage studied in this work) and binds a different anionic guest. However, concerning the four-stranded lantern shape and structure of the photoswitches, both cages share similar features. The use of a chiral camphor sulfonate guest in that study helped in exhibiting that the guest leaves the cage after the first ligand is switched to its closed form through a set of experiments based on a guest-to-host chirality transfer. Our data suggest that the cage studied here behaves similarly.
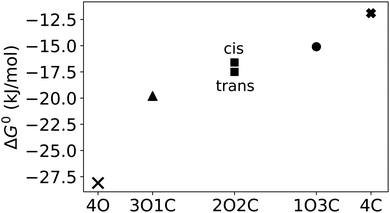
In addition to the binding free energies discussed so far, more mechanistic details of the (un-)binding pathways can be extracted from the shape of the PMF profiles. All PMFs show a minimum at 0.25 nm (Fig. 2), where the guest is buried inside the cavity, slightly displaced from the centre of the cage (Fig. 4a). This inside bound minimum is separated by a barrier, in which the guest is in between two ligands (Fig. 4b), from a more loosely bound minimum at 1.4 nm, in which the guest is associated with one of the Pd ions (outside the bound structure, Fig. 4c and Movie in the ESI†). In the unbound state, the host and guest are separated from each other and individually solvated (Fig. 4d).
Interestingly, the barrier height varies significantly between the different photoisomeric forms of the cage, and it also depends on the guest exit pathway (Fig. 2). The barriers for unbinding are the highest for the fully closed cage (4C) and the fully open cage (4O). For all mixed cages, the barriers are substantially lower. Interestingly, the barrier height is significantly altered already by the first photoswitching step, i.e., ring-closure in the first DTE ligand upon the transition from 4O to 3O1C. The lowering of the unbinding barrier leads to faster kinetics, supporting the notion that, starting from the 4O cage, the guest can readily unbind from the cavity after the first ligand is photoswitched. In the 3O1C cage, there are two possible guest exit pathways, one between 2 open ligands (oo pathway) and the other between one closed and one open ligand (co pathway). The exit pathway influences the barrier height, which is significantly lower for the pathway in which the guest leaves the cavity at the interface of one open and one closed ligand. Hence, the co pathway is the preferred exit route.
Compared to the binding equilibrium (Table 1), the barrier heights from the PMFs are discussed only at a more qualitative level. Our reservation to quantitatively interpret ΔG is linked to the restraining potential UR applied in the umbrella sampling simulations (eqn (1)). While UR was constructed such that it did not affect the inside-bound state, the motion in the plane orthogonal to the reaction coordinate is restricted differentially at distinct values of the reaction coordinate when the guest leaves the cavity of the cage. The corresponding entropy penalty is analytically corrected for in ΔGbind (eqn (2)), but it is inherently present in the PMF profiles shown in Fig. 2. Although being close to the bound minimum, the barrier region could in principle be affected by UR, both in terms of its location and its height.
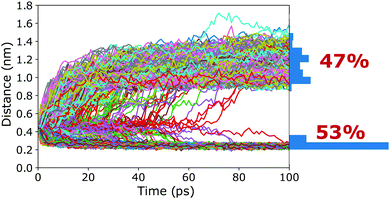
To verify that the barrier found in the PMFs actually corresponds to a true transition state region, a committor analysis was carried out. Using the closed cage (4C) as an example system, a total of 15 different snapshots were extracted from the umbrella window that corresponds to the maximum of the PMF. For each of these 15 structures, 100 independent 100 ps long simulations without any restraints were carried out, using different random seeds for generating the initial atomic velocities. The host–guest 3-dimensional COM–COM distance was then monitored to analyse whether the guest moves into or out of the cage cavity (Fig. 5). If the maximum of the PMF corresponds to a true transition state region, the binding should be observed in 50% of the trajectories and unbinding in the other 50%. The committor analysis shows that 53% of the simulations end up in the bound state and 47% in the unbound state (Fig. 5). Within the expected statistical noise, this is close to the ideal 50/50 ratio, and we conclude that the barrier in the PMF indeed corresponds to a true transition state region separating the bound and unbound states on the free energy landscape. This result shows that the setup used in the free energy simulations, including the reaction coordinate chosen and also the restraining potentials applied, is not only suitable to capture the endpoints of the binding process but also the location of the barrier. As opposed to its location, the committor analysis cannot reveal whether the height of the barrier is affected by the restraining potentials. However, even if UR had an influence on the barrier heights, all photoisomers can be expected to be affected similarly, and thus barrier differences between the photoisomers can be compared (at least at a qualitative level), as done above.
To summarize the results from a mechanistic viewpoint, a key insight obtained from the PMFs is that switching of the first DTE ligand in the 4O cage, i.e., the 4O to 3O1C transition, promotes guest unbinding from both the thermodynamic and kinetic perspectives.
3.2 Enthalpy and entropy
Next, to obtain deeper insights into the thermodynamic driving forces behind the host–guest binding, the free energy was separated into enthalpy and entropy contributions. First, for the 4O and 4C cages, the enthalpy of binding was calculated from the PMFs according to eqn (6). The entropy contribution to the binding free energy, TΔSbind, was obtained as ΔHbind − ΔGbind. The values are summarized in Table 2, together with the experimental values.| Cage | ITC | NMR | MD | |||
|---|---|---|---|---|---|---|
| ΔHbind | TΔSbind | ΔHbind | TΔSbind | ΔHbind | TΔSbind | |
| 4O | 6 | 33 | 30 | 56.1 | 3.6 | 31.7 |
| 4C | 10 | 28.5 | 0.6 | 16.8 | 2.6 | 14.5 |
While the values from ITC and NMR differ significantly from each other, both experimental methods agree that binding is driven by entropy, i.e., ΔHbind is positive. This qualitative result is also obtained from the simulations. One aspect to consider in the interpretation of the experimental values is that they do not necessarily measure the same sum of contributions from all events following the mixture of host and guest solutions, including the binding reaction. In ITC, the outside association and inside binding cannot be differentiated, while it is clearly separable in the NMR results, as the latter method allows individually following the chemical shifts of inward and outward pointing hydrogen atoms of the host. With regard to the simulations, the integral in eqn (6) is calculated over the entire PMF, and thus the outside bound minimum contributes to the ΔHbind value obtained. This is in line with the observation that the binding enthalpies from the simulations are in better agreement with the ITC values than with the ones derived from NMR, at least when considering both 4O and 4C cages together. However, instead of dwelling on the comparison of the ΔHbind values obtained from the simulations with the ones obtained from the two different experimental methods, we turn to the decomposition of the enthalpy into the individual energetic contributions, namely electrostatic, van der Waals, and bonded interactions. Furthermore, the contributions of the individual parts of the system were analysed, i.e., the cage, the guest, and the solvent (acetonitrile). These analyses can provide deeper insights into the driving forces underlying the binding process.
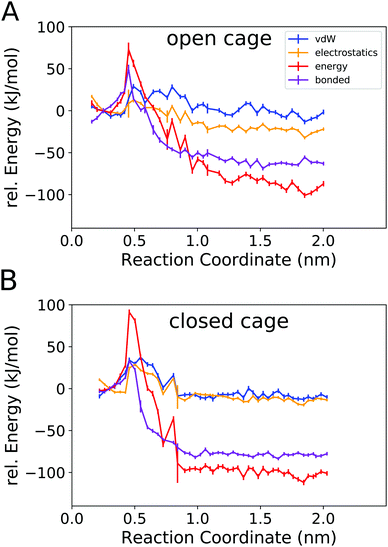
Fig. 6 shows the total potential energy of the system (red curves), and the separate energy contributions from the bonded, van der Waals, and electrostatic interactions.
The total potential energy is lower in the unbound state than for the bound complex, in line with the finding that guest binding is unfavourable in enthalpic terms. Fig. 6 also shows that the binding/unbinding barrier is largely caused by bonded interactions, especially for the open cage (4O). For the closed cage (4C), the bonded terms also play an important role in the barrier, but here the van der Waals and electrostatic interactions also contribute. The observation that the bonded interactions are important for the barrier height can be attributed to the increased strain in the barrier region, where the guest is in between two ligands (Fig. 4b). Interestingly, when comparing the bound and unbound regions, it appears that the nonbonded interactions (van der Waals and electrostatic) are similar and hence do not contribute to the binding energy. This result may seem somewhat surprising at first because Coulombic attraction between the cationic cage and the anionic guest could be expected to contribute favorably to the binding energy. However, as shown in the following, the – indeed attractive – Coulomb interaction between the cage and guest is compensated by cage–solvent and guest–solvent interactions, which are more favourable in the unbound state. Hence, the bonded interactions not only contribute the most to the barrier but are also responsible for the positive enthalpy of binding, as they are more unfavourable in the bound state than in the unbound state. This suggests that there is a structural strain present in the bound complex and, hence, the shape complementarity of this host–guest system may not be ideal. This effect is more pronounced in the more rigid closed cage (4C) than in the open cage (4O), possibly contributing to the lower binding affinity of the former. These findings open a possible way for the targeted optimization of this (and related) host–guest systems in terms of binding enthalpy. Since the guest is very rigid in the present case, modifying the cage could be a promising approach for lowering the deformation energy penalty. However, designing a cage with improved shape complementarity is beyond the scope of this work.
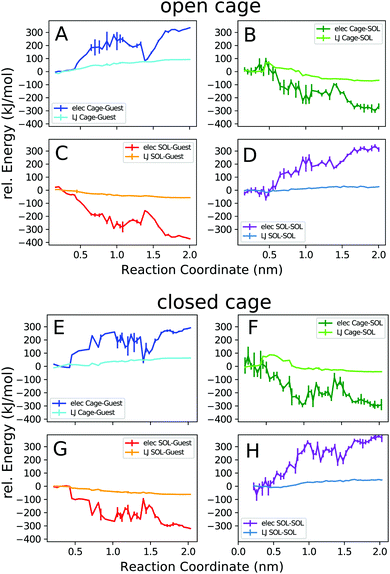
Next, we decomposed the potential energy profiles into the pairwise contributions from the different parts of the system. Fig. 7 shows the cage–guest, cage–solvent, guest–solvent, and solvent–solvent interaction energies.
The trends observed in the open and closed cages are similar. In general, the electrostatic interaction energies are stronger than the van der Waals interactions, as expected for this ionic complex. The cage–guest electrostatic energy (A, E) is most favourable for the bound state. This expected result is due to the attractive Coulomb interactions of the cationic host with the anionic guest, which are strongest in the bound state. The dip in the host–guest electrostatic energy curve at 1.4 nm corresponds to the outside bound structure (Fig. 4c). The acetonitrile solvent more favourably interacts with the guest and also with the cage when unbound. The solvent-accessible area increases upon unbinding until the cage and the guest are fully solvated when separated from each other. The local maximum in the cage–solvent and guest–solvent electrostatic energy (B, C, F, G) at 1.4 nm is due to the partial shielding of the cage and guest from solvent interactions in the outside bound structure.
The solvent–solvent interaction energy curves (D, H) show that this solvent energy contribution favours the bound complex. This is because solvating only a single entity, the cage–guest complex, requires less solvent reorganization compared to solvating the individual cage and guest molecules. However, for the interpretation of this result, it is important to bear in mind that the solvent–solvent energy is exactly compensated by an equally large TΔS term.63,64 Thus, in terms of the overall free energy change associated with the process, the solvent–solvent reorganization does not play a role.
The above analyses revealed in detail the different energy (enthalpy) contributions that play a role in the binding process. However, a microscopic explanation for the observation that binding is driven by entropy is still lacking. The present work focuses on the enthalpy aspects, and fully resolving this intricate question is beyond the scope of this study, as it would require explicit calculation of the (solvent) entropy, e.g., using the 2-phase thermodynamics approach.65–68 However, on the basis of the above results, one can discuss the following aspects. The configurational entropy change of the cage itself is expected to be unfavourable because, if at all, the cage would become more rigid (instead of more flexible) upon binding. The same applies to the guest, which however is anyway very rigid in the present case. Furthermore, translational entropy will also be diminished upon complex formation. Thus, the favourable binding entropy is most likely not due to the cage or the guest themselves but linked to the solvent. To investigate this further, the number of acetonitrile molecules located inside the cage cavity and the number of solvent molecules in the first solvation layer around the guest were counted along the reaction coordinate. Fig. 8A shows that the number of solvent molecules within the cavity of the open (4O) cage increases from an average of 1.5 for the cage/guest complex to about 2.2 for the empty cage. Interestingly, although the number of acetonitrile molecules inside the cage cavity has already reached 2, immediately after the guest leaves the cage (i.e., at around 1.0 nm along the reaction coordinate), it again reduces to about 1 solvent molecule for the outside bound state (at around 1.4 nm). Concerning the geometry of the cavity, as described by the Pd–Pd distance and the S–S distances across the cage, the outside bound structure does not show any prominent features (Fig. S11, ESI†). A possible explanation for this unexpected behaviour is that the association of the B12F122− anion to the Pd(II) ion from the outside lowers the positive charge density close to that Pd centre. As acetonitrile associates with Pd preferentially with its (partially negatively charged) N-atom (Fig. S12, ESI†), this would explain the lowered propensity of a solvent molecule to associate from the inside.
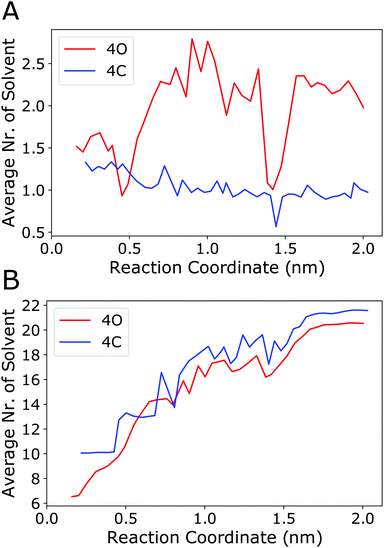 | ||
| Fig. 8 (A) Number of acetonitrile molecules inside the cavity of the open cage (4O, red curve) or inside the closed cage (4C, blue curve) along the reaction coordinate (averaging was done over the 50 ns sampled in every umbrella window). An acetonitrile molecule was considered to be inside the cavity if any of its atoms was within a sphere of radius 0.5 nm centred at either of the two Pd centers and, at the same time, any of its atoms was within a sphere of radius 0.4 nm positioned at the centre of mass of the two Pd atoms. (B) Number of acetonitrile molecules in direct contact with the guest. An acetonitrile molecule was considered to be in contact with the guest if any of its atoms was within a distance of 0.4 nm to any of the fluoride atoms of the guest. Fig. S12 (ESI†) shows the radial distribution functions of acetonitrile around the guest. | ||
To check the energetics of this suggested “Coulomb knock-off mechanism”, the association energy of an acetonitrile molecule inside the cavity to one of the Pd centres was calculated using force field energy minimisations. These were performed for two systems, (a) the open cage (4O) with the B12F122− guest is associated from the outside (outside bound minimum, Fig. 4c), and (b) the open cage (4O) where the Pd centre is associated from the outside with another acetonitrile molecule (instead of the guest). The difference in the association energy of the acetonitrile molecule inside the cavity amounts to +1.7 kJ mol−1, supporting the notion that guest association from the outside lowers the affinity of the Pd centre towards acetonitrile. This reduced affinity is also reflected in a longer distance between the N-atom of the acetonitrile inside the cavity to the Pd centre, which increased to 0.5 nm during the energy minimisation of the outside bound system. The other acetonitrile molecule inside the cavity is not affected, as it is associated with the other Pd centre at the opposite side of the cage. In contrast to the open cage, for the closed cage (4C) the average number of solvent molecules does not increase upon unbinding of the guest (Fig. 8A, blue curve). The Pd–Pd and S–S distances (Fig. S11, ESI†) show that the closed cage has a slightly smaller cavity than the open cage, and hence the 4C cage can host only one solvent molecule even in the unbound state.
Fig. 8A shows that, for the open cage, one acetonitrile molecule is freed up upon guest binding. The release of that confined solvent molecule might be linked to an entropy increase. However, since this is only a single solvent molecule, the contribution is not expected to be large. Instead, we expect a larger entropy gain due to the release of a greater number of acetonitrile molecules in the solvation layer of the guest, which is largely desolvated upon binding inside the host cavity. Fig. 8B shows that the number of acetonitrile molecules in the first solvation layer of the guest is indeed substantially reduced upon binding, from about 20 in the unbound state to about 6 (for 4O) or 10 (for 4C). Interestingly, this partial desolvation of the guest is more pronounced for the open cage than for the closed cage. This is attributed to the fact that the more flexible open cage can enclose the guest more effectively, and hence shield the guest from the solvent, than the more rigid closed cage. The acetonitrile molecules in the solvation shell of the guest are preferentially oriented with their methyl-groups towards the fluoride atoms (Fig. S12, ESI†), and the release of these solvent molecules upon binding is therefore expected to lead to a gain in entropy. Taken together, both from the solvation layer of the guest and from the cavity of the cage, a larger number of acetonitrile molecules is freed up upon guest binding to the open cage than to the closed cage. This is in line with the observed more favourable entropy change upon binding to the open cage, see TΔSbind values in Table 2.
4 Summary and conclusions
In this work, a force field was parametrized and used for free energy simulations of binding of a B12F122− guest to a photoswitchable palladium coordination cage. Umbrella sampling simulations were performed to obtain PMFs of the binding/unbinding process for all photoisomers of the cage. These simulations provide detailed insights into the link between the photoisomeric state of the cage and the thermodynamics governing guest binding. The free energies of binding, obtained through the integration of the PMFs, are directly comparable to the experiment and show that the all-ligand-open cage (4O) binds the guest most favourably, while the all-ligand-closed (4C) cage binds the guest least favourably. The binding free energies obtained from the simulations agree with the experimental data.Starting from the open cage (4O), stepwise photoinduced closure of the DTE ligands gradually diminishes the binding affinity. The largest loss in affinity is associated with the closing of the first ligand in the cage. Every ligand that is closed after the initial one further decreases the affinity, but the magnitude of the effect is significantly smaller. This result suggests that the guest preferably leaves the cavity after the first ligand is closed, which agrees with the study of a similar host–guest complex performed by the Clever group,41 where a chiral guest was observed to leave the cavity of a very similar host to the one studied here after the first photoswitching step.
In addition to the standard free energies of binding, the PMFs also provide information on the underlying kinetics of the unbinding process. The barrier height for unbinding varies depending on the photoisomeric state of the cage and on the pathway along which the guest leaves the cavity. The cages consisting of only one photoisomeric form of the ligand (4O, 4C) have higher unbinding barriers than the “mixed” cages comprised of different ligand photoisomers. The lowest barrier for unbinding was found in the 3O1C cage, which further supports the notion that the guest leaves the cavity after the first photoswitching event.
Analyses of the enthalpies of guest binding to the 4O and 4C cages provide further insights into the thermodynamic driving forces of the binding process. The enthalpy of binding was found to be positive (i.e., unfavourable) in both cases, and hence the process is driven by a favourable entropy change, as also found experimentally. The favourable binding entropy is presumably linked to solvation, with the release of solvent molecules from the solvation shell of the guest upon binding presumably playing a more important role than changes in cage cavity solvation. However, further investigations are required for a deeper understanding of entropy. Concerning the enthalpy contributions, separately analysing the van der Waals, electrostatic, and bonded interactions in the force field provided deeper insights into the energetic processes at play. Both the unbinding barrier and the enthalpically more unfavourable bound state are largely caused by bonded interactions. The bonded interactions favour the unbound state, suggesting the presence of structural strain in the bound complex. This strain is larger in the more rigid all-ligand-closed cage (4C) than in the all-ligand-open (4O) system, in line with the observed more negative binding free energy of the latter. These findings might offer an approach for the design of these (and related) host–guest systems, as improving shape complementarity might help in optimising the enthalpy of binding.
Taken together, the simulations agree with the experimental data and provide missing microscopic insights into the thermodynamics of guest binding to the photoswitchable cage. The first photoclosure event has the largest effect. Ultrafast spectroscopy studies are currently performed in our laboratories to investigate whether this trend is also reflected in differing photodynamics of the cages' DTE ligands in the presence of guest molecules. From a more general perspective, this work contributes to the detailed understanding of the complex host–guest chemistry of supramolecular assemblies that involve multiple, experimentally difficult to assess intermediate states. The atomistic insights, as provided by molecular simulations, are important for the design of novel structures, serving the future development of tailor-made functional materials, stimuli-responsive receptors, controllable catalysts and molecular machines.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Daniel Markthaler and Niels Hansen (University of Stuttgart) for sharing their PLUMED input files and for useful discussions. This work was supported by the Research Training Group Confinement-controlled Chemistry, funded by the Deutsche Forschungsgemeinschaft (DFG) under Grant GRK2376/331085229.Notes and references
- M. J. Wiester, P. A. Ulmann and C. A. Mirkin, Angew. Chem., Int. Ed., 2011, 50, 114–137 CrossRef CAS PubMed.
- T. R. Cook, Y.-R. Zheng and P. J. Stang, Chem. Rev., 2012, 113, 734–777 CrossRef PubMed.
- S. Saha, I. Regeni and G. H. Clever, Coord. Chem. Rev., 2018, 374, 1–14 CrossRef CAS.
- M. M. Smulders, I. A. Riddell, C. Browne and J. R. Nitschke, Chem. Soc. Rev., 2013, 42, 1728–1754 RSC.
- M. Yoshizawa, J. K. Klosterman and M. Fujita, Angew. Chem., Int. Ed., 2009, 48, 3418–3438 CrossRef CAS PubMed.
- C. M. Hong, R. G. Bergman, K. N. Raymond and F. Dean Toste, Acc. Chem. Res., 2018, 51, 2447–2455 CrossRef CAS PubMed.
- L. Pauling, Nature, 1948, 161, 707–709 CrossRef CAS PubMed.
- J. K. M. Sanders, Chem. – Eur. J., 1998, 4, 1378–1383 CrossRef CAS.
- Y. Fang, J. A. Powell, E. Li, Q. Wang, Z. Perry, A. Kirchon, X. Yang, Z. Xiao, C. Zhu, L. Zhang, F. Huang and H. C. Zhou, Chem. Soc. Rev., 2019, 48, 4707–4730 RSC.
- W. Cullen, M. C. Misuraca, C. A. Hunter, N. H. Williams and M. D. Ward, Nat. Chem., 2016, 8, 231–236 CrossRef CAS PubMed.
- V. Martí-Centelles, A. L. Lawrence and P. J. Lusby, J. Am. Chem. Soc., 2018, 140, 2862–2868 CrossRef PubMed.
- V. V. Welborn, W.-L. Li and T. Head-Gordon, Nat. Commun., 2020, 11, 415 CrossRef CAS PubMed.
- V. V. Welborn and T. Head-Gordon, J. Phys. Chem. Lett., 2018, 9, 3814–3818 CrossRef PubMed.
- T. A. Young, V. Martí-Centelles, J. Wang, P. J. Lusby and F. Duarte, J. Am. Chem. Soc., 2020, 142, 1300–1310 CrossRef PubMed.
- J. Wang, T. A. Young, F. Duarte and P. J. Lusby, J. Am. Chem. Soc., 2020, 142, 17743–17750 CrossRef CAS PubMed.
- R. L. Spicer, A. D. Stergiou, T. A. Young, F. Duarte, M. D. Symes and P. J. Lusby, J. Am. Chem. Soc., 2020, 142, 2134–2139 CrossRef CAS PubMed.
- W. Moormann, T. Tellkamp, E. Stadler, F. Röhricht, C. Näther, R. Puttreddy, K. Rissanen, G. Gescheidt and R. Herges, Angew. Chem., Int. Ed., 2020, 59, 15081–15086 CrossRef CAS PubMed.
- A. J. McConnell, C. S. Wood, P. P. Neelakandan and J. R. Nitschke, Chem. Rev., 2015, 115, 7729–7793 CrossRef CAS PubMed.
- L. J. Chen and H. B. Yang, Acc. Chem. Res., 2018, 51, 2699–2710 CrossRef CAS PubMed.
- A. Díaz-Moscoso and P. Ballester, Chem. Commun., 2017, 53, 4635–4652 RSC.
- S. J. Wezenberg, Chem. Lett., 2020, 49, 609–615 CrossRef CAS.
- M. Han, R. Michel, B. He, Y. S. Chen, D. Stalke, M. John and G. H. Clever, Angew. Chem., Int. Ed., 2013, 52, 1319–1323 CrossRef CAS PubMed.
- M. Irie, Chem. Rev., 2000, 100, 1685–1716 CrossRef CAS PubMed.
- M. Irie, T. Fukaminato, K. Matsuda and S. Kobatake, Chem. Rev., 2014, 114, 12174–12277 CrossRef CAS PubMed.
- M. Takeshita and M. Irie, Chem. Commun., 1997, 2265–2266 RSC.
- M. Takeshita, N. Kato, S. Kawauchi, T. Imase, J. Watanabe and M. Irie, J. Org. Chem., 1998, 63, 9306–9313 CrossRef CAS.
- I. Hamdi, G. Buntinx, A. Perrier, O. Devos, N. Jaïdane, S. Delbaere, A. K. Tiwari, J. Dubois, M. Takeshita, Y. Wada and S. Aloïse, Phys. Chem. Chem. Phys., 2016, 18, 28091–28100 RSC.
- I. Hamdi, G. Buntinx, O. Poizat, S. Delbaere, A. Perrier, R. Yamashita, K.-I. Muraoka, M. Takeshita and S. Aloïse, Phys. Chem. Chem. Phys., 2019, 21, 6407–6414 RSC.
- N. Tamai, T. Saika, T. Shimidzu and M. Irie, J. Phys. Chem., 1996, 100, 4689–4692 CrossRef CAS.
- Y. Ishibashi, M. Fujiwara, T. Umesato, H. Saito, S. Kobatake, M. Irie and H. Miyasaka, J. Phys. Chem. C, 2011, 115, 4265–4272 CrossRef CAS.
- J. Ern, A. T. Bens, H. D. Martin, S. Mukamel, D. Schmid, S. Tretiak, E. Tsiper and C. Kryschi, Chem. Phys., 1999, 246, 115–125 CrossRef CAS.
- J. Ern, A. T. Bens, H.-D. Martin, S. Mukamel, S. Tretiak, K. Tsyganenko, K. Kuldova, H. P. Trommsdorff and C. Kryschi, J. Phys. Chem. A, 2001, 105, 1741–1749 CrossRef CAS.
- J. Ern, A. T. Bens, H.-D. Martin, K. Kuldova, H. P. Trommsdorff and C. Kryschi, J. Phys. Chem. A, 2002, 106, 1654–1660 CrossRef CAS.
- H. Jean-Ruel, R. R. Cooney, M. Gao, C. Lu, M. A. Kochman, C. A. Morrison and R. J. D. Miller, J. Phys. Chem. A, 2011, 115, 13158–13168 CrossRef CAS PubMed.
- C. L. Ward and C. G. Elles, J. Phys. Chem. A, 2014, 118, 10011–10019 CrossRef CAS PubMed.
- E. Pontecorvo, C. Ferrante, C. G. Elles and T. Scopigno, J. Phys. Chem. B, 2014, 118, 6915–6921 CrossRef CAS PubMed.
- D. T. Valley, D. P. Hoffman and R. A. Mathies, Phys. Chem. Chem. Phys., 2015, 17, 9231–9240 RSC.
- C. Schweigert, O. Babii, S. Afonin, T. Schober, J. Leier, N. C. Michenfelder, I. V. Komarov, A. S. Ulrich and A. N. Unterreiner, ChemPhotoChem, 2019, 3, 403–410 CrossRef CAS.
- R. Li, M. Han, J. Tessarolo, J. J. Holstein, J. Lübben, B. Dittrich, C. Volkmann, M. Finze, C. Jenne and G. H. Clever, ChemPhotoChem, 2019, 3, 378–383 CrossRef CAS.
- C. Sgarlata, J. S. Mugridge, M. D. Pluth, B. E. F. Tiedemann, V. Zito, G. Arena and K. N. Raymond, J. Am. Chem. Soc., 2010, 132, 1005–1009 CrossRef CAS PubMed.
- R. J. Li, J. J. Holstein, W. G. Hiller, J. Andréasson and G. H. Clever, J. Am. Chem. Soc., 2019, 141, 2097–2103 CrossRef CAS PubMed.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed.
- D. A. Case, J. M. Wang, R. M. Wolf, J. W. Caldwell and P. A. Kollman, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef PubMed.
- A. Jakalian, D. B. Jack and C. I. Bayly, J. Comput. Chem., 2002, 23, 1623–1641 CrossRef CAS PubMed.
- A. Bergner, M. Dolg, W. Küchle, H. Stoll and H. Preuß, Mol. Phys., 1993, 80, 1431–1441 CrossRef CAS.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- M. Yoneya, S. Tsuzuki, T. Yamaguchi, S. Sato and M. Fujita, ACS Nano, 2014, 114, 1290–1296 CrossRef PubMed.
- J. de Andrade, E. S. Böes and H. Stassen, J. Phys. Chem. B, 2002, 106, 13344–13351 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1-2, 19–25 Search PubMed.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef CAS.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- C. Caleman, P. J. van Maaren, M. Hong, J. S. Hub, L. T. Costa and D. van der Spoel, J. Chem. Theory Comput., 2012, 8, 61–74 CrossRef CAS PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- J. S. Hub, B. L. de Groot and D. van der Spoel, J. Chem. Theory Comput., 2010, 6, 3713–3720 CrossRef CAS.
- K. K. Irikura and M. K. Gilson, J. Phys. Chem. B, 2010, 114, 16304–16317 CrossRef PubMed.
- M. K. Gilson, J. A. Given, B. L. Bush and J. A. McCammon, Biophys. J., 1997, 72, 1047–1069 CrossRef CAS PubMed.
- D. H. de Jong, L. V. Schäfer, A. H. de Vries, S. J. Marrink, H. J. C. Berendsen and H. Grubmüller, J. Comput. Chem., 2011, 32, 1919–1928 CrossRef CAS PubMed.
- S. Doudou, N. A. Burton and R. H. Henchman, J. Chem. Theory Comput., 2009, 5, 909–918 CrossRef CAS PubMed.
- D. Markthaler, J. Gebhardt, S. Jakobtorweihen and N. Hansen, Chem. Ing. Tech., 2017, 89, 1306–1314 CrossRef CAS.
- D. M. Heyes, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 755–764 CrossRef CAS PubMed.
- T. Zhang, H. Tan, C. Hetényi and D. van der Spoel, J. Chem. Theory Comput., 2013, 9, 4542–4551 CrossRef PubMed.
- A. Ben-Naim, Biopolymers, 1975, 14, 1337–1355 CrossRef CAS.
- D. Ben-Amotz and R. Underwood, Acc. Chem. Res., 2008, 41, 957–967 CrossRef CAS PubMed.
- S.-T. Lin, M. Blanco and W. A. Goddard, J. Chem. Phys., 2003, 119, 11792–11805 CrossRef CAS.
- T. A. Pascal, S.-T. Lin and W. A. Goddard, Phys. Chem. Chem. Phys., 2011, 13, 169–181 RSC.
- O. Fisette, C. Päslack, R. Barnes, J. M. Isas, R. Langen, M. Heyden, S. Han and L. V. Schäfer, J. Am. Chem. Soc., 2016, 138, 11526–11535 CrossRef CAS PubMed.
- R. A. X. Persson, V. Pattni, A. Singh, S. M. Kast and M. Heyden, J. Chem. Theory Comput., 2017, 13, 4467–4481 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp06495e |
| This journal is © the Owner Societies 2021 |