Protein flexibility reduces solvent-mediated friction barriers of ligand binding to a hydrophobic surface patch

Abstract

Solvent fluctuations have been explored in detail for idealized and rigid hydrophobic model systems, but so far it has remained unclear how internal protein motions and their coupling to the surrounding solvent affect the dynamics of ligand binding to biomolecular surfaces. Here, molecular dynamics simulations were used to elucidate the solvent-mediated binding of a model ligand to the hydrophobic surface patch of ubiquitin. The ligand's friction profiles reveal pronounced long-time correlations and enhanced friction in the vicinity of the protein, similar to idealized hydrophobic surfaces. Interestingly, these effects are shaped by internal protein motions. Protein flexibility modulates water density fluctuations near the hydrophobic surface patch and smooths out the friction profile of ligand binding.

---

1 Introduction

Water plays an important role in molecular recognition and receptor–ligand binding.^1,2 The properties of water in the hydration shell of biomolecules such as proteins and membranes as well as the couplings between them have been the subject of numerous studies.^3–15 Altered solvent dynamics were found to be important for ligand binding by mediating the interactions between receptor and ligand.^16–22 In addition, near hydrophobic protein surfaces or in confinement, “dewetting” and capillary fluctuations were shown to contribute to driving forces of self-assembly and association,^23,24i.e., the partial dewetting (or desolvation) of a binding site contributes to the thermodynamics and kinetics of binding. Protein vibrations and conformational fluctuations have also been shown to bear the potential for non-trivial contributions to ligand binding, for example due to changes in the protein conformational entropy that have been probed in pioneering NMR relaxation experiments as well as in molecular simulations.^25–28 The relationship between protein conformational fluctuations and binding dynamics has been studied in the context of the solvent viscosity, which led to the concept of solvent slaving²⁹ that is an active field of debate.^30,31 However, more direct correlations between protein flexibility and the dynamics of ligand binding have not yet been studied in detail.

The role of solvent fluctuations in idealized hydrophobic cavity–ligand systems was investigated computationally by Setny et al.³² The stochastic motion of the ligand is intimately coupled to the wet/dry oscillations of the hydrophobic binding cavity, which introduces long-time correlations in the random force auto-correlation function. Dry ligand-binding cavities were also observed in proteins using magnetic relaxation dispersion,³³ and Mössbauer and neutron scattering experiments showed that solvent fluctuations in a protein hydration shell can control protein motion and function.³⁴ Furthermore, it was shown how proteins can use hydrophobicity to shape biomolecular interactions by driving solvated binding sites away or towards the wet state depending on their chemistry and topology,³⁵ thereby rendering the hydration shells susceptible to perturbations.³⁶

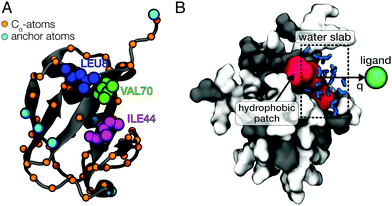
In this work, we use all-atom molecular dynamics (MD) simulations to characterize the atomic-level details of the coupling of ligand motion to solvent fluctuations in a protein–ligand system. Ubiquitin (UBQ) was used as a model protein to investigate the impact of protein flexibility on the dynamics of ligand binding to a hydrophobic protein surface patch. The residues Leu-8, Ile-44 and Val-70 are known as the hydrophobic patch (HP) of UBQ (Fig. 1A), which is essential for proteosomal degradation.³⁷ The model ligand used in this study was a single van der Waals sphere with a moderate binding free energy to the HP (simulation details can be found in ESI†). Our simulations reveal that protein flexibility can facilitate ligand binding by reducing the solvent-mediated friction on the ligand and altering the water density fluctuations near the HP surface.

Fig. 1 Structure of ubiquitin. (A) The secondary structure (gray) and the residues forming the HP, Leu-8 (blue), Ile-44 (magenta) and Val-70 (green). C_α-atoms are shown in orange and anchor atoms in cyan. (B) The hydrophobic patch (red) and the reaction coordinate q describing the binding of the ligand (q is roughly normal to the HP surface). Hydrophilic protein surfaces are shown in light gray and hydrophobic parts are shown in dark gray. The dashed box highlights the water molecules (blue) within 4.5 Å of the hydrophobic surface patch, which were selected for density fluctuation analyses.

2 Methods

2.1 Simulation protocol

All simulations were performed using the GROMACS software package (version 4.6.1).³⁸ The CHARMM27³⁹ protein force field and the TIP4P/2005 water model⁴⁰ were used. Our specific choice of the TIP4P/2005 water model was motivated by its realistic description of dynamical properties such as the water self-diffusion.⁴⁰ The Lennard-Jones (12,6) potential parameters for the spherical model ligand were σ = 4 Å and ε = 0.025 kJ mol⁻¹, while its mass was set to 39.95 g mol⁻¹. The protein was placed in a large 80 Å × 80 Å × 80 Å cubic box and was solvated with 16 545 water molecules. Umbrella sampling⁴¹ was then performed in the canonical ensemble (NVT) at 300 K using 15 windows with 1 Å-spacings of the ligand position on the reaction coordinate q, which was defined as the distance between the ligand and the center of mass (COM) of the amino acid residues forming the HP with a negative offset of 3 Å (i.e., surface contact for q = 0 Å). The ligand was positioned on a vector perpendicular to the HP surface and the system was oriented to align this vector with the x-axis (see Fig. 1B). The force constant of the harmonic biasing potential was 1000 kJ mol⁻¹ nm⁻² and the ligand was restrained by harmonic restraining potentials in the orthogonal directions (y, z) with force constants of 1500 kJ mol⁻¹ nm⁻². Each umbrella window was simulated for 2.1 ns (10 ns for the frozen protein). These simulation times are sufficient to sample picosecond timescale hydration water dynamics and, at the same time, short enough to minimize protein side-chain fluctuations and other conformational changes. Slow protein conformational dynamics – on multi-nanosecond timescales and beyond – are not expected to dynamically couple to intermolecular vibrations and picosecond processes in hydration water due to the separation of timescales. Dynamical coupling, such as correlated vibrational motion in the protein and its hydration shell, primarily occurs on the sub-picosecond and picosecond timescale and was analyzed in previous work.^13,42 The first 100 ps of all production simulations were considered additional equilibration time and were therefore excluded from the subsequent analyses. We verified the convergence by performing longer simulations (4.2 ns, with the first 200 ps omitted from analysis) for a few selected umbrella windows. For a detailed description of the methods, see ESI.†

2.2 Potentials of mean force

To obtain the potential of mean force (PMF) of ligand binding, umbrella sampling (US) simulations were performed in which the ligand motion was restricted to a one-dimensional reaction coordinate q roughly normal to the HP surface (Fig. 1B). The PMFs were computed from the umbrella sampling simulations using the weighted histogram analysis method (WHAM).^43,44 The effect of protein flexibility was studied by performing three independent sets of simulations with (1) a completely frozen protein (frozen), (2) harmonic restraining potentials applied to all C_α-atoms of UBQ (restrained) and (3) position restraints only applied to 6 selected anchoring C_α-atoms of UBQ that are far away from the HP (flexible). Fig. 1A shows the restrained atoms. In case of the flexible protein, the restraining potentials eliminated overall rotation and translation of the protein but affected protein flexibility only marginally. This was verified by a comparison of the root mean square fluctuations (RMSF) of the flexible protein with those of an entirely unrestrained protein (see Fig. S1, ESI†).

2.3 One-body friction profiles

The friction profiles of the ligand along the reaction coordinate were computed from the fluctuations of the random force, as described by Setny et al.³² The instantaneous random force R_q(t) was obtained by subtracting the mean force and the biasing force due to the umbrella potential from the total force on the reaction coordinate, R_q0(t) = F_q(t) + k_umb(q(t) − q₀) + ∂PMF(q)/∂q, where F_q is the total force on the ligand (stored every 10 fs). According to the second fluctuation–dissipation theorem,⁴⁵ static one-body friction profiles ξ(q) of the ligand can be straightforwardly obtained from the time auto-correlation of the random force, C_RR(t) = 〈R_q0(t₀ + t)R_q0(t₀)〉_t0. The integration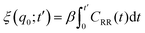 was carried out until the integrals converged to a pseudo-plateau.⁴⁶

2.4 Solvent fluctuations

Solvent fluctuations near the hydrophobic patch of UBQ were analyzed in terms of the instantaneous number of water molecules, N_wat(t), that are within a distance of 4.5 Å from the residues Ile-44 or Val-70 (Fig. 1A). The density fluctuations in the vicinity of the HP surface were calculated as a function of the ligand position on the reaction coordinate (Fig. 1B). Semi-logarithmic representations of the probability distributions P_v(N_wat) provide useful visual comparisons of the water density fluctuations between distinct simulations. For bulk water and near hydrophilic surfaces, P_v(N_wat) is typically Gaussian-shaped. However, near hydrophobic surfaces it can either become non-Gaussian, i.e., having an increased probability for low values of N_wat, or the entire distribution can be shifted towards lower occupation numbers, and both cases are markers for desolvation.^35,36 Furthermore, average occupancy fluctuations were analyzed via the reduced local compressibility χ_r = 〈δN²〉/〈N〉, where δN(t) = N(t) − 〈N〉.^47,48 This reduced compressibility quantifies the magnitude of solvent fluctuations of confined water molecules. The timescale of solvent fluctuations was estimated using the time auto-correlation function of δN(t), C_δNδN(t) = 〈δN(τ)·δN(τ + t)〉_τ/〈δN²〉. The correlation times τ_δN were estimated from double-exponential fits A exp[−t/τ_A] + B exp[−t/τ_B] to account for multiple timescales. For validation purposes, τ_δN was also estimated directly as C_δNδN(τ_δN) = 1/e, i.e., without fitting to an (assumed) exponential form. Reference data for bulk water were obtained from separate simulations of a pure water box by selecting water molecules in a similar volume V.

3 Results and discussion

3.1 Protein dynamics modulate the binding free energy landscape

Fig. 2 shows the PMF for the flexible (green), restrained (red) and frozen (blue) proteins (convergence tests are shown in Fig. S2, ESI†). In all cases, there is a pronounced free energy minimum very close to the protein surface. For the restrained protein, the minimum is located around q ≈ 0.5 Å with a depth of −6.5 kJ mol⁻¹. In case of the flexible protein, the minimum is located at q ≈ 1.0 Å and has a depth of −8.0 kJ mol⁻¹. Interestingly, the barrier at around 4 Å is roughly twice as high for the restrained protein compared to the flexible case, indicating that protein flexibility facilitates the binding of the ligand. Finally, for the frozen protein the energy barrier is even higher than for the restrained protein, and the energy minimum has a smaller depth of around −3.0 kJ mol⁻¹. This less pronounced minimum indicates that the frozen protein is unable to respond to the presence of the ligand in order to optimize its interactions, which is allowed in simulations with a flexible protein and to a lesser degree for the restrained protein.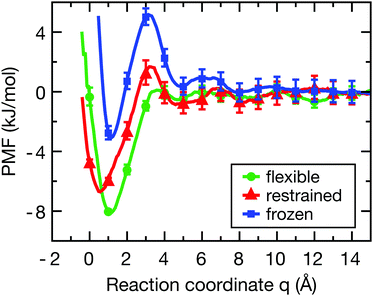

Fig. 2 Potentials of mean force of ligand-binding to the HP for the flexible (green), restrained (red) and frozen (blue) proteins along the reaction coordinate q, which can be directly interpreted as the width of the solvation region separating the ligand and the protein surface. Error bars were estimated from a bootstrap analysis.⁴⁹ The histograms of ligand positions (Fig. S3, ESI†) show sufficient overlap between the distributions to properly sample the reaction coordinate.

Although the frozen protein is an artificial, or even unphysical system (zero kinetic energy, violation of Newton's third law), it was included here as an extreme case in order to study the influence of protein dynamics. Furthermore, a fully rigid system was also used by Setny et al. in their studies of an idealized hydrophobic model cavity,^32,50 and thus the frozen protein simulations facilitate the comparison of our results with the literature. As also shown below, the results for the frozen protein are qualitatively similar to those for the restrained protein, but the observed effects are somewhat more pronounced. Taken together, the differences in the binding free energy profiles between the flexible, restrained, and frozen proteins are expected to affect both the dynamics of the ligand and the layers of hydration water around the HP, which shall be investigated next.

3.2 Protein flexibility reduces friction barriers

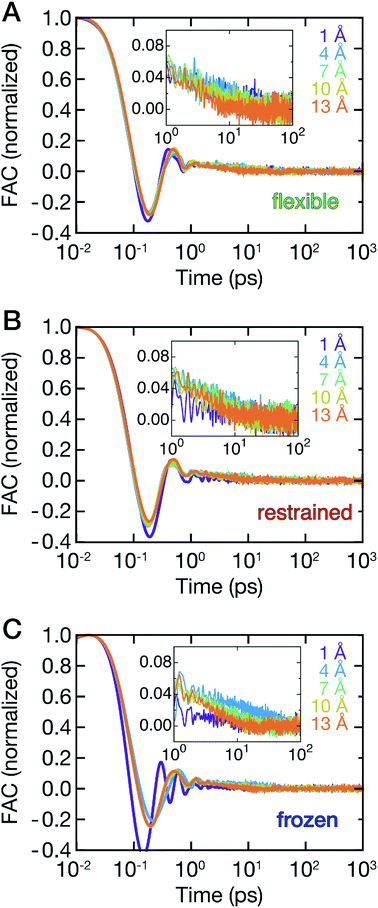
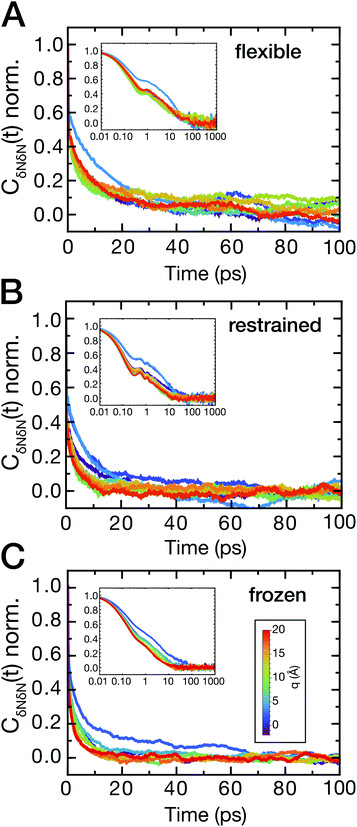
The ligand dynamics can be described based on PMFs shown in Fig. 2 combined with information on the friction experienced by the ligand as it approaches the protein along the reaction coordinate. The latter was probed via fluctuations of the time-dependent random force R_q0(t) for each reference position q₀. Specifically, the time auto-correlation functions of the random force (FAC) were computed to assess the degree of non-Markovian motion, which are shown in Fig. 3 for selected ligand positions q.

Fig. 3 Random force auto-correlation functions for selected ligand positions q. Shown are the normalized results for the (A) flexible, (B) restrained and (C) frozen proteins. Insets show the long-time behavior of the correlation functions. Plot colors indicate results from simulations with varying reference positions of the ligand on the reaction coordinate.

For large separations (q ≥ 10 Å, i.e., ligand in bulk-like water), the FACs oscillate on the sub-ps timescale and decay exponentially within 10 ps. Interestingly, the FACs exhibit additional long-time decays for short protein–ligand distances (q < 10 Å), similar to the observations made by Setny et al.³² for an idealized and rigid hydrophobic model cavity. The change of timescales is most obvious for the frozen protein at short distances, likely due to strongly retarded water dynamics in the first hydration shell around the frozen protein. The long-time decay can be traced back to the distributions of the random force presented in Fig. S4–S6 (ESI†). Especially for short separation distances, the distributions are non-Gaussian, displaying the non-Markovianity of the ligand's motion.

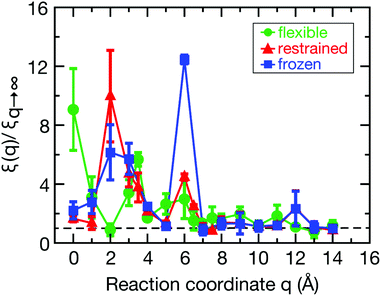
The spatial dependence of ligand dynamics with respect to protein flexibility was assessed through the friction profiles of the ligand along the reaction coordinate. To this end, static one-body friction profiles ξ(q) were computed from the FACs as described above. The friction profiles ξ(q) were obtained for the flexible, restrained and frozen proteins, respectively, and are shown in Fig. 4. All data were normalized by the value at q = 14 Å for the restrained protein (ξ_q→∞), which is nearly identical for the three systems. Fig. 4 reveals that for a more rigid protein, i.e., restrained and frozen, the ligand experiences substantially enhanced friction upon approaching the protein surface at short distances before reaching the bound state (see minimum of the corresponding PMF in Fig. 2). The friction is increased by a factor of around 8–13 compared to large distances, with two distinct maxima at around 2–4 Å and 6 Å distance to the HP. Notably, the separations between the maxima correspond to the size of a single hydration layer, supporting the notion that the friction enhancement is related to the step-wise removal of hydration layers from the binding site. This assumption is supported by an analysis of the average number of water molecules near the HP surface. 〈N_wat〉 was determined within 4.5 Å, 6.0 Å, and 7.0 Å of the HP surface (Fig. S7, ESI†). When taking more than one hydration shell into account (i.e., 6–7 Å), the data show that there is a variation of the water count in line with variations of the friction along the reaction coordinate. Increased friction is also observed for the flexible protein, but the enhancement is less pronounced than for the restrained and frozen proteins. We do not go beyond this qualitative comparison, because the correlation functions (Fig. 3) are oscillatory and somewhat noisy, which is also reflected in the FAC integral (Fig. S8, ESI†). However, the distinction between the flexible protein (small friction enhancement) and the restrained/frozen proteins (large friction enhancement) is significant. The convergence of the friction profiles was verified by repeating the analysis for longer, 4 ns trajectories for selected positions, yielding values that differed by no more than 8% from those of the shorter, 2 ns trajectories. This low variation is understandable, because the force fluctuations occur on the ps timescale. Overall, protein flexibility is found to reduce the solvent-mediated friction acting on the ligand during binding, which may be a general mechanism to facilitate binding in large and flexible biomolecular systems.

Fig. 4 Friction profiles ξ(q) along the reaction coordinate q evaluated by integrating the random force time auto-correlation function. Error bars signify the standard deviations calculated by partitioning the 2 ns trajectories into 2 parts of 1 ns each.

3.3 The dynamic hydration shell shapes ligand binding dynamics

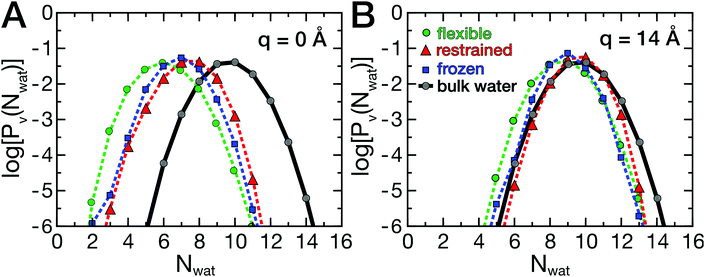
As described above, the ligand binding involves removal of water molecules from the HP, which may be underlying the friction barriers. Therefore, the dynamics of the hydration water around the HP was investigated. As described by Patel and co-workers,^35,36 the probability distribution P_v(N_wat) provides information on the sensitivity of water molecules to external perturbations, such as the presence of a ligand or a protein. In fact, bulk water at ambient conditions is close to a liquid–vapor phase transition, which leads to the well known capillary evaporation near hydrophobic, concave binding pockets.^18,51 Here, deviations from the bulk water distribution, which are expected in the hydration shell of a protein, were analyzed as a function of ligand position and compared between flexible and rigid proteins. The probability distributions P_v(N_wat) are shown in Fig. 5A and B.

Fig. 5 Probability distributions P_v(N_wat) of water molecules in a small volume V near the hydrophobic patch of UBQ. Shown is P_v(N_wat) of water with the ligand at q = 0 Å (A) and q = 14 Å (B) along the reaction coordinate. Reference data for bulk water is shown in gray. Data points signify simulation data, and lines are shown as a guide to the eye.

The data are shown in a semi-logarithmic representation, therefore a parabolic shape for bulk water is found (Fig. 5, gray curves), as reported earlier.^35,36 In Fig. 5, log[P_v(N_wat)] is shown for two ligand positions, q = 0 Å (A) and q = 14 Å (B). At large protein–ligand distances, the distributions deviate only moderately from those of bulk water, with a slightly smaller mean water number 〈N_wat〉 than in bulk due to the presence of the protein. At short distances, the ligand induces the partial desolvation of the HP, which is most pronounced for the flexible protein (green curve). The protein's hydrophobic surface shifts the distributions to smaller values and changes the width asymmetrically, favoring lower water occupancies.

The sensitivity to perturbations, as displayed by the altered shape of log[P_v(N_wat)] compared to bulk water, is seen in both the magnitude and the timescale of solvent fluctuations. To analyze the timescales, the time auto-correlation functions C_δNδN(t) were computed (Fig. 6A–C). Generally, the correlation functions have a long-time decay on a timescale of several tens of picoseconds for short protein–ligand distances. In addition, fast oscillations on the sub-picosecond timescale can be observed for all protein–ligand separation distances for simulations of the flexible and restrained protein, which are absent in simulations of the frozen protein. These oscillations indicate a coupling of low-frequency protein vibrations to water dynamics and resulting density fluctuations near the hydrophobic binding site.

Fig. 6 Normalized time auto-correlation functions of solvent fluctuations C_δNδN(t) near the HP surface with the ligand at several distances to the binding site. (A) flexible protein, (B) restrained protein and (C) frozen protein. Insets show semi-logarithmic representations of the same correlation functions.

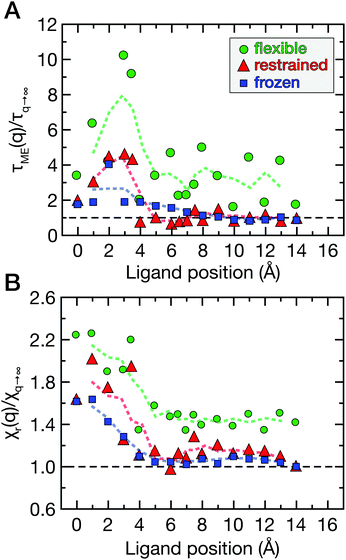
Fig. 7A shows the correlation times τ_δN obtained from the correlation functions in Fig. 6 as a function of q. Overall, the double-exponential fits yielded one ps-decay and one very fast decay on the fs timescale; the former are in good agreement with the correlation times directly obtained from C_δNδN(τ_δN) = 1/e. Therefore, we focus on the picosecond dynamics, which is also in accordance with data for purely hydrophobic cavities.³² The correlation time of solvent occupancy fluctuations in bulk water is τ_δN ≃ 0.4 ps (analyzed in a similar volume element V as was used for the hydration water around the HP, see above). To reveal ligand effects on the solvent dynamics, all data in Fig. 7A are normalized with respect to the “ligand-in-bulk” value, i.e., normalized by the value at q = 14 Å for the restrained protein (τ_q→∞ ≃ 0.9 ps). The value for the frozen protein is also τ_q→∞ ≃ 0.9 ps, and for the flexible protein it is τ_q→∞ ≃ 1.7 ps.

Fig. 7 Dynamics of water molecules near the HP as a function of ligand position. (A) Time scales of solvent fluctuations τ_δN(q). Dashed lines show the moving average over 3 values applied to the data (represented as a scatter plot) and are included as a guide to the eye. (B) Reduced local compressibility χ_r(q) describing the magnitude of solvent fluctuations. All data is normalized by the “ligand-in-bulk” value at q = 14 Å for the restrained protein.

For ligand positions of 2–4 Å distance to the restrained protein (Fig. 7A, red data points), where the ligand expels the final layers of hydration water from the HP upon binding, the solvent fluctuations are slowed down by a factor of up to 5 compared to large distances. This retardation coincides with the position of the free energy barrier (Fig. 2), indicating the onset of partial desolvation. For the frozen protein (Fig. 7A, blue data points), the ligand does not seem to affect the fluctuation timescale as much, even for short distances. On the contrary, for the flexible protein (Fig. 7A, green data points) the correlation times are slower than for the restrained and frozen proteins, and the slow-down of water fluctuations near the HP surface at short protein–ligand distances (q < 6 Å) is up to around 10-fold compared to the reference value obtained for large protein–ligand distances in the restrained system. Again, the removal of water molecules upon protein–ligand binding coincides with the free energy barrier (Fig. 2).

Finally, the magnitude of the solvent fluctuations was determined via the reduced local compressibility χ_r(q) of the water molecules in the volume element V close to the HP (Fig. 1B). The reference compressibility of bulk water is χ_r = 0.25. The reduced local compressibility χ_r(q) depends both on the size and shape of the volume element V used for the analysis, even for bulk systems. Only in the thermodynamic limit, χ_r(q) equals the local compressibility χ(q) = ρ(q)⁻¹(∂ρ(q)/∂P)_T,V.⁴⁷ Again, the data were normalized by the ligand-in-bulk value, i.e., at large separation distances. The compressibilities obtained for the restrained and frozen proteins are almost identical (χ_q→∞ = 0.18), and for the flexible protein it is χ_q→∞ = 0.25. The reduced local compressibility χ_r(q) of water molecules near the HP as a function of ligand position is shown in Fig. 7B.

For the restrained and frozen proteins (Fig. 7B, red and blue data points, respectively), the χ_r(q) profiles are similar. Notably, for the flexible protein (green data points), the solvent fluctuations are overall more strongly enhanced even for large separation distances between the ligand and the HP surface. At short protein–ligand distances (q<5 Å), χ_r(q) is about twofold larger than for large q. When the ligand approaches the HP, the partial desolvation increases the magnitude of solvent fluctuations, in line with the observed changes of the probability distributions P_v(N_wat) (see Fig. 5).

4 Conclusions

In this study, we analyzed the influence of protein flexibility on the dynamics of ligand binding to a hydrophobic surface patch of ubiquitin. Our results indicate that increased protein flexibility not only enhances the ligand binding affinity, but also lowers free energy barriers associated with the dewetting of the binding interface. The reduced free energy barriers upon binding to the flexible protein are rationalized by the simultaneous observation of enhanced water density fluctuations in the vicinity of the binding site in the presence of the ligand, which feature longer relaxation times but result in an increased local compressibility that facilitates dewetting. Friction profiles computed along the binding coordinate from random force correlations further indicate reduced friction and thus faster binding dynamics in simulations of a fully flexible protein compared to simulations with a restrained or fully frozen protein.

Previous research has focused on idealized hydrophobic model surfaces^17,32,35,50 and on small proteins.^36,52 In biological protein–ligand systems, the complete dewetting observed for hydrophobic model cavities^18,24,51 usually reduces to a partial desolvation of a binding site, which is also observed here.

Our study provides atomic-level insights into the dynamic coupling between a protein, its hydration shell and nearby ligands and how this coupling can facilitate binding processes. These observations are particularly interesting in the context of correlated protein–water vibrations, which we found in previous work to persist up to distances of 10–25 Å from the protein.^13,42,53 The explicit consideration of vibrational modes in the receptor at frequencies compatible to intermolecular vibrations in the water hydrogen bond network may complement previous observations from simulations with rigid binding site models.³² The results of the present study could thus open the way for future work aiming to quantify the effects of receptor flexibility on ligand binding for more realistic ligand-receptor pairs. Further it will be of interest to deduce the detailed mechanisms behind these effects and the mechanistic roles of correlated and/or collective dynamics and vibrations.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – EXC 2033 – 390677874 – RESOLV.

Notes and references

1. D. Chandler, Nature, 2005, 437, 640–647.
2. G. Hummer, Nat. Chem., 2010, 2, 906–907.
3. S. K. Pal, J. Peon, B. Bagchi and A. H. Zewail, J. Phys. Chem. B, 2002, 106, 12376–12395.
4. B. Bagchi, Chem. Rev., 2005, 105, 3197–3219.
5. M. Chaplin, Nat. Rev. Mol. Cell Biol., 2006, 7, 861–866.
6. J. C. Rasaiah, S. Garde and G. Hummer, Annu. Rev. Phys. Chem., 2008, 59, 713–740.
7. J. Qvist, E. Persson, C. Mattea and B. Halle, Faraday Discuss., 2009, 141, 131–144.
8. J. T. King and K. J. Kubarych, J. Am. Chem. Soc., 2012, 134, 18705–18712.
9. M.-C. Bellissent-Funel, A. Hassanali, M. Havenith, R. Henchman, P. Pohl, F. Sterpone, D. van der Spoel, Y. Xu and A. E. Garcia, Chem. Rev., 2016, 116, 7673–7697.
10. O. Fisette, C. Päslack, R. Barnes, J. M. Isas, R. Langen, M. Heyden, S. Han and L. V. Schäfer, J. Am. Chem. Soc., 2016, 138, 11526–11535.
11. D. Laage, T. Elsaesser and J. T. Hynes, Chem. Rev., 2017, 117, 10694–10725.
12. V. Pattni, T. Vasilevskaya, W. Thiel and M. Heyden, J. Phys. Chem. B, 2017, 121, 7431–7442.
13. C. Päslack, L. V. Schäfer and M. Heyden, Phys. Chem. Chem. Phys., 2019, 21, 15958–15965.
14. C. Päslack, J. C. Smith, M. Heyden and L. V. Schäfer, Phys. Chem. Chem. Phys., 2019, 21, 10370–10376.
15. S. Mukherjee, S. Mondal and B. Bagchi, Phys. Rev. Lett., 2019, 122, 058101.
16. Y. Levy and J. N. Onuchic, Annu. Rev. Biophys. Biomol. Struct., 2006, 35, 389–415.
17. S. N. Jamadagni, R. Godawat and S. Garde, Annu. Rev. Chem. Biomol. Eng., 2011, 2, 147–171.
18. R. Baron, P. Setny and F. Paesani, J. Phys. Chem. B, 2012, 116, 13774–13780.
19. R. Baron and J. A. McCammon, Annu. Rev. Phys. Chem., 2013, 64, 151–175.
20. M. S. Bodnarchuk, R. Viner, J. Michel and J. W. Essex, J. Chem. Inf. Model., 2014, 54, 1623–1633.
21. G. Gerogiokas, M. Southey, M. Mazanetz, A. Hefeitz, M. Bodkin, R. Law and J. Michel, Phys. Chem. Chem. Phys., 2015, 17, 8416–8426.
22. S. M. Gopal, F. Klumpers, C. Herrmann and L. V. Schäfer, Phys. Chem. Chem. Phys., 2017, 19, 10753–10766.
23. B. J. Berne, J. D. Weeks and R. Zhou, Annu. Rev. Phys. Chem., 2009, 60, 85–103.
24. P. Setny, R. Baron and J. A. McCammon, J. Chem. Theory Comput., 2010, 6, 2866–2871.
25. L. Zdek, M. V. Novotny and M. J. Stone, Nat. Struct. Biol., 1999, 6, 1118–1121.
26. A. Bhowmick and T. Head-Gordon, Structure, 2015, 23, 44–55.
27. J. A. Caro, K. W. Harpole, V. Kasinath, J. Lim, J. Granja, K. G. Valentine, K. A. Sharp and A. J. Wand, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 6563–6568.
28. M. L. Verteramo, O. Stenström, M. M. Ignjatović, O. Caldararu, M. A. Olsson, F. Manzoni, H. Leffler, E. Oksanen, D. T. Logan and U. J. Nilsson, et al. , J. Am. Chem. Soc., 2019, 141, 2012–2026.
29. P. W. Fenimore, H. Frauenfelder, B. H. McMahon and F. G. Parak, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 16047–16051.
30. L. Zhao, W. Li and P. Tian, PLoS One, 2013, 8, e60553.
31. M.-C. Bellissent-Funel, A. Hassanali, M. Havenith, R. Henchman, P. Pohl, F. Sterpone, D. Van Der Spoel, Y. Xu and A. E. Garcia, Chem. Rev., 2016, 116, 7673–7697.
32. P. Setny, R. Baron, P. M. Kekenes-Huskey, J. A. McCammon and J. Dzubiella, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1197–1202.
33. J. Qvist, M. Davidovic, D. Hamelberg and B. Halle, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 6296–6301.
34. P. W. Fenimore, H. Frauenfelder, B. H. McMahon and R. D. Young, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 14408–14413.
35. A. J. Patel, P. Varilly, S. N. Jamadagni, M. F. Hagan, D. Chandler and S. Garde, J. Phys. Chem. B, 2012, 116, 2498–2503.
36. N. B. Rego, E. Xi and A. J. Patel, J. Am. Chem. Soc., 2019, 141, 2080–2086.
37. C. T. Archer and T. Kodadek, Nucleic Acids Res., 2009, 38, 789–796.
38. S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854.
39. B. R. Brooks, C. L. Brooks, A. D. Mackerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614.
40. J. L. F. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505.
41. G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199.
42. M. Heyden and D. J. Tobias, Phys. Rev. Lett., 2013, 111, 218101.
43. S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021.
44. J. S. Hub, B. L. de Groot and D. van der Spoel, J. Chem. Theory Comput., 2010, 6, 3713–3720.
45. R. Kubo, Rep. Prog. Phys., 1966, 29, 255.
46. R. Vogelsang and C. Hoheisel, J. Stat. Phys., 1987, 47, 193–207.
47. H. Acharya, S. Vembanur, S. N. Jamadagni and S. Garde, Faraday Discuss., 2010, 146, 353–365.
48. R. Evans and M. C. Stewart, J. Phys.: Condens. Matter, 2015, 27, 194111.
49. B. Efron, Ann. Stat., 1979, 7, 1–26.
50. P. Setny, Z. Wang, L.-T. Cheng, B. Li, J. A. McCammon and J. Dzubiella, Phys. Rev. Lett., 2009, 103, 187801.
51. R. Baron, P. Setny and J. A. McCammon, J. Am. Chem. Soc., 2010, 132, 12091–12097.
52. S. Sarupria and S. Garde, Phys. Rev. Lett., 2009, 103, 037803.
53. M. Heyden, J. Chem. Phys., 2014, 141, 22D509.

---

Footnote

† Electronic supplementary information (ESI) available: MD simulation protocol, protein RMSF, details on the analysis procedures, PMF convergence tests, and extended water occupancy analyses. See DOI: 10.1039/d1cp00181g

---