Open Access Article
Open Access ArticleA coarse-grained xDLVO model for colloidal protein–protein interactions†
Srdjan
Pusara
 a,
Peyman
Yamin‡
a,
Wolfgang
Wenzel
a,
Peyman
Yamin‡
a,
Wolfgang
Wenzel
 *a,
Marjan
Krstić
*a,
Marjan
Krstić
 ab and
Mariana
Kozlowska
ab and
Mariana
Kozlowska
 *a
*a
aInstitute of Nanotechnology, Karlsruhe Institute of Technology (KIT), Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany. E-mail: mariana.kozlowska@kit.edu
bInstitute of Theoretical Solid State Physics, Karlsruhe Institute of Technology (KIT), Wolfgang-Gaede-Str. 1, 76131 Karlsruhe, Germany
First published on 24th May 2021
Abstract
Colloidal protein–protein interactions (PPIs) of attractive and repulsive nature modulate the solubility of proteins, their aggregation, precipitation and crystallization. Such interactions are very important for many biotechnological processes, but are complex and hard to control, therefore, difficult to be understood in terms of measurements alone. In diluted protein solutions, PPIs can be estimated from the osmotic second virial coefficient, B22, which has been calculated using different methods and levels of theory. The most popular approach is based on the Derjaguin–Landau–Verwey–Overbeek (DLVO) theory and its extended versions, i.e. xDLVO. Despite much efforts, these models are not fully quantitative and must be fitted to experiments, which limits their predictive value. Here, we report an extended xDLVO-CG model, which extends existing models by a coarse-grained representation of proteins and the inclusion of an additional ion–protein dispersion interaction term. We demonstrate for four proteins, i.e. lysozyme (LYZ), subtilisin (Subs), bovine serum albumin (BSA) and immunoglobulin (IgG1), that semi-quantitative agreement with experimental values without the need to fit to experimental B22 values. While most likely not the final step in the nearly hundred years of research in PPIs, xDLVO-CG is a step towards predictive PPIs calculations that are transferable to different proteins.
1 Introduction
Protein–protein interactions play an important role in biological function and processes in biotechnology. Specific interactions, known as “lock-and-key”, are characterized by a strong binding affinity and occur during processes such as antigen binding to the antibody or ligand binding to a receptor. In contrast, the state of proteins in solution, including the propensity to aggregate, is steered mostly by the weak non-specific interactions, i.e. colloidal protein–protein interactions (PPIs). These include steric repulsion, van der Waals or hydrophobic interactions, as well as long- or short-ranged electrostatic repulsion and attraction, all of which are modulated by the solution pH, temperature, ionic strength, protein concentration and the presence of excipients. The balance between attractive and repulsive forces determines the stability of protein solutions and their precipitation and crystallization, when the screening of the repulsive forces is achieved. Both processes are complex and not fully understood, yet, they are extremely important for protein processing and manufacturing, especially in health care or food applications.1,2 Control and design of such processes and the assessment of the PPIs during the pre-formulation development phase require information regarding protein solubility and its modulation by the solution conditions.3,4The solubility of molecules is affected by their solid–liquid equilibrium, which depends on solute–solute and solute–solvent interactions.5 Macroscopic deviation of the osmotic pressure from that on an ideal solution can give information about solute–solute interactions. This deviation is characterized by virial coefficients. Here, the most relevant quantity is the second virial coefficient, known in diluted systems as B22, which gives information about average two-body interactions between protein molecules. B22 is a measure of the non-specific protein binding capacity6 and stickiness, and it has been investigated widely as a semi-quantitative approach to characterize protein solubility,7–12 phase behavior13–16 and crystallization.2,7,9,16–18 Positive values of the B22 coefficient indicate the dominance of repulsion interactions between proteins and correspond to good protein solubility. When attractive interactions between proteins increase, enabling protein assembly and aggregation, the B22 values become negative. A quantitative relation between the B22 and the ideal protein crystallization conditions was proposed by George and Wilson,19 who determined a narrow range of the B22, when crystallization occurs.7,8,20 Since then, several empirical models were proposed aiming to correlate B22 quantitatively with solubility and self-assembly with parameters fitted from experimental data.11,18,21 Moreover, thermodynamic relations between the protein solubility and B22 were developed,7,12 where the solubility, S, is calculated from the measured B22 using:
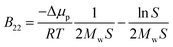 | (1) |
Experimentally, the osmotic second virial coefficient is often measured using membrane osmometry, static light scattering, cloud-point measurements, fluorescence-anisotropy, self-interaction chromatography or by sedimentation equilibrium.14,22–24 As an example, the functional form to relate PPIs with Rayleigh scattering in static light scattering (SLS) is the following:25
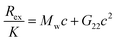 | (2) |
Unfortunately, the experimentally determined values of B22 cannot be decomposed into the specific PPI contributions, limiting the systematic understanding of PPI. Presently, the number of reported B22 coefficients is still limited to specific examples, therefore, considering the huge number of proteins of industrial interest and the various conditions occurring in industrial processes, there is a huge space for improved models and theories for the B22 calculation. Quantitative models to compute the B22 coefficients for specific proteins and environmental conditions can accelerate the optimization of the industrial processing towards the stability of the protein solutions or protein crystallization beyond the current “trial and error” experiments based on the several empirical rules.28,29
From the perspective of thermodynamics, the osmotic second virial coefficient is the solvent-averaged free energy of interaction between a pair of proteins, which is Boltzmann-averaged over the relative protein orientations and separations. It has been estimated by the integration over the configuration space, Monte-Carlo simulations30,31 with the Mayer sampling,13,32–36 from molecular simulations27,37,38 using radial distribution functions or potentials of mean force or by counting all configurations in which proteins interact.36 Among available theoretical tools aimed to calculate B22 coefficients, one of the most commonly used approach is the DLVO theory, that was originally developed by Derjaguin–Landau and Verwey–Overbeek for colloidal systems.39 It models PPI by representing proteins by spheres and accounts for van der Waals and electrostatic interactions in protein solutions of a specific ionic strength. The protein is represented by the charged sphere using a Debye–Hückel model for the screening by hydrated salts and a continuum representation of the solvent. When fitted to experimental B22 data, DLVO theory represents the overall trends well.1 Several improvements of DLVO were reported, including introduction of the multiple binding sites to other proteins40 or addition of a salt-induced osmotic attraction potential.41 The latter model was also extended to compute B22 of protein solutions with excipients42 in the presence of polymers.43 Details of the extended DLVO (xDLVO) method are given in Section 2.2.
Since proteins exist in a variety of different shapes with an inhomogeneous charge distribution, resulting in anisotropic PPIs,31,44 the spherical approximation in xDLVO may be one of the reasons, why such models fail to quantitatively describe B22 coefficients without fitting to an experimental baseline. Moreover, even for the globular proteins, the surface roughness can play significant role on the solvent accessible area, and therefore, on the total potential of mean force (PMF) and B22.45 Anisotropic shape is also important for the protein surface complementarity during the assembly and crystallization processes.46 Methods using coarse-grained (CG) representations of proteins improve the accuracy of B22 calculation for different types of proteins,27,47,48 starting from the small globular lysozyme to monoclonal antibodies. In most cases, the protein model was parameterized based on the experimental data.13,27,30–36 One might assume that using a fully atomistic, but computationally costly representation would fully resolve the difficulties stemming from the spherical approximation, but this is not the case: investigations with fine-grained protein models using atomistic and MARTINI force fields have shown significant deviations from experiment, in particular they result in a large overestimation of the PMF well depths.31,37,38
Here, we aim to develop a transferable model for reasonably efficient B22 calculations using optimized coarse-grained (CG) representation for the protein that is better able to account for the shape of non-spherical proteins, while not incurring the cost of fully atomistic models. We show that a shape based representation of the protein and the introduction of an additional term representing ion–protein dispersion interactions improve an agreement between experiment and model, both in values and limiting behavior. Going beyond spherical models we must sample the conformational space of the relative orientations of the proteins. We validate the model on lysozyme (LYZ), subtilisin (Subs), bovine serum albumin (BSA) and immunoglobulin type 1 (IgG1), where we find a good agreement with the available experimental data.
2 Theory
2.1 B 22 from the potential of mean force
The osmotic second virial coefficient, B22, can be defined via the virial expansion of the osmotic pressure as: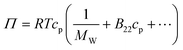 | (3) |
McMillan and Mayer used a statistical mechanics approach to describe the osmotic properties of solutions, reducing the virial equation of state to the osmotic equation of state, where the solute particles interact with each other via effective potentials.49 Therefore, the relationship between the osmotic second virial coefficient and the potential of mean force (PMF), W22, between two proteins in solution can be derived as:49,50
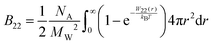 | (4) |
2.2 DLVO and xDLVO theory
DLVO theory is a traditional approach that is often used also to compute B22 as a function of ionic strength.39 Proteins are represented by spheres, which interact via van der Waals interactions (Hamaker model) and electrical double layer forces (Debye–Hückel). When fitted to experimental B22 data, DLVO theory represents the overall trends well with larger discrepancies at higher ionic strengths.1 Extended DLVO models (xDLVO) as, for example, reported by Herhut et al.,41 overcome some of the limitations of DLVO by adding salt effects via osmotic potential, while retaining the spherical model for the proteins. Here, by fitting of the Hamaker constant and B22 to experiments at low ionic strengths, they improved B22 coefficients at high ionic strengths. Their model included the contribution of a hard sphere potential WHS(r), a dispersion potential Wdisp(r), an electrostatic potential Wel(r), and an osmotic potential Wosm(r):51| W22(r) = WHS(r) + Wdisp(r) + Wel(r) + Wosm(r) | (5) |
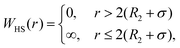 | (6) |
The dispersion potential:
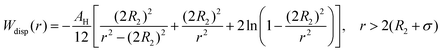 | (7) |
The electrostatic potential was derived from Debye–Hückel theory,53 which models the repulsive forces of two identical protein molecules:
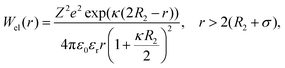 | (8) |
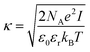 | (9) |
Eqn (8) cannot take into account the effect of electrolytes at ionic strengths higher than 10 mM, therefore, the salt effects were modeled via the osmotic potential,54Wosm(r):
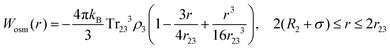 | (10) |
The traditional xDLVO model41 allowed to describe the B22 of proteins in aqueous solution as a function of pH, salt type, salt concentration and temperature by fitting to experimental B22 data. In order to compare it with the new model developed here, we re-implemented this approach, but do not fit the parameters. Instead, we use just one value of the Hamaker constant, taken from the literature (see Table 1 in Appendix), to represent dispersion interactions and we implemented new potential term, i.e. for ion–protein dispersion interactions, that improves the salt induced attractive PPIs in PMF. The detailed description of the new model is given in the next Section.
| Protein | Conditions | A H [kBT] |
|---|---|---|
| LYZ | All pH and salts | 8.0 |
| BSA | All pH and salts | 3.0 |
| Subs | NaCl | 5.1 |
| Subs | NaSCN | 6.8 |
| IgG1 | All pH and salts | 3.0 |
3 A coarse-grained xDLVO model
3.1 Coarse-grained model
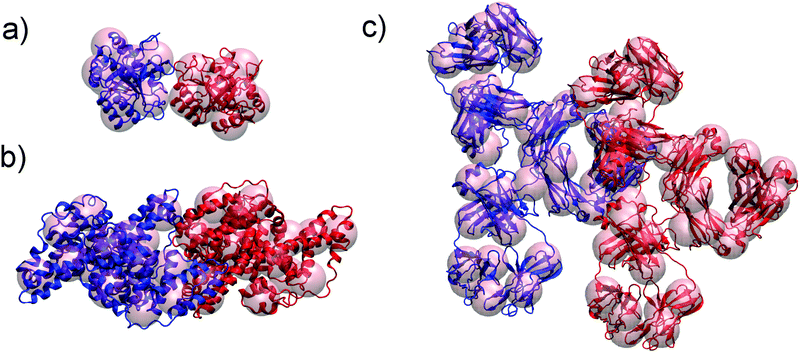
We investigate here a model that tries to improve upon some approximations in xDLVO. Clearly, most proteins are not spherical and, therefore, their interactions are anisotropic. This means that many configurations contribute to the conformational ensemble. In order to account for these effects we introduce a coarse-grained model of the proteins built from the respective all-atom structures. We investigate here lysozyme (LYZ), subtilisin properase (Subs), bovine serum albumin (BSA) and human immunoglobulin type I (IgG1) with the PDB codes 4nhi, 4f5s, 1ndu and 1mco. The selected PDB structures contain all residues and have at least two protein units in the unit cell. Hydrogen atoms were added according to the pH of interest (see Table S1, ESI†) using PROPKA method55,56 implemented in PDB2PQR web-server.57,58All-atom structures of proteins were mapped to a coarse-grained (CG) representations using a shape-based model with a self-organizing neural network topology building algorithm,59 implemented in the VMD program (version 1.9.3).60 The neural network was initialized by two variables, ε and λ, used for the learning algorithm. The starting and the final values of ε and λ were 0.3 and 0.05 and 20 and 0.01, respectively. One CG bead represented approximately 500 atoms of a particular protein, resulting in 5, 10, 20, 40 CG beads for LYZ, Subs, BSA and IgG1 (see Fig. 1a and 5), respectively. CG beads were placed at the center of mass of atoms represented by each bead. Partial charges of atoms in each bead, as calculated by PROPKA, were used to calculate the charge of each CG bead (see Fig. S1, ESI†). Several mapping schemes were tested (see Fig. S2, ESI†). We find that there is little difference in B22 between 500-to-1 mapping compared to a calculation that used a 150-to-1 mapping, while the computational cost of B22 was reduced from 57.76 minutes to 7.7 minutes for 150-to-1 and 500-to-1 model of BSA (for one relative orientation). For this reason we opted for a 500-to-1 mapping for this investigation.
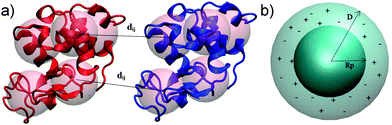 | ||
| Fig. 1 Improvements of xDLVO approach implemented in xDLVO-CG: shape-based coarse-grained model of proteins, shown for lysozyme (PDB code 4nhi) represented by 5 CG beads per a protein unit (a) and continuum model of ion–protein dispersion interactions (b). Rp and D denote protein radius and maximum thickness of a shell, at which ion–protein interactions are considered. | ||
3.2 Potential of mean force in xDLVO-CG
The xDLVO model, described in Section 2.2, was adapted for the shape-based CG model of proteins. Interaction potentials (eqn (7)–(10)) between all beads of one protein and all beads of another protein (schematically shown in Fig. 1a) were implemented using pairwise terms between beads as opposed to the protein as a whole. The implementation of these terms is discussed in detail below.In order to go beyond the fitting of the Hamaker constant to protein specific B22 data in xDLVO, we aim here for a model, where the Hamaker constant is independently measured or computed and do not depend on pH and salt concentrations. Even in a CG representation we need to account for the “missing” interactions and additional terms must be considered to model the observed dependence on pH and salt concentration. To account for this effect we investigate, whether an additional ion–protein dispersion potential (Section 3.2.4), mimicking the impact of ion type on the protein salting out, as known from the Hofmeister series, can compensate for the missing effects. For the dispersion interactions, we still use a Hamaker-approach for most of the paper, but, at the end, we discuss replacing this term altogether by a Lennard-Jones potential. Therefore, the total PMF between two proteins, W22 (eqn (4)), was determined as the sum of electrostatic, dispersion (Hamaker or Lennard-Jones), osmotic and ion–protein interactions as in
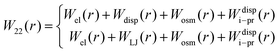 | (11) |
The PMF was calculated at salt concentrations from 0 to 1 M (every 0.01 M) on the center-of-mass distances between the proteins starting from the separation in the initial crystal structure (R0) up to R0 + 30 nm using 0.1 nm step (see Fig S3, ESI†). All calculations were performed at 298.15 K. The PMF and the corresponding B22 coefficients were calculated by an in-house developed code.
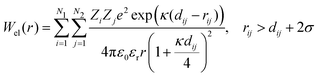 | (12) |
The impact of the low dielectric core, which was shown to give a rise to the short-range image-charge-based repulsion of the charged polyelectrolyte chain, adsorbed on the spherical substrates,61 was not included. The image repulsion for the ion–protein electrostatics is low: Slight contributions are noticeable only at low salt concentrations (see Fig. S4, ESI†) without the influence on the B22 values. Image-charge-based repulsion is negligible at moderate ionic strengths. This is consistent with other studies in this field.62,63
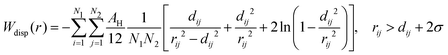 | (13) |
| AH = π2λq1q2, | (14) |
Since the Hamaker equation needs experimentally measured values of AH, we attempted to generate a parameter-free substitute by implementing the Lennard-Jones potential:
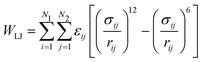 | (15) |
The Lennard-Jones parameters of each bead: εi and σi, were assigned according to Arkhipov et al.,66 as implemented in the SBCG builder in VMD. According to this model, the interaction strength of each bead was assigned based on the hydrophobic solvent accessible surface area (SASA) for the protein domain represented by a bead:
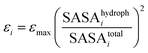 | (16) |
The LJ radius for each bead, σi, was obtained as a radius of gyration of the groups of atoms represented by a CG bead, increased by a constant value, Δσ, of 0.1 nm, to mimic atoms at the edges of the bead. LJ parameters between specific beads pairs were obtained by standard combination rules:
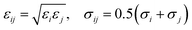 | (17) |
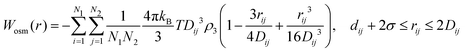 | (18) |
| Dij = dij + R3 + σ | (19) |
| Salt | R 3 [nm] | Ion | B i–pr × 10−50 [J m3] |
|---|---|---|---|
| NaCl | 0.442 | Na+ | 0.454 |
| KCl | 0.436 | K+ | 1.888 |
| NaI | 0.464 | Cl− | 3.574 |
| NaSCN | 0.460 | I− | 4.440 |
| SCN− | 10.000 |
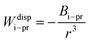 | (20) |
The number of ions in an infinitely thin spherical shell around the protein is given by cbulk![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−zϕ(r)/r)dV, where dV = 4πr2dr is the shell volume, z is the charge of an anion or a cation and ϕ(r) is the electrostatic potential felt by ion at distance r from the protein center (approximated by eqn (8)). As a result, the total magnitude of the ion–protein dispersion interaction in xDLVO-CG is obtained by the integration of contributions of all ions, placed in the spherical shell around the protein:
exp(−zϕ(r)/r)dV, where dV = 4πr2dr is the shell volume, z is the charge of an anion or a cation and ϕ(r) is the electrostatic potential felt by ion at distance r from the protein center (approximated by eqn (8)). As a result, the total magnitude of the ion–protein dispersion interaction in xDLVO-CG is obtained by the integration of contributions of all ions, placed in the spherical shell around the protein:
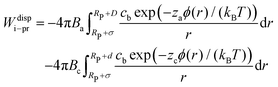 | (21) |
3.3 Protein–protein sampling scheme
When proteins are represented as non-spherical molecules, the orientational dependence of B22 is accounted by the generalization of eqn (4):46,50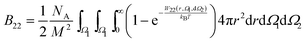 | (22) |
We employ two sampling schemes: the data labelled just with the name of the PDB code refers to a sampling of the PPI, where the protein is pulled along a linear trajectory outwards along the line connecting the respective center-of-mass of the proteins starting with the crystal structure up to a distance of R0 + 30 nm. The other data was generated as follows: To sample the protein pair interactions for the relevant relative arrangements we used a statistical sampling scheme over the configuration space. This approach results in a fast evaluation of the protein–protein configurations with on-the-fly calculation of the corresponding contributions to the PMF. For this, the initial crystal structure of the protein (see Section 3.1) was used, such that the first protein was kept at a fixed position (x1, y1, z1), while the second protein (with the center at (x2, y2, z2)) was uniformly moved around the first one on the fixed distance r0. The radial sampling of the second protein was performed by varying (θ, ϕ, r) coordinates in the spherical coordinate system with the center at (x1, y1, z1). Ten values of θ, ϕ angles were taken uniformly from θ = [0,2π] and v = [−1,1] → ϕ = −arccos(v) intervals, which resulted in 83 unique starting configurations (including the protein position in the crystal). In addition, the second protein was subsequently rotated by five different angles 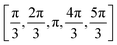 around (x − x2), (y − y2) or (z − z2) axis, respectively. These resulted in 16 differently rotated structures, therefore, in the total amount of different starting protein configurations of 83·16( = 1328). From these starting configurations, again the protein is pulled along a linear trajectory outwards, up to a distance of R0 + 30 nm, along the line connecting the respective center-of-mass. All configurations were checked for the possible sterical overlap that could have been generated after the radial movements and rotations. Two proteins were considered overlapping, if the distance between any bead pairs (belonging to different proteins) was smaller than the sum of radii of gyration of the corresponding beads. Overlapping structures were excluded from further calculations. The total PMF was obtained via averaging of all the angular orientations defined by the starting structures, resulting in the PMF as a function of the COM: W22(r,Ω1,Ω2) → W22(r). The second osmotic coefficient as a function of ionic strength was calculated by numerical integration of the averaged PMF at different salt conditions according to eqn (4).
around (x − x2), (y − y2) or (z − z2) axis, respectively. These resulted in 16 differently rotated structures, therefore, in the total amount of different starting protein configurations of 83·16( = 1328). From these starting configurations, again the protein is pulled along a linear trajectory outwards, up to a distance of R0 + 30 nm, along the line connecting the respective center-of-mass. All configurations were checked for the possible sterical overlap that could have been generated after the radial movements and rotations. Two proteins were considered overlapping, if the distance between any bead pairs (belonging to different proteins) was smaller than the sum of radii of gyration of the corresponding beads. Overlapping structures were excluded from further calculations. The total PMF was obtained via averaging of all the angular orientations defined by the starting structures, resulting in the PMF as a function of the COM: W22(r,Ω1,Ω2) → W22(r). The second osmotic coefficient as a function of ionic strength was calculated by numerical integration of the averaged PMF at different salt conditions according to eqn (4).
4 Results and discussion
4.1 pH dependence of B22 for lysozyme
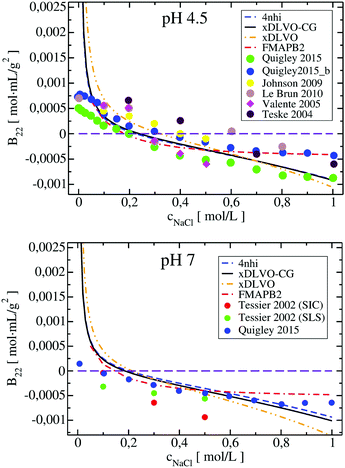
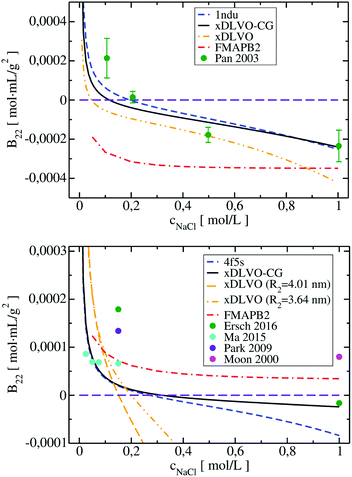
Four proteins of different size, shape and physicochemical properties were used for the osmotic second virial coefficient calculations with the new xDLVO-CG model. The choice of the proteins investigated was mainly based on the availability of experimental measurements of the B22 coefficients. An in-depth analysis of the literature revealed significant variation in the B22 values for the same protein and in similar solution conditions, often the data was obtained using different measurement techniques. To provide a generalized picture of the available data and correlations between the computed B22 in the present study, we included data originating from the several reports, as indicated. Moreover, we compared xDLVO-CG results with other theoretical models for B22 calculations, i.e. with a spherical xDLVO model that replicated the model reported in ref. 41, as discussed in Section 2.2. Secondly, we compared to FMAPB2 (FFT-based Modeling of Atomistic Protein–protein interactions),38 an all-atom model for the protein and implicit solvent model. FMAPB2 incorporates much higher structural resolution in comparison to the spherical or CG models. FMAPB2 calculations were performed using publicly available web-server (http://pipe.rcc.fsu.edu/fmapb2). In the xDLVO-CG calculations we did not fit the Hamaker constant, but used values discussed in the sections for each protein and listed in Table 1 in Appendix.Lysozyme (LYZ) is a small globular protein (Fig. 1a) that consists of 129 residues and exists as a monomer in solution for a wide range of conditions. Its main physiological function is hydrolysis of the glycosidic bonds in peptidoglycans that can be found in bacteria. LYZ was the first enzyme to be fully sequenced79 and it is the second protein for which the crystal structure was solved.80 Due to its size and simplicity of processing, LYZ is the most studied protein also in terms of its solubility via the osmotic second virial coefficients.10,14,22,81–83 As all proteins, LYZ is of zwitterionic nature and its PPIs, and therefore the solubility, are highly dependent on the pH of the solution. The main change induced by pH is the charge of the protein, resulting in a positive B22 for highly charged proteins and a negative B22 when the charge is screened enabling further attractive PPIs. To understand the aggregation propensity of LYZ as a function of pH, we perform calculations at five different pH values: pH 3, pH 4.5, pH 5, pH 7 and pH 8, for which exhaustive experimental data is available.
The B22 coefficients of LYZ at pH 4.5 and pH 7 are shown in Fig. 2. Values at low ionic strengths are positive and decrease towards negative with an increase of the salt concentration. Due to relatively slight decrease of the positive charge of a protein, i.e. from +11 to +9 at pH 4.5 and pH 7, as obtained using PROPKA protonation method (see Table S1, ESI†), the general trend for the B22 change with increasing ionic strength is similar in both cases. The data obtained correlates well with the measured B22, no fitting to experiment is required. For xDLVO-CG, we used one AH value for all pH and salt concentrations (Table 1 in Appendix), and the calculated B22 reproduces experimental observations. We have used the same AH value for xDLVO and wee see that it also works well without any additional fitting. We find that calculations using one starting protein–protein configuration from the crystal (PDB code: 4nhi, data marked with dashed blue curve) result in nearly identical results to those obtained via the sampling protocol (marked with solid black curve). This likely results from the globular and symmetrical shape of LYZ with a low level of charge anisotropy. From the same reason, the xDLVO model considered here works also well for LYZ (data marked with orange dashed curve in Fig. 2). There is a slight overestimation of B22 for concentrations lower than 200 mM, thereafter it decreases as in experiment and xDLVO-CG. This overestimation was improved in xDLVO theory reported by Herhut et al.,41 which fitted the Hamaker constant depending on pH value and salt concentration.
B 22 values, calculated with xDLVO-CG, correlate with FMAPB2 results (data marked with red dashed curve in Fig. 2), especially at low ionic strengths. Larger deviations are observed starting from 500 mM NaCl concentrations, where FMAPB2 data flattens out. It is hard to judge, which model performs better since experimental results vary widely. The computational cost of B22 calculations at one pH value using xDLVO-CG and FMAPB2 is ca. 1.85 h (on 1 desktop CPU i5-7500, 3.40 GHz) for hundred salt concentrations (in the range of 0.0–1.0 M) and 4 h on the FMAPB2 server (single node with 16 Intel Xeon E5-2650 cores) for one salt concentration, respectively.
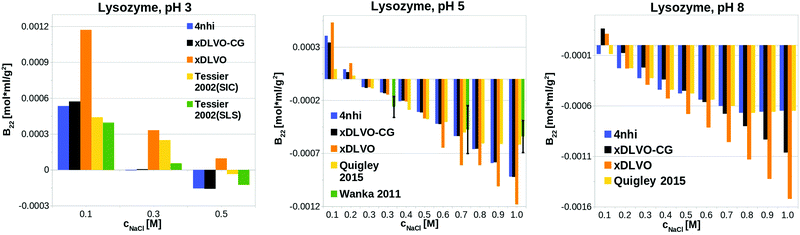
xDLVO-CG has good semi-quantitative agreement with experimental data also at other pH values (see Fig. 3). We observe larger deviations from either experimental data from size exclusion chromatography (SIC) or static light scattering (SLS), to both xDLVO and xDLVO-CG at 300 mM NaCl at pH 3 (histogram on the left in Fig. 3). The same observation was reported by Kalyuzhnyi et al.,84 who accounted all interacting species: proteins, ions and water molecules, explicitly in the model. They also reported overestimation of calculated B22 at pH larger than 7, which agrees with our observations for lysozyme at pH 8, where probably ion-specific effects are more pronounced than we can presently account for in the model.
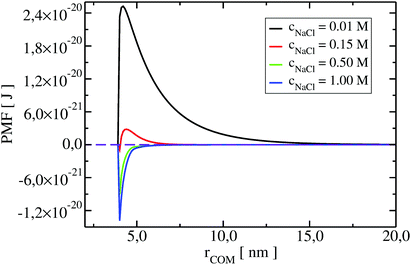
To understand the impact of different colloidal PPIs modulating the observed changes of the B22, interaction potentials contributing in the total PMF (Section 3.2) at specific salt conditions can be analyzed (see Fig. 10 and 11 in Appendix). From this data, we see the strong impact of the electrostatic repulsion interactions at low ionic strength and their decrease with stronger charge screening induced by an increase of the salt ions. For LYZ at pH 4.5 and 10 mM NaCl, the electrostatic potential (ca. 4.4 × 10−20 J) is approximately 5 times stronger than the dispersion potential (ca. −9 × 10−21 J). This is the reason why the total PMF (see Fig. 4) at 10 mM NaCl is dominated by repulsive interactions, resulting in positive B22 (Fig. 2).
The situation changes with the increase of the salt concentration, which results in more pronounced attractive dispersion interactions (PMF depicted in green and blue in Fig. 4), inducing negative values of B22 and protein aggregation. The impact of osmotic and ion–protein interactions is smaller, however, it increases at higher ionic strengths (Fig. 10 and 11 in Appendix), where protein salting out occurs. Inclusion of ion–protein dispersion interactions in xDLVO-CG improves the calculated B22 values (see Section 4.3).
4.2 Application to non-spherical proteins
LYZ is a globular protein, which results in relatively good description of its solubility even by pure DLVO theory. The predictive power of DLVO and xDLVO is limited for solubility predictions for non-spherical proteins, where parameters must be fitted to experiment. We tested our model for subtilisin properase (Subs), bovine serum albumin (BSA) and human immunoglobulin type 1 (IgG1). The coarse-grained representation of the proteins is depicted in Fig. 5, where protein monomers in dimer models used for the PPIs sampling are colored in blue and red, respectively.In the B22 data for Subs at pH 5.5 (upper panel in Fig. 6), we see significant differences between calculations made with xDLVO and FMAPB2 in comparison to xDLVO-CG. The B22 crossing point, indicating a change between solubilized proteins and induction of aggregation, is shifted to the lower ionic strengths in xDLVO and shows stronger increase of attractive PPIs towards aggregation. This is caused by the representation of the charge by a sphere in xDLVO, while the protein has a significant anisotropy that is better represented by xDLVO-CG (see Fig. S1, ESI†). B22 from xDLVO, with the experimental Hamaker constant of 5.1kBT, matches the experimental B22 at 500 mM NaCl (−1.83 × 10−4 and −1.78 × 10−4 mol mL g−2, respectively), but this is the only data point that matches. Another xDLVO methodology to calculate B22 was used by Pan et al.12 They used the MacroDox program to calculate the charge of Subs and fitted the Hamaker constant to achieve nearly quantitative agreement between the experimental measurements and their xDLVO. The protein charge they obtained is higher by 2.7–3.5e (i.e. is +8.7 to +9.42e) than we obtained using PROPKA (+6e). Since there is no information about the Subs charge from experimental measurements, we cannot validate the protonation schemes used in either approach. Moreover, fits of the Hamaker constant for each protein charge and radius12 complicates the decomposition of PPIs originating from protein–protein dispersion interactions and other interactions (see Section 4.3).
B 22 calculated using FMAPB2, with an all atom protein representation, are shifted far to the negative B22 range, this model deviates far from the B22 range from experiment. This was observed only in the case of Subs. Double data check via repeated FMAPB2 calculations did not result in improved results.
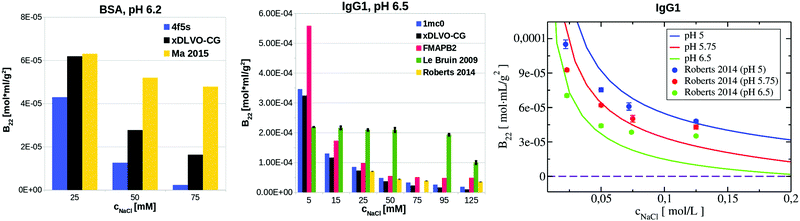 | ||
| Fig. 7 Comparison of B22 coefficients for BSA at pH 6.2 and IgG1 at pH 5, pH 5.75 and pH 6.5 calculated using xDLVO-CG, xDLVO and FMAPB2 with respect to the reported experimental measurements. | ||
xDLVO, fails to reproduce the B22 coefficients at salt concentrations higher than 100 mM NaCl (data marked in orange in Fig. 6), even if the total charge of the sphere in xDLVO (−20.06e, see Table S1, ESI†) better reproduces the experimentally reported value (−20.30e88). The xDLVO data depends strongly on the protein radius used, R2, which is known for BSA to be in the range of 3.5–4.1 nm89 as a function of pH and ionic strength. In Fig. 6, xDLVO calculations of B22 for BSA with radius of 3.64 nm90 and 4.01 nm (from 4f5s) are shown. xDLVO calculations with either radius cannot capture the experimental B22 trends.
Human immunoglobulin IgG1, used in the present studies, consists of 644 residues and has a characteristic T-shaped structure (see Fig. 5c). Its shape cannot be represented well by a spherical approach in xDLVO without fitting to the experimental data. Coarse-graining IgG1 by 40 CG beads nicely mimics the shape of this protein. We calculated B22 of IgG1 at pH 5, 5.75 and 6.5 (Fig. 7) using the Hamaker constant of 3kBT, which is in the range of a typical AH values in protein–water–protein systems.92,93
The B22 data obtained are shown in Fig. 7. Both xDLVO-CG and FMAPB2 give comparable results and similar trends for salt concentrations higher than 25 mM, despite the fact that the methodologies are very different. B22 values, calculated by xDLVO-CG, agree well with the experimental data reported by Roberts et al.,94 while B22 coefficients reported by Le Bruin et al.95 are higher and show low degree of salt concentration dependence. Calculated B22 indicate preferred attractive interactions (lower B22) of IgG1 at higher pH values (see panel on the right in Fig. 7). This is caused by the higher protein charge at lower pH, promoting solubilization of monomers in solution.
B 22 coefficients of IgG1, calculated using xDLVO without fitting fail completely to reproduce the experimental data and are totally out of the range of the values obtained by xDLVO-CG and other methods (see Fig. S5, ESI†). This again demonstrates that xDLVO methods, with protein represented as a sphere, are highly dependent on experimental data and loose their ability to accurately model PPIs and the corresponding osmotic second virial coefficients for aspherical proteins without fitting procedures.
Still, the calculated second virial coefficients for IgG1 and BSA in xDLVO-CG deviate more from experiment than for LYZ and Subs. This may result from the higher conformational flexibility of these large proteins and larger deviations in the total charge of the protein, calculated using PROPKA method, in comparison to the experimentally reported data (see Table S1, ESI†). H++ protonation improved the partial charges of BSA, so we used it to parametrize the CG beads, but still these deviations may introduce discrepancies in the electrostatic potential, therefore, the calculated B22. However, it seems that the overall trends and the behaviour at physiological ionic strengths agree better with the available experimental data. Further developments of xDLVO-CG and the inclusion of the solvent accessibility corrections, e.g. as available in the TKSA-MC server96 or GBSA,97 and other solvent effects, modulated by the change of the ionic strength,98 are required to improve the quality of predictions and enable better correlations with the experimental observations.
4.3 Impact of ion–protein interactions
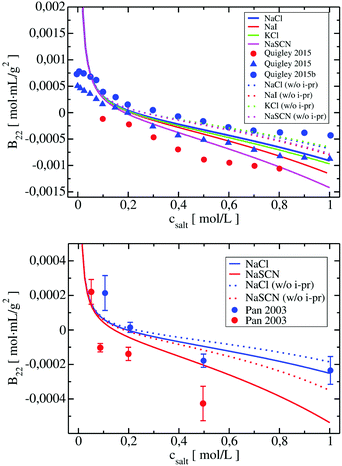
Conventional xDLVO models consider the influence of different salts on the osmotic second virial coefficients by osmotic and electrostatic potentials, which use hydrated salt radii and ionic strength as an input for the calculations. However, radii of hydrated monovalent salts do not differ significantly and the absolute value of the osmotic term is overall small. Therefore the osmotic effect alone cannot explain the observed salt-dependence of B22.These discrepancies are presently overcome by fitting the Hamaker constant to the experimental data measured at each desired pH and salt conditions, limiting the detailed understanding of PPIs and to recover the trends according to the Hofmeister series.99,100 According to its original definition, the Hamaker constant describes attractive London-var der Waals interactions that should arise from the interactions between charge-neutral proteins64,65 and should not depend on the ionic strength. The impact of salt ions in promoting attractive PPIs results from the ion–protein dispersion interaction, which, in the most basic form, are insensitive towards the protein type and depend on the properties of salt ions.75
We included these interactions in xDLVO-CG using the model described in Section 3.2.4. In Fig. 8, the B22 coefficients calculated for LYZ (at pH 4.5) and Subs (at pH 5.5), using xDLVO-CG with (solid curves) and without (dotted curves) ion–protein interactions, are depicted. It is clearly seen that the attractive PPIs in LYZ, arising only from the ion type (different hydrated radii accounted in the osmotic attraction potential), are similar (see upper panel in Fig. 8) and cannot explain more pronounced differences to the experimental B22 data. Adding the ion–protein dispersion term in the PMF differentiates the salting out efficiency of ions, induces stronger separation between the data obtained using different salts and better correlation to the experiments. The same effect is seen also for Subs (bottom panel in Fig. 8), showing stronger tendency of SCN− to promote aggregation of proteins, which agrees with the trends reported by the Hofmeister series, where thiocyanate anion is known as a strong salting out agent causing protein precipitation. This is connected to the ion–protein dispersion coefficients, Bi–pr (eqn (20)), of SCN−, which is 2.8 times larger than in the case of Cl−,70 resulting in stronger ion–protein dispersion interactions.75 This interaction also relates to the lower ion hydration propensity of SCN−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 that affects PPIs stronger, resulting in a decrease of the B22 coefficients and more efficient salting out. Both ion hydration and ion–protein dispersion coefficients are modulated by the ion polarizability.73
40 that affects PPIs stronger, resulting in a decrease of the B22 coefficients and more efficient salting out. Both ion hydration and ion–protein dispersion coefficients are modulated by the ion polarizability.73
B 22 coefficients of LYZ at pH 4.5 using NaCl and KCl (data in blue and green in the upper panel in Fig. 8) are similar and differ mostly at higher salt concentrations. The same observation was reported by Kalyuzhnyi et al.,84 which relate it to the small differences in the water binding by Na+ and K+ (dependent also on the polarizability) and generally smaller salting out introduced by cations. At the same time, I− ions show stronger salting out efficiency of LYZ than Cl−, resulting in faster decrease of B22, indicating that our model is consistent with the Hofmeister series trend, i.e. Cl− < I− < SCN−.
4.4 Beyond Hamaker constant
There are several expressions that attempt to calculate dispersion interactions between proteins on the basis of continuum models. Most models use the Hamaker constant, AH, which according to its original definition, depends on the chemical composition and density of the protein. In most models, however, AH is used as an adjustable parameter in (x)DLVO and is fitted to the experimental data at different pH and salt conditions. The Hamaker constant can be also calculated, e.g. using robust McLachlans formulation of Lifshitzs van der Waals forces,101 where the excess polarizability in dielectric medium is accounted, but this approach is less widely implemented.With the use of fitted AH, the obtained B22 coefficients are in good agreement with the experiments, however, such adjustments of AH include error compensations arising from the electrostatic, osmotic and ion–protein dispersion terms, as explained in Section 4.3. Moreover, experimental measurements for different proteins at specific solution conditions are required to parameterize the model.
In the present study, we validated xDLVO-CG using Hamaker constants reported previously (Table 1 in Appendix) and we have not changed their values at different salt and pH conditions (two AH used only for Subs). We show good correlations between the calculated and the experimental B22 using this approach. However, we aim to introduce the protein solubility model using standard potential energy functions without designed fitting to the experimental data points. Therefore, we attempted to replace Hamaker dispersion interactions in the total PMF by the Lennard-Jones interactions (eqn (11) and (15)) parameterized according to Arkhipov et al.,59 as described in Section 3.2.2.
Both dispersion potentials for LYZ at pH 7 and Subs at pH 5.5 are depicted in Fig. 9. We see that the strength of the dispersion interactions, introduced by the Hamaker constant, is decreasing faster than in the case of the Lennard-Jones interactions. This results in stronger binding of the proteins in the LJ potential model and a small shift of the calculated second virial coefficients towards negative values (see panel on the right in Fig. 9). Overall, the potential depth and the corresponding COM distance of the most attractive interactions between the proteins are similar in both cases, resulting in B22 coefficients in the range of the reported experimental data. Analysis of the B22 changes as a function of the sampled protein–protein structures indicates higher sensitivity of the PMF with LJ (Fig. S6, ESI†), that arises from the fact that all bead-bead dispersion interactions were parametrized based on the chemical composition of the residues included in a CG bead, and not by uniform values of the Hamaker constant.
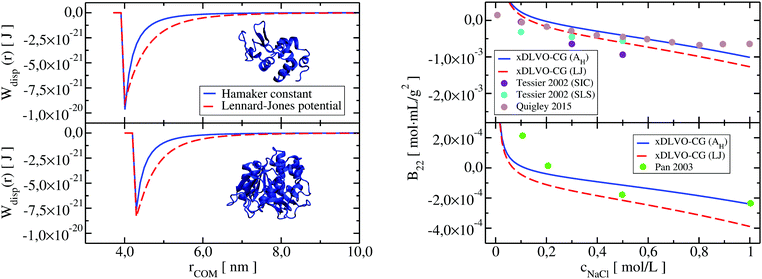 | ||
| Fig. 9 Dispersion potential in PPIs of LYZ (upper panel) and Subs (lower panel) represented by the Hamaker constant (in blue), taken from experimental measurements (see Table 1 in Appendix) and implemented according to eqn (13), and by the Lennard-Jones potential (in red) from the shape-based coarse-grained model (xDLVO-CG(LJ)). The B22 coefficients for LYZ at pH 7 and Subs at pH 5.5 using both potentials, eqn (11), are shown correspondingly on the right panel. | ||
Larger deviations between the B22 values calculated using the Hamaker constant in xDLVO-CG and xDLVO-CG(LJ) are observed for BSA and IgG1 (Fig. S7, ESI†). It appears that the standard parameterization of the LJ potentials for these large proteins is inadequate to capture PPIs that are measured experimentally. The LJ potential is significantly wider (Fig. S8, ESI†), resulting in overbinding of the proteins and more negative B22, therefore, faster protein precipitation. Such observations are also typical for the PMF calculated by all-atom force fields.31,37,38 However, this is the first attempt, to our knowledge, to replace the Hamaker dispersion interactions in xDLVO models by the LJ potential. More rigorously, the dispersion interactions and the Hamaker constant can be calculated by the continuum Lifshitz theory102 using, for example, McLachlans formulation. We hope that, with better parameterization and further improvements, the predictive power of xDLVO-CG can be further increased.
5 Conclusions
We reported a novel xDLVO-CG model for the calculation of the osmotic second virial coefficients, B22 for proteins, as a function of pH, ionic strength and the protein type. xDLVO-CG can be used to predict the stability of the protein solutions and the salt induced dependencies. It complements the experimental measurements of B22 and enables the understanding of the origin of the protein solubility as a function of diverse colloidal PPIs.The developed model was derived from the extended DLVO theory and includes a new term for ion–protein dispersion interactions, which is shown to be relevant when the Hamaker constant is not fitted for every environmental condition. xDLVO-CG was implemented with a shape-based coarse-grained representation to better account for anisotropic protein–protein interactions. Combined, this approach reduces and, in some examples, eliminates the need to fit the experimental B22 data. Such an approach may accelerate the investigations of the protein processing conditions, starting from pharmaceutical up to food industry applications.
The unified CG protein mapping scheme in xDLVO-CG introduces a generally applicable parametrization procedure, which improves transferability of the model among proteins of different shape and physicochemical characteristics. CG bead mapping is free from experimental B22 parameters and builds directly on the all atom structure of the protein. This allows the use of the xDLVO-CG to various proteins without the need of the special model adjustments. In order to account for the anisotropic nature of the interactions, calculations of the osmotic second virial coefficients require the integration of the potential of mean force over many configurations in a model that includes electrostatic, dispersion, osmotic and ion–protein dispersion interactions.
The xDLVO-CG calculations for lysozyme, subtilisin, bovine serum albumin and immunoglobulin type 1 at different solution conditions, show that the model agrees with the experimental measurements of the B22 coefficients of lysozyme in the wide range of pH. The model is transferable to larger, irregular and non-spherical proteins and results in semi-quantitative correlations of the B22 for subtilisin, BSA and IgG1. The observed differences for the latter may result from difficulties to correctly compute the charge of the protein. However, using experimental values for the protein charge, results in a worse fit to the data. Overall, xDLVO-CG demonstrates significant improvements of the B22 modeling in comparison with the regular xDLVO models and it does not require fitting to experimental B22 values.
We believe that with further implementations in the PMF and the introduction of better dispersion terms, more accurate models for electrostatic and solvent effects, xDLVO-CG has the potential to better predict B22 coefficients of different proteins without time-consuming experiments. The developed computational scheme can be adjusted also for the calculation of the aqueous stability of other colloidal particles. Indeed, special CG parameterization scheme should be proposed as the first.
Conflicts of interest
There are no conflicts to declare.Appendix
The potential of mean force in xDLVO-CG, calculated according to eqn (11) and depicted in Fig. 4, consists of interaction potentials of different salt induced dependencies. The change of the potentials steering colloidal protein interactions of LYZ at pH 4.5 and pH 7.0 are shown in Fig. 10 and 11, respectively.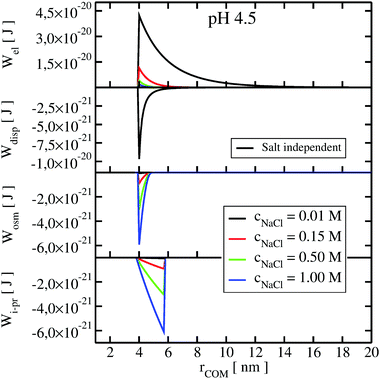 | ||
| Fig. 10 The change of the interaction potentials, accounted in xDLVO-CG, with the increase of the salt concentration of the LYZ at pH 4.5. | ||
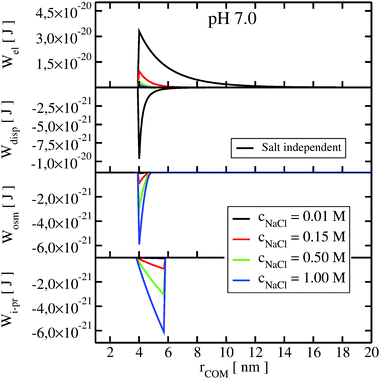 | ||
| Fig. 11 The change of the interaction potentials, accounted in xDLVO-CG, with the increase of the salt concentration of the LYZ at pH 7.0. | ||
Literature reported values of the parameters used to calculate the dispersion, osmotic and ion–protein dispersion potentials are listed in Tables 1 and 2.
Acknowledgements
This research has been funded by Deutsche Forschungsgemeinschaft (DFG) SPP priority programme DiSPBiotech (SPP1934, project number WE1863/30-2). M. K. acknowledges funding by the Ministry of Science, Research and Art of Baden-Württemberg (Germany) under Brigitte-Schlieben-Lange-Programm. W. W. and M. K. acknowledge funding by the DFG under the GRK 2450 “Scale bridging methods of computational nanoscience”.Notes and references
- T. L. Moore, L. Rodriguez-Lorenzo, V. Hirsch, S. Balog, D. Urban, C. Jud, B. Rothen-Rutishauser, M. Lattuada and A. Petri-Fink, Chem. Soc. Rev., 2015, 44, 6287–6305 RSC
.
- N. Rakel, K. C. Bauer, L. Galm and J. Hubbuch, Biotechnol. Prog., 2015, 31, 438–451 CrossRef CAS PubMed
.
- S. D. Durbin and G. Feher, Annu. Rev. Phys. Chem., 1996, 47, 171–204 CrossRef CAS PubMed
.
- R.-B. Zhou, H.-L. Cao, C.-Y. Zhang and D.-C. Yin, CrystEngComm, 2017, 19, 1143–1155 RSC
.
- M. Kozlowska, P. Rodziewicz, T. Utesch, M. A. Mroginski and A. Kaczmarek-Kedziera, Phys. Chem. Chem. Phys., 2018, 20, 8629–8639 RSC
.
- D. Roberts, R. Keeling, M. Tracka, C. F. van der Walle, S. Uddin, J. Warwicker and R. Curtis, Mol. Pharm., 2014, 11, 2475–2489 CrossRef CAS PubMed
.
- B. Guo, S. Kao, H. McDonald, A. Asanov, L. Combs and W. William Wilson, J. Cryst. Growth, 1999, 196, 424–433 CrossRef CAS
.
- C. Haas, J. Drenth and W. W. Wilson, J. Phys. Chem. B, 1999, 103, 2808–2811 CrossRef CAS
.
- S. Ruppert, S. I. Sandler and A. M. Lenhoff, Biotechnol. Prog., 2001, 17, 182–187 CrossRef CAS PubMed
.
- V. Le Brun, W. Friess, S. Bassarab and P. Garidel, Pharm. Dev. Technol., 2010, 15(4), 421–430 CrossRef CAS PubMed
.
- L. F. M. Franco and P. d. A. Pessôa Filho, Braz. J. Chem. Eng., 2013, 30, 95–104 CrossRef CAS
.
- X. Pan and C. E. Glatz, Cryst. Growth Des., 2003, 3, 203–207 CrossRef CAS
.
- M. A. Woldeyes, C. Calero-Rubio, E. M. Furst and C. J. Roberts, J. Phys. Chem. B, 2017, 121, 4756–4767 CrossRef CAS PubMed
.
- A. Quigley and D. Williams, Eur. J. Pharm. Biopharm., 2015, 96, 282–290 CrossRef CAS PubMed
.
- E. Sahin, A. O. Grillo, M. D. Perkins and C. J. Roberts, J. Pharm. Sci., 2010, 99, 4830–4848 CrossRef CAS PubMed
.
- A. C. Dumetz, A. M. Snellinger-O'Brien, E. W. Kaler and A. M. Lenhoff, Protein Sci., 2007, 16, 1867–1877 CrossRef CAS PubMed
.
- B. Neal, D. Asthagiri, O. Velev, A. Lenhoff and E. Kaler, J. Cryst. Growth, 1999, 196, 377–387 CrossRef CAS
.
- C. M. Mehta, E. T. White and J. D. Litster, Biotechnol. Prog., 2012, 28, 163–170 CrossRef CAS PubMed
.
- A. George and W. W. Wilson, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1994, 50, 361–365 CrossRef CAS PubMed
.
- K. Demoruelle, B. Guo, S. Kao, H. M. McDonald, D. B. Nikic, S. C. Holman and W. W. Wilson, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2002, 58, 1544–1548 CrossRef PubMed
.
- A. D. Naik and S. S. Bhagwat, J. Chem. Eng. Data, 2005, 50, 460–467 CrossRef CAS
.
- C. A. Teske, H. W. Blanch and J. M. Prausnitz, J. Phys. Chem. B, 2004, 108, 7437–7444 CrossRef CAS
.
- C. Ersch, L. L. Meijvogel, E. van der Linden, A. Martin and P. Venema, Food Hydrocolloids, 2016, 52, 982–990 CrossRef CAS
.
- Y. Ma, D. M. Acosta, J. R. Whitney, R. Podgornik, N. F. Steinmetz, R. H. French and V. A. Parsegian, J. Biol. Phys., 2015, 41, 85–97 CrossRef CAS PubMed
.
- M. A. Blanco, E. Sahin, Y. Li and C. J. Roberts, J. Chem. Phys., 2011, 134, 225103 CrossRef PubMed
.
-
A. Ben-Naim, Statistical Thermodynamics for Chemists and Biochemists, Plenum Press, New York, NY, 1992 Search PubMed
.
- M. A. Blanco, E. Sahin, A. S. Robinson and C. J. Roberts, J. Phys. Chem. B, 2013, 117, 16013–16028 CrossRef CAS PubMed
.
- X. X. Li, X. D. Xu, Y. Y. Dan and M. L. Zhang, Crystallogr. Rep., 2008, 53, 1261–1266 CrossRef CAS
.
- E. Ruckenstein and I. L. Shulgin, Adv. Colloid Interface Sci., 2006, 123–126, 97–103 CrossRef CAS PubMed
.
- W. Li and M. Z. Oskolkova, J. Phys. Chem. B, 2015, 6 Search PubMed
.
- L. J. Quang, S. I. Sandler and A. M. Lenhoff, J. Chem. Theory Comput., 2014, 10, 835–845 CrossRef CAS PubMed
.
- C. Calero-Rubio, A. Saluja and C. J. Roberts, J. Phys. Chem. B, 2016, 120, 6592–6605 CrossRef CAS PubMed
.
- C. Calero-Rubio, R. Ghosh, A. Saluja and C. J. Roberts, J. Pharm. Sci., 2018, 107, 1269–1281 CrossRef CAS PubMed
.
- C. Calero-Rubio, A. Saluja, E. Sahin and C. J. Roberts, J. Phys. Chem. B, 2019, 123, 5709–5720 CrossRef CAS PubMed
.
- C. J. O'Brien, C. Calero-Rubio, V. I. Razinkov, A. S. Robinson and C. J. Roberts, Protein Sci., 2018, 27, 1275–1285 CrossRef PubMed
.
- A. Jost Lopez, P. K. Quoika, M. Linke, G. Hummer and J. Köfinger, J. Phys. Chem. B, 2020, 124, 4673–4685 CrossRef CAS PubMed
.
- A. C. Stark, C. T. Andrews and A. H. Elcock, J. Chem. Theory Comput., 2013, 9, 4176–4185 CrossRef CAS PubMed
.
- S. Qin and H.-X. Zhou, J. Phys. Chem. B, 2019, 123, 8203–8215 CrossRef CAS PubMed
.
-
E. J. W. Verwey and J. T. G. Overbreek, Theory of the stability of lyophobic colloids, Elsevier, 1948, vol. 6 Search PubMed
.
- M. Kastelic, Y. V. Kalyuzhnyi, B. Hribar-Lee, K. A. Dill and V. Vlachy, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 6766–6770 CrossRef CAS PubMed
.
- M. Herhut, C. Brandenbusch and G. Sadowski, Fluid Phase Equilib., 2016, 422, 32–42 CrossRef CAS
.
- M. Schleinitz, G. Sadowski and C. Brandenbusch, Int. J. Pharm., 2019, 569, 118608 CrossRef CAS PubMed
.
- M. Herhut, C. Brandenbusch and G. Sadowski, Biotechnol. J., 2016, 11, 146–154 CrossRef CAS PubMed
.
- C. J. Roberts and M. A. Blanco, J. Phys. Chem. B, 2014, 118, 12599–12611 CrossRef CAS PubMed
.
- C. Roth, B. Neal and A. Lenhoff, Biophys. J., 1996, 70, 977–987 CrossRef CAS PubMed
.
- B. Neal, D. Asthagiri and A. Lenhoff, Biophys. J., 1998, 75, 2469–2477 CrossRef CAS PubMed
.
- O. Velev, E. Kaler and A. Lenhoff, Biophys. J., 1998, 75, 2682–2697 CrossRef CAS PubMed
.
- A. H. Elcock and J. A. McCammon, Biophys. J., 2001, 80, 613–625 CrossRef CAS PubMed
.
- W. G. McMillan and J. E. Mayer, J. Chem. Phys., 1945, 13, 276–305 CrossRef CAS
.
-
D. A. McQuarrie, Statistical mechanics, University Science Books, Sausalito, Calif, 2000 Search PubMed
.
- R. A. Curtis, J. M. Prausnitz and H. W. Blanch, Biotechnol. Bioeng., 1998, 57, 12 CrossRef
.
- Y. Georgalis, A. Zouni, W. Eberstein and W. Saenger, J. Cryst. Growth, 1993, 126, 245–260 CrossRef CAS
.
-
E. Hückel, Ergebnisse der exakten naturwissenschaften, Springer Berlin Heidelberg, Berlin, Heidelberg, 1924, vol. 3, pp. 199–276 Search PubMed
.
- S. Asakura and F. Oosawa, J. Polym. Sci., 1958, 33, 183–192 CrossRef CAS
.
- C. R. Søndergaard, M. H. M. Olsson, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 2284–2295 CrossRef PubMed
.
- H. Li, A. D. Robertson and J. H. Jensen, Proteins: Struct., Funct., Bioinf., 2005, 61, 704–721 CrossRef CAS PubMed
.
- T. J. Dolinsky, P. Czodrowski, H. Li, J. E. Nielsen, J. H. Jensen, G. Klebe and N. A. Baker, Nucleic Acids Res., 2007, 35, W522–W525 CrossRef PubMed
.
- T. J. Dolinsky, J. E. Nielsen, J. A. McCammon and N. A. Baker, Nucleic Acids Res., 2004, 32, W665–W667 CrossRef CAS PubMed
.
- A. Arkhipov, P. L. Freddolino and K. Schulten, Structure, 2006, 14, 1767–1777 CrossRef CAS PubMed
.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed
.
- A. G. Cherstvy and R. G. Winkler, J. Phys. Chem. B, 2012, 116, 9838–9845 CrossRef CAS PubMed
.
- K. Karraker and C. Radke, Adv. Colloid Interface Sci., 2002, 96, 231–264 CrossRef CAS PubMed
.
- M. Boström, V. Deniz, G. Franks and B. Ninham, Adv. Colloid Interface Sci., 2006, 123–126, 5–15 CrossRef PubMed
.
- H. Hamaker, Physica, 1937, 4, 1058–1072 CrossRef CAS
.
- S. Nir and M. Andersen, J. Membr. Biol., 1977, 31, 1–18 CrossRef CAS PubMed
.
- A. Arkhipov, Y. Yin and K. Schulten, Biophys. J., 2008, 95, 2806–2821 CrossRef CAS PubMed
.
- Y. Marcus, Biophys. Chem., 1994, 51, 111–127 CrossRef CAS
.
- Y. Zhang and P. S. Cremer, Curr. Opin. Chem. Biol., 2006, 10, 658–663 CrossRef CAS PubMed
.
- H. I. Okur, J. Hladílková, K. B. Rembert, Y. Cho, J. Heyda, J. Dzubiella, P. S. Cremer and P. Jungwirth, J. Phys. Chem. B, 2017, 121, 1997–2014 CrossRef CAS PubMed
.
- M. Boström, F. W. Tavares, B. W. Ninham and J. M. Prausnitz, J. Phys. Chem. B, 2006, 110, 24757–24760 CrossRef PubMed
.
- M. Boström, D. R. M. Williams and B. W. Ninham, Langmuir, 2001, 17, 4475–4478 CrossRef
.
- L. A. Moreira, M. Boström, B. W. Ninham, E. C. Biscaia and F. W. Tavares, J. Braz. Chem. Soc., 2007, 18, 223–230 CrossRef CAS
.
- B. W. Ninham and V. Yaminsky, Langmuir, 1997, 13, 2097–2108 CrossRef CAS
.
- L. Moreira, M. Boström, B. Ninham, E. Biscaia and F. Tavares, Colloids Surf., A, 2006, 282–283, 457–463 CrossRef
.
- D. F. Parsons, M. Boström, P. L. Nostro and B. W. Ninham, Phys. Chem. Chem. Phys., 2011, 13, 12352 RSC
.
- M. Boström, F. Tavares, S. Finet, F. Skouri-Panet, A. Tardieu and B. Ninham, Biophys. Chem., 2005, 117, 217–224 CrossRef PubMed
.
- A. Salis and B. W. Ninham, Chem. Soc. Rev., 2014, 43, 7358–7377 RSC
.
- M. P. Crosio, J. Janin and M. Jullien, J. Mol. Biol., 1992, 228, 243–251 CrossRef CAS PubMed
.
- R. E. Canfield, J. Biol. Chem., 1963, 238, 2698–2707 CrossRef CAS
.
- C. C. F. Blake, D. F. Koenig, G. A. Mair, A. C. T. North, D. C. Phillips and V. R. Sarma, Nature, 1965, 206, 757–761 CrossRef CAS PubMed
.
- D. H. Johnson, A. Parupudi, W. W. Wilson and L. J. DeLucas, Pharm. Res., 2009, 26, 296–305 CrossRef CAS PubMed
.
- J. J. Valente, B. G. Fryksdale, D. A. Dale, A. L. Gaertner and C. S. Henry, Anal. Biochem., 2006, 357, 35–42 CrossRef CAS PubMed
.
- P. M. Tessier, A. M. Lenhoff and S. I. Sandler, Biophys. J., 2002, 82, 1620–1631 CrossRef CAS PubMed
.
- Y. V. Kalyuzhnyi and V. Vlachy, J. Chem. Phys., 2016, 144, 215101 CrossRef PubMed
.
- Y. Park and G. Choi, Korean J. Chem. Eng., 2009, 26, 193–198 CrossRef CAS
.
- Y. U. Moon, R. A. Curtis, C. O. Anderson, H. W. Blanch and J. M. Prausnitz, J. Solution Chem., 2000, 29, 699–718 CrossRef CAS
.
- R. Anandakrishnan, B. Aguilar and A. V. Onufriev, Nucleic Acids Res., 2012, 40, W537–W541 CrossRef CAS PubMed
.
- V. L. Vilker, C. K. Colton and K. A. Smith, J. Colloid Interface Sci., 1981, 79, 548–566 CrossRef CAS
.
- O. V. Khorolskyi, N. P. Malomuzh, O. V. Khorolskyi and N. P. Malomuzh, AIMS Biophys., 2020, 7, 219–235 CAS
.
- P. M. Blanco, S. Madurga, J. L. Garcés, F. Mas and R. S. Dias, Soft Matter, 2021, 17, 655–669 RSC
.
- P. Singh, A. Roche, C. F. van der Walle, S. Uddin, J. Du, J. Warwicker, A. Pluen and R. Curtis, Mol. Pharmaceutics, 2019, 16, 4775–4786 CrossRef CAS PubMed
.
- S. Nir, Prog. Surf. Sci., 1977, 8, 1–58 CrossRef CAS
.
- C. M. Roth and A. M. Lenhoff, J. Colloid Interface Sci., 1996, 179, 637–639 CrossRef CAS
.
- D. Roberts, R. Keeling, M. Tracka, C. F. van der Walle, S. Uddin, J. Warwicker and R. Curtis, Mol. Pharm., 2015, 12, 179–193 CrossRef CAS PubMed
.
- V. Le Brun, W. Friess, S. Bassarab, S. Mühlau and P. Garidel, Eur. J. Pharm. Biopharm., 2010, 75, 16–25 CrossRef CAS PubMed
.
- V. G. Contessoto, V. M. d. Oliveira, B. R. Fernandes, G. G. Slade and V. B. P. Leite, Proteins: Struct., Funct., Bioinf., 2018, 86, 1184–1188 CrossRef CAS PubMed
.
- M. Brieg, J. Setzler, S. Albert and W. Wenzel, Phys. Chem. Chem. Phys., 2017, 19, 1677–1685 RSC
.
- A. Levy, D. Andelman and H. Orland, Phys. Rev. Lett., 2012, 108, 227801 CrossRef PubMed
.
- F. Hofmeister, Archiv für experimentelle Pathologie und Pharmakologie, 1888, 24, 247–260 Search PubMed
.
- W. Kunz, J. Henle and B. W. Ninham, Curr. Opin. Colloid Interface Sci., 2004, 9, 19–37 CrossRef CAS
.
- S. Damodaran, Langmuir, 2012, 28, 9475–9486 CrossRef CAS PubMed
.
-
E. Lifshitz and M. Hamermesh, Perspectives in Theoretical Physics, Elsevier, 1992, pp. 329–349 Search PubMed
.
- M. Muschol and F. Rosenberger, J. Chem. Phys., 1995, 103, 10424–10432 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp01573g |
| ‡ The author passed away before the paper was completed. |
| This journal is © the Owner Societies 2021 |