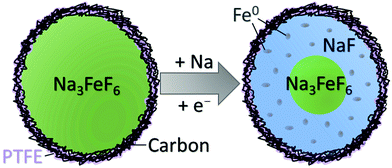
Probing reaction processes and reversibility in Earth-abundant Na3FeF6 for Na-ion batteries†
Emily E.
Foley
 ab,
Anthony
Wong
ab,
Anthony
Wong
 c,
Rebecca C.
Vincent
c,
Rebecca C.
Vincent
 ab,
Alexis
Manche‡
ab,
Aryan
Zaveri
abd,
Eliovardo
Gonzalez-Correa
ab,
Gabriel
Ménard
ab,
Alexis
Manche‡
ab,
Aryan
Zaveri
abd,
Eliovardo
Gonzalez-Correa
ab,
Gabriel
Ménard
 c and
Raphaële J.
Clément
c and
Raphaële J.
Clément
 *ab
*ab
aMaterials Department, University of California Santa Barbara, California 93106, USA. E-mail: rclement@ucsb.edu
bMaterials Research Laboratory, University of California Santa Barbara, California 93106, USA
cDepartment of Chemistry and Biochemistry, University of California Santa Barbara, California 93106, USA
dPhysics Department, University of California Santa Barbara, California 93106, USA
First published on 1st July 2021
Abstract
Sodium (Na)-ion batteries are the most explored ‘beyond-Li’ battery systems, yet their energy densities are still largely limited by the positive electrode material. Na3FeF6 is a promising Earth-abundant containing electrode and operates through a conversion-type charge–discharge reaction associated with a high theoretical capacity (336 mA h g−1). In practice, however, only a third of this capacity is achieved during electrochemical cycling. In this study, we demonstrate a new rapid and environmentally-friendly assisted-microwave method for the preparation of Na3FeF6. A comprehensive understanding of charge–discharge processes and of the reactivity of the cycled electrode samples is achieved using a combination of electrochemical tests, synchrotron X-ray diffraction, 57Fe Mössbauer spectroscopy, X-ray photoelectron spectroscopy, magnetometry, and 23Na/19F solid-state nuclear magnetic resonance (NMR) complemented with first principles calculations of NMR properties. We find that the primary performance limitation of the Na3FeF6 electrode is the sluggish kinetics of the conversion reaction, while the methods employed for materials synthesis and electrode preparation do not have a significant impact on the conversion efficiency and reversibility. Our work confirms that Na3FeF6 undergoes conversion into NaF and Fe(s) nanoparticles. The latter are found to be prone to oxidation prior to ex situ measurements, thus necessitating a robust analysis of the stable phases (here, NaF) formed upon conversion.
Introduction
Lithium (Li)-ion batteries (LIBs) have enabled the successful electrification of numerous devices ranging from laptops to electric vehicles to large-scale energy storage systems. However, with the continually increasing demand for these batteries, the sustainability, security, and economics of their comprising materials must be considered. Significant progress has been made towards utilizing more abundant transition metals in the cathode, rather than expensive cobalt, as well as increasing the energy density of LIBs.1 However, an alternate solution entails transitioning to entirely non-lithium-based battery technologies. Sodium (Na)-ion batteries (NIBs) are the most explored beyond-Li battery systems. Due to the chemical similarity of sodium to lithium,2 initial work on Na-ion electrodes has focused on Li-ion electrode analogues, namely layered sodium transition metal oxides and polyanion systems. However, transition metal oxides and polyanionic systems exhibit low theoretical energy densities (520 W h kg−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 475 W h kg−1,4 respectively). Therefore, new Na-ion electrode materials with high energy densities are needed. Several promising alternatives have been reported including conversion-type SnS nanospheres5 and insertion-type disordered rocksalts6,7 and weberites.8,9 However, there has been no conclusive Earth-abundant, energy dense, and inexpensive electrode material found for NIBs prompting further investigation.
3 and 475 W h kg−1,4 respectively). Therefore, new Na-ion electrode materials with high energy densities are needed. Several promising alternatives have been reported including conversion-type SnS nanospheres5 and insertion-type disordered rocksalts6,7 and weberites.8,9 However, there has been no conclusive Earth-abundant, energy dense, and inexpensive electrode material found for NIBs prompting further investigation.
Fluoride-based conversion-type NIB electrodes may reach energy densities up to 1400 W h kg−1 on account of multi-electron redox processes10 and thus present a promising direction for NIB electrodes. Yet, conversion reactions lead to a redistribution of all species in the electrode material, as recently shown by Grey and coauthors for LixFeyF3.11 Thus, these materials generally require a greater driving force (overpotential) and cause more irreversible behavior than intercalation reactions. Further, conversion-type electrodes are often more kinetically-limited than intercalation-type electrodes, leading to sluggish redox reaction kinetics that are exacerbated by the insulating fluoride compounds. As a result, significant discrepancies are observed between theoretically-computed thermodynamic pathways and the experimentally-observed kinetically-limited phenomena, making it difficult to identify conversion reaction mechanisms.12,13 Furthermore, the structural changes that occur on cycling often result in the formation of amorphous and metastable phases that are difficult to capture via diffraction and ex situ methods. For these reasons, the majority of fluoride-based conversion electrodes for NIBs do not have well-established reaction pathways.10 In turn, a poor understanding of reaction mechanisms makes it difficult to distinguish between intrinsic limitations imposed by the conversion reaction, and practical losses due to the starting particle morphology and electrode preparation. Thus, to understand the reaction mechanisms and limitations of current conversion materials in NIBs, and to enable the rational design of next-generation systems combining high capacity and long cycle life, local structure probes are warranted.
Na3FeF6 is a particularly attractive candidate electrode material for NIBs, as it is exclusively composed of Earth-abundant species. This compound was first explored as a conversion-type NIB electrode by Shakoor et al. and displayed a first discharge capacity of 125 mA h g−1 with very low reversibility.14 Two follow-up studies used solution-phase syntheses and obtained more stable cycling with initial reversible capacities of 140 mA h g−1 and ≈64% capacity retention after 400 cycles.15,16 These studies have focused on electrochemical characterization of Na3FeF6, with the only additional characterization reported being ex situ X-ray diffraction (XRD) by Shakoor et al.14 The ex situ XRD data collected on cycled electrode samples were used as evidence that NaF and Fe formed on discharge, and the following conversion reaction was proposed:
| Na3FeF6 + 3Na ⇄ 6NaF + Fe. |
However, the NaF and Fe peaks in the ex situ XRD are nearly indistinguishable from the baseline and incommensurate with the reported capacity, which suggests an incomplete understanding of the conversion mechanism at play. Thus, a closer investigation of the reaction process and limitations of Na3FeF6 is warranted.
In the present work, we revisit Na3FeF6 and aim for a complete understanding of key performance limitations to inform the design of next-generation NIB conversion electrodes. Here, Na3FeF6 is prepared through a similar mechanochemical method as Shakoor et al.,14 as well as a new assisted-microwave synthesis method. The latter is a rapid, environmentally-friendly, all solid-state synthesis method allowing for the facile preparation of inorganic materials,17 and this work demonstrates its promise for the preparation of battery electrode materials. Inspired by the need to test NIB materials in practical electrode setups and determine the intrinsic charge storage capacity of the conversion material in composite electrodes, we investigate the dependence of the electrochemical reversibility of Na3FeF6 on the electrode loading density and separate the capacity contributions associated with Na3FeF6 and with the conductive carbon matrix. We answer the question of why this material cannot reach its full conversion capacity based on Shakoor et al.'s proposed mechanism14 through an in-depth characterization of the long- and short-range chemical changes occurring on cycling. For this, we employ a suite of tools sensitive to both amorphous and crystalline phases, including synchrotron X-ray diffraction (SXRD), 23Na/19F solid-state nuclear magnetic resonance (NMR) complemented with first principles calculations of NMR parameters, 57Fe Mössbauer spectroscopy, magnetometry, and X-ray photoelectron spectroscopy (XPS). Our results indicate that the primary performance bottleneck of Na3FeF6 is the kinetic limitations of the conversion process due to the formation of insulating NaF domains that are also poorly Na+ conducting on discharge, leading to a low discharge capacity and rapid capacity decay on subsequent cycles. Interestingly, the impact of the electrode film thickness on the capacity and its retention is minimal, indicating that the kinetic limitations are already present at the (≤100 nm) particle scale. We also find that ex situ characterization of the electrode samples is complicated by the spontaneous oxidation of metastable Fe conversion phases during cell disassembly and sample handling (even in an inert environment), and develop a novel and robust analytical framework based on local structure probes and galvanostatic cycling to determine the true underlying conversion processes.
Results & discussion
Characterization of as-synthesized Na3FeF6
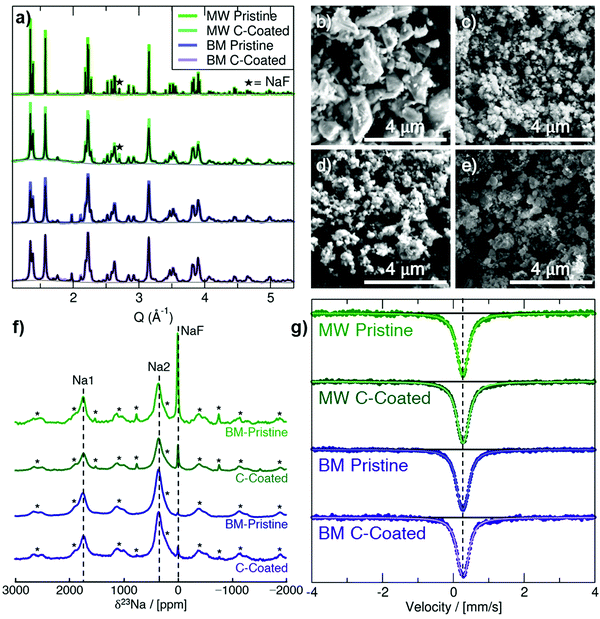
Na3FeF6 forms a distorted ordered double perovskite structure, more clearly written as (Na2)2(Na1)FeF6, with space group P21. This structure (Fig. S1, ESI†) is characterized by tilted corner-sharing (Na1)F6 and FeF6 octahedra, with the two remaining Na atoms filling the Na2 sites between the octahedral chains. Synchrotron XRD (SXRD) patterns collected on pristine and C-coated Na3FeF6 samples prepared via mechanochemical/ball-mill (BM) and microwave (MW) synthesis are shown in Fig. 1a along with their Rietveld refinements. A small NaF precursor impurity phase is seen at Q = 2.71 Å−1 for the MW samples and a ZrO2 impurity is seen at Q = 1.98 and 2.12 Å−1 for the BM samples from the jars used for the milling. As summarized in Table S1 (ESI†), the Na3FeF6 lattice parameters for the as-synthesized materials show little variation between samples and are in good agreement with previously reported structures. The peak broadening observed for the BM and C-coated samples obtained by ball-milling with a conductive carbon additive is attributed to the formation of ≤100 nm particles upon high-energy milling, as shown in the scanning electron microscopy (SEM) images in Fig. 1b–e. This procedure may also result in strained particles and an overall decrease in crystallinity, which could also contribute to peak broadening. The greater size of the particle agglomerates in the C-coated materials (Fig. 1c and e) indicates successful formation of a C nanocomposite.1823Na and 19F solid-state NMR experiments were conducted to obtain further insights into the local structure of Na3FeF6. The presence of open-shell Fe3+ species in these compounds results in strong paramagnetic interactions between unpaired electron spins nominally present in the Fe 3d orbitals and 23Na/19F nuclear spins. These strong interactions result in significant NMR line broadening and large chemical shifts, complicating the attribution of spectral features to specific local environments in the material. Here, the assignment of the complex NMR spectra is assisted by first principles hybrid density functional theory (DFT)/Hartree Fock (HF) calculations of paramagnetic 23Na and 19F NMR parameters using the CRYSTAL17 code on the optimized Na3FeF6 structure (details of the analysis in the ESI†). The isotropic chemical shift (δiso) of 23Na and 19F nuclei in Na3FeF6 is dominated by the paramagnetic (Fermi contact) shift resulting from delocalization of unpaired electron spin density from the Fe 3d orbitals to the 23Na/19F s orbitals. For an I = 3/2 quadrupolar nucleus such as 23Na, the interaction between the nuclear quadrupole moment and the electric field gradient (EFG) present at the nucleus leads to a further broadening of the spectrum and to a shift of the 23Na resonant frequency due to second-order effects (denoted δQ). The observed chemical shift (δobs) is then the sum of the isotropic Fermi contact shift and of the second-order quadrupolar shift: δobs = δiso + δQ. In contrast, 19F is a spin-1/2 nucleus with no quadrupole moment and so δobs = δiso.
23Na NMR characterization of the as-synthesized and C-coated materials is shown in Fig. 1f. There are three main signals in the 23Na NMR spectra: a diamagnetic signal at 0 ppm assigned to NaF and two paramagnetic signals near 350 ppm and 1750 ppm. The 350 and 1750 ppm signals observed experimentally are consistent with the computed NMR shifts for Na2 and Na1 sites in the Na3FeF6 structure, respectively, as summarized in Table 1. We note that two calculations were performed using two different hybrid DFT/HF exchange–correlation functionals (H20 and H35) as it has been shown that paramagnetic NMR shifts computed using the H20 and H35 functionals provide approximate upper and lower bounds to the observed shift, respectively. This is confirmed here with, e.g., the 350 ppm experimental shift lying in between the 120 ppm (H35) and 457 ppm (H20) values computed for Na2. By fitting the spectra in Fig. 1f to extract the relative integrated intensity of each 23Na resonance, scaled by the transverse relaxation time (T2′) to account for signal loss over the course of the experiment, we can deduce the population of NaF, Na1 and Na2 environments in the sample. We find that <1% of the integrated 23Na signal intensity corresponds to NaF for the two BM samples, whereas about 7% (±3%) of the integrated 23Na signal intensity corresponds to NaF for the two MW samples. In all spectra, the ratio of Na2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na1 present is 2 (±0.2)
Na1 present is 2 (±0.2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, consistent with the multiplicity of Na1 and Na2 sites in the Na3FeF6 = (Na2)2(Na1)FeF6 crystal structure.
1, consistent with the multiplicity of Na1 and Na2 sites in the Na3FeF6 = (Na2)2(Na1)FeF6 crystal structure.
| Environment | Parameter | OPT H20 | OPT H35 |
|---|---|---|---|
| Na1 (x1) | δ iso/ppm | 2564 | 1923 |
| δ Q/ppm | −20 | −20 | |
| δ obs/ppm | 2544 | 1903 | |
| Na2 (x2) | δ iso/ppm | 484 | 148 |
| δ Q/ppm | −27 | −28 | |
| δ obs/ppm | 457 | 120 | |
The only signal observed in 19F NMR data shown in in Fig. S2a (ESI†) is the NaF impurity phase at −224 ppm. In agreement with the SXRD and 23Na NMR data, this impurity does not appear for the BM samples and decreases for the MW samples after C-coating. No paramagnetic 19F NMR signal attributable to the Na3FeF6 phase is observed in the spectra. While this result may be surprising at first, it can easily be explained by the fact that NMR resonances associated with 19F nuclei directly bonded to paramagnetic species (here, Fe3+) are too broad and too short lived to be observed, as we recently showed in related electrode compounds.19
57Fe Mössbauer spectra are shown in Fig. 1g for the as-synthesized materials. All Mössbauer spectra exhibit a singlet with an isomer shift (δ) of about 0.27 mm s−1 and a small quadrupole splitting (ΔEQ) of 0.1 to 0.15 mm s−1 (exact values shown in Table S4, ESI†). This signal can be assigned to octahedrally-coordinated Fe3+ (Oh-Fe3+) surrounded by six F− anions,20 in good agreement with the Na3FeF6 crystal structure. The slightly larger quadrupole splitting in the BM samples is likely due to an increased amount of structural disorder, as expected from high-energy milling.
The magnetic susceptibility data collected on the pristine BM and MW Na3FeF6 powders are shown in Fig. S2b (ESI†). The susceptibility χ of the BM sample exhibits Curie–Weiss-like behavior, i.e., 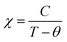 , where C is the Curie constant, T is the temperature, and θ is the Weiss constant. A fit of the susceptibility data obtained between 150 and 350 K yields C = 4.211 emu K mol−1 Oe−1 and θ = −10 K. The value of C correlates with an effective magnetic moment (μeff) of 5.85 μB per Fe atom, indicating the presence of high-spin Fe3+ (theoretical spin-only magnetic moment μtheoSO(Fe3+) = 5.92 μB), which is consistent with the 57Fe Mössbauer results. The small and negative θ = −10 K obtained for BM-Na3FeF6 is consistent with the previously reported value of θ = −12 K21 and suggests that this material is weakly antiferromagnetic. In contrast to BM-Na3FeF6, attempts to fit the susceptibility of MW-Na3FeF6 with the Curie–Weiss equation resulted in nonphysical properties. We suspect that this sample contains a small amount of an amorphous, unreacted FeF3 phase compensating for the NaF impurity phase observed via NMR. This impurity is impossible to distinguish from the major Na3FeF6 phase via57Fe Mössbauer spectroscopy, as both compounds have similar local Fe3+ environments and therefore similar resonances.
, where C is the Curie constant, T is the temperature, and θ is the Weiss constant. A fit of the susceptibility data obtained between 150 and 350 K yields C = 4.211 emu K mol−1 Oe−1 and θ = −10 K. The value of C correlates with an effective magnetic moment (μeff) of 5.85 μB per Fe atom, indicating the presence of high-spin Fe3+ (theoretical spin-only magnetic moment μtheoSO(Fe3+) = 5.92 μB), which is consistent with the 57Fe Mössbauer results. The small and negative θ = −10 K obtained for BM-Na3FeF6 is consistent with the previously reported value of θ = −12 K21 and suggests that this material is weakly antiferromagnetic. In contrast to BM-Na3FeF6, attempts to fit the susceptibility of MW-Na3FeF6 with the Curie–Weiss equation resulted in nonphysical properties. We suspect that this sample contains a small amount of an amorphous, unreacted FeF3 phase compensating for the NaF impurity phase observed via NMR. This impurity is impossible to distinguish from the major Na3FeF6 phase via57Fe Mössbauer spectroscopy, as both compounds have similar local Fe3+ environments and therefore similar resonances.
In summary, we have demonstrated that high-energy ball-milling and assisted-microwave synthesis are two possible preparation routes for Na3FeF6. While BM-Na3FeF6 is almost completely phase pure (with less than 1% of the total Na molar content in NaF domains), MW-Na3FeF6 has a moderate amount of NaF and FeF3 impurities detected by 23Na/19F NMR and magnetometry, respectively. Thus, despite being a fast and environmentally-friendly synthesis method,17 the assisted-microwave synthesis protocol used here is unable to produce as high purity of a material as mechanochemical synthesis.
Electrochemical properties
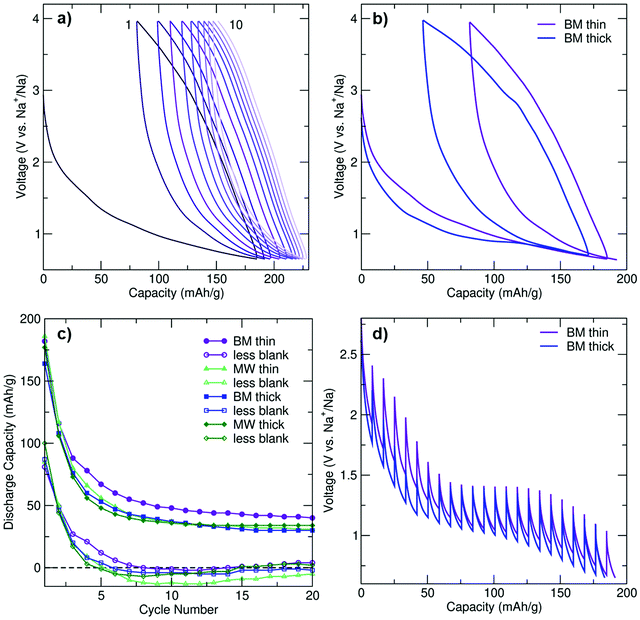
To determine the role of the electrode loading density on performance, the electrochemical properties of thin and thick (3 and 12 mg cm−2 loading density, respectively) electrode films composed of BM and MW C-coated Na3FeF6 were investigated using galvanostatic cycling at a rate of C/20 (full (dis)charge in 20 hours) between 0.65 and 4 V vs. Na+/Na. Negligible capacity (<14 mA h g−1) was observed when the cells were charged first (Fig. S3a, ESI†), indicating that a very small amount of Na (if any) can be extracted from the pristine structure. A rate of C/20 was used throughout as faster rates resulted in decreased capacities and reversibility (Fig. S3a, ESI†). Hence, all of the data shown in Fig. 2 and Fig. S3b–d (ESI†) were obtained on cells discharged first at a rate of C/20. As shown in Fig. S3b (ESI†), particle size reduction and C coating is required to achieve appreciable electrochemical activity from the intrinsically insulating Na3FeF6 phase.Galvanostatic electrochemical profiles are shown in Fig. 2a and b for the BM thin and BM thick electrodes, and Fig. S3c (ESI†) for the MW thin and MW thick electrodes. All cells exhibit first discharge capacities between 160 and 190 mA h g−1, with significant capacity fade (>36%) on second discharge. The discharge capacity retention of BM and MW thin and thick electrodes over the first 20 cycles is shown in Fig. 2c. For each electrode type, the total capacity and the actual Na3FeF6 active material capacity obtained after subtracting the capacity of a thin or thick blank cell (as appropriate) are depicted. The blank cells (NaF in place of Na3FeF6) provide an estimate of the capacity due to the presence of a significant amount of conductive carbon additive in the composite Na3FeF6 electrodes (32 wt%). Galvanostatic cycling (Fig. S3d, ESI†) of these blank cells results in sloping electrochemical profiles with an average potential of 1.3 V and an initial reversible capacity of 75 and 100 mA h g−1 for the thick and thin blank cells, respectively, that gradually decays on subsequent cycles. Thus, a significant fraction of the capacity observed for the Na3FeF6 electrodes arises from Na intercalation into the C matrix rather than the conversion process, as shown in Fig. 2c, with more Na intercalation into C expected for the thin electrodes. MW Na3FeF6 electrodes feature higher initial discharge capacities, but also faster capacity fade compared to their BM counterparts, likely due to the presence of an electrochemically active FeF3 impurity.22,23 Notably, the BM thin cell exhibits less capacity fade and a higher average potential (1.2 V vs. 1.1 V) compared to all other electrode formulations, and a more sloping discharge profile compared to that of the BM thick cell, as supported by the dQ/dV comparison shown in Fig. S3f (ESI†). Hence, for the high purity BM Na3FeF6 electrodes, thinner electrode films appear to enhance the reversibility of the charge–discharge reactions.
To investigate the origin of this loading density-dependent performance, galvanostatic intermittent titration technique (GITT) tests were conducted on BM-Na3FeF6 thin and thick electrodes, as shown in Fig. 2d. Following a 30 minute C/20 current pulse, the voltage was allowed to equilibrate for 4 hours to obtain an estimate of the equilibrium voltage and overpotential. A clear equilibrium voltage plateau is observed at 1.4 V for both electrodes in the GITT tests. In contrast, this plateau is only clearly visible in the galvanostatic voltage profile of the thick electrode cell and at a lower voltage of 0.95 V (see Fig. 2b), presumably due to the significant polarization upon galvanostatic discharge at a rate of C/20.
The evolution of the polarization or overpotential during the first discharge process as obtained from the GITT tests is plotted in Fig. S3e (ESI†). For the thick electrode, the overpotential initially decreases from 0.55 V at 10 mA h g−1 to 0.3 V at 50 mA h g−1. For the thin electrode, a similar albeit delayed decrease in the overpotential is observed from 30 mA h g−1 to 60 mA h g−1. We attribute this electrochemical region (≤50–60 mA h g−1 of capacity) to Na intercalation into the C matrix and explain the decrease in overpotential to gradually more facile Na insertion upon discharge. The delay in the overpotential decrease in the case of the BM thin electrode may be due to side reactions and/or greater Na intercalation into C during the initial stages of discharge (at high voltage), which is consistent with the higher average potential observed for the thin BM electrode (Fig. 2b). Furthermore, greater Na intercalation into the C matrix of the thin BM electrode is consistent with its more sloping voltage profile and the absence of a clear electrochemical plateau in its galvanostatic profile.
The 1.4 V equilibrium voltage plateau region (50–60 to 150 mA h g−1 of capacity) of the GITT curves in Fig. 2d is assigned to bulk Na3FeF6 conversion, and the steady increase in the overpotential up to 0.45 V for both electrodes is attributed to a kinetically-hindered conversion process and the build-up of insulating NaF domains that are also poorly Na+ conducting, as will be discussed later. Perhaps unsurprisingly, the 0.45 V overpotential value matches the voltage difference between the 0.95 V electrochemical plateau observed during galvanostatic cycling for the thick BM electrode and the 1.4 V equilibrium voltage obtained from GITT tests, indicating that kinetic limitations are important when cycling at a rate of C/20. The thin BM electrode results suggest that, at low electrode loading densities, Na intercalation into the C matrix is kinetically-preferred over Na3FeF6 conversion over the plateau region. Indeed, Na intercalation into C is more prevalent when the cell is discharged at C/20 without resting periods, resulting in a sloping galvanostatic profile and no voltage plateau (Fig. 2b). Yet, when the cell is allowed to rest at regular intervals (GITT results), or for thicker electrode films, differences in the rate of Na intercalation and Na3FeF6 conversion are reduced and a clear electrochemical plateau is observed (Fig. 2d).
In summary, the electrochemical performance is improved in the higher purity BM electrodes although the rapidly prepared MW electrodes perform comparably. While electrodes prepared with a lower loading density (e.g., BM thin) result in greater Na intercalation into the carbon matrix at practical C rates, leading to more sloping profiles and a greater average potential, the electrode loading density does not seem to affect the Na3FeF6 conversion mechanism nor its efficiency. The capacity fades quickly for all cells likely due to the significant kinetic limitations and irreversibility of the conversion process. Our comparison of the electrochemical activity of the C-coated Na3FeF6 cells with blank cells is particularly informative in this regard (Fig. 2c), as it clearly shows some electrochemical activity from the Na3FeF6 active material for the first 5 cycles, but past cycle 5 most of the capacity is attributable to Na intercalation into carbon. Thus, we conclude that Na3FeF6 suffers from severe charge–discharge irreversibility and is only electrochemically-active for about 5 cycles.
Characterization of conversion processes
To elucidate the reaction processes and causes of charge–discharge irreversibility for the Na3FeF6 conversion-type electrode, we carried out an in-depth characterization of ex situ electrode samples collected over the first 10 cycles, through a combination of solid-state NMR, SXRD, XPS, magnetometry and 57Fe Mössbauer measurements.High resolution ex situ SXRD was performed on several MW thick Na3FeF6 electrodes at various states of charge to identify the crystalline phases forming on (dis)charge as shown in Fig. S4 (ESI†). All patterns can be successfully fitted with contributions from Na3FeF6 (P21) and NaF (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) phases. The amount of NaF increases on discharge and decreases on charge, consistent with a conversion process. Moreover, low intensity reflections at Q ≈ 1.3, 1.9, 2.1, 2.4, 3.1, and 3.8 Å−1 indicate the formation of a small amount of (a) crystalline phase(s) on discharge that is only partially reversible on subsequent charge. Yet, none of our attempts to match these reflections to any of the known Na-, Fe-, O- or F-containing phases in the International Crystal Structure Database (ICSD) database were successful (full list of attempted phases in Table S5, ESI†). The unidentifiable crystalline phase(s) appear(s) to only account for a small fraction of the sample and could potentially arise from side-reactions (e.g., electrolyte decomposition). A broad baseline is noticeable in all but the pristine sample due to its significantly higher signal intensity. This baseline is predominantly attributed to the Kapton capillary used to hold the sample, although contributions from amorphous phase(s) formed during the conversion process cannot be excluded for patterns collected on ex situ cycled sample. Notably, we could not detect any crystalline α-Fe in our ex situ samples, in contrast to Shakoor et al.'s findings.14 Yet, in this previous study, the claimed Fe reflections are extremely difficult to discern from the noise in the ex situ patterns. Overall, our results exemplify the limited utility of long-range diffraction techniques to monitor conversion processes, and warrant the implementation of more local and quantitative probes to gain insights into nano-sized and disordered/amorphous phases during cycling. Specifically, our ex situ SXRD results indicate the conversion of Na3FeF6 to NaF on discharge, yet are unable to identify any Fe-containing crystalline phase and cannot rule out the possibility of forming amorphous Fe nanoparticles, as has been reported in related conversion electrodes.24,25
m) phases. The amount of NaF increases on discharge and decreases on charge, consistent with a conversion process. Moreover, low intensity reflections at Q ≈ 1.3, 1.9, 2.1, 2.4, 3.1, and 3.8 Å−1 indicate the formation of a small amount of (a) crystalline phase(s) on discharge that is only partially reversible on subsequent charge. Yet, none of our attempts to match these reflections to any of the known Na-, Fe-, O- or F-containing phases in the International Crystal Structure Database (ICSD) database were successful (full list of attempted phases in Table S5, ESI†). The unidentifiable crystalline phase(s) appear(s) to only account for a small fraction of the sample and could potentially arise from side-reactions (e.g., electrolyte decomposition). A broad baseline is noticeable in all but the pristine sample due to its significantly higher signal intensity. This baseline is predominantly attributed to the Kapton capillary used to hold the sample, although contributions from amorphous phase(s) formed during the conversion process cannot be excluded for patterns collected on ex situ cycled sample. Notably, we could not detect any crystalline α-Fe in our ex situ samples, in contrast to Shakoor et al.'s findings.14 Yet, in this previous study, the claimed Fe reflections are extremely difficult to discern from the noise in the ex situ patterns. Overall, our results exemplify the limited utility of long-range diffraction techniques to monitor conversion processes, and warrant the implementation of more local and quantitative probes to gain insights into nano-sized and disordered/amorphous phases during cycling. Specifically, our ex situ SXRD results indicate the conversion of Na3FeF6 to NaF on discharge, yet are unable to identify any Fe-containing crystalline phase and cannot rule out the possibility of forming amorphous Fe nanoparticles, as has been reported in related conversion electrodes.24,25
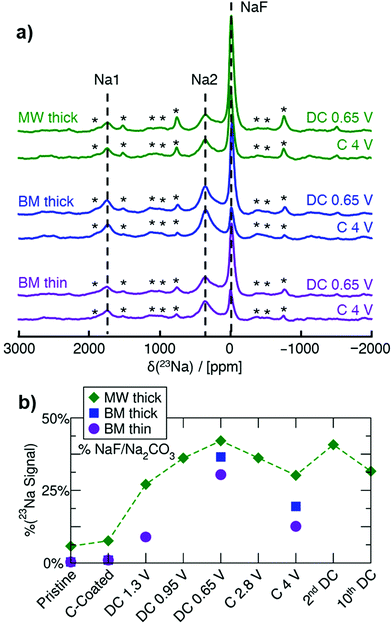
Ex situ 23Na NMR is key in understanding the conversion behavior of Na3FeF6, as it enables us to identify and quantify both crystalline and amorphous Na-containing phases formed on (dis)charge. MW thick, BM thick and BM thin electrodes are examined here to investigate the impact of synthesis and electrode loading density on the degree of conversion during cycling. 23Na spin echo spectra collected on ex situ samples stopped at the end of the initial discharge to 0.65 V, and upon subsequent charge to 4 V, for the three electrode types, are shown in Fig. 3. A more in-depth NMR analysis of a series of ex situ thick MW electrodes is shown in Fig. S5 (ESI†). The three main resonances at ≈0 ppm (NaF), 1750 ppm (Na1), and 350 ppm (Na2), present in the spectra collected on the as-synthesized materials (Fig. 1f) are also observed in the ex situ spectra, albeit with varying relative intensities as expected from the conversion process. Notably, no new 23Na NMR signal appears on cycling. The evolution of the amount of diamagnetic Na-containing phase during cycling is obtained from the fitted 23Na signal intensity at ≈0 ppm and shown in Fig. 3b, with the remainder of the 23Na NMR signal intensity attributed to Na3FeF6. Although most of the diamagnetic 23Na signal can be attributed to NaF present in the pristine MW sample or formed on discharge, we cannot rule out a small contribution to the 0 ppm signal intensity from Na2CO3 formed upon decomposition of the carbonate electrolyte and reaction with Na during cycling. Overall, the NaF signal increases on discharge and decreases on charge, with at least 50% of the total 23Na signal intensity arising from the Na3FeF6 phase even at the bottom of discharge. Thus, Na3FeF6 conversion is incomplete on discharge and only partially reversible on subsequent charge.
Complementary ex situ19F NMR experiments were performed to gain further insights into NaF formation during cycling. The 19F NMR spectra are shown in Fig. S6 (ESI†) and exhibit three main signals: the NaF resonance at −224 ppm, the PTFE binder resonance at −122 ppm, and a resonance at −74.5 ppm indicating adsorption of electrolyte salt (e.g. PF6−) at the surface of the particles.26 Overall, the relative intensity of the NaF signal, as shown in Fig. S6d (ESI†), follows the same trend as that already discussed for NaF through 23Na NMR, confirming that Na2CO3 contributes minimally to the diamagnetic (≈0 ppm) resonance in the 23Na NMR data.
After adjusting for the presence of NaF in the as-synthesized materials (see Table S6, ESI†), 23Na and 19F NMR results indicate that high purity BM Na3FeF6 electrodes result in a higher degree of reconversion of NaF on charge (24 mol%) compared to MW Na3FeF6 (14 mol%), and therefore a higher degree of reversibility. Consistent with the electrochemical results presented earlier, the thinner BM electrode exhibits a low amount of conversion to NaF when discharged to 1.3 V (14 mol%) whereas the thicker MW electrode shows much more conversion (40 mol%), indicating that a larger amount of the observed electrochemical capacity in the thin electrodes is attributable to the carbon additive rather than Na3FeF6 conversion. Thus, the higher reversibility of the thinner electrode is partially attributed to Na+ intercalation into carbon27,28 and/or capacitive storage at the surface of particles,29,30 as these processes are fairly reversible.
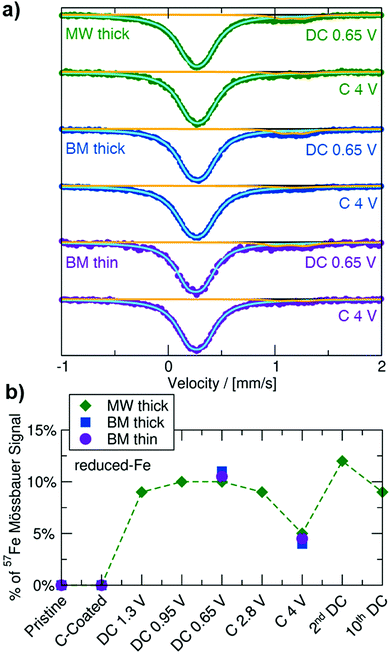
To monitor changes to the Fe redox state and local coordination environment on cycling, and to facilitate the identification of (a) new Fe-containing phase(s) formed during electrochemical cycling, 57Fe Mössbauer experiments were performed on ex situ MW thick, BM thick and BM thin electrode samples collected at the end of the initial discharge to 0.65 V, and upon subsequent charge to 4 V, with results shown in Fig. 4 and values summarized in Table S4 (ESI†). All ex situ spectra exhibit a main (≥88%) resonance with similar δ and ΔEQ values as the Oh-Fe3+ signal observed for the pristine Na3FeF6 powders. A minority (≤12%) doublet signal at δ ≈ 1.16 mm s−1 with ΔEQ ≈ 0.2 mm s−1 is present in the spectra obtained on discharge and is attributed to a “reduced-Fe” species. Additional characterization of samples discharged to 0.65 V via XPS and magnetometry (details in Note S2, ESI†) suggests the presence of an amorphous Fe2+-containing phase that may also contain Fe3+ species. The evolution of the total 57Fe Mössbauer signal throughout (dis)charge, as seen in Fig. 4b, shows minimal change in this “reduced-Fe” signal. Clearly, the absence of a significant change to the main 57Fe Mössbauer resonance upon cycling cannot simply be interpreted as a lack of electrochemical conversion, as 23Na NMR indicated significant Na3FeF6 conversion to NaF upon cycling. Instead, part of the main Oh-Fe3+ signal may come from relaxation24,31 and/or oxidation32,33 of the newly formed metastable conversion products to (a) Oh-Fe3+ containing phase(s) upon removal from the cell for ex situ characterization, complicating the analysis of the Fe redox behavior by ex situ57Fe Mössbauer spectroscopy, XPS, and magnetometry.
Na3FeF6 conversion process and key insights into performance limitations
The reactive nature of the Fe-containing discharged products prevents the exploration of the electrochemical conversion mechanism using ex situ Fe probes, such as Mössbauer, XPS and magnetometry. Thus, the way to obtain insights into the conversion mechanism is to carry out real-time operando measurements or focus on ex situ experiments capable of identifying and quantifying stable conversion products (here, NaF). We employ the latter strategy here, and recall that 23Na NMR is uniquely suited to quantitatively characterize all crystalline and amorphous Na-containing phases appearing upon (dis)charge. The only signals observed via23Na NMR (Fig. 3) are NaF and Na3FeF6. Thus, NaF is the only Na-containing phase formed on discharge. Regarding Fe-containing phase(s) formed upon conversion, we consider two possible processes:| Mechanism A: Na3FeF6 + 3Na ⇄ 6NaF + Fe |
| Mechanism B: Na3FeF6 + Na ⇄ 4NaF + FeF2. |
To distinguish between these two reaction pathways, 23Na NMR can be used to compute the expected capacity based on mechanisms A and B (with theoretical capacities of 337 and 112 mA h g−1, respectively) and on the observed mol% of NaF formed at various states of charge (SOCs), and compare the expected capacities to the observed capacity at these SOCs. We note here that the observed capacity is the actual Na3FeF6 active material capacity obtained after subtracting the capacity of the blank cell. Table S6 (ESI†) shows the details of this analysis at various SOCs for MW thick, BM thick, and BM thin electrodes. Clearly, the observed capacity at the end of discharge is much larger than what would be expected for mechanism B, whereas the expected capacity for mechanism A is in much better agreement with what is observed experimentally, albeit still moderately lower. The good agreement between the expected capacity based on mechanism A and the observed capacity leads us to conclude that Na3FeF6 + 3Na ⇄ 6NaF + Fe is the likely reaction pathway. The small discrepancies between the expected and observed capacities in this scenario can be explained by the intrinsic limitations of our fits of the NMR data (the mol% of NaF phase in the samples extracted from the fits is accurate to ±5%), and how we have estimated the capacity solely attributable to Na3FeF6 conversion by subtracting out the blank cell capacity. Additionally, the presence of a small amount of electrochemically active FeF3 in the MW Na3FeF6 electrode, which is unobservable in 23Na/19F NMR, also likely contributes additional experimental capacity that we have not accounted for in our calculations. Overall, our analysis suggests the incomplete conversion of Na3FeF6 (no more than 60%) to NaF and Fe on discharge through mechanism A. As these Fe nanoparticles are likely less than a few nanometers in diameter,34 they are metastable and oxidize upon ex situ analysis, even upon minimal exposure to ambient air (electrodes opened and samples handled in an inert atmosphere at all times). Additionally, 57Fe Mössbauer analysis of a chemically reduced BM Na3FeF6 powder sample (Fig. S8, ESI†) shows a clear Fe0 singlet at δ = 0 mm s−1, confirming that Fe0 does in fact form on chemical reduction, with a small reduced-Fe signal similar to our previous Mössbauer results (Fig. 4) also observed. We hypothesize that this Fe0 phase is still present in the chemically reduced ex situ Mössbauer spectra as these Fe particles are much larger than those obtained electrochemically and thus spontaneous Fe oxidation only occurs around the exterior of the particles.
The present work demonstrates that Na3FeF6 undergoes a conversion reaction to NaF and Fe on discharge, with the reverse transformation occurring on subsequent charge. While this process should provide a high capacity of 337 mA h g−1, the electrochemical performance is limited by incomplete and poorly reversible phase transformations during cycling. Despite all particles in the C-coated starting materials being ≤100 nm in size, the sluggish conversion kinetics are exacerbated by the formation of NaF domains on the exterior of the Na3FeF6 particles. A schematic of the expected conversion process throughout a Na3FeF6 electrode particle is shown in Fig. 5. The exterior of the particles is expected to undergo conversion through mechanism A, but the interior of the particles is unable to convert on the time-scale of the electrochemical experiments as this process hinges on both Na diffusion and electron tunneling through the poorly Na+ conducting and insulating NaF. Indeed, NaF is a wide bandgap insulator, with a reported bandgap of 11.5 eV,35,36 as well as a very poor Na+ conductor, with large predicted Na+ migration barriers (>1 eV) at room temperature,37 indicating that both transport processes are exceedingly kinetically limited.
In an effort to facilitate more facile Na+ and electron transport, we have attempted to further decrease the Na3FeF6 particle size through an additional ball-milling step with a mixture of grinding ball sizes. SEM images of the resultant particles are shown in Fig. S9a (ESI†) where the particles are now reduced to about 60 nm. The first charge–discharge cycle for this extended ball-milling compared to the BM thin electrodes is shown in Fig. S9b (ESI†) with the capacity fade in Fig. S9c (ESI†). While the initial discharge capacity is not improved with these decreased particles, the reversibility is increased, albeit, still quickly fading with little to no capacity attributed to Na3FeF6 past cycle 15. Cycling this sample at faster rates (Fig. S9d, ESI†) results in comparable discharge capacities observed for C/20 and C/10 rates but with faster capacity fade observed for the higher rates. Thus, despite further reducing the particle sizes, Na3FeF6 is still intrinsically plagued by poor transport properties.
As the dominant kinetic limitation for Na3FeF6 prepared in this study is charge transport (Na+ ions and electrons) into the interior of the particles, rather than through the bulk of the electrode film, the film thickness does not affect the kinetics nor the reversibility of the Na3FeF6 conversion process. In fact, lower loading densities lead to more facile Na intercalation into the carbon additive rather than more conversion of the Na3FeF6 material. These results suggest that the energy density of Na3FeF6 and other fluoride-type Na-based conversion electrodes may be further increased through the preparation of thick electrodes utilizing nanosized particles of the active material embedded into a carbon matrix (e.g. carbon nanotubes), to further enhance the electronic conductivity of the composite. Ultimately, both the electronic conductivity and the Na+ diffusion properties of the discharged products are key considerations for the design of higher rate and reversible conversion electrodes, and sulfide- and oxide-type conversion electrodes may compare more favorably than fluoride-based compounds.
Conclusion
For the first time, Na3FeF6 was prepared through a rapid and sustainable assisted-MW preparation method. Electrochemical testing revealed that several distinct electrochemical processes occur in Na3FeF6 composite electrodes. Notably, carbon additives in the electrode film account for a large fraction of the observed capacity in this and other conversion-type fluoride electrodes, and thus should be accounted for in future studies of this class of materials. We identified that Na3FeF6 converts to NaF and Fe on discharge, as previously proposed. While this mechanism should yield a high theoretical capacity, conversion is incomplete and only moderately reversible due to sluggish conversion reaction kinetics that are exacerbated by the formation of insulating NaF domains with poor Na+ diffusion properties on the exterior of the Na3FeF6 particles. Further, we found that ex situ characterization data on the metastable Fe-containing phases formed on discharge are challenging to interpret due to spontaneous oxidation processes occurring during cell disassembly and/or sample handling, even in an inert environment. We devised a simple ex situ analytical method that relies on the quantification of stable conversion products using local structure probes (here, NaF characterized through 23Na NMR) and a comparison with the observed capacity, to determine the conversion mechanism at play. This novel analytical framework holds promise for the study of a wide range of conversion processes that are often plagued by severe relaxation and oxidation processes during ex situ characterization. Ultimately, in situ and operando studies are better suited for the elucidation of conversion type processes and should be employed in the future for a more in-depth understanding of the thermodynamics and kinetics of conversion processes.Experimental
Materials synthesis
Na3FeF6 was prepared via both microwave-assisted and mechanochemical methods using stoichiometric ratios of NaF (Strem, 99.99%) and FeF3 (Sigma, 99.5%). For the microwave-assisted synthesis method, 300 mg of a ground stoichiometric mixture of the precursors was pressed into 6 mm pellets, placed inside BN crucibles, and sealed in vitreous silica ampules under 0.25 atm of Ar. The ampules were placed in a carbon-filled crucible and heated in a 1200 W domestic microwave oven (Panasonic, model NN-SN651WAZ) at 30% power (360 W) for 6 min. For the mechanochemical synthesis method, 1 g of a ground stoichiometric mixture of the precursors was placed in a 50 mL ZrO2 ball-milling jar along with five 10 mm ZrO2 balls and ten 5 mm ZrO2 balls and sealed inside an Ar glovebox. The material was then ball-milled at 500 rpm for 24 h.Electrochemical characterization
For all samples the Na3FeF6 active material was ball-milled for 24 h at 300 rpm with five 10 mm ZrO2 balls with 34 wt% carbon (0.5 g in total) to form an electronically conductive carbon nanocomposite.18 This nanocomposite was then hand-ground with polytetrafluoroethylene (PTFE) for 15 minutes and made into electrodes with a 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 weight ratio of Na3FeF6
5 weight ratio of Na3FeF6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C Super P
C Super P![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PTFE. The thick electrodes were prepared by pressing the electrode material into a thin 10 mm diameter pellet whereas for the thin electrodes the electrode material was hand-rolled into a film and punched into 6 mm disks. Their loading densities were 12 mg cm−2 and 3 mg cm−2, respectively. Blank cells were prepared in an analogous manner but now replacing the Na3FeF6 with NaF. All electrochemical testing occurred in Swagelok-type cells with an excess of 1 M NaPF6 (≥99% Strem Chemicals) in EC
PTFE. The thick electrodes were prepared by pressing the electrode material into a thin 10 mm diameter pellet whereas for the thin electrodes the electrode material was hand-rolled into a film and punched into 6 mm disks. Their loading densities were 12 mg cm−2 and 3 mg cm−2, respectively. Blank cells were prepared in an analogous manner but now replacing the Na3FeF6 with NaF. All electrochemical testing occurred in Swagelok-type cells with an excess of 1 M NaPF6 (≥99% Strem Chemicals) in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC (1
DMC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 w/w, ≥99% Sigma-Aldrich) electrolyte with <25 ppm water content, a Na metal (Sigma-Aldrich) counter-electrode, and a glass fiber separator (Whatman GF/D).
1 w/w, ≥99% Sigma-Aldrich) electrolyte with <25 ppm water content, a Na metal (Sigma-Aldrich) counter-electrode, and a glass fiber separator (Whatman GF/D).
Chemical reduction of the BM Na3FeF6 material was achieved by stirring a suspension of BM Na3FeF6 (25.0 mg, 0.1046 mmol) in anhydrous THF (2 mL) followed by the addition of Na metal (14.4 mg, 0.6281 mmol) and naphthalene (80.5 mg, 0.6281 mmol). The resulting green mixture was stirred at room temperature under an inert nitrogen atmosphere for three days, where the green coloration of the sodium naphthalenide had faded. The volatile components were then removed in vacuo, and the crude solid residue was analyzed spectroscopically.
Structural characterization
Calculation of NMR parameters
Spin-unrestricted hybrid density functional theory (DFT)/Hartree Fock (HF) calculations were performed using the CRYSTAL17 all-electron linear combination of atomic orbital code42,43 to determine 23Na and 19F NMR parameters in Na3FeF6. Two spin-polarized exchange–correlation functionals based upon the B3LYP form,44–47 and with Fock exchange weights of F0 = 20% (B3LYP or H20) and 35% (H35) were chosen for their good performance for the electronic structure and band gaps of transition metal compounds (B3LYP or H20),48,49 and for their accurate description of the magnetic properties of related compounds (H35).50–52 Besides, previous studies have shown that the hyperfine shifts calculated with the H20 and the H35 functionals on similar compounds are in good agreement with experiment.53,54All-electron atom-centered basis sets comprising fixed contractions of Gaussian primitive functions were employed throughout. Two types of basis sets were used: a smaller basis set (BS-I) was employed for structural optimizations, and a larger basis set (BS-II) was used for computing 23Na and 19F NMR parameters which require an accurate description of the occupation of core-like electronic states. For BS-I, individual atomic sets are of the form (15s7p)/[1s3sp] for Na, (20s12p5d)/[1s4sp2d] for Fe, and (10s6p1d)/[4s3p1d] for F the values in parentheses denote the number of Gaussian primitives and the values in square brackets the contraction scheme. All BS-I sets were obtained from the CRYSTAL online repository and were unmodified from their previous use in a broad range of compounds.42 For BS-II, modified IGLO-III and (10s6p2d)/[6s5p2d] sets were adopted for F, a flexible and extended TZDP-derived (11s7p)/[7s3p] set was used for Na, and an Ahlrichs DZP-derived55 (13s9p5d)/[7s5p3d] was adopted for Fe.
NMR parameters were computed on the fully optimized (atomic positions and cell parameters) Na3FeF6 structure (P21).56 All first principles structural optimizations were carried out in the ferromagnetic (FM) state, after removal of all symmetry constraints (within the P1 space group) and using the H20 and H35 hybrid functionals. A 160 atom 2 × 2 × 2 supercell was used throughout. Structural optimizations were pursued using the quasi-Newton algorithm with RMS convergence tolerances of 10−7, 0.0003, and 0.0012 a.u. for total energy, root-mean-square (rms) force, and rms displacement, respectively. Tolerances for maximum force and displacement components were set to 1.5 times the respective rms values. Sufficient convergence in total energies and spin densities was obtained by application of integral series truncation thresholds of 10−7, 10−7, 10−7, 10−7, and 10−14 for Coulomb overlap and penetration, exchange overlap, and g- and n-series exchange penetration, respectively, as defined in the CRYSTAL17 documentation.42 The final total energies and spin and charge distributions were obtained in the absence of any spin and eigenvalue constraints. NMR parameters were obtained on ferromagnetically aligned supercells, and on supercells in which one Fe spin was flipped, using BS-II sets and a method identical to that described in Middlemiss et al.'s work.54 Anisotropic Monkhorst–Pack reciprocal space meshes57 with shrinking factors 6 9 3 were used for both H20 and H35 calculations. The lattice parameters for the Na3FeF6 structures relaxed using the H20 and H35 functionals are compared to the experimental (EXP) unit cell parameters56 in Table S4 (ESI†).
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work made use of the shared facilities of the UC Santa Barbara MRSEC (DMR 1720256), a member of the Materials Research Facilities Network (http://www.mrfn.org) and the computational facilities administered by the Center for Scientific Computing at the CNSI and MRL (an NSF MRSEC; CNS 1725797, DMR 1720256). E. E. Foley, R. C. Vincent, and E. Gonzalez-Correa were supported by the NSF Graduate Research Fellowship Program under Grant No. DGE 1650114. Synchrotron diffraction data was collected at beamlines 11-BM at the Advanced Photon Source, Argonne National Laboratory, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. We gratefully acknowledge Howie Nguyen and Dr Ram Seshadri for the helpful discussions regarding magnetic measurements.References
- N. Nitta, F. Wu, J. T. Lee and G. Yushin, Li-ion battery materials: present and future, Mater. Today, 2015, 18, 252–264 CrossRef CAS.
- K. Kubota and S. Komaba, Review-Practical Issues and Future Perspective for Na-Ion Batteries, J. Electrochem. Soc., 2015, 162, A2538–A2550 CrossRef CAS.
- M. Keller, D. Buchholz and S. Passerini, Layered Na-Ion Cathodes with Outstanding Performance Resulting from the Synergetic Effect of Mixed P- and O-Type Phases, Adv. Energy Mater., 2016, 6, 1501555 CrossRef PubMed.
- M. Bianchini, F. Fauth, N. Brisset, F. Weill, E. Suard, C. Masquelier and L. Croguennec, Comprehensive investigation of the Na3V2(PO4)2F3-NaV2(PO4)2F3 system by operando high resolution synchrotron X-ray diffraction, Chem. Mater., 2015, 27, 3009–3020 CrossRef CAS.
- Y. Wang, Y. Zhang, J. Shi, A. Pan, F. Jiang, S. Liang and G. Cao, S-doped porous carbon confined SnS nanospheres with enhanced electrochemical performance for sodium-ion batteries, J. Mater. Chem. A, 2018, 6, 18286–18292 RSC.
- K. Sato, M. Nakayama, A. M. Glushenkov, T. Mukai, Y. Hashimoto, K. Yamanaka, M. Yoshimura, T. Ohta and N. Yabuuchi, Na-Excess Cation-Disordered Rocksalt Oxide: Na1.3Nb0.3Mn0.4O2, Chem. Mater., 2017, 29, 5043–5047 CrossRef CAS.
- T. Sato, K. Sato, W. Zhao, Y. Kajiya and N. Yabuuchi, Metastable and nanosize cation-disordered rocksalt-type oxides: revisit of stoichiometric LiMnO2 and NaMnO2, J. Mater. Chem. A, 2018, 6, 13943–13951 RSC.
- H. Park, Y. Lee, M.-K. Cho, J. Kang, W. Ko, Y. H. Jung, T.-Y. Jeon, J. Hong, H. Kim, S.-T. Myung and J. Kim, Na2Fe2F7: a fluoride-based cathode for high power and long life Na-ion batteries, Energy Environ. Sci., 2021, 14, 1469–1479 RSC.
- H. Euchner, O. Clemens and M. A. Reddy, Unlocking the potential of weberite-type metal fluorides in electrochemical energy storage, npj Comput. Mater., 2019, 5, 31 CrossRef.
- M. A. Reddy and M. Fichtner, Advanced Fluoride-Based Materials for Energy Conversion, Elsevier Inc., 2015, pp. 51–76 Search PubMed.
- X. Hua, A. S. Eggeman, E. Castillo-Martínez, R. Robert, H. S. Geddes, Z. Lu, C. J. Pickard, W. Meng, K. M. Wiaderek, N. Pereira, G. G. Amatucci, P. A. Midgley, K. W. Chapman, U. Steiner, A. L. Goodwin and C. P. Grey, Revisiting metal fluorides as lithium-ion battery cathodes, Nat. Mater., 2021, 20, 841–850 CrossRef CAS PubMed.
- R. E. Doe, K. A. Persson, Y. S. Meng and G. Ceder, First-principles investigation of the Li-Fe-F phase diagram and equilibrium and nonequilibrium conversion reactions of iron fluorides with lithium, Chem. Mater., 2008, 20, 5274–5283 CrossRef CAS.
- V. L. Chevrier, G. Hautier, S. P. Ong, R. E. Doe and G. Ceder, First-principles study of iron oxyfluorides and lithiation of FeOF, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 94118 CrossRef.
- R. A. Shakoor, S. Y. Lim, H. Kim, K. W. Nam, J. K. Kang, K. Kang and J. W. Choi, Mechanochemical synthesis and electrochemical behavior of Na3FeF6 in sodium and lithium batteries, Solid State Ionics, 2012, 218, 35–40 CrossRef CAS.
- H. Guo, W. Liu, M. Qin, J. Tang, J. Cheng and Y. Ling, Room-temperature liquid-phase synthesis of Na3FeF6 and its lithium/sodium storage properties, Mater. Res. Express, 2019, 6, 085507 CrossRef CAS.
- W. Liu, W. Wang, M. Qin and B. Shen, Successive synthesis and electrochemical properties of Na3FeF6 and NaFeF3/C cathode materials for lithium-ion and sodium-ion batteries, Ceram. Int., 2020, 46, 11436–11440 CrossRef CAS.
- E. E. Levin, J. H. Grebenkemper, T. M. Pollock and R. Seshadri, Protocols for High Temperature Assisted-Microwave Preparation of Inorganic Compounds, Chem. Mater., 2019, 31, 7151–7159 CrossRef CAS.
- F. Badway, N. Pereira, F. Cosandey and G. G. Amatucci, Carbon-Metal Fluoride Nanocomposites: Structure and Electrochemistry of FeF3:C, J. Electrochem. Soc., 2003, 150, A1209 CrossRef CAS.
- R. J. Clément, D. Kitchaev and J. Lee, and Gerbrand Ceder, Short-Range Order and Unusual Modes of Nickel Redox in a Fluorine-Substituted Disordered Rocksalt Oxide Lithium-Ion Cathode, Chem. Mater., 2018, 30, 6945–6956 CrossRef.
- P. Gütlich, Fifty years of Mössbauer spectroscopy in solid state research - Remarkable achievements, future perspectives, Z. Anorg. Allg. Chem., 2012, 638, 15–43 CrossRef.
- A. Tressaud, J. Portier, S. Shearer-Turrell, J. L. Dupin and P. Hagenmuller, Les hexafluoferrites M3FeF6 (M = Li, Na, K, Rb, Cs, Ag, Tl, NH4): Etude radiocristallographique, spectroscopique et magnetique, J. Inorg. Nucl. Chem., 1970, 32, 2179–2186 CrossRef CAS.
- H. Arai, S. Okada, Y. Sakurai and J. I. Yamaki, Cathode performance and voltage estimation of metal trihalides, J. Power Sources, 1997, 68, 716–719 CrossRef CAS.
- C. P. Guntlin, Z. Tanja, V. Kostiantyn Kravchyk, W. Michael, M. I. Bodnarchuk and M. V. Kovalenko, Nanocrystalline FeF3 and MF2 (M = Fe, Co, and Mn) from metal trifluoroacetates and their Li(Na)-ion storage properties, J. Mater. Chem. A, 2017, 5, 7383–7393 RSC.
- G. Gershinsky, E. Bar, L. Monconduit and D. Zitoun, Operando electron magnetic measurements of Li-ion batteries, Energy Environ. Sci., 2014, 7, 2012–2016 RSC.
- K. M. Wiaderek, O. J. Borkiewicz, E. Castillo-Martínez, R. Robert, N. Pereira, G. G. Amatucci, C. P. Grey, P. J. Chupas and K. W. Chapman, Comprehensive insights into the structural and chemical changes in mixed-anion FeOF electrodes by using operando pdf and NMR spectroscopy, J. Am. Chem. Soc., 2013, 135, 4070–4078 CrossRef CAS PubMed.
- N. Dupre, M. Cuisinier and D. Guyomard, Electrode/Electrolyte Interface Studies in Lithium Batteries Using NMR, Interface Mag., 2011, 20, 61–67 CrossRef CAS.
- K. A. See, M. A. Lumley, G. D. Stucky, C. P. Grey and R. Seshadri, Reversible Capacity of Conductive Carbon Additives at Low Potentials: Caveats for Testing Alternative Anode Materials for Li-Ion Batteries, J. Electrochem. Soc., 2017, 164, 327–333 CrossRef.
- J. M. Stratford, P. K. Allan, O. Pecher, P. A. Chater and C. P. Grey, Mechanistic insights into sodium storage in hard carbon anodes using local structure probes, Chem. Commun., 2016, 52, 12430–12433 RSC.
- J. Nava-Avendaño, M. E. Arroyo-De Dompablo, C. Frontera, J. A. Ayllón and M. R. Palacín, Study of sodium manganese fluorides as positive electrodes for Na-ion batteries, Solid State Ionics, 2015, 278, 106–113 CrossRef.
- N. Dimov, A. Nishimura, K. Chihara, A. Kitajou, I. D. Gocheva and S. Okada, Transition metal NaMF3 compounds as model systems for studying the feasibility of ternary Li-M-F and Na-M-F single phases as cathodes for lithium-ion and sodium-ion batteries, Electrochim. Acta, 2013, 110, 214–220 CrossRef CAS.
- K. E. Johnston, M. T. Sougrati, L. Stievano, A. Darwiche, N. Dupré, C. P. Grey and L. Monconduit, Effects of Relaxation on Conversion Negative Electrode Materials for Li-Ion Batteries: A Study of TiSnSb Using 119Sn Mössbauer and 7Li MAS NMR Spectroscopies, Chem. Mater., 2016, 28, 4032–4041 CrossRef CAS.
- K. Haneda, X. Z. Zhou, A. H. Morrish and R. J. Pollard, Mössbauer study of ultrafine FeF2 particles, Hyperfine Interact., 1990, 54, 551–556 CrossRef CAS.
- S. Ramasamy, J. Jiang, H. Gleiter, R. Birringer and U. Gonser, Investigation of nanocrystalline FeF2 by Mössbauer spectroscopy, Solid State Commun., 1990, 74, 851–855 CrossRef CAS.
- K. He, Y. Zhou, P. Gao, L. Wang, N. Pereira, G. G. Amatucci, K. W. Nam, X. Q. Yang, Y. Zhu, F. Wang and D. Su, Sodiation via heterogeneous disproportionation in FeF2 electrodes for sodium-ion batteries, ACS Nano, 2014, 8, 7251–7259 CrossRef CAS PubMed.
- F. C. Brown, C. Gähwiller, H. Fujita, A. B. Kunz, W. Scheifley and N. Carrera, Extreme-ultraviolet spectra of ionic crystals, Phys. Rev. B: Solid State, 1970, 2, 2126–2138 CrossRef.
- G. Roy, G. Singh and T. E. Gallon, The electron energy loss spectra of some alkali halides in the band gap region, Surf. Sci., 1985, 152–153, 1042–1050 CrossRef CAS.
- H. Yildirim, A. Kinaci, M. K. Y. Chan and J. P. Greeley, First-Principles Analysis of Defect Thermodynamics and Ion Transport in Inorganic SEI Compounds: LiF and NaF, ACS Appl. Mater. Interfaces, 2015, 7, 18985–18996 CrossRef CAS PubMed.
- B. H. Toby and R. B. Von, Dreele, GSAS-II: The genesis of a modern open-source all purpose crystallography software package, J. Appl. Crystallogr., 2013, 46, 544–549 CrossRef CAS.
- I. Hung, L. Zhou, F. Pourpoint, C. P. Grey and Z. Gan, Isotropic High Field NMR Spectra of Li-Ion Battery Materials with Anisotropy > 1 MHz, J. Am. Chem. Soc., 2012, 134, 1898–1901 CrossRef CAS PubMed.
- C. Prescher, C. McCammon and L. Dubrovinsky, MossA: A program for analyzing energy-domain Mössbauer spectra from conventional and synchrotron sources, J. Appl. Crystallogr., 2012, 45, 329–331 CrossRef CAS.
- P. M. T. M. Van Attekum and G. K. Wertheim, Excitonic effects in core-hole screening, Phys. Rev. Lett., 1979, 43, 1896–1898 CrossRef CAS.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D’Arco, M. Llunel, M. Causà, Y. Noël, L. Maschio, A. Erba, M. Rérat and S. Casassa, CRYSTAL17 User's Manual, 2018 Search PubMed.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Quantum-mechanical condensed matter simulations with CRYSTAL, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360 Search PubMed.
- A. D. Becke, A new mixing of Hartree-Fock and local density-functional theories, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, 1994, vol. 98 Search PubMed.
- F. Corà, M. Alfredsson, G. Mallia, D. S. Middlemiss, W. C. Mackrodt, R. Dovesi and R. Orlando, Structure and Bonding, Springer, Berlin, Heidelberg, 2012, vol. 113, pp. 171–232 Search PubMed.
- J. Muscat, A. Wander and N. M. Harrison, On the prediction of band gaps from hybrid functional theory, Chem. Phys. Lett., 2001, 342, 397–401 CrossRef CAS.
- X. Feng and N. M. Harrison, Magnetic coupling constants from a hybrid density functional with 35% Hartree-Fock exchange, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 092402 CrossRef.
- D. S. Middlemiss, L. M. Lawton and C. C. Wilson, A solid-state hybrid density functional theory study of Prussian blue analogues and related chlorides at pressure, J. Phys.: Condens. Matter, 2008, 20, 335231 CrossRef.
- I. de, P. R. Moreira, F. Illas and R. L. Martin, Effect of Fock exchange on the electronic structure and magnetic coupling in NiO, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 1551021 CrossRef.
- J. Kim, D. S. Middlemiss, N. A. Chernova, B. Y. X. Zhu, C. Masquelier and C. P. Grey, Linking local environments and hyperfine shifts: A combined experimental and theoretical 31P and 7Li solid-state NMR study of paramagnetic Fe(III) phosphates, J. Am. Chem. Soc., 2010, 132, 16825–16840 CrossRef CAS PubMed.
- D. S. Middlemiss, A. J. Ilott, R. J. Clément, F. C. Strobridge and C. P. Grey, Density functional theory-based bond pathway decompositions of hyperfine shifts: Equipping solid-state NMR to characterize atomic environments in paramagnetic materials, Chem. Mater., 2013, 25, 1723–1734 CrossRef CAS.
- A. Schäfer, H. Horn and R. Ahlrichs, Fully optimized contracted Gaussian basis sets for atoms Li to Kr, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- E. N. Matvienko, O. V. Yakubovich, M. A. Simonov, A. N. Ivashchenko, O. K. Mel’nikov and N. V. Belov, The crystal structure of the synthetic Fe-cryolite Na3FeF6, Dokl. Akad. Nauk SSSR, 1981, 257, 105–108 CAS.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02763h |
| ‡ Present address: School of Chemistry, University of St-Andrews, North Haugh, St-Andrews, KY16 9ST, UK. |
| This journal is © the Owner Societies 2021 |