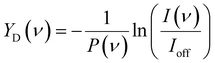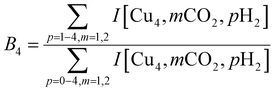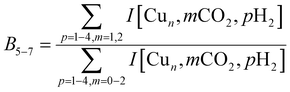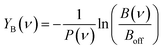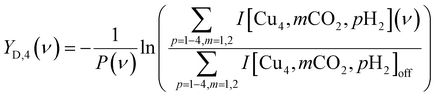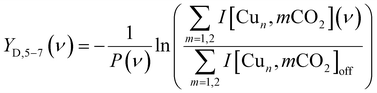IR spectroscopic characterization of the co-adsorption of CO₂ and H₂ onto cationic Cu_n⁺ clusters

Abstract

To understand elementary reaction steps in the hydrogenation of CO₂ over copper-based catalysts, we experimentally study the adsorption of CO₂ and H₂ onto cationic Cu_n⁺ clusters. For this, we react Cu_n⁺ clusters formed by laser ablation with a mixture of H₂ and CO₂ in a flow tube-type reaction channel and characterize the products formed by IR multiple-photon dissociation spectroscopy employing the IR free-electron laser FELICE. We analyze the spectra by comparing them to literature spectra of Cu_n⁺ clusters reacted with H₂ and with new spectra of Cu_n⁺ clusters reacted with CO₂. The latter indicate that CO₂ is physisorbed in an end-on configuration when reacted with the clusters alone. Although the spectra for the co-adsorption products evidence H₂ dissociation, no signs for CO₂ activation or reduction are observed. This lack of reactivity for CO₂ is rationalized by density functional theory calculations, which indicate that CO₂ dissociation is hindered by a large reaction barrier. CO₂ reduction to formate should energetically be possible, but the lack of formate observation is attributed to kinetic hindering.

---

Introduction

The rapid development of the urbanized world has resulted in the constant growth of the atmospheric CO₂ concentration. On its own, CO₂ is a harmless molecule, which is part of the natural carbon cycle. In large concentrations, CO₂ acts as thermal isolation for our planet and is one of the main causes of global warming. Therefore, a reduction of the global carbon footprint is of great significance to reduce the societal impact of global warming.¹

Since CO₂ is non-toxic, renewable, and cheap, it has the potential to serve as a feedstock for the industrial production of value-added chemicals. The bottleneck of CO₂ utilization is its kinetic inertness due to the high C=O bonding energy of 7.8 eV.² Almost a century ago, syngas, a mixture of CO₂, CO, and H₂, was used for the first time for methanol production.³ This reaction required a catalyst, and elevated pressure (up to 350 bar) and temperature. Ever since, the search has been ongoing for more efficient catalyst materials that can reduce production costs, increase methanol selectivity, and minimize environmental impact.

The widely used Cu/ZnO/Al₂O₃ catalyst for commercial methanol production made it possible to reduce the reaction pressure to 50–100 bar at a temperature around 200–300 °C.⁴ Wide ranges of other catalysts have been investigated; a recent summary was given by Zhang et al.⁵ Overall, Cu based catalysts still show the best performance. However, the exact mechanism of methanol formation over the catalyst remains elusive. Theoretical studies have discussed several reaction paths.^6–8 Some require the dissociation of hydrogen before CO₂ activation, while others are initiated by direct CO₂ activation or even water involvement. It is now widely accepted that the most profitable path for hydrogenation of CO₂ to methanol over Cu-based catalysts proceeds via a formate (HCOO) intermediate.^4,6,9–12

The surface chemistry of CO₂ as studied under high vacuum conditions has been reviewed by various authors.^13–15 Surface studies agree that the electronic and geometric structures determine the activity of the catalyst.^2,16–18 Experimentally, it was shown that crystalline Cu(100) surfaces are relatively inert towards CO₂.^16,19 In the Cu/ZnO catalyst, Cu atoms are dispersed and Cu⁺ is stabilized,^20,21 where a correlation was found between the concentration of Cu⁺ species on the catalyst surface and methanol production rates.^19,21–24 Cu clusters deposited on a ZnO/Al₂O₃ surface were demonstrated to significantly reduce the pressure required for methanol formation.^25,26 Concomitant density functional theory (DFT) modeling showed that the Cu clusters deposited on Al₂O₃ and SiO₂ are slightly positively charged, which is attributed to the cluster–support interaction.²⁶ Theoretical studies also emphasize that the size of the deposited cluster has a large influence on its activity, with smaller clusters showing a higher activity.^26–28

Complete control over the structure and charge of the clusters is achieved in gas-phase studies. Here, metal clusters can mimic the catalyst active sites to study the elementary steps of methanol formation at the molecular level. Understanding the binding nature of CO₂ to different metal ions has attracted broad research interest. The chemistry between cationic metal ions and a single CO₂ molecule has been studied employing guided ion beam and flow tube reactor based mass spectrometry;^29–36 a summary can be found elsewhere.⁷ IR spectroscopic studies have aimed to obtain structural insight into the solvent-driven activation of CO₂ by various metal cations.^37–47 The general picture that emerges is that metal cations mostly bind CO₂ molecules intact, in end-on configuration via one of the oxygen atoms through quadrupole-related electrostatic interactions.

It can thus be expected that CO₂ adsorption onto metal clusters is also dominated by a weak electrostatic interaction resulting in physisorption. However, what is unclear is how this situation changes when hydrogen atoms are present on the cluster surface. Hu et al. simulated methanol formation over a Cu₈ cluster and compared it to the Cu(100) surface.⁴⁸ According to this work, H₂ and CO₂ are co-adsorbed on the surface, where H₂ is dissociated and CO₂ is chemisorbed in the form of CO₂⁻. This leads to a Langmuir–Hinshelwood type reaction between atomic hydrogen, H(a), and CO₂⁻ resulting in a formate intermediate. Yang et al. also found that methanol formation will proceed via a formate intermediate, both over a Cu₂₉ cluster, and over Cu(111).⁴⁹ However, in this study the reaction proceeds via an Eley–Rideal-type mechanism. First, H₂ dissociatively binds to the surface, and then CO₂ directly reacts with the H(a) to form formate. Another mechanism of methanol formation over Cu/ZnO catalyst is proposed by Kakumoto.¹¹ His calculations suggest that CO₂ is first linearly absorbed on Cu⁺, followed by an attack of H(a) on the C atom, leading to the formate intermediate.¹¹ Therefore, three alternative routes of the formation of the formate intermediate are proposed by the theoretical investigations.

Previously, we have shown that the adsorption of H₂ onto cationic Cu_n⁺ (n = 4–7) clusters can lead to a significant fraction of cluster population with dissociatively bound H₂, with a size-dependent propensity for dissociation.⁵⁰ In this work, we investigate the co-adsorption of CO₂ and H₂ on cationic Cu_n⁺ clusters employing IRMPD spectroscopy. To interpret the co-adsorption spectra we compare them to equivalent spectra separately obtained for the adsorption products of the individual molecules. For H₂ adsorbed on cationic Cu_n⁺ we use spectra from our previous work;⁵⁰ for CO₂, we present new spectra. Furthermore, we have carried out extensive DFT calculations to rationalize and corroborate our interpretations.

Methods

Experimental

The experiments are performed using a molecular beam instrument placed within the cavity of a free-electron laser (FELICE).^51,52 Cu clusters are produced in a Smalley–type laser ablation source, where a Cu rod is rotated and translated while being irradiated by the second harmonic (532 nm) of a pulsed Nd: YAG laser, focused on the rod to ablate metal atoms. For the spectroscopy of CO₂ adsorption only, a rod of naturally abundant Cu (69% ⁶³Cu and 31% ⁶⁵Cu) is used. In the experiments utilizing both H₂ and CO₂, mass spectral overlap is prevented by employing a foil of isotopically enriched ⁶⁵Cu (99.9%, STB Isotope GmbH) attached to a stainless steel rod. The plasma formed in the ablation process is collisionally cooled by a carrier gas pulse consisting of a mixture of 1% Ar in He for the CO₂ experiment (to facilitate the formation of larger clusters) and of pure He for the co-adsorption experiment. The carrier gas is introduced via a pulsed valve (General Valve series 9) with a stagnation pressure of 6 bar. The created clusters are reacted with either pure CO₂ or a mixture of 1% CO₂ in H₂, introduced approximately 50 mm downstream by a second pulsed valve with a 1 bar stagnation pressure. The reacting mixture is confined in the flow channel by a converging–diverging nozzle (diameter ∼0.7 mm), which is located 10 mm further downstream, through which the gas mixture eventually is expanded into vacuum, forming a molecular beam. The formed beam is subsequently collimated by a 2 mm diameter skimmer and shaped by a horizontal slit aperture (8 × 0.45 mm) to ensure optimum overlap with the (horizontal) IR beam, which it crosses at a 35° angle; both shaping elements are electrically grounded. The irradiated cationic species are extracted by two pulsed, high voltage plates into a reflectron time-of-flight mass spectrometer and registered by a multichannel plate (MCP) detector. The experiment is operated at 10 Hz, which is double the FELICE macropulse repetition rate. Therefore, for every mass spectrum of irradiated clusters recorded, a reference mass spectrum is recorded to correct for fluctuations in cluster production. When the IR light is resonant with an optically allowed vibrational mode of the complex, the sequential absorption of IR photons can lead to fragmentation, resulting in the loss of CO₂, H₂, or both.

The FELICE IR light employed in this work is in the 120–2100 cm⁻¹ spectral range. Each FELICE macropulse is formed by a 10 μs duration pulse train of 1 ns spaced picosecond duration, near-transform limited optical pulses. The spectral bandwidth is adjusted to a full-width at half-maximum (FWHM) of about 0.7% of the central frequency, thus ∼7 cm⁻¹ at 1000 cm⁻¹. The typical macropulse energy used is between 0.5–0.8 J. The use of the intracavity instrument allows performing experiments, where high pulse energies are required for photofragmentation, as one could expect for complexes where CO₂ and/or H₂ adsorb dissociatively. For systems with lower binding energies, the instrument can be positioned well out of the focus of the IR laser to reduce the IR intensity. The IRMPD spectra presented in this paper are measured out of focus.⁵¹

The IRMPD spectra for CO₂ adsorption are presented as the pulse energy-normalized depletion yield Y_D, defined as

where I(ν) is the ion intensity of the mass channel under study with IR radiation at frequency ν, I_off the intensity without IR laser, and P the macropulse energy, respectively. If no fragmentation takes place, the ratio I(ν)/I_off is unity and Y is consequently zero.

To construct spectra for [Cu_n, CO₂, H₂]⁺, loss of H₂ from [Cu_n, CO₂, pH₂]⁺ (p > 1) and of CO₂ from [Cu_n, mCO₂, H₂]⁺ (m > 1) leads to contamination of the mass channel of interest. To account for this, we inspected the IR-induced loss and growth signals for all relevant mass channels to identify the fragmentation pathways, which are summarized in Scheme 1; they are substantiated by depletion spectra per individual mass channel in the ESI.† We then calculate the branching ratio B(ν) of all clusters with m CO₂ and p H₂ molecules adsorbed to all these species plus the channel into which the [Cu_n, CO₂, H₂]⁺ fragments. Because this channel is different for n = 4 (dominant loss channel [Cu₄, CO₂, H₂]⁺ → [Cu₄, CO₂]⁺ + H₂) than for n = 5–7 ([Cu_n, CO₂, H₂]⁺ → [Cu_n, H₂]⁺ + CO₂) the branching ratios are also different:

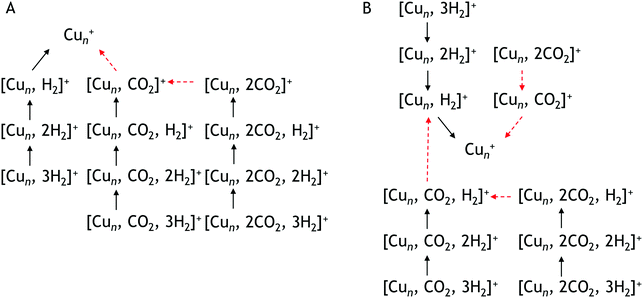Scheme 1 Observed fragmentation pathways. Pathway A is observed for Cu₄⁺ pathway B for Cu₅⁺, Cu₆⁺, Cu₇⁺. Black solid arrows indicate H₂ loss, red dashed arrows CO₂ loss.

The IRMPD yield Y_B is then obtained as the logarithmic depletion ratio of the branching ratios with and without IR irradiation:

This approach assumes that no direct loss of multiple H₂ or CO₂ occurs from [Cu_n, mCO₂, pH₂]⁺ (m,p > 1) induced by IR absorption, and was used previously.⁵³ By employing it, ingrowth effects from higher order complexes are reduced, as are shot-to-shot fluctuations in cluster production.

To construct spectra for [Cu_n, CO₂]⁺ in the co-adsorption experiments, neither of the described methods is suitable. The depletion yield Y cannot be used since there is significant ingrowth from fragmentation from the different complexes into the [Cu_n, CO₂]⁺ mass channel. The depletion of the branching ratio also fails, because the final fragment in this case, the bare cluster, has competing ingrowth from fragmentation of [Cu_n, pH₂]⁺, which will contaminate the final spectrum. Therefore, the depletion yield Y_D of [Cu_n, CO₂]⁺ plus all species fragmenting into the [Cu_n, CO₂]⁺ mass channel has been calculated:

Throughout the manuscript, we employ the bracketed notation introduced here to indicate no structural knowledge of the products is known, only its mass.

Computational

Quantum chemical computations were carried out using the Q-Chem 5.3 program package,⁵⁴ and were mostly focused on the Cu₄⁺ cluster. We performed optimizations on different initial cluster geometries (rhombohedral, tetrahedral, etc.) to locate the lowest energy bare Cu₄⁺ cluster. Cluster geometries with different metal cluster cores and different CO₂ and H₂ binding motifs (i.e., intact and dissociated H₂ and CO₂, CO₂ bound with its oxygen or in di-σ binding mode) were systematically generated using our in-house code. This code, successfully used in other combined experimental and theoretical work on activation reactions involving metal clusters,^55–58 systematically generates the initial cluster-adsorbate structures in different binding modes (see the ESI,† for the details). A publication detailing and benchmarking this software is forthcoming. The structures generated were optimized at the TPSSh/def2-TZVP + D3 level of theory.⁵⁹ All calculations were done at the lowest spin multiplicity, i.e., doublet for even and singlet for odd numbers of Cu atoms. The effect of the level of correlation for Cu₄⁺ with CO₂ or H₂ adducts is compared to CCSD(T)/def2-QZVPPD benchmarks, while the finite basis size in DFT computations and relativistic effects were estimated using relativistic full-potential linearized augmented wave computations (see the ESI† for the details). We explored the reaction mechanisms between stable intermediates. Harmonic vibrational frequencies of the structures were computed for comparison with the experimental spectra, and to confirm that all minima and transition structures have zero or one imaginary vibrational frequency, respectively. The stability of the Self Consistent Field solution was confirmed. Intrinsic Reaction Coordinates were computed starting from the transition structures. To compare experimental spectra to calculated spectra, the harmonic frequencies were scaled by a factor 0.968 to correct for anharmonicity of the vibrational potential and inaccuracies of the employed level of theory. This factor was determined by fitting experimental band positions of [Cu₅, H₂]⁺,⁵⁰ to calculated band positions of the assigned isomer at the current level of theory (see Fig. S4 in the ESI†). The scaled harmonic stick spectra were then convoluted with a 20 cm⁻¹ full-width at half-maximum Gaussian line shape function. Enthalpies and Gibbs-free energies were computed at 298 K and 1 atm using the rigid rotor harmonic oscillator approximation and treating all internal degrees of freedoms as vibrations, i.e., not considering hindered internal rotors. They are compiled in Table S1 in the ESI.†

Results and discussion

CO₂ adsorption onto Cu_n⁺ clusters

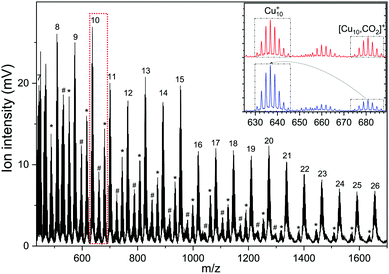
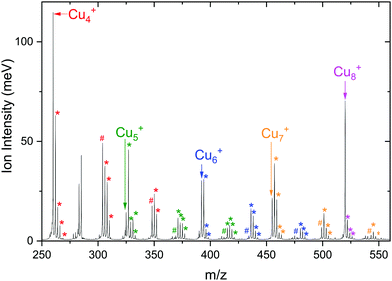
A typical mass spectrum resulting from the reaction of cationic copper clusters Cu_n⁺ (n = 7–25) with CO₂ is shown in Fig. 1. We have found that production of Cu_n⁺ (n = 1–4) in the presence of only a helium carrier gas yields significant signals for n ≤ 4; the production of larger Cu_n⁺ clusters is facilitated by admixing a few % of Ar into the helium carrier gas. Since Ar readily binds to Cu_n⁺ clusters, and especially so for the smaller clusters where the total charge is distributed over only a few atoms as was shown in our previous work,^50,60 a competition between complexation of Cu_n⁺ with Ar and CO₂ results in a rather complex mass spectrum, with substantial mass overlap for the smaller cluster sizes. This overlap prevents us from completely disentangling depletion and growth for n < 7. In the mass spectrum shown, we observe that Cu_n⁺ with 7 < n < 19 binds up to two CO₂ with appreciable efficiency, and only one for n > 19. For the whole mass range, we observe no significant binding of Cu_n⁺ with Ar, indicating that binding of CO₂ is preferred here and that the binding energy thus likely exceeds the 0.2 eV found for Ar.⁶⁰ The inset shows two mass spectra zoomed into the region of the Cu₁₀⁺ cluster, where the isotopic distributions of Cu₁₀⁺, [Cu₉, 2CO₂]⁺, and [Cu₁₀, CO₂]⁺ are visible. Upon resonant IR irradiation at a frequency of 657 cm⁻¹, the distribution without IR light (top trace) changes such that the intensity of the [Cu₁₀, CO₂]⁺ distribution reduces, coinciding with an increase of the Cu₁₀⁺ bare cluster distribution, as indicated with boxes and arrows in the bottom trace. This is indicative of photoinduced loss of CO₂via the reaction [Cu₁₀, CO₂]⁺+ k·hν → Cu₁₀⁺, with k an unknown number of IR photons.

Fig. 1 Time-of-flight mass spectrum of the [Cu_n, mCO₂]⁺ (n = 7–25, m = 0–2) complexes. Bare copper clusters are indicated by their number of constituent atoms n, complexes with m = 1 by a hash tag (#), with m = 2 with an asterisk (*). The inset shows a zoom-in displaying the isotopic distribution for Cu₁₀⁺, [Cu₉, 2CO₂]⁺, and [Cu₁₀,CO₂]⁺, with IR light at 657 cm⁻¹ (red trace) and without (blue trace), respectively.

In Fig. 2 the IRMPD spectra for [Cu_n, CO₂]⁺ (n = 7–25) are displayed. Whereas the adsorption of CO₂ onto extended surfaces was shown either to lead to chemisorption or carbonate formation, depending on the surface morphology,⁶¹ clusters provide often very diverse structural motifs, and it can therefore a priori not be predicted whether the binding motif of CO₂ will be similar for each cluster size. However, inspection of the spectra for different size n tells there are no significant differences. Although the signal-to-noise ratio gradually decreases with cluster size (a result of the decrease in production efficiency), it is evident that all spectra are very similar. We therefore discuss the spectrum of one cluster size in detail as a representative example for the other sizes. Cu₁₀⁺ is chosen because a) the Cu₁₀⁺ geometry is already known from our previous work on the spectroscopy of Cu_n⁺·Ar clusters,⁶² and b) since a direct comparison between the spectrum of Cu₁₀⁺·Ar and [Cu₁₀, CO₂]⁺ may allow to determine whether the adsorption of CO₂ – be it dissociative adsorption, molecular chemisorption or physisorption – affects the structure of the cluster itself.

Fig. 2 Experimental IRMPD spectra of [Cu_n,CO₂]⁺ (n = 7–25) in the 400–1500 cm⁻¹ spectral range (the line a five-point adjacent-average). Dashed vertical lines are shown as guide to the eye.

Fig. 3 shows the IRMPD spectrum of [Cu₁₀, CO₂]⁺ in the 120–1600 cm⁻¹ spectral range (panel A) together with the IR photodissociation spectrum of Cu₁₀⁺·Ar.⁶² Additionally, calculated spectra for two possible geometries, one with molecularly adsorbed CO₂ (panel C) and one where one of the C=O bonds has been ruptured, and the eliminated O is separately adsorbed (panel D). The spectrum for [Cu₁₀, CO₂]⁺ exhibits seven clear bands with maxima at 134, 175, 231, 650, 1185, 1274, and 1378 cm⁻¹, respectively, with a typical FWHM of 15–30 cm⁻¹, with the exception of the band at 231 cm⁻¹, for which the FWHM is about 50 cm⁻¹. We attribute the oscillations in the spectrum above 1500 cm⁻¹ to background noise that is amplified by normalization of the yield on the reduced IR laser pulse energies in this spectral area.

Fig. 3 Experimental IRMPD spectra of [Cu₁₀,CO₂]⁺, [Cu₄,CO₂]⁺ (panels A/E, solid dots, the line a five-point adjacent-average) and Cu₁₀⁺–Ar (panel B, in the metal–metal vibration range only). Panels C and D show the calculated vibrational spectra (red line) for two low-energy structures for complexes of Cu₁₀⁺ with molecularly (panel C) and dissociatively absorbed (D) CO₂, respectively. Panel F represents the calculated spectrum for [Cu₄,CO₂]⁺ with molecularly absorbed CO₂. The green bar in panels C, D and F represents half the frequency of the CO₂ asymmetric stretch vibration with the IR intensity divided by 100. The structures responsible for these spectra are shown with their relative energies of formation. The vibrational modes of free CO₂ are indicated by vertical marks and their conventional mode labeling.

The typical vibrational modes of the Cu₁₀⁺ cluster are in the 120–350 cm⁻¹ region. Therefore, the first three bands (134, 175, and 231 cm⁻¹) can readily be attributed to vibrations of the Cu₁₀⁺ cluster. Comparison with the spectrum of Cu₁₀⁺-Ar in Fig. 3B shows that the main bands are at the same line positions. The bands for [Cu₁₀, CO₂]⁺ are, however, significantly broader since the average FWHM of Cu₁₀⁺–Ar is 11 cm⁻¹.⁶² This band broadening could be caused by the higher binding energy of CO₂ compared to that of Ar, but also by the larger pulse energies employed here. Nevertheless, the similarity between the spectra of the two complexes in the 120–350 cm⁻¹ range strongly suggests that the cluster structure is not much affected by CO₂ adsorption.

Before considering the current spectrum further, it is useful to discuss the vibrational structure of free CO₂ in the gas phase. Free CO₂ has three fundamental modes: the symmetric and anti-symmetric stretch vibrations ν₁ and ν₃, and the bending vibration ν₂. Due to the symmetry of CO₂, only ν₂ and ν₃ are IR-active, and they have been experimentally observed at 667 cm⁻¹, and 2349 cm⁻¹, respectively.⁶³ The symmetric stretch is symmetry–forbidden in IR, but not in Raman spectroscopy. Here, not one but two bands are found, at 1388 cm⁻¹ and 1285 cm⁻¹, respectively. These bands are due to a Fermi resonance between ν₁ and 2ν₂.⁶³

A rapid look at the experimental spectrum already indicates that the band at 650 cm⁻¹ likely corresponds to the bending vibration of free CO₂ (667 cm⁻¹). Further, the series of three bands at 1185, 1274 and 1378 cm⁻¹ are all in the region where the IR-forbidden symmetric vibrations are expected, which become IR active due to the cluster breaking the symmetry. However, for intact CO₂ only two bands are expected, namely the two characteristic bands of the Fermi dyad. It is most likely that this dyad corresponds to the bands observed at 1274 and 1378 cm⁻¹ for [Cu₁₀, CO₂]⁺.

Thus, only the band at 1185 cm⁻¹ remains. This band cannot be a CO₂ fundamental. It is also not an overtone of the bending vibration (667 cm⁻¹ in free CO₂) since this is already part of the Fermi dyad. Another possibility, a combination between the bending mode and a cluster vibration can be ruled out as none of the conceivable combination bands would have a frequency exceeding 1000 cm⁻¹.

To seek a plausible explanation for the 1185 cm⁻¹ band, we turn to DFT calculations. We did not do an extensive structure search, but rather limited ourselves to two possible structures, one with CO₂ attached molecularly, and one where one of the CO bonds has ruptured, leaving a carbonyl and a separate O atom. In both cases, we assumed that the Cu₁₀⁺ structure is the one found in experiments on Cu₁₀⁺–Ar clusters.⁶² We first discuss the physisorbed species, for which the spectrum is shown in Fig. 3C. The binding energy of CO₂ to Cu₁₀⁺ in this species amounts to a mere 0.26 eV, which is only a little more than the Ar binding energy of 0.17 eV.⁶⁰ Its calculated spectrum is dominated by a strong band at 645 cm⁻¹, which is associated with the O=C=O bending motion. The bands at lower frequencies are the cluster vibrations, with little involvement of the CO₂ ligand, or the vibrations involving the CO₂–cluster bond (below 70 cm⁻¹). The final bands are the modes associated with the CO₂ symmetric (1352 cm⁻¹) and anti-symmetric (2406 cm⁻¹) stretching vibrations. Since this is a calculation in the harmonic approximation, a Fermi doublet caused by anharmonic couplings is not reproduced. The symmetric stretching mode at 1352 cm⁻¹ is falling much closer to the higher two of the three bands in the 1100–1400 cm⁻¹ spectral range, confirming that the 1274 and 1378 cm⁻¹ experimental bands are indeed the Fermi dyad. Nevertheless, this species still does not provide a satisfactory explanation for the 1185 cm⁻¹ band. Further trial structures of molecularly absorbed CO₂ on Cu₁₀⁺, all within 0.1 eV from the minimum shown here, have near-identical vibrational frequencies. An alternative structure conceivable is that of a dissociatively adsorbed CO₂ where a separate O atom is bound to several Cu atoms, and a carbonyl CO is bound on an on-top site. While the on-top binding is typical for late transition metal surfaces, it is energetically quite unfavorable with a formation energy of 1.4 eV higher than the physisorption complex, and thus unlikely given its endothermicity. Indeed, the calculated spectrum does not give reason to suspect the species in the experiment is this structure, for instance an intense band at 378 cm⁻¹ is not detected.

Thus, we find little reason to suspect the CO₂ molecule is adsorbed in any other way than the physisorption complex shown in Fig. 3C. What is then the cause of the band at 1185 cm⁻¹? For this, we have to critically evaluate the IR excitation laser and the possible presence of higher harmonics. It is well-known that any free-electron laser contains spontaneously emitted radiation at higher harmonic wavelengths, see e.g.,⁶⁴ and lasing was achieved early on at the third harmonic.⁶⁵ In contrast to odd harmonics, even harmonics have zero gain on the favored on-axis TEM₀₀ optical mode. However, the less favorable TEM₀₁ was demonstrated to have gain, and eventually lasing on the second harmonic was achieved at Jefferson Lab.⁶⁶ Overall, one can thus expect that the second harmonic is present, albeit at substantially reduced intensity when compared to the harmonic. Inspection using a grating spectrometer indeed confirms that there is second harmonic radiation present with an intensity of ∼1% of the fundamental, making the observation of bands of similar oscillator strength as the ones discussed above unlikely. However, the one fundamental band not discussed as it is seemingly out of the spectral range probed, the CO₂ anti-symmetric stretching vibration, has a much higher intensity than, e.g., the bending mode (predicted 1203 and 17.4 km mol⁻¹ for the physisorbed complex shown in Fig. 3C, respectively), and can thus plausibly be observed if the intensity of the second harmonic radiation is no less than three orders of magnitude lower. Thus, we assign the observed band at 1185 cm⁻¹ to the anti-symmetric CO₂ stretching mode, which thus has its band maximum at 2370 cm⁻¹. This is slightly lower than the 2406 cm⁻¹ predicted for the physisorbed Cu₁₀⁺–CO₂ complex, shown at half its frequency and 1/100 its calculated IR intensity by the green trace in Fig. 3C, but still altogether acceptable. Unfortunately, we are unable to verify this assignment experimentally with the FEL fundamental, since this is out of the spectral range covered by FELICE. Nevertheless, we can unambiguously conclude that the Cu₁₀⁺–CO₂ reaction product adopts a physisorption complex. Given the similarity of all spectra shown in Fig. 2, we conclude that the intermediate size cationic Cu_n⁺ clusters all weakly bind CO₂ and no significant activation takes place.

Panel E shows the spectrum recorded for [Cu₄, CO₂]⁺ using pure helium as carrier gas over the 600–1600 cm⁻¹ spectral range. It essentially shows the same four bands as observed for [Cu₁₀, CO₂]⁺. The band at 630 cm⁻¹ is somewhat broader and shows a high-frequency shoulder. The calculated IR spectrum for the Cu₄⁺·CO₂ physisorption complex shows the two CO₂ bending and symmetric stretch vibrations at near-identical frequencies as for Cu₁₀⁺·CO₂ (panel C). In summary, like the larger Cu_n⁺ clusters, CO₂ adsorbs molecularly on Cu₄⁺.

Co-adsorption of H₂ and CO₂ onto Cu_n⁺ clusters

To see whether co-adsorption of H₂ can activate CO₂, we have examined the products formed upon reacting Cu_n⁺ (n = 4–7) with a gas mixture of H₂ and CO₂. In the resulting mass spectrum, presented in Fig. 4, it is evident that apart from masses indicative for binding of the individual CO₂ and H₂ molecules, also co-adsorption complexes [Cu_n, mCO₂, pH₂]⁺, typically with m = 1,2 and p = 1–4, are formed. The ion intensity of the complexes formed upon the adsorption of a single H₂ molecule for n = 4 and 5 is much lower than that of the bare cluster, while for n = 6 and 7 it is the opposite. Complexes with p > 1 are always much lower in intensity than complexes with a single H₂ adsorbed. For the sole adsorption of CO₂, only the product [Cu₄, CO₂]⁺ is significantly higher in intensity than [Cu₄, CO₂, pH₂]⁺. For other complexes, the intensity of just CO₂ adsorbed on the cluster is lower than for the co-adsorption complexes: the intensity of [Cu₇, CO₂]⁺ is about half that of [Cu₇, CO₂, H₂]⁺, while the intensities of [Cu_n, CO₂]⁺n = 5, 6 are almost negligible. The adsorption of a second CO₂ leads to dominance of [Cu_n, 2CO₂, H₂]⁺ for all n. Still, the ratio [Cu₄, 2CO₂]⁺ : [Cu₄, 2CO₂, H₂]⁺ is significantly higher than the equivalent for other n. These patterns suggest that Cu₄⁺ binds H₂ more weakly than Cu_5–7⁺, consistent with our earlier work.⁵⁰

Fig. 4 Mass spectrum of [Cu_n, mCO₂, pH₂]⁺ with n = 4–8, m = 0–2, and p = 0–4 obtained using isotopically enriched ⁶⁵Cu. Masses corresponding to complexes are color-coded according to the color of the bare cluster. The hash tag (#) indicates attachment of CO₂ and the asterisk (*) of H₂.

This is also expressed in the observed photofragmentation: the fragmentation pattern of co-adsorption complexes with Cu₄⁺ suggests the sequential loss of H₂ from [Cu₄, 2CO₂, pH₂]⁺ until [Cu₄, mCO₂]⁺ is formed followed by the sequential loss of CO₂, as illustrated in Scheme 1A. For Cu_n⁺n = 5–7 a different fragmentation pattern was observed (Scheme 1B). The co-adsorption complexes first fragment via sequential loss of H₂ to end as [Cu_n, mCO₂, H₂]⁺. Then, rather than shedding the last H₂, fragmentation continues by sequential CO₂ loss to form [Cu_n, H₂]⁺. The bare cluster can be formed after the fragmentation of [Cu_n, pH₂]⁺ or [Cu_n, mCO₂]⁺. It is important to note that no loss of other fragments than H₂ and CO₂ has been observed. The difference in the fragmentation patterns suggests that the first H₂ binds more strongly to Cu_5–7⁺ than CO₂. In contrast, CO₂ binds more strongly to Cu₄⁺ as also suggested by the intensity distribution of the measured mass channels.

IR spectroscopy of [Cu₄, CO₂, H₂]⁺

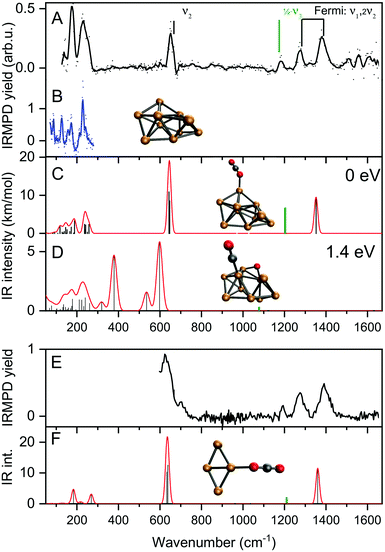
The focus of this work lies on reaction products where one H₂ and one CO₂ molecule are adsorbed on the cluster Cu_n⁺. The obtained experimental spectrum for [Cu₄, CO₂, H₂]⁺ is shown in Fig. 5 (top panel). This spectrum exhibits six bands at 641, 713, 1098, 1184, 1270, and 1391 cm⁻¹. To interpret this spectrum, we compare it to experimental spectra of the cluster reacted with the individual molecules. Simultaneous with recording the spectrum for [Cu₄, CO₂, H₂]⁺, we have obtained a spectrum for [Cu₄, CO₂]⁺. Note that this spectrum is reconstructed using the depletion of all fragments including higher-order complexes with multiple H₂ and CO₂ as illustrated in Scheme 1A. This method was applied in order to account for all possible ingrowth from [Cu₄, mCO₂, pH₂]⁺ into this channel. The [Cu₄, CO₂]⁺ spectrum, shown in Fig. 5B (black trace), shows bands at 644, 1262, 1376, and 1573 cm⁻¹. In green, the spectrum of [Cu₄, CO₂]⁺ from Fig. 3E is reproduced. In that experiment, no higher-order complexes were present and, therefore, this spectrum does not suffer from ingrowth. This spectrum of [Cu₄, CO₂]⁺ obtained during the co-adsorption experiment is fairly similar to that from Fig. 3E, but there are some minor differences. The spectrum in green exhibits two additional low-intensity bands. The band attributed to the CO₂ bending vibration at 644 cm⁻¹ gets a small shoulder at 704 cm⁻¹ and the band at 1186 cm⁻¹ probably originates from the antisymmetric stretch of CO₂ probed with the second harmonic of FELICE. Similar bands were found in the data presented earlier in Fig. 2 for the Cu_n⁺ (n = 7–25). The [Cu₄, CO₂]⁺ spectrum obtained from the co-adsorption experiments also has an additional feature at 1573 cm⁻¹, but we interpret this as an artifact, just like the noisy (and in fact negative) signal just above 1600 cm⁻¹. Therefore, the reference spectrum seems more reliable and we conclude that CO₂ is bound to Cu₄⁺ in end-on configuration, in the same manner as on Cu_n⁺ (n = 7–25). If we compare spectra of the co-adsorbed complex [Cu₄, CO₂, H₂]⁺ and the reference spectrum of [Cu₄, CO₂]⁺ it becomes clear that the bands at 641, 1184, 1270, and 1391 cm⁻¹ in the [Cu₄, CO₂, H₂]⁺ spectrum originate from intact CO₂.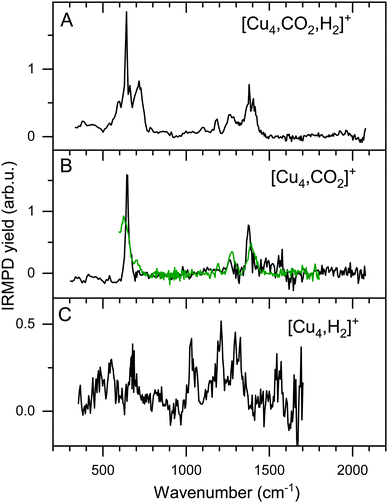

Fig. 5 Experimental IRMPD spectra of [Cu₄, CO₂, H₂]⁺ (A) and [Cu₄, CO₂]⁺ (B, black). Panel B also shows the [Cu₄, CO₂]⁺ reference spectrum from Fig. 3E (green trace), and Panel C that for [Cu₄, H₂]⁺ from ref. 50.

To interpret the remaining bands we turn to the spectrum of [Cu₄, H₂]⁺ we reported earlier,⁵⁰ shown in Fig. 5C. This spectrum exhibits seven bands at 485, 551, 670, 1030, 1200, 1290 and 1555 cm⁻¹. It is of interest to note that the spectrum of [Cu₄, CO₂, H₂]⁺ was recorded with a lower laser power to prevent saturation of the strongest bands (now identified as originating from CO₂ vibrations). Nevertheless, the remaining bands at 713 and 1098 cm⁻¹ in the spectrum of [Cu₄, CO₂, H₂]⁺, and the unresolved structure between 800 and 1050 cm⁻¹, are similar to those observed for [Cu₄, H₂]⁺. The resemblance between the spectrum of [Cu₄, H₂]⁺ and that of the co-adsorption complex suggests that CO₂ is weakly bound to the cluster, while H₂ is molecularly or dissociative adsorbed, as found previously for [Cu₄, H₂]⁺.⁵⁰

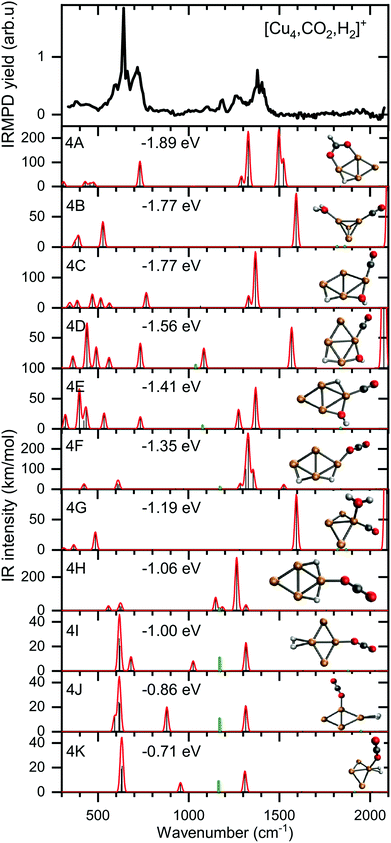
To verify and rationalize this, we compare the experimental spectrum of [Cu₄, CO₂, H₂]⁺ to calculated spectra of different isomers in Fig. 6. In the structure search, it was found that the majority of structures is based on the 2D rhombic geometry of the Cu₄⁺ cluster, which was found to be present in the molecular beam in complexes with Ar and H₂.^50,62 The exception is formed by structure 4B, the second-lowest in energy, and the only one based on a pyramidal cluster structure. Low-energy structures are dominated by isomers where reduction of CO₂ has led to the formation of water or hydroxyl and CO; structure 4A, the lowest energy structure found, has a formate on the cluster. Only the sixth-lowest energy isomer 4F has an intact CO₂. The energy of formation of 4F (−1.35 eV with respect to the reactants Cu₄⁺, H₂, and CO₂) is only 0.5 eV higher than that of 4A, suggesting CO₂ reduction is thermodynamically favored, but not by very much.

Fig. 6 Experimental spectrum of [Cu₄, CO₂, H₂]⁺ (top panel) compared to theoretical spectra of possible isomers. The calculated modes (black sticks) are complemented by a 20 cm⁻¹ Gaussian convolution. The frequencies of calculated modes outside the spectral range probed (above 2100 cm⁻¹) were divided by a factor of two and the intensities multiplied by 1% (green sticks) simulating the measurement with the second harmonic of FELICE. The energy relative to the free reactants of the corresponding structure is also shown.

When comparing the experimental spectrum with theoretical spectra, it is evident that among the lowest energy structures 4B–E and 4G cannot be the dominant species in the molecular beam. The spectra of these structures all exhibit quite strong bands below 600 cm⁻¹ for which no evidence is found in the experimental spectrum. Of the remaining structures, 4A can also be ruled out since it exhibits strong bands above 1500 cm⁻¹, while the highest frequency band on the experimental spectrum is at 1391 cm⁻¹. The experimental band at 641 cm⁻¹ could be assigned to strong bands at 638, 640, or 652 cm⁻¹ from 4I, 4J, or 4K, respectively, or to the low-intensity bands at 634 (4F) and 647 cm⁻¹ (4H). Structure 4J appears to be ruled out due to a strong band predicted at 910 cm⁻¹, for which no experimental evidence is found. The band at 1391 cm⁻¹ could be due to bands for 4F, 4H, 4I, and 4K (1372, 1307, 1361, and 1351 cm⁻¹). A word of caution is in place here: these calculations are all done in the harmonic approximation, and inherently do not reproduce the CO₂ Fermi resonance, which is likely still present for isomers 4F, 4H, 4I, and 4K, and it could thus also be seen back in the bump at 1270 cm⁻¹. The experimental sideband of the strong 641 cm⁻¹ resonance, centered at 713 cm⁻¹, appears most plausibly assigned to 4I's band predicted at 703 cm⁻¹. The 4I band at 1059 cm⁻¹ could cause the experimental band at 1098 cm⁻¹. We cannot rule out 4K despite its band at 986 cm⁻¹, which could simply be too weak to detect. The experimental band at 1186 cm⁻¹ could potentially originate from a FELICE second harmonic probing of the antisymmetric stretch of CO₂ in isomers 4I and 4K, predicted at 2418 and 2404 cm⁻¹, respectively.

All structures that could be responsible for the spectrum are formed by the reaction of rhombic Cu₄⁺, which was found to be the most stable isomer,⁶² with CO₂ and H₂. In all cases, CO₂ is bound to the cluster in a linear end-on configuration, as was seen earlier for bare Cu_n⁺ clusters. The H₂ is either molecularly bound to the obtuse apex of the cluster with CO₂ bound to the same (structure 4K) or opposite Cu atom (4I), or dissociated on the obtuse apex and bound in-plane on bridge sites with CO₂ bound to the acute apex for 4F. All these configurations of H₂ are consistent with the previous work.⁵⁰ The presence of structure 4H is difficult to rule out or confirm: its principal bands are all consistent with the structure above 1000 cm⁻¹ in the experimental spectrum.

Potential energy surface for the adsorption and activation reaction of CO₂ and H₂ on Cu₄⁺ clusters

To understand how the co-adsorption of CO₂ and H₂ proceeds and which products can be formed, the potential energy surface (PES) for this reaction is calculated and presented in Fig. 7, with the energies, ZPE corrected energies, enthalpies and Gibbs free energies in Table S1 (ESI†). The inclusion of the ZPE and the thermal effects in enthalpies play a relatively small role, while the entropy part is more important, especially when both CO₂ and H₂ are added to the cluster and the reactions progress. All structures included in the PES are numbered, the structures used for assignment of the [Cu₄, CO₂, H₂]⁺ IRMPD spectrum in Fig. 6 are also labeled with the corresponding letters.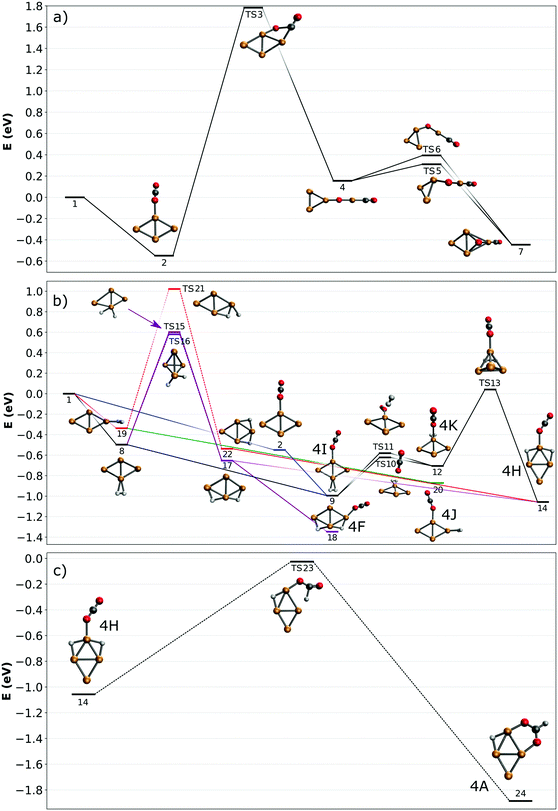

Fig. 7 Potential energy surfaces describing adsorption reactions on Cu₄⁺. (a) CO₂ adsorption and dissociation; (b) co-adsorption of H₂ and CO₂ (color codes are used to identify different pathways in the text; dashed lines denote simplified pathways for which full path are shown in the ESI†); (c) CO₂ reduction to formate. All energies are given with respect to the reactants.

First, the adsorption and dissociation of CO₂ over the bare cluster are evaluated in Fig. 7A. The entrance complex (2) is formed by linear CO₂ adsorbed on the obtuse apex of rhombic Cu₄⁺, with a CO₂ binding energy of 0.54 eV. Adsorption on the acute apex (not shown) is only 0.08 eV higher in energy. Of all structures found, the entrance complex is thermodynamically the most favorable, followed by one (7, +0.09 eV) where CO₂ is dissociated, with CO attached to the acute apex of the still close to rhombic cluster, and the loose O on a hollow site. Although both structures are exothermic with respect to the reactants, for CO₂ to dissociate it has to overcome a barrier at +1.79 eV associated with transition state (TS3). The dissociation pathway involves a rearrangement of the cluster to allow the CO₂ molecule to bend, leading to the insertion of a Cu atom into the C=O bond in structure (4). This barrier is obviously too high to be overcome, as is experimentally evidenced above.

In Fig. 7B, potential reaction paths for forming the co-adsorption complexes are explored. If the entrance complex (2) reacts with the H₂, a co-adsorption complex 4I, with intact H₂ adsorbed on the opposite obtuse apex of the cluster, can be formed barrierless as indicated by the blue route. This complex is more favorable than (2) by 0.46 eV. 4I can of course also be formed by first adsorbing H₂, and then CO₂ (route indicated in black). Entrance complex 4I can further rearrange to the slightly less favorable (0.29 eV) structure 4K, also an entrance complex, by transfer of either H₂ or CO₂ over the short axis of the cluster so that both molecules are bound on the same obtuse apex. Structure 4K can likely also be directly formed by adsorption of H₂ onto structure (2), but it requires a bending of the CO₂ ligand, which may not be energetically more favourable than the formation from structure 4I, given it is relatively low barriers. The H₂ on 4K can dissociate by crossing transition state (TS13) at 0.74 eV with respect to 4K to form complex 4H. This reaction involves a compression–elongation-type interconversion of the horizontally oriented rhombus into a vertically oriented one, via a tetrahedron in TS13, again showing the cluster's dynamic nature. Although this barrier is the highest in this reaction path, it is only 0.04 eV higher than the energy of the reactants and might be overcome at room temperature. 4H has two H atoms on bridging sites, sharing the acute apex, with CO₂ in end-on configuration in-between. This configuration is thermodynamically more favorable than 4I by 0.07 eV. There is an alternative pathway to form 4H, but it requires H₂ dissociation before CO₂ adsorption. In the current calculations, the barrier towards dissociation is at least 0.58 eV above the energy of the reactants, making it difficult to see this as a viable pathway. However, this barrier was at the PBE/QZV4P level calculated to be only 0.15 eV, making the reaction much more plausible. In fact, structure (22) was one of the assigned species for the spectrum of H₂ adsorbed onto Cu₄⁺.⁵⁰ To investigate this somewhat better, we benchmarked this barrier for the two functionals PBE, TPSSh with various (larger) basis sets and with CCSD(T) (ESI†). We find that the level of correlation and relativistic effects each lead to an error of ∼0.2 eV in the computed relative energies, and that the barrier height is very sensitive to the structures. Given the earlier assignment of (22) to a H₂ adsorption product of Cu₄⁺,⁵⁰ we assume that this route is open in the current experiment, too. The adsorption of CO₂ onto structure (22) will directly lead to 4H, that onto structure 17 to 4F, at −1.35 eV the lowest energy structure in this PES.

To summarize: complexes 4H, 4I, 4K, and 4F, which are viable candidate structures for assignment of the experimental bands, can all be formed relatively easily. Each pathway leads to the formation of complexes with linear CO₂ bound in end-on configuration. Structures 4I and K are formed most easily, requiring no H₂ dissociation, whereas formation of structure 4H can proceed via several paths, which often requires the crossing of a relatively high, but not insurmountable, barrier. The energetically most feasible (black) route for 4H also allows the formation of structures 4I and 4K. Of these, the former is the most stable, and appears the most important candidate for assignment. The energetically most favorable structure, 4F, also requires dissociation (purple route).

The co-adsorption complexes discussed above (4F, I–K) could of course also lead to dissociation of CO₂. However, if we assume that the corresponding barrier is similar to the one calculated for CO₂ on bare Cu₄⁺ (Fig. 7A), it can be expected that, even starting from the lowest energy structure 4F, the transition state lies around 1 eV higher than the reactants. Therefore, the energetic gain from the adsorption of H₂ is not enough to overcome this barrier, and dissociation of CO₂ will not be examined further.

In contrast, the barrier for CO₂ reduction to formate, which is energetically also more favorable than CO₂ dissociation, is almost isoenergetic with the reactants, making this route more plausible than dissociation. A reduction pathway starting from 4H is illustrated in Fig. 7C. Here, the CO₂ ligand leans over to one of the bridging H atoms, abstracting it to form HCOO (formate), which then rotates along the Cu–O–C bond to bind via the second O atom in a η² bidentate configuration to Cu₄⁺. An additional minimum and transition state were located on the potential energy surface (see Fig. S11 in the ESI†), however the minimum is shallow and thus expected to play a negligible role in the reaction. Since many routes in Fig. 7B lead to the formation of 4H, it acts as a ‘gateway’ structure for the formation of formate. Although we can rule out CO₂ reduction as the dominant pathway in the current experiments, the pathway calculated suggests it is not entirely out of reach. While the decreased entropy of the formate adduct compared to the free reactants has certainly an adverse effect, its Gibbs-free energy is still negative (see Table S1 in the ESI†), so its formation is thermodynamically allowed at 298 K. Thus, we can speculate that its formation under thermalized conditions in an ion trap only requires moderate temperatures. Because several computational studies of CO₂ hydrogenation to methanol over Cu clusters suggest that the methanol formation proceeds via formate,^11,48,49 this opens up the possibility to complete a full catalytic cycle over Cu₄⁺.

IR spectroscopy of [Cu_n, CO₂,H₂]⁺ (n = 5–7)

The experimental spectra for the co-adsorption of CO₂ and H₂ onto Cu_n⁺ (n = 5–7) are presented in Fig. 8 (top panels), together with spectra for the individual adsorption of CO₂ (middle) and H₂ (bottom). The depletion yield spectrum of [Cu₅, CO₂]⁺ has been reconstructed from the same measurement, but in contrast to the spectrum for [Cu₄, CO₂]⁺, here only the signals of [Cu₅, mC, 2mO]⁺ (m = 1,2) have been used, since complexes with H₂ do not fragment into these mass channels (see Scheme 1B).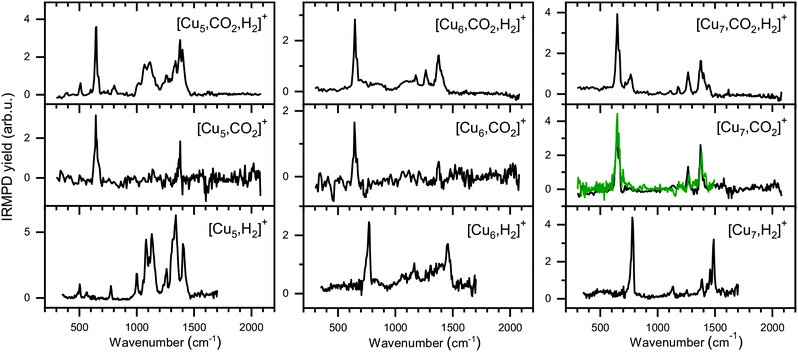

Fig. 8 Experimental spectra of [Cu_n, CO₂, H₂]⁺, [Cu_n, CO₂]⁺, and [Cu_n, H₂]⁺ for n = 5–7 presented in a similar manner as for the Cu₄⁺ complexes in Fig. 6. The green trace on the [Cu₇, CO₂]⁺ spectrum is the reference spectrum from Fig. 3 obtained during individual CO₂ adsorption experiments.

The spectrum of [Cu₅, CO₂, H₂]⁺ shows ten bands at 511, 646, 802, 1008, 1068, 1118, 1260, 1335, 1384 and 1640 cm⁻¹, where bands between 950 and 1500 cm⁻¹ strongly overlap. Bands at 646 cm⁻¹, 1260 and 1335 cm⁻¹ can safely be assigned to the CO₂ bending vibration and the Fermi dyad, even though the spectrum of [Cu₅, CO₂]⁺ only shows one of the Fermi dyad bands, with the second probably hidden in the relatively high noise level. The other bands are lower in intensity, but their overlap with the bands measured for [Cu₅, H₂]⁺ is recognizable: bands at 503, 775, 1002, 1081, 1135, 1260, and 1330 cm⁻¹ for [Cu₅, H₂]⁺ appear to correspond to bands at 511, 802, 1008, 1068, 1118, and 1335 cm⁻¹ in the spectrum of the co-adsorption product; other bands visible in the [Cu₅, H₂]⁺ spectrum are likely hidden in the shoulders of the strong CO₂ bands. Interestingly, a new potential band is observed for the co-adsorption product around 1640 cm⁻¹. This band is absent in the experimental spectra of the individual complexes or in the calculated spectra of complexes with H₂. This might be indicative of a reaction between CO₂ and H₂ on the cluster surface, but we are unable to assign this band without calculated structures. Nevertheless, based on a comparison between experimental spectra alone, it is clear that the spectrum is dominated by the vibrations of both molecularly and dissociatively chemisorbed H₂ together with CO₂ adsorbed in the end-on configuration as it is found for Cu₄⁺.

The case for Cu₆⁺ is not much different. The experimental spectrum of [Cu₆, CO₂, H₂]⁺ (Fig. 8, middle) exhibits seven bands at 647, 720, 860, 1086, 1175, 1264 and 1377 cm⁻¹. Bands in the region between 700 and 1150 cm⁻¹ are rather broad and, therefore, not so well defined. The quality of the spectrum of [Cu₆, CO₂]⁺ is not the greatest, but it also shows two bands at 646 and 1377 cm⁻¹. Therefore, we interpret the bands at 647, 1264, and 1377 cm⁻¹ in the [Cu₆, CO₂, H₂]⁺ spectrum as vibrations of intact CO₂. The remaining bands in the [Cu₆, CO₂, H₂]⁺ spectrum exhibit a pattern quite similar to the spectrum of [Cu₆, H₂]⁺. The 720 cm⁻¹ band has a rather broad structure (FWHM at least 90 cm⁻¹), and forms a shoulder of the band at 647 cm⁻¹ and its origin could be similar to the band observed for [Cu₆, H₂]⁺ at 770 cm⁻¹. The weak band around 860 cm⁻¹ observed for [Cu₆, CO₂, H₂]⁺ can probably be linked to a shoulder of the 770 cm⁻¹ bands in the [Cu₆, H₂]⁺ spectrum which peaks around 830 cm⁻¹. Bands at 1067 and 1166 cm⁻¹ in the [Cu₆, H₂]⁺ spectrum could correspond to the bands at 1086 and 1175 cm⁻¹ on the [Cu₆, CO₂, H₂]⁺ spectrum, respectively, while bands at 1306 and 1392 cm⁻¹ for [Cu₆, H₂]⁺ could be hidden in the elevated baseline of overlapping bands. The exception is formed by the band at 1453 cm⁻¹ in [Cu₆, H₂]⁺ spectrum, which is absent in the co-adsorption spectrum or shifted by more than 50 cm⁻¹ forming the shoulder of an asymmetric band at 1377 cm⁻¹. The origin of this band in the [Cu₆, H₂]⁺ spectrum is still unclear, and even after an extensive search no structure was found that could explain it.⁵⁰ Nevertheless, we conclude that Cu₆⁺ binds CO₂ in end-on configuration with H₂ co-adsorbed.

Finally, the spectrum for [Cu₇, CO₂, H₂]⁺ is compared to its counterparts in Fig. 8 (right panels). The spectrum of the co-adsorption product is better resolved than those for [Cu_n, CO₂, H₂]⁺ (n = 4–6), showing bands at 646, 766, 1117, 1182, 1264 and 1377 cm⁻¹. The band at 1377 cm⁻¹ has shoulders peaking at 1402 and 1444 cm⁻¹. The spectrum for [Cu₇, CO₂]⁺ is in good agreement with the spectrum presented in Fig. 2, reproduced as a green trace in Fig. 8, and shows bands that are probably the same as the band 646, 1264 and 1377 cm⁻¹ observed for [Cu₇, CO₂, H₂]⁺. The strongest band for [Cu₇, H₂]⁺ at 784 cm⁻¹, can be linked to the 766 cm⁻¹ band for [Cu₇, CO₂, H₂]⁺, slightly shifted but still clearly visible. The same is valid for the 1135 and 1488 cm⁻¹ bands of [Cu₇, H₂]⁺, which correspond to a band at 1117 cm⁻¹ and a shoulder of the 1377 cm⁻¹ band for [Cu₇, CO₂, H₂]⁺. The [Cu₇, H₂]⁺ bands at 1255 and 1386 cm⁻¹ lie fairly close to the Fermi dyad of CO₂ and therefore probably overlap. The only unexplained low-intensity bands in the [Cu₇, CO₂, H₂]⁺ spectrum are found at 1182 and potentially at 1622 cm⁻¹. We speculate that the band at 1182 cm⁻¹ is caused by the antisymmetric stretch of CO₂ excited by the second harmonic of FELICE (found at 1185 cm⁻¹ in Fig. 3). We have no clear explanation for the 1622 cm⁻¹ band, but due to its weakness, we do not regard this as crucial. We conclude again that CO₂ binds only weakly to Cu_n⁺ clusters (n = 4–7), even when H₂ is co-adsorbed.

Conclusion

We have recorded experimental IRMPD spectra for the products resulting from reacting Cu_n⁺ (n = 4–7) clusters with CO₂, and with CO₂ and H₂ simultaneously. The spectra of the clusters with only CO₂ adsorbed are indicative for simple physisorption of the CO₂ molecule in an end-on configuration, leaving the CO₂ fundamental vibrations largely unchanged. This is in agreement with DFT calculations, which predict the activation of CO₂ by cationic clusters is hindered by a barrier of at least 2.33 eV relative to the energies of the reactants. This inactivity of Cu_n⁺ cations towards CO₂ is also consistent with previous calculations, suggesting that CO₂ only gets activated by a significant amount of charge transfer that goes hand in hand with stronger bonding.

When both H₂ and CO₂ co-adsorb onto the clusters, CO₂ activation is not achieved either. No size-dependent effects have been observed in the binding of CO₂ to either bare and H₂ preloaded clusters. On the other hand, co-adsorption of CO₂ does not affect the cluster size dependence of H₂ adsorption as identified in ref. 50. DFT calculations of the reaction pathway for CO₂ reduction over Cu₄⁺ in which dissociative adsorption of H₂ leads to H(a) being formed that could react with CO₂ after migration from its absorption site on the cluster, thereby following a Langmuir–Hinshelwood type mechanism. The transition states along this reaction path are only slightly higher than the energy of the reactants, but the barriers might be in the order of 1 eV. This suggests that, although CO₂ reduction under the current experimental conditions may not be feasible or dominant, it could be observed at only slightly higher temperatures and longer reaction times that can be provided by an ion trap. If such experiments would be successful, a study of the efficiency of CO₂ reduction on more complex cluster materials could provide an understanding of e.g., the promotor materials in the real catalyst.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge financial support from the Nether-lands Organization for Scientific Research (NWO) under grant no. 739.017.008 (Mat4Sus), and the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 955650. We also gratefully acknowledge NWO for the support of the FELIX Laboratory and CPU time at the Dutch National Supercomputer Cartesius (project number EINF-216). TH and MSz thank Prof. László Nyulászi for fruitful discussions.

Notes and references

1. H. Arakawa, et al. , Chem. Rev., 2001, 101, 953–996.
2. S. Xie, Q. Zhang, G. Liu and Y. Wang, Chem. Commun., 2016, 52, 35–59.
3. K. C. Waugh, Catal. Today, 1992, 15, 51–75.
4. M. Behrens, et al. , Science, 2012, 759, 893–898.
5. J. Zhong, X. Yang, Z. Wu, B. Liang, Y. Huang and T. Zhang, Chem. Soc. Rev., 2020, 49, 1385–1413.
6. P. Liu, Y. Yang and M. G. White, Surf. Sci. Rep., 2013, 68, 233–272.
7. H. Schwarz, Coord. Chem. Rev., 2017, 334, 112–123.
8. A. M. Appel, et al. , Chem. Rev., 2013, 113, 6621–6658.
9. R. Burch, S. E. Golunski and M. S. Spencer, Catal. Lett., 1990, 5, 55–60.
10. J. Yoshihara and C. T. Campbell, J. Catal., 1996, 161, 776–782.
11. T. Kakumoto, Energy Convers. Manage., 1995, 36, 661–664.
12. L. C. Grabow and M. Mavrikakis, ACS Catal., 2011, 1, 365–384.
13. H.-J. Freund and M. W. Roberts, Surf. Sci. Rep., 1996, 25, 225–273.
14. W. Taifan, J.-F. Boily and J. Baltrusaitis, Surf. Sci. Rep., 2016, 71, 595–671.
15. U. Burghaus, Prog. Surf. Sci., 2014, 89, 161–217.
16. L. E. Y. Nonneman and V. Ponec, Catal. Lett., 1990, 7, 213–217.
17. S. S. Fu and G. A. Somorjai, Surf. Sci., 1992, 262, 68–76.
18. O. Klaja, J. Szczygieł, J. Trawczyński and B. M. Szyja, Theor. Chem. Acc., 2017, 136.
19. J. Szanyi and D. W. Goodman, Catal. Lett., 1991, 10, 383–390.
20. Y. Okamoto, K. Fukino, T. Imanaka and S. Teranishi, J. Phys. Chem., 1983, 87, 3740–3747.
21. Y. Okamoto, K. Fukino, T. Imanaka and S. Teranishi, J. Phys. Chem., 1983, 87, 3747–3754.
22. J. Szanyi and D. W. Goodman, Catal. Lett., 1991, 10, 383–390.
23. J. Nakamura, I. Nakamura, T. Uchijima, Y. Kanai, T. Watanabe, M. Saito and T. Fujitani, Catal. Lett., 1995, 31, 325–331.
24. T. Fujitani, M. Saito, Y. Kanai, M. Takeuchi, K. Moriya, T. Watanabe, M. Kawai and T. Kakumoto, Chem. Lett., 1993, 1079–1080.
25. C. Liu, et al. , J. Am. Chem. Soc., 2015, 137, 8676–8679.
26. B. Yang, et al. , J. Phys. Chem. C, 2017, 121, 10406–10412.
27. A. A. B. Padama, J. D. Ocon, H. Nakanishi and H. Kasai, J. Phys.: Condens. Matter, 2019, 31, 415201.
28. N. T. Thu, Ha, V. T. Minh Hue, B. C. Trinh, N. N. Ha and L. M. Cam, J. Chem., 2019, 2019, 1–10.
29. D. E. Clemmer, M. E. Weber and P. B. Armentrout, J. Phys. Chem., 1992, 96, 10888–10893.
30. F. Meyer, Y. M. Chen and P. B. Armentrout, J. Am. Chem. Soc., 1995, 117, 4071–4081.
31. M. R. Sievers and P. B. Armentrout, J. Chem. Phys., 1995, 102, 754–762.
32. M. R. Sievers and P. B. Armentrout, J. Phys. Chem. A, 1998, 102, 10754–10762.
33. M. R. Sievers and P. B. Armentrout, Inorg. Chem., 1999, 38, 397–402.
34. J. Herman, J. D. Foutch and G. E. Davico, J. Phys. Chem. A, 2007, 111, 2461–2468.
35. G. K. Koyanagi and D. K. Bohme, J. Phys. Chem. A, 2006, 110, 1232–1241.
36. P. Cheng, G. K. Koyanagi and D. K. Bohme, J. Phys. Chem. A, 2006, 110, 12832–12838.
37. B. Bandyopadhyay and M. A. Duncan, Chem. Phys. Lett., 2012, 530, 10–15.
38. N. R. Walker, R. S. Walters and M. A. Duncan, J. Chem. Phys., 2004, 120, 10037–10045.
39. A. Iskra, A. S. Gentleman, A. Kartouzian, M. J. Kent, A. P. Sharp and S. R. Mackenzie, J. Phys. Chem. A, 2017, 121, 133–140.
40. N. R. Walker, R. S. Walters, G. A. Grieves and M. A. Duncan, J. Chem. Phys., 2004, 121, 10498–10507.
41. G. Gregoire, N. R. Brinkmann, D. Van Heijnsbergen, H. F. Schaefer and M. A. Duncan, J. Phys. Chem. A, 2003, 107, 218–227.
42. R. S. Walters, N. R. Brinkmann, H. F. Schaefer and M. A. Duncan, J. Phys. Chem. A, 2003, 107, 7396–7405.
43. G. Gregoire and M. A. Duncan, J. Chem. Phys., 2002, 117, 2120–2130.
44. G. Gregoire, J. Velasquez and M. A. Duncan, Chem. Phys. Lett., 2001, 349, 451–457.
45. J. B. Jaeger, T. D. Jaeger, N. R. Brinkmann, H. F. Schaefer and M. A. Duncan, Can. J. Chem., 2004, 82, 934–946.
46. X. P. Xing, G. J. Wang, C. X. Wang and M. F. Zhou, Chin. J. Chem. Phys., 2013, 26, 687–693.
47. Z. Zhao, X. Kong, D. Yang, Q. Yuan, H. Xie, H. Fan, J. Zhao and L. Jiang, J. Phys. Chem. A, 2017, 121, 3220–3226.
48. Z. M. Hu, K. Takahashi and H. Nakatsuji, Surf. Sci., 1999, 442, 90–106.
49. Y. Yang, J. Evans, J. A. Rodriguez, M. G. White and P. Liu, Phys. Chem. Chem. Phys., 2010, 12, 9909.
50. O. V. Lushchikova, H. Tahmasbi, S. Reijmer, R. Platte, J. Meyer and J. M. Bakker, J. Phys. Chem. A, 2021, 125, 2836–2848.
51. J. M. Bakker, et al. , J. Chem. Phys., 2010, 132, 074305.
52. M. Haertelt, V. J. F. Lapoutre, J. M. Bakker, B. Redlich, D. J. Harding, A. Fielicke and G. Meijer, J. Phys. Chem. Lett., 2011, 2, 1720–1724.
53. T. Nagata, K. Koyama, S. Kudoh, K. Miyajima, J. M. Bakker and F. Mafuné, J. Phys. Chem. C, 2017, 121, 27417–27426.
54. Y. Shao, et al. , Mol. Phys., 2015, 113, 184–215.
55. J. Barabás, P. Ferrari, V. Kaydashev, J. Vanbuel, E. Janssens and T. Höltzl, RSC Adv., 2021, 11, 29186–29195.
56. J. Barabás and T. Höltzl, J. Phys. Chem. A, 2016, 120, 8862–8870.
57. J. Barabás, J. Vanbuel, P. Ferrari, E. Janssens and T. Höltzl, Chem. – Eur. J., 2019, 25, 15795–15804.
58. G. Hou, E. Faragó, D. Buzsáki, L. Nyulászi, T. Höltzl and E. Janssens, Angew. Chem., Int. Ed., 2021, 60, 4756–4763.
59. F. Liu, E. Proynov, J.-G. Yu, T. R. Furlani and J. Kong, J. Chem. Phys., 2012, 137, 114104.
60. Z. Jamshidi, O. V. Lushchikova, J. M. Bakker and L. Visscher, J. Phys. Chem. A, 2020, 124, 9004–9010.
61. W. Taifan, J. F. Boily and J. Baltrusaitis, Surf. Sci. Rep., 2016, 71, 595–671.
62. O. V. Lushchikova, D. M. M. Huitema, P. López-Tarifa, L. Visscher, Z. Jamshidi and J. M. Bakker, J. Phys. Chem. Lett., 2019, 10, 2151–2155.
63. T. Shimanouchi, Natl. Bur. Stand., 1972, 1–160.
64. D. J. Bamford and D. A. G. Deacon, Phys. Rev. Lett., 1989, 62, 1106–1109.
65. S. V. Benson and J. M. J. Madey, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 1579–1581.
66. G. R. Neil, S. V. Benson, G. Biallas, J. Gubeli, K. Jordan, S. Myers and M. D. Shinn, Phys. Rev. Lett., 2001, 87, 84801.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp03119h

---