Trajectory surface hopping molecular dynamics simulations for retinal protonated Schiff-base photoisomerization†
Yuxiu
Liu
a and
Chaoyuan
Zhu
 *ab
*ab
aDepartment of Applied Chemistry and Institute of Molecular Science, National Chiao-Tung University, Hsinchu 30010, Taiwan. E-mail: cyzhu@mail.nctu.edu.tw
bDepartment of Applied Chemistry and Center for Emergent Functional Matter Science, National Yang Ming Chiao Tung University, Hsinchu 30010, Taiwan
First published on 4th October 2021
Abstract
Global switching trajectory surface hopping molecular dynamics simulations are performed using accurate on-the-fly (TD)CAM-B3LYP/6-31G potential energy surfaces to study retinal protonated Schiff-base photoisomerization up to S1 excitation. The simulations detected two-layer conical intersection networks: one is at an energy as high as 8 eV and the other is in the energy range around 3–4 eV. Six conical intersections within the low-layer energy region that correspond to active conical intersections under experimental conditions are found via the use of pairwise isomers, within which nonadiabatic molecular dynamics simulations are performed. Eight isomer products are populated with simulated sampling trajectories from which the simulated quantum yield in the gas phase is estimated to be 0.11 (0.08) moving from the all-trans isomer to the 11-cis (11-cis to all-trans) isomer in comparison with an experimental value of 0.09 (0.2) in the solution phase. Each conical intersection is related to one specific twist angle accompanying a related C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond motion during photoisomerization. Nonplanar distortion of the entire dynamic process has a significant role in the formation of the relevant photoisomerization products. The present simulation indicates that all hopping points show well-behaved potential energy surface topology, as calculated via the conventional TDDFT method, at conical intersections between S1 and S0 states. Therefore, the present nonadiabatic dynamics simulations with the TDDFT method are very encouraging for simulating various large systems related to retinal Schiff-base photoisomerization in the real world.
C double bond motion during photoisomerization. Nonplanar distortion of the entire dynamic process has a significant role in the formation of the relevant photoisomerization products. The present simulation indicates that all hopping points show well-behaved potential energy surface topology, as calculated via the conventional TDDFT method, at conical intersections between S1 and S0 states. Therefore, the present nonadiabatic dynamics simulations with the TDDFT method are very encouraging for simulating various large systems related to retinal Schiff-base photoisomerization in the real world.
1. Introduction
The retinal protonated Schiff-base (RPSB) in its all-trans form is found in bacterial rhodopsin, and it is isomerized upon photoexcitation from its native all-trans form to the 13-cis form with an ultrafast speed of 500 fs and a quantum yield of about 0.6–0.7.1–3 In contrast, the analogous photoisomerization process in solution is slow with a speed of about 4 ps and a poor total quantum yield of about 0.1–0.3;2,4,5 it also involves the formation of the isomerized products: the 9-cis form with a quantum yield of 0.02, the 11-cis form with a quantum yield of 0.09, and the 13-cis form with a quantum yield of 0.04. In addition, the 11-cis RPSB chromophore is found in the retinal protein rhodopsin, exhibiting almost barrierless dynamics on the first excited state (S1) potential energy surface (PES),6,7 and the 11-cis form is isomerized to the all-trans form within as little as 200 fs, and the quantum yield is 0.65 via a low-lying S1/S0 conical intersection (CI).8–10 However, in methanol solution, 11-cis RPSB isomerization also takes as long as 4 ps.11–13 Current experimental measurements and theoretical estimations show that the RPSB in protein environments can be isomerized with an ultrafast speed and high quantum yields and, especially for 11-cis RPSB, the protein frame can adjust the ground-state chromophore conformation, resulting in more reactive decay channels.14 It is realized that the surrounding environment of the RPSB can have a significant influence on the photoisomerization processes related to the intrinsic retinal properties. Experimental studies in the gas phase of RPSB isomerization mainly focused on the absorption spectrum15 and action spectroscopy;16,17 in the cases of all-trans and 11-cis RPSB, experiments show that the energy gaps between the S1 and S0 states are about 420–680 nm,16 and the lifetimes of electronically excited states manifest that the decay times are temperature dependent.17 There is a fast decay component with a lifetime of about 650 ± 160 fs geared toward 11-cis RPSB and a slow component with a lifetime of around 4.7 ± 3 ps aimed toward all-trans RPSB. Therefore, all-trans RPSB is inclined to isomerize into the 11-cis form, while the fast photoresponse of the retinal chromophore is straightforwardly related to intrinsic retinal properties.17Theoretical studies have been carried out for calculating the Franck–Condon excitation energies, equilibrium geometries, and photoisomerization reaction pathways in relation to conical intersection (CI) in the gas phase.17–24 Meanwhile, photoisomerization processes that take place on the potential energy surface are mostly related to the ground state S0 and the first excited-state S1, due to the fact that the energy gap between S1 and S2 is very large for RPSB chromophores in the gas phase.18,20 Density functional theory (DFT) can easily be employed to optimize the equilibrium structures in the ground state, while time-dependent (TD)-DFT is utilized for calculating vertical excitation energies. Complete-active-space self-consistent-field (CASSCF) multireference, spin–flip (SF)-DFT, and SF-TD-DFT methods are usually employed to calculate the geometries of CI points and to scan related photoisomerization reaction pathways. High-level theoretical methods, such as CASPT2, NEVPT2, CR-EOM-CCSD(T), and EOM-CCSD, are employed to correct single-point energies via including dynamic electronic correlation for related geometry structures.19,21Via employing these high-level calculations, Kiefer and coworkers17 reported small (30 cm−1) and big (∼300 cm−1) potential barriers during internal conversion processes, starting from the Franck–Condon regions in the S1 state, from the 11-cis and all-trans forms, respectively, consistent with similar high-level calculations performed by Aguilar and coworkers.22 Actually, experiments and calculations have shown isomerization from the all-trans form to the 9-cis, 11-cis, and 13-cis forms, in which the cis isomers of RPSB have almost-barrierless fast 400 fs decay and the all-trans isomer exhibits barrier-controlled slow 3 ps decay.17 Park and Shiozaki23 performed XMS-CASPT2 calculations along the minimum CI energy path (MECI), and they found that the potential barrier from all-trans to 11-cis is lower than from all-trans to 13-cis. Regarding isomerization starting from 11-cis RPSB, however, most studies accepted the viewpoint of a nearly barrierless process on the S1 PES with a sub-picosecond excited-state lifetime.24–26 In contrast, Han and coworkers19 performed SF-DTDFT calculations along the constructed linearly interpolated internal coordinate (LIIC) pathway of MECI and they found that there is a higher potential barrier of about 10 kcal mol−1 starting from the 11-cis form. This large potential energy barrier is not realistic, and large error might arise from spin contamination in the SF-TDDFT method.
Nonadiabatic ab initio dynamics simulation can be performed only using a simplified RPSB model.24,27–31 In this way, Buss and coworkers28 performed trajectory surface hopping dynamics simulations with the TDDFT method, and they found that chromophore distortion severely impacted the results of the photoreaction; in comparison with the reaction rate of the relaxed chromophore, the torsional characteristic dihedral angle increased the rate to some extent. Barbatti and coworkers29 performed trajectory surface hopping dynamics simulations with the CASSCF method, and they found that the bond length alternation, defined as the difference between the averages of single bond and double bond lengths, was obviously altered in the process of excitation, as was the twisted special dihedral angle; this is a significant finding due to the conical intersection within the photoisomerization dynamics. These model studies have claimed that lower photoproduct specificity during 11-cis and all-trans isomerization processes in the gas phase was obtained because isomerization is an intrinsic property of retinal chromophores. Meanwhile, due to the truncated model used, the acquired lower average excited-state lifetime of about 100 fs is inconsistent with experimental results.17
In the present work, we performed global trajectory surface hopping dynamic simulations with conventional TDDFT on-the-fly potential energy surfaces based on a real system (not a model system) of RPSB photoisomerization, including eight different isomers (all-trans, 7_8-cis, 8_11-cis, 9_11-cis, 11-cis, 11_14-cis, 9-cis, and 8-cis forms). We have demonstrated that a method based on a global switching algorithm (without calculating nonadiabatic vectors) plus TDDFT could be successfully applied to ultrafast photoisomerization dynamics simulations of a large dMe-OMe-NAIP system.32 We first identify each conical intersection mainly related to one torsional dihedral angle that connects two photoproducts, and we then construct a conical intersection network, based on which real-system RPSB photoisomerization can be interpreted and analyzed.
2. Computational methods and detailed analysis
A global switching algorithm33 (with simple and accurate Zhu-Nakamura analytical formulas34,35) is employed in cooperation with trajectory surface hopping molecular dynamics simulations associated with TDDFT using on-the-fly potential energy surfaces for real-system RPSB photoisomerization. Potential energy surfaces and their gradients are computed via employing the Gaussian 16 computational package.36 The long-range corrected CAM-B3LYP hybrid functional is an encouraging method to calculate the excited states with a charge-transfer component37 presented by retinal chromophores, and the 6-31G basis set of moderate size is employed.The (TD)CAM-B3LYP/6-31G method (with charge of +1 and multiplicity of 1 for RPSB isomers) was employed for both optimizing the electronic structures of ground and first excited states and performing on-the-fly trajectory surface dynamics simulations. Vibrational frequency calculations are carried out to characterize the minima and saddle points with zero imaginary vibrational frequencies and one imaginary vibrational frequency, respectively. However, the conical intersection zones are found via running a few tens of sampling trajectories using the global-switching trajectory surface hopping method, and in each CI zone, one CI that has a minimum energy gap is identified as a representative conical intersection (the definition of CI used in this section is used throughout the present work).
Under the Born–Oppenheimer approximation, electronic motion is much faster than nuclear motion in molecules and, thus, a molecule with equilibrium geometry that absorbs light energy in the electronic ground state will be vertically excited to an electronic excited state instantaneously. This means that nuclear motion is frozen when the molecule is excited from the ground state to the excited state, and this phenomenon is called the Franck–Condon principle. Theoretically speaking, we prepare initial conditions for the coordinates and velocities of sampling trajectories at the ground-state S0 minimum (this region is called the Franck–Condon region), and then we vertically move these initial conditions to the excited S1 state where the sampling trajectories start running. In order to localize the conical intersections, we preliminarily performed 20 sampling trajectories via dynamic simulations for up to 4000 fs starting from the all-trans Franck–Condon regions in the S1 state with a total initial kinetic energy as high as 14 eV (above the all-trans energy as the energy zero point). All those sampling trajectories increase the potential energy in the S1 state rapidly within a few femtoseconds, and then they oscillate around a potential energy of 8 eV in the S1 state. None of them are able to make hops during the 4000 fs simulation time, and the minimum energy separation is kept much larger than 0.5 eV along all sampling trajectories. Fig. S1 (ESI†) shows that one such resonance trajectory keeps an oscillating structure starting from the all-trans form. Although the total initial kinetic energy of 14 eV is much higher than the potential energy barrier around the Franck–Condon regions in the all-trans form for all sampling trajectories, they still cannot overcome this potential energy barrier to run via conical intersection zones, and we believe that the effective kinetic energy projected from the total kinetic energy in a particular vibration mode is still not high enough to reach a transition state along the trajectory evolution pathway. This is because the total kinetic energy quickly dissipates into all vibrational modes during trajectory evolution. On the other hand, we also performed 20 sampling trajectories via dynamic simulations for up to 1000 fs starting from the 11-cis Franck–Condon regions in the S1 state with a total initial kinetic energy of around 14 eV and we found 6 sampling trajectories making hops at around 8 eV. Fig. S2 (ESI†) shows that one such hopping trajectory makes a hop at 900 fs upon initially starting from the 11-cis form. This confirms that the potential energy barrier in the S1 state is lower in the 11-cis form than in the all-trans form. The sampling trajectories starting from all-trans and 11-cis forms could only detect CI zones around 8 eV that do not correspond to situations seen under experimental conditions. We realized that CI zones might be classified into a high-layer-energy zone at around 8 eV and a low-layer-energy zone at around 3.5 eV. However, the sampling trajectories starting from the Franck–Condon regions of the all-trans and 11-cis forms do not lead to finding the CI in the low-layer-energy zone. We will figure out a new sampling scheme in the following discussion.
We found eight isomers in the ground state via optimization, and these are the all-trans, 7_8-cis, 8_11-cis, 9_11-cis, 11-cis, 11_14-cis, 9-cis, and 8-cis forms, as shown in Table 1 (the corresponding Cartesian coordinates are given in Table S1 (ESI†)). For each ground-state structure, we optimized the corresponding first-excited-state geometry (expect for the 7_8-cis form), as shown in Table 1, with blue colored text relating to the geometries of the dihedral angles of excited states. Fig. 1 shows that seven dihedral angles (five of them, α, β, γ, δ, and ε, are listed in Table 1) are the most important ones relating to specific conical intersections. The global minimum is in the all-trans ground state, which is considered to be the energy zero point. In general, the single-cis isomers are lower in energy than the double-cis isomers; the S0 potential energy values are 0.21 eV, 0.08 eV, and 0.11 eV for the 11-cis, 9-cis, and 8-cis isomers, respectively, in comparison with values of 0.28 eV, 0.24 eV, and 0.41 eV for the 8_11-cis, 9_11-cis, and 11_14-cis isomers, respectively. This conclusion is consistent with results discussed by Bieske and coworkers,38 and it simply indicates that a cisoid conformation results in more steric hindrance effects on the molecular skeleton, especially along polyene conjugated chains, thus increasing the energy systematically. Vertical excitation energies in the S0 state for all isomers calculated via the present CAM-B3LYP/6-31G method agree well with previous M06-2X/cc-pVDZ benchmark calculations,38 as shown in Table 2. Actually, we made calculations using the TD-B3LYP method (not given in Table 2) as well, and we found that the results from TD-CAM-B3LYP are better than those from TD-B3LYP. On the contrary, vertical excitation energy calculations showed that TD-B3LYP is better than TD-CAM-B3LYP in comparison with the experimental results for a dMe-OMe-NAIP system.32 The vertical excitation energies for all isomers are below 3 eV in the visible light range with significant oscillator strengths in the Franck–Condon regions, as shown in Table 1. For the 11-cis isomer, the vertical excitation energy in the present calculations in the gas phase is 2.79 eV in comparison with a maximum absorption of 2.81 eV observed in methanol solution2,39 and 2.49 eV observed in rhodopsin.40 For the all-trans isomer, the vertical excitation energy in the present calculations in the gas phase is 2.57 eV in comparison with a maximum absorption of 2.79 eV observed in methanol solution2,39 and 2.18 eV observed in bacteriorhodopsin.41 The vertical and adiabatic excitation energies in the S1 state for each isomer are very close to each other, and this implies that the optimized S0 and S1 electronic structures for each isomer are very similar to each other in terms of the five important dihedral angles, as shown in Table 1. The calculated results are consistent with results simulated via quantum Monte Carlo (QMC), coupled cluster (CC), and CASPT2 methods where the bond-length pattern of the S0 state is preserved in the S1 state based on a truncated RPSB model.42–46
| Structure | Potential energy | Dihedral angle | ||||||
|---|---|---|---|---|---|---|---|---|
| S0 | S1(VE) | S1(MIN) | α | β | γ | δ | ε | |
| All-trans | 0.00 | 2.57 (1.60) | 2.48 (1.69) | −179.90 | 0.05 | −180.00 | 179.99 | −177.90 |
| 179.75 | 0.01 | 179.36 | 179.85 | −176.11 | ||||
| RS(AT/7_8-cis) | 5.09 | 5.40 | −179.84 | 0.17 | −179.13 | 179.73 | −100.92 | |
| 7_8-cis | 0.25 | 2.82 (0.92) | −179.78 | 0.30 | −178.15 | 179.43 | −13.42 | |
| CI(AT/7_8-cis) | 5.26 | 5.34 | −179.54 | −0.05 | −179.53 | 179.38 | −100.61 | |
| TS(AT/11-cis) | 0.78 | 2.78 | −133.77 | 47.24 | 176.69 | −176.25 | 175.64 | |
| CI(AT/11-cis) | 2.94 | 3.13 | −99.18 | 98.12 | 170.36 | −170.65 | −172.79 | |
| CI(AT/8_11-cis) | 3.92 | 3.94 | −88.74 | 87.70 | 177.52 | 179.77 | −98.62 | |
| RS(AT/8_11-cis) | 3.42 | 3.84 | −88.55 | 91.66 | 177.83 | 179.95 | −98.18 | |
| CI(AT/9_11-cis) | 3.48 | 3.63 | −80.25 | 85.64 | −11.42 | 172.31 | 168.44 | |
| RS(AT/9_11-cis) | 1.81 | 3.83 | −54.04 | 125.93 | −53.92 | 179.96 | −177.68 | |
| 8_11-cis | 0.28 | 2.81 (1.37) | 2.69 (1.41) | −0.78 | 179.67 | 175.74 | 179.92 | −21.59 |
| −8.27 | 173.81 | 177.67 | 176.02 | −9.95 | ||||
| 9_11-cis | 0.24 | 2.78 (1.54) | 2.70 (1.35) | −0.10 | 179.88 | 0.11 | 179.94 | −177.59 |
| 10.35 | −173.46 | 6.80 | −172.39 | −176.28 | ||||
| TS(11-cis/11_14-cis) | 1.20 | 3.33 | −0.09 | 179.96 | 179.97 | 178.90 | −178.23 | |
| 11-cis | 0.21 | 2.79 (1.69) | 2.68 (1.59) | 0.52 | −179.59 | 180.00 | 180.00 | −177.54 |
| −10.75 | 172.85 | 175.27 | 172.29 | −174.59 | ||||
| CI(11-cis/11_14-cis) | 3.96 | 4.09 | 1.97 | −173.95 | −175.72 | 174.95 | 173.30 | |
| 11_14-cis | 0.41 | 2.89 (1.39) | 2.82 (1.35) | 10.45 | −173.52 | −177.03 | −171.66 | −176.22 |
| 13.74 | −170.61 | −174.42 | −168.58 | −178.10 | ||||
| TS(11-cis/9_11-cis) | 1.59 | 2.23 | 17.21 | −164.28 | 92.72 | −178.23 | 175.97 | |
| CI(11-cis/9_11-cis) | 2.74 | 2.78 | 23.55 | −164.21 | 92.75 | 178.97 | 175.37 | |
| CI(AT/9-cis) | 2.94 | 3.10 | 178.61 | 0.49 | −84.38 | −175.70 | −173.32 | |
| 9-cis | 0.08 | 2.61 (1.33) | 2.53 (1.35) | 179.75 | −0.08 | −0.43 | −179.93 | 177.60 |
| 179.97 | 0.06 | −0.17 | 179.88 | 178.10 | ||||
| 8-cis | 0.11 | 2.65 (1.73) | 2.51 (1.73) | 179.79 | −0.26 | −177.69 | −179.66 | 17.21 |
| −179.87 | 0.12 | −178.92 | −179.62 | 5.41 | ||||
| RS(AT/9-cis) | 3.13 | 3.68 | 179.92 | −0.02 | −86.62 | −179.97 | 179.76 | |
In order to localize each conical intersection that might connect two or three photoproducts of RPSB isomers, we first attempted to find transition states that connect two RPSB isomers. The 11-cis, 9-cis, and 8-cis isomers are the main photoisomerization products from the all-trans isomer because of the lower energies calculated in the gas phase along the minimum energy CI (MECI).22,23,48 Meanwhile, the double-cis isomers, including 7_8-cis, 8_11-cis, 9_11-cis, and 11_14-cis, are also important in terms of the photoisomerization products as well.38 We searched each CI zone between every pair of isomers among the 8 isomers, and we neglected all CI zones that have energy as high as 8 eV. This analysis led us to find seven CI zones within the lower energy conditions. We first optimized the transition states for every isomer pair, and then we obtained three transition states (TS(all-trans/11-cis), TS(11-cis/11_14-cis), and TS(11-cis/9_11-cis)) and four rotation states (RS(all-trans/7_8-cis), RS(all-trans/8_11-cis), RS(all-trans/9_11-cis), and RS(all-trans/9-cis)). Then, we carried out frequency calculations for these seven transition states: a transition state that has one imaginary frequency is named TS, while a transition state that has more than one imaginary frequency is named RS. The three transition states and four rotation states are summarized in Table 1, and the corresponding Cartesian coordinates are given in Table S2 (ESI†). The main focus in photoisomerization dynamics is to find conical intersections, so a real transition state (TS) and an approximated transition state (RS) are just intermediate processes equally good for finding CIs in the present study.
Now, we performed global trajectory surface hopping dynamics simulations, initially starting from each transition and rotation state vertically excited to the S1 state, and for each TS or RS we ran a few tens of sampling trajectories and determined the hopping zone from which one representative CI can be specified. We finally found seven conical intersections, namely CI(all-trans/7_8-cis) with (α, μ) = (−179.9°, 91.8°), CI(all-trans/11-cis) with α = −99.2°, CI(all-trans/8_11-cis) with (α, ε) = (−88.7°, −98.6°), CI(all-trans/9_11-cis) with (α, β) = (−80.3°, 85.6°), CI(11-cis/11_14-cis) with (α, θ) = (2°, 104.5°), CI(11-cis/9_11-cis) with (α, γ) = (23.6°, 92.8°), and CI(all-trans/9-cis) with (α, γ) = (178.6°, −84.4°), as shown in Table 1, and the corresponding Cartesian coordinates are given in Table S3 (ESI†). The electronic structures of all seven conical intersections are drawn in Fig. S3 (ESI†). We carried out calculations of the natural transition orbitals at each representative conical intersection, as shown in Fig. S4 (ESI†), and we found that the S0 → S1 electronic transition at each CI is dominantly contributed to by HOMO to LUMO transfer. The HOMO and LUMO charge distributions are mostly concentrated at the side-chain chromophore around the α dihedral angle, with charge transfer to the LUMO around the other dihedral angle for each of the six low-layer-energy CI zones (not including CI(all-trans/7_8-cis) in Fig. S4a (ESI†), which is in the high-energy zone). This confirms again that the six low-layer-energy CI zones correspond to photoisomerization dynamics under experimental conditions.
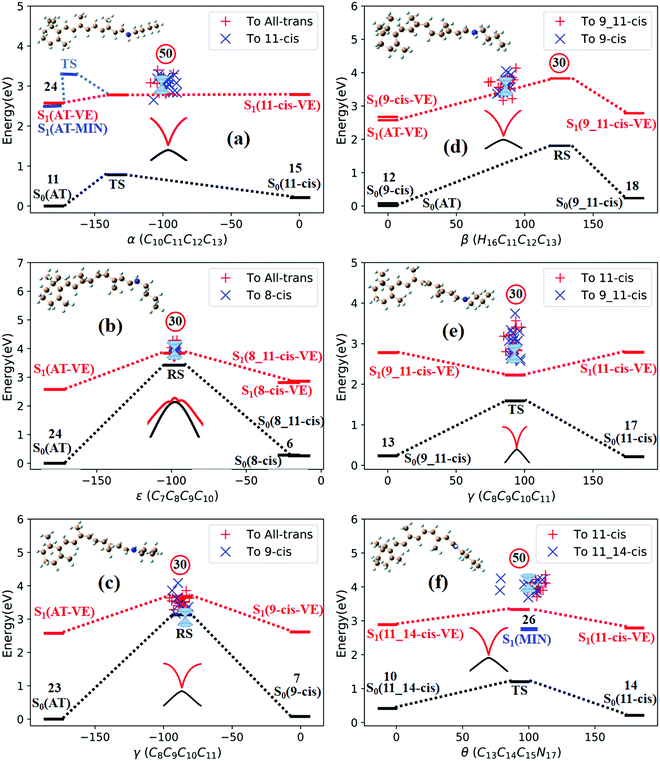
All eight isomers in the ground state, three transition states, four rotation states, and seven conical intersections are summarized in Table 1, ranked from smallest to largest dihedral angle (α = C10C11C12C13). Fig. 2 shows the potential energy profiles of all critical structure points in Table 1 arranged from an α dihedral angle of −180° to +180°. We noticed that six of the conical intersections have a crossing energy of around 3–4 eV, belonging to the low-layer-energy region, but the other one, CI(all-trans/7_8-cis), has an energy of 5.3 eV, belonging to the high-energy region, as the total energy for sampling trajectories is close to 8 eV in this case (this example will not be discussed below since we have already neglected high-layer-energy CIs). All sampling trajectories are performed with a total energy of around 5 eV for the other six CIs.
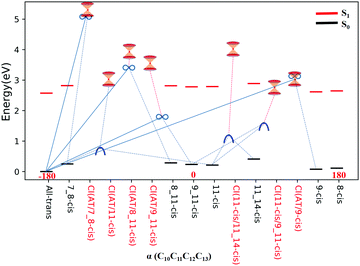 | ||
| Fig. 2 Potential energy profiles for the RPSB isomers given in Table 1, the seven representative CIs, three TSs, and four RSs, and eight S0 minima with respect to the α dihedral angle. The vertical excitation energies at the eight S0 minima are marked with red dashes. The seven double funnels represent CIs. The three blue convex curves represent TSs and the four black ∞ symbols represent RSs. Each TS or RS is linked with the pairwise isomer where it was originally found. | ||
3. Results and discussion
For realistic trajectory surface hopping molecular dynamics simulations of real RPSB systems, the initial conditions for sampling trajectories have to match TS and RS geometries vertically excited to the S1 state (not in the Franck–Condon region), and only in this way can the present simulation reach lower-energy conical intersection zones. The choice of the initial conditions for sampling trajectories in the TS or RS can involve problems relating to the initial velocity direction in the dimension associated with the imaginary frequency direction. We developed a scheme to choose the correct ratio between forward and backward velocity directions along the reaction coordinate (the imaginary frequency direction) via satisfying the correct quantum flux boundary conditions.49 However, we do not use this scheme in the present simulation with these six CIs because we know that effects will get smaller and smaller as the number of dimensions in the system gets larger and larger. In fact, we compared the simulated results for sampling trajectories with and without this scheme in ref. 49, and we found no noticeable differences. Simulated quantum yields can still be meaningful as the potential energy surface topology around the CI basically determines the trajectory bifurcation ratios. However, the lifetime of the dynamics is not able to be estimated. Initial velocities of sampling trajectories are randomly generated via distributing an initial kinetic energy of 2 eV equally to all degrees of freedom at 300 K in the gas phase.47 A total of 220 sampling trajectories, initially starting from three RS and three TS, as shown in Fig. 3, are performed with a time step of 0.5 fs up to the time constant of 1000 fs. After hopping to the S0 state for all sampling trajectories, the products are collected and identified when sampling trajectories involve structures with regular oscillating motion.3.1. Photo isomerization mechanism and quantum yields
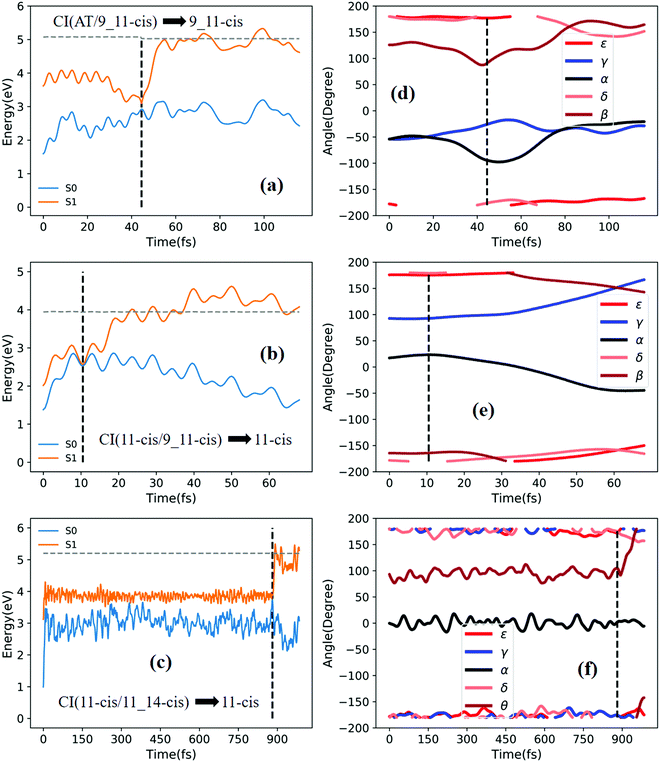
Fig. 3a shows that total 50 sampling trajectories start from TS(all-trans/11-cis) vertically excited to the S1 state, and 26 make hops around CI(all-trans/11-cis) to the S0 state at two dihedral angles α (−100°) and β (92°); the hopping spots are plotted in Fig. 4a. Finally, 15 trajectories end at the 11-cis isomer and 11 end at the all-trans isomer, but 24 trajectories run over a potential energy barrier of 12 kcal mol−1 in the S1 state and are trapped in an all-trans S1 minimum as resonance trajectories. Synchronous twisting clockwise C11-H, anticlockwise C12-H, and C13-CH3 motion can facilitate the generation of the 11-cis product, while the all-trans product is generated via clockwise rotation around C11-H first followed by clockwise rotation around C12-H.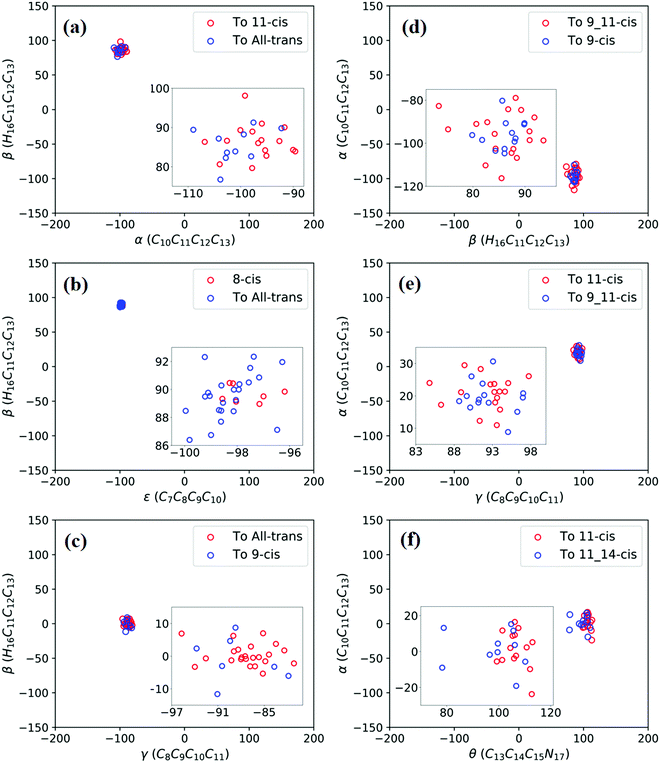 | ||
| Fig. 4 Trajectories of hopping-spot distributions with respect to two characteristic dihedral angles for each CI shown in Fig. 3. Enlarged views of the distributions are also plotted. (a) TS(all-trans/11-cis), (b) RS(all-trans/8_11-cis), (c) RS(all-trans/9-cis), (d) RS(all-trans/9_11-cis), (e) TS(11-cis/9_11-cis), and (f) TS(11-cis/11_14-cis). | ||
Fig. 3b shows that 30 total sampling trajectories start from RS(all-trans/8_11-cis) vertically excited to the S1 state, and all make hops around CI(all-trans/8_11-cis) to the S0 state at two dihedral angles ε (−98°) and β (89°); the hopping spots are plotted in Fig. 4b. Finally, 24 trajectories end in the all-trans isomer and 6 end in the 8-cis isomer (none end at 8_11-cis). Anticlockwise rotation around C10-H followed by the synchronous clockwise twisting motion of C7-H and C8-H can facilitate the generation of the 8-cis product, while the all-trans product is generated by the synchronous anticlockwise twisting motion of C7-H and C8-H.
Fig. 3c shows that a total of 30 sampling trajectories start from RS(all-trans/9-cis) vertically excited to the S1 state, and all make hops around CI(all-trans/9-cis) to the S0 state at two dihedral angles γ (−90°) and β (0°); the hopping spots are plotted in Fig. 4c. Finally, 23 trajectories end in the all-trans isomer and 7 end in the 9-cis isomer. The synchronous twisting clockwise C10-H and anticlockwise C11-H motion can facilitate the generation of both 9-cis and all-trans products.
Fig. 3d shows that a total of 30 sampling trajectories start from RS(all-trans/9_11-cis) vertically excited to the S1 state, and all make hops around CI(all-trans/9_11-cis) to the S0 state at two dihedral angles β (85°) and α (−100°); the hopping spots are plotted in Fig. 4d. Finally, 12 trajectories end in the 9-cis isomer and 18 end in the 9_11-cis isomer (none end in all-trans). The synchronous anticlockwise twisting motion of C10-H, C11-H, C12-H, and C13-CH3 can facilitate the generation of the 9_11-cis product, while the synchronous twisting anticlockwise C10-H and C11-H motion and clockwise C12-H and C13-CH3 motion can facilitate the generation of the 9-cis product.
Fig. 3e shows that a total of 30 sampling trajectories start from TS(11-cis/9_11-cis) vertically excited to the S1 state, and all make hops around CI(11-cis/9_11-cis) to the S0 state at two dihedral angles γ (92°) and α (20°); the hopping spots are plotted in Fig. 4e. Finally, 17 trajectories end in the 11-cis isomer and 13 end in the 9_11-cis isomer. The synchronous clockwise twisting motion of C10-H, C11-H, C12-H, and C13-CH3 can facilitate the generation of the 9_11-cis product, while the synchronous anticlockwise twisting motion of C10-H, C11-H, C12-H, and C13-CH3 can facilitate the generation of the 11-cis product.
Fig. 3f shows that a total of 50 sampling trajectories start from TS(11-cis/11_14-cis) vertically excited to the S1 state, and 24 make hops around CI(11-cis/11_14-cis) to the S0 state at two dihedral angles θ (110°) and α (0°); the hopping spots are plotted in Fig. 4d. Finally, 14 trajectories end in the 11-cis isomer and 10 end in the 11_14-cis isomer, but 26 trajectories are trapped in the S1 minimum at θ = 100° around TS(11-cis/11_14-cis) as resonance trajectories. The synchronous clockwise twisting motion of C15-H and N17-H can facilitate the generation of the 11_14-cis product, while the synchronous anticlockwise twisting motion of C15-H and N17-H can facilitate the generation of the 11-cis product.
The quantum yields of RPSB photoisomerization can be estimated from a way in which the sampling trajectories starting from a TS or RS in Fig. 3 can be considered as initial sampling trajectories starting from either side of a TS or RS. Then, we can collect 140 sampling trajectories starting from the all-trans region (see Fig. 3a–d) and 130 sampling trajectories starting from the 11-cis region (see Fig. 3a, e and f). Therefore, we can estimate a quantum yield of 0.11 from all-trans to 11-cis, which agrees with the measured value of 0.09 in methanol solution2 and a yield of 0.08 from 11-cis to all-trans, which is slightly smaller than the measured value of 0.2 in methanol solution.11 Simulated quantum yields to various isomer photoproducts are also summarized in Table 3. Potential energy surfaces along MECI at each CI are scanned via (TD)-CAM-B3LYP/6-31G with respect to the characteristic dihedral angle for CI(all-trans/11-cis), CI(all-trans/8_11-cis), CI(all-trans/9-cis), CI(all-trans/9_11-cis), CI(11-cis/9_11-cis), and CI(11-cis/11_14-cis). They all show well-behaved potential energy surface topology at conical intersections between the S1 and S0 states, as shown in Fig. S5 (ESI†).
3.2. Typical trajectories in terms of five characteristic dihedral angles
A total of 220 sampling trajectories are initially started from three TSs and three RSs, vertically excited to the S1 state; 170 sampling trajectories hop to the ground S0 state and 50 sampling trajectories are trapped in potential energy wells in the S1 state. We discuss how some typical trajectories propagate on the S0 and S1 potential energy surfaces in terms of changes to five characteristic dihedral angles (α, β, γ, δ, and ε) and reveal some properties of reactive and nonreactive photoisomerization.
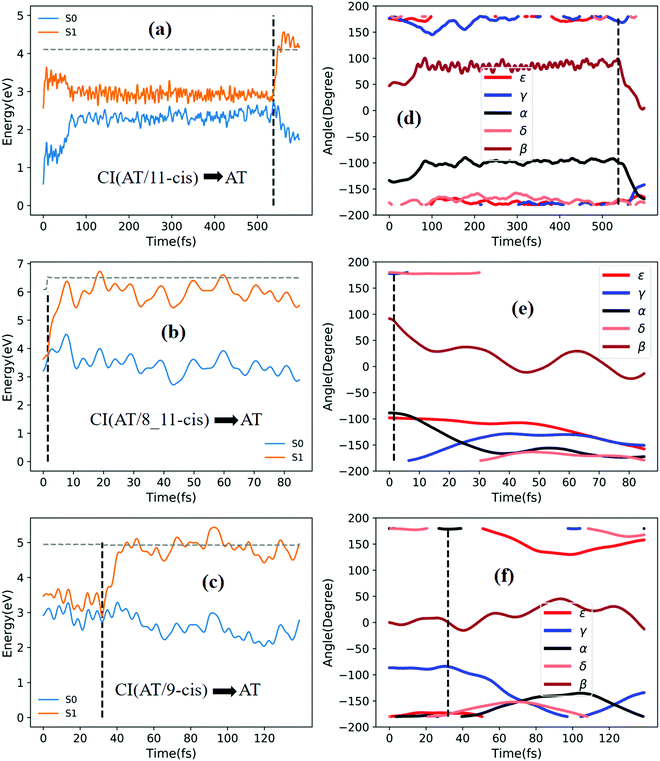
Fig. 5a shows that a typical trajectory starting from TS(all-trans/11-cis) vertically excited to the S1 state hops to the S0 state at 537.5 fs via a CI(all-trans/11-cis)-related event, as shown in Fig. 3a, and it then quickly relaxes to the all-trans isomer at 600 fs, as shown in Fig. 5d, where α goes to −180° from −120° and β goes to 0° from 50° (the other three angles γ, δ, and ε are almost unchanged with only small vibrations). Four double bonds (C7![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C8, C9
C8, C9![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C10, C11
C10, C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12, and C13
C12, and C13![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C14) vibrate within the range of 0.05 Å, as shown in Fig. S6a (ESI†). Fig. 5b shows that a typical trajectory starting from RS(all-trans/8_11-cis) vertically excited to the S1 state hops to the S0 state at 1.5 fs via a CI(all-trans/8_11-cis)-related event, as shown in Fig. 3b, and it then relaxes to the all-trans isomer at 80 fs, as shown in Fig. 5e, where ε and α go to −180° from −100° and β goes to 0° from 90° (the other two angles γ and δ are almost unchanged). Two double bonds (C11
C14) vibrate within the range of 0.05 Å, as shown in Fig. S6a (ESI†). Fig. 5b shows that a typical trajectory starting from RS(all-trans/8_11-cis) vertically excited to the S1 state hops to the S0 state at 1.5 fs via a CI(all-trans/8_11-cis)-related event, as shown in Fig. 3b, and it then relaxes to the all-trans isomer at 80 fs, as shown in Fig. 5e, where ε and α go to −180° from −100° and β goes to 0° from 90° (the other two angles γ and δ are almost unchanged). Two double bonds (C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12 and C13
C12 and C13![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C14) vibrate within a large range of 0.2 Å, as shown in Fig. S6b (ESI†). Fig. 5c shows that a typical trajectory starting from RS(all-trans/9-cis) vertically excited to the S1 state hops to the S0 state at 32 fs via a CI(all-trans/9-cis)-related event, as shown in Fig. 3c, and it then slowly relaxes to the all-trans isomer beyond 140 fs, as shown in Fig. 5f, where γ goes to −180° from −100° with slow oscillation (the other four angles α, β, ε, and δ are almost unchanged). The double bond C9
C14) vibrate within a large range of 0.2 Å, as shown in Fig. S6b (ESI†). Fig. 5c shows that a typical trajectory starting from RS(all-trans/9-cis) vertically excited to the S1 state hops to the S0 state at 32 fs via a CI(all-trans/9-cis)-related event, as shown in Fig. 3c, and it then slowly relaxes to the all-trans isomer beyond 140 fs, as shown in Fig. 5f, where γ goes to −180° from −100° with slow oscillation (the other four angles α, β, ε, and δ are almost unchanged). The double bond C9![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C10 vibrates within the range of 0.3 Å (the other three bonds C7
C10 vibrates within the range of 0.3 Å (the other three bonds C7![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C8, C11
C8, C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12, and C13
C12, and C13![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C14 vibrate within the range of 0.1 Å), as shown in Fig. S6c (ESI†).
C14 vibrate within the range of 0.1 Å), as shown in Fig. S6c (ESI†).
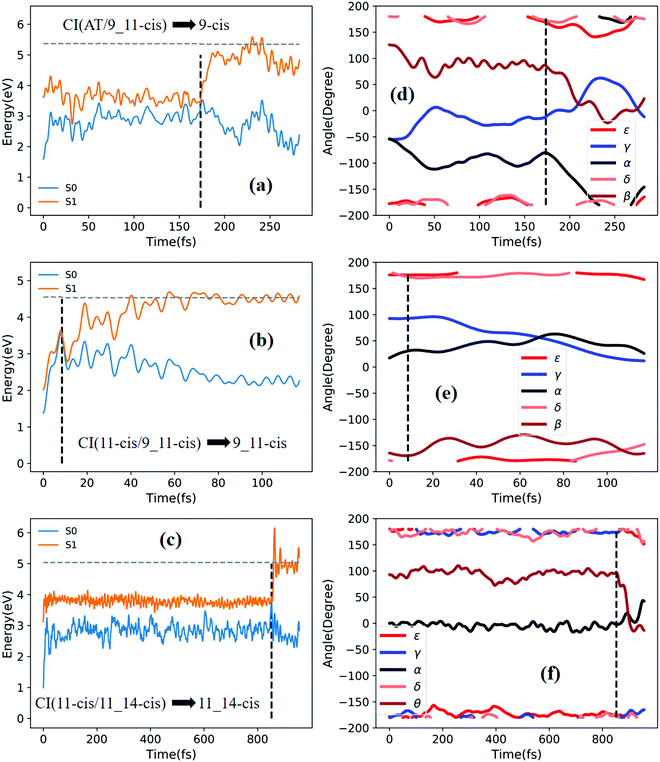
Fig. 6a shows that a typical trajectory starting from TS(all-trans/11-cis) vertically excited to the S1 state hops to the S0 state at 100 fs via a CI(all-trans/11-cis)-related event, as shown in Fig. 3a, and it then relaxes to the 11-cis isomer at 300 fs, as shown in Fig. 6d, where α goes to 0° from −140° and β goes to 180° from 50° (the other three angles γ, δ, and ε are almost unchanged with only small vibrations). Four double bonds (C7![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C8, C9
C8, C9![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C10, C11
C10, C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12, and C13
C12, and C13![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C14) vibrate within the range of 0.05 Å, as shown in Fig. S6d (ESI†). Fig. 6b shows that a typical trajectory starting from RS(all-trans/8_11-cis) vertically excited to the S1 state hops to the S0 state at 1.5 fs via a CI(all-trans/8_11-cis)-related event, as shown in Fig. 3b, and it then slowly relaxes to the 8-cis isomer at 180 fs, as shown in Fig. 6e, where ε (β) goes to 0° from −100° (100°), and α goes to −180° from −100° (the other two angles γ and δ are almost unchanged). The double bond C11
C14) vibrate within the range of 0.05 Å, as shown in Fig. S6d (ESI†). Fig. 6b shows that a typical trajectory starting from RS(all-trans/8_11-cis) vertically excited to the S1 state hops to the S0 state at 1.5 fs via a CI(all-trans/8_11-cis)-related event, as shown in Fig. 3b, and it then slowly relaxes to the 8-cis isomer at 180 fs, as shown in Fig. 6e, where ε (β) goes to 0° from −100° (100°), and α goes to −180° from −100° (the other two angles γ and δ are almost unchanged). The double bond C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12 vibrates within the large range of 0.2 Å, as shown in Fig. S6e (ESI†). Fig. 6c shows that a typical trajectory starting from RS(all-trans/9-cis) vertically excited to the S1 state hops to the S0 state at 29.5 fs via a CI(all-trans/9-cis)-related event, as shown in Fig. 3c, and it then relaxes to the 9-cis isomer at 120 fs, as shown in Fig. 6f, where γ goes to 0° from −100° smoothly (the other four angles α, β, ε, and δ are almost unchanged). The double bond C9
C12 vibrates within the large range of 0.2 Å, as shown in Fig. S6e (ESI†). Fig. 6c shows that a typical trajectory starting from RS(all-trans/9-cis) vertically excited to the S1 state hops to the S0 state at 29.5 fs via a CI(all-trans/9-cis)-related event, as shown in Fig. 3c, and it then relaxes to the 9-cis isomer at 120 fs, as shown in Fig. 6f, where γ goes to 0° from −100° smoothly (the other four angles α, β, ε, and δ are almost unchanged). The double bond C9![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C10 vibrates within the range of 0.3 Å (the other three bonds C7
C10 vibrates within the range of 0.3 Å (the other three bonds C7![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C8, C11
C8, C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12, and C13
C12, and C13![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C14 vibrate within the range of 0.1 Å), as shown in Fig. S6f (ESI†).
C14 vibrate within the range of 0.1 Å), as shown in Fig. S6f (ESI†).
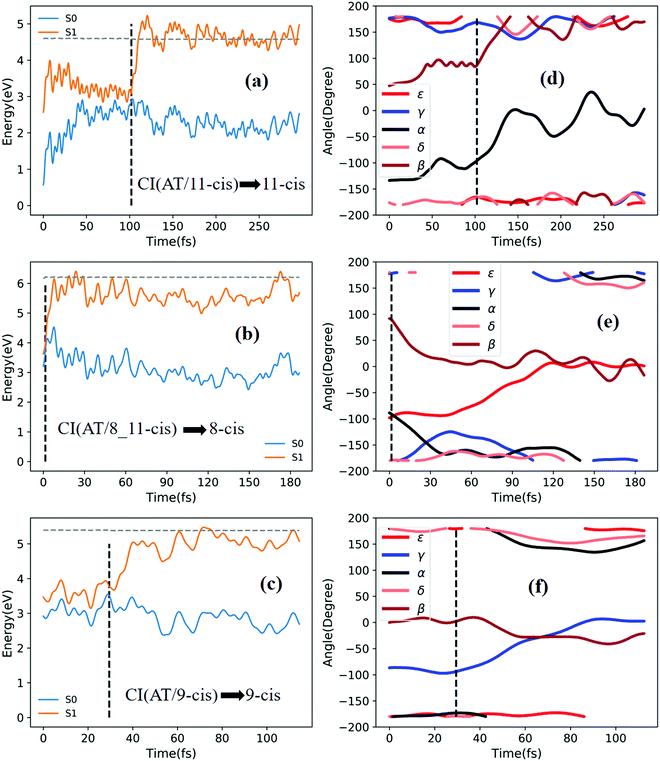
Fig. 7a shows that a typical trajectory starting from RS(all-trans/9_11-cis) vertically excited to the S1 state hops to the S0 state at 44.5 fs via a CI(all-trans/9_11-cis)-related event, as shown in Fig. 3d, and it then relaxes to the 9_11-cis isomer at 120 fs, as shown in Fig. 7d, where α and γ go to 0° from −60° and β goes to 180° from 120° (the other two angles δ and ε are almost unchanged with only small vibrations). Two double bonds (C9![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C10 and C11
C10 and C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12) vibrate within the range of 0.25 Å, as shown in Fig. S7a (ESI†). Fig. 7b shows that a typical trajectory starting from TS(11-cis/9_11-cis) vertically excited to the S1 state hops to the S0 state at 10.5 fs via a CI(11-cis/9_11-cis)-related event, as shown in Fig. 3e, and it then relaxes to the 11-cis isomer at 70 fs, as shown in Fig. 7e, where γ goes to 180° from 90° and α goes to −10° from 10° (the other three angles β, δ, and ε are almost unchanged with only small vibrations). Two double bonds (C9
C12) vibrate within the range of 0.25 Å, as shown in Fig. S7a (ESI†). Fig. 7b shows that a typical trajectory starting from TS(11-cis/9_11-cis) vertically excited to the S1 state hops to the S0 state at 10.5 fs via a CI(11-cis/9_11-cis)-related event, as shown in Fig. 3e, and it then relaxes to the 11-cis isomer at 70 fs, as shown in Fig. 7e, where γ goes to 180° from 90° and α goes to −10° from 10° (the other three angles β, δ, and ε are almost unchanged with only small vibrations). Two double bonds (C9![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C10 and C11
C10 and C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12) vibrate within the range of 0.15 Å, as shown in Fig. S7b (ESI†). Fig. 7c shows that a typical trajectory starting from TS(11-cis/11_14-cis) vertically excited to the S1 state hops to the S0 state at 881 fs via a CI(11-cis/11_14-cis)-related event, as shown in Fig. 3f, and it then relaxes to the 11-cis isomer at 1000 fs, as shown in Fig. 7f where θ (not given in Table 1), as seen in Fig. 1, goes to 180° from 90° (the five angles α, β, γ, δ, and ε are almost unchanged with only small vibrations). Four double bonds (C7
C12) vibrate within the range of 0.15 Å, as shown in Fig. S7b (ESI†). Fig. 7c shows that a typical trajectory starting from TS(11-cis/11_14-cis) vertically excited to the S1 state hops to the S0 state at 881 fs via a CI(11-cis/11_14-cis)-related event, as shown in Fig. 3f, and it then relaxes to the 11-cis isomer at 1000 fs, as shown in Fig. 7f where θ (not given in Table 1), as seen in Fig. 1, goes to 180° from 90° (the five angles α, β, γ, δ, and ε are almost unchanged with only small vibrations). Four double bonds (C7![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C8, C9
C8, C9![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C10, C11
C10, C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12, and C13
C12, and C13![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C14) vibrate rapidly within the range of 0.10 Å, as shown in Fig. S7c (ESI†).
C14) vibrate rapidly within the range of 0.10 Å, as shown in Fig. S7c (ESI†).
Fig. 8a shows that a typical trajectory starting from RS(all-trans/9_11-cis) vertically excited to the S1 state hops to the S0 state at 173.5 fs via a CI(all-trans/9_11-cis)-related event, as shown in Fig. 3d, and it then relaxes to the 9-cis isomer at 280 fs, as shown in Fig. 8d, where α goes to −180° from −50°, γ goes to 0° from −60°, and β goes to 120° from 0° (the other two angles δ and ε are almost unchanged with only small vibrations). Two double bonds (C9![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C10 and C11
C10 and C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12) vibrate within the range of 0.20 Å, as shown in Fig. S7d (ESI†). Fig. 8b shows that a typical trajectory starting from TS(11-cis/9_11-cis) vertically excited to the S1 state hops to the S0 state at 8.5 fs via a CI(11-cis/9_11-cis)-related event, as shown in Fig. 3e, and it then relaxes to the 9_11-cis isomer at 120 fs, as shown in Fig. 8e, where γ goes to 0° from 100° (the other four angles α, β, δ, and ε are almost unchanged with only small vibrations). Three double bonds (C9
C12) vibrate within the range of 0.20 Å, as shown in Fig. S7d (ESI†). Fig. 8b shows that a typical trajectory starting from TS(11-cis/9_11-cis) vertically excited to the S1 state hops to the S0 state at 8.5 fs via a CI(11-cis/9_11-cis)-related event, as shown in Fig. 3e, and it then relaxes to the 9_11-cis isomer at 120 fs, as shown in Fig. 8e, where γ goes to 0° from 100° (the other four angles α, β, δ, and ε are almost unchanged with only small vibrations). Three double bonds (C9![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C10, C11
C10, C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12, and C13
C12, and C13![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C14) vibrate within the range of 0.2 Å, as shown in Fig. S7e (ESI†). Fig. 8c shows that a typical trajectory starting from TS(11-cis/11_14-cis) vertically excited to the S1 state hops to the S0 state at 852 fs via CI(11-cis/11_14-cis), as shown in Fig. 3f, and it then relaxes to the 11_14-cis isomer at 1000 fs, as shown in Fig. 8f, where θ (not given in Table 1), as seen in Fig. 1, goes to 0° from 100° (the five angles α, β, γ, δ, and ε are almost unchanged with only small vibrations). Four double bonds (C7
C14) vibrate within the range of 0.2 Å, as shown in Fig. S7e (ESI†). Fig. 8c shows that a typical trajectory starting from TS(11-cis/11_14-cis) vertically excited to the S1 state hops to the S0 state at 852 fs via CI(11-cis/11_14-cis), as shown in Fig. 3f, and it then relaxes to the 11_14-cis isomer at 1000 fs, as shown in Fig. 8f, where θ (not given in Table 1), as seen in Fig. 1, goes to 0° from 100° (the five angles α, β, γ, δ, and ε are almost unchanged with only small vibrations). Four double bonds (C7![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C8, C9
C8, C9![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C10, C11
C10, C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C12, and C13
C12, and C13![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C14) vibrate rapidly within the range of 0.10 Å, as shown in Fig. S7f (ESI†).
C14) vibrate rapidly within the range of 0.10 Å, as shown in Fig. S7f (ESI†).
We have discussed 12 typical sampling trajectories and their dynamic evolution, hopping from the S1 state to the S0 state via six conical intersections and then bifurcating into the two product regions connected to each CI. The final product distributions for all sampling trajectories are summarized in Fig. S8 (ESI†), connected to Fig. 3.
4. Concluding remarks
Via performing global switching trajectory surface hopping molecular dynamics simulations using on-the-fly (TD)CAM-B3LYP/6-31G potential energy surfaces for the first-exited S1 and ground S0 states, we have simulated real RPSB photoisomerization dynamics up to S1 excitation via finding the conical intersection networks spanned by six representative CIs. We have found that there are two layers of conical intersection clouds: one layer has energies as high as 8 eV (above all-trans S0) and the other has low energies of around 3–4 eV. In the present work, we have probed RPSB photoisomerization mechanisms via only focusing on low-layer-energy CIs. The present simulation gives a quantum yield of 0.11 (0.08) in the gas phase in comparison to an experimental value of 0.09 (0.2) in solution for all-trans to 11-cis (11-cis to all-trans) photoisomerization. The present simulation using (TD)-DFT methods indeed detected potential barriers in both the all-trans and 11-cis Franck–Condon regions, and the barrier energy in 11-cis form is lower than that in all-trans-form. In addition, for this real RPSB system with 63 atoms, there are 183 vibrational degrees of freedom, so the total kinetic energy can quickly dissipate into massive vibrational modes in the Franck–Condon regions; thus, even a small potential barrier can prevent sampling trajectories from crossing over. Instead, we carried out simulations starting from transition states based on each pair of isomers. We found six transition states (although three of them are called rotation states) via optimization; in such a way we can determine the lower-layer-energy conical intersections and dynamic simulations using transition states vertically excited to S1 states can actually be performed. We found that different geometries at the hopping points give rise to the twisting of specific torsional angles accompanied by variations of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds; as a result, electronic quenching occurs near a CI where one or two of the related dihedral angles related to specific double bonds twist close to 90°. The photoisomerization reaction is not stereoselective in the gas phase but presents a mixture of isomers compared to the high specificity obtained with proteins.
C double bonds; as a result, electronic quenching occurs near a CI where one or two of the related dihedral angles related to specific double bonds twist close to 90°. The photoisomerization reaction is not stereoselective in the gas phase but presents a mixture of isomers compared to the high specificity obtained with proteins.
The present simulation indicated again that the (TD)CAM-B3LYP/6-31G method can show all hopping points with well-behaved potential energy surface topology at conical intersections between S1 and S0 states. This can be seen from the scanned potential energy surfaces along MECI with respect to the characteristic dihedral angles for CI(all-trans/11-cis), CI(all-trans/8_11-cis), CI(all-trans/9-cis), CI(all-trans/9_11-cis), CI(11-cis/9_11-cis), and C I(11-cis/11_14-cis). The present simulation method is very encouraging and may allow us to simulate even larger systems with conventional TD-DFT methods to examine various retinal Schiff-base photoisomerization dynamics in the real world.
Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
This work is supported by the Ministry of Science and Technology, Taiwan (grant no. MOST 109-2113-M-009-019, 110-2113-M-A49-022 and 110-2634-F-009-026) and the Center for Emergent Functional Matter Science of National Yang Ming Chiao Tung University from The Featured Areas Research Center Program within the framework of the Higher Education Sprout Project by the Ministry of Education (MOE) in Taiwan.Notes and references
- R. Mathies, C. Brito Cruz, W. Pollard and C. Shank, Science, 1988, 240, 777–779 CrossRef CAS PubMed.
- K. A. Freedman and R. S. Becker, J. Am. Chem. Soc., 1986, 108, 1245–1251 CrossRef CAS.
- S. L. Logunov and M. A. El-Sayed, J. Phys. Chem. B, 1997, 101, 6629–6633 CrossRef CAS.
- S. L. Logunov, L. Song and M. A. El-Sayed, J. Phys. Chem., 1996, 100, 18586–18591 CrossRef CAS.
- H. Kandori and H. Sasabe, Chem. Phys. Lett., 1993, 216, 126–172 CrossRef CAS.
- M. Garavelli, F. Negri and M. Olivucci, J. Am. Chem. Soc., 1999, 121, 1023–1029 CrossRef CAS.
- C. Punwong, J. Owens and T. J. Martínez, J. Phys. Chem. B, 2015, 119, 704–714 CrossRef CAS PubMed.
- R. Schoenlein, L. Peteanu, R. Mathies and C. Shank, Science, 1991, 254, 412–415 CrossRef CAS PubMed.
- L. Peteanu, R. Schoenlein, Q. Wang, R. Mathies and C. Shank, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 11762–11766 CrossRef CAS PubMed.
- D. Polli, P. Altoè, O. Weingart, K. M. Spillane, C. Manzoni, D. Brida, G. Tomasello, G. Orlandi, P. Kukura, R. A. Mathies, M. Garavelli and G. Cerullo, Nature, 2010, 467, 440–443 CrossRef CAS PubMed.
- R. S. Becker and K. Freedman, J. Am. Chem. Soc., 1985, 107, 1477–1485 CrossRef CAS.
- H. Kandori, Y. Katsuta, M. Ito and H. Sasabe, J. Am. Chem. Soc., 1995, 117, 2669–2670 CrossRef CAS.
- G. Bassolino, T. Sovdat, A. Soares Duarte, J. M. Lim, C. Schnedermann, M. Liebel, B. Odell, T. D. W. Claridge, S. P. Fletcher and P. Kukura, J. Am. Chem. Soc., 2015, 137, 12434–12437 CrossRef CAS PubMed.
- G. Zgrablić, A. M. Novello and F. Parmigiani, J. Am. Chem. Soc., 2012, 134, 955–961 CrossRef PubMed.
- J. Rajput, D. Rahbek, L. Andersen, A. Hirshfeld, M. Sheves, P. Altoè, G. Orlandi and M. Garavelli, Angew. Chem., Int. Ed., 2010, 49, 1790–1793 CrossRef CAS PubMed.
- N. J. A. Coughlan, K. J. Catani, B. D. Adamson, U. Wille and E. J. Bieske, J. Chem. Phys., 2014, 140, 164307 CrossRef CAS PubMed.
- H. V. Kiefer, E. Gruber, J. Langeland, P. A. Kusochek, A. V. Bochenkova and L. H. Andersen, Nat. Commun., 2019, 10, 1210 CrossRef PubMed.
- M. Sun, Y. Ding, G. Cui and Y. Liu, J. Phys. Chem. A, 2007, 111, 2946–2950 CrossRef CAS PubMed.
- P. Zhou, J. Liu, K. Han and G. He, J. Comput. Chem., 2014, 35, 109–120 CrossRef CAS PubMed.
- A. Cembran, R. González-Luque, P. Altoè, M. Merchán, F. Bernardi, M. Olivucci and M. Garavelli, J. Phys. Chem. A, 2005, 109, 6597–6605 CrossRef CAS PubMed.
- A. Cembran, R. González-Luque, L. Serrano-Andrés, M. Merchán and M. Garavelli, Theor. Chem. Acc., 2007, 118, 173–183 Search PubMed.
- R. Barata-Morgado, M. L. Sánchez, A. Muñoz-Losa, M. E. Martín, F. J. Olivares del Valle and M. A. Aguilar, J. Phys. Chem. A, 2018, 122, 3096–3106 CrossRef CAS PubMed.
- J. W. Park and T. Shiozaki, Mol. Phys., 2018, 116, 2583–2590 CrossRef CAS.
- T. Ishida, S. Nanbu and H. Nakamura, J. Phys. Chem. A, 2009, 113, 4356–4366 CrossRef CAS PubMed.
- O. Weingart, J. Am. Chem. Soc., 2007, 129, 10618–10619 CrossRef CAS PubMed.
- W. C. Chung, S. Nanbu and T. Ishida, J. Phys. Chem. A, 2010, 114, 8190–8201 CrossRef CAS PubMed.
- T. Vreven, F. Bernardi, M. Garavelli, M. Olivucci, M. A. Robb and H. B. Schlegel, J. Am. Chem. Soc., 1997, 119, 12687–12688 CrossRef CAS.
- O. Weingart, I. Schapiro and V. Buss, J. Phys. Chem. B, 2007, 111, 3782–3788 CrossRef CAS PubMed.
- M. Barbatti, G. Granucci, M. Persico, M. Ruckenbauer, M. Vazdar, M. Eckert-Maksić and H. Lischka, J. Photochem. Photobiol., A, 2007, 190, 228–240 CrossRef CAS.
- M. Barbatti, M. Ruckenbauer, J. J. Szymczak, A. J. A. Aquino and H. Lischka, Phys. Chem. Chem. Phys., 2008, 10, 482–494 RSC.
- O. Weingart, I. Schapiro and V. Buss, J. Mol. Model., 2006, 12, 713–721 CrossRef CAS PubMed.
- Y. Hu, C. Xu, L. Ye, F. L. Gu and C. Zhu, Phys. Chem. Chem. Phys., 2021, 23, 5236–5243 RSC.
- L. Yu, C. Xu, Y. Lei, C. Zhu and Z. Wen, Phys. Chem. Chem. Phys., 2014, 16, 25883–25895 RSC.
- C. Zhu and H. Nakamura, J. Chem. Phys., 1992, 97, 8497 CrossRef CAS.
- C. Zhu and H. Nakamura, J. Chem. Phys., 1993, 98, 6208 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 (Revision B.01), Inc., Wallingford CT, 2016 Search PubMed.
- Z. Cai, M. J. Crossley, J. R. Reimers, R. Kobayashi and R. D. Amos, J. Phys. Chem. B, 2006, 110, 15624–15632 CrossRef CAS PubMed.
- N. J. A. Coughlan, B. D. Adamson, L. Gamon, K. Catani and E. J. Bieske, Phys. Chem. Chem. Phys., 2015, 17, 22623–22631 RSC.
- P. Hamm, M. Zurek, T. Röschinger, H. Patzelt, D. Oesterhelt and W. Zinth, Chem. Phys. Lett., 1996, 263, 613–621 CrossRef CAS.
- G. Wald and P. K. Brown, Science, 1958, 127, 222–249 CrossRef CAS PubMed.
- J. K. Lanyi, Nature, 1995, 375, 461–463 CrossRef CAS PubMed.
- R. Send, D. Sundholm, M. P. Johansson and F. Paw lowski, J. Chem. Theory Comput., 2009, 5, 2401–2414 CrossRef CAS PubMed.
- O. Valsson and C. Filippi, J. Chem. Theory Comput., 2010, 6, 1275–1292 CrossRef CAS.
- R. Send and D. Sundholm, J. Phys. Chem. A, 2007, 111, 27–33 CrossRef CAS PubMed.
- R. Send and D. Sundholm, J. Phys. Chem. A, 2007, 111, 8766–8773 CrossRef CAS PubMed.
- R. Send and D. Sundholm, J. Mol. Model., 2008, 14, 717–726 CrossRef CAS PubMed.
- B. Sellner, M. Barbatti and H. Lischka, J. Chem. Phys., 2009, 131, 024312 CrossRef PubMed.
- O. Weingart, A. Migani, M. Olivucci, M. A. Robb, V. Buss and P. Hunt, J. Phys. Chem. A, 2004, 108, 4685–4693 CrossRef CAS.
- L. Yue, L. Yu, C. Xu, C. Zhu and Y. Liu, Phys. Chem. Chem. Phys., 2020, 22, 11440–11451 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp03401d |
| This journal is © the Owner Societies 2021 |