Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Radiative lifetime of a BODIPY dye as calculated by TDDFT and EOM-CCSD methods: solvent and vibronic effects
Rengel Cane E.
Sia
 a,
Ruben Arturo
Arellano-Reyes
a,
Ruben Arturo
Arellano-Reyes
 b,
Tia E.
Keyes
b,
Tia E.
Keyes
 b and
Julien
Guthmuller
b and
Julien
Guthmuller
 *a
*a
aInstitute of Physics and Computer Science, Faculty of Applied Physics and Mathematics, Gdańsk University of Technology, Narutowicza 11/12, 80233 Gdańsk, Poland. E-mail: julien.guthmuller@pg.edu.pl
bSchool of Chemical Sciences, National Centre for Sensor Research, Dublin City University, Glasnevin, Dublin 9, Ireland
First published on 17th November 2021
Abstract
The radiative emission lifetime and associated S1 excited state properties of a BODIPY dye are investigated with TDDFT and EOM-CCSD calculations. The effects of a solvent are described with the polarizable continuum model using the linear response (LR) approach as well as state-specific methods. The Franck–Condon (FC), Herzberg–Teller (HT) and Duschinsky vibronic effects are evaluated for the absorption and emission spectra, and for the radiative lifetime. The transition energies, spectra shapes and radiative lifetime are assessed with respect to experimental results. It is found that the TDDFT transition energies are overestimated by about 0.4–0.5 eV, whereas EOM-CCSD improves the vertical emission energy by about 0.1 eV in comparison to TDDFT. The solvatochromic and Stokes shifts are better reproduced by the state-specific solvation methods, which show that these methods are more suited than the LR model to describe the solvent effects on the BODIPY dye. The vibronic effects lead to an increase of the radiative lifetime of about 0.4 to 1.0 ns depending on the theoretical approach, which highlights the importance of such effects. Moreover, the HT effects are negligible on both the spectra and lifetime, which demonstrates that the FC approximation is accurate for the BODIPY dye. Finally, the comparison with experimental data shows that the radiative lifetimes predicted by EOM-CCSD and TDDFT have comparable accuracy.
1. Introduction
The synthesis of 4,4-difluoro-4-bora-3a,4a-diaza-s-indacene (BODIPY) dyes can be traced back as early as1 1968 but it was actually in 2009, that the first unsubstituted BODIPY core was produced.2–4 Nowadays, the study and synthesis of BODIPY dyes have become widespread owing to their favorable properties such as large molar absorption coefficients, high fluorescence quantum yields, excellent thermal and photochemical stability, and good solubility as well as versatile functionalization.5–8 These properties make the BODIPY-based compounds highly suitable for many applications, in particular as probes or contrast agents in the biological environment. For example, BODIPY dyes were employed as luminophore for bioimaging and labelling of biological components, such as proteins, peptides, amino acids and lipid membranes.9–11 They have also been used as photosensitizers in solar energy conversion devices,12–14 as fluorescent switches, as chemical sensors, as laser dyes, and as components of molecular logic gates.15,16BODIPY dyes have been the subject of a number of theoretical studies in the past two decades (see e.g. ref. 12, 14 and 17–36). These works focused on determining the most suitable computational methods to perform reliable predictions, have contributed to the interpretation and analysis of experimental results, and have been used to design new dyes with desired absorption, emission and photochemical properties. In particular, an important effort has concerned the benchmarking of methods for the calculation of vertical and 0-0 transition energies (usually for the S1 state) in different series of BODIPY-based compounds.18,20,23,24,30,31,35,36 These studies have shown that time dependent density functional theory (TDDFT) calculations generally significantly overestimate the S1 excitation energy by about 0.3–0.5 eV. Nevertheless, because of the rather systematic nature of this deviation, the TDDFT method usually performs well in predicting the shifts in energy induced by various substituents or by chemical modifications of the BODIPY core. In this respect, long-range corrected exchange–correlation (XC) functionals or hybrid functionals including a large amount of exact exchange perform better than pure XC functionals. The rather large overestimation of the S1 excitation energy was ascribed to the difficulties of TDDFT in describing the differential electron correlation, and to contributions of double excitations and of multireference character to the wavefunction.30 These correlation effects can in principle be accounted for by wavefunction-based methods such as the configuration interaction (CI), coupled-cluster (CC) and complete active space self-consistent field (CASSCF) methods. Therefore, several calculations were performed using correlated methods including double excitations17,24,28,30,31,36 (CIS(D), SOS-CIS(D), CC2, LCC2*, EOM-CCSD, SAC-CI, etc) and describing the multiconfigurational character14,27,30,32 (CASPT2, RASPT2). For example, a very accurate reproduction of 0-0 energies (mean absolute error below 0.1 eV) was obtained using SOS-CIS(D) for a series of BODIPY dyes,24 provided that the solvent and vibronic effects (calculated with PCM/TDDFT) are included. Additionally, the LCC2*, SAC-CI and CASPT2 methods provided a good accuracy for vertical excitation energies (mean absolute error below 0.2 eV) in another series of BODIPY compounds.30 However, the results obtained from different wavefunction-based methods with double excitations (CIS(D), LCC2*, EOM-CCSD, SAC-CI) also shows significant variations for the calculated mean absolute errors (∼0.3 eV). This indicates that higher-order excitations or multiconfigurational contributions are required to properly account for the complicated correlation effects in BODIPY systems.28,30 The effects of solvent on the excitation energies were mostly described with a polarizable continuum model (PCM) in conjunction with TDDFT calculations.18,20,23,24 These studies have shown that state-specific approaches for the solvent effects usually provide more consistent results than the standard linear response (LR) theory. Several studies have also concentrated on the simulation of the absorption and emission vibronic spectra within the Franck–Condon (FC) or Herzberg–Teller (HT) approaches.20,23,24,33 It was observed that TDDFT calculations satisfactorily reproduce the vibronic band shape in the spectra.
An important property for the application of BODIPY dyes is the fluorescence quantum yield,37ΦF = kr/(kr + knr). This quantity provides a measure of the fluorescence efficiency of the dye and is determined by the radiative (kr) and nonradiative (knr) rates, which are associated to the relaxation pathways of the excited state. First principle calculations of quantum yields for different dyes were reported in the literature.38–47 In most studies, the radiative rate was estimated from the Einstein coefficient by assuming a two states approximation involving only the electronic parts of the ground and first excited states. In a few cases (e.g. ref. 39, 48 and 49), the vibronic coupling effects on the radiative rate were also considered using the Strickler and Berg50 equation, which is defined within the FC approximation. However, much less is known concerning the accuracy of different theoretical methods to calculate radiative rates, and fewer studies still have concerned BODIPY dyes.51
The main goal of the paper is to investigate the effects of several theoretical approaches to estimate the radiative rate (and the associated radiative lifetime) of a BODIPY dye (Fig. 1B). This compound was selected for study as it is a versatile synthon that through the carboxyl group modified to append functionality to the BODIPY core with only modest impact on photophysical properties. For example, the BODIPY-Ar-Chol (Fig. 1A) dye was employed as a fluorescent probe for the imaging of lipid membrane, and it has been shown to target almost exclusively liquid-ordered domains.11 Generally, the radiative rate depends on the emission energy and on the transition dipole moment between the initial and final states. Therefore, the accuracy of the TDDFT, CIS(D) and EOM-CCSD methods is first assessed for the S1 state transition energies. Next, the effects of the solvent on the energies and on the electronic transition dipole moments are investigated with the PCM by employing the standard LR theory as well as state-specific approaches. Then, the vibronic structure of the absorption and emission spectra is simulated within the FC and HT approximations using different XC functionals. Finally, the impact of the quantum chemistry method (i.e. choice of the XC functional, inclusion of double excitations), of the solvent (i.e. described by the LR and state-specific approaches) and of the vibronic couplings (i.e. Duschinsky effect, FC and HT contributions) on the radiative rate are discussed. The calculated transition energies, vibronic spectra and radiative lifetimes are compared to experimental results in order to assess their accuracy.
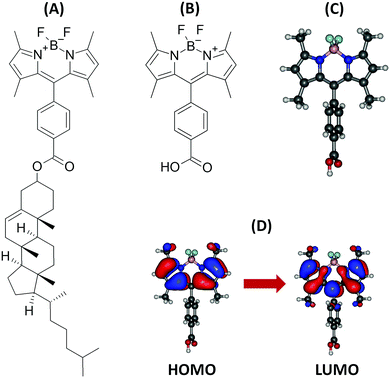 | ||
| Fig. 1 Structure of the BODIPY-Ar-Chol dye (A), investigated BODIPY compound (B), optimized structure (C), and orbitals involved in the first singlet excited state (D). | ||
2. Methods
2.1. Theoretical methods
The quantum chemical calculations were performed with the Gaussian 16 program52 using standard procedures described in the Gaussian 16 manual. Density functional theory was employed to calculate the geometry and the harmonic vibrational frequencies of the ground state (S0), while time-dependent DFT was used to compute the first singlet excited state (S1) properties (i.e. energy, transition dipole moment, geometry, vibrational frequencies). The DFT and TDDFT calculations were done with the B3LYP,53,54 CAM-B3LYP,55 M06-2X,56 MN1557 and PBE058–60 exchange–correlation (XC) functionals in association with the 6-311++G(2d,p) basis set. Density functional dispersion corrections were included using the GD3 model61 for the XC functionals B3LYP, CAM-B3LYP, M06-2X and PBE0, whereas such corrections were not considered for MN15 due to the lack of defined GD3 parameters for this XC functional. However, it was shown that MN15 alone provides a good performance for noncovalent interactions.57 Unless stated otherwise, the calculations were performed by assuming Cs symmetry of the compound, in which the plane of symmetry contains the atoms of the BF2 and of the phenyl-COOH groups. Additional excited state calculations were performed with the CIS(D)62 and EOM-CCSD63 methods using the S1 state geometry optimized with MN15. The CIS(D) calculations provided the vertical emission energy, whereas EOM-CCSD gave both the excited state energy and the transition dipole moment. This latter quantity was also estimated from the linear response transition densities.64In a first step, the calculations were executed in a vacuum. Then, in the second step the effects of the solvent (water, ε = 78.3553) were taken into account by the polarizable continuum model65 (PCM). The geometry and the harmonic vibrational frequencies of the S0 and S1 states were calculated using the integral equation formalism of the PCM. In particular, the S1 excited state properties were obtained from the conventional linear response (LR) theory employing the equilibrium procedure of solvation. These calculations provided the vertical emission (VE) energy, the adiabatic (AD) energy as well as the adiabatic energy including the zero-point vibrational energy correction (AD + ZPVE). Additionally, the vertical absorption (VA) energy and oscillator strength were calculated at the S0 geometry using the non-equilibrium procedure of solvation.
In addition to the LR results, the VA, VE and AD energies were also estimated using the state-specific (SS) approach66,67 as implemented in Gaussian 16 via the External Iteration keyword. In this method the VA energy is calculated – at the S0 geometry – from the difference between the S1 energy obtained from a non-equilibrium SS calculation (using the solvent reaction field in equilibrium with S0) and the S0 equilibrium energy. Similarly, the VE energy is calculated – at the S1 geometry – from the difference between the S1 energy obtained from an equilibrium SS calculation and the S0 non-equilibrium energy (using the solvent reaction field in equilibrium with S1). The AD energy is calculated from the difference between the S1 energy obtained from an equilibrium SS calculation and the S0 equilibrium energy. The AD + ZPVE energy is obtained by applying the same ZPVE correction as calculated previously with the LR theory. Moreover, state-specific effects on the VA, VE and AD energies were also estimated using the corrected linear response (cLR) method68 by following the procedure described in ref. 69.
The vibronic structure of the absorption and emission spectra were simulated with the Franck–Condon (FC) and FC-Herzberg–Teller (FCHT) methods70,71 using the geometries and vibrational frequencies of the S0 and S1 states. The potential energy surfaces (PESs) of the ground and excited states were represented by the adiabatic hessian (AH) and adiabatic shift (AS) methods. These simulations were performed in a vacuum as well as in solution using the LR approach. A temperature T = 0 K was assumed in the simulations (i.e. only the vibrational ground state of S0 and S1 is initially populated for the absorption and emission processes, respectively). The mode with an imaginary frequency in the S1 state (present in Cs symmetry) and several low frequency modes (mainly associated to rotations of the phenyl and methyl groups) were removed from FC overlap integrals calculations in order to obtain converged spectra (i.e. sum of FC factors above 0.99). The convergence of the FC factors is required to estimate the vibronic effect on the radiative rate. Furthermore, the removal of low frequency modes (<∼100 cm−1) is justified by the fact that the PESs along these modes cannot be properly described within the harmonic model. Calculations of the vibronic structure without symmetry constraints (i.e. C1 symmetry) were attempted with the MN15 functional but failed to provide proper convergence of the FC factors. Therefore, the vibronic effects on the spectra and on the radiative rate were only estimated assuming Cs symmetry.
The radiative rate kr (in SI units) for a transition from state |i〉 to state |f〉, assuming photon emission over all directions and polarizations, and after a rotational average over randomly oriented molecules, is given by the Einstein Aif coefficient72
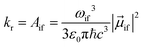 | (1) |
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) if is the transition dipole moment. ε0, c and ħ are the vacuum permittivity, the speed of light and the reduced Planck constant (ħ = h/2π), respectively.
if is the transition dipole moment. ε0, c and ħ are the vacuum permittivity, the speed of light and the reduced Planck constant (ħ = h/2π), respectively.
The radiative lifetime τr is defined as the inverse of the radiative rate, τr = 1/kr. Within the two-states approximation of eqn (1), the radiative lifetime was estimated using the VE energy (i.e. ħωif) and the electronic transition dipole moment at the S1 geometry.
The radiative rate kr for transitions from a single initial vibronic state |i〉 to an ensemble of final vibronic states |f〉, is given by
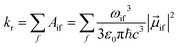 | (2) |
| |i〉 = |φe〉|θe0〉, |f〉 = |φg〉|θgu〉 | (3) |
| 〈i|μρ|f〉 = 〈θe0|(μρ)eg|θgu〉 | (4) |
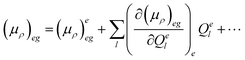 | (5) |
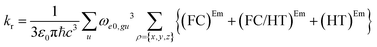 | (6) |
| (FC)Em = (μρ)eeg(μρ)eeg〈θe0|θgu〉2 | (7.1) |
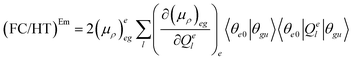 | (7.2) |
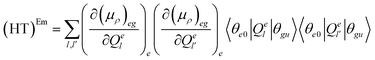 | (7.3) |
The (FC)Em term describes the FC contribution to the radiative rate, whereas the (FC/HT)Em and (HT)Em terms describe the HT correction. The radiative rate and the associated radiative lifetime were calculated with a local program employing the data obtained with Gaussian 16.
2.2. Experimental methods
1H and 13C NMR spectra were recorder on a 600 MHz Bruker spectrometer and residual DMSO was used as reference (2.50 ppm for 1H and 39.52 ppm for 13C) and are reported as follows: δ (ppm), multiplicity (s = singlet, d = doublet, m = multiplet), relative integration.
A Varian Cary 50 spectrometer was used to record the absorbance spectra and a Varian Cary Eclipse spectrometer was used to record emission spectra using slid widths of 2.5 nm. Hellma quartz cuvettes (10 mm × 10 mm) were used to record all data and a background correction was done beforehand. A PicoQuantFluoTime 100 Compact FLS TCSPC system using a 450 nm pulsed laser source generated from a PicoQuant PDL800-B box was used to determine the lifetime of the excited state.
A 7.0615 mM stock solution of BODIPY-Ar-COOH (Fig. 1B) in DMSO was prepared and further dilutions were prepared in the appropriate solvents. Luminesence lifetime data were recorded using 5 μM solutions of BODIPY-Ar-COOH in chloroform and in methanol. Quantum yield was determined using the slope method and fluorescein as the standard.75
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EtAcO (8
EtAcO (8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) as eluent. The product was obtained as a red powder in 14% yield, 176 mg. 1H-NMR (600 MHz, DMSO-d6) δ (ppm): 13.26 (1H), 8.11–8.08 (m, 2H), 7.55–7.52 (m, 2H), 6.20 (s, 2H), 2.45 (s, 6H), 1.32 (s, 6H). 13C-NMR (600 MHz, DMSO-d6) δ (ppm): 166.8, 155.3, 142.6, 140.8, 138.4, 131.5, 130.3, 130.1, 128.4, 121.6, 14.2, 14.0.
2) as eluent. The product was obtained as a red powder in 14% yield, 176 mg. 1H-NMR (600 MHz, DMSO-d6) δ (ppm): 13.26 (1H), 8.11–8.08 (m, 2H), 7.55–7.52 (m, 2H), 6.20 (s, 2H), 2.45 (s, 6H), 1.32 (s, 6H). 13C-NMR (600 MHz, DMSO-d6) δ (ppm): 166.8, 155.3, 142.6, 140.8, 138.4, 131.5, 130.3, 130.1, 128.4, 121.6, 14.2, 14.0.
3. Results
3.1. Excited state properties
Table 1 presents the VA, VE, AD and AD + ZPVE (i.e. 0-0 transition) energies associated to the S1 state, together with the transition dipole moments calculated at the S0 and S1 geometries. The computations were performed in a vacuum with five different XC functionals and were then repeated using the LR, cLR and SS solvent models. The S1 state corresponds mainly to a transition from the HOMO towards the LUMO (Fig. 1D).| Method | VA (eV) | VA (nm) | f | μ 01 (a.u.) | VE (eV) | VE (nm) | μ 01 (a.u.) | AD (eV) | AD + ZPVEc (eV) | AD + ZPVEc (nm) |
|---|---|---|---|---|---|---|---|---|---|---|
| a Calculated at the S0 geometry. b Calculated at the S1 geometry. c Includes the zero-point vibrational energy (ZPVE) correction. d Calculated in methanol. e Calculated in water with C1 symmetry. f Experimental energies/wavelengths at the maximum of absorption and emission in methanol and chloroform. g Estimated 0–0 transition from the absorption/fluorescence crossing point. | ||||||||||
| B3LYP | ||||||||||
| Vacuum | 2.98 | 416 | 0.482 | 2.57 | 2.90 | 428 | 2.50 | 2.94 | 2.80 | 443 |
| LR | 2.88 | 431 | 0.580 | 2.87 | 2.56 | 485 | 3.61 | 2.60 | 2.49 | 498 |
| cLR | 2.99 | 415 | — | — | 2.91 | 427 | — | 2.95 | 2.84 | 437 |
| SS | 2.99 | 415 | — | — | 2.91 | 427 | — | 2.95 | 2.84 | 437 |
| CAM-B3LYP | ||||||||||
| Vacuum | 3.00 | 413 | 0.531 | 2.69 | 2.91 | 427 | 2.69 | 2.95 | 2.85 | 435 |
| LR | 2.89 | 429 | 0.625 | 2.97 | 2.53 | 490 | 3.70 | 2.58 | 2.51 | 494 |
| cLR | 3.00 | 413 | — | — | 2.91 | 427 | — | 2.96 | 2.89 | 429 |
| SS | 3.02 | 411 | — | — | 2.92 | 425 | — | 2.97 | 2.90 | 428 |
| M06-2X | ||||||||||
| Vacuum | 2.98 | 416 | 0.520 | 2.67 | 2.89 | 429 | 2.66 | 2.93 | 2.84 | 437 |
| LR | 2.87 | 432 | 0.615 | 2.96 | 2.52 | 491 | 3.67 | 2.57 | 2.49 | 498 |
| cLR | 2.99 | 415 | — | — | 2.89 | 429 | — | 2.94 | 2.87 | 432 |
| SS | 3.00 | 413 | — | — | 2.90 | 428 | — | 2.95 | 2.87 | 432 |
| MN15 | ||||||||||
| Vacuum | 2.94 | 422 | 0.500 | 2.63 | 2.86 | 434 | 2.62 | 2.90 | 2.80 | 443 |
| LR | 2.84 | 437 | 0.595 | 2.92 | 2.50 | 496 | 3.65 | 2.55 | 2.46 | 503 |
| LRd | 2.84 | 437 | 0.592 | 2.92 | 2.51 | 493 | 3.62 | 2.56 | 2.48 | 500 |
| LRe | 2.84 | 437 | 0.589 | 2.91 | 2.44 | 508 | 3.57 | 2.52 | 2.45 | 506 |
| cLR | 2.95 | 420 | — | — | 2.86 | 433 | — | 2.91 | 2.83 | 438 |
| SS | 2.96 | 419 | — | — | 2.87 | 432 | — | 2.91 | 2.83 | 438 |
| PBE0 | ||||||||||
| Vacuum | 3.02 | 411 | 0.506 | 2.61 | 2.94 | 422 | 2.59 | 2.98 | 2.85 | 435 |
| LR | 2.92 | 425 | 0.604 | 2.91 | 2.58 | 480 | 3.64 | 2.63 | 2.53 | 490 |
| cLR | 3.03 | 409 | — | — | 2.94 | 422 | — | 2.99 | 2.89 | 429 |
| SS | 3.04 | 408 | — | — | 2.95 | 420 | — | 2.99 | 2.89 | 429 |
| Experimentf | ||||||||||
| Methanol | 2.49 | 497 | 2.43 | 511 | 2.46g | |||||
| Chloroform | 2.46 | 503 | 2.38 | 520 | 2.43g | |||||
The results in a vacuum show that changing the XC functional modifies the VA, VE, AD and AD + ZPVE energies by less than 0.1 eV. The lowest energies are obtained with MN15, whereas PBE0 provides the largest energies about 0.05–0.08 eV above the MN15 values. The transition energies of the BODIPY dye are overestimated by about 0.4–0.5 eV in comparison to the experimental values. This behavior is in agreement with previous TDDFT studies (see Introduction). For each XC functional, the transition dipole moment presents rather small variations between the S0 and S1 states geometries. The values differ at the most by 0.02 a.u., except for B3LYP, which displays a difference of 0.07 a.u. The effect of the XC functional is more pronounced. The largest difference of 0.19 a.u. is obtained between B3LYP and CAM-B3LYP at the S1 geometry. The fact that CAM-B3LYP provides the largest transition dipole moments and B3LYP the smallest is likely related to the amount of exact exchange in the functional.
The calculations were performed in water in order to estimate the effects of a polar solvent on the properties and because the dye has applications in biological environment.11 The calculations were also done in methanol using the MN15 functional and the LR solvent model (Table 1). No significant differences are obtained between the results in water and in methanol. Indeed, the energies and transition dipole moments differ at most by 0.02 eV and 0.03 a.u., respectively. Moreover, the effect of releasing the Cs symmetry was investigated with the MN15 functional and the LR solvent model. In C1 symmetry, the dihedral angle describing the rotation of the phenyl-COOH group with respect to the BODIPY core is decreased from 90° (Cs symmetry) to 82.6° and 66.4° for the S0 and S1 geometries, respectively. The VA energy and transition dipole moment at the S0 geometry are nearly identical to the values obtained with the Cs symmetry (Table 1). The VE energy and the transition dipole moment at the S1 geometry are decreased by 0.06 eV and 0.10 a.u. in comparison to the Cs symmetry results, respectively. However, the AD + ZPVE energy calculated at 2.45 eV with C1 symmetry is only 0.01 eV lower than the Cs symmetry value of 2.46 eV. This shows that the effect of releasing the Cs symmetry remains rather limited on these properties and justifies the use of geometries having Cs symmetry. From all the tested XC functionals, MN15 provides the lowest energies in solution, and therefore the best agreement with the experimental values. In particular, the PBE0 transition energies are about 0.06–0.08 eV larger than the MN15 values.
In the following, the discussion is restricted to the MN15 results, because the data obtained with the other functionals display comparable evolutions. The Stokes shift estimated with the LR method (−0.34 eV), as the difference between the VE and VA energies, is strongly overestimated in comparison to the experimental value (−0.06 eV in methanol). The calculated LR solvatochromic shifts (i.e., difference between the LR energy and the energy in a vacuum) for the VA, VE and 0-0 energies are −0.10 eV, −0.36 eV and −0.34 eV, respectively. These large values are in disagreement with the small solvatochromic shifts observed in experiment. Indeed, the experimental shifts are comprised between +0.03 eV (absorption maximum and 0-0 transition) and +0.05 eV (emission maximum) when going from the non-polar solvent chloroform to the solvent methanol (Table 1). Therefore, it appears that the LR method overestimates the solvent effects. This is particularly the case at the S1 geometry when using the equilibrium procedure of solvation. As a consequence, the excellent agreement between the AD + ZPVE energy (2.46 eV) and the experimental estimation of the 0-0 transition (2.46 eV in methanol) occurs due to a cancellation of errors on the transition energy, which involves the errors arising from the approximate TDDFT electron correlation (positive deviation) and the LR solvent effect (negative deviation). Additionally, the LR transition dipole moment is larger in comparison to the value in a vacuum. An increase of 0.29 a.u. is obtained at the S0 geometry using non-equilibrium solvation, whereas a larger increase of 1.03 a.u. is computed at the S1 geometry using equilibrium solvation. The cLR and SS models give very similar energies, which differ at most by 0.01 eV. This shows that the perturbative cLR method is efficient for the investigated dye. The solvent effect predicted by the cLR and SS approaches is much smaller than the one calculated with the LR method. Indeed, the MN15/SS energies differ at most by 0.03 eV in comparison to the energies in a vacuum. As a consequence, the cLR and SS results provide a better reproduction of the Stokes and solvatochromic shifts. With MN15/SS, the Stokes and solvatochromic shifts are −0.09 eV and +0.02/+0.01/+0.03 eV (VA/VE/0-0 transition), respectively. These results are in good agreement with the experimental estimations of −0.06 eV (in methanol) and +0.03/+0.05/+0.03 eV, respectively. Therefore, it can be concluded that (i) the cLR and SS methods are more suited than the LR model for the description of the solvent effects in this compound, (ii) TDDFT is accurate in reproducing the Stokes shift if associated with the cLR or SS solvent model, and (iii) the systematic overestimation of the transition energies can be predominantly ascribed to the approximate treatment of electron correlation by the TDDFT method.
The electron correlation should be better described using wavefunction-based methods including double excitations effects (see Introduction). To this aim, the CIS(D) and EOM-CCSD methods are employed to calculate the VE energy (Table 2). The calculations were performed in a vacuum with different basis sets by using the S1 geometry optimized with MN15. The basis set effect on the CIS(D) VE energy is moderate and leads to a stabilization of 0.04 eV going from the 6-311G(d) to the 6-311++G(2d,p) basis sets. The best value (2.69 eV) obtained with the largest basis set improves the MN15 results (2.86 eV) by 0.17 eV. However, the CIS(D) VE energy is still overestimated in comparison to experiment (2.38 eV in chloroform) by 0.31 eV. This indicates that the inclusion of additional electron correlation effects is required to accurately predict the transition energies. The deviation from experiment cannot be explained by solvent effects, which are expected to increase the calculated energy even further by about +0.01 eV to +0.05 eV according to the TDDFT/SS and experimental results. Only the two basis sets 6-31G(d) and 6-311G(d) were considered with EOM-CCSD because of the large computational cost of such calculations. The basis set effects on the EOM-CCSD results is very small for both the VE energy and the transition dipole moment. The EOM-CCSD method does not improve the VE energy in comparison to CIS(D) (0.04 eV larger than CIS(D) with 6-311G(d)) but performs better than TDDFT (0.09 eV lower than MN15). However, EOM-CCSD allows the calculations of the transition dipole moment both with the standard approach and using linear response transition densities. The former method provides transition dipole moments about 0.1 a.u. larger than the latter.
| Method | VE (eV) | VE (nm) | μ 01 (a.u.) |
|---|---|---|---|
| a The S1 geometry obtained with MN15 was employed in the CIS(D) and EOM-CCSD calculations. b Calculated with the LR transition densities method. | |||
| CIS(D) | |||
| 6-311G(d) | 2.73 | 455 | — |
| 6-311+G(d) | 2.70 | 459 | — |
| 6-311++G(2d,p) | 2.69 | 461 | — |
| EOM-CCSD | |||
| 6-31G(d) | 2.77 | 447 | 2.83; 2.75b |
| 6-311G(d) | 2.77 | 447 | 2.85; 2.77b |
3.2. Vibronic effects on the absorption and emission spectra.
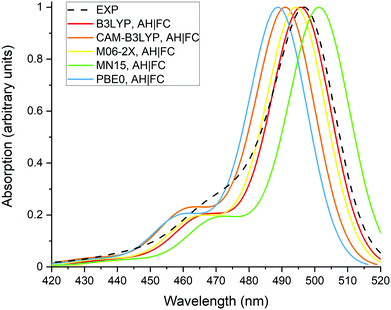
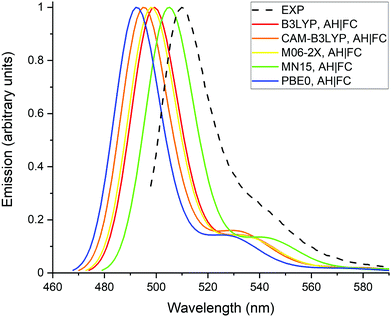
Fig. 2 presents the normalized absorption spectra calculated with the different XC functionals as well as the experimental spectrum recorded in methanol. The theoretical spectra were obtained with the AH|FC vibronic model and the LR solvation method. The spectra have a typical shape for BODIPY dyes, with a maximum of absorption located close to the 0-0 transition and a vibronic shoulder at shorter wavelengths. All the XC functionals predict the shoulder with a nearly similar intensity, which is partially underestimated in comparison to the experimental spectrum. The position of the absorption maximum follows the values of the 0-0 transition energies reported in Table 1. Moreover, the position of experimental maximum is well reproduced by the different XC functionals with a deviation below 0.1 eV. However, as discussed in the previous section, this agreement originates from a cancellation of errors between the approximate TDDFT electron correlation and the LR solvent effect.The calculated and experimental emission spectra are reported on Fig. 3. Similar observations can be made as for the absorption spectra, (i) the vibronic shoulders have a comparable intensity for all tested XC functionals, (ii) the vibronic structure is in reasonable agreement with the experimental spectrum and, (iii) MN15 gives the best prediction of the emission maximum.
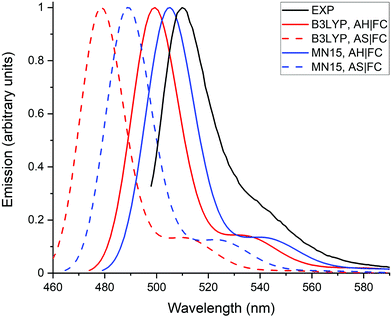
Fig. 4 compares the emission spectra calculated with the AH|FC and the AS|FC vibronic models for both the B3LYP and MN15 XC functionals. The simpler AS model provides a vibronic shoulder of nearly similar intensity as the AH model. This shows that the modifications of vibrational frequencies and of normal coordinates (Duschinsky effects) between the S0 and S1 states have a negligible impact on the spectrum, and consequently that the vibronic structure originates predominantly from the changes of geometry. The shorter wavelengths obtained for the maximum of emission with the AS model are related to the neglect of the ZPVE correction, i.e., the AS model makes use of the AD energies (Table 1). The ZPVE correction (∼0.1 eV) is not negligible and provides an improvement of the transition energy accuracy.
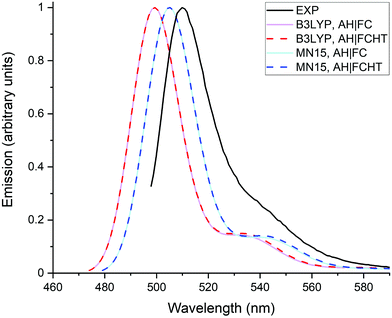
Fig. 5 compares the emission spectra calculated with the AH|FC and the AH|FCHT vibronic models. It is directly seen that the HT effects are negligible on the emission spectra. This result is likely related to the rather large transition dipole moment of the dye, which explains why the FC contribution dominates.
3.3. Radiative lifetimes.
Table 3 presents the radiative emission lifetimes calculated with different theoretical approaches as well as experimental radiative lifetimes. The experimental values for the radiative lifetimes were determined from the measured fluorescence lifetime (τF) (2.79 ± 0.003 and 2.34 ± 0.04 ns in methanol and chloroform, respectively) and quantum yield (ΦF) (0.46 ± 0.038 and 0.41 ± 0.1) according to the relation τr = τF/ΦF as 6.1 ± 0.08 ns in methanol and 5.7 ± 0.24 ns in chloroform.| Method | Two-states method τr (ns) | AS|FC τr (ns) | AH|FC τr (ns) | AS|FCHT τr (ns) | AH|FCHT τr (ns) |
|---|---|---|---|---|---|
| a Calculated in water with C1 symmetry. b Calculated with the 6-31G(d) basis set. c Calculated with the 6-311G(d) basis set. d Calculated with the linear response transition densities method. | |||||
| B3LYP | |||||
| Vacuum | 6.18 | 6.12 | 7.25 | 6.07 | 7.17 |
| LR | 4.32 | 4.27 | 4.91 | 4.27 | 4.91 |
| cLR | 2.93 | ||||
| SS | 2.93 | ||||
| CAM-B3LYP | |||||
| Vacuum | 5.28 | 5.24 | 5.86 | 5.23 | 5.86 |
| LR | 4.22 | 4.18 | 4.60 | 4.18 | 4.60 |
| cLR | 2.79 | ||||
| SS | 2.77 | ||||
| M06-2X | |||||
| Vacuum | 5.53 | 5.48 | 6.13 | 5.47 | 6.11 |
| LR | 4.35 | 4.31 | 4.73 | 4.31 | 4.73 |
| cLR | 2.88 | ||||
| SS | 2.86 | ||||
| MN15 | |||||
| Vacuum | 5.88 | 5.83 | 6.60 | 5.82 | 6.58 |
| LR | 4.51 | 4.47 | 4.99 | 4.47 | 4.99 |
| LRa | 5.09 | ||||
| cLR | 3.01 | ||||
| SS | 2.99 | ||||
| PBE0 | |||||
| Vacuum | 5.51 | 5.46 | 6.34 | 5.44 | 6.31 |
| LR | 4.12 | 4.08 | 4.65 | 4.08 | 4.65 |
| cLR | 2.78 | ||||
| SS | 2.77 | ||||
| EOM-CCSD | |||||
| Vacuumb | 5.53; 5.85d | ||||
| Vacuumc | 5.43; 5.75d | ||||
| Experiment | |||||
| Methanol | 6.1 ± 0.08 | ||||
| Chloroform | 5.7 ± 0.24 | ||||
The results calculated with the two-states approximation and TDDFT are first described. The two-states approximation radiative lifetime depends on the accuracy of the VE energy and of the transition dipole moment (eqn (1)). In a vacuum, the effect of changing the XC functional leads to differences as large as 0.9 ns between B3LYP and CAM-B3LYP. The differences in solution are smaller, the largest being of 0.29 ns between MN15 and CAM-B3LYP with the LR solvation model. Overall, the radiative lifetimes are decreased going from a vacuum to the solvent. Indeed, the LR method predicts differences of about 1.06 to 1.86 ns depending on the XC functional. This decrease of the radiative lifetime is due to the larger transition dipole moment in the solvent (by about 1 a.u., see Table 1). However, this effect is partially compensated by the lower VE energy in solution (0.34 to 0.38 eV lower than in a vacuum). The cLR and SS radiative lifetimes were calculated using the LR transition dipole moments (3.6–3.7 a.u.). As expected from the close VE energies (Table 1), the cLR and SS radiative lifetimes are found with nearly similar values. These radiative lifetimes are even smaller than those obtained with the LR method because in that case the VE energy is almost unchanged (+0.01 to +0.02 eV) going from a vacuum to the solvent. Therefore, the small cLR and SS radiative lifetimes (2.77–3.01 ns) originate almost entirely from the large LR transition dipole moment. The radiative lifetime was also estimated without symmetry constraints (i.e. C1 symmetry) using the MN15 functional and the LR solvent model. A value of 5.09 ns is obtained with the C1 symmetry, which is 0.58 ns larger than the radiative lifetime calculated with Cs symmetry. This effect is not negligible and arises from the lower VE energy and transition dipole moment calculated with C1 symmetry (Table 1).
The effects of the vibronic structure on the radiative lifetimes are now described. The AS|FC vibronic model gives radiative lifetimes slightly decreased by about 0.02–0.06 ns in comparison to the two-states approximation. However, the AH|FC model provides larger radiative lifetimes than the two-states approximation, with increases in the ranges 0.38–0.59 ns in solution and 0.58–1.07 ns in a vacuum. Because the vibronic structures in the AS|FC and AH|FC emission spectra are nearly the same (see Section 3.2), the differences of radiative lifetime between the AS|FC and AH|FC models are mainly ascribed to the differences in AD and AD + ZPVE energies. This shows that the ZPVE correction is important for the estimation of the radiative lifetime. Similarly to the emission spectra, the HT effects are negligible on the radiative lifetime, which shows that the FC approximation is sufficient for the investigated BODIPY dye.
The radiative lifetime was also calculated with the EOM-CCSD method in a vacuum using the two-states approximation. Increasing the basis set size from 6-31G(d) to 6-311G(d) leads to a small decrease of the lifetime of 0.1 ns. The radiative lifetimes calculated using the linear response transition densities formalism are larger by about 0.32 ns in comparison to the radiative lifetimes obtained with the standard EOM-CCSD method for the transition dipole moment. The linear response transition densities formalism is expected to be more accurate for the transition dipole moment. Therefore, the radiative lifetime calculated with the largest basis set (5.75 ns) should provide the best theoretical estimate for EOM-CCSD. This value is within the radiative lifetimes calculated with TDDFT (e.g. the MN15 radiative lifetime is 5.88 ns).
The comparison with experimental values shows that the radiative lifetimes calculated in a vacuum agree better with experiment. However, this rather good agreement likely originates from cancellation of errors between the overestimated transition energy and underestimated transition dipole moment. For example, a radiative lifetime of 8.52 ns is obtained if the experimental VE energy (2.43 eV) is employed with the two-states approximation and the EOM-CCSD transition dipole moment (2.77 a.u.). Including an additional vibronic effect of about 0.7 ns leads to a radiative lifetime significantly larger than experiment, which indicates that the EOM-CCSD transition dipole moment is underestimated. A similar conclusion applies for the TDDFT transition dipole moment in a vacuum. The LR method predicts more accurate VE and 0-0 transition energies (e.g. MN15 gives deviations of 0.07 eV and 0.00 eV for these two quantities, respectively, when compared to experiment in methanol). Nevertheless, the radiative lifetime is underestimated even after inclusion of vibronic effects (e.g. τr = 4.99 ns with MN15 and AH|FC). This indicates that the transition dipole moment calculated with the LR solvent model is too large. One can roughly estimate the correct value of the transition dipole moment in solution by using the two-states approximation with the experimental VE energy (2.43 eV in methanol), and by assuming a vibronic effect of +0.5 ns (value taken from MN15 in solution). To obtain a radiative lifetime equal to the experimental estimation (i.e. 6.1 ns in methanol), a transition dipole moments of 3.42 a.u. should be employed.
4. Conclusion
The S1 excited state properties, absorption and emission spectra, as well as the radiative emission lifetime of a BODIPY dye were investigated with TDDFT, CIS(D) and EOM-CCSD calculations. The effects of a solvent were included with the PCM using the standard LR model and state-specific approaches (cLR and SS). The vibronic effects on the spectra and on the radiative lifetime were accounted for with the AS and AH harmonic models by including both the FC and HT contributions. The transition energies, spectra shapes and radiative lifetime were assessed with respect to experimental results recorded in methanol and chloroform solutions.It was found that the TDDFT transition energies are overestimated by about 0.4–0.5 eV. From all the tested XC functionals, MN15 provides the lowest energies, and therefore gives the best agreement with the experimental values. The CIS(D) and EOM-CCSD methods provide improved VE energies in comparison to TDDFT, but the CIS(D) and EOM-CCSD values remain overestimated by 0.31 and 0.39 eV in comparison to experiment, respectively. Therefore, the overestimation of the transition energies can be predominantly ascribed to the approximate treatment of electron correlation by the TDDFT, CIS(D) and EOM-CCSD methods. Regarding the solvent effects, it was observed that the cLR and SS methods are more suited than the LR model in reproducing the solvatochromic and Stokes shifts. From the vibronic structure effects, in can be concluded that, (i) the vibronic shoulders in the absorption and emission spectra have a comparable intensity for all tested XC functionals, and are in reasonable agreement with the experimental spectra, (ii) the vibronic effect on the radiative lifetime (i.e. going from the two-states approximation to the AH|FC model) leads to an increase of about 0.4 to 1.0 ns depending on the XC functional and the environment, which demonstrates that such effects are important and should be incorporated in radiative lifetime calculations and, (iii) the HT effects are negligible on both the spectra and radiative lifetime, which shows that the FC contribution is sufficient for the BODIPY dye. The EOM-CCSD and TDDFT methods predict radiative lifetimes (calculated in a vacuum with the two-states approximation) of comparable accuracy. The analysis of the data reveals that the TDDFT and EOM-CCSD transition dipole moments in a vacuum are underestimated, whereas the TDDFT transition dipole moments calculated with the LR solvent model are overestimated. Similar to the transition energy, this suggests that additional electron correlation effects and state specific solvation effects should be included to improve the accuracy of the transition dipole moment in solution.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The calculations were performed at the Wrocław Centre for Networking and Supercomputing (grant No. 384) and at the Academic Computer Centre TASK in Gdańsk. This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 813920.References
- A. Treibs and F.-H. Kreuzer, Difluorboryl-Komplexe von Di- und Tripyrrylmethenen, Justus Liebigs Ann. Chem., 1968, 178, 208–223 CrossRef.
- K. Tram, H. Yan, H. A. Jenkins, S. Vassiliev and D. Bruce, The synthesis and crystal structure of unsubstituted 4,4-difluoro-4-bora-3a,4a-diaza-s-indacene (BODIPY), Dyes Pigm., 2009, 82, 392–395 CrossRef CAS.
- A. Schmitt, B. Hinkeldey, M. Wild and G. Jung, Synthesis of the core compound of the BODIPY dye class: 4,4′-difluoro-4-bora-(3a,4a)-diaza-s-indacene, J. Fluoresc., 2009, 19, 755–758 CrossRef CAS PubMed.
- I. J. Arroyo, R. Hu, G. Merino, B. Z. Tang and E. Peña-Cabrera, The smallest and one of the brightest. Efficient preparation and optical description of the parent borondipyrromethene system, J. Org. Chem., 2009, 74, 5719–5722 CrossRef CAS PubMed.
- A. Loudet and K. Burgess, BODIPY Dyes and Their Derivatives: Syntheses and Spectroscopic Properties, Chem. Rev., 2007, 107, 4891–4932 CrossRef CAS PubMed.
- R. Ziessel, G. Ulrich and A. Harriman, The chemistry of Bodipy: a new El Dorado for fluorescence tools, New J. Chem., 2007, 31, 496–501 RSC.
- G. Ulrich, R. Ziessel and A. Harriman, The chemistry of fluorescent bodipy dyes: versatility unsurpassed, Angew. Chem., Int. Ed., 2008, 47, 1184–1201 CrossRef CAS PubMed.
- H. Lu, J. MacK, Y. Yang and Z. Shen, Structural modification strategies for the rational design of red/NIR region BODIPYs, Chem. Soc. Rev., 2014, 43, 4778–4823 RSC.
- T. Kowada, H. Maeda and K. Kikuchi, BODIPY-based probes for the fluorescence imaging of biomolecules in living cells, Chem. Soc. Rev., 2015, 44, 4953–4972 RSC.
- M. Grossi, M. Morgunova, S. Cheung, D. Scholz, E. Conroy, M. Terrile, A. Panarella, J. C. Simpson, W. M. Gallagher and D. F. O’Shea, Lysosome triggered near-infrared fluorescence imaging of cellular trafficking processes in real time, Nat. Commun., 2016, 7, 10855 CrossRef CAS PubMed.
- D. O’Connor, A. Byrne and T. E. Keyes, Linker length in fluorophore-cholesterol conjugates directs phase selectivity and cellular localisation in GUVs and live cells, RSC Adv., 2019, 9, 22805–22816 RSC.
- R. P. Sabatini, T. M. McCormick, T. Lazarides, K. C. Wilson, R. Eisenberg and D. W. McCamant, Intersystem Crossing in Halogenated Bodipy Chromophores Used for Solar Hydrogen Production, J. Phys. Chem. Lett., 2011, 2, 223–227 CrossRef CAS.
- G.-G. Luo, H. Lu, X.-L. Zhang, J.-C. Dai, J.-H. Wu and J.-J. Wu, The relationship between the boron dipyrromethene (BODIPY) structure and the effectiveness of homogeneous and heterogeneous solar hydrogen-generating systems as well as DSSCs, Phys. Chem. Chem. Phys., 2015, 17, 9716–9729 RSC.
- L. Dura, M. Wächtler, S. Kupfer, J. Kübel, J. Ahrens, S. Höfler, M. Bröring, B. Dietzek and T. Beweries, Photophysics of BODIPY Dyes as Readily-Designable Photosensitisers in Light-Driven Proton Reduction, Inorganics, 2017, 5, 21 CrossRef.
- A. P. De Silva, Molecular Logic-based Computation, Royal Society of Chemistry, Cambridge, UK, 2013 Search PubMed.
- S. Erbas-Cakmak, S. Kolemen, A. C. Sedgwick, T. Gunnlaugsson, T. D. James, J. Yoon and E. U. Akkaya, Molecular logic gates: the past, present and future, Chem. Soc. Rev., 2018, 47, 2228–2248 RSC.
- P. Acebal, S. Blaya and L. Carretero, Ab initio study of absorption and emission spectra of PM567, Chem. Phys. Lett., 2003, 374, 206–214 CrossRef CAS.
- N. Boens, V. Leen, W. Dehaen, L. Wang, K. Robeyns, W. Qin, X. Tang, D. Beljonne, C. Tonnelé, J. M. Paredes, M. J. Ruedas-Rama, A. Orte, L. Crovetto, E. M. Talavera and J. M. Alvarez-Pez, Visible absorption and fluorescence spectroscopy of conformationally constrained, annulated BODIPY dyes, J. Phys. Chem. A, 2012, 116, 9621–9631 CrossRef CAS PubMed.
- Y. Chen, J. Zhao, H. Guo and L. Xie, Geometry relaxation-induced large Stokes shift in red-emitting borondipyrromethenes (BODIPY) and applications in fluorescent thiol probes, J. Org. Chem., 2012, 77, 2192–2206 CrossRef CAS PubMed.
- S. Chibani, B. Le Guennic, A. Charaf-Eddin, O. Maury, C. Andraud and D. Jacquemin, On the computation of adiabatic energies in Aza-Boron-dipyrromethene dyes, J. Chem. Theory Comput., 2012, 8, 3303–3313 CrossRef CAS PubMed.
- J. L. Jin, H. Bin Li, Y. Geng, Y. Wu, Y. A. Duan and Z. M. Su, Theoretical insight into the origin of large Stokes shift and photophysical properties of anilido-pyridine boron difluoride dyes, ChemPhysChem, 2012, 13, 3714–3722 CrossRef CAS PubMed.
- M. J. Calhorda, D. Suresh, P. T. Gomes, R. E. Di Paolo and A. L. Maçanita, Photophysical properties of iminopyrrolyl boron complexes: a DFT interpretation, Dalton Trans., 2012, 41, 13210–13217 RSC.
- S. Chibani, B. Le Guennic, A. Charaf-Eddin, A. D. Laurent and D. Jacquemin, Revisiting the optical signatures of BODIPY with ab initio tools, Chem. Sci., 2013, 4, 1950–1963 RSC.
- S. Chibani, A. D. Laurent, B. Le Guennic and D. Jacquemin, Improving the accuracy of excited-state simulations of BODIPY and Aza-BODIPY dyes with a joint SOS-CIS(D) and TD-DFT approach, J. Chem. Theory Comput., 2014, 10, 4574–4582 CrossRef CAS PubMed.
- J. C. Manton, C. Long, J. G. Vos and M. T. Pryce, A photo- and electrochemical investigation of BODIPY-cobaloxime complexes for hydrogen production, coupled with quantum chemical calculations, Phys. Chem. Chem. Phys., 2014, 16, 5229–5236 RSC.
- B. Le Guennic and D. Jacquemin, Taking Up the Cyanine Challenge with Quantum Tools, Acc. Chem. Res., 2015, 48, 530–537 CrossRef CAS PubMed.
- E. A. Briggs, N. A. Besley and D. Robinson, QM/MM Excited State Molecular Dynamics and Fluorescence Spectroscopy of BODIPY, J. Phys. Chem. A, 2013, 117, 2644–2650 CrossRef CAS PubMed.
- R. R. Valiev, A. N. Sinelnikov, Y. V. Aksenova, R. T. Kuznetsova, M. B. Berezin, A. S. Semeikin and V. N. Cherepanov, The computational and experimental investigations of photophysical and spectroscopic properties of BF2 dipyrromethene complexes, Spectrochim. Acta, Part, 2014, 117, 323–329 CrossRef CAS PubMed.
- S. Ji, J. Ge, D. Escudero, Z. Wang, J. Zhao and D. Jacquemin, Molecular structure-intersystem crossing relationship of heavy-atom-free bodipy triplet photosensitizers, J. Org. Chem., 2015, 80, 5958–5963 CrossRef CAS PubMed.
- M. R. Momeni and A. Brown, Why do TD-DFT excitation energies of BODIPY/aza-BODIPY families largely deviate from experiment? Answers from electron correlated and multireference methods, J. Chem. Theory Comput., 2015, 11, 2619–2632 CrossRef CAS PubMed.
- I. K. Petrushenko and K. B. Petrushenko, Effect of meso-substituents on the electronic transitions of BODIPY dyes: DFT and RI-CC2 study, Spectrochim. Acta, Part A, 2015, 138, 623–627 CrossRef CAS PubMed.
- K. M. Ziems, S. Gräfe and S. Kupfer, Photo-Induced Charge Separation vs. Degradation of a BODIPY-Based Photosensitizer Assessed by TDDFT and RASPT2, Catalysts, 2018, 8, 520 CrossRef.
- M. Fortino, J. Bloino, E. Collini, L. Bolzonello, M. Trapani, F. Faglioni and A. Pedone, On the simulation of vibrationally resolved electronic spectra of medium-size molecules: The case of styryl substituted BODIPYs, Phys. Chem. Chem. Phys., 2019, 21, 3512–3526 RSC.
- D. Tzeli, I. D. Petsalakis and G. Theodorakopoulos, The solvent effect on a styryl-bodipy derivative functioning as an AND molecular logic gate, Int. J. Quantum Chem., 2020, 120, e26181 CrossRef CAS.
- V. E. Matulis, E. G. Ragoyja and O. A. Ivashkevich, Accurate theoretical prediction of optical properties of BODIPY dyes, Int. J. Quantum Chem., 2020, 120, e26159 CrossRef CAS.
- I. K. Petrushenko and K. B. Petrushenko, Theoretical predictions of the spectroscopic properties of BODIPY dyes: effects of the fused aromatic and heteroaromatic rings at the b, g bonds, Spectrochim. Acta, Part A, 2021, 247, 119125 CrossRef PubMed.
- M. Y. Berezin and S. Achilefu, Fluorescence lifetime measurements and biological imaging, Chem. Rev., 2010, 110, 2641–2684 CrossRef CAS PubMed.
- S. Yin, Q. Peng, Z. Shuai, W. Fang, Y.-H. Wang and Y. Luo, Aggregation-enhanced luminescence and vibronic coupling of silole molecules from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205409 CrossRef.
- Q. Peng, Y. Yi, Z. Shuai and J. Shao, Toward quantitative prediction of molecular fluorescence quantum efficiency: role of Duschinsky rotation, J. Am. Chem. Soc., 2007, 129, 9333–9339 CrossRef CAS PubMed.
- Y. Niu, Q. Peng, C. Deng, X. Gao and Z. Shuai, Theory of Excited State Decays and Optical Spectra: Application to Polyatomic Molecules, J. Phys. Chem. A, 2010, 114, 7817–7831 CrossRef CAS PubMed.
- R. R. Valiev, V. N. Cherepanov, V. Y. Artyukhov and D. Sundholm, Computational studies of photophysical properties of porphin, tetraphenylporphyrin and tetrabenzoporphyrin, Phys. Chem. Chem. Phys., 2012, 14, 11508–11517 RSC.
- M. Humbert-Droz, C. Piguet and T. A. Wesolowski, Fluorescence quantum yield rationalized by the magnitude of the charge transfer in π-conjugated terpyridine derivatives, Phys. Chem. Chem. Phys., 2016, 18, 29387–29394 RSC.
- N. K. Swenson, M. A. Ratner and E. A. Weiss, Computational Study of the Influence of the Binding Geometries of Organic Ligands on the Photoluminescence Quantum Yield of CdSe Clusters, J. Phys. Chem. C, 2016, 120, 6859–6868 CrossRef CAS.
- Q. Wu, Q. Peng, Y. Niu, X. Gao and Z. Shuai, Theoretical insights into the aggregation-induced emission by hydrogen bonding: a QM/MM study, J. Phys. Chem. A, 2012, 116, 3881–3888 CrossRef CAS PubMed.
- Q. Ou, Q. Peng and Z. Shuai, Toward Quantitative Prediction of Fluorescence Quantum Efficiency by Combining Direct Vibrational Conversion and Surface Crossing: BODIPYs as an Example, J. Phys. Chem. Lett., 2020, 11, 7790–7797 CrossRef CAS PubMed.
- Z. Lin, A. W. Kohn and T. Van Voorhis, Toward Prediction of Nonradiative Decay Pathways in Organic Compounds II: Two Internal Conversion Channels in BODIPYs, J. Phys. Chem. C, 2020, 124, 3925–3938 CrossRef CAS.
- K. Veys and D. Escudero, Computational Protocol to Predict Anti-Kasha Emissions: The Case of Azulene Derivatives, J. Phys. Chem. A, 2020, 124, 7228–7237 CrossRef CAS PubMed.
- Z. C. Wong, W. Y. Fan, T. S. Chwee and M. B. Sullivan, Modelling fluorescence lifetimes with TD-DFT: a case study with syn-bimanes, RSC Adv., 2016, 6, 87237–87245 RSC.
- J. Preiss, D. Kage, K. Hoffmann, T. J. Martínez, U. Resch-Genger and M. Presselt, Ab Initio Prediction of Fluorescence Lifetimes Involving Solvent Environments by Means of COSMO and Vibrational Broadening, J. Phys. Chem. A, 2018, 122, 9813–9820 CrossRef CAS PubMed.
- S. J. Strickler and R. A. Berg, Relationship between absorption intensity and fluorescence lifetime of molecules, J. Chem. Phys., 1962, 37, 814–822 CrossRef CAS.
- W. Qin, T. Rohand, W. Dehaen, J. N. Clifford, K. Driesen, D. Beljonne, B. Van Averbeke, M. Van Der Auweraer and N. Boens, Boron Dipyrromethene Analogs with Phenyl, Styryl, and Ethynylphenyl Substituents: Synthesis, Photophysics, Electrochemistry, and Quantum-Chemical Calculations, J. Phys. Chem. A, 2007, 111, 8588–8597 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2019 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other function, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- H. S. Yu, X. He, S. L. Li and D. G. Truhlar, MN15: A Kohn-Sham global-hybrid exchange-correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions, Chem. Sci., 2016, 7, 5032–5051 RSC.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, ERRATA: Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: the PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. Head-Gordon, R. J. Rico, M. Oumi and T. J. Lee, A doubles correction to electronic excited states from configuration interaction in the space of single substitutions, Chem. Phys. Lett., 1994, 219, 21–24 CrossRef CAS.
- J. F. Stanton and R. J. Bartlett, The equation of motion coupled-cluster method. A systematic biorthogonal approach to molecular excitation energies, transition probabilities, and excited state properties, J. Chem. Phys., 1993, 98, 7029–7039 CrossRef CAS.
- H. Koch, R. Kobayashi, A. Sanchez de Merás and P. Jorgensen, Calculation of size-intensive transition moments from the coupled cluster singles and doubles linear response function, J. Chem. Phys., 1994, 100, 4393–4400 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Quantum mechanical continuum solvation models, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- R. Improta, V. Barone, G. Scalmani and M. J. Frisch, A state-specific polarizable continuum model time dependent density functional theory method for excited state calculations in solution, J. Chem. Phys., 2006, 125, 054103 CrossRef PubMed.
- R. Improta, G. Scalmani, M. J. Frisch and V. Barone, Toward effective and reliable fluorescence energies in solution by a new state specific polarizable continuum model time dependent density functional theory approach, J. Chem. Phys., 2007, 127, 074504 CrossRef PubMed.
- M. Caricato, B. Mennucci, J. Tomasi, F. Ingrosso, R. Cammi, S. Corni and G. Scalmani, Formation and relaxation of excited states in solution: a new time dependent polarizable continuum model based on time dependent density functional theory, J. Chem. Phys., 2006, 124, 124520 CrossRef PubMed.
- C. Guido and S. Caprasecca, Corrected Linear Response State-specific correction to solvent polarization response, http://www.dcci.unipi.it/molecolab/tools/white-papers/pisalr.
- F. Santoro, A. Lami, R. Improta, J. Bloino and V. Barone, Effective method for the computation of optical spectra of large molecules at finite temperature including the Duschinsky and Herzberg-Teller effect: the Qx band of porphyrin as a case study, J. Chem. Phys., 2008, 128, 224311 CrossRef PubMed.
- V. Barone, J. Bloino, M. Biczysko and F. Santoro, Fully integrated approach to compute vibrationally resolved optical spectra: from small molecules to macrosystems, J. Chem. Theory Comput., 2009, 5, 540–554 CrossRef CAS PubMed.
- D. P. Craig and T. Thirunamachandran, Molecular Quantum Electrodynamics: An Introduction to Radiation Molecule Interaction, Dover Publications, Mineola, NY, 1984 Search PubMed.
- J. Guthmuller, Comparison of simplified sum-over-state expressions to calculate resonance Raman intensities including Franck-Condon and Herzberg-Teller effects, J. Chem. Phys., 2016, 144, 064106 CrossRef PubMed.
- J. Guthmuller, in Molecular Spectroscopy: A Quantum Chemistry Approach, ed. Y. Ozaki, M. J. Wójcik and J. Popp, Wiley-VCH, 2019, pp. 497–536 Search PubMed.
- C. Würth, M. Grabolle, J. Pauli, M. Spieles and U. Resch-Genger, Relative and absolute determination of fluorescence quantum yields of transparent samples, Nat. Protoc., 2013, 8, 1535–1550 CrossRef PubMed.
| This journal is © the Owner Societies 2021 |