 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
C–H bond activation in light alkanes: a theoretical perspective
Yalan
Wang
a,
Ping
Hu
b,
Jia
Yang
a,
Yi-An
Zhu
 *b and
De
Chen
*b and
De
Chen
 *a
*a
aDepartment of Chemical Engineering, Norwegian University of Science and Technology, Trondheim, 7491, Norway. E-mail: de.chen@ntnu.no
bUNILAB, State Key Laboratory of Chemical Engineering, School of Chemical Engineering, East China University of Science and Technology, Shanghai, 200237, China. E-mail: yanzhu@ecust.edu.cn
First published on 17th February 2021
Abstract
Alkanes are the major constituents of natural gas and crude oil, the feedstocks for the chemical industry. The efficient and selective activation of C–H bonds can convert abundant and low-cost hydrocarbon feedstocks into value-added products. Due to the increasing global demand for light alkenes and their corresponding polymers as well as synthesis gas and hydrogen production, C–H bond activation of light alkanes has attracted widespread attention. A theoretical understanding of C–H bond activation in light hydrocarbons via density functional theory (DFT) and microkinetic modeling provides a feasible approach to gain insight into the process and guidelines for designing more efficient catalysts to promote light alkane transformation. This review describes the recent progress in computational catalysis that has addressed the C–H bond activation of light alkanes. We start with direct and oxidative C–H bond activation of methane, with emphasis placed on kinetic and mechanistic insights obtained from DFT assisted microkinetic analysis into steam and dry reforming, and the partial oxidation dependence on metal/oxide surfaces and nanoparticle size. Direct and oxidative activation of the C–H bond of ethane and propane on various metal and oxide surfaces are subsequently reviewed, including the elucidation of active sites, intriguing mechanisms, microkinetic modeling, and electronic features of the ethane and propane conversion processes with a focus on suppressing the side reaction and coke formation. The main target of this review is to give fundamental insight into C–H bond activation of light alkanes, which can provide useful guidance for the optimization of catalysts in future research.
1. Introduction
Alkanes or paraffins (CnH2n+2) are acyclic saturated hydrocarbons and are the major constituents of natural gas and crude oil. Alkanes have the simplest structure among organic molecules, where each carbon atom is sp3-hybridized with four sigma bonds (either C–C or C–H), and each hydrogen atom joins to one of the carbon atoms (in a C–H bond). The efficient and selective activation of C–H bonds can directly convert abundant and low-cost hydrocarbon feedstocks into value-added products as commodity, intermediate, and fine chemicals, which have the potential to have a substantial economic impact. However, there is a formidable challenge for the sufficient activation of C–H bonds in alkanes into more sophisticated value-added architectures due to the thermodynamically strong C–H bonds and thus a high energy barrier to break the bonds. The bond strength of C–H bonds depends slightly on the structure, and the bond dissociation energies (BDEs) of the primary (1°), secondary (2°), and tertiary (3°) C sp3–H bonds of alkanes fall in the range of 4.16 to 4.38 eV, with the 1° C–H bonds being stronger than the 2° and 3° bonds.1 Methane molecules, as the main constituent of natural gas, have four primary C–H bonds which are highly stable and thus are the most difficult to activate. Moreover, the C–H bonds of alkanes functionalized products (such as alkenes and oxygenates) are not as stable as alkanes, which presents a challenge for gaining a high selectivity in alkane conversions.Catalysts play a privileged role in selective C–H bond activation and controlling the reaction pathways to improve the selectivity and lower the carbon footprint. Many catalytic routes have been developed to convert alkanes to high value-added chemicals, which form the technological foundation of the modern chemical industry and meet the demand of certain substances in a transition from petroleum to natural gas and shale gas and liquids. The global demand for light alkenes has increased due to the increasing demand of their corresponding polymers. The light olefin market across the globe is expected to reach USD 475.8 million at a compound annual growth rate of 5.85% by the end of 2027. Besides, with a shift of the feedstock from naphtha to natural gas feedstocks, the supply of certain chemicals such as propylene, butadiene, and BTX has become constrained. Their shortage in the market is the main driving force for the renewed interest in producing them from alkanes, as low-cost feedstocks for chemical production. Synthesis gas and hydrogen production via steam reforming, dry reforming, and partial oxidation from methane, and dehydrogenation reactions have been often used by industry for the on-purpose production of hydrogen and light alkenes like ethylene, propylene, and butylene. Catalytic dehydrogenation of light alkanes is becoming increasingly important with the exploitation of shale gas, which provides a significant amount of ethane and propane feedstocks. The dehydrogenation is one of the major routes to fill the lower olefin gap in terms of future production and demands.
Catalytic dehydrogenation reaction is an endothermic reaction, and high equilibrium conversion is favored by high temperature and low alkane pressure.2 However, hydrogenolysis also occurs at the high temperature, forming methane and other lower carbon number species leading to low olefin selectivity. Both transition metals (TMs) and metal oxides are active for the dehydrogenation of light alkanes. Oxidative dehydrogenation (ODH) is an alternative process to break down the thermodynamic limitation. The main challenge is to control the consecutive oxidation of alkanes/alkenes to carbon oxides due to the much higher reactivity of products than the reactants. The critical issue in the development of catalysts is, therefore, how to selectively activate the C–H bonds of alkane molecules.3
During the last few decades, great progress has been made in developing catalysts and catalytic processes of alkane conversion to value-added chemicals. Amounts of reviews have been reported for homogeneous catalysis regarding C–H bond activation of alkanes on organometallic and/or inorganic complexes,4–10 which are not covered in this review. In contrast, we focus on heterogeneous catalysis. So far, many comprehensive reviews on methane conversion11–13 and ethane and propane conversion on metal,2,14 oxide,2,3,15–18 metal-free,19,20 and bifunctional catalysts21 have been reported towards heterogeneous systems, covered mainly catalysts,2,12,17,21,22 kinetics,3,15 and processes.2,17 These reviews deal with progress in the experimental studies of chemistry and catalysis, focusing on key challenges related to light alkane activation in terms of activity, selectivity, and carbon formation. Despite their successful applications at an industrial scale, several central questions remain unanswered, such as active sites effectively activating C–H bonds, the detailed reaction mechanism of catalytic cycles, rate-determining steps (RDSs), and factors governing the selectivity and carbon formation in activation and conversion processes of methane and light alkanes.
A better understanding of the factors governing the fundamental aspects mentioned above is important to design more efficient catalyst systems to promote selective C–H activation. The design of new effective catalysts and/or improvement of industrial catalysts rely on a better understanding of the surface reactions at a molecular level. Great efforts have been devoted to assessing the structure–property–performance relationship. However, it is still challenging because the experimental approach can severely restrict the range of catalyst structures and compositions to be examined. An effective strategy for developing useful catalysts should involve simultaneous consideration of all structure–function relationships that are related to stability, activity, and selectivity in the design of catalyst and reaction systems.23
Theoretical heterogeneous catalysis and surface science have witnessed significant development toward a molecular-level understanding of the working catalysts. Electronic structure calculations based primarily on ab initio density functional theory (DFT) calculations have been widely applied in heterogeneous catalysis.24 Over the past decade, DFT combined with microkinetic modeling is widely used to provide vital fundamental data regarding the properties of the active sites, mechanisms of surface reactions, RDSs, trends in reactivity, etc.25–28 The development and application of DFT in heterogeneous catalysis29,30 as well as microkinetic modeling for catalyst design31,32 have been reported in several excellent reviews. Generally, microkinetic models are constructed based on DFT estimated energetics of elementary steps involved in reaction mechanisms for targeted reactions. Particularly, in recent years, the rapidly developed scaling relationships27,33–36 make the combination of microkinetic modeling with DFT more convenient due to much addressed computational complexity. That is, based on the DFT calculated energetics, the scaling relationships are obtained and used to predict the energetics of other adsorbates or on other catalyst surfaces, which are further employed as input parameters of the microkinetic model. DFT calculations have shown that the energetics of crucial reaction intermediates are linked by linear scaling relationships that have been applied for rationalizing trends in C–H bond activation of light alkanes across different catalyst surfaces. Gong and coworkers29 reviewed the mechanistic insights into heterogeneous catalytic dehydrogenation of light alkanes obtained from DFT calculations in 2015. Owing to the rapid development of scaling relationship-based microkinetic modeling, the molecular level understanding of surface catalyzed reactions involved in C–H activation of light alkanes has been dramatically improved across metal, alloy, oxide, and metal–oxide hybrid catalysts. A comprehensive review of the theoretical heterogeneous catalysis of C–H activation of methane, ethane, and propane on various catalysts is highly desired to provide fundamental insights into industrial catalytic processes and guidelines for the rational design of new catalysts and/or improvement of industrial catalysts.
The purpose of this review is to describe the recent progress in computational catalysis that has addressed the C–H bond activation of light alkanes, such as methane, ethane, and propane by heterogeneous transition metal, oxide, and metal/oxide catalysts, with emphasis on activity, selectivity and coke formation in light alkane conversion. This review describes the detailed understanding of kinetic and mechanistic insights into catalytic dehydrogenation of light alkanes at atomic and molecular levels obtained from DFT calculations and microkinetic modeling across various catalyst surfaces. It unravels the basic electronic features of the C–H cleavage process to the targeted products. The results of the mechanistic studies depend on temperature, pressure, and reactant composition. Finally, the design of new catalysts and improvement of the catalysts are reviewed and proposed based on the fundamental understanding and theory-driven catalyst design.
The first part of the review addresses direct and oxidative C–H bond activation of methane via σ–d interaction on metals and oxides. The mechanistic insights obtained from DFT assisted microkinetic analysis into steam and dry reforming, and the partial oxidation dependence on metal/oxide surfaces and nanoparticle (NP) size are summarized and analyzed. The theory-driven catalyst design is reviewed and discussed. The second and third parts describe direct and oxidative activation of the C–H bonds of ethane and propane towards light alkene formation on various metal and oxide surfaces. The emphasis is on the elucidation of active sites, intriguing mechanisms, microkinetic modeling, and electronic features of the ethane and propane conversion processes with a focus on suppressing the side reaction and coke formation.
2. C–H bond activation in methane
Methane is the simplest hydrocarbon, which is the predominant constituent (approximately 70–90%) of natural gas.37 Recent advances in hydraulic fracturing have led to the effective extraction of natural gas from shale rock and triggered the so-called ‘shale gas revolution’.29,38,39 This increased supply of natural gas makes methane very attractive as both an energy source and feedstock to produce fuels and chemicals. Apart from natural gas reserves, methane is also a central component of biogas produced by the anaerobic digestion of organic materials.38,40,41 Moreover, methane can be found in crystalline hydrates existing in permafrost areas as well as the continental slopes of many oceans.38 In view of its abundant reserves and resources, and with the depletion of oil reserves, methane activation will play a key role in ensuring the supply of energy, fuels, and chemicals in the future.Methane activation can be carried out through both direct and indirect conversion routes. To date, the industrial direct conversion routes of methane into fuels and chemicals have been limited. The challenges associated with these routes arise from the phenomenon that methane is very stable and requires very aggressive operating conditions to activate its C–H bonds, which facilitates undesirable reactions, thus resulting in a loss in activity, selectivity, and yields of desired products.39 Moreover, the products are more reactive than methane, which necessitates the selective separation of the products and brings more challenges in the chemical process.42 Despite the great challenges, significant progress has been made in the direct conversion of methane to chemicals, especially in the production of hydrocarbons, such as olefins and aromatics. Direct conversion to olefins can be realized via oxidative coupling of methane (OCM),43–45 and to aromatics can be realized via methane dehydroaromatization (MDA).46 Since recently Schwach et al.12 published an excellent review on direct conversion of methane into value-added chemicals, we will not include this in our review. They gave the fundamentals of C–H activation, analyzed the reaction pathways regarding selective routes of OCM, MDA, and MTOAH (methane conversion to olefins, aromatics, and hydrogen),47 and provided insights into the reaction mechanisms. Readers who are specifically interested in direct conversion of methane are directed to this review article.
The indirect conversion routes of methane into more valuable chemicals via synthesis gas are economically feasible and currently industrially applied. The production of synthesis gas from methane can be realized through three reactions,42,48,49 namely steam reforming (SRM, eqn (1)), dry reforming (DRM, eqn (2)), and partial oxidation (POM, eqn (3)), which are summarized as follows:
SRM: CH4 + H2O → CO + 3H2 ΔH298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 2.14 eV K = 2.14 eV | (1) |
DRM: CH4 + CO2 → 2CO + 2H2 ΔH298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 2.56 eV K = 2.56 eV | (2) |
POM: CH4 + 0.5O2 → CO + 2H2 ΔH298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = −0.37 eV K = −0.37 eV | (3) |
All three processes are found to be active over noble metal catalysts such as Rh, Ru, Ir, Pt, and Pd, and over non-noble metal catalysts like Ni and Co. Moreover, the oxide is one of the crucial types of catalysts to promote methane conversion. So far, the catalyst performance, support effect, promoter effect, deactivation, and kinetics and mechanisms of SRM,38,39,52–58 DRM,40,49–51,59–65 and POM48,66–71 over both noble and non-noble metal catalysts as well as oxide catalysts16,18,72–74 have been summarized in many reviews. However, these reviews are mostly introduced from experimental points of view, and a systematic understanding of these reactions from a theoretical perspective is still missing. Herein, we mainly review these reactions based on DFT calculations and microkinetic modeling, with the kinetic studies briefly introduced. C–H bond activation in methane is first elucidated.
2.1 Activation of C–H bonds in methane on metal and oxide surfaces
A methane molecule has four H atoms bonded to a single C atom in a tetrahedral orientation. The CH4 molecule is geometrically highly symmetrical and nonpolar, and it is neither an electron donor nor acceptor. The unique structural and electronic features of the methane molecule make it weakly interact with catalytic surfaces. A high bond dissociation energy of the C–H bond makes methane a relatively unreactive starting material. The first C–H bond activation is the critical step in methane conversion, which has been reported to be the RDS for methane decomposition, oxidation, and steam and dry reforming on different catalysts (Ni, Pd, Ru, and Rh), according to the kinetic studies by Wei and Iglesia75–80 and other researchers.81–90 Therefore, understanding the mechanism for C–H bond activation is essential for further comprehending SRM, DRM, and POM reactions.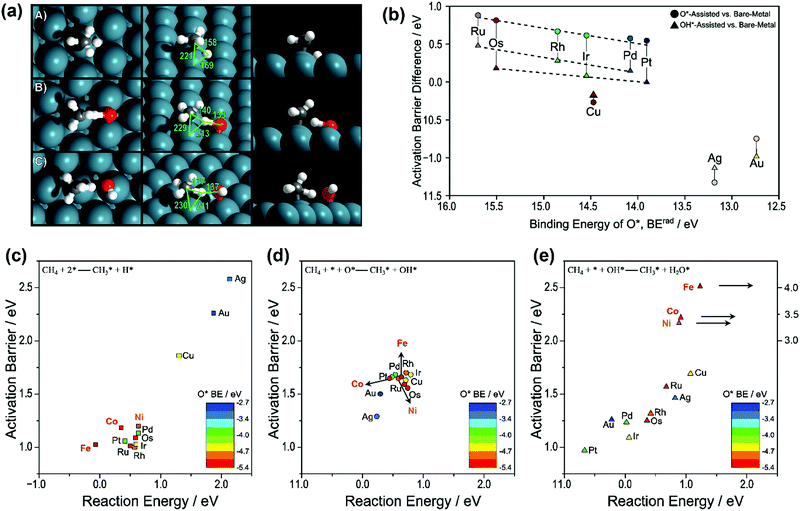 | ||
| Fig. 1 (a) Transition-state structures for the activation of the C–H bond in CH4 over (A) metal–metal site pairs (direct), (B) metal–O* site pairs (O*-assisted), and (C) metal–OH* (OH*-assisted) on the Pd(111) surface. Reported bond lengths are given in pm. (b) Difference between the O*-assisted and direct CH4 activation barriers (●) and the difference between OH*-assisted and direct CH4 activation (▲) compared to the binding energy of O*. Activation barriers and reaction energies for the CH4 activation via (c) direct CH4 activation (■), (d) O*-assisted CH4 activation (●), and (e) OH*-assisted CH4 activation (▲). Points are colored by the trends in O* binding energy, where red refers to the most strongly bound O* and blue refers to the most weakly bound O* (BErad, eV). The data of Ni, Co, and Fe in (c), (d), and (e) were obtained from our previous work.36,87,89,92 The others were reported by Hibbitts et al.91 Adapted from ref. 91 with permission from Elsevier, copyright 2016. | ||
Fig. 1(b) gives the activation barrier differences between the three routes as a function of O* binding energy. The respective activation barriers as a function of reaction energy for the three routes are shown as Fig. 1(c–e), respectively. The data of Ru, Rh, Pd, Os, Ir, Pt, Cu, Ag, and Au were reported by Hibbitts et al.,91 and those of Ni, Co, and Fe were obtained from our previous work.36,87,89,92 For group 8–10 metals (Ru, Rh, Pd, Os, and Ir), the DFT calculated activation barriers of O*-assisted CH4 dissociation were much higher than those of OH*-assisted CH4 dissociation, both higher than those of direct CH4 dissociation. Hibbitts et al.91 also compared the activation barriers for CH3* dissociation of the three pathways, where the direct route exhibited the lowest activation barrier for the above group 8–10 metals.
Similarly, Niu et al.92 also found that the first C–H bond activation via direct CH4 dissociation (activation energy Ea: 1.21 eV) was more energetically favorable than O-assisted (Ea: 1.66 eV) and OH-assisted CH4 dissociation (Ea: 3.39 eV) on a Ni(111) surface (Fig. 1c–e). Moreover, the C–H bond activation of CH3* and CH2* via direct dissociation was energetically preferred over the other two pathways. The observation is in good agreement with those reported by Zhu et al.93 on a Ni(111) surface, by Fan et al.94 on Ni(111), Ni(211), and Ni(100) surfaces, by Wang et al.87,89 on Ni, Rh, Pd, and Pt(111), (211), and (100) surfaces, by Jørgensen et al.86 on Pd(111) and Pd(100) surfaces, by Yoo et al.95 on a Pd(111) surface, and by Wang et al.88 on a Pt(111) surface. Like on Ni, the activation barriers of direct CH4 dissociation on Co and Fe were also much lower than those of the other two pathways (Fig. 1c–e), and extremely high activation barriers of OH*-assisted CH4 dissociation (3–4 eV) were observed (Fig. 1e).36,89 It is worth mentioning that even though the direct CH4 dissociation was also calculated as the energetically most favorable pathway on Co catalysts, Tu et al.96 suggested that the O*-assisted route dominated CH4 activation on Co and Ni–Co clusters because of their high oxophilicities, resulting in their surfaces covered with oxygen adatoms.
For group 11 metals, the O*- and OH*-assisted routes were energetically preferred over the direct CH4 dissociation route for both CH4 and CH3* dissociation. However, the activation energies of O*- and OH*-assisted C–H activation are still higher than that of the direct dissociation of methane on other groups of metals (8–10). The promotional effects of O* and OH* in activating C–H bonds on the group 11 metals were related to the M–O/M–OH binding energy and their basicity when binding with metal. The weakly bound O* and OH* often participate and assist in C–H bond activation. As such, enhanced promotional effects were observed on the group 11 metal surfaces by O*/OH* over direct metal activation due to their weak M–O/M–OH bonding. Moreover, the O* and OH* are more negatively charged when binding with the group 11 metals, thus increasing their basicity and ability to promote C–H activation. In contrast, the basicity of O* and OH* over the group 8–10 metal surfaces is not strong enough to aid C–H bond activation. As a result, the presence of O* or OH* will reduce the overall reaction rate since they will block active surface sites.
The Pt(111) surface is an exception, where the activation barrier for OH*-assisted CH4 dissociation was lower than those for the direct dissociation and the O*-assisted route.91,92,97 On the Pt(211) surface, the direct CH4 dissociation was the energetically most favorable pathway.97 However, the preferred reaction pathways need to be determined based on the whole catalytic cycle. Chen and Vlachos97 proposed that the reactions involving OH*-assisted C–H bond activation and addition were most probably the minor reaction pathways, because the OH coverage was low in methane reforming and oxidation and the direct CH4 dissociation was suggested as a dominant pathway on both the Pt(211) and Pt(111) surfaces. Similarly, the recent DFT study of Niu et al.92 indicated that the OH*-assisted CH4 activation was considered as an attractive alternative route for SRM on a Pt(111) surface. However, taking the coverage effect of OH* into account could reasonably lead to the direct CH4 dissociation route being dominant.
C–H bond activation via direct CH4 dissociation dominates methane activation on group 8–10 metals, which are active catalysts for SRM, DRM, and POM reactions. Gong and coworkers29 gave a detailed review of the theoretical study of methane dehydrogenation over various transition-metal surfaces, including fcc(111), hcp(0001), fcc(100), and fcc(211). The difference in activation energy between different elementary steps was found to be related to electronic and geometric effects, and the difference between other metals could be associated with the metal d-band center. Therefore, we only give a brief overview here. For instance, the geometries of the transition states (TSs) for CH4 dehydrogenation on close-packed Ni(111) and stepped Ni(211) surfaces are shown in Fig. 2(a and b), with the corresponding activation energies listed.94 Among the four elementary steps, the step CH → C + H showed the highest activation barrier for both Ni(111) and Ni(211) surfaces, consistent with that summarized by Gong and coworkers.29 The high barrier of CH → C + H results mainly from the stability of CH* (electronic effect) coupled with the perpendicular nature of CH* (geometrical effect). As shown in Fig. 2(c), CH* is perpendicular to the Ni(211) surface, where an energy penalty is required to bend the structure parallel to the metal surface in the transition state, and therefore geometrically not favorable for further dehydrogenation. The Ni(211) surface exhibits lower activation energies than the Ni(111) surface due to the existence of under-coordinated atoms on the stepped (211) surface, leading to higher binding strengths of surface intermediates and more stabilization of transition states and final states. Moreover, the geometric effect also influences the activation barriers between stepped and terrace surfaces. The partial charge densities projected onto the bonding states in Fig. 2(c and d) show that the CH species forms bonds with 4 Ni atoms, while 5-coordinated bonding is achieved between the C atom and Ni(211), demonstrating the strong binding of C on the stepped Ni(211) surface.98
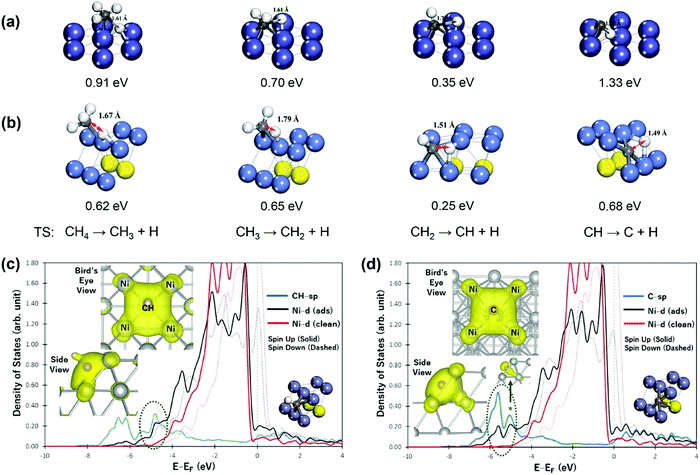 | ||
| Fig. 2 Geometries of the transition states (TS) for CH4 dehydrogenation on (a) Ni(111) and (b) Ni(211) surfaces. The values below the geometries are the activation energies of the corresponding elementary steps reported by Zhu et al.93 and Fan et al.94 Reproduced from ref. 93 with permission from Elsevier, copyright 2009. Reproduced from ref. 94 with permission from the American Chemical Society, copyright 2015. The densities of states (DOS) projected onto the sp states of CH (c) and C (d) and the d-band of stepped Ni(211) surfaces. “ads” and “clean” denote the surface with and without an adsorbate, respectively. The left inset figures show the side and bird's eye views of the partial charge density projected onto bonding states within an energy range bound by a dashed ellipse. The right inset figures show the geometries of CH and C on Ni(211) surfaces.98 Adapted from ref. 98 with permission from Springer Nature, copyright 2017. | ||
The activation energy of the C–H activation depends on the metal surfaces (Fig. 1) and the metal dependence follows the Brønsted–Evans–Polanyi (BEP) relationship that the activation energy of the elementary step scales linearly with reaction heat. Nørskov and co-workers found that the C binding energy can be used as a descriptor for the linear scaling relations (LSRs) of CHx (x = 1, 2, 3) adsorption energies and transition-state energies with respect to their gas-phase energies over various transition-metal surfaces.33,99,100 The linear relation could also be established between the activation energies and C adsorption energies, as shown in Fig. 3(a), based on our data.36 CH* dissociation shows the highest activation energy among the dehydrogenation steps, with the energy barriers for CH4, CH3, and CH2 dissociation gradually reduced on the close-packed surfaces. The C–metal binding energy can be simply characterized by the metal d-band center, as shown in Fig. 3(b). This underlines the theory that the binding energy of an adsorbate to a metal surface is strongly dependent on the electronic structure of the surface itself. When the C–H σ bond interacts with the metal d bond, the metal d-band hybridizes with the C–H bonding (σ) orbital to form bonding (d–σ) and antibonding (d–σ)* states. The metal–adsorbate interaction depends on the extent of filling of the (d–σ)* or the location of the d-band center. The energetically higher d-band center results in a higher C binding energy. The higher C binding energy leads to more negative CHx adsorption energy and its transition-state energy and a lower CHx dissociation barrier.
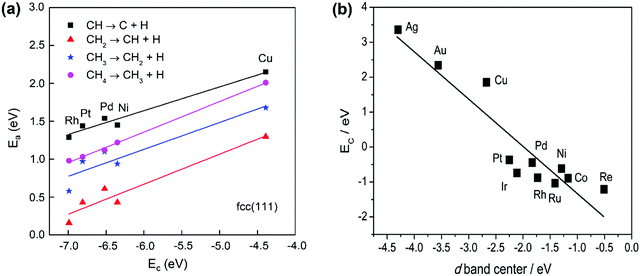 | ||
| Fig. 3 (a) Activation energies of CH4 dehydrogenation steps as a function of carbon adsorption energies on an fcc(111) surface, with the data obtained from our previous work.36 (b) Relationship between C binding energy and the metal d-band center.29 Published by the Royal Society of Chemistry, copyright 2015. | ||
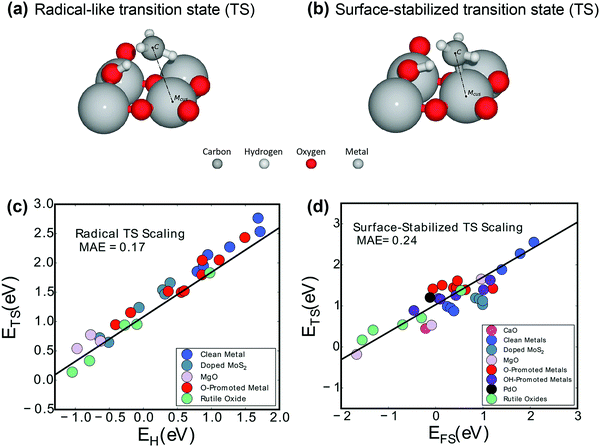 | ||
| Fig. 4 Two activation mechanisms on rutile-type metal oxide (110) surfaces are exhibited: (a) the radical-like transition state (TS) and (b) the surface-stabilized transition state (TS).104 Reproduced from ref. 104 with permission from the American Chemical Society, copyright 2019. Universal scaling relations for (c) the radical pathway (0.75EH + 1.09) and (d) the surface-stabilized pathway (0.67EFS + 1.04).103 Reproduced from ref. 103 with permission from the PCCP Owner Societies, copyright 2017. | ||
More interestingly, Latimer et al.103,106 proposed a universal scaling relationship for C–H bond activation (ETS) across reactants and catalysts that depends only on the hydrogen affinity of the catalyst (EH) and the C–H bond energy of the reactant (EC–H):
| ETS = 0.75EH − 1.26EC–H − 4.93 | (4) |
The relationship predicts well the C–H bond activation energies compared to the DFT-calculated ones across a wide variety of reactants and catalysts. The C–H activation energy of methane is the highest due to the more negative C–H bond energy.
Aljama et al. studied the role of alkaline metal oxides (MgO, CaO, and SrO)107 and alkaline earth metal oxides (AEMOs) with an alkaline earth metal (AEM) or a TM as a dopant108 in breaking the C–H bond in methane. The dopant can change the TS structure. Microkinetic modeling and analysis were performed using the binding energies of H and CH3 as two descriptors, and a volcano plot was obtained. Even for the surface-stabilized TS on pure alkaline metal oxides, the hydrogen binding energy was found to be a more appropriate descriptor. This suggested that at weak H binding strength, the reaction was limited by C–H bond activation. However, at strong H binding strength, the reaction was limited by poisoning of the active site.
Perovskite oxides with the formula ABO3 have gained increasing attention in applications in energy-related processes, such as solid fuel cells and chemical looping reforming of methane due to the massive family of combinations of A and B, well-defined structures, and excellent tunability of properties. Fung et al.109 investigated a broad set of perovskite compositions via descriptors of O reactivity such as the H adsorption energy, vacancy formation energy, and first C–H activation energy of methane using DFT calculations. The cubic perovskite (001) surface has both ‘A’ and ‘B’ terminations, as shown in Fig. 5(a). On each model termination, one possible lattice O site exists for catalysis. On the ‘A’ termination surface, the O is fourfold-coordinated to the surface A cation and onefold-coordinated to the subsurface B cation. On the ‘B’ termination surface, the O is twofold-coordinated to both the surface B cation and subsurface A cation. The reactive lattice O activates the methane molecule via a homolytic C–H bond cleavage, as illustrated in the upper part of Fig. 5(a). The typical geometries of C–H activation transition states over the perovskite(001) surface A and B terminations can be found in the lower part of Fig. 5(a). A strong linear relationship between the H adsorption energy or hydrogen affinity and the O vacancy formation energy was observed, as shown in Fig. 5(b). Both parameters can be used as descriptors for C–H bond activation of methane, as shown in Fig. 5(c) and (d), in good agreement with the universal scaling relationship.103,106 The stronger the hydrogen adsorption on the lattice O or the easier the O vacancy formation at the lattice-O site, the lower the C–H activation barrier of methane. The oxygen vacancy formation energy has been widely used as a descriptor of the C–H activation energy of methane on CeO2(111) doped with TMs, TbOx(111), ZnO, doped TiO2, and doped MgO;101 on pure CeO2(111), (100) and (110) surfaces and surfaces with Pd or Zr substituted in Ce lattice positions;110 on lanthanum oxides doped with Fe, Mg, Zn, Cu, Nb, Ti, Zr, and Ta; and on undoped catalysts.111 Oxides doped with low-valence atoms decreased the oxygen vacancy formation energy, which enhanced C–H bond activation. The lowered methane activation barrier was also observed for La2O3 catalyst doped with Cu, Zn, or Mg112 and for CeO2 doped with Pt.113 It can be generally proposed that oxides doped with low-valence metals are better methane activation catalysts than the undoped oxides.
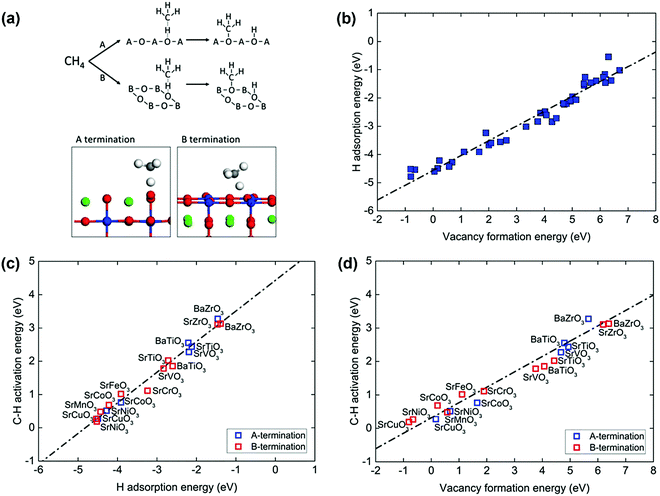 | ||
| Fig. 5 (a) Top: CH4 activation on the perovskite (001) A and B terminations. Bottom: The homolytic C–H pathway and the typical transition states (A, green; B, blue; O, red; C, grey; H, white). (b) Correlation between the hydrogen adsorption and vacancy formation energy of the lattice oxygen. Correlations between the homolytic C–H activation energy of CH4 and (c) hydrogen adsorption energy and (d) oxygen vacancy formation energy. The black dotted line represents the linear best fit.109 Reproduced from ref. 109 with permission from the Royal Society of Chemistry, copyright 2018. | ||
2.2 Methane conversion on metal surfaces
Great efforts have been devoted to the first-principles study of the C–H bond-breaking step of methane in a multistep process,91,98,103,106,114–120 because the C–H bond activation is often the RDS of the methane conversion. However, studying only the C–H activation step is insufficient to gain insight into the reaction mechanism, carbon formation, and RDSs, which can change with catalysts and operating conditions. Calculating the energy profile for the entire catalytic cycle is a demanding task, but it provides the activation barriers for the elementary steps. Microkinetic modeling and analysis of the whole cycle allow us to assess the preferential reaction pathways, RDSs, and dominating surface intermediates. Besides, the scaling relationships related to the binding energies of a wide variety of catalytic intermediates across a range of catalyst surfaces enable us to conduct theory-driven catalyst design. In the next sections, we will review the progress in the first-principles study and descriptor-based microkinetic modeling and analysis of the entire catalytic cycles in steam and dry methane reforming and partial oxidation of methane across a range of catalyst surfaces and catalyst nanoparticles.Metal dependence of activity. Steam reforming of methane is one of the main processes for hydrogen production.121 To date, many efforts have been devoted to investigating the SRM reaction from both experimental75,76,78,122–129 and theoretical87,89,97,126–128,130–135 points of view. The reaction is active over various transition-metal catalysts. For these metals, most studies demonstrated an activity trend of Ru, Rh > Ni, Ir > Pt, Pd > Co, Fe with a temperature range of 673–1173 K and atmospheric pressure.87,123,124,127,136Fig. 6(a) gives the microkinetic modeling results of SRM, reported by Jones et al.,127 and plots log10(TOF) as a function of C and O binding energies as two descriptors. The microkinetic model was built based on the energetics estimated by the linear scaling relationships and BEP relationships over the fcc(211) and bcc(210) surfaces. The descriptor-based microkinetic modeling provided a volcano curve as a function of C and O binding energies as descriptors. Ru, Rh and Ni(211) were found to be active for SRM and the activity is near the predicted optimum activity. It can be explored to design new catalysts with high performance.
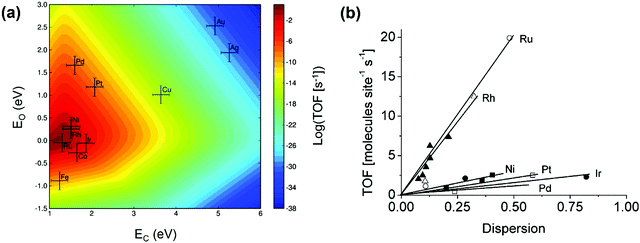 | ||
| Fig. 6 (a) Microkinetic modeling predicted log10(TOF) as a function of C and O binding energies for SRM. Reaction conditions: T = 773 K, P = 1 bar, 10% conversion. (b) Experimentally measured TOF as a function of dispersion for SRM across Ru (○), 5 wt% Rh (▲), 1 wt% Rh (Δ), Ni (■), Pt (□), Ir (•) and Pd (♦) catalysts. Reaction conditions: T = 773 K, PCH4 = 0.19 bar, PH2O = 0.74 bar, PH2 = 0.07 bar.127 Reproduced from ref. 127 with permission from Elsevier, copyright 2008. | ||
At 773 K, 1 bar, and 10% conversion, the model-predicted activity trend is Ru > Rh > Ni > Ir > Pt ∼ Pd. In addition to theoretical calculations, the authors also investigated the activity employing experimental measurements. By assuming that support effects were negligible, the obtained experimental activity trend at 773 K was Ru ∼ Rh > Ni ∼ Ir ∼ Pt ∼ Pd (Fig. 6b). Although the modeling results are not exactly the same as the experimental results, the general trends are consistent. The difference between the theoretical and experimental results might be caused by some sources of errors both in the modeling and in the experiments. The combined DFT, scaling relationship, and descriptor-based microkinetic modeling can effectively describe catalytic reactions at surfaces with the detail and accuracy required for the predicted activity tendency comparable to experiments.
It seems that among these pure metals, Ru and Rh are the most active catalysts, Ni and Ir are moderately active, and Pd and Pt are less active. However, the kinetic studies of Wei and Iglesia75–80 illustrated a different result, with the activity order as Pt > Ir > Rh > Ru, Ni at 873 K. In their studies, Pt is the most active catalyst. Despite the controversy about the metal activity, Ni, Rh, Ru, Pt and Pd are among the focuses of research for SRM. Ni is the most studied catalyst due to its low cost, abundance, and relatively high activity, and is a commercial and mature industrial SRM catalyst.58,137 Rh and Ru are normally studied because of their high reforming activity and coke-resistant performance.133 Pt is also a potential SRM catalyst with high activity, according to Wei and Iglesia's work.75 A better understanding of the SRM mechanism on these metal surfaces serves as an important step in revealing the nature of this reaction and in aiding the rational design of catalysts.
Metal dependence of the reaction mechanism. The reaction mechanism of steam methane reforming has been long studied both experimentally and theoretically, due to its industrial importance. The reaction mechanism of SRM typically involves methane activation (three C–H activation pathways as discussed above), and CH*/C* oxidation by OH* or O* to form CO. As a result, the mechanism involves many elementary steps, leading to many reaction pathways to form synthesis gas, as shown in Fig. 7.
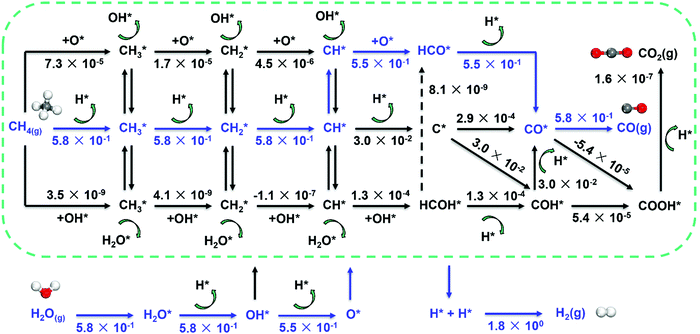 | ||
| Fig. 7 Reaction network for SRM over Ni catalyst and estimated net turnover frequency (TOFNet) for elementary steps involved in the microkinetic model over the Ni(211) surface. The dominant reaction pathway is colored blue. Reaction conditions: 773 K, 1 bar, S/C = 3.5, and CH4/H2 = 1.0.87 Reproduced from ref. 87 with permission from Elsevier, copyright 2019. | ||
The activation of C–H bonds in methane generates surface CHx (x = 1–3), and CH* and C* have been identified as the critical intermediates for CO formation. The CH*/C* may follow five routes to form CO by using O*/OH* as an oxidant (Fig. 7). They are (1) the direct C* and O* combination route (C–O route: CH* → C* → CO*), (2) hydrogen insertion via HCO* (CH–O route: CH* → HCO* → CO*) and (3) COH* (C–OH route: CH* → C* → COH* → CO*), and routes that involve the HCOH* intermediate like (4) the HCO–H route (CH* → HCOH* → HCO* → CO*) and (5) the H–COH route (CH* → HCOH* → COH* → CO*). The O* and OH* are provided by the dissociation of H2O.
DFT calculations and microkinetic modeling are powerful tools for elucidating the reaction pathways for syngas formation via the complex reaction mechanism and identifying the RDS, as it is difficult or almost impossible to gain a full picture on the basis of only experimental work. However, due to the coverage or surface concentration effect, it is difficult to determine the dominating reaction mechanisms purely based on DFT-calculated barriers under reaction conditions.29 The microkinetic modeling is therefore employed to clarify further the mechanistic scenario, which provides opportunities to directly acquire the reaction rate by taking into account both energy and coverage.87,94,130,132,138 Recently, Wang et al.89 conducted comprehensive microkinetic modeling to gain unified insight into the SRM mechanism on different metal surfaces with energetics estimated by combining a DFT-modified UBI-QEP (unity bond index-quadratic exponential potential) method and BEP relationships. The unified 2D mapping of the dominant reaction pathway and the RDS as a function of C and O formation energies is shown in Fig. 8 at 773 K (a) and 1073 K (b). The lower formation energy corresponds to a higher binding energy. The map can be divided into three areas in terms of the dominant reaction pathways. The O*-assisted C–H activation can only be for the catalysts with high C formation energy and low O formation energy. For most of the catalysts, the direct C–H dissociation is the preferred pathway for methane activation. RDSs such as H–CH3, H–CH2, C–OH, and CH–O were observed. This clearly shows that the RDS can change with catalysts or conditions. Based on the 2D map, the dominant reaction pathway and the RDS on transition metals Ni, Pt, Pd, and Rh with different surfaces such as (111), (100) and (211) were analyzed. It was found that the direct CH4 dissociation was the dominant pathway for methane activation for all the metal surfaces concerned, independent of temperature. CO formation mainly takes place via the C–OH route on the (100) surface due to the strong C binding strength and relatively weak binding of O, except for Ni(100) with H–CH3 activation as the RDS. On Pt(111) and (211), CH–O (HCO* formation) is the RDS, while on Ni(211), H–CH3 activation is the RDS. On Ni(111) and Rh surfaces, with increasing temperature, the RDS changes from HCO* formation to CH4 dissociation. The change in RDS with temperature agrees with the microkinetic modeling results reported by Jones et al.127
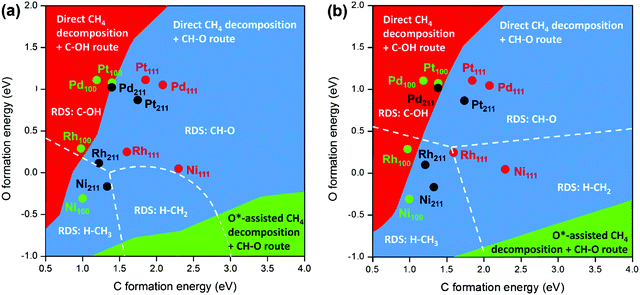 | ||
| Fig. 8 Schematic diagrams of the dominant reaction pathways (divided by colors) and rate-determining steps (divided by the dashed lines) as functions of C and O formation energies on different metal surfaces for SRM (a) at 773 K, 1 bar, with 18.2% CH4, 63.6% H2O, 18.2% H2, and (b) at 1073 K, 10 bar, with 18.2% CH4, 63.6% H2O, 18.2% H2.89 Adapted from ref. 89 with permission from the American Chemical Society, copyright 2020. | ||
The reaction mechanism and microkinetics have been intensively studied on Ni, Rh, Ru, Pt, and Pd catalysts. We will review the recent progress in the understanding of the mechanism and RDS on these catalysts.
Ni catalysts. Ni catalyst is the most widely studied catalyst due to its importance in industry where the Ni(111) surface is the most studied surface. In 1997, Aparicio125 carried out transient isotopic and microkinetic modeling to investigate the SRM mechanism over Ni catalysts. Direct dissociation of methane was experimentally demonstrated to be the main C–H bond activation pathway. The results suggested that there was no unified RDS for SRM. Both the first C–H activation and CO formation could all be kinetically relevant steps depending on the reaction conditions. In some cases, one of them can be the RDS, but in most cases, a combination of them determines the reaction rate. Later, Wei and Iglesia75–80 conducted a series of kinetic investigations for SRM on a range of metal catalysts (including Ni), which indicated that the first C–H bond activation was the RDS at high temperature (823–1023 K). However, at relatively low temperatures (<773 K), CO formation was expected as the RDS for most metals (including Ni), according to the thermodynamic analysis reported by Jones et al.127 The change in the RDS from CO formation to methane dissociation is caused by the increased reaction barrier of methane dissociation (related to entropy contribution) as the temperature increases.
More detailed theoretical studies relevant to SRM on Ni catalysts have been extensively carried out on Ni(211), Ni(111), and Ni(100) surfaces. In 2002, Bengaard et al.126 combined DFT calculations, microkinetic and Monte Carlo simulations, kinetic measurements, thermogravimetric analysis (TGA), and extended X-ray absorption spectroscopy (EXAFS) to present a comprehensive mechanistic picture of the SRM process on a Ni catalyst. DFT calculations were performed on step Ni(211) and flat Ni(111) surfaces, based on which potential energy diagrams of the full reaction were obtained. The methane activation was considered to be among the RDSs on the Ni(211) surface,125 which is consistent with the general RDS mapping in Fig. 8. Although Ni(111) exhibited a higher barrier, it has more available active sites because of more facet sites than step sites in a normal particle (except for extremely small particles). Therefore, the authors concluded that there are at least two types of active sites on a Ni catalyst: one is very active, related to certain step and surface defect sites; and the other is less active, related to the close-packed surfaces.
It is generally agreed that the CH–O route was energetically the most preferred pathway on the Ni(111) surface for CO formation.81,92,93,130,139–141 Wang et al.87 also confirmed the CH–O route as an energetically favorable pathway on Ni(211) as well as Ni(100) and Ni(111) surfaces from 773 to 848 K by microkinetic modeling. However, Blaylock et al.132 illustrated by multi-facet microkinetic modeling of Ni NPs consisting of Ni(111), Ni(211), and Ni(100) that the favorable reaction pathway depends on the reaction temperature. The C–O route was the most preferred pathway at high temperatures; however, at low temperatures, CH–O and C–OH routes were predicted to be more important. Dissociative chemisorption of methane and CO*/HCO*/COH* formation were the RDSs. Xu et al.133 compared the C–O route, CH–O route, and C–OH route on twelve TM stepped (211) surfaces by means of microkinetic modeling and demonstrated that the C–O route was the most favorable pathway owing to the highest estimated rates. CO formation was the RDS at 773 K. In summary, for Ni catalysts, direct CH4 dissociation is accepted as a dominant route for methane activation, although the exact reaction mechanism for CO formation is still under debate. The RDS can change with temperature and with Ni surfaces.
Rh, Ru, Pt, and Pd catalysts. Mei et al.128 obtained a lower activation barrier for the CH–O route (1.37 eV) than the C–O route (1.59 eV) on a Rh(111) surface. van Grootel et al.131 reported competition between the CH–O route and C–O route on a Rh(111) surface and that the CH–O route was slightly more favorable on a Rh(211) surface through a comparison of DFT calculated activation barriers. Inderwildi et al.142 observed a much lower activation barrier for the CH–O route (0.99 eV) than the C–O route (2.23 eV) on a Ru(0001) surface. Chen et al.97 suggested a dominant pathway of the C–O route on Pt(111) and Pt(211) surfaces. Wang et al.88 demonstrated a primary reaction pathway of the CH–O route involving HCOO* on a Pt(111) surface, while the route involving a CHOH* intermediate turned to be dominant in a moist environment, based on the DFT-calculated activation barrier. Since the SRM mechanism is controversial on different metal surfaces, and it is insufficient to determine the dominant pathway solely based on the activation barrier; microkinetic modeling was employed to further elucidate the mechanism by taking into account both energy and coverage effects.
The microkinetic modeling of steam and dry reforming by Maestri et al.83 predicted that the direct dissociation of the C–H bond was the main pathway of methane activation on Rh catalyst. The microkinetic can describe well the experimental results over a wide range. The microkinetic analysis showed that the CO formation took place by oxidation of the surface C* via C* + OH* → CO* + H*, and the CH3* dehydrogenation (CH3* + * → CH2* + H*) was the RDS for both steam and dry reforming.
Towards CO formation, the DFT calculations and microkinetic modeling study of Zhu et al.134 showed that the C–O route was the dominant pathway on Rh(211), Rh(111), Pt(533), and Pt(111) surfaces. The microkinetic modeling of Xu et al.133 indicated that the C–O route was more favorable on Ru and Rh(211) surfaces and that the C–OH route was more preferred on a Pt(211) surface. The DFT-based microkinetic modeling of Jørgensen et al.86 illustrated that the C–O route was more favorable at high temperatures and the C–OH route involving COH* and OCOH* intermediates was more preferred at low temperatures on Pd(111) and Pd(100) surfaces. The DFT and microkinetic study of Yoo et al.95 revealed that the HCO–H route dominated the reaction on a Pd(111) surface under mildly oxidizing conditions. Trinchero et al.84 reported a C–O route on (111), (100), (211), and (321) surfaces of Pt and Pd using DFT and microkinetic modeling. All the analyses point out that C–H bond activation in methane is among the RDSs, although there is a difference in the exact RDS. As shown in Fig. 8, the RDSs on Rh surfaces change with operating temperature. At relatively high temperatures, the H–CH3 could be the RDS, in accord with the microkinetic analysis by Maestri et al.83 The microkinetic analysis results agree with the experimental observation reported in the literature.77,123,143,144
To sum up, it seems that direct CH4 dissociation dominates methane activation for Ni, Rh, Ru, Pt, and Pd. The OH-assisted CH4 dissociation is limited by low OH* surface coverage, although sometimes it is energetically favorable. At the same time, the dominant routes for CO formation are dependent on the catalysts and the metal surfaces. The RDS of the total SRM reaction can change with temperature and with catalysts. The change in RDS with temperature is mainly caused by the large entropy loss of methane, which raises the reaction barrier of methane dissociation as the temperature increases. The change in the RDS with catalysts results from the distinct C–metal and O–metal binding energies on different metal surfaces, which are descriptors to probe the catalyst activity.
Size dependence of activity. In addition to mechanistic research, the metal particle size-dependent activity of SRM also attracted much attention in the previous study. The early work concerning the particle size effect on metal activity for SRM was mainly carried out through experimental measurements. Wei and Iglesia75–78,80 investigated the effects of metal dispersion on CH4 reforming turnover rates for Pt, Ir, Rh, Ru, and Ni catalysts. The forward CH4 turnover rates were observed to increase monotonically with the metal dispersions. Similarly, Jones et al.127 observed a linear relationship between the TOF and dispersion for Ru, Rh, Ni, Pt, Pd, and Ir catalysts, as shown in Fig. 6(b). Since dispersion is inversely proportional to particle size for not too small particles, the particle size effect on activity could be easily obtained; that is, the smaller the particle size, the higher the activity (turnover number) for the investigated metals. The activity was therefore considered to depend on the surface structure of the NPs, and the under-coordination sites (edges, kinks, and defects) were expected to be the active sites for SRM because of the larger fraction of under-coordinated surface sites exposed on small particles than larger particles.127,145,146 The DFT-based microkinetic modeling was subsequently employed to investigate the size-dependent activity. DFT calculations provide the reaction mechanism and kinetic parameters on specific surfaces such as Ni(111), Ni(100), and Ni(211). The multifaceted microkinetic model brings the bridge between the DFT calculation and the kinetics of nanoparticles.87,89,123
To gain insight into the size-dependent activity, Wang et al.87,89 reported an approach that combined microkinetic modeling with a truncated octahedron model to calculate the total activity based on the surface fraction and individual surface activity. The schematic diagram of a truncated octahedron model is shown in Fig. 9, which consists of fcc(111) and fcc(100) surfaces, where steps, edges, and corners are treated as an fcc(211) surface. The total reaction rate (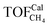 ) can be estimated by the sum of surface fraction (fi) times individual reaction rate (TOFi):
) can be estimated by the sum of surface fraction (fi) times individual reaction rate (TOFi):
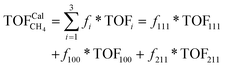 | (5) |
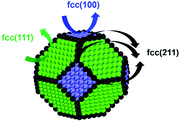 | ||
| Fig. 9 A truncated octahedron model consisting of fcc(111), fcc(100), and fcc(211) surfaces.89 Adapted from ref. 89 with permission from the American Chemical Society, copyright 2020. | ||
For Ni catalyst, the modeling well reproduced the size-dependent activity observed from the kinetic study, namely lower activity on larger sized Ni particles (Fig. 10b).87 The size-dependent activity was found to result from the surface-dependent activity. Ni(211) was the most active surface for SRM (Fig. 10a), and the decreased Ni(211) surface fraction with increasing particle size resulted in reduced Ni activity (Fig. 10b). The Ni(111) activity was limited by a high energy barrier, and the Ni(100) activity was limited by surface blockage related to C* and CH* deposition (Fig. 11a). The study also demonstrated that stabilizing Ni catalysts with particle sizes ≤6 nm (Fig. 10b) could be a good strategy to achieve high activity for SRM reaction. The apparent activation energies calculated from the modeling were 1.13–1.21 eV with the Ni particle size in the range of 8 nm to 12 nm, which was in good agreement with the results measured by experiments, 1.06–1.17 eV for 8–12 nm. These values were also close to the experimental data reported by Wei and Iglesia (1.06 eV),80 Nikolla et al. (1.05 ± 0.04 eV),147 Zeppieri et al. (1.00 ± 0.02 eV),148 and Niu et al. (1.08 eV).92 Moreover, the combined model predicted well the change in the apparent activation energy with Ni particle size, i.e., lower activation energy on larger sized Ni particles. Niu et al.92 reported an effective activation energy of 1.12 eV based on a DFT calculated G plot, also consistent with the experimental values on Ni catalysts. This demonstrated that microkinetic modeling and/or DFT are feasible approaches to characterize the real kinetic properties.
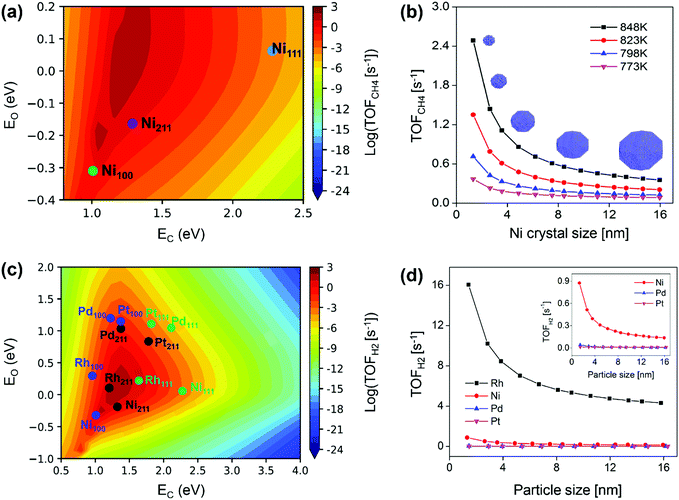 | ||
| Fig. 10 Modeling predicted forward CH4 turnover frequency as a function of (a) C and O formation energies in SRM on Ni(111), Ni(211), and Ni(100) surfaces at 773 K, and (b) Ni particle size (1.3–16 nm) at 773, 798, 823, and 848 K.87 Reproduced from ref. 87 with permission from Elsevier, copyright 2019. (c) Predicted activity for H2 production over M(111) (green), M(211) (black), and M(100) (blue) surfaces. M denotes Ni, Pd, Pt, and Rh. (d) TOFH2 as a function of particle size for Ni, Pd, Pt, and Rh NPs. Reaction conditions: 773 K, 1 bar, S/C = 3.5, and CH4/H2 = 1.0.89 Reproduced from ref. 89 with permission from the American Chemical Society, copyright 2020. | ||
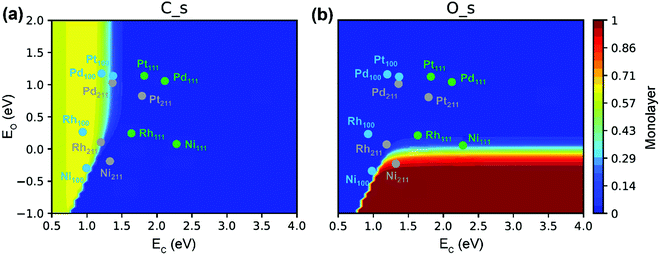 | ||
| Fig. 11 (a) O* and (b) C* site coverages as functions of C- and O-metal formation energies in SRM. Reaction conditions: 773 K, 1 bar, 18.2% CH4, 63.6% H2O, 18.2% H2.89 Adapted from ref. 89 with permission from the American Chemical Society, copyright 2020. | ||
The size-dependent activity of SRM on Rh, Ru and Pt catalysts follows the same trend as that on Ni, namely, the smaller the particle size, the higher the activity.75–77,80,127,149 Wang et al.89 also provided a systematic and in-depth understanding of the size-dependent activity on Rh, Ni, Pd, and Pt catalysts by combining microkinetic modeling with a truncated octahedron model. The modeling predicted activity of H2 production in SRM on each metal surface is shown in Fig. 10(c). It was found that the M(211) surface is most active for Rh, Ni, and Pd catalysts, while for Pt, the M(100) surface is most active. The total activity was estimated by the sum of individual TOF on each surface multiplied by the surface fraction, based on that, the total TOF against particle size is plotted in Fig. 10(d). The TOFs were observed to be inversely proportional to particle size and linearly related to dispersion, in good agreement with reported experimental results.75–77,80,127,149 The linear scaling between TOFs and dispersion was associated with a linear relationship between surface fractions and dispersion. M(211) was the active surface, and the increased M(211) surface fraction along with increased dispersion led to enhanced NP activity at smaller NP size. As for metal-dependent activity, the catalytic activity of SRM followed Rh > Ni > Pd ∼ Pt for both small and large particles. Compared to Rh, the activity of Ni was limited by surface blocking, and the activities of Pt and Pd were limited by high free energy barriers. Although Rh exhibits very high activity, other noble metals such as Ru, Pt, Pd, and Ir are also active for SRM, but these metals are usually too expensive to be applied in conventional industrial reformers. Developing appropriate methods to combine Ni-based catalysts with these noble metals to achieve both enhanced activity and catalyst resistance to carbon deposition seems like a cost-effective way and a promising subject of SRM study in the future.
Catalysts improving carbon formation resistance. Although the use of Ni-based catalysts for SRM is a relatively mature technology, catalyst deactivation through carbon formation, poisoning and sintering tends to occur on the Ni surface, which is an important challenge and is among the subjects of active research.133 Among them, carbon formation is the most common and significant challenge for Ni-based catalysts. Several types of carbon have been reported on the catalysts towards methane reforming and decomposition,150 with atomic carbon, encapsulating carbon, and filamentous carbon being the most important.151 It is generally accepted that the growth of filamentous carbon involves decomposition of the carbon-containing gas to carbon adsorbed on the metal surface, dissolution/segregation of carbon into the bulk, diffusion of carbon through Ni particles to surfaces that are suitable for filament growth, and precipitation of filaments.152 Chen et al.151 performed a microkinetic analysis of deactivation during DRM over Ni catalyst, where both filamentous carbon and encapsulating carbon were assumed to generate from a surface carbon (C*) precursor. The carbon formation was dependent on the concentration of surface C*, and different operating conditions affected the coking rate through changes in *C site coverage. It was suggested that the formation of monolayer encapsulating carbon blocked the active sites and hence deactivated the methane reforming, the filamentous carbon formation and the encapsulating carbon formation itself.
The C* site coverage is an important parameter to characterize carbon formation. Both experimental and DFT studies of Nørskov and co-workers126,153 suggested that the nucleation of graphene on Ni catalysts was initiated at the stepped Ni(211) sites. If the surfaces or step edges are too small, the nucleation cannot proceed, thereby further inhibiting the graphene formation. This explains why very small particles cannot grow filamentous carbon under normal conditions. However, the recent microkinetic modeling of Wang et al.89 demonstrated carbon deposition on a Ni(100) surface (Fig. 11a). The absence of graphene formation on very small particles is related to the very low surface fraction of Ni(100), which is an energetically preferred facet of Ni for the formation of carbon. The carbon deposition phenomenon on Ni(100) has also been reported by Schouten et al. towards methane decomposition reaction.154,155 Moreover, Eizenberg and Blakely observed the formation of monolayer graphene on a Ni(100) surface in experiments.156,157 According to Fig. 11(a), in addition to Ni(100), the Rh(100), Pt(100) and Pd(100) surfaces as well as Rh(211) and Pd(211) surfaces could also suffer from carbon deposition because of the strong carbon binding energy. In contrast, the Ni(211) surface is poisoned primarily by surface O* due to relatively strong O binding energy (Fig. 11b). The active surface for carbon formation is, therefore, still under debate.
High temperature and pressure are beneficial to the removal of carbon formation, based on the thermodynamic analysis.158,159 It was found that for temperatures above 1100 K there is no possibility of carbon formation for the steam-to-methane ratios above unity. For temperatures below 1100 K, carbon formation removal could be done by increasing the pressure. Therefore, for large-scale hydrogen production through SRM, the pressure is above 10 bar.
Ni-based bimetallic catalysts by alloying Ni (the active metal) with another metal (e.g. Au,160 Ru,161 Rh,55 Co,162 Pt,163,164 Ag,165 and Sn166) are generally used to reduce methane dissociation and enhance the surface reaction of carbon removal, which could effectively increase catalyst resistance to deactivation and improve catalyst stability. Besenbacher et al.160 combined molecular beam scattering experiments, scanning tunneling microscopy (STM), and DFT calculations to design a surface alloy for steam reforming. It was demonstrated that alloying Au into the surface layer of Ni could effectively improve the catalyst performance, achieving high resistance to carbon formation, which was confirmed by experimental results. Nikolla et al.166 conducted a DFT study to investigate the effect of a Ni-containing alloy on C deposition relative to monometallic Ni and indicated that the growth of carbon deposits was inhibited by Sn alloying of Ni.
Ni-Based bimetallic catalysts with alloy metals such as Ru, Rh, Pd, Ag, Pt, Cu, and Au were investigated by Fan et al.167 for methane dissociation. The DFT-calculated potential energy diagrams are shown in Fig. 12. They demonstrated that the Cu- and Ag-modified surfaces were energetically more favorable than the bare Ni surface for dissociation reactions. For CH4* dissociation, the activation barriers on Ru/Ni(111) (0.65 eV), Rh/Ni(111) (0.77 eV), and Cu/Ni(111) (0.88 eV) were lower than that on Ni(111) (0.92 eV). On the other hand, the DFT-calculated C adsorption energies on Pt/Ni(111), Pd/Ni(111), Au/Ni(111), and Rh/Ni(111) were less negative than that on Ni(111), indicating that coke formation was suppressed to a certain extent on these bimetallic catalysts. The Ni–Rh bimetallic catalyst was therefore suggested as a good candidate for methane dissociation due to improvement in both activity and stability, which has been verified by experimental observations.168,169
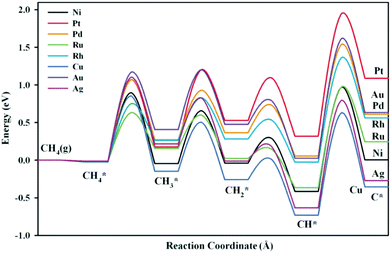 | ||
| Fig. 12 Potential energy diagrams for methane dissociation on Ni-based bimetallic surfaces. The chemisorbed H atoms required to balance adsorption states have been omitted to simplify the notation.167 Reproduced from ref. 167 with permission from AIP Publishing, copyright 2012. | ||
Xu et al.170 studied the effect of Ag on the control of Ni-catalyzed carbon formation by DFT calculations. The addition of Ag into Ni catalysts reduced the catalytic activity towards SRM but enhanced coke formation resistance. Liu et al.171 reported that segregated NiCu was a good SRM catalyst to suppress coke formation, which displayed the highest carbon deposition resistance among Ni, Fe, Co, Cu, NiFe, NiCo, NiCu, and segregated NiCu catalysts via DFT study. Yoon et al.135 compared Ni, Ni–Ru, and Ni–Rh bimetallic catalysts for SRM through DFT calculations, which demonstrated that alloying Ni with Ru could be an effective way to greatly enhance the catalytic efficiency and reduce carbon deposition. Niu et al.92 performed DFT studies on Ni, Pt, and Ni@Pt catalysts for SRM reaction, which revealed that core–shell structured Ni@Pt showed a lower activation barrier for CH and C oxidation but a higher activation barrier for CH dissociation to form C. The Ni@Pt catalyst was found to significantly inhibit carbon formation without sacrificing much activity. To summarize, the Ni–Rh, Ni–Ru, and Ni–Pt alloys are promising bimetallic catalysts to effectively increase catalyst resistance to carbon deposition without sacrificing much activity or even with enhanced activity for SRM reaction.
Reaction mechanism of DRM. The mechanism of DRM over Ni catalysts has been extensively investigated experimentally. The isotopic kinetics study of Wei and Iglesia80 indicated that the initial C–H bond activation of methane was the sole kinetically-relevant step for DRM on Ni catalysts. However, some other researchers argued that carbon oxidation,173–175 the surface reaction between CHx* and O*,176 or CHxO decomposition177,178 could be the RDS for Ni-based catalysts. The controversial observation could be related to the factor that the mechanism is a function of operating conditions. Using transient isotopic approaches and microkinetic modeling, Aparicio125 suggested that there was no single RDS in methane reforming over Ni catalysts. Under certain conditions, the availability of surface oxygen may play a key role in determining the rate. Bradford and Vannice179 proposed a reaction model for DRM, where CH4 dissociation and CHxO decomposition were assumed as RDSs, which correlates experimental data successfully. The same RDSs were obtained by Nandini et al.180 over the Ni–K/CeO2–Al2O3 catalyst. The kinetic study of Cui et al.181 indicated that CH4 dissociation was the RDS at low temperature, while the reaction between CO2 and CHx became the RDS at high temperature. Zhang et al.182 developed a Langmuir–Hinshelwood (L–H) model, assuming CH4 dissociation and the reaction between activated CO2 and the C species as RDSs over a Ni–Co/Al–Mg–O catalyst, which agrees well with the experimental data. Despite the numerous experimental studies devoted to investigating the mechanism of DRM, there are still arguments between different researchers. The theoretical studies were therefore employed to further elucidate the reaction mechanism of DRM.
The theoretical DRM mechanism is usually interpreted in terms of CH4 activation, CO2 activation, and CO formation. CH4 activation was generally believed to take place via the direct dissociation route, which has been reviewed in detail in Section 2.1.1. CO formation pathways are the same as those in SRM reaction. CH* and C* are the critical intermediates for surface oxidation by O* or OH*. CO2 activation is the key step that is different from SRM.
CO2 activation. Concerning CO2 activation, the direct decomposition (CO2 → CO + O) and H-induced CO2 decomposition (CO2 + H → COOH → CO + OH) were considered by Zhu et al.93 on a Ni(111) surface. The geometries of the initial states, intermediates, and transition states for CO2 decomposition obtained from DFT calculations are shown in Fig. 13(a–f). The total energy and free energy diagrams for the two routes on the Ni(111) surface are given in Fig. 13(g). It was observed that the CO2 direct decomposition was energetically more favorable than H-induced CO2 decomposition. The CO2 direct decomposition was also supported by Jiao and co-workers on both Ni(111) and Ni(211) surfaces.81,82,183,184
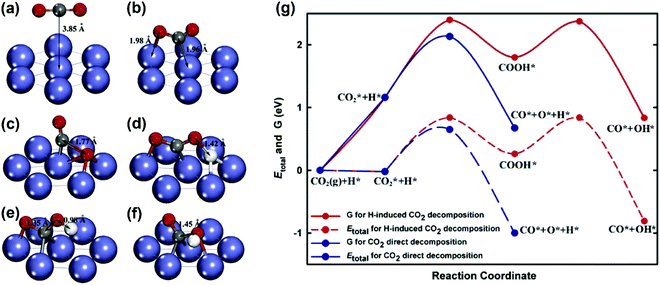 | ||
| Fig. 13 Geometries of (a) the physisorbed CO2 on Ni(111), (b) the chemisorbed CO2 on Ni(111), (c) the transition state for CO2 decomposition via the direct pathway, (d) the transition state for the H-inducted CO2 decomposition, (e) the intermediate for the H-induced CO2 decomposition, and (f) the transition state for COOH dissociation to generate CO and OH, and (g) total energy and Gibbs free energy diagrams for the CO2 direct decomposition and H-induced CO2 decomposition on Ni(111).93 Reproduced from ref. 93 with permission from Elsevier, copyright 2009. | ||
CO2 activation on other metals has also attracted some attention.185,186 Ko et al.185 systematically investigated CO2 activation and dissociation on a series of pure metal surfaces and bimetallic alloy surfaces by using DFT calculations. The scaling relations (Fig. 14a) were obtained, where the reaction heat ΔE(CO2δ−) of CO2 dissociation scaled linearly with the sum of the adsorption heats of CO and O over various pure metal surfaces. Meanwhile, the BEP relationships were suitable (see Fig. 14b), with the CO2δ− dissociation barrier linearly correlated with ΔE(CO2δ−). In light of this fact, the activation energies of CO2 dissociation over pure metal and bimetallic surfaces could be rapidly predicted by combining the surface mixing rule, scaling relation, and BEP relationship, as illustrated in Fig. 14(c). The barrier increases from left to right and from top to bottom. Fe, Ru, Co, Ni, Rh, and Ir pure metals as well as Fe-, Ru-, Co-, Ni-, Rh-, and Ir-based bimetallic alloys exhibited relatively low Eacta values (∼0.75 eV). Pd, Pt, and Cu pure metals as well as Ru-, Co-, Ni-, Rh-, Ir-, and Cu-based bimetallic alloys showed moderate Eacta values (0.76–1.50 eV). Au and Ag pure metals as well as Pd-, Pt-, and Cu-based bimetallic alloys were observed to take high Eacta values (1.51 eV).
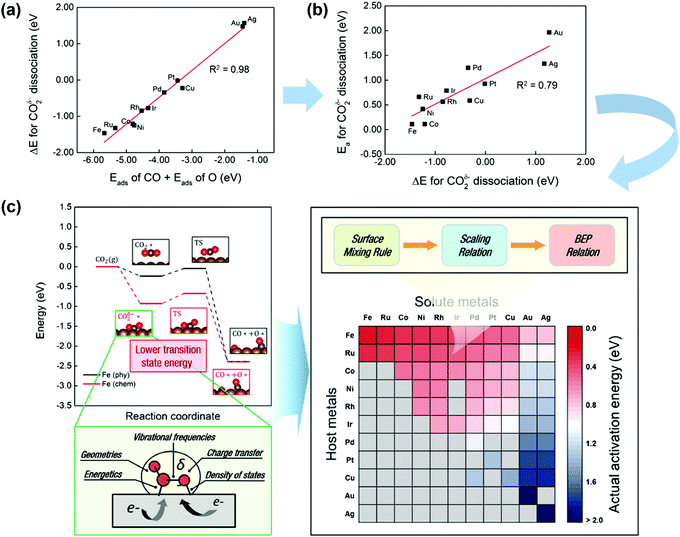 | ||
| Fig. 14 (a) Scaling relations between Eads(CO) + Eads(O) and ΔE(CO2δ−) on TM surfaces. (b) BEP relationships for CO2δ− dissociation. (c) CO2 activation pathways and screening for Eacta for CO2 dissociation on pure metals and bimetallic alloys. Gray cells indicate that the bimetallic alloys are not preferred for the surface segregation of solute atoms. Here, Eacta is estimated by combining the BEP relation, scaling relation, and surface mixing rule.185 Reproduced from ref. 185 with permission from the American Chemical Society, copyright 2016. | ||
Support and promoter effects are important factors in facilitating CO2 activation. Kattel et al.187 combined DFT calculations, kinetic Monte Carlo (kMC) simulations, and experimental measurements to investigate CO2 hydrogenation over Pt, Pt/SiO2, and Pt/TiO2 catalysts. It was found that Pt NPs alone were not able to catalyze CO2 activation due to the weak bonding with CO2. Once CO2 was stabilized, for example by using SiO2 or defected TiO2 with O vacancy as the support for Pt NPs, the overall CO2 conversion would be enhanced via increased CO2 binding. Pt/TiO2 exhibited more significant enhancement than Pt/SiO2 and thus higher activity. Yang et al.188 studied the reduction of CO2 by hydrogen over Au/TiO2 and Au/CeOx/TiO2 surfaces. On Au3/TiO2, the reaction was suppressed by the relatively large barrier (1.23 eV) for the activation of *CO2 to **CO2, which was significantly promoted in the presence of CeOx (0.16 eV). On Au/CeOx/TiO2, an electronic metal–support interaction resulted in a charge redistribution in the metal around the Au–ceria interface. Such surface electronic polarization at the metal–oxide interface enhanced both CO2 adsorption and activation. Niu et al.189 employed both kinetic studies and DFT calculations to investigate the effect of oxide additives (CeO2, ZrO2, ZnO) on hydrotalcite-derived Ni catalysts for DRM reaction. Regarding CO2 activation, the apparent activation energies obtained from the Arrhenius plot for CeO2–Ni (0.62 eV) and ZrO2–Ni (0.64 eV) were lower than that of Ni (0.68 eV). In contrast, ZnO–Ni exhibited a higher activation barrier (0.77 eV) than Ni. It was suggested that the addition of CeO2 and ZrO2 could lower the CO2 activation energy on Ni catalyst, thus promoting CO2 dissociation to CO and O. The authors also calculated the TOF based on Gibbs free energy, which was 5.92 s−1 at 1023 K for CO2 activation on the support, very close to the experimental value (6.13 s−1 at 1023 K), but much higher than that on the Ni surface (4.42 × 10−6 s−1). This demonstrated that the oxides played a significant role in CO2 activation in DRM reaction.
For the overall DRM reaction, DFT-based microkinetic modeling was applied to explore the mechanism on various metal surfaces such as Ni(111),85,94 Ni(100),94 Ni(211),94 Pt(111),85,190 and Pd(111).85 Regardless of the catalyst surface, direct dissociation was favored for C–H bond activation of methane. Direct dissociation is a preferred route for CO2 activation on Ni,85,94 but the H-assisted route via the COOH* intermediate is preferred for Pt and Pd catalysts.85,190 However, different preferred routes for CO formation such as C* + O* on Ni,94 CH* + O* on Ni(111), Pt(111) and Pt(111),85 and CH* + OH* on Pt(111)190 were proposed by different studies. The mechanism is very similar to the one of SRM. The RDS was dependent on operating conditions. At high CH4 and CO2 partial pressures, carbon oxidation was suggested as the RDS, while at low pressures, both CH4 dissociative adsorption and C oxidation would jointly determine the overall reaction rate for the DRM reaction.94 Since DRM has attracted more and more attention due to environmental effects, the DRM mechanism is still under debate, and more theoretical studies are essential to gain insight into the reaction, further aiding the rational design of catalysts.
Metal dependence of activity. Like SRM, the DRM reaction is active on metal catalysts, such as Ni, Ru, Rh, Pt, Pd, Ir, and Co.123,191–193 As discussed above, the C–H activation and CH and/or C reaction with surface O* are kinetically relevant steps in DRM. Besides, the CO2 activation leading to surface O* formation is a function of support. Therefore, the metal dependence of the dry reforming activity depends also on the support used. Rostrup–Nielsen and Bak Hansen obtained an activity tendency on a TOF basis as Ru > Rh > Ni > Ir > Pt > Pd on a MgO support123 like SRM.127 Solymosi et al. reported an activity (in terms of turnover number) trend in the order of Ru > Pd > Rh > Pt > Ir on an Al2O3 support for the DRM process.193 Ferreira-Aparicio et al. observed a TOF tendency of Rh > Ni > Ir > Ru–Pt > Co on an Al2O3 support, and Ni > Ru > Rh–Ir > Co–Pt on a SiO2 support.191 Although the metal performances have some differences among different supports and different studies, Ni catalyst is of particular interest in DRM because it is less expensive than noble metals and exhibits relatively high activity.63
Size dependence of activity. The kinetic study of Wei and Iglesia75,80 illustrated a positive size-dependent activity for DRM on Pt, Ir, Ni, Rh, and Ru catalysts, namely the smaller the metal NPs, the higher the activities. The size dependence of the activity of DRM is similar to the one of SRM, as discussed in Section 2.2.1. Similarly, Lustemberg et al.194 reported that Ni–ceria systems involving the smallest highly dispersed Ni particles were more efficient for methane activation and reforming than larger particles. This is related to the strong metal–support interactions, which affect the charge transfer between Ni particles and ceria. Small Ni particles on stoichiometric ceria undergo large electronic perturbations, which lead to a relatively low activation barrier of the first C–H bond cleavage of methane, compared to extended Ni surfaces. However, recently, Vogt et al.195 established a volcano behavior of size-dependent activity for SRM and DRM at 773 and 873 K, and 5 bar, where the optimal Ni particle size was approximately 2–3 nm. Ni particles smaller than 2.5 nm exhibited a different structure sensitivity from that expected from the above literature. CH4 activation, CO2 activation, and CO formation were possibly important kinetically limiting steps for DRM.
Catalyst improvement. Carbon formation on Ni-based catalysts is the main obstacle to the commercialization of DRM.140 To investigate the carbon formation scheme on Ni-based catalysts, Wang et al.140 compared the whole reaction network of DRM over flat Ni(111) and step Ni(211) surfaces, as well as flat Ni3C(001) and step Ni3C(111) by DFT calculations. The kinetic analysis illustrated an activity order of Ni(111) > Ni3C(001) > Ni(211) > Ni3C(111) for DRM. That is, flat surfaces were more active than step surfaces, and metallic Ni catalysts were more active than nickel carbide. Therefore, the formation of nickel carbide would reduce the catalytic activity on both flat and step surfaces. With respect to carbon formation, the authors suggested that the rate ratio of the CH oxidation route to the C oxidation route (rCH/rC) coupled with the CO dissociation barrier could be used to measure the carbon formation probability. Ni(111) was found to exhibit both the highest activity and the best carbon resistance.
In addition to pure metal catalysts, a few theoretical studies have been employed to investigate the mechanism on Ni catalysts with supports, promoters, and Ni-based bimetallic catalysts for DRM reaction with improved performance. The experimental and computational studies of Akri et al. revealed that Ni atomically dispersed over Ce-doped hydroxyapatite (HAP-Ce) was highly active and intrinsically coke-resistant due to strong metal–support interactions, which favor only the first C–H bond activation in methane and stabilize Ni single atoms towards sintering.196 The DFT studies of Rodriguez and coworkers194,197,198 indicated that the effective barrier of methane activation decreased from 0.9 eV over a Ni(111) surface to only 0.15 eV over a Ni/CeO2−x(111) surface (Fig. 15). The electronic or chemical properties of Ni were modified with CeO2 through strong metal–support interactions. The strong interactions enhanced the Ni reactivity for methane dissociation and probably prevented carbon deposition and deactivation during DRM.197 Moreover, a decrease in the barrier of the first C–H bond activation of methane from 1.07 eV over the Co(0001) surface to 0.87 eV over the Co2+/CeO2(111) surface, and to only 0.05 eV over the Co0/CeO2−x(111) surface, was obtained by Liu et al.198 through DFT calculations. This suggests that the reduction degree of the CeO2 or oxygen vacancy is vital for the activity of Ni/Co sites. The Ni/Co cation on CeO2 shows a much lower activity for C–H activation of methane compared to the Ni/Co cation on reduced CeO2 (Ce2O3). CO2 dissociation was observed to take place on the oxide surface at 700 K, under DRM conditions, and no coke deposition was found in the catalytic cycle. CeO2 is an efficient support that can play an essential role in the DRM process. In contrast, single-site Ni1/Mg(100) was not active for CO2 and CH4 dissociation, while Ni4/MgO(100) enabled the formation of H2, CO, and H2O under DRM reaction, revealed by combined DFT, kMC simulation, and experimental studies.199 The Ni cluster provided the active sites, and MgO offered the Mgvac as an anchor for Ni clusters to prevent Ni aggregation. The study revealed that the oxygen vacancy enhanced the C–H activation of methane. However, the whole catalytic cycle involving the oxygen vacancy was not analyzed. It is highly desired to analyze the elementary reaction steps at the metal–oxide interface in the catalytic cycle to gain a better understanding of the role of the interface in DRM.
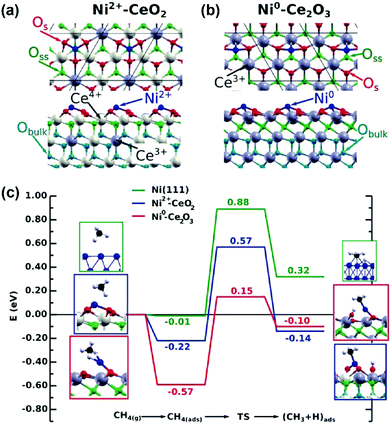 | ||
| Fig. 15 Atomic structures of Ni adsorbed on (a) CeO2(111) and (b) Ce2O3(0001). (c) Reaction energy profiles for the CH4 → CH3 + H reaction on Ni(111), Ni2+/CeO2(111), and Ni0/Ce2O3(0001). The structures shown on the left and right of the reaction pathways correspond to the side views of the optimized initial (molecularly adsorbed) and final (dissociated) states used in search of the transition state. Os = surface oxygen atoms, Oss = subsurface oxygen atoms, and Obulk = bulk oxygen atoms.197 Reproduced from ref. 197 with permission from Wiley-VCH, copyright 2016. | ||
Foppa et al.200 employed a multiscale (DFT and microkinetic) modeling approach to investigate the role of a Ni/Al2O3 interface in WGS (water–gas shift) and DRM. The Ni/Al2O3 interface provided the active site for WGS, while all Ni atoms were active for DRM, which was confirmed by the experimental measurements. Li et al.201 combined DFT, CO2-TPD, and in situ DRIFTS to investigate the interfacial synergism of Ni/La2O3 catalysts towards CO2 activation in DRM. They proposed a mechanism that CH4 activation occurred on the Ni surface to form H2 and activated coke precursors. CO2 activation took place at the Ni/La2O3 interface to generate bidentate carbonate. Then bidentate carbonate underwent a reaction with adjacent activated coke precursors to generate CO. Therefore, carbon deposition was avoided at the Ni/La2O3 interface. The more the Ni/La2O3 interface existed, the better the stability by inhibiting the coke deposition.
Li et al.202 combined DFT and microkinetic modeling to investigate the DRM reaction mechanism on a Ni(111) surface with La and La2O3 as promoters. For La modified Ni(111), the dominant pathway was CH4 + CO2 → CH + 3H + CO + O → CHO + 3H + CO → 2CO + 2H2, with CH + O → CHO as the RDS. For La2O3 modified Ni(111), CH4 + CO2 + La2O3 → CH + CO2(La2O2–O) + 3H CHO + CO2(La2O2) + 3H → 2CO + 2H2 + La2O3 was the dominant reaction pathway, with CH4 → CH3 + H as the RDS. The modified catalysts improved the DRM reaction both thermodynamically and kinetically. Moreover, the carbon deposition was inhibited on La2O3 modified Ni(111) because of the lower reaction rate in CH → C + H, compared to that on La modified Ni(111).
For Ni-based bimetallic catalysts, NiSn was observed to favor methane dissociation,203 and reduce coke formation204 more than pure Ni catalysts for DRM via both theoretical and experimental studies. NiFe bimetallic catalysts suppressed coke deposition due to the increased energy barrier of CH → C + H, in comparison to that on a pure Ni(111) surface.205 Furthermore, under DRM conditions, Fe was oxidized partially to FeO, leading to a partial dealloying. FeO could react with surface carbon deposits to form CO, where the reduced Fe returned to the original NiFe alloy.205,206 The FeO/Ni(111) interface exhibited easier C–O bond cleavage of CO2 and dehydrogenation of CHx (x = 1–3). Therefore, both improved DRM reactivity and coke resistance were obtained on NiFe catalysts. The Ni2Cu(111) catalyst displayed superior carbon deposition resistance compared to Ni(111) and Ni2Fe(111) due to the higher energy barrier of CH dissociation. It could also improve carbon elimination by enhancing C* + O* reaction, resulting in improved catalyst stability.207 NiPt bimetallic catalysts showed higher reaction barriers for CH cracking and lower carbon adsorption energy than that on pure Ni(111), which decreased the possibility of coke formation. It can be concluded that the use of supports, promoters, and Ni-based bimetallic catalysts can effectively suppress coke formation on Ni surfaces. Meanwhile, some supports, such as CeO2, promoters such as La2O3, and Ni-based bimetallic catalysts such as NiSn and NiFe can improve the metal activity for DRM due to enhanced methane activation.
Metal dependence of the reaction mechanism. Although many studies have been carried out to elucidate the mechanism of POM reaction, the mechanism of synthesis gas formation is not yet completely clarified. In the literature, two reaction mechanisms have been proposed for POM reaction: one is the “direct partial oxidation” (DPO) mechanism, in which CH4 and O2 react on the catalyst surface to generate CO and H2 directly; and the other is the “combustion and reforming reaction” (CRR) mechanism, which involves total methane combustion to form H2O and CO2 first, followed by SRM and DRM to produce CO and H2.38,48,69,70,211,212 The latter mechanism was suggested by Prettre et al.213 as early as 1945, but due to the highly desired direct selective route to produce synthesis gas, significant efforts have been made towards investigating whether this can be achieved in practice.69
Rh and Pt are two of the most widely used catalysts in POM reaction.214 The first simulations on POM over Pt and Rh surfaces were reported by Hickmann and Schmidt,69,215,216 using a model with 19 elementary steps containing adsorption, desorption, and surface reactions. The reaction parameters were obtained from the literature or from fitting to previous experiments. The model results demonstrated that at high temperatures with CH4-rich conditions, CO and H2 were primary products of direct methane oxidation via a pyrolysis mechanism. The superiority of Rh over Pt towards the direct oxidation of methane to CO and H2 was due primarily to the much lower activation barrier of OH formation from O* and H* on Pt than that on Rh (0.11 eV for Pt vs. 0.87 eV for Rh).
Boucouvalas et al.217 conducted a kinetic study of POM over supported Rh catalysts. The calculated apparent activation energy of CO2 formation was around 0.35 eV, which was close to that of methane conversion (∼0.39 eV). In contrast, the apparent activation energy of CO formation was 0.88–1.13 eV, close to those for CO production from SRM and DRM,123,217–219 and much higher than that for CO2 formation. It was suggested that the POM followed an indirect (CRR) mechanism; namely, the reaction initially involved total oxidation of methane to CO2 and H2O, followed by reforming reactions to synthesis gas. The kinetic study reported by Kondratenko et al.210 also illustrated that CO and H2 were mainly produced through SRM and DRM at least in the case of complete oxygen conversion. Donazzi et al.143 carried out a kinetic study of POM over a Rh/α-Al2O3 catalyst, with SRM, DRM, WGS, reverse-WGS, CO and H2 combustion tests also conducted to refine the study. It was found that under the POM conditions the kinetic role of DRM is negligible; therefore SRM and CH4 total combustion account for the consumption of methane.
Mallens et al.220 employed a transient kinetic study to investigate the reaction mechanism of POM to synthesis gas over Pt. The methane decomposition took place on reduced platinum and resulted in surface C* and H*, which produced CO and CO2 in parallel by the involvement of different oxygen species. In the presence of both CH4 and O2 at a stoichiometric feed ratio, the major reaction pathways were the direct formation of H2 and CO followed by their consecutive oxidation. Based on the study, a Mars–van Krevelen (MVK) redox cycle221 was postulated for POM over Pt: the methane oxidation was accompanied by the reduction of platinum oxide, which was re-oxidized via incorporation of dioxygen into the catalyst.
In view of the controversy in the POM mechanism, it is of great significance to further elucidate the reaction from a microscopic perspective. Mhadeshwar and Vlachos222 developed a thermodynamically consistent C1 microkinetic model for POM, SRM, DRM, and oxygenate decomposition on Rh using a hierarchical multiscale methodology with parameters obtained from combined UBI-QEP and DFT calculations. The model predicted distinct oxidation and reforming zones, where CO and H2O were the primary products that existed in the oxidation zone. H2 was produced from methane reforming by H2O generated in the oxidation zone. Matteo et al.223 integrated a microkinetic model224 with detailed reactor models225 to investigate the dominant reaction pathways for syngas production in POM on Rh. Three reaction zones were suggested: deep combustion of a methane zone (O* is the most abundant reactive intermediate), followed by a zone where both direct formation of synthesis gas and catalytic combustion occur, and, finally, a SRM and WGS zone (oxygen is no longer available). Zone II and zone III were supported by the microkinetic study of spatially resolved autothermal POM experiments reported by Donazzi et al.226 over Rh-coated foams. Besides, the reaction pathway analysis of Donazzi et al.226 showed that methane was activated via pyrolytic decomposition, and the main oxidizer was OH* rather than O*. In the oxidation zone (zone II), OH* was generated from O* and H* combination, while in the reforming zone (zone III), OH* was formed by H2O dissociation.
Mhadeshwar and Vlachos214 developed a predictive CH4 (C1) mechanism on Pt by using a hierarchical multiscale approach. They concluded that POM on Pt was indirect, where total oxidation occurred first to form CO2 and H2O, followed by SRM and DRM to generate CO and H2, consistent with modeled experimental data. The combined kinetic and DFT studies of CH4 oxidation on Pt and Rh clusters by Chin et al.227 confirmed that POM to CO and H2 followed an indirect mechanism at the molecular scale. CO and H2 were predominantly produced upon complete O2 consumption from the sequential reforming steps. Based on the above kinetic and microkinetic studies, it is generally accepted that there is no unified mechanism of POM to synthesis gas and that even for the same catalyst the process might follow different reaction routes depending on the reaction conditions and the state of the catalyst.
Au et al.228 gave a detailed theoretical study of POM to synthesis gas on Ni, Pd, Pt and Cu catalysts, where adsorption energies were calculated using the Amsterdam density functional (ADF) program system, and activation energies were estimated by the UBI-QEP method. These metals were simulated by Ni7, Pd10, Pt10, and Cu10 clusters. The calculated total methane dissociation energies followed the trend of Ni < Pd ≈ Pt, corresponding to the experimental tendency in methane conversions as Ni > Pd ≈ Pt. The rather high activation energy of discrete dehydrogenation steps on Cu explains why Cu is not active for methane dissociation. C* + O* → CO* was the RDS on Ni due to the higher activation energy than those of dehydrogenations (CHx,s → CHx−1,s). On the other hand, on Pd, Pt, and Cu, CH* dissociation (CH* → C* + H*) was the RDS because of the highest activation energies. The calculation also indicated that gas-phase CO could easily combine with O* to form CO2. The CO2 selectivity was, therefore, dependent on the amount of adsorbed O* present on the surface. High CO selectivity can be obtained in an oxygen-depleted environment.
Metal dependence of the activity. Like SRM, POM reaction is active on noble metals such as Rh, Ru, Ir, Pt, and Pd, with Rh and Ru being the most active, and on non-noble metals like Ni and Co.38,42,70,210,211 For non-noble metal catalysts, Ni-based catalysts display the highest activity, which is even comparable to that of noble metal catalysts.42 Nevertheless, rapid catalyst deactivation caused by carbon deposition as well as loss and sintering of Ni under POM reaction conditions is a major problem that occurred on Ni-based catalysts.141 Consistent with the mechanism of POM with total oxidation followed with SRM, the activity order of POM on these metals is similar to that of SRM, namely Rh ≈ Ru > Ni ≥ Ir ≥ Pt, Pd,48,127,210 which has been discussed in Section 2.2.1. The relative order of carbon formation was observed as Ni > Pd ≫ Rh, Ru, Ir, Pt, reported by Claridge and Battle et al.48,229
Yoo et al.95 employed DFT and microkinetic modeling to investigate methane oxidation to CO, CO2, CH2O, and CH3OH over a Pd(111) surface under mildly oxidizing conditions. CO and CH2O were found to be the main products. The CO selectivity was greater than 0.5 and normally increased with increasing temperature, while the CH2O selectivity was less than 0.4 with a maximum at 550 K. In addition to Pd(111), the authors also extended the study to other metal fcc(111) surfaces by employing linear scaling relations in the microkinetic model. The obtained volcano plots of the product reaction rates are given in Fig. 16. Pd, Pt, and Rh(111) surfaces were selective to CO and/or CH2O productions, where the metallic site led to CO production, and the surface O* site led to CH2O production. Ag, Au, and Cu(111) surfaces were selective to CH2O and/or CH3OH productions, with the O*-assisted mechanism preferred for all dehydrogenation steps.
 | ||
| Fig. 16 Logarithms of the calculated production rates (s−1 per site) of (a) CO2, (b) CO, (c) CH2O, and (d) CH3OH during CH4 oxidation at T = 523 K, PCH4 = 0.91 bar, PO2 = 0.11 bar, PH2O = 0.02 bar, and PH2, PCH3OH, PCH2O, PCO, and PCO2 = 10−39 bar. ΔEC and ΔEO are taken relative to gas-phase CH4, H2O, and H2.95 Reproduced from ref. 95 with permission from the American Chemical Society, copyright 2018. | ||
Catalysts improving carbon formation resistance. Like SRM and DRM, carbon deposition is a commonly encountered phenomenon occurring in the POM process that results in catalyst deactivation, especially for Ni-based catalysts. The application of bimetallic catalysts could effectively reduce the carbon deposition problem and sometimes also improve the catalyst activity. For instance, the DFT calculations of He et al.230 revealed an improved performance of Ni by alloying it with Co, which enhanced both catalyst activity and carbon formation resistance for methane oxidation. Alloying Ni with Cu could also improve the catalyst carbon formation resistance but with reduced activity as a cost.
Concerning direct partial oxidation to synthesis gas, theoretical studies mainly focus on single-atom alloy (SAA) catalysts rather than traditional bimetallic catalysts. Zhang et al.141 investigated the effect of Ni(111) alloying with Pt on this reaction via a DFT study. It was found that by doping Pt on Ni(111) methane dissociation was greatly promoted. However, the activation energy of CO formation (RDS: CH + O → CHO) and that of H2 formation (H + H → H2) were both observed to increase on the NiPt(111) surface, indicating that alloying Ni(111) with Pt might cause suppressed CO and H2 production. The results demonstrated that NiPt bimetallic catalysts were beneficial to methane adsorption and dissociation and atomic C/H adsorption, but might be less favorable for synthesis gas formation.71,141
Meng et al.90 investigated POM to synthesis gas over a D-Pd/Cu(111) (doped Pd/Cu(111)) catalyst and over an A-Pd/Cu(111) (adsorbed Pd/Cu(111)) catalyst via DFT calculations. Through comparison, the D-Pd/Cu(111) catalyst showed more thermodynamic stability and exhibited a higher capacity for sintering resistance. In their other study,231 Pt was doped on Cu(111) and Ni(111) surfaces to understand the bimetallic catalyst activity and coke-resistance during POM using DFT calculations. Fig. 17 gives a comparison of methane dissociation reaction pathways on Cu(111), Ni(111), Pt1Cu(111) and Pt1Ni(111) surfaces. The activation barriers of CH4 dissociation were largely reduced by the introduction of a single Pt atom on the Cu(111) surface. Compared to Pt1Ni(111) and Ni(111), Pt1Cu(111) displayed similar activation barriers of CH4 dissociation to CH3, but a higher barrier of CH dehydrogenation to C. These results indicated that Pt1Cu(111) can effectively promote methane activation, but not affect the excellent coke resistance. Towards CO formation, the dominant pathway was CH → CHO → CO on both Pt1Cu(111) and Pt1Ni(111), with CH + O → CHO as the RDS. The lower activation energy of CH + O → CHO on Pt1Cu(111) than on Pt1Ni(111) illustrated a higher potential of CO formation on Pt1Cu(111), which prevented C formation and resulted in a better coke-resistance. The performance of the Pt single-alloy Cu catalyst was significantly enhanced, compared with that of commercial Ni-based catalysts.
 | ||
| Fig. 17 Comparison of methane dissociation reaction pathways on Pt1Cu(111) and Pt1Ni(111) surfaces.231 Reproduced from ref. 231 with permission from the Centre National de la Recherche Scientifique (CNRS) and the Royal Society of Chemistry, copyright 2020. | ||
In addition to bimetallic catalysts, the employment of supports could also effectively improve the performance of the catalysts. Guo et al.232 investigated methane dissociation and partial oxidation on Rh4/Ana-Ov (oxygen-defective anatase TiO2 supported Rh) and Rh4/Rut-Ov (rutile TiO2 supported Rh) by DFT, with emphasis put on carbon deposition resistance. Rh4/Ana-Ov showed a higher activation barrier of C–H bond breaking in methane decomposition and a lower energy barrier of CH2 + O → CH2O (RDS for CO formation) compared to that on Rh4/Rut-Ov, implying a strong carbon deposition resistance and a high synthesis gas formation activity of the Rh4/Ana-Ov catalyst. The microkinetic modeling of Rh4/Ana-Ov illustrated a high (up to 90%) CO selectivity, which was increased with temperature. In another study of Guo et al.,233 DFT calculations were used to analyze the size-dependent carbon deposition resistance of Rh-clusters supported on anatase (Rhx/Ana-Ov) for POM. Rh1/Ana-Ov, Rh4/Ana-Ov, and Rh13/Ana-Ov were applied to simulate different cluster sizes. It was found that Rh1/Ana-Ov displayed a much higher apparent energy barrier of methane dissociation and lower energy barrier of CH2 + O → CH2O (RDS for CO formation) among the three models, which could be the one owing to the strong carbon deposition resistance and high catalytic activity. Therefore, SAA catalysts were suggested as candidates to reduce carbon deposition for POM processes.
Size dependence of activity. The kinetic study of Kondratenko et al.210 investigated the size effect on activity and selectivity for POM to synthesis gas over γ-Al2O3 supported Rh NPs. As the particle size increased, the methane conversion and H2/CO ratio were decreased. Meanwhile, the apparent TOF of CO formation and CO selectivity were strongly reduced, indicating a size-dependent kinetics of this process on the supported Rh NPs. However, the overall mechanism of POM was size-independent, which mainly followed an indirect (CRR) mechanism through methane combustion and reforming to form CO and H2.
According to the above kinetic, DFT and microkinetic studies, the mechanism of POM to synthesis gas is still under debate. The exothermic property of POM reaction makes it a challenge to elucidate the reaction mechanism. Nevertheless, owing to the potential of POM in methane conversion, there is a great possibility to attract more attention to this process in the future.
2.3 Methane conversion on oxides
There are extensive pieces of literature on methane activation over various oxide catalysts, some of which have been reviewed previously39,63,234–239 and among which methane oxidation was found to be the most studied reaction. Methane oxidation catalysis involves the introduction of methane and gaseous molecular oxygen into the reactor. Since both the adsorbed oxygen from the gas phase and lattice oxygen from the oxide catalyst can possibly participate in the reactions, it is essential to understand the relative role between them. It was earlier proposed that, instead of the adsorbed oxygen from the gas phase, the concentration of lattice oxygen controls the selectivity of the metal oxide catalyst for total oxidation.239,240 This opinion is consistent with the MVK mechanism.As early as 1993, Otsuka et al.241 reported that CeO2 could be used as an oxidant to transform methane into synthesis gas with a H2/CO ratio of 2 at 873–1073 K. During the redox cycle of cerium oxide, methane was directly converted to CO and H2, and CeO2 was partially reduced to CeO2−n, as shown in eqn (6):
| CeO2 + nCH4 → CeO2−n + nCO + 2nH2 | (6) |
The reduced CeO2−n could be used to convert CO2 into CO, with oxygen recovery to CeO2, as shown in eqn (7):
| CeO2−n + nCO2 → CeO2 + nCO | (7) |
Encouraged by experimental results on CeO2 oxides, methane oxidation has been studied by DFT calculations on CeO2,110,242 and CeO2 doped with Zr or Pd,110,242,243 and Pt.113 As discussed in Section 2.1.2, the C–H bond activation of methane is well correlated with the surface reducibility of CeO2 measured by the formation energy of O vacancy. A comparative study of methane oxidation was performed by a DFT+U on PdxCe1−xO2(111), CeO2(111) and PdO(100) surfaces.242 The reaction mechanism is similar to that on transition-metal surfaces, where methane oxidation took place via CH4 → CH3* → CH2* → CH* → HCO* → CO* → CO2 at low coverage as shown in the free energy diagrams in Fig. 18. C–H bond activation in methane is the RDS on all three surfaces. Carbon formation was not favored over any surface, and the formation of POM products was also not thermodynamically favorable, which, however, was different from the results obtained by Otsuka et al.241 that synthesis gas was the primary product on the CeO2 surface.
 | ||
| Fig. 18 Reaction free energy diagrams for CH4(g) + 2O2(g) → CO2(g) + 2H2O(g) over (a) PdxCe1−xO2(111), (b) CeO2(111) and (c) PdO(100) at T = 298 K and PCH4 = 0.01 atm, PO2 = 0.04 atm, PH2O = PCO2 = 10−6 atm. Insets show the most stable intermediates in methane oxidation over the three surfaces. Ce is displayed as tan (light), Pd as light blue (gray), O as red (dark), and H as white.242 Reproduced from ref. 242 with permission from Elsevier, copyright 2011. | ||
Importantly, doping CeO2 with Zr or Pd,110,242,243 and Pt113 decreased the formation energy of O vacancy of the neighboring oxygen atoms and thus reduced the C–H activation energy barrier. Doping with metals is an effective method to increase the activity of C–H bond activation. The methane activation barrier was the lowest on the PdxCe1−xO2(111) surface, lower than those on CeO2(111), PdO(100), and Pd*/CeO2(111), and even lower than those on Pd(111) and stepped and kinked Pd(211) surfaces.243
Jin et al.244 conducted experimental and theoretical studies of oxidation of ventilation air methane on Fe2O3 and CuO catalysts. The mechanism schematics of CH4 oxidation on the two surfaces are given in Fig. 19(a), together with calculated reaction energies. They implied that CH4 dissociation was the RDS, with reaction energies as 2.76 eV for Fe2O3(0001) and 0.47 eV for CuO(110), due to the strong C–H bonding. It also revealed that the oxygen vacancy (OV) could recover quickly when additional O2 molecules reached the metal oxide surface conducting adsorption and dissociation. Therefore, the reduction of Fe2O3 and CuO could rarely occur, which remained stable without transition to the reduced phase. The schematic configurations of surface bonding for methane oxidation on the O-terminated Fe2O3(0001) are presented in Fig. 19(b). An OV was generated when H2O was released (Fig. 19b(A–C)), followed by O2 filling in the OV to generate –Fe–O–O (Fig. 19b(D)). The formation of C–O bonding in Fig. 19b(F) was favorable to activate the C–H bond of CHx due to the spontaneous transfer of the C–O single bond to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond with the breakage of C–H. The DOS profiles in their work showed that OVs generated more local states over reduced metal surfaces, which were the active sites for O2 adsorption and thus made the C–H activation and O2 splitting more feasible. The under-coordinated metal atoms and OVs could stabilize CHx radicals to promote CH4 dissociation (RDS), which are therefore essential for potential high-performance CH4 oxidation catalysts.
O double bond with the breakage of C–H. The DOS profiles in their work showed that OVs generated more local states over reduced metal surfaces, which were the active sites for O2 adsorption and thus made the C–H activation and O2 splitting more feasible. The under-coordinated metal atoms and OVs could stabilize CHx radicals to promote CH4 dissociation (RDS), which are therefore essential for potential high-performance CH4 oxidation catalysts.
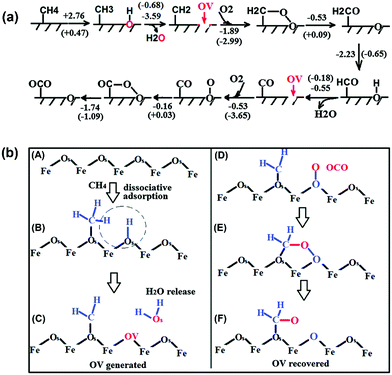 | ||
| Fig. 19 (a) Mechanism schematics of CH4 oxidation on the surfaces of Fe2O3 and CuO under the reaction atmosphere with abundant oxygen, together with calculated reaction energies in units of eV. Two values of the reaction energy are labelled for each elementary reaction: one is for Fe2O3, and the other given in the parentheses is for CuO. Red O indicates that the oxygen is from Fe2O3 or CuO, rather than adsorbed O2. (b) Schematic configurations of surface bonding for CH4 oxidation on the O-terminated Fe2O3(0001) surface. (A–C) show the generation of an OV, and (D–F) describe the recovery of the OV from O2 dissociative adsorption. Os represents the surface oxygen and OCO denotes one-coordinated oxygen.244 Reproduced from ref. 244 with permission from the PCCP Owner Societies, copyright 2015. | ||
In addition to the above metal oxide catalysts, IrO2 was also reported to be an effective catalyst to activate the C–H bond of methane.245 According to the DFT study of Yeh et al.,246 formaldehyde formation was the most favorable reaction for methane oxidation. The reaction was limited by formaldehyde desorption, with a desorption energy of 1.10 eV on an IrO2(110) surface, and the reaction barrier was lower than 0.70 eV. An external electric field was employed to modify the reactivity of IrO2(110), which was found to have no apparent influence on methane dehydrogenation and C–O coupling but could regulate the desorption energy of the adsorbates, especially promoting methane oxidation to formaldehyde over an O-rich IrO2(110) surface.
Despite the most cases that lattice O was favorable for methane oxidation, surface oxygen adsorbed or “activated” O played an important role in the POM reaction on oxides with high formation energies of oxygen vacancy, such as MoO3(100)247 and SiO2 surfaces.248
Perovskite oxides (ABO3) have stimulated interest in various redox cycle reactions (e.g. methane oxidation) due to their excellent crystal structure and redox reversibility.249–251 Methane oxidation has been studied on LaFeO3 based perovskites by DFT calculations focused on the active sites and oxygen mobility and their effects on catalyst activity and selectivity.252,253 The mechanism and structure requirements of selective and total oxidation of methane in a chemical looping process are both experimentally and theoretically examined on La0.5Sr0.5Fe1−xCoxO3−δ perovskites. The substitution of Sr for La at the A site and the substitution of Co for Fe at the B site of the ABO3 perovskites significantly reduced the formation energy of oxygen vacancy. The lattice O diffusion rate and the activity of methane conversion increased, and the selectivity decreased upon decreasing the formation energy of oxygen vacancy. The formation energy of oxygen vacancy increased upon increasing the lattice oxygen charge. Recently, Zhang et al.252 employed combined electrical conductivity relaxation measurements and DFT calculations to study the influence of FeO6 octahedral distortion on lattice oxygen in La1−xCexFeO3 perovskites for POM coupled with a CO2 splitting process. It was found that changing the content of Ce3+ substitution in La1−xCexFeO3 (x = 0, 0.25 0.5, 0.75, 1) resulted in a change in Fe–O bond-length variance, which could tune the FeO6 octahedral distortion degree in La1−xCexFeO3, activate the lattice oxygen and significantly improve the catalysts’ performance in chemical looping POM-CO2 splitting.
Methane oxidation on spinel structured oxides such as CaFe2O4254 and NiCo2O4255 was studied experimentally and theoretically. The deep reduction of calcium ferrite facilitated the production of synthesis gas through methane dehydrogenation and selective oxidation of C to CO. The mechanism difference of POM to form CO and H2 with the CaFe2O4 carrier can be associated with the differences in the oxide phases existing during the reduction process, oxygen species concentration, and bonding in the lattice structure.254 The metal total combustion on NiCo2O4 was observed to follow (1) O2 dissociation on surface O vacancies; (2) the dissociated O atoms filled into O vacancies and coupled with H atoms to form OH and H2O; (3) CH4 dissociation to form CH3* on Ni cations with a subsequent oxidation to CH3O*; (4) CH3O* dehydrogenation to form CH2O* with a subsequent ODH (with the O species of the nearby Co site) to form CHO*; and (5) transformation of CHO* to products (CO2 and H2O) via two subpathways including OCHO dehydrogenation and CO oxidation. The high activity of NiCo2O4 in CH4 conversion to H2O and CO2 at a relatively low temperature together with its low cost leads to NiCo2O4 being very promising for the removal of CH4 in the exhaust gas of a natural gas engine through complete oxidation.
Unlike the extensive literature reported for methane oxidation, only a few theoretical studies have been conducted for SRM and DRM reactions on oxide catalysts, such as SRM on a Ce0.90Ni0.05Ru0.05O2 (CNR) catalyst,256 and DRM on Rh-substituted lanthanum zirconate pyrochlore (LRhZ),257 NiO–MgO,258 and Ni–CaO.259 In SRM and DRM, the metal oxides are normally used as supports to favor possible H2O92,200,260,261 or CO2 activation40,189,262,263 coupled with methane activation on transition metal surfaces. The relatively high activity and low cost of Ni-based catalysts, as well as good performance of other metal catalysts for SRM and DRM, make the research mainly focused on metal surfaces.
3. C–H bond activation in ethane
Ethylene is the most critical chemical building block which could be applied to synthesize various downstream products. It can be produced by noncatalytic thermal dehydrogenation, catalytic dehydrogenation, and oxidative dehydrogenation. Steam cracking is still the dominating route for industrial production of ethylene, but other technologies have also gained increasing attention. Several excellent reviews have addressed the progress in ethane dehydrogenation and oxidative dehydrogenation of ethane.3,264–273 Here we summarize the progress of theoretical catalysis on C–H activation of ethane.3.1 Ethane dehydrogenation on metal surfaces
Ethane is physisorbed on various metal and metal oxide surfaces, and the composition of the catalyst changes the physisorption very much. The C–H bond activation of ethane is similar to the C–H activation of methane and follows the universal scaling relationship of the activation energy of C–H activation of light alkanes. The C–H activation of ethane deals with the secondary C sp3–H bond cleavage. The C–H activation energy of ethane is generally lower than the one of methane, due to the weaker strength of 2° than 1° C–H bonds.The geometries of the transition states for activation of ethane and ethyl C–H bonds on Pt(111) and Pt(211) surfaces are shown in Fig. 20, with the corresponding activation barriers summarized in Table 1.279 The C–H bond activation of ethane on both surfaces occurs through the simultaneous interaction of C and H with a surface Pt atom, forming a C–Pt–H three-membered ring structure (Fig. 20a and d). The C–Pt–H three-membered ring structures are also found in ethyl to ethylene on both surfaces (Fig. 20c and f) and ethyl to CH3CH* on the Pt(211) surface (Fig. 20e). For the transition states of ethyl to CH3CH* on the Pt(111) surface, ethyl is bonded to Pt surfaces via the C atom, where the H in C–H is bonded to adjunct Pt (Fig. 20b). The energy barriers of the three steps follow the order Pt(211) < Pt(111), as shown in Table 1. Similarly, the energy barriers of Pt(433) step < Pt(433) terrace,280 and Pt55 < Pt(111)281 are obtained. The stepped Pt surfaces (or small Pt particles) having coordinatively unsaturated Pt atoms are therefore kinetically more active for the dehydrogenation of ethane to form ethylene than the flat surfaces.
 | ||
| Fig. 20 Geometries of the transition states for the activation of ethane and ethyl C–H bonds on Pt(111): (a) CH3CH2–H, (b) CH3CH–H, and (c) CH2CH2–H; and on Pt(211): (c) CH3CH2–H, (d) CH3CH–H, and (e) CH2CH2–H.279 Reproduced from ref. 279 with permission from the American Chemical Society, copyright 2010. | ||
| Surface | E act (eV) | XC functional | k points | Unit cell | Ref. | ||
|---|---|---|---|---|---|---|---|
| CH3CH3(g) → CH3CH2* | CH3CH2* → CH3CH* | CH3CH2* → CH2CH2* | |||||
| Pt(111) | 0.54 | 0.88 | 0.81 | PBE | 5 × 5 × 1 | 2 × 2 | 279 |
| Pt(211) | 0.08 | 0.27 | 0.44 | 3 × 4 × 1 | 2 × 1 | ||
| Pt(110)-(1 × 2) | 0.38 | 0.33 | 0.29 | PW91 | — | 2 × 2 | 285 and 286 |
| Pt(433) terrace | 0.65 | 0.81 | 0.71 | PW91 | 1 × 2 × 1 | 1 × 3 | 280 |
| Pt(433) step | 0.33 | 0.08 | 0.27 | ||||
| Al6O11 decorated Pt(433) | 0.69 | 0.78 | 0.73 | ||||
| Pt(111) | 0.84 | — | 0.67 | PBE | 3 × 3 × 1 | 4 × 4 | 281 |
| Pt55 | 0.57 | — | 0.48 | 1 × 1 × 1 | — | ||
| Pt(111) | 0.91 | 0.91 | 0.89 | PW91 | 6 × 6 × 1 | 2 × 2 | 282 and 283 |
| Pt3Sn/Pt(111) | 1.19 | 1.04 | 1.07 | ||||
| PtSn/Pt(111) | 1.58 | 1.28 | 1.28 | ||||
| Pt(111) | 0.90 | 0.95 | 0.88 | PW91 | 6 × 6 × 1 | 2 × 2 | 284 |
| Pt3Sn/Pt(111) | 1.18 | 1.30 | 1.08 | ||||
| Pt3Sn(111) | 1.08 | 0.84 | 0.88 | ||||
In addition to activity, ethylene selectivity is another important factor in characterizing ethane dehydrogenation. From Table 1, one can see that the energy barrier of CH3CH2* → CH3CH* is lower than that of CH3CH2* → CH2CH2* for both the Pt(211) and Pt(433) steps. It means that these under-coordinated step sites preferably promote deep dehydrogenation, resulting in coke formation and catalyst deactivation.280 By decorating the step with AlOx species (Al6O11 decorated Pt(433)), the step sites can be blocked, leading to suppression of deep dehydrogenation and coke formation. The deep hydrogenation can also be suppressed by doping Pt with Sn. As shown in Table 1, Pt–Sn surface alloys with different site coverages of Sn and Pt–Sn bulk alloy have been investigated for ethane dehydrogenation via DFT calculations.282–284 The activation energies of the first and second C–H bond cleavage steps for ethylene formation were calculated as Pt(111) < Pt3Sn(111) (bulk alloy) < Pt3Sn/Pt(111) (surface alloy) < PtSn/Pt(111) (surface alloy). The addition of Sn into Pt increases the C–H and C–C bond cleavage barriers, which inhibits the catalyst activity but favors ethylene selectivity over carbon formation. A more detailed discussion on the site coverage of Sn and the location of the Sn on Pt catalyst for ethane dehydrogenation can be seen in Section 3.1.2.
Nørskov and co-workers287 developed a descriptor based microkinetic model for ethane dehydrogenation over close-packed metal surfaces and varied reaction conditions. The C2H4 turnover frequency and selectivity can be predicted as functions of the adsorption energies of two key intermediates CH3CH* and CH2CH2*. The model results showed that Pt and Pt alloys were among the most active catalysts for ethane dehydrogenation, as shown in Fig. 21(a). The catalytic activity followed the order IrPt3 ≈ Pt > Re > Ir > Ru > Rh > Ni, Co, while Cu, Zn, Au, In, and Ag were almost inactive. The Sn–Pt and Zn–Pt alloys showed reasonable activity, but it was lower than that of Pt. The Sn and Zn alloyed with Pt lowered the adsorption strength of CH2CH2*, and thus significantly enhanced ethylene selectivity, as shown in Fig. 21(b). The activity trend predicted by micro-kinetic modeling is in general agreement with experimental results.
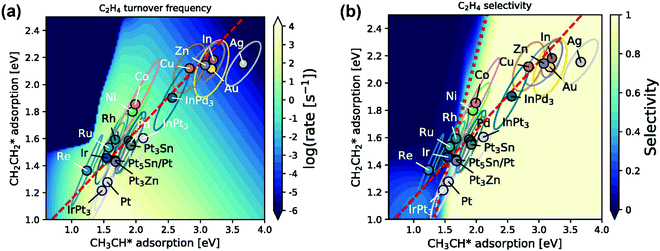 | ||
| Fig. 21 (a) Activity volcano for ethylene production at 873 K, 0.2 bar C2H6(g), 2 × 10−4 bar C2H4 (1% carbon conversion), 0.6 bar H2(g), and 10−9 bar CH4 and 10−12 bar C2H2. (b) Map of carbon-specific selectivity.287 Reproduced from ref. 287 with permission from Elsevier, copyright 2019. | ||
Bell and co-workers288 applied tetrahedral metal clusters in DFT calculations to represent metal NPs to study the elementary processes involved in ethane dehydrogenation. The DFT estimated free energy activation barrier for the dissociative adsorption of ethane to present activity trend followed Pt3Sn > Pt3Ir > Pt4, which agreed relatively well with the experimentally measured activity order. The same group investigated the effects of intermetallic interaction on alkane dehydrogenation systematically using Pt-based, subnanometer-sized alloy cluster catalysts.289 The alloys were modeled with Pt3X (X = Pd, Sn, Ge, Si, In, Ga, Au, Ag, Cu, and Ir). For all the alloy catalysts, the RDS was found to be the same, namely the first C–H bond cleavage. The activation energy of the first C–H cleavage on the alloy clusters was predicted to be in the order of Pt3Si < Pt3Ge < Pt3Sn < Pt3Ir < Pt. No significant BEP relationship could be found with respect to atomic H or CH3 group binding energy for the Pt alloys. However, the catalyst activity correlated well with the HOMO–LUMO gap of the clean catalyst. Smaller HOMO–LUMO gaps indicated higher activity due to the increased flexibility of the valence electron at the active site.
The cluster model289 predicted relatively high ethylene selectivity on Pt-based catalysts due to their relatively high barriers for direct C–C bond cleavage compared to C–H bond breaking. A natural bond orbital analysis revealed that the d-orbital shape of the HOMO with its pronounced nodal features better facilitated the breaking of a C–H bond than that of a C–C bond due to better overlap with the C–H anti-binding orbital.
The site coverage of Sn and the location of the Sn on Pt catalyst do influence the catalyst performances for ethane dehydrogenation.282–284 Kinetic reaction barriers were calculated for potential energy surfaces of C1 and C2 intermediates from C–H and C–C bond cleavage of ethane with ¼ and ½ surface monolayers of Sn.282 Sn weakened the binding energies of all species at both coverages. At the lower Sn coverage (¼ monolayer), the effect was purely electronic since the binding geometries had not changed compared to those on the Pt(111) surface. At the higher coverage of Sn, a larger effect on reaction energies was observed due to the changes in the binding geometries as a result of the elimination of 3-fold hollow sites that consist of Pt atoms. In terms of the electronic effect, Sn can donate electrons to Pt atoms and reduce the binding energies of adsorbates to Pt and increase the barrier for C–H and C–C cleavage, as shown in Table 1. The increase in the barriers favors ethylene selectivity over carbon formation. The same group further studied the effect of tin in the bulk of PtSn alloys for ethane dehydrogenation.284 DFT calculations were performed on pristine Pt(111), a Pt3Sn/Pt(111) surface alloy, and a Pt3Sn(111) bulk alloy. The binding energies of adsorbates weakened on both Sn alloys. But on the bulk alloy, the binding energy was weaker than that on pure Pt but stronger than that on the surface alloy. Therefore, the activity trend for ethylene formation was predicted as pure Pt > bulk alloy > surface alloy based on the activation energies of the first and second C–H bond cleavage steps (Table 1). A selectivity descriptor was defined for ethane dehydrogenation as the energy difference between the activation energy for ethylene dehydrogenation (Ea, CH2CH2* → CH2CH*) and the desorption energy of ethylene (ΔEdes, CH2CH2*) for several substitutional surface alloys. A smaller value indicates that further ethylene dehydrogenation is more favored over desorption and therefore predicts poor selectivity towards ethylene. The selectivity descriptor was calculated as −0.12, 0.04, and +0.36 eV for Pt, the bulk alloy, and the surface alloy, respectively. Therefore, the ethylene selectivity was highest on the surface alloy, followed by the bulk alloy and pure Pt.
The selectivity descriptor has been used to study a broader range of Pt–M surface alloys at low and high M coverages, including metals from groups 7–15.283 The Pt3M/Pt(111) alloy surface was created by replacing one surface Pt atom with alloying element M, giving 1/4 ML surface coverage for M. There were two types of 3-fold hollow sites, namely Pt3 and Pt2M sites on Pt3M/Pt(111) surfaces. A PtM/Pt(111) surface was created by replacing two surface Pt atoms with M, giving 1/2 ML surface coverage for M. On the PtM/Pt(111) surface, the 3-fold Pt3 sites were removed, and 3-fold binding sites included Pt2M and PtM2 sites. 27 elements (M) were selected for this study, which comprised the TMs from groups 7–11 and the post-transition (P-T) metals from groups 12–15. The P-T metals included Zn, Cd, Hg, Al, Ga, In, Tl, Ge, Sn, Pb, Sb, and Bi. The TMs were further classified as nonpreferred transition (NT) metals and carbon-preferred transition (CT) metals based on the preferred binding site of a carbon atom (Fig. 22a). NT metals were transition metals where a carbon atom placed on Pt3M/Pt(111) preferred to bind on Pt3 sites. Conversely, the transition metals where C preferred to bind on Pt2M sites over Pt3M/Pt(111) were labeled CT metals. The NT metals included Mn, Fe, Co, Ni, Pd, (Pt), Cu, Ag, and Au. The CT metals included Tc, Re, Ru, Os, Rh, and Ir. On P–T and NT alloys, C, H, and CH preferred to bind to Pt3 at 1/4 ML coverage and Pt2M at 1/2 ML coverage. CH3 preferred to bind to top sites of Pt at both coverages. On CT alloys, C, H, and CH preferred to bind to Pt2M at 1/4 ML coverage and PtM2 at 1/2 ML coverage. CH3 preferred to bind to top sites of the M atom at both coverages. The scaling relationship was established between the desorption energy of ethylene and methyl binding energy (BECH3) (Fig. 22b and c) as well as the activation energy of ethylene dehydrogenation and the methylidyne dehydrogenation reaction energy (ΔECH) plus the methyl binding energy (BECH3) (Fig. 22d) on various Pt3–M alloys. It indicated that alloying Pt with Pb, Bi, Tl, Sn, Sb, Hg, and In decreased the ethylene desorption energy and increased the activation energy of C–H activation of ethylene, thus resulting in higher ethylene selectivity.283
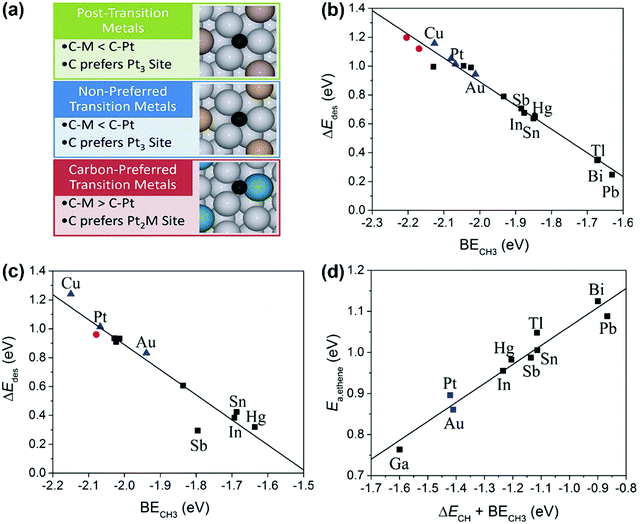 | ||
| Fig. 22 (a) Binding site preferences of carbon atoms on three categories of alloying elements: post-transition (P-T) metals, nonpreferred transition (NT) metals, and carbon-preferred transition (CT) metals. Relationships between the methyl binding energy (BECH3) and the desorption energy of ethylene (ΔEdes) at (b) ¼ ML and (c) ½ ML coverage. (d) Relationships between the methylidyne dehydrogenation reaction energy (ΔECH) plus methyl binding energy (BECH3) and the ethylene dehydrogenation barrier (Ea, ethylene) for alloys at ¼ ML coverage. NT alloys in blue, P–T alloys in black, and CT alloys in red.283 Reproduced from ref. 283 with permission from the American Chemical Society, copyright 2017. | ||
Cybulskis et al.290 investigated Zn promotion of platinum for ethane dehydrogenation by combining DFT, kinetic, and in situ spectroscopies. DFT calculations could accurately predict the electronic structure of Pt 5d valence orbitals in Pt/SiO2 and PtZn/SiO2. Zn lowers the energy of filled states of the Pt surface and weakens the binding energy between adsorbates and the Pt surface as well as increases the turnover rate of the reaction. In addition, Zn has a geometric effect, leading to the formation of a Pt1Zn1 intermetallic alloy with uniformly isolated Pt surface sites, which effectively suppresses hydrogenolysis and cracking reactions.
Ko et al.291 investigated the influence of P doping into Ni-based catalysts on ethane dehydrogenation by combined DFT and experimental study. DFT calculations revealed that a Ni2P(001) surface exhibited a similar CH3CH2–H activation barrier to, but a much greater CH2CH–H activation barrier (an indicator of the coking tendency) than a Ni(111) surface. Meanwhile, the experimental study demonstrated a much higher ethylene selectivity (<80%) and less carbon deposition on the Ni2P(2)/SBA-15 catalyst compared to Ni/SBA-15 (<1% ethylene selectivity). This highlights the potential of using metal phosphides as robust and selective catalysts for alkane dehydrogenation.
Ge is another promising promoter. It can enhance the catalyst selectivity without decreasing the catalytic activity. DFT calculations were performed on MgO-supported Pt3 and Pt7 with Pt2Ge and Pt7Ge clusters.278 It was found the Pt2Ge could elongate the C–H bond more than Pt and had a lower activation barrier of 0.05 eV compared to 0.17 eV for pure Pt. Therefore, the activity of ethane dehydrogenation was not negatively affected by Ge. On the other hand, Ge quenched the unpaired electrons in the metal clusters, which were needed to activate alkenes for dehydrogenation. Ge in alloys made Pt interact less strongly with ethylene and therefore increased ethylene selectivity. For the smallest cluster size, the C binding energy was significantly reduced and increased catalyst resistance to deactivation due to coking.
Carbon deposition is also dependent on the particle size of Pt and PtSn alloy, as well as the Sn content. In general, carbon deposition under reaction conditions increases with increasing particle size, but higher Sn content suppresses carbon formation.292
3.2 Oxidative dehydrogenation of ethane
Oxidative dehydrogenation, which couples the endothermic dehydration of ethane with the strongly exothermic oxidation of hydrogen, exhibits higher ethane conversion and lower operation temperature compared to steam cracking, which leads to growing interest in this process. However, major practical challenges with ODH reaction still occur, which are (1) additional safety measures associated with O2 in the feed and (2) the development of highly active and selective catalysts due to the high reactivity of olefins compared with the corresponding paraffins.265 The ODH of ethane has not been practiced on a large scale yet. The relatively higher reactivity of olefins is attributed to the direct interaction of the olefin with catalytic surfaces. Typical undesired side reaction involves total oxidation to form CO, CO2, and water. The reaction occurs through oxygen insertion into the C–H bond or from the addition of oxygen to olefins.The only feedstock that can achieve high selectivity to olefins is ethane because ethylene is sufficiently unreactive towards oxygen compared to ethane. This is evidenced by the bonding strength difference in paraffins and olefins. The weakest C–H bond in ethane has a bond energy of 4.35 eV, whereas the weakest C–H bond in ethylene has an energy of 4.60 eV. For propane and propylene, the weakest C–H bond has a bond energy of 4.16 and 3.74 eV respectively. A more significant difference exists for C–C bond energy; the weakest C–C bond in ethylene is a double bond with a bond energy of 7.46 eV compared to 4.29 eV in propylene, in which the weakest C–C bond is a single bond. In general, to achieve high selectivity, the weakest C–H or C–C bond in the olefin has to be less than 0.31 eV weaker than the weakest C–H bond in the reacting paraffin.293 This is true for ethane and ethylene, but not for propane and propylene.
| CnH2n+2 + 1/2O2 → CnH2n + H2O | (8) |
ODH normally accompanies the combustion of hydrocarbons, producing CO and CO2. To avoid over-oxidation of hydrocarbons, lattice oxygen in metal oxides can be used as the alternative oxygen supplier for the ODH process, which is often called a chemical looping ODH process. Most of the catalysts that are active for the ODH of ethane fall into redox-active metal oxides such as V2O5,295 MoO3,294 MoVTeNb mixed metal oxides,296 Co oxides,297 Ni oxides,298 and IrO2.299 There is a general consensus that ODH of ethane on such materials follows a MVK221 mechanism and the reactivity of oxygen plays a vital role in the C–H activation of ethane. That is, the lattice oxygen of metal oxides interacts with hydrocarbons to form oxygen vacancies (eqn (9)), followed by the regeneration process (eqn (10)).
| CnH2n+2 + MxOy → CnH2n + MxOy−1 + H2O | (9) |
| MxPy−1 + 1/2O2 → MxOy | (10) |
V2O5 catalysts. The most prominent redox metal oxides for ethane ODH are supported V2O5 catalysts. The oxide support does not participate in the reaction, but it does influence the reactivity and stability of the oxygen bonded to V.300 Three types of metal–oxygen bond have been identified in the surface vanadium species as illustrated in Fig. 23, including terminal V
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds, bridging O atoms between V and the support (V–O–S), and bridging O atoms between two V cations (V–O–V).301 The isolated VO4 species on the support contains the first two types of V–O bonds, while the polymeric VO4 species contains all three V–O bonds.
O bonds, bridging O atoms between V and the support (V–O–S), and bridging O atoms between two V cations (V–O–V).301 The isolated VO4 species on the support contains the first two types of V–O bonds, while the polymeric VO4 species contains all three V–O bonds.
 | ||
| Fig. 23 Isolated and polymeric VO4 species in supports.301 Reproduced from ref. 301 with permission from the Royal Society of Chemistry, copyright 2011. | ||
Ethane ODH pathways on vanadium oxide catalysts were elucidated by kinetic and isotopic tracer and exchange measurements.302 The lack of exchange products (C2H6−xDx or C2H4−xDx isotopomers) revealed that the first C–H bond cleavage in ethane and ethylene was an irreversible and kinetically relevant step in ODH and combustion reactions. 16O2–18O2–C2H6 reactions on supported V16Ox domains led to the initial appearance of 16O from the lattice in the products H2O, CO, and CO2, evidencing the involvement of lattice oxygen in C–H bond activation steps. The emerging paradigm is that the development of suitable catalysts requires fundamental insight into the reaction mechanism on a molecular level, including the details of the interactions with the catalytic surfaces and the associated gas-phase reactions. The theoretical calculation has been used to provide a molecular understanding of active sites and reaction mechanisms on vanadium-based oxides. Similar activity of oxygen species and reaction mechanisms of C–H bond activation have been found on ethane ODH295 as well as propane ODH303 on the V2O5(001) surface. The most favorable pathway occurred on the O(1) (V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) site through a radical mechanism with an activation energy of 1.52 eV;295 V–O–V was less active toward C–H bond activation (1.63 eV) through an oxo-insertion mechanism but much more selective towards ethylene formation. However, the terminal O site exhibited a more favorable side reaction leading to acetaldehyde than to ethylene. The first C–H activation step was the RDS, in good agreement with the experimental observation.302 Water and acetaldehyde would desorb from the surface to create vacant O(1) sites easily. The oxygen molecule can re-oxidize the reduced vanadium, which is exothermic by 3.77 eV, with a barrier of 1.52 eV. Obviously, the surface of the catalyst can be re-oxidized easily at high temperatures when it is exposed to O2. A more detailed discussion on the active sites, the reactivity of surface oxygen species, and the reaction mechanism of C–H bond activation of light alkanes can be seen in Section 4.2.
O) site through a radical mechanism with an activation energy of 1.52 eV;295 V–O–V was less active toward C–H bond activation (1.63 eV) through an oxo-insertion mechanism but much more selective towards ethylene formation. However, the terminal O site exhibited a more favorable side reaction leading to acetaldehyde than to ethylene. The first C–H activation step was the RDS, in good agreement with the experimental observation.302 Water and acetaldehyde would desorb from the surface to create vacant O(1) sites easily. The oxygen molecule can re-oxidize the reduced vanadium, which is exothermic by 3.77 eV, with a barrier of 1.52 eV. Obviously, the surface of the catalyst can be re-oxidized easily at high temperatures when it is exposed to O2. A more detailed discussion on the active sites, the reactivity of surface oxygen species, and the reaction mechanism of C–H bond activation of light alkanes can be seen in Section 4.2.
MoO3 catalysts. The surface stability and equilibrium morphology of MoO3 have been investigated by DFT calculations.304 The (010) surface has the lowest surface energy among the surfaces exposed to the gas.304 The ethane ODH mechanism on the MoO3(010) surface was investigated by the first-principles study using the on-site Coulomb correction.294 There are three types of surface oxygens, namely terminal O and symmetric and unsymmetric Mo–O–Mo, and the terminal O is the main active site. Two stable configurations of ethylene adsorption on the MoO3(010) surface, namely horizontally and vertically adsorbed ethylenes, were identified. The horizontal adsorption favors ethylene formation with a barrier of 1.36 eV, which is lower than that of V2O5. The vertical adsorption of ethane favors acetaldehyde formation along the α-ODH pathway, and the ethylene oxide formation along the β-ODH pathway. The β-ODH pathway may also produce ethylene from the CH2CH2O intermediate, with the second C–H bond activation of ethane as the RDS. Towards horizontal C2H6 ODH reaction (the dominant ethylene formation pathway), the first C–H bond activation of ethane is the RDS. This is in agreement with the kinetic study that irrespective of the oxidant's chemical identity (O2, CO2 or H2O), ethane activation occurs via the kinetically relevant C–H activation of C2H6 on the lattice O of MoOx, forming ethylene.305
MoVTeNb mixed metal oxides. MoVTeNb mixed metal oxides have exhibited high selectivity and yields to C2H4. The catalyst is typically composed of two compounds Mo7.8V1.2Te0.937NbO28.9 and Mo4.31V1.36Te1.81Nb0.33O19.81, which are referred to as M1 and M2 phases, respectively.306 The structure of the M1 phase is illustrated in Fig. 24(a). It is generally accepted that the M1 crystalline phase is responsible for high activity and selectivity due to its ability to catalyze the initial homolytic H abstraction from alkanes.307 Both the basal [001] plane308 and lateral surface309,310 have been reported to be responsible for the activation of alkanes. The S2–S4–S7 metal positions were proposed as the catalytic centers for alkane activation. The crystal termination of the M1 phase did have an impact on the intrinsic activity of ethane ODH.296 A quantitative correlation was found between the sum of the surface areas of facets (001), (120), and (210) at the surfaces of the M1 crystals and the activity, demonstrating that multiple facets were involved in the reaction. Different facets would have different degrees of exposed active sites, and therefore different catalytic activities. The number of different facets can be tuned by changing the crystal morphology of the M1 phase of MoVTeNbOx catalysts.
 | ||
| Fig. 24 (a) Two-dimensional diagram of the MoVTeNbOx M1 unit cell viewed in the [001] direction with 13 cation sites labelled as in the literature.311 Active site centers are composed of metal positions S2–S4–S7 (red and green), located between unit cells.296 Reproduced from ref. 296 with permission from Wiley-VCH, copyright 2016. (b) Accessibility of surface catalytic sites to reactants on VOx/SiO2 and MoVTeNbO as well as C2H6/C6H12 rate ratios on MoVTeNbO relative to the corresponding values on VOx/SiO2. (c) vdW-DF2 derived electronic energies and (d) structures of transition states for C2H6 ODH (TS1, TS2), parallel O-insertion in ˙C2H5 (TS3) and sequential O-insertion in C2H4 (TS4) at O-atoms exposed in heptagonal pores of double-layer MoVTeNbO.312 Reproduced from ref. 312 with permission from the American Chemical Society, copyright 2018. | ||
In addition to the surface reaction, C2H6 ODH can also occur on M1 phase MoVTeNb mixed oxides’ micropores, which was considered to be the reason for the high ethylene yields at moderate temperatures.312,313 Deshlahra and co-workers312 assessed the role of the M1 phase heptagonal channel micropores in regulating reactivity and selectivity using reactant size-dependent kinetic probes and DFT treatments for C2H6 and C6H12 (cyclohexane) activations inside and outside the micropores and compared with nonmicroporous vanadium oxides (VOx/SiO2). As shown in Fig. 24(b), both C2H6 and C6H12 activations can take place on the VOx/SiO2 surface and MoVTeNbO external surfaces. Inside the MoVTeNbO micropores, C2H6 activation is possible due to a tight guest–host fit, while C6H12 cannot access intrapore sites because of the large kinetic diameter. The measured C2H6/C6H12 activation rate ratios on MoVTeNbO were much higher than those measured on VOx/SiO2 and estimated by DFT calculations on the external surfaces, demonstrating that most C2H6 activations on MoVTeNbO occur inside the micropores under typical conditions. MoVTeNbO and VOx/SiO2 exhibited similar product selectivities for C6H12 oxidation, while for C2H6 oxidation, the ethylene selectivity was much higher on the former oxide. This suggested that the external surfaces of MoVTeNbO displayed a similar ability to activate C–H bonds and prevent O-insertion in products with VOx/SiO2, but the micropores in MoVTeNbO are more selective for C–H activation, which was confirmed by DFT calculations. The DFT calculated electronic energies and structures of transition states for C–H activation and O-insertion in C2H6 and C2H4 inside the heptagonal pores of MoVTeNbO are shown in Fig. 24(c) and (d), respectively. C2H6 ODH is the dominant reaction pathway, with the first C–H activation as the RDS and ethylene as the product. The C–O bond formation via two O-insertion pathways is hindered due to steric hindrances, which require much bulkier CH2 groups in close contact with concave pore walls (top views of TS3 and TS4 in Fig. 24d). Therefore, the heptagonal pores of MoVTeNbO enhance ethylene selectivity by enhancing C–H activation and suppressing O-insertion reactions via a combination of van der Waals (vdW) and steric effects.
 | ||
| Fig. 25 DFT calculated energy profiles of reforming and ODH of ethane on (a) Pt-terminated CoPt(111) and (b) mixed FeNi(111).323 Reproduced from ref. 323 with permission from Elsevier, copyright 2016. | ||
The same group investigated lattice O atom coordination effects and pore confinement on selectivity limitations for ethane ODH catalyzed by vanadium–oxo species.313 DFT was used to calculate C–H activation and C–O formation in ethane ODH on (001) surfaces of V2O5 and MoVTeNb oxides and in pores of MoVTeNb oxides. High C2H4 selectivity depended strongly on the O atom coordination and H atom addition energies of the oxides. C–O formation preferably occurred at V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O terminal O atoms due to their significantly lower energy than V–O–V, V–O–Mo bridging or V2–O–V tri-coordinated O atoms. In contrast, the C–H activations on MoVTeNbO(001) surfaces exhibited similar activation energies between bridging O atoms and terminal O atoms. Terminal O atoms are inaccessible in MoVTeNbO bulk oxide micropores, which leads to high ethane activation rates and ethylene selectivity.
O terminal O atoms due to their significantly lower energy than V–O–V, V–O–Mo bridging or V2–O–V tri-coordinated O atoms. In contrast, the C–H activations on MoVTeNbO(001) surfaces exhibited similar activation energies between bridging O atoms and terminal O atoms. Terminal O atoms are inaccessible in MoVTeNbO bulk oxide micropores, which leads to high ethane activation rates and ethylene selectivity.
Co oxides. Co3O4 is a good oxidation catalyst. Its high activity has been attributed to the weak metal–O bond among other transition metal oxides314 and the easy formation of oxygen vacancies at the catalyst surfaces.315 Co3O4 is also active for ODH. Surface termination can have an impact on the catalyst activity and selectivity of ODH. Experimental and theoretical calculations have identified several stable Co3O4 surfaces, such as (110), (111), and (100). Fung et al. developed a full catalytic cycle of ODH based on first-principles calculations on a thermodynamically stable Co3O4(111) surface.297 The full catalytic cycle includes the first and second C–H bond activations, hydroxyl clustering, water formation, water desorption, and lattice oxygen-site regeneration. On the most stable terminal surface, there are two types of lattice oxygen: OA, which is triply coordinated to the subsurface cobalt (Co3+); and OB, which is not only doubly coordinated to the subsurface Co but also singly coordinated to the surface Co. There are also two types of C–H activation of ethane, namely the homolytic pathway where the lattice O is the active site, and the heterolytic pathway where the O and Co pair is the active site. The C–H activity depends on the lattice oxygen reactivity. The formation energy of oxygen vacancy and Bader charges are good descriptors to predict well the higher reactivity of OA. The first C–H activation was more favorable on more reactive lattice oxygen and had a lower barrier for the homolytic pathway (∼0.62 eV), but the barrier for the second C–H activation was lower for the heterolytic pathway. The water formation step of the catalytic cycle on the pure (111) surface was found to be the RDS, possibly due to the highly oxyphilic nature of the Co surface.
The same group investigated the effects of Co3O4 doping on oxygen reactivity and ethane C–H activation energies over Co3O4(111) and (311) surfaces for a series of dopants.316 The DFT calculations illustrated that the O vacancy formation energy and H adsorption energy were descriptors for oxygen reactivity, which were directly correlated with the ethane C–H activation energy and the TS geometry. The group also discovered that the surface orientation had a significant influence on dopant efficacy.
Ni oxides. The reaction mechanism of ODH of ethane has also been studied on nickel-based oxides, namely Ni3Ox (x = 1, 2, 3) by DFT calculations using the cluster model.298 Ethylnickel species have been identified as main reaction intermediates through a concerted mechanism involving two sites for the C–H bond activation step. Subsequent pathways include beta-H elimination, alpha-H abstraction, C–C bond cleavage, and isomerization to ethoxide species. The selectivity of ethylene depends on the relative rates of the four pathways. According to the calculation, the SC2H4 selectivity increases from 37% to over 99% with decreasing x value. The oxygen vacancy has a significant influence on the selectivity and more oxygen vacancies in Ni oxides enhance remarkably the ethylene selectivity. An important issue for transition-metal catalyzed oxidation of hydrocarbons is the type of primary species generated from the C–H bond activation step and the types of species directly responsible for the initial product selectivity observed in the experiment.14 The adsorbed ethane on oxygen sites forms ethoxide, which leads to ethylene formation. The high selectivity in the Ni3O1 case is due to the absence of a bare O atom nearby the α-Ni site and block isomerization from ethyl-nickel to ethoxide, which is more likely to undergo C–C bond cleavage.
Doping of NiO with Sn, Ti, and W has been shown to increase the catalytic activity and selectivity.317 DFT calculations show that doping these metals into the NiO structure are thermodynamically feasible. The dopant, on the one hand, can decrease the particle size of NiO and open up more active sites. The incorporation of these metals into the NiO lattice, on the other hand, reduces the number of holes (h+), resulting in a significant decrease of nonstoichiometric oxygen (O˙−) in the NiO structure. The low concentration of nonstoichiometric oxygen contributes to the improved catalytic selectivity (O˙− is known to favor complete ethane oxidation to CO2). Based on this study, a design criterion has been proposed; an optimum concentration of nonstoichiometric oxygen at the NiO surface exists. A too high oxygen concentration leads to total oxidation of ethylene to CO2, while a too low oxygen concentration leads to difficulty in activating ethylene at a lower temperature.
Doping of NiO with Nb in ethane ODH was found to form NbO2 groups, considered to be the dopant, predicted by DFT calculations.318 The NbO2 groups were created because the Nb-doped NiO adsorbed oxygen very strongly from the gas phase and dissociated it to generate two chemisorbed O atoms, with each making an Nb–O–Ni bond. The calculated activation energies of dissociative adsorption of ethane on the NbO2-doped oxide were substantially lower than that on undoped NiO. This is because the NbO2-doped oxide was more reactive in breaking the C–H bond of ethane than undoped NiO. However, this is different from the experimental results319,320 in that even adding a small amount of Nb decreased the ethane conversion per unit area and per unit time for NiO catalysts. The difference between the experimental observation and the DFT prediction might be due to the formation of NbOx clusters on the surface or NiNb2O6 (instead of NbO2 groups used in the model) during the calcination in oxygen for catalyst preparation. Experiments found that the slow deactivation of the catalyst was attributed to the formation of NiNb2O6.
IrO2 catalysts. In contrast to most metal oxides, where initial C–H bond activation is the RDS of ethane ODH, the first C–H bond activation of ethane is a fast reaction over IrO2 catalysts. A DFT study of ethane activation over an IrO2(110) surface reported by Pham et al.321 indicated that ethane was most stably adsorbed on IrO2(110) by interacting with two adjacent Ircus (five-fold coordinated Ir) atoms, and ethane activation on IrO2(110) was both thermodynamically (ΔE, PBE: −1.12 eV; optB88-vdW: −1.13 eV) and kinetically (Ea, PBE: 0.50 eV; optB88-vdW: 0.57 eV) favorable, which was expected to occur at low temperature. Similarly, the temperature-programmed reaction spectroscopy (TPRS) and DFT results reported by Bian et al.299 showed that ethylene desorption was the RDS in the conversion of ethane to ethylene over IrO2(110) during the TPRS. The DFT calculated barrier of ethane C–H bond cleavage over clean IrO2(110) (0.39 eV) was much lower than that of ethylene desorption (1.96 eV). However, the DFT calculation predicted that the oxygen vacancy plays a significant role in ethane conversion. Partial hydrogenation of IrO2(110) was found to enhance ethane conversion to ethylene while suppressing ethane oxidation to COx species. According to DFT, hydrogenation of reactive O atoms of IrO2(110) to OH groups effectively inhibited these sites as H atom acceptors, resulting in ethylene desorption being favored over further dehydrogenation. The study revealed that IrO2(110) displayed an exceptional ability to promote C2H6 dehydrogenation to C2H4 near room temperature, and controlled deactivation of reactive O atoms was an effective way to facilitate ethylene production from ethane on IrO2(110).
| C2H6(g) + CO2(g) → C2H4(g) + CO(g) + H2O(l) ΔH25° = 1.39 eV | (11) |
In addition to producing ethylene via an ODH pathway through C–H bond scission, the interaction of ethane with CO2 can also produce synthesis gas via a dry reforming pathway through C–C bond scission. High ethylene selectivity can be achieved by using different catalysts to selectively promote the C–H bond scission and preserve the C–C bond scission. Chen and co-workers have done a lot of work on it.323–326 They studied the dry reforming and ODH of ethane with CO2 as a soft oxidant on CeO2 supported bimetallic catalysts.323 It was found that CoPt/CeO2, CoMo/CeO2, and NiMo/CeO2 bimetallic catalysts favored the reforming pathway to produce synthesis gas via the C–C bond cleavage, while FeNi/CeO2 favored the ODH pathway to produce ethylene via the C–H bond cleavage. The DFT calculated energy profiles shown in Fig. 25 clearly demonstrate different pathways on the CoPt/CeO2 catalyst compared to the FeNi/CeO2 catalyst.
The most likely active sites over CeO2-supported NiFe catalysts were further elucidated by the same group by combining in situ characterization with DFT calculations.324 Both the experimental and theoretical results revealed that the Ni–FeOx interfacial sites could selectively break the C–H bonds and preserve the C–C bond of C2H6 to produce ethylene, while the Ni–CeOx interfacial sites efficiently cleaved all of the C–H and C–C bonds to produce synthesis gas. Similar work has been done on non-precious FeNi and precious NiPt catalysts supported on CeO2 for ODH of propane by CO2 of propane and dry reforming.327 DFT was performed on three representative surfaces: Fe3Ni, FeO/Ni(111), and Ni3Pt. The FeO/Ni(111) surface was used to represent potential FeO–Ni interfacial active sites due to the observation of the FeO layer on the Ni surface during the reaction conditions. DFT results revealed that on bulk-terminated-Fe3Ni(111) the ODH reaction (ΔE = 0.29 eV and Ea = 1.02 eV) had lower reaction energy and activation energy than *O insertion reaction (ΔE = 0.43 eV and Ea = 3.30 eV). Therefore, the ODH reaction is more favorable along the C–H bond cleavage pathway than the *O insertion reaction along the C–C bond cleavage pathway. Similarly, on the FeO/Ni(111) surface, ODH reaction is favored over the C–C bond cleavage dry reforming reaction. However, on the Ni3Pt catalyst, the C–C bond cleavage is favored over C–H bond cleavage dehydrogenation reaction.
Chen and co-workers also found that the Mo2C/γ-Al2O3 catalyst preserved the C–C bond cleavage of ethane to produce ethylene, while Pt/CeO2 preferably produced synthesis gas.325 These findings agreed with DFT results that the Mo2C(001) surface led to ethylene formation, and the CeO2/Pt(111) surface preferentially generated synthesis gas. Besides, the authors demonstrated that a MoOx modified Mo2C surface was related to ethylene formation in ethane ODH with CO2.326 Oxygen modification was able to inhibit the C–C bond cleavage and reduce coke formation. The Fe promoter could accelerate the formation of the surface MoOx layer and stabilize it, leading to a higher ethylene yield and improved stability.
An ab initio microkinetic model (MKM) was constructed to investigate the reactivity trends of transition metal catalysts for ethane dehydrogenation with CO2 as a mild oxidant.328 Both direct ethane dehydrogenation and O-assisted ethane dehydrogenation on terrace (111) and step (211) surfaces were studied. Ethane was predominantly converted to ethylene via direct dehydrogenation on both surfaces. Towards O-assisted ethane dehydrogenation (CO2 consumption), Co, Ru, Ni, and Rh were more active than other transition metals on both surfaces (Fig. 26a and b). In an attempt to screen bimetallic alloys to achieve greater CO2 consumption activity with reduced coke formation, three potential bimetallic alloys (Ni3Fe, Ni3Co and Pt3Co) were selected (Fig. 26c). Out of them, two were tested experimentally, and FeNi/CeO2 has shown some promise for ethane dehydrogenation along with CO2 reduction.
 | ||
| Fig. 26 Elementary reaction rate for oxygen assisted ethane dehydrogenation (C2H6 + O → C2H5 + OH) over the (a) (111) surface and (b) (211) surface of transition metal catalysts; and (c) screened alloy candidates.328 Reproduced from ref. 328 with permission from the Royal Society of Chemistry, copyright 2020. | ||
4. Activation of C–H bonds of propane and propylene
Propylene is one of the vital petrochemical building blocks for producing various chemical products, such as propylene oxide, polypropylene, and acrylonitrile. The conventional production processes of propylene are mainly steam cracking and fluidized catalytic cracking of light diesel, naphtha, and other oil byproducts.329,330 Along with the large-scale revolution of shale gas and the growth of the global propylene demand (which is expected to increase to 130 million metric tons by 2023), on-purpose propylene production, specifically propane dehydrogenation (PDH), seems to be a promising alternative.331 The PDH process is an endothermic reaction, and successfully commercialized PDH catalysts can be categorized into two groups: Pt- and Cr-based catalysts. The reaction is normally performed at around 600 °C on Al2O3 supported Pt–Sn or CrOx catalysts. Pt-Based catalysts are commonly used commercial catalysts for PDH because of their high catalytic activity. Still, they suffer from unsatisfactory propylene selectivity, fast deactivation, and poor catalyst stability caused by coke formation and catalyst sintering at high reaction temperatures.277,289,292,332 Thus, significant efforts have been devoted to improving the performance of Pt-based catalysts, generally by doping with additional promoters, such as late TMs and main-group metals (including Ga and Sn) and by modifying carriers.333,334The oxidative dehydrogenation of propane generally follows the MVK mechanism,221,335,336 also known as the lattice oxygen mechanism. This mechanism holds that reactants with reducing properties react with highly reactive oxygen atoms in the catalyst surface to generate oxidation products and thus form oxygen vacancies on the surface. Then, followed by O2 or CO2 adsorption at the oxygen vacancy sites, the sites can be oxidized or filled with oxygen, forming a catalytic cycle. Besides, in order to break the thermodynamic limitations of the propane dehydrogenation reaction, an oxidant that is added to the reaction feed or system will react with the intermediate species hydrogen or the product H2 to produce water, releasing a large amount of heat.337,338 However, for the ODH of propane, the reaction products are easily oxidized to produce CO and CO2, so the reaction has to be carried out at a lower temperature in order to obtain a higher selectivity.339 Also, propane dehydrogenation is a kinetically controlled reaction, and the activation of the C–H bond in propane is usually a rate-determining step, which requires the reaction at a higher temperature.340
Currently, in the PDH and ODH systems, the nature of the reaction mechanisms and reaction pathways on the catalysts remains elusive, and many side reactions such as deep dehydrogenation, C–C bond cleavage, H migration, and H2O formation also need to be taken into consideration. By DFT calculations, the surface electronic structures of catalysts can be studied, mainly for exploring the active sites, stability, and modulation mechanism on the surface. Then, the elementary steps of dehydrogenation reaction involved in the network of the main and side reactions, together with the migration of H on the catalyst surface, are investigated to identify a favorable reaction pathway. Besides, the kinetic analysis can further convert the rate constants of the elementary steps calculated with DFT to the corresponding turnover rates under the reaction conditions, and consequently, it can determine the activity trend and rate-determining steps. It is therefore of great interest to employ theoretical calculations as a tool for investigating how the PDH and ODH catalysts function on an atomic scale. We will see that, by using microkinetic analysis combined with results from DFT calculations, the crucial roles of different active sites, promoters, and supports, and reaction pathways and RDSs29 can be explained, which guides the investigation toward a more effective catalyst for PDH and ODH. The progress in computational catalysis of PDH and ODH is reviewed in Sections 4.1 and 4.2, respectively.
4.1 C–H bond activation in propane on metals
| Surface | Propylene | XC functional | Ref. | |||||
|---|---|---|---|---|---|---|---|---|
| Propane | di-σ | π | ||||||
| E ads (eV) | E ads (eV) | d C1=C2 (Å) | d Pt–C1 (Å) | d Pt–C2 (Å) | E ads (eV) | |||
| Pt(111) | −0.34 | −0.83 | 1.501 | 2.145 | 2.178 | — | vdW_DF | 350 |
| Pt3Sn/Pt(111) | −0.39 | −0.48 | 1.504 | 2.159 | 2.174 | — | ||
| Pt3Sn(111) | −0.28 | −0.54 | 1.497 | 2.159 | 2.193 | — | ||
| PtSn2(111) | −0.24 | −0.23 | — | — | — | — | ||
| Pt(111) | — | −0.64 | 1.48 | 2.12 | 2.14 | 0.06 | B3LYP | 356 |
| Pt(111) | −0.06 | −0.93 | 1.50 | 2.11 | — | −0.66 | PBE | 349 |
| Pt(100) | −0.04 | −1.22 | — | — | — | −1.07 | PBE | 357 |
| Pt(111) | −0.04 | −0.97 | — | — | — | −0.67 | ||
| Pt(211) | −0.04 | −1.43 | — | — | — | — | PBE | 347 |
A crucial point in the dehydrogenation reaction is the examination of the competition between propylene dehydrogenation and desorption, which provides the key to understanding how the selectivity of catalyst surfaces can be tuned.358 Compared to propane, propylene has a half-saturated double bond (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), which could be readily decomposed on metal surfaces. Valcárcel et al. proposed a schematic representation of adsorbed propylene on Pt(111), where these surface structures mainly depend on coverage and temperature.359 At temperatures below 230 K, propylene is undissociated to adsorb on the metal surface, as is the case for ethylene. The di–σ and π models are the most common propylene chemisorption configurations on metal surfaces, as shown in Fig. 27(a). The adsorption configuration depends on the site coverage of propylene, and the di–σ mode through its unsaturated C
C), which could be readily decomposed on metal surfaces. Valcárcel et al. proposed a schematic representation of adsorbed propylene on Pt(111), where these surface structures mainly depend on coverage and temperature.359 At temperatures below 230 K, propylene is undissociated to adsorb on the metal surface, as is the case for ethylene. The di–σ and π models are the most common propylene chemisorption configurations on metal surfaces, as shown in Fig. 27(a). The adsorption configuration depends on the site coverage of propylene, and the di–σ mode through its unsaturated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond at a short bridge site is predominant below half-saturation coverage, with the C
C bond at a short bridge site is predominant below half-saturation coverage, with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond being nearly parallel to the surface, and the methyl group would tilt away from the surface as the site coverage is close to saturation. The adsorption energy of the di–σ adsorption is generally more negative than that of the π adsorption.349,350,353,357,359 This can be explained by the larger valence charge density between the C and metal surface in the di–σ bond than in the π adsorption, indicating a stronger C–metal bond, as shown in Fig. 27(b). The strong adsorption weakens the C
C bond being nearly parallel to the surface, and the methyl group would tilt away from the surface as the site coverage is close to saturation. The adsorption energy of the di–σ adsorption is generally more negative than that of the π adsorption.349,350,353,357,359 This can be explained by the larger valence charge density between the C and metal surface in the di–σ bond than in the π adsorption, indicating a stronger C–metal bond, as shown in Fig. 27(b). The strong adsorption weakens the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond.360 Upon the di–σ adsorption over metal surfaces, the length of the double C
C bond.360 Upon the di–σ adsorption over metal surfaces, the length of the double C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond in propylene increases from 1.36 (in gas-phase propylene) to about 1.50 Å,349,351,353 which is close to the single C–C bond length of propane. This change, together with the fact that propylene loses its “planarity” as the C–H bonds bend away from the surface plane, indicates the rehybridization of the C atom from sp2 to sp3, and the C
C bond in propylene increases from 1.36 (in gas-phase propylene) to about 1.50 Å,349,351,353 which is close to the single C–C bond length of propane. This change, together with the fact that propylene loses its “planarity” as the C–H bonds bend away from the surface plane, indicates the rehybridization of the C atom from sp2 to sp3, and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond is therefore weakened by forming covalent bonds with Pt atoms. On Pt(100)357 and Pt(211) surfaces,347 propylene adsorption also prefers the di–σ mode to the π mode. The adsorption energy of propylene follows the order of Pt(211) > Pt(100) > Pt(111), as can be seen in Table 2. Although the estimated adsorption energy depends on the functionals used, it does not change the trend on the different surfaces. The adsorption energy on Pt(111) obtained with the vdW–DF functional agrees well with the experimental desorption energy determined using temperature-programmed desorption (TPD) measurements.350
C bond is therefore weakened by forming covalent bonds with Pt atoms. On Pt(100)357 and Pt(211) surfaces,347 propylene adsorption also prefers the di–σ mode to the π mode. The adsorption energy of propylene follows the order of Pt(211) > Pt(100) > Pt(111), as can be seen in Table 2. Although the estimated adsorption energy depends on the functionals used, it does not change the trend on the different surfaces. The adsorption energy on Pt(111) obtained with the vdW–DF functional agrees well with the experimental desorption energy determined using temperature-programmed desorption (TPD) measurements.350
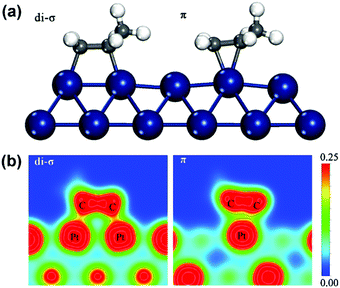 | ||
| Fig. 27 (a) Adsorption modes of propylene on Pt surfaces.357 Reproduced from ref. 357 with permission from Elsevier, copyright 2014. (b) The valence charge densities calculated for different propylene adsorption modes.349 Reproduced from ref. 349 with permission from Elsevier, copyright 2010. | ||
Alloying Pt(111) with less reactive metal Sn leads to weaker propylene adsorption, as can be seen in Table 2.350 Propylene binds preferentially to the Pt3Sn(111) surface in the di–σ mode, similar to that on Pt(111), but the adsorption is weak on the PtSn2(111) surface and dominated by vdW interactions. This result is mainly attributed to the geometric effect of introduced Sn, which reduces the number of Pt–Pt di–σ sites accessible by propylene, whereas the electronic effect that originated from the interaction energy of the Pt–Pt di–σ sites was found to be small.
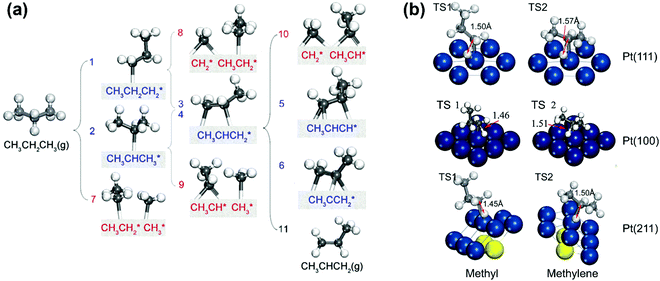 | ||
| Fig. 28 (a) Reaction network for propane dehydrogenation to propenyl and (b) geometries of the transition states for the initial activation of the propane C–H bonds at the methyl and methylene groups on Pt(111), Pt(100), and Pt(211). The detached H atoms are not included for clarity. The numbers signify the sequence numbers of the elementary steps.347,357 Reproduced from ref. 347 with permission from the PCCP Owner Societies, copyright 2011. Adapted from ref. 357 with permission from Elsevier, copyright 2014. | ||
The C–H bond dissociation energy of propane is 4.35 and 4.17 eV for the primary and secondary C–H bond scission, respectively. In the catalytic system, the energy barriers for the initial activation of the propane C–H bonds at the methyl and methylene groups are 0.69 and 0.70 eV on Pt(111), respectively, which indicates that there is no particular preference for the activation of C–H bonds on the surface.347 For the transition states of propane activation on Pt surfaces, propane is bonded to Pt surfaces via the C atom, where the H in C–H is bonded to adjunct Pt. The C–H bonds at the methyl group are stretched by 1.50 Å (see Fig. 28b), as compared to the C–H bond length in gas-phase propane (1.10 Å). The geometries of the transition states on Pt(111), Pt(100), and Pt(211) are almost identical, as shown in Fig. 28(b). The C–H bond activation follows the universal scaling relationship, as shown in eqn (4). The lower C–H bond energy leads to a lower activation energy of propane activation than ethane and methane activation. The activation energies of the first dehydrogenation steps on Pt(211) are lower than those on Pt(100) and Pt(111) due to the higher hydrogen affinity on the unsaturated surfaces, where the lower activation energies for propane give higher dehydrogenation activity on these three surfaces. The activated C–H bonds are stretched by 0.36–0.41 Å. The energy barriers for the activation of C–H bonds occurring at the two groups are calculated to be 0.32 and 0.28 eV on stepped Pt(211), and 0.43 and 0.42 eV on Pt(100), respectively.357
The addition of one or more main-group metals or TMs is an effective way to modify Pt-based catalysts.350,361,362 DFT calculations revealed that the Sn component could broaden the d-band of Pt, giving rise to a downshift of the d-band center, and the dehydrogenation activity ranked in the descending order is: Pt(111) > Pt3Sn(111) (bulk alloy) > Pt3Sn/Pt(111) (surface alloy) > PtSn2(111) (bulk alloy) > Pt2Sn/Pt(111) (surface alloy).348 In addition to Pt-based catalysts, other metal catalysts, such as metal Ni, intermetallic Pd–Zn, and Pd–Cu, have also been studied for the activation of C–H bonds.351,363,364 Saelee et al. reported that the activation energy for the first dehydrogenation of propane on Ni(111) (0.69 eV) is close to that on Pt(111) (0.70 eV). Single Pd atoms at the edge site of Cu55 clusters can facilitate the first C–H bond cleavage, and the energy barrier predicted using the PBE functional is 1.06 eV, approximately 0.25 eV lower than the corresponding barrier on pure Cu55 clusters. With the correction of the vdW–DF functional, this energy barrier is increased to 1.17 eV.364
| Surface | E act (eV) | XC functional | k points | Unit cell | Ref. | |||
|---|---|---|---|---|---|---|---|---|
| C3H8 → 1-C3H7 | C3H8 → 2-C3H7 | 1-C3H7 → C3H6 | 2-C3H7 → C3H6 | |||||
| Pt(111) | 0.69 | 0.70 | 0.70 | 0.68 | PBE | 7 × 7 × 1 | 3 × 3 | 347 |
| Pt(211) | 0.32 | 0.28 | 0.34 | 0.33 | PBE | 4 × 2 × 1 | 1 × 3 | 347 |
| Pt(100) | 0.43 | 0.42 | 0.39 | 0.39 | PBE | 7 × 7 × 1 | 3 × 3 | 357 |
| Pt(111) | 0.59 | — | 0.66 | — | PBE | 5 × 5 × 1 | 3 × 3 | 331 |
| Pt(111) | 0.92 | 0.92 | 0.90 | 0.94 | BEEF-vdW | 3 × 3 × 1 | 3 × 3 | 353 |
| Pt(111) | 0.75 | 0.60 | 0.74 | 0.78 | opt-PBE vdW–DF | 3 × 5 × 1 | 4 × 2 | 340 |
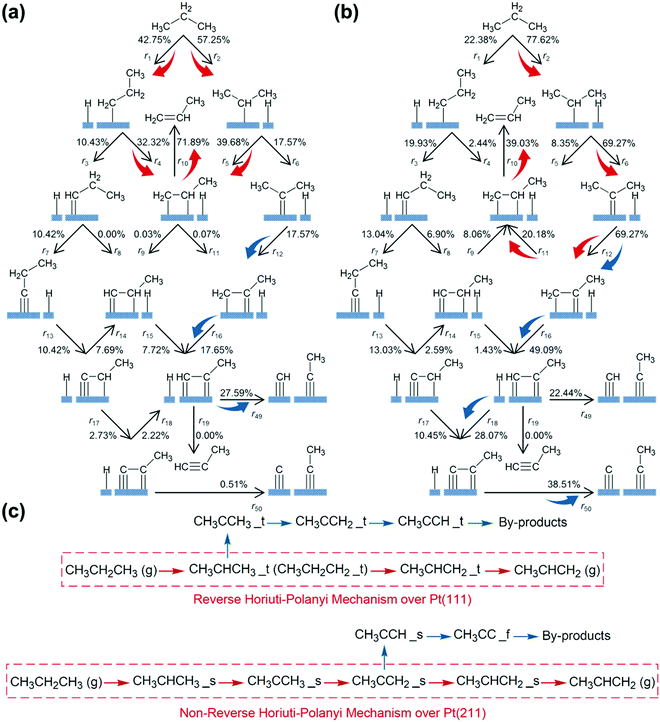 | ||
| Fig. 29 Flux analysis of PDH under experimental reactor inlet conditions (723.15 K, 0.03 bar propane, and 0.04 bar hydrogen) over (a) Pt(111) and (b) Pt(211) with adsorbate–adsorbate interactions considered. The arrows which are labelled with the percentage of the total reaction flux indicate the direction in which the reversible elementary steps actually proceed. The percentage of the reaction flux is calculated as the absolute value of the net rate for that elementary step divided by the rate for propane consumption. (c) Simplified reaction networks for PDH over Pt(111) and Pt(211).365 Reproduced from ref. 365 with permission from the American Chemical Society, copyright 2020. | ||
In addition, the strongly endothermic nature of PDH (ΔrH° = 1.28 eV, under standard conditions at 298 K) requires high reaction temperature (800–980 K) to achieve a reasonable propane conversion.366 However, side reactions, such as cracking, hydrogenolysis, deep dehydrogenation, oligomerization, cyclization, and coke formation, can be promoted even more dramatically by the increase in temperature.332,367 As a result, ethylene (or ethane), methane, and coke are often produced in the PDH reaction as byproducts. The critical challenge for the catalysis of PDH is to reduce the selectivity to byproducts and to maintain the catalytic stability of the catalyst. It is thus essential to include not only the C–H bond activation but also the C–C bond cleavage in the whole catalytic cycle of PDH for the kinetic analysis. Yang et al. systematically investigated the PDH process on flat and stepped Pt surfaces, including Pt(111), Pt(100), and Pt(211).347,349,357 They focused on the kinetics of the C–H bond activation of all the C3 intermediates in PDH, containing 17 dehydrogenation elementary reactions (see Fig. 30) and 12 C–C bond-breaking steps. As an example, the energy profile for PDH on Pt(111) is shown in Fig. 30(b). The insights provided by these studies are summarized as follows:
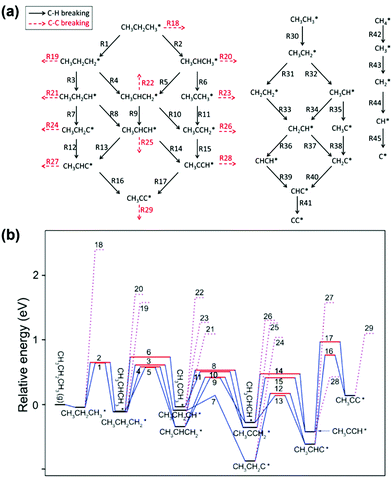 | ||
| Fig. 30 (a) The network of surface reactions of PDH, not including the adsorption reactions of gases and dissociation of H2. All elementary reactions are reversible, and asterisks indicate surface adsorbed species.353 Reproduced from ref. 353 with permission from the American Chemical Society, copyright 2018. (b) Energy profile for propane dehydrogenation on Pt(111) including both the dehydrogenation steps (the solid lines) and the C–C cracking steps (the dotted lines).347 Reproduced from ref. 347 with permission from the PCCP Owner Societies, copyright 2011. | ||
(1) A good scaling relation was found between the transition-state energy and the final-state energy for C3Hx (x = 3–9) dehydrogenation. C–C bond cleavage steps have higher transition state energy and hence higher activation energy than C–H activation.347 The adsorption strength of the intermediates is the key parameter in tuning the activity and selectivity. The stepped Pt surfaces are kinetically more favorable than the flat surfaces for the dehydrogenation of propane because of the stronger adsorption of intermediates on Pt(211).347,368
(2) The activation energy difference between propylene dehydrogenation and desorption was identified as the selectivity descriptor. Lowering the desorption energy and increasing the C–H bond activation barrier of propylene are crucial for increasing the propylene selectivity. Both quantities are closely related to the adsorption strength of propylene. The selectivity towards propylene is substantially lowered in the presence of the coordinatively unsaturated surface Pt atoms due to the strong adsorption of propylene, which has recently been widely used to screen promising candidates as the catalysts for PDH.331,345,354,369
(3) The deeply dehydrogenated intermediate of propyne (CH3CCH*) was identified as an important surface species for the C–C bond breaking because it is the sole C3 species that energetically prefers the cleavage of the C–C bond to the C–H bond breaking, which has also been determined by the microkinetic analysis on Pt(111).340,353
(4) PDH to propylene follows the generally accepted reverse Horiuti–Polanyi mechanism over Pt(111), while over Pt(211), a non-reverse Horiuti–Polanyi mechanism dominates.365 The experimental354 and theoretical analyses of Gibbs energy profiles of the PDH reaction340,353 suggest that the first C–H bond activation is the RDS on Pt(211) and Pt(100) for smaller Pt cluster sizes, while the second C–H bond activation is the RDS on Pt(111). The first C–H activation of propane was identified as the RDS on the Pt(111) by a microkinetic analysis.340 It should be noted that the energy barriers for the first and second C–H bond activations are quite close on Pt(111). The RDS could change with the reaction conditions.
So far, there have been only three microkinetic studies of PDH based on a relatively full description of the reaction pathway of dehydrogenation to propylene, deep dehydrogenation, and C–C bond cracking over Pt(111) surfaces, which were carried out by Saerens et al.,340 Lian et al.,353 and Xiao et al.,365 respectively. The DFT-based kMC simulations by Lian et al. reveal that there are quick deactivation and steady states during the PDH process.353 The precursor of coke is mainly formed during the rapid deactivation, which originates from the coverage of cracking products at the active sites. Then, the surface species and active sites covered by the hardly removed coke lead to the steady-state after quick deactivation. Saerens et al.340 focused their studies on the influence of hydrogen co-feeding on the reaction mechanism of PDH. They pointed out that the increasing the co-feeding hydrogen pressure can decrease the coverage of deeply dehydrogenated coke precursors and increase the number of free sites on the Pt(111) surface; moreover, this increase in free sites can lead to higher catalytic activity. The modeling results rationalized the experimental observation of the reduced coke formation and enhanced propylene selectivity by co-feeding hydrogen in PDH.340,353 By using microkinetic analysis in combination with results from DFT calculations, Xiao et al.365 found that a non-reverse Horiuti–Polanyi mechanism accounts for more than half the propylene production at the under-coordinated active sites that dominate the kinetics of PDH (see Fig. 29), which consists of three dehydrogenation steps that have two β-H and one α-H atoms removed from propane, followed by the hydrogenation of CH3CCH2, and at this species the deep dehydrogenation reaction competes with the production of propylene.
The microkinetic modeling of the side reactions of C–C bond cracking and deep dehydrogenation, and coke formation indicates that the catalyst deactivation is due to the formation of CH3CC* and C*, which lead to cracking and eventual coke formation, respectively.340,353 The formed C1 and C2 species could desorb to form ethane, ethylene, and methane or serve as coke precursors.340 Then, the formation of coke could block the active sites of the catalyst, impede the catalytic activity, and eventually deactivate the catalyst.331,353 Lian et al. studied the detailed reaction pathway of propylene formation, deep dehydrogenation, and C–C bond cracking for understanding the origin of coke formation.353 The deep dehydrogenations are via R6 → R11 and R10 and finally lead to the cracking of C3 species, mainly starting from propyne (see Fig. 30). The coke precursors are mainly formed during the quick deactivation, and the active sites are mainly occupied by C2 and C1 species, which are hardly removed from the surface. However, the covered active sites, after quick deactivation, can lead to a stable state, which can hinder the side reactions to achieve a stable selectivity. Besides, the co-adsorption of carbon can shift the d-band centers of the surface Pt atoms further below the Fermi level, leading to a decrease in the catalytic activity for PDH.340 Zhu et al. proposed that coke formation is not structure-sensitive, as coke can be formed by all Pt facets and can preferentially cover the under-coordinated active sites.354 The higher coking rate on small Pt clusters is due to the larger Pt surface area, and the faster coke formation resulted in faster deactivation. Therefore, the rational construction of a Pt surface structure can be a crucial factor in improving catalytic selectivity and controlling coke formation.353
Under high-temperature reaction conditions, the interaction between Pt and propylene is strong, and side reactions readily occur to form coke and deactivate the catalyst, so the propylene selectivity is around 60–80%, and the catalyst stability is poor.370 To increase the selectivity toward propylene at relatively high catalytic activity, various attempts have been made to modify the geometrical and electronic structures of Pt-based catalysts,2,371,372 such as controlling the size and shape of Pt NPs, alloying Pt with TMs or main-group metals, and selecting appropriate catalyst supports. For example, Zhu et al. reported that the Pt catalysts of larger cluster sizes with (111) dominating the surface have higher selectivity toward propylene and better stability than the smaller clusters where (211) is dominant on the surface. This is due to the weakened binding strength of propylene and the higher energy barrier for deep dehydrogenation on Pt(111). Yang et al.354,357 proposed that the introduction of H can decrease the desorption barrier for propylene, and therefore, the selectivity toward gaseous propylene is improved. The Gibbs free energy of the dominant reaction pathways of propane to propynyl (CCCH3) on Pt(111) shows that with increasing H coverage the propylene adsorption strength decreases, while the energy barrier for the further dehydrogenation of propylene increases, leading to a higher catalytic selectivity.340
Previous studies have proved that alloying of Pt with one or more TMs, such as Sn, Ti, Ga, Cu, Co, Zn, Ir, and In, is an effective way to improve the catalytic performance in PDH.2,290,373–377 Among them, Sn is most widely studied due to its application in the industrial process. Yang et al.348 reported that with the increase in Sn content in Pt–Sn alloys, the d-band centers of surface Pt atoms are shifted farther below the Fermi level, as shown in Fig. 31(a), which changes the adsorption properties of Pt. According to the d-band model,378 downshifting the d-band center of surface atoms would reduce the interaction strength between the surface and adsorbates, whereas upshifting the d-band center of surface atoms may cause the antibonding states to, at least in part, shift up through the Fermi level and become empty, which eventually leads to a stronger binding strength of the adsorbate to the metal surface. Therefore, from the figure, one can see that an upshift of the d-band center gives rise to stronger binding of 1-propyl to the surface and a lower energy barrier for PDH to 1-propyl, which lowers the catalytic activity for PDH. Moreover, the step sites of Pt modified by adding Sn show more profound electron transfer from Sn to Pt on the Pt–Sn alloy surfaces. In addition, the authors also investigated the competition between propylene dehydrogenation and propylene desorption. They found that the introduction of Sn into Pt(111) can lower the energy barrier for propylene desorption and simultaneously increase the activation energy for propylene dehydrogenation (see Fig. 31b). The electronic effect, i.e., the decrease in the interaction energy of the available Pt–Pt di–σ sites, and the geometric effect of the introduced Sn reducing the number of Pt–Pt di–σ sites accessible by propylene can weaken propylene adsorption, leading to a lower desorption barrier than the dehydrogenation barrier of propylene, and thus higher propylene selectivity than Pt(111).379 By considering the compromise between the catalytic activity and selectivity, the Pt3Sn bulk alloy is proposed to be the best candidate for PDH. The related experiments also proved that the Sn component added as a promoter in the Pt/γ-Al2O3 catalyst can achieve higher propylene selectivity and minimize coke formation.334,373,380,381 The work also reported that the addition of Sn can help Pt re-disperse in the catalyst regeneration by providing nucleation sites on the γ-Al2O3 surface to achieve superior catalyst stability.381
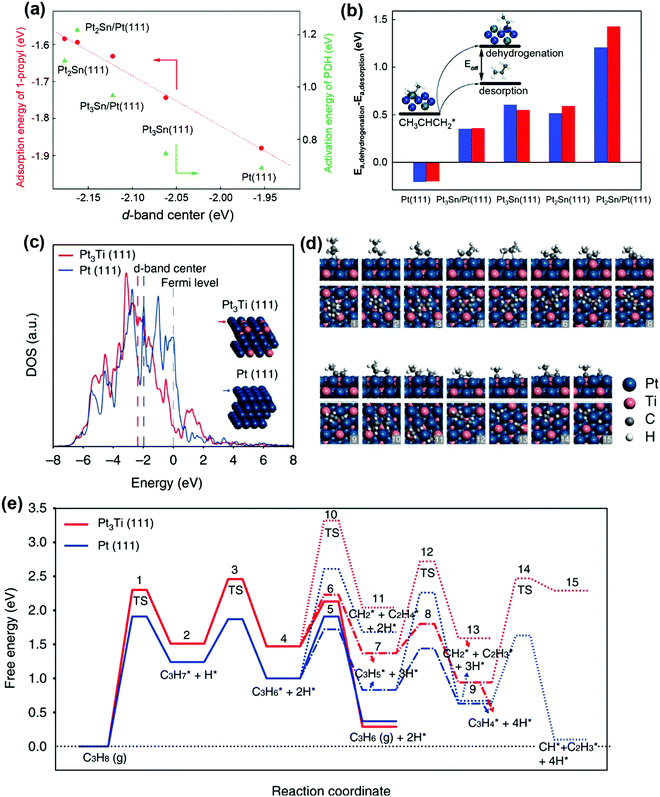 | ||
| Fig. 31 (a) Plots of the binding energies of 1-propyl (red dots) and the energy barriers for propylene dehydrogenation to 1-propyl (green dots) against the d-band centers over Pt(111) and PtSn surfaces. (b) Energy barrier difference (Ediff) between propylene dehydrogenation and propylene desorption. Blue and red bars indicate pathways to 1- and 2-propenyls, respectively.348 Reproduced from ref. 348 with permission from the American Chemical Society, copyright 2012. (c) DFT calculated projected DOS for the 5d orbitals of Pt in the top-layer Pt3Ti(111) and Pt(111). (d) Optimized structures as numbered in (e) from the side and top views (H* is not shown). (e) Free energy diagrams of relevant (side-)reaction steps in PDH on Pt3Ti(111) and Pt(111) surfaces. The dotted lines denote the C–C cracking of C3H6*, C3H5*, and C3H4*, and the dashed-dotted lines denote the deep dehydrogenation of C3H6* and C3H5*.382 Reproduced from ref. 382 with permission from Springer Nature, copyright 2018. | ||
Similarly, an improved catalytic performance was also reported on the Pt3Ti catalyst.382 As shown in Fig. 31(c), the d-band center of Pt(111) is located at −1.97 eV relative to the Fermi level, whereas that of Pt3Ti(111) downshifts to −2.37 eV due to the strong Pt–Ti d–d orbital coupling, giving rise to weaker adsorption of reaction intermediates and changes in the relative free energy and barriers of the reaction steps during dehydrogenation and side reactions (see Fig. 31d and e). From the figure, one can see that the barrier for propylene desorption on Pt3Ti(111) is 0.25 eV lower than that on Pt(111), but the energy barrier for deep propylene dehydrogenation is increased by the introduction of Ti into Pt. Moreover, on the Pt3Ti(111) surface, the C–C bond cracking steps are all endergonic and hence are hindered compared to Pt(111), where C3H5* and C3H4* cracking are exergonic and much more favorable. These results indicate that Pt3Ti has higher selectivity toward propylene for PDH compared to pure Pt. Wang et al. also studied the effect of Ga as a promoter of Pt/CeO2–Al2O3 catalysts on PDH, indicating that introduced Ga can decorate Pt NPs by forming Pt–Ga alloys and, meanwhile, the Ga component can be incorporated into the cubic fluorite structure of CeO2. The metal Ga promoter on Pt–Ga alloys can decrease the size of Pt ensembles or block the low-coordinated defect active sites, lower the desorption barrier of propylene and coke precursors by donating electrons to Pt atoms, and thus suppress undesirable side reactions to achieve better propylene selectivity. Besides, the promoter towards CeO2 can enhance both lattice oxygen storage capacity and surface oxygen mobility to increase the reducibility of CeO2 and consequently reduce the coke deposition and improve the catalyst stability.376
Besides, the addition of one or more main-group metals or TMs, such as Sn, In, Cu, and Ga, is also an effective way to reduce the tendency to form coke.343,350,361,362 The dopants can promote the dispersion of Pt particles and thus prevent their sintering, suppress the structure-sensitive side reactions including hydrogenolysis and deep dehydrogenation to reduce the rate of carbon deposition, and promote the migration of carbon deposition from active metal components to the carrier, etc.380,383,384
In addition, some novel core–shell Pt-based catalysts can not only improve the catalytic performance but also effectively increase the utilization efficiency of precious metals. Note that near-surface alloys (NSAs) having a host metal (such as Pt) as the subsurface and solute metals as the overlayer exhibit unique chemical and physical properties distinct from those of their constituent metals. Xiao et al.331 reported that by substituting late TMs for the Pt atoms in the core region, the adsorption and catalytic properties of the surface Pt atoms in M@Pt core–shell catalysts could be tuned, which is attributed to the modification of the electronic structure of metal surfaces through the strain effect and electron transfer. The core–shell catalysts were found to have less negative propylene adsorption energies and higher activation energies for the dehydrogenation reactions than Pt, thus giving rise to lower catalytic activity and a higher selectivity toward propylene, as shown in Fig. 32(a). This figure also indicates that higher catalyst selectivity toward propylene can be attained at the expense of a lower catalytic activity for PDH. Co@Pt is proposed to be the best core–shell catalyst for PDH if a compromise is made between catalytic activity and catalyst selectivity. Cesar et al.370 prepared bimetallic Pt–Co NPs for PDH with and without added H2 and studied the effect of the Co loading amount on the core structure from Pt to Pt3Co to PtCo. The result shows that bimetallic NPs have significantly better olefin selectivity than either single metal, suggesting that Co that acts as a less active promoter can utilize the geometric effects to enhance the selectivity by breaking up large Pt ensembles in the bimetallic catalysts. Therefore, through the experimental exploration for Pt–Co alloy catalysts, it is found that the catalysts exhibit superior PDH performance, especially catalytic selectivity, consistent with the results obtained by Xiao et al.331 Besides, Sun et al.385 pointed out that the isolated Pt atoms dispersed in Cu NPs can break the PtM alloy scaling relationship, which is different from the scaling for conventional Pt alloys during the PDH (see Fig. 32b). In other words, the Pt/Cu single atom alloy maintains a reasonable dehydrogenation activation barrier and at the same time displays quite a high selectivity, which is reflected by the low free energy barrier difference between the propylene desorption and deep dehydrogenation. Therefore, the use of dopants can improve the selectivity of Pt-based catalysts, suppress catalyst deactivation, and extend the use time of catalysts.
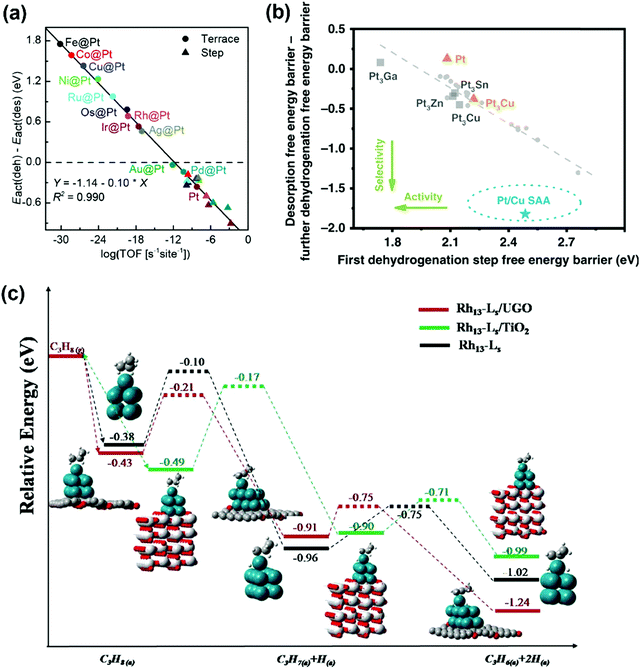 | ||
| Fig. 32 (a) Linear scaling relation between catalytic activity and selectivity for PDH over 12 core–shell alloy catalysts.331 Reproduced from ref. 331 with permission from Elsevier, copyright 2019. (b) Screening of Pt-based bimetallic catalysts for PDH, where SAA denotes the single atom alloy.385 Reproduced from ref. 385 with permission from Springer Nature, copyright 2018. (c) Profiles of the potential-energy surface for PDH on Rh13-Ls, Rh13-Ls/UGO and Rh13-Ls/TiO2, where Rh13-Ls is the low-symmetry Rh13 cluster and UGO is the unzipped graphene–oxide.386 Reproduced from ref. 386 with permission from the PCCP Owner Societies, copyright 2017. | ||
Moreover, selecting suitable catalyst supports is also an effective way to modify the catalytic performance of metal catalysts for PDH.387,388 Chang et al.386 investigated the PDH over Rh13-Ls (low-symmetry Rh13 cluster), Rh13-Ls/UGO (Rh13-Ls cluster supported on a sheet of unzipped graphene oxide), and Rh13-Ls/TiO2 catalysts. They found that although electrons flowed from the Rh13 cluster towards both supports, the UGO support induced an electronic redistribution of the Rh13 cluster rather than just abstracting electronic charge from the Rh13 cluster to the support, as compared with the TiO2 counterparts. UGO would induce an electronic accumulation onto the top area of the Rh13 cluster, while TiO2 induced electronic depletion, which dictates different results for PDH. As shown in Fig. 32(c), for the Rh13-Ls/UGO system, the energy barrier for the dehydrogenation of propane to propyl is 0.22 eV, and the calculated energy barrier for the dehydrogenation of propyl is 0.16 eV. UGO as a support could lower the energy barriers for both two dehydrogenation steps of propane, but TiO2 as a support increased the energy barriers for both dehydrogenation steps, indicating that the UGO sheet is a more suitable support for the Rh13-Ls cluster and for activation of the C–H bond in PDH. Besides, Jiang et al.389 found that the addition of an appropriate amount of TiO2 in Pt/TiO2–Al2O3 catalysts can improve propylene selectivity and catalyst stability. The reasons are that the electrons could be transferred from the partially reduced TiOx (x < 2) to the Pt atoms, and the partial coverage of the metal surface by TiOx species, and thus the increased electron density of Pt can hinder propylene adsorption on active metal sites and facilitate coke migration from the active sites to the carrier.
4.2 C–H oxidative activation on metal oxides
Although the direct dehydrogenation of propane to propylene (PDH) is a rather promising solution, the ODH of propane has some advantages: ODH is thermodynamically favored even at low temperatures and can avoid the formation of coke.303,390,391 Besides, unlike the PDH reaction, the ODH of propane is mainly based on the following two mechanisms: first, lattice oxygen is involved in the reaction, and then the oxygen vacancies formed can be filled by the added oxidants (removal of lattice oxygen anions and their reinsertion); second, lattice oxygen is not involved in the reaction; however, the oxidants can be adsorbed on the surface to react with the reactants or intermediates.392,393 Supported vanadium oxides are known to be one of the best catalysts for the ODH reaction with high thermal stability and a relatively large surface area. Several research groups have studied the mechanism of ODH reaction on metal oxide catalysts, usually following the MVK redox mechanism involving lattice oxygen in C–H bond activation.394–396 This redox mechanism mostly occurs on transition-metal oxide catalysts with relatively high reducibility. It can be generally described as a two-step mechanism: (1) the reduction of the oxide surface by the dehydrogenation of the hydrocarbon – the catalyst in the oxidation state activates the C–H bond and therefore the dissociated H atoms combine with the lattice oxygen atoms to desorb in the form of H2O; and (2) the subsequent reoxidation by gas-phase oxygen – the generated oxygen vacancies complete the circulation process of the catalyst surface under the action of oxygen.29,397,398 The C–H bond activation in propane on (un)supported metal oxides such as VOx, Cr2O3, ZnO, V2O3, and Ga2O32,303,339,391,399–406 has been studied theoretically by using DFT calculations in which the active sites and reaction mechanism were focused. The reduction step has comprehensively been studied, and the full catalytic cycle is not considered because the oxidation of the substrate is typically a fast step.336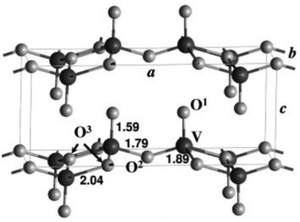 | ||
| Fig. 33 V2O5 bulk surface.408a, b, and c of the orthorhombic unit cells are parallel to the (100), (010), and (001) directions, respectively. V atoms are depicted as the white circles and O atoms as the smaller gray circles. O1, O2, and O3 denote the single, 2-fold, and 3-fold coordinated oxygen atoms, respectively. Bond lengths in Å. Reproduced from ref. 408 with permission from the American Chemical Society, copyright 2005. | ||
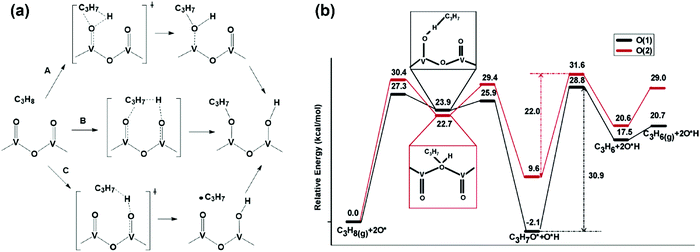 | ||
| Fig. 34 (a) Three homolytic cleavage mechanisms for the C–H bond activation of propane: an oxo-insertion mechanism (A), a concerted mechanism (B), and a radical mechanism (C); and (b) lowest-energy pathways of the propane ODH process that occurred on O1 and O2 on the V2O5(001) surface.303 Reproduced from ref. 303 with permission from the American Chemical Society, copyright 2006. | ||
The reactivity of O sitting on V2O5(001) follows the order of O1 > O2 > O3. The energy barriers of activation of the first C–H bond in propane are 1.18 and 1.32 eV at the O1 and O2 sites, respectively, as shown in Fig. 34(b). The threefold-coordinated oxygen (O3) is the least active for C–H bond activation and almost inert.303 The i-propoxide can much more easily further decompose into propylene at the O2 site, releasing an H atom to a neighboring O2 or O3 atom, and the corresponding energy barrier is 0.95 eV lower than that at the O1 site (>1.30 eV). The H2O formation through the recombination of two OH groups at the O1 site is facile, and H2O desorption is endothermic with a relatively low reaction energy of 0.56 eV, leading to the formation of oxygen vacancies on the oxide surface. As the lattice oxygen is removed, the structure of the catalyst may collapse, indicating that the V2O5(001) surface is fully dynamic.
For the second H abstraction step, the reaction energy is −1.58 eV, and the estimated activation barrier is 0.65 eV, where the surface reconstruction is not taken into account.399,409 Gas-phase reactions of propane with VO2+ and V3O7+ have also been studied.410,411 When considering the more complex reaction conditions of vanadium oxide catalysts involving supports and O2 adsorption, some of the energy barriers could be affected, such as propane adsorption and H2O elimination. However, the terminal O1 is too active to release propylene and therefore shows poor propylene selectivity.
Active sites. Depending on the loading of VOx on the support, the VOx can present as an isolated monomer, dimer, and polymer (sub-monolayer, a monolayer) and crystalline structure.404,413 Three types of lattice O are identified, such as (a) terminal V
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O sites, (b) bridging V–O–V sites, and (c) V–O–support sites.403,414 The active sites depend on the catalyst structure on the surface. On the supported monomeric VOx, there are two different types of available active O sites, namely terminal V
O sites, (b) bridging V–O–V sites, and (c) V–O–support sites.403,414 The active sites depend on the catalyst structure on the surface. On the supported monomeric VOx, there are two different types of available active O sites, namely terminal V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O sites and V–O–support interface sites. For the dimer and polymer VOx, there are additional bridging V–O–V sites. Activation of propane requires a pair of oxygen sites denoted as OA–OB as the active sites, where V is inert.414 The active sites are highly dynamic, and there are a large number of combinations of two oxygen sites among the three O sites.
O sites and V–O–support interface sites. For the dimer and polymer VOx, there are additional bridging V–O–V sites. Activation of propane requires a pair of oxygen sites denoted as OA–OB as the active sites, where V is inert.414 The active sites are highly dynamic, and there are a large number of combinations of two oxygen sites among the three O sites.
Activation of propane and propylene. The activation of propane has been studied on the isolated monomeric O
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) V(O–)3 supported on SiO2,401 a VOx monolayer on TiO2(001),403 and monomeric and dimeric VOx species supported on the (001) and (100) surfaces of anatase TiO2.414 Regardless of the supports, propane undergoes preliminary weak physical adsorption on the surface prior to dissociation. Unlike the non-selective activation on the metal surfaces, the secondary C–H bond activation is energetically preferred compared to the primary C–H bond activation, in agreement with the order of the C–H bond dissociation energies in propane. C–H bond activation follows similar mechanisms on the unsupported V2O5(001). The activation energies for hydrogen abstraction are almost the same at the different active sites of the unsupported catalyst, i.e., O1 ≈ O2 ≈ O3, while they increase in the order O1 < O2 < O3 on the supported catalyst.403
V(O–)3 supported on SiO2,401 a VOx monolayer on TiO2(001),403 and monomeric and dimeric VOx species supported on the (001) and (100) surfaces of anatase TiO2.414 Regardless of the supports, propane undergoes preliminary weak physical adsorption on the surface prior to dissociation. Unlike the non-selective activation on the metal surfaces, the secondary C–H bond activation is energetically preferred compared to the primary C–H bond activation, in agreement with the order of the C–H bond dissociation energies in propane. C–H bond activation follows similar mechanisms on the unsupported V2O5(001). The activation energies for hydrogen abstraction are almost the same at the different active sites of the unsupported catalyst, i.e., O1 ≈ O2 ≈ O3, while they increase in the order O1 < O2 < O3 on the supported catalyst.403
On the supported VOx monolayer on TiO2(001), the C–H bond activation in propane is via a concerted mechanism at the V–O site, leading to the formation of the metal hydride and adsorbed propoxide.403 The vanadyl site (V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) is the most active site on V2O5(001) and V2O5/TiO2, while the bridging V–O–V sites are more selective towards propylene. The rate-limiting step of oxidative PDH is the activation of propane via a direct H abstraction from the methylene C–H, based on the reaction path analysis at 0 K. The TiO2 support enhances the C–H bond activation as compared to unsupported V2O5 by lowering the activation energy of the RDS as shown in Fig. 35 and influences the selectivity of the supported monolayer VOx catalyst towards propylene production rather than propanol and acetone.
O) is the most active site on V2O5(001) and V2O5/TiO2, while the bridging V–O–V sites are more selective towards propylene. The rate-limiting step of oxidative PDH is the activation of propane via a direct H abstraction from the methylene C–H, based on the reaction path analysis at 0 K. The TiO2 support enhances the C–H bond activation as compared to unsupported V2O5 by lowering the activation energy of the RDS as shown in Fig. 35 and influences the selectivity of the supported monolayer VOx catalyst towards propylene production rather than propanol and acetone.
 | ||
| Fig. 35 (a) Investigated pathways for propane oxidation over the vanadia surface; the corresponding energy diagrams for propane oxidation to propylene on (b) V2O5 and (c) V2O5/TiO2.403 Reproduced from ref. 403 with permission from Elsevier, copyright 2012. | ||
The VOx monomers and dimers supported on SiO2 have also been studied by Rozanska et al.415 The first H abstraction from propane is the RDS and yields activation barriers at 750 K, which are lower for dimeric VOx (1.18 eV) than for monomeric VOx (1.29 eV). Using the reaction energy as a reactivity descriptor, the energy barriers for propane ODH decrease with increasing VOx coverage from dimers to larger oligomers. Besides, VV/VIV redox cycles are preferred over VV/VIII cycles.
Dependence of activity on supports and cluster size. Various oxides such as TiO2, SiO2, CeO2 and γ-Al2O3 have been studied as the supports of VOx.394,416–418 The activity of the active sites in VOx depends strongly on the supports, which is ascribed to the electronic modification of active oxygen sites.414 TiO2 is the most widely studied support owing to the highest activity of VOx/TiO2. Du et al. observed that propane ODH activity can be tuned by supporting on anatase TiO2 surface and changing VOx dispersion.414 The activation energy of the first C–H activation and the formation energy of propylene on the monomeric and dimeric VOx species supported on the anatase TiO2(001) and (100) surfaces are summarized in Table 4.
| VOx/TiO2(001) | VOx/TiO2(100) | |||
|---|---|---|---|---|
| First C–H activation | Propylene formation | First C–H activation | Propylene formation | |
| a R represents the radical propyl mechanism and C represents the concerted propoxide mechanism. Values in the brackets for the monomeric and dimeric VOx/TiO2(100) surfaces are ZPE corrected (unit: eV). | ||||
| Monomer | OV–Ti (1.58) | R: OV–Ti (1.83) | OV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) (1.37)[1.14] (1.37)[1.14] |
R: OV–Ti (1.86)[1.65] |
| C: OV–Ti (1.85) | OV–Ti (1.36)[1.19] | C: OV–Ti (1.86)[1.69] | ||
| Dimer | OV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) (1.62) (1.62) |
C: OV–Ti (2.02) | OV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) (1.05)[0.86] (1.05)[0.86] |
C: OV–Ti (1.19)[1.08] |
By comparing the energy barrier of the first C–H activation step and the overall energy barrier of propylene formation on TiO2(001) and (100) surfaces given in Table 4,414 it can be seen that the catalysts supported on the (100) surface show higher activity than those on the (001) surface. For the monomer, dimer, and monolayer of VOx, the valence bond formed at the interface of VOx and support surfaces. The interface electronic transfer resulted in the modification of the electronic structure of VOx species, as evidenced by the projected p-DOS plots where the centers of the valence bands of the VOx/TiO2(100) surfaces are closer to the Fermi level than those of the VOx/TiO2(001) surfaces. This is also reflected in more negative Bader charges of oxygen sites on the (100) than (001) surfaces. This indicates that the oxygen sites are the nucleophilic centers to attack the positively charged H atoms and activate the C–H bond. The stronger basic oxygen sites with more negative charges in VOx supported on (100) attack more efficiently the acidic C–H bond, and thus result in higher activities than those on the (001) surfaces. In addition, the support changed the relative charge of the oxygen sites. For example, the higher activity of the terminal V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O sites than that of the V–O–Ti interface sites on the dimeric VOx/TiO2(001) can be ascribed to the more negatively charged O on the former sites.
O sites than that of the V–O–Ti interface sites on the dimeric VOx/TiO2(001) can be ascribed to the more negatively charged O on the former sites.
A comparative study of PDH on monomeric and dimeric VOx supported on γ-Al2O3 and V2O5 crystal, as shown in Fig. 36, revealed that the cluster size has a remarkable influence on the relative activity of oxygen sites and the rate-determining step.404 The first C–H bond activation has a lower activation barrier than the secondary C–H activation on the supported V2O5, while both C–H bond activations have similar energy barriers on the supported VO3. Besides, the O p-band center could correlate with the dehydrogenation barrier of the O sites to predict the dehydrogenation activity. Luo et al. also reported that mixed CaO and γ-Al2O3 supported VOx is beneficial to the propylene formation compared to pure CaO supported VOx, which is attributed to the moderate level of acidity and metal–support interaction.419
 | ||
Fig. 36 Reaction energy profiles of C3H6* formation and CH3COCH3* formation by two successive H ruptures of C3H8* over (a) supported monomeric VO3/Al2O3, (b) supported dimeric V2O5/Al2O3, and (c) slab V2O5(001) surfaces. (d) Proposed reaction mechanisms over the different degrees of vanadium polymerization in different periods of reaction. The structures of transition states and adsorbed C3H6* are shown in the diagram. The black line denotes the C–H rupture by the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, while the red line denotes the C–H rupture by V–O–Al (or by the V–O–V bond). The blue line denotes the CH3CO*CH3 formation catalyzed by the V O bond, while the red line denotes the C–H rupture by V–O–Al (or by the V–O–V bond). The blue line denotes the CH3CO*CH3 formation catalyzed by the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. The structures of transition states and adsorbed C3H6* are shown in the diagram. Color scheme: H white; Al green; V gray; O red; C gray.404 Reproduced from ref. 404 with permission from the American Chemical Society, copyright 2019. O bond. The structures of transition states and adsorbed C3H6* are shown in the diagram. Color scheme: H white; Al green; V gray; O red; C gray.404 Reproduced from ref. 404 with permission from the American Chemical Society, copyright 2019. | ||
Moreover, p-DOS analysis suggests that the electronic structure depends on the VOx cluster size or dispersion, which rationalizes the activity dependence of the cluster size of VOx on the support. The monomer dispersed VOx is more active than the dimer dispersed VOx on the TiO2(001) surface, while the dimer dispersed VOx is more active than the monomer dispersed VOx on the TiO2(100) surface.414 Cheng et al.420 reported that the coordination number of the vanadium atom was the key structural parameter in predicting the catalytic activity, showing that the activation energy of the first dehydrogenation step for propane on anatase-supported vanadium oxide monomers and dimers is 1.73 eV and 1.91 eV, respectively.
The above discussion reveals that the support surface and the dispersion of the VOx catalyst change the electronic properties of the oxygen sites and thus change their activity in activating the C–H bond of propane. The oxygen activity in VOx seems to be of vital importance for C–H bond activation.
The activity of the lattice oxygen can also be described by the formation energy of the oxygen vacancy. The formation energy of surface oxygen vacancy can be identified as a dominant parameter in determining the adsorption mode and the catalytic activity of metal oxides.421 Li et al. reported that the formation energy of surface oxygen vacancy could be used as a descriptor to explain the adsorption behaviors, which is more sensitive to the change in the electronic structure of perovskites, arising from the fact that the actual partial charges the oxygen and transition-metal ions carry determine the adsorption behaviors of the oxygen and transition-metal ions.422 The estimated formation energies of oxygen vacancy of VOx are summarized in Table 5.
| Model | O* → * + 1/2O2(g) | |||||
|---|---|---|---|---|---|---|
| O1 | O2 | O3 | O2–support | O3–support | Ref. | |
| V2O5(001) | 2.04 | 3.37 | 3.78 | — | — | 403 |
| V2O5/TiO2 | 2.44 | 4.50 | 3.49 | — | — | |
| V2O5(001) | 1.67 | 3.30 | — | — | — | 413 |
| VO3/TiO2 | 1.86 | — | — | 0.77 | — | |
| V2O5/TiO2 | 2.63 | — | — | 2.76 | 2.23 | |
| V3O6/TiO2 | 2.86 | 4.16 | — | 2.85 | 4.29 | |
| V4O8/TiO2 | 2.68 | 3.92 | — | — | — | |
| 1 mL VOx/TiO2 | 2.89 | 4.77 | — | — | — | |
| Monomeric OVSi7O12H7 | 2.98 | — | — | — | — | 423 |
| Dimeric O2V2Si6O12H6 | 2.87 | — | — | — | — | |
| Octameric V8O20 | 2.65 | — | — | — | — | |
When going from monomeric through dimeric and eventually to octameric VOx species, the reaction energy for VOx species yielding an O defect site changes from 2.98 through 2.87 and eventually to 2.65 eV, as shown in Table 5, while the reaction energy for H abstraction in propane at the corresponding V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O site decreases from 1.06 through 0.90 and eventually to 0.52 eV.415,423 The lower formation energy of oxygen vacancy corresponds to a higher oxygen activity. Likewise, the TiO2 support lowered the formation energy of oxygen vacancy, thus increasing the activity. The formation energy of the oxygen vacancy can therefore be used as a descriptor when searching for new catalysts for ODH of propane.
O site decreases from 1.06 through 0.90 and eventually to 0.52 eV.415,423 The lower formation energy of oxygen vacancy corresponds to a higher oxygen activity. Likewise, the TiO2 support lowered the formation energy of oxygen vacancy, thus increasing the activity. The formation energy of the oxygen vacancy can therefore be used as a descriptor when searching for new catalysts for ODH of propane.
Dependence of activity and selectivity on the cluster size and valence state. The selectivity of propylene remains a challenge in ODH of propane. A study of deep oxidation of propane to CO2 on V2O5(001)424 revealed that the terminal V
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O sites are the active sites for the formation of acetone from i-propoxide and the further combustion of acetone to CO2. The V–O–support is the main active site for propylene formation. It provides a guideline for the rational design of new catalysts with improved selectivity. The ratio of the terminal V
O sites are the active sites for the formation of acetone from i-propoxide and the further combustion of acetone to CO2. The V–O–support is the main active site for propylene formation. It provides a guideline for the rational design of new catalysts with improved selectivity. The ratio of the terminal V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O to the other two oxygen sites is a key parameter in the catalyst design. Small cluster VOx with a low V
O to the other two oxygen sites is a key parameter in the catalyst design. Small cluster VOx with a low V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O ratio could increase the propylene selectivity at the expense of lowering the activity, while polymeric VOx with a high V
O ratio could increase the propylene selectivity at the expense of lowering the activity, while polymeric VOx with a high V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O ratio could lower the propylene selectivity. The cluster size needs to be compromised between the activity and selectivity, and sub-monolayer VOx could provide a high propylene yield, which has been very recently confirmed experimentally by Gong and coworkers.413
O ratio could lower the propylene selectivity. The cluster size needs to be compromised between the activity and selectivity, and sub-monolayer VOx could provide a high propylene yield, which has been very recently confirmed experimentally by Gong and coworkers.413
Very recently, Xiong and co-workers found that the PDH reaction can be divided into two periods in the VOx reduction by propane: the initial ODH dominant period leading to propylene, water and CO2 formation and the non-ODH dominant period (see Fig. 36d).404 Over γ-Al2O3 supported VOx, the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O mainly contributes to H2O and CH3CO*CH3 formation and deep oxidation to CO2 in the ODH dominant period. With the consumption of the V
O mainly contributes to H2O and CH3CO*CH3 formation and deep oxidation to CO2 in the ODH dominant period. With the consumption of the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O during the reaction, the Al–O–V sites become dominating active sites for propylene formation. Note that the PDH ability should be related to their corresponding valence state.420,425 It has been illustrated that the oxygen vacancy modified the electronic structure of active species and even change the reaction mechanism.426
O during the reaction, the Al–O–V sites become dominating active sites for propylene formation. Note that the PDH ability should be related to their corresponding valence state.420,425 It has been illustrated that the oxygen vacancy modified the electronic structure of active species and even change the reaction mechanism.426
Gas-phase O2 in the reactant mixture reoxidizes the reduced V species and removes carbon deposits. The lattice O of VOx species provides pathways toward desired propylene formation, while the surface O mainly forms undesired COx species. Propane conversion and the propylene yield could be described by a kinetic model including propane ODH, parallel propane combustion, and sequential propylene combustion. Propylene is the most abundant primary product. CO and CO2 are formed by the secondary combustion of propylene, which is the main source of carbon oxides in the studied reaction, and CO2 also forms by direct combustion of propane.335,427,428 The activation energies of CO and CO2 formation from secondary propylene combustion are less than the activation energy for propylene formation on TiO2/SiO2-supported VOx catalysts, leading to the inverse conversion versus selectivity relationship.429 This result is different from the energy profiles for propane ODH and propylene combustion over VOx/Al2O3 catalysts, as shown in Fig. 37.15 The C–H bond activation and the recombination of the remaining OH groups to form H2O are irreversible.427,428 For the propane ODH reaction over VOx involving the participation of the O2 molecule, the energy barriers for H2O elimination on the surface can be reduced.409 The rate of propane ODH reaction is proportional to C3H8 partial pressure and independent of O2 partial pressure in the limit of very low H2O concentrations, and therefore propane activation is a kinetically relevant step. However, the rates acquire a more complex dependence on C3H8 and O2 pressures when H2O is present at higher concentrations. On V2O5 powders and supported VOx, the dependencies of reaction rates on C3H8, O2, and H2O concentrations are identical, indicating that both surfaces have similar active centers.427
 | ||
| Fig. 37 Energy profile for propane ODH (left) and rate determining step of propene combustion over VOx/Al2O3 catalysts.15 Reproduced from ref. 15 with permission from the American Chemical Society, copyright 2014. | ||
In addition to these studies, significant efforts have been devoted to improving the activity of the different O sites for propane ODH of the supported VOx catalyst. Alkali metal additives have been found to improve the propylene selectivity for propane ODH on V-based and Mo-based catalysts; the effect is explained by a modification of the acid–base properties of the catalysts.335,430–432 On VOx/SiO2 catalysts, the potassium additive by blocking active centers on the catalyst surface exhibits a strong inhibitory effect on the consecutive propylene and parallel propane combustion and has a lower influence on ethylene and ethane combustion.335 Thus, potassium does not change the ethylene selectivity but has a distinct influence on the propylene selectivity, and thus leads to high initial selectivity (−95%). Zhao et al.433 also reported that OH groups on supported VOx catalysts can lead to lower PDH activity and less coke formation by combined experimental and calculational studies, but the fresh VOx catalysts under a C3H8 atmosphere are directly reduced to V2O3.
Fu et al.400 also reported that the initial propane activation on molybdenum oxides follows the same ODH mechanism as V-based catalysts in that lattice oxygens participate the C–H activation, where 6 possible mechanisms of the C–H bond activation on metal oxides are considered on Mo3O9, leading to 17 transition states involving C–H activations from the methyl and methylene groups in propane. For example, this activation step can specifically take place at M–O ion pairs by a heterolytic mechanism or at O–O pairs by a homolytic mechanism or at the terminal M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O site by an oxygen insertion mechanism. On the surface, it is found that the most feasible reaction pathway for the initial propane activation is H abstraction by the terminal Mo
O site by an oxygen insertion mechanism. On the surface, it is found that the most feasible reaction pathway for the initial propane activation is H abstraction by the terminal Mo![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O site and the C–H activation for methylene is 0.20 eV more favorable than that for the methyl C–H bond. The calculated activation enthalpy and entropy for the methylene C–H bond are 32.3 kcal mol−1 and −28.6 cal (mol K−1)−1, respectively.
O site and the C–H activation for methylene is 0.20 eV more favorable than that for the methyl C–H bond. The calculated activation enthalpy and entropy for the methylene C–H bond are 32.3 kcal mol−1 and −28.6 cal (mol K−1)−1, respectively.
Also, for MoOx catalysts, similar active centers are present on supported MoOx, MoO3, and ZrMo2O8.428 Surface O and OH groups are the most abundant surface intermediates that can lead to a rate expression to accurately describe the measured kinetics of propane ODH.427,428 On MoOx and VOx catalysts, similar kinetic rate expressions confirm that propane ODH occurs via similar pathways, using lattice oxygen atoms to abstract hydrogen atoms from propane in the RDS of irreversible C–H bond activation.339 For the transition state for this elementary step, the electrons are transferred from lattice oxygens to metal centers as an i-propoxide and an OH group from propane.438 Propane ODH activation energies (1.03–1.31 eV) are higher than those for propylene combustion (0.53–0.67 eV), where the measured difference in activation energy (0.50–0.63 eV) between the both is larger than the difference in the weakest C–H bond dissociation enthalpy between propane and propylene (0.42 eV).
The activation energies for propane primary dehydrogenation and propylene secondary combustion increase as the Lewis acidity of the cations increases (V5+ < Mo6+ < W6+), while the corresponding reaction rates decrease. Therefore, metal oxides having high redox properties exhibit high catalytic activity, and less acidic metal oxides lead to higher propylene yields.339 Chen et al. also reported that VOx catalysts are much more active than MoOx catalysts with similar H2 reduction rates.438
Zhu et al.358,391,405,439 systematically studied the catalytic performance of PDH on Cr2O3, ZnO, V2O3, and Ga2O3. There are oxygen vacancies that can exist on the ZnO surfaces, also implying that the reaction path of the ODH mechanism could occur in the initial reaction stage.405 Besides, oxygen vacancies may modify their electronic structure, thereby positively affecting the reactivity of α-Cr2O3, but negatively affecting ZnO mainly due to the weaker Lewis acid–base interaction on ZnO(10−10). Therefore, for the dehydrogenation reaction over some transition metal oxides without oxidants (such as O2 and CO2) introduced into the reaction gas mixture, active lattice oxygen can participate in the C–H bond activation, possibly following an ODH mechanism in the initial stage of the reaction before the oxide surfaces reach a steady state. However, if oxidants are introduced into the reaction gas, the dehydrogenation reaction could follow the ODH mechanism to remove the H atoms absorbed on the surface.337,440,441 For example, Atanga et al.442 proposed that CO2 as a mild oxidant for the ODH of propane can reactivate deactivated redox catalysts caused by metal oxide reduction, and the introduction of CO2 can also overcome the problems of over-oxidation and low propylene selectivity.
4.3 C–H activation on single atom–oxide hybrids
Single-atom catalysis is an area of intense current research.443–445 On the one hand, single-atom catalysts (SACs) exhibit properties that are distinctly different from those of supported nanoclusters. On the other hand, single-atom catalysts have well-defined local structures, and therefore provide an opportunity for establishing the structure–reactivity relationship.446–448 However, because of the low coordination environment, the surfaces of SACs have a high surface free energy, and single atoms tend to migrate and aggregate to form clusters. Recently, several research efforts have been devoted to synthesizing thermally stable SACs, such as the proposal of strong metal–support interactions (SMSI), which can play a role in keeping single atoms from sintering on the surface.446,449 Lang et al. found that isolated Pt atoms or PtO2 units can be trapped on an Fe2O3 support through SMSI during high-temperature calcination (800 °C, 5 h).450Single metal atoms have been deposited onto transition metal, graphene, and metal oxides, among which singly dispersed metal atoms on metal oxides have received much attention in catalyzing PDH.364,385,451–455 As has been observed by Xiong et al.,451 isolated single atoms of Pt can be steadily trapped on CeO2 catalysts, while the catalyst is not selective towards propylene. DFT calculations show that the strongly adsorbed propylene is expected to undergo further reactions, leading eventually to C–C bond cleavage. To prevent a further reaction, Sn is added to the Pt single-atom catalyst. They found that propylene showed much lower adsorption energy on small Pt–Sn clusters than that on single Pt atoms. Consequently, a higher selectivity is obtained on Pt–Sn–CeO2. Sun et al.385 directly dispersed single Pt atoms on Cu NPs to form SAA catalysts, which exhibit high propylene selectivity (∼90%) and great stability at 520 °C. In addition to the use of SAA catalysts, other SACs that provide excellent catalytic performance for PDH are still under theoretical research.
Some supports have been considered to anchor single metal atoms by theoretical calculations.358,391,405,439 For instance, Pt1–Cr2O3(0001) and Pt1–ZnO(10−10) oxides were constructed by Chang et al.,405 and show higher activity than their pristine surfaces by lowering the activation energy for the RDS and promoting H2 desorption, and on these two types of oxide surfaces single Pt atoms act as promoters (see Fig. 38). These findings are in line with experimental and DFT studies by Liu et al. and Sattler et al.,333,456 which clearly showed that the addition of a trace amount of Pt could accelerate H2 desorption over ZnO/Al2O3 catalysts and affect the distribution of Ga3+, thereby leading to a higher activity than the pristine surfaces.2,456 This may be attributed to the interactions between Pt and ZnO (or TiO2). On the Pt1–Ga2O3(100) surface, a Pt-doped Ga2O3 catalyst shows a bifunctional character in PDH where the Pt–O site brings about dehydrogenation, while the Ga–O site is active for desorbing H2.439
 | ||
| Fig. 38 Energy profiles for PDH on pristine, oxygen-deficient, and Pt-doped (a) Cr2O3 and (b) ZnO surfaces. All the potential energies are referenced to gas-phase propane.405 Reproduced from ref. 405 with permission from the American Chemical Society, copyright 2019. | ||
The kinetics of the PDH reaction over M1–V2O3 (M = Mn–Cu, Ru–Ag, and Os–Au) were studied by Zhang et al.391 In their model, surface V and O atoms are replaced with single atoms, including M1–(Vvac)–V2O3(0001) (M = Mn, Fe, Co, Ni, and Cu) and M1–(Ovac)–V2O3(0001) (M = Pd, Pt, and Au). Moreover, it shows that the V–O(o) site is the dominant active site over V2O3(0001). These findings agree well with the experimental studies by Liu et al. who found that V3+ was more active for PDH over VOx/Al2O3, which, to some extent, explains why a VOx catalyst without H2 reduction shows higher initial activity.394 Besides, on M1–(Vvac)–V2O3(0001), the active site for PDH is V–O(o) and M acts as the promoter, while on M1–(Ovac)–V2O3(0001) the M and V ion pairs act as the active site. Apart from the work by Zhang et al., Ma et al. systemically examined the structural stability, catalytic activity and selectivity of 13 M1–ZnO (M = Mn, Fe, Co, Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, and Au).358 By applying linear scaling relations of chemisorption energy and transition-state energy, it is found that the formation energies of H and 2-propyl can be used to measure the binding strengths of all the reaction intermediates and activated complexes and can therefore be used as descriptors to describe the kinetics of PDH over M1–ZnO. As indicated in Fig. 39, theoretical calculations predict that most of the single-atom-doped ZnO catalysts except for Fe- and Os-doped ZnO exhibit higher activity than pristine ZnO. Such a study can not only offer new opportunities to develop a more cost-effective heterogeneous catalyst but also help guide future experiments.
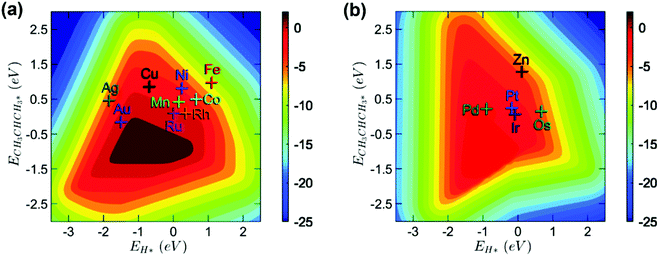 | ||
| Fig. 39 TOFs for propane dehydrogenation to propylene as a function of the formation energies of adsorbed H at the O site and adsorbed 2-propyl at the M site on the (a) first and (b) second groups of doped oxide surfaces.358 Reproduced from ref. 358 with permission from the Royal Society of Chemistry, copyright 2020. | ||
5. Conclusions and perspectives
The paper reviews the computational catalysis of the C–H bond activation of light alkanes such as methane, ethane, and propane towards synthesis gas and light olefins, as the important building blocks of the chemical industry. Quantum chemical calculations have grown into a technique of extraordinary power that pervades all current discussions of heterogeneous catalysis. In particular, computational approaches that use results from DFT calculations combined with descriptor-based scaling relationships as inputs to microkinetic analysis or kinetic Monte Carlo simulations not only play a significant role in developing a step-by-step, molecular-level view of the pathway leading to products but also provide an effective way to rationally screen potential catalyst candidates for a given catalytic reaction. A highly integrated approach using DFT, linear scaling relations, and microkinetic modeling successfully accounts for the way catalyst compositions like various metals, alloys, single atoms, metal–oxide interfaces, and locally coordinated oxygen in oxides modify the electronic properties of the active sites and their relations to the catalytic performance of alkane conversion. DFT-based microkinetic analysis extends the computational catalysis from model surfaces to industrially relevant catalysts. In this review, we attempted to illustrate the recent substantial progress made by using such theoretical methods in understanding the effects of geometrical and electronic structures on the activation of C–H bonds of light alkanes and in the discovery of new and more effective catalysts for light alkane conversion on metal and metal oxides. Special efforts have been devoted to recognizing the patterns of catalytic activity and selectivity for a class of substances applied in commercially important reactions.Despite the fact that many different reactions and different types of catalysts have been applied to convert light alkanes to valuable products, it is common that the light alkane transformation initiates from C–H cleavage. The C–H bond activation of methane, ethane, and propane on metal and metal oxides was summarized and compared. A universal scaling relationship of C–H bond activation across C1–C3 alkanes and various catalysts was discussed.
Some mechanistic insights into methane conversion to synthesis gas are common for steam reforming, dry reforming and partial oxidation, involving C–H bond cleavage to form CHx followed by subsequent oxidation of CH* or C* by O* or OH*. The preferred reaction pathways and rate-determining step depend on the catalysts and operating conditions. DFT calculations and microkinetic modeling provide a guideline to manipulate the catalyst surface to reduce the carbon formation by lowering the surface carbon coverage. The lowered surface carbon coverage benefits from the enhanced CH* oxidation and the reduced CH* formation and its decomposition to surface carbon.
The critical challenges in ethane and propane dehydrogenation and oxidative dehydrogenation are the selectivities to olefins and coke formation. The DFT calculations and kinetic analysis unravel useful fundamental insights into these key challenges at the molecular level, where the difference in the desorption energy of olefins and the activation energy of deep dehydrogenation of surface intermediates is used as the descriptor. Computational catalysis suggested Pt-based alloys as the best candidates for industrial catalysts by lowering the olefin desorption energy.
Oxidative dehydrogenation on oxides is an attractive alternative for light alkane dehydrogenation to olefins due to the breaking of the thermodynamic limitation and in situ supply of heat for highly endothermic dehydrogenation reactions. However, the critical challenge in olefin selectivity still remains due to the high reactivity of olefins. DFT calculations elucidated the active sites and surface reactions responsible for the formation of olefins, COx, and other byproducts. The lattice oxygen is the main active site. It significantly adds complexity in DFT modeling, where the activity of oxygen depends on the local structure and coordination as well as oxygen vacancy. However, it also provides huge opportunities to tune the oxygen activity to reduce the C–C bond cleavage and oxidation to COx. Oxides are a large family and present numerous oxide structures. The experimental and theoretical studies revealed the catalyst's activity dependence on the oxide identity, doping, cluster size, and supports. The formation energy of oxygen vacancy or hydrogen affinity was identified as the descriptor to describe the oxygen activity. However, a thorough screening of a huge number of oxide structures to find appropriate catalyst candidates for a given reaction remains a formidable challenge. Most of the studies have been performed only addressing the C–H bond activation. DFT calculations of elementary steps involved in the whole catalytic cycle, including by-product formation, are essential to address the selectivity. In addition, the active sites are highly dynamic on oxides due to their redox nature, with generation and filling of the oxygen vacancy. The oxygen vacancy in the steady-state can be changed with reaction conditions. Full modeling of reactions accounting for active site dynamics is also extremely challenging. Better scaling relationships for adsorption energy and activation energy on oxides need to be explored based on a big dataset. Machine learning and artificial intelligence could be explored to significantly accelerate catalyst development.
There is generally a strongly constrained relation between the C–H bond activation of light paraffins, olefin desorption, and deep C–H bond activation, which presents a challenge in catalyst design to maintain high activity, selectivity, and stability with a high coking resistance, simultaneously. The alloy of Pt with a second metal and a core–shell structure is an effective way to lower the ethylene and propylene desorption energy and increase the olefin selectivity and lower the coking potential, but at the expense of lower activity. The single metal or metal clusters on oxides could be explored to break down the constrained relation to enhance the catalytic performance. However, the active sites at the metal–oxide interface largely increase the complexity of the modeling. There are much more possible sites for adsorption and elementary reactions compared to the metal and oxide alone.
There remain several challenges in theoretical catalysis, which makes it difficult to discuss the chemistry of light alkane conversion in a more quantitative way. First, DFT has its complexity and a lot of physics hidden inside the approximate exchange–correlation functional. This term works surprisingly well given its simplicity and holds the key to the success of the theory. However, it is still challenging to quantitatively reproduce the reaction rates obtained from experiments, since the values of the calculated reaction heat and activation energy obtained by DFT calculations have an uncertainty of 0.1–0.2 eV.457,458
Second, the structure of active sites on catalysts is generally represented by simple low-index surfaces in computational studies. A gap still exists between realistic catalysts under reaction conditions and model surfaces. In situ characterization of working catalysts can provide more detailed structural information to help build more reliable structures close to industrial catalysts. Even though computational modeling of the surface structure of industrial catalysts needs to be carried out with caution, there is no doubt that DFT calculations are able to suggest mechanisms and structure–activity–selectivity relations, and rationalize a considerable amount of experimental observations, which are often difficult to understand. Finally, the microkinetic analysis of reactions is necessary to present the experimental conditions appropriately to understand important industrial reactions. The DFT calculations and microkinetic modeling need to be even more tightly associated with multiscale modeling at catalyst pellet and reactor levels, as well as the experimental study for searching for new catalysts and improving industrial catalysts.
Despite many challenges, with advances in density functional theory, scaling relationships, and descriptor-based microkinetic modeling, it is now possible to describe catalytic reactions at surfaces with the detail and accuracy required for computational results to compare favorably with experiments.28 The computational approach has become an effective tool for the design of catalysts with high activity, selectivity, and stability. It is interesting to note that the advanced computational catalysis approach has predicted the most active pure metals for methane and propane activation, and some bimetallic alloys are screened based on the volcano curve obtained from pure metals for ethane activation. The highly integrated computational and experimental approach will be explored to accelerate the development of next-generation catalysts for alkane conversion.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The supports from NTNU energy, the Centre for Industrial Catalysis Science and Innovation (iCSI), which receives financial support from the Norwegian Research Council, the Natural Science Foundation of China (No. 91645122 and 22073027), and the Natural Science Foundation of Shanghai (No. 20ZR1415800), as well as the computational time provided by the Notur project (nn4685k), are gratefully acknowledged.Notes and references
- X. Tang, X. Jia and Z. Huang, Chem. Sci., 2018, 9, 288–299 RSC
.
- J. J. H. B. Sattler, J. Ruiz-Martinez, E. Santillan-Jimenez and B. M. Weckhuysen, Chem. Rev., 2014, 114, 10613–10653 CrossRef CAS
.
- R. Grabowski, Catal. Rev., 2006, 48, 199–268 CrossRef CAS
.
- B. A. Arndtsen, R. G. Bergman, T. A. Mobley and T. H. Peterson, Acc. Chem. Res., 1995, 28, 154–162 CrossRef CAS
.
- A. E. Shilov and G. B. Shul'pin, Chem. Rev., 1997, 97, 2879–2932 CrossRef CAS
.
- S. S. Stahl, J. A. Labinger and J. E. Bercaw, Angew. Chem., Int. Ed., 1998, 37, 2180–2192 CrossRef
.
- B. G. Hashiguchi, S. M. Bischof, M. M. Konnick and R. A. Periana, Acc. Chem. Res., 2012, 45, 885–898 CrossRef CAS
.
- J. A. Labinger and J. E. Bercaw, J. Organomet. Chem., 2015, 793, 47–53 CrossRef CAS
.
- N. J. Gunsalus, A. Koppaka, S. H. Park, S. M. Bischof, B. G. Hashiguchi and R. A. Periana, Chem. Rev., 2017, 117, 8521–8573 CrossRef CAS
.
- R. G. Bergman, Nature, 2007, 446, 391–393 CrossRef CAS
.
- H. Schwarz, Angew. Chem., Int. Ed., 2011, 50, 10096–10115 CrossRef CAS
.
- P. Schwach, X. Pan and X. Bao, Chem. Rev., 2017, 117, 8497–8520 CrossRef CAS
.
- A. Obradović, J. W. Thybaut and G. B. Marin, Chem. Eng. Technol., 2016, 39, 1996–2010 CrossRef
.
- D. Balcells, E. Clot and O. Eisenstein, Chem. Rev., 2010, 110, 749–823 CrossRef CAS
.
- C. A. Carrero, R. Schloegl, I. E. Wachs and R. Schomaecker, ACS Catal., 2014, 4, 3357–3380 CrossRef CAS
.
- J. F. Weaver, C. Hakanoglu, A. Antony and A. Asthagiri, Chem. Soc. Rev., 2014, 43, 7536–7547 RSC
.
- Z. Nawaz, Rev. Chem. Eng., 2015, 31, 413–436 CAS
.
- J. T. Grant, J. M. Venegas, W. P. McDermott and I. Hermans, Chem. Rev., 2018, 118, 2769–2815 CrossRef CAS
.
- JCPDS—Joint Committee on Powder Diffraction Standards, International Center of Diffraction Data, CD-ROM, 1994, Pensilvânia, USA.
- X. Sun, P. Han, B. Li, S. Mao, T. Liu, S. Ali, Z. Lian and D. Su, Chem. Commun., 2018, 54, 864–875 RSC
.
- G. Caeiro, R. H. Carvalho, X. Wang, M. A. N. D. A. Lemos, F. Lemos, M. Guisnet and F. Ramôa Ribeiro, J. Mol. Catal., A, 2006, 255, 131–158 CrossRef CAS
.
- J. M. Venegas, W. P. McDermott and I. Hermans, Acc. Chem. Res., 2018, 51, 2556–2564 CrossRef CAS
.
- R. A. Periana, G. Bhalla, W. J. Tenn, K. J. H. Young, X. Y. Liu, O. Mironov, C. J. Jones and V. R. Ziatdinov, J. Mol. Catal., A, 2004, 220, 7–25 CrossRef CAS
.
- F. J. Keil, Comput. Math. Appl., 2013, 65, 1674–1697 CrossRef
.
- J. K. Norskov, Nature, 2001, 414, 405–406 CrossRef CAS
.
- J. K. Norskov, M. Scheffler and H. Toulhoat, MRS Bull., 2006, 31, 669–674 CrossRef CAS
.
- J. K. Norskov, T. Bligaard, B. Hvolbaek, F. Abild-Pedersen, I. Chorkendorff and C. H. Christensen, Chem. Soc. Rev., 2008, 37, 2163–2171 RSC
.
- J. K. Norskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef CAS
.
- Z. J. Zhao, C. C. Chiu and J. Gong, Chem. Sci., 2015, 6, 4403–4425 RSC
.
- C. A. Gaggioli, S. J. Stoneburner, C. J. Cramer and L. Gagliardi, ACS Catal., 2019, 9, 8481–8502 CrossRef CAS
.
- A. H. Motagamwala, M. R. Ball and J. A. Dumesic, Annu. Rev. Chem. Biomol. Eng., 2018, 9, 413–450 CrossRef
.
- L. Grajciar, C. J. Heard, A. A. Bondarenko, M. V. Polynski, J. Meeprasert, E. A. Pidko and P. Nachtigall, Chem. Soc. Rev., 2018, 47, 8307–8348 RSC
.
- F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skulason, T. Bligaard and J. K. Norskov, Phys. Rev. Lett., 2007, 99, 016105 CrossRef CAS
.
- A. Michaelides, Z.-P. Liu, C. Zhang, A. Alavi, D. A. King and P. Hu, J. Am. Chem. Soc., 2003, 125, 3704–3705 CrossRef CAS
.
- J. Greeley, Annu. Rev. Chem. Biomol. Eng., 2016, 7, 605–635 CrossRef
.
- Y. Wang, L. Xiao, Y. Qi, M. Mahmoodinia, X. Feng, J. Yang, Y. A. Zhu and D. Chen, Phys. Chem. Chem. Phys., 2019, 21, 19269–19280 RSC
.
- M. Ravi, M. Ranocchiari and J. A. van Bokhoven, Angew. Chem., Int. Ed., 2017, 56, 16464–16483 CrossRef CAS
.
- R. Horn and R. Schlögl, Catal. Lett., 2014, 145, 23–39 CrossRef
.
- B. Wang, S. Albarracín-Suazo, Y. Pagán-Torres and E. Nikolla, Catal. Today, 2017, 285, 147–158 CrossRef CAS
.
- D. Pakhare and J. Spivey, Chem. Soc. Rev., 2014, 43, 7813–7837 RSC
.
- F. J. Keil, Nat. Chem., 2013, 5, 91–92 CrossRef CAS
.
- P. Tang, Q. Zhu, Z. Wu and D. Ma, Energy Environ. Sci., 2014, 7, 2580–2591 RSC
.
- G. Keller and M. Bhasin, J. Catal., 1982, 73, 9–19 CrossRef CAS
.
- D. J. Driscoll, W. Martir, J. X. Wang and J. H. Lunsford, J. Am. Chem. Soc., 1985, 107, 58–63 CrossRef CAS
.
- T. Ito, J. Wang, C. H. Lin and J. H. Lunsford, J. Am. Chem. Soc., 1985, 107, 5062–5068 CrossRef CAS
.
- L. Wang, L. Tao, M. Xie, G. Xu, J. Huang and Y. Xu, Catal. Lett., 1993, 21, 35–41 CrossRef CAS
.
- X. Guo, G. Fang, G. Li, H. Ma, H. Fan, L. Yu, C. Ma, X. Wu, D. Deng and M. Wei, Science, 2014, 344, 616–619 CrossRef CAS
.
- A. P. E. York, T. Xiao and M. L. H. Green, Top. Catal., 2003, 22, 345–358 CrossRef CAS
.
- A. W. Budiman, S.-H. Song, T.-S. Chang, C.-H. Shin and M.-J. Choi, Catal. Surv. Asia, 2012, 16, 183–197 CrossRef CAS
.
- B. Abdullah, N. A. Abd Ghani and D.-V. N. Vo, J. Cleaner Prod., 2017, 162, 170–185 CrossRef CAS
.
- W.-J. Jang, J.-O. Shim, H.-M. Kim, S.-Y. Yoo and H.-S. Roh, Catal. Today, 2019, 324, 15–26 CrossRef CAS
.
- P. V. Beurden, On the Catalytic Aspects of Steam–Methane Reforming – A Literature Surve, 2004 Search PubMed.
- J. P. Van Hook, Catal. Rev., 2006, 21, 1–51 CrossRef
.
- J. Liu, Kinetics, catalysis and mechanism of methane steam reforming, 2007 Search PubMed.
- D. Li, Y. Nakagawa and K. Tomishige, Appl. Catal., A, 2011, 408, 1–24 CrossRef CAS
.
- S. D. Angeli, G. Monteleone, A. Giaconia and A. A. Lemonidou, Int. J. Hydrogen Energy, 2014, 39, 1979–1997 CrossRef CAS
.
- T. L. LeValley, A. R. Richard and M. Fan, Int. J. Hydrogen Energy, 2014, 39, 16983–17000 CrossRef CAS
.
- E. Meloni, M. Martino and V. Palma, Catalysts, 2020, 10, 352 CrossRef CAS
.
- Y. Kathiraser, U. Oemar, E. T. Saw, Z. Li and S. Kawi, Chem. Eng. J., 2015, 278, 62–78 CrossRef CAS
.
- M. Usman, W. M. A. Wan Daud and H. F. Abbas, Renewable Sustainable Energy Rev., 2015, 45, 710–744 CrossRef CAS
.
- Z. Bian, S. Das, M. H. Wai, P. Hongmanorom and S. Kawi, ChemPhysChem, 2017, 18, 3117–3134 CrossRef CAS
.
- N. A. K. Aramouni, J. G. Touma, B. A. Tarboush, J. Zeaiter and M. N. Ahmad, Renewable Sustainable Energy Rev., 2018, 82, 2570–2585 CrossRef CAS
.
- T. Yabe and Y. Sekine, Fuel Process. Technol., 2018, 181, 187–198 CrossRef CAS
.
- Y. Wang, L. Yao, S. Wang, D. Mao and C. Hu, Fuel Process. Technol., 2018, 169, 199–206 CrossRef CAS
.
- A. Abdulrasheed, A. A. Jalil, Y. Gambo, M. Ibrahim, H. U. Hambali and M. Y. Shahul Hamid, Renewable Sustainable Energy Rev., 2019, 108, 175–193 CrossRef CAS
.
- R. Pitchai and K. Klier, Catal. Rev., 1986, 28, 13–88 CrossRef CAS
.
- V. D. Sokolovskii, N. J. Coville, A. Parmaliana, I. Eskendirov and M. Makoa, Catal. Today, 1998, 42, 191–195 CrossRef CAS
.
- C. R. H. de Smet, Partial oxidation of methane to synthesis gas: reaction kinetics and reactor modelling, 2000 DOI:10.6100/IR535178.
- B. Christian Enger, R. Lødeng and A. Holmen, Appl. Catal., A, 2008, 346, 1–27 CrossRef
.
- S. A. Al-Sayari, Open Catal. J., 2013, 6, 17–28 CrossRef CAS
.
- R. Wang, J. Chen, W. Zhao, X. Zhang and J. Ran, Theor. Chem. Acc., 2019, 138, 38–51 Search PubMed
.
- J. Védrine, Catalysts, 2016, 6, 22 Search PubMed
.
- J. C. Vedrine, J. Energy Chem., 2016, 25, 936–946 Search PubMed
.
- J. C. Védrine and I. Fechete, C. R. Chim., 2016, 19, 1203–1225 CrossRef
.
- J. Wei and E. Iglesia, J. Phys. Chem. B, 2004, 108, 4094–4103 CrossRef CAS
.
- J. Wei and E. Iglesia, J. Phys. Chem. B, 2004, 108, 7253–7262 CrossRef CAS
.
- J. Wei, J. Catal., 2004, 225, 116–127 CrossRef CAS
.
- J. Wei and E. Iglesia, Angew. Chem., Int. Ed., 2004, 43, 3685–3688 CrossRef CAS
.
- J. Wei and E. Iglesia, Phys. Chem. Chem. Phys., 2004, 6, 3754–3759 RSC
.
- J. Wei and E. Iglesia, J. Catal., 2004, 224, 370–383 CrossRef CAS
.
- S.-G. Wang, D.-B. Cao, Y.-W. Li, J. Wang and H. Jiao, J. Phys. Chem. B, 2006, 110, 9976–9983 CrossRef CAS
.
- S.-G. Wang, X.-Y. Liao, J. Hu, D.-B. Cao, Y.-W. Li, J. Wang and H. Jiao, Surf. Sci., 2007, 601, 1271–1284 CrossRef CAS
.
- M. Maestri, D. Vlachos, A. Beretta, G. Groppi and E. Tronconi, J. Catal., 2008, 259, 211–222 CrossRef CAS
.
- A. Trinchero, A. Hellman and H. Grönbeck, Surf. Sci., 2013, 616, 206–213 CrossRef CAS
.
- L. Foppa, M.-C. Silaghi, K. Larmier and A. Comas-Vives, J. Catal., 2016, 343, 196–207 CrossRef CAS
.
- M. Jørgensen and H. Grönbeck, ACS Catal., 2016, 6, 6730–6738 CrossRef
.
- Y. Wang, H. Wang, A. H. Dam, L. Xiao, Y. Qi, J. Niu, J. Yang, Y.-A. Zhu, A. Holmen and D. Chen, Catal. Today, 2020, 355, 139–147 CrossRef CAS
.
- R. Wang, J. Chen, W. Zhao, J. Wen, H. Li, L. Li and J. Ran, Appl. Surf. Sci., 2019, 471, 566–586 CrossRef CAS
.
- Y. Wang, L. Xiao, Y. Qi, J. Yang, Y.-A. Zhu and D. Chen, J. Phys. Chem. C, 2020, 124, 2501–2512 CrossRef CAS
.
- Y. Meng, C. Ding, X. Gao, L. Ma, K. Zhang, J. Wang and Z. Li, Appl. Surf. Sci., 2020, 513, 145724 CrossRef CAS
.
- D. Hibbitts and M. Neurock, Surf. Sci., 2016, 650, 210–220 CrossRef CAS
.
- J. Niu, Y. Wang, Y. Qi, A. H. Dam, H. Wang, Y.-A. Zhu, A. Holmen, J. Ran and D. Chen, Fuel, 2020, 266, 117143 CrossRef CAS
.
- Y.-A. Zhu, D. Chen, X.-G. Zhou and W.-K. Yuan, Catal. Today, 2009, 148, 260–267 CrossRef CAS
.
- C. Fan, Y.-A. Zhu, M.-L. Yang, Z.-J. Sui, X.-G. Zhou and D. Chen, Ind. Eng. Chem. Res., 2015, 54, 5901–5913 CrossRef CAS
.
- J. S. Yoo, J. Schumann, F. Studt, F. Abild-Pedersen and J. K. Nørskov, J. Phys. Chem. C, 2018, 122, 16023–16032 CrossRef CAS
.
- W. Tu, M. Ghoussoub, C. V. Singh and Y. C. Chin, J. Am. Chem. Soc., 2017, 139, 6928–6945 CrossRef CAS
.
- Y. Chen and D. G. Vlachos, Ind. Eng. Chem. Res., 2012, 51, 12244–12252 CAS
.
- R. L. Arevalo, S. M. Aspera, M. C. S. Escano, H. Nakanishi and H. Kasai, Sci. Rep., 2017, 7, 13963–13970 CrossRef
.
- G. Jones, T. Bligaard, F. Abild-Pedersen and J. K. Norskov, J. Phys.: Condens. Matter, 2008, 20, 064239 CrossRef CAS
.
- S. Wang, V. Petzold, V. Tripkovic, J. Kleis, J. G. Howalt, E. Skulason, E. M. Fernandez, B. Hvolbaek, G. Jones, A. Toftelund, H. Falsig, M. Bjorketun, F. Studt, F. Abild-Pedersen, J. Rossmeisl, J. K. Norskov and T. Bligaard, Phys. Chem. Chem. Phys., 2011, 13, 20760–20765 RSC
.
- G. Kumar, S. L. J. Lau, M. D. Krcha and M. J. Janik, ACS Catal., 2016, 6, 1812–1821 CrossRef CAS
.
- N. Shi, Y. Xie, Y. Yang, S. Xue, X. Li, K. Zhu, D. Huan, R. Peng, C. Xia and Y. Lu, Mater. Renewable Sustainable Energy, 2020, 9, 1–18 CrossRef
.
- A. A. Latimer, H. Aljama, A. Kakekhani, J. S. Yoo, A. Kulkarni, C. Tsai, M. Garcia-Melchor, F. Abild-Pedersen and J. K. Norskov, Phys. Chem. Chem. Phys., 2017, 19, 3575–3581 RSC
.
- J. Xu, X.-M. Cao and P. Hu, J. Phys. Chem. C, 2019, 123, 28802–28810 CrossRef
.
- R. K. Singha, Y. Tsuji, M. H. Mahyuddin and K. Yoshizawa, J. Phys. Chem. C, 2019, 123, 9788–9798 CrossRef CAS
.
- A. A. Latimer, A. R. Kulkarni, H. Aljama, J. H. Montoya, J. S. Yoo, C. Tsai, F. Abild-Pedersen, F. Studt and J. K. Norskov, Nat. Mater., 2017, 16, 225–229 CrossRef CAS
.
- H. Aljama, J. K. Nørskov and F. Abild-Pedersen, J. Phys. Chem. C, 2017, 121, 16440–16446 CrossRef CAS
.
- H. Aljama, J. K. Nørskov and F. Abild-Pedersen, J. Phys. Chem. C, 2018, 122, 22544–22548 CrossRef CAS
.
- V. Fung, F. Polo-Garzon, Z. Wu and D.-E. Jiang, Catal.: Sci. Technol., 2018, 8, 702–709 RSC
.
- A. D. Mayernick and M. J. Janik, J. Phys. Chem. C, 2008, 112, 14955–14964 CrossRef CAS
.
- A. R. Derk, B. Li, S. Sharma, G. M. Moore, E. W. McFarland and H. Metiu, Catal. Lett., 2013, 143, 406–410 CrossRef CAS
.
- B. Li and H. Metiu, J. Phys. Chem. C, 2011, 115, 18239–18246 CrossRef CAS
.
- W. Tang, Z. Hu, M. Wang, G. D. Stucky, H. Metiu and E. W. McFarland, J. Catal., 2010, 273, 125–137 CrossRef CAS
.
- I. M. Ciobîcă, F. Frechard, R. A. V. Santen, A. W. Kleyn and J. Hafner, J. Phys. Chem. B, 2000, 104, 3364–3369 CrossRef
.
- I. M. Ciobica and R. A. V. Santen, J. Phys. Chem. B, 2002, 106, 6200–6205 CrossRef CAS
.
- L. Xiao and L. Wang, J. Phys. Chem. B, 2007, 111, 1657–1663 CrossRef CAS
.
- M. F. Fellah and I. Onal, Catal. Today, 2011, 171, 52–59 CrossRef CAS
.
- J. Li, E. Croiset and L. Ricardez-Sandoval, J. Mol. Catal.,
A, 2012, 365, 103–114 CrossRef CAS
.
- J. Niu, J. Ran, X. Du, W. Qi, P. Zhang and L. Yang, Mol. Catal., 2017, 434, 206–218 CrossRef CAS
.
- Z. Jiang, Z. Wu, T. Fang and C. Yi, Chem. Phys. Lett., 2019, 715, 323–329 CrossRef CAS
.
- R. L. Arevalo, S. M. Aspera, M. C. Sison Escano, H. Nakanishi and H. Kasai, ACS Omega, 2017, 2, 1295–1301 CrossRef CAS
.
- J. R. Rostrup-Nielsen, J. Catal., 1973, 31, 173–199 CrossRef CAS
.
- J. R. Rostrupnielsen and J. H. B. Hansen, J. Catal., 1993, 144, 38–49 CrossRef CAS
.
- D. Qin and J. Lapszewicz, Catal. Today, 1994, 21, 551–560 CrossRef CAS
.
- L. M. Aparicio, J. Catal., 1997, 165, 262–274 CrossRef CAS
.
- H. S. Bengaard, J. K. Nørskov, J. Sehested, B. S. Clausen, L. P. Nielsen, A. M. Molenbroek and J. R. Rostrup-Nielsen, J. Catal., 2002, 209, 365–384 CrossRef CAS
.
- G. Jones, J. Jakobsen, S. Shim, J. Kleis, M. Andersson, J. Rossmeisl, F. Abildpedersen, T. Bligaard, S. Helveg and B. Hinnemann, J. Catal., 2008, 259, 147–160 CrossRef CAS
.
- D. Mei, V.-A. Glezakou, V. Lebarbier, L. Kovarik, H. Wan, K. O. Albrecht, M. Gerber, R. Rousseau and R. A. Dagle, J. Catal., 2014, 316, 11–23 CrossRef CAS
.
- L. Maier, B. Schädel, K. H. Delgado, S. Tischer and O. Deutschmann, Top. Catal., 2011, 54, 845 CrossRef CAS
.
- D. W. Blaylock, T. Ogura, W. H. Green and G. J. O. Beran, J. Phys. Chem. C, 2009, 113, 4898–4908 CrossRef CAS
.
- P. W. van Grootel, E. J. Hensen and R. A. van Santen, Langmuir, 2010, 26, 16339–16348 CrossRef CAS
.
- D. W. Blaylock, Y.-A. Zhu and W. H. Green, Top. Catal., 2011, 54, 828–844 CrossRef CAS
.
- Y. Xu, A. C. Lausche, S. Wang, T. S. Khan, F. Abild-Pedersen, F. Studt, J. K. Nørskov and T. Bligaard, New J. Phys., 2013, 15, 125021 CrossRef
.
- T. Zhu, P. W. van Grootel, I. A. W. Filot, S.-G. Sun, R. A. van Santen and E. J. M. Hensen, J. Catal., 2013, 297, 227–235 CrossRef CAS
.
- Y. Yoon, H. Kim and J. Lee, J. Power Sources, 2017, 359, 450–457 CrossRef CAS
.
- E. Kikuchi, S. Tanaka, Y. Yamazaki and Y. Morita, Bull. Jpn. Pet. Inst., 1974, 16, 95–98 CrossRef CAS
.
- J. K. Norskov and C. H. Christensen, Science, 2006, 312, 1322–1323 CrossRef CAS
.
- D. Chen, R. Lødeng, H. Svendsen and A. Holmen, Ind. Eng. Chem. Res., 2011, 50, 2600–2612 CrossRef CAS
.
- C. Pistonesi, A. Juan, B. Irigoyen and N. Amadeo, Appl. Surf. Sci., 2007, 253, 4427–4437 CrossRef CAS
.
- Z. Wang, X. M. Cao, J. Zhu and P. Hu, J. Catal., 2014, 311, 469–480 CrossRef CAS
.
- M. Zhang, K. Yang, X. Zhang and Y. Yu, Surf. Sci., 2014, 630, 236–243 CrossRef CAS
.
- O. R. Inderwildi, S. J. Jenkins and D. A. King, Angew. Chem., Int. Ed., 2008, 47, 5253–5255 CrossRef CAS
.
- A. Donazzi, A. Beretta, G. Groppi and P. Forzatti, J. Catal., 2008, 255, 241–258 CrossRef CAS
.
- A. Donazzi, A. Beretta, G. Groppi and P. Forzatti, J. Catal., 2008, 255, 259–268 CrossRef CAS
.
- C. J. H. Jacobsen, S. Dahl, P. L. Hansen, E. Törnqvist, L. Jensen, H. Topsøe, D. V. Prip, P. B. Møenshaug and I. Chorkendorff, J. Mol. Catal., A, 2000, 163, 19–26 CrossRef CAS
.
- K. Honkala, A. Hellman, I. N. Remediakis, A. Logadottir, A. Carlsson, S. Dahl, C. H. Christensen and J. K. Nørskov, Science, 2005, 307, 555–558 CrossRef CAS
.
- E. Nikolla, J. Schwank and S. Linic, J. Catal., 2009, 263, 220–227 CrossRef CAS
.
- M. Zeppieri, P. L. Villa, N. Verdone, M. Scarsella and P. De Filippis, Appl. Catal., A, 2010, 387, 147–154 CrossRef CAS
.
- D. A. J. M. Ligthart, R. A. van Santen and E. J. M. Hensen, J. Catal., 2011, 280, 206–220 CrossRef CAS
.
- V. C. H. Kroll, H. M. Swaan and C. Mirodatos, J. Catal., 1996, 161, 409–422 CrossRef CAS
.
- D. Chen, R. Lødeng, A. Anundskås, O. Olsvik and A. Holmen, Chem. Eng. Sci., 2001, 56, 1371–1379 CrossRef CAS
.
- J.-W. Snoeck, G. F. Froment and M. Fowles, J. Catal., 1997, 169, 240–249 CrossRef CAS
.
- F. Abild-Pedersen, J. K. Nørskov, J. R. Rostrup-Nielsen, J. Sehested and S. Helveg, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 115419 CrossRef
.
- F. C. Schouten, O. L. J. Gijzeman and G. A. Bootsma, Bull. Soc. Chim. Belg., 1979, 88, 541–547 CrossRef CAS
.
- F. C. Schouten, O. L. J. Gijzeman and G. A. Bootsma, Surf. Sci., 1979, 87, 1–12 CrossRef CAS
.
- M. Eizenberg and J. M. Blakely, J. Chem. Phys., 1979, 71, 3467–3477 CrossRef CAS
.
- I. Alstrup, J. Catal., 1988, 109, 241–251 CrossRef CAS
.
- F. F. Tabrizi, S. A. H. S. Mousavi and H. Atashi, Energy Convers. Manage., 2015, 103, 1065–1077 CrossRef
.
- D. Pashchenko, Int. J. Energy Res., 2020, 44, 438–447 CrossRef CAS
.
- F. Besenbacher, I. Chorkendorff, B. Clausen, B. Hammer, A. Molenbroek, J. K. Nørskov and I. Stensgaard, Science, 1998, 279, 1913–1915 CrossRef CAS
.
- J. H. Jeong, J. W. Lee, D. J. Seo, Y. Seo, W. L. Yoon, D. K. Lee and D. H. Kim, Appl. Catal., A, 2006, 302, 151–156 CrossRef CAS
.
- X. You, X. Wang, Y. Ma, J. Liu, W. Liu, X. Xu, H. Peng, C. Li, W. Zhou, P. Yuan and X. Chen, ChemCatChem, 2014, 6, 3377–3386 CrossRef CAS
.
- D. Li, Y. Zhan, K. Nishida, Y. Oumi, T. Sano, T. Shishido and K. Takehira, Appl. Catal., A, 2009, 363, 169–179 CrossRef CAS
.
- Y. Zhan, D. Li, K. Nishida, T. Shishido, Y. Oumi, T. Sano and K. Takehira, Appl. Clay Sci., 2009, 45, 147–154 CrossRef CAS
.
- N. V. Parizotto, K. O. Rocha, S. Damyanova, F. B. Passos, D. Zanchet, C. M. P. Marques and J. M. C. Bueno, Appl. Catal., A, 2007, 330, 12–22 CrossRef CAS
.
- E. Nikolla, A. Holewinski, J. Schwank and S. Linic, J. Am. Chem. Soc., 2006, 128, 11354–11355 CrossRef CAS
.
- C. Fan, Y. A. Zhu, Y. Xu, Y. Zhou, X. G. Zhou and D. Chen, J. Chem. Phys., 2012, 137, 014703 CrossRef
.
- J. C. S. Wu and H.-C. Chou, Chem. Eng. J., 2009, 148, 539–545 CrossRef CAS
.
- H. Arbag, S. Yasyerli, N. Yasyerli and G. Dogu, Int. J. Hydrogen Energy, 2010, 35, 2296–2304 CrossRef CAS
.
- Y. Xu, C. Fan, Y.-A. Zhu, P. Li, X.-G. Zhou, D. Chen and W.-K. Yuan, Catal. Today, 2012, 186, 54–62 CrossRef CAS
.
- H. Liu, B. Wang, M. Fan, N. Henson, Y. Zhang, B. F. Towler and H. Gordon Harris, Fuel, 2013, 113, 712–718 CrossRef CAS
.
- L. Chen, Z. Qi, S. Zhang, J. Su and G. A. Somorjai, Catalysts, 2020, 10, 858 CrossRef CAS
.
- V. C. H. Kroll, H. M. Swaan, S. Lacombe and C. Mirodatos, J. Catal., 1996, 164, 387–398 CrossRef CAS
.
- Y. Schuurman, V. C. H. Kroll, P. Ferreira-Aparicio and C. Mirodatos, Catal. Today, 1997, 38, 129–135 CrossRef CAS
.
- J.-S. Chang, S.-E. Park, J. W. Yoo and J.-N. Park, J. Catal., 2000, 195, 1–11 CrossRef CAS
.
- T. Osaki, T. Horiuchi, K. Suzuki and T. Mori, J. Chem. Soc., Faraday Trans., 1996, 92, 1627–1631 RSC
.
- J. Z. Luo, Z. L. Yu, C. F. Ng and C. T. Au, J. Catal., 2000, 194, 198–210 CrossRef CAS
.
- T. Osaki and T. Mori, J. Catal., 2001, 204, 89–97 CrossRef CAS
.
- M. C. J. Bradford and M. A. Vannice, Appl. Catal., A, 1996, 142, 97–122 CrossRef CAS
.
- A. Nandini, K. K. Pant and S. C. Dhingra, Appl. Catal., A, 2006, 308, 119–127 CrossRef CAS
.
- Y. Cui, H. Zhang, H. Xu and W. Li, Appl. Catal., A, 2007, 318, 79–88 CrossRef CAS
.
- J. Zhang, H. Wang and A. K. Dalai, Ind. Eng. Chem. Res., 2009, 48, 677–684 CrossRef CAS
.
- S.-G. Wang, D.-B. Cao, Y.-W. Li, J. Wang and H. Jiao, J. Phys. Chem. B, 2005, 109, 18956–18963 CrossRef CAS
.
- D.-B. Cao, Y.-W. Li, J. Wang and H. Jiao, Surf. Sci., 2009, 603, 2991–2998 CrossRef CAS
.
- J. Ko, B.-K. Kim and J. W. Han, J. Phys. Chem. C, 2016, 120, 3438–3447 CrossRef CAS
.
- P. Schlexer, H.-Y. T. Chen and G. Pacchioni, Catal. Lett., 2017, 147, 1871–1881 CrossRef CAS
.
- S. Kattel, B. Yan, J. G. Chen and P. Liu, J. Catal., 2016, 343, 115–126 CrossRef CAS
.
- X. Yang, S. Kattel, S. D. Senanayake, J. A. Boscoboinik, X. Nie, J. Graciani, J. A. Rodriguez, P. Liu, D. J. Stacchiola and J. G. Chen, J. Am. Chem. Soc., 2015, 137, 10104–10107 CrossRef CAS
.
- J. Niu, S. E. Liland, J. Yang, K. R. Rout, J. Ran and D. Chen, Chem. Eng. J., 2019, 377, 119763 CrossRef CAS
.
- J. Niu, X. Du, J. Ran and R. Wang, Appl. Surf. Sci., 2016, 376, 79–90 CrossRef CAS
.
- P. Ferreira-Aparicio, A. Guerrero-Ruiz and I. Rodríguez-Ramos, Appl. Catal., A, 1998, 170, 177–187 CrossRef CAS
.
- J. H. Edwards and A. M. Maitra, Fuel Process. Technol., 1995, 42, 269–289 CrossRef CAS
.
- F. Solymosi, G. Kutsán and A. Erdöhelyi, Catal. Lett., 1991, 11, 149–156 CrossRef CAS
.
- P. G. Lustemberg, P. J. Ramírez, Z. Liu, R. A. Gutiérrez, D. G. Grinter, J. Carrasco, S. D. Senanayake, J. A. Rodriguez and M. V. Ganduglia-Pirovano, ACS Catal., 2016, 6, 8184–8191 CrossRef CAS
.
- C. Vogt, J. Kranenborg, M. Monai and B. M. Weckhuysen, ACS Catal., 2019, 10, 1428–1438 CrossRef
.
- M. Akri, S. Zhao, X. Li, K. Zang, A. F. Lee, M. A. Isaacs, W. Xi, Y. Gangarajula, J. Luo and Y. Ren, Nat. Commun., 2019, 10, 1–10 CrossRef CAS
.
- Z. Liu, D. C. Grinter, P. G. Lustemberg, T. D. Nguyen-Phan, Y. Zhou, S. Luo, I. Waluyo, E. J. Crumlin, D. J. Stacchiola, J. Zhou, J. Carrasco, H. F. Busnengo, M. V. Ganduglia-Pirovano, S. D. Senanayake and J. A. Rodriguez, Angew. Chem., Int. Ed., 2016, 55, 7455–7459 CrossRef CAS
.
- Z. Liu, P. Lustemberg, R. A. Gutierrez, J. J. Carey, R. M. Palomino, M. Vorokhta, D. C. Grinter, P. J. Ramirez, V. Matolin, M. Nolan, M. V. Ganduglia-Pirovano, S. D. Senanayake and J. A. Rodriguez, Angew. Chem., Int. Ed., 2017, 56, 13041–13046 CrossRef CAS
.
- Z. Zuo, S. Liu, Z. Wang, C. Liu, W. Huang, J. Huang and P. Liu, ACS Catal., 2018, 8, 9821–9835 CrossRef CAS
.
- L. Foppa, T. Margossian, S. M. Kim, C. Muller, C. Coperet, K. Larmier and A. Comas-Vives, J. Am. Chem. Soc., 2017, 139, 17128–17139 CrossRef CAS
.
- K. Li, X. Chang, C. Pei, X. Li, S. Chen, X. Zhang, S. Assabumrungrat, Z.-J. Zhao, L. Zeng and J. Gong, Appl. Catal., B, 2019, 259, 118092 CrossRef CAS
.
- K. Li, F. He, H. Yu, Y. Wang and Z. Wu, J. Catal., 2018, 364, 248–261 CrossRef CAS
.
- M. A. L. Ferreira, N. N. Nichio and O. A. Ferretti, J. Mol. Catal., A, 2003, 202, 197–213 CrossRef CAS
.
- U. Guharoy, E. Le Saché, Q. Cai, T. R. Reina and S. Gu, J. CO2 Util., 2018, 27, 1–10 CrossRef CAS
.
- L.-l. Xu, H. Wen, X. Jin, Q.-m. Bing and J.-y. Liu, Appl. Surf. Sci., 2018, 443, 515–524 CrossRef CAS
.
- S. M. Kim, P. M. Abdala, T. Margossian, D. Hosseini, L. Foppa, A. Armutlulu, W. van Beek, A. Comas-Vives, C. Coperet and C. Muller, J. Am. Chem. Soc., 2017, 139, 1937–1949 CrossRef CAS
.
- A. Omran, S. H. Yoon, M. Khan, M. Ghouri, A. Chatla and N. Elbashir, Catalysts, 2020, 10, 1043 CrossRef CAS
.
- S.-H. Kye, H. S. Park, R. Zhang, H. J. Yang, K. H. Lee, H. Suh, J.-G. Kim, M. G. Kim, G. S. Hwang and N. H. Hur, J. Chem. Phys., 2020, 152, 054715 CrossRef CAS
.
- R. Sharma, H. Poelman, G. B. Marin and V. V. Galvita, Catalysts, 2020, 10, 194 CrossRef CAS
.
- V. A. Kondratenko, C. Berger-Karin and E. V. Kondratenko, ACS Catal., 2014, 4, 3136–3144 CrossRef CAS
.
- P. Aghalayam, Y. K. Park and D. G. Vlachos, Catalysis, 2000, 98–137, 10.1039/9781847553270-00098
.
- J. Zhu, D. Zhang and K. D. King, Fuel, 2001, 80, 899–905 CrossRef CAS
.
- M. Prettre, C. Eichner and M. Perrin, Trans. Faraday Soc., 1946, 42, 335–339 RSC
.
- A. B. Mhadeshwar and D. G. Vlachos, Ind. Eng. Chem. Res., 2007, 46, 5310–5324 CrossRef CAS
.
- D. A. Hickman and L. D. Schmidt, AIChE J., 1993, 39, 1164–1177 CrossRef CAS
.
- D. A. Hickman and L. D. Schmidt, Science, 1993, 259, 343–346 CrossRef CAS
.
- Y. Boucouvalas, Z. Zhang and X. E. Verykios, Catal. Lett., 1994, 27, 131–142 CrossRef CAS
.
- J. T. Richardson and S. A. Paripatyadar, Appl. Catal., 1990, 61, 293–309 CrossRef CAS
.
- A. Erdohelyi, J. Cserenyi and F. Solymosi, J. Catal., 1993, 141, 287–299 CrossRef CAS
.
- E. P. J. Mallens, J. H. B. J. Hoebink and G. B. Marin, Catal. Lett., 1995, 33, 291–304 CrossRef CAS
.
- P. Mars and D. W. van Krevelen, Chem. Eng. Sci., 1954, 3, 41–59 CrossRef CAS
.
- A. B. Mhadeshwar and D. G. Vlachos, J. Phys. Chem. B, 2005, 109, 16819–16835 CrossRef CAS
.
- M. Maestri, D. G. Vlachos, A. Beretta, P. Forzatti, G. Groppi and E. Tronconi, Top. Catal., 2009, 52, 1983–1988 CrossRef CAS
.
- M. Maestri, D. G. Vlachos, A. Beretta, G. Groppi and E. Tronconi, AIChE J., 2009, 55, 993–1008 CrossRef CAS
.
- M. Maestri, A. Beretta, T. Faravelli, G. Groppi, E. Tronconi and D. G. Vlachos, Chem. Eng. Sci., 2008, 63, 2657–2669 CrossRef CAS
.
- A. Donazzi, M. Maestri, B. C. Michael, A. Beretta, P. Forzatti, G. Groppi, E. Tronconi, L. D. Schmidt and D. G. Vlachos, J. Catal., 2010, 275, 270–279 CrossRef CAS
.
- Y.-H. Chin, C. Buda, M. Neurock and E. Iglesia, J. Catal., 2011, 283, 10–24 CrossRef CAS
.
- C.-T. Au, M.-S. Liao and C.-F. Ng, J. Phys. Chem. A, 1998, 102, 3959–3969 CrossRef CAS
.
- J. B. Claridge, M. L. H. Green, S. C. Tsang, A. P. E. York, A. T. Ashcroft and P. D. Battle, Catal. Lett., 1993, 22, 299–305 CrossRef CAS
.
- J. He, Z. Yang, C. Ding, L. Zhang, Y. Yan and X. Du, Fuel, 2018, 226, 400–409 CrossRef CAS
.
- Y. Meng, C. Ding, Y. Xue, X. Gao, K. Zhang, J. Wang and Z. Li, New J. Chem., 2020, 44, 3922–3929 RSC
.
- D. Guo and G.-C. Wang, J. Phys. Chem. C, 2017, 121, 26308–26320 CrossRef
.
- D. Guo, J.-H. Wen and G.-C. Wang, Catal. Today, 2020, 355, 422–434 CrossRef CAS
.
- G. J. Hutchings, M. S. Scurrell and J. R. Woodhouse, Chem. Soc. Rev., 1989, 18, 251–283 RSC
.
- J. G. McCarty and H. Wiseb, Catal. Today, 1990, 8, 231–248 CrossRef CAS
.
- T. Seiyama, Catal. Rev., 1992, 34, 281–300 CrossRef CAS
.
- Q. Zhu, X. Zhao and Y. Deng, J. Nat. Gas Chem., 2004, 13, 191–203 CAS
.
- E. W. McFarland and H. Metiu, Chem. Rev., 2013, 113, 4391–4427 CrossRef CAS
.
- T. M. Gür, Prog. Energy Combust. Sci., 2016, 54, 1–64 CrossRef
.
- J. L. Callahan and R. K. Grasselli, AIChE J., 1963, 9, 755–760 CrossRef CAS
.
- O. Kiyoshi, U. Tetsuya and Y. Ichiro, Chem. Lett., 1993, 1517–1520 Search PubMed
.
- A. D. Mayernick and M. J. Janik, J. Catal., 2011, 278, 16–25 CrossRef CAS
.
- Z.-P. Liu and P. Hu, J. Am. Chem. Soc., 2003, 125, 1958–1967 CrossRef CAS
.
- Y. Jin, C. Sun and S. Su, Phys. Chem. Chem. Phys., 2015, 17, 16277–16284 RSC
.
- Y. Tsuji and K. Yoshizawa, J. Phys. Chem. C, 2018, 122, 15359–15381 CrossRef CAS
.
- C.-H. Yeh, T. M. L. Pham, S. Nachimuthu and J.-C. Jiang, ACS Catal., 2019, 9, 8230–8242 CrossRef CAS
.
- B. Irigoyen, N. Castellani and A. Juan, J. Mol. Catal., A, 1998, 129, 297–310 CrossRef CAS
.
- S. Ozturk, I. Onal and S. Senkan, Ind. Eng. Chem. Res., 2000, 39, 250–258 CrossRef CAS
.
- M. A. Peña and J. L. G. Fierro, Chem. Rev., 2001, 101, 1981–2018 CrossRef
.
- S. Royer, D. Duprez, F. Can, X. Courtois, C. Batiot-Dupeyrat, S. Laassiri and H. Alamdari, Chem. Rev., 2014, 114, 10292–10368 CrossRef CAS
.
- K. Kousi, D. Neagu, L. Bekris, E. I. Papaioannou and I. S. Metcalfe, Angew. Chem., Int. Ed., 2020, 59, 2510–2519 CrossRef CAS
.
- X. Zhang, C. Pei, X. Chang, S. Chen, R. Liu, Z. J. Zhao, R. Mu and J. Gong, J. Am. Chem. Soc., 2020, 142, 11540–11549 CrossRef CAS
.
- H. Chang, E. Bjorgum, O. Mihai, J. Yang, H. L. Lein, T. Grande, S. Raaen, Y. A. Zhu, A. Holmen and D. Chen, ACS Catal., 2020, 10, 3707–3719 CrossRef CAS
.
- D. D. Miller, J. Riley and R. Siriwardane, Energy Fuels, 2019, 34, 2193–2204 CrossRef
.
- F. F. Tao, J. J. Shan, L. Nguyen, Z. Wang, S. Zhang, L. Zhang, Z. Wu, W. Huang, S. Zeng and P. Hu, Nat. Commun., 2015, 6, 7798–7807 CrossRef CAS
.
- Y. Chen, B. deGlee, Y. Tang, Z. Wang, B. Zhao, Y. Wei, L. Zhang, S. Yoo, K. Pei, J. H. Kim, Y. Ding, P. Hu, F. F. Tao and M. Liu, Nat. Energy, 2018, 3, 1042–1050 CrossRef CAS
.
- F. Polo-Garzon, M. He and D. A. Bruce, J. Catal., 2016, 333, 59–70 CrossRef CAS
.
- S. Jiang, Y. Lu, S. Wang, Y. Zhao and X. Ma, Appl. Surf. Sci., 2017, 416, 59–68 CrossRef CAS
.
- P. Wu, Y. Tao, H. Ling, Z. Chen, J. Ding, X. Zeng, X. Liao, C. Stampfl and J. Huang, ACS Catal., 2019, 9, 10060–10069 CrossRef CAS
.
- V. A. Ranea, I. Carmichael and W. F. Schneider, J. Phys. Chem. C, 2009, 113, 2149–2158 CrossRef CAS
.
- R. S. Alvim, I. Borges, D. G. Costa and A. A. Leitão, J. Phys. Chem. C, 2011, 116, 738–744 CrossRef
.
- J. H. Bitter, K. Seshan and J. A. Lercher, J. Catal., 1998, 176, 93–101 CrossRef CAS
.
- J. Guo, H. Lou, L. Mo and X. Zheng, J. Mol. Catal. A: Chem., 2010, 316, 1–7 CrossRef CAS
.
-
H. H. Kung, Advances in Catalysis, Elsevier, 1994, vol. 40, pp. 1–38 Search PubMed
.
- C. A. Gärtner, A. C. van Veen and J. A. Lercher, ChemCatChem, 2013, 5, 3196–3217 CrossRef
.
- F. Cavani and F. Trifiro, Catal. Today, 1995, 24, 307–313 CrossRef CAS
.
- F. Cavani and F. Trifiro, Catal. Today, 1999, 51, 561–580 CrossRef CAS
.
- S. Wang and Z. Zhu, Energy Fuels, 2004, 18, 1126–1139 CrossRef CAS
.
- A. Alamdari, R. Karimzadeh and S. Abbasizadeh, Rev. Chem. Eng., 2019, 1 DOI:10.1515/revce-2017-0109
.
- D. Mukherjee, S.-E. Park and B. M. Reddy, J. CO2 Util., 2016, 16, 301–312 CrossRef CAS
.
- L. Shi, Y. Wang, B. Yan, W. Song, D. Shao and A.-H. Lu, Chem. Commun., 2018, 54, 10936–10946 RSC
.
- E. Gomez, B. Yan, S. Kattel and J. G. Chen, Nat. Rev. Chem., 2019, 1–12 CAS
.
- A. M. Gaffney, Q. An, W. A. Goddard, W. Diao and M. V. Glazoff, Top. Catal., 2020, 1–15 Search PubMed
.
- I. Horiuti and M. Polanyi, Trans. Faraday Soc., 1934, 30, 1164–1172 RSC
.
- R. D. Cortright, P. E. Levin and J. A. Dumesic, Ind. Eng. Chem. Res., 1998, 37, 1717–1723 CrossRef CAS
.
- Q. Li, Z. Sui, X. Zhou and D. Chen, Appl. Catal., A, 2011, 398, 18–26 CrossRef CAS
.
- A. W. Hauser, J. Gomes, M. Bajdich, M. Head-Gordon and A. T. Bell, Phys. Chem. Chem. Phys., 2013, 15, 20727–20734 RSC
.
- E. Jimenez-Izal, J.-Y. Liu and A. N. Alexandrova, J. Catal., 2019, 374, 93–100 CrossRef CAS
.
- Y. Chen and D. G. Vlachos, J. Phys. Chem. C, 2010, 114, 4973–4982 CrossRef CAS
.
- G. Peng, D. Gerceker, M. Kumbhalkar, J. A. Dumesic and M. Mavrikakis, Catal.: Sci. Technol., 2018, 8, 2159–2174 RSC
.
- X. Ding, H. Zhu, H. Ren, D. Liu, Z. Yu, N. Shi and W. Guo, Phys. Chem. Chem. Phys., 2020, 22, 21835–21843 RSC
.
- A. Hook, J. D. Massa and F. E. Celik, J. Phys. Chem. C, 2016, 120, 27307–27318 CrossRef CAS
.
- A. Hook and F. E. Celik, J. Phys. Chem. C, 2017, 121, 17882–17892 CrossRef CAS
.
- J. Nam and F. E. Celik, Top. Catal., 2020, 63, 700–713 CrossRef CAS
.
- A. Anghel, D. Wales, S. Jenkins and D. King, Chem. Phys. Lett., 2005, 413, 289–293 CrossRef CAS
.
- A. Anghel, D. Wales, S. Jenkins and D. King, J. Chem. Phys., 2007, 126, 044710 CrossRef CAS
.
- M. H. Hansen, J. K. Nørskov and T. Bligaard, J. Catal., 2019, 374, 161–170 CrossRef CAS
.
- J. Wu, S. M. Sharada, C. Ho, A. W. Hauser, M. Head-Gordon and A. T. Bell, Appl. Catal., A, 2015, 506, 25–32 CrossRef CAS
.
- A. W. Hauser, P. R. Horn, M. Head-Gordon and A. T. Bell, Phys. Chem. Chem. Phys., 2016, 18, 10906–10917 RSC
.
- V. J. Cybulskis, B. C. Bukowski, H.-T. Tseng, J. R. Gallagher, Z. Wu, E. Wegener, A. J. Kropf, B. Ravel, F. H. Ribeiro, J. Greeley and J. T. Miller, ACS Catal., 2017, 7, 4173–4181 CrossRef CAS
.
- J. Ko, J. A. Muhlenkamp, Y. Bonita, N. J. LiBretto, J. T. Miller, J. C. Hicks and W. F. Schneider, Ind. Eng. Chem. Res., 2020, 59, 12666–12676 CrossRef CAS
.
- J. Wu, Z. Peng and A. T. Bell, J. Catal., 2014, 311, 161–168 CrossRef CAS
.
- C. Batiot and B. K. Hodnett, Appl. Catal., A, 1996, 137, 179–191 CrossRef CAS
.
- C.-C. Liao, C.-C. Chang, Y. Choi and M.-K. Tsai, Surf. Sci., 2018, 674, 45–50 CrossRef CAS
.
- G.-L. Dai, Z.-P. Liu, W.-N. Wang, J. Lu and K.-N. Fan, J. Phys. Chem. C, 2008, 112, 3719–3725 CrossRef CAS
.
- D. Melzer, P. Xu, D. Hartmann, Y. Zhu, N. D. Browning, M. Sanchez-Sanchez and J. A. Lercher, Angew. Chem., Int. Ed., 2016, 55, 8873–8877 CrossRef CAS
.
- V. Fung, F. Tao and D.-E. Jiang, Catal.: Sci. Technol., 2016, 6, 6861–6869 RSC
.
- X. Lin, Y. Xi and J. Sun, J. Phys. Chem. C, 2012, 116, 3503–3516 CrossRef CAS
.
- Y. Bian, M. Kim, T. Li, A. Asthagiri and J. F. Weaver, J. Am. Chem. Soc., 2018, 140, 2665–2672 CrossRef CAS
.
- M. Banares, M. Martınez-Huerta, X. Gao, J. Fierro and I. Wachs, Catal. Today, 2000, 61, 295–301 CrossRef CAS
.
-
J. A. Lercher and F. N. Naraschewski, Nanostructured Catalysts: Selective Oxidations, The Royal Society of Chemistry, 2011, pp. 5–32, 10.1039/9781847559876-00005
.
- M. D. Argyle, K. Chen, A. T. Bell and E. Iglesia, J. Phys. Chem. B, 2002, 106, 5421–5427 CrossRef CAS
.
- H. Fu, Z. P. Liu, Z. H. Li, W. N. Wang and K. N. Fan, J. Am. Chem. Soc., 2006, 128, 11114–11123 CrossRef CAS
.
- S. P. Sun, J. L. Zhu, S. Gu, X. P. Li, W. N. Lei, Y. Jiang, D. Q. Yi and G. H. Chen, Appl. Surf. Sci., 2019, 467–468, 753–759 CrossRef CAS
.
- R. Yao, J. E. Herrera, L. Chen and Y.-H. C. Chin, ACS Catal., 2020, 10, 6952–6968 CrossRef CAS
.
- Y. V. Kolen’ko, W. Zhang, R. N. d’Alnoncourt, F. Girgsdies, T. W. Hansen, T. Wolfram, R. Schlögl and A. Trunschke, ChemCatChem, 2011, 3, 1597–1606 CrossRef
.
- D. Vitry, Y. Morikawa, J. L. Dubois and W. Ueda, Top. Catal., 2003, 23, 47–53 CrossRef CAS
.
- N. R. Shiju, X. Liang, A. W. Weimer, C. Liang, S. Dai and V. V. Guliants, J. Am. Chem. Soc., 2008, 130, 5850–5851 CrossRef CAS
.
- A. Celaya Sanfiz, T. W. Hansen, A. Sakthivel, A. Trunschke, R. Schlögl, A. Knoester, H. H. Brongersma, M. H. Looi and S. B. A. Hamid, J. Catal., 2008, 258, 35–43 CrossRef CAS
.
- R. Schlögl, Top. Catal., 2011, 54, 627–638 CrossRef
.
- K. Muthukumar, J. Yu, Y. Xu and V. V. Guliants, Top. Catal., 2011, 54, 605–613 CrossRef CAS
.
- L. Annamalai, Y. Liu, S. Ezenwa, Y. Dang, S. L. Suib and P. Deshlahra, ACS Catal., 2018, 8, 7051–7067 CrossRef CAS
.
- Y. Liu, L. Annamalai and P. Deshlahra, J. Phys. Chem. C, 2019, 123, 28168–28191 CrossRef CAS
.
- S. Zhang, J.-j. Shan, Y. Zhu, A. I. Frenkel, A. Patlolla, W. Huang, S. J. Yoon, L. Wang, H. Yoshida, S. Takeda and F. Tao, J. Am. Chem. Soc., 2013, 135, 8283–8293 CrossRef CAS
.
- D.-e. Jiang and S. Dai, Phys. Chem. Chem. Phys., 2011, 13, 978–984 RSC
.
- V. Fung, F. Tao and D. E. Jiang, ChemCatChem, 2018, 10, 244–249 CrossRef CAS
.
- H. Zhu, D. C. Rosenfeld, M. Harb, D. H. Anjum, M. N. Hedhili, S. Ould-Chikh and J.-M. Basset, ACS Catal., 2016, 6, 2852–2866 CrossRef CAS
.
- X. Sun, B. Li and H. Metiu, J. Phys. Chem. C, 2013, 117, 23597–23608 CrossRef CAS
.
- B. Savova, S. Loridant, D. Filkova and J. Millet, Appl. Catal., A, 2010, 390, 148–157 CrossRef CAS
.
- H. Zhu, S. Ould-Chikh, D. H. Anjum, M. Sun, G. Biausque, J.-M. Basset and V. Caps, J. Catal., 2012, 285, 292–303 CrossRef CAS
.
- T. L. M. Pham, S. Nachimuthu, J.-L. Kuo and J.-C. Jiang, Appl. Catal., A, 2017, 541, 8–14 CrossRef CAS
.
- T. A. Bugrova, V. V. Dutov, V. A. Svetlichnyi, V. Cortés Corberán and G. V. Mamontov, Catal. Today, 2019, 333, 71–80 CrossRef CAS
.
- M. Myint, B. Yan, J. Wan, S. Zhao and J. G. Chen, J. Catal., 2016, 343, 168–177 CrossRef CAS
.
- B. Yan, S. Yao, S. Kattel, Q. Wu, Z. Xie, E. Gomez, P. Liu, D. Su and J. G. Chen, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 8278–8283 CrossRef CAS
.
- M. D. Porosoff, M. N. Z. Myint, S. Kattel, Z. Xie, E. Gomez, P. Liu and J. G. Chen, Angew. Chem., 2015, 127, 15721–15725 CrossRef
.
- S. Yao, B. Yan, Z. Jiang, Z. Liu, Q. Wu, J. H. Lee and J. G. Chen, ACS Catal., 2018, 8, 5374–5381 CrossRef CAS
.
- E. Gomez, S. Kattel, B. Yan, S. Yao, P. Liu and J. G. Chen, Nat. Commun., 2018, 9, 1398–1403 CrossRef
.
- F. Jalid, T. S. Khan and M. A. Haider, Catal.: Sci. Technol., 2021, 11, 97–115 RSC
.
- O. O. James, S. Mandal, N. Alele, B. Chowdhury and S. Maity, Fuel Process. Technol., 2016, 149, 239–255 CrossRef CAS
.
- Y. He, Y. J. Song, D. A. Cullen and S. Laursen, J. Am. Chem. Soc., 2018, 140, 14010–14014 CrossRef CAS
.
- L. Xiao, F. Ma, Y.-A. Zhu, Z.-J. Sui, J.-H. Zhou, X.-G. Zhou, D. Chen and W.-K. Yuan, Chem. Eng. J., 2019, 377, 120049 CrossRef CAS
.
- J. Im and M. Choi, ACS Catal., 2016, 6, 2819–2826 CrossRef CAS
.
- J. J. H. B. Sattler, I. D. Gonzalez-Jimenez, L. Luo, B. A. Stears, A. Malek, D. G. Barton, B. A. Kilos, M. P. Kaminsky, T. W. G. M. Verhoeven, E. J. Koers, M. Baldus and B. M. Weckhuysen, Angew. Chem., Int. Ed., 2014, 53, 9251–9256 CrossRef CAS
.
- N. Kaylor and R. J. Davis, J. Catal., 2018, 367, 181–193 CrossRef CAS
.
- R. Grabowski and J. Słoczyński, Chem. Eng. Process., 2005, 44, 1082–1093 CrossRef CAS
.
- M. M. Hossain, Ind. Eng. Chem. Res., 2017, 56, 4309–4318 CrossRef CAS
.
- J. Baek, H. J. Yun, D. Yun, Y. Choi and J. Yi, ACS Catal., 2012, 2, 1893–1903 CrossRef CAS
.
- F. Cavani, N. Ballarini and A. Cericola, Catal. Today, 2007, 127, 113–131 CrossRef CAS
.
- K. Chen, A. T. Bell and E. Iglesia, J. Phys. Chem. B, 2000, 104, 1292–1299 CrossRef CAS
.
- S. Saerens, M. K. Sabbe, V. V. Galvita, E. A. Redekop, M.-F. Reyniers and G. B. Marin, ACS Catal., 2017, 7, 7495–7508 CrossRef CAS
.
- Y. J. Wang, Y. M. Wang, S. R. Wang, X. Z. Guo, S. M. Zhang, W. P. Huang and S. H. Wu, Catal. Lett., 2009, 132, 472–479 CrossRef CAS
.
- A. Iglesias-Juez, A. M. Beale, K. Maaijen, T. C. Weng, P. Glatzel and B. M. Weckhuysen, J. Catal., 2010, 276, 268–279 CrossRef CAS
.
- P. Sun, G. Siddiqi, W. C. Vining, M. Chi and A. T. Bell, J. Catal., 2011, 282, 165–174 CrossRef CAS
.
- J. C. Li, J. M. Li, Z. Zhao, X. Q. Fan, J. Liu, Y. C. Wei, A. J. Duan, Z. Xie and Q. L. Liu, J. Catal., 2017, 352, 361–370 CrossRef CAS
.
- S. Zha, G. Sun, T. Wu, J. Zhao, Z.-J. Zhao and J. Gong, Chem. Sci., 2018, 9, 3925–3931 RSC
.
- C. Yang, Z. Wu, G. Zhang, H. Sheng, J. Tian, Z. Duan, H. Sohn, A. J. Kropf, T. Wu, T. R. Krause and J. T. Miller, Catal. Today, 2019, 323, 123–128 CrossRef CAS
.
- M.-L. Yang, Y.-A. Zhu, C. Fan, Z.-J. Sui, D. Chen and X.-G. Zhou, Phys. Chem. Chem. Phys., 2011, 13, 3257–3267 RSC
.
- M.-L. Yang, Y.-A. Zhu, X.-G. Zhou, Z.-J. Sui and D. Chen, ACS Catal., 2012, 2, 1247–1258 CrossRef CAS
.
- M.-L. Yang, Y.-A. Zhu, C. Fan, Z.-J. Sui, D. Chen and X.-G. Zhou, J. Mol. Catal. A: Chem., 2010, 321, 42–49 CrossRef CAS
.
- L. Nykänen and K. Honkala, J. Phys. Chem. C, 2011, 115, 9578–9586 CrossRef
.
- T. Saelee, S. Namuangruk, N. Kungwan and A. Junkaew, J. Phys. Chem. C, 2018, 122, 14678–14690 CrossRef CAS
.
- X. Cao, RSC Adv., 2016, 6, 65524–65532 RSC
.
- Z. Lian, S. Ali, T. Liu, C. Si, B. Li and D. S. Su, ACS Catal., 2018, 8, 4694–4704 CrossRef CAS
.
- J. Zhu, M.-L. Yang, Y. Yu, Y.-A. Zhu, Z. J. Sui, X. Zhou, A. Holmen and D. Chen, ACS Catal., 2015, 5, 6310–6319 CrossRef CAS
.
-
Z.-J. Sui, Y.-A. Zhu, P. Li, X.-G. Zhou and D. Chen, in Advances in Chemical Engineering, ed. G. B. Marin, Academic Press, 2014, vol. 44, pp. 61–125 Search PubMed
.
- A. Valcárcel, J. M. Ricart, A. Clotet, A. Markovits, C. Minot and F. Illas, Surf. Sci., 2002, 519, 250–258 CrossRef
.
- M.-L. Yang, J. Zhu, Y.-A. Zhu, Z.-J. Sui, Y.-D. Yu, X.-G. Zhou and D. Chen, J. Mol. Catal., A, 2014, 395, 329–336 CrossRef CAS
.
- F. Ma, Q.-Y. Chang, Q. Yin, Z.-J. Sui, X.-G. Zhou, D. Chen and Y.-A. Zhu, Catal.: Sci. Technol., 2020, 10, 4938–4951 RSC
.
- A. Valcárcel, J. M. Ricart, A. Clotet, F. Illas, A. Markovits and C. Minot, J. Catal., 2006, 241, 115–122 CrossRef
.
- A. Valcárcel, A. Gil, J. M. Ricart and A. Clotet, Chem. Phys. Lett., 2004, 399, 295–299 CrossRef
.
- L. Shi, G. M. Deng, W. C. Li, S. Miao, Q. N. Wang, W. P. Zhang and A. H. Lu, Angew. Chem., Int. Ed., 2015, 54, 13994–13998 CrossRef CAS
.
- L. Rochlitz, K. Searles, J. Alfke, D. Zemlyanov, O. V. Safonova and C. Copéret, Chem. Sci., 2020, 11, 1549–1555 RSC
.
- J. R. Gallagher, D. J. Childers, H. Zhao, R. E. Winans, R. J. Meyer and J. T. Miller, Phys. Chem. Chem. Phys., 2015, 17, 28144–28153 RSC
.
- X. Cao, Y. Ji and Y. Luo, J. Phys. Chem. C, 2015, 119, 1016–1023 CrossRef CAS
.
- L. Xiao, Y.-L. Shan, Z.-J. Sui, D. Chen, X.-G. Zhou, W.-K. Yuan and Y.-A. Zhu, ACS Catal., 2020, 10, 14887–14902 CrossRef CAS
.
- M. Heinritz-Adrian, S. Wenzel and F. Youssef, Pet. Technol. Quart., 2008, 13, 83–92 Search PubMed
.
- Y. Zhu, Z. An, H. Song, X. Xiang, W. Yan and J. He, ACS Catal., 2017, 7, 6973–6978 CrossRef CAS
.
- C.-c. Chiu, A. Genest and N. Rösch, ChemCatChem, 2013, 5, 3299–3308 CrossRef CAS
.
- M.-L. Yang, C. Fan, Y.-A. Zhu, Z.-J. Sui, X.-G. Zhou and D. Chen, J. Phys. Chem. C, 2015, 119, 21386–21394 CrossRef CAS
.
- L. G. Cesar, C. Yang, Z. Lu, Y. Ren, G. Zhang and J. T. Miller, ACS Catal., 2019, 9, 5231–5244 CrossRef CAS
.
- M. S. Kumar, D. Chen, J. C. Walmsley and A. Holmen, Catal. Commun., 2008, 9, 747–750 CrossRef CAS
.
- T. Bauer, S. Maisel, D. Blaumeiser, J. Vecchietti, N. Taccardi, P. Wasserscheid, A. Bonivardi, A. Gorling and J. Libuda, ACS Catal., 2019, 9, 2842–2853 CrossRef CAS
.
- O. A. Bariås, A. Holmen and E. A. Blekkan, J. Catal., 1996, 158, 1–12 CrossRef
.
- Z. Han, S. Li, F. Jiang, T. Wang, X. Ma and J. Gong, Nanoscale, 2014, 6, 10000–10008 RSC
.
- K. Xia, W.-Z. Lang, P.-P. Li, X. Yan and Y.-J. Guo, J. Catal., 2016, 338, 104–114 CrossRef CAS
.
- T. Wang, F. Jiang, G. Liu, L. Zeng, Z. J. Zhao and J. Gong, AIChE J., 2016, 62, 4365–4376 CrossRef CAS
.
- S. Furukawa and T. Komatsu, ACS Catal., 2016, 7, 735–765 CrossRef
.
- B. Hammer and J. K. Nørskov, Adv. Catal., 2000, 45, 71–129 CAS
.
- L. Nykänen and K. Honkala, ACS Catal., 2013, 3, 3026–3030 CrossRef
.
- M.-H. Lee, B. M. Nagaraja, P. Natarajan, N. T. Truong, K. Y. Lee, S. Yoon and K.-D. Jung, Res. Chem. Intermed., 2016, 42, 123–140 CrossRef CAS
.
- H. N. Pham, J. J. H. B. Sattler, B. M. Weckhuysen and A. K. Datye, ACS Catal., 2016, 6, 2257–2264 CrossRef CAS
.
- Z. Li, L. Yu, C. Milligan, T. Ma, L. Zhou, Y. Cui, Z. Qi, N. Libretto, B. Xu, J. Luo, E. Shi, Z. Wu, H. Xin, W. N. Delgass, J. T. Miller and Y. Wu, Nat. Commun., 2018, 9, 5258–5265 CrossRef CAS
.
- B. K. Vu, M. B. Song, I. Y. Ahn, Y.-W. Suh, D. J. Suh, J. S. Kim and E. W. Shin, J. Ind. Eng. Chem., 2011, 17, 71–76 CrossRef CAS
.
- Y. Zhang, M. Xue, Y. Zhou, H. Zhang, W. Wang, Q. Wang and X. Sheng, RSC Adv., 2016, 6, 29410–29422 RSC
.
- G. Sun, Z.-J. Zhao, R. Mu, S. Zha, L. Li, S. Chen, K. Zang, J. Luo, Z. Li, S. C. Purdy, A. J. Kropf, J. T. Miller, L. Zeng and J. Gong, Nat. Commun., 2018, 9, 4454 CrossRef
.
- C. C. Chang, C. Y. Liu, S. Y. Wu and M. K. Tsai, Phys. Chem. Chem. Phys., 2017, 19, 4989–4996 RSC
.
- K. Xia, W.-Z. Lang, P.-P. Li, L.-L. Long, X. Yan and Y.-J. Guo, Chem. Eng. J., 2016, 284, 1068–1079 CrossRef CAS
.
- J. Liu, Y. Yue, H. Liu, Z. Da, C. Liu, A. Ma, J. Rong, D. Su, X. Bao and H. Zheng, ACS Catal., 2017, 7, 3349–3355 CrossRef CAS
.
- F. Jiang, L. Zeng, S. Li, G. Liu, S. Wang and J. Gong, ACS Catal., 2015, 5, 438–447 CrossRef CAS
.
- M. M. Bhasin, J. H. McCain, B. V. Vora, T. Imai and P. R. Pujado, Appl. Catal., A, 2001, 221, 397–419 CrossRef CAS
.
- J. Zhang, R.-J. Zhou, Q.-Y. Chang, Z.-J. Sui, X.-G. Zhou, D. Chen and Y.-A. Zhu, Catal. Today, 2020 DOI:10.1016/j.cattod.2020.02.023
.
- C. Coperet, Chem. Rev., 2010, 110, 656–680 CrossRef CAS
.
- J. Védrine, Catalysts, 2017, 7, 341–365 CrossRef
.
- G. Liu, Z. J. Zhao, T. F. Wu, L. Zeng and J. L. Gong, ACS Catal., 2016, 6, 5207–5214 CrossRef CAS
.
- A. H. Elbadawi, M. S. Ba-Shammakh, S. Al-Ghamdi, S. A. Razzak and M. M. Hossain, Chem. Eng. J., 2016, 284, 448–457 CrossRef CAS
.
- S. Barman, N. Maity, K. Bhatte, S. Ould-Chikh, O. Dachwald, C. Haeßner, Y. Saih, E. Abou-Hamad, I. Llorens, J.-L. Hazemann, K. Köhler, V. D’ Elia and J.-M. Basset, ACS Catal., 2016, 6, 5908–5921 CrossRef CAS
.
- Y. Gambo, A. A. Jalil, S. Triwahyono and A. A. Abdulrasheed, J. Ind. Eng. Chem., 2018, 59, 218–229 CrossRef CAS
.
- P. Gandeepan, T. Müller, D. Zell, G. Cera, S. Warratz and L. Ackermann, Chem. Rev., 2019, 119, 2192–2452 CrossRef CAS
.
- F. Gilardoni, A. T. Bell, A. Chakraborty and P. Boulet, J. Phys. Chem. B, 2000, 104, 12250–12255 CrossRef CAS
.
- G. Fu, X. Xu, X. Lu and H. Wan, J. Phys. Chem. B, 2005, 109, 6416–6421 CrossRef CAS
.
- R. m. F. Xavier Rozanska and J. Sauer, J. Phys. Chem. C, 2007, 111, 6041–6050 CrossRef
.
- Y. Liu, Z. H. Li, J. Lu and K. N. Fan, J. Phys. Chem. C, 2008, 112, 20382–20392 CrossRef CAS
.
- K. Alexopoulos, M.-F. Reyniers and G. B. Marin, J. Catal., 2012, 289, 127–139 CrossRef CAS
.
- C. Xiong, S. Chen, P. Yang, S. Zha, Z.-J. Zhao and J. Gong, ACS Catal., 2019, 9, 5816–5827 CrossRef CAS
.
- Q.-Y. Chang, Q. Yin, F. Ma, Y.-A. Zhu, Z.-J. Sui, X.-G. Zhou, D. Chen and W.-K. Yuan, Ind. Eng. Chem. Res., 2019, 58, 10199–10209 CrossRef CAS
.
- M. Hus, D. Kopac and B. Likozar, J. Catal., 2020, 386, 126–138 CrossRef CAS
.
- A. Kämper, A. Auroux and M. Baerns, Phys. Chem. Chem. Phys., 2000, 2, 1069–1075 RSC
.
- M. V. Ganduglia-Pirovano and J. Sauer, J. Phys. Chem. B, 2005, 109, 374–380 CrossRef CAS
.
- P. C. Redfern, P. Zapol, M. Sternberg, S. P. Adiga, S. A. Zygmunt and L. A. Curtiss, J. Phys. Chem. B, 2006, 110, 8363–8371 CrossRef CAS
.
- M. Engeser, M. Schlangen, D. Schröder, H. Schwarz, T. Yumura and K. Yoshizawa, Organometallics, 2003, 22, 3933–3943 CrossRef CAS
.
- S. Feyel, D. Schroder, X. Rozanska, J. Sauer and H. Schwarz, Angew. Chem., Int. Ed., 2006, 45, 4677–4681 CrossRef CAS
.
- J. Scholz, A. Walter and T. Ressler, J. Catal., 2014, 309, 105–114 CrossRef CAS
.
- J. Gong, Angew. Chem., Int. Ed., 2020, 59, 22072–22079 CrossRef
.
- Y.-J. Du, Z. H. Li and K.-N. Fan, J. Mol. Catal., A, 2013, 379, 122–138 CrossRef CAS
.
- X. Rozanska, R. Fortrie and J. Sauer, J. Am. Chem. Soc., 2014, 136, 7751–7761 CrossRef CAS
.
- J.-L. Sánchez-García, B. E. Handy, I. N. Ávila-Hernández, A. G. Rodríguez and R. García-Alamilla, Catalysts, 2020, 10, 550 CrossRef
.
- H. Kazerooni, J. T. Darian, Y. Mortazavi, A. A. Khadadadi and R. Asadi, Catal. Lett., 2020, 150, 2807–2822 CrossRef CAS
.
- X. Wu, Z. Chen, X. Yu, Z. Huang, H. Shen and G. Jing, Chem. Eng. J., 2020, 125629 CrossRef CAS
.
- Q.-X. Luo, X.-K. Zhang, B.-L. Hou, J.-G. Chen, C. Zhu, Z.-W. Liu, Z.-T. Liu and J. Lu, Catal.: Sci. Technol., 2018, 8, 4864–4876 RSC
.
- L. Cheng, G. A. Ferguson, S. A. Zygmunt and L. A. Curtiss, J. Catal., 2013, 302, 31–36 CrossRef CAS
.
- Y. Hinuma, T. Toyao, T. Kamachi, Z. Maeno, S. Takakusagi, S. Furukawa, I. Takigawa and K.-I. Shimizu, J. Phys. Chem. C, 2018, 122, 29435–29444 CrossRef CAS
.
- Y. Li, W. Cheng, Z.-J. Sui, X.-G. Zhou, D. Chen, W.-K. Yuan and Y.-A. Zhu, J. Phys. Chem. C, 2019, 123, 28275–28283 CrossRef CAS
.
- J. Sauer and J. Dobler, Dalton Trans., 2004, 3116–3121, 10.1039/b402873b
.
- G.-L. Dai, Z.-H. Li, J. Lu, W.-N. Wang and K.-N. Fan, J. Phys. Chem. C, 2012, 116, 807–817 CrossRef CAS
.
- H.-S. Kim, S. A. Zygmunt, P. C. Stair, P. Zapol and L. A. Curtiss, J. Phys. Chem. C, 2009, 113, 8836–8843 CrossRef CAS
.
- Y. Y. Zhang, Y. Zhao, T. Otroshchenko, H. Lund, M. M. Pohl, U. Rodemerck, D. Linke, H. J. Jiao, G. Y. Jiang and E. V. Kondratenko, Nat. Commun., 2018, 9, 3794–3803 CrossRef
.
- K. Chen, A. Khodakov, J. Yang, A. T. Bell and E. Iglesia, J. Catal., 1999, 186, 325–333 CrossRef CAS
.
- K. Chen, E. Iglesia and A. T. Bell, J. Phys. Chem. B, 2001, 105, 646–653 CrossRef CAS
.
- S. Chakraborty, S. C. Nayak and G. Deo, Catal. Today, 2015, 254, 62–71 CrossRef CAS
.
- M. De and D. Kunzru, Catal. Lett., 2005, 102, 237–246 CrossRef CAS
.
- S. N. Koc, G. Gurdag, S. Geissler, M. Guraya, M. Orbay and M. Muhler, J. Mol. Catal., A, 2005, 225, 197–202 CrossRef CAS
.
- A. Held, J. Kowalska-Kuś, K. Nowińska and K. Góra-Marek, J. Catal., 2017, 347, 21–35 CrossRef CAS
.
- Z.-J. Zhao, T. Wu, C. Xiong, G. Sun, R. Mu, L. Zeng and J. Gong, Angew. Chem., Int. Ed., 2018, 57, 6791–6795 CrossRef CAS
.
- Z. Bai, P. Li, L. Liu and G. Xiong, ChemCatChem, 2012, 4, 260–264 CrossRef CAS
.
- G. Wu, F. Hei, N. Guan and L. Li, Catal.: Sci. Technol., 2013, 3, 1333 RSC
.
- M. J. Cheng and W. A. Goddard, 3rd, J. Am. Chem. Soc., 2015, 137, 13224–13227 CrossRef CAS
.
- M. Aly, E. L. Fornero, A. R. Leon-Garzon, V. V. Galvita and M. Saeys, ACS Catal., 2020, 10, 5208–5216 CrossRef CAS
.
- K. Chen, A. T. Bell and E. Iglesia, J. Catal., 2002, 209, 35–42 CrossRef CAS
.
- Q.-Y. Chang, K.-Q. Wang, P. Hu, Z.-J. Sui, X.-G. Zhou, D. Chen, W.-K. Yuan and Y.-A. Zhu, AIChE J., 2020, 66, 16232 Search PubMed
.
- T. Shishido, K. Shimamura, K. Teramura and T. Tanaka, Catal. Today, 2012, 185, 151–156 CrossRef CAS
.
- H. M. Wang, Y. Chen, X. Yan, W. Z. Lang and Y. J. Guo, Microporous Mesoporous Mater., 2019, 284, 69–77 CrossRef CAS
.
- M. A. Atanga, F. Rezaei, A. Jawad, M. Fitch and A. A. Rownaghi, Appl. Catal., B, 2018, 220, 429–445 CrossRef CAS
.
- L. Wang, L. Huang, F. Liang, S. Liu, Y. Wang and H. Zhang, Chin. J. Catal., 2017, 38, 1528–1539 CrossRef CAS
.
- J. Y. Liu, ACS Catal., 2017, 7, 34–59 CrossRef CAS
.
- N. J. O’Connor, A. S. M. Jonayat, M. J. Janik and T. P. Senftle, Nat. Catal., 2018, 1, 531–539 CrossRef
.
- X. F. Yang, A. Wang, B. Qiao, J. Li, J. Liu and T. Zhang, Acc. Chem. Res., 2013, 46, 1740–1748 CrossRef CAS
.
- X.-K. Gu, B. Qiao, C.-Q. Huang, W.-C. Ding, K. Sun, E. Zhan, T. Zhang, J. Liu and W.-X. Li, ACS Catal., 2014, 4, 3886–3890 CrossRef CAS
.
- C. Riley, S. Zhou, D. Kunwar, A. De La Riva, E. Peterson, R. Payne, L. Gao, S. Lin, H. Guo and A. Datye, J. Am. Chem. Soc., 2018, 140, 12964–12973 CrossRef CAS
.
- Z. K. Han and Y. Gao, Chem. – Eur. J., 2016, 22, 2092–2099 CrossRef CAS
.
- R. Lang, W. Xi, J. C. Liu, Y. T. Cui, T. Li, A. F. Lee, F. Chen, Y. Chen, L. Li, L. Li, J. Lin, S. Miao, X. Liu, A. Q. Wang, X. Wang, J. Luo, B. Qiao, J. Li and T. Zhang, Nat. Commun., 2019, 10, 234 CrossRef
.
- H. Xiong, S. Lin, J. Goetze, P. Pletcher, H. Guo, L. Kovarik, K. Artyushkova, B. M. Weckhuysen and A. K. Datye, Angew. Chem., Int. Ed., 2017, 56, 8986–8991 CrossRef CAS
.
- X. Sun, P. Han, B. Li and Z. Zhao, J. Phys. Chem. C, 2018, 122, 1570–1576 CrossRef CAS
.
- X. Y. Sun, M. J. Liu, Y. Y. Huang, B. Li and Z. Zhao, Chin. J. Catal., 2019, 40, 819–825 CrossRef CAS
.
- N. Kong, X. Fan, F. Liu, L. Wang, H. Lin, Y. Li and S.-T. Lee, ACS Nano, 2020, 14, 5772–5779 CrossRef CAS
.
- W. Zhang, H. Wang, J. Jiang, Z. Sui, Y. Zhu, D. Chen and X. Zhou, ACS Catal., 2020, 10, 12932–12942 CrossRef CAS
.
- G. Liu, L. Zeng, Z.-J. Zhao, H. Tian, T. Wu and J. Gong, ACS Catal., 2016, 6, 2158–2162 CrossRef CAS
.
-
J. K. Nørskov, F. Studt, F. Abild-Pedersen and T. Bligaard, Fundamental concepts in heterogeneous catalysis, John Wiley & Sons, 2014 Search PubMed
.
- B. Hammer and J. K. Norskov, Nature, 1995, 376, 238–240 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2021 |





