Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The joint effect of electrical conductivity and surface oxygen functionalities of carbon supports on the oxygen reduction reaction studied over bare supports and Mn–Co spinel/carbon catalysts in alkaline media†
Aldona
Kostuch
 ,
Sebastian
Jarczewski
,
Sebastian
Jarczewski
 ,
Marcin K.
Surówka
,
Marcin K.
Surówka
 ,
Piotr
Kuśtrowski
,
Piotr
Kuśtrowski
 ,
Zbigniew
Sojka
,
Zbigniew
Sojka
 and
Krzysztof
Kruczała
and
Krzysztof
Kruczała
 *
*
Faculty of Chemistry, Jagiellonian University in Krakow, Gronostajowa 2, 30-387 Krakow, Poland. E-mail: kruczala@chemia.uj.edu.pl; Tel: (+48) 12 686 2498
First published on 7th October 2021
Abstract
Supported manganese–cobalt spinel catalysts and the corresponding mesoporous carbon supports were examined in order to reveal the effect of electrical conductivity and surface oxygen functionalities on the oxygen reduction reaction (ORR) in alkaline media. Carbon replicas of comparable porosity were obtained from sucrose by nano-replication of a silica template followed by carbonization at different temperatures (650–1050 °C). The degree of their graphitization was assessed by deconvolution of the Raman spectra (1000–1800 cm−1), whereas relative electrical conductivity measurements were performed by means of the contactless microwave cavity quality factor perturbation technique. The electrocatalytic activities of the obtained materials towards the ORR (gauged by the ORR onset potential and the number of transferred electrons) were tested in alkaline media using standard hydrodynamic methods. It was found that with increasing carbonization temperature, the electrical conductivity of the examined carbon materials increased, in parallel with their growing crystallinity. For the carbon samples calcined in the temperature range 650–850 °C, the ORR onset potential initially rises as the electrical conductivity increases, passes through a maximum at around 850 °C, and then falls. Such a volcano-type shape was found also in the case of manganese–cobalt spinel catalysts deposited on the examined carbon supports. The observed non-monotonous electrocatalytic behavior was accounted for by two descriptors: the carbon support electrical conductivity and the amount of surface carbonyl and quinone groups, changing in the opposite way with the carbonization temperature. It was shown that variation of the electrical conductivity multiplied by the amount of carboxyl and quinone groups with the carbon calcination temperature exhibits the same behavior as the number of electrons exchanged in the ORR, confirming that an optimal conjunction of these properties plays a decisive role. The prime advantage of the dispersed spinel active phase lies in a significant enhancement of the 4-electron reduction pathway. To the best of our knowledge, the role of electrical conductivity and the nature of the surface oxygen-bearing functional groups in the ORR were elucidated for the first time.
Introduction
In the rapidly developing modern society, there is an urgent need for wide-ranging availability of advanced and eco-friendly energy sources. One of the possible alternatives is the application of anion exchange membrane fuel cells (AEMFCs) with a catalyst reducing efficiently dioxygen. These promising devices can revolutionize the energy sector since they produce little pollution. However, to make them more widely used, several obstacles must be overcome. As a result, vast-ranging investigations focus on improving the properties of conductive polymer membranes1–7 and catalysts for the oxygen reduction reaction (ORR).8–15 Due to the slow ORR kinetics, which is usually attributed to the high stability of the oxygen molecule, with an O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond strength of 498 kJ mol−1, it is necessary to use efficient electrocatalysts to accomplish this process. One of the main impediments in this field is the development of cheap and highly efficient materials to catalyze the ORR, which plays a key role in fuel cell systems. Therefore, non-noble metal electrocatalysts, such as metal macrocyclic compounds (phthalocyanines and porphyrins in particular), transition metal oxides, transition metals (e.g. silver, nickel), and nitrogen co-doped carbons have been investigated and used as the ORR catalysts.16–24 Transition metal oxides (TMOs) of spinel structure are commonly applied as catalysts for the ORR in AEMFCs. Numerous TMOs exhibit satisfactory catalytic activity in the ORR and the oxygen evolution reaction (OER) with the advantages of being inexpensive, naturally abundant, and environmentally benign. However, due to their low conductivity, carbon-based supports are usually used to circumvent this obstacle. The properties of carbon supports, such as porosity, electrical conductivity, surface area, degree of graphitization, and the presence of surface functional groups are crucial for the prospective catalytic performance.25–30 A great deal of research has been devoted to the investigation of ordered nanoporous carbons due to their desired porosity.31,32 It is considered that the presence of mesopores enhances the mass transfer of the electrolyte with dissolved oxygen and provides access to the active sites for the reactants, whereas micropores can improve the catalytic process through the adsorption phenomenon.33–36 Additionally, it has been shown that synthesis of the spinel active phase in the presence of such carbon carriers results in smaller grain dimensions, which is favorable for catalyzing the ORR process.27 Enhancement of the carbon support performance can be achieved by oxidizing its surface to form various oxygen-containing functional groups8 and/or by doping or co-doping it with heteroatoms such as nitrogen,37 boron,38 and sulfur.39 The introduction of oxygen groups on the carbon surface seems to be an efficient way of increasing the catalytic efficiency of spinel materials deposited on the carbon supports. This kind of functionalization allows activation of the chemically inert carbon surfaces and improves dispersion and adhesion between the support and the deposited spinel active phase, which appear to be crucial for enhanced durability of the resultant catalyst.40 It is also believed that surface C/O groups generate more active ORR sites, enhancing the electrode–spinel electron transfer,14,29 and are able to stabilize intermediate products of the reaction.8,41 DFT calculations also suggest that particularly active are the –COOH functional groups located at edges of the armchair shape and the C–O–C groups placed on the basal planes of the graphene domains.41 Another important factor gauging the ORR activity is good electrical conductivity of the catalyst's support, which is correlated with the graphitization degree.31,42,43 It does not only reduce the electrode resistance, promoting an efficient electron transport, but also helps to prevent carbon oxidation.44,45 However, the electrical conductivity measurements of powder carbon samples encounter several obstacles. The classic two- or four-point probe method requires establishing fair and reproducible contacts between the powder and the probe, which is usually quite challenging and inconvenient for handling. Furthermore, the results obtained depend substantially on the quality of the contacts between the examined catalyst and the electrodes. For these reasons, we have applied a contactless method for determining the relative electrical conductivity, based on the microwave cavity quality factor perturbation (MCQP) technique,46 which has scarcely been applied for conductivity measurements of powders so far.47 The MCQP method enables probing the electric/dielectric properties of the sample under a contact-free fashion.
O bond strength of 498 kJ mol−1, it is necessary to use efficient electrocatalysts to accomplish this process. One of the main impediments in this field is the development of cheap and highly efficient materials to catalyze the ORR, which plays a key role in fuel cell systems. Therefore, non-noble metal electrocatalysts, such as metal macrocyclic compounds (phthalocyanines and porphyrins in particular), transition metal oxides, transition metals (e.g. silver, nickel), and nitrogen co-doped carbons have been investigated and used as the ORR catalysts.16–24 Transition metal oxides (TMOs) of spinel structure are commonly applied as catalysts for the ORR in AEMFCs. Numerous TMOs exhibit satisfactory catalytic activity in the ORR and the oxygen evolution reaction (OER) with the advantages of being inexpensive, naturally abundant, and environmentally benign. However, due to their low conductivity, carbon-based supports are usually used to circumvent this obstacle. The properties of carbon supports, such as porosity, electrical conductivity, surface area, degree of graphitization, and the presence of surface functional groups are crucial for the prospective catalytic performance.25–30 A great deal of research has been devoted to the investigation of ordered nanoporous carbons due to their desired porosity.31,32 It is considered that the presence of mesopores enhances the mass transfer of the electrolyte with dissolved oxygen and provides access to the active sites for the reactants, whereas micropores can improve the catalytic process through the adsorption phenomenon.33–36 Additionally, it has been shown that synthesis of the spinel active phase in the presence of such carbon carriers results in smaller grain dimensions, which is favorable for catalyzing the ORR process.27 Enhancement of the carbon support performance can be achieved by oxidizing its surface to form various oxygen-containing functional groups8 and/or by doping or co-doping it with heteroatoms such as nitrogen,37 boron,38 and sulfur.39 The introduction of oxygen groups on the carbon surface seems to be an efficient way of increasing the catalytic efficiency of spinel materials deposited on the carbon supports. This kind of functionalization allows activation of the chemically inert carbon surfaces and improves dispersion and adhesion between the support and the deposited spinel active phase, which appear to be crucial for enhanced durability of the resultant catalyst.40 It is also believed that surface C/O groups generate more active ORR sites, enhancing the electrode–spinel electron transfer,14,29 and are able to stabilize intermediate products of the reaction.8,41 DFT calculations also suggest that particularly active are the –COOH functional groups located at edges of the armchair shape and the C–O–C groups placed on the basal planes of the graphene domains.41 Another important factor gauging the ORR activity is good electrical conductivity of the catalyst's support, which is correlated with the graphitization degree.31,42,43 It does not only reduce the electrode resistance, promoting an efficient electron transport, but also helps to prevent carbon oxidation.44,45 However, the electrical conductivity measurements of powder carbon samples encounter several obstacles. The classic two- or four-point probe method requires establishing fair and reproducible contacts between the powder and the probe, which is usually quite challenging and inconvenient for handling. Furthermore, the results obtained depend substantially on the quality of the contacts between the examined catalyst and the electrodes. For these reasons, we have applied a contactless method for determining the relative electrical conductivity, based on the microwave cavity quality factor perturbation (MCQP) technique,46 which has scarcely been applied for conductivity measurements of powders so far.47 The MCQP method enables probing the electric/dielectric properties of the sample under a contact-free fashion.
The aim of the present study was to evaluate the influence of the electrical conductivity of carbon supports and the role of the surface functional oxygen-bearing groups in the performance of the bare and cobalt–manganese spinel functionalized carbon supports acting as electrocatalysts in the ORR process.
Materials and methods
Carbon support and catalyst preparation
Mesoporous carbons were obtained by structural nano-replication using spherical silica (40–75 μm particle size, Supelco) as a template and sucrose (POCH) as a carbon precursor (more details are available in the ESI†). Prior to etching with HF, the template–precursor composites were carbonized at 650, 750, 850, 950 or 1050 °C for 4 h. The resultant carbon supports are denoted as C-SPH_x, where x corresponds to the carbonization temperature, e.g., C-SPH_650. The electrocatalysts based on the manganese–cobalt spinel (Mn–Co) active phase deposited on the obtained mesoporous carbon supports (C-SPH) were prepared using a one-pot microwave-assisted hydrothermal method14 (see the ESI† for more details). The obtained catalysts are labeled as, e.g., Mn–Co/C-SPH_650.Physicochemical characterization methods
The as-prepared catalytic and reference materials were characterized for their phase structure and crystallinity by X-ray powder diffraction. The XRD patterns of the C-SPH samples and the supported Mn–Co spinel catalysts were obtained using Bruker D2 Phaser and Rigaku MiniFlex diffractometers, respectively. The surface area and porosity of the synthesized carbon replicas were determined based on low-temperature nitrogen adsorption–desorption isotherms, collected at −196 °C using a Micromeritics ASAP 2020 instrument. In order to assess the degree of graphitization of the obtained C-SPH samples and to determine the spinel-to-carbon support mass ratio, thermogravimetric (TGA) measurements of the mass changes of the examined materials were performed. The analysis was conducted by means of a SDT Q600 thermo-balance (TA Instruments) and a Mettler Toledo instrument (TGA/DSC1). Temperature-programmed desorption (TPD) measurements were performed up to 800 °C in a flow of helium. Evolving CO and CO2 were analyzed on-line using a quadrupole mass spectrometer (PREVAC). Raman measurements were carried out under ambient conditions using a Renishaw InVia spectrometer equipped with a Leica DMLM confocal microscope and a CCD detector. The surface composition of the synthesized samples was studied by means of X-ray photoelectron spectroscopy (XPS) using a Prevac photoelectron spectrometer equipped with a hemispherical analyzer (VG SCIENTA R3000). The elemental composition of the samples (Mn/Co ratio) was determined by the X-ray fluorescence method (XRF) using an ARL Quant'X (Thermo Science) spectrometer equipped with the commercial UniQuant analysis software. For quantitative analysis, calibration was performed for pure cobalt and manganese oxides. Diffuse reflectance spectra were collected in the range of 200–2000 nm using a UV-vis-IR spectrophotometer (Shimadzu UV-3600) equipped with a 15 cm diameter integrating sphere. The morphology of the Mn–Co/C-SPH_850 sample was examined with the use of a FEI Tecnai Osiris microscope. More experimental details are available in the ESI.†The relative electrical conductivity of the carbon materials was measured using the microwave cavity Q-factor perturbation technique. The measurement is based on the changes of quality factor of the loaded (Qs) vs. empty (Q0) microwave cavity operating at the resonance frequency ν0.
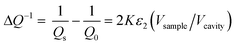 | (1) |
A quartz tube (4 mm inner diameter) sealed on one side was put into the microwave cavity (microwave frequency Q-meter, QWED, Poland) and the initial quality factor (Q0) was recorded. Next, 50 mg of the examined sample was put into the tube and pressed to obtain the same height of the sample in the tube each time (ca. 2 cm). The filled tube was placed again in the microwave cavity to measure the Qs value.
RRDE measurements
The electrocatalytic activity of the obtained materials towards the ORR was determined using an Autolab PGSTAT 302 N potentiostat and the rotating ring disk electrode (RRDE) method. The electrochemical measurements were conducted in a standard three-electrode electrochemical cell equipped with a glassy carbon disk working electrode, concentrically surrounded by a platinum ring (GCE-Pt, surface area GCE = 0.1256 cm2), a Pt wire counter electrode, and an Ag/AgCl reference electrode. The electrolyte was a 0.1 M KOH aqueous solution saturated with either O2 or Ar by bubbling the corresponding gas prior to each experiment and then during the tests. In order to obtain an electrochemically clean and stable catalyst surface, a modified working electrode, prepared according to the procedure described in the ESI† in detail, was activated by performing several full voltammetric potential cycles in the potential range from 0 to 1.2 V vs. RHE (reversible hydrogen electrode) in an Ar-saturated electrolyte (at 100 mV s−1) until stable results were obtained. The electrochemical properties of the obtained materials were determined by cyclic voltammetry (CV). The measurements were carried out in a deoxygenated 0.1 M KOH electrolyte at a scan rate of 10 mV s−1. The ORR activity of the prepared materials was tested in an O2-saturated KOH solution using linear-sweep voltammetry (LSV) at a scan rate of 5 mV s−1 on the disc electrode, while the constant potential of 1.2 V vs. RHE was applied to the ring electrode, with several rotating speeds ranging between 800 and 2000 rpm. The applied potential ranges were iR-corrected and converted to the RHE scale. The registered currents were normalized to the geometric area of the electrode and additionally corrected to the background currents measured in an Ar atmosphere. The onset potential values were determined as the potential at the current density of −0.1 mA cm−2 for the measurement with electrode spinning at 1600 rpm.Results and discussion
Physicochemical characterization of carbon supports
The results of the XRD measurements for the carbon C-SPH series, summarized in Fig. S1A,† revealed the highly amorphous character of the investigated materials. Nevertheless, for each sample two broad reflections at 2θ ∼23° and ∼44° are visible and are associated with the (002) and (101) lattice planes of the hexagonal graphite domains, respectively.48–50 Furthermore, the degree of carbon graphitization/crystallinity increases with the calcination temperature, as revealed by the decrease of the FWHM values of the observed peaks.In order to determine the textural parameters of the synthesized carbon materials, N2 adsorption measurements were performed. The obtained materials exhibit a distinct micro-mesoporous character, as implied by the shape of their isotherms that belong to type IV(a) according to the IUPAC classification (Fig. S1B†).51,52 The observed hysteresis loop can be classified as type H2(b), which indicates that the distribution of the neck widths is relatively large. The desorption branch reveals that pore shapes are rather of a slit than a cylindrical type. The isotherms at lower relative pressures indicate a small contribution of micropores with narrow diameters, as can be inferred from the distinct sharpness of the inflection point. The BET surface area determination was performed following the IUPAC criteria,52 and the obtained results together with the pore volumes are collated in Table 1. Remarkably, the determined textural parameters are very similar for all samples, and only a negligible decrease in their values with rising carbonization temperature was observed. The observed similarity of the textural parameters is beneficial for further investigations into the influence of electrical conductivity on the ORR performance, as the effect of the porosity variation is minimized thereby.
| T carbonization/°C | Textural parameters | Ratio of the Raman integral intensities | ||||
|---|---|---|---|---|---|---|
| S BET /m2 g−1 | V total /cm3 g−1 | V micro /cm3 g−1 | V meso /cm3 g−1 | I D3/IG | I D1/IG | |
| a S BET – specific surface area determined using the BET model. b Total pore volume (Vtotal), micropore volume (Vmicro) and mesopore volume (Vmeso) calculated using one-point, t-plot and BJH models, respectively. | ||||||
| 650 | 1446 | 2.935 | 0.155 | 2.780 | 1.799 | 2.759 |
| 750 | 1439 | 3.270 | 0.163 | 3.107 | 1.164 | 2.462 |
| 850 | 1406 | 3.098 | 0.161 | 2.937 | 1.063 | 2.362 |
| 950 | 1412 | 3.372 | 0.167 | 3.205 | 1.058 | 2.519 |
| 1050 | 1396 | 3.281 | 0.173 | 3.108 | 0.894 | 2.605 |
The degree of graphitization was also investigated by the TGA method by monitoring the temperature of the oxidation onset (Fig. S1C†).53 The oxidation temperature for the particular samples increases in the following order: C-SPH_650 < C-SPH_750 < C-SPH_850 < C-SPH_950 < C-SPH_1050, indicating an increase in the crystallinity of graphitic domains that are most resistant to oxidation as the carbonization temperature increases. Furthermore, the TGA analysis revealed that the obtained mesoporous spherical carbons contain no silica residue or only in trace amounts. The corroborative UV-vis measurements (Fig. S2†) allowed for the determination of the optical bandgaps of the synthetized carbon materials, which decrease from 0.74 eV to 0.62 eV as the carbonization temperature increases from 650 °C to 1050 °C (Table S1†). Using an empirical formula published elsewhere54 (see the ESI†), the average number of aromatic rings in the graphitic domains was calculated. This number increases with the carbonization temperature from less than nine hundred (C-SPH_650) up to above five thousand (C-SPH_1050) (Fig. S3†). All these results are self-consistent and indicate definitely better carbon support crystallinity when it is obtained at higher temperature, in good agreement with earlier literature reports.26
Raman spectra show two dominant bands at ∼1340 cm−1 and ∼1590 cm−1, characteristic of carbon materials (Fig. S4A†).55 Due to their complexity, the obtained spectra were next deconvoluted into five individual components of mixed Lorentzian and Gaussian shape (Fig. S4B–F†). The resultant bands were assigned to a well-developed graphitic lattice (G, 1579 cm−1), graphene edges (D1, 1339 cm−1), graphene planes (D2, 1601 cm−1), amorphous carbon (D3, 1492 cm−1) and a disordered graphitic lattice (D4, 1206 cm−1). Depending on the carbonization temperature, changes in the relative contribution of the individual bands were observed. Based on the integral intensities of the individual components, the degree of graphitization (inversely proportional to ID1/IG) and the relative content of the amorphous carbon (directly proportional to ID3/IG) in the investigated materials were determined,14,55,56 and the results are summarized in Table 1.
In general, the obtained data confirm an increase in the degree of the C-SPH graphitization and a simultaneous decrease in the content of the amorphous carbon fraction with increasing carbonization temperature. Furthermore, based on the ID1/IG ratio that is related to the degree of disorder in the crystalline structure of carbonaceous materials, a higher content of structural defects was determined for the C-SPH_950 and C-SPH_1050 samples calcined at the highest temperatures.33 It may also correspond to the presence of some oxygen-bearing entities on the surface of the heat-treated carbon materials, produced spontaneously during the cooling to ambient temperature. Indeed, according to the literature, it is presumed that surface defects arising upon removal of the oxygen during heat treatment constitute active sites for oxygen re-adsorption as soon as the heat-treated carbon materials come into contact with the atmosphere.57,58
The presence of surface oxygen functional groups was confirmed by XPS analysis of the C-SPH samples (Fig. S5†). The total oxygen content was found to be relatively small for all the examined carbon materials and varied in the range from ∼1.7% to ∼3% (Table 2).
| E/eV | C-SPH_650/at% | C-SPH_750/at% | C-SPH_850/at% | C-SPH_950/at% | C-SPH_1050/at% | |
|---|---|---|---|---|---|---|
| 284.4 | C 1s | 96.98 | 97.81 | 98.27 | 97.88 | 98.11 |
| O 1s | 3.02 | 2.19 | 1.73 | 2.12 | 1.89 | |
| 530.7 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
0.47 | 0.35 | 0.28 | 0.37 | 0.18 |
| 532.6 | C–![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) H, C H, C![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) OH OH |
1.69 | 1.52 | 1.10 | 1.35 | 1.38 |
| 533.8 | CO![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) H H |
0.63 | 0.32 | 0.35 | 0.40 | 0.33 |
| 535.9 | H2O | 0.23 | — | — | — | — |
Deconvolution of the O 1s spectrum exhibited the presence of four types of surface oxygen species, identified as carbonyl groups (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, 530.7 eV), hydroxyl groups (C–
O, 530.7 eV), hydroxyl groups (C–![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) H), oxygen atoms double bonded to carbon atoms in carboxyl groups (C
H), oxygen atoms double bonded to carbon atoms in carboxyl groups (C![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) OH, 532.6 eV), oxygen atoms single bonded to carbon atoms in carboxyl groups (CO
OH, 532.6 eV), oxygen atoms single bonded to carbon atoms in carboxyl groups (CO![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) H, 533.8 eV), and oxygen atoms in the adsorbed water molecules (H2O, 535.9 eV).58–60
H, 533.8 eV), and oxygen atoms in the adsorbed water molecules (H2O, 535.9 eV).58–60
The TPD measurements allowed us to quantify the amount of the particular surface oxygen-containing functional groups in the C-SPH samples. CO appears as a product of the decomposition of the surface carbonyl/quinone species at high temperatures as well as phenols and anhydrides at slightly lower temperatures. CO2 is formed by decomposition of carboxylic functional groups in a low-temperature region, and lactones/anhydrides at higher temperatures.61,62 The m/z lines of 28 (CO) and 44 (CO2) collected during the TPD study are presented in Fig. S6A and B in the ESI,† respectively. The peaks originating from the decomposition of the carbonyl/quinone and carboxylic functional groups (that are crucial for the discussed ORR, see below) are observed at 707–792 °C (CO profiles) and 277–383 °C (CO2 profiles), respectively. As expected, the peaks observed at other temperatures confirm the presence of additional oxygen functional groups like phenols, anhydrides and lactones. In order to evaluate the amount of the particular oxygen-bearing entities, the obtained TPD profiles were deconvoluted and integrated. The results of the analysis are summarized in Table 3. The highest amount of carbonyls/quinones was found for the sample carbonized at 650 °C (100 μmol g−1), and it decreases with increasing carbonization temperature. The amount of carboxylic groups is rather constant (89–114 μmol g−1) regardless of the carbonization conditions. The latter finding is apparently not fully compatible with the XPS results. However, one should take into account that whereas the TPD technique probes the entire sample, XPS is limited to its near surface region only. As a consequence, the results collected by these techniques in many cases described in the literature are quite divergent.59–61 In general, the total amount of evolved CO and CO2 decreases with rising carbonization temperature: for CO from 381 to 83 μmol g−1 and for CO2 from 408 to 257 μmol g−1 (cf.Table 3).
| Sample | CO (carbonyls/quinones) | CO2 (carboxylic groups) | ||||
|---|---|---|---|---|---|---|
| T | A | S | T | A | S | |
| a Temperature of the peak maximum/maxima (°C). b Amount of particular surface oxygen functional group (μmol g−1). c Total amount of evolved CO/CO2. | ||||||
| C-SPH_650 | 758 | 100 | 381 | 274–366 | 109 | 408 |
| C-SPH_750 | 792 | 48 | 191 | 280–375 | 90 | 329 |
| C-SPH_850 | 767 | 40 | 120 | 277–379 | 97 | 254 |
| C-SPH_950 | 707 | 8 | 87 | 288–384 | 89 | 222 |
| C-SPH_1050 | 784 | 11 | 83 | 282–372 | 114 | 257 |
The changes in the relative electrical conductivity of the examined carbon materials as a function of the calcination temperature are presented in Fig. 1. Obviously, higher carbonization temperature promotes the graphitization of the samples and therefore enhances their electrical conductivities. Vulcan XC-72R carbon was used as a reference here. Its measured ΔQ−1 value is equal to 1.49 × 10−4, which corresponds to the electrical conductivity of 2.77 S cm–1.44 Thus, the electrical conductivities of the investigated materials differ by three orders of magnitude, and the extreme values correspond to 10−2 S cm−1 for the sample obtained at 650 °C and to 101 S cm−1 for that carbonized at 1050 °C.
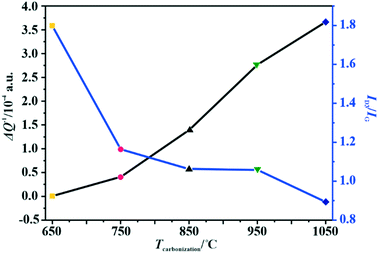 | ||
| Fig. 1 Variation of the amorphous carbon content determined by Raman spectroscopy and the relative electrical conductivity (MCPT) with the carbonization temperature of the C-SPH carbon supports. | ||
As implied in Fig. 1, the electrical conductivity of the calcined carbon support increases with increasing carbonization temperature, in parallel with the increasing support crystallinity, as can be inferred from the TGA, UV and Raman measurements. Thus, the electrical conductivity is a good descriptor of the overall crystallinity of carbon materials as well.
Physicochemical characterization of catalysts
The phase structure of the spinel catalysts was confirmed by XRD measurements (Fig. 2A). The observed reflections are assigned to the crystalline manganese–cobalt spinel cubic Fd3m structure (ICDD 23-1237).63 The carbon support exhibits a wide peak at ∼25°, which corresponds to the graphite (002) plane.64 The apparent broadening of the diffraction peaks indicates the nanometric character of the dispersed spinel phase. The average size of the crystallites for each sample, estimated by means of the Scherrer formula, is presented in Table 4.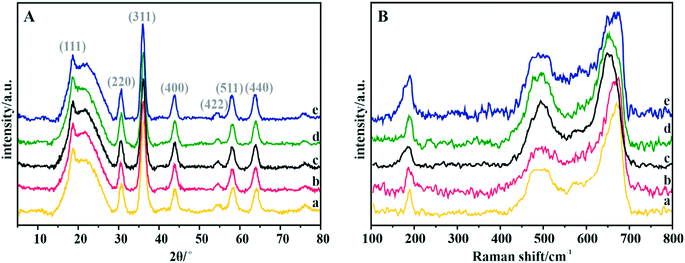 | ||
| Fig. 2 (A) XRD patterns and (B) Raman spectra of the Mn–Co spinel deposited on the C-SPH carbon supports, carbonized at different temperatures: (a) 650, (b) 750, (c) 850, (d) 950, and (e) 1050 °C. | ||
| Catalyst | D Scherrer/nm | Spinel loading on carbon support (TGA)/wt% | XRF elemental composition/at% | Spinel empirical formula | |
|---|---|---|---|---|---|
| Mn | Co | ||||
| Mn–Co/C-SPH_650 | 7 | 14 | 22 | 78 | Mn0.66Co2.34O4 |
| Mn–Co/C-SPH_750 | 7 | 19 | 22 | 78 | Mn0.66Co2.34O4 |
| Mn–Co/C-SPH_850 | 7 | 18 | 24 | 76 | Mn0.72Co2.28O4 |
| Mn–Co/C-SPH_950 | 7 | 16 | 23 | 77 | Mn0.69Co2.31O4 |
| Mn–Co/C-SPH_1050 | 8 | 20 | 23 | 77 | Mn0.69Co2.31O4 |
The Raman spectra confirm the manganese–cobalt spinel crystal structure and the absence of any spurious oxide phases65,66 (Fig. 2B).
In the case of bare Co3O4, the Raman spectra exhibit five bands at 194, 477, 517, 615 and 685 cm−1, which correspond to the Eg, 3F2g and A1g vibrational modes. The bands in the range of 600–700 cm−1 correspond to the vibrations of oxygen atoms in the Co–O6 octahedral positions, while the band at 194 cm−1 is associated with the Co–O4 vibrations in the tetrahedral sites.67 The Raman spectra of the manganese–cobalt spinel samples show only three intense bands (∼189, 494 and 663 cm−1), which are related to the incorporation of Mn into the Co3O4 lattice, leading to broadening and shifting in the peak positions towards the lower wavenumber.65,66 In particular, the observed changes in the shape and position of the A1g band indicate a successful substitution of Mn3+ for the octahedral Co3+ ions. To reveal the dispersion, elemental composition, and morphology of the oxide active phase detailed microscopic (HR) TEM, HAADF STEM, and EDX analyses for the Mn–Co/C-SPH_850 sample were performed (Fig. S7†). Both TEM and STEM analyses (Fig. S7A and B,† respectively) show that nanometric spinel particles are well dispersed on the carbon support. The HR TEM image (Fig. S7A,† inset) shows polyhedral cobalt–manganese spinel crystallites with a Mn/Co ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (determined from EDX) and a size less than 10 nm. EDX mapping (Fig. S7C†) confirmed the lack of segregation of cobalt and manganese. The elemental composition of the obtained manganese–cobalt spinels was determined by the XRF method (Table 4).
3 (determined from EDX) and a size less than 10 nm. EDX mapping (Fig. S7C†) confirmed the lack of segregation of cobalt and manganese. The elemental composition of the obtained manganese–cobalt spinels was determined by the XRF method (Table 4).
For all investigated materials, the Mn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Co mass ratios are in good agreement with the expected values. The amount of Mn–Co spinel deposited on the carbon supports was determined by the TGA method (Fig. S8†), and the results are listed in Table 4. The obtained TG profiles show a similar trend, with small differences for the individual samples. The main weight loss of ∼80%, which starts in the temperature range of about 300–325 °C, related to oxidation of the carbon support, is similar for all the examined catalysts and confirms the expected spinel loading.
Co mass ratios are in good agreement with the expected values. The amount of Mn–Co spinel deposited on the carbon supports was determined by the TGA method (Fig. S8†), and the results are listed in Table 4. The obtained TG profiles show a similar trend, with small differences for the individual samples. The main weight loss of ∼80%, which starts in the temperature range of about 300–325 °C, related to oxidation of the carbon support, is similar for all the examined catalysts and confirms the expected spinel loading.
Electrochemical characterization
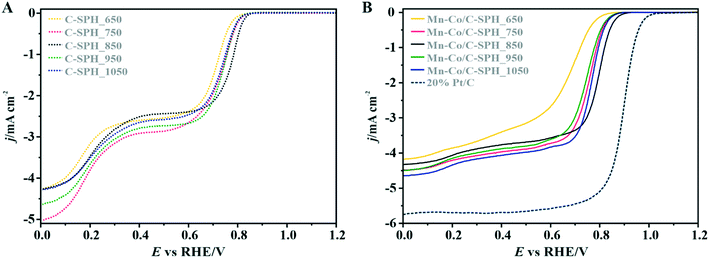
In order to identify active redox pairs of the investigated materials, the CV curves were measured in an Ar-saturated 0.1 M KOH solution (Fig. S9†). The observed high capacitive currents for each tested sample are related to the large specific surface area of the used carbon supports. Furthermore, the presence of surface oxygen species is responsible for the surface pseudo-capacitive phenomena, which lead to enhancement of the capacitive currents.33,68 As can be seen in Fig. S9A,† humps representing the faradaic reactions, which are attributed to reduction/oxidation of the surface groups, are observed at the potential range of 0.3–0.7 V vs. RHE for all the tested C-SPH samples. In the case of the catalysts with the spinel active phase deposited on the C-SPH supports (Fig. S9B†), the observed well-defined redox peaks correspond to the valence state changes associated with the Co2+/Co3+ oxidation (0.9–1.23 V vs. RHE), Mn3+/Mn2+ reduction (0.4–0.7 V vs. RHE) and Mn2+/Mn3+ oxidation (0.65–0.8 V vs. RHE).69,70 The absence of a Co3+/Co2+ reduction peak and asymmetry in the anodic and cathodic current densities of the manganese redox pairs suggest quasi-reversibility or irreversibility of the involved redox processes.71The electrocatalytic activity of the obtained bare carbon supports and the Mn–Co spinel supported catalysts in the ORR was evaluated by RRDE measurements in an O2-saturated 0.1 M KOH aqueous solution at room temperature (Fig. 3).
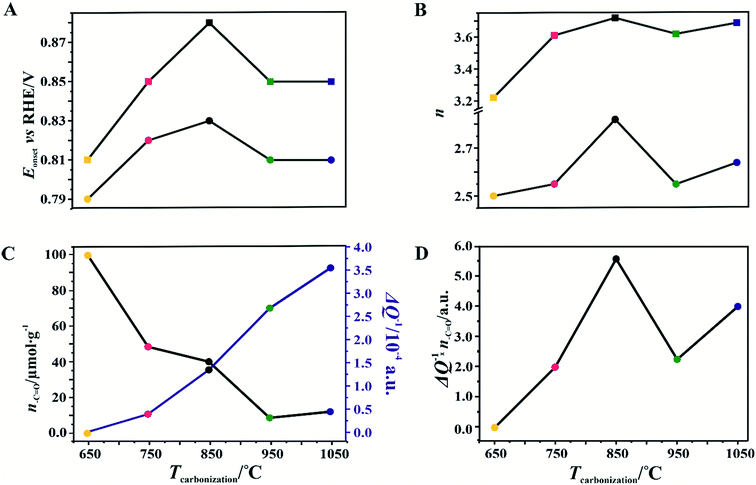
As a reference, a commercial platinum catalyst (20 wt% Pt/Vulcan XC-72) was used. The recorded LSV curves for the C-SPH samples, presented in Fig. 3A, are characterized by a similar shape, indicating the kinetic limitation of the process even at high overpotentials. The onset potential of the ORR (Eonset), which is defined as the threshold potential at which the current density of 0.1 mA cm−2 is generated in a steady-state RRDE/RDE experiment,72 changes in the following order: C-SPH_650 (0.79 V) < C-SPH_950 = C-SPH_1050 (0.81 V) < C-SPH_750 (0.82 V) < C-SPH_850 (0.83 V).
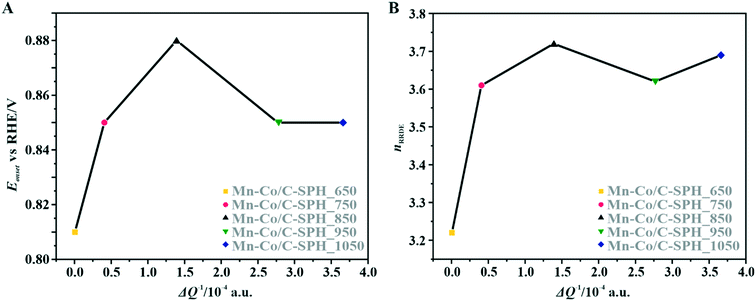
The correlation of the onset potential versus the electrical conductivity of carbon supports exhibits a volcano-type dependence, with the maximum corresponding to the C-SPH_850 (0.83 V) sample (Fig. 4).
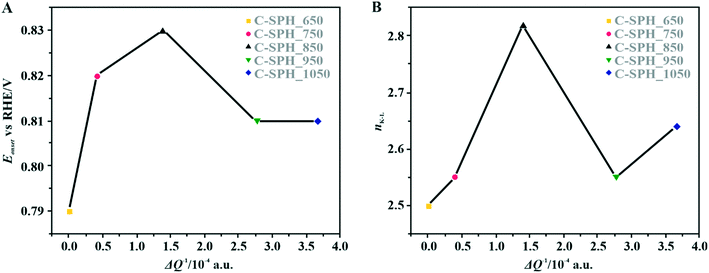 | ||
| Fig. 4 Correlation between the electrical conductivity of the C-SPH carbon supports and the reduction onset potential (A) and the number of transferred electrons, calculated based on K–L plots (B). | ||
Apparently, the electrical conductivity of the sample is not the sole factor that actually determines its electrocatalytic behavior. Indeed, the relatively high activity of the tested carbon materials has been related to the presence of the surface oxygen groups73 (vide infra). In addition, two characteristic reduction waves were registered for each of the C-SPH supports. This corresponds to the changes in the oxygen reduction pathway with the decreasing potential. The carbon materials are able to electro-reduce oxygen to peroxide, mainly through a two-electron pathway in an alkaline environment. However, at the more negative potentials, a fraction of the produced HO2− intermediates could be further reduced to O2−, augmenting the contribution of the sequential (2e− + 2e−) reaction pathway to the whole reduction process.73 This was confirmed by means of K–L analysis (for more details see the ESI,† Fig. S10), which indicated that at the pre-wave potentials values of n close to 2 were observed, whereas for potentials ≤0.2 V vs. RHE, the number of the transferred electrons is increased. For the Mn–Co/C-SPH_750, Mn–Co/C-SPH_850, Mn–Co/C-SPH_950 and Mn–Co/C-SPH_1050 samples, similar potentiodynamic ORR profiles were observed, with maximum current densities of around 4.5 mA cm−2 (Fig. 3B). In the case of these catalysts, at the potential below ∼0.55 V vs. RHE a diffusion-controlled electron transfer process dominates, while a mixed kinetic-diffusion region appears in the potential range between 0.55 and 0.8 V vs. RHE. The kinetic control region (independent of the rotation rate) takes place at more positive potentials (above 0.8 V vs. RHE). A different slope in the mixed kinetic-diffusion control region compared to the other samples was recorded for the Mn–Co/C-SPH_650 sample, with a lower maximum current density of ∼4 mA cm−2. In order to define the performance of the ORR catalysts based on the registered LSV curves, the onset and the half-wave (E1/2) potentials were used as concise descriptor parameters. As summarized in Table 5, the Mn–Co/C-SPH_850 catalyst outperformed all the other samples in terms of the Eonset (0.88 V vs. RHE) and E1/2 (0.78 V vs. RHE) values. In the case of this catalyst, the observed reduction potential is negatively shifted compared to the commercial Pt/C by about 100 mV. Among the tested catalysts, the Mn–Co/C-SPH_650 sample showed the lowest activity, with Eonset and E1/2 equal to 0.81 and 0.66 V vs. RHE, respectively. The obtained results are comparable to the behavior of similar electrocatalysts based on transition metal oxides published previously.14,74,75 Additionally, the ORR activities of the supported manganese–cobalt catalysts are higher, in comparison to the corresponding supports alone. The Tafel plot, presented in Fig. 5, was used to elucidate the ORR kinetics. The Tafel slopes were calculated for all the investigated catalysts (Table 5), taking into account the mass transport correction for calculation of the kinetic current density:76,77
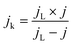 | (2) |
| Catalyst | E onset/V | E 1/2/V | n RRDE (0.1–0.5 V) | % HO2− (max) | Tafel slopea/mV dec−1 |
|---|---|---|---|---|---|
| a At the low overpotential region (∼0.88–0.75 V vs. RHE). | |||||
| 20% Pt/Vulcan XC-72 | 0.98 | 0.89 | 3.88 | 12 | 58.2 (ref. 14) |
| Mn–Co/C-SPH_650 | 0.81 | 0.66 | 3.22 | 41 | 73.3 |
| Mn–Co/C-SPH_750 | 0.85 | 0.75 | 3.61 | 20 | 53.4 |
| Mn–Co/C-SPH_850 | 0.88 | 0.78 | 3.72 | 14 | 52.6 |
| Mn–Co/C-SPH_950 | 0.85 | 0.73 | 3.62 | 20 | 57.6 |
| Mn–Co/C-SPH_1050 | 0.85 | 0.76 | 3.69 | 17 | 54.0 |
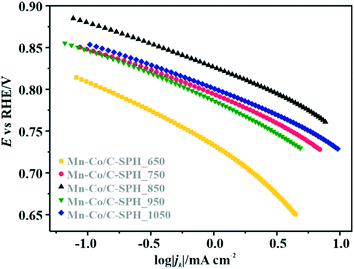 | ||
| Fig. 5 Tafel plots based on the data reported in Fig. 3B. | ||
The obtained results slightly varied between the individual samples, implying the presence of the same type of active sites capable of activating oxygen molecules. Due to the very low electrical conductivity of C-SPH_650, the Tafel slope for the Mn–Co spinel deposited on this carbon sample is considerably higher, reaching the value of ∼73 mV dec−1, which indicates transport limitations in the electron transfer. Moreover, an increase of the slope at higher overpotentials (∼0.78–0.73 V vs. RHE) is observed for each electrocatalyst (Mn–Co/C-SPH_650 ∼103 mV dec−1, Mn–Co/C-SPH_750 ∼87 mV dec−1, Mn–Co/C-SPH_850 ∼91 mV dec−1, Mn–Co/C-SPH_950 ∼85 mV dec−1 and Mn–Co/C-SPH_1050 ∼83 mV dec−1), which is usually associated with the change in the extent of surface coverage by the oxygen species.80,81
To investigate the ORR pathway on the obtained catalysts based on the recorded RRDE data, the number of the transferred electrons and the percentage of the HO2− species with respect to the total ORR products were calculated according to eqn (3)82 and (4),83 respectively:
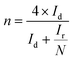 | (3) |
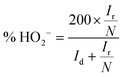 | (4) |
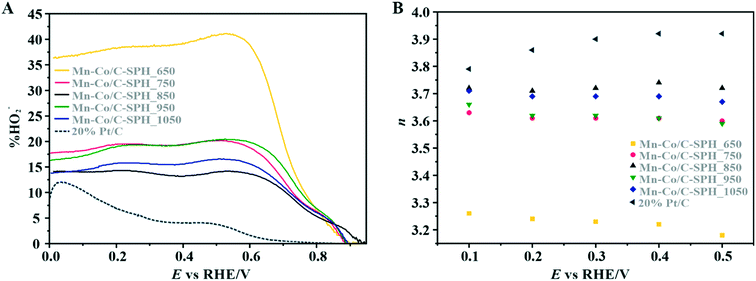
The data presented in Fig. 6A illustrate the amount (%) of HO2− formed during the ORR process versus the potential applied to the disk electrode at 800 rpm. Again, the 20 wt% Pt/C catalyst was also analyzed for the sake of comparison. In the case of the reference Pt/C catalyst, the beginning of the intermediate peroxide production is observed at the potential below 0.8 V vs. RHE and increases when it approaches the region of the hydrogen underpotential. This phenomenon is related to Pt–OH formation due to specific adsorption of hydroxide anions, with an outer-sphere electron transfer mechanism being involved.84 The maximum yield of the peroxide species observed for the 20 wt% Pt on Vulcan XC-72 sample was equal to ∼12%.
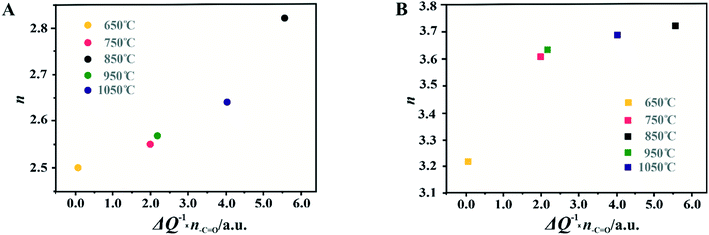
For the obtained spinel-based catalysts, production of the HO2− intermediate starts at the potential below 0.85 V vs. RHE and systematically increases until reaching the maximum values at around 0.55 V vs. RHE. According to the literature, the maximum yield of the peroxide species observed at this potential is associated with the carbon support, which itself catalyzes partial oxygen reduction through a two-electron pathway in an alkaline medium.84,85 The HO2− amount changes in the following order: Mn–Co/C-SPH_850 (∼14%) < Mn–Co/C-SPH_1050 (∼17%) < Mn–Co/C-SPH_750 (∼20%) < Mn–Co/C-SPH_950 (∼20%) < Mn–Co/C-SPH_650 (∼41%). The calculated average value of n was equal to 3.22 for Mn–Co/C-SPH_650, 3.61 for Mn–Co/C-SPH_750, 3.72 for Mn–Co/C-SPH_850, 3.62 for Mn–Co/C-SPH_950, and 3.69 for Mn–Co/C-SPH_1050 at the potential range between 0.1 and 0.5 V vs. RHE. In the considered potential window, the lowest amount of the HO2− intermediate, thus the highest number of transferred electrons, was observed for the Mn–Co spinel deposited on the C-SPH support carbonized at 850 °C, whereas the highest amount of HO2− species was detected in the case of Mn–Co/C-SPH_650, which reached a value about two times higher in comparison to all the other samples (Fig. 6B). The values of n <4 indicate that the ORR proceeds along two parallel pathways: by four- and two-electron reduction processes. Apart from the Mn–Co/C-SPH_650 sample of the lowest electrical conductivity, for the other catalysts the direct 4e− pathway dominates. The spinel catalyst dispersed on the carbon C-SPH_650 support carbonized at the lowest temperature (650 °C) is characterized by the smaller activity and selectivity in the oxygen reduction reaction, in comparison to the other investigated samples. It is related to the low electrical conductivity and thereby to the highly amorphous nature of this carbon material. It is usually considered that both parameters, the electrical conductivity and high crystallinity, significantly influence the catalyst activity in the ORR.14,26 The relations between the electrical conductivity and the ORR onset potential as well as the number of transferred electrons for the examined supported spinel catalysts are similar to those observed for the bare carbon supports (Fig. 7A and B).
A non-monotonic effect of the electrical conductivity of the carbon supports on the oxygen reduction reaction in alkaline media was detected with a distinct maximum for the sample calcined at 850 °C. A similar relationship between the catalytic activity and the carbonization temperature of the carbon support and its electrical conductivity (measured using a four-point probe) has recently been described for nitrogen-doped carbon materials elsewhere.86 The observed non-linear dependence of the catalyst activity with the carbonization temperature was explained therein by a decrease in the nitrogen content with increasing calcination temperature. However, in our carbon samples, there are no nitrogen or sulfur heteroatoms, as proved by the XPS measurements of the C-SPH_850 sample in the binding energy regions typical of nitrogen (N 1s, Fig. S11A†) and sulfur (S 2p, Fig. S11B†). Thus, only oxygen plays the role of a heteroatom. It implies that from the temperature-programmed desorption measurements the relative content and the ratio of the carboxyl, hydroxyl, and carbonyl groups in the examined carbon carries are sensibly derived. Following the literature,87 an electrophilic O2 molecule would preferentially adsorb at a nucleophilic carbon site with available labile electrons to be donated rather than to electron-deficient carbon atoms. Such sites of favorable O2 attachment are presumably created in the vicinity of the electron-withdrawing carboxyl and carbonyl groups, in line with the Garten and Weiss mechanism of the ORR on the quinone-functionalized graphitic carbon surface, confirmed later by Yeager.88 Taking into account such a conjecture, which is also supported by recent reports that enhanced ORR activity may be related to the formation of C–O bonds on the carbon surface,8,89 we used the content of carboxyl and quinone groups (denoted as –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) in the samples as another descriptor of the ORR activity of the oxygen-functionalized carbon materials, apart from the electrical conductivity (Fig. 8).
O) in the samples as another descriptor of the ORR activity of the oxygen-functionalized carbon materials, apart from the electrical conductivity (Fig. 8).
In the case of the support carbonized at 650 °C, the amount of –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups is the highest; however, the poor electrical conductivity of the carbon support resulted in low electrocatalytic activity (the smallest Eonset and n values). For the samples carbonized at temperatures from 650 to 850 °C, an increase in the electrical conductivity (more than one order of magnitude) correlates well with the concomitant boosting of the ORR performance for the spinel catalysts and the bare C-SPH supports. The highest activity is exhibited by the samples carbonized at 850 °C. Further increase of the carbonization temperature (950–1050 °C), despite steadily increasing electrical conductivity and the associated support crystallinity, leads to lowering of the catalyst activity, which is apparently congruent with a drop in the amount of the carboxyl and quinone groups in the examined samples. Such a non-monotonous behavior implies that once a sufficiently good electrical conductivity of the carbon material is achieved, surface oxygen functionalities (–C
O groups is the highest; however, the poor electrical conductivity of the carbon support resulted in low electrocatalytic activity (the smallest Eonset and n values). For the samples carbonized at temperatures from 650 to 850 °C, an increase in the electrical conductivity (more than one order of magnitude) correlates well with the concomitant boosting of the ORR performance for the spinel catalysts and the bare C-SPH supports. The highest activity is exhibited by the samples carbonized at 850 °C. Further increase of the carbonization temperature (950–1050 °C), despite steadily increasing electrical conductivity and the associated support crystallinity, leads to lowering of the catalyst activity, which is apparently congruent with a drop in the amount of the carboxyl and quinone groups in the examined samples. Such a non-monotonous behavior implies that once a sufficiently good electrical conductivity of the carbon material is achieved, surface oxygen functionalities (–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups) control the ORR activity. This statement is strongly supported by the data presented in Fig. 8D, where variation of the sample electrical conductivity multiplied by the amount of the carboxyl and quinone groups as a function of the carbon calcination temperature exhibits the same shape as the plot of the number of electrons exchanged in the ORR, showing that an optimal conjunction of both these properties plays a decisive role here. The role of the spinel nanocrystals supported on the carbon materials consists in enhancing the number of the transferred electrons by favoring the 4e− pathway of the reaction. As can be seen in Fig. 9A, in the case of the bare carbon samples, the number of exchange electrons strongly depends on the carbon conductivity and the content of the oxygen functional groups, reaching a distinct maximum for the sample calcinated at 850 °C. In the case of the spinel/carbon catalysts, the selectivity is controlled mostly by the presence of the manganese–cobalt spinel catalyst and improves only slightly with the product of the conductivity and the amount of the carboxyl/quinone groups, except for the sample obtained at 650 °C. The lowest selectivity and activity of the Mo–Co/C-SPH_650 catalyst is caused by the very low support conductivity, being two orders of magnitude smaller than for the other samples.
O groups) control the ORR activity. This statement is strongly supported by the data presented in Fig. 8D, where variation of the sample electrical conductivity multiplied by the amount of the carboxyl and quinone groups as a function of the carbon calcination temperature exhibits the same shape as the plot of the number of electrons exchanged in the ORR, showing that an optimal conjunction of both these properties plays a decisive role here. The role of the spinel nanocrystals supported on the carbon materials consists in enhancing the number of the transferred electrons by favoring the 4e− pathway of the reaction. As can be seen in Fig. 9A, in the case of the bare carbon samples, the number of exchange electrons strongly depends on the carbon conductivity and the content of the oxygen functional groups, reaching a distinct maximum for the sample calcinated at 850 °C. In the case of the spinel/carbon catalysts, the selectivity is controlled mostly by the presence of the manganese–cobalt spinel catalyst and improves only slightly with the product of the conductivity and the amount of the carboxyl/quinone groups, except for the sample obtained at 650 °C. The lowest selectivity and activity of the Mo–Co/C-SPH_650 catalyst is caused by the very low support conductivity, being two orders of magnitude smaller than for the other samples.
It is worth noting that the electrical conductivity of the carrier exhibits a greater effect on the number of electrons exchanged90 than on the Eonset value, which is manifested by a slight increase in the n value for the sample activated at 1050 °C, observed for both the bare support and the spinel catalyst.
Conclusions
A series of mesoporous carbon materials were obtained using spherical silica as a template and sucrose as a carbon precursor, followed by calcination at temperatures in the range of 650–1050 °C. It was shown that with the increasing carbonization temperature of the carbon support the electrical conductivity increased in parallel with the extent of crystallization. The electrocatalytic performance of the carbon carriers and the supported cobalt manganese spinels exhibits a volcano-type shape, reaching the maximum for carbon materials obtained at 850 °C. Such a dependence results from two descriptors changing in opposite ways with the carbonization temperature: an increasing electrical conductivity and a decreasing amount of carbonyl and quinone groups in the sample. The electrical conductivity multiplied by the amount of the carboxyl and quinone groups exhibits the same variation with the carbon calcination temperature as the number of electrons exchanged in the ORR, confirming that an optimal conjunction of both these properties plays a decisive role in this process. The dispersed spinel active phase favors the direct 4e− pathway of the ORR and improves the value of the Eonset potential distinctly. To the best of our knowledge, the role of electrical conductivity and surface oxygen functionalities in the ORR activity over carbon materials and supported spinel electrocatalysts was disentangled for the first time in this study.Author contributions
The manuscript was written through the contributions of all authors. All authors have approved the final version of the manuscript.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This work was supported by the Polish National Science Centre under grant no. 2017/27/B/ST5/01004. We would like to thank Dr. Joanna Gryboś for performing TEM experiments. The open-access publication of this article was funded by the Priority Research Area SciMat under the program “Excellence Initiative – Research University” at the Jagiellonian University in Krakow.References
- E. A. Astaf'ev, Russ. J. Electrochem., 2018, 54, 554–560 CrossRef.
- S. Gottesfeld, D. R. Dekel, M. Page, C. Bae, Y. Yan, P. Zelenay and Y. S. Kim, J. Power Sources, 2018, 375, 170–184 CrossRef CAS.
- D. R. Dekel, J. Power Sources, 2018, 375, 158–169 CrossRef CAS.
- D. R. Dekel, I. G. Rasin and S. Brandon, J. Power Sources, 2019, 420, 118–123 CrossRef CAS.
- Ł. Łańcucki and K. Kruczała, Polym. Degrad. Stab., 2014, 109, 327–335 CrossRef.
- Ł. Łańcucki, S. Schlick, M. Danilczuk, F. D. Coms and K. Kruczała, Polym. Degrad. Stab., 2013, 98, 3–11 CrossRef.
- S. Wierzbicki, J. C. Douglin, A. Kostuch, D. R. Dekel and K. Kruczała, J. Phys. Chem. Lett., 2020, 11, 7630–7636 CrossRef CAS PubMed.
- C. Ouyang, B. Ni, Z. Sun, J. Zhuang, H. Xiao and X. Wang, Chem. Sci., 2019, 10, 2118–2123 RSC.
- R. Shibuya, T. Kondo and J. Nakamura, Carbon-Based Metal-Free Catalysts: Design and Applications, I, ed. L. Dai, 2018, ch. 8, vol. 1–2, pp. 227–249 Search PubMed.
- L. Yang, D. Cheng, H. Xu, X. Zeng, X. Wan, J. Shui, Z. Xiang and D. Cao, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 6626–6631 CrossRef CAS PubMed.
- H. Wang, R. Liu, Y. Li, X. Lü, Q. Wang, S. Zhao, K. Yuan, Z. Cui, X. Li, S. Xin, R. Zhang, M. Lei and Z. Lin, Joule, 2018, 2, 337–348 CrossRef CAS.
- P. Sivakumar, P. Subramanian, T. Maiyalagan, A. Gedanken and A. Schechter, Mater. Chem. Phys., 2019, 229, 190–196 CrossRef CAS.
- R. Praats, M. Käärik, A. Kikas, V. Kisand, J. Aruväli, P. Paiste, M. Merisalu, A. Sarapuu, J. Leis, V. Sammelselg, J. C. Douglin, D. R. Dekel and K. Tammeveski, J. Solid State Electrochem., 2021, 25, 57–71 CrossRef CAS.
- A. Kostuch, J. Gryboś, P. Indyka, L. Osmieri, S. Specchia, Z. Sojka and K. Kruczała, Catal. Sci. Technol., 2018, 8, 642–655 RSC.
- L. Osmieri, R. Escudero-Cid, M. Armandi, A. H. A. Monteverde Videla, J. L. G. Fierro, P. Ocón and S. Specchia, Appl. Catal., B, 2017, 205, 637–653 CrossRef CAS.
- J. Lilloja, E. Kibena-Põldsepp, A. Sarapuu, J. C. Douglin, M. Käärik, J. Kozlova, P. Paiste, A. Kikas, J. Aruväli, J. Leis, V. Sammelselg, D. R. Dekel and K. Tammeveski, ACS Catal., 2021, 11, 1920–1931 CrossRef CAS.
- J. Tang, C. Su, Y. Zhong and Z. Shao, J. Mater. Chem. A, 2021, 9, 3151–3179 RSC.
- N. Ralbag, M. Mann-Lahav, E. S. Davydova, U. Ash, R. Galed, M. Handl, R. Hiesgen, E. Magliocca, W. Mustain, J. He, P. Cong, A. M. Beale, G. S. Grader, D. Avnir and D. R. Dekel, Matter, 2019, 1, 959–975 CrossRef.
- K. Kaare, I. Kruusenberg, M. Merisalu, L. Matisen, V. Sammelselg and K. Tammeveski, J. Solid State Electrochem., 2016, 20, 921–929 CrossRef CAS.
- P. Lang, N. Yuan, Q. Jiang, Y. Zhang and J. Tang, Energy Technol., 2020, 8, 1900984 CrossRef CAS.
- H. Wang and H. D. Abruña, Appl. Catal., B, 2020, 277, 119149 CrossRef CAS.
- W. Kiciński, B. Dembinska, M. Norek, B. Budner, M. Polański, P. J. Kulesza and S. Dyjak, Carbon, 2017, 116, 655–669 CrossRef.
- B. Dembinska and P. J. Kulesza, Electrochim. Acta, 2009, 54, 4682–4687 CrossRef CAS.
- J. Ho, Y. Li, Y. Dai, T. Kim, J. Wang, J. Ren, H. Yun and X. Liu, Int. J. Hydrogen Energy, 2021, 46, 20503–20515 CrossRef CAS.
- D. W. Wang and D. Su, Energy Environ. Sci., 2014, 7, 576–591 RSC.
- J. C. Li, D. M. Tang, P. X. Hou, G. X. Li, M. Cheng, C. Liu and H. M. Cheng, MRS Commun., 2018, 8, 1158–1166 CrossRef CAS.
- X. Bo, Y. Zhang, M. Li, A. Nsabimana and L. Guo, J. Power Sources, 2015, 288, 1–8 CrossRef CAS.
- F. Rodríguez-Reinoso, Carbon, 1998, 36, 159–175 CrossRef.
- A. Pendashteh, J. Palma, M. Anderson and R. Marcilla, Appl. Catal., B, 2017, 201, 241–252 CrossRef CAS.
- A. Kostuch, J. Gryboś, S. Wierzbicki, Z. Sojka and K. Kruczała, Materials, 2021, 14, 820 CrossRef CAS PubMed.
- W. Zhang, C. Yang, W. Liu, H. Wang, S. Wei, J. Qi, P. Bai, B. Jin and L. Xu, Appl. Catal., B, 2021, 293, 120199 CrossRef CAS.
- W. Y. Noh, J. H. Lee and J. S. Lee, Appl. Catal., B, 2020, 268, 118415 CrossRef CAS.
- D. Barrera, M. Florent, K. Sapag and T. J. Bandosz, ACS Appl. Energy Mater., 2019, 2, 7412–7424 CrossRef CAS.
- C. O. Ania, P. A. Armstrong, T. J. Bandosz, F. Beguin, A. P. Carvalho, A. Celzard, E. Frackowiak, M. A. Gilarranz, K. László, J. Matos and M. F. R. Pereira, Carbon, 2020, 164, 69–84 CrossRef CAS.
- M. Florent, R. Wallace and T. J. Bandosz, ChemCatChem, 2019, 11, 851–860 CrossRef CAS.
- A. H. A. Monteverde Videla, L. Zhang, J. Kim, J. Zeng, C. Francia, J. Zhang and S. Specchia, J. Appl. Electrochem., 2013, 43, 159–169 CrossRef CAS.
- K. Yokoyama, Y. Sato, M. Yamamoto, T. Nishida, K. Motomiya, K. Tohji and Y. Sato, Carbon N. Y., 2019, 142, 518–527 CrossRef CAS.
- J. S. Han, D. Y. Chung, D. G. Ha, J. H. Kim, K. Choi, Y. E. Sung and S. H. Kang, Carbon, 2016, 105, 1–7 CrossRef CAS.
- J. C. Li, X. Qin, P. X. Hou, M. Cheng, C. Shi, C. Liu, H. M. Cheng and M. Shao, Carbon, 2019, 147, 303–311 CrossRef CAS.
- J. H. Kim, J. Y. Cheon, T. J. Shin, J. Y. Park and S. H. Joo, Carbon, 2016, 101, 449–457 CrossRef CAS.
- Z. Lu, G. Chen, S. Siahrostami, Z. Chen, K. Liu, J. Xie, L. Liao, T. Wu, D. Lin, Y. Liu, T. F. Jaramillo, J. K. Nørskov and Y. Cui, Nat. Catal., 2018, 1, 156–162 CrossRef CAS.
- R. Paul, L. Zhu, H. Chen, J. Qu and L. Dai, Adv. Mater., 2019, 31, 1–24 Search PubMed.
- D. He, K. Cheng, T. Peng, X. Sun, M. Pan and S. Mu, J. Mater. Chem., 2012, 22, 21298–21304 RSC.
- S. Tang, G. Sun, J. Qi, S. Sun, J. Guo, Q. Xin and G. M. Haarberg, Chin. J. Catal., 2010, 31, 12–17 CrossRef CAS.
- H. Li, N. Cheng, Y. Zheng, X. Zhang, H. Lv, D. He, M. Pan, F. Kleitz, S. Z. Qiao and S. Mu, Adv. Energy Mater., 2013, 3, 1176–1179 CrossRef CAS.
- J. C. Slater, Rev. Mod. Phys., 1946, 18, 441–512 CrossRef.
- M. Eichelbaum, R. Stößer, A. Karpov, C.-K. Dobner, F. Rosowski, A. Trunschke and R. Schlögl, Phys. Chem. Chem. Phys., 2012, 14, 1302–1312 RSC.
- S. Rodrigues, M. Marques, I. Suárez-Ruiz, I. Camean, D. Flores and B. Kwiecinska, Int. J. Coal Geol., 2013, 111, 67–79 CrossRef CAS.
- D. H. Kwak, S. B. Han, Y. W. Lee, H. S. Park, I. A. Choi, K. B. Ma, M. C. Kim, S. J. Kim, D. H. Kim, J. I. Sohn and K. W. Park, Appl. Catal., B, 2017, 203, 889–898 CrossRef CAS.
- X. Chen, X. Deng, N. Y. Kim, Y. Wang, Y. Huang, L. Peng, M. Huang, X. Zhang, X. Chen, D. Luo, B. Wang, X. Wu, Y. Ma, Z. Lee and R. S. Ruoff, Carbon, 2018, 132, 294–303 CrossRef CAS.
- K. S. W. Sing, D. H. Everett, R. A. W. Haul, L. Moscou, R. A. Pierotti, J. Rouquerol and T. Siemieniewska, Pure Appl. Chem., 1985, 57, 603–619 CAS.
- M. Thommes, K. Kaneko, A. V. Neimark, J. P. Olivier, F. Rodriguez-Reinoso, J. Rouquerol and K. S. W. Sing, Pure Appl. Chem., 2015, 87, 1051–1069 CAS.
- H. Bi, K. C. Kou, K. Ostrikov and J. Q. Zhang, J. Appl. Phys., 2008, 104, 1–7 CrossRef.
- H. A. Michelsen, Proc. Combust. Inst., 2017, 36, 717–735 CrossRef CAS.
- A. Sadezky, H. Muckenhuber, H. Grothe, R. Niessner and U. Pöschl, Carbon, 2005, 43, 1731–1742 CrossRef CAS.
- M. Lezańska, P. Pietrzyk, A. Dudek and J. Włoch, Mater. Chem. Phys., 2015, 149, 539–552 CrossRef.
- J. A. Menéndez, J. Phillips, B. Xia and L. R. Radovic, Langmuir, 1996, 12, 4404–4410 CrossRef.
- H. Darmstadt, C. Roy, S. Kaliaguine, S. J. Choi and R. Ryoo, Carbon, 2002, 40, 2673–2683 CrossRef CAS.
- P. Niebrzydowska, R. Janus, P. Kuśtrowski, S. Jarczewski, A. Wach, A. M. Silvestre-Albero and F. Rodríguez-Reinoso, Carbon, 2013, 64, 252–261 CrossRef CAS.
- J. L. Figueiredo and M. F. R. Pereira, Catal. Today, 2010, 150, 2–7 CrossRef CAS.
- J. L. Figueiredo, M. F. R. Pereira, M. M. A. Freitas and J. J. M. Órfão, Carbon, 1999, 37, 1379–1389 CrossRef CAS.
- G. Hotová, V. Slovák, O. S. G. P. Soares, J. L. Figueiredo and M. F. R. Pereira, Carbon, 2018, 134, 255–263 CrossRef.
- A. Restovic, E. Rios, S. Barbato, J. Ortiz and J. L. Gautier, J. Electroanal. Chem., 2002, 522, 141–151 CrossRef CAS.
- Z. Yang, X. Zhou, H. Nie, Z. Yao and S. Huang, ACS Appl. Mater. Interfaces, 2011, 3, 2601–2606 CrossRef CAS PubMed.
- F. Kovanda, T. Rojka, J. Dobešová, V. MacHovič, P. Bezdička, L. Obalová, K. Jirátová and T. Grygar, J. Solid State Chem., 2006, 179, 812–823 CrossRef CAS.
- P. L. Meena, S. Pal, K. Sreenivas and R. A. Kumar, Adv. Sci. Lett., 2015, 21, 2760–2763 CrossRef.
- V. G. Hadjiev, M. N. Iliev and I. V. Vergilov, J. Phys. C: Solid State Phys., 1988, 21, L199–L201 CrossRef.
- L. Osmieri, A. M. Videla and S. Specchia, Int. J. Hydrogen Energy, 2015, 41, 19610–19628 CrossRef.
- E. Lee, J.-H. Jang and Y.-U. Kwon, J. Power Sources, 2015, 273, 735–741 CrossRef CAS.
- Y. Wang, X. Ma, L. Lu, Y. He, X. Qi and Y. Deng, Int. J. Hydrogen Energy, 2013, 38, 13611–13616 CrossRef CAS.
- A. N. Naveen and S. Selladurai, Electrochim. Acta, 2014, 125, 404–414 CrossRef CAS.
- G. Wu, K. L. More, C. M. Johnston and P. Zelenay, Science, 2011, 332, 443–447 CrossRef CAS PubMed.
- I. Kruusenberg, J. Leis, M. Arulepp and K. Tammeveski, J. Solid State Electrochem., 2010, 14, 1269–1277 CrossRef CAS.
- T. Sönmez, S. J. Thompson, S. W. T. Price, D. Pletcher and A. E. Russell, J. Electrochem. Soc., 2016, 163, 884–890 CrossRef.
- X. Cao, C. Jin, F. Lu, Z. Yang, M. Shen and R. Yang, J. Electrochem. Soc., 2014, 161, H296–H300 CrossRef CAS.
- J. Masa, C. Batchelor-McAuley, W. Schuhmann and R. G. Compton, Nano Res., 2014, 7, 71–78 CrossRef CAS.
- H. A. Gasteiger, S. S. Kocha, B. Sompalli and F. T. Wagner, Appl. Catal., B, 2005, 56, 9–35 CrossRef CAS.
- P. W. Menezes, A. Indra, N. R. Sahraie, A. Bergmann, P. Strasser and M. Driess, ChemSusChem, 2015, 8, 164–167 CrossRef CAS PubMed.
- Y. Liang, Y. Li, H. Wang, J. Zhou, J. Wang, T. Regier and H. Dai, Nat. Mater., 2011, 10, 780–786 CrossRef CAS PubMed.
- S. Gottesfeld, ECS Trans., 2014, 61, 1–13 CrossRef CAS.
- F. H. B. Lima, M. L. Calegaro and E. A. Ticianelli, J. Electroanal. Chem., 2006, 590, 152–160 CrossRef CAS.
- E. Claude, T. Addou, J. Latour and P. Aldebert, J. Appl. Electrochem., 1998, 28, 57–64 CrossRef CAS.
- M. Bron, P. Bogdanoff, S. Fiechter, I. Dorbandt, M. Hilgendorff, H. Schulenburg and H. Tributsch, J. Electroanal. Chem., 2001, 500, 510–517 CrossRef CAS.
- N. Ramaswamy and S. Mukerjee, Adv. Phys. Chem., 2021, 491604 Search PubMed.
- L. Osmieri, A. H. A. Monteverde Videla, M. Armandi and S. Specchia, Int. J. Hydrogen Energy, 2016, 41, 22570–22588 CrossRef CAS.
- M. Gehring, H. Tempel, A. Merlen, R. Schierholz, R. A. Eichel and H. Kungl, RSC Adv., 2019, 9, 27231–27241 RSC.
- L. R. Radovic, F. Beguin and E. Frackowiak, Carbons for Electrochemical Energy Storage and Conversion Systems, 2010 Search PubMed.
- E. Yeager, J. Mol. Catal., 1986, 38, 5–25 CrossRef CAS.
- H. Zhang, K. Lv, B. Fang, M. C. Forster, R. Dervişoğlu, L. B. Andreas, K. Zhang and S. Chen, Electrochim. Acta, 2018, 292, 942–950 CrossRef CAS.
- D. G. Lee, O. Gwon, H. S. Park, S. H. Kim, J. Yang, S. K. Kwak, G. Kim and H. K. Song, Angew. Chem., Int. Ed., 2015, 54, 15730–15733 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cy01115d |
| This journal is © The Royal Society of Chemistry 2021 |