Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The impact of boron atoms on clathrate-I silicides: composition range of the borosilicide K8−xBySi46−y†
Walter
Jung
ab,
Bodo
Böhme
a,
Julia M.
Hübner
a,
Ulrich
Burkhardt
a,
Horst
Borrmann
a,
Matej
Bobnar
a,
Hong Duong
Nguyen
ac,
Ingo
Pantenburg
b,
Martin
Etter
d,
Ulrich
Schwarz
 a,
Yuri
Grin
a and
Michael
Baitinger
a,
Yuri
Grin
a and
Michael
Baitinger
 *a
*a
aMax-Planck-Institut für Chemische Physik fester Stoffe, Nöthnitzer Straße 40, 01187 Dresden, Germany. E-mail: Michael.Baitinger@cpfs.mpg.de
bDepartment für Chemie, Institut für Anorganische Chemie, Universität zu Köln, Greinstraße 6, 50939 Köln, Germany
cEnviromental and Ressources Management Department, Quang Ninh Economic Zone Authority, Ha Long City, Vietnam
dDeutsches Elektronen-Synchrotron (DESY), 22607 Hamburg, Germany
First published on 4th January 2021
Abstract
The clathrate-I borosilicide K8−xBySi46−y (0.8 ≤ x ≤ 1.2 and 6.4 ≤ y ≤ 7.2; space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n) was prepared in sealed tantalum ampoules between 900 °C and 1000 °C. By high-pressure preparation at 8 GPa and 1000 °C, a higher boron content is achieved (x = 0.2, y = 7.8). Crystal structure and composition were established from X-ray diffraction data, chemical analysis, WDX spectroscopy, and confirmed by 11B and 29Si NMR, and magnetic susceptibility measurements. The compositions are electron-balanced according to the Zintl rule within one estimated standard deviation. The lattice parameter varies with composition from a = 9.905 Å for K7.85(2)B7.8(1)Si38.2(1) to a = 9.968(1) Å for K6.80(2)B6.4(5)Si39.6(5).
n) was prepared in sealed tantalum ampoules between 900 °C and 1000 °C. By high-pressure preparation at 8 GPa and 1000 °C, a higher boron content is achieved (x = 0.2, y = 7.8). Crystal structure and composition were established from X-ray diffraction data, chemical analysis, WDX spectroscopy, and confirmed by 11B and 29Si NMR, and magnetic susceptibility measurements. The compositions are electron-balanced according to the Zintl rule within one estimated standard deviation. The lattice parameter varies with composition from a = 9.905 Å for K7.85(2)B7.8(1)Si38.2(1) to a = 9.968(1) Å for K6.80(2)B6.4(5)Si39.6(5).
1. Introduction
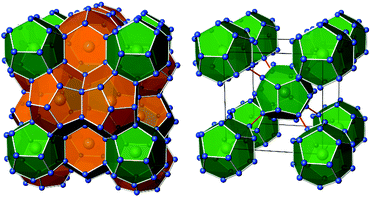
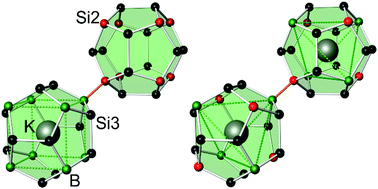
Intermetallic clathrate-I phases comprise covalent frameworks of four-bonded atoms, which host electropositive metal atoms in 20-atom and 24-atom cages (Fig. 1). The framework topology matches the connectivity of group 14 atoms 4b(E14)0 and group 13 Zintl-anions 4b(E13)−, which form a variety of ternary representatives.1–4 In particular, ternary silicon and germanium clathrates with E13 = Al,5–11 Ga,12–17 In18–20 have been studied thoroughly, often motivated by the search for new thermoelectric materials.12,13 Clathrate compounds often exhibit a broad homogeneity range, and their compositions do not necessarily follow the Zintl rule. For example, in the ternary system Ba–Al–Si, the homogeneity range covers compositions from Ba8Al6.9Si39.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 to Ba8Al15Si31,9 while the Zintl-rule composition Ba8Al16Si30 seems inaccessible. However, the rare clathrate-I representatives with boron atoms, K7B7Si39
10 to Ba8Al15Si31,9 while the Zintl-rule composition Ba8Al16Si30 seems inaccessible. However, the rare clathrate-I representatives with boron atoms, K7B7Si39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 and Rb8B8Si38,22 were found to follow the Zintl-Klemm concept. With four-bonded boron atoms, the electron balances are [K1+]7[B1−]7[Si0]39, and [Rb1+]8[B1−]8[Si0]38, respectively. In both cases, the distribution of boron and silicon atoms is exceptional for intermetallic clathrates. Substitution atoms or vacancies in clathrate-I phases usually appear in the tetrakaidecahedral cages first,23 but the boron atoms in K7B7Si39 and Rb8B8Si38 solely contribute to the pentagonal dodecahedral cages. In this work, we have prepared the clathrate-I phase K8−xBySi46−y with different compositions and studied the crystal structure adaption to the boron content. We show that borosilicide clathrates constitute an own branch of the intermetallic clathrate-I family with a unique atomic order.
21 and Rb8B8Si38,22 were found to follow the Zintl-Klemm concept. With four-bonded boron atoms, the electron balances are [K1+]7[B1−]7[Si0]39, and [Rb1+]8[B1−]8[Si0]38, respectively. In both cases, the distribution of boron and silicon atoms is exceptional for intermetallic clathrates. Substitution atoms or vacancies in clathrate-I phases usually appear in the tetrakaidecahedral cages first,23 but the boron atoms in K7B7Si39 and Rb8B8Si38 solely contribute to the pentagonal dodecahedral cages. In this work, we have prepared the clathrate-I phase K8−xBySi46−y with different compositions and studied the crystal structure adaption to the boron content. We show that borosilicide clathrates constitute an own branch of the intermetallic clathrate-I family with a unique atomic order.
2. Results and discussion
2.1. Preparation
A challenge in the preparation of alkali metal borosilicides was the high reactivity of the elemental components with the common crucible materials. Using tantalum ampoules at reaction temperatures of ≈1000 °C, annealing times did not exceed 2 days to prevent the formation of byproducts such as TaB2 or TaSi2 (Table 1). For shorter annealing times, the reactivity of boron affected product formation. By using plasma activated amorphous boron,24 clathrates can be formed with higher B and K content than from precursor alloys of boron and silicon. Although the clathrate product always yielded sharp and symmetric reflections in XRPD, crystallites of the boron-rich samples typically contained inclusions of boron (Fig. 2), which were not removed by washing with aqua regia. Therefore, the boron content of bulk samples was generally higher than the boron content of the clathrate phase. WDX spectroscopy confirmed the ratio nK/nSi obtained from crystal structure refinement, and the presence of boron in the clathrate phase (Table 1). The quantification of boron was outside of the reliable measuring range. For the high-pressure product, the WDXS analysis was affected by the small grain size and contamination by the boron nitride crucible material. | ||
| Fig. 2 Microstructure of sample 2 (cf.Table 1); back-scattered electron images. (Left) Polished clathrate grains (white) in a polymer matrix (black); boron inclusions appear as black spots within the white grains. (Right) Surface morphology of the as-grown sample. | ||
| Composition from structure refinement | Composition from analysis | Preparation | |||||||
|---|---|---|---|---|---|---|---|---|---|
| No. | a/Å | Composition | n(K)/n(B) | n(K)/n(Si) | n(K)/n(B) | n(K)/n(Si) | Educts | Conditionsa | |
K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si (at. %) Si (at. %) |
|||||||||
| a Bam: amorphous boron; Bcryst: crystalline boron. b Preparation in an iron crucible | |||||||||
| 1 | 9.9366(3) | K7.18(2)B7.2(5)Si38.8(5) | 0.9972(20) | 0.1851(20) | WDXS | 0.79(10) | 0.181(2) | 15.4/24.6/60.0 | 900 °C |
| CA | 1.048(6) | 0.1808(12) | 48 h; Bam | ||||||
| 2 | 9.9393(2) | K7.12(4)B7.1(6)Si38.9(6) | 1.003(3) | 0.183(3) | WDXS | 0.91(3) | 0.191(4) | 20.0/40.0/40.0 | 950 °C |
| 20 h; Bam | |||||||||
| 3 | 9.9470(2) | K6.98(4)B6.4(5)Si39.6(5) | 1.108(2) | 0.176(2) | WDXS | 0.90(3) | 0.185(2) | 17.9/14.3/67.9 | 1000 °Cb |
| 44 h; Bcryst | |||||||||
| 4 | 9.952(1) | K7.08(1)B6.8(3)Si39.2(3) | 1.0412(14) | 0.1806(14) | EDXS | — | 0.1707 [1] | 20.7/13.8/65.5 | 950 °C |
| 48 h; Bcryst | |||||||||
| 5 | 9.968(1) | K6.80(2)B6.4(5)Si39.6(5) | 1.063(2) | 0.172(2) | WDXS | 0.96(3) | 0.183(5) | 17.3/7.7/75.0 | 1000 °C |
| CA | 1.161(13) | 0.1687(17) | 56 h; Bam | ||||||
| 6 | 9.9055(1) | K7.85(2)B7.8(1)Si38.2(1) | 1.01(3) | 0.204(5) | WDXS | 0.815(7) | 0.214(2) | 41.7/16.7/41.7 | 1000 °C |
| 5 h; Bam, 8 GPa | |||||||||
Thermogravimetry experiments on a washed clathrate sample revealed an onset of continuous weight loss at ca. 870 °C. The sample was not molten a this temperature. The total amount is consistent with the complete elimination of potassium, while the residue showed the reflections of boron-doped α-Si in XRPD. For comparison, samples were heated in open Ta crucibles enclosed in silica glass ampoules for one day at various temperatures. Under these conditions, the decomposition was observed at similar temperatures, as evidenced by the reaction of potassium vapor with the glass vessel.
2.2 Crystal structure and composition
In the first part of this section, we outline the basic structure refinement strategy using crystal 4 (Table 1). The refinement was performed for a binary structure model K8Si46−x. Assuming the absence of vacancies, the number of Boron atoms was calculated subsequently (see ESI, section 1†). By refining the boron content directly, the results depended on the refinement strategy. In the starting model, all positions were fully occupied (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n; 6 Si1 in 6c, 16 Si2 in 16i, 24 Si3 in 24k, 2 K1 in 2a, 6 K2 in 6d). The refinement with 872 symmetry independent reflections (up to sin
n; 6 Si1 in 6c, 16 Si2 in 16i, 24 Si3 in 24k, 2 K1 in 2a, 6 K2 in 6d). The refinement with 872 symmetry independent reflections (up to sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θλ−1 = 1.2) and anisotropic approximation of atomic displacement parameters (ADP) yielded the residual value RF = 0.085. Characteristic features of the model at that stage were Ueq(K1) > Ueq(K2), and Ueq(Si1) ≪ Ueq(Si3) < Ueq(Si2). Because the 20-atom cage of K1 is smaller than the 24-atom cage of K2, suggesting the reverse ratio of the ADP, the ratio U(K1) > U(K2) indicates partial site occupancy of K1. Consequently, the site occupancy factor of K1 was refined to 0.54, while the R-value decreased to RF = 0.075, and the displacement parameters converged to the expected ratio U(K1) < U(K2). The ADP values of K2 indicated a disc-like shape, which adequately reflects the larger volume and the anisotropic shape of the K2 cage.
θλ−1 = 1.2) and anisotropic approximation of atomic displacement parameters (ADP) yielded the residual value RF = 0.085. Characteristic features of the model at that stage were Ueq(K1) > Ueq(K2), and Ueq(Si1) ≪ Ueq(Si3) < Ueq(Si2). Because the 20-atom cage of K1 is smaller than the 24-atom cage of K2, suggesting the reverse ratio of the ADP, the ratio U(K1) > U(K2) indicates partial site occupancy of K1. Consequently, the site occupancy factor of K1 was refined to 0.54, while the R-value decreased to RF = 0.075, and the displacement parameters converged to the expected ratio U(K1) < U(K2). The ADP values of K2 indicated a disc-like shape, which adequately reflects the larger volume and the anisotropic shape of the K2 cage.
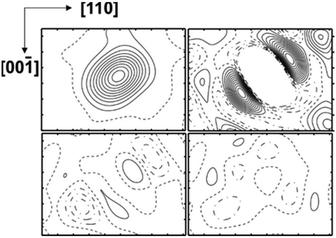
Occupancy refinement for the framework positions resulted in a distinctly reduced electron density for Si2, a minor reduction for Si3, and a RF value of 0.042. The ADP ratio for the framework positions did not change. The results reveal local disorder as the reason for the enhanced ADP of Si2 and Si3 positions and a mixed occupancy with Si and B atoms. The calculated residual density without occupancy of Si2 displayed a non-spherical distribution (Fig. 3, top left). When the Si2 position was occupied with a with a mixture of Si and B atoms in isotropic approximation, the refinement revealed residual density along the space diagonal (Fig. 3 top right), which was not removed by applying anisotropic ADP (Fig. 3, bottom left). Only by introducing two 16i split positions (Si + B), the refinement resulted in a ‘flat’ residual density map and a residual value of RF = 0.039. The occupancy of site Si3 was estimated in a similar fashion. The residual density calculated without atoms at this position revealed a non-spherical distribution in two directions – approximately along the diagonal in the (010) plane and perpendicular to it in (100) (Fig. 4a). Neither anisotropic approximation for ADPs for a single mixed occupied position (Fig. 4b and c) nor a model with two positions located in the (010) plane (Fig. 4d) yielded an acceptable description of the electron density in this region. However, it was satisfactorily described applying two silicon occupied split positions – one in the (010) plane (24k), and another one out of plane (48l) (Fig. 4e). Thereby, the residual value dropped to 0.031 (ESI, Table S4†). The final atomic coordinates and displacement parameters for all crystal structures K8−xBySi46−y, which were refined applying the same strategy, are listed in the (ESI, Tables S1–S6†).
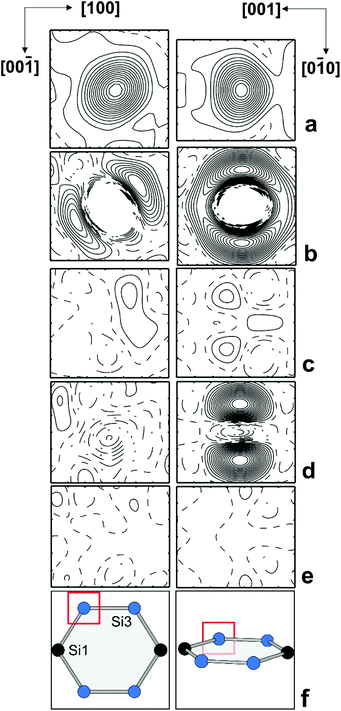 | ||
| Fig. 4 Distribution of the difference electron density around Si3 in two perpendicular planes: (a) without any atoms; (b) with one mixed occupied position in the (010) plane in isotropic approximation; (c) with one mixed occupied position in the (010) plane in anisotropic approximation; (d) with two mixed occupied positions in the (010) plane in isotropic approximation; (e) with two silicon occupied positions (one on the (010) plane, the other one out of plane, cf. ESI Table 5†); (f) position of the selected planes in the structure. The center of each panel is located at (0.30, 0.00, 0.12). The step of the isolines is 5 e Å−3 in (a) and 0.5 e Å−3 in all other panels. | ||
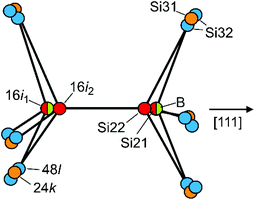
The preferred substitution of Si2 by B atoms at site 16i is a feature that only occurs for clathrate-I borosilicides so far. Typically, the replacement of group 14 elements in intermetallic clathrates by heteroatoms starts at site 6c (Si1). As in all binary clathrate silicides M8−xSi46 the Si2 atoms show the shortest framework distances,22,23 this site should be the most suitable one for boron atoms. However, the partial substitution at site 16i inevitably causes a structural disorder, because 16i atoms appear as bonded pairs. Assuming that direct contacts of negatively charged boron anions are energetically unfavourable, the pairs mainly consist of B–Si contacts in two orientations plus, for y < 8, a minority of Si–Si pairs. The bond distances d(B–Si) ≈ 2.0 Å and d(Si–Si) ≈ 2.3 Å differ substantially. The experimental electron density at sites 16i and 24k thus represents a sum of local configurations, which is reflected by the apparently large and anisotropic ADPs (Fig. 3 and 4). After introducing split positions for Si2 (16i1 + 16i2) the question arises, which of them is the favourable one for boron atoms (Fig. 5).
When boron occupies the split site 16i1, the neighbouring site 16i2 is occupied by silicon (Si22). In this case, all B–Si distances are favourably short: one to the silicon atom at 16i2, and three to the Si32 at 48l with values of ≈2.0 Å. Site 16i2 is less favourable for B atoms because of three longer distances of ca. 2.2 Å to the Si32 atoms. The minority case without boron atoms is represented by Si21–Si21 pairs. Here, the Si21 atoms are connected to three Si31 at site 24k. The Si22 atoms at 16i2 are connected to boron at 16i1, to Si31 atoms at 24k or to the Si32 atoms at 48l out of the mirror plane. To interpret the refined site occupancies, we extend the split-site model and consider the possible local configurations of the Si20−xBx dodecahedron around K1, which is composed of B21, Si21, Si22, Si31 and Si32 atoms (Fig. 6a–f).
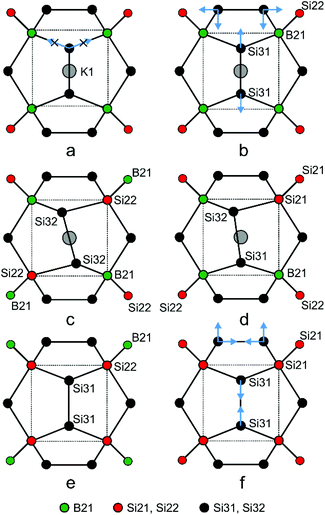 | ||
| Fig. 6 Local atomic arrangements derived from the Si3 split sites in the crystal structure of K8−xBySi46−y. The examples show how the Si20−xBx dodecahedra may respond to the composition. | ||
A frequently occurring situation, which cannot be explained in Fig. 5, is that the Si3 atom has two adjacent B atoms (Fig. 6a). Here, a shift towards Si32 is no longer possible, because the approach to one of the boron atom would enlarge the distance to the other one. In this case, a short distance to both boron atoms can still be realized by stretching the Si3–Si3 bond and shifting the pair at the same time towards the cage center (Fig. 6b, blue arrows). With equal distances to both boron atoms, such Si3 atoms contribute to the electron density at Si31 and not, as Fig. 5 may suggest, at Si32. Only in such cases, where the Si3 atoms are connected to a B atom and a Si atom (Fig. 6c and d), they shift towards the B atom and occupy the Si32 position. As a consequence, the Si3–Si3 bond line deviates from the [100] direction. This can even occur for a Si31–Si31 bond when the Si3 atoms are connected to a closer Si21 and a more distant Si22 atom (Fig. 6e and f). In the refined structure model, site Si31 represents all cases, for which the 24k atoms are connected to 16i atoms of the same type (Fig. 6b), while Si32 represents the asymmetrical local configuration (Fig. 6c). As the asymmetric arrangements occur more frequently, the Si32 site (48l) features a higher occupancy than Si31 (24k).
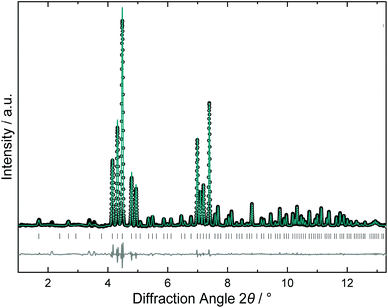
The crystal structure of the high-pressure product was refined from synchrotron X-ray powder diffraction data. The powder pattern (Fig. 7) was fully indexed with a primitive unit cell so that the structure model was developed in space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n applying a similar refinement strategy as described above. The tetrakaidecahedral cages were found fully occupied with K2, while the K1 atoms in the smaller dodecahedral showed a minor deficiency. In the framework, position Si1 was fully occupied by silicon, but both Si2 and also Si3 showed mixed B/Si occupancy. However, the lower resolution of the method did not allow for resolving the split positions. Therefore, the bond distances represent mean values from the superposition of B–Si and Si–Si bonds. Remarkably, the refined composition K7.85(2)B7.8(1)Si38.2(1) fits the Zintl rule within one experimental error. Thermal analysis of the high-pressure product was similar to those of the ambient pressure products and did not show any exothermic decomposition effect on heating, which would have indicated a metastable phase.
n applying a similar refinement strategy as described above. The tetrakaidecahedral cages were found fully occupied with K2, while the K1 atoms in the smaller dodecahedral showed a minor deficiency. In the framework, position Si1 was fully occupied by silicon, but both Si2 and also Si3 showed mixed B/Si occupancy. However, the lower resolution of the method did not allow for resolving the split positions. Therefore, the bond distances represent mean values from the superposition of B–Si and Si–Si bonds. Remarkably, the refined composition K7.85(2)B7.8(1)Si38.2(1) fits the Zintl rule within one experimental error. Thermal analysis of the high-pressure product was similar to those of the ambient pressure products and did not show any exothermic decomposition effect on heating, which would have indicated a metastable phase.
The lattice parameter of the borosilicide clathrates with the remarkable minimum for K7.85(2)B7.8(1)Si38.2(1) (a ≈ 9.905 Å) is considerably smaller than that of the corresponding binary silicon clathrate K8−xSi46 (a ≈ 10.26 Å). The lattice parameter decreases with increasing boron content, which is expected from the short d(B–Si) distances (Fig. 8). Surprisingly, the decrease is not hindered by the increasing potassium content, which suggests an attractive interaction between the four-bonded boron anions and the K1 cations in the dodecahedral cages. So far, a decrease of lattice parameter with an increasing number of filler atoms has been observed only for the oversized Si28 cages in the clathrate-II structure of Na24−xSi136.25
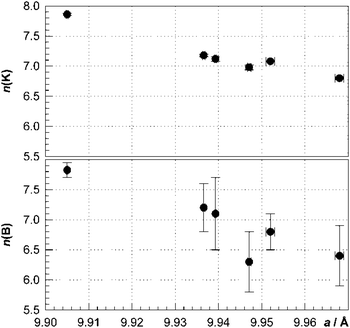 | ||
| Fig. 8 Number of potassium and boron atoms per unit cell of K8−xBySi46−y obtained from crystal structure refinement vs. lattice parameter. | ||
For compositions with partial occupancy of position K1, the crystal structure comprises empty and filled dodecahedral cages. Hence, an attractive interaction between K1 and B atoms would imply that the B atoms of B-Si22 pairs are oriented towards the K1 atoms. A complete separation into Si20 and K1@Si12B8 cages could be achieved for the hypothetical composition K7B8Si38 (Fig. 9, left). For the nearly filled composition K7.8B7.8Si38.2 a tetrahedral coordination of K1 by B atoms is most probable (Fig. 9, right). An ordered distribution of boron atoms may cause superstructures. For example, the ideal arrangement of B atoms derived for the compositions K7B8Si38 corresponds to space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (Fig. 9, left), and for K8B8Si38 to space group P4
(Fig. 9, left), and for K8B8Si38 to space group P4![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n (Fig. 9, right). But so far, there is no evidence for a superstructure formation in our experiments. In the local structure, the distortions caused by short distances d(B–Si22) should favor arrangements with a uniform shortening of all four space diagonals. Moreover, the direct connection of silicon rich dodecahedra (Fig. 6f) is unfavorable due the very short distance Si21–Si31 (ESI, Table S4d†) which might also explain the existence of a lower limit for the boron content in K8−xBySi46−y.
n (Fig. 9, right). But so far, there is no evidence for a superstructure formation in our experiments. In the local structure, the distortions caused by short distances d(B–Si22) should favor arrangements with a uniform shortening of all four space diagonals. Moreover, the direct connection of silicon rich dodecahedra (Fig. 6f) is unfavorable due the very short distance Si21–Si31 (ESI, Table S4d†) which might also explain the existence of a lower limit for the boron content in K8−xBySi46−y.
2.3 Chemical bonding
Two ordered models in the space group P4![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n were investigated for the idealized composition K8B8Si38, which is close to the composition K7.85(2)B7.8(1)Si38.2(1) of the high-pressure product. In the acentric space group P4
n were investigated for the idealized composition K8B8Si38, which is close to the composition K7.85(2)B7.8(1)Si38.2(1) of the high-pressure product. In the acentric space group P4![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n, the former position Si2 of space group Pm
n, the former position Si2 of space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n is represented by two eight-fold positions Si21 and Si22 which are fully occupied either by boron or by silicon atoms (for atomic parameters see ESI, Table S7†). In both models, the boron atoms are arranged tetrahedrally around K1 (Fig. 9, right). The positions Si1 and Si3 are occupied by silicon only. For the chosen model, the outer position Si21 is more favorable for boron than Si22 (Fig. 5), which is consistent with the structure discussion above.
n is represented by two eight-fold positions Si21 and Si22 which are fully occupied either by boron or by silicon atoms (for atomic parameters see ESI, Table S7†). In both models, the boron atoms are arranged tetrahedrally around K1 (Fig. 9, right). The positions Si1 and Si3 are occupied by silicon only. For the chosen model, the outer position Si21 is more favorable for boron than Si22 (Fig. 5), which is consistent with the structure discussion above.
In order to study the redistribution of the charges within the framework for different local arrangements, and the charge ratio between boron ad silicon atoms, the analysis of the calculated electron density was performed within the Quantum Theory of Atoms in Molecules.26 For both hypothetical models, the calculation reveals that the potassium atoms have nearly the same positive charge and transfer, thus, their valence electron to the framework. Rather unexpectedly, the distribution of the electrons within the framework does not completely follow the Zintl count (Fig. 10). The charges of the four-bonded silicon atoms deviate from the expected zero value and are between −0.52 and +0.55 in model 1 and between −0.09 and +0.67 in model 2. Independently from the effective silicon charges, boron atoms have more negative charges as expected from the Zintl count and electronegativity.
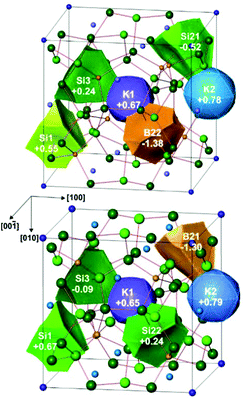 | ||
| Fig. 10 QTAIM charges in K8B8Si38 models 1 (top) and 2 (bottom) with different distributions of boron and silicon atoms at the Si2 position. | ||
2.4 11B NMR and 29Si NMR investigations
To study the local arrangement of the boron atoms, samples 1, 3 and 5 (Table 1) were investigated by 11B NMR spectroscopy in static mode. For all samples, one sharp signal with a slightly asymmetric peak shape is observed (Fig. 11, left). The signal shape and the shifts of −15 ppm to −24 ppm are close to the former result (−5 ppm for K7B7Si39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21).
21).
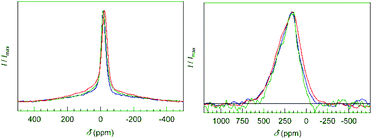 | ||
| Fig. 11 NMR spectra (static echo measurements) of the clathrates with composition K7.18(2)B7.2(5)Si38.8(5) (blue), K6.98(4)B6.4(5)Si39.6(5) (green) and K6.80(2)B6.4(5)Si39.6(5) (red). (Left) 11B NMR signals are sharp and slightly asymmetric. The broad background is attributed to the presence of amorphous boron inclusions. (Right) 29Si NMR signals (static echo measurements) show a small Knight shift typical for widely electronically balanced silicon clathrate-I compounds.28–30 | ||
By using echo measurements, contributions of amorphous boron appearing as a broad background signal were separated. For the quantitative analysis of the boron content, the samples were measured at standardized conditions. The integrated intensity of the 11B NMR signals was normalized by the nominal sample weight as the clathrate content in the bulk samples was always close to 100%. The results confirm the range of boron content found by X-ray diffraction (Table 9, ESI†). The single, sharp signal points to only one dominating local environment of four-bonded boron atoms. Therefore, the presence of B–B bonds besides B–Si bonds at site 16i is ruled out. The slight asymmetry in the 11B signals is explained by the differences in bond angles, bonding distances and local symmetry due to the different connection patterns of the Si–B pairs (Fig. 5 and 6). 29Si NMR spectroscopy reveals a broad signal, which does not allow for an assignment of individual contributions of framework sites (Fig. 11, right). The signals have a smaller Knight shift than Ba8−xSi46 or Na8Si46.27,31 This indicates bad-metal behavior of the clathrate phase for all samples, which is in agreement with electronically widely (but not exactly) balanced chemical compositions.28–30
2.5 Magnetic susceptibility
The samples 1, 3 and 5 (Table 10, ESI†) show diamagnetic behavior at room temperature, but with an upturn towards low temperatures which is assigned to Curie-like paramagnetic impurities. The extracted temperature independent susceptibility values are negative and similar to those calculated on the basis of diamagnetic increments for K+ cations, B3+ and α-Si32,33 for the refined composition. However, the sum of the increments underestimates the diamagnetism, as only the core value is used for boron and the increment of silicon in the anionic framework of the clathrate structure is expected to be more negative than for α-Si. Deviation of the measured data toward less negative values (sample 5) are attributed to contributions of conduction electrons (Pauli paramagnetism) caused by n(K) > n(B). Sample 3, prepared in an iron crucible, had a lower purity than the other samples. The result confirms the absence of framework vacancies in the structure as the diamagnetic contributions of (3b)Si− anions23 would exceed the elemental increments of (4b)Si0 significantly.343. Experimental
Synthesis. Potassium (Chempur, 99.95%), silicon (Chempur, 99.9999%), and crystalline boron (Chempur, 99.95%) were used without further refinement. Amorphous boron powder (Alfa Aesar), which typically contains oxidic impurities in the range of 1–3 mass%, was purified in a streaming hydrogen plasma.23 For this purpose, the boron powder was placed in a corundum crucible situated in a silica glass Schlenk-tube. Plasma treatment under controlled H2 flow was realized in a microwave furnace (MLS) for 20 minutes (P = 1200 W, p(H2) ≈ 2 mbar) at temperatures below 300 °C. The purified boron powder was free of oxygen and hydrogen according to chemical analysis and still amorphous. Preparation of the clathrate phase at ambient pressure proceeded via two different routes. Using amorphous boron, silicon powder was admixed in different atomic ratios. The mixture was homogenized in an agate mortar and directly filled into a tantalum ampoule with an excess of potassium (Table 1). Alternatively, mixtures of crystalline boron and silicon were melted in an arc furnace before grinding. An excess of potassium was placed at the bottom of a tantalum tube and covered by the B/Si precursor alloy as described earlier.21 In both preparation routes, the sealed tantalum ampoules were placed in quartz glass vessels under Ar atmosphere and heated to 650 °C for ten hours. After this pre-reaction, the temperature was raised by 20 K h−1 to maxima between 900 °C and 1000 °C. An exception is the sample 3, which was prepared 30 years ago in an iron crucible. The iron content in the sample was ca. 1 wt% according to WDXS. After annealing for 1–2 days, the ampoules were removed from the hot furnace. While the operations up to this stage were performed either at a Schlenk line or in an argon-filled glove box, the elimination of residual potassium silicide is performed in normal atmosphere with isopropanol in an atmosphere of streaming Ar. After the first, normally violent reaction, the process is continued with ethanol. Residual elemental silicon and boron were removed successively with 1 M aqueous NaOH solution and boiling aqua regia, respectively. After washing, the remaining clathrate-I phase showed well-shaped crystals with metallic luster (Fig. 2).High-pressure preparation started from a finely ground mixture of K4Si4 and amorphous boron powder with atomic ratio K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B
B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si = 5
Si = 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5. The powder was mechanically closed in a boron nitride crucible (d = 3 mm) and plugged in the drilled hole of a MgO octahedron (l = 18 mm). The synthesis was conducted using a multi-anvil press comprising a Walker-type module.35 Before the experiment, pressure and temperature measurements were calibrated by recording resistance changes of bismuth and thermocouple-calibrated runs, respectively. A pressure of at p = 8(±1) GPa was applied, and the sample was heated to T = 1273(±127) K within 15 min. After annealing for 60 min, the sample was quenched under load. To remove side products, the sample was first washed with ethanol, then with deionized water and finally with acetone, and dried at room temperature. The high-pressure product is air-stable and inert against strong acids and bases.
5. The powder was mechanically closed in a boron nitride crucible (d = 3 mm) and plugged in the drilled hole of a MgO octahedron (l = 18 mm). The synthesis was conducted using a multi-anvil press comprising a Walker-type module.35 Before the experiment, pressure and temperature measurements were calibrated by recording resistance changes of bismuth and thermocouple-calibrated runs, respectively. A pressure of at p = 8(±1) GPa was applied, and the sample was heated to T = 1273(±127) K within 15 min. After annealing for 60 min, the sample was quenched under load. To remove side products, the sample was first washed with ethanol, then with deionized water and finally with acetone, and dried at room temperature. The high-pressure product is air-stable and inert against strong acids and bases.
Elemental analysis. The clathrate phase is stable against aqua regia and NaOH solutions. Samples were dissolved in aqueous HNO3/HF by using a microwave-assisted procedure (ETHOS, MLS) in closed Teflon vessels and analyzed by using optical emission spectrometry (ICP-OES, VISTA RL, Varian). Standardization was performed with a matrix-matched standard. For determination of O and H in amorphous boron, specimens of about 25 mg were loaded into tin capsules and analyzed by carrier gas hot extraction with IR spectrometry of CO, CO2, and H2O (TCH 600, LECO). The carbon content was analyzed after the combustion of the sample in oxygen stream (CHLH 200, LECO).
Powder X-Ray diffraction (PXRD). Diffraction experiments on powder samples were performed with a Guinier camera (Huber G670, Cu Kα1 radiation, λ = 1.54056 Å, germanium monochromator, 5° ≤ 2θ ≤ 100°, Δ2θ = 0.005). Reflection positions were corrected by using LaB6 standard (NIST), and the unit cell parameters were calculated from least-square refinement. Rietveld refinements were performed using synchrotron data (Desy Hamburg, PETRA III, Beamline P02.1, λ = 0.20720 Å) recorded at room temperature. All calculations were performed with the WinCSD software.36
X-ray single crystal diffraction. Five single crystals obtained from samples with different lattice parameters were investigated by single-crystal X-ray diffraction. The crystals were selected under paraffin oil and fixed onto a glass capillary. The measurements were performed on a IPDS diffractometer (Stoe, MoKα radiation, λ = 0.71073 Å), a CAD4 diffractometer (Enraf-Nonius, Mo Kα radiation) or a Rigaku Spider diffractometer (rotating anode and Varimax optics, AgKα radiation, λ = 0.560871 Å). Absorption correction was performed with a multi-scan procedure. The crystal structures were refined using WinCSD software.36 Details concerning the data collection, structure refinement, and interatomic distances are given in the ESI.†
Scanning electron microscopy (SEM). Bulk samples were embedded in epoxy resin with conductive carbon filler and polished. Energy-dispersive X-ray spectroscopy (EDXS) was performed with an attached EDAX Si (Li) detector, wavelength dispersive X-ray spectroscopy (WDXS) by using a Cameca SX100 electron microprobe. The Kα lines of the elements were measured and evaluated using Ni3B, Mg2Si, and KBr as standards.
Thermogravimetry (TG). The thermal stability of the clathrate phase was investigated using a thermo balance (Netzsch STA 409 CD). The substance was filled in a Ta crucible and heated with a rate of 10 K min−1 up to 1200 °C.
Magnetic susceptibility. Specimens of m = 50 mg–90 mg were measured in closed silica tubes using a SQUID magnetometer (MPMS XL-7, Quantum Design) at external fields of 3.5 T and 7 T. The diamagnetic contribution of the silica tube was determined prior to the measurements and subtracted. The samples contained tiny amounts of ferromagnetic impurities with a mass content of about 1 ppm, which may originate, e.g., from the usage of steel tools in sample preparation. Therefore, an extrapolation to infinite external field was performed by applying the Honda-Owen method.37 Afterward, the temperature-independent contribution was extracted by a polynomial fit.
Nuclear Magnetic Resonance Spectroscopy. NMR experiments were performed with a Bruker Avance 500 spectrometer in a magnetic field of B0 = 11.74 T. A standard Bruker Magic Angle Spinning (MAS) probe for 2.5 mm ZrO2 rotors was used for spinning experiments while the static experiments were performed in probes built by NMR Service GmbH, Erfurt. The external reference frequencies for 11B and 29Si nuclei were 160.458 MHz and 99.360 MHz, corresponding to the signals of BF3·Et2O and TMS solutions in CCl3D, respectively. In the case of 11B, the signal was collected either after a single pulse or as an echo after two pulses of equal length (6 μs) applying a recovery time of 30 s–60 s. The single pulse experiments were performed for signal assignment, while the quantitative evaluation bases on the echo measurements. In the case of 29Si, Hahn echoes were obtained after a pulse sequence, in which the second pulse had twice the length of the first one (1.8 μs and 3.6 μs), applying a recovery time of 10 s.
Chemical bonding. For the electronic structure calculations, the TB-LMTO-ASA software was used.38 Analysis of the chemical bonding is performed by the electron localizability approach in position space.39 The electron localizability indicator (ELI) in its ELI-D representation40 is calculated together with the electron density (ED), using a specialized module implemented in the TB-LMTO-ASA package. The topology of the three-dimensional distributions of ELI-D and ED was evaluated with the program DGrid.41 Integration of the electron density in the basins bounded by zero-flux surfaces of the electron density or ELI-D gradient fields yield the atomic charges or bond populations, respectively. This procedure follows the quantum theory of atoms in molecules (QTAIM).26
4. Conclusions
Different compositions of the clathrate borosilicide K8−xBySi46−y were investigated by combining X-ray diffraction experiments, solid state NMR and magnetic susceptibility measurements. Borosilicide clathrates constitute an own branch of intermetallic clathrates with the unique structural feature that boron atoms first substitute atoms at site 16i and not at site 6c as it is observed in other clathrate-I phases. The complex structural order was investigated and a structure model was established. The correlation between lattice parameter, boron and potassium content points to an attractive interaction between potassium cations and four-bonded boron anions. The unit cell volume shrinks distinctly with boron content. In particular, the sample with the highest boron content, K7.8B7.8Si38.2, features an extraordinary small lattice parameter compared to other clathrate-I silicides (a = 9.9055(1) Å). By trend, the compositions within the homogeneity range follow the Zintl-rule with n(K) ≈ n(B). Chemical bonding analysis with the electron localizability indicator reveals the Zintl-like behavior of the B− anions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the competence groups structure and metallography at MPI CPfS for providing experimental support. Open Access funding provided by the Max Planck Society.References
- The Physics and Chemistry of Inorganic Clathrates, ed. G. S. Nolas, Springer Series in Materials Science, 2014 Search PubMed.
- J. Dolyniuk, B. Owens-Baird, J. Wang, J. V. Zaikina and K. Kovnir, Mater. Sci. Eng., R, 2016, 108, 1 CrossRef.
- S. Cros and M. Pouchard, C. R. Chim., 2009, 12, 1014 CrossRef.
- M. Christensen, S. Johnsen and B. B. Iversen, Dalton Trans., 2010, 39, 978 RSC.
- B. Eisenmann, H. Schäfer and R. Zagler, J. Less-Common Met., 1986, 118, 43 CrossRef CAS.
- C. L. Condron, J. Martin, G. S. Nolas, P. M. B. Piccoli, A. J. Schultz and S. M. Kauzlarich, Inorg. Chem., 2006, 45, 9381 CrossRef CAS.
- C. L. Condron, S. M. Kauzlarich, T. Ikeda, G. J. Snyder, F. Haarmann and P. Jeglic, Inorg. Chem., 2008, 47, 8204 CrossRef CAS.
- E. N. Nenghabi and C. W. Myles, J. Phys.: Condens. Matter, 2008, 20, 415214 CrossRef.
- J. H. Roudebush, C. de la Cruz, B. C. Chakoumakos and S. M. Kauzlarich, Inorg. Chem., 2012, 51, 1805 CrossRef CAS.
- M. Bobnar, B. Böhme, M. Wedel, U. Burkhardt, A. Ormeci, Y. Prots, C. Drathen, Y. Liang, H. D. Nguyen, M. Baitinger and Y. Grin, Dalton Trans., 2015, 44, 12680 RSC.
- M. Troppenz, S. Rigamonti and C. Draxl, Chem. Mater., 2017, 29, 2414 CrossRef CAS.
- J. Martin, H. Wang and G. S. Nolas, Appl. Phys. Lett., 2008, 92, 222110 CrossRef.
- E. S. Toberer, M. Christensen, B. B. Iversen and G. J. Snyder, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 075203 CrossRef.
- G. S. Nolas, J. L. Cohn, G. A. Slack and S. B. Schujman, Appl. Phys. Lett., 1998, 73, 178 CrossRef CAS.
- B. C. Chakoumakos, B. C. Sales, D. G. Mandrus and G. S. Nolas, J. Alloys Compd., 2000, 296, 80 CrossRef CAS.
- B. C. Sales, B. C. Chakoumakos, R. Jin, J. R. Thompson and D. G. Mandrus, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245113 CrossRef.
- S. Paschen, W. Carrillo-Cabrera, A. Bentien, V. H. Tran, M. Baenitz, Yu. Grin and F. Steglich, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 214404 CrossRef.
- A. Czybulka, B. Kuhl and H.-U. Schuster, Z. Anorg. Allg. Chem., 1991, 594, 23 CrossRef CAS.
- Ya. Mudryk, P. Rogl, C. Paul, S. Berger, E. Bauer, G. Hilscher, C. Godart and H. Noël, J. Phys.: Condens. Matter, 2002, 14, 7991 CrossRef CAS.
- A. Bentien, E. Nishibori, S. Paschen and B. B. Iversen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 144107 CrossRef.
- W. Jung, J. Loerincz, R. Ramlau, H. Borrmann, Yu. Prots, F. Haarmann, W. Schnelle, U. Burkhardt, M. Baitinger and Yu. Grin, Angew. Chem., Int. Ed., 2007, 46, 6725 ( Angew. Chem. , 2007 , 119 , 6846 ) CrossRef CAS.
- J. M. Hübner, W. Jung, M. Schmidt, M. Bobnar, P. Koželj, B. Böhme, M. Baitinger, M. Etter, Yu. Grin and U. Schwarz, Inorg. Chem., 2020 DOI:10.1021/acs.inorgchem.0c02357.
- M. Baitinger, B. Böhme, F. R. Wagner and U. Schwarz, Z. Anorg. Allg. Chem., 2020, 646, 1034 CrossRef CAS.
- A. Alekseeva, K. Kovnir, P. Chizhov, M. Baitinger and Yu. Grin, European Patent, EP1893320B8, 2010 Search PubMed.
- M. Beekman, E. N. Nenghabi, K. Biswas, C. W. Myles, M. Baitinger, Yu. Grin and G. S. Nolas, Inorg. Chem., 2010, 49, 5338 CrossRef CAS.
- F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, New York, 1990 Search PubMed.
- R. Castillo, W. Schnelle, M. Bobnar, U. Burkhardt, B. Böhme, M. Baitinger, U. Schwarz and Y. Grin, Z. Anorg. Allg. Chem., 2015, 641, 206 CrossRef CAS.
- H. Sakamoto, H. Tou, H. Ishii, Y. Maniwa, E. A. Reny and S. Yamanaka, Physica C, 2000, 341, 2135 CrossRef.
- Y. Maniwa, H. Sakamoto, H. Tou, Y. Aoki, H. Sato, F. Shimizu, H. Kawaji and S. Yamanaka, Mol. Cryst. Liq. Cryst., 2000, 341, 497 CrossRef CAS.
- B. Böhme, M. Bobnar, A. Ormeci, K. Peters, W. Schnelle, M. Baitinger and Yu. Grin, Z. Kristallogr. – Cryst. Mater., 2017, 232, 223 Search PubMed.
- J. He, D. D. Klug, K. Uehara, K. F. Preston, C. I. Ratcliffe and J. S. Tse, J. Phys. Chem. B, 2001, 105, 3475 CrossRef CAS.
- P. W. Selwood, Magnetochemistry, Interscience, New York, USA, 2nd edn, 1956, p. 78 Search PubMed.
- S. Hudgens, M. Kastner and H. Fritzsche, Phys. Rev. Lett., 1974, 33, 1552 CrossRef CAS.
- Y. Liang, B. Böhme, A. Ormeci, H. Borrmann, O. Pecher, F. Haarmann, W. Schnelle, M. Baitinger and Yu. Grin, Chem. – Eur. J., 2012, 18, 9818 CrossRef CAS.
- D. Walker, M. A. Carpenter and C. M. Hitch, Am. Mineral., 1990, 75, 1020 Search PubMed.
- L. Akselrud and Yu. Grin, J. Appl. Crystallogr., 2014, 47, 803 CrossRef CAS.
- K. Honda, Ann. Phys., 1910, 337, 1027 CrossRef.
- O. Jepsen, A. Burkhardt and O. K. Andersen, The Program TB-LMTO-ASA. Vers. 4.7, Stuttgart, 1999 Search PubMed.
- M. Kohout, Int. J. Quantum Chem., 2004, 97, 651 CrossRef CAS.
- F. R. Wagner, V. Bezugly, M. Kohout and Yu. Grin, Chem. – Eur. J., 2007, 13, 5724 CrossRef CAS.
- M. Kohout, DGrid, versions 4.6–5.0, 2018 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: CSD numbers: High-pressure sample K7.85(2)B7.8(1)Si38.2(1), CSD 2006316; crystal 1: K7.18(2)B7.2(5)Si38.8(5), CSD 2046329; crystal 2: K7.12(4)B7.1(6)Si38.9(6), CSD 2046333; crystal 3: K6.98(4)B6.4(5)Si39.6(5), CSD 2046330; crystal 4, K7.08(1)B6.8(3)Si39.2(3), CSD 2046332; crystal 5: K6.80(2)B6.4(5)Si39.6(5), CSD 2046331. CCDC 2006316–2046333. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0dt03339a |
| This journal is © The Royal Society of Chemistry 2021 |