Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Condensation sink of atmospheric vapors: the effect of vapor properties and the resulting uncertainties
Santeri
Tuovinen
 a,
Jenni
Kontkanen
a,
Jenni
Kontkanen
 a,
Runlong
Cai
a and
Markku
Kulmala
a,
Runlong
Cai
a and
Markku
Kulmala
 *abcd
*abcd
aInstitute for Atmospheric and Earth System Research, University of Helsinki, Helsinki, 00014, Finland. E-mail: markku.kulmala@helsinki.fi
bJoint International Research Laboratory of Atmospheric and Earth System Sciences, School of Atmospheric Sciences, Nanjing University, Nanjing, China
cAerosol and Haze Laboratory, Beijing Advanced Innovation Center for Soft Matter Sciences and Engineering, Beijing University of Chemical Technology (BUCT), Beijing, China
dFaculty of Geography, Lomonosov Moscow State University, Moscow, Russia
First published on 23rd September 2021
Abstract
Aerosol particles affect the climate and human health. Thus, understanding and accurately quantifying the processes associated with secondary formation of aerosol particles is highly important. The loss rate of vapor to aerosol particles affects the mass balance of that vapor in the atmosphere. The condensation sink (CS) describes the condensation rate of vapor to particles while the effective condensation sink (CSeff) describes the loss rate including both condensation and evaporation of vapor. When the CS is determined, the mass accommodation coefficient (α) is usually assumed to be unity and the condensing vapor is often assumed to be sulfuric acid. In addition, evaporation is assumed to be negligible (CSeff = CS) and the total loss rate of vapor is described by the CS. To study the possible uncertainties resulting from these assumptions, we investigate how vapor properties such as vapor mass and α affect the CS. In addition, the influence of evaporation on the CSeff is evaluated. The CS and CSeff are determined using particle number size distribution data from Beijing, China. Vapors are observed to have differing CSs depending on molecular mass and diffusivity volume and larger molecules are lost at a slower rate. If the condensing vapor is composed, for example, of oxidized organic molecules, which often have larger masses than sulfuric acid molecules, the CS is smaller than for pure sulfuric acid vapor. We find that if α is smaller than unity, the CS can be significantly overestimated if unity is assumed. Evaporation can significantly influence the CSeff for volatile and semi-volatile vapors. Neglecting the evaporation may result in an overestimation of vapor loss rate and hence an underestimation of the fraction of vapor molecules that is left to form clusters.
Environmental significanceThe condensation sink (CS) affects the mass balance of atmospheric vapors and it can also influence the number of vapor molecules that form molecular clusters. These clusters can, if the conditions are suitable, grow to aerosol particles in a phenomenon called atmospheric New Particle Formation (NPF). Atmospheric NPF can influence climate and potentially also air quality. The CS is often determined making multiple assumptions and we evaluate the uncertainty arising from these assumptions. Our results can be applied to determine the CS more accurately for example in aerosol models, leading to a more comprehensive understanding of NPF. |
1 Introduction
New Particle Formation (NPF), the formation and following growth of aerosol particles from atmospheric vapors,1 is globally a major source of atmospheric aerosol particles.1–4 Atmospheric aerosol particles have many effects both on climate2,4–6 and human health.2,7 For example, exposure to aerosol particles is associated with cardiovascular and respiratory diseases and leads to an increase in premature mortality.7 To improve the understanding of impacts of NPF, the processes affecting NPF need to be well understood.For NPF to occur, the availability of atmospheric vapors is essential and thus one of the important parameters for understanding NPF is the condensation sink (CS).8–10 The CS, characterizing the loss rate of atmospheric vapor to aerosol particles, is widely used when studying aerosol dynamics.11 The CS may strongly affect the concentrations of atmospheric vapors and it can, for example, be used in estimating the source rates of atmospheric vapors, or in proxies for their concentrations.12,13 The CS is also important for understanding the mass balance of vapors in chamber studies.14 In addition, the coagulation sink (CoagS), the loss rate of small aerosol particles to larger aerosol particles, can be approximated using the CS.15
The CS depends, in addition to the number size distribution of aerosol particles, on environmental properties such as temperature and atmospheric pressure, and, more significantly, on vapor properties. The vapor properties include the molecular mass and mass accommodation coefficient, which has also been called the sticking probability.16 Several previous studies indicate that the mass accommodation coefficient is very likely close or equal to unity.17–20 However, there is still no consensus on values of the mass accommodation coefficient for atmospherically relevant vapors on aerosol particles in different environments.21,22 Because of this element of uncertainty, it is relevant to consider how much the CS could be reduced if the mass accommodation coefficient differs from unity.
The CS is often determined for a vapor consisting of sulfuric acid molecules, due to the key role of sulfuric acid in the formation of new aerosol particles.23–25 Sulfuric acid in the atmosphere is also expected to often be present clustered with bases and water.26–28 In addition to sulfuric acid and sulfuric acid clusters, organic compounds can have an important role in NPF by participating in cluster formation or by contributing to the growth of freshly formed clusters.29–31 Because the CS depends on the properties of the vapor, the loss rate of atmospheric vapors is expected to vary based on the condensing vapor.
The CS, describing the condensation rate to aerosol particles, is determined assuming irreversible condensation,9,11,13 however, in addition to condensation, there can be evaporation of vapors from the surface of the aerosol particles.9,32 This can affect the net flux of vapor to the particles if evaporation is considerable and thus the CS might not describe the total net loss rate of vapor accurately. In the case of sulfuric acid, this effect of evaporation on the loss rate is likely negligible due to the presence of stabilizing base sources.33–35 However, for atmospheric organic vapors with higher volatilities, evaporation could be significant and affect their loss rate.14,36–38 To describe the net loss rate accounting both for condensation and evaporation fluxes, we use the effective condensation sink (CSeff).
For NPF to occur, molecular clusters need to be formed at a sufficiently high rate. The fraction of vapor molecules that can form clusters is influenced by the loss rate of vapor to pre-existing particles. Thus, the overestimation of the CS and CSeff can lead to inaccurate description of clustering.
The objective of this study is to provide a more comprehensive understanding of the condensation loss rate of atmospheric vapor to aerosol particles: (1) we investigate the dependency of the CS on vapor properties and compare values of the CS for different atmospherically relevant compounds. (2) We determine the dependency of the CS on the mass accommodation coefficient and (3) evaluate the effect of evaporation on the CSeff of atmospheric vapors such as sulfuric acid and oxidized organic vapors. (4) Finally, we determine the effect of mass accommodation coefficient and non-negligible evaporation on the fractions of sulfuric acid molecules that are lost to pre-existing aerosol particles and that form clusters.
2 Methods
2.1 Condensation sink and effective condensation sink
The condensation sink (CS) was calculated using particle number size distribution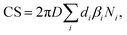 | (1) |
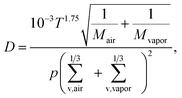 | (2) |
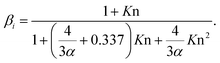 | (3) |
The CS describes the flux of vapor to particles due to condensation. However, in addition there can be a non-negligible flux of the same vapor from particles due to evaporation. The vapor mass balance equation is10
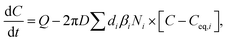 | (4) |
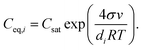 | (5) |
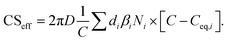 | (6) |
Using CSeff, the vapor mass balance equation is
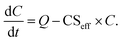 | (7) |
If the influence of Kelvin effect can be assumed to be negligible across the particle number size distribution, Ceq,i ≈ Csat and
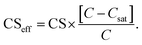 | (8) |
If Csat approaches zero, evaporation flux is negligible, the CSeff approaches the CS and the total loss rate of vapor to particles is only affected by the condensation flux described by the CS. In this work we used the CSeff to describe the total vapor loss rate when evaporation is not assumed to be negligible while the CS was used when evaporation was not considered or when we assumed it to be negligible (CSeff = CS).
2.2 Particle number size distribution
To calculate the CS and CSeff, we used particle number size distribution data measured at the station of Beijing University of Chemical Technology (39°56′31′′N, 116°17′50′′E, Beijing). The number size distributions between 1 nm and 1 μm were measured with a Diethylene Glycol Scanning Mobility Particle Sizer36 and a custom-made Particle Size Distribution system37 between January 2018 and March 2019. In the Beijing measurements, the relative humidity (RH) of the aerosol sample was conditioned to be below 40% by using a Nafion dryer. The hygroscopic growth factor for accumulation mode particles in Beijing has been estimated to be 1.3 at RH = 90%.38 Thus, for our case the error resulting from neglecting hygroscopic growth is likely small. However, it should be noted that depending on the composition of background particles hygroscopic growth can be significant and result in underestimation of the CS and CSeff if it is neglected. The CS and CSeff were calculated from median particle number size distributions between 9 and 12 am (local time, UTC + 8) from data for NPF events and non-NPF days separately. The day was classified as an NPF event day if a new particle mode below 25 nm appeared and growth of that mode was observed in the following hours.39 The days, on which there were clearly no NPF events, were classified as non-NPF days. More details on the particle size distribution measurements and NPF event classification are presented by Zhou et al.40For comparison, we also calculated the CS from a median NPF event day particle number size distribution between January 2018 and March 2019 (9–12 am, UTC + 2) from Hyytiälä, Finland. The particle number size distribution data used to determine the median size distribution was measured at the Station for Measuring Forest Ecosystem-Atmosphere Relations (SMEAR) II (61°5′N, 24°170′E) using a twin DMPS (Mobility Particle Sizer) system.41 For more details on the measurements see e.g. Aalto et al.41
The median particle number size distributions used in this work are presented in Fig. 1. To consider the influence of shape of the particle number size distribution on the CS and CSeff, three different particle number size distributions from two different locations were used. Only particles below 500 nm in diameter are considered to eliminate error resulting from differences in measurement set-ups between the two locations. In this work we did not investigate the dependency of the vapor loss on the particle number size distribution in more depth.
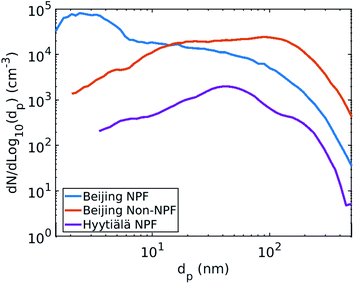 | ||
| Fig. 1 Median particle number size distribution in Beijing, China during NPF event days and non-NPF days, and in Hyytiälä, Finland during NPF event days (9–12 am) from January 2018 to March 2019. | ||
2.3 Investigated cases and system properties
We calculated the CS according to eqn (1). We investigated the sensitivity of the CS on the molecular mass (m) and diffusivity volume (Σv) of the vapor and on the vapor diffusivity (D), which depends on the two aforementioned properties. To demonstrate the effect of vapor properties on the CS, we determined the CS for clusters of sulfuric acid and dimethylamine (DMA) or ammonia, and for the oxidation products of monoterpenes with chemical formulas of C8–10H12–18O4–9 (monomers) and C16–20H24–36O8–14 (dimers).42 In addition, a model oxidized organic molecule (OOM) was used to represent an average atmospheric organic molecule. Properties of model OOM were chosen based on the work by Ehn et al.43 In addition, vapors of oleic acid and C5H10O5, which is an oxidation product of isoprene, were used in Section 3.5. The compounds and their properties are presented in Table 1.| Compound | m (u) | Σ v (cm3) | γ (N m−1) | ρ (kg m−3) |
|---|---|---|---|---|
| Sulfuric acid (SA) | 98.1 | 52.0 | 0.055 | 1830.0 |
| DMA | 45.1 | 52.5 | ||
| Ammonia (NH3) | 18.0 | 11.5 | ||
| 1 SA + 1 DMA | 143.2 | 104.5 | 0.023 | 1500 |
| 2–5 SA + 0–4 DMA | 196.2–670.9 | 104.0–470.0 | ||
| 1–5 SA + 0–4 NH3 | 98.1–562.5 | 52.0–275.5 | ||
| C8–10H12–18O4–9 | 172.0–182.0 | 179.4–255.6 | 0.020 | 1500 |
| C16–20H24–36O8–14 | 344.0–502.0 | 358.7–486.7 | 0.020 | 1500 |
| Model OOM | 325.0 | 300.0 | 0.020 | 1500 |
| Oleic acid | 282.5 | 377.0 | 0.033 | 895.0 |
| C5H10O5 | 150.1 | 133.2 | 0.020 | 1500 |
We also investigated the dependency of the CS on the mass accommodation coefficient α (see eqn (3)). In the calculations, the value of α was assumed to be independent of the particle diameter. α is often assumed to be equal to unity and we estimated the resulting uncertainty if in some case this assumption is inaccurate.
We note that while we have investigated the dependency of vapor loss rates on Σv, m, D and α using the CS, the same dependencies also apply to the total vapor loss rate, CSeff.
Finally, we investigated how much vapor evaporation can affect the vapor loss rate by determining the CSeff according to eqn (6). Both sulfuric acid vapor and model OOM were used to calculate the CSeff. We divided OOMs based on their saturation concentrations to extremely low volatile organic compounds (ELVOCs), low volatile organic compounds (LVOCs) and semi-volatile organic compounds (SVOCs) using a classification based on previous research.42,44,45 For our model OOM if Nsat < 5.56 × 104 cm−3 it was classified as ELVOC, and if Nsat > 5.56 × 108 cm−3 it was classified as SVOC. If Nsat was in between these two limits, model OOM was classified as LVOCs.
To obtain saturation vapor pressures in a system consisting of sulfuric acid and ammonia, we used the E-AIM model (version II; http://www.aim.env.uea.ac.uk, last access: 30.07.2021). For more details on the model see e.g. Clegg et al.46 The sum of sulfuric acid concentrations in the gaseous and aerosol phase was assumed to be equal to 4 × 10−8 mol m−3 (corresponding to 3.9 μg m−3). Relative humidities RH = 10%, 30%, 50% and 70%, and temperatures T = 285 K and 298 K were used. It should be noted that values of vapor pressure were not sensitive to the assumed concentration of sulfuric acid. For example, setting the total concentration of sulfuric acid to 1 × 10−7 mol m−3 instead would not change our results significantly.
It should be noted that atmospheric aerosol particles consist of mixtures of different chemical compounds, which affect the Csat of the condensing species. The interactions of the molecules of the studied condensing species and the molecules of other compounds in the particle phase vary depending on the identity of the compounds, which can be accounted for by using the activity coefficient.35 In this work, we do not explicitly include the activity coefficient in eqn (5). For model OOM, we do not consider the effect of activity. For the system with sulfuric acid and ammonia, Csat obtained from the E-AIM model accounts for activity in a simplified system of water, ammonia and sulfuric acid. However, in a real atmospheric system the chemical composition of particles varies resulting in varying activities and Csat values.
We used atmospheric pressure P = 101![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 Pa in all of our calculations. Temperature T = 285 K was used if not otherwise stated. Choice of T and P had only a minor influence on our results.
325 Pa in all of our calculations. Temperature T = 285 K was used if not otherwise stated. Choice of T and P had only a minor influence on our results.
2.4 Losses of sulfuric acid monomers
To illustrate the effect of changes in the CS on the dynamics of atmospheric systems, we determined the fractions of sulfuric acid monomers lost by condensation to aerosol particles and by clustering of vapor monomers at different CS values, assuming that these are the only loss processes of sulfuric acid monomers and there is for example no losses due to deposition or chemical reactions.We used the kinetic model presented by Cai et al.47 The losses of sulfuric acid monomers due to condensation are determined as
| LCS = CSA(CSSA(1 − η) + CS1SA+DMAη) | (9) |
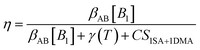 | (10) |
At the kinetic limit the losses due to clustering are
| LKL = β11[A1,tot]2 | (11) |
| L = LKLη(2 − η). | (12) |
3 Results
3.1 Dependency of the CS on vapor properties
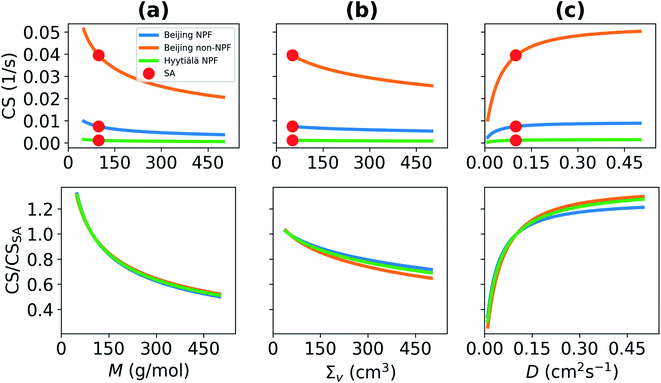
The condensation loss rate of vapor depends on its properties. We investigate the sensitivity of the condensation sink (CS) on the molar mass (M), diffusivity volume (Σv) and on the diffusion coefficient (D), which depends on the former two quantities (Fig. 2). In all cases other properties are assumed to correspond to properties of sulfuric acid vapor (M = 98.08 g mol−1, Σv = 51.96 cm3). We used the median particle number size distributions of NPF days in Beijing and in Hyytiälä, and the median particle number size distribution of non-NPF days in Beijing to determine CS. With increasing M, the CS decreases (Fig. 2a). If M increases to 300 g mol−1, or more, from M of the sulfuric acid monomer, Beijing median NPF day CS decreases by more than 37%. This corresponds to a CS < 0.0046 s−1 instead of a CS = 0.0074 s−1. M and Σv are both properties related to the size and composition of a molecule or a cluster and if M increases, in most cases Σv also changes. However, in this study, we studied the dependency on M and Σv separately. The CS is shown to also decrease with increasing Σv (Fig. 2b). If Σv > 300 cm3, CS < 0.006 s−1, which means that the CS is decreased by around 20% compared to the CS for sulfuric acid. If M and Σv of vapor increase, the diffusion of vapor molecules becomes slower and D decreases. This results in decreasing CS (Fig. 2c).We also see from Fig. 2 that while the choice of particle number size distribution has a large effect on the absolute values of the CS, it has only a minor effect on the behavior of the CS as a function of M, Σv and D. At the most, the ratio of the CS and CSSA differs by less than 10% between the three particle number size distributions. Because of this, we do not include the non-NPF Beijing and NPF Hyytiälä size distributions in further analysis of the CS for different atmospherically relevant compounds (Section 3.2).
Overall, these results illustrate that the CS can get significantly different values depending on vapor properties, and thus inaccurate assumptions about properties of the condensing vapor can lead to significant error in CS. In practice, if the vapor molecule has a larger molecular mass than the sulfuric acid monomer, which is for example the case for many organic vapors, the corresponding CS will be significantly lower than for the CS for sulfuric acid monomers (see Section 3.2). If a vapor has lower molecular mass than sulfuric acid, its CS will be higher than the CS for sulfuric acid.
3.2 CS of different atmospheric vapors and clusters
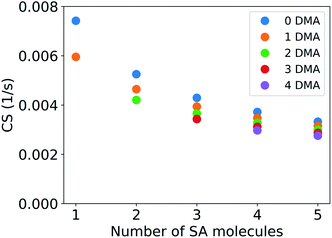
Atmospheric sulfuric acid can be present in clusters consisting of sulfuric acid and other compounds such as dimethylamine (DMA) or ammonia.24,26,27,50,51 The CS of these clusters is different from that of pure sulfuric acid molecules due to their larger mass. For example, if a major fraction of sulfuric acid monomers is present in clusters with DMA, the loss rate of sulfuric acid monomers is decreased as a result.Fig. 3 shows the CS for clusters composed of sulfuric acid and DMA. In the results presented here the CS has been determined using the median NPF day particle number size distribution for Beijing, China. The mass accommodation coefficient (α) is assumed to be equal to unity and evaporation of vapor from particles is assumed to be negligible. A cluster of two sulfuric acid molecules and one DMA has a CS of 0.0046 s−1, which is 62% of the loss rate for the sulfuric acid monomer. A large cluster composed of five sulfuric acid molecules and four DMA has a CS of 0.0028 s−1, which is 38% of the CS for the sulfuric acid monomer. The CS of clusters with one to five sulfuric acid molecules and one to four DMA molecules varies between 19% and 38% of the loss rate for pure sulfuric acid monomers. As discussed in Section 2.1, the CS decreases with increasing molecular number due to increasing mass and diffusivity volume of the cluster. The addition of a sulfuric acid molecule to the cluster changes the CS more compared to the addition of a DMA due to the larger size of the molecules. In the atmosphere sulfuric acid–DMA clusters may also contain water,28 but the addition of water should have relatively little effect on the value of the CS due to the small size of water molecules and is not considered in this study.
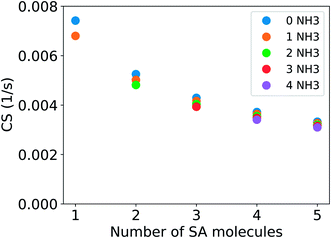
Fig. 4 shows the CS for clusters consisting of sulfuric acid and ammonia. The CS has been determined using the median NPF day particle number size distribution from Beijing, China. For a cluster with two sulfuric acid molecules and one ammonia molecule, CS = 0.0050 s−1, which is 68% of the CS for sulfuric acid monomers. If the vapor consists of clusters of one to five sulfuric acid and one to four ammonia molecules, the CS is between 0.0068 s−1 and 0.0031 s−1, i.e., between 92% and 42% of the CS for pure sulfuric acid monomers. Similar to addition of DMA, addition of ammonia also decreases the CS. However, the change is smaller due to the smaller molecular size of ammonia compared to DMA.
If a major fraction of condensing vapor is expected to be other than sulfuric acid, this should to be taken into account when determining the CS. In Table 2 we have included the CS of some other atmospherically relevant compounds. The CS has been determined using median NPF day particle number size distribution from Beijing, China and we assumed α = 1 and that evaporation is negligible. The CS of the model OOM is 0.0038 s−1, which is 51% of the CS for sulfuric acid. For an oxidized organic monomer with 8–10 carbon atoms, the CS is between 0.0052 and 0.0041 s−1, depending on the composition. For the oxidized organic dimers the CS is 0.0037–0.0031 s−1. Due to their larger mass, many organic vapors are lost to particles at slower rates compared to sulfuric acid vapor.
| Compound | CS (s−1) |
|---|---|
| Sulfuric acid | 7.4 × 10−3 |
| (1–5) sulfuric acid + (0–4) DMA | 7.4 × 10−3 – 2.8 × 10−3 |
| (1–5) sulfuric acid + (0–4) ammonia | 7.5 × 10−3 – 3.1 × 10−3 |
| C8–10H12–18O4–9 | 5.2 × 10−3 − 4.1 × 10−3 |
| C16–20H24–36O8–14 | 3.7 × 10−3 – 3.1 × 10−3 |
| Model OOM | 3.8 × 10−3 |
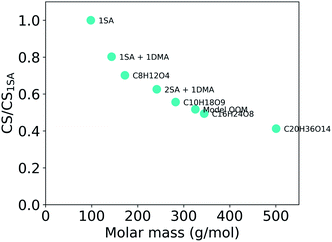
Overall, the CS strongly depends on the composition of the condensing vapor due to the differences in molecular mass and diffusivity. Fig. 5 presents the ratio of CS between different compounds, or clusters, and sulfuric acid as a function of molar mass. It shows a decreasing CS with increasing molar mass of these clusters and compounds. Because the CS varies with the properties of the vapor, the accuracy of assumptions about the properties of condensing vapor should be taken into consideration. For example, if the CS has been calculated for sulfuric acid monomers, that value only characterizes the sink of sulfuric acid monomers and not the sink of sulfuric acid clustered with water or base. In addition, various compounds other than sulfuric acid, such as OOMs, play important roles in atmospheric cluster formation and growth.29–31,44 All of these different vapors have differing loss rates. If the CS is for example used to evaluate the formation of atmospheric clusters, it is worth considering whether the CS should be determined taking into account sulfuric acid molecules, sulfuric acid clustered with bases or water or even OOMs.
One should note that the dependency of the CS on the vapor molecule size is analogous to the dependency of coagulation sink on the particle size. With increasing mass and particle size, the diffusivity of the particle decreases resulting in a lower coagulation sink.8,15 In this work we have treated small clusters similarly to vapor molecules.
3.3 Dependency of the CS on the mass accommodation coefficient
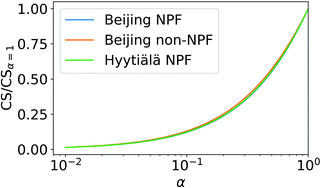
The value of the CS is a function of the mass accommodation coefficient α (see eqn (3)). The significance of this dependency is investigated in this section.Fig. 6 shows the ratio of sulfuric acid CS with varying α to CS assuming α = 1. The CS is determined using median NPF size distributions from Beijing and Hyytiälä and median non-NPF size distribution from Beijing. CS/CSα=1 does not show major dependency on the used particle number size distribution. Thus, we only include the median NPF number size distribution from Beijing for further discussion.
Fig. 7 shows how the CS of sulfuric acid depends on α. If α = 1, CS = 0.0074 s−1. If α < 0.5 then the CS < 0.0041 s−1. Thus, if α < 0.5, the CS is below 56% of the corresponding value when α = 1. Therefore, if a significant fraction of collisions of vapor molecules onto particles does not result in the uptake of molecules, i.e., α < 1, assuming α = 1 results in an overestimation of the vapor loss rate.
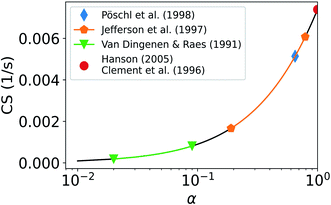
Fig. 7 also includes ranges for α as given by previous studies. Pöschl et al.21 reported the best fit for α of sulfuric acid vapor on aqueous sulfuric acid to be 0.65. If α = 0.65, CS = 0.0051 s−1, and if in this case we then assume α = 1, we will overestimate the CS by 45%. Van Dingenen and Raes52 reported α to be between 0.02 and 0.09 for sulfuric acid vapor on particles of sulfuric acid and water. Using this range of α, the calculated CS ranges from 1.8 × 10−4 s−1 to 8.1 × 10−4 s−1. Jefferson et al.53 reported α to be 0.79 for sulfuric acid on NaCl particles and between 0.19 and 0.31 for sulfuric acid on NaCl particles coated with stearic acid. If α is between 0.19 and 0.79, the CS is between 0.0017 s−1 and 0.0061 s−1. If in these cases α = 1 is assumed, the CS is overestimated by 335% to 21%. Clement et al.17 suggested that for sulfuric acid on atmospheric droplets, α should be near unity. Several more recent studies also suggest that α is close to, or equals, unity for sulfuric acid, organic vapors and water vapor.18,54,55,56 Roy et al.22 reported α of water vapor on organics to be 0.25 at 296 K and to decrease strongly with increasing temperature. Using predictions for α based on multiple previous studies, it becomes apparent that the CS differs strongly based on the assumed value of α.
We assumed the value of α to be constant across all the particle diameters. However, some studies suggest that α increases with increasing particle size.57 Since larger particles cause a larger sink compared to smaller particles, using α that increases with diameter instead of constant α would decrease the effect of non-unity α on CS.
Although several studies suggest that α is unity and that collisions between vapor molecules and aerosol particles stick, there is still no consensus. There is also no research on variance of α between different environments such as boreal forests and megacities. It is possible that atmospheric α could vary for example based on both vapor properties and the properties of background aerosol particles, such as their chemical composition. It is also possible that α varies depending on the size and atmospheric age of the aerosol particles. It is thus important to consider how the assumptions about α influence the value of CS.
In addition to being reduced due to collisions between vapor molecules and particles not sticking, the CS can be increased due to attractive intermolecular forces resulting in an increased number of collisions between molecules and particles.48,49 This enhancement resulting from van der Waals forces has been estimated to be 1.3 for collisions between sulfuric acid molecules and Aitken mode particles.49 Because the CS is dominated by Aitken and accumulation mode particles, we have chosen to neglect this enhancement. However, accounting for it would lead to a minor enhancement of the CS and would result in all CS and CSeff values being slightly larger.
3.4 Influence of evaporation on the total vapor loss rate
Fig. 8 shows the CS as a function of COOM and Csat. With lower COOM and higher Csat, and thus lower saturation, the effect of evaporation becomes significant. Assuming COOM = 108 cm−3 and Csat = 107 cm−3, CSeff = 0.0034 s−1 and it is only 11% lower than CS. At COOM = 108 cm−3 and Csat = 5 × 107 cm−3, CS = 0.0019 s−1, which is 50% of the CS. From Fig. 8 we can also see that for ELVOCs the effect of evaporation on the total vapor loss rate to particles is negligible for all COOM in the test range, but for SVOCs the effect of evaporation on the loss rate can be significant even for COOM up to 1010 cm−3. For both LVOCs and SVOCs in low COOM the evaporation flux can also be larger than the condensation flux and thus there is no condensation losses of vapors to particles. In these cases, the CSeff acts as a rate constant of total evaporation of vapor from aerosol particles, increasing vapor concentration. We have chosen not to show negative CSeff values to keep the focus of this study on vapor losses due to condensation.
We do not take into account in this study that the Csat generally decreases with molecular mass. Therefore, we may overestimate the loss rate of high-volatility molecules such as SVOCs and higher volatility LVOCs whereas underestimate the sink of low-volatility molecules such as ELVOCs. In addition, we do not consider the possible variability in Csat due to differences in particle chemical composition. However, it is clear that when either COOM is low or Csat is high, resulting in low saturation ratio, evaporation considerably reduces the rate that the vapor is lost to the particles.
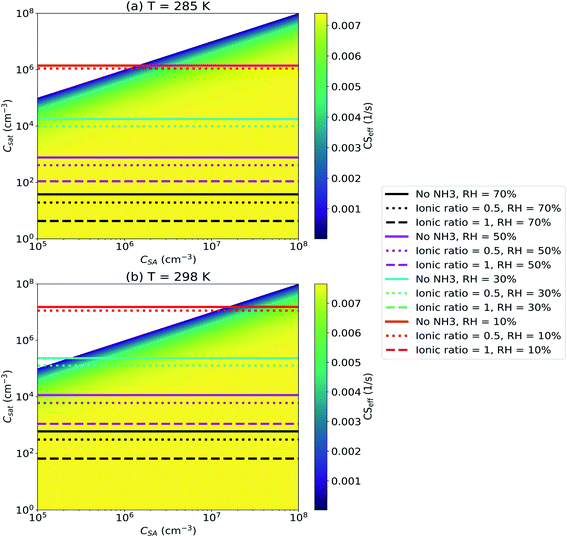
Fig. 9 shows that RH has a major influence on Csat and evaporation only affects the CSeff for low RH due to the large lowering effect of water on SA Csat. At T = 285 K, evaporation has any effect on the CSeff only for RH as low as 10% and for a system with [NH4+]/[SO42−] ≤ 0.5. In systems with higher RH evaporation has no significant effect on the CSeff. At T = 298 K, evaporation lowers the CS if [NH4+]/[SO42−] ≤ 0.5, RH ≤ 30% and CSA < 106 cm−3. It is apparent that the CSeff can be significantly affected by evaporation only if [NH4+]/[SO42−] and RH are low and T is sufficiently high.
We note that we have only considered a system with sulfuric acid, water and ammonia and have not studied systems with other basic components. Saturation concentration of sulfuric acid depends not just on the concentration of basic components but also on the chemical species. Addition of other bases than ammonia such as DMA to the system changes Csat. DMA is a stronger base than ammonia and if the system includes DMA in addition to, or instead of, ammonia, Csat is likely lower and evaporation has less effect on the CSeff.58 The studied system also includes only particles consisting of sulfuric acid, ammonia and water while real atmospheric aerosol particles have varying compositions and consist of a wide range of chemical compounds. Thus, in the atmosphere Csat can vary while here we assume it to be constant.
It appears that in most atmospheric, especially urban, environments the sulfuric acid CSeff is likely not affected by evaporation. Water by itself effectively lowers sulfuric acid Csat and bases such as ammonia, or stronger bases such as DMA, additionally lower Csat resulting in evaporation being negligible compared to condensation. However, it is still possible that in some environments with both low humidity and low concentrations of bases, the sulfuric acid CSeff is significantly reduced due to non-negligible evaporation of sulfuric acid from aerosol particles.
3.5 Relevance of results and implications
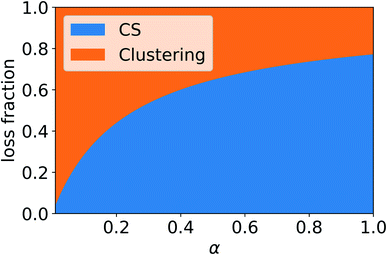
In addition to condensation on pre-existing particles, in the atmosphere vapor can be lost due to other processes, including the formation of molecular clusters, which may grow to larger particles. Therefore, if no other loss processes are considered, reduced vapor loss rate due to non-unity mass accommodation or significant evaporation from particles can increase the rate at which vapor forms molecular clusters. Fig. 10 shows the fraction of sulfuric acid (SA) monomers, including both SA molecules and clusters of one SA and DMA molecule, lost due to the CS and dimer formation as a function of the mass accommodation coefficient α. We can see that as α decreases, reducing the CS, the fraction of monomers lost to dimer formation increases. Compared to the case of α = 1, α has to be around 0.4 or less for the loss fraction due to the CS to decrease by more than 20%, If the CS is reduced due to non-unity α, or other factors such as evaporation affect the loss rate of vapor to particles, a larger number of monomers are potentially left to form dimers, which can then form larger clusters.Table 3 summarizes the CSeff of some atmospheric compounds, considering both previously reported values of α and the possibility of evaporation from particles using Csat values based on previous studies. The CSeff has been determined using the median NPF day particle number size distribution from Beijing, China. These compounds all have different CSeff ranging from 0.0074 s−1 for pure sulfuric acid at Cvapor ≥ 1 × 105 cm−3 to just 0.0018 s−1 at Cvapor = 2.5 × 1010 cm−3 for oleic acid. It is apparent that the vapors are lost to particles at different rates depending on their properties.
| Vapor | α | C sat (cm−3) | C vapor (cm−3) | CSeff (s−1) | % of CS for SA (α = 1) | |
|---|---|---|---|---|---|---|
| SA (no bases, RH = 50%) | 1.0 (0.44) | 770.0 | ≥1 × 105 | 0.0074 (0.0036) | 100 (49) | 17, 18, 21, 52 and 53 |
| SA + DMA | 1.0 (0.44) | 0 | 0.0060 (0.0030) | 81 (41) | 26 and 50 | |
| C10H18O9 | 1.0 | 1.98 × 108 | 1 × 108 | Evaporation > condensation | 30 | 14, 55 and 56 |
| 5 × 108 | 0.0022 | 43 | ||||
| 1 × 109 | 0.0032 | 54 | ||||
| 1 × 1010 | 0.0040 | |||||
| C20H36O14 | 1.0 | 2.6 × 105 | ≥1 × 108 | 0.0031 | 42 | 14, 54 and 55 |
| C5H10O5 | 1.0 | 1.36 × 109 | 1 × 109 | Evaporation > condensation | 32 | 55, 56 and 59 |
| 2.5 × 109 | 0.0024 | 54 | ||||
| 5 × 109 | 0.0040 | 66 | ||||
| 1 × 1010 | 0.0049 | |||||
| Oleic acid | 1.0 | 4.62 × 108 | 1 × 1010 | Evaporation > condensation | 24 | 55 and 60 |
| 2.5 × 1010 | 0.0018 | 39 | ||||
| 5 × 1010 | 0.0029 | 46 | ||||
| 1 × 1011 | 0.0034 |
The lifetime of vapors, and thus also their mass balance, is influenced by their CSeff (eqn (7)). If the vapor source rate and other loss rates are the same, a vapor with smaller CSeff will have a higher vapor concentration. Therefore, the CSeff significantly lower than the estimated value, due to inaccurate assumptions, could lead to the misinterpretation of the results. For example, when estimating the source rate (Q) of vapors in a chamber study using mass balance methods with known vapor concentrations, the source rate is determined using the theoretical loss rate.14 If the loss rate is overestimated due to inaccurate assumptions for CSeff, the source rate will be overestimated. This is demonstrated in Fig. 11, which shows Q needed to maintain constant vapor concentrations of the model OOM (COOM) for different Csat. Q has been determined based on eqn (7). We see that with increasing Csat, Q first appears to stay constant after reaching a certain point after which evaporation of vapor from particles becomes more and more significant and Q needed to maintain COOM steeply decreases.
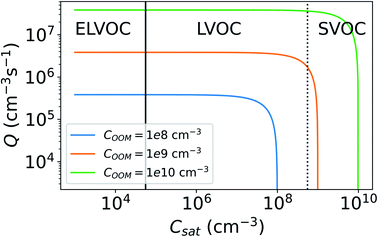 | ||
| Fig. 11 Vapor source rate (Q) needed to maintain a constant vapor concentration (COOM) for different saturation concentrations (Csat). For the vapor balance equations used see eqn (4) and (7). Lines indicate whether the model oxidized organic molecule (OOM) with certain Csat would be categorized as an extremely low volatile organic compound (ELVOC), low volatile organic compound (LVOC) or semi-volatile organic compound (SVOC) (see Sect 2.3). | ||
Differences in the CS and CSeff can also lead to differences in the rate at which vapor forms molecular clusters. If we want to describe the dynamics of atmospheric vapors and aerosol particles as accurately as possible, for example in an atmospheric model, we should account for the differences in the loss rates to particles of different vapors. The differences caused by different sizes of molecules can usually be taken into account if the chemical composition is known, but due to the lack of reported values of evaporation rates or saturation concentrations of vapors, accounting for evaporation of vapor from particles it is often difficult. Similarly, there's still uncertainty related to α and it is unclear whether its values could for example differ between rural and urban areas.
When determining the CS, the choice of the condensing vapor should be considered. If the CS is for example used to characterize and compare the pre-existing particle surface area, which also acts as a sink for freshly formed particles, in different locations, then staying consistent with the choice of condensing vapor and its properties is of more importance than the exact choice of the vapor species. However, if the CS is used to calculate the rate at which vapor is lost to the particles, then the choice of vapor properties is important.
If we are interested in the loss rate of vapors taking part in new particle formation, we should consider whether the vapor is SA or some other compounds such as ELVOCs and choose the properties accordingly. It should also be considered whether the condensing SA is present as pure SA molecules or in clusters with bases, such as ammonia and DMA, or water. For example, if the average cluster consists of one SA molecule and one DMA molecule, error in the CS is around 20% if properties for pure sulfuric acid molecule are used to determine the CS.
Many studies suggest that α = 1 and unless more specific information available it is usually the best assumption when determining the CS and CSeff. However, if the vapor appears to be lost at a lower rate than the CS or CSeff suggests, α being lower than unity could be a potential explanation for this.
Finally, we recommend considering whether the CS or CSeff should be used. If evaporation of the vapor of interest from particles is non-negligible, the CSeff and CS are different and the CS does not describe the net loss rate of the vapor accurately. This can result in a significant error if we are for example interested in the atmospheric vapor mass balance. In most atmospheric environments, the CS and CSeff for SA are likely equal due to the low volatility of SA and thus using the CS to describe the total loss rate of vapor does not result in error. However, if the considered environment has both low RH and base concentrations, it is possible that CSeff is lower than CS. For organic vapors, the CSeff can be considerably lower than the CS. For ELVOCs, CS ≈ CSeff, but for LVOC and SVOC evaporation can considerably affect the loss rate of vapor to particles. When determining the loss rate of LVOCs and SVOCs, we recommend using the CSeff instead of the CS.
4 Conclusions
In this study, we investigate how vapor properties, such as vapor molecular mass, influence the condensation sink (CS). We also evaluate the dependency of the CS on the mass accommodation coefficient (α), characterizing the fraction of collisions between molecules and particles that stick. We also study the effect of evaporation on the total net vapor loss rate to particles, characterized by the effective condensation sink (CSeff). Often, when determining the vapor loss rate, condensing vapor is assumed to be sulfuric acid, α is assumed to be equal to unity and evaporation is neglected. We evaluate the uncertainty arising from these assumptions.We determine the CS and CSeff using median NPF and non-NPF day particle number size distributions from Beijing, China between January 2018 and March 2019. In addition, we use a median NPF day particle number size distribution from Hyytiälä, Finland. The differences in qualitative behavior of our results between the different size distributions are minor suggesting that our results are applicable to environments with different size distributions of background aerosol particles.
Our results show that the CS depends on the size of the vapor molecule or cluster: compounds with larger molecular mass are lost at a slower rate compared to compounds with smaller masses. For example, if a major fraction of the condensing vapor is oxidized organic compounds with large molecular masses, but their properties for CS calculation are assumed to be those of sulfuric acid, the loss rate of the condensing vapor will be overestimated. In addition, if a significant fraction of sulfuric acid is present in clusters with bases, such as dimethylamine, the CS is lower than for pure sulfuric acid molecules.
We demonstrate that if α differs from unity, the CS can be significantly overestimated if unity is assumed. Many studies suggest that α is close or equal to unity and thus this is likely not a significant source of error in reported values of CS. However, until there is a more unified agreement on values of α in different atmospheric environments, this element of uncertainty remains.
We show that the net loss rate of vapor can be influenced by evaporation of vapor from particles and thus the CS determined assuming irreversible condensation is an upper limit for the vapor loss rate. The CSeff may be significantly lower than the CS for example for semi-volatile organic compounds. However, in most urban and rural tropospheric environments evaporation can be expected to have a little effect on the net loss rate of sulfuric acid due to the presence of stabilizing bases and water.
The investigated assumptions are shown to be able to cause significant uncertainty in the CS and CSeff. Overestimation of the condensation loss rate due to inaccurate assumptions can lead to inaccurate understanding of the vapor mass balance and to underestimation of the fraction of vapor molecules that forms clusters. Thus, it is important to take into consideration the properties of the condensing vapor when determining the CS. In addition, possible uncertainty in the CS due to α should be kept in mind. If saturation concentrations of vapors are known, it is also recommended to account for evaporation for organic vapors, when considering the net loss rate of vapor to particles. Our results can in future be applied in describing the vapor loss rates more accurately, for example in atmospheric clustering and particle formation models. Overall, our results increase the understanding of the factors influencing the vapor condensation loss rate in the atmosphere.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We acknowledge the following projects: ACCC Flagship funded by the Academy of Finland (grant no. 337549), Russian Mega Grant project “Megapolis - heat and pollution island: interdisciplinary hydroclimatic, geochemical and ecological analysis” (application reference 2020-220-08–5835), “Quantifying carbon sink, CarbonSink+ and their interaction with air quality” funded by Jane and Aatos Erkko Foundation, European Research Council (ERC) project ATM-GTP (grant no. 742206) and Academy of Finland project no. 316114 and 332547.References
- V.-M. Kerminen, X. Chen, V. Vakkari, T. Petäjä, M. Kulmala and F. Bianchi, Atmospheric new particle formation and growth: review of field observations, Environ. Res. Lett., 2018, 13, 103003 CrossRef.
- U. Pöschl, Atmospheric Aerosols: Composition, Transformation, Climate and Health Effects, Angew. Chem., Int. Ed., 2005, 44, 7520–7540 CrossRef PubMed.
- D. V. Spracklen, K. S. Carslaw, J. Merikanto, G. W. Mann, C. L. Reddington, S. Pickering, J. A. Ogren, E. Andrews, U. Baltensperger, E. Weingartner, M. Boy, M. Kulmala, L. Laakso, H. Lihavainen, N. Kivekäs, M. Komppula, N. Mihalopoulos, G. Kouvarakis, S. G. Jennings, C. O'Dowd, W. Birmili, A. Wiedensohler, R. Weller, J. Gras, P. Laj, K. Sellegri, B. Bonn, R. Krejci, A. Laaksonen, A. Hamed, A. Minikin, R. M. Harrison, R. Talbot and J. Sun, Explaining global surface aerosol number concentrations in terms of primary emissions and particle formation, Atmos. Chem. Phys., 2010, 10, 4775–4793 CrossRef CAS.
- E. M. Dunne, H. Gordon, A. Kürten, J. Almeida, J. Duplissy, C. Williamson, I. K. Ortega, K. J. Pringle, A. Adamov, U. Baltensperger, P. Barmet, F. Benduhn, F. Bianchi, M. Breitenlechner, A. Clarke, J. Curtius, J. Dommen, N. M. Donahue, S. Ehrhart, R. C. Flagan, A. Franchin, R. Guida, J. Hakala, A. Hansel, M. Heinritzi, T. Jokinen, J. Kangasluoma, J. Kirkby, M. Kulmala, A. Kupc, M. J. Lawler, K. Lehtipalo, V. Makhmutov, G. Mann, S. Mathot, J. Merikanto, P. Miettinen, A. Nenes, A. Onnela, A. Rap, C. L. S. Reddington, F. Riccobono, N. A. D. Richards, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, K. Sengupta, M. Simon, M. Sipilä, J. N. Smith, Y. Stozkhov, A. Tomé, J. Tröstl, P. E. Wagner, D. Wimmer, P. M. Winkler, D. R. Worsnop and K. S. Carslaw, Global atmospheric particle formation from CERN CLOUD measurements, Science, 2016, 354, 1119–1124 CrossRef CAS PubMed.
- D. Rosenfeld, S. Sherwood, R. Wood and L. Donner, Climate Effects of Aerosol-Cloud Interactions, Science, 2014, 343, 379–380 CrossRef CAS PubMed.
- N. Bellouin, J. Quaas, E. Gryspeerdt, S. Kinne, P. Stier, D. Watson-Parris, O. Boucher, K. S. Carslaw, M. Christensen, A. -L. Daniau, J. -L. Dufresne, G. Feingold, S. Fiedler, P. Forster, A. Gettelman, J. M. Haywood, U. Lohmann, F. Malavelle, T. Mauritsen, D. T. McCoy, G. Myhre, J. Mülmenstädt, D. Neubauer, A. Possner, M. Rugenstein, Y. Sato, M. Schulz, S. E. Schwartz, O. Sourdeval, T. Storelvmo, V. Toll, D. Winker and B. Stevens, Bounding Global Aerosol Radiative Forcing of Climate Change, Rev. Geophys., 2020, 58(1), e2019RG000660 CrossRef CAS PubMed.
- M. Shiraiwa, K. Ueda, A. Pozzer, G. Lammel, C. J. Kampf, A. Fushimi, S. Enami, A. M. Arangio, J. Fröhlich-Nowoisky, Y. Fujitani, A. Furuyama, P. S. J. Lakey, J. Lelieveld, K. Lucas, Y. Morino, U. Pöschl, S. Takahama, A. Takami, H. Tong, B. Weber, A. Yoshino and K. Sato, Aerosol Health Effects from Molecular to Global Scales, Environ. Sci. Technol., 2017, 51, 13545–13567 CrossRef CAS PubMed.
- M. Kulmala, M. D. Maso, J. M. Mäkelä, L. Pirjola, M. Väkevä, P. Aalto, P. Miikkulainen, K. Hämeri and C. D. O’dowd, On the formation, growth and composition of nucleation mode particles, Tellus B, 2001, 53, 479–490 CrossRef.
- L. Pirjola, M. Kulmala, M. Wilck, A. Bischoff, F. Stratmann and E. Otto, Effects of aerosol dynamics on the formation of sulphuric acid aerosols and cloud condensation nuclei, J. Aerosol Sci., 1999, 30, 1079–1094 CrossRef CAS.
- L. Pirjola, M. Kulmala, M. Wilck, A. Bischoff, F. Stratmann and E. Otto, Formation of sulphuric acid aerosols and cloud condensation nuclei: an expression for significant nucleation and model comparison, J. Aerosol Sci., 1999, 30, 1079–1094 CrossRef CAS.
- M. Kulmala, T. Petäjä, T. Nieminen, M. Sipilä, H. E. Manninen, K. Lehtipalo, M. Dal Maso, P. P. Aalto, H. Junninen, P. Paasonen, I. Riipinen, K. E. J. Lehtinen, A. Laaksonen and V.-M. Kerminen, Measurement of the nucleation of atmospheric aerosol particles, Nat. Protoc., 2012, 7, 1651–1667 CrossRef CAS PubMed.
- L. Dada, I. Ylivinkka, R. Baalbaki, C. Li, Y. Guo, C. Yan, L. Yao, N. Sarnela, T. Jokinen, K. R. Daellenbach, R. Yin, C. Deng, B. Chu, T. Nieminen, Y. Wang, Z. Lin, R. C. Thakur, J. Kontkanen, D. Stolzenburg, M. Sipilä, T. Hussein, P. Paasonen, F. Bianchi, I. Salma, T. Weidinger, M. Pikridas, J. Sciare, J. Jiang, Y. Liu, T. Petäjä, V.-M. Kerminen and M. Kulmala, Sources and sinks driving sulfuric acid concentrations in contrasting environments: implications on proxy calculations, Atmos. Chem. Phys., 2020, 20, 11747–11766 CrossRef CAS.
- M. Kulmala, T. Petäjä, P. Mönkkönen, I. K. Koponen, M. Dal Maso, P. P. Aalto, K. E. J. Lehtinen and V.-M. Kerminen, On the growth of nucleation mode particles: source rates of condensable vapor in polluted and clean environments, Atmos. Chem. Phys., 2005, 5, 409–416 CrossRef CAS.
- O. Peräkylä, M. Riva, L. Heikkinen, L. Quéléver, P. Roldin and M. Ehn, Experimental investigation into the volatilities of highly oxygenated organic molecules (HOMs), Atmos. Chem. Phys., 2020, 20, 649–669 CrossRef.
- K. E. J. Lehtinen, M. Dal Maso, M. Kulmala and V.-M. Kerminen, Estimating nucleation rates from apparent particle formation rates and vice versa: Revised formulation of the Kerminen–Kulmala equation, J. Aerosol Sci., 2007, 38, 988–994 CrossRef CAS.
- N. A. Fuchs and A. G. Sutugin, Highly dispersed aerosols, Topics in Current Aerosol Research, ed. G. M. Hidy and J. R. Brock, Pergamon, vol. 2, 1971 Search PubMed.
- C. F. Clement, M. Kulmala and T. Vesala, Theoretical consideration on sticking probabilities, J. Aerosol Sci., 1996, 27, 869–882 CrossRef CAS.
- D. R. Hanson, Mass Accommodation of H2SO4 and CH3SO3H on Water−Sulfuric Acid Solutions from 6% to 97% RH, J. Phys. Chem. A, 2005, 109, 6919–6927 CrossRef CAS PubMed.
- A. Laaksonen, T. Vesala, M. Kulmala, P. M. Winkler and P. E. Wagner, On cloud modelling and the mass accommodation coefficient of water, Atmos. Chem. Phys., 2004, 4, 7281–7290 Search PubMed.
- P. M. Winkler, A. Vrtala, P. E. Wagner, M. Kulmala, K. E. J. Lehtinen and T. Vesala, Mass and Thermal Accommodation during Gas-Liquid Condensation of Water, Phys. Rev. Lett., 2004, 93, 075701 CrossRef PubMed.
- U. Pöschl, M. Canagaratna, J. T. Jayne, L. T. Molina, D. R. Worsnop, C. E. Kolb and M. J. Molina, Mass Accommodation Coefficient of H2SO4 Vapor on Aqueous Sulfuric Acid Surfaces and Gaseous Diffusion Coefficient of H2SO4 in N2/H2O, J. Phys. Chem. A, 1998, 102, 10082–10089 CrossRef.
- S. Roy, M. E. Diveky and R. Signorell, Mass Accommodation Coefficients of Water on Organics from Complementary Photoacoustic and Light Scattering Measurements on Laser-Trapped Droplets, J. Phys. Chem. C, 2020, 124, 2481–2489 CrossRef.
- Z. B. Wang, M. Hu, D. L. Yue, J. Zheng, R. Y. Zhang, A. Wiedensohler, Z. J. Wu, T. Nieminen and M. Boy, Evaluation on the role of sulfuric acid in the mechanisms of new particle formation for Beijing case, Atmos. Chem. Phys., 2011, 11, 12663–12671 CrossRef CAS.
- L. Yao, O. Garmash, F. Bianchi, J. Zheng, C. Yan, J. Kontkanen, H. Junninen, S. B. Mazon, M. Ehn, P. Paasonen, M. Sipilä, M. Wang, X. Wang, S. Xiao, H. Chen, Y. Lu, B. Zhang, D. Wang, Q. Fu, F. Geng, L. Li, H. Wang, L. Qiao, X. Yang, J. Chen, V.-M. Kerminen, T. Petäjä, D. R. Worsnop, M. Kulmala and L. Wang, Atmospheric new particle formation from sulfuric acid and amines in a Chinese megacity, Science, 2018, 361, 278–281 CrossRef CAS PubMed.
- D. L. Yue, M. Hu, R. Y. Zhang, Z. B. Wang, J. Zheng, Z. J. Wu, A. Wiedensohler, L. Y. He, X. F. Huang and T. Zhu, The roles of sulfuric acid in new particle formation and growth in the mega-city of Beijing, Atmos. Chem. Phys., 2010, 10, 4953–4960 CrossRef CAS.
- A. Kürten, T. Jokinen, M. Simon, M. Sipilä, N. Sarnela, H. Junninen, A. Adamov, J. Almeida, A. Amorim, F. Bianchi, M. Breitenlechner, J. Dommen, N. M. Donahue, J. Duplissy, S. Ehrhart, R. C. Flagan, A. Franchin, J. Hakala, A. Hansel, M. Heinritzi, M. Hutterli, J. Kangasluoma, J. Kirkby, A. Laaksonen, K. Lehtipalo, M. Leiminger, V. Makhmutov, S. Mathot, A. Onnela, T. Petäjä, A. P. Praplan, F. Riccobono, M. P. Rissanen, L. Rondo, S. Schobesberger, J. H. Seinfeld, G. Steiner, A. Tomé, J. Tröstl, P. M. Winkler, C. Williamson, D. Wimmer, P. Ye, U. Baltensperger, K. S. Carslaw, M. Kulmala, D. R. Worsnop and J. Curtius, Neutral molecular cluster formation of sulfuric acid–dimethylamine observed in real time under atmospheric conditions, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15019–15024 CrossRef PubMed.
- S. Schobesberger, A. Franchin, F. Bianchi, L. Rondo, J. Duplissy, A. Kürten, I. K. Ortega, A. Metzger, R. Schnitzhofer, J. Almeida, A. Amorim, J. Dommen, E. M. Dunne, M. Ehn, S. Gagné, L. Ickes, H. Junninen, A. Hansel, V.-M. Kerminen, J. Kirkby, A. Kupc, A. Laaksonen, K. Lehtipalo, S. Mathot, A. Onnela, T. Petäjä, F. Riccobono, F. D. Santos, M. Sipilä, A. Tomé, G. Tsagkogeorgas, Y. Viisanen, P. E. Wagner, D. Wimmer, J. Curtius, N. M. Donahue, U. Baltensperger, M. Kulmala and D. R. Worsnop, On the composition of ammonia–sulfuric-acid ion clusters during aerosol particle formation, Atmos. Chem. Phys., 2015, 15, 55–78 CrossRef.
- H. Henschel, T. Kurtén and H. Vehkamäki, Computational Study on the Effect of Hydration on New Particle Formation in the Sulfuric Acid/Ammonia and Sulfuric Acid/Dimethylamine Systems, J. Phys. Chem. A, 2016, 120, 1886–1896 CrossRef CAS PubMed.
- P. Paasonen, T. Nieminen, E. Asmi, H. E. Manninen, T. Petäjä, C. Plass-Dülmer, H. Flentje, W. Birmili, A. Wiedensohler, U. Hõrrak, A. Metzger, A. Hamed, A. Laaksonen, M. C. Facchini, V.-M. Kerminen and M. Kulmala, On the roles of sulphuric acid and low-volatility organic vapours in the initial steps of atmospheric new particle formation, Atmos. Chem. Phys., 2010, 10, 11223–11242 CrossRef CAS.
- Z. B. Wang, M. Hu, X. Y. Pei, R. Y. Zhang, P. Paasonen, J. Zheng, D. L. Yue, Z. J. Wu, M. Boy and A. Wiedensohler, Connection of organics to atmospheric new particle formation and growth at an urban site of Beijing, Atmos. Environ., 2015, 103, 7–17 CrossRef CAS.
- R. Zhang, I. Suh, J. Zhao, D. Zhang, E. C. Fortner, X. Tie, L. T. Molina and M. J. Molina, Atmospheric New Particle Formation Enhanced by Organic Acids, Science, 2004, 304, 1487–1490 CrossRef CAS PubMed.
- J. C. Barrett and C. F. Clement, Growth rates for liquid drops, J. Aerosol Sci., 1988, 19, 223–242 CrossRef CAS.
- E. N. Fuller, K. Ensley and J. C. Giddings, Diffusion of halogenated hydrocarbons in helium. The effect of structure on collision cross sections, J. Phys. Chem., 1969, 73, 3679–3685 CrossRef CAS.
- R. C. Reid, J. M. Prausnitz and B. E. Poling, The Properties of Gases and Liquids, 4th edn, 1987 Search PubMed.
- J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics: from Air Pollution to Climate Change, John Wiley & Sons, 2016 Search PubMed.
- J. Jiang, M. Chen, C. Kuang, M. Attoui and P. H. McMurry, Electrical Mobility Spectrometer Using a Diethylene Glycol Condensation Particle Counter for Measurement of Aerosol Size Distributions Down to 1 nm, Aerosol. Sci. Tech., 2011, 45, 510–521 CrossRef CAS.
- J. Liu, J. Jiang, Q. Zhang, J. Deng and J. Hao, A spectrometer for measuring particle size distributions in the range of 3 nm to 10 μm, Front. Environ. Sci. Eng., 2016, 10, 63–72 CrossRef CAS.
- J. Meier, B. Wehner, A. Massling, W. Birmili, A. Nowak, T. Gnauk, E. Brüggemann, H. Herrmann, H. Min and A. Wiedensohler, Hygroscopic growth of urban aerosol particles in Beijing (China) during wintertime: a comparison of three experimental methods, Atmos. Chem. Phys., 2009, 9, 6865–6880 CrossRef CAS.
- M. D. Maso, M. Kulmala, I. Riipinen, R. Wagner, T. Hussein, P. P. Aalto and K. E. J. Lehtinen, Formation and growth of fresh atmospheric aerosols: eight years of aerosol size distribution data from SMEAR II, Hyytiälä, Finland, Boreal Environ. Res., 2005, 10, 323–336 Search PubMed.
- Y. Zhou, L. Dada, Y. Liu, Y. Fu, J. Kangasluoma, T. Chan, C. Yan, B. Chu, K. R. Daellenbach, F. Bianchi, T. V. Kokkonen, Y. Liu, J. Kujansuu, V.-M. Kerminen, T. Petäjä, L. Wang, J. Jiang and M. Kulmala, Variation of size-segregated particle number concentrations in wintertime Beijing, Atmos. Chem. Phys., 2020, 20, 1201–1216 CrossRef CAS.
- P. Aalto, K. Hämeri, E. Becker, R. Weber, J. Salm, J. M. Mäkelä, C. Hoell, C. D. O’dowd, H.-C. Hansson, M. Väkevä, I. K. Koponen, G. Buzorius and M. Kulmala, Physical characterization of aerosol particles during nucleation events, Tellus B, 2001, 53, 344–358 CrossRef.
- F. Bianchi, T. Kurtén, M. Riva, C. Mohr, M. P. Rissanen, P. Roldin, T. Berndt, J. D. Crounse, P. O. Wennberg, T. F. Mentel, J. Wildt, H. Junninen, T. Jokinen, M. Kulmala, D. R. Worsnop, J. A. Thornton, N. Donahue, H. G. Kjaergaard and M. Ehn, Highly Oxygenated Organic Molecules (HOM) from Gas-Phase Autoxidation Involving Peroxy Radicals: A Key Contributor to Atmospheric Aerosol, Chem. Rev., 2019, 119, 3472–3509 CrossRef CAS PubMed.
- M. Ehn, J. A. Thornton, E. Kleist, M. Sipilä, H. Junninen, I. Pullinen, M. Springer, F. Rubach, R. Tillmann, B. Lee, F. Lopez-Hilfiker, S. Andres, I.-H. Acir, M. Rissanen, T. Jokinen, S. Schobesberger, J. Kangasluoma, J. Kontkanen, T. Nieminen, T. Kurtén, L. B. Nielsen, S. Jørgensen, H. G. Kjaergaard, M. Canagaratna, M. D. Maso, T. Berndt, T. Petäjä, A. Wahner, V.-M. Kerminen, M. Kulmala, D. R. Worsnop, J. Wildt and T. F. Mentel, A large source of low-volatility secondary organic aerosol, Nature, 2014, 506, 476–479 CrossRef CAS PubMed.
- J. Tröstl, W. K. Chuang, H. Gordon, M. Heinritzi, C. Yan, U. Molteni, L. Ahlm, C. Frege, F. Bianchi, R. Wagner, M. Simon, K. Lehtipalo, C. Williamson, J. S. Craven, J. Duplissy, A. Adamov, J. Almeida, A.-K. Bernhammer, M. Breitenlechner, S. Brilke, A. Dias, S. Ehrhart, R. C. Flagan, A. Franchin, C. Fuchs, R. Guida, M. Gysel, A. Hansel, C. R. Hoyle, T. Jokinen, H. Junninen, J. Kangasluoma, H. Keskinen, J. Kim, M. Krapf, A. Kürten, A. Laaksonen, M. Lawler, M. Leiminger, S. Mathot, O. Möhler, T. Nieminen, A. Onnela, T. Petäjä, F. M. Piel, P. Miettinen, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, K. Sengupta, M. Sipilä, J. N. Smith, G. Steiner, A. Tomè, A. Virtanen, A. C. Wagner, E. Weingartner, D. Wimmer, P. M. Winkler, P. Ye, K. S. Carslaw, J. Curtius, J. Dommen, J. Kirkby, M. Kulmala, I. Riipinen, D. R. Worsnop, N. M. Donahue and U. Baltensperger, The role of low-volatility organic compounds in initial particle growth in the atmosphere, Nature, 2016, 533, 527–531 CrossRef PubMed.
- N. M. Donahue, J. H. Kroll, S. N. Pandis and A. L. Robinson, A two-dimensional volatility basis set – Part 2: Diagnostics of organic-aerosol evolution, Atmos. Chem. Phys., 2012, 12, 615–634 CrossRef CAS.
- S. L. Clegg, P. Brimblecombe and A. S. Wexler, Thermodynamic Model of the System H+–NH4+–SO42−–NO3–H2O at Tropospheric Temperatures, J. Phys. Chem. A, 1998, 102, 2137–2154 CrossRef CAS.
- R. Cai, C. Yan, D. Yang, R. Yin, Y. Lu, C. Deng, Y. Fu, J. Ruan, X. Li, J. Kontkanen, Q. Zhang, J. Kangasluoma, Y. Ma, J. Hao, D. R. Worsnop, F. Bianchi, P. Paasonen, V.-M. Kerminen, Y. Liu, L. Wang, J. Zheng, M. Kulmala and J. Jiang, Sulfuric acid–amine nucleation in urban Beijing, Atmos. Chem. Phys., 2021, 21, 2457–2468 CrossRef CAS.
- T. W. Chan and M. Mozurkewich, Measurement of the coagulation rate constant for sulfuric acid particles as a function of particle size using tandem differential mobility analysis, J. Aerosol Sci., 2001, 32, 321–339 CrossRef CAS.
- D. Stolzenburg, M. Simon, A. Ranjithkumar, A. Kürten, K. Lehtipalo, H. Gordon, S. Ehrhart, H. Finkenzeller, L. Pichelstorfer, T. Nieminen, X.-C. He, S. Brilke, M. Xiao, A. Amorim, R. Baalbaki, A. Baccarini, L. Beck, S. Bräkling, L. Caudillo Murillo, D. Chen, B. Chu, L. Dada, A. Dias, J. Dommen, J. Duplissy, I. El Haddad, L. Fischer, L. Gonzalez Carracedo, M. Heinritzi, C. Kim, T. K. Koenig, W. Kong, H. Lamkaddam, C. P. Lee, M. Leiminger, Z. Li, V. Makhmutov, H. E. Manninen, G. Marie, R. Marten, T. Müller, W. Nie, E. Partoll, T. Petäjä, J. Pfeifer, M. Philippov, M. P. Rissanen, B. Rörup, S. Schobesberger, S. Schuchmann, J. Shen, M. Sipilä, G. Steiner, Y. Stozhkov, C. Tauber, Y. J. Tham, A. Tomé, M. Vazquez-Pufleau, A. C. Wagner, M. Wang, Y. Wang, S. K. Weber, D. Wimmer, P. J. Wlasits, Y. Wu, Q. Ye, M. Zauner-Wieczorek, U. Baltensperger, K. S. Carslaw, J. Curtius, N. M. Donahue, R. C. Flagan, A. Hansel, M. Kulmala, J. Lelieveld, R. Volkamer, J. Kirkby and P. M. Winkler, Enhanced growth rate of atmospheric particles from sulfuric acid, Atmos. Chem. Phys., 2020, 20, 7359–7372 CrossRef CAS.
- C. N. Jen, P. H. McMurry and D. R. Hanson, Stabilization of sulfuric acid dimers by ammonia, methylamine, dimethylamine, and trimethylamine, J. Geophys. Res.: Atmos., 2014, 119, 7502–7514 CAS.
- K. Lehtipalo, L. Rondo, J. Kontkanen, S. Schobesberger, T. Jokinen, N. Sarnela, A. Kürten, S. Ehrhart, A. Franchin, T. Nieminen, F. Riccobono, M. Sipilä, T. Yli-Juuti, J. Duplissy, A. Adamov, L. Ahlm, J. Almeida, A. Amorim, F. Bianchi, M. Breitenlechner, J. Dommen, A. J. Downard, E. M. Dunne, R. C. Flagan, R. Guida, J. Hakala, A. Hansel, W. Jud, J. Kangasluoma, V.-M. Kerminen, H. Keskinen, J. Kim, J. Kirkby, A. Kupc, O. Kupiainen-Määttä, A. Laaksonen, M. J. Lawler, M. Leiminger, S. Mathot, T. Olenius, I. K. Ortega, A. Onnela, T. Petäjä, A. Praplan, M. P. Rissanen, T. Ruuskanen, F. D. Santos, S. Schallhart, R. Schnitzhofer, M. Simon, J. N. Smith, J. Tröstl, G. Tsagkogeorgas, A. Tomé, P. Vaattovaara, H. Vehkamäki, A. E. Vrtala, P. E. Wagner, C. Williamson, D. Wimmer, P. M. Winkler, A. Virtanen, N. M. Donahue, K. S. Carslaw, U. Baltensperger, I. Riipinen, J. Curtius, D. R. Worsnop and M. Kulmala, The effect of acid–base clustering and ions on the growth of atmospheric nano-particles, Nat. Commun., 2016, 7, 11594 CrossRef CAS PubMed.
- R. Van Dingenen and F. Raes, Determination of the condensation accommodation coefficient of sulfuric acid on water-sulfuric acid aerosol, Aerosol. Sci. Tech., 1991, 15, 93–106 CrossRef CAS.
- A. Jefferson, F. L. Eisele, P. J. Ziemann, R. J. Weber, J. J. Marti and P. H. McMurry, Measurements of the H2SO4 mass accommodation coefficient onto polydisperse aerosol, J. Geophys. Res.: Atmos., 1997, 102, 19021–19028 CrossRef CAS.
- J. Julin, M. Shiraiwa, R. E. H. Miles, J. P. Reid, U. Pöschl and I. Riipinen, Mass Accommodation of Water: Bridging the Gap Between Molecular Dynamics Simulations and Kinetic Condensation Models, J. Phys. Chem. A, 2013, 117, 410–420 CrossRef CAS PubMed.
- J. Julin, P. M. Winkler, N. M. Donahue, P. E. Wagner and I. Riipinen, Near-unity mass accommodation coefficient of organic molecules of varying structure, Environ. Sci. Technol., 2014, 48, 12083–12089 CrossRef CAS PubMed.
- X. Liu, D. A. Day, J. E. Krechmer, W. Brown, Z. Peng, P. J. Ziemann and J. L. Jimenez, Direct measurements of semi-volatile organic compound dynamics show near-unity mass accommodation coefficients for diverse aerosols, Commun. Chem., 2019, 2, 1–9 CrossRef.
- P. L. Barclay and J. R. Lukes, Curvature Dependence of the Mass Accommodation Coefficient, Langmuir, 2019, 35, 6196–6202 CrossRef CAS PubMed.
- T. Kurtén, V. Loukonen, H. Vehkamäki and M. Kulmala, Amines are likely to enhance neutral and ion-induced sulfuric acid-water nucleation in the atmosphere more effectively than ammonia, Atmos. Chem. Phys., 2008, 8, 4095–4103 CrossRef.
- J. E. Krechmer, M. M. Coggon, P. Massoli, T. B. Nguyen, J. D. Crounse, W. Hu, D. A. Day, G. S. Tyndall, D. K. Henze, J. C. Rivera-Rios, J. B. Nowak, J. R. Kimmel, R. L. Mauldin, H. Stark, J. T. Jayne, M. Sipilä, H. Junninen, J. M. St. Clair, X. Zhang, P. A. Feiner, L. Zhang, D. O. Miller, W. H. Brune, F. N. Keutsch, P. O. Wennberg, J. H. Seinfeld, D. R. Worsnop, J. L. Jimenez and M. R. Canagaratna, Formation of Low Volatility Organic Compounds and Secondary Organic Aerosol from Isoprene Hydroxyhydroperoxide Low-NO Oxidation, Environ. Sci. Technol., 2015, 49, 10330–10339 CrossRef CAS PubMed.
- C. D. Cappa, E. R. Lovejoy and A. R. Ravishankara, Evaporation Rates and Vapor Pressures of the Even-Numbered C8−C18 Monocarboxylic Acids, J. Phys. Chem. A, 2008, 112, 3959–3964 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2021 |