Towards controlling the reversibility of anionic redox in transition metal oxides for high-energy Li-ion positive electrodes

Abstract

Anionic redox in positive electrode materials in Li-ion batteries provides an additional redox couple besides conventional metal redox, which can be harvested to further boost the energy density of current Li-ion batteries. However, the requirement for the reversible anionic redox activity remains under debate, hindering the rational design of new materials with reversible anionic redox. In this work, we employed differential electrochemical mass spectrometry (DEMS) to monitor the release of oxygen and to quantify the reversibility of the anionic redox of Li₂Ru_0.75M_0.25O₃ (M = Ti, Cr, Mn, Fe, Ru, Sn, Pt, Ir) upon first charge. X-ray absorption spectroscopy, coupled with density functional theory (DFT) calculations, show that various substituents have a minimal effect on the nominal metal redox, yet more ionic substituents and reduced metal–oxygen covalency introduce irreversible oxygen redox, accompanied with easier distortion of the M–O octahedron and a smaller barrier for forming an oxygen dimer within the octahedron. Therefore, a strong metal–oxygen covalency is needed to enhance the reversible oxygen redox. We proposed an electron–phonon-coupled descriptor for the reversibility of oxygen redox, laying the foundation for high-throughput screening of novel materials that enable reversible anionic redox activity.

---

Broader context

Li-rich positive electrodes exhibiting anionic redox have enhanced the energy densities of Li-ion batteries, yet there is no clear understanding of the factors controlling the reversibility of the anionic redox process and enhancing the cycling stability of these materials. In this work, by employing 3d, 4d and 5d transition metal substituted Li₂RuO₃ oxides, we observe that the energetic overlap between the metal and oxygen density of states dictates the rigidity of the oxide sublattice upon lithium deintercalation. Therefore, a large metal–oxygen covalency is necessary for increasing the thermodynamic barrier to form molecular oxygen and to stabilize the oxygen redox intermediates, which is also the key to less disorder introduced in the M–O octahedron upon lithium deintercalation, as shown by X-ray absorption spectroscopies. The experimental oxygen redox reversibility quantified through mass spectrometry thus directly scales with the metal–oxygen covalency and lattice rigidity upon lithium removal. An electron–phonon-coupled descriptor for anionic redox reversibility is proposed, providing opportunities for further screening of low-cost, high-energy electrode materials leveraging anionic redox, to further improve the energy density of Li-ion batteries.

1. Introduction

Positive electrode materials used in commercial lithium-ion batteries are based on layered LiMO₂ (M = Co, Ni, Mn), where the reversible redox of 3d transition metals, including Co³⁺/Co⁴⁺,^1,2 Ni²⁺/Ni⁴⁺ (or Ni³⁺/Ni⁴⁺)^3–5 and Mn³⁺/Mn⁴⁺,^6,7 can deliver capacities of up to 200 mA h g⁻¹. Thackeray et al.^8,9 have synthesized Li₂MnO₃-derived materials such as Li(Li_xMn_yNi_zCo_{1−x−y−z})O₂ (Li-rich Mn-rich NMC)^10–14 which have shown enhanced discharge capacities of ∼300 mA h g⁻¹, coming from cationic redox as well as lattice oxygen redox.^12,13,15,16 The cycling stability of Li-rich Mn-rich NMC shows a significant voltage decay as well as a capacity fade over subsequent cycles, which is related to diminishing oxygen redox upon extended cycling.^10,17 Fundamental understanding for the origin of oxygen redox is needed for the development of novel and non-noble oxides that employ reversible oxygen redox to boost the capacity and energy density of Li-ion batteries.^15,18–21

Li₂MO₃ (M = Ru and Ir)^22–25 has been used as a model system to understand oxygen redox in oxides. Li₂RuO₃^22,24,26 and Li₂IrO₃^25,27 show reversible capacities with a two-electron transfer process and high cycling stability. For example, Tarascon and co-workers have shown that Li₂Ru_1−xMn_xO₃²⁴ and Li₂Ru_1−xSn_xO₃^11,22 deliver first discharge capacities as high as 250 mA h g⁻¹, and capacity retention capabilities higher than 80% after 100 cycles. The capacity corresponding to the second electron transfer has been attributed to reversible lattice oxygen oxidation into peroxo- and superoxo-like species in the bulk.^26,28 Currently, there are two schools of seemingly contradictory thought on the requirement for reversible anionic redox. In the first school of thought, the reversible oxygen redox is proposed to scale with the ionicity of the metal–oxygen bond. Yabuuchi et al.^29,30 have reported that increasing the ionicity of the transition metal and oxygen bond can reduce the overlap between the metal and oxygen electronic density-of-states (DOS),²⁹ forbidding the oxidation of oxygen ion to molecular oxygen. This thinking is exemplified in the superior cycling stability of more ionic oxides Li_1.2Ti_0.4Mn_0.4O₂ and the more depressed oxygen evolution of this material upon charging to 4.8 V_Li, compared with those of Li_1.2Ti_0.4Fe_0.4O₂.²⁹ Further support comes from density functional theory (DFT) calculation results by Doublet et al.,^20,31 where it has been shown that as the charge transfer gap decreases, the covalency of the transition metal and oxygen increases. As a result, this lower charge transfer gap induces more oxygen character at the Fermi level, resulting in a larger degree of charge compensation coming from the oxygen, shortening of the O–O bond, and eventually leading to irreversible oxygen release.²⁰ A certain ionicity between metal and oxygen is needed to maintain reversible oxygen redox.²⁰

The second school of thought argues that more reversible anionic redox activity comes from a more covalent interaction between the transition metal and oxygen bond in the oxide. Saubanère et al.²⁸ have reported from crystal orbital overlap population (COOP) analysis that greater covalent bonding between Ru and O in Li_2−xRuO₃ stabilizes the peroxo-like species upon oxidation more than that in Li_2−xMnO₃. This idea has also been further explored by Bruce and coworkers.¹⁶ In this work, an O K-edge resonant inelastic X-ray scattering (RIXS) study on Li-rich Mn-rich NMC showed an electronic structure fingerprint, which was assigned to the formation of oxygen-localized electron holes, where these researchers concluded that the reversibility of the anionic redox relies on more delocalized M–O bonds from higher M–O covalency. In our previous work by combining X-ray absorption and emission spectra as well as excited states calculations on charged Li_2−xRuO₃,³² we were able to pinpoint the experimental electronic fingerprint of (O–O) σ* states coordinated with Ru d states in core-level spectroscopies. Such type of signature is missing in charged Li_2−xMnO₃,^32,33 which suffers irreversible oxygen redox and molecular oxygen evolution, again highlighting the importance of metal–oxygen covalency in stabilizing anionic redox. In our follow-up work,³³ we showed that such Ru–O covalency results in phonon hardening in the oxide lattice upon lithium deintercalation, resulting in a more stable oxygen sublattice towards oxygen redox intermediates, inducing more reversible oxygen redox. In this work, we hypothesize that the larger degree of overlap between the transition metal and oxygen electronic states introduces a more rigid oxygen sublattice upon lithium deintercalation, resulting in a more reversible oxygen redox.

In this study, for the systematic examination of the role of M–O covalency in reversible anionic redox, we employ Li₂RuO₃ as the host lattice to substitute in different transition metal elements, to slightly tune the covalency between the transition metal and oxygen. We characterize the redox behavior and structural changes using X-ray absorption spectroscopy (XAS). Coupled with differential electrochemical mass spectrometry (DEMS) measurements and electrochemistry, we are able to identify the reversible component of anionic redox in each of the substituted materials and quantify the reversibility of the anionic redox. Through DFT calculations, an electron–phonon-coupled descriptor for the reversibility of anionic redox is then proposed, which allows for future high-throughput screening of next generation high-energy density Li-ion positive electrode materials.

2. Result and discussion

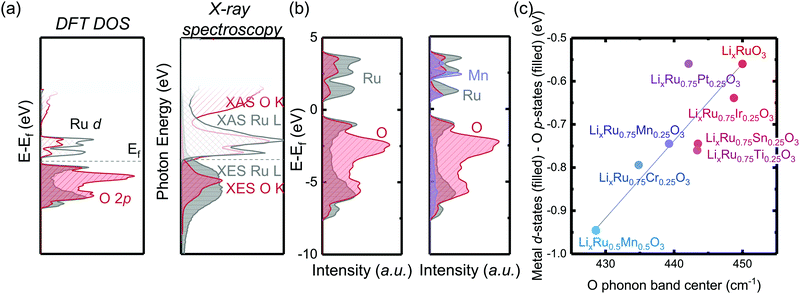
Coupled electronic and phononic trend in M-substituted Li₂RuO₃

By substituting different transition metal elements into the Li₂RuO₃ host lattice, the oxygen phonon band center of delithiated LiRu_xM_1−xO₃, which describes the oxygen lattice integrity upon lithium deintercalation, has a strong positive correlation with the metal–oxygen covalency, characterized by the energetic overlap between metal d states and O p electronic states. From DFT calculations of the projected density of states (pDOS) and experimental density of states from X-ray spectroscopies in Fig. 1(a), Ru has a large degree of overlap with the oxygen states, which is quite different from 3d transition metals such as Mn, where in Li₂MnO₃ it is primarily the nonbonding oxygen, without the presence of Mn states, pinned at the Fermi level, as shown in previous work.³³ The larger degree of overlap between Ru and O electronic states is also manifested when we compare the computed pDOS of Li₂RuO₃ and substituted Li₂Ru_0.75Mn_0.25O₃ in Fig. 1(b), whereby introducing Mn substituents, the total metal d band center of the transition metal shifts downwards, reducing the energetic overlap between oxygen and the transition metal. Such a decrease of energetic overlap between the transition metal and oxygen at the Fermi level induces a more flexible lattice upon lithium deintercalation, as shown in Fig. 1(c). As we decrease the energetic overlap between metal and oxygen near the Fermi level, the O phonon band center of metal oxides upon lithium deintercalation also shifts toward lower frequency, marking a less rigid M–O framework in the delithiated oxides. In our previous works,³³ Li₂(Ru,Ir)O₃, which exhibits reversible lattice oxygen redox, in comparison with Li₂(Mn,Sn)O₃, which releases molecular oxygen upon lithium deintercalation, shows a larger degree of energetic overlap at the Fermi level, leading to more covalent M–O bonds as well as a hardened oxide lattice upon lithium deintercalation. Therefore, we propose that the lattice oxygen redox reversibility scales directly with the metal oxygen energetic overlap near the Fermi level as well as the oxygen phonon band center upon lithium deintercalation. To test this hypothesis, in the next section we will discuss quantification methods of the reversibility of anionic redox and qualify our hypothesis based on substituted Li₂Ru_xM_1−xO₃ (M = Ti, Cr, Mn, Fe, Ru, Sn, Ir, Pt).

Fig. 1 (a) DFT computed pDOS and X-ray absorption and emission spectroscopy (XAS and XES) showing the projected electronic density of states of Li₂RuO₃, where due to the covalent nature of the Ru–O bond, there is a large degree of energetic overlap between the Ru d states and O p states at the Fermi level (dashed line). (b) Computed pDOS of Li₂RuO₃ (left) and Li₂Ru_0.75Mn_0.25O₃ (right), whereby introducing 3d metal dopants, such as Mn⁴⁺, which are in general more electronegative compared with Ru⁴⁺, results in less overlap between the metal and oxygen around the Fermi level. (c) Correlation between the center of mass difference of filled metal d-states and O p-states of fully lithiated M-substituted Li₂Ru_0.75M_0.25O₃ (filled circles) versus the O phonon band center of partially lithiated M-substituted Li₁Ru_0.75M_0.25O₃, where we observed a strong correlation between the M d–O p states and the O phonon band center. This correlation indicates that a smaller difference between M and O electronic states induces a greater overlap at the Fermi level of the oxide, inducing a stiffer oxide lattice upon lithium deintercalation and a larger frequency of the oxygen phonon band center.

Greater oxygen redox reversibility in M-substituted Li₂RuO₃ with increasing metal–oxygen covalency and oxygen lattice hardening

To evaluate the reversibility of anionic redox, DEMS measurements were conducted on the composite Li₂Ru_xM_1−xO₃ electrodes to detect the evolution of molecular oxygen, where by substituting different transition metal elements, the amount of oxygen evolved in general increases with more electronegative substituents (Fig. 2). DEMS data reveal similar onset potentials and amounts of CO₂ outgassing for the charged composite Li₂Ru_xM_1−xO₃ (M = Ti, Cr, Mn, Fe, Ru, Sn, Ir, Pt) electrodes (Fig. 2 and Fig. S1, ESI†), which are typically attributed to the decomposition of the electrolyte at high potentials.^34,35 The similar amount of CO₂ evolution across different chemistries is rooted in the same amount of electrolyte in the cell and similar surface area of the positive electrode active materials. The voltage onset of CO₂ evolution around 4.1 V_Li is comparable to other Ru based systems such as Li_1.2Ni_0.2Ru_0.6O₂ reported in the literature,³⁶ yet is not detected in Li₂Ru_0.75Sn_0.25O₂ in Sathiya et al.²² due to the potential insensitivity of their measurement and a lower amount of electrolyte used in the cell. Such CO₂ potential onset occurs slightly earlier than that for 3d-based Li-rich systems, which is around 4.5 V_Li for Li-rich NMC Li_1.17[Ni_0.22Co_0.12Mn_0.66]_0.83O₂,³⁴ Li_1.2Ni_0.2Mn_0.6O₂³⁷ and disordered rock-salt Li₂Mn_2/3Nb_1/3O₂F.³⁸ While the oxygen evolution profile varies drastically across different chemistries, for Li₂Ru_xM_1−xO₃ (M = Ru, Pt, Ir, Ti) with relatively more covalent metal–oxygen interactions, we observe a similar oxygen evolution profile, where after the onset of oxygen evolution, there is a continuous and steady-rate oxygen evolution without any obvious peak feature (Fig. S1, ESI†). Materials represented by Li₂Ru_xM_1−xO₃ (M = Cr, Mn, Fe, Sn) with slightly less covalent M–O bonds have a much more well-defined oxygen evolution peak, with an onset at a higher state-of-charge compared with the other materials, also with a relatively larger amount of oxygen evolved (Fig. 2). The oxygen evolution profile we observed in Li₂Ru_0.75Sn_0.25O₂ is also very close to what was observed by Sathiya et al.²² However, the difference in oxygen evolution profiles, which seems to depend on the electronic structures of the oxides, is not pointed out in previous works on the Li-rich systems and requires more detailed studies in the future to understand the physical origin.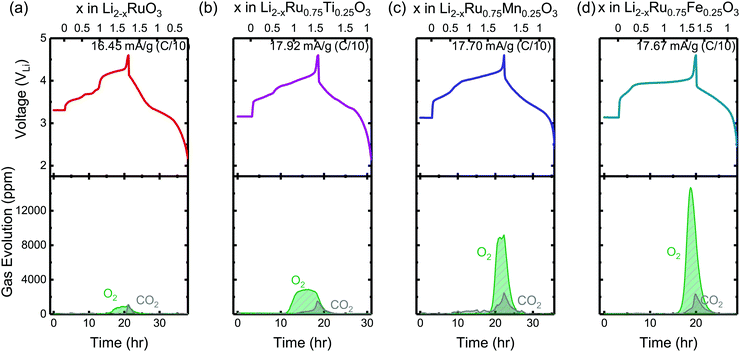

Fig. 2 The charge and discharge voltage profiles (top panels) of (a) Li₂RuO₃, (b) Li₂Ru_0.75Ti_0.25O₃, (c) Li₂Ru_0.75Mn_0.25O₃ and (d) Li₂Ru_0.75Fe_0.25O₃ composite electrodes in two-electrode cells with lithium as the counter electrode as well as the concentration of CO₂ and O₂ (ppm) detected upon charging from DEMS (bottom panels). The cell volume is controlled around 6 cm³ and the cell is pressurized with argon to 22 psi with a flushing interval of 10 min. The electrodes were charged at a C/10 rate (∼16.45–17.92 mA g⁻¹) during DEMS measurements with current density labeled on the right corner of the top panels. The DEMS data of other substituted systems Li₂Ru_xM_1−xO₃ (M = Ir, Sn, Pt, Cr, Mn) are shown in Fig. S1 (ESI†).

The reversibility of the anionic redox activity defined in this work is shown to increase for more covalent metal substituted Li₂Ru_xM_1−xO₃ (M = Ti, Cr, Mn, Fe, Ru, Sn, Pt, Ir) and a more rigid oxygen lattice upon lithium deintercalation. To quantify the reversibility of the anionic redox process experimentally, we here first define the anionic reversibility figure of merit as 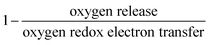, where oxygen release could be measured as the integrated total oxygen released during the first charge cycle, as measured by DEMS (detailed methods and quantification methods are discussed in the Methodology section), and the electron transfer can be obtained by integrating the dQ/dV curve for the second plateau, which has been shown in earlier works^11,32 associated with oxygen redox, upon first charge (shown in Methods in details). The larger this figure of merit, suggesting a smaller oxygen release with respect to the total electron transfer associated with oxygen, the more reversible is the anionic redox. Such a definition can more effectively decouple the oxygen redox from the metal redox, where one could alternatively define a such figure of merit by using , yet such definition introduces the complexity that substituent metals and Ru might also be reduced in addition to oxygen redox upon discharge,^11,15,17,22 where the discharge profile typically has one convoluted plateau.¹¹ As a result, this definition would introduce more complexity in separating the metal reduction and oxygen reduction process upon discharge.¹¹ In the definition employed in our work, we only use the information from the first charge, and the high-voltage plateau has been shown clearly to be related to the oxygen-redox plateau in previous work,^11,32 which is quite easy to separate from the cationic redox that is represented by the lower-voltage plateau.^11,22,27,32 Here we examine this defined figure of merit as a function of the computed energetic difference between filled M d and O p states and the O phononic band center in Fig. 3(a) and (b). As we increase the distance between the metal d states and oxygen p states, we are decreasing the covalency and bond strength between metal and oxygen around the Fermi level, resulting in less reversible oxygen redox activity. (Fig. 3(a)) This decrease of bond covalency between M and O is also evident in the simultaneous drop in the stiffness of the M–O framework upon lithium extraction (Fig 1(c)), inducing a lower oxygen phonon band center for the delithiated oxides. This coupling between the electronic structure and lattice dynamics has shown that the reversibility of the anionic redox also trends nicely with the oxygen phonon band center, where a softer oxygen lattice upon lithium removal induces generally more irreversible oxygen redox behavior. It is worth noting that lithium deintercalation from Li₁MO₃ to Li_0.5MO₃ results in a softening of the oxygen lattice for most of the substituted systems. We believe that such an observation is due to the incapability of the transition metals to be further oxidized from 5+ to 6+ in an octahedral environment,^32,39 therefore the oxide lattice become less rigid upon lithium deintercalation,³³ which is the case for M = Ti, Mn, Ru, Sn. However, for the case of the Cr-substituted system, Cr can be oxidized all the way up to 6+ in solid state,⁴⁰ further increasing the covalency between M–O and the oxide lattice stiffness, pushing up the oxygen phonon band center. Moreover, the oxygen phonon band center for Li_0.5CrO₃ is also shifted upwards by the high frequency of the short O–O vibration upon lithium deintercalation as shown in Fig. S3(c) (ESI†). Furthermore, the observed trend is not dependent on the method we use to calculate the electron transfer correlated with the oxygen redox. If we calculate the oxygen redox electron transfer by alternatively integrating the total electrons transferred after the onset of oxygen gas evolution, the reversibility still trends with the electronic structure and phononic descriptors as shown in Fig. S5 (ESI†).

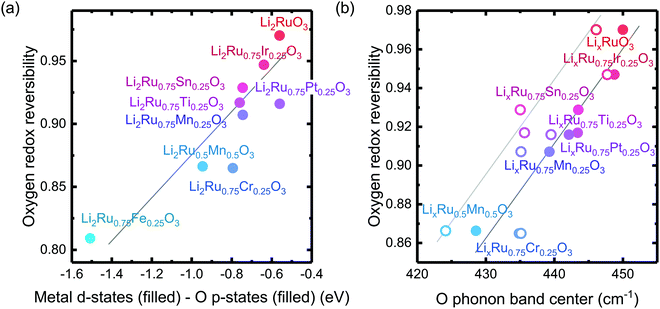Fig. 3 Oxygen redox reversibility 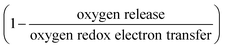as a function of (a) DFT calculated M d–O p states (eV) and (b) oxygen phonon band center of Li₂Ru_0.75Fe_0.25O₃, Li₂Ru_0.75Mn_0.25O₃, Li₂Ru_0.75Pt_0.25O₃, Li₂Ru_0.75Sn_0.25O₃, Li₂RuO₃, Li₂Ru_0.75Ir_0.25O₃, Li₂Ru_0.75Ti_0.25O₃, Li₂Ru_0.75Cr_0.25O₃, Li₂Ru_0.5Mn_0.5O₃, where the raw DEMS spectra and the corresponding electrochemical profile of those compounds to calculate the reversibility figure of merit are shown in Fig. S1 (ESI†). The open circles represent the calculated O phonon band center of Li_0.5Ru_0.75M_0.25O₃ and the closed circles represent the calculated O phonon band center of Li₁Ru_0.75M_0.25O₃. The raw electronic pDOS of those compounds to calculate the M d–O p states are shown in Fig. S2 (ESI†). The oxygen phonon band center is obtained from our previous work³³ and additional calculations are shown in Fig. S3 and S4 (ESI†), where for the substituted compounds, the phonon band center is taken as the weighted sum of the two endpoint compounds to simplify the calculations, as shown in previous work.⁴¹ The methodology of calculating the figure of merit is shown in the Methods section. The trend still stands as we switch to another method of integrating the charge based on the DEMS information, as shown in Fig. S5 (ESI†). The oxygen redox reversibility follows a linear trend with M–O covalency, described by the electronic structure, as well as the rigidity of the delithiated oxides lattice, as described by the phonon structure. A more covalent metal oxide induces a more rigid lattice upon lithium intercalation, resulting in a more reversible oxygen redox.

Ru/metal and oxygen redox from XAS of Li_2−xRu_0.75M_0.25O₃ (M = Mn, Ti, Fe)

To further understand the underlying mechanism for the observed trend, XAS was conducted on Ru and other transition metal substituents to reveal the redox process and structural evolution upon lithium deintercalation. XAS Ru L₃-edge data for Li_2−xRu_0.75M_0.25O₃ (M = Mn, Ti and Fe) revealed comparable oxidation of Ru to that of Li_2−xRuO₃ with lithium de-intercalation, as shown in Fig. 4(a)–(c), respectively. The spectra of oxide-only Li_2−xRu_0.75M_0.25O₃ (M = Mn, Ti and Fe) pellets are comprised of two major features:⁴² one at a lower photon energy, corresponding to the MO interaction with electrons with t_2g parentage, and the other at a higher photon energy, corresponding to the MO interaction with electrons with e_g parentage, which are similar to those reported previously for Li_2−xRuO₃.³² The onset energy of Ru L₃-edge for Li_2−xRu_0.75M_0.25O₃ (M = Mn, Ti and Fe) was found to shift towards a higher photon energy (upon removing ∼0.8 Li for Mn and Fe substitution and ∼0.5 Li for Ti substitution), indicating Ru oxidation during the first plateau, and then a shift towards a lower photon energy with further lithium de-intercalation, as shown in Fig. 4(d). This trend found for the onset energy of the Ru L₃-edge of charged Li_2−xRu_0.75M_0.25O₃ is similar to that of Li_2−xRuO₃ reported previously,³² which has been attributed to Ru oxidation followed by reductive coupling triggered by lattice oxygen redox.^22,27,32 This consistent Ru redox trend across different layered chemistries studied in this work highlights the limitation of the Ru redox, where Ru⁴⁺ is only able to be oxidized to Ru⁵⁺ upon removing 1 e⁻/Ru, followed by Ru reduction upon further oxidation associated with oxygen redox. Moreover, as observed in our previous work,³² such observed Ru redox process is not dependent on the quantification methods that we employ to represent the Ru oxidation state. Further support of this observed redox process comes from the analysis of the t_2g/e_g peak ratio (Fig. 4(e)) and t_2g–e_g splitting (Fig. S7, ESI†) as well as the white-line centroid (Fig. S8, ESI†). From those analyses, Ru was first oxidized, accompanied by a larger t_2g/e_g peak ratio and t_2g–e_g splitting, with the pre-peak centroid shifting towards a higher photon energy; Ru was then reduced after removing ∼0.8 Li, coupled with a smaller t_2g/e_g peak ratio and t_2g–e_g splitting (Fig. S7, ESI†), and the centroid shifted back to a lower photon energy (Fig. S8, ESI†). As we pointed out in a previous study,³² such reductive coupling observed in Ru is not necessarily the sole result of molecular oxygen evolution (Fig. 4(d)), as the amount of oxygen released cannot explain such a large degree of metal reduction. Moreover, the oxygen release onset observed in the DEMS measurements is at a higher state-of-charge than was observed for the inflection point of the Ru L-edge energy of the charged oxides. Furthermore, different metal substituted systems exhibit drastically different amounts of oxygen release, where Li_2−xRu_0.75Fe_0.25O₃ evolves ∼0.16 mol O₂ per f.u., in contrast with Li_2−xRuO₃, which evolves 0.02 mol O₂ per f.u., yet the degree of Ru backshift observed in those systems upon lithium deintercalation is quite close, at around 0.15 eV. Therefore, the Ru reduction/backshift upon lithium removal in the second plateau is not necessarily the result of molecular oxygen evolution, but more of lattice oxygen redox. It is interesting to note, as we pointed out previously,³² that lattice oxygen redox results in a broadening of the e_g peak towards a high photon energy. By quantifying the FWHM of the e_g peak through peak fitting (Fig. S12, ESI†), we observe that there is a sharp increase in the e_g peak width upon removing 1 e⁻/Ru after entering the high-voltage plateau, further verifying the assumption that the high-voltage plateau represents the lattice oxygen redox pointed out in previous publications.^11,32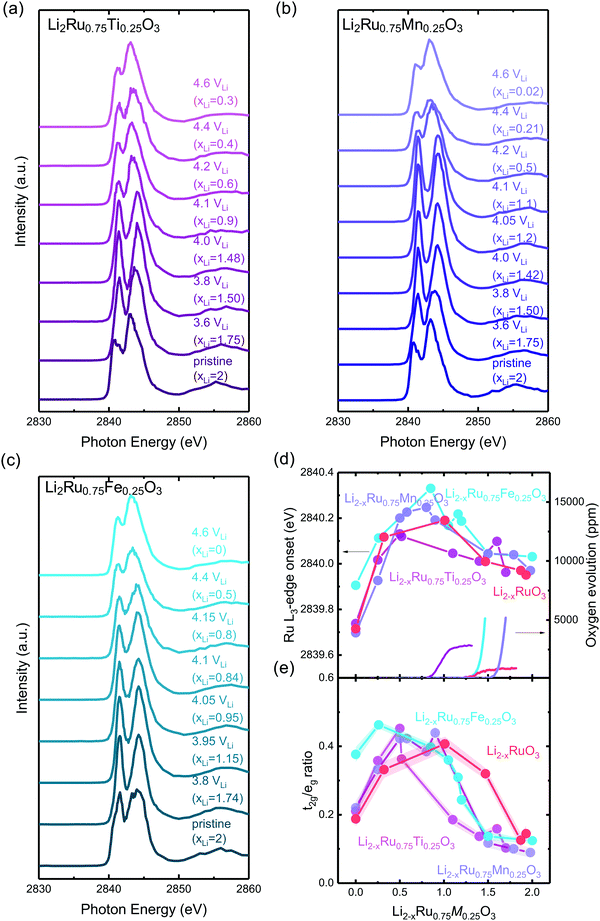

Fig. 4 Ru L₃-edge spectra of (a) Li₂Ru_0.75Ti_0.25O₃ pristine and charged pellets to 3.6, 3.8, 4.0, 4.1, 4.2, 4.4, 4.6 V_Li, (b) Li₂Ru_0.75Mn_0.25O₃ pristine and charged oxide-only pellets to 3.6, 3.8, 4.0, 4.05, 4.1, 4.2, 4.4, 4.6 V_Li and (c) Li₂Ru_0.75Fe_0.25O₃ pristine and charged pellets to 3.8, 3.95, 4.05, 4.1, 4.15, 4.4, 4.6 V_Li, where the quantification of the Ru oxidation states using the edge onset and t_2g/e_g ratio is shown in (d) and (e), respectively. The t_2g and e_g areas are determined by fitting two Gaussian peaks with a linear background removed. Quantification of the Ru oxidation state using an alternative method with t_2g and e_g centroids are shown in Fig. S7 and S8 (ESI†), where we have shown similar oxidation and reduction trends to that shown in (d). Details of the Gaussian fitting are shown in Fig. S9–S11 (ESI†). The quantification of previously reported Li₂RuO₃³² is also shown for comparison for the substituted systems in (d) and (e), where the edge onset is manually shifted by 0.7 eV for better comparison because Li₂RuO₃ and Li₂Ru_0.75M_0.25O₃ (M = Ti, Mn, Fe) were measured at two different beamtimes, and there is a slight shift in the beam energy.

Hard X-ray XAS on the transition metal K-edge shows minimal involvement of the substituted metals in Li₂Ru_0.75M_0.25O₃ (M = Mn, Ti, Fe). XAS of Ti and Mn in the substituted systems shows a similar slight reduction upon charging in Li₂Ru_0.75M_0.25O₃ (M = Mn, Ti), whereas Fe K-edge data show a slight oxidation of Fe³⁺ upon Li removal in Li₂Ru_0.75Fe_0.25O₃ (Fig. S13, ESI†). As we remove Li from the oxide-only pellets of Li₂Ru_0.75M_0.25O₃ (M = Mn, Ti), we observe a slight shift towards a lower photon energy, which is captured in the quantification of the oxidation state using the edge onset in Fig. S6(c) (ESI†), indicating a slight reduction of Mn or Ti upon charging. As a result, due to the incapability of both Mn⁴⁺ and Ti⁴⁺ being further oxidized in the octahedral environment, we observed minimal changes in the oxidation state of Mn and Ti upon removing most of the Li in the lattice (Fig. S13(b) and (d), ESI†). On the other hand, in the Fe system, due to the instability of Fe⁴⁺ in the solid-state, the pristine Li₂Ru_0.75Fe_0.25O₃ shows an oxidation state of Fe³⁺. Upon lithium deintercalation by removing around 1.75 Li per f.u. in Li₂Ru_0.75Fe_0.25O₃, there is a clear oxidation, yet such oxidation of Fe is quite subtle, reaching an edge of 7124.3 eV at half-rise, compared with an edge of around 7128–7129 eV, which is roughly the theoretical Fe⁴⁺ edge onset by linear extrapolation of the edge energy of Fe²⁺ and Fe³⁺. As a result, even though the charged Li₂Ru_0.75Fe_0.25O₃ shows a slightly different trend in Fe oxidation compared with Mn and Ti in charged Li₂Ru_0.75Mn_0.25O₃ and Li₂Ru_0.75Ti_0.25O₃, the degree of involvement of those transition metals in redox is negligible compared to Ru in those substituted systems, as shown in Fig. 4.

Disorder in the first-shell M–O coordination from metal K-edge EXAFS of Li_2−xRu_0.75M_0.25O₃

Transition metal K-edge extended X-ray absorption fine structure spectroscopy (EXAFS) reveals a significant reduction in intensity in the first-shell coordination of Ti–O and Fe–O in Li_2−xRu_0.75M_0.25O₃ (M = Ti and Fe) with lithium de-intercalation in Fig. 5(b) and (d), respectively, in contrast to that of Ru–O in Li_2−xRuO₃ and Mn–O in Li_2−xRu_0.75Mn_0.25O₃ in Fig. 5(a) and (c), respectively. Fourier-transformed spectra in the R-space (Fig. 5(a)–(d)) show two major contributions, one located at a reduced distance of around 1.5 Å, representing M–O coordination, and the other located at a reduced distance of around 2.5 Å, representing M–M coordination. Similarly, Fourier-transformed Ti K-edge EXAFS of Li_2−xRu_0.75Ti_0.25O₃ (Fig. 5(b)) and Fourier-transformed Fe K-edge EXAFS of Li_2−xRu_0.75Fe_0.25O₃ (Fig. 5(d)) reveal significant decreases in the Ti–O and Fe–O coordination upon charging, respectively. On the other hand, substituting Ru with Mn in Li_2−xRuO₃ led to an insignificant reduction in the Mn–O coordination in the first shell from Mn K-edge EXAFS, as shown in Fig. 5(c), having a slight reduction of Mn–O coordination by ∼20% in intensity upon lithium removal in charged Li_2−xRu_0.75Mn_0.25O₃. The insignificant reduction in the Mn–O coordination in the first shell of Li_2−xRu_0.75Mn_0.25O₃ is accompanied with minimal changes observed in the Ru–O coordination in the Fourier-transformed Ru K-edge EXAFS of Li_2−xRu_0.75Mn_0.25O₃ in Fig. S19(a) (ESI†), compared with that in Li_2−xRuO₃ (Fig. 5(a)).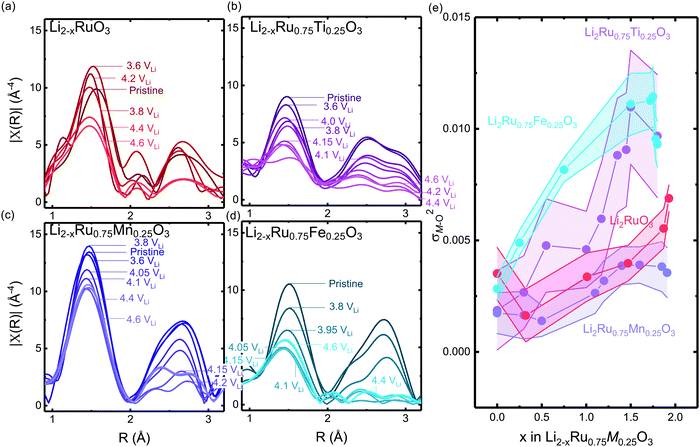

Fig. 5 (a) Fourier-transformed Ru K-edge EXAFS spectra in the R space of pristine Li_2−xRuO₃ and pellets charged to 3.6 (x_Li = 1.68), 3.8 (x_Li = 0.99), 4.2 (x_Li = 0.53), 4.4 (x_Li = 0.13), 4.6 V_Li (x_Li = 0.07). (b) Fourier-transformed Ti K-edge EXAFS spectra in the R space of oxide-only pristine Li_2−xRu_0.75Ti_0.25O₃ and pellets charged to 3.6 (x_Li = 1.7), 3.8 (x_Li = 1.45), 4.0 (x_Li = 1), 4.1 (x_Li = 0.83), 4.15 (x_Li = 0.65), 4.2 (x_Li = 0.55), 4.4 (x_Li = 0.5), 4.6 V_Li (x_Li = 0.2), where the k-space raw data are shown in Fig. S14(a) (ESI†). (c) Fourier-transformed Mn K-edge EXAFS spectra in the R space of oxide-only pristine Li₂Ru_0.75Mn_0.25O₃ and pellets charged to 3.6 (x_Li = 1.7), 3.8 (x_Li = 1.5), 4.05 (x_Li = 0.9), 4.1 (x_Li = 0.8), 4.15 (x_Li = 0.6), 4.2 (x_Li = 0.4), 4.4 (x_Li = 0.15), 4.6 V_Li (x_Li = 0.09), where the k-space raw data are shown in Fig. S14(b) and the detailed fitting parameter is shown in Table S3 (ESI†). (d) Fourier-transformed Fe K-edge EXAFS spectra in the R space of pristine Li₂Ru_0.75Fe_0.25O₃ and pellets charged to 3.8 (x_Li = 1.75), 3.95 (x_Li = 1.25), 4.05 (x_Li = 0.5), 4.1 (x_Li = 0.28), 4.15 (x_Li = 0.25), 4.4 (x_Li = 0.22), 4.6 V_Li (x_Li = 0.2), where the k-space raw data are shown in Fig. S14(c) (ESI†). (e) Fitted pseudo Debye–Waller factor of Ru–O, Ti–O, Mn–O and Fe–O from the EXAFS data shown in (a)–(d), and the detailed fitting results are summarized in Fig. S15–S18 (ESI†), respectively, and in Tables S1–S4 (ESI†). Here, Li₂Ru_0.75Ti_0.25O₃ and Li₂Ru_0.75Fe_0.25O₃ show a significant reduction in the M–O peak intensity compared with Li₂Ru_0.75Mn_0.25O₃ at a high state-of-charge, which is responsible for the difference in the increase of the pseudo Debye–Waller factor.

The decrease in the M–O intensity^43–45 and metal–oxygen coordination in the first shell (MO₆) for Ti–O (Fig. 5(b)) can be attributed to the considerable disordering in the first-shell introduced by lithium deintercalation, compared with Mn–O (Fig. 5(c)). The creation of considerable oxygen vacancies cannot be used to explain the observed large reduction in Ti–O in comparison with Mn–O coordination in the EXAFS spectra. Li_2−xRu_0.75Ti_0.25O₃ (with an oxygen release of 0.08 mol O₂/mol_oxide) has an oxygen evolution that is very comparable to Li_2−xRu_0.75Mn_0.25O₃ (with an oxygen release of 0.12 mol O₂/mol_oxide) based on the DEMS measurements shown in Fig. 2. If we assume that the oxygen vacancies created were distributed uniformly throughout the bulk of particles instead of being concentrated near the surface region, the similarity in the amount of oxygen evolved cannot explain the drastic difference in M–O contribution evolution upon charge. Moreover, the transition metal vacancy induced by metal dissolution as a parasitic reaction upon charging can also not be the likely reason for the difference observed in the metal K-edge EXAFS, because previous studies have shown that it is more difficult to dissolve Ti⁴⁺ in comparison with Mn⁴⁺ by substituting Ti into 0.5Li₂MnO₃–0.5LiNi_0.5Mn_0.5O₂.⁴⁶ Therefore, the increased reduction in the first-shell Ti–O coordination can be attributed to a greater pseudo Debye–Waller factor of M–O coordination extracted from the EXAFS spectra for Li_2−xRu_0.75Ti_0.25O₃ than Li₂RuO₃ and Li_2−xRu_0.75Mn_0.25O₃ (Fig. 5(a) and (c)), coming from a distorted M–O octahedron upon lithium deintercalation. On the other hand, for charged Li_2−xRu_0.75Fe_0.25O₃, which evolves a more significant amount of oxygen (∼0.16 mol per f.u.) compared with other systems studied by EXAFS, the more significant reduction in the Fe–O contribution in Fe EXAFS spectra compared with Mn and Ru based systems might be the compounded result of oxygen vacancy creations and octahedral distortion. To verify the hypothesis on the differences in tendency toward octahedral distortion across different substituted Li_2−xRu_0.75M_0.25O₃ upon lithium deintercalation, the systematic tuning of oxygen framework distortion is studied using DFT in the next section.

Tuning of the O–O distance shows evidence of two competing mechanisms of irreversible oxygen redox

Computational tuning of the oxygen–oxygen distance in Li₀Ru_0.75M_0.25O₃ (M = Ti, Mn, Ru) shows that by introducing less covalent substitutions from Ru to Ti or Mn, the barrier of forming oxygen dimers within the MO octahedron is reduced. Moreover, the observed more depressed M–O contribution in the Ti-substituted system at high states-of-charge from EXAFS comes from an easier MO octahedral distortion for Ti compared with Ru and Mn. Here, we employed the fully delithiated structures as the starting structures, where we selected an oxygen–oxygen pair, either within the oxygen octahedron or across two layers (shown schematically in Fig. 6(a) and (b) insets), where we forced that pair to have a fixed shorter distance, while allowing the other atoms in the unit cell to relax. Therefore, we are able to probe the barrier of O–O bond formation either within the MO octahedron or across the layer in the substituted systems. As we tune the oxygen–oxygen distance within the octahedron in Li₂Ru_0.75M_0.25O₃ (M = Mn, Ti, Ru), the Mn-substituted case shows a relatively big barrier of around 0.6 eV towards a reduction in bond distance to 1.3 Å. Such a dimerization barrier with Li₂Ru_0.75Mn_0.25O₃ lies roughly between the two end-point compounds Li₂RuO₃ (red circle) and Li₂MnO₃ (grey circle) in Fig. 6(a). Compared with Li₂Ru_0.75Mn_0.25O₃, Li₂Ru_0.75Ti_0.25O₃ basically shows the absence of such a barrier for octahedral distortion, which is the root cause of the increase in the Ti–O first shell disorder upon lithium deintercalation in charged Li₂Ru_0.75Ti_0.25O₃ as observed in EXAFS (Fig. 5(b) and (e)). On the other hand, imposing such a short oxygen–oxygen distance across the layer (across different octahedrons) (Fig. 6(b)) induces a less obvious metal substituent dependency, where Ti shows a slightly higher barrier towards forming shorter oxygen bonds across the layer. Therefore, we can generalize that materials with a slightly smaller degree of metal and oxygen DOS overlap near the Fermi level have a higher tendency to form an O–O dimer within the octahedron due to less-directional M–O bonding.^47,48 As summarized in Fig. 6(c), the barrier of forming O–O within the M–O octahedron is highly dependent on the energetic overlap between metal and oxygen DOS center of mass distance, whereas the barrier to forming an O–O bond across different layers is weakly dependent on the transition metal substituents introduced in the system. Therefore, as we decrease the energetic overlap between the transition metal and oxygen, there is a transition from forming the O–O dimer across the layer towards forming O–O bonds within the octahedron. As a result, as we decrease the M–O energetic overlap, we are decreasing the overall energetic barrier to form shorter O–O bonds, inducing a higher tendency in forming molecular oxygen and a less reversible anionic redox. This observation explains the linear dependence of the oxygen redox reversibility on both the electronic DOS overlap as well as the oxygen phonon band center, observed in Fig. 3(a) and (b), respectively.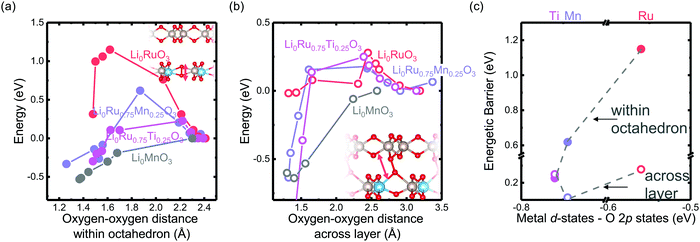

Fig. 6 Computed energetic evolution as a function of the oxygen–oxygen distance (a) within the octahedron and (b) across the layer in Li₀Ru_0.75M_0.25O₃ (M = Mn, Ti, Ru) and Li₀MnO₃ from the literature,³³ where the insets show schematics of the structures. The Li₀MnO₃ data from previous work are normalized by a factor of four due to the inclusion of four dimers created in the super cell compared with only one dimer created in this work. (c) The barrier of Li₂Ru_0.75M_0.25O₃ (M = Mn, Ti, Ru). Here we can see that, compared with the Ti-substituted case, Mn has a higher barrier to forming the oxygen dimer within the octahedron due to the rigidity of the metal–oxygen lattice, where the barrier of dimerization across the layer does not show a strong dependence of the energetic overlap between the M d states and O p states.

Insights into design guidelines for novel high-energy positive electrode materials

The observations in this work again highlight the importance of maintaining the large degree of energetic overlap between the metal and oxygen DOS near the Fermi level for introducing a rigid lattice upon lithium deintercalation and a higher barrier to irreversible oxygen dimers. This requirement poses two clear strategies in designing new, Li-rich, high-energy electrode materials. The first strategy relies on using less correlated and more delocalized transition metal ions (4d and 5d transition metals) which have some degree of redox capability upon lithium deintercalation. Such transition metals include previously explored Ru⁴⁺,^22–24,36 Ir⁴⁺,^25,27 and Mo^4+/3+,⁴⁹ which show promising performance, as well as those not yet explored such as Rh⁴⁺. From what we have observed in this study, early 4d and 5d transition metals would not be good candidates as due to the absence of d electrons, since there are no accessible metal states around the Fermi level, leading to the de-coordination of oxygen redox intermediates. However, a single transition metal redox center poses a large limitation on redox center choice and cost challenges related to those feasible noble transition metals. Therefore, another strategy for the design of reversible anionic redox positive electrodes involves substituting 3d Li-rich positive electrodes with less correlated transition metals such as Ru⁴⁺, Ir⁴⁺, Mo^4+/3+, and W³⁺ to introduce a larger degree of energetic overlap between M and O to increase the barrier to oxygen dimerization. The integration of Mo³⁺ and Ru⁴⁺ into the Li-rich Li_1.2Ni_0.2Mn_0.6O₂ has been previously explored experimentally and computationally,⁵⁰ and was shown to have much more improved reversibility compared with pristine Li_1.2Ni_0.2Mn_0.6O₂. To systematically explore the substitution options that improve the oxygen redox reversibility beyond chemical intuition, a high-throughput computational and/or experimental approach are needed for identifying oxide compositions with a large degree of energetic overlap between the transition metal and oxygen in future studies.

3. Conclusions

In our work, we examined an electronic and phononic descriptor for the anionic redox activity of the Li₂Ru_0.75M_0.25O₃ (M = Ti, Cr, Mn, Fe, Ru, Sn, Pt, Ir) system. Through DEMS measurements, coupled with electrochemistry profiles, we proposed a methodology to quantify the reversibility of anionic redox based on the ratio of oxygen release with respect to oxygen electron transfer. We demonstrated that for the substituted systems, the electronic structure is coupled with the rigidity of the oxide sublattice upon lithium deintercalation, where a larger degree of energetic overlap between the transition metal and oxygen induces a more rigid oxygen lattice upon lithium deintercalation from phonon calculations. As a result, the reversibility of anionic redox scales with the degree of overlap between the M d and O 2p states of the oxides. Employing EXAFS measurements and DFT calculations, we observed that such a trend is rooted in the more ionic substituents with a smaller energetic overlap between the M d and O 2p states being able to introduce easier distortion of M–O octahedron, thus giving a smaller barrier to forming an oxygen dimer within the octahedron, thus inducing oxygen release and irreversible oxygen redox. Moreover, the barrier to forming oxygen dimer across different layers show minimal metal dependence. As a result, as we increase the separation between metal and oxygen DOS below the Fermi level, there is a transition from the preference towards forming O–O bonds across the layer to forming O–O bonds within the octahedron. A more ionic substituent introduces a decrease in the oxygen dimerization barrier and a less reversible oxygen redox. Therefore, an optimized M d–O p DOS distance is needed for the harvesting of reversible anionic activity. Through this study, we were able to propose some new design strategies that can potentially induce more reversible anionic redox, providing guidance for future rational high-energy electrode exploration.

4. Methods

Experimental methods

Solid-state synthesis. The pristine Li₂RuO₃, Li₂Ru_0.75Cr_0.25O₃ and Li₂Ru_0.75Ir_0.25O₃ were synthesized through the solid-state route previously undertaken by Goodenough et al.⁵¹ and Tarascon et al.²² Li₂CO₃ (Sigma-Aldrich, ACS reagent ≥99.0%) and RuO₂ (Sigma-Aldrich and Alfa Aesar, anhydrous 99.9% trace metal basis) precursors are first dried under air flow at 300 °C for 4 h. The precursors (Li₂CO₃, RuO₂, CrO₂ (Sigma-Aldrich, Magtrieve™), and IrO₂ (Sigma-Aldrich, anhydrous 99.9% trace metal basis)) were then mixed in stoichiometric amounts, but with a Li excess of 10%, using a mortar and a pestle for 1 h in an argon-filled glovebox (H₂O, O₂ < 0.5 ppm). The resultant powder was pelletized under 1 MPa pressure and calcined and sintered at 1000 °C and 900 °C under air with heating rate of 2 °C min⁻¹ for 24 h and 48 h (24 h for Cr), respectively, with intermediate grinding. The pristine Li₂Ru_0.75Mn_0.25O₃, Li₂Ru_0.5Mn_0.5O₃ and Li₂Ru_0.75Sn_0.25O₃ are synthesized with precursors (Li₂CO₃, RuO₂, MnCO₃ (Sigma-Aldrich, 99.9% trace metal basis)), and SnC₂O₄ (Sigma-Aldrich, 98%) mixed in stoichiometric amounts, but with a Li excess of 10%, using a mortar and a pestle for 1 h in an argon-filled glovebox (H₂O, O₂ < 0.5 ppm). The resultant powder was pelletized under 1 MPa pressure and calcined and sintered at 800, 900 and 1100 °C under air with heating rate of 2 °C min⁻¹ for 6, 12 and 12 h, respectively, with intermediate grinding. The pristine Li₂Ru_0.75Pt_0.25O₃ was synthesized with precursors (Li₂CO₃, RuO₂, Pt (Tanaka Precious Metal)) mixed in stoichiometric amounts, but with a Li excess of 10%, using a mortar and a pestle for 1 h in an argon-filled glovebox (H₂O, O₂ < 0.5 ppm). The resultant powder was pelletized under 1 MPa pressure and calcined and sintered at 750 °C and 1050 °C under air with heating rate of 2 °C min⁻¹ for 12 h and 12 h, respectively, with intermediate grinding. The pristine Li₂Ru_0.75Fe_0.25O₃ was synthesized with precursors mixed (Li₂CO₃, RuO₂, Fe₂O₃ (Acros Organics, 99.999% trace metal basis)) in stoichiometric amounts, but with a Li excess of 10%, using a mortar and a pestle for 1 h in an argon-filled glovebox (H₂O, O₂ < 0.5 ppm). The resultant powder was pelletized under 1 MPa pressure and calcined and sintered at 1000 °C and 900 °C under air with heating rate of 2 °C min⁻¹ for 24 h and 24 h, respectively, with intermediate grinding. All of the resultant powder is stored inside the glovebox and the phase purity of Li₂Ru_xM_1−xO₃ is confirmed through X-ray diffraction (XRD) using a PANalyt’cal X'Pert PRO diffractometer (Fig. S20, ESI†).

Positive electrode preparation. The pellet electrode was prepared by pelletizing around 48 mg of active material using a 6 mm diameter pressing die set (Across International) for 15 min. The pellets were then sintered under air at 800 °C (Li₂Ru_0.75Mn_0.25O₃, Li₂Ru_0.75Ti_0.25O₃ and Li₂Ru_0.5Mn_0.5O₃) and 900 °C for all the other chemistries for 6 hours. The cooling and heating rates were 2 °C min⁻¹. The pellet electrodes were then broken into pieces of around 3 mg each and dried under vacuum under 120 °C overnight before being transferred into an argon-filled glovebox (<0.5 ppm of H₂O and O₂). The pellet electrodes were used for the X-ray measurements to remove any ambiguities introduced by the conductive carbon and binder.

Composite electrodes for DEMS measurements were prepared by mixing the active material (80% mass fraction), 10% acetylene black (AB) and 10% polyvinylidene fluoride (PVDF) (Solvay 6020) dispersed in N-methyl-2-pyrrolidone (NMP) using a Fritsch Minimill 23 homogenizer. The resulting slurry was then blade-coated onto a stainless steel 304 mesh with an opening of 0.0012′′ with a wire diameter of 0.008′′ with an aluminium sheet underneath, and with a gap of 15 μ m. The electrodes were then dried and separated from the aluminium sheet underneath and punched into 15 mm diameter discs. The DEMS electrodes were pressed at 4.53 T cm⁻² under a hydraulic press. Finally, the electrodes were dried completely at 120 °C under vacuum for 12 h before being transferred into an argon-filled glovebox (<0.5 ppm of H₂O and O₂). The active loading of the composite electrodes for the DEMS experiments was around 10 mg cm⁻², which is higher than the usual loading of common composite electrodes to ensure that enough gaseous species were evolved to be detected during cycling.

Electrochemical measurements. Electrochemical behavior of the pellet electrodes was confirmed by galvanostatic measurements in two-electrode cells (Tomcell type TJ-AC). Cells were assembled in an argon-filled glovebox (<0.5 ppm of H₂O and O₂) and comprised a lithium metal foil as the negative electrode and the positive electrode, separated by two pieces of polypropylene separator (2500 Celgard), impregnated with 150 μL of LP57 (1 M LiPF₆ in a 3 : 7 ethylene carbonate (EC) : ethyl methyl carbonate (EMC) electrolyte (BASF)). After assembly, the cells rested for 6 h prior to measurement and then were charged with different end-of-charge potentials at a rate of ∼1.6–1.9 mA g⁻¹, depending on the specific chemistry. This rate of charge corresponds to a rate of C/100 based on the theoretical capacity calculated assuming one lithium extraction per Li₂Ru_xM_1−xO₃. The cell was held at the end-of-charge potential for 5 h before disassembly inside the glovebox.

Differential electrochemistry mass spectrometry measurements. The DEMS setup was constructed in-house based on the design reported by McCloskey et al.⁵² and used for the detection of gas evolution including CO₂ and O₂ in the head space of the electrochemistry cell along with pressure monitoring. Details on the DEMS setup and cell design are documented in Harding et al.⁵³ The cell volume is around 6 cm³ for the measurement and argon (Airgas, 99.999% pure, O₂, H₂O, CO₂ < 1 ppm) was used as the carrier gas. The DEMS cells were prepared inside an argon-filled glovebox (<0.5 ppm of H₂O and O₂) and comprised a lithium metal foil as the negative electrode and the DEMS positive electrodes, separated by two pieces of polypropylene separator (2500 Celgard), impregnated with 150 μL of LP57. The cell was first pressurized with argon to around 22 psi and allowed to rest for 8 h prior to electrochemical measurements to check for any potential leakage. DEMS measurement started 4 h after pressurization with a time interval of 10 min of collecting the gas from the headspace to obtain a CO₂ evolution background from the evaporated EMC fragments. The gas evolution profile upon charge/discharge as a function of time presented in this work were already background subtracted by fitting the gas evolution profile collected in the open circuit voltage stage after pressurizing with a polynomial function. The electrochemical measurements were carried out at a current density of 14–19 mA g⁻¹, depending on the specific chemistry for charge and discharge (corresponding to a C/10 rate by assuming 1 C = extracting 1 Li⁺ per f.u.), and a time interval of 10 min was set between each DEMS sequence. Please note that due to updating of previous DEMS system, the measured total volume of gas evolution is around 1.5 times the measured values from our previous work.³²

Quantification of the reversibility of anionic redox

In our definition of the figure of merit, the quantification of electrons transferred from oxygen redox is obtained through the electrochemistry profile upon first charge obtained from the DEMS measurement. As shown schematically in Fig. S6(a) (ESI†) the dQ/dV is obtained from the electrochemistry profile. All the charges are integrated after around 3.9 V_Li. The exception applies to Li₂Ru_0.75Cr_0.25O₃ and Li₂Ru_0.75Fe_0.25O₃, where the peaks at ca. 4.1 V_Li and 4.0 V_Li are not integrated due to the presence of Cr³⁺ and Fe³⁺, respectively, where the Cr^3+/4+,5+ and Fe^3+/4+ redox potential is around 4.0–4.1 V_Li.^54,55

Alternatively, we have also shown that the quantification of electrons transferred from oxygen redox can be defined strictly as all the charges after the O₂ gas onset upon first charge, which is also shown schematically in Fig. S6(b) (ESI†), and such a type of quantification method does not alter the trend in Fig. 3 as we observed in Fig. S5 (ESI†).

Synchrotron measurements. After rinsing and drying, the dried pellet electrodes were mixed with sucrose or BN powder to make 10 mm pellets. The pellets were wrapped around with Kapton tape for protection during transportation for hard X-ray absorption measurements.

High-energy resolution fluorescence detected Ru L₃-edge XAS was conducted at the Stanford Synchrotron Radiation Lightsource (SSRL) at the SLAC National Accelerator Laboratory Station 6-2b. The measurements were performed with a high-resolution tender X-ray spectrometer developed on a dispersive Johansson geometry in a 500 mm Rowland circle using a Si(111) analyzer.⁵⁶ The spectrometer recorded in dispersive mode the overall Ru Lα emission line; for extracting the HERFD spectrum, the peak intensity of the Lα emission line is plotted as a function of the incident photon energy. By using the Si(111) monochromator of the SSRL beamline 6-2, an overall energy resolution of 0.6 eV was achieved enabling the sharpening of the Ru-L₃ XAS features when compared with conventional X-ray absorption spectroscopy, i.e., total fluorescence yield or transmission mode XAS. The incident beam was about 400 μm × 800 μm (FWHM) and the photon flux ∼10¹² s⁻¹. The dried electrode material was mixed with sucrose to minimize any self-absorption effects across the very intense Ru L₃-edge resonances, resulting in pressed pellets with an active material mass fraction concentration of 0.5%.

Transition metal Ti, Fe, Mn K-edge EXAFS was conducted at beamline 6-2b of SSRL in fluorescence mode with an active material mass fraction of around 1.5%, diluted with sucrose, using a Si(111) analyzer. The spectra are aligned using the Si(111) glitches. Ru K-edge EXAFS was conducted at beamline 20-BM-B of Advanced Photon Source (APS) in Argonne National Laboratory in transmission mode with an active material concentration of 10 wt%, where a Ru metal foil was used as the reference. All spectroscopy data were normalized and processed using the ATHENA software package.⁵⁷ The EXAFS fitting was conducted using a k-space window of 3 Å⁻¹ to 11 Å⁻¹, and an R-space window of 1 to 3 Å to include both the first and second coordination shell of the metal center for Mn- and Fe-substituted cases. The EXAFS fitting was conducted using a k-space window of 3 Å⁻¹ to 10 Å⁻¹, and an R-space window of 1.1 to 3.1 Å to include both the first and second coordination shell of the metal center for Ti-substituted cases to avoid the impact of spurious interaction observed around 0.9 Å in the EXAFS spectra in R space. To have a more consistent estimation of the pseudo Debye–Waller factor, the coordination number S₀² is fixed to be same as the pristine oxide for the fitting of charged oxides. The details of the fitting are shown in Tables S1–S4 (ESI†).

Computational methods

DFT calculations. We used the Perdew–Burke–Ernzerhof (PBE)⁵⁸ formulation of generalized gradient approximations (GGA) and projected augmented wave (PAW) potentials implemented in the Vienna ab initio Simulation Package (VASP),^59–61 with Dudarev's rotationally invariant Hubbard-type U⁶² applied on the transition metal where the following U values of 5 eV, 3.5 eV, 3.9 eV, 4 eV, 4 eV and 4 eV on Ti, Cr, Mn, Fe, Ru and Ir are based on the literature.^28,48 A cutoff energy of 520 eV and a k-point per reciprocal atom of at least 4000 were used. The following pseudopotentials are used: Li_sv, Ti_sv, Cr_pv, Mn_pv, Fe, Ru_pv, Ir, Sn_d, O. The delithiated structures were generated with a primitive cell with 4 formula units of Li₂RuO₃, where for each different lithium content, the most energetically favorable configuration was taken.

The computed M d–O 2p difference was based on the difference of center of mass of the metal d states from −10 to 0 eV versus the Fermi level and that of the oxygen p states from −10 to 0 eV versus the Fermi level. Most of the computed phonon density-of-states is taken from previous work by calculating the center of mass of the oxygen projected non-imaginary phonon density of states.³³ For the substituted compounds, the phonon density-of-states is taken as the weighted sum of the two end compounds, as employed in previous work.⁴¹ We did not include Li₂Ru_0.75Fe_0.25O₃ because the phonon density of states of Li₁Fe⁵⁺O₃ and Li_0.5Fe^5.5+O₃ results in a significant amount of imaginary frequency and most of the modes are not well converged. The observed imaginary frequency comes from the instability of Fe⁵⁺ and above at room temperature and 0 K, which can only be synthesized through high pressure and high temperature synthesis.⁶³ Therefore, we did not include the phonon datapoint from Li_xRu_0.75Fe_0.25O₃ (x = 1 and 0.5) due to the unstable nature of Fe⁵⁺ and phononic imaginary modes in the layered structure.

Computational tuning of the oxygen–oxygen dimer was conducted on the fully delithiated structures where the oxygen–oxygen distance of a specific oxygen–oxygen pair was either within the octahedron or across the layer. This specific oxygen pair was not allowed to relax during computation while the other atoms as well as the cell volume and cell shape are allowed to relax to full degree of freedom.

Author contributions

Conceptualization: Y. Y. and Y. S.-H. Methodology: Y. Y., P. K., D. S., R. K., C.-J. S. and Y. S.-H. Investigation: Y. Y., P. K., D. S., R. K., C.-J. S. and Y. S.-H. Writing: Y. Y. and Y. S.-H. Review & editing: Y. Y., P. K., D. S., L. G., R. K., C.-J. S., R. J., F. G., F. M. and Y. S.-H. Supervision: Y. S.-H. Funding acquisition: Y. S.-H.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work made use of the MRSEC Shared Experimental Facilities at MIT, supported by the National Science Foundation under award number DMR-1419807. Research at MIT related to this work was supported financially by BMW and MIT-Indonesia Seed Fund. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. This work also used resources of the Extreme Science and Engineering Discovery Environment (XSEDE),⁶⁴ which is supported by National Science Foundation grant number ACI-1548562. Use of the Stanford Synchrotron Radiation Lightsource (SSRL), SLAC National Accelerator Laboratory, was supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences (contract no. DE-AC02-76SF00515). Part of the instrument used for this study was supported by U.S. Department of Energy, Office of Energy Efficiency & Renewable Energy, Solar Energy Technology Office BRIDGE Program. This research used resources of the Advanced Photon Source, an Office of Science User Facility operated for the U.S. Department of Energy (DOE) Office of Science by Argonne National Laboratory, and was supported by the U.S.DOE under Contract No. DE-AC02-06CH11357, and the Canadian Light Source and its funding partners. This research used resources of the Advanced Light Source, which is a DOE Office of Science User Facility under contract no. DE-AC02-05CH11231. The authors are thankful for the supply of the Pt precursors from Tanaka Precious Metal.

References

1. K. Mizushima, P. C. Jones, P. J. Wiseman and J. B. Goodenough, Mater. Res. Bull., 1980, 15, 783–789.
2. W.-S. Yoon, K.-B. Kim, M.-G. Kim, M.-K. Lee, H.-J. Shin, J.-M. Lee, J.-S. Lee and C.-H. Yo, J. Phys. Chem. B, 2002, 106, 2526–2532.
3. M. Broussely, F. Perton, P. Biensan, J. M. Bodet, J. Labat, A. Lecerf, C. Delmas, A. Rougier and J. P. Peres, J. Power Sources, 1995, 54, 109–114.
4. C. Delmas, I. Saadoune and A. Rougier, J. Power Sources, 1993, 44, 595–602.
5. H.-J. Noh, S. Youn, C. S. Yoon and Y.-K. Sun, J. Power Sources, 2013, 233, 121–130.
6. I. Koetschau, M. N. Richard, J. R. Dahn, J. B. Soupart and J. C. Rousche, J. Electrochem. Soc., 1995, 142, 2906–2910.
7. Y. Shao-Horn, S. A. Hackney, A. R. Armstrong, P. G. Bruce, R. Gitzendanner, C. S. Johnson and M. M. Thackeray, J. Electrochem. Soc., 1999, 146, 2404–2412.
8. M. M. Thackeray, S.-H. Kang, C. S. Johnson, J. T. Vaughey and R. Benedek, and S. Hackney, J. Mater. Chem., 2007, 17, 3112–3125.
9. M. M. Thackeray, C. S. Johnson, J. T. Vaughey, N. Li and S. A. Hackney, J. Mater. Chem., 2005, 15, 2257–2267.
10. C. S. Johnson, N. Li, C. Lefief, J. T. Vaughey and M. M. Thackeray, Chem. Mater., 2008, 20, 6095–6106.
11. G. Assat, A. Iadecola, C. Delacourt, R. Dedryvère and J.-M. Tarascon, Chem. Mater., 2017, 29, 9714–9724.
12. W. E. Gent, K. Lim, Y. Liang, Q. Li, T. Barnes, S.-J. Ahn, K. H. Stone, M. McIntire, J. Hong and J. H. Song, Nat. Commun., 2017, 8, 2091.
13. C. S. Johnson, N. Li, C. Lefief and M. M. Thackeray, Electrochem. Commun., 2007, 9, 787–795.
14. C. S. Johnson, J. S. Kim, C. Lefief, N. Li, J. T. Vaughey and M. M. Thackeray, Electrochem. Commun., 2004, 6, 1085–1091.
15. K. Dai, J. Wu, Z. Zhuo, Q. Li, S. Sallis, J. Mao, G. Ai, C. Sun, Z. Li, W. E. Gent, W. C. Chueh, Y. Chuang, R. Zeng, Z. Shen, F. Pan, S. Yan, L. F. J. Piper, Z. Hussain, G. Liu and W. Yang, Joule, 2019, 3, 518–541.
16. K. Luo, M. R. Roberts, R. Hao, N. Guerrini, D. M. Pickup, Y.-S. Liu, K. Edström, J. Guo, A. V. Chadwick and L. C. Duda, Nat. Chem., 2016, 8, 684.
17. E. Hu, X. Yu, R. Lin, X. Bi, J. Lu, S. Bak, K.-W. Nam, H. L. Xin, C. Jaye and D. A. Fischer, Nat. Energy, 2018, 3, 690.
18. G. Assat and J.-M. Tarascon, Nat. Energy, 2018, 1.
19. A. Grimaud, W. T. Hong, Y. Shao-Horn and J.-M. Tarascon, Nat. Mater., 2016, 15, 121.
20. M. B. Yahia, J. Vergnet, M. Saubanère and M.-L. Doublet, Nat. Mater., 2019, 18, 496–502.
21. C. Zhan, Z. Yao, J. Lu, L. Ma, V. A. Maroni, L. Li, E. Lee, E. E. Alp, T. Wu and J. Wen, Nat. Energy, 2017, 2, 963.
22. M. Sathiya, A. M. Abakumov, D. Foix, G. Rousse, K. Ramesha, M. Saubanère, M. L. Doublet, H. Vezin, C. P. Laisa and A. S. Prakash, Nat. Mater., 2015, 14, 230.
23. M. Sathiya, J.-B. Leriche, E. Salager, D. Gourier, J.-M. Tarascon and H. Vezin, Nat. Commun., 2015, 6, 6276.
24. M. Sathiya, K. Ramesha, G. Rousse, D. Foix, D. Gonbeau, A. S. Prakash, M. L. Doublet, K. Hemalatha and J.-M. Tarascon, Chem. Mater., 2013, 25, 1121–1131.
25. E. McCalla, A. M. Abakumov, M. Saubanère, D. Foix, E. J. Berg, G. Rousse, M.-L. Doublet, D. Gonbeau, P. Novák and G. Van Tendeloo, Science, 2015, 350, 1516–1521.
26. M. Sathiya, G. Rousse, K. Ramesha, C. P. Laisa, H. Vezin, M. T. Sougrati, M.-L. Doublet, D. Foix, D. Gonbeau and W. Walker, Nat. Mater., 2013, 12, 827–835.
27. J. Hong, W. E. Gent, P. Xiao, K. Lim, D.-H. Seo, J. Wu, P. M. Csernica, C. J. Takacs, D. Nordlund and C.-J. Sun, Nat. Mater., 2019, 1.
28. M. Saubanère, E. McCalla, J.-M. Tarascon and M.-L. Doublet, Energy Environ. Sci., 2016, 9, 984–991.
29. N. Yabuuchi, M. Nakayama, M. Takeuchi, S. Komaba, Y. Hashimoto, T. Mukai, H. Shiiba, K. Sato, Y. Kobayashi and A. Nakao, Nat. Commun., 2016, 7, 13814.
30. N. Yabuuchi, M. Takeuchi, M. Nakayama, H. Shiiba, M. Ogawa, K. Nakayama, T. Ohta, D. Endo, T. Ozaki and T. Inamasu, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7650–7655.
31. Y. Xie, M. Saubanere and M.-L. Doublet, Energy Environ. Sci., 2017, 10, 266–274.
32. Y. Yu, P. Karayaylali, S. H. Nowak, L. Giordano, M. Gauthier, W. Hong, R. Kou, Q. Li, J. Vinson and T. Kroll, Chem. Mater., 2019, 31, 7864–7876.
33. N. Charles, Y. Yu, L. Giordano, R. Jung, F. Maglia and Y. Shao-Horn, Chem. Mater., 2020, 32, 5502–5514.
34. J. Wandt, A. T. Freiberg, A. Ogrodnik and H. A. Gasteiger, Mater. Today, 2018, 21, 825–833.
35. R. Jung, M. Metzger, F. Maglia, C. Stinner and H. A. Gasteiger, J. Electrochem. Soc., 2017, 164, A1361–A1377.
36. J. Xu, M. Sun, R. Qiao, S. E. Renfrew, L. Ma, T. Wu, S. Hwang, D. Nordlund, D. Su and K. Amine, Nat. Commun., 2018, 9, 947.
37. F. Wu, G.-T. Kim, T. Diemant, M. Kuenzel, A. R. Schür, X. Gao, B. Qin, D. Alwast, Z. Jusys and R. J. Behm, et al. , Adv. Energy Mater., 2020, 10, 2001830.
38. J. Lee, D. A. Kitchaev, D.-H. Kwon, C.-W. Lee, J. K. Papp, Y.-S. Liu, Z. Lun, R. J. Clément, T. Shi and B. D. McCloskey, et al. , Nature, 2018, 556, 185–190.
39. B. Ammundsen and J. Paulsen, Adv. Mater., 2001, 13, 943–956.
40. Y. Lyu, N. Zhao, E. Hu, R. Xiao, X. Yu, L. Gu, X.-Q. Yang and H. Li, Chem. Mater., 2015, 27, 5238–5252.
41. S. Muy, J. C. Bachman, L. Giordano, H.-H. Chang, D. L. Abernathy, D. Bansal, O. Delaire, S. Hori, R. Kanno and F. Maglia, et al. , Energy Environ. Sci., 2018, 11, 850–859.
42. Z. Hu, H. Von Lips, M. Golden, J. Fink, G. Kaindl, F. De Groot, S. Ebbinghaus and A. Reller, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 5262.
43. M. Risch, A. Grimaud, K. J. May, K. A. Stoerzinger, T. J. Chen, A. N. Mansour and Y. Shao-Horn, J. Phys. Chem. C, 2013, 117, 8628–8635.
44. M. Risch, K. A. Stoerzinger, B. Han, T. Z. Regier, D. Peak, S. Y. Sayed, C. Wei, Z. Xu and Y. Shao-Horn, J. Phys. Chem. C, 2017, 121, 17682–17692.
45. S. Calvin, XAFS for Everyone, CRC Press, 2013, pp. 345–362.
46. S. Yamamoto, H. Noguchi and W. Zhao, J. Power Sources, 2015, 278, 76–86.
47. A. Urban, A. Abdellahi, S. Dacek, N. Artrith and G. Ceder, Phys. Rev. Lett., 2017, 119, 176402.
48. D.-H. Seo, J. Lee, A. Urban, R. Malik, S. Kang and G. Ceder, Nat. Chem., 2016, 8, 692–697.
49. S. Hoshino, A. M. Glushenkov, S. Ichikawa, T. Ozaki, T. Inamasu and N. Yabuuchi, ACS Energy Lett., 2017, 2, 733–738.
50. T. A. Wynn, C. Fang, M. Zhang, H. Liu, D. M. Davies, X. Wang, D. Lau, J. Z. Lee, B.-Y. Huang and K.-Z. Fung, et al. , J. Mater. Chem. A, 2018, 6, 24651–24659.
51. A. James and J. B. Goodenough, J. Solid State Chem., 1988, 74, 287–294.
52. B. D. McCloskey, D. S. Bethune, R. M. Shelby, G. Girishkumar and A. C. Luntz, J. Phys. Chem. Lett., 2011, 2, 1161–1166.
53. J. R. Harding, PhD thesis, Massachusetts Institute of Technology, 2015.
54. S. Komaba, C. Takei, T. Nakayama, A. Ogata and N. Yabuuchi, Electrochem. Commun., 2010, 12, 355–358.
55. Y. Sakurai, H. Arai, S. Okada and J. Yamaki, J. Power Sources, 1997, 68, 711–715.
56. S. Nowak, R. Armenta, C. Schwartz, A. Gallo, B. Abraham, A. Garcia-Esparza, E. Biasin, A. Prado, A. Maciel and D. Zhang, et al. , Rev. Sci. Instrum., 2020, 91, 033101.
57. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
58. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
59. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
60. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
61. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
62. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505.
63. P. Xiong, H. Seki, H. Guo, Y. Hosaka, T. Saito, M. Mizumaki and Y. Shimakawa, Inorg. Chem., 2016, 55, 6218–6222.
64. J. Towns, T. Cockerill, M. Dahan, I. Foster, K. Gaither, A. Grimshaw, V. Hazlewood, S. Lathrop, D. Lifka and G. D. Peterson, Comput. Sci. Eng., 2014, 16, 62–74.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ee03765f

‡ Current address: Faurecia Clean Mobility, Biberbachstraße 9, 86154, Augsburg, Germany.

---