Open Access Article
Open Access ArticleTechnological learning for resource efficient terawatt scale photovoltaics
Jan Christoph
Goldschmidt
 *a,
Lukas
Wagner
*a,
Lukas
Wagner
 a,
Robert
Pietzcker
a,
Robert
Pietzcker
 b and
Lorenz
Friedrich
b and
Lorenz
Friedrich
 a
a
aFraunhofer Institute for Solar Energy Systems, Heidenhofstr. 2, 79110 Freiburg, Germany. E-mail: jan.christoph.goldschmidt@ise.fraunhofer.de; lukas.wagner@ise.fraunhofer.de; lorenz.friedrich@ise.fraunhofer.de
bPotsdam Institute for Climate Impact Research, P.O. Box 60 12 03, 14412 Potsdam, Germany. E-mail: pietzcker@pik-potsdam.de
First published on 17th September 2021
Abstract
Cost efficient climate change mitigation requires installing a total of 20–80 TWp photovoltaics until 2050 and 80–170 TWp until 2100. The question is, whether the projected growth is feasible from a resource point of view – and if so, under which conditions. We assess demand for fundamental resources until the year 2100, which are necessary independently from the specific nature of the used PV technology, i.e. energy, float-glass, and capital investments, and addtionally silver. Without technological learning serious resource constraints will arise. On the other hand, continued technological learning at current rates would be sufficient to stay within reasonable boundaries. With such technological learning, energy demand for production will correspond to 2–5% of global energy consumption leading to cumulative greenhouse gas emissions of 4–11% of the 1.5 °C emission budget. Glass demand might still exceed current float-glass production, requiring capacity expansion; and silver consumption could be kept at current levels. Installations costs would be 300–600 billion $US2020 per year. Technological solutions enabling such learning are foreseeable, nevertheless current and future investments must not only be targeted at capacity expansion but also at upholding the currently high rate of innovation.
Broader contextPhotovoltaics – the direct conversion of solar radiation into electricity – is the major energy conversion technology for cost efficient climate change mitigation. To achieve this goal a huge number of systems must be installed, which is associated with a high resource demand, e.g in terms of energy, float-glass, metals, and capital investments, as well as with associated greenhouse gas emissions. In this paper, we investigate whether the projected growth is feasible from a resource point of view – and if so, under which conditions. In this analysis, we consider that the photovoltaic technology is constantly evolving, and new generations of systems are more efficient and consume less resources during production. We find that without technological learning, resource limitations will most likely occur. Those limitations can be avoided if technological learning continues with its current speed also in the long-term future. Already now, technological solutions like perovskite-based tandem solar cells are foreseeable that promise high efficiencies at low-costs and low resource consumption. Therefore, we conclude that current and future investments must not only be targeted at capacity expansion but also at upholding the currently high rate of innovation. |
Introduction
Several papers have identified photovoltaics (PV) as the most important renewable energy technology for cost optimized climate change mitigation.1–3 Accordingly, huge numbers of total PV installations ranging from 20 to 80 TWp in the year 2050 are an integral part global of progressive energy scenarios.1–5 However, the associated massive demand for resources for these PV installations is rarely discussed in these scenarios. Most existing literature on resource limitations for PV, on the other hand, only considered significantly lower PV installations of typically below 10 TWp (see also following section) so resource limitations might be underestimated. Then again, the literature often also failed to properly consider technological learning, leading to an exaggeration of resource constraints. Given the relevance of PV for electricity decarbonization in many scenarios, a well-founded answer to the question whether the projected growth is feasible from a resource point of view – and if so, under which conditions – is of great importance for the development of robust climate change mitigation strategies and as guiding principle for future technological developments.Therefore, in this work, we estimate the resource demand for photovoltaic systems along a path towards a TWp scale PV industry for the 21st century. The precise technological development is difficult to foresee over such an extended period of time. Hence, we base our analysis on three main resources necessary independently from the specific nature of the used PV technology, i.e. energy, float-glass, and capital investments. Additionally, we included Ag in our analysis, because Ag has been identified as critical in previous analyses6–10 and is relevant both for the currently dominant silicon technology and might also be for future technologies, which will require a form of metallic electrical contact.
To reflect the dynamic development of PV technology, we use deployment dependent technological learning in our future projections. We consider ongoing efficiency increases, cost reduction as well as reduction in energy and in per-piece silver consumption. The plausibility of the resulting improved characteristics is substantiated for the short term and the long term by describing technological solutions that might drive the technological progress and by pointing out fundamental technological boundaries. This analysis is based on the dominant silicon technology and on the emerging perovskite technology, that, up to now, has not been considered in resource limitation studies yet.
Resource demands of terawatt scale photovoltaics
Review of existing literature
Many works have investigated resource limitations for a large-scale PV deployment or complete renewable energy systems. Table 1 gives an overview on the literature considered for this work.6–23 The table lists considered deployment levels, considered resources as well as resources found to be critical. Apparently, only few works considered PV deployment in the range of 20–80 TWp necessary for reaching ambitious climate goals. Only about half of the works consider technological learning. This is surprising, as it has been one key characteristic of photovoltaics in the past, that cost and resource efficiency has been continuously improved over time. For many categories, the development can be described by learning rates, which state how much a certain quantity is changed, when the cumulative production is doubled. In photovoltaics, the best-known learning rate is that the price for PV modules was decreased by 25% for every doubling of cumulative module production, which has been observed now for the last 40 years.24 Such learning rates can also be found for inverter prices, energy consumption for production, silver usages per solar cell and efficiency.20,24–26 In literature, hardly any fundamental resources like energy and glass are investigated. Instead, many works provide more detail in terms of considered elements, especially elements like In, Te, Se, Ga, Cd, Ni, and Sn. In these works, possible resource constraints have been identified for Te and Se, already for lower levels of PV installations. These materials, however, are only relevant for the CdTe and CIGS thin film technologies, with current market shares of 5%.25 The resource constraints and failure to increase market share in the past 12 years, make it very likely that these technologies are not relevant for reaching several TWp installations levels, and therefore where not considered in the present analysis. The same applies for Ga which is necessary for III–V multijunction solar cells used in concentrator PV.| 1st Author (year) | Title | Deployment | Technological Learning | Energy | Glass | Capital | Silicon | Silver | Indium | Others | Considered Critical |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Feltrin (2008) | Material considerations for terawatt level deployment of photovoltaics | 2.5 TWp/a possible for crystalline c-Si, >10 TWp/a possible for in-free a-Si | — | ✗ | ✗ | ✗ | Te, Sn, Pt, Ge, Ga, Au, Cd, Se | Te, In | |||
| Dale (2013) | Energy balance of the global photovoltaic (PV) industry—is the PV industry a net electricity producer? | 0.3 TWp in 2015 | CED learning rates | x | |||||||
| Elshkaki (2013) | Dynamic analysis of the global metals flows and stocks in electricity generation technologies | 2 TWp in 2050 | — | ✗ | ✗ | Te, Se, Ga, Ge, Cu, Cd, Pb, Ni | Ag, In, Te | ||||
| Woodhouse (2013) | Supply-chain dynamics of tellurium, indium, and gallium within the context of PV manufacturing costs | x00 GWp – TWp | — | ✗ | ✗ | Te, Ga | Te, In, Ga | ||||
| Moss (2013) | The potential risks from metals bottlenecks to the deployment of strategic energy technologies | 630 GWp in 2030 in Europe | — | ✗ | ✗ | Te, Sn, Ga, Cd, Se, Cu | Te, In, Ga | ||||
| Kavlak (2015) | Metal production requirements for rapid photovoltaics deployment | 1.850 TWp in 2030 | Decrease of material intensities till 2030. | ✗ | ✗ | Cd, Te, Ga, Se | Te, In, Se, Ga | ||||
| Jean (2015) | Pathways for solar photovoltaics | 25 TWp in 2050 | — | ✗ | ✗ | ✗ | Ge, Ga, Cu, Cd, Se, Te, Zn, Pb, Sn | In, Te, Ga | |||
| Viebahn (2015) | Assessing the need for critical minerals to shift the German energy system towards a high proportion of renewables | 0.4 TWp in 2050 in Germany | Decrease of material intensity and increase of efficiency | ✗ | Ga, Se, Cd, Te | Se, In | |||||
| Needleman (2016) | Economically sustainable scaling of photovoltaics | 10 TWp in 2030 | Technology scenarios and consequential costs | ✗ | |||||||
| Louwen (2016) | Re-assessment of net energy production and greenhouse gas emissions avoidance after 40 years of photovoltaics development | 1.6 TWp in 2040 | Learning rates from past 40 years | ✗ | ✗ | CO2 | |||||
| Grandell (2016) | Role of critical metals in the future markets of clean energy technologies | 10 TWp in 2050 | - | ✗ | ✗ | Te,Ru, Pt | Ag, In, Te | ||||
| Davidsson (2017) | Material requirements and availability for multi-terawatt deployment of photovoltaics | 9.3 TWp in 2050 | Decrease in material intensity until lower limit reached | ✗ | ✗ | ✗ | Ga, Se, Te, Cd | Ag, In, Te | |||
| Valero (2018) | Material bottlenecks in the future development of green technologies | 3.5 TWp in 2050 | - | ✗ | ✗ | Cd, Cu, Ga, Gd, Ge, Mg, Mo, Ni, Se, Sn, Te | Te, Ag, Cd, Ga, In, Ni, Sn | ||||
| Månberger (2018) | Global metal flows in the renewable energy transition: exploring the effects of substitutes, technological mix and development | 6.9 TWp in 2060 | 5% yearly decrease in material intensity | ✗ | ✗ | Te, Ga, Se | |||||
| Tokimatsu (2018) | Energy modeling approach to the global energy-mineral nexus: Exploring metal requirements and the well-below 2 °C target with 100 percent renewable energy | ∼50 TWp in 2100 | — | ✗ | ✗ | ✗ | Ga, Se, Cd, Te, Cu | Se, In, Te | |||
| Moreau (2019) | Enough metals? Resource constraints to supply a fully renewable energy system | ∼25 TWp in 2050 | — | ✗ | ✗ | Cd, Cu, Ga, Mg, Mo, Ni, Sn, Te,Pb | Cd, Ag, Ni, Sn | ||||
| Gervais (2021) | Raw material needs for the large-scale deployment of photovoltaics – effects of innovation-driven roadmaps on material constraints until 2050 | ∼7.5 TWp in 2050 | Two scenarios for technological evolution | ✗ | ✗ | ✗ | Al, Cu, As, Sn, Bi, Ga, Pb, Se, Zn, Ni, Cd | Ga, In, As, Bi, Se, Ag, Si |
Silicon, on the other hand, is currently the dominant material for the production of solar cells. Resource constraints for elemental silicon do not occur, as silicon is the second most abundant element in the earth crust. One has to consider, nevertheless, that silicon does most commonly occur not in its elemental form in nature. Naturally occurring silicate minerals need to be purified to solar grade polysilicon which requires large amount of energy, which has been considered in this study. Note that currently still over 90% of Si-PV modules contain an aluminium frame. Yet, there is an increasing trend towards frameless modules and the market share of aluminium frames is expected to continuously fall to below 75% by 2029.27 Thus, the development of aluminium consumption for future PV production is not considered in this work.
Photovoltaic growth scenarios
Two scenarios for future installed PV capacity, which are compatible with limiting climate change to 1.5 °C, are the basis of our analysis (see Fig. 1 left). They were calculated with the REMIND model, which is extensively used for analyses of climate policies.28,29 REMIND is a global inter-temporally optimizing energy-economy model that calculates investments and vintaging of energy conversion technologies, including important features that influence the dynamics of the energy transition such as integration challenges of wind and solar power or technological learning.30–33 Both scenarios were calculated by setting a maximum CO2 budget of 600 GtCO2 for the period 2011–2100, and then letting the model endogenously invest into energy conversion technologies in order to maximize welfare. The scenarios thus represent cost-optimal pathways that limit the total CO2 emissions. Given the uncertainty surrounding the long-term evolution of many technological and societal characteristics that influence PV deployment, two scenarios were calculated: Scenario 1 assumes model parameters describing an evolution that is not so favourable for PV deployment, while scenario 2 uses parameter values that are more favourable for PV deployment. The two scenarios span a plausible range of values for parameters describing the price learning curve of PV, the size of system integration challenges, the upscaling dynamics of Carbon Capture and Sequestration (CCS), and the development of electrification of end-use demands (see Methods for details). As can be seen in Fig. 1 left, Scenario 1 and 2 cover well the range of ref. 1–5. In the scenarios, the years until 2030/2040 see a rapid growth of PV capacity driven by low prices for PV technology and the implementation of high CO2 prices. PV quickly replaces other, more expensive technologies and reaches 30–60% electricity generation share in most world regions. Subsequently, growth slows down because integration costs (storage, curtailment) become relevant. Still, economic and population growth drive a continued expansion of total electricity demand, leading to an approximately linear growth of PV capacity. Fig. 1 right displays the annual installation necessary to realize this growth. Because older systems must be replaced, the actual installation of PV systems is larger than the active capacity expansion. In the nearly exponential growth until 2030 this effect is not very significant, but during slower growth periods replacements become a major share of the PV market. The waviness observed in the gross capacity additions in the right panel of Fig. 1 is due to the very fast ramp-up of active capacity until 2030 followed by periods of varying deployment speed as described above, together with the time-shifted need to replace old installations. If a lifetime of 25 years is assumed, the installations built in 2020–2030 will be retired in 2045–2055 and thus increase the total required PV production in these years. The same retirement/installation wave again occurs 25 years later, from 2070–2080. We choose to perform the following analyses for the rather conservative scenario in the context of resource criticality of 25 years because of the following reasons: (i) the overwhelmingly majority of modules currently installed are younger than 25 years, so we cannot be sure whether such long periods are realized in the field (ii) performance does degrade, creating need for earlier addition of new modules. We choose not to model this explicitly, but rather taking a shorter lifetime (iii) in the future it may be economically favorable to repower a piece of land with the latest generation of PV (e.g. with a higher efficiency) although the lifetime and/or warranty has not expired yet. (iv) new technologies e.g. perovskite based device might feature a shorter lifetime. On the other hand, it is also possible that considerably longer lifetimes of 40 maybe 50 years are achieved. In any case, we would like to point out that in our assessment the question of lifetime becomes only relevant after 2040 (cf.Fig. 1) and therefore after the initial rapid growth period.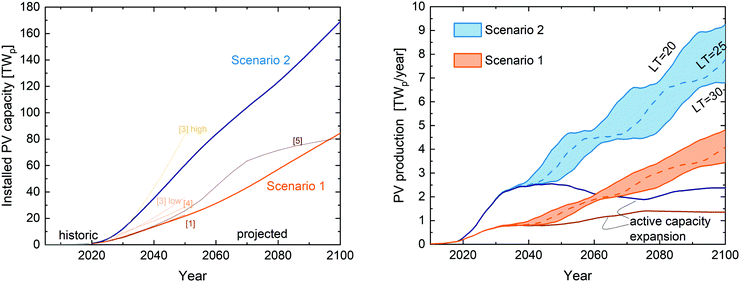 | ||
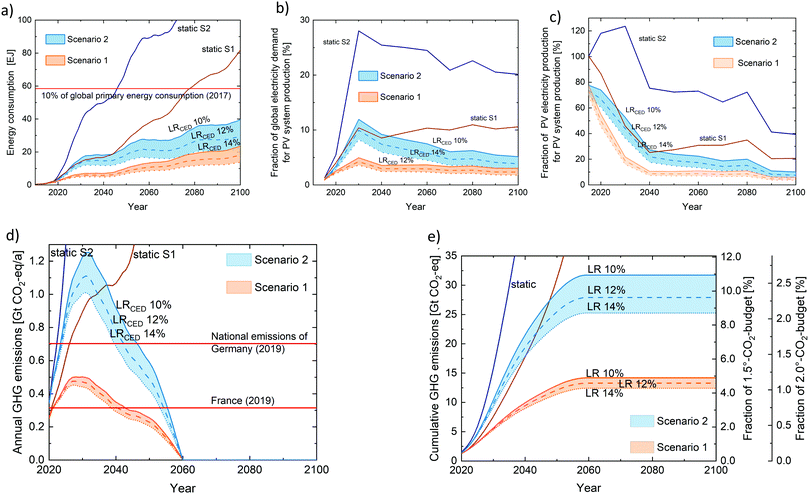
| Fig. 1 Left: Modelled installed PV capacity at end of year for two scenarios in comparison to scenarios from literature. Depending on the scenario assumptions, the global actively operating PV capacity is reaching 80–170 TWp in the year 2100. The projected range in the two scenarios is covering well the range of the ambitious growth scenarios published in ref. 1–5. Right: To realize the described growth the active capacity is increased by roughly 1–2 TWp per year after 2030. Because older systems must also be replaced at the end of their lifetime (LT in years) the actual production of new PV modules and systems is increasing to 3–9 TWp per year in 2100. Periods of faster and slower growth, which then also influence periods of higher or lower replacement needs, result in somewhat wavy curves, which differ from the often very smooth projections in other scenarios. | ||
Energy consumption and greenhouse gas emissions
PV systems will be installed to generate electricity, but it is an important question, how much energy is actually necessary to manufacture and install those systems and how large the energy surplus is. We estimate that the cumulative primary energy demand (CED) for production and installation of a PV system was 20 GJ per kWp in 2010. This value was obtained by averaging data from different sources34,35 and by accounting for the market shares of multi-crystalline and mono-crystalline silicon solar cells. If we assumed that CED would stay at this level, in Scenario 2 by 2049 global PV production will require 58.7 EJ per year, which is more than 10% of the global primary energy consumption of 2017 (585 EJ)36 (Fig. 2a). However, over the past decades, CED for PV production continuously decreased with learning rates (LR) determined between 12–14%,20,26 meaning that for every doubling of cumulative installed PV system capacity CED was reduced by 12–14%. If we assume continued learning rates LRCED of 10%, 12%, or 14%, the annual energy consumption of the PV industry will reach values of 23.6, 18.1, or 13.8 EJ per year, respectively, in Scenario 1 and 39.8, 29.8, or 22.1 EJ per year in Scenario 2 for the year 2100.Fig. 2(b) relates the primary energy required for PV production with the expected global electricity consumption within our scenarios. Depending on learning rates, energy demand for PV production will peak at values between 8 and 12% of the total global electricity production in the year 2030, for the ambitious Scenario 2, and at 3–5% for Scenario 1, while the static curves without learning remain at a high levels above 20% and 10%, respectively. Fig. 2c shows that for the static case the energy required for PV production would currently be at the same level (Scenario 1) or would even exceed the PV electricity production in the year 2035 by 24% (Scenario 2). Considering technological learning, however, PV electricity production already exceeds the energy demand that drives the rapid growth. A rising amount of PV electricity and decreasing energy demand for the production lead to a fast decrease of the fraction necessary for the production of new modules, which drops to 4–6% in Scenario 1 or 6–11%, respectively, in Scenario 2 after 2080. This, if you will, “own-consumption” is of a comparable order of magnitude as for fossil technologies. It is estimated, for example, that the own-consumption of coal power plants is in the order of 4–10%37 of its electricity production, while the coal mining consumes an additional 2.5–5%.38 Nuclear power plants tend to have an even higher own-consumption.37
The energy usage is closely linked to the emission of greenhouse gases (GHG). Due to rapid capacity expansion, by 2030 the GHG emissions of the global PV industry might surpass the national emissions of France or even Germany.39 (Fig. 2c) However, GHG emissions drop sharply after 2030, due to a slowdown of the growth of annual production of PV systems combined with an increasing share of renewables in the energy mix.
Fig. 2(e) displays the corresponding development of the cumulative GHG emissions, which, from 2060 on, stabilize at values around 12 Gt CO2-eq. for Scenario 1 and between approximately 25 to 30 Gt CO2-eq. for Scenario 2. The right axis of the plot represents the corresponding fraction of the carbon dioxide budget. As of January 2021, the CO2 budget to contain the anthropogenic global warming below 1.5 °C (1.5-degree goal) at a likelihood of 67% was approximately 290 Gt. For the 2 °C goal (probability of 67%), the remaining CO2 budget was 1040 Gt. Note that this representation can only be a snapshot as the budget is steadily reducing at a current rate of 1.3 kt s−1.40,41 On the other hand, a future removal of CO2 from the atmosphere could lead to larger budget being available for photovoltaics. In consequence, depending on the assumptions, building the global PV infrastructure will consume 4–11% of the remaining emission budget compatible with limiting global warming to 1.5 °C. To be clear here, not building such a PV infrastructure would most certainly lead to much higher emissions.
Glass
Currently, essentially all commercial PV modules use at least one glass sheet. The massive expansion of PV production thus directly increases glass demand. On the other hand, continuous increase in solar cell and module efficiency reduces area needed per Wp of installed power, and hence glass demand. We project the development of the power conversion efficiency with a learning rate of 6.7%,27 starting from a module efficiency of 20% in 2020. We estimate an annually produced module area of 1000–1300 km2 in 2020, which increases to 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–22
000–22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 km2 by 2100, depending on the scenario. Looking at the total area of the active PV capacity, the values increase from 4200–4600 km2 in 2020 to 252
000 km2 by 2100, depending on the scenario. Looking at the total area of the active PV capacity, the values increase from 4200–4600 km2 in 2020 to 252![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–466
000–466![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 km2 by 2100. To put this in perspective, the values for 2100 correspond roughly to the land area of the UK or Sweden, respectively.
000 km2 by 2100. To put this in perspective, the values for 2100 correspond roughly to the land area of the UK or Sweden, respectively.
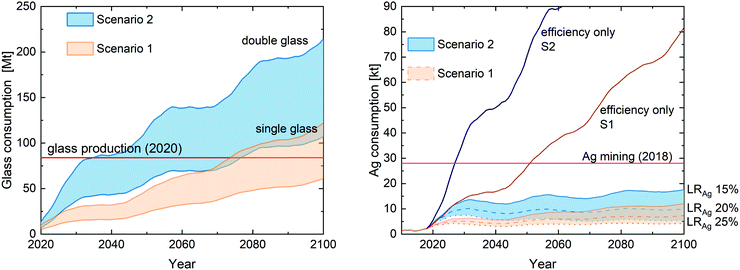
Currently, most modules are single-glass modules with front glass thickness of 3 mm. However trends are in the direction of 2 mm sheets on the one hand and double glass modules with glass back-sheets on the other hand.27 As shown in Fig. 3 left, for 2 mm float glass, a fully double glass based PV production will require amounts of float-glass exceeding todays overall annual glass production of 84 Mt42 as early as 2034 for Scenario 2 and in 2074 for Scenario 1. In 2100, glass consumption would reach 122–215 Mt. Correspondingly, in the single glass case consumption would reach 61–117 Mt by 2100. From a resource perspective, this is probably not critical since sand reserves for glass manufacturing are abundant and widespread43 and glass can be also be recycled, but it certainly requires a serious expansion of production facilities within the next ten years.
Silver consumption
Current commercial silicon PV products rely on a screen-printable silver front metallization. As for 2018, a typical 156 × 156 mm2 cell comprised of 100 mg silver.27 There is, however, a strong trend to reduce the amount of silver motivated by high prices and driven by improvements in printing technologies, with learnings rates LRAg in the order of 20%. On top of this development comes the continuous improvement of solar cell efficiencies, further reducing the needed amount of silver per Wp installed power. We estimate that the annual silver consumption of the PV industry was 1959 t in 2018, corresponding to 7.9% of the total annual silver mine production of 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 037 t.44 If the silver consumption per cell remained constant such that only device efficiency increases reduce the per Wp silver consumption, the demand of the PV industry will exceed today's global silver production as early as in the year 2027 (Scenario 2) or in the year 2051 (Scenario 1) (see Fig. 3 right). This effect can be drastically mitigated if learning rates in the silver consumption by technological and scientific improvements can be maintained. Depending on the learning rate LRAg the total silver consumption of the PV industry will remain below 18
037 t.44 If the silver consumption per cell remained constant such that only device efficiency increases reduce the per Wp silver consumption, the demand of the PV industry will exceed today's global silver production as early as in the year 2027 (Scenario 2) or in the year 2051 (Scenario 1) (see Fig. 3 right). This effect can be drastically mitigated if learning rates in the silver consumption by technological and scientific improvements can be maintained. Depending on the learning rate LRAg the total silver consumption of the PV industry will remain below 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 t (Scenario 2 LRAg 15%), or will stay roughly at today's level (Scenario 1 LRAg 25%), respectively. If, by technological learning, silver consumption is saturating in the long term, this would also enable to cover a large fraction by recycling of old modules.
000 t (Scenario 2 LRAg 15%), or will stay roughly at today's level (Scenario 1 LRAg 25%), respectively. If, by technological learning, silver consumption is saturating in the long term, this would also enable to cover a large fraction by recycling of old modules.
Capital expenditure
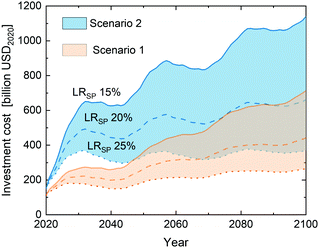
From a fast-increasing number of PV installations, one can expect a fast increase in necessary capital investment. On the other hand, PV technologies profit from fast technological learning also in terms of costs. A long-term learning rate of 24% can be determined for the time span from 1980–2018 for inflation adjusted silicon module prices.45 In the last years, however, the price has decreased more rapidly, with learning rates between 29.6% to 38.6%, depending on which starting year between 2003 to 2008 the analysis is based.46 Also for other system components, technological learning occurs. For inverter a learning rate of 18.9% was reported,25 and other system costs components become cheaper on a Wp basis because of increasing module efficiencies. Learning rates for system prices (SP) of LRSP 15%, 20%, and 25% result in yearly investments of 361, 263, or 188 billion US$2020, respectively, by 2050 for Scenario 1 and accordingly 766, 515, or 337 billion US$2020 for Scenario 2 (see Fig. 4). In the year 2100 the extreme values are 1140 billion US$2020 (Scenario 2, LRSP 15%) and 265 billion US$2020 (Scenario 1, LRSP 25%). The very high cost scenarios are unlikely, however, because high prices would reduce PV capacity expansion. To put this in perspective, the largest six oil and gas companies have each annual revenues between 300 and 400 billion US$,47 so one could conclude that the energy market roughly stays in the same order of magnitude.Technological solution for resource efficient photovoltaics
In the previous section, it has become clear that continued technological learning is crucial for resource demands to stay within reasonable limits. In this section, we compare the outcomes of the assumed learning rates with technology-detailed progress estimations in order to assess the plausibility of such continued technological learning.Efficiency
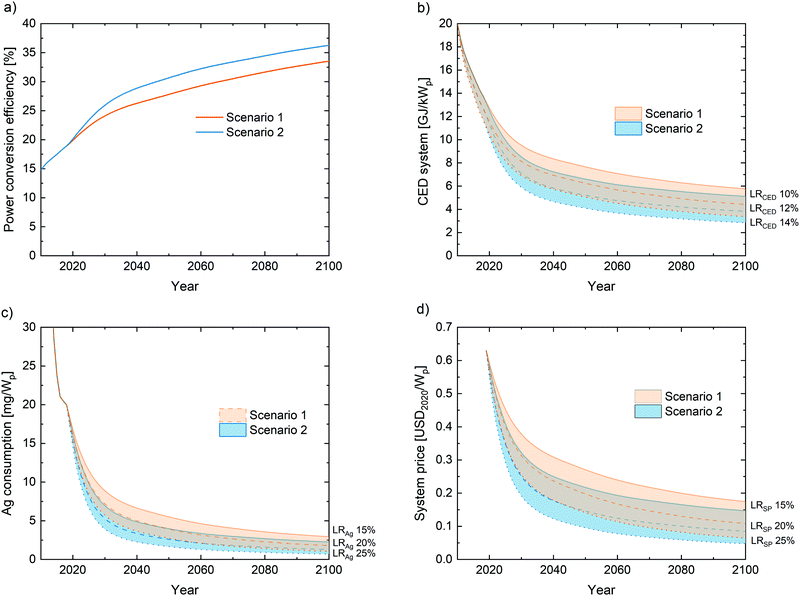
Our projections of the necessary glass and silver amount are based on an increase in power conversion efficiency with a learning rate of 6.7%.27 Also the other learning rates implicitly require increases in efficiency. In the short term, the projected learning results in module efficiencies of 24.1% and 25.9% by 2030 for Scenarios 1 and 2, respectively (see Fig. 5a), which is well in agreement with the forecast of the International Technology Roadmap for Photovoltaic (ITRPV) of 2020.48 This roadmap foresees solar cell efficiencies in the range of 25% for leading products of both n- and p-type products of monocrystalline Si-PV. These products achieve already today efficiencies beyond 22%,20 and currently efficiency increases of 0.5%abs per year are reported by the industry.21 However, as discussed in the Methods section, currently additional losses must be considered when going from the solar cell to the module level. On the other hand, these losses are predicted to decrease considerably with more transparent front glasses, reduced packaging and series resistance losses with half-cells and shingle modules, resulting in expected cell-to-module power ratios above 100%.20 Furthermore, a high market share of 70% of bifacial modules is predicted.20 These modules can harvest light reflected from the ground with their rear side. While strictly speaking this is not increasing the efficiency, the energy yield, i.e., the produced power is going up. In our simplified calculations this would have the same effect as a substantial efficiency increase.By 2050, the assumed learning rates leads to projected module efficiencies of 27.8% (Scenario 1) and 30.7% (Scenario 2). Until 2100, the projected efficiencies are 33.5% and 36.3% for Scenario 1 and 2, respectively, surpassing the maximum theoretical efficiency limits of single-junction Si-PV cells of 29.4%.49 Hence, the targeted learning rate can only be maintained by the implementation of novel technological concepts of which the most promising are multi-junction PV modules. III-V on silicon tandem devices are already achieving more than 32% with two junctions and more than 35% with three junction,50 while pure III–V solar cells with six junctions have achieved 47.1% efficiency under 143 suns concentration51 Unfortunately, no technologies to produce III–V multijunction solar cells with low costs are available yet. In contrast, perovskite-based tandem structure promise to reach high efficiencies at low costs. Perovskites are an emerging thin-film PV technology, which has reached high efficiency values at unprecedented speeds and substantial commercialisation efforts are underway. Laboratory perovskite silicon tandem solar cells have reached efficiencies of 29.5%,52 and dual junction perovskite on silicon53 and triple junction perovskite solar cells54 have already been developed. This makes it plausible that the targeted module efficiencies can be reached during the next 30 years with cheap production technologies by the ongoing technological development. Especially, since the theoretical efficiency limit for 2-junction and 3-junction devices for terrestrial conditions without concentration are at 42% and 49%,55 respectively, leaving plenty of room for further improvements.
Glass demand
Only little change to thinner glass substrates48 and the trend to bifacial modules requiring double glass modules keep glass demand high. Therefore, we did not project any glass specific technological learning. In consequence, the substantial efficiency increase discussed above is crucial to reduce the projected glass demand. Furthermore, glass-recycling needs to be addressed. On the other hand, there are technological innovations that could dramatically reduce the necessary glass amount. Perovskite solar cells have been produced on thin polymer substrates56 and also on 100 μm thin flexible substrates.57 Just recently, major commercialisation efforts have been announced for thin double glass perovskite module, which would reduce glass demand by an order of magnitude.58Energy consumption
By 2030, the extrapolation based on learning rates LRCED of 10, 12, and 14%, respectively, leads to CED ranging between 9.4, 8.1, and 6.7 GJ kWp−1 for Scenario 1 and 8.5, 7.1 and 5.9 GJ kWp−1 for Scenario 2. These values could be reached by ongoing technological developments. The purification of polysilicon feedstock and ingot crystal growth was estimated to consume three quarters of the total energy for the production of wafer based silicon PV modules.34 Therefore, a reduction of silicon use per wafer of 22% as predicted by the ITRPV 2020 and the projected increase in module efficiency would already be sufficient to reach CED values of around 8 GJ kWp−1 in the year 2030.By 2050, we project CEDs between 4.1–7.7 GJ kWp−1. These values can be achieved by the combination of efficiency enhancement, reducing wafer thickness to 150 μm and a 20% reduction of the dicing loss. These technological steps are already anticipated for the next decade by the ITRPV. The projected high efficiencies, however, require a multijunction approach. An additional perovskite top solar cell would only add 0.6 GJ kWp−1 under the assumption of a tandem module efficiency of 29.5%. Provided they achieve the same efficiency, perovskite–perovskite tandem modules which do not require an energy intensive silicon wafer could reach a CED as low as 2.8 GJ kWp−1, which would be in line with our most optimistic projections for the year 2100. These low values show that, in the long term, it is not unlikely that wafer-based Si-PV will have been replaced by a thin-film technology where the energy demand is substantially reduced to that of the float-glass substrate.39
There is one other aspect to consider when extrapolating the CED. In the past, the primary energy demand has mainly been reduced because the production of especially the solar cells has become less energy intensive and simultaneously the efficiency of the module has increased, thus producing more output from the same energy input. These effects are contained in the learning rate and thus considered in our extrapolation. In the future, there will be an additional effect that affects the calculated primary energy demand: the switch to renewable energies. On the one hand side, as renewable energies are considered in typical CED calculations with an efficiency of 100%, the CED value would go down, even if e.g. the same amount of electricity is consumed in solar cell production. On the other hand, if e.g. natural gas used for heating was directly replaced by synthetic natural gas produced from renewable electricity the CED would go up. The efficiency of energy conversion from electricity to synthetic natural gas is 54–78% according to.59 The average CED of natural gas following the Ecoinvent method60 is 38.3 MJ-eq. N−1 m−3, so using renewable energy, the CED of synthetic natural gas would be 49.1–70.9 MJ-eq. N−1 m−3. On the other already now electricity is used in glass production.61 So, it is difficult to foresee, which effect does dominate at which point in time. As these effects were not important in the past, they are not contained in the learning rates and thus not in our extrapolation. We do, however, consider the switch to renewables explicitly in the assessment of greenhouse gas emissions in the next section.
Greenhouse gas emissions
We base our assessment of the development of greenhouse gas (GHG) emissions from industrial production of PV systems on latest life cycle assessment (LCA) data for mono-crystalline silicon (Cz-Si) PERC PV systems,62 which can be regarded as a representative of the current and near future PV technologies for at least the next decade.48 Assuming a production in China, which represents the largest proportion of today's global PV production,25 the specific global warming potential (GWP) of Cz-Si PERC PV systems is 1.27 kg CO2-eq Wp−1.62The static case in Fig. 2(d and e) represents the evolution of the annual GHG emissions in Scenarios 1 and 2, if the specific GWP is assumed to stay constant. However, there are two main drivers that will lead to a reduction of specific GWP: first the processes for the production become more efficient and less materials and energy are consumed. Second, with a more widespread usage of renewable energies the GHG emissions from the energy used in the different production processes (and which is also the main driver for the GWP of the used materials) will decrease additionally.
The assessment of the learning rates of the GWP is challenging as it can only be based on a range of different LCA approaches that date back as far as to the 1970s. Louwen et al. presented a comprehensive overview of historical LCAs and assessed the learning rate to range between 16.5% and 23.6% for multi- and mono-crystalline Si PV, respectively.20 This learning rate development includes both effects described above, more efficient production and change in the specific GHG emissions for the energy used. These learning rates, however, seem to reflect a rather optimistic scenario as thy would imply a GWP of well below 1 kg CO2-eq. Wp−1 for mono-crystalline Si PV produced today (installed capacity >500 GWp), which is only the case, for a production within the EU.62 Thus, for our analysis we chose a different approach. As most GHG emissions for the production of PV systems are energy related, we take the same learning rates as for the CED, i.e. 10–14%. Additionally, we account for the dramatic shift towards renewable energies not only for electricity production but also for industrial processes, which we foresee to happen, but for which there is no historic precedent. We start the assumed development with the values calculated for China, which is a conservative assessment, as emission intensity for production is lower on other regions. For example, a production in the EU is associated with approximately half the GWP of a production in China.34,62 Based on the ambitious plans of China to reach a net zero CO2-emissions by 2060 and the EU's target to be GHG neutral until 2050, we assume a linear decrease of the GHG intensity for energy reaching zero by 2060. Regarding electricity, such a linear scenario has also been reported by Pehl et al.,63 yet we point out that besides the transformation of the electricity infrastructure, one critical challenge for the transformation towards net CO2-neutrality of PV product will lie in the replacement of the currently natural gas powered melting processes for flat-glass production, e.g. by the use of hydrogen produced from renewable electricity. On the other hand, the linear extrapolation is also a conservative estimate, as the data within our REMIND model shows an initially faster than linear decrease in carbon intensity for the energy sector in China and cheap renewable electricity could be a strong driver for a fast switch away from gas.
Silver and indium consumption
The learning curve assumed for the amount of silver used per solar cell and the increasing efficiency led to projected silver demands of 3.9–8.9 mg Wp−1 in 2030, and 0.7–2.9 mg Wp−1 in 2100 averaged over all produced modules. Based on48 it is expected that 7.8 mg Wp−1 could be reached with improvements of the screen-printing technology like a reduced silver content in printing pastes. A further reduction could be achieved with plating48 or advanced printing technologies, such as FlexTrail printing, with 0.05 mg Wp−1.64 Furthermore, perovskite technologies exist that allow for the realisation of modules without any silver, be it by the use of aluminium, or by innovative module concepts.39 So, it appears that a significant reduction in silver consumption for the average of the PV industry as described by the projected values or even a silver free PV industry is possible with known technologies. One has to note, however, that having less silver per module and thus a higher dilution would lower the incentive for recycling and might require also an advancement in recycling technologies.In terms of rare metals, however, another element could become critical with the emergence of multi-junction devices. In perovskite–silicon and perovskite–perovskite tandem solar cells – the currently most promising technological options – indium containing transparent conductive oxide (TCO) are used as front contact and as recombination contact between the two sub-cells. Indium has been identified as critical for much lower installed capacities. To solve this issue, the recombination contact could be replaced e.g. by tunnel diodes made from silicon in perovskite-silicon tandem solar cells,65 or by an innovative material combination like a C60/SnO2−x recombination contact in all-perovskite tandems.66 However, up to now the front TCO in the highest efficiency tandem solar cells all contain indium, because the TCO also enhances device stability. Clearly more research is necessary to achieve the goals of high efficiencies, good resource availability and low costs (which implies long lifetimes) simultaneously.
Costs
The assumed technological learning leads to a cost range between 0.19–0.38 US$2020 Wp−1 for installed utility systems in the year 2030, 0.10–0.27 US$2020 Wp−1 in the year 2050 and 0.05–0.17 US$2020 Wp−1 in 2100. In ref. 46 a detailed bottom up cost analysis projected system costs of 0.37–0.44 US$2020 Wp−1 for utility installations in the year 2025, with perovskite and perovskite-silicon tandem solar cell at the lower end, and single junction silicon solar cells at the upper end. These values could be considered on route towards the cost range projected for 2030. Based on ref. 46, one can estimate 23.5 US$2020 m−2 production costs for a perovskite-perovskite tandem module. In combination with the upper limit of efficiencies projected above, this result in production costs of the module alone of 0.08 US$2020 Wp−1 and 0.02 US$2020 Wp−1 in the years 2050 and 2100, respectively. This is only slightly below the lower limit of the projected cost ranges. Thus, reaching these limits would require very substantial to unlikely reductions in balance of system costs (BOS). In this context, one could speculate on substantially higher efficiencies, integration in multifunctional elements where part of the BOS is already accounted for (e.g. vehicles) and/or automatization in the installation and economy of scale in ultra-large PV power plants. On the other hand, reaching medium values within the projected cost ranges appears fully plausible.Conclusions
Cost efficient climate change mitigation requires total photovoltaic installations in the range of 20–80 TWp in the year 2050 and 80–170 TWp until 2100. Based on the current technology, such a TW-scale PV industry would be running into resource constraints. On the other hand, with continued technological learning at its current rate the resource demands could be kept within reasonable boundaries. With technological learning, during the initial rapid growth, the energy consumed for PV system production corresponds to close to 80% of the electricity produced by PV. This rate is dropping fast and stabilizes at 4–11%. Accordingly, the fraction of the overall energy demand used for PV production stabilizes at 2–5%. Nevertheless, building the global PV infrastructure will consume 4–11% of the remaining greenhouse gas emission budget compatible with limiting global warming to 1.5 °C. Hence, developing low-emission PV technologies should become a priority. The demand for float-glass for photovoltaics will be in the order of the entire current global float-glass production or more than double that amount if there is switch to glass–glass modules without a reduction in glass thickness. Therefore, a rapid expansion in float glass production capacity within the next 10 years is necessary. Depending on the learning rate, the global silver demand used for PV production could stay at roughly current levels, or increase by a factor of 9, which most likely would not be feasible. Recycling facilities that can cope with the enormous materials flow, will also be necessary. Finally, yearly investments will be in the range of 300–600 billion $US2020 for likely scenarios and therefore in the same order of magnitude as the revenues of the largest oil and gas companies. Technologies to realize the anticipated developments are available. Multi-junction solar cells already achieve the necessary efficiencies in the range of 35%. Perovskite-perovskite devices, for instance, could develop to a level where high efficiencies together with low energy consumption, production on thinner substrates and low or no silver usage are achieved simultaneously. However, replacement of indium in transparent conductive layers is still a challenge. Despite all uncertainties inherent of such long-term scenarios, one can conclude that current and future investments must not only be targeted at capacity expansion but also at upholding the currently high rate of innovation with a focus on sustainability.Methods
REMIND model and PV installation data
We use the global multi-regional energy-economy-climate model REMIND Version 2.1.0 for our analysis.29,30 REMIND is open source and available on GitHub at https://github.com/remindmodel/remind. The technical documentation of the equation structure can be found at https://rse.pik-potsdam.de/doc/remind/2.1.0/. In REMIND, each single region is modelled as a hybrid energy-economy system and is able to interact with the other regions by means of trade. Tradable goods are the exhaustible primary energy carriers coal, oil, gas and uranium, emission permits, and a composite good that represents all other tradeable goods.The economy sector is modelled by a Ramsey-type growth model which maximizes utility, a function of consumption. Labor, capital and end-use energy generate the macroeconomic output, i.e., GDP. The produced GDP covers the costs of the energy system, the macroeconomic investments, the export of a composite good and consumption.
The energy sector is described with high technological detail. It uses exhaustible and renewable primary energy carriers and converts them to final energy types such as electricity, heat and fuels. Various conversion technologies are available, including technologies with carbon capture and storage (CCS).
The model includes cost mark-ups for the fast up-scaling of investments into individual technologies; therefore, a more realistic phasing in and out of technologies is achieved. The model allows for premature retirement of capacities before the end of their technological lifetime, and the lifetimes of capacities differ between various types of technologies. If capacities are phased out for economic reasons before they reach the end of their technical lifetime, these assets are then stranded. Furthermore, capacities of conversion technologies age realistically from an engineering point of view: depreciation rates are very low in the first half of the lifetime and increase strongly thereafter.
The two scenarios differ in a number of assumptions:
• PV learning parameters that determine the capital cost evolution: Until 2050, investment costs only decrease to 40 $cent2020 Wp−1 in Scenario 1, while going down to 10 $cent2020 Wp−1 in Scenario 2.
• Additionally, the non-linear cost mark-ups penalizing very fast upscaling of PV are four times as large in Scenario 1 compared to Scenario 2.
• Integration challenges in Scenario 2 are set to half the value of Scenario 1.
• Electrification options in the transport, buildings and industry sectors are assumed to be substantially more expensive and limited in Scenario 1 than in Scenario 2.
• CCS usage is substantially more expensive in Scenario 2: investment costs are 50% higher, up-scaling cost mark-ups are 4 times as large.
To match the historic data in the year 2020, 47 GWp were added to the REMIND data in each year. Furthermore, the REMIND model delivers the cumulative installed PV capacity in time steps of 5 years until 2060 and in time steps of 10 years until 2100. To obtain data with a yearly resolution, in a first step preliminary installed PV capacity data was estimated for the intermediate years using the compound annual growth rate (CAGR) calculated for the 5 or 10 years time period. Lower CAGR values in a following time period then sometimes lead to a sharp drop in the annual active capacity expansion, when going from one time period to the next. To avoid these artificial oscillations, the data for the annual active capacity expansion was smoothed by a moving average over ±4 years. Finally, by integrating over these values and smoothing with a moving average over ±1 year we obtained the data for the installed PV capacity data without implausible jumps at the transition between time periods, which is used in the present study. While there is a certain discrepancy in the transition from the historic to the projected data, after 2025 the deviation from the REMIND data-points lies below 2.7% and 2.4% for Scenario 1 and 2, respectively. The discrepancy decreases steadily and is below 1% from 2045 on. Respective data for annual active capacity expansion was calculated from the difference in installed PV capacity to the previous year.
To account for the module lifetime τ, the PV production in year t, Pτ(t), is calculated from the sum of the active capacity expansion in the same year P(t) and the production from τ years ago.
| Pτ(t) = P(t) + Pτ(t − τ) | (1) |
Learning rate calculations for energy demand, GHG emissions and PV system costs
The development of the prices of PV system components, but also the cumulative primary energy demand (CED) for production and installation of a PV system can be described by a learning rate LR.20,24–26 Each time the cumulative produced capacity Pτcum(t) doubles, the price or CED is reduced by LR. The cumulative produced capacity Pτcum(t) is higher than the installed PV capacity shown in Fig. 1 left, which only shows the active PV capacity, while Pτcum(t) considers also the already decommissioned systems and is derived by integrating over Pτ(t). The learning rate calculations were carried out under the assumption of a module lifetime of τ = 25 years. For the CED the data was available for the year 2010, thus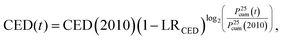 | (2) |
The majority of the GHG gas emission associated for the production of PV systems are based on energy consumption, either for direct processes during solar cell, module and system production, or in the processes for material production, e.g. silicon purification. Hence, we assume that the development of the GHG emissions GHG(t), can be modelled based on CED(t), with
| GHG(t) = CED(t)ECI(t), | (3) |
For the system price SP(t) we assumed 63 $cent Wp−1 from our own analysis published in ref. 30 for utility scale installations in the year 2019, thus
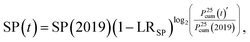 | (4) |
Power conversion efficiency
The efficiencies for solar cells in mass production of the base year 2018 were obtained from ref. 27. The most representative devices showed an efficiency of 20.2% for multi-crystalline Si-PERC and an efficiency of 22.0% for monocrystalline Si-PERC technology. The average efficiency was calculated accounting for the market share of mono-and multi-crystalline silicon PV in 2017 of 60.8% and 32.2%, respectively.25 The resulting module efficiency was calculated by accounting for 1.3% cell to module efficiency loss and 8% packaging loss, resulting in 18.91% module efficiency 2018.The development of the power conversion efficiency was calculated based on the efficiency of the year 2018 and on the basis of the historical learning rate, LRη. The learning rate was applied to the cumulative produced capacity Pτcum(t) for module lifetimes of τ = 25 years, thus
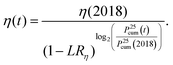 | (5) |
Silver demand
The silver demand per solar cell in 2018 was assumed to be 100 mg silver based on ref. 27. Learning rates for the reduction of the silver consumption LRAg are typically given per cell Agcell(t) in literature. Thus, the development of the module efficiency has to be considered additionally, to obtain the silver demand on a Wp basis AgWp(t). In this calculation the solar cell area Areacell and the packaging loss LossPack as described above have to be considered as well: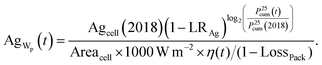 | (6) |
Author contributions
J. C. G. and L. W. performed the conceptualization, investigation, and methodology development. L. F. performed the LCA analysis and R. P. the REMIND modelling. All authors contributed the writing of the original draft and the reviewing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Fraunhofer Lighthouse Project MaNiTU. R.P. gratefully acknowledges funding from the European Union's Horizon 2020 research and innovation programme under grant agreement No 730403 (INNOPATHS) and the Kopernikus-Projekt Ariadne (FKZ 03SFK5A) by the German Federal Ministry of Education and Research. L.W. acknowledges the scholarship support of the German Federal Environmental Foundation (DBU).References
- F. Creutzig, P. Agoston, J. C. Goldschmidt, G. Luderer, G. Nemet and R. C. Pietzcker, Nat. Energy, 2017, 2, 17140 CrossRef.
- N. M. Haegel, R. Margolis, T. Buonassisi, D. Feldman, A. Froitzheim, R. Garabedian, M. Green, S. Glunz, H.-M. Henning, B. Holder, I. Kaizuka, B. Kroposki, K. Matsubara, S. Niki, K. Sakurai, R. A. Schindler, W. Tumas, E. R. Weber, G. Wilson, M. Woodhouse and S. Kurtz, Science, 2017, 356, 141–143 CrossRef CAS PubMed.
- N. M. Haegel, H. Atwater, T. Barnes, C. Breyer, A. Burrell, Y.-M. Chiang, S. de Wolf, B. Dimmler, D. Feldman, S. Glunz, J. C. Goldschmidt, D. Hochschild, R. Inzunza, I. Kaizuka, B. Kroposki, S. Kurtz, S. Leu, R. Margolis, K. Matsubara, A. Metz, W. K. Metzger, M. Morjaria, S. Niki, S. Nowak, I. M. Peters, S. Philipps, T. Reindl, A. Richter, D. Rose, K. Sakurai, R. Schlatmann, M. Shikano, W. Sinke, R. Sinton, B. J. Stanbery, M. Topic, W. Tumas, Y. Ueda, J. van de Lagemaat, P. Verlinden, M. Vetter, E. Warren, M. Werner, M. Yamaguchi and A. W. Bett, Science, 2019, 364, 836–838 CrossRef CAS PubMed.
- C. Breyer, D. Bogdanov, A. Gulagi, A. Aghahosseini, L. S. Barbosa, O. Koskinen, M. Barasa, U. Caldera, S. Afanasyeva, M. Child, J. Farfan and P. Vainikka, Prog. Photovoltaics, 2017, 25, 727–745 Search PubMed.
- Shell Scenarios, Sky – Meeting the Goals of the Paris Agreement, 2018.
- S. Davidsson and M. Höök, Energy Policy, 2017, 108, 574–582 CrossRef CAS.
- A. Valero, A. Valero, G. Calvo and A. Ortego, Renewable Sustainable Energy Rev., 2018, 93, 178–200 CrossRef.
- V. Moreau, P. Dos Reis and F. Vuille, Resources, 2019, 8, 29 CrossRef.
- A. Elshkaki and T. E. Graedel, J. Cleaner Prod., 2013, 59, 260–273 CrossRef.
- L. Grandell, A. Lehtilä, M. Kivinen, T. Koljonen, S. Kihlman and L. S. Lauri, Renewable Energy, 2016, 95, 53–62 CrossRef CAS.
- A. Feltrin and A. Freundlich, Renewable Energy, 2008, 33, 180–185 CrossRef CAS.
- J. I. Goldstein, D. E. Newbury, P. Echlin, D. C. Joy, A. D. Romig, C. E. Lyman, C. Fiori and E. Lifshin, Scanning Electron Microscopy and X-Ray Microanalysis. A Text for Biologists, Materials Scientists, and Geologists, 2nd edn, Springer US, Boston, MA, 1992 Search PubMed.
- M. Dale and S. M. Benson, Environ. Sci. Technol., 2013, 47, 3482–3489 CrossRef CAS PubMed.
- M. Woodhouse, A. Goodrich, R. Margolis, T. L. James, M. Lokanc and R. Eggert, IEEE J. Photovolt., 2013, 3, 833–837 Search PubMed.
- R. L. Moss, E. Tzimas, H. Kara, P. Willis and J. Kooroshy, Energy Policy, 2013, 55, 556–564 CrossRef CAS.
- G. Kavlak, J. McNerney, R. L. Jaffe and J. E. Trancik, Energy Environ. Sci., 2015, 8, 1651–1659 RSC.
- J. Jean, P. R. Brown, R. L. Jaffe, T. Buonassisi and V. Bulović, Energy Environ. Sci., 2015, 8, 1200–1219 RSC.
- P. Viebahn, O. Soukup, S. Samadi, J. Teubler, K. Wiesen and M. Ritthoff, Renewable Sustainable Energy Rev., 2015, 49, 655–671 CrossRef CAS.
- D. Berney Needleman, J. R. Poindexter, R. C. Kurchin, I. M. Peters, G. Wilson and T. Buonassisi, Energy Environ. Sci., 2016, 9, 2122–2129 RSC.
- A. Louwen, W. G. J. H. M. van Sark, A. P. C. Faaij and R. E. I. Schropp, Nat. Commun., 2016, 7, 13728 CrossRef CAS PubMed.
- A. Månberger and B. Stenqvist, Energy Policy, 2018, 119, 226–241 CrossRef.
- K. Tokimatsu, M. Höök, B. McLellan, H. Wachtmeister, S. Murakami, R. Yasuoka and M. Nishio, Appl. Energy, 2018, 225, 1158–1175 CrossRef.
- E. Gervais, S. Shammugam, L. Friedrich and T. Schlegl, Renewable Sustainable Energy Rev., 2021, 137, 110589 CrossRef CAS.
- S. Philipps and W. Warmuth, Photovoltaics Report.
- Fraunhofer Institut für Solare Energiesysteme ISE, Current and Future Cost of Photovoltaics, 2015.
- M. Görig and C. Breyer, Environ. Prog. Sustainable Energy, 2016, 35, 914–923 CrossRef.
- ITRPV, International Technology Roadmap for Photovoltaic, 2018 Results 10th Edition, 2019 Search PubMed.
- G. Luderer, M. Pehl, A. Arvesen, T. Gibon, B. L. Bodirsky, H. S. de Boer, O. Fricko, M. Hejazi, F. Humpenöder, G. Iyer, S. Mima, I. Mouratiadou, R. C. Pietzcker, A. Popp, M. van den Berg, D. van Vuuren and E. G. Hertwich, Nat. Commun., 2019, 10, 5229 CrossRef PubMed.
- C. Bertram, G. Luderer, R. C. Pietzcker, E. Schmid, E. Kriegler and O. Edenhofer, Nat. Clim. Change, 2015, 5, 235–239 CrossRef CAS.
- G. Luderer, C. Auer, N. Bauer, L. Baumstark, C. Bertram, S. Bi, A. Dirnaichner, A. Giannousakis, J. Hilaire, D. Klein, J. Koch, M. Leimbach, A. Levesque, A. Malik, L. Merfort, M. Pehl, R. Pietzker, F. Piontek, S. Rauner, R. Rodrigues, M. Rottoli, F. Schreyer, B. Sörgel, J. Strefler and F. Ueckerdt, REMIND v2.1.0 - Model documentation, Zenodo, 2020 Search PubMed.
- T. Aboumahboub, C. Auer, N. Bauer, L. Baumstark, C. Bertram, S. Bi, J. Dietrich, A. Dirnaichner, A. Giannousakis, M. Haller, J. Hilaire, D. Klein, J. Koch, A. Körner, E. Kriegler, M. Leimbach, A. Levesque, A. Lorenz, G. Luderer, S. Ludig, M. Lüken, A. Malik, S. Manger, L. Merfort, I. Mouratiadou, M. Pehl, R. Pietzker, F. Piontek, L. Popin, S. Rauner, R. Rodrigues, N. Roming, M. Rottoli, E. Schmidt, F. Schreyer, A. Schultes, B. Sörgel, J. Strefler and F. Ueckerdt, REMIND – REgional Model of INvestments and Development, Zenodo, 2020 Search PubMed.
- F. Ueckerdt, R. Pietzcker, Y. Scholz, D. Stetter, A. Giannousakis and G. Luderer, Energy Economics, 2017, 64, 665–684 CrossRef.
- R. C. Pietzcker, D. Stetter, S. Manger and G. Luderer, Appl. Energy, 2014, 135, 704–720 CrossRef.
- M. J. de Wild-Scholten, Photovoltaics, Solar Energy Materials, and Technologies: Cancun 2010, 2013, vol. 119, pp. 296–305 Search PubMed.
- N. Jungbluth, M. Tuchschmid and M. J. de Wild-Scholten, 2008, http://www.esu-services.ch.
- International Energy Agency, World Energy Outlook 2018, Paris, 2018 Search PubMed.
- R. Flosdorff and G. Hilgarth, Elektrische Energieverteilung, 8th edn, Teubner, Stuttgart, Leipzig, Wiesbaden, 2003 Search PubMed.
- Wikipedia, Kohlekraftwerk, available at: https://de.wikipedia.org/w/index.php?title=Kohlekraftwerk&oldid=204189894, accessed 23 December 2020.
- L. Wagner, S. Mastroianni and A. Hinsch, Joule, 2020, 4, 882–901 CrossRef CAS.
- Remaining carbon budget - Mercator Research Institute on Global Commons and Climate Change (MCC), available at: https://www.mcc-berlin.net/en/research/co2-budget.html, accessed 8 February 2021.
- M. Allen, M. Babiker, Y. Chen, H. de Coninck and S. Conors, Global Warming of 1.5 °C. An IPCC Special Report on the impacts of global warming of 1.5 °C above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change, sustainable development, and efforts to eradicate poverty, IPCC Special Report, 2018 Search PubMed.
- International Year of Glass 2022, The global glass economy and its wider social consequences, 2020.
- US Geological Survey, Mineral commodity summaries 2019, United States Government Printing Office, Reston, Virginia, 2019 Search PubMed.
- T. J. Brown, N. E. Idoine, C. E. Wrighton, E. R. Raycraft, S. F. Hobbs, R. A. Shaw, P. Everett, C. Kresse, E. A. Deady and T. Bide, World Mineral Production 2014–2018, British Geological Survey, Keyworth, Nottingham, 2019 Search PubMed.
- S. Philipps and W. Warmuth, Photovoltaics Report, available at: https://www.ise.fraunhofer.de/content/dam/ise/de/documents/publications/studies/Photovoltaics-Report.pdf, accessed 5 April 2019.
- L. A. Zafoschnig, S. Nold and J. C. Goldschmidt, IEEE Journal of Photovoltaics, 2020, 10, 1632–1641 Search PubMed.
- Fortune Media IP Limited, Fortune Global 500, available at: https://fortune.com/global500/2019/, accessed 13 January 2020.
- ITRPV, International Technology Roadmap for Photovoltaic. 2019 Results 11th Edition, 2020 Search PubMed.
- A. Richter, M. Hermle and S. W. Glunz, IEEE J. Photovolt., 2013, 3, 1184–1191 Search PubMed.
- S. Essig, C. Allebé, T. Remo, J. F. Geisz, M. A. Steiner, K. Horowitz, L. Barraud, J. S. Ward, M. Schnabel, A. Descoeudres, D. L. Young, M. Woodhouse, M. Despeisse, C. Ballif and A. Tamboli, Nat. Energy, 2017, 2, 17144 CrossRef CAS.
- J. F. Geisz, R. M. France, K. L. Schulte, M. A. Steiner, A. G. Norman, H. L. Guthrey, M. R. Young, T. Song and T. Moriarty, Nat. Energy, 2020, 5, 326–335 CrossRef CAS.
- National Renewable Energy Laboratory (NREL), Best Research-Cell Efficiency Chart, available at: https://www.nrel.gov/pv/cell-efficiency.html, accessed 18 December 2020.
- J. Werner, F. Sahli, F. Fu, J. J. Diaz Leon, A. Walter, B. A. Kamino, B. Niesen, S. Nicolay, Q. Jeangros and C. Ballif, ACS Energy Lett., 2018, 3, 2052–2058 CrossRef CAS.
- K. Xiao, J. Wen, Q. Han, R. Lin, Y. Gao, S. Gu, Y. Zang, Y. Nie, J. Zhu, J. Xu and H. Tan, ACS Energy Lett., 2020, 5, 2819–2826 CrossRef CAS.
- A. de Vos, J. Phys. D: Appl. Phys., 1980, 13, 839–846 CrossRef.
- C. Wu, D. Wang, Y. Zhang, F. Gu, G. Liu, N. Zhu, W. Luo, D. Han, X. Guo, B. Qu, S. Wang, Z. Bian, Z. Chen and L. Xiao, Adv. Funct. Mater., 2019, 29, 1902974 CrossRef.
- X. Dai, Y. Deng, C. H. van Brackle, S. Chen, P. N. Rudd, X. Xiao, Y. Lin, B. Chen and J. Huang, Adv. Energy Mater., 2020, 10, 1903108 CrossRef CAS.
- W. Driscoll, US start-up pursues roll-to-roll printing of perovskite on flexible glass, available at: https://www.pv-magazine.com/2020/11/18/us-start-up-pursues-roll-to-roll-printing-of-perovskite-on-flexible-glass/, accessed 23 December 2020.
- S. Fendt, A. Buttler, M. Gaderer and H. Spliethoff, WIREs Energy Environ., 2016, 5, 327–350 CrossRef CAS.
- R. Frischknecht, N. Jungbluth, H.-J. Althaus, R. Hischier, G. Doka, C. Bauer, R. Dones, T. Nemecek, S. Hellweg, S. Humbert, M. Margni, T. Koellner and Y. Loerincik, Implementation of life cycle impact assessment methods. Data v2.0 (2007). Ecoinvent report No. 3, Swiss Federal Office of Agriculture (BLW) INIS-CH-10091, 2007.
- M. Leisin, Energiewende in der Industrie Potenziale und Wechselwirkungen mit dem Energiesektor. Branchensteckbrief der Glasindustrie, Universität Stuttgart, Institut für Energiewirtschaft und rationelle Energieanwendung, 2019 Search PubMed.
- L. Friedrich, S. Nold, A. Müller, J. Rentsch and R. Preu, 2021, under review.
- M. Pehl, A. Arvesen, F. Humpenöder, A. Popp, E. G. Hertwich and G. Luderer, Nat. Energy, 2017, 2, 939–945 CrossRef CAS.
- J. Schube, T. Fellmeth, M. Jahn, R. Keding and S. W. Glunz, in International Symposium on Green and Sustainable Technology (ISGST2019), AIP Publishing, 2019, p. 20007 Search PubMed.
- F. Sahli, B. A. Kamino, J. Werner, M. Bräuninger, B. Paviet-Salomon, L. Barraud, R. Monnard, J. P. Seif, A. Tomasi, Q. Jeangros, A. Hessler-Wyser, S. de Wolf, M. Despeisse, S. Nicolay, B. Niesen and C. Ballif, Adv. Energy Mater., 2018, 8, 1701609 CrossRef.
- Z. Yu, Z. Yang, Z. Ni, Y. Shao, B. Chen, Y. Lin, H. Wei, Z. J. Yu, Z. Holman and J. Huang, Nat. Energy, 2020, 5, 657–665 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |