Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Refinement and extension of COSMO-RS-trained fragment contribution models for predicting the partition properties of C10–20 chlorinated paraffin congeners†
Satoshi
Endo
 *
*
Health and Environmental Risk Division, National Institute for Environmental Studies (NIES), Onogawa 16-2, 305-8506 Tsukuba, Ibaraki, Japan. E-mail: endo.satoshi@nies.go.jp; Tel: +81-29-850-2695
First published on 21st May 2021
Abstract
COSMO-RS-trained fragment contribution models (FCMs) to predict the partition properties of chlorinated paraffin (CP) congeners were refined and extended. The improvement includes (i) the use of an improved conformer generation method for COSMO-RS, (ii) extension of training and validation sets for FCMs up to C20 congeners covering short-chain (SCCPs), medium-chain (MCCPs) and long-chain CPs (LCCPs), and (iii) more realistic simulation of industrial CP mixture compositions by using a stochastic algorithm. Extension of the training set markedly improved the accuracy of model predictions for MCCPs and LCCPs, as compared to the previous study. The predicted values of the log octanol/water partition coefficients (Kow) for CP mixtures agreed well with experimentally determined values from the literature. Using the established FCMs, this study provided a set of quantum chemically based predictions for 193 congener groups (C10–20 and Cl0–21) regarding Kow, air/water (Kaw), and octanol/air (Koa) partition coefficients, subcooled liquid vapor pressure (VP) and aqueous solubility (Sw) in a temperature range of 5–45 °C as well as the respective enthalpy and internal energy changes.
Environmental significanceThe partition properties for chlorinated paraffins (CPs) are difficult to determine both experimentally and theoretically due to the extremely high complexity of CP mixtures. COSMO-RS-trained fragment contribution models refined in this study enabled rapid calculations of partition properties for an extended set of individual CP congeners. Using FCMs, this work generated a large data set of quantum-chemically based predictions of partition properties for 193 congener groups (i.e., homologue sets). These data can be used for, e.g., environmental fate and bioaccumulation models or be compared to field monitoring data to understand the environmental behavior of CPs. |
1 Introduction
Chlorinated paraffins (CPs) are mixtures of polychlorinated n-alkanes with different carbon chain lengths and chlorination patterns. Depending on the length of the carbon chain, CPs are classified into short-chain (SCCPs, C10–13), medium-chain (MCCPs, C14–17) and long-chain CPs (LCCPs, C18+). SCCPs are restricted under the Stockholm Convention due to their recognized persistent, bioaccumulative and toxic properties.1 MCCPs and LCCPs are also of environmental concern because of their frequent detection in various environmental and biological samples2–5 including samples from humans.6,7 Environmental property values such as equilibrium partition coefficients (K) need to be known for environmental fate and risk assessments, although the extremely high complexity of CP mixtures hampers the use of conventional experimental and theoretical approaches to obtain their property data.In the previous study,8 we proposed to calibrate a fragment contribution model (FCM) with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values predicted by the COSMO-RS (conductor-like screening model for real solvents) method for developing property prediction models for individual CP congeners. This approach combines the advantages of both FCM and COSMO-RS methods. Thus, FCMs are an empirical model that is computationally simple and fast but need to be trained with a large and diverse set of data. FCMs are usually trained with experimental data,9,10 which however are not sufficiently available for CP congeners. COSMO-RS is quantum-chemically based prediction theory for solute activity in solvent and can provide accurate predictions for partition properties such as K values.11 Glüge et al.12 demonstrated that COSMO-RS was the most accurate of the three methods that they compared for predicting partition properties of CPs. Our previous work8 also showed that COSMO-RS predictions for partition coefficients of individual CP congeners were mostly within 1 log unit of the experimental data available. A strong advantage of COSMO-RS is that it can calculate properties from the molecular structure and does not need any additional empirical calibration. Nevertheless, the quantum chemical calculations are highly time-demanding for CP molecules and cannot be performed for thousands of congeners possibly present in CP industrial mixtures. The previous work8 demonstrated that FCMs trained with 815 COSMO-RS-predicted K values can predict the original COSMO-RS calculations within an RMSE of 0.1–0.3 log units. The trained FCMs were able to provide predictions for octanol/water (Kow), air/water (Kaw) and octanol/air (Koa) partition coefficients for as many as 52
K values predicted by the COSMO-RS (conductor-like screening model for real solvents) method for developing property prediction models for individual CP congeners. This approach combines the advantages of both FCM and COSMO-RS methods. Thus, FCMs are an empirical model that is computationally simple and fast but need to be trained with a large and diverse set of data. FCMs are usually trained with experimental data,9,10 which however are not sufficiently available for CP congeners. COSMO-RS is quantum-chemically based prediction theory for solute activity in solvent and can provide accurate predictions for partition properties such as K values.11 Glüge et al.12 demonstrated that COSMO-RS was the most accurate of the three methods that they compared for predicting partition properties of CPs. Our previous work8 also showed that COSMO-RS predictions for partition coefficients of individual CP congeners were mostly within 1 log unit of the experimental data available. A strong advantage of COSMO-RS is that it can calculate properties from the molecular structure and does not need any additional empirical calibration. Nevertheless, the quantum chemical calculations are highly time-demanding for CP molecules and cannot be performed for thousands of congeners possibly present in CP industrial mixtures. The previous work8 demonstrated that FCMs trained with 815 COSMO-RS-predicted K values can predict the original COSMO-RS calculations within an RMSE of 0.1–0.3 log units. The trained FCMs were able to provide predictions for octanol/water (Kow), air/water (Kaw) and octanol/air (Koa) partition coefficients for as many as 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 CP congeners within a reasonable time. The predicted values were shown to agree well with available experimental log
000 CP congeners within a reasonable time. The predicted values were shown to agree well with available experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values for individual congeners.
K values for individual congeners.
To provide even more useful sets of property data for individual CP congeners, congener groups (defined here as congeners with the same molecular formula; also referred to as homologue groups or as isomers), and whole mixtures, the present work refined and extended the COSMO-RS-trained FCM approach in the following regards. First, the training and validation sets for FCM development were revised, covering MCCPs and LCCPs, which were left out of consideration in the previous work.8 Second, COSMO-RS-trained FCMs for subcooled liquid saturation vapor pressure (VP) and aqueous solubility (Sw) were developed in addition to Kow, Kaw, and Koa. Third, the present work calibrated FCMs for these properties at differing temperatures as well as enthalpy changes (ΔH) and internal energy changes (ΔU). Fourth, a Monte Carlo method was introduced that simulates synthetic pathways of CP molecules and predicts congener compositions of technical mixtures with varying degree of chlorination.13 Combined with the trained FCMs, this stochastic method should offer more realistic property distributions of CP mixtures in comparison to the random generation of congeners as adopted in the previous study. All predicted data are provided as tables and figures in the ESI† together with R scripts for additional calculations to facilitate the use of outputs from this work.
2 Methods
2.1 Method overview
The workflow of this study is summarized in Fig. 1. The properties considered are log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow, log
Kow, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kaw, log
Kaw, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Koa, log
Koa, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) VP (in Pa), and log
VP (in Pa), and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sw (in mol L−1) at 5, 15, 25, 35 and 45 °C and corresponding temperature-dependence values which are required for interpolation of these properties (ΔHow, ΔUaw, ΔUoa, ΔHvap, and ΔHdiss, respectively). COSMO-RS was used to generate training and validation data for FCMs. A set of congener structures built by the Monte Carlo model was passed to the trained FCMs to predict property distributions for CP mixtures. Details are explained in the following sections.
Sw (in mol L−1) at 5, 15, 25, 35 and 45 °C and corresponding temperature-dependence values which are required for interpolation of these properties (ΔHow, ΔUaw, ΔUoa, ΔHvap, and ΔHdiss, respectively). COSMO-RS was used to generate training and validation data for FCMs. A set of congener structures built by the Monte Carlo model was passed to the trained FCMs to predict property distributions for CP mixtures. Details are explained in the following sections.
2.2 COSMO-RS
In this work, COSMOconfX 20, TURBOMOLE 7.4 and COSMOthermX 20 (all from COSMOlogic, Biovia, Dassault Systèmes) were used for implementation of COSMO-RS. The first two programs provide an optimal set of conformers of each chemical and derive the cosmo and energy files that contain the information (e.g., energy, and surface screening charge density) needed for successive calculations in COSMOthermX. COSMOconfX and TURBOMOLE were run on the NIES supercomputer system (HPE Apollo 2000 System). COSMOthermX with the BP_TZVPD_FINE_20 parameterization was used to calculate the property values. Sw was calculated as VP/(RTKaw) for consistency and computational efficiency, where R is the gas constant and T is the absolute temperature. Sw calculated here is for dry, pure subcooled liquid and does not consider mutual saturation with the water phase. The effect of mutual saturation is expected to be small because of low Sw of CP congeners. Note that Kow was calculated with wet octanol and Koa with dry octanol. Temperature dependence was evaluated by calculating the properties for 278.15, 288.15, 298.15, 308.15 and 318.15 K. As the log of the COSMOtherm-predicted values was linear against 1/T, the slope of the following equation was used to derive ΔH and ΔU,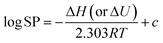 | (1) |
CP congeners can have many stereoisomers because each −CHCl– group can be chiral. Moreover, all CP molecules have many rotatable bonds and thus an enormous number of possible conformers exist. Due to these structural features, two considerations appear to be necessary when COSMOconfX is used. First, the default algorithm of the COSMOconfX sometimes generates stereochemically inconsistent output structures as compared to the original input structure, as stated in the previous article.8 This problem can be circumvented by using the Windows version of COSMOconfX, removing the RDKit conformer generation step, and running only the Balloon method to generate initial candidate conformers. Second, COSMOtherm prediction for CPs sometimes depends on the original input structure entered in the COSMOconfX program. It appears that the default algorithm of COSMOconfX cannot always find the optimal conformation of a CP molecule in the gas phase. This results in sporadically large solvent–air (or low air–solvent) partition coefficients (up to 0.47 log unit difference). Some examples are provided in ESI-1 (see ESI-A, Fig. S1, S2†). Indeed, by increasing the number of initial candidate conformers to consider (ca. 4 times), it was possible to reduce variability and obtain more repeatable predictions (Fig. S1, S2†).
2.3 Fragment contribution models (FCMs)
FCMs are a linear regression model that uses the numbers of molecular substructures (i.e., fragments) as independent variables to describe the properties of interest. The implementation of FCMs for CP congeners was described in the previous article.8 In brief, molecular fragments with one to four C atoms were counted for each CP congener. In total, 310 fragment types were considered, including 78 fragments that describe the diastereomeric structure (see the next paragraph for more explanation). For training of the FCMs, COSMOtherm-predicted property values were regressed against these fragment counts. The forward and backward stepwise approach was performed with Akaike's Information Criterion (AIC) as the evaluation metric to select an optimal set of fragments. In contrast to the previous work, this work only reports the model that uses all C1–C4 fragments, denoted as the Level 4 model in the previous article, because this model always performed the best. The partial least squares regression (PLSR) was also computed but external validation showed that the PLSR-derived model was not better than the model directly from the stepwise regression; thus, the PLSR results are not reported here. Fragment counting and statistical analysis were all performed with R (3.6.2) using ChemmineR (3.38.0), ChemmineOB (1.24.0),14 pls (2.7.2)15 and their dependent packages.Some more explanations for fragments that include the diastereomeric structure may be useful. A C2-fragment -CHCl-CHCl- is the simplest example of fragments with a diastereomeric structure. Both C atoms can be chiral, and depending on their rotational configurations, two diastereomeric structures are possible: one with the two C atoms having the same rotational configuration and the other having the opposite rotational configurations. Thus, this study counted “the total number of (stereometrically nonspecific) –CHCl–CHCl–” and “the number of –CHCl–CHCl– with the same rotational configuration” and used these counts as FCM variables. C3- and C4-fragments are obviously more complicated. The principle is that, for each fragment, all possible stereometrically specific structures are listed, meso- structures are identified to avoid double counting, and the numbers of enantiomeric structures are combined to account for difference in diastereomers.
2.4 Training and validation sets for FCMs
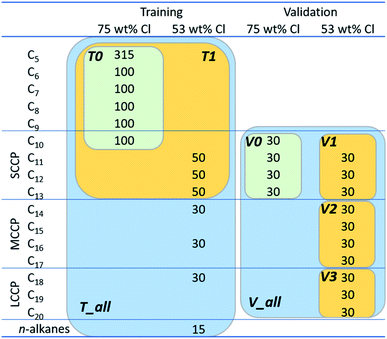
Overall, 1070 congeners for training and 420 congeners for validation were prepared for this work (Fig. 2). Among these, 815 training (grouped as “T0” in Fig. 2) and 120 validation congeners (V0) are those used in the previous study.8 These original congeners are short and were chosen before because of relatively fast quantum chemical computation. Note, cosmo and energy files for T0 and V0 were all updated in this work using the refined COSMOconfX procedure, as discussed above. In addition, this work prepared 50 congeners each for C11–13 and 30 congeners each for C14, C16, and C18 as additional training compounds. Moreover, 15 n-alkanes (C6–20) were added to enlarge the domain of training. The validation set was also extended by adding 30 congeners each for C11–20 congeners.For a given carbon chain length, structures of training and validation congeners were generated in a random manner. In the previous study,8 H or Cl was assigned to a substitution position at a probability of 50%. Thus, on average, half of the positions were substituted with Cl, equivalent to the mean chlorination degree of 75 wt%. This is relatively high as compared to typical compositions of industrial mixtures (i.e., 30–70 wt%). Moreover, there was an indication that the FCMs trained in the previous study were comparatively inaccurate for low chlorinated congeners.8 Therefore, for generation of additional training and validation congeners, the current study adopted a reduced probability of chlorination (53 wt% Cl on average) so that lower chlorinated congeners could be better represented.
To test the influence of the training set on the prediction accuracy, training congeners were grouped into 3 sets (T0, T1, and T_all) and validation congeners into 5 sets (V0, V1, V2, V3 and V_All), as shown in Fig. 2, and the FCM results of all combinations were compared.
2.5 Monte Carlo model
Industrial CP mixtures contain an unknown number of congeners with differing molecular structures. To predict the property distributions of mixtures using FCMs, a set of molecular structures that represents the composition of the mixture needs to be prepared. In the previous study,8 molecular structures were generated on a random basis. However, past studies have shown that Cl substitution does not randomly occur.16,17To obtain a more representative ensemble of molecular structures, this work used the Monte Carlo approach developed by Jensen et al.13 The algorithm of Jensen et al. starts with a set of say 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 n-alkane molecules and simulates the free-radical chlorination reaction as a series of substitution of H with Cl. Different probabilities for Cl substitution are assigned to C atoms in the alkane chain, depending on the neighboring Cl substitution patterns. The probabilities were set based on the available experimental data.13 As this stochastic simulation proceeds, the n-alkane molecules are increasingly chlorinated, exhibiting different substitution patterns, and lead to a final set of CP structures which is expected to mimic the composition of the actual CP mixture.
000 n-alkane molecules and simulates the free-radical chlorination reaction as a series of substitution of H with Cl. Different probabilities for Cl substitution are assigned to C atoms in the alkane chain, depending on the neighboring Cl substitution patterns. The probabilities were set based on the available experimental data.13 As this stochastic simulation proceeds, the n-alkane molecules are increasingly chlorinated, exhibiting different substitution patterns, and lead to a final set of CP structures which is expected to mimic the composition of the actual CP mixture.
In this work, the algorithm from Jensen et al. was used with some modifications. First, while the original model randomly selected a C atom to be challenged by chlorine, this work randomly selected an H position instead. This change was made to generate stereoisomers. The two H atoms at a C atom were assumed to have the same probability for Cl substitution (i.e., the same probability to obtain R and S configurations). Second, the three H positions of a terminal C atom were attacked at 2/3 probability of the H positions inside the chain, so that the probability remains uniform with regard to all C atoms. Third, at each reaction step, 1% of the total alkane molecules were selected for possible reaction, instead of one molecule by Jensen's approach, in order to speed up the simulation. The reaction cycle was repeated until the wt% of Cl exceeded the pre-set value (e.g., 40 wt%). A list of SMILES strings was then generated according to the results of simulation and passed to the FCMs to predict the distributions of physicochemical properties for the given mixture. An R code is provided in the ESI zip fie to run this Monte Carlo simulation.
The simulation was performed for C10–20 alkanes with 30–70 wt% Cl. On the basis of preliminary test runs (see ESI-B, Fig. S3†), the number of n-alkane molecules was set to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for each combination of the chain length and Cl wt% so that we can obtain reliable K distributions for all congener groups that make up more than 1 mol% of the mixture.
000 for each combination of the chain length and Cl wt% so that we can obtain reliable K distributions for all congener groups that make up more than 1 mol% of the mixture.
3 Results and discussion
3.1 Training and validation sets for FCMs
Prediction accuracy of trained FCMs as evaluated by root mean squared errors (RMSEs) depended on the combination of training and validation sets. RMSEs for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kaw at 25 °C are presented in Fig. 3 as an example (see more data in Fig. S4 and Table S1†). T0–V0 is the combination of training and validation sets used in the previous study.8 RMSEs for this combination appreciably improved; thus, RMSEs were 0.095, 0.246 and 0.190 for log
Kaw at 25 °C are presented in Fig. 3 as an example (see more data in Fig. S4 and Table S1†). T0–V0 is the combination of training and validation sets used in the previous study.8 RMSEs for this combination appreciably improved; thus, RMSEs were 0.095, 0.246 and 0.190 for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow, log
Kow, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kaw and log
Kaw and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Koa, respectively, in this study, while they were 0.123, 0.286 and 0.207, respectively, in the previous study. This improvement should result from more accurate calculations of COSMOtherm due to the improved COSMOconfX procedure because nothing has changed in the FCM method.
Koa, respectively, in this study, while they were 0.123, 0.286 and 0.207, respectively, in the previous study. This improvement should result from more accurate calculations of COSMOtherm due to the improved COSMOconfX procedure because nothing has changed in the FCM method.
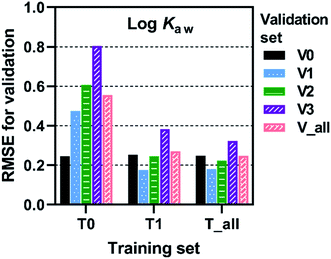 | ||
| Fig. 3 Root mean squared errors (RMSE) for validation of FCM models. Training and validation sets are explained in Fig. 2. | ||
Training set T0 resulted in elevated RMSEs for validation sets V1, V2 and V3 (Fig. 3). Thus, the use of congeners with the mean Cl content of 75 wt% (T0) as training compounds led to less accurate predictions for congeners with 53 wt% Cl (V1, V2, V3). Training FCMs with T1 (including congeners with 75 and 53 wt% Cl) resulted in a marked improvement in predicting the V1, V2, and V3 sets. Still, predictions were less accurate for MCCPs (V2) and LCCPs (V3) compared to for SCCPs (V1). The inclusion of M/LCCPs in the training set (i.e., T_all) resulted in only a minor improvement in the prediction of V2 and V3 congeners, suggesting that extrapolation to longer congeners is less of a problem. Higher RMSEs for V2 and V3 could be related, in part, to lower precision of COSMOtherm predictions for long molecules with a large number of possible conformers (see Section 2.2). Overall, it can be concluded that extending the training set from T0 to T_all substantially improved the domain of applicability of the trained FCMs.
3.2 FCMs for Kow, Kaw, Koa, VP and Sw at 5–45 °C and the respective ΔH and ΔU
FCMs for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow, log
Kow, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kaw, log
Kaw, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Koa, log
Koa, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) VP and log
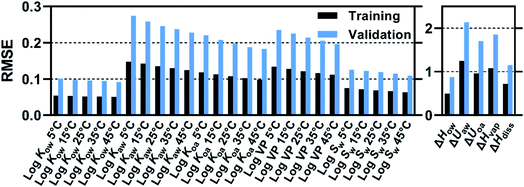
VP and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sw at 5–45 °C as well as their respective ΔH or ΔU were calibrated with the T_all set and validated with the V_all set. All results are presented in Fig. S5 and Tables S2.† RMSE values for training and validation are summarized in Fig. 4. An R code and its associated files are provided in the ESI zip file so that the reader can use the trained FCMs to obtain predictions for all properties considered here for given CP congeners.
Sw at 5–45 °C as well as their respective ΔH or ΔU were calibrated with the T_all set and validated with the V_all set. All results are presented in Fig. S5 and Tables S2.† RMSE values for training and validation are summarized in Fig. 4. An R code and its associated files are provided in the ESI zip file so that the reader can use the trained FCMs to obtain predictions for all properties considered here for given CP congeners.
RMSE values for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K's, log
K's, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) VP and log
VP and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sw were 0.05–0.15 for training and 0.09–0.28 for validation. These ranges are similar to those of the previous work.8 The FCM fitted well with the COSMOtherm-predicted values in the entire range of property values (Fig. S5†). The validation RMSEs indicate that the trained FCMs can predict the COSMOtherm-predicted values for C10–20 CP congeners to the accuracy of 0.1–0.3 log units on average. RMSE values for ΔH's and ΔU's were 0.5–1.3 kJ mol−1 for training and 0.9–2.1 kJ mol−1 for validation. Generally, the RMSE tends to be lower for liquid/liquid partition properties (i.e., Kow, Sw, ΔHow, ΔHdiss) than for liquid/air partition properties (i.e., Kaw, Koa, VP, ΔUaw, ΔUoa, and ΔHvap). This trend may be related to COSMOtherm's precision which is expected to be higher for the liquid/liquid partition properties, because energy terms and their errors calculated for the two liquid phases tend to be cancelled, whereas such cancelation does not occur for liquid/air partitioning. Fig. 4 also shows that RMSEs for both training and validation decrease with temperature. As the intermolecular interaction energy generally diminishes with temperature, the contribution of each fragment decreases, and so does the fitting error.
Sw were 0.05–0.15 for training and 0.09–0.28 for validation. These ranges are similar to those of the previous work.8 The FCM fitted well with the COSMOtherm-predicted values in the entire range of property values (Fig. S5†). The validation RMSEs indicate that the trained FCMs can predict the COSMOtherm-predicted values for C10–20 CP congeners to the accuracy of 0.1–0.3 log units on average. RMSE values for ΔH's and ΔU's were 0.5–1.3 kJ mol−1 for training and 0.9–2.1 kJ mol−1 for validation. Generally, the RMSE tends to be lower for liquid/liquid partition properties (i.e., Kow, Sw, ΔHow, ΔHdiss) than for liquid/air partition properties (i.e., Kaw, Koa, VP, ΔUaw, ΔUoa, and ΔHvap). This trend may be related to COSMOtherm's precision which is expected to be higher for the liquid/liquid partition properties, because energy terms and their errors calculated for the two liquid phases tend to be cancelled, whereas such cancelation does not occur for liquid/air partitioning. Fig. 4 also shows that RMSEs for both training and validation decrease with temperature. As the intermolecular interaction energy generally diminishes with temperature, the contribution of each fragment decreases, and so does the fitting error.
FCM predictions are compared to the available experimental data for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow and log
Kow and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kaw of SCCP congeners (Fig. S6†). FCM predictions in the previous work already agreed well with the experimental data, and FCM predictions from this study agreed well similarly. Nevertheless, clear improvement can be found for prediction of log
Kaw of SCCP congeners (Fig. S6†). FCM predictions in the previous work already agreed well with the experimental data, and FCM predictions from this study agreed well similarly. Nevertheless, clear improvement can be found for prediction of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kaw for 1,2,9,10-tetrachlorodecane and 1,2,10,11-tetrachloroundecane. While the repeated –CH2– units were not well calibrated previously,8 this shortcoming was apparently overcome in the current work by adding more of low chlorinated congeners in the training set.
Kaw for 1,2,9,10-tetrachlorodecane and 1,2,10,11-tetrachloroundecane. While the repeated –CH2– units were not well calibrated previously,8 this shortcoming was apparently overcome in the current work by adding more of low chlorinated congeners in the training set.
3.3 Monte Carlo model for simulating the congener compositions of CP mixtures
Before predicting the property distributions of mixtures, it may be useful to evaluate the Monte Carlo model itself. To test the relevance of the model outputs, experimental composition data for 14 CP mixtures reported recently in the literature18 were predicted by the model. The CP congeners generated by the Monte Carlo simulations for a given Cl wt% were sorted according to the numbers of C and Cl atoms and were compared to the experimental data (Fig. 5; see Fig. S7† for all 14 mixtures from ref. 18). The Monte Carlo model excellently reproduced the numbers of Cl for each carbon chain length, supporting the validity of the model.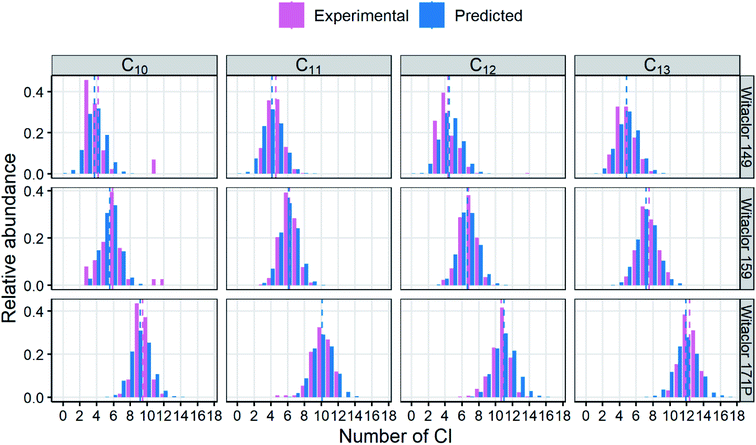 | ||
| Fig. 5 Experimental and predicted congener profiles in CP mixtures. Experimental data are from Yuan et al.18 Predictions were derived with the Monte Carlo method13 with 3000 molecules for each number of C. Dashed lines indicate the mean number of Cl. | ||
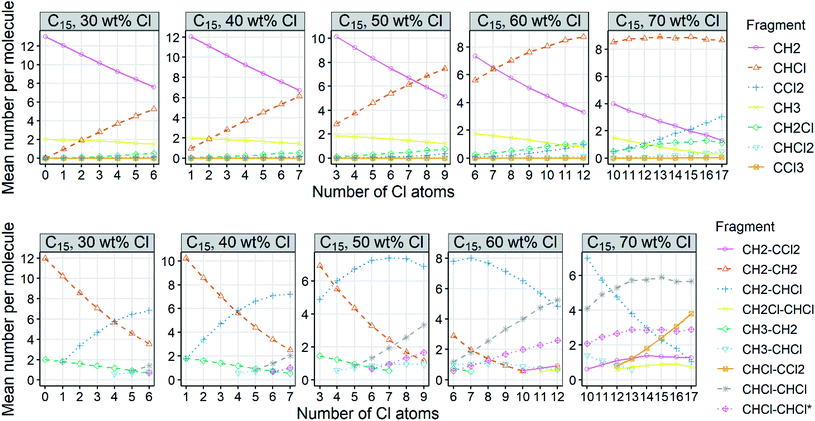
To give an overview of the abundance of fragment types generated by the Monte Carlo simulations, the mean numbers of the C1 and C2 fragments per molecule are plotted (Fig. 6; see Fig. S8 and S9† for other carbon chain lengths). CH2 is the most abundant C1 fragment in low-chlorinated mixtures (≤50 wt% Cl). The number of CHCl increases with increasing degree of chlorination, and CHCl is the major C1 fragment for mixtures with ≥60 wt% Cl. CCl2 is minor except for highly chlorinated congener groups (i.e., the number of Cl ≥ the number of C). The terminal fragments are always minor because there can only be two per molecule. The terminal C atoms can also be chlorinated, but they are less often chlorinated than C atoms within the chain. Distributions of the C2 fragments show that CH2–CHCl is often the major C2 fragment that carries Cl. CHCl–CHCl rather than CH2–CCl2 emerges when the number of CH2–CHCl approaches the total number of C atoms divided by 2. C2-fragments with double chlorinated C (CH2–CCl2 and CHCl–CCl2) occur only in highly chlorinated congeners. These fragment patterns reflect the model parameterization that is based on the knowledge of the varying probabilities for chlorination of C atoms.
3.4 Property distributions for CP technical mixtures
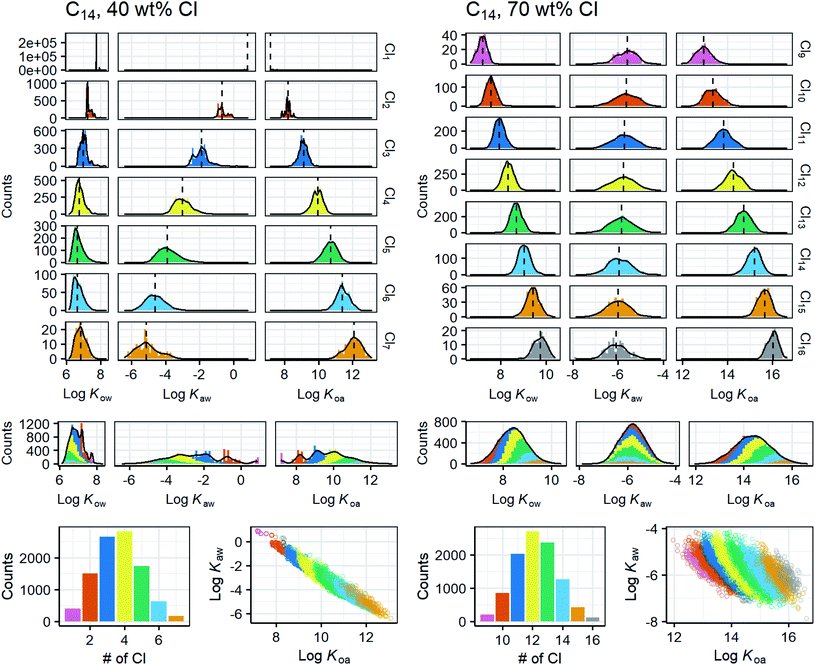
For each mixture with a given combination of a carbon chain length (C10–20) and degree of chlorination (30–70 wt% Cl), 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 CP molecules were generated by the Monte Carlo approach. Then, property values were predicted by the FCMs. The results for the 55 mixtures (11 C lengths × 5 Cl degrees) were sorted according to the congener groups (i.e., molecular formula) and are shown with histograms and probability density curves (ESI-2†). Fig. 7 shows two examples of the distributions of Kow, Kaw, and Koa. Low chlorinated (30, 40 wt% Cl) mixtures are characterized by (i) bell-shape overall K distributions with some sharp spikes originating from low chlorinated (Cl0–3) congeners, (ii) a narrow range (2 log units) of log
000 CP molecules were generated by the Monte Carlo approach. Then, property values were predicted by the FCMs. The results for the 55 mixtures (11 C lengths × 5 Cl degrees) were sorted according to the congener groups (i.e., molecular formula) and are shown with histograms and probability density curves (ESI-2†). Fig. 7 shows two examples of the distributions of Kow, Kaw, and Koa. Low chlorinated (30, 40 wt% Cl) mixtures are characterized by (i) bell-shape overall K distributions with some sharp spikes originating from low chlorinated (Cl0–3) congeners, (ii) a narrow range (2 log units) of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow, (iii) a wide range (6 log units) of log
Kow, (iii) a wide range (6 log units) of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kaw, and (iv) a strong correlation between log
Kaw, and (iv) a strong correlation between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kaw and log
Kaw and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Koa. In contrast, highly chlorinated (60, 70 wt% Cl) mixtures are characterized by (i) symmetric, bell-shaped overall K distributions for all three log
Koa. In contrast, highly chlorinated (60, 70 wt% Cl) mixtures are characterized by (i) symmetric, bell-shaped overall K distributions for all three log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values, (ii) an increase of log
K values, (ii) an increase of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow with the number of Cl, (iii) broad but Cl-independent log
Kow with the number of Cl, (iii) broad but Cl-independent log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kaw, and (iv) no or an only weak correlation between log
Kaw, and (iv) no or an only weak correlation between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kaw and log
Kaw and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Koa. Interestingly, these qualitative trends were common for all chain lengths from C10 to C20. That is to say, while the absolute values of log
Koa. Interestingly, these qualitative trends were common for all chain lengths from C10 to C20. That is to say, while the absolute values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K depend on the chain lengths, the relative distribution patterns as shown in Fig. 7 do not depend on the chain lengths. The distribution patterns of log
K depend on the chain lengths, the relative distribution patterns as shown in Fig. 7 do not depend on the chain lengths. The distribution patterns of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) VP and log
VP and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sw are only shown in the ESI,† but the former is similar to log
Sw are only shown in the ESI,† but the former is similar to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Koa and the latter to log
Koa and the latter to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow.
Kow.
3.5 Does the property distribution of each congener group depend on the mixtures?
Identifying whether the property distribution of a congener group in one mixture is equivalent to that in another mixture is of interest. For instance, C10Cl4 congeners exist in any of C10-mixtures with 30, 40, 50 and 60 wt% Cl in an amount greater than 1 mol%, according to the Monte Carlo simulations. In the 30 wt% Cl mixture, C10Cl4 congeners represent an “advanced” fraction, having undergone the chlorination reaction to a greater extent than the majority of the other molecules in the mixture. In contrast, C10Cl4 congeners in 60 wt% Cl mixture are “left behind” in the reaction and represent a relatively low chlorinated fraction in the mixture. There could be difference in the structure profiles and thus in the property distributions. The property distributions predicted by the COSMO-trained-FCMs, however, show that such a difference is small if any (Fig. S10†). The medians of the property values vary only within 0.2 log units for any congener group from C10 to C20, suggesting that the partition properties of each congener group are virtually independent of the source CP mixtures.Representative property values for specific congener groups were calculated by summing the predictions for 30, 40, 50, 60, and 70 wt% Cl mixtures. Table 1 lists the medians of the property values at 25 °C for all congener groups considered. The ESI excel file provides other quantiles as well as values at temperatures other than 25 °C. These data represent the largest and most comprehensive set of COSMO-RS based property values for CP congener groups that consider congener profiles in the CP technical mixtures. It is notable that the property values have nonlinear relationships with the number of Cl atoms, as reported previously8 and can also be seen in Fig. 8. Note however that the congener profile could change in environmental processes such as partitioning and transformation and thus property distributions may also vary in the environment.
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow (25 °C) Kow (25 °C) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kaw (25 °C) Kaw (25 °C) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Koa (25 °C) Koa (25 °C) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) VP (Pa, 25 °C) VP (Pa, 25 °C) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sw (M, 25 °C) Sw (M, 25 °C) |
ΔHow (kJ mol−1) | ΔUaw (kJ mol−1) | ΔUoa (kJ mol−1) | ΔHvap (kJ mol−1) | ΔHdiss (kJ mol−1) | |
|---|---|---|---|---|---|---|---|---|---|---|
| C10Cl0 | 6.04 | 2.01 | 4.24 | 2.53 | −5.87 | −5.81 | 38.9 | −46.6 | 49.9 | 8.6 |
| C10Cl1 | 5.53 | 0.44 | 5.26 | 1.42 | −5.41 | −4.59 | 47.3 | −54.3 | 58.8 | 8.6 |
| C10Cl2 | 5.12 | −1.08 | 6.24 | 0.35 | −5.09 | −3.66 | 56.2 | −61.8 | 67.6 | 8.8 |
| C10Cl3 | 4.90 | −2.17 | 7.17 | −0.64 | −4.88 | −2.64 | 63.7 | −68.6 | 75.4 | 8.7 |
| C10Cl4 | 4.78 | −3.00 | 7.95 | −1.44 | −4.81 | −1.82 | 70.9 | −75.0 | 82.0 | 8.3 |
| C10Cl5 | 4.89 | −3.61 | 8.59 | −2.07 | −4.88 | −1.39 | 77.2 | −80.6 | 87.2 | 7.4 |
| C10Cl6 | 5.14 | −3.93 | 9.18 | −2.60 | −5.06 | −1.35 | 82.8 | −85.8 | 91.8 | 6.7 |
| C10Cl7 | 5.48 | −4.09 | 9.66 | −3.00 | −5.31 | −0.89 | 87.6 | −90.1 | 95.3 | 5.1 |
| C10Cl8 | 5.86 | −4.15 | 10.10 | −3.37 | −5.62 | −0.67 | 91.9 | −94.1 | 98.5 | 4.1 |
| C10Cl9 | 6.24 | −4.28 | 10.60 | −3.82 | −5.96 | −0.79 | 96.5 | −98.3 | 102.1 | 3.5 |
| C10Cl10 | 6.61 | −4.40 | 11.11 | −4.30 | −6.31 | −0.87 | 100.5 | −102.7 | 106.3 | 3.0 |
| C10Cl11 | 7.00 | −4.42 | 11.57 | −4.74 | −6.70 | −1.20 | 104.3 | −106.7 | 110.1 | 3.2 |
| C10Cl12 | 7.33 | −4.62 | 12.08 | −5.24 | −7.07 | −1.47 | 108.2 | −110.9 | 114.1 | 3.3 |
| C11Cl0 | 6.60 | 2.10 | 4.73 | 2.01 | −6.49 | −7.02 | 42.0 | −51.1 | 54.6 | 10.1 |
| C11Cl1 | 6.08 | 0.56 | 5.71 | 0.96 | −6.02 | −5.80 | 50.4 | −58.3 | 62.9 | 10.1 |
| C11Cl2 | 5.66 | −0.98 | 6.73 | −0.15 | −5.65 | −4.78 | 59.2 | −66.0 | 71.9 | 10.3 |
| C11Cl3 | 5.42 | −2.10 | 7.63 | −1.14 | −5.44 | −3.60 | 67.0 | −73.0 | 79.7 | 10.2 |
| C11Cl4 | 5.27 | −3.03 | 8.44 | −1.96 | −5.34 | −2.74 | 74.3 | −79.4 | 86.7 | 9.6 |
| C11Cl5 | 5.27 | −3.72 | 9.12 | −2.66 | −5.33 | −2.09 | 81.0 | −85.1 | 92.4 | 9.0 |
| C11Cl6 | 5.47 | −4.14 | 9.72 | −3.21 | −5.47 | −1.67 | 86.8 | −90.3 | 97.1 | 7.6 |
| C11Cl7 | 5.75 | −4.41 | 10.26 | −3.69 | −5.67 | −1.56 | 91.9 | −95.2 | 101.2 | 7.0 |
| C11Cl8 | 6.09 | −4.53 | 10.72 | −4.07 | −5.94 | −1.05 | 96.7 | −99.3 | 104.5 | 5.3 |
| C11Cl9 | 6.48 | −4.55 | 11.15 | −4.43 | −6.28 | −0.94 | 100.8 | −103.2 | 107.5 | 4.4 |
| C11Cl10 | 6.86 | −4.66 | 11.64 | −4.88 | −6.62 | −0.98 | 105.1 | −107.3 | 111.2 | 3.8 |
| C11Cl11 | 7.21 | −4.77 | 12.12 | −5.33 | −6.95 | −1.13 | 108.8 | −111.3 | 115.1 | 3.5 |
| C11Cl12 | 7.58 | −4.86 | 12.58 | −5.78 | −7.32 | −1.47 | 112.7 | −115.4 | 118.9 | 3.6 |
| C11Cl13 | 7.93 | −4.97 | 13.02 | −6.23 | −7.71 | −1.92 | 116.0 | −119.2 | 122.7 | 4.0 |
| C12Cl0 | 7.15 | 2.19 | 5.22 | 1.49 | −7.10 | −8.23 | 45.2 | −55.5 | 59.3 | 11.6 |
| C12Cl1 | 6.64 | 0.65 | 6.20 | 0.44 | −6.63 | −7.01 | 53.6 | −62.8 | 67.6 | 11.6 |
| C12Cl2 | 6.19 | −0.89 | 7.20 | −0.67 | −6.24 | −5.99 | 62.4 | −70.5 | 76.5 | 11.8 |
| C12Cl3 | 5.94 | −2.03 | 8.12 | −1.66 | −6.02 | −4.76 | 70.2 | −77.4 | 84.4 | 11.7 |
| C12Cl4 | 5.76 | −3.03 | 8.92 | −2.50 | −5.88 | −3.68 | 77.7 | −83.7 | 91.3 | 11.1 |
| C12Cl5 | 5.71 | −3.82 | 9.67 | −3.26 | −5.83 | −2.91 | 84.5 | −89.9 | 97.6 | 10.4 |
| C12Cl6 | 5.81 | −4.36 | 10.29 | −3.85 | −5.90 | −2.26 | 90.7 | −95.1 | 102.6 | 9.3 |
| C12Cl7 | 6.04 | −4.68 | 10.83 | −4.34 | −6.06 | −2.00 | 96.2 | −100.0 | 106.8 | 8.0 |
| C12Cl8 | 6.36 | −4.86 | 11.34 | −4.78 | −6.31 | −1.74 | 101.2 | −104.6 | 110.6 | 7.1 |
| C12Cl9 | 6.72 | −4.91 | 11.76 | −5.12 | −6.60 | −1.28 | 105.5 | −108.4 | 113.5 | 5.6 |
| C12Cl10 | 7.09 | −5.00 | 12.22 | −5.51 | −6.91 | −1.28 | 109.6 | −112.4 | 116.8 | 4.8 |
| C12Cl11 | 7.47 | −5.06 | 12.68 | −5.94 | −7.26 | −1.27 | 113.6 | −116.4 | 120.4 | 4.2 |
| C12Cl12 | 7.83 | −5.17 | 13.14 | −6.38 | −7.60 | −1.43 | 117.4 | −120.3 | 124.2 | 4.1 |
| C12Cl13 | 8.20 | −5.25 | 13.60 | −6.81 | −7.98 | −1.94 | 120.9 | −124.3 | 127.8 | 4.3 |
| C12Cl14 | 8.50 | −5.31 | 14.05 | −7.30 | −8.33 | −2.35 | 124.4 | −128.2 | 131.6 | 4.4 |
| C13Cl0 | 7.71 | 2.28 | 5.70 | 0.96 | −7.71 | −9.45 | 48.4 | −60.0 | 64.0 | 13.1 |
| C13Cl1 | 7.19 | 0.74 | 6.69 | −0.08 | −7.24 | −8.22 | 56.7 | −67.3 | 72.3 | 13.1 |
| C13Cl2 | 6.68 | −0.80 | 7.69 | −1.20 | −6.81 | −7.00 | 65.5 | −74.8 | 81.2 | 13.2 |
| C13Cl3 | 6.45 | −1.96 | 8.59 | −2.14 | −6.60 | −5.91 | 73.4 | −81.8 | 88.9 | 13.2 |
| C13Cl4 | 6.24 | −3.04 | 9.43 | −3.05 | −6.42 | −4.80 | 81.0 | −88.4 | 96.3 | 12.6 |
| C13Cl5 | 6.15 | −3.89 | 10.18 | −3.82 | −6.34 | −3.87 | 88.1 | −94.4 | 102.6 | 11.9 |
| C13Cl6 | 6.19 | −4.51 | 10.84 | −4.46 | −6.36 | −3.05 | 94.5 | −99.9 | 108.0 | 10.9 |
| C13Cl7 | 6.36 | −4.92 | 11.42 | −5.00 | −6.48 | −2.51 | 100.4 | −104.9 | 112.5 | 9.5 |
| C13Cl8 | 6.64 | −5.17 | 11.93 | −5.45 | −6.69 | −2.24 | 105.6 | −109.5 | 116.4 | 8.6 |
| C13Cl9 | 6.97 | −5.30 | 12.39 | −5.84 | −6.94 | −1.82 | 110.1 | −113.8 | 119.7 | 7.1 |
| C13Cl10 | 7.33 | −5.33 | 12.80 | −6.17 | −7.23 | −1.42 | 114.3 | −117.4 | 122.6 | 5.8 |
| C13Cl11 | 7.71 | −5.36 | 13.23 | −6.52 | −7.56 | −1.47 | 118.2 | −121.2 | 125.6 | 5.1 |
| C13Cl12 | 8.08 | −5.47 | 13.69 | −6.97 | −7.90 | −1.54 | 122.1 | −125.2 | 129.3 | 4.6 |
| C13Cl13 | 8.43 | −5.56 | 14.16 | −7.41 | −8.24 | −1.75 | 125.7 | −129.1 | 132.9 | 4.4 |
| C13Cl14 | 8.78 | −5.65 | 14.63 | −7.86 | −8.59 | −2.29 | 129.2 | −133.0 | 136.7 | 4.7 |
| C13Cl15 | 9.10 | −5.78 | 15.11 | −8.35 | −8.96 | −2.65 | 132.6 | −136.6 | 140.8 | 5.0 |
| C14Cl0 | 8.26 | 2.37 | 6.19 | 0.44 | −8.32 | −10.66 | 51.5 | −64.5 | 68.6 | 14.6 |
| C14Cl1 | 7.75 | 0.83 | 7.18 | −0.60 | −7.85 | −9.43 | 59.9 | −71.8 | 77.0 | 14.6 |
| C14Cl2 | 7.24 | −0.71 | 8.18 | −1.72 | −7.41 | −8.21 | 68.6 | −79.3 | 85.9 | 14.7 |
| C14Cl3 | 6.97 | −1.88 | 9.11 | −2.71 | −7.20 | −7.13 | 76.6 | −86.4 | 93.7 | 14.7 |
| C14Cl4 | 6.72 | −3.03 | 9.95 | −3.62 | −6.98 | −5.87 | 84.3 | −93.0 | 101.1 | 14.1 |
| C14Cl5 | 6.61 | −3.91 | 10.69 | −4.38 | −6.87 | −4.85 | 91.5 | −98.9 | 107.4 | 13.4 |
| C14Cl6 | 6.60 | −4.63 | 11.38 | −5.07 | −6.85 | −3.95 | 98.2 | −104.6 | 113.3 | 12.5 |
| C14Cl7 | 6.71 | −5.15 | 11.99 | −5.66 | −6.92 | −3.35 | 104.3 | −109.8 | 118.2 | 11.3 |
| C14Cl8 | 6.94 | −5.43 | 12.52 | −6.11 | −7.08 | −2.88 | 109.8 | −114.6 | 122.2 | 9.8 |
| C14Cl9 | 7.24 | −5.64 | 13.02 | −6.55 | −7.30 | −2.48 | 114.7 | −119.1 | 125.9 | 8.8 |
| C14Cl10 | 7.58 | −5.71 | 13.44 | −6.88 | −7.56 | −1.95 | 119.0 | −122.9 | 128.8 | 7.2 |
| C14Cl11 | 7.94 | −5.74 | 13.84 | −7.22 | −7.87 | −1.73 | 123.1 | −126.6 | 131.6 | 6.1 |
| C14Cl12 | 8.33 | −5.75 | 14.26 | −7.57 | −8.21 | −1.75 | 126.9 | −130.2 | 134.7 | 5.4 |
| C14Cl13 | 8.69 | −5.85 | 14.72 | −8.01 | −8.54 | −1.80 | 130.7 | −134.0 | 138.2 | 5.0 |
| C14Cl14 | 9.04 | −5.97 | 15.19 | −8.46 | −8.90 | −2.04 | 134.3 | −138.0 | 142.0 | 4.9 |
| C14Cl15 | 9.42 | −6.00 | 15.63 | −8.90 | −9.28 | −2.56 | 137.8 | −141.9 | 145.7 | 5.0 |
| C14Cl16 | 9.77 | −6.09 | 16.02 | −9.29 | −9.61 | −3.13 | 140.8 | −145.2 | 149.0 | 5.7 |
| C15Cl0 | 8.82 | 2.45 | 6.68 | −0.08 | −8.93 | −11.87 | 54.7 | −69.0 | 73.3 | 16.1 |
| C15Cl1 | 8.30 | 0.95 | 7.64 | −1.13 | −8.46 | −10.64 | 62.9 | −76.1 | 81.6 | 16.2 |
| C15Cl2 | 7.79 | −0.62 | 8.66 | −2.24 | −8.03 | −9.42 | 71.6 | −83.8 | 90.5 | 16.2 |
| C15Cl3 | 7.51 | −1.82 | 9.60 | −3.24 | −7.78 | −8.24 | 79.8 | −90.9 | 98.6 | 16.3 |
| C15Cl4 | 7.24 | −2.99 | 10.44 | −4.14 | −7.54 | −6.99 | 87.5 | −97.3 | 105.8 | 15.6 |
| C15Cl5 | 7.09 | −3.95 | 11.22 | −4.95 | −7.41 | −5.91 | 94.8 | −103.6 | 112.6 | 14.9 |
| C15Cl6 | 7.04 | −4.72 | 11.92 | −5.66 | −7.35 | −4.97 | 101.7 | −109.3 | 118.4 | 14.0 |
| C15Cl7 | 7.11 | −5.28 | 12.54 | −6.27 | −7.39 | −4.17 | 108.1 | −114.6 | 123.5 | 12.9 |
| C15Cl8 | 7.25 | −5.70 | 13.11 | −6.79 | −7.50 | −3.45 | 113.9 | −119.6 | 128.0 | 11.4 |
| C15Cl9 | 7.52 | −5.95 | 13.64 | −7.24 | −7.68 | −3.07 | 119.2 | −124.2 | 131.9 | 10.2 |
| C15Cl10 | 7.84 | −6.09 | 14.07 | −7.61 | −7.93 | −2.63 | 123.7 | −128.3 | 135.0 | 8.9 |
| C15Cl11 | 8.20 | −6.10 | 14.44 | −7.90 | −8.20 | −2.05 | 127.9 | −131.7 | 137.6 | 7.3 |
| C15Cl12 | 8.56 | −6.12 | 14.85 | −8.25 | −8.50 | −1.93 | 131.8 | −135.4 | 140.5 | 6.3 |
| C15Cl13 | 8.94 | −6.19 | 15.30 | −8.65 | −8.86 | −1.96 | 135.6 | −139.2 | 143.9 | 5.8 |
| C15Cl14 | 9.30 | −6.28 | 15.76 | −9.08 | −9.19 | −2.21 | 139.3 | −143.1 | 147.4 | 5.5 |
| C15Cl15 | 9.65 | −6.35 | 16.19 | −9.48 | −9.53 | −2.39 | 142.7 | −146.9 | 150.9 | 5.4 |
| C15Cl16 | 10.01 | −6.42 | 16.64 | −9.92 | −9.90 | −2.86 | 146.1 | −150.5 | 154.5 | 5.6 |
| C15Cl17 | 10.31 | −6.51 | 17.09 | −10.35 | −10.22 | −3.44 | 149.3 | −153.8 | 157.6 | 6.4 |
| C16Cl0 | 9.37 | 2.54 | 7.17 | −0.61 | −9.54 | −13.08 | 57.9 | −73.5 | 78.0 | 17.6 |
| C16Cl1 | 8.86 | 1.03 | 8.13 | −1.65 | −9.07 | −11.85 | 66.1 | −80.6 | 86.3 | 17.7 |
| C16Cl2 | 8.35 | −0.50 | 9.15 | −2.76 | −8.64 | −10.63 | 74.6 | −88.3 | 95.2 | 17.7 |
| C16Cl3 | 8.06 | −1.74 | 10.09 | −3.76 | −8.38 | −9.40 | 83.0 | −95.4 | 103.3 | 17.7 |
| C16Cl4 | 7.77 | −2.95 | 10.94 | −4.67 | −8.12 | −8.18 | 90.7 | −101.9 | 110.6 | 17.2 |
| C16Cl5 | 7.58 | −3.94 | 11.72 | −5.50 | −7.96 | −6.97 | 98.2 | −108.1 | 117.4 | 16.4 |
| C16Cl6 | 7.49 | −4.78 | 12.46 | −6.25 | −7.86 | −5.95 | 105.2 | −114.1 | 123.6 | 15.6 |
| C16Cl7 | 7.51 | −5.42 | 13.10 | −6.88 | −7.87 | −5.00 | 111.7 | −119.4 | 128.8 | 14.5 |
| C16Cl8 | 7.64 | −5.88 | 13.67 | −7.42 | −7.95 | −4.16 | 117.8 | −124.4 | 133.4 | 13.1 |
| C16Cl9 | 7.83 | −6.21 | 14.20 | −7.90 | −8.08 | −3.70 | 123.2 | −129.1 | 137.6 | 11.6 |
| C16Cl10 | 8.12 | −6.45 | 14.73 | −8.36 | −8.31 | −3.30 | 128.4 | −133.8 | 141.4 | 10.7 |
| C16Cl11 | 8.46 | −6.49 | 15.10 | −8.65 | −8.55 | −2.72 | 132.7 | −137.4 | 144.1 | 9.0 |
| C16Cl12 | 8.80 | −6.51 | 15.50 | −8.96 | −8.84 | −2.33 | 136.7 | −140.9 | 146.8 | 7.7 |
| C16Cl13 | 9.20 | −6.49 | 15.88 | −9.28 | −9.17 | −2.19 | 140.4 | −144.4 | 149.5 | 6.7 |
| C16Cl14 | 9.56 | −6.57 | 16.32 | −9.68 | −9.50 | −2.23 | 144.2 | −148.1 | 152.8 | 6.1 |
| C16Cl15 | 9.92 | −6.67 | 16.77 | −10.11 | −9.84 | −2.46 | 147.9 | −151.8 | 156.3 | 5.8 |
| C16Cl16 | 10.28 | −6.75 | 17.23 | −10.54 | −10.18 | −2.80 | 151.2 | −155.7 | 159.9 | 5.8 |
| C16Cl17 | 10.62 | −6.85 | 17.68 | −10.96 | −10.55 | −3.04 | 154.7 | −159.3 | 163.4 | 5.8 |
| C17Cl0 | 9.93 | 2.63 | 7.66 | −1.13 | −10.15 | −14.29 | 61.0 | −78.0 | 82.7 | 19.2 |
| C17Cl1 | 9.41 | 1.12 | 8.62 | −2.17 | −9.69 | −13.07 | 69.3 | −85.1 | 91.0 | 19.2 |
| C17Cl2 | 8.90 | −0.42 | 9.61 | −3.24 | −9.25 | −11.84 | 77.8 | −92.8 | 99.8 | 19.2 |
| C17Cl3 | 8.60 | −1.67 | 10.57 | −4.28 | −8.97 | −10.62 | 86.1 | −99.8 | 107.9 | 19.2 |
| C17Cl4 | 8.27 | −2.92 | 11.44 | −5.20 | −8.70 | −9.32 | 93.9 | −106.4 | 115.4 | 18.7 |
| C17Cl5 | 8.08 | −3.95 | 12.24 | −6.05 | −8.52 | −8.09 | 101.6 | −112.8 | 122.3 | 18.0 |
| C17Cl6 | 7.96 | −4.81 | 12.99 | −6.82 | −8.40 | −6.97 | 108.7 | −118.7 | 128.6 | 17.1 |
| C17Cl7 | 7.95 | −5.53 | 13.66 | −7.51 | −8.37 | −6.04 | 115.3 | −124.3 | 134.2 | 16.1 |
| C17Cl8 | 8.02 | −6.09 | 14.28 | −8.09 | −8.42 | −5.23 | 121.7 | −129.6 | 139.2 | 14.9 |
| C17Cl9 | 8.18 | −6.47 | 14.82 | −8.59 | −8.52 | −4.42 | 127.5 | −134.2 | 143.5 | 13.4 |
| C17Cl10 | 8.41 | −6.71 | 15.32 | −9.02 | −8.69 | −3.87 | 132.7 | −138.7 | 147.2 | 12.0 |
| C17Cl11 | 8.73 | −6.88 | 15.78 | −9.41 | −8.92 | −3.38 | 137.5 | −143.0 | 150.6 | 10.7 |
| C17Cl12 | 9.05 | −6.93 | 16.17 | −9.71 | −9.17 | −2.92 | 141.5 | −146.5 | 153.1 | 9.3 |
| C17Cl13 | 9.40 | −6.94 | 16.52 | −10.00 | −9.46 | −2.50 | 145.4 | −149.8 | 155.7 | 7.9 |
| C17Cl14 | 9.79 | −6.94 | 16.93 | −10.34 | −9.80 | −2.45 | 149.1 | −153.4 | 158.6 | 7.1 |
| C17Cl15 | 10.17 | −7.00 | 17.35 | −10.73 | −10.14 | −2.52 | 152.8 | −157.1 | 161.8 | 6.5 |
| C17Cl16 | 10.53 | −7.07 | 17.79 | −11.15 | −10.48 | −2.68 | 156.5 | −160.8 | 165.3 | 6.2 |
| C17Cl17 | 10.87 | −7.17 | 18.25 | −11.58 | −10.82 | −3.06 | 160.1 | −164.6 | 168.9 | 6.3 |
| C17Cl18 | 11.19 | −7.21 | 18.70 | −12.02 | −11.18 | −3.47 | 163.0 | −168.2 | 172.4 | 6.7 |
| C18Cl0 | 10.48 | 2.72 | 8.15 | −1.65 | −10.77 | −15.50 | 64.2 | −82.5 | 87.3 | 20.7 |
| C18Cl1 | 9.97 | 1.21 | 9.11 | −2.69 | −10.30 | −14.28 | 72.4 | −89.6 | 95.7 | 20.7 |
| C18Cl2 | 9.45 | −0.33 | 10.09 | −3.74 | −9.84 | −13.05 | 80.8 | −97.0 | 104.0 | 20.7 |
| C18Cl3 | 9.12 | −1.63 | 11.06 | −4.80 | −9.58 | −11.83 | 89.3 | −104.2 | 112.6 | 20.7 |
| C18Cl4 | 8.80 | −2.85 | 11.93 | −5.72 | −9.29 | −10.50 | 97.1 | −110.9 | 120.1 | 20.2 |
| C18Cl5 | 8.58 | −3.92 | 12.74 | −6.60 | −9.08 | −9.25 | 104.8 | −117.3 | 127.0 | 19.6 |
| C18Cl6 | 8.44 | −4.84 | 13.49 | −7.37 | −8.95 | −8.10 | 112.0 | −123.3 | 133.5 | 18.7 |
| C18Cl7 | 8.38 | −5.60 | 14.20 | −8.08 | −8.88 | −7.03 | 119.0 | −129.0 | 139.3 | 17.7 |
| C18Cl8 | 8.42 | −6.23 | 14.83 | −8.70 | −8.90 | −6.07 | 125.4 | −134.3 | 144.5 | 16.6 |
| C18Cl9 | 8.52 | −6.66 | 15.38 | −9.22 | −8.95 | −5.15 | 131.4 | −139.1 | 148.9 | 15.0 |
| C18Cl10 | 8.72 | −6.99 | 15.91 | −9.69 | −9.09 | −4.49 | 136.8 | −143.7 | 152.9 | 13.5 |
| C18Cl11 | 8.99 | −7.20 | 16.38 | −10.10 | −9.29 | −3.98 | 141.8 | −148.1 | 156.5 | 12.3 |
| C18Cl12 | 9.34 | −7.31 | 16.84 | −10.46 | −9.56 | −3.51 | 146.6 | −152.1 | 159.6 | 10.8 |
| C18Cl13 | 9.67 | −7.30 | 17.17 | −10.72 | −9.81 | −2.92 | 150.5 | −155.4 | 162.1 | 9.2 |
| C18Cl14 | 10.03 | −7.32 | 17.55 | −11.03 | −10.11 | −2.77 | 154.2 | −158.9 | 164.7 | 8.2 |
| C18Cl15 | 10.41 | −7.33 | 17.96 | −11.39 | −10.45 | −2.74 | 157.8 | −162.3 | 167.7 | 7.4 |
| C18Cl16 | 10.79 | −7.40 | 18.40 | −11.80 | −10.79 | −2.81 | 161.5 | −166.1 | 171.0 | 6.8 |
| C18Cl17 | 11.13 | −7.46 | 18.82 | −12.19 | −11.12 | −3.04 | 164.7 | −169.6 | 174.2 | 6.7 |
| C18Cl18 | 11.48 | −7.53 | 19.26 | −12.61 | −11.47 | −3.34 | 168.2 | −173.4 | 177.7 | 6.7 |
| C18Cl19 | 11.85 | −7.64 | 19.74 | −13.06 | −11.84 | −3.93 | 171.7 | −177.2 | 181.5 | 7.1 |
| C19Cl0 | 11.04 | 2.80 | 8.64 | −2.17 | −11.38 | −16.71 | 67.4 | −87.0 | 92.0 | 22.2 |
| C19Cl1 | 10.52 | 1.30 | 9.60 | −3.22 | −10.91 | −15.49 | 75.6 | −94.1 | 100.4 | 22.2 |
| C19Cl2 | 10.01 | −0.24 | 10.58 | −4.26 | −10.44 | −14.26 | 84.0 | −101.3 | 108.7 | 22.2 |
| C19Cl3 | 9.67 | −1.55 | 11.54 | −5.32 | −10.18 | −13.04 | 92.4 | −108.7 | 117.1 | 22.3 |
| C19Cl4 | 9.34 | −2.81 | 12.42 | −6.27 | −9.86 | −11.71 | 100.3 | −115.4 | 124.9 | 21.8 |
| C19Cl5 | 9.09 | −3.89 | 13.23 | −7.12 | −9.65 | −10.40 | 108.0 | −121.7 | 131.7 | 21.0 |
| C19Cl6 | 8.92 | −4.86 | 14.02 | −7.94 | −9.49 | −9.23 | 115.4 | −127.9 | 138.5 | 20.4 |
| C19Cl7 | 8.85 | −5.64 | 14.72 | −8.66 | −9.42 | −8.08 | 122.4 | −133.6 | 144.4 | 19.2 |
| C19Cl8 | 8.84 | −6.33 | 15.38 | −9.31 | −9.39 | −7.04 | 129.1 | −139.1 | 149.9 | 18.1 |
| C19Cl9 | 8.91 | −6.84 | 15.98 | −9.89 | −9.43 | −6.22 | 135.2 | −144.2 | 154.7 | 16.9 |
| C19Cl10 | 9.07 | −7.25 | 16.52 | −10.38 | −9.53 | −5.29 | 141.0 | −148.9 | 158.9 | 15.3 |
| C19Cl11 | 9.31 | −7.50 | 17.01 | −10.80 | −9.70 | −4.68 | 146.2 | −153.4 | 162.6 | 13.7 |
| C19Cl12 | 9.62 | −7.62 | 17.45 | −11.17 | −9.93 | −4.14 | 151.0 | −157.4 | 165.7 | 12.4 |
| C19Cl13 | 9.95 | −7.68 | 17.85 | −11.49 | −10.18 | −3.66 | 155.1 | −161.1 | 168.5 | 10.9 |
| C19Cl14 | 10.30 | −7.70 | 18.20 | −11.75 | −10.45 | −3.07 | 159.2 | −164.4 | 170.9 | 9.2 |
| C19Cl15 | 10.67 | −7.69 | 18.58 | −12.08 | −10.78 | −2.91 | 162.7 | −167.7 | 173.7 | 8.4 |
| C19Cl16 | 11.02 | −7.76 | 19.00 | −12.45 | −11.08 | −2.96 | 166.5 | −171.5 | 176.8 | 7.7 |
| C19Cl17 | 11.40 | −7.77 | 19.43 | −12.83 | −11.43 | −3.07 | 170.1 | −175.0 | 179.9 | 7.2 |
| C19Cl18 | 11.75 | −7.88 | 19.87 | −13.26 | −11.77 | −3.32 | 173.6 | −178.7 | 183.4 | 7.1 |
| C19Cl19 | 12.10 | −7.91 | 20.26 | −13.64 | −12.12 | −3.70 | 176.5 | −182.0 | 186.5 | 7.3 |
| C19Cl20 | 12.43 | −8.05 | 20.71 | −14.05 | −12.42 | −4.32 | 179.2 | −185.4 | 189.9 | 7.9 |
| C20Cl0 | 11.59 | 2.89 | 9.13 | −2.70 | −11.99 | −17.92 | 70.5 | −91.5 | 96.7 | 23.7 |
| C20Cl1 | 11.08 | 1.38 | 10.09 | −3.74 | −11.52 | −16.70 | 78.8 | −98.6 | 105.0 | 23.7 |
| C20Cl2 | 10.56 | −0.15 | 11.07 | −4.78 | −11.05 | −15.48 | 87.1 | −105.8 | 113.4 | 23.7 |
| C20Cl3 | 10.18 | −1.50 | 12.03 | −5.85 | −10.74 | −14.25 | 95.5 | −113.2 | 122.0 | 23.8 |
| C20Cl4 | 9.88 | −2.73 | 12.90 | −6.77 | −10.45 | −12.90 | 103.6 | −119.8 | 129.5 | 23.2 |
| C20Cl5 | 9.61 | −3.84 | 13.73 | −7.66 | −10.23 | −11.58 | 111.3 | −126.3 | 136.6 | 22.6 |
| C20Cl6 | 9.41 | −4.85 | 14.53 | −8.49 | −10.05 | −10.36 | 118.8 | −132.4 | 143.3 | 21.9 |
| C20Cl7 | 9.30 | −5.69 | 15.24 | −9.22 | −9.94 | −9.17 | 125.8 | −138.2 | 149.4 | 20.8 |
| C20Cl8 | 9.29 | −6.39 | 15.91 | −9.89 | −9.91 | −8.04 | 132.6 | −143.8 | 154.9 | 19.6 |
| C20Cl9 | 9.33 | −7.00 | 16.54 | −10.51 | −9.92 | −7.11 | 138.9 | −149.0 | 160.1 | 18.5 |
| C20Cl10 | 9.44 | −7.44 | 17.11 | −11.04 | −9.99 | −6.24 | 145.0 | −153.9 | 164.6 | 17.1 |
| C20Cl11 | 9.64 | −7.76 | 17.62 | −11.48 | −10.13 | −5.36 | 150.4 | −158.5 | 168.5 | 15.3 |
| C20Cl12 | 9.90 | −7.97 | 18.08 | −11.88 | −10.32 | −4.89 | 155.4 | −162.6 | 171.9 | 14.1 |
| C20Cl13 | 10.21 | −8.10 | 18.53 | −12.26 | −10.54 | −4.30 | 160.2 | −167.0 | 175.2 | 12.6 |
| C20Cl14 | 10.55 | −8.13 | 18.90 | −12.55 | −10.79 | −3.80 | 164.2 | −170.2 | 177.6 | 11.2 |
| C20Cl15 | 10.89 | −8.08 | 19.22 | −12.80 | −11.09 | −3.37 | 167.9 | −173.3 | 179.9 | 9.7 |
| C20Cl16 | 11.29 | −8.08 | 19.60 | −13.11 | −11.42 | −3.20 | 171.4 | −176.7 | 182.6 | 8.8 |
| C20Cl17 | 11.65 | −8.14 | 20.03 | −13.49 | −11.74 | −3.20 | 175.1 | −180.3 | 185.7 | 8.1 |
| C20Cl18 | 12.02 | −8.18 | 20.43 | −13.86 | −12.09 | −3.35 | 178.6 | −183.8 | 188.9 | 7.7 |
| C20Cl19 | 12.37 | −8.23 | 20.87 | −14.27 | −12.42 | −3.64 | 182.0 | −187.4 | 192.2 | 7.7 |
| C20Cl20 | 12.74 | −8.29 | 21.30 | −14.70 | −12.79 | −4.05 | 185.4 | −191.1 | 195.6 | 7.8 |
| C20Cl21 | 13.04 | −8.45 | 21.74 | −15.13 | −13.09 | −4.72 | 188.0 | −194.5 | 199.0 | 8.2 |
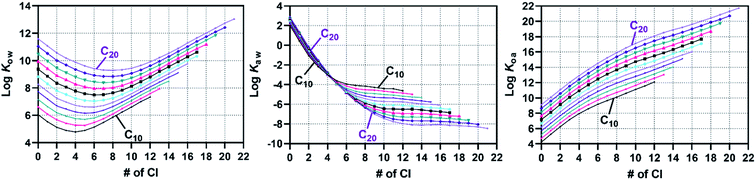 | ||
Fig. 8 Medians of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow, log Kow, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kaw, and log Kaw, and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Koa at 25 °C for each congener group predicted by COSMO-RS-trained FCMs and the Monte Carlo model. Data plots for the other properties are shown in Fig. S11.† Koa at 25 °C for each congener group predicted by COSMO-RS-trained FCMs and the Monte Carlo model. Data plots for the other properties are shown in Fig. S11.† | ||
3.6 Comparing experimental and predicted Kow distributions for technical mixtures
The predicted distributions of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow for a CP mixture with a given C length and Cl wt% were compared to the experimental data from Hilger et al.,19 who measured the range of log
Kow for a CP mixture with a given C length and Cl wt% were compared to the experimental data from Hilger et al.,19 who measured the range of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow for a CP mixture using an HPLC retention method (Fig. 9). Their data set includes the mixtures that contain congeners of a single chain length (C10, C11, C12, or C13) with varying degrees of chlorination (45–75 wt% Cl). The predicted medians of log
Kow for a CP mixture using an HPLC retention method (Fig. 9). Their data set includes the mixtures that contain congeners of a single chain length (C10, C11, C12, or C13) with varying degrees of chlorination (45–75 wt% Cl). The predicted medians of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow agree well with the experimental values that correspond to the HPLC peak top times within 1.1 log unit in the worst case. The agreement is particularly high for relatively short and low chlorinated mixtures. Less accurate predictions for highly chlorinated mixtures could be related to the relatively low accuracy of the Monte Carlo method for highly chlorinated congeners. The authors of the paper13 admitted that the model parameters for the reactivity of highly chlorinated molecules were not well based on any experimental data.
Kow agree well with the experimental values that correspond to the HPLC peak top times within 1.1 log unit in the worst case. The agreement is particularly high for relatively short and low chlorinated mixtures. Less accurate predictions for highly chlorinated mixtures could be related to the relatively low accuracy of the Monte Carlo method for highly chlorinated congeners. The authors of the paper13 admitted that the model parameters for the reactivity of highly chlorinated molecules were not well based on any experimental data.
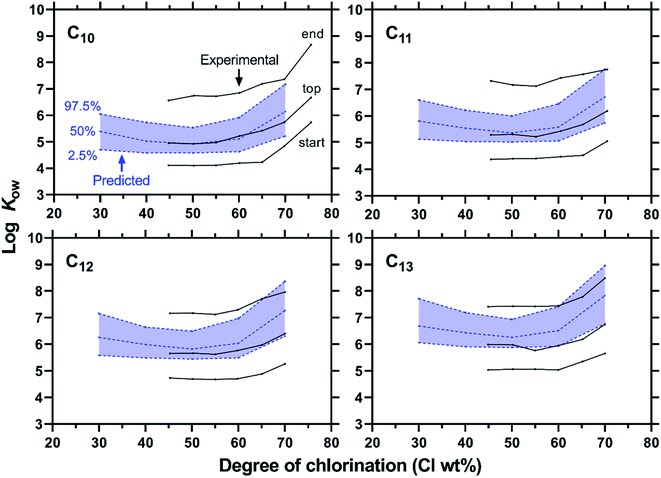 | ||
Fig. 9 Experimental and predicted ranges of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow for CP mixtures. Experimental Kow data as described by Hilger et al.19 using an HPLC retention method corresponding to the peak start, top and end are compared to the 2.5, 50, and 97.5 percentiles of log Kow for CP mixtures. Experimental Kow data as described by Hilger et al.19 using an HPLC retention method corresponding to the peak start, top and end are compared to the 2.5, 50, and 97.5 percentiles of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow predicted by COSMO-RS-trained FCMs. Kow predicted by COSMO-RS-trained FCMs. | ||
Fig. 9 also shows that the predicted range of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow (as 2.5–97.5 percentiles) is generally narrower than the measured range. This result could be taken as an indication that real CP mixtures contain more diverse congeners than predicted by the Monte Carlo model. It should however be noted that both predicted and measured ranges are somewhat arbitrarily defined. The predicted range was set between 2.5 and 97.5 percentiles here, but a wider range (e.g., 1–99 percentiles) could also be considered. In the HPLC measurements, the start and end times had to be assigned to a broad HPLC peak. Moreover, peak broadening can, in general, occur due to diffusion and dispersion in addition to the variation of properties of mixture components.
Kow (as 2.5–97.5 percentiles) is generally narrower than the measured range. This result could be taken as an indication that real CP mixtures contain more diverse congeners than predicted by the Monte Carlo model. It should however be noted that both predicted and measured ranges are somewhat arbitrarily defined. The predicted range was set between 2.5 and 97.5 percentiles here, but a wider range (e.g., 1–99 percentiles) could also be considered. In the HPLC measurements, the start and end times had to be assigned to a broad HPLC peak. Moreover, peak broadening can, in general, occur due to diffusion and dispersion in addition to the variation of properties of mixture components.
4 Conclusions
This study extended the COSMO-RS-trained FCM approach to CP congeners with a carbon chain length up to C20. The quantum chemically based predictions for Kow, Kaw, Koa, VP, and Sw and their temperature dependence for each congener group were offered, in consideration of varying congener compositions in technical mixtures. These predictions may be used for various environmental fate models or correlated with field-measured environmental partition coefficients such as organic carbon/water partition coefficients and gas/particle partition coefficients to understand the environmental behavior of CPs. Further validation of the model predictions with congener (group)-specific experimental data would be desirable, particularly for data-poor MCCPs and LCCPs.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Environment Research and Technology Development Fund SII-3-1 (JPMEERF18S20300) of the Environmental Restoration and Conservation Agency, Japan. COSMOconfX and TURBOMOLE calculations were run with the NIES supercomputer system.References
- UNEP, Decision SC-8/11, Listing of short-chain chlorinated paraffins, 2017, UNEP/POPS/COP.8/SC-8/11 Search PubMed.
- B. Yuan, K. Vorkamp, A. M. Roos, S. Faxneld, C. Sonne, S. E. Garbus, Y. Lind, I. Eulaers, P. Hellström, R. Dietz, S. Persson, R. Bossi and C. A. de Wit, Accumulation of Short-, Medium-, and Long-Chain Chlorinated Paraffins in Marine and Terrestrial Animals from Scandinavia, Environ. Sci. Technol., 2019, 53, 3526–3537 CrossRef CAS.
- C. Bogdal, N. Niggeler, J. Glüge, P. S. Diefenbacher, D. Wächter and K. Hungerbühler, Temporal trends of chlorinated paraffins and polychlorinated biphenyls in Swiss soils, Environ. Pollut., 2017, 220, 891–899 CrossRef CAS PubMed.
- S. H. Brandsma, L. van Mourik, J. W. O'Brien, G. Eaglesham, P. E. Leonards, J. de Boer, C. Gallen, J. Mueller, C. Gaus and C. Bogdal, Medium-Chain Chlorinated Paraffins (CPs) Dominate in Australian Sewage Sludge, Environ. Sci. Technol., 2017, 51, 3364–3372 CrossRef CAS.
- X. Du, B. Yuan, Y. Zhou, J. P. Benskin, Y. Qiu, G. Yin and J. Zhao, Short-, Medium-, and Long-Chain Chlorinated Paraffins in Wildlife from Paddy Fields in the Yangtze River Delta, Environ. Sci. Technol., 2018, 52, 1072–1080 CrossRef CAS PubMed.
- M. Aamir, S. Yin, F. Guo, K. Liu, C. Xu and W. Liu, Congener-Specific Mother-Fetus Distribution, Placental Retention, and Transport of C10-13 and C14-17 Chlorinated Paraffins in Pregnant Women, Environ. Sci. Technol., 2019, 53, 11458–11466 CrossRef CAS.
- Y. Wang, W. Gao, Y. W. Wang and G. B. Jiang, Distribution and Pattern Profiles of Chlorinated Paraffins in Human Placenta of Henan Province, China, Environ. Sci. Technol. Lett., 2018, 5, 9–13 CrossRef CAS.
- S. Endo and J. Hammer, Predicting Partition Coefficients of Short-Chain Chlorinated Paraffin Congeners by COSMO-RS-Trained Fragment Contribution Models, Environ. Sci. Technol., 2020, 54, 15162–15169 CrossRef CAS.
- W. M. Meylan and P. H. Howard, Atom/fragment contribution method for estimating octanol-water partition coefficients, J. Pharm. Sci., 1995, 84, 83–92 CrossRef CAS PubMed.
- T. N. Brown, J. A. Arnot and F. Wania, Iterative fragment selection: a group contribution approach to predicting fish biotransformation half-lives, Environ. Sci. Technol., 2012, 46, 8253–8260 CrossRef CAS PubMed.
- A. Klamt, Conductor-like screening model for real solvents: A new approach to the quantitative calculation of solvation phenomena, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- J. Glüge, C. Bogdal, M. Scheringer, A. M. Buser and K. Hungerbühler, Calculation of Physicochemical Properties for Short- and Medium-Chain Chlorinated Paraffins, J. Phys. Chem. Ref. Data, 2013, 42, 023103 CrossRef.
- S. R. Jensen, W. A. Brown, E. Heath and D. G. Cooper, Characterization of polychlorinated alkane mixtures-a Monte Carlo modeling approach, Biodegradation, 2007, 18, 703–717 CrossRef CAS PubMed.
- Y. Cao, A. Charisi, L. C. Cheng, T. Jiang and T. Girke, ChemmineR: a compound mining framework for R, Bioinformatics, 2008, 24, 1733–1734 CrossRef CAS PubMed.
- B.-H. Mevik, R. Wehrens and K. H. Liland, pls: Partial Least Squares and Principal Component Regression, R package version 2.7-2., 2019 Search PubMed.
- J. Sprengel, N. Wiedmaier-Czerny and W. Vetter, Characterization of single chain length chlorinated paraffin mixtures with nuclear magnetic resonance spectroscopy (NMR), Chemosphere, 2019, 228, 762–768 CrossRef CAS PubMed.
- B. Yuan, D. H. Lysak, R. Soong, A. Haddad, A. Hisatsune, A. Moser, S. Golotvin, D. Argyropoulos, A. J. Simpson and D. C. G. Muir, Chlorines Are Not Evenly Substituted in Chlorinated Paraffins: A Predicted NMR Pattern Matching Framework for Isomeric Discrimination in Complex Contaminant Mixtures, Environ. Sci. Technol. Lett., 2020, 7, 496–503 CrossRef CAS PubMed.
- B. Yuan, C. Bogdal, U. Berger, M. MacLeod, W. A. Gebbink, T. Alsberg and C. A. de Wit, Quantifying Short-Chain Chlorinated Paraffin Congener Groups, Environ. Sci. Technol., 2017, 51, 10633–10641 CrossRef CAS PubMed.
- B. Hilger, H. Fromme, W. Volkel and M. Coelhan, Effects of chain length, chlorination degree, and structure on the octanol-water partition coefficients of polychlorinated n-alkanes, Environ. Sci. Technol., 2011, 45, 2842–2849 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1em00123j |
| This journal is © The Royal Society of Chemistry 2021 |