Effect of disinfectant residual, pH, and temperature on microbial abundance in disinfected drinking water distribution systems

Abstract

In piped drinking water distribution systems, microbial water quality depends on the quantities and types of microorganisms present as well as the physicochemical conditions that influence them. Accurately assessing microbial water quality in these systems is important to maintain water quality throughout distribution. Microbial water quality can be assessed directly, using measures of microbial abundance, and indirectly, by measuring pH, temperature, and disinfectant residual. In the United States, total coliform bacteria measurement is the only regulated parameter for microbial abundance, but because levels are required to be maintained below the quantification limit, this parameter provides little insight into the total microbial abundance. In this study, alternate measures of microbial abundance were assessed in six drinking water distribution systems with a wide range of free chlorine (<0.02 to 2.14 mg L⁻¹ as Cl₂) and total chlorine residuals (<0.02 to 2.9 mg L⁻¹ as Cl₂). Five measures of microbial abundance were compared for quantifiability and variability throughout distribution: total and intact cell counts, total and intracellular ATP concentrations, and heterotrophic plate counts. We found that: intracellular ATP and intact cell counts had significant and strong correlations with disinfectant concentration; these correlations were stronger in chlorinated systems compared to chloraminated systems; 97.6% of samples had a quantifiable intact cell counts, with only four samples below the intact cell count quantifiaction limit at the highest residual concentration in chlorinated drinking water distribution systems (1.5–2.0 mg L⁻¹ as Cl₂); and variance between technical replicates was lowest for total ATP followed by total and intact cell counts, as compared to heterotrophic plate counts and intracellular ATP. We also demonstrated that a generalized linear mixed model could be used to estimate the combined effect of common water quality parameters on intact cell counts in a chloraminated distribution system: total chlorine had the greatest inverse effect on intact cells with a greater positive effect of temperature at lower levels of total chlorine. We discuss the purpose and interpretation of typical microbial water quality parameters, such as heterotrophic plate count and disinfectant residual, and consider the future role of ATP and flow cytometry-based methods.

---

Water impact

Maintaining sustainable drinking water distribution systems will require enhanced monitoring methods that can quickly reveal when water quality is compromised. Methods for quantifying microbial abundance,like flow cytometry-based cell counts and ATP assays, have tremendous potential to transform the way drinking water quality is monitored in drinking water distribution systems. Yet, research applying these novel tools to disinfected systems is scarce. This work demonstrates the unique insights gained from monitoring absolute microbial abundance in several full-scale disinfected distribution systems and lays a foundation for statistical approaches that could provide a basis for applying these tools through water quality monitoring.

1 Introduction

Microbial water quality in piped drinking water distribution systems depends on complex interactions between the microbial community (composition, abundance, and growth rates of microorganisms) and chemical and physical conditions. Over the last five years, researchers have made great progress to better understand these interactions with the common goal of guiding drinking water providers toward more efficient management of microbial water quality in piped drinking water systems with continuous or intermittent flow.^1–11 Advances in meta-omics techniques allow researchers to characterize changes in the microbial community composition throughout piped distribution,^12,13 but these techniques often do not quantify absolute microbial abundance. Increases in microbial abundance in piped drinking water distribution systems can signal mobilization of loose deposits,^14,15 loss of disinfectant residual,^16–18 treatment breakthrough,¹⁹ nitrification,^20,21 stagnation,^22,23 and intrusion or backflow.¹ It is important to pair measures of microbial abundance with compositional data to better characterize microbial water quality in drinking water systems.

In the United States, total coliform bacteria are the only regulated parameter for microbial abundance, but because levels are required to be maintained below the quantifiaction limit, this parameter provides little insight into the total microbial abundance. Given this limitation, other measures of microbial abundance have been used that include heterotrophic plate counts (HPC), which are the most common,^9,24 and newer methods that aim to capture the entire microbial community such as adenosine triphosphate (ATP) assays^25,26 and flow cytometry-based assays.^27,28 Each assay has its limitations. The World Health Organization recommends HPC for monitoring the “general bacterial content” of water,²⁴ but the HPC assay has been shown to quantify a varied fraction of total bacteria in drinking water²⁹ that can be several orders of magnitude smaller than total cell counts and usually requires two days to complete.³⁰ However, HPC may require less technical skill than ATP or cell counts if user-friendly proprietary HPC kits are used. As an alternative to HPC, the quantification of intracellular ATP has been used to estimate the viable biomass in water samples.^31–33 However, ATP concentration depends on the types of microorganisms present³⁴ and local conditions,^35,36 which hinders accurate quantification of microbial abundance. In addition, ATP assays require an extra filtration step during sample processing to measure total ATP (both intracellular and extracellular) as well as extracellular ATP (ATP in 0.1 μm filtered sample), which is subtracted from total ATP to obtain intracellular ATP.²⁵ In contrast, flow cytometry-based methods can be used to quantify microbial cells^37,38 with high reproducibility (<5% error³⁹), low limits of quantification (<25 cells per mL (ref. 40)), and rapid sample turnaround. Flow cytometry-based monitoring has been estimated to cost twice that of standard monitoring methods using HPC,⁴¹ and that cost does not include the cost of instruments needed, which for flow cytometry are currently more expensive than for HPC. For flow cytometry-based monitoring, an assessment of viability can be included by distinguishing between total cells and intact cells through staining procedures.

Drinking water distribution systems are dynamic, and changes in physical and chemical conditions in full-scale systems also influence the microbial abundance. For example, seasonal variations in drinking water quality have been linked to changes in intact cell count in a full-scale system without disinfectant residual.²⁸ In drinking water systems with residual disinfectants, characterizing these impacts can be difficult because environmental factors that can impact microorganisms can also impact the efficacy of disinfection (e.g., temperature, pH).⁴² In addition, high levels of residual disinfectant can make microbial abundance difficult to quantify because it might drive the quantity of microorganisms below the quantification limit of the assay. Flow cytometry-based methods have only been applied in full-scale systems with relatively low residual concentrations (<0.9 mg L⁻¹ free chlorine and <1.8 mg L⁻¹ combined chlorine),^{8,16,18,43–45} while drinking water systems in the United States have reported free chlorine concentrations of up to 4 mg L⁻¹ as Cl₂ after primary disinfection.⁴⁶ The understanding of disinfectant residual, and its interaction with other physical and chemical parameters, on total microbial abundance is still far from complete. Nonetheless, measures of microbial abundance that better reflect the entire microbial community, rather than a small fraction, and that are quantifiable throughout the range of conditions encountered in piped drinking water distribution systems, have the potential to provide more insight to guide the safe management of drinking water.

In this study, we compared five measures of microbial abundance (total and intact cell counts, total and intracellular ATP, and HPC) in six piped drinking water distribution systems. The drinking water systems had different treatment trains and used either free chlorine or chloramine as a residual disinfectant. We surveyed these systems to: 1. assess the impact of commonly measured parameters (disinfectant concentration, pH, and temperature) on microbial abundance, including statistical approaches to account for interactions between parameters; and 2. compare the quantifiability and variability of five measures of microbial abundance under the conditions of distribution. To our knowledge, this study is the first to apply flow cytometry-based total and intact cell counts in drinking water distribution systems with high disinfectant residual concentrations (>0.9 mg L⁻¹ free chlorine and >1.8 mg L⁻¹ total chlorine). These data will serve as points of comparison for future studies applying these methods in similar water systems.

2 Methods

2.1 Sampling locations

Piped drinking water distribution systems in California and Texas were sampled as indicated in Table S1.† Treatment processes and other metadata for these systems are shown in Table 1. Sampling efforts were coordinated with drinking water providers, and samples were collected from a subset of their routine monitoring locations. Systems A and B were sampled one time each in both 2016 and 2018. Systems C, D, and E were sampled one time in 2016. System F was sampled six times in 2018 (Table S1†). Prior to bulk water grab sampling, drinking water distribution system site taps were flushed for 10 minutes and 500 mL grab samples of bulk water were aseptically collected in autoclaved-sterilized glass bottles. pH (Electrode Sealed SJ F; Fisher Scientific) was determined within eight hours of sampling. Temperature (Electrode Sealed SJ F; Fisher Scientific) and free and total chlorine measurements (HACH pocket colorimeter II) were determined onsite at the time of sampling. Samples for quantification of microbial abundance were treated with sodium thiosulfate in excess to quench disinfectant residual and kept at 4 °C until processing within 24 hours of sampling. For DWDS F, water ages for each site were provided by the utility based on an internal model of the full distribution system developed using SynerGEE Water (v4.7.0). Consumables, including filtered pipette tips (RAININ TerraRack or Finntip Flex) and 2 mL microcentrifuge tubes (Thermo Scientific) used for microbial analyses were purchased presterilized and free of DNA, DNase, and RNase as well as of ATP when available.

Table 1 Treatment processes for each drinking water distribution system sampled in this study, presented in their sequential order at the treatment plant, where source water type is either surface water (S) and/or ground water (G)

System	Source water type	Maximum capacity (million gallons per day)	Treatment process											Secondary disinfectant
			Free chlorine	Coagulation, flocculation, sedimentation	Ozone	Free chlorine	Filtration(anthracite & sand)	Filtration(granular activated carbon & sand)	Filtration(granular activated carbon)	Membrane filtration (ultrafiltration)	Chlorine dioxide	Free chlorine	Ammonia
a These systems also have free chlorine addition at several locations in the distribution system. b Both chlorine dioxide and free chlorine are used as primary disinfectants. c System B had two parallel trains fed with the same source water that are combined before distribution with about 40% of flow from B1 and 60% of flow from B2.
A	S	12		X				X				X		Free chlorine
B1^c	S	5.5		X			X					X		Free chlorine
B2^c	S	5.5		X						X		X		Free chlorine
C	S	200	X	X			X					X	X	Chloramine
D	S/G	40		X					X		X^b	X^b		Free chlorine
E	G	30		X					X			X		Free chlorine^a
F	S	144		X	X	X	X					X	X	Chloramine

---

2.2 Cell counts by fluorescent staining and flow cytometry

Total and intact cell concentrations were measured following the methods of Miller et al.⁴⁰ Briefly, cell concentrations were measured using flow cytometry with SYBR® Green I (S9430; Sigma-Aldrich, St. Louis, MO) and propidium iodide (30 mM P1304MP; Life Technologies, Carlsbad, CA) to distinguish cells with intact membranes. From each bulk water grab sample, a 1000-μL aliquot of each triplicate was processed and the geometric mean and geometric standard deviation were calculated. Measurements were performed on two separate flow cytometers, an Accuri C6 flow cytometer (Accuri; BD Biosciences, San Jose, CA) and a BD FACSCanto cell analyzer (Canto; BD Biosciences, San Jose, CA). The Accuri was used to sample all locations but had to be sent in for repair during field sampling at DWDS F. While the Accuri was not available the Canto was used, which was during sampling of DWDS F (data files in the supplemental information include which cytometer was used to generate each data point). The Accuri was equipped with a 50 mW laser emitting a fixed wavelength of 488 nm, and measurements were performed at the “fast” flow rate of 66 μL per minute on sample volumes of 50 μL. Microbial cell signals were distinguished and enumerated from background and instrument noise on density plots of green (FL1; 533 ± 30 nm) and red (FL3; >670 nm) fluorescence using FlowJo gating software (v 10.5.3). Gate positions were modified slightly from a template publicly available for the BD Accuri C6 (ref. 38) to adapt for FlowJo software. The Canto was equipped with a 20 mW laser emitting a fixed wavelength of 488 nm, and measurements were performed at a flow rate of 1 μL s⁻¹ for 50 seconds. Microbial cell signals were distinguished and enumerated from background and instrument noise on density plots of green (FTIC; 530 ± 30 nm) and red (PerCP; 695 ± 40 nm) fluorescence using FlowJo gating software. Gate positions were modified slightly compared to BD Accuri C6 gating based on calibration beads (Spherotech, Catalog #NFPPS-52-4 K, Lake Forest, IL). For the Accuri, the lower quantification limits were determined for intact cell count (22 cells per mL) and total cell count (12 cells per mL) by Miller et al. using the same instrument used in this study.⁴⁰ All data from the Canto were deemed detectable based on the recommended lower quantification limit (>10² cells per mL;³⁸) after gate adjustment (more information can be found in the Supplemental Information). All of our flow cytometric measurements were at least an order of magnitude lower than the upper recommended upper quantification limit (<10⁷ cells per mL;³⁸). For a negative control, 0.22 μm filtered, Millipore Milli-Q water was used.

2.3 Adenosine tri-phosphate concentrations

Total and intracellular ATP concentrations were measured following the methods of Miller et al.⁴⁰ Briefly, ATP concentrations were measured using the BacTiter-Glo™ Microbial Cell Viability Assay (G8231, Promega Corporation, Madison, WI) and GloMax® 20/20 Luminometer (Turner BioSystems, Sunnyvale, CA). From each bulk water grab sample, a 500-μL aliquot of each triplicate was processed and the geometric mean and geometric standard deviation were calculated. Relative light units from the luminometer were converted to ATP concentrations using calibration curves made with a pure ATP standard (P1132; Promega Corporation, Madison, WI). Extracellular ATP was separated from total ATP prior to sample incubation through removal of microbial cells by filtration (0.1 μm, Millex-VV Syringe Filter Unit; Millipore, Billerica, MA). For total and extracellular ATP, the quantification limits were set by the standard curve, which ranged from 1 × 10⁻⁴ nM to 10 nM. No total or extracellular ATP measurement was higher than the upper quantification limit. The lower quantification limit for intracellular ATP was determined by Miller et al.⁴⁰ as 1.83 × 10⁻⁵ nM. Empty tube measurements and reagent-only measurements were used as negative controls and reagent controls respectfully.

2.4 Heterotrophic plate counts

Heterotrophic plate counts (HPC) were determined using Quanti-Tray 2000 (IDEXX US; Westbrook, Maine) with HPC for Quanti-Tray media (IDEXX US; Westbrook, Maine) following the manufacturer's instructions with the trays incubated at 37 °C for 44–72 hours. 100 mL of bulk water grab sample was transferred to autoclave sterilized bottles for each replicate and the geometric mean and geometric standard deviation were calculated. Technical duplicates of all samples were completed except samples from distribution system B in 2016, for which there were no replicates. The lower limit of quantification was set using the IDEXX Quanti-Tray format at a most probable number of one cell per 100 mL. The upper limit of quantification was set at a most probable number of 2419.6 cells per 100 mL (a fully positive IDEXX tray).

2.5 Statistical analyses

Our dataset had inherent dependencies for which we needed to account in our analysis, including dependent variables that may be correlated with each other (e.g., pH, temperature, chlorine residual), samples collected from the same drinking water distribution system on the same day, or at the same location within a distribution system over time. Thus, relationships between microbial abundance and water quality parameters were assessed via correlation analyses and generalized linear mixed models using R (3.6.2).⁴⁷ To investigate potential multicollinearity, Spearman's Correlation values of all chemical and microbial water quality parameters were determined using Hmisc (4.3–0)⁴⁸ and GGally (1.4.0).⁴⁹ Data exploration was completed following Zuur et al.⁵⁰ using Cleveland dot plots to detect outliers, GGgally to assess colinearity, and scatter plots of all covariates to visualize relationships.^50,51 Outliers and collinearity between covariates were not detected. Generalized linear mixed model (GLMM) analysis and validation was completed following the methods of Zuur et al.^51,52 Prior to analysis, microbial abundance metrics were tested for goodness of fit to a normal distribution, log-normal distribution, and gamma distribution⁵³ using goft (1.3.4).⁵⁴ The GLMM was fitted to raw intact cell counts from distribution system F with centered and scaled predictors (to improve the parameter optimization process) using lme4 (1.1–23)⁵⁵ with site as a random variable. The most optimal model was selected based on minimizing conditional Akaike information criterion with MuMIn (1.43.15)⁵⁶ through backward stepwise model selection. Wald confidence intervals for fixed effects were calculated using lme4. For correlation, GLMM, and summary statistic calculations, values below the quantification limit of intracellular ATP, total ATP, intact cell counts, total cell counts, HPC, free chlorine and total chlorine were replaced with the respective lower quantification limit for the assay to be conservative. However, for calculations of the coefficient of variation, only the quantifiable samples were used (Table 4). In figures, these data were plotted at a value below the quantification limit for visualization. Four HPC samples were above the quantification limit and were removed from all statistical analyses and figures. Plotting was completed using ggplot2 (3.2.1),⁵⁷ tables were generated using stargazer (5.2.2),⁵⁸ plot fonts were set using extrafont (0.17),⁵⁹ figures with multiple plots were generated using ggpubr (0.4.0),⁶⁰ and color palettes were chosen from viridis (0.5.1).⁶¹ The full reproducible code and csv files that have all data used in this paper is available in the ESI† Materials as well as through GitHub (https://zenodo.org/record/3993877#.X5n0Qy9h1TZ).

3 Results

3.1 Impacts of physicochemical parameters on microbial abundance

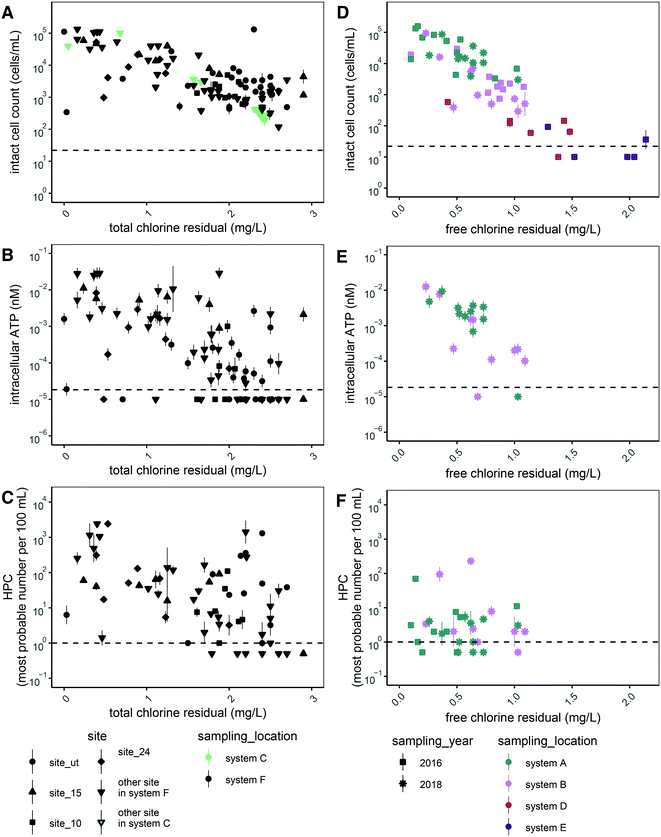
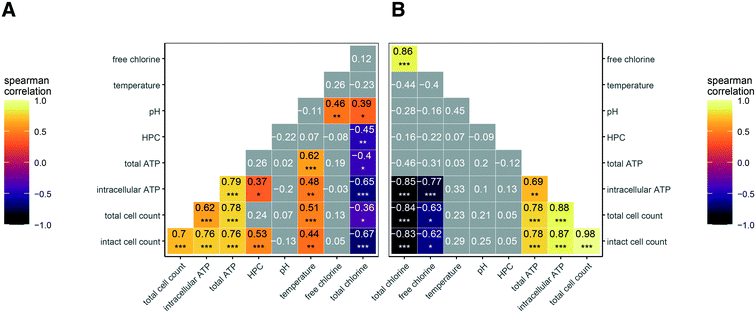
We expected disinfectant residual concentration to be a master variable affecting microbial abundance across the various the drinking water distribution systems that were sampled. Thus, we plotted all data for each measure of microbial abundance as a function of disinfectant residual concentration. Of the five measurements of microbial abundance we applied, we observed inverse trends for two of them: intact cell counts (Fig. 1A and D) and intracellular ATP (Fig. 1B and E). The trends for HPC (Fig. 1C and F), total cell counts in chloraminated systems (Fig. S1A†), and total ATP (Fig. S1C and D†) were less clear. In free chlorinated systems, a similar trend was observed for total cell count (Fig. S1B†) as for intact cell count (Fig. 1D), likely because free chlorine is a stronger disinfectant than chloramine.⁴² Thus, signal from non-viable cells and free DNA likely decreases more rapidly than in chlorinated systems. We also did not observe a trend for proportion of potentially viable cells (intact:total cells) (Fig. S2†).

Fig. 1 Microbial abundance measures in the drinking water distribution systems sampled in this study by disinfectant concentration. Left (chloraminated systems): intact cell counts (A), intracellular ATP (B), and HPC (C) in distribution system C (A) and distribution system F (A–C). Shapes denote sites in distribution system F that were sampled at least six times between august 2017 and april 2018. Right (chlorinated systems): intact cell counts (D), intracellular ATP (E), and HPC (F) in distribution system A (D–F), distribution system B (D–F), and distribution systems D and E (D). Shapes denote locations in distribution systems A and B that were sampled once in 2016 and repeated in 2018. Horizontal dashed lines denote quantification limits for each assay. Points are the geometric mean of the technical replicates and error bars represent the variation associated with technical replicates as quantified by the geometric standard deviation for technical replicates.

In addition to disinfectant residual concentration, we recognized that temperature and pH might influence microbial abundance. To explore these relationships statistically, we used Spearman's correlation coefficients (r_s) to assess the strength of correlation between the various microbial abundance metrics, disinfectant concentration, temperature, and pH (Fig. 2A and B). The correlation between microbial abundance metrics and residual disinfectant concentration is discussed first. In both chloraminated and chlorinated systems, total chlorine concentration was significantly and inversely correlated with both intracellular ATP and intact cell counts (r_s values between −0.65 and −0.85; p-values <0.0001; Fig. 2A and B), consistent with the visual trends in Fig. 1. HPC were only significantly correlated with disinfectant residual in chloraminated systems (r_s = −0.45; p < 0.001; Fig. 2A). In contrast, we found that intracellular ATP was more strongly correlated with disinfectant concentration in chlorinated systems (r_s value −0.77; p < 0.0001; Fig. 2B) compared to chloraminated systems (r_s value −0.65; p < 0.0001; Fig. 2A), but intact cell count was similar in both chlorinated (r_s values −0.62; p < 0.01; Fig. 2B) and chloraminated (r_s value −0.67; p < 0.0001; Fig. 2A) systems. In chlorinated systems, the majority of the total chlorine concentration consisted of free chlorine except for in two cases for which total chlorine concentrations were <0.3 mg L⁻¹ as Cl₂. Thus free and total chlorine concentrations were strongly correlated and appear to have similar impacts on measures of microbial abundance (Fig. 2B). However, in chloraminated systems free chlorine concentration varied and was not significantly correlated with any microbial abundance parameters (Fig. 2A).

Fig. 2 A) Spearman's correlation coefficient heat map for all samples with complete water quality data collected from a chloraminated drinking water distribution system (n = 61) (B) Spearman's correlation coefficient heat map for all samples with complete water quality data collected from chlorinated drinking water distribution systems (n = 21). Insignificant coefficients are shown in grey where significance is coded as * p < 0.01; ** p < 0.001; *** p < 0.0001.

In terms of the other two commonly monitored water quality variables, we observed significant correlations in chloraminated systems of temperature with intact cell counts (r_s = 0.44; p < 0.001) and with intracellular ATP (r_s = 0.48; p <0.001), but temperature was not correlated with any measures of microbial abundance in chlorinated systems (Fig. 2A and B). pH was not significantly correlated with any measure of microbial abundance. We note that our dataset included ranges for disinfectant residual, temperature, and pH that are typical of drinking water distribution systems located in the Western/Southwestern United States (Table S2†).

In the chloraminated distribution system, microbial abundance measures were strongly correlated with both disinfect residual and temperature, and pH was strongly correlated with disinfectant residual. We wanted to assess relationships between these variables using a model. However, we needed to account for interactions between variables and for measurements from the same location that were not independent. For this approach, we focused on intact cell counts and developed a mixed model using data from distribution system F (n = 80). Raw intact cell counts were not normally or log normally distributed, but the fit to a gamma distribution was not rejected.⁵³ Thus, scaled and centered predictor variables (pH, temperature, free and total chlorine) and raw intact cell counts were used in a generalized linear mixed model with log link function (eqn (1)). The log link function was chosen because it requires positive fitted values. Sampling location within distribution system F (“site”) was used as a random intercept to account for dependency associated with samples taken from the same site.

ICC_ij ∼ Gamma (μ_ij, τ) (1)

log(μ_ij) = total chlorine_ij + free chlorine_ij + pH_ij + temperature_ij + total chlorine_ij × pH_ij + free chlorine_ij × pH_ij + free chlorine_ij × temperature_ij + total chlorine_ij × temperature_ij + site_i

site_i ∼ N(0, σ²_site)

In eqn (1), ICC_ij is the intact cell count (with mean μ_ij) for the jth observation of site_i. ICC_ij is assumed to follow a gamma distribution with scale parameter, μ_ij, and shape parameter, τ. The random intercept, site_i, is assumed to be normally distributed with mean of 0 and variance of σ²_site. Fixed effects include total chlorine, free chlorine, pH, temperature, and their interactions (included as interaction terms). We applied stepwise model selection (Table S3†) to determine the most optimal model (eqn (2)) with parameter estimates in Table 2.

ICC_ij ∼ Gamma (μ_ij, τ) (2)

log(μ_ij) = total chlorine_ij + pH_ij + temperature_ij + free chlorine_ij × pH_ij + total chlorine_ij × temperature_ij + site_i

site_i ∼ N(0, σ²_site)

The most optimal model shows that lower total chlorine concentrations resulted in higher intact cell counts; as expected, there was also an interaction with temperature that could result in higher intact cell counts at lower total chlorine values and higher temperatures (Fig. 3). In Fig. 3, quantiles of temperature, from lowest (purple line) to highest (yellow line), are used in eqn (2) at a range of total chlorine concentrations. The total chlorine term was the largest parameter estimate for a fixed effect in this model (Table 2), which indicates that total chlorine had a large inverse effect on intact cell counts. In addition, higher pH and temperature values resulted in higher intact cell counts (Fig. S3† and Table 2). However, the effect of temperature and pH on intact cell counts was smaller than that of total chlorine (Table 2). In addition, the interaction between pH and free chlorine in the optimized model was indistinguishable from 0 (0 falls within the confidence intervals shown in Table 2). It is known that free chlorine disinfection is more effective at pH values below 7.5,⁴² but the minimum pH value in system F was 7.67 (Table S4†). Thus, the pH in this system likely did not vary enough to produce an accurate estimate for this interaction term (Table S4†).

Table 2 Estimated parameters, standard errors, and confidence intervals for each covariate of the most optimal model of intact cell counts in distribution system F (eqn (2)). Generalized linear mixed model for intact cell counts with sampling location (“site”) as a random variable, where σ²_site = 0.26 and τ = 1.72. X denotes interaction

Parameter	Estimate	Standard error	Lower confidence interval (5%)	Upper confidence interval (95%)
Intercept	8.6	0.19	8.3	9.0
Total chlorine	−1.3	0.13	−1.6	−1.1
pH	0.40	0.17	0.062	0.73
Temperature	0.35	0.097	0.16	0.54
pH × free chlorine	0.39	0.23	−0.066	0.84
Total chlorine × temperature	−0.24	0.12	−0.47	−0.0087

---

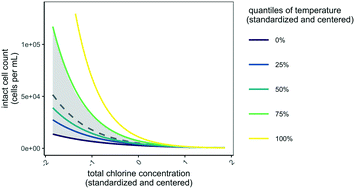Fig. 3 Visual representation of the most optimal model of intact cell counts in distribution system F (eqn (2)). To generate dashed grey line, all fixed effects were held constant at their average value except for total chlorine (with bootstrapped 95% confidence intervals are shown in grey). To generate other lines, temperature was varied in the model at each quantile value (−1.9, −0.10, −0.53, 0.87, and 2.1). In Fig. S3†, other fixed effects are shown.

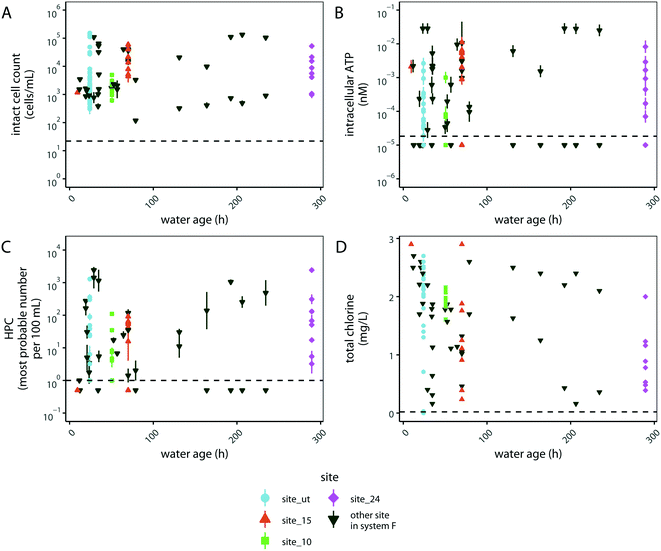
We hypothesized that another variable in drinking water distribution systems that may correlate with microbial abundance is water age, given that the concentration of chlorine residual is known to diminish with water age, which could have substantial impacts on microbial abundance.⁶² To investigate the impacts of water age on water quality, we compared water age with intact cell counts, intracellular ATP, HPC, and total chlorine concentration in distribution system F (Fig. 4). Surprisingly, the measures of microbial abundance generally did not trend with water age (Fig. 4A–C). However, total chlorine generally decreased with water age during each specific sampling event (Fig. S4†). To investigate the variability in chlorine residual at individual sampling sites, we aggregated data from a year of sampling at 21 sites in distribution system F (Fig. S5†). Total chlorine at each sited varied over the course of a year depending on the location sampled and was not directly correlated with the water age at that site (Fig. S5†). These results suggest that total chlorine had a large impact on microbial abundance that was independent of water age in distribution system F.

Fig. 4 Intact cell counts (A), intracellular ATP (B), HPC (C), and total chlorine concentration (D) by water age (hours) in distribution system F. Shapes denote locations in distribution system F that were sampled at least six times between August 2017 and April 2018. Horizontal dashed lines denote quantification limits for each assay. Points are the geometric mean of the technical replicates and error bars represent the variation associated with technical replicates as quantified by the geometric standard deviation for technical replicates.

3.2 Quantifiability and variability of five measures of microbial abundance

To evaluate the utility of the microbial abundance assays, we determined which measures of microbial abundance were most frequently quantifiable in disinfected drinking water systems. Intact cell counts yielded the highest percentage of results that were above lower quantification limits (97.6% of samples, n = 166; Table 3). In contrast, intracellular ATP was quantifiable in only 69.6% of samples (n = 115), and HPC were quantifiable in only 81.4% of samples (n = 102; 18.6% of samples either above or below limits of quantification). Total ATP and total cell counts were quantifiable in 100% of samples, as no samples were below the limit of quantification (Table 3). Interestingly, quantifiability of intracellular ATP was dependent on the system sampled (Tables S5 and S6†). In particular, we saw a greater fraction of samples with concentrations of intracellular ATP above lower quantification limits from distribution system A (90.9% of samples with n = 11; Table S5†) and distribution system B (90% of samples with n = 10; Table S5†) and lower quantifiability in samples from distribution system F (64.9% of samples with n = 94; Table S5†).

Table 3 Percent of samples above quantification limit, below quantification limit, and quantifiable in all drinking water distribution systems sampled for this study for each microbial water quality assessment method. “n” is the number of samples per assay

Assay	n	Percent quantifiable	Percent below quantification limit	Percent above quantification limit
Intact cell counts	166	97.6	2.4	0
Total cell counts	166	100	0	0
Intracellular ATP	115	69.6	30.4	0
Total ATP	115	100	0	0
HPC	102	81.4	14.7	3.9

---

To evaluate the variability of the microbial abundance assays, we determined which measures of microbial abundance had the lowest average coefficients of variation. The coefficient of variation is commonly used to assess variability in quantitative bioassays and is reported as a percentage with a higher percentage indicating more variation among replicates.⁶³ To summarize the variability across all samples taken in this study, we calculated an average coefficient of variation for each of the measures of microbial abundance by taking the arithmetic mean of all sample coefficients of variation (Table 4). Notably, variability was lower for total ATP (9.30%; Table 4), total cell counts (17.0%; Table 4), and intact cell counts (16.9%; Table 4), compared to intracellular ATP (56.0%; Table 4) and HPC (49.4%; Table 4).

Table 4 Ranges in coefficient of variation determined by geometric mean (%; min, median, and max) and average coefficient of variation (%) for replicates taken in all drinking water distribution systems sampled for this study for each microbial water quality assessment method. “n” is the number of samples per assay

Assay	n	Min coefficient of variation	Median coefficient of variation	Max coefficient of variation	Average coefficient of variation
Intact cell counts	162	0.0266	9.78	148	16.9
Total cell counts	166	0.318	6.15	255	17.0
Intracellular ATP	80	42.9	48.6	328	56.0
Total ATP	115	0.389	4.81	66.0	9.30
HPC	73	0	27.1	293	49.4

---

4 Discussion

We compared five measures of microbial abundance by surveying drinking water systems that apply residual disinfectants in California and Texas. In one chloraminated system, we used a generalized linear mixed model to estimate the effect of commonly measured water quality parameters on intact cell counts. In the following sections, we discuss the purpose and interpretation of typical microbial water quality factors and consider the future role of enhanced measures of microbial water quality for three applications: routine monitoring, diagnostics, and research.

4.1 Considerations for routine monitoring of drinking water systems

A key finding from this study is that disinfectant concentration in drinking water distribution systems provided an indirect measure of microbial abundance, which has useful implications for routine monitoring of distribution systems. Disinfectant residual had the largest inverse correlation coefficient regardless of residual type (Fig. 2A and B). Furthermore, total chlorine had the greatest inverse effect on intact cell counts in a chloraminated drinking water distribution system (distribution system F). Gillespie et al.¹⁶ and Nescerecka et al.¹⁸ also surveyed disinfected distribution systems, but did not report trends between intact cell counts and disinfectant residual. Gillespie et al.¹⁶ sampled in chlorinated systems with free chlorine <0.8 mg L⁻¹ as Cl₂ and recommend maintaining free chlorine above 0.5 mg L⁻¹ as Cl₂ to keep the fraction of potentially viable cells below 0.2. In contrast, we did not observe a similar trend with the fraction of viable cells (Fig. S2†), but we did find that intact cell count decreased to <100 cells per mL at free chlorine concentrations above 1.5 mg L⁻¹ as Cl₂. We assessed intact cell counts at a wider range of disinfectant concentrations and observed a clear trend between disinfectant residual and intact cell counts.

We presented a proof of concept that development of mixed models could help relate routinely monitored physicochemical data to intact cell counts in drinking water distribution systems. Drinking water providers in the United States commonly monitor pH, temperature, free chlorine, and total chorine, and we incorporated these data into a model to estimate intact cell counts using data from a chloraminated distribution system. The most optimal model (eqn (2)) suggests that total chlorine had the largest effect on intact cell counts and that this effect depended on temperature. Zhang et al.⁶⁴ also found that disinfectant concentration had an inverse effect on log-transformed HPC and visually observed higher values of log transformed HPC in the summer than in the winter, but statistical results were inconsistent, likely due to variability in HPC results. Using intact cell counts, instead of just the small fraction of total coliform bacteria or HPC, holds promise to model a commonly observed phenomenon: in summer, a higher residual disinfectant is necessary to maintain microbial water quality.⁶⁵ This study focused on routinely measured parameters in drinking water distribution systems in the Southwestern United States, but more research is needed to expand the dataset and modeling approach. This approach could include a dataset that accounts for seasonal variability and source water quality changes as well as includes additional biological (e.g., assimilable organic carbon) and physicochemical parameters (e.g., total organic carbon concentration). However, including more parameters would require a larger sample size than we collected for our model (n = 80). In addition, modeling completed using data from multiple distribution systems will introduce a nested dependency structure in which both samples from the same system will be correlated as well as samples from the same site within a distribution system over time. With a more complete dataset, it might be possible to generate a model for which consistent deviations from model predictions at specific sites may be indicative of water quality problems, such as pipe corrosion or nitrification.

4.2 Intact cell counts and intracellular ATP assays as diagnostic tools

To better understand observed or expected changes in water quality, such the impact of nitrification, upgrading treatment processes, or incorporating a new treated water source (e.g., potable reuse), diagnostic monitoring can be necessary. However, the culturing methods commonly employed in routine monitoring, such as for total coliforms and HPC, often produce unquantifiable or unrepresentative results. For example, in a survey of U.S. drinking water providers, 57% of respondents reported never detecting total coliforms while the other 43% reported having fewer than 12 positive samples per year (n = 256 respondents⁴⁶). Similarly, our results support previous claims that HPC vastly underestimates drinking water microbial abundance as compared with intact cell counts.³⁰ HPC only quantifies bacteria that can utilize organic nutrients for growth^29,41 and they have been shown to comprise <1% of bacteria in some drinking water samples.^31,66 Prest et al.²⁸ reported a very high fraction of treated drinking water samples with HPC results below 5 CFU per mL while total cell counts ranged from 9.0 × 10⁴ to 4.5 × 10⁵ cells per mL.

For diagnostic purposes, use of intact cell counts would allow drinking water providers to detect changes in microbial water quality that are not observable using traditional microbial monitoring methods like HPC or total coliform quantification.^{30,41,43,67–69} In this study, 97.6% of samples had quantifiable intact cell counts. Only four samples were below the intact cell count quantification limit, which occurred at the highest residual concentration observed in chlorinated drinking water distribution systems (1.5–2.0 mg L⁻¹ as Cl₂; Fig. 1). Intact cell counts spanned four orders of magnitude in chloraminated systems (from <22 cells per mL to 1.09 × 10⁵ cells per mL) and more than two orders of magnitude in the chlorinated systems (<22 cells per mL to 2.12 × 10³ cells per mL). As might be expected, these cell counts were lower than those reported in other studies with lower maximum residual disinfectant values or in systems without disinfectant residuals. For chlorinated distribution systems, the maximum cell counts from this study are about 1000 times less than those reported in Gillespie et al.¹⁶ In addition, the geometric mean of intact cell counts of all distribution system samples in our study (3 × 10³ cells per mL) was about 100 times lower than that of total cell counts reported for a system that does not apply a residual disinfectant (1 × 10⁵ cells per mL).⁷⁰

Intracellular ATP may also be useful for diagnostic purposes because the values measured in this study correlated strongly with intact cell counts and ATP assays are less expensive. Drinking water providers monitoring microbial abundance for diagnostic purposes will need to choose measures of microbial abundance that maximize information gained and minimize expense. For this reason, it is important to consider how much each technique overlaps with other measures of microbial abundance and with chemical or physical water quality parameters. Intact cell counts and intracellular ATP results were strongly correlated (Fig. 2A and 4B), and other studies have found similar correlations between ATP and intact cell counts among both chloraminated and chlorinated systems.^18,28,30,66 Our results support the likelihood that most microbial abundance information will be obtained if either intact cell counts or intracellular ATP is measured. However, intact cell count was still more quantifiable and consistent compared to intracellular ATP. Intracellular ATP was quantifiable in only 69.6% of samples (Table 3) and technical replicates varied considerably (average coefficient of variation = 56%; Table 4). Thus, intracellular ATP may only be preferable when expense is a primary concern.

4.3 Assessment of biostability and risk in disinfected drinking water systems

While there is no evidence that the safety of drinking water is compromised simply due to variations in microbial abundance, microbial growth in distribution systems is generally considered to be a risk.^27,71,72 Choosing universal guidelines to maintain microbial water quality is not straightforward because microbial abundance is not directly linked to specific risks to infrastructure or public health. For example, setting a numerical operational limit for cell counts (e.g., 100 cells per mL) is not logical because microbial abundance varies considerably by water source and even within the same distribution system.¹⁷ In lieu of numerical operational limits, researchers have proposed maintaining biologically stable water, in which microbial abundance and composition does not significantly change throughout a distribution system.^70,73 However, biologically stable drinking water is difficult to maintain in disinfected drinking water distribution systems^17,18 because disinfectant residual concentration has been shown to degrade in drinking water distribution systems as it reacts with pipe walls and organic matter (Fig. S4†).⁶² In this study, disinfectant residual varied over a large range within chloraminated and chlorinated distribution systems, and there was a strong inverse correlation between the residual concentration and the microbial abundance.

Instead of maintaining biologically stable water, setting more subjective operational limits might be necessary in disinfected drinking water systems. Subjective operational limits have been set for HPC in the United Kingdom, France, the Netherlands, and Belgium where the upper limit is “no abnormal change” in HPC.³⁰ While it is difficult to define “normal” in drinking water systems, normal can be operationally defined by measuring microbial water quality under a range of conditions encountered in the system to establish a baseline and to discern contamination events from the natural fluctuations^74,75 that have been well documented in drinking water distribution systems.⁷⁶ To establish a baseline microbial abundance in drinking water systems, water providers could monitor intact cell counts or intracellular ATP data throughout the range of chemical and physical water quality conditions encountered in their systems under routine operations. The generalized linear mixed model presented in this paper represents one way to establish such a baseline and the methodology could be applied in other systems.

To more thoroughly assess health risk in drinking water systems, more research is needed to pair absolute microbial abundance measures with assessments of microbial community composition and the concentration of specific pathogens of concern. Significant research is underway to characterize microbial communities in drinking water using high-throughput sequencing technologies (e.g., 16S rRNA gene amplicon and metagenomic sequencing). Some researchers have paired microbial abundance data with sequencing data using quantitative polymerase chain reaction (qPCR) methods to provide a deeper characterization of microbial water quality.^77–79 Combining qPCR with viability dyes brings a similar benefit as cell counts and ATP assays in that cell membrane damage can be used as a viability metric.⁸⁰ However, these methods have limitations discussed previously,⁸¹ including limited resolution (twofold changes in gene copies;⁸²), bias introduced from assay design,^82,83 and bias introduced with PCR.⁸⁴ Others have paired flow cytometry with sequencing data to provide a similar characterization of microbial water quality without bias introduced from PCR.^39,81,85 Ultimately, these studies may provide a sophisticated understanding of the complex interactions and factors that govern microbial ecology in drinking water systems. However, not all microbial ecology studies report absolute microbial abundance data. Pairing measures of microbial abundance with sequencing results has the potential to characterize microbial water quality in greater resolution than using any single method. This approach can provide more insight into risk in drinking water distribution systems including potential exposure to opportunistic pathogens and other microbially induced issues, such as pipe corrosion,^86,87 nitrification,^88,89 and aesthetic deterioration of finished water.⁹⁰

For meta-omics research, we believe that the microbial abundance measures we studied that will be most useful to include are intact and total cell counts. Our flow cytometry results indicate that a varied fraction of cells in the sites we sampled were viable (Fig. S2†). Intact and total cell counts are quantified by a fluorescent dye that intercalates with DNA⁹¹ and are a more direct measure of microbial abundance compared to ATP assays. Though cell count data were correlated with ATP data, ATP results were varied and often unquantifiable in these systems. While total cell count is more reflective of the sequenced microbial community, intact cell count is more reflective of the risk imposed by the microbial community. Thus, both total and intact cell counts could be useful to pair with meta-omics data and provide a more informative assessment of microbial water quality in drinking water systems.

5 Conclusions

Applying measures of microbial abundance in piped drinking water systems can be useful for routine monitoring, diagnostics, and research. Our results support that disinfectant residual is an indirect measure of microbial abundance, and the necessity of pairing it with direct measures is questionable for routine monitoring. However, for diagnostic purposes, additional monitoring data in systems with large ranges in microbial and physicochemical water quality conditions could help drinking water providers diagnose issues early and move beyond the goal of ensuring total coliforms are not detectable.^92,93 For research, pairing meta-omics data with measures of microbial abundance can help researchers better characterize microbial water quality. Our results support that HPC assays are uninformative in these systems because these results are variable and often unquantifiable. Microorganisms are present throughout drinking water systems, and by limiting analyses to HPC, the true microbial water quality cannot be observed. Instead, we recommend using either intracellular ATP or intact cell counts for diagnostic purposes and both intact and total cell counts to pair with meta-omics data. Our main findings are summarized as follows:

• Intact cells were measured in all six piped drinking water distribution systems, including chloraminated sites with total chlorine >2.5 mg L⁻¹ as Cl₂.

• Only 2.4% of sampling sites, with the highest free chlorine concentrations (i.e., 1.5–2 mg L⁻¹ as Cl₂), had intact cell counts below quantification limits.

• Residual disinfectant concentration was significantly and strongly correlated with intracellular ATP and intact cell counts in distribution systems.

• Negative correlations between residual disinfectant concentration and intracellular ATP were stronger in chlorinated systems than in chloraminated systems.

• The parameter that had the greatest impact on intact cell counts in a chloraminated drinking water distribution system was total chlorine concentration, which interacted with temperature.

• Of the five measures of microbial abundance, only total cell counts and total ATP were quantifiable in all samples, but these assays do not assess viability of cells.

• Total ATP had the least variability among technical replicates followed by intact cell counts and total cell counts.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank our utility partners for facilitating and assisting with sampling campaigns, including Terance Hodge and Richard Wilcox as well as others. We also thank Hannah Greenwald and Lorelay Mendoza for assisting with sample collection and Emily Cook and Casey Finnerty for helpful discussions. In addition, we thank the San Diego State University Flow Cytometry Core Facility for their efforts.

This material is based upon work supported by the National Science Foundation Graduate Research Fellowship under Grant No. DGE-1752814 & No. DGE-1106400. In addition, this work was supported by the National Science Foundation through the Engineering Research Center for Reinventing the Nation's Urban Water Infrastructure under Grant No. EEC-1028968.

References

1. Q. M. Bautista-de los Santos, K. A. Chavarria and K. L. Nelson, Understanding the impacts of intermittent supply on the drinking water microbiome, Curr. Opin. Biotechnol., 2019, 57, 167–174.
2. Q. M. Bautista-de los Santos, J. L. Schroeder, M. C. Sevillano-Rivera, R. Sungthong, U. Z. Ijaz and W. T. Sloan, et al. Emerging investigators series: microbial communities in full-scale drinking water distribution systems – a meta-analysis, Environ. Sci.: Water Res. Technol., 2016, 2(4), 631–644.
3. Z. Dai, M. C. Sevillano-Rivera, S. T. Calus, Q. M. Bautista-de los Santos, A. M. Eren and P. W. J. J. van der Wielen, et al. Disinfection exhibits systematic impacts on the drinking water microbiome, Microbiome, 2020, 8(1), 42.
4. V. C. Dias, A.-A. Durand, P. Constant, M. Prévost and E. Bédard, Identification of factors affecting bacterial abundance and community structures in a full-scale chlorinated drinking water distribution system, Water, 2019, 11(3), 627.
5. I. Douterelo, C. Calero-Preciado, V. Soria-Carrasco and J. B. Boxall, Whole metagenome sequencing of chlorinated drinking water distribution systems, Environ. Sci.: Water Res. Technol., 2018, 4(12), 2080–2091.
6. N. M. Hull, F. Ling, A. J. Pinto, M. Albertsen, H. G. Jang and P.-Y. Hong, et al., Drinking water microbiome project: is it time?, Trends Microbiol., 2019, 27(8), 670–677.
7. E. Kumpel and K. L. Nelson, Intermittent water supply: prevalence, practice, and microbial water quality, Environ. Sci. Technol., 2015, 50(2), 542–553.
8. W. Li, J. Zhang, F. Wang, L. Qian, Y. Zhou and W. Qi, et al., Effect of disinfectant residual on the interaction between bacterial growth and assimilable organic carbon in a drinking water distribution system, Chemosphere, 2018, 202, 586–597.
9. Y. Perrin, D. Bouchon, V. Delafont, L. Moulin and Y. Héchard, Microbiome of drinking water: A full-scale spatio-temporal study to monitor water quality in the Paris distribution system, Water Res., 2019, 149, 375–385.
10. C. R. Proctor and F. Hammes, Drinking water microbiology—from measurement to management, Curr. Opin. Biotechnol., 2015, 33, 87–94.
11. Y. Zhang, S. Oh and W.-T. Liu, Impact of drinking water treatment and distribution on the microbiome continuum: an ecological disturbance's perspective, Environ. Microbiol., 2017, 19(8), 3163–3174.
12. Y. Zhang and W.-T. Liu, The application of molecular tools to study the drinking water microbiome – Current understanding and future needs, Crit. Rev. Environ. Sci. Technol., 2019, 49(13), 1188–1235.
13. F. Ju and T. Zhang, Experimental design and bioinformatics analysis for the application of metagenomics in environmental sciences and biotechnology, Environ. Sci. Technol., 2015, 49(21), 12628–12640.
14. E. Torvinen, S. Suomalainen, M. J. Lehtola, I. T. Miettinen, O. Zacheus and L. Paulin, et al., Mycobacteria in water and loose deposits of drinking water distribution systems in finland, Appl. Environ. Microbiol., 2004, 70(4), 1973.
15. L. Chen, F. Ling, G. Bakker, W.-T. Liu, G. Medema and W. van der Meer, et al. Assessing the transition effects in a drinking water distribution system caused by changing supply water quality: an indirect approach by characterizing suspended solids, Water Res., 2020, 168, 115159.
16. S. Gillespie, P. Lipphaus, J. Green, S. Parsons, P. Weir and K. Juskowiak, et al. Assessing microbiological water quality in drinking water distribution systems with disinfectant residual using flow cytometry, Water Res., 2014, 65 IS, 224–234.
17. A. Nescerecka, T. Juhna and F. Hammes, Identifying the underlying causes of biological instability in a full-scale drinking water supply system, Water Res., 2018, 135, 11–21.
18. A. Nescerecka, J. Rubulis, M. Vital, T. Juhna, F. Hammes and J. L. Balcazar, Biological instability in a chlorinated drinking water distribution network, PLoS One, 2014, 9(5), e96354.
19. P. Payment and W. Robertson, The microbiology of piped distribution systems and public health, in Safe Piped Water: Managing Microbial Water Quality in Piped DistributionSystems, ed. R. Ainsworth, World Health Organization, London, IWA Publishing, Citeseer, 2004.
20. L. H. Odell, G. J. Kirmeyer, A. Wilczak, J. G. Jacangelo, J. P. Marcinko and R. L. Wolfe, Controlling nitrification in chloraminated systems, J. - Am. Water Works Assoc., 1996, 88(7), 86–98.
21. A. Wilczak, J. G. Jacangelo, J. P. Marcinko, L. H. Odell and G. J. Kirmeyer, Occurrence of nitrification in chloraminated distribution systems, J. - Am. Water Works Assoc., 1996, 88(7), 74–85.
22. F. Ling, R. Whitaker, M. W. LeChevallier and W.-T. Liu, Drinking water microbiome assembly induced by water stagnation, ISME J., 2018, 12(6), 1520–1531.
23. K. Lautenschlager, N. Boon, Y. Wang, T. Egli and F. Hammes, Overnight stagnation of drinking water in household taps induces microbial growth and changes in community composition, Water Res., 2010, 44(17), 4868–4877.
24. J. Bartram, J. A. Cotruvo, M. Exner, C. Fricker and A. Glasmacher, Heterotrophic plate counts and drinking-water safety, IWA publishing, 2003.
25. F. Hammes, F. Goldschmidt, M. Vital, Y. Wang and T. Egli, Measurement and interpretation of microbial adenosine tri-phosphate (ATP) in aquatic environments, Water Res., 2010, 44(13), 3915–3923.
26. K. Zhang, R. Pan, T. Zhang, J. Xu, X. Zhou and Y. Yang, A novel method: using an adenosine triphosphate (ATP) luminescence–based assay to rapidly assess the biological stability of drinking water, Appl. Microbiol. Biotechnol., 2019, 103(11), 4269–4277.
27. F. Hammes, M. Berney, Y. Wang, M. Vital, O. Köster and T. Egli, Flow-cytometric total bacterial cell counts as a descriptive microbiological parameter for drinking water treatment processes, Water Res., 2008, 42(1), 269–277.
28. E. I. Prest, D. G. Weissbrodt, F. Hammes, M. C. M. van Loosdrecht, J. S. Vrouwenvelder and R. Paranhos, Long-term bacterial dynamics in a full-scale drinking water distribution system, PLoS One, 2016, 11(10), e0164445.
29. M. J. Allen, S. C. Edberg and D. J. Reasoner, Heterotrophic plate count bacteria—what is their significance in drinking water?, Int. J. Food Microbiol., 2004, 92(3), 265–274.
30. S. Van Nevel, S. Koetzsch, C. R. Proctor, M. D. Besmer, E. I. Prest and J. S. Vrouwenvelder, et al. Flow cytometric bacterial cell counts challenge conventional heterotrophic plate counts for routine microbiological drinking water monitoring, Water Res., 2017, 113, 191–206.
31. D. van der Kooij, H. R. Veenendaal, C. Baars-Lorist, D. W. van der Klift and Y. C. Drost, Biofilm formation on surfaces of glass and Teflon exposed to treated water, Water Res., 1995, 29(7), 1655–1662.
32. A. Thore, S. Anséhn, A. Lundin and S. Bergman, Detection of bacteriuria by luciferase assay of adenosine triphosphate, J. Clin. Microbiol., 1975, 1(1), 1.
33. O. Holm-Hansen, Determination of microbial biomass in deep ocean profiles, Limnol. Oceanogr., 1969, 14(5), 740–747.
34. D. M. Karl, Cellular nucleotide measurements and applications in microbial ecology, Microbiol. Rev., 1980, 44(4), 739–796.
35. H. S. C. Eydal and K. Pedersen, Use of an ATP assay to determine viable microbial biomass in Fennoscandian Shield groundwater from depths of 3–1000 m, J. Microbiol. Methods, 2007, 70(2), 363–373.
36. P. W. J. J. van der Wielen, G. Bakker, A. Atsma, M. Lut, G. Roeselers and B. de Graaf, A survey of indicator parameters to monitor regrowth in unchlorinated drinking water, Environ. Sci.: Water Res. Technol., 2016, 2(4), 683–692.
37. E. I. Prest, F. Hammes, S. Kötzsch, M. C. M. van Loosdrecht and J. S. Vrouwenvelder, Monitoring microbiological changes in drinking water systems using a fast and reproducible flow cytometric method, Water Res., 2013, 47(19), 7131–7142.
38. E. Gatza, F. Hammes and E. Prest, Assessing water quality with the BD Accuri™ C6 flow cytometer, White paper BD Biosciences, 2013.
39. E. I. Prest, J. El-Chakhtoura, F. Hammes, P. E. Saikaly, M. C. M. van Loosdrecht and J. S. Vrouwenvelder, Combining flow cytometry and 16S rRNA gene pyrosequencing: A promising approach for drinking water monitoring and characterization, Water Res., 2014, 63 IS, 179–189.
40. S. E. Miller, R. A. Rodriguez and K. L. Nelson, Removal and growth of microorganisms across treatment and simulated distribution at a pilot-scale direct potable reuse facility, Environ. Sci.: Water Res. Technol., 2020, 107(11), 36.
41. K. Helmi, A. Watt, P. Jacob, I. Ben-Hadj-Salah, A. Henry and G. Méheut, et al., Monitoring of three drinking water treatment plants using flow cytometry, Water Sci. Technol.: Water Supply, 2014, 14(5), 850–856.
42. J. C. Crittenden, R. R. Trussell, D. W. Hand, K. J. Howe and G. Tchobanoglous, MWH's water treatment: principles and design, John Wiley & Sons, 2012.
43. R. Cheswick, E. Cartmell, S. Lee, A. Upton, P. Weir and G. Moore, et al., Comparing flow cytometry with culture-based methods for microbial monitoring and as a diagnostic tool for assessing drinking water treatment processes, Environ. Int., 2019, 130, 104893.
44. K. Lautenschlager, C. Hwang, W.-T. Liu, N. Boon, O. Köster and H. Vrouwenvelder, et al., A microbiology-based multi-parametric approach towards assessing biological stability in drinking water distribution networks, Water Res., 2013, 47(9), 3015–3025.
45. T. Liu, W. Kong, N. Chen, J. Zhu, J. Wang and X. He, et al., Bacterial characterization of Beijing drinking water by flow cytometry and MiSeq sequencing of the 16S rRNA gene, Ecol. Evol., 2016, 6(4), 923–934.
46. A. Pifer, D. Rindal, G. M. Lohse, M. C. Gibson, J. A. Starke and J. Springer, et al.2017 Water utility disinfection survey report, 2018.
47. R Core Team, R: A Language and Environment for Statistical Computing, Vienna, Austria, 2019.
48. F. E. Harrell Jr. , Hmisc: Harrell Miscellaneous, 2020.
49. B. Schloerke, J. Crowley, D. Cook, F. Briatte, M. Marbach and E. Thoen, et al.GGally: Extension to “ggplot2.”, 2018.
50. A. F. Zuur, E. N. Ieno and C. S. Elphick, A protocol for data exploration to avoid common statistical problems, Methods Ecol. Evol., 2009, 1(1), 3–14.
51. A. F. Zuur, J. Hilbe, E. N. Ieno, A. F. Zuur, J. M. Hilbe and E. N. Leno, A beginner's guide to glm and glmm with r: a frequentist and bayesian perspective for ecologists, 2013.
52. A. F. Zuur and E. N. Ieno, A protocol for conducting and presenting results of regression-type analyses, Methods Ecol. Evol., 2016, 7(6), 636–645.
53. J. A. Villaseñor and E. González-Estrada, A variance ratio test of fit for Gamma distributions, Stat. Probab. Lett., 2015, 96, 281–286.
54. E. González-Estrada and J. A. Villasenor-Alva, goft: Tests of fit for some probability distributions, 2017.
55. D. Bates, M. Maechler, B. Bolker and S. Walker, lme4: Linear mixed-effects models using 'Eigen' and S4, 2020.
56. K. Bartoń, MuMIn: multi-model inference, 2019.
57. H. Wickham, W. Chang, L. Henry, T. L. Pedersen, K. Takahashi and C. Wilke, et al.ggplot2: Create elegant data visualisations using the grammar of graphics, 2020.
58. M. Hlavac, stargazer: stargazer: Well-formatted regression and summary statistics tables, 2018.
59. W. Chang, extrafont: Tools for using fonts, 2014.
60. A. Kassambara, ggpubr: ggplot2 based publication ready plots, 2020.
61. S. Garnier, viridis: Default color maps from 'matplotlib.', 2018.
62. J. J. Vasconcelos, L. A. Rossman, W. M. Grayman, P. F. Boulos and R. M. Clark, Kinetics of chlorine decay, J. - Am. Water Works Assoc., 1997, 89(7), 54–65.
63. G. F. Reed, F. Lynn and B. D. Meade, Use of coefficient of variation in assessing variability of quantitative assays, Clin. Vaccine Immunol., 2002, 9(6), 1235.
64. W. Zhang and F. A. DiGiano, Comparison of bacterial regrowth in distribution systems using free chlorine and chloramine: a statistical study of causative factors, Water Res., 2002, 36(6), 1469–1482.
65. M. W. LeChevallier, Conditions favouring coliform and HPC bacterial growth in drinking, in Heterotrophic Plate Counts and Drinking-water Safety: The Significance of HPCs for Water Quality and Human Health, World Health Organization, 2003, p. 177.
66. E. Siebel, Y. Wang, T. Egli and F. Hammes, Correlations between total cell concentration, total adenosine tri-phosphate concentration and heterotrophic plate counts during microbial monitoring of drinking water, Drinking Water Eng. Sci., 2008, 1(1), 1–6.
67. M. Berney, F. Hammes, F. Bosshard, H.-U. Weilenmann and T. Egli, Assessment and interpretation of bacterial viability by using the LIVE/DEAD BacLight Kit in combination with flow cytometry, Appl. Environ. Microbiol., 2007, 73(10), 3283–3290.
68. P. Foladori, L. Bruni, S. Tamburini, V. Menapace and G. Ziglio, Surrogate parameters for the rapid microbial monitoring in a civil protection module used for drinking water production, Chem. Eng. J., 2015, 265, 67–74.
69. F. Hammes, M. Berney, Y. Wang, M. Vital, O. Köster and T. Egli, Flow-cytometric total bacterial cell counts as a descriptive microbiological parameter for drinking water treatment processes, Water Res., 2008, 42(1), 269–277.
70. F. Hammes, C. Berger, O. Köster and T. Egli, Assessing biological stability of drinking water without disinfectant residuals in a full-scale water supply system, J. Water Supply: Res. Technol.--AQUA, 2010, 59(1), 31–40.
71. D. Van Der Kooij, Biological stability: A multidimensional quality aspect of treated water, Water, Air, Soil Pollut., 2000, 123(1), 25–34.
72. E. I. Prest, F. Hammes, M. C. M. van Loosdrecht and J. S. Vrouwenvelder, Biological stability of drinking water: controlling factors, methods, and challenges, Front. Microbiol., 2016, 7(41), 133.
73. B. E. Rittmann and V. L. Snoeyink, Achieving biologically stable drinking water, J. - Am. Water Works Assoc., 1984, 76(10), 106–114.
74. M. D. Besmer, F. Hammes, J. A. Sigrist and C. Ort, Evaluating monitoring strategies to detect precipitation-induced microbial contamination events in karstic springs used for drinking water, Front. Microbiol., 2017, 8, 81.
75. M. D. Besmer, J. A. Sigrist, R. Props, B. Buysschaert, G. Mao and N. Boon, et al., Laboratory-Scale Simulation and Real-Time Tracking of a Microbial Contamination Event and Subsequent Shock-Chlorination in Drinking Water, Front. Microbiol., 2017, 8, 366.
76. H. R. Safford and H. N. Bischel, Flow cytometry applications in water treatment, distribution, and reuse: A review, Water Res., 2019, 151, 110–133.
77. A. Bruno, A. Sandionigi, M. Bernasconi, A. Panio, M. Labra and M. Casiraghi, Changes in the Drinking Water Microbiome: Effects of Water Treatments Along the Flow of Two Drinking Water Treatment Plants in a Urbanized Area, Milan (Italy), Front. Microbiol., 2018, 9, 631.
78. N. M. Hull, E. P. Holinger, K. A. Ross, C. E. Robertson, J. K. Harris and M. J. Stevens, et al. Longitudinal and Source-to-Tap New Orleans, LA, U.S.A. Drinking Water Microbiology, Environ. Sci. Technol., 2017, 51(8), 4220–4229.
79. M. B. Waak, R. M. Hozalski, C. Hallé and T. M. LaPara, Comparison of the microbiomes of two drinking water distribution systems-with and without residual chloramine disinfection, Microbiome, 2019, 7(1), 87.
80. J. B. Emerson, R. I. Adams, C. M. B. Román, B. Brooks, D. A. Coil and K. Dahlhausen, et al., Schrödinger's microbes: Tools for distinguishing the living from the dead in microbial ecosystems, Microbiome, 2017, 5(1), 86.
81. R. Props, F.-M. Kerckhof, P. Rubbens, J. De Vrieze, E. Hernandez Sanabria and W. Waegeman, et al. Absolute quantification of microbial taxon abundances, ISME J., 2017, 11(2), 584–587.
82. R. Brankatschk, N. Bodenhausen, J. Zeyer and H. Bürgmann, Simple Absolute Quantification Method Correcting for Quantitative PCR Efficiency Variations for Microbial Community Samples, Appl. Environ. Microbiol., 2012, 78(12), 4481–4489.
83. C. J. Smith and A. M. Osborn, Advantages and limitations of quantitative PCR (Q-PCR)-based approaches in microbial ecology, FEMS Microbiol. Ecol., 2009, 67(1), 6–20.
84. V. F. Wintzingerode, U. B. Göbel and E. Stackebrandt, Determination of microbial diversity in environmental samples: pitfalls of PCR-based rRNA analysis, FEMS Microbiol. Rev., 1997, 21(3), 213–229.
85. R. S. Kantor, S. E. Miller and K. L. Nelson, The water microbiome through a pilot scale advanced treatment facility for direct potable reuse, Front. Microbiol., 2019, 10, 21.
86. S. H. Lee, J. T. O'Connor and S. K. Banerji, Biologically mediated corrosion and its effects on water quality in distribution systems, J. - Am. Water Works Assoc., 1980, 72(11), 636–645.
87. I. B. Beech and J. Sunner, Biocorrosion: towards understanding interactions between biofilms and metals, Curr. Opin. Biotechnol., 2004, 15(3), 181–186.
88. P. W. J. J. van der Wielen, S. Voost and D. van der Kooij, Ammonia-oxidizing bacteria and archaea in groundwater treatment and drinking water distribution systems, Appl. Environ. Microbiol., 2009, 75(14), 4687.
89. J. M. Regan, G. W. Harrington, H. Baribeau, R. D. Leon and D. R. Noguera, Diversity of nitrifying bacteria in full-scale chloraminated distribution systems, Water Res., 2003, 37(1), 197–205.
90. J. C. Block, K. Haudidier, J. L. Paquin, J. Miazga and Y. Levi, Biofilm accumulation in drinking water distribution systems, Biofouling, 1993, 6(4), 333–343.
91. H. Zipper, H. Brunner, J. Bernhagen and F. Vitzthum, Investigations on DNA intercalation and surface binding by SYBR Green I, its structure determination and methodological implications, Nucleic Acids Res., 2004, 32(12), e103.
92. H. R. Safford and H. N. Bischel, Flow cytometry applications in water treatment, distribution, and reuse: A review, Water Res., 2019, 151, 110–133.
93. R. Fabris, K. Braun, L. Ho, J. Q. J. C. Verberk and M. Drikas, Bacteriological water quality changes in parallel pilot distribution systems, Water Sci. Technol.: Water Supply, 2016, 16(6), 1710–1720.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ew00809e

---