Three calibration techniques combined with sample-effective design of experiment based on Latin hypercube sampling for direct detection of lanthanides in REE-rich ores using TXRF and WDXRF
Timur F.
Akhmetzhanov
a,
Galina V.
Pashkova
*b,
Victor M.
Chubarov
 c,
Timur A.
Labutin
c,
Timur A.
Labutin
 a and
Andrey M.
Popov
a and
Andrey M.
Popov
 *a
*a
aDepartment of Chemistry, Lomonosov Moscow State University, 119234, Leninskie Gory, 1-3, Moscow, Russia. E-mail: popov@laser.chem.msu.ru
bInstitute of the Earth's Crust, SB RAS, Lermontov St., 128, Irkutsk, 664033, Russia. E-mail: pashkova.gv@yandex.ru
cVinogradov Institute of Geochemistry, SB RAS, Favorsky St., 1A, Irkutsk, 664033, Russia
First published on 26th November 2020
Abstract
This study concerns the simultaneous detection of five rare-earth elements (REEs) – Ce, La, Nd, Pr, Sm – in ores and nodules using two X-ray fluorescence techniques (XRF): total reflection (TXRF) and wavelength-dispersive (WDXRF). The issues of high pairwise correlation between REE contents in certified reference materials of natural origin, resulting in a poor quality of calibration sample set, and the significant overlapping of REE lines, especially in TXRF spectra, which have low spectral resolution, are addressed in the study. For the first time, this is done by employing a specially designed calibration set, based on Latin hypercube sampling. Its applicability was assessed for univariate and multivariate (PCR, PLS) calibration models to overcome the above issues. A feature of our calibration set is the use of artificial mixtures of REE oxides and Fe2O3 + TiO2 (as a matrix) providing extremely low correlation (<0.03) between the content of different REEs. Simultaneously, the validation set consists of natural certified reference materials of REE-rich ores and oceanic ferromanganese nodules. The content of each REE in the calibration set varies in the range of 0–40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm. Our PLS/PCR-based calibration models provide a quantitative determination of Ce, La, and Nd content using both XRF techniques. Pr and Sm were special cases, which cannot be quantitatively determined using univariate calibration, while our multivariate models were able to detect these REEs at a level above 100 ppm.
000 ppm. Our PLS/PCR-based calibration models provide a quantitative determination of Ce, La, and Nd content using both XRF techniques. Pr and Sm were special cases, which cannot be quantitatively determined using univariate calibration, while our multivariate models were able to detect these REEs at a level above 100 ppm.
Introduction
Ultrapure rare earth element (REE) compounds are used in many branches of technology as components in high-tech devices, catalysts, magnets, batteries, steel alloys and others.1 The determination of REE concentration is essential for geochemical exploration studies, mining, and for on-line and laboratory control in industry.2,3 The “working horse” for REE analysis is inductively coupled plasma mass spectrometry (ICP-MS), which provides extremely high sensitivity in a wide range of applications.4,5 Optical emission spectrometry with inductively coupled plasma (ICP-OES)6,7 or microwave plasma (MP-AES)8 is a feasible alternative for ICP-MS because it provides adequate sensitivity in some applications. The abovementioned techniques require acid digestion or preliminary matrix separation and pre-concentration, and cannot, therefore, be used for rapid analysis outside the laboratory. Instrumental neutron activation analysis (INAA)9 can be used a sensitive direct technique for determining REE content in geological materials serving, thus, as a reliable reference analytical technique, but it is a time-consuming technique that requires a nuclear reactor.At the same time, laser-induced breakdown spectrometry (LIBS) and X-ray fluorescence (XRF) spectrometry can also provide direct, rapid determination of REE content in solids with minimal pre-treatment. LIBS was mainly used to determine REEs in solutions10,11 or in artificial samples with relatively simple matrices12 due to significant spectral interferences. Only light REEs (e.g. La, Y) were detected in geological materials using LIBS.13–15 Generally, XRF spectra of REEs are less complicated than optical ones, making XRF more suitable for analyzing a mixture of REEs. Wavelength-dispersive XRF (WDXRF) provides high resolution that allows for the simultaneous quantification of REEs. However, WDXRF spectrometers are more expensive than energy-dispersive XRF (EDXRF) ones and are hardly adaptable to field applications.16 Different configurations of handheld and benchtop EDXRF spectrometers, including total reflection XRF (TXRF) spectrometers, are currently available. Although portable EDXRF instruments have revolutionized the practice of geochemical exploration,17,18 their low sensitivity, strong matrix effects, and mutual spectral interferences still complicate obtaining quantitative results.19–25 Reducing these effects seems to be of vital importance for EDXRF to provide accurate and precise REE content.26
Multivariate calibration is widely used to improve accuracy, especially for overlapping signals.27 The most common chemometric techniques for multivariate data processing are Partial Least Squares Regression (PLSR) and Principal Component Regression (PCR). These techniques are versatile tools to overcome spectral interferences28–31 and distinguish samples by matrixes through Principal component analysis (PCA).32,33 A crucial part of chemometric data analysis is data pre-processing, the aim of which is to remove unwanted variations (such as instrumental artifacts) and thereby focus on the variation of interest.34 Common ways to prepare data for carrying out multivariate algorithms include baseline correction, scatter correction, noise removal, mean-centering, and scaling.
Another problem is that the typical calibration set, consisting of certified standards of ores, used in XRF techniques for determining REE has strong correlations between the content of different REEs. Thus, implementing the design of experiment (DoE) concept is helpful in order to build a good regression model which will yield accurate predictions by avoiding correlations between the REE contents of the new calibration set. The design can implement the expected variation of the REE content within the range where good prediction is important for a particular application.35 A full factorial design36 uses levels to the power of factors and, as a result, covers the whole hyperspace, and finds all possible relations between the factors and the levels. For example, 205 experiments are needed to uniformly fill the hyperspace for 20 concentrations (levels) for 5 elements (factors). This huge number of experiments obviously exceeds the set needed for a stable PLS/PCR predictive model. A fractional factorial design is aimed at excluding a large part of the possible combinations.37 An orthogonal matrix design can exclude all correlations between the element concentrations.38 This design is, however, best suited for a small concentration range due to quadratic growth of the calibration set dimension as the number of levels increases. By applying the orthogonal matrix design to the above example, only 52 = 25 samples are needed for a 5th level design, while 202 = 400 samples are required for 20 levels, which corresponds the range of several orders of magnitude needed for reliable calibration. Shulyumova et al.39 have applied Brereton's DoE to determine the concentration of Cd, Co, Hg, As, Pb, and Ni in solutions in a range of 0–2 mg L−1 using TXRF with multivariate calibration. Kirsanov et al.40 have applied an alternative DoE,41 based on the uniform distribution of experimental points in a multidimensional space, to analyze lanthanides in aqueous solutions using TXRF. This DoE uses a simple iterative algorithm for calculation and is not computationally demanding. However, a serious drawback of the approach is high pairwise correlation (up to 0.2), which adds uncertainty to the model of multivariate calibration and reduces its stability. Generally, space-filling designs, used in computer simulation experiments, spread the points uniformly throughout the region of experimentation, and do not contain any duplicates.37 These features would also be useful in the preparation of a calibration set of samples. Latin hypercube sampling (LHS), first proposed by McKay et al.,42 can be constructed with low correlation of both first-order and second-order terms for a large number of factors.43
The goal of this study is to overcome the problems of the quantitative determination of REEs using different variants of XRF, i.e. EDXRF (specifically TXRF) and WDXRF, using multivariate calibration with a specially designed and prepared calibration set of solid samples based on LHS. As a result, our DoE and the preparation of our calibration set with very low correlation between REE content improve the accuracy of determining the REE content in ores using XRF. This would allow cheaper, but at the same time sensitive and accurate, direct analysis of five REEs (Ce, La, Nd, Pr, Sm) using TXRF. Additionally, we would like to reduce the number of samples in the calibration set for WDXRF, covering a range of three orders of magnitude with the use of a sample-effective DoE.
Materials and methods
Calibration set
Powders of CeO2 (99.95%), La2O3 (99.99%), Nd2O3 (99.99%), Sm2O3 (99.9%), and Pr6O11 (99.9%) purchased from Sigma Aldrich (Germany) were carefully mixed in different ratios to produce a set of samples corresponding to our DoE (see description in section “Design of experiment”). Oxide powders of Fe2O3 (chemical grade) and TiO2 (chemical grade) produced by Reachem (Russia) roughly simulated the same matrix as found in a validation set of samples with concentrations of 62–67 wt% and 1.8 wt% in mixture, respectively. The content of REEs in the calibration set are given in Table 1.| No. mixture | Ce | La | Nd | Pr | Sm |
|---|---|---|---|---|---|
| 1 | 3.37 | 0.99 | 0.07 | 0.27 | 0.23 |
| 2 | 1.06 | 0.71 | 0.35 | 0.32 | 0.17 |
| 3 | 0 | 2.11 | 1.19 | 0.21 | 0.34 |
| 4 | 1.27 | 1.41 | 0.42 | 0.25 | 0.04 |
| 5 | 0.22 | 0 | 0.63 | 0.09 | 0.38 |
| 6 | 2.95 | 0.57 | 1.05 | 0.30 | 0.25 |
| 7 | 2.32 | 2.67 | 0.98 | 0.11 | 0.21 |
| 8 | 2.74 | 2.53 | 0.49 | 0.17 | 0.06 |
| 9 | 1.48 | 1.83 | 0.91 | 0.13 | 0.02 |
| 10 | 3.58 | 2.25 | 0.56 | 0.15 | 0.36 |
| 11 | 2.53 | 1.97 | 0.28 | 0.38 | 0.27 |
| 12 | 3.16 | 0.85 | 1.26 | 0.04 | 0 |
| 13 | 0.43 | 1.55 | 0.14 | 0 | 0.13 |
| 14 | 0.85 | 2.39 | 0.70 | 0.40 | 0.11 |
| 15 | 4.00 | 0.29 | 1.12 | 0.34 | 0.09 |
| 16 | 2.11 | 1.27 | 0.21 | 0.23 | 0.30 |
| 17 | 1.90 | 0.43 | 0 | 0.19 | 0.19 |
| 18 | 3.79 | 1.69 | 0.84 | 0.02 | 0.40 |
| 19 | 1.69 | 0.15 | 0.77 | 0.06 | 0.15 |
| 20 | 0.64 | 1.13 | 1.33 | 0.36 | 0.32 |
Validation set
The certified reference materials (CRMs) of carbonatite Supergene REE-Nb ore (OREAS 460–465) and U ore (OREAS 100a, 101a, 101b, 102a) produced by Ore Research & Exploration Pty Ltd (Australia) were used as a validation set. For several REEs (see below), the validation set was expanded with ferromanganese nodules CRM 408-10 (GMK-1, GMK-2), OOPE601, OOPE602, OOPE603, ore crust OOPE604, and cobalt-bearing ferromanganese crusts CRM 409-10 (KMK-1 and KMK-2) developed by Fedorovsky All-Russian Scientific Research Institute of Mineral Raw Materials, Institute of Applied Physics of Irkutsk State University and P. P. Shirshov Institute of Oceanology of RAS. The content of REEs in the validation set of CRMs are given in Table 2. Note that the certified content of titanium and iron in CRMs were 0.2–6.3 wt% and 4.6–37 wt%, respectively.| Standards | Ce | La | Nd | Pr | Sm |
|---|---|---|---|---|---|
| Niobium ores | |||||
| OREAS 460 | 1830 ± 10 | 1330 ± 10 | 800 ± 30 | 240 ± 10 | 104 ± 5 |
| OREAS 461 | 3510 ± 10 | 2590 ± 10 | 1630 ± 40 | 480 ± 30 | 214 ± 8 |
| OREAS 462 | 4950 ± 100 | 3790 ± 30 | 2560 ± 70 | 740 ± 20 | 369 ± 5 |
| OREAS 463 | 6590 ± 70 | 4966 ± 69 | 3610 ± 70 | 1000 ± 20 | 538 ± 4 |
| OREAS 464 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 ± 300 300 ± 300 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 ± 100 700 ± 100 |
9940 ± 160 | 2600 ± 60 | 1500 ± 20 |
| OREAS 465 | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 ± 800 500 ± 800 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 ± 500 100 ± 500 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 ± 300 800 ± 300 |
3800 ± 100 | 1360 ± 20 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Uranium ores | |||||
| OREAS 100a | 460 ± 20 | 260 ± 10 | 152 ± 8 | 47 ± 2 | 24 ± 0.4 |
| OREAS 101a | 1400 ± 90 | 820 ± 30 | 400 ± 20 | 134 ± 7 | 49 ± 1 |
| OREAS 101b | 1330 ± 70 | 750 ± 30 | 390 ± 20 | 127 ± 6 | 48 ± 3 |
| OREAS 102a | 590 ± 30 | 320 ± 10 | 180 ± 9 | 58 ± 3 | 25 ± 0.7 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Ferromanganese nodules and crusts | |||||
| OOPE 601 | 500 ± 200 | 150 ± 40 | 150 ± 40 | 40 | 40 ± 10 |
| OOPE 602 | 200 ± 50 | 90 ± 20 | 80 ± 30 | 33 | 22 ± 7 |
| OOPE 603 | 900 ± 200 | 140 ± 40 | 140 ± 40 | 30 | 30 ± 10 |
| OOPE 604 | 1000 ± 300 | 120 ± 30 | 100 ± 30 | 41 | 27 ± 8 |
| KMK-1 | 1120 ± 100 | 320 ± 40 | 260 ± 30 | 61 ± 6 | 50 ± 3 |
| KMK-2 | 720 ± 70 | 270 ± 30 | 190 ± 20 | 46 ± 4 | 36 ± 2 |
| GMK-1 | 360 ± 40 | 100 ± 10 | 140 ± 10 | 35 ± 4 | 34 ± 3 |
| GMK-2 | 390 ± 50 | 100 ± 10 | 140 ± 10 | 34 ± 4 | 34 ± 3 |
Sample preparation
Preparing a suspension is a common way to evaluate solid samples during TXRF analysis.44,45 20 mg of material was placed in an agate mortar and, then, several drops of ethanol and 100 μL of Ga(NO3)3 (1 g L−1, CertiPUR®, Merck) were added to the powder. After grinding the mixture, a few more drops of ethanol were used to wash residues off from the pestle. Then, 5 mL of 1% non-ionic surfactant Triton X-100 solution (reagent grade, Amresco) was added to the mortar. The particulates, stuck to the walls of the mortar, were carefully scraped off and mixed. An aliquot of 10 μL of the prepared mixture was pipetted onto a quartz carrier and dried at room temperature. For WDXRF measurements, about 1 g of the sample powder was pressed with 100 kN of force to obtain a 40 mm diameter pellet. Analytical grade crystalline boric acid was used as a binder. All CRMs were preliminarily dried for 2 hours to remove hygroscopic moisture before pressing.Equipment
TXRF spectra were obtained using a S2 PICOFOX spectrometer (Bruker Nano GmbH, Germany) equipped with a micro-focus X-ray tube (Mo-anode and air-cooling), multilayer monochromator (Ni/C), and Si drift detector (SDD) XFlash® (area 30 mm2 and 150 eV resolution for Mn Kα line). Operating voltage and current were 50 kV and 500 μA for 500 s per sample, respectively. The X-ray spectra were treated using the manufacturer software SPECTRA 6 with the Bayesian deconvolution thoroughly described by Sievers et al.46 The analyte content, Ci, can be described using the ratio: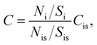 | (1) |
The WDXRF spectra were obtained using a S8 Tiger spectrometer (Bruker AXS, Germany, 60 kV, 40 mA) under the conditions specified in Table 3 for analytical lines including the most significant spectral overlaps. The total measurement time was about 11 minutes per sample. Although the K-series lines of REEs can be used for quantitative analysis, observation of these lines requires irradiating the samples using a synchrotron source.47 Conventional WDXRF spectrometers equipped with Rh-anode X-ray tube do not allow accurate measurement of the lines due to high background intensity (bremsstrahlung) and poor excitation. The most intense spectral lines from the L-series (Lα and Lβ) were chosen as analytical ones. Spectral overlapping with other L-series lines (Ll, Lγ) was considered to be negligible. Different crystals (see Table 3) provided a compromise between achieving the highest intensity, the highest spectral resolution, and the spectral region, in which there was no analytical signal to measure background. The collimator provided maximal intensity at 0.23° excluding spectral interferences. The scintillation detector, made it possible to record spectra at wavelengths less than 2.4 Å, while longer wavelength spectra were obtained using a gas-flow proportional counter with an argon–methane mixture. The software SPECTRAPLUS, which is integrated in the WDXRF spectrometer, was used to build the univariate calibration. The content of the analyte, Ci, when not correcting for matrix effects, is linearly proportional to the measured intensity of the ith-analyte, Ii:
| Ci = a0 + a1 × Ii | (2) |
| a SC indicates that a scintillation detector was used, FC indicates the same for a gas-flow proportional counter. | |||||
|---|---|---|---|---|---|
| Line | La Lα1 | Ce Lα1 | Pr Lα1 | Nd Lα1 | Sm Lα1 |
| Wavelength, Å | 2.6673 | 2.5621 | 2.4634 | 2.3710 | 2.2002 |
| Crystal | LiF 200 | LiF 200 | LiF 200 | LiF 200 | LiF 220 |
| Detectora | FC | FC | FC | SC | SC |
| Peak position (2θ), ° | 82.917 | 79.036 | 75.419 | 72.154 | 101.144 |
| Background position (2θ), ° | 84.500 | 80.873 | 74.293 | 74.000 | 100.137 |
| Overlaps | La Lβ1 | Ce Lβ1 | Ce Lβ2 | ||
| Exposition, s | 10 | 10 | 30 | 10 | 50 |
The fundamental parameters (FP)16,19,48 method is used to correct for matrix effects (this is the option “variable alphas” of the spectrometer software)49 using the equation:
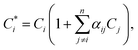 | (3) |
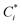 , Cj, and αij are the corrected content of i-th-analyte, the content of the j-th-element of the matrix, and the matrix effect correction coefficients, respectively. Spectral overlapping is considered to be:
, Cj, and αij are the corrected content of i-th-analyte, the content of the j-th-element of the matrix, and the matrix effect correction coefficients, respectively. Spectral overlapping is considered to be: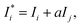 | (4) |
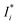 , Ij, and a are the corrected intensity of the i-th-analyte, the intensity of the interfering j-th-component, and an empirical coefficient, respectively. Our calculations of the relative standard deviation (RSD) values as a ratio of root mean square values obtained with the use of the FP method and without matrix correction show that the correction decreases the RSD values in general, and in some cases up to 5 fold. This notwithstanding, the FP method can cause biases in the αij values in the calibration set, giving inaccurate results when analyzing the real samples, because they contain many other elements as well as lanthanides. To avoid these biases, we used eqn (2) without correcting for matrix effects as the univariate calibration model.
, Ij, and a are the corrected intensity of the i-th-analyte, the intensity of the interfering j-th-component, and an empirical coefficient, respectively. Our calculations of the relative standard deviation (RSD) values as a ratio of root mean square values obtained with the use of the FP method and without matrix correction show that the correction decreases the RSD values in general, and in some cases up to 5 fold. This notwithstanding, the FP method can cause biases in the αij values in the calibration set, giving inaccurate results when analyzing the real samples, because they contain many other elements as well as lanthanides. To avoid these biases, we used eqn (2) without correcting for matrix effects as the univariate calibration model.
Multivariate regression
We have built two multivariate calibration models based on partial least squares (PLS) and principal component regression (PCR) to predict the content of REEs in a sample. For this purpose, we developed an algorithm, thoroughly described elsewhere,50–52 using the OjAlgo library for matrix operations in Java.53 We omit the description of both algorithms as they are well established and described in a large number of papers (see, for example, the book by Pomerantsev52). The main difference between PCR and PLS is that the former uses only spectral intensities, while the latter projects the predicted variables (content) and the signals to a new space. The number of principal components (PCs) included in PCR is chosen, judging by the value of R2 from the prediction plot and the root-mean square error of calibration (RMSEc), such that a robust calibration model can be constructed. The root-mean square error of the prediction (RMSEp) was used as a measure to validate the model. Since the range of REE content exceeds three orders of magnitude, prediction plots can provide a general understanding of the quality of the model.40 The baseline was corrected to decrease false correlations that PLS/PCR might find. However, we did not use scaling in order to preserve the nature of the low noise signal, which aids in avoiding possible false correlations.34,52Design of experiment
We used a DoE based on LHS, thoroughly described by McKay et al.,42 in order to avoid false correlations between the signals of different elements. This design, where the experimental hyperspace was filled uniformly with points, is suitable for completing an accurate PLS/PCR analysis while avoiding the dramatic growth of the number of samples as the number of both levels and needed factors increases.38 We used the Matlab™ software to create a matrix containing 5 factors (elements) and 20 levels (contents) with a maximum pairwise correlation of 0.03. Our correlation limit (0.03) was almost an order of magnitude better than those for DoE proposed by Kirsanov et al.40 The content range of every analyte in our DoE (see Table 1) completely covers those for ores (see Table 2) and seems to be suitable for analytical practice.There are different physical effects that influence the accuracy of WDXRF and TXRF. In the former case, such effects like absorption and secondary fluorescence are dominant. For the latter, however, these effects are negligible assuming infinitely thin samples, but in TXRF overlapping between strong lines arises because of the low-resolution of the detector, as can be seen by comparing the WDXRF and TXRF spectra shown in Fig. 1. If a correlation of elemental content in CRMs is observed (this is typical for REEs in ores, see Table 2), the accuracy of the determined REE content using either XRF technique with univariate calibration using certified standards of ores will worsen dramatically. Therefore, preparing the calibration set with very low correlation between the content of different REEs could improve the accuracy, irrespective of whether there is a strong correlation between them in the analyzed set. Our DoE makes it possible to prepare a virtually uncorrelated set of calibration samples avoiding, therefore, influence from any dominant physical effects.
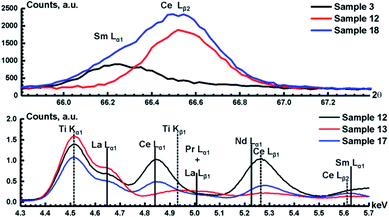 | ||
| Fig. 1 WDXRF (top) and TXRF (bottom) spectra of mixtures from the calibration set. Solid and dotted lines correspond to the peak positions of analytical lines and interfering lines, respectively. | ||
Results and discussions
X-ray fluorescence spectra
Raw TXRF spectra of the calibration set are shown in Fig. 1. All lines of REEs are in the range of 4.75–5.70 keV, and they are listed in Table 4 along with possible interfering lines. We did not use the Lα1 line of La, which overlaps with the Kα1 line of Ti, due to a strong correlation between the elements (0.45), since Ti content was constant in the calibration set (see section “Calibration set”). Instead of the La Lα1 line, we used a combination of several La lines (Lβ1–3) that influence the shape of the spectrum in a wide spectral range (5.00–5.50 keV). Since the position of the analytical line of each REE is known, we have split the observed spectral range into several parts containing as few peaks of other elements as possible to avoid false correlation. Thus, only two things can result in a false correlation. Firstly, LHS does not produce a completely orthogonal matrix, which can lead to correlations in the DoE. Secondly, there may be a correlation of the REE content with the signals of elements that are not included in the DoE: namely, either the Ti Kα1 line, or an “escape-peak” of the strong Fe Kα1 line or even its low-energy wing. Before building calibration models, the TXRF spectra were normalized to the intensity of Ga peak (internal standard).| Analytical line | Interfering lines | Ranges, keV | ||
|---|---|---|---|---|
| Ce | TXRF | L α1 | Ti Kβ1 | 4.75–4.94 |
| WDXRF | L α1 | — | 4.786–4.883 | |
| La | TXRF | L β1–3 | Pr Lα1, Nd Lα1, Ce Lβ1 | 5.00–5.50 |
| WDXRF | L α1 | — | 4.593–4.690 | |
| Nd | TXRF | L α1 | Ce Lβ1 | 5.17–5.50 |
| WDXRF | L α1 | Ce Lβ1 | 5.173–5.320 | |
| Pr | TXRF | L α1 | La Lβ1 | 5.00–5.13 |
| WDXRF | L α1 | La Lβ1 | 4.977–5.093 | |
| Sm | TXRF | L α1 | Nd Lβ1, Ce Lβ2 | 5.50–5.70 |
| WDXRF | L α1 | Ce Lβ2 | 5.538–5.670 | |
Raw WDXRF spectra of several mixtures from the calibration set are shown in Fig. 1. In this case, the influence of the Fe/Ti Kα1 lines on analytical lines is negligible due to the high spectral resolution. We can note several features of the WDXRF spectra. Unlike in TXRF spectra, there is no strong iron “escape-peak”, nor is there overlap between the Ce and La Lα1 lines. However, there are strong spectral interferences observed for several analytical lines (Table 4). For example, the Sm Lα1 line strongly overlaps the weak Ce Lβ2 line (top part of Fig. 1); these two peaks can, however, be separated using an appropriate deconvolution procedure. We have split the measured spectra into the several narrow ranges similar to the TXRF spectra, and, then, background corrections for all calibration models using PLS/PCR was performed.
Univariate and multivariate calibration in TXRF
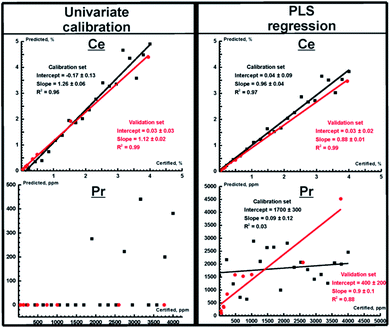
To build a robust calibration model for the prediction of REE content in ores, we chose the optimal number of PCs, defined as the number resulting in the smallest value of RMSEc/RMSEp. In the first step, we analyzed the decay rate of RMSEc taking into account that the number of PCs cannot exceed the number of overlapping lines. The last assumption seems to be physically reasonable because the calibration set has a pre-defined number of constituents. For example, four PCs were selected in this step for La since four lines overlapped in this case (see Table 4). In the second step, the number of PCs, chosen in the previous step, was tested using the validation set. If the values of RMSEp were close for several numbers of PCs, we validated the model with the smaller number of PCs to avoid overfitting (see Table 5). A similar procedure was implemented for the PCR calibration models.| REE | Sample type | Univariatea | PLSa | PCRa | ||||
|---|---|---|---|---|---|---|---|---|
| RMSEp | PCs | RMSEc | RMSEp | PCs | RMSEc | RMSEp | ||
| a Data obtained from TXRF and WDXRF spectra are separated by a slash in the format (TXRF)/(WDXRF). | ||||||||
| Ce | Ores | 1963/1610 | 2/1 | 2183/820 | 1549/712 | 3/1 | 2166/820 | 1313/712 |
| Nodules | —/633 | —/113 | —/173 | |||||
| La | Ores | 2230/1191 | 4/1 | 2759/711 | 885/634 | 4/1 | 2597/711 | 593/634 |
| Nodules | —/63 | —/37 | —/37 | |||||
| Nd | Ores | 1863/934 | 2/3 | 1518/485 | 215/273 | 3/3 | 1360/291 | 588/580 |
| Nodules | —/120 | —/13 | —/16 | |||||
| Pr | Ores | —/661 | 2/3 | 1070/217 | 593/79 | 2/3 | 1001/158 | 671/134 |
| Nodules | —/— | —/13 | —/14 | |||||
| Sm | Ores | —/160 | 3/3 | 1016/267 | 227/64 | 3/3 | 1008/186 | 220/41 |
| Nodules | —/— | —/24 | —/25 | |||||
The prediction plots obtained using univariate and PLS regressions for TXRF measurements are shown in Fig. 2 for Ce and Pr. We selected them to represent the two most extreme cases, i.e. the best prediction plot (Ce) and the worst plot (Pr). The parameters of the prediction plots are given in Table 5 for all REEs. As one can see, the PLS regression and PCR demonstrate similar performance, which is significantly higher than the performance of the univariate calibration integrated into the TXRF spectrometer software (eqn (1)). In particular, in contrast to univariate calibration, multivariate calibration provides a significant enhancement of measurement accuracy (RMSEp decreases by almost 2.5 and 9 times for La and Nd, respectively), making quantitative determination of the content of Pr and Sm possible. It should be noted that univariate regression works better for intense lines without strong interferences like Ce Lα1. For these lines, the superiority of multivariate calibration is not as evident. But even in the best case of Ce, the slope of the prediction plot (compare Fig. 2, top left) clearly demonstrates that the univariate model gives wrong results. The point scattering in the PLS prediction plot (Fig. 2, top right) may be caused by the negative impact of the heterogeneity of our suspensions on the TXRF measurements (see sections “Calibration set” and “Validation set”) and high background level. Thus, we can conclude that a chemometric approach can be considered to be a reliable way to improve the accuracy of EDXRF and TXRF analysis.
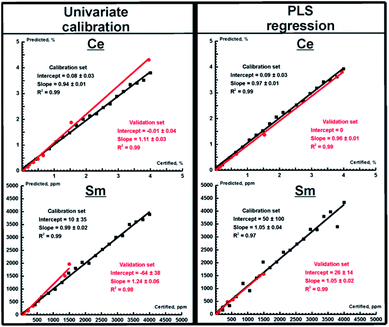
Univariate and multivariate calibration in WDXRF
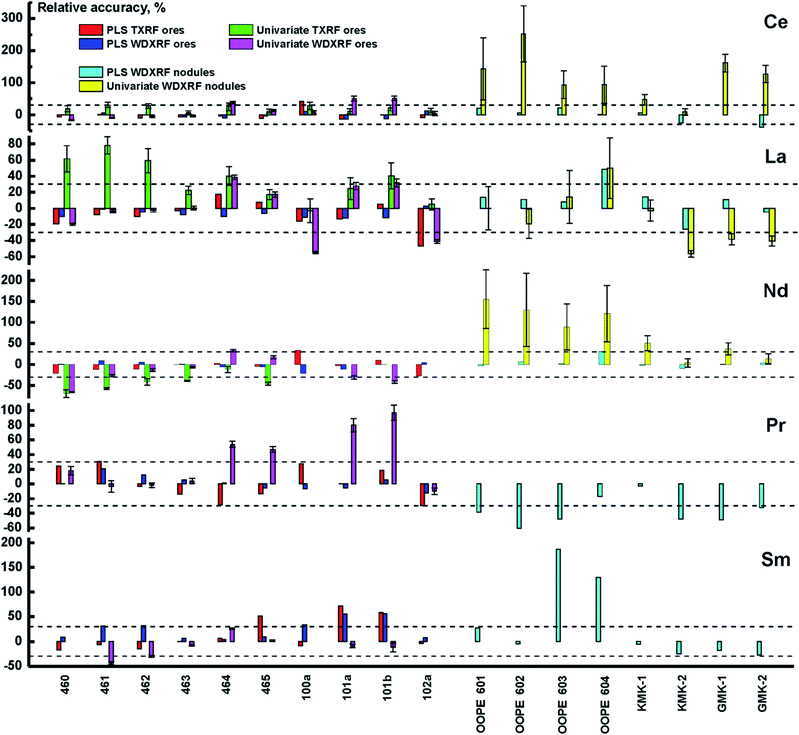
As one can expect, WDXRF provides much more accurate results for determining the REE content both in ores and in nodules (see Table 5, values after a slash) because of its high spectral resolution. Both PLS and PCR provided more accurate results for all REEs (as evidenced by lower values of RMSEp) than the univariate calibration, and the best (Ce) and the worst (Sm) prediction plots obtained using WDXRF are shown in Fig. 3. Determining the concentrations of Pr and Sm are of special interest, since this cannot be done using TXRF with univariate regression, while it is evident that the multivariate calibration models for WDXRF are reliable even for these worst cases. It should be noted, here, that a LiF 220 crystal was used for univariate calibration to eliminate spectral interferences, while a LiF 200 crystal was used for the PLS/PCR models. The latter crystal has a lower resolution power, but this feature makes WDXRF more sensitive in detecting weak lines. Thus, we were able to determine low concentrations for Sm, Pr, and Nd (10–100 ppm). The concentrations of the investigated REEs determined using all calibration strategies for OREAS ores (OREAS 100a-102b, 460–465) are compared to certified concentrations in Fig. 4. To clearly represent the advantages of multivariate models in terms of accuracy, the relative accuracy (%) was calculated as follows:| relative accuracy = 100 × (Cpredicted − Creference)/Creference, | (5) |
Another analytical feature of WDXRF is the possibility to quantitatively determine the REE content in ferromanganese nodules. Their TXRF spectra are, expectedly, rich in Mn lines which completely suppress the REE lines. The high spectral resolution of WDXRF, however, makes it possible to determine the concentration of REEs even with this adverse factor. In this study, we determined the content of REEs using the above calibration models (Fig. 4). In all cases, PLS provided more accurate results than the univariate model, with the values of RMSEp for PLS/PCR models remaining below those of the univariate model. It is interesting to note that the concentrations of Sm and Pr cannot be determined in nodules using univariate calibration, which is not true for ores. This case seems to be similar to TXRF analysis with univariate calibration. Nevertheless, both elements can be measured semi-quantitatively (with an uncertainty of about 30%) using PLS regression. This means that Ce, La, Nd, Pr, and Sm can be analyzed using WDXRF in different types of samples with the same multivariate model (PLS). This is the main advantage of the chemometric approach in comparison with univariate calibration integrated into the software of WDXRF spectrometer. Another advantage is that this is the same calibration set of artificial samples that provides minimal matrix effects.
Conclusions
A comparison of three regression methods (univariate, PLS and PCR) for the quantification of five REEs in three types of samples (niobium and uranium ores, and oceanic nodules) was performed using two XRF techniques (WDXRF and TXRF). The DoE based on LHS (20 levels and 5 factors) with extremely low correlation (<0.03) enabled the construction of a robust calibration model using artificial mixtures of REE compounds (iron and titanium oxides as a matrix). The main features of the suggested approach are (1) a relatively small number of calibration samples (20 samples), which cover the desired concentration range for the analysis of ores and nodules preserving a low level of paired correlation, and (2) the use of artificial mixtures of REE oxides, the applicability of which was proven for different sample types. It was clearly demonstrated that multivariate calibration provided better analytical performance for both XRF techniques than univariate calibration, especially for low concentrations. Multivariate calibration for TXRF makes it possible to quantify the content of major REE elements (Ce, La and Nd) in ores, while WDXRF is capable of yielding quantitative analysis of Ce, La, Nd, Pr, and Sm in both nodules and ores because of the higher spectral resolution and sensitivity of the technique. Another improvement in WDXRF analysis is the possibility of using the same calibration set to analyze three different types of samples (niobium and uranium ores, and oceanic nodules). The above features are expected to simultaneously simplify WDXRF analysis and make it more accurate. At the same time, we have demonstrated that simultaneous quantitative evaluation of Ce, La, and Nd content in niobium and uranium ores within the range of content 100–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm does not require an expensive WDXRF spectrometer, showing that TXRF is sufficient to the task. The more accurate determination of the concentrations of other REE (Pr and Sm) using TXRF still remains an issue to be solved in the future.
000 ppm does not require an expensive WDXRF spectrometer, showing that TXRF is sufficient to the task. The more accurate determination of the concentrations of other REE (Pr and Sm) using TXRF still remains an issue to be solved in the future.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research was performed using equipment of the of the Siberian Branch of the Russian Academy of Sciences Joint use centers (Geodynamics and Geochronology Center and Isotope-geochemical Research Center) and was funded by Russian Foundation for Basic Research according to the research projects No. 19-33-50065, No. 18-33-20104, and No. 19-33-90242.References
- V. Balaram, Geosci. Front., 2019, 10, 1285 CrossRef CAS.
- B. Zawisza, K. Pytlakowska, B. Feist, M. Polowniak, A. Kita and R. Sitko, J. Anal. At. Spectrom., 2011, 26, 2373 RSC.
- J. R. Bacon, O. T. Butler, W. R. L. Cairns, J. M. Cook, R. Mertz-Kraus and J. F. Tyson, J. Anal. At. Spectrom., 2019, 34, 9 RSC.
- Q. Ma, M. Yang, H. Zhao, N. J. Evans, Z. Y. Chu, L. W. Xie, C. Huang, Z. D. Zhao and Y. H. Yang, J. Anal. At. Spectrom., 2019, 34, 1256 RSC.
- X. H. Liao, Z. C. Hu, T. Luo, W. Zhang, Y. S. Liu, K. Q. Zong, L. Zhou and J. F. Zhang, J. Anal. At. Spectrom., 2019, 34, 1126 RSC.
- F. O. Leme, L. C. Lima, R. Papai, N. Akiba, B. L. Batista and I. Gaubeur, J. Anal. At. Spectrom., 2018, 33, 2000 RSC.
- B. Ticova, K. Novotny and V. Kanicky, Chem. Pap., 2019, 73, 2913 CrossRef CAS.
- E. Helmeczi, Y. Wang and I. D. Brindle, Talanta, 2016, 160, 521 CrossRef CAS.
- A. El-Taher, W. M. Badawy, A. E. M. Khater and H. A. Madkour, Appl. Radiat. Isot., 2019, 151, 171 CrossRef CAS.
- C. R. Bhatt, J. C. Jain, C. L. Goueguel, D. L. McIntyre and J. P. Singh, Spectrochim. Acta, Part B, 2017, 137, 8 CrossRef CAS.
- X. Yang, Z. Hao, M. Shen, R. Yi, J. Li, H. Yu, L. Guo, X. Li, X. Zeng and Y. Lu, Talanta, 2017, 163, 127 CrossRef CAS.
- M. Martin, R. C. Martin, S. Allman, D. Brice, A. Wymore and N. Andre, Spectrochim. Acta, Part B, 2015, 114, 65 CrossRef CAS.
- T. A. Labutin, S. M. Zaytsev, A. M. Popov and N. B. Zorov, J. Anal. At. Spectrom., 2016, 31, 2223 RSC.
- C. Fabre, D. Devismes, S. Moncayo, F. Pelascini, F. Trichard, A. Lecomte, B. Bousquet, J. Cauzid and V. Motto-Ros, J. Anal. At. Spectrom., 2018, 33, 1345 RSC.
- S. Romppanen, H. Häkkänen and S. Kaski, Spectrochim. Acta, Part B, 2017, 134, 69 CrossRef CAS.
- R. M. Rousseau, Spectrochim. Acta, Part B, 2006, 61, 759 CrossRef.
- B. Lemière, J. Geochem. Explor., 2018, 188, 350 CrossRef.
- C. Vanhoof, J. R. Bacon, A. T. Ellis, L. Vincze and P. Wobrauschek, J. Anal. At. Spectrom., 2018, 33, 1413 RSC.
- R. Sitko, B. Zawisz and M. Czajain, J. Anal. At. Spectrom., 2005, 20, 741 RSC.
- A. Smoliński, M. Stempin and N. Howaniec, Spectrochim. Acta, Part B, 2016, 116, 63 CrossRef.
- D. Suvorova, E. Khudonogova and A. Revenko, X-Ray Spectrom., 2017, 46, 200 CrossRef CAS.
- W. Wenqi, X. U. Tao, H. Qian, W. Qiang, Z. Shujie and Z. Changyu, J. Rare Earths, 2010, 28, 30 Search PubMed.
- K. Nakayama and T. Nakamura, Anal. Sci., 2005, 21, 815 CrossRef CAS.
- E. De Pauw, P. Tack, M. Lindner, A. Ashauer, J. Garrevoet, B. Vekemans, G. Falkenberg, F. E. Brenker and L. Vincze, Anal. Chem., 2020, 92, 1106 CrossRef CAS.
- I. E. De Vito, R. A. Olsina and A. N. Masi, Fresenius. J. Anal. Chem., 2000, 368, 392 CrossRef CAS.
- G. E. Hall, G. F. Bonham-Carter and A. Buchar, Geochem. Explor. Environ. Anal., 2014, 14, 99 CrossRef CAS.
- R. G. Brereton, Chemometrics: data analysis for the laboratory and chemical plant, Wiley, New York, 2003 Search PubMed.
- K. Molt and R. Schramm, Fresenius. J. Anal. Chem., 1997, 359, 61 CrossRef CAS.
- R. Schramm, Anal. Chim. Acta, 2000, 420, 197 CrossRef CAS.
- J. Moros, A. Gredilla, S. Fdez-Ortiz de Vallejuelo, A. de Diego, J. M. Madariaga, S. Garrigues and M. de la Guardia, Talanta, 2010, 82, 1254 CrossRef CAS.
- S. Akbulut, J. Anal. At. Spectrom., 2014, 29, 853 RSC.
- J. M. Soriano-Disla, L. Janik, M. J. McLaughlin, S. Forrester, J. Kirby and C. Reimann, Appl. Geochem., 2013, 29, 135 CrossRef CAS.
- J. Malherbe and F. Claverie, Anal. Chim. Acta, 2013, 773, 37 CrossRef CAS.
- J. Engel, J. Gerretzen, E. Szymańska, J. J. Jansen, G. Downey, L. Blanchet and L. M. C. Buydens, Trac. Trends Anal. Chem., 2013, 50, 96 CrossRef CAS.
- K. Kjeldahl and R. Bro, J. Chemometr., 2010, 24, 558 CrossRef CAS.
- V. Panchuk, I. Yaroshenko, A. Legin, V. Semenov and D. Kirsanov, Anal. Chim. Acta, 2018, 1040, 19 CrossRef CAS.
- D. C. Montgomery, Design and analysis of experiments, Wiley, New York, 2017 Search PubMed.
- R. G. Brereton, Analyst, 1997, 122, 1521 RSC.
- A. Shulyumova, A. Maltsev and N. Umarova, X Ray Spectrom., 2018, 47, 396 CrossRef CAS.
- D. Kirsanov, V. Panchuk, A. Goydenko, M. Khaydukova, V. Semenov and A. Legin, Spectrochim. Acta, Part B, 2015, 113, 126 CrossRef CAS.
- D. Kirsanov, V. Panchuk, M. Agafonova-Moroz, M. Khaydukova, A. Lumpov, V. Semenov and A. Legin, Analyst, 2014, 139, 4303 RSC.
- M. D. McKay, R. J. Beckman and W. J. Conover, Technometrics, 1979, 21, 239 Search PubMed.
- D. M. Steinberg and D. K. Lin, A construction method for orthogonal Latin hypercube designs, Biometrika, 2006, 93, 279 CrossRef.
- T. Yu. Cherkashina, S. V. Panteeva and G. V. Pashkova, Spectrochim. Acta, Part B, 2014, 99, 59–66 CrossRef CAS.
- G. V. Pashkova, V. M. Chubarov, T. F. Akhmetzhanov, A. N. Zhilicheva, M. M. Mukhamedova, A. L. Finkelshtein and O. Y. Belozerova, Spectrochim. Acta, Part B, 2020, 168, 105856 CrossRef CAS.
- P. Sievers, T. Weber, T. Michel, J. Klammer, L. Büermann and G. Anton, J. Instrum., 2012, 7, P03003 Search PubMed.
- K. Sakurai, M. Mizusawa and Y. Terada, Rev. Sci. Instrum., 2007, 78, 066108 CrossRef.
- D. K. G. De Boer, J. J. M. Borstrok, A. J. G. Leenaers, H. A. Van Sprang and P. N. Brouwer, X-Ray Spectrom., 1993, 22, 33 CrossRef CAS.
- Software Package for X-Ray Spectrometers, SPECTRAplus Version 2.2.3.1, Bruker AXS Karlsruhe, Germany, 2010 Search PubMed.
- S. Wold, M. Sjostrom and L. Eriksson, Chemometr. Intell. Lab. Syst., 2001, 58, 109 CrossRef CAS.
- R. G. Brereton, Applied chemometrics for scientists, Wiley, New York, 2007 Search PubMed.
- A. L. Pomerantsev, Chemometrics in Excel, Wiley, New York, 2014 Search PubMed.
- Open Source Java code oj! Algorithms, https://www.ojalgo.org/, 2020, May 27 Search PubMed.
| This journal is © The Royal Society of Chemistry 2021 |