Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Microfluidic formation of crystal-like structures
Francesco
Del Giudice
 *a,
Gaetano
D'Avino
*a,
Gaetano
D'Avino
 b and
Pier Luca
Maffettone
b and
Pier Luca
Maffettone
 b
b
aSystem and Process Engineering Centre, College of Engineering, Fabian Way, Swansea, SA1 8EN, UK. E-mail: francesco.delgiudice@swansea.ac.uk; Tel: +44 (0)1792 604027
bDipartimento di Ingegneria Chimica, dei Materiali e della Produzione Industriale, Universitá degli Studi di Napoli Federico II, Piazzale Tecchio 80, 80125 Naples, Italy
First published on 14th May 2021
Abstract
Crystal-like structures find application in several fields ranging from biomedical engineering to material science. For instance, droplet crystals are critical for high throughput assays and material synthesis, while particle crystals are important for particles and cell encapsulation, Drop-seq technologies, and single-cell analysis. Formation of crystal-like structures relies entirely on the possibility of manipulating with great accuracy the micrometer-size objects forming the crystal. In this context, microfluidic devices offer versatile tools for the precise manipulation of droplets and particles, thus enabling fabrication of crystal-like structures that form due to hydrodynamic interactions among droplets or particles. In this review, we aim at providing an holistic representation of crystal-like structure formation mediated by hydrodynamic interactions in microfluidic devices. We also discuss the physical origin of these hydrodynamic interactions and their relation to parameters such as device geometry, fluid properties, and flow conditions.
1 Introduction
Crystals are defined as homogeneous pieces of solid substance having a natural geometrical regular form with symmetrically arranged planes.1 The term crystal has seen a substantial evolution over time, and nowadays it refers to systems, either liquid or solid, that display a certain degree of regularity or order. In this context, microfluidics emerged as a very suitable field to enable the formation and the study of crystal-like structures owing to the possibility of controlling fluid and solid elements at the sub-micrometer scale.Crystal-like structures in microfluidic devices, hereafter microfluidic crystals, can either be formed thanks to external fields (e.g., electric or magnetic field) or because of hydrodynamic interactions among the different objects forming the crystal. In order to experience hydrodynamic interactions, the objects need to ‘feel’ each other, meaning that the local concentration should be sufficiently large to enable hydrodynamic interactions to take place. In such conditions, hydrodynamic interactions can promote the self-assembly of individual objects in crystal-like structures depending on several parameters such as channel geometry, fluid properties, and flow rate.
Microfluidic crystals, especially droplet and particle crystals, are not only important from a fundamental point of view, as they are found in a variety of microfluidic applications including digital PCR, synthesis of colloidal structures and single-cell analysis. So far, however, droplet and particle crystals have never been presented under a unified framework, which is helpful in understanding the self-assembly phenomena mediated by hydrodynamic interactions with the ultimate goal of generating new optimised technologies.
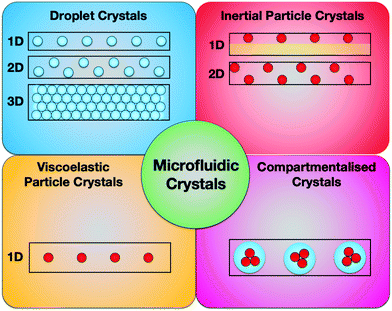
In this review, we aim at providing a holistic view of microfluidic crystals formed as results of droplet and particle self-assembly promoted by hydrodynamic interactions (Fig. 1). We believe that a multidisciplinary approach to microfluidic manipulation of crystals could open up the way to new microfluidic applications. We will mainly focus on microfluidic crystals and their applications, while referring the reader to other recent reviews to receive a broader overview about the advancements of each specific application.
The review is organized as follows. In section 2, we will first present the relevant dimensionless numbers required to understand the effect of the parameters governing the self-assembly dynamics. In section 3, we will discuss the formation of droplet crystals covering fundamental and application aspects. Similarly, in section 4, we will focus on self-assembly of particle crystals. In section 5, we will discuss recent applications in compartmentalisation involving both droplet and particle crystals. Finally, we will draw some conclusions and suggest future directions.
2 Dimensionless numbers
In this section, we introduce some dimensionless numbers helpful to understand the effect of the relevant parameters on the self-assembly dynamics and commonly used in many of the reviewed works. In general, dimensionless numbers are very useful to compare the relevant forces operating in a system, as well as to offer an easy way to compare experiments and simulations carried out at different operating conditions. We will follow the definitions reported in the review by Squires and Quake.2The importance of inertial and viscous forces during flow can be quantified by the Reynolds number defined as:
 | (1) |
When the fluid presents a certain amount of elasticity, for instance as in the case of aqueous solutions with the addition of polymers, the dimensionless number employed to characterise the strength of the elastic forces is the Deborah number defined as:
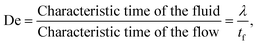 | (2) |
The ratio between inertial and viscoelastic forces is quantified by the elasticity number defined as:
 | (3) |
In a multiphase system made of two non-miscible liquids interfacial properties play a relevant role. The ratio between viscous forces and interfacial forces is quantified using the capillary number:
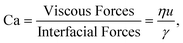 | (4) |
We also introduce the particle Reynolds number that is widely employed in the discussion of particle crystals formed during inertial flow (section 4):
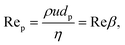 | (5) |
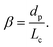 | (6) |
3 Droplet crystals
Before reviewing the literature on droplet crystals, it is worth to introduce here few concepts regarding droplet formation. Droplets are generally formed when two non-miscible liquids ‘meet’ at a microfluidic junction: the competition between capillary forces and viscous forces at the interface between the two liquids results in the formation of droplets having different sizes.2 The fluid that surrounds the droplet is referred to as the continuous phase, while the fluid forming the droplet is the dispersed phase. It has been shown that droplets can form in microfluidic devices having, among others, three geometries: coaxial, flow focusing, and T-junction.3 The size of the droplets as well as the droplet regime investigated (e.g., dripping or jetting regime) strongly depend upon the microfluidic geometry, the fluid properties, and the flow conditions.3 A detailed description of the droplet formation mechanism falls outside the scope of this review; we refer the interested reader to the review by Nunes et al.3 or the more recent ones by Zhu et al.4 and Guerrero et al.53.1 Formation and stability of droplet crystals: hydrodynamic interactions among droplets
In this section, we review the literature related to the effect of hydrodynamic interactions among droplets on the overall stability of the droplet crystal. This is especially important to control the formation of droplet crystals used for analytical chemistry applications as well as for the fabrication of colloidal structures (see section 3.3 for more details). We will focus on the available techniques and the experimental results on droplet crystal self-assembly, without going into the details of the mathematical model involved in the descriptions of the hydrodynamic potentials and the flow fields. The interested reader may refer to the two reviews6,7 by Beatus, Bar-ziv and Tlusty, where the full details regarding the physical equations describing interactions among droplets are reported and discussed.The first observation of droplet generation in a microfluidic device together with the first evidence of crystal-like structures formation was presented by Thorsen et al.11 A T-junction with width w = 30 μm and height h = 9 μm followed by an expansion region having the same height but width w = 60 μm was used to generate water in oil droplets. The droplets were formed at a frequency of 20–80 hertz and, depending on the average imposed pressure between oil and water, they observed a variety of crystal-like structures in the expansion region. In particular, they observed 1D crystals made by equally spaced droplets, 1D crystals formed by necklace of droplets attached to each other, and 2D crystals made of adjacent droplets forming a crystal along the expansion width. Despite the work of Thorsen et al.11 was the first to show the formation of droplet crystals, the main outcome of their work was the formation of uniformly distributed droplets (a significant improvement over macroscopic techniques); they did not investigate the stability of the crystals, nor clarified the origin behind the formation of such crystals. In several microfluidic applications such as digital polymerase chain reaction PCR, particle/cell encapsulation and synthesis of particles, the relation among external flow parameters, hydrodynamic interactions, and resulting crystal is very important to establish a general framework to create ad hoc crystal-like structures that target specific applications (see section 3.3 for a more detailed discussion). Beatus et al.8 were the first to study the stability of 1D droplet crystals as a function of the hydrodynamic interactions between adjacent droplets (Fig. 2a). Similarly to Thorsen et al.,11 they formed water in oil droplets using a T-junction having a height of h = 10 μm and a width of w = 35 μm, followed by an expansion with the same height and a width of w = 250 μm (when the width of the channel is significantly larger than its height, the device is also referred as ‘Hele-Shaw’ cell,12 because the flow can be approximated as a Poiseuille-like flow along the height h and as a potential flow along the width w). The diameter of the droplet formed at the T-junction was larger than the height of the microfluidic device: therefore, as the droplets approached the expansion area, the droplet assumed a ‘pancake’ configuration, i.e., more squeezed along the height than the width (Fig. 2b). The 1D crystal observed by Beatus et al.8 was stable only near the beginning of the expansion area, while displaying both transversal and longitudinal oscillations further downstream (Fig. 2c and d). These acoustic waves reminded the authors of the acoustic ‘phonons’ observed in solid-state physics. The origin of these waves were ascribed to the hydrodynamic interactions between consecutive droplets. In particular, for droplets confined along one direction, as in the case of pancake-like droplets, they observed a strong mismatch between the velocity of the droplets and that of the continuous phase. This was due to the drag experienced by the droplets because of their confinement between the floor and the ceiling of the microfluidic device: in these conditions, the droplets disturbed the flow of the continuous phase, resulting in the formation of a dipole-like flow field around the droplet (Fig. 2b). The hydrodynamic interactions between subsequent droplets were the result of superposition of flow dipoles that generated a long-range propagation of a wave that disrupted the stability of the crystal. The same authors also observed that the flow-disturbance around the droplets propagated longitudinally over the expansion area causing the destruction of the 1D crystal formed at the T-junction. Similar results were obtained by Liu et al.13 that performed numerical simulations aimed at studying the stability of a system of confined droplets. They concluded that the instability in the droplet configuration was due to two factors: i) the non-linearity in the hydrodynamic potential and ii) interactions between longitudinal and transversal waves. The analytical expression for the interaction forces between two closely spaced droplets has been obtained by Sarig et al.14 with a follow up analysis carried out by Green.15 From an application point of view, the results presented above are extremely important because they provide some arguments on how to design the microfluidic device for targeted applications. For instance, for the fabrication of crystals made of pancake-like structure using UV (see the recent review by Wang and Wang16), it is important to design the expansion channel short enough so that the photo-polymerisation takes place before any longitudinal or transversal instability begins. For applications such as digital PCR,17 it is important to fill in the expansion area of the microfluidic device with as many droplets as possible: if both transversal and longitudinal waves take place simultaneously, they may result in a chaotic behaviour8 that leads to the destruction of the crystal, thus making the whole process of filling in the expansion area with droplets unpredictable and not optimised, with negative implications on the throughput of a digital-PCR assay.
 | ||
| Fig. 2 a) 1D microfluidic crystal made of water droplets (dispersed phase) surrounded by oil (continuous phase). The height of the channel is h = 10 μm. The width at the T-junction is w = 35 μm, while that along the expansion area is 250 μm. Scale bar is 100 μm b) schematic of a droplet in a ‘pancake’ configuration as a result of the confinement along the z-direction. The continuous phase flows along the x-direction. The velocity profile is parabolic along the z-direction and a potential flow in the xy-plane. c) Image of transversal acoustic waves. d) Image of longitudinal acoustic waves. Panels a)–d) are reprinted by permission from Springer Nature: Nature Physics, Beatus et al.,8 Phonons in a one-dimensional microfluidic crystal, Copyright Springer Nature, 2006. e) Droplets of water in oil subjected to strong lateral confinement. f) Confined droplets exhibit longitudinal wave motion. g) Confined droplets exhibit transversal wave motion. Panels e)–g) are reprinted with permission from Beatus et al.,9Physical Review Letter, 99, 124502, Copyright 2007 by the American Physical Society. h) Generation of microfluidic crystals using a step-emulsification geometry. i) Flow field determined by particle image velocimetry in the lab frame. The relevant dipolar flow fields around each droplet in the co-moving frame of the droplets are sketched by white arrows. The second half of the dipolar flow field close to the channel wall is omitted for the sake of clarity. The transverse forces resulting from the dipolar flow fields from leading and trailing droplets are shown as grey and black arrows, respectively. j) Microscopy time series showing the droplet reorganization at a 90° bend. The boundaries of the bend were indicated in the first image. The droplet marked with a dot is repelled from the corner due to its hydrodynamic image and the trailing droplet marked with a circle is squeezed between the leading droplet and the wall and propelled longitudinally out of the corner. k and l) Travelling sine waves with different wavelength as generated by periodic defects for two different droplet sizes. The width of all microfluidic channels is w = 210 μm. Panels h)–l) are reprinted from Fleury et al.,10 Mode coupling of phonons in a dense one-dimensional microfluidic crystal, New Journal of Physics, 16, 063029, 2014, https://doi.org/10.1088/1367-2630/16/6/063029. | ||
In their pioneering work, Beatus et al.8 mainly focused on pancake droplets that were practically unconfined along the channel width in the expansion. In a follow-up study,9 the same authors analysed the effect of the confinement on the stability of the 1D crystal-like structures (Fig. 2e–g). The 1D crystal-like structures were formed by water in oil droplets flowing in a microfluidic channel with constant height of h = 10 μm and different values of the expansion width to simulate the transition from unconfined (w = 250 μm) to confined (w = 50 μm) conditions. They observed that the 1D crystal was more stable compared to the one reported in the previous work8 because the interactions that caused the vibrational modes along the channel width were screened exponentially by the lateral walls. Under a physical point of view, an increase in the confinement resulted in a symmetry breaking between longitudinal and transversal vibration modes, with the transversal modes being stronger in magnitude than the longitudinal ones. The screening of the long-range interactions also resulted in the strengthening of the hydrodynamic interactions between consecutive droplets due to the crystal incompressibility in plug-flow configuration, i.e., when the channel was nearly blocked by the droplets.
Stable production of droplet crystals is the foundation for a vast range of optimised microfluidic applications. For this reason, it is important to know in which flow conditions droplet crystals are stable and what would be the effect of flow perturbations (i.e., channel defects, geometrical changes, etc.) on the stability of the crystal. This aspect has been considered by Fleury et al.,10 who employed a step emulsification geometry18 to produce a stable 2D zig-zag crystal made of water droplets with radius R ≈ 64 μm in n-hexadecane (Fig. 2h). When the droplets entered the expansion area with height of h = 120 μm and width of w = 210 μm, they were squeezed between the floor and the ceiling of the channel, with a velocity lower than the continuous phase velocity, thus generating a flow dipole similarly to Beatus et al.8 When a new droplet entered the expansion area, the hydrodynamic interactions between the flow dipole of the entering droplet and that of the leading droplet resulted into the formation of a stable zig-zag 2D crystal (Fig. 2i). Such crystal was found to be very stable along the expansion area. The introduction of a 90° bend following the expansion area (Fig. 2j), however, resulted in the droplets to become closer, and it also promoted sinusoidal waves along the full width of the microfluidic channel (Fig. 2k and l). Even though it is not possible to clearly appreciate the actual sinusoidal motion from the experimental snapshots, we invite the interested reader to access the ESI video provided by the authors.10 In a different work,19 the authors also performed additional experiments and numerical simulations that demonstrated the possibility of using defect patterns to excite transversal or longitudinal vibrations starting from an initial zig-zag 2D crystal. From a practical point of view, the results presented above suggest that the stability of a crystal should not be taken for granted as flow perturbations can modify the overall stability of the crystal. For instance, imperfections in the microchannel fabrication can lead to local flow modifications that propagate along the crystal with a destabilising effect (see also Thutupalli et al.20 for more details).
Once the crystal has been formed within the microfluidic device, it is worth to ask whether it is stable when subjected to an applied flow. Gai et al.21 studied the overall motion of a 2D droplet crystal in a microfluidic ‘tapered’ channel with a 5° angle leading to a constriction of 30 μm. When the crystal approached the constriction, a spatial periodicity of the droplet rearrangement was observed that could be described by the Read–Shockley model22 for low-angle grain boundaries. They also observed that the geometry of the tapered channel, and especially the taper angle, was very important to preserve the periodicity of the spatial rearrangement in the crystal. If the taper angle was too large, a chaotic behaviour of the crystal rearrangement appeared.
The volumetric flow rate had also an effect on the dynamic of rearrangement of the microfluidic crystal.23 At sufficiently large flow rate values, which are often essential in microfluidic high-throughput applications, the overall crystal dynamics moved from liquid-like to solid-like, and this resulted in a non-localised spatial distribution, where the local order was lost.
3.2 Formation of droplet crystals in microfluidic flows: from 1D to 3D crystals
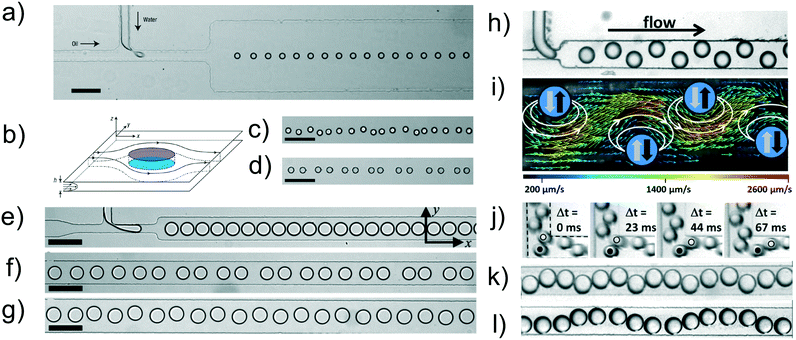
The formation of droplet crystals in microfluidic devices strongly depends on the geometry of the microfluidic device as well as on the ratio between the flow rate of the continuous phase Qc and the dispersed phase Qd, as well as the capillary number Ca. Jose and Cubaud24 employed a microfluidic device with constant height h = 250 μm having a square-shaped flow focusing droplet formation area followed by a diverging/converging channel (expansion chamber) with an angle of 45° and maximum width w = 20 h = 5000 μm. Depending on the capillary number Ca and the ratio Qc/(Qc + Qd) at the flow focusing area, spherical droplets with diameter h < d0 < 2 h and uniform size distribution were formed. These droplets first travelled along a square-shaped 5 mm long microchannel and then entered the diverging/converging geometry, where 1D-crystals and 2D-crystal formation was observed (Fig. 3a). The dynamic of formation of the 2D-crystals arranged in a multi-layered structure was similar to the one described in previous works.8,10 The authors tracked a series of droplets entering the diverging/converging area (Fig. 3b) and observed that such droplets where deflected from their centreline positions because of the hydrodynamic interactions with the droplets already in the chamber. The first droplet travelled towards the upper part of the chamber while the second one was deflected on the second row and so on, similarly to the zig-zag 2D crystals observed by Beatus et al.8 and by Fleury et al.10 An interesting consideration is that the droplet confinement in Jose and Cubaud24 was significantly smaller than the one in Fleury et al.:10 despite such difference, hydrodynamic interactions were still significant and led to the formation of 2D crystals. In other words, even values of the droplet confinement that do not force a significant pancake-like droplet shape are sufficient to generate hydrodynamic interactions aimed at the formation of droplet crystals. Similar results regarding occurrence of hydrodynamic interactions between droplets having different type of confinement can be found comparing the work of Shen et al.28 with the one of Ohmura et al.:29 both works analysed hydrodynamic interactions between two droplets in i) strong confinement28 and ii) more mild confinement.29 An important aspect arising from the analysis of Fig. 3a is the occurrence of a transition from 1D-crystal to 2D-crystal formation when changing the flow rate of the continuous phase Qc. Jose and Cubaud24 reported a phase diagram linking the crystal formation to both capillary number Ca and frequency of droplet formation expressed as distance between consecutive droplets L0 normalised by the droplet initial diameter d0 (i.e., at the flow focusing area), as reported in Fig. 3c. The main message arising from this analysis was that the formation of 1D crystals occurred at low droplet formation frequency values, with L0/d0 ≥ 10: in this case, the first droplet entering the diverging/converging geometry had sufficient time to travel along the axis before another droplet arrived. When increasing the frequency of droplet formation, meaning an increase of Qd, the flow dipole generated by the first droplet entering the diverging/converging area interacted with the one generated by the upcoming droplets, resulting in a multi-layered 2D crystal configuration. We expect the phase diagram reported in Fig. 3c to be valid only for the geometry described in the corresponding work. A variation of geometrical parameters in the device such as channel height, angle in the diverging/converging chamber are expected to modify the transition between 1D to 2D crystals and also the type of multi-layer crystals observed because of a variation of the hydrodynamic interactions among droplets.25 While the results by Jose and Cubaud24 can be qualitatively explained using the same arguments presented in the seminal paper by Beatus et al.,8 a more quantitative analysis has been carried out with the aid of numerical simulations (Fig. 3d and e).25 The interacting drop-traffic model solved in creeping flow (i.e., at very low Reynolds number values) was employed to describe the different forces acting on droplets flowing in the same geometry of Jose and Cubaud.24 This model assumes that the droplets are subjected to three forces: i) a force exerted by the continuous phase, ii) a force due to the presence of other droplets when the distance between the two centres of gravity approach the droplet diameter, and iii) the force due to the geometrical boundaries. By solving the resulting equations, the results by Jose and Cubaud24 were replicated in full (Fig. 3d and e). The authors also demonstrated that droplet crystal configurations observed in the diverging–converging geometry depended upon the frequency of droplet formation, as originally reported by Jose and Cubaud.24 Specifically, when the initial spacing between consecutive droplet was small, i.e., at large droplet formation frequencies (high throughput), there was a tendency to form 2D crystal-like structures. On the contrary, when the spacing between droplets was large, i.e., at small droplet formation frequencies (low throughput), 1D crystal-like structures were formed. More interestingly, the authors evaluated the resulting crystal-like structures when changing the geometry of the diverging–converging area: they found that the midsection of the microchannel, where the velocity profile was nearly flat along the channel width, had the largest effect on pattern formation rather than the ‘shape’ of the inlet and outlet of the expansion area. The transition from 1D to 2D crystals as function of droplet size and volumetric flow rates has also been reported in other works.30–32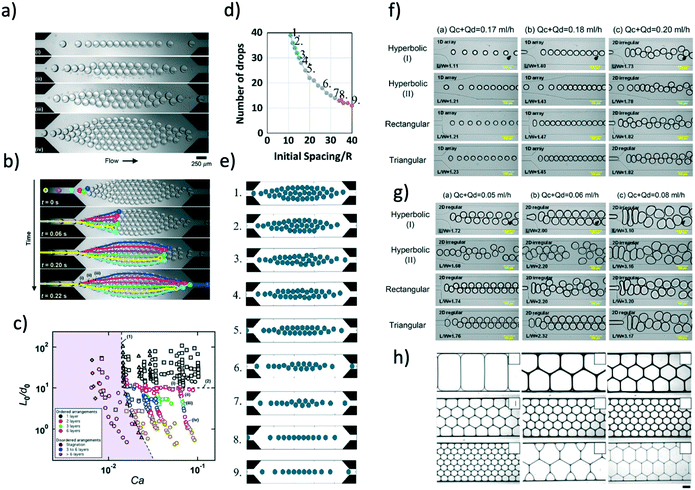 | ||
| Fig. 3 a) Formation of multiple layers in the microfluidic chamber at different flow rates of the dispersed phase and a constant flow rate of the continuous phase of Qc = 400 μl min−1: flow rate values of the dispersed phase are Qd = 14 μl min−1 (i), Qd = 30 μl min−1 (ii), Qd = 40 μl min−1 (iii) and Qd = 85 μl min−1 (iv). b) Temporal evolution of the trajectories of six successive droplets in a six-layer arrangement for Qc = 400 μl min−1 and Qd = 85 μl min−1. c) General phase diagram to obtain droplet crystals with different layouts. L0 is the distance between consecutive droplets, d0 is the diameter of the droplet and Ca is the capillary number. Panels a)–c) are reprinted with permission from Springer Nature: Microfluidics and Nanofluidics, Droplet arrangement and coalescence in diverging/converging microchannels, Jose and Cubaud,24 Copyright Springer Nature, 2012. d) Number of drops as a function of the initial spacing between consecutive droplets. e) Numerical snapshots of the crystal configuration resulting from the combination between droplet number and initial spacing. Numbers in (e) refers to the data points in (d). Panels d) and e) are reprinted with permission from Springer Nature: Microfluidics and Nanofluidics, Understanding drop-pattern formation in 2-D microchannels: a multi-agent approach, Danny Raj and Rengaswamy,25 Copyright Springer Nature, 2014. f) Snapshot of droplet crystals generation within microfluidic devices with different funnels for a constant flow rate of the continuous phase equal to Qc = 0.16 ml h−1. The flow rate of the dispersed phase was regulated as: Qd = 0.01 ml h−1 (i), Qd = 0.02 ml h−1 (ii) and Qd = 0.04 ml h−1 (iii). g) Experimental snapshots as in (f) for a constant flow rate of the continuous phase Qc = 0.04 ml h−1. The flow rate of the dispersed phase is Qd = 0.01 ml h−1 (i), Qd = 0.02 ml h−1 (ii) and Qd = 0.04 ml h−1 (iii). Panels f) and g) are reprinted with permission from Springer Nature: Korea-Australia Rheology Journal, Effect of local kinematic history on the dynamic self-assembly of droplets in micro-expansion channels, Yang et al.,26 Copyright Springer Nature, 2011. h) Optical microscopy images of hexagonal lattices formed by droplets having different volume. Reprinted with permission from Seo et al.,27 Microfluidics: from dynamic lattices to periodic arrays of polymer disks, 21(11), Copyright 2005, American Chemical Society. | ||
The effect of the shape of the inlet and outlet of the expansion area was experimentally investigated by Yang et al.26 (Fig. 3f and g) using devices with uniform height h = 200 μm. They referred to the different shapes as ‘local kinematic history’, meaning the history that each droplet experienced before entering the expansion area. For a fixed geometry, an increase of the dispersed phase flow rate Qd resulted in the transition from 1D crystal-like structures to 2D structures (not necessarily crystals), in agreement with the findings presented previously.24,25 At variance with previous experimental evidence, though, the ‘regularity’ of the 2D structure depended upon the kinematic history. With reference to Fig. 3f, 1D structures were all crystal-like regardless of the geometry, whereas 2D crystal-like structures were only observed for the triangular inlet to the expansion area; in all the other cases, at large values of Qd, the pattern was always irregular, thus preventing the formation of any crystal-like structure. The formation of droplet crystals at low capillary number values was also explored (Fig. 3g). The formation of regular 2D crystal-like structures was only found in devices denoted as hyperbolic (I) (Fig. 3f) or in those with rectangular shape. The aforementioned results show that the geometrical design of the channel has a strong impact on the formation of 1D or 2D crystal-like structures. While a more general framework relating flow parameters to droplet formation in different geometries exists,3 the same is not true for crystal-like formation due to the complexity of the multi-body system. A comprehensive framework addressing the formation of crystal-like structure would enable deterministic formation of microfluidic crystals, thus opening new opportunities for microfluidic applications.
All the microfluidic crystals introduced so far were made by droplets with a circular cross-section, either in a pancake configuration or in a more spherical shape. In some microfluidic applications such as digital PCR,17 2D crystals are organised in the expansion area of the microfluidic device in order to fill in the whole space. Of course, if the 2D crystal is made of circular droplets, there will be empty spaces in the device with consequent reduction of assay throughput. In such circumstances, it would be beneficial to employ 2D crystals made of drops with rectangular or hexagonal cross-section or any other suitable shape that can fill in a rectangular chamber entirely, without leaving empty spaces. Seo et al.27,36 fabricated 2D microfluidic crystals made of different internal shapes, with the aim of forming 2D lattices (Fig. 3h). They observed that by changing the volume of the formed droplets, it was possible to generate2D crystals with pentagonal or hexagonal shapes. They employed silicone oil with viscosities in the range of 0.64 to 50 cP in an aqueous 2 wt% sodium dodecyl sulfate solution; the interfacial tension was γ = 2.71 mN m−1. The imposed flow conditions resulting in a capillary number Ca ≃ 1 × 10−4, meaning very small values of the imposed flow rate (0.1 to 2 μL min−1).
For small values of the droplet volume (0.53 to 1.12 nL), the 2D crystals were made by droplets with a circular shape.36 When increasing the droplet volume above 1.52 nL, the circular droplets deformed into different shapes (because of the confinement) and filled in the entire chamber, even in the case of bimodal droplet distributions (see the two bottom-left panels in Fig. 3h). The potential formation of 2D crystals fitting the entire expansion area solved the problem of empty spaces caused by spherical droplets. However, shapes different from the circular one in 2D crystals have been generated only for very small flow rate values, which somehow limits the applications to low throughput ones. Even more recent attempts37 to form honeycomb microfluidic crystals using surfactants with two different adsorption rates were limited by low flow rate values (same range as Seo et al.27,36); furthermore, the honeycomb structure in Fujiwara et al.37 was not perfectly uniform and changed over time because of the absorption of the second surfactant on the droplet surface. Very recently, the morphology of microfluidic crystals observed by Raven and Marmottant38 were numerically reproduced39 using a multicomponent Lattice Boltzmann method augmented by a forcing term representing the near-contact forces at the interface between two droplets.
Until now, we mainly focused on the formation of 1D and 2D crystals. Intuitively, to produce 3D structures, the droplets need to have some ‘free space’ along the height of the microchannel, a condition that has never been fulfilled in the works discussed above. Hatch et al.33 demonstrated the formation of 3D droplet crystals in microfluidic devices (Fig. 4a and b). More specifically, they either changed the flow rate value of both continuous and dispersed phase in order to obtain droplets with diameter smaller than the channel height, or changed the height of the microfluidic device compared to the size of the droplet. By doing so, they demonstrated the transition from 2D to 3D microfluidic droplet crystals. The type of crystals formed depended upon the ratio between chamber height and droplet size, as reported in Fig. 4a. A different approach was followed by Priest et al.34 who employed a step emulsification device (Fig. 4c) to produce 3D crystal lattices made of pentagons (Fig. 4d). They employed water or glycerol water with the addition of 2 wt% of NaCl as dispersed phase and Isopar low viscosity organic liquid with Span 80 as continuous phase. When the droplets entered the ‘step’ in the microfluidic device, they settled because of density difference, thus occupying the floor of the device; additional droplets settled above the ones occupying the floor leading to the formation of 3D droplet crystals (Fig. 4d). A potential disadvantage of the systems employed by Hatch et al.33 and by Priest et al.34 is that the formation of the 3D crystal was delayed by the presence of the continuous phase that needed to be replaced by new droplets. A way around this problem has been proposed by Wang et al.40 and then significantly optimised by Parthiban et al.35 Wang et al.40 simply added some tiny lateral channels to the expansion region with the goal of removing the continuous phase, thus ‘accelerating’ the formation of the 3D droplet crystal. They employed a microfluidic device with constant height h = 50 μm where water-in-oil droplets were formed using a flow-focusing geometry: the droplets then reached an expansion area where strong hydrodynamic interactions took place, facilitated by the removal of the oil via the lateral channels. The resulting 3D crystals was not perfectly uniform across the expansion area, thus leaving room for design optimisation. In this respect, Parthiban et al.35 recently demonstrated production of uniform 3D droplet crystals using an expansion area that changed the height gradually from h = 500 μm to h = 2000 μm; before the expansion area, a single lateral channel was used to subtract the continuous phase. With reference to Fig. 4e, the authors demonstrated that when not removing the continuous phase (oil, in their case) water droplets tended to form only 2D microfluidic crystals. When increasing the amount of continuous phase subtracted before approaching the expansion area (meaning a reduction of the distance between consecutive droplets), the droplets arranged to form 3D closely packed microfluidic crystals that were uniform across the expansion area. It is interesting to notice the analogy between the results of Parthiban et al.35 with those of Jose and Cubaud:24 in both cases a transition between different crystal orders was obtained by reducing the distance between consecutive droplets in order to enhance hydrodynamic interactions. Parthiban et al.35 also demonstrated that the kinematic history of the liquid entering the expansion area was important to generate 3D crystals, echoing the results for 2D droplet crystals introduced by Yang et al.26 When using a sudden expansion area (without the gradual change from h = 500 μm to h = 2000 μm), it was not possible to obtain stable 3D crystals, thus further strengthening the argument that the local kinematic history remain a crucial parameter to achieve crystals with a well defined order and regularity.
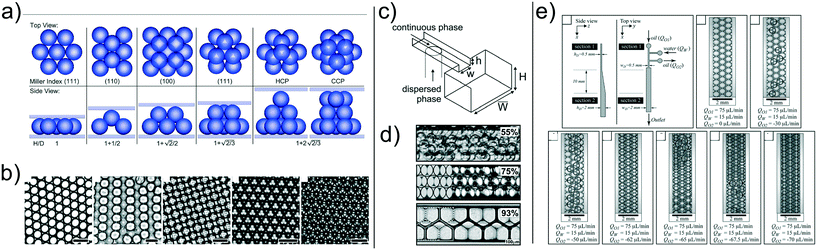 | ||
| Fig. 4 a) Three-dimensional droplet sphere packing configurations. Illustration of self-assembled droplet sphere packing configurations as a function of chamber height/droplet diameter ratio, H/D. b) Brightfield images of single layer to triple layer self-assembled droplet sphere packing configurations. Scale bars are 100 μm. Panels a) and b) are reproduced from ref. 33 with permission from The Royal Society of Chemistry. c) Schematic of the single step emulsification geometry, where w = 200 μm, h = 10, 22 or 43 μm, while H = W = 250 μm. d) Self-assembly of gel emulsions in microchannels. As the dispersed phase volume fraction increases (top to bottom), the structural order of the emulsion increases substantially. Panels c) and d) are reprinted from Priest et al.,34 Generation of monodisperse gel emulsions in a microfluidic device, 88(2), 2006 with permission of AIP publishing. e) Schematic illustration of 3D microfluidic devices used for self-assembly of water droplets into 2D and 3D ordered array. Experimental snapshots of the microfluidic crystals obtained for different volumetric flow rate values of the inlets/outlets. Reproduced from ref. 35 with permission from The Royal Society of Chemistry. | ||
Before closing this section, we make a final consideration regarding droplet crystals made of droplets having different properties. In applications such as synthesis of anisotropic particles41,42 or microfluidic crystals43 formed by polymerised droplets having different properties, it is important to know how to inject the two droplets types in order to obtain the desired final structures. Numerical simulations carried out by Danny Raj et al.44 using the same geometry of Jose and Cubaud24 studied the effect of the injection policy of two droplets types called ‘A’ and ‘B’, obtaining also some counterintuitive results. For instance, they demonstrated that an injection policy ABAB led to a microfluidic crystal where the succession of particles follow the order ABAB only when the crystal was 1D. For 2D droplet crystals with 6 layers (such as those in Fig. 3a) the injection policy ABAB led to a 6 layer crystal where the top 3 layers were formed by droplet A and the bottom 3 layers formed by droplet B. The observed layering (a symmetry breaking instability) was caused by the infinitesimal local perturbations around the droplets entering the expansion channel. The results by Danny Raj et al.44 demonstrated even further the complexity of the formation of crystal-like structures in microfluidic device and called for further studies targeting a general framework to describe the observed structures.
3.3 Applications of droplet crystals
In this section, we discuss some applications of droplet crystals. In the majority of cases, these applications have been characterised as ‘droplet microfluidics’, thus somehow overlooking the importance of having a crystal-like structures to obtain, for instance, high throughput assays and to avoid cross-contamination in analytical chemistry applications. A notable exception is the commercialised PCR system by Stilla Technologies, which is labelled as Crystal Digital PCR. It is our intention to highlight some recent works in the field where droplet crystals play a crucial role, while we will refer the interested reader to other more comprehensive reviews on the topic at large.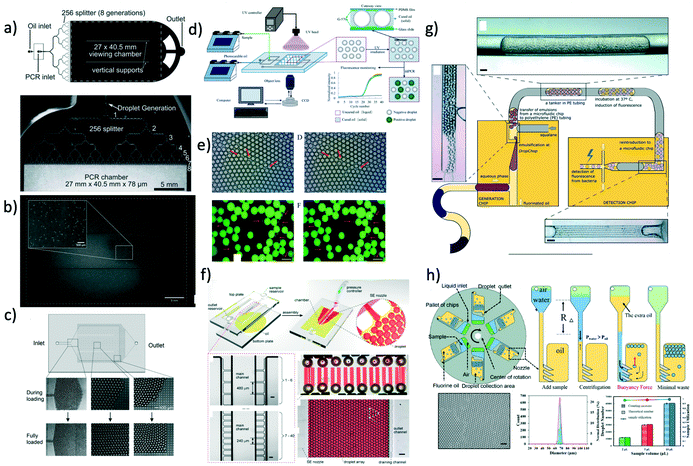 | ||
| Fig. 5 a) Schematic of the microfluidic device with 256 splitting parts used to generate 1 million droplets in few minutes. b) Image of the fluorescent signal derived from the PCR analysis occurring in the microfluidic crystal. Panels a) and b) are reproduced from ref. 33 with permission from The Royal Society of Chemistry. c) Droplets are self-assembled with the help of a grid where the continuous phase is filtered. Upon removal of the continuous phase, the crystal self-assemble in a uniform 2D droplet crystal. Reprinted with permission from O'Keefe et al.,45 Highly efficient real-time droplet analysis platform for high-throughput interrogation of DNA sequences by melt, Analytical Chemistry, 91, 17, 11275, Copyright 2019, American Chemical Society. d) Droplets are ‘frozen’ in space by curing the photocurable oil (continuous phase) using a UV lamp. This approach prevented coalescence during the PCR thermo cycle. e) Experimental snapshots of the 2D droplet crystal before (left) and after (right) the PCR thermo cycle. Top and bottom image refer to the fluorescence signal obtained before (left) and after (right) 40 PCR cycles. Panels d) and e) are reprinted with permission from He et al.,46 Rapid in situ photoimmobilization of a planar droplet array for digital PCR, Analytical Chemistry, 92, 8530, Copyright 2020, American Chemical Society. f) Schematic of the step emulsification droplet PCR device. At variance with other microfluidic device, here the droplet are formed by employing only a single syringe pump with the continuous phase being preloaded in the device. This arrangement leads to the formation of 2D droplet crystals. Reprinted with permission from Nie et al.,47 Assembled step emulsification device for multiplex droplet digital polymerase chain reaction, Analytical Chemistry, 91, 1779, Copyright 2019, American Chemical Society. g) Schematic of the experimental setup to generate droplet tankers each containing droplet crystals. Reproduced from ref. 48 with permission from The Royal Society of Chemistry. h) Schematic of the centrifugal-driven droplet generation. The centrifugal force pushes the water (dispersed phase) through the oil (continuous phase): this is similar to a step emulsification device where the syringe pump is replaced by the centrifugal-driven flow. Scale bar in the experimental snapshot is 200 μm. Reprinted with permission from Li et al.,49 Centrifugal-driven droplet generation method with minimal waste for single-cell whole genome amplification, Analytical Chemistry, 91, Copyright 2019, American Society of Chemistry. | ||
During the PCR cycle, the reagent needs to undergo different thermal cycles where the temperature is changed significantly with ΔT ≈ 40 °C. Such abrupt temperature change affects the integrity of the 3D crystal-like structure, as the droplets tend to coalesce.17 From an application point of view, droplet coalescence means cross-contamination among different micro-reactors. A solution to this problem was proposed by Bian et al.55 that employed a microfluidic device made of polydimethylsiloxane (PDMS) saturated with mineral oil on a silicon mould fabricated using conventional lithography. This step was critical to avoid droplet evaporation under many rounds of thermal cycling, thus preserving the integrity of their 2D crystal, meaning larger throughput and no cross-contamination. They also employed two-colour fluorescent probes for simultaneous detection of E. coli O157:H7 and L. monocytogenes. A different approach aimed at overcoming the problem of coalescing droplets has recently been introduced by He et al.46 They employed a flow-focusing droplet formation technique to create a 2D droplet crystal made of polyurethane droplets (dispersed phase) in photocurable oil (continuous phase). By using a UV lamp, they polymerised the oil surrounding the droplets, thus ‘freezing’ the 2D crystal (Fig. 5d and e). This technique remains valuable to avoid droplet coalescence during PCR thermocycle but also to prevent droplet free movements, thus making real-time analysis possible without the use of a sieve as presented by O'Keefe et al.45 By using this technique, highly efficient PCR fluorescent readout was demonstrated. We expect that a further improvement in terms of throughput can be realised by creating a 3D crystal structure in the PCR chamber rather than a 2D crystal. Of course, there are some foreseeable challenges associated to the formation of the 3D crystals during photopolymerisation process. Apart from direct PCR applications, 2D droplet crystals have also been recently employed to detect cancer biomarkers56 and circulating tumour DNA.57 Similar considerations remain regarding increasing the assay throughput by adding an extra dimensionality to the crystal, from 2D to 3D.
In all the applications presented so far, the formation of droplet crystals occurred after the formation of individual droplets using either a T-junction geometry or a flow-focusing geometry. However, this often requires very sensitive control of the applied volumetric flow rate in order to obtain uniform droplets that can then self-assemble in a droplet crystal. This problem has been addressed firstly by Xu et al.58 that generated droplets by using a microfluidic device with a single inlet, leading to a rectangular channel with aspect ratio larger than 3.5 followed by an expansion area (this technique was named ‘step emulsification’). The expansion chamber of the microfluidic device was first filled with the continuous phase (oil); the dispersed phase (water) was then pumped via the single channel and, upon reaching the expansion, it formed a droplet that was pinched off because the equilibrium Laplace pressure acting on the droplet could not be maintained thanks to the abrupt expansion. The authors employed this technique to perform PCR analysis aimed at identification of the targeted genomic DNA purified from lung cancer lines H1579. This concept has been also recently pushed further by Nie et al.47 that designed are usable multiplex microfluidic device for PCR analysis in 2D droplet crystals (Fig. 5f). The device was made of two soda-lime glass plates patterned by standard photolithography and wet chemical etching techniques. The two pieces of glass were simply bonded using binder clips: after each use, the device could be easily cleaned and then reused. The oil (continuous phase) was pre-loaded in the microfluidic device before clamping the two pieces of glass. Then, the dispersed phase was injected using a single inlet that ended in several lateral channels with different diameters: when the dispersed phase was in contact with the oil, droplets were formed as for the step emulsification technique described by Xu et al.58 Moreover, the formed droplets interacted forming a 2D droplet crystal: together with an additional parallelisation (eight parallel channels), the authors achieved a very large throughput. They employed this device to detect template DNA at concentrations as low as 10 copies per μL and they also performed quantitative assessment of HER2 copy number variation, important for targeted therapy and prognosis of breast cancer.
The majority of droplet crystals employed for PCR applications, either 2D or 3D, were very valuable for the analysis of a single sample via droplet parallelisation. A different approach is needed when a simultaneous analysis of different samples is required. An example is the evaluation of the minimum inhibitory concentration (MIC), meaning the lowest concentration of antibiotic in which the growth of bacteria cannot be observed. The MIC strongly depends upon the initial bacteria concentration, and such phenomenon is called inoculum effect (IE). The IE is very important in the clinical practice because it can lead to an overestimation of the MIC in vitro, thus causing an increased mortality among patients. To correctly evaluate the MIC, analysis with different amount of antibiotics are required, thus making the devices introduced so far not optimal unless when using several of them in parallel. In an attempt to solve this problem, Postek et al.48 recently employed a microfluidic system for the formation of droplet tankers each containing a 3D droplet crystal (Fig. 5g). The authors first prepared off-chip microliter mother droplets, each with a different chemical environment. The droplets were then aspirated from a well plate with emulsification taking place using the Drop Chop device introduced previously by the same authors.59 These droplets were then injected in another channel where they were encapsulated in a larger droplet called tanker using immiscible squalene (Fig. 5g). Once within the tanker, the encapsulated droplets self-assembled in a 3D microfluidic crystal that was then subjected to incubation at 37 °C while flowing in a tube, and then re-injected in the microfluidic device for detection. Since the mother droplets were all presenting different chemical environments, it was possible to simultaneously run MIC assays. Another advantage of the approach employed by the authors is that each reactor tanker contained a 3D droplet crystal, meaning a very large amount of individual micro-reactors in parallel, thus making the whole procedure high-throughput. In terms of stability of the 3D droplet crystal within the tanker, no significant variation in droplet number and shape after 16 hours at 37 °C was reported. However, follow up studies should analyse the effect of large temperature differences (such as those experienced during PCR) on the stability of the tanker, in order to expand the range of applicability of this platform.
The advent of step emulsification droplet formation using a single channel opened the way to a different approach for droplet formation where the motion of the dispersed phase was not imposed by an external syringe pump but rather by the centrifugal force experienced by the fluid during the ‘spinning’ of the microfluidic device. Centrifugal step emulsification was employed by Schuler et al.60 to produce individual droplets that then self-assembled in a 2D crystals made of hexagons, where recombinase polymerase amplification (RPA), i.e., a DNA amplification technique occurring at the constant temperature of ∼39 °C, took place. In a successive work,61 the authors also performed PCR on a disk using a centrifugal step emulsification technique to form 2D crystals. The 2D crystal was formed by changing the speed of the centrifuge in order to change the balance between centrifugal and capillary forces: air bubbles were then removed using a bubble drain, thus allowing formation of a large 2D crystal occupying the whole PCR readout area. A similar result was also obtained by Peng et al.62 who designed a microfluidic device with an oil-storage structure for the regulation of the thickness of the oil film (continuous phase) between neighbouring water droplets. An example of parallelisation of microfluidic devices subjected to centrifugal force has recently been presented by Li et al.,49 who performed PCR analysis with 98% of sample utilisation as well as a single-cell whole genome amplification. With reference to Fig. 5h, oil was first added to the device followed by water and air. During centrifugation, water droplets were formed in the continuous oil phase; to minimise the waste, additional oil used to push the remaining water to form other droplets in oil was added. The advantage of this approach was that more droplets could be formed, thus leading to strong hydrodynamic interactions which formed a uniform 2D crystal for both PCR and whole genome analysis. Some limitations encountered in centrifugal microfluidic for the formation of droplet crystals include the possibility of controlling droplet size and droplet formation without changing the rotational speed. As extensively discussed, the injection policy may alter the dimensionality of the microfluidic crystal,24 while the possibility of changing the droplet size compared to the height of the microfluidic device can lead to a reacher variety of droplet crystals.33 The first problem has been addressed by Wang et al.63 who designed a centrifugal microfluidic pressure regulator scheme to control droplet formation without changing the rotational speed. Specifically, they employed an air chamber as pressure regulator to control the droplet crystal formation. The second problem has been recently addressed by Clime et al.64 who employed pneumatic actuation for fluid displacement. They demonstrated formation of uniform 2D droplet crystals, each having individual droplets with different diameter and narrow standard deviation.
Before concluding this section, we want to highlight a recent work by Kao et al.65 where the microfluidic crystal was formed without the support of any type of external flow equipment, nor syringe pump, nor centrifugal force. The device was still based on the step emulsification process where the continuous phase was, as usual, added in the droplet generation chamber; moreover, the dispersed phase as well was added to a reservoir in the microfluidic device using a pipette. The flow was then initiated by orienting the device vertically, with the gravity driving the dispersed phase in the continuous phase chamber, thus leading to the formation of droplets that then self-assembled in 2D crystals. The same device was used for digital enumeration of bacteria and for antibiotic susceptibility testing. We believe that similar approaches will be required in the future in the attempt to use microfluidic devices in places where expensive pieces of equipment are not available.
So far, we discussed findings related to the formation of droplet crystals having either different dimensionality (1D, 2D, 3D) or having individual crystal components with different shape (circle, hexagon, pentagon, etc.). However, while such crystals have been advantageous in analytical chemistry, they find limited interest when seeking to fabricate small colloidal crystal-like structures. Shen et al.66 presented the first experimental evidence of formation of colloidal crystal-like structures resulting from the hydrodynamic interactions of the single droplet units (Fig. 6a and b). They employed a microfluidic device with two different heights, in analogy with the aforementioned step emulsification geometry. In the first part of the channel, droplet plugs were formed using a flow-focusing geometry; when entering the wider chamber with larger channel height, the plug dissociated in different circular droplet units. After adding a large amount of surfactant, far above the critical micellar concentration, the so-formed droplets remained in contact and began to interact hydrodynamically to form a variety of colloidal structures depending on the initial configuration of the separated droplets (Fig. 6b). The authors were also able to solidify the formed structures by using acrylate-based polymers and by adjusting the solubilities so that the polymerisation could occur in both continuous and dispersed phase. The potentiality of this approach is that colloidal crystals with different shapes or properties could be easily fabricated with a throughput of up to 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures per hour. Shen et al.66 suggested the potential of fabricating photonic materials by reducing the dimensions of the individual droplet size down to 400 nm and below. This hypothesis has recently been explored further by Morozov and Leshansky,70 who suggested to encapsulate the colloidal crystals formed by Shen et al.66 in a droplet, and then use hydrodynamic interactions among droplets to generate different crystals, by using a modified version of the setup by Postek et al.48 Morozov and Leshansky70 demonstrated numerically the emergence of the omnidirectional band gap in the cubic face centred (fcc) lattice dumbbells. They also reported that encapsulating tetrahedrons over fcc-templated dumbbells caused a reduction of the photonic properties. The results by Shen et al.66 remain, to the best of our knowledge, the only experimental data on the subject. More recently, numerical simulations67,71 have been carried out to replicate the experimental results of Shen et al.66 Ge et al.71 employed confined simple shear and Poiseuille flow as reference flows and showed that the crystal formation is mostly affected by the shear-induced cross-stream migration as long as attractive forces between droplets are present. The Poiseuille flow approximation is valid in 3D flow, meaning that the droplets do not ‘feel’ the presence of the walls and do not assume a ‘pancake’ shape: in such conditions, depletion forces between droplets are more relevant than the long-range dipolar interactions.67 The results by Ge et al.71 clarified that the crystal formation was a result of hydrodynamic interactions in 3D flow, but they did not provide a predictive framework that would allow crystal design a priori. Some steps in this direction have been made by Danny Raj et al.67 They first performed numerical simulations to evaluate the stability of the crystal-like structures introduced by Shen et al.66 (Fig. 6c). At time zero, the droplet configuration was the one by Shen et al.66 (first column in Fig. 6c); after a local perturbation, they studied the variation over time of the structure (second column in Fig. 6c), and quantified the modification using the structure parameter Φd (third column in Fig. 6c). Besides the mathematical definition of Φd (not reported here), the meaning of this parameter was that structural changes of the colloidal structure were reflected in a change of the Φd value. With reference to Fig. 6c, it is clear that there are some structures that are stable over time, while others evolve into a different crystal. Under an experimental point of view, this means that the design of the microfluidic device needs to account for the residence time of the desired crystal. If a metastable configuration is desired, optimisation of the channel design and photo polimerisation time is crucial to achieve the desired crystal. The authors also attempted to introduce a general framework based on the optimisation analysis, solving a large combinatorial problem after fixing a suitable objective function. By doing so, they obtained a non-trivial relation among channel geometry, injection policy, and the resulting geometry; however, their results could not be generalised in a unified framework due to the complexity of the original problem. We agree with the authors that the introduction of machine learning techniques can actually be able to transform the current problem in a deterministic one, where a desired crystal configuration can be achieved by using a specific channel design coupled to a specific injection policy. Future experimental and numerical works are still required to provide a unified framework of action to fabricate microfluidic crystals using hydrodynamic interactions among droplets.
000 structures per hour. Shen et al.66 suggested the potential of fabricating photonic materials by reducing the dimensions of the individual droplet size down to 400 nm and below. This hypothesis has recently been explored further by Morozov and Leshansky,70 who suggested to encapsulate the colloidal crystals formed by Shen et al.66 in a droplet, and then use hydrodynamic interactions among droplets to generate different crystals, by using a modified version of the setup by Postek et al.48 Morozov and Leshansky70 demonstrated numerically the emergence of the omnidirectional band gap in the cubic face centred (fcc) lattice dumbbells. They also reported that encapsulating tetrahedrons over fcc-templated dumbbells caused a reduction of the photonic properties. The results by Shen et al.66 remain, to the best of our knowledge, the only experimental data on the subject. More recently, numerical simulations67,71 have been carried out to replicate the experimental results of Shen et al.66 Ge et al.71 employed confined simple shear and Poiseuille flow as reference flows and showed that the crystal formation is mostly affected by the shear-induced cross-stream migration as long as attractive forces between droplets are present. The Poiseuille flow approximation is valid in 3D flow, meaning that the droplets do not ‘feel’ the presence of the walls and do not assume a ‘pancake’ shape: in such conditions, depletion forces between droplets are more relevant than the long-range dipolar interactions.67 The results by Ge et al.71 clarified that the crystal formation was a result of hydrodynamic interactions in 3D flow, but they did not provide a predictive framework that would allow crystal design a priori. Some steps in this direction have been made by Danny Raj et al.67 They first performed numerical simulations to evaluate the stability of the crystal-like structures introduced by Shen et al.66 (Fig. 6c). At time zero, the droplet configuration was the one by Shen et al.66 (first column in Fig. 6c); after a local perturbation, they studied the variation over time of the structure (second column in Fig. 6c), and quantified the modification using the structure parameter Φd (third column in Fig. 6c). Besides the mathematical definition of Φd (not reported here), the meaning of this parameter was that structural changes of the colloidal structure were reflected in a change of the Φd value. With reference to Fig. 6c, it is clear that there are some structures that are stable over time, while others evolve into a different crystal. Under an experimental point of view, this means that the design of the microfluidic device needs to account for the residence time of the desired crystal. If a metastable configuration is desired, optimisation of the channel design and photo polimerisation time is crucial to achieve the desired crystal. The authors also attempted to introduce a general framework based on the optimisation analysis, solving a large combinatorial problem after fixing a suitable objective function. By doing so, they obtained a non-trivial relation among channel geometry, injection policy, and the resulting geometry; however, their results could not be generalised in a unified framework due to the complexity of the original problem. We agree with the authors that the introduction of machine learning techniques can actually be able to transform the current problem in a deterministic one, where a desired crystal configuration can be achieved by using a specific channel design coupled to a specific injection policy. Future experimental and numerical works are still required to provide a unified framework of action to fabricate microfluidic crystals using hydrodynamic interactions among droplets.
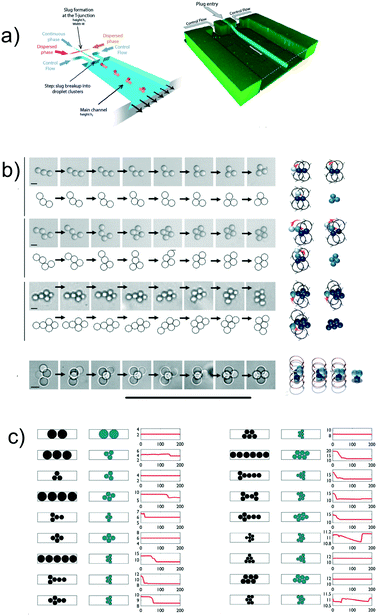 | ||
| Fig. 6 a) Schematic of the two-level microfluidic device (left) and confocal image of the system taken over long exposure times and comparison with numerical simulations (right). b) Rearrangement kinetic of several crystals with different initial configurations. Top panels are experimental snapshots with scale bar of 50 μm, while the bottom panels are obtained from numerical simulations. Panels a) and b) are reprinted from Shen et al.66 c) Structure configuration observed by Shen et al.66 and used as initial conditions for the numerical simulations by Danny Raj et al.67 (first column). Numerical simulation results outlining the equilibrium conditions resulting from a slight perturbation of the initial conditions (second column). Evolution of the form factor Φd defined in the text (third column). Reprinted from ref. 67, with permission of the Royal Society of Chemistry. | ||
4 Particle crystals
We now proceed to review crystal-like structures made of rigid particles. The most important difference between droplet and particle crystals is the way they are obtained. While the formation of droplets can be accurately controlled in a variety of microfluidic geometries,3 the same is not true for rigid particles. In other words, the interactions among droplet crystals can be controlled at the micrometer level, while the interactions among rigid particles depend upon their position along the microchannel cross-section and their mutual distances. The spatial distribution of the suspended particles cannot be controlled during the injection process, being the latter a random process. A way to manipulate the position of the particles along the channel cross-section is to exploit non-linear forces such as inertial and viscoelastic forces. Indeed, both forces are able to drive the flowing particles towards specific equilibrium positions depending on the channel geometry, flow rate, and properties of the suspending liquid, as well documented in several reviews.72–78 Once the particles reached the equilibrium position, at sufficiently large concentrations, they begin to interact, possibly leading to the formation of crystal-like structures. In this stage, the overall dynamics depends upon the mutual distance between all the interacting particles. This results in a complex collective motion even for the simplest case of an inertialess Newtonian fluid where pairing instabilities, cascades of pair-switching events, propagation of displacement waves occur.8,9,79,80 These phenomena prevent the formation of equally-spaced structures. On the other hand, inertia or viscoelasticity introduce strong non-linearities that, at some extent, might lead to a stable ordered microstructure. As a result, particle crystals can either be formed on a single fluid line (1D crystals) or on multiple flow lines (2D crystals), and they find several applications in particle/cell encapsulation, flow cytometry and material science, as described in section 5.In the following sections, we review the self-assembly of particles suspended in a fluid flowing in a microfluidic device induced by inertial or viscoelastic effects. We begin from the dynamics of a particle pair, that is the starting point to understand the particle–particle hydrodynamic interactions. The analysis is then extended to the more complex phenomenon of train formation with a focus on the capability of inertia or viscoelasticity to form stable ordered structures and the effect of the relevant parameters on the particle microstructure.
4.1 Inertial ordering
Before presenting the recent advancements in inertial ordering, it is worth to briefly mention the inertial particle focusing phenomenon. Particles suspended in a Newtonian fluid and flowing in a straight microchannel under inertial flow conditions experience a combination of forces which result in a net lift force FL quantified as FL = fLρu2dp4/DH2, where fL is a net lift force coefficient, u is the average flow velocity, dp is the particle diameter and DH is the hydraulic diameter. A full description of the inertial focusing process, which depends among several parameters, falls outside the scope of this review. In general, particles will migrate towards a variety of equilibrium positions depending upon the Reynolds number and the geometry of the microchannel. We refer the interested reader to the recent review by Tang et al.85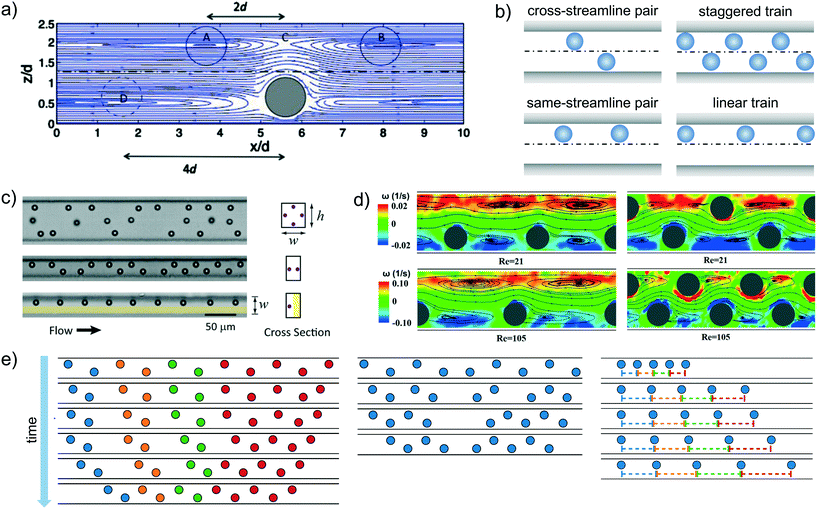 | ||
| Fig. 7 a) Streamlines around an isolated particle in the flow-gradient plane computed by numerical simulations. The solid and dotted circles suggest the equilibrium positions of adjacent particles. The channel has a rectangular cross-section 4 × 2.5 particle diameters and the particle Reynolds number is 1.25. Reprinted from Humphry et al.,81 Axial and lateral particle ordering in finite Reynolds number channel flows, Physics of Fluids, 22, 081703, 2010, with the permission of AIP publishing. b) Schematic representation of the cross-streamline and same-streamline pair configurations, and staggered and linear trains. c) Visualization of particle microstructure in a square-shaped microchannel with four equilibrium positions (top panel), a rectangular microchannel with two equilibrium positions (middle panel), in a rectangular microchannel with a coflow of a particle-free fluid that confines the particles on one side of the channel resulting in a single equilibrium position (bottom panel). Reprinted with permission from Lee et al.,82 Dynamic self-assembly and control of microfluidic particle crystals, Proceeding of the National Academy of Science, 2010, 07(52), 22413. d) Microscale flow structures around in-line (left) and staggered (right) particle trains obtained from micro-particle image velocimetry experiments at Re = 21 and Re = 105 on the middle plane of a rectangular microchannel. The streamlines of fluid flow relative to the particles are plotted with background contours indicating the vorticity magnitude. Reprinted from Pan et al.,83 Direct measurement of microscale flow structures induced by inertial focusing of single particle and particle trains in a confined microchannel, Physics of Fluids, 30, 102005, 2018, with the permission of AIP publishing. e) Evolution of staggered (left), staggered with defect (middle), and linear particle trains in time obtained by numerical simulations. Reprinted from Schaaf et al.,84 Particle pairs and trains in inertial microfluidics, The European Physical Journal E, 43, 2020. | ||
The stability of staggered particle pairs was also confirmed by detailed numerical simulations.84,87,88 The particles attracted each other over large distances without significant changes of the cross-stream position. Specifically, depending on the initial lateral positions and axial distance, four different kinds of trajectories were possible.88 If the leading particle was closer to the channel midline than the trailing one, it travelled faster and the two particles separated, migrating independently towards the inertial equilibrium position up to reach a distance so that they did not interact anymore. A second scenario occurred when the distance between the trailing particle and the channel midplane was much lower than that between the leading particle and the midplane. In this case, the trailing sphere travelled faster and overtook the leading one. Due to the strong hydrodynamic interactions, the particles were displaced along the cross-stream direction and the trailing sphere passed the leading one, and then separated. A third kind of dynamics was observed when the trailing sphere was again closer to the channel midplane than the leading one but the two distances were more similar. In this case, the faster trailing particle approached the leading one without passing. The strong hydrodynamic interactions determined a swapping of the lateral position, making the leading particle faster and the pair separated. Obviously these three scenarios do not lead to a stable configuration. In a range of initial positions where the distances between the two particles and the midplane was similar, the particles followed damped oscillatory trajectories up to reach an equilibrium position. The axial distance was about four times the particle radius, and it was independent of the initial particle positions and the Reynolds number.
The stability of a linear particle pair, i.e., the two particles are aligned along the same streamline of the flow field (Fig. 7b), is less clear. Numerical simulations showed that two aligned particles form a stable configuration with a preferential distance of 5 and 2.5 times the particle diameter at low and high particle Reynolds number, respectively.89 The stability of a same-streamline pair was also confirmed by the theoretical analysis of Hood and Roper86 and explained in terms of minimization of the fluid kinetic energy. In contrast, more recent numerical works did not find any stable fixed point in a linear particle pair.84,87,88 The two particles moved away one to each other up to reach a distance such that the hydrodynamic interactions vanished. This behavior was also observed in experiments where the interparticle spacing increased as the pair travelled along the channel.82 Detailed experiments have been recently performed in an oscillatory flow field aimed at increasing the distance travelled by the particles using a relatively small microchannel length.90 Both staggered and linear pairs were considered. In the former case, pair formation quickly occurred when the interparticle spacing reached a critical value, and the equilibrium configuration was very robust against external perturbations. Furthermore, a variation of the line concentration (defined as the particle diameter times the number of particles in the field of view and divided by the length of the field of view) did not affect the equilibrium distance. In contrast, the linear pair formed gradually and the interparticle distance fluctuated as the two particles travelled along the channel. In this same-streamline arrangement, the shape and the mean value of the interparticle spacing distribution strongly depend on the line concentration: lower concentrations spread out the distribution and move the peak towards larger distances.
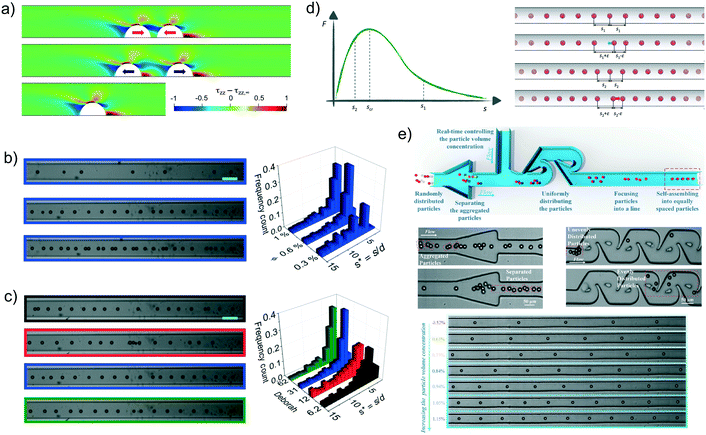
Regarding the stability of the trains, both experimental and numerical results confirmed that a staggered configuration is stable83,84,87,97 in line with the pair particle dynamics. Numerical simulations on a regular staggered configuration (left panel of Fig. 7e) and on a train with all the particles in a staggered arrangement except two middle particles that are placed on the same streamline (middle panel of Fig. 7e) clarified the train formation dynamics.84 In the case of a regular staggered structure with initial distances higher than the equilibrium one, the train contracts starting from the front and back in a non-uniform way, leading to a ‘cascade’ of pair formation. The overall velocity of a cluster of staggered particles is lower than that of isolated particles or pairs due to a reduction of the viscous drag, allowing the joining of isolated particles to the train. Regarding the case of a staggered configuration with two middle particles on the same line, the two particles increase their distance and the two parts of the train contract. Once the two small trains achieve the equilibrium configuration, the following dynamics depends on how many particles form the two trains. If the trailing train is made of less particles than the leading one, the latter is slower due to the enhanced viscous drag reduction and the trailing one joins. The equilibrium distance between the two in-line particles is about twice the axial distance between the staggered particles in agreement with experimental observations.93,94 An opposite scenario occurs if the trailing train has more particles than the leading one. In this case the trailing train moves faster and the two trains separate.
As for the particle pair, the available results assessing the stability of linear trains are controversial. Simulations reported that only linear trains formed by a limited number of particles were stable, where this number was between 2 and 4 depending on the particle Reynolds number and the confinement ratio.98 Numerical simulations with several aligned particles confirmed (right panel of Fig. 7e) that the interparticle spacing progressively increased without reaching a stable configuration.84,97 On the other hand, stable linear trains were observed in experiments.89,95 It has to be pointed out, however, that the train dynamics computed by numerical simulations84 showed an initial fast variation of the interparticle distances up to a value of about twice the distance between consecutive particles in a staggered configuration in line with experimental observations.89 In the second stage, the particles continued to drift apart from each other at a much lower rate, making the separation dynamics hardly detectable through experimental observations. Interestingly, the distribution of the particle spacing in random linear trains well reproduced the experimental one,89 confirming the robustness of the numerical predictions.
4.2 Viscoelastic ordering
Before presenting the recent advancements in viscoelastic ordering, we briefly describe the viscoelastic particle focusing phenomenon. When the viscoelastic suspending liquid presents a near constant-viscosity, particles migrate transversally to the flow direction towards the centreline of a circular or square-shaped channel with a migration velocity given by78,102VM ∼ dp2∇![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) /η, where η is the fluid viscosity, dp is the particle diameter and ∇
/η, where η is the fluid viscosity, dp is the particle diameter and ∇![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) is the shear rate gradient along the channel cross-section. When particles are suspended in a near constant-viscosity liquid, the direction of the particle migration does not depend upon the particle diameter, meaning that the particles will always migrate towards the centreline of a circular or square-shaped straight microchannel.75,78,103 When the viscoelastic suspending liquid presents shear-thinning features (i.e., the viscosity decreases with increasing the shear rate
is the shear rate gradient along the channel cross-section. When particles are suspended in a near constant-viscosity liquid, the direction of the particle migration does not depend upon the particle diameter, meaning that the particles will always migrate towards the centreline of a circular or square-shaped straight microchannel.75,78,103 When the viscoelastic suspending liquid presents shear-thinning features (i.e., the viscosity decreases with increasing the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) ), it was found104,105 that particles migrate towards the centreline of a square-shaped microchannel only if β ≥ 0.2, while migrating towards both the centreline and the four corners of the channel when β ≤ 0.2 (for a cylindrical geometry, the four corners are replaced by the circular walls). In the case of shear-thinning suspending liquids, there are no explicit expression relating the migration velocity to the properties of the suspending liquids. The interested reader can find more details regarding viscoelastic focusing in the recent review by Zhou and Papautsky.78
), it was found104,105 that particles migrate towards the centreline of a square-shaped microchannel only if β ≥ 0.2, while migrating towards both the centreline and the four corners of the channel when β ≤ 0.2 (for a cylindrical geometry, the four corners are replaced by the circular walls). In the case of shear-thinning suspending liquids, there are no explicit expression relating the migration velocity to the properties of the suspending liquids. The interested reader can find more details regarding viscoelastic focusing in the recent review by Zhou and Papautsky.78
 | ||
| Fig. 8 a) Difference between the zz-component of the viscoelastic stress tensor and the same component of the unperturbed fluid for a particle pair (top and middle panel) or a single sphere (bottom panel) in a viscoelastic fluid modelled with the Giesekus constitutive equation. The Deborah number is De = 1, the confinement ratio is β = 0.4, and the Giesekus mobility parameter is α = 0.2. The pairs in the top and middle panels have an initial center-to-center distance of 1.25 and 2 particle diameters, respectively. Adapted by permission from Springer Nature: Microfluidics and Nanofluidics: Numerical simulations on the dynamics of a particle pair in a viscoelastic fluid in a microchannel: effect of rheology, particle shape, and confinement, D'Avino et al.,99 Copyright 2019. b) and c) Visualization of particle microstructure and interparticle distance distributions for a suspension of polystyrene particles in a shear-thinning solution of 1% wt hyaluronic acid in PBS at De = 31 and different volume fractions (b) and at ϕ = 0.6% and different Deborah numbers (c). Reproduced from Del Giudice et al.,100 Copyright 2018, American Physical Society. d) (Left) Sketch of the repulsive force between two particles in a viscoelastic fluid for a sufficiently high Deborah number. (Right) Schematic representation of the stability analysis of a particle train: a train of equally spaced particles at a distance s1 > scr is considered (first panel). A particle of the train is displaced by a small amount ε and experiences two different repulsive forces from the trailing and the leading sphere. Since s1 is in the branch where the force F has a negative slope, the force between the displaced particle and the leading one is lower than the force between the particle and the trailing sphere. The net force is, then, toward the trailing sphere (blue arrow) and the interparticle distances are restored to the original value s1 (second panel). The same scenario is considered with an equilibrium distance s2 < scr (third panel). After displacing the particle, the force between the displaced sphere and the leading one is higher than the force between the particle and the trailing sphere. Thus, the displaced sphere moves toward the leading one and a pair is formed (fourth panel). Reprinted with permission from Del Giudice et al.,100Physical Review Applied, 10, 064058, 2018 Copyright (2018) by the American Physical Society. e) Schematic illustration of the microfluidic channel based on an array of swirl mixing channels. Snapshots of the particle arrangements in the array of inverted triangular microchannels, in an array of swirl mixing channels, and in the final straight microchannel (at different particle concentrations) are shown. Reprinted from ref. 101 with permission from the Royal Society of Chemistry. | ||
The case of three aligned particles showed a richer behavior106 as the dynamics depends on two relative distances. For a Newtonian inertialess fluid, the long-time configuration consists in a pair made of the trailing and middle sphere whereas the leading one moves far away until becoming isolated.80,106 The distance of the particles forming the pair achieves a constant value depending on the two initial relative distances. In a viscoelastic fluid, the triplet dynamics is more complex and, as for the pair, the Deborah number is the most relevant parameter in order to identify possible scenarios. For values lower than a threshold Decr, the triplet dynamics is determined by the two relative distances. For an initial configuration such that at least one of these two distances is below a critical value, the leading and middle sphere reduce their distance, whereas the leading one moves away. The long-time configuration is then made of a doublet (trailing and middle particles) and an isolated sphere (leading particle). In contrast, for initial distances higher than a critical value, both relative distances increase in time leading to the formation of three isolated particles. The latter is the only possible scenario for a Deborah number higher than Decr.
The theoretical analysis of the dynamics of pairs and triplets of particles aligned at the centerline of a microchannel and immersed in a viscoelastic liquid showed the existence of an unstable critical distance. Consequently, two particles can reduce their distance while traveling along the channel forming a doublet or move far away until becoming isolated. The latter scenario is favored at high Deborah numbers and for strongly shear-thinning fluids. In a system made of several aligned particles at a sufficiently high volume fraction, each particle is surrounded by a trailing and leading particle. Let us assume that two particles of the train are at a distance higher than the critical one so that they move away. At some point both particles will ‘feel’ the presence of the surrounding particles, preventing the formation of isolated particles. As one particle starts to hydrodynamically interact with the next (or the previous) one, viscoelasticity immediately prevents them to approach as the distance between the new pair is of course higher than the critical one. A balance of these ‘repulsive forces’ suggests the possibility to generate a microstructure made of equally-spaced particles.
Numerical simulations have been also carried out to understand the train dynamics.100,108 To follow the motion of a large number of particles, the simulations assumed that each particle of the train hydrodynamically interacted with the previous and the next one, ignoring the presence of the other particles. Hence, the train could be decomposed in several systems made of three particles for which the relative velocities needed to update the relative distances were computed through direct numerical simulations.106 The simulation results confirmed the experimental evidences, reporting no relevant ordering at low volume fractions, a preferential distance at higher volume fractions, and a more and more frequents of doublets as the volume fraction is further increased. An interesting outcome of the simulations was the formation of doublets even at a Deborah number higher than the critical value Decr where two or three spheres repelled regardless of their relative distances. A qualitative argument based on a stability analysis was proposed to justify this behavior.100 With reference to Fig. 8d, a train of equally-spaced particles at some distance s1 is considered. In the left panel of Fig. 8d, a schematic of the interparticle force between a pair as a function of the relative distance is sketched for De > Decr based on direct simulation results.106 The force is positive for any distance denoting that the two particles separate. Let us also assume that the equilibrium distance of the train is larger than the critical distance corresponding to the maximum in Fig. 8d. If one particle of the train was displaced approaching the leading one, the relative distance between these two particles reduce, corresponding to an increase of the repulsive force. Similarly, as the displaced particle moves far away from the trailing one, the distance increases corresponding in a lower force. As a result, the net force acting on the displaced particle is opposite to the direction of the displacement and the original train is restored. On the contrary, for a train characterized by an equilibrium distance lower than the maximum, a displaced particle feels a force directed towards the direction of the displacement, forming a doublet (bottom panel of Fig. 8d).
Experiments and simulations also highlighted the importance of the initial distribution of the interparticle distances. Indeed, once aligned at the centerline, particles that ended up very close one to each other were hardly separated while traveling through the channel,100,101,108 obviously reducing the ordering efficiency. The microfluidic device must be properly designed in order to prevent the injection of agglomerates of particles from the reservoir or to separate the aligned particles before ordering takes place. The latter was accomplished by designing a channel with an array of swirl mixing channels101 shown in Fig. 8e. The overall device was made of a sequence of inverted triangular microchannels and straight microchannels aimed at separating the particles. The suspension then passed through the array of swirl mixing channels, leading to a spatial uniform distribution of the flowing particles. Finally, the suspension reached a straight channel where first focusing and then ordering took place. A lateral channel where the suspending fluid was injected was placed between the two sets of geometrical elements in order to adjust the volume fraction. The results showed the formation of highly equally-spaced structures for particle volume concentration from 0.5% to 1.15% (bottom panel of Fig. 8e).
The aforementioned studies clearly showed the capability of viscoelastic fluids to self-assemble particles in equally-spaced aligned structures. A relevant aspect of using elastic effects was that focusing and then ordering took place in the same microchannel. At variance with inertial ordering, the formation of a train was along the channel centerline with several advantages for a variety of microfluidic applications. For instance, at the channel centerline the shear stresses experienced by the particles are minimal, allowing the processing of soft cells. Also, the rotation rate of the aligned particles/cells is small (in theory nil for a perfect alignment) avoiding blurred images in cytometry applications that employ line-scan based interrogation.
Several aspects, however, need to be further investigated. The formation of doublets or, more in general, of strings of particles in contact, is a critical issue. The presence of strings is due to the direction of the viscoelastic normal forces acting between two aligned particles. Crucial is the initial distribution of the particle distances and, in particular, the presence of close particles after the focusing mechanism. Even when the elastic forces between adjacent particles tend to separate them regardless the relative distance, string formation is still observed. A properly design of the feeding process aimed at avoiding the formation of agglomerates of particles is required. An important parameter affecting the probability of string formation is the particle volume concentration. A relatively large value promotes particle pairing with a detrimental effect on the ordering efficiency. On the other side, a low value of particle volume concentration may result in large average interparticle distances and weak hydrodynamic interactions so that the train microstructure does not change. Hence, viscoelastic ordering properly works in a window of solid volume concentration. In fact, rather than the nominal particle volume concentration, a more relevant quantity to be considered to assess the quality of the ordering is the local volume concentration, i.e., the concentration of particles along the train. Such a quantity may strongly vary during an experiment due to disturbances of the applied flow rate or pressure drop, or to the presence of an agglomerate of particles in the reservoir. These disturbances may lead to zones of the train with or without several particles, reducing in both cases the ordering efficiency.
The re-arrangement of the microstructure hopefully leading to an equally-spaced train is due to a difference of the translational velocity of the flowing particles, resulting in a continuous variation of their mutual distances. The relative velocity between consecutive particles is 3–4 orders of magnitude lower than their translational velocity. Hence, microchannels with a length much larger than the characteristic size of the cross-section are required to obtain an appreciable modification of the interparticle distance distribution. For instance, in a straight microchannel with length one thousand times higher than the side of the cross-section the distance distribution is still evolving as the train reaches the end of the channel.100,108 Curved or spiraling microchannels could help in extending the total length while keeping the overall chip surface small. In this case, the effect of a curvature of the streamlines of the flow field on the ordering dynamics should be investigated. Another possibility could be the periodical inversion of the flow field in a straight channel to mimic an infinite length as adopted for inertial ordering90 or for enhancing the viscoelastic focusing.109 An inversion of the flow, however, leads to a transient redistribution of the viscoelastic stresses between the particles, likely affecting the ordering mechanism.
The physical mechanism behind the dynamics of the pair is quite well-understood and the effect of the relevant parameters (rheology, flow rate, confinement ratio) has been thoroughly investigated. A similar in-depth theoretical analysis for the triplet dynamics is not available and only a couple of Deborah numbers have been analyzed. Since the train dynamics is determined by the interaction of each particle with at least the trailing and leading one, a more detailed study on the three-particle system is required. Similarly, the experimental and numerical studies on the train dynamics are limited to a couple of suspending fluids and to a fixed value of the confinement ratio. Regarding the fluid rheology, experiments have evidenced that ordering is possible in a shear-thinning fluid, while a sequence of particle strings are observed in an elastic fluid characterized by a constant viscosity. Although this is partially confirmed by the theoretical analysis on the pair dynamics, a clear explanation is missing. Similarly, the effect of the confinement ratio on the train dynamics is not yet explored. A useful information comes from the pair dynamics where lowering the confinement ratio results in a significant reduction of the relative velocity. This is expected as the hydrodynamic interactions between smaller particles are weaker. Furthermore, a lower confinement ratio also leads to an extension of the attractive region between the particles of the pair at higher Deborah numbers. On the basis of these results, a suspension of smaller particles would require much longer channels to re-arrange the microstructure and the formation of strings is favored.
Finally, it has to be mentioned that the available results have investigated the possibility to achieve ordering by exploiting purely viscoelastic effects. The flow and fluid conditions, indeed, are such that the Reynolds number is much less than unity, ruling out inertial effects. Motivated by the successful combination of inertia and viscoelasticity to enhance particle focusing,76,78 the ‘inertio-elastic ordering’ might have interesting potentialities. For instance, inertial effects, that generally produce opposite results with respect to elastic ones, could reduce (or even revert) the direction of the repulsive interparticle forces and promote the formation of more stable trains. This possibility definitely merits further investigation.
5 Microfluidic crystals and compartmentalisation
Formation of droplet and particle crystals can be seen as the ‘prelude’ to a vast range of applications featuring both types of crystals. On the one hand, microfluidic crystals can be used to enhance the compartmentalisation efficiency of particles and cells in order to defeat the Poisson statistic problem, which is a very important aspect when targeting single-cell analysis.93,110–113 On the other hand, compartmentalisation of either rigid particles or liquid droplets in another larger droplet where they can self-assemble in ordered crystals (similarly to the work by Postek et al.48) is appealing for the fabrication of colloidal crystals114,115 and photonic materials.116 In this section, we review some of the most recent advances in microfluidic crystals and compartmentalisation, citing also some pioneering works in the field. A broader overview of the applications related to microfluidic compartmentalisation (not only crystals) can be found in the following recent reviews: encapsulation,117 single-cell analysis,118 multiple emulsions,119,120 self-assembly,121 and production of biomaterials.1225.1 Deterministic encapsulation
Deterministic encapsulation (or compartmentalisation) is a procedure where a constant pre-defined number of objects (particles or cells) are encapsulated in each single droplet without empty droplets nor a different number of objects per droplet. The deterministic encapsulation can take place when the frequency of droplet formation is proportional to the frequency of the objects reaching the encapsulation area. For instance, to encapsulate one particle in one droplet, the frequency of the particle crystal approaching the encapsulation area should be equal to the droplet crystal formation frequency. A purely hydrodynamic deterministic encapsulation can then take place when droplet crystals ‘meet’ particle crystals at the encapsulation area. Edd et al.93 were among the firsts to introduce this concept and demonstrated that inertially-formed particle trains flowing on two equilibrium lines (2D particle crystal) coupled to a flow focusing droplet geometry for the generation of 1D droplet crystals led to the controlled encapsulation of particles in droplets with an efficiency of over 80%. This approach has been perfected later by Kemna et al.110 that employed a spiral microfluidic channel to form 1D particle crystals by reducing the focusing equilibrium position of the particles from two (as in Edd et al.93) to one. Other ways to increase the encapsulation efficiency such as complex geometries,112 and multi-droplet merging113 have been also introduced. However, these studies mainly focused on the encapsulation of a single object, whereas in applications such as drop-sequencing,125 where barcoded beads are encapsulated together with cells for single-cell analysis, it is important to encapsulate two objects simultaneously (e.g., one particle and one cell). Lagus and Edd111 employed a microfluidic device where two sets of particles or cells were encapsulated simultaneously in a single droplet with an efficiency of 65%, 5-folds larger than the one dictated by the Poisson statistic. We now highlight two recent works that successfully employed 1D particle and cell train crystals for single-cell analysis using Drop-seq techniques. Moon et al.126 used a spiral microfluidic channel to obtain inertial-driven 1D particle crystals; the spiral channel was coupled to a flow-focusing geometry where flowing cells were then encapsulated together with the barcoded particles with an efficiency of roughly 98%. In this way, the authors performed single-cell RNA extraction from HEK293 and IH3T3 mouse cell lines. Despite a substantial efficiency improvement, a step further was introduced by Li et al.123 that employed two independent spiral channels to self-order both particles and cells prior to the encapsulation area (Fig. 9a). By synchronising the frequency of particle and cell arrival with that of droplet formation, they obtained up to 300% increase in cell-utilisation rate compared to conventional Drop-seq techniques. To the best of our knowledge, the two works above are the only ones that employed inertial ordering finalised to Drop-seq analysis. Follow-up works will need to achieve truly deterministic encapsulation, meaning an efficiency of 100%, which would lead to the identification of rare cells such as circulating tumour cells. Moreover, the formation of particle crystals in viscoelastic solutions is an entirely new field that is awaiting further developments. We are currently not aware of any work featuring the encapsulation of particles or cells in polymer solutions: we ascribe this to the fact that droplets made of polymer solutions are difficult to form because of the elastic stresses that delay the droplet formation at the microfluidic junction.127 An interesting variation to the encapsulation strategies presented above has been introduced by Clark and Abate128 where droplet formation was ‘triggered’ by the beads and the cells during their flow. The authors successfully achieved bead-cell encapsulation at a rate of 20 kHz. We expect that this method can be optimised to account for different cell lines as well as different cell types. It also offers a promising route to achieve Drop-seq technologies in a centrifugal microfluidic device, as the continuous phase could be pre-loaded, while the dispersed phase containing the particles could then trigger the encapsulation. This is particularly challenging because, to our knowledge, there are no works featuring train formation in centrifugal microfluidic devices: addressing this issue can open new opportunities for centrifugal microfluidics.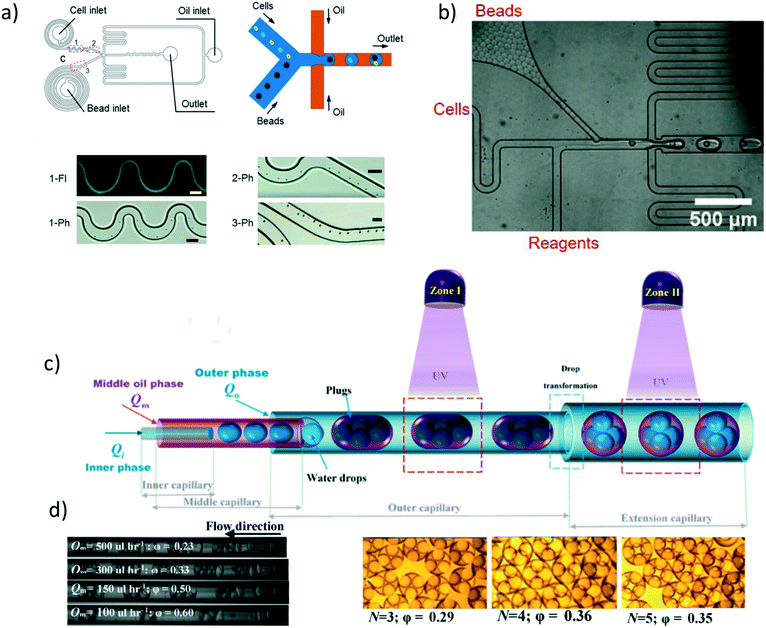 | ||
| Fig. 9 a) Dean-flow assisted 1D cell and particle inertial crystal formation for Drop-seq analysis. Schematic of the device and experimental snapshots are also reported. Reprinted with permission from Li et al.,123 Dean flow assisted single cell and bead encapsulation for high performance single cell expression profiling, ACS Sensors, 4, 1299, Copyright 2019, American Chemical Society. b) Microfluidic device employed to deterministically dissolve polyacrylamide barcoded beads in droplets containing cells. Reprinted from Wang et al.,124 Dissolvable polyacrylamide beads for high-throughput droplet DNA barcoding, Advanced Science, 7(8), 1903463, 2020. c) ‘On the fly’ fabrication of porous microparticles using double emulsions. Droplets self-assemble in crystals within another larger droplet and are photopolymerised. d) Experimental snapshots of double emulsions in different flow conditions (left) and self-assembled structures (right). Panels c) and d) are reprinted with permission from Sajjadi et al.,115 ‘On-the-fly’ fabrication of highly-ordered interconnected cylindrical and spherical porous microparticles via dual polymerization zone microfluidics, Langmuir, 35, 12731, Copyright 2019, American Chemical Society. | ||
Another technique to encapsulate cells together with particles was introduced by Abate et al.129 Instead of using rigid particles that can clog the channel at large concentrations, the authors employed deformable microgels that were self-assembled to form a 2D droplet crystal in a near-tapered geometry (similarly to Gai et al.21). The 2D crystal was then forced to flow in a channel with size equal to that of a single microgel while two lateral channels pumping water contributed to equally-space the microgels in a 1D microgel crystal. Finally, the microgels in the 1D crystal were encapsulated using downstream flow-focusing droplet formation, with 98% efficiency. This approach, however, could not be used for Drop-seq applications as there was the need of introducing easy to fabricate deformable barcoded particles (in contrast with the most common rigid ones). Very recently, this problem has been addressed by Wang et al.124 that reported continuous microfluidic fabrication of dissolvable barcoded polyacrylamide beads. They employed a device where the dissolvable beads were arranged in a 2D crystal using a nearly tapered device (Fig. 9b). The authors employed the beads for single cell RNA protein analysis. Considering that the production of soft barcoded beads has been presented only recently and that cells were not ordered in the work by Wang et al.,124 we soon expect new works featuring the deterministic Drop-seq of cells using dissolvable barcoded beads.
5.2 Crystal formation in droplets
The possibility of forming crystal-like structures within droplets in microfluidic devices has been introduced by Yi et al.130 The authors first encapsulated microspheres using the same device of Thorsen et al.;11 while moving downstream, the water layer of the droplet surrounding the microspheres was slowly absorbed by the oil (continuous phase) causing droplet shrinkage and self-assembly of the particles in the droplet. Similar approaches have been also explored for the formation of colloidosomes,131 celloidosomes,132 photonic materials116 and three-tier hierarchical assemblies.133 However, with the exception of the work by Yi et al.,130 these approaches required a step external to the microfluidic device in order to facilitate the droplet evaporation with consequent self-assembly of the compartmentalised particles. Controlled self-assembly of several structures containing chemically functionalised particles has instead been introduced by Xu et al.114 In their work, the authors were able to fabricate droplet crystals having different structures based on the combination of chemical particle properties and self-assembly internal to the droplets. The final configuration of the crystal was expected to depend upon the chemical composition of the particles, thus requiring future works in order to clarify how chemical properties of the particles affect the crystal formation.A more controlled approach for the fabrication of compartmentalised crystal structures is based on doublet emulsions, i.e., a multiple-phase dispersion in which droplets enclosing fined droplets are suspended in a continuous liquid phase134,135 (the interested reader is referred to the recent review by Sattari et al.119). An interesting development has been presented by Sajjadi et al.115 who introduced a microfluidic device for the formation of double emulsions based on the co-flow droplet generation geometry. With reference to Fig. 9c, the double emulsions were formed first; then, the shape of their external droplet changed according to the diameter of the two series of capillaries. Two photopolymerisation zones were added to then polymerise the assembled structures. The advantage of this approach over others was the fact that the large droplet relaxed in a more spherical configuration when the double emulsion reached the last microchannel: consequently, the internal droplets self-assembled within the larger droplet in crystals that were thermodynamically favoured, thus making the whole process pseudo-deterministic, with very well defined crystal-like structures (left snapshots in Fig. 9d). After polymerisation, the external layer of the large droplet ruptured, resulting in the formation of hollow particles. We expect this approach to be useful also for the fabrication of plasmonic materials as previously suggested by Morozov and Leshansky.70 A similar technique can be coupled to that by Shen et al.66 to obtain a rich portfolio of colloidal structures having different properties. Recent advances in the understanding of the fluid dynamics of the fluid inside the double emulsions136,137 is also expected to simplify the fabrication of colloidal structures.
6 Conclusions and perspectives
The advent of microfluidics contributed to introduce a vast range of tools to control the position of objects down to the sub-micrometer scale, thus enabling the generation of crystal-like structures in confined flows. A significant amount of literature has been published on microfluidic crystals. Some of these works highlight the physical mechanisms behind the self-assembly of droplets/particles mediated by hydrodynamic interactions, the stability of the microstructure, and the effect of the relevant parameters. Other works focus on the engineerization of the crystal-like structures introducing new droplet-based technologies for single-cell analysis or colloidal synthesis, devices for deterministic encapsulation, etc. The physical mechanism governing the collective motion of droplets is of different nature as compared to that involved in self-assembly of particles induced by inertia or viscoelasticity. In the former case, the inter-droplets forces are generated by the disturbance of the flow field induced by the droplet motion coupled with confinement effects, resulting in a dipole–dipole interaction. Inertial ordering of particles is, instead, driven by inertial forces that push the particles to equilibrium positions and repulsive viscous forces that stabilize the microstructure setting the inter-particle spacing. Elastic forces, originated by the orientation and stretching of polymer chains under flow, rule viscoelastic ordering. These forces lead to the alignment of particles along the channel centreline and modulate the inter-particle spacing. The different underlying self-assembly mechanisms reflect on different stability properties of the formed crystals as well as on the dimensionality of the resulting structures. Droplets can arrange in 1D, 2D, and 3D structures depending on the microchannel geometry. 1D equally-spaced structures can be easily generated with a well-controlled spacing. However, their stability requires strong confinements in two directions. In unconfined geometries, transversal local fluctuations of the droplet crystal may grow, leading to crystal instability. In contrast, 1D structures of particles are more stable as a transversally displaced particle is restored to its equilibrium position along the train by an inertial or viscoelastic lateral force component. Since particles are not formed but are randomly injected in the microchannel, the control of the inter-particle spacing is not straightforward. Research is active in this direction to understand the conditions leading to equally-spaced structures in inertial and viscoelastic ordering, required to design efficient particle-in-droplet encapsulation devices.Despite the different mechanisms involved in droplet and particle crystal formation, the underlying physics have several common features. First, all the governing forces are of hydrodynamic nature, leading to the formation of the microstructure without the need of external forces. Furthermore, the formation and evolution of both droplet and particle crystals is strongly affected by confinement effects, making microfluidics the natural framework to work with. Finally, the phonon-like behaviour in 1D structures has been observed in droplet crystals, inertial and viscoelastic ordering. We believe that there is a need to tackle the phenomenon of microfluidic crystal formation under a more holistic point of view, where a detailed understanding of the hydrodynamic interactions among different objects (i.e., particles, cells, droplets) can lead to a generalised framework to design a priori microfluidic devices for targeted applications.
There is room for developing new technologies that are currently missing. The recent fabrication of barcoded dissolvable beads124 together with the principles of deterministic encapsulation129 may open a new generation of optimised Drop-seq technologies. The experimental evidence of particle ordering on the centreline of a straight microchannel when the suspending liquid is viscoelastic and shear-thinning is expected to drive new research.
Continuous generation of viscoelastic droplets will also close the gap with inertial microfluidics, enabling further studies on viscoelastic Drop-seq technologies. The capability of self-order different kinds of particles and encapsulate them in a multi-droplet system would generate an isolated environment where complex reactions, mass transfer, biological activity, controlled drug release, etc. could take place. Similarly, recent advances in colloidal crystal fabrication can prompt new directions in material science for the production of photonic materials, provide new tools for drug delivery applications, generate complex structures from simple building blocks, combine objects with different physical or chemical properties to create a material with unique characteristics. Very recently, an interest in the self-assembly of ‘active’ droplets and particles arose,138–140 with potential advancements in the field yet to be explored.
Finally, the advent of machine learning and artificial intelligence can provide a significant boost to the field (see the recent review by Isozaki et al.141). The complexity of solving a multi-body problem associated to crystal formation could be tackled by using machine learning techniques with predictive outcomes, thus leading to a AI-aided technology for crystal design. Similarly, deterministic encapsulation could be triggered by artificial intelligence consequently to object recognition.142,143 The capacity of elaborating large amount of data together with intrinsic predictive functionalities, makes artificial intelligence among the most suitable candidates to face the challenges associated to the derivation of a general framework for the production of microfluidic crystals.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
FDG acknowledges support from EPSRC New Investigator Award (Grant Ref. No. EP/S036490/1).References
- A. Stevenson, Oxford dictionary of English, Oxford University Press, USA, 2010 Search PubMed.
- T. M. Squires and S. R. Quake, Rev. Mod. Phys., 2005, 77, 977 CrossRef CAS.
- J. Nunes, S. Tsai, L. D. Landau, E. M. Lifshitz, J. Wan and H. A. Stone, J. Phys. D: Appl. Phys., 2013, 46, 114002 CrossRef PubMed.
- P. Zhu and L. Wang, Lab Chip, 2017, 17, 34–75 RSC.
- J. Guerrero, Y.-W. Chang, A. A. Fragkopoulos and A. Fernandez-Nieves, Small, 2020, 16, 1904344 CrossRef CAS PubMed.
- T. Beatus, R. H. Bar-Ziv and T. Tlusty, Phys. Rep., 2012, 516, 103–145 CrossRef.
- T. Beatus, I. Shani, R. H. Bar-Ziv and T. Tlusty, Chem. Soc. Rev., 2017, 46, 5620–5646 RSC.
- T. Beatus, T. Tlusty and R. Bar-Ziv, Nat. Phys., 2006, 2, 743–748 Search PubMed.
- T. Beatus, R. Bar-Ziv and T. Tlusty, Phys. Rev. Lett., 2007, 99, 124502 CrossRef PubMed.
- J.-B. Fleury, U. D. Schiller, S. Thutupalli, G. Gompper and R. Seemann, New J. Phys., 2014, 16, 063029 CrossRef.
- T. Thorsen, R. W. Roberts, F. H. Arnold and S. R. Quake, Phys. Rev. Lett., 2001, 86, 4163 CrossRef CAS PubMed.
- L. D. Landau and E. M. Lifshitz, Fluid Mechanics, Pergamon Press, 1987.
- B. Liu, J. Goree and Y. Feng, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 046309 CrossRef PubMed.
- I. Sarig, Y. Starosvetsky and A. D. Gat, J. Fluid Mech., 2016, 800, 264–277 CrossRef.
- Y. Green, J. Fluid Mech., 2018, 853, 253–270 CrossRef CAS.
- L. Wang and J. Wang, Nanoscale, 2019, 11, 16708–16722 RSC.
- A. C. Hatch, J. S. Fisher, A. R. Tovar, A. T. Hsieh, R. Lin, S. L. Pentoney, D. L. Yang and A. P. Lee, Lab Chip, 2011, 11, 3838–3845 RSC.
- V. Chokkalingam, S. Herminghaus and R. Seemann, Appl. Phys. Lett., 2008, 93, 254101 CrossRef.
- U. D. Schiller, J.-B. Fleury, R. Seemann and G. Gompper, Soft Matter, 2015, 11, 5850–5861 RSC.
- S. Thutupalli, J.-B. Fleury, U. D. Schiller, G. Gompper, S. Herminghaus and R. Seemann, in Engineering of Chemical Complexity II, World Sci., Singapore, 2014, vol. 12, p. 125 Search PubMed.
- Y. Gai, C. M. Leong, W. Cai and S. K. Tang, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 12082–12087 CrossRef CAS PubMed.
- W. T. Read and W. Shockley, Phys. Rev., 1950, 78, 275 CrossRef CAS.
- Y. Gai, A. Bick and S. K. Tang, Phys. Rev. Fluids, 2019, 4, 014201 CrossRef.
- B. M. Jose and T. Cubaud, Microfluid. Nanofluid., 2012, 12, 687–696 CrossRef CAS.
- M. D. Raj and R. Rengaswamy, Microfluid. Nanofluid., 2014, 17, 527–537 CrossRef.
- S. Yang, S. W. Ahn, A. R. Kang, D. Lee, S. S. Lee, J. M. Kim, K. H. Ahn and S. J. Lee, Korea Aust. Rheol. J., 2011, 23, 119 CrossRef.
- M. Seo, Z. Nie, S. Xu, P. C. Lewis and E. Kumacheva, Langmuir, 2005, 21, 4773–4775 CrossRef CAS PubMed.
- B. Shen, M. Leman, M. Reyssat and P. Tabeling, Exp. Fluids, 2014, 55, 1728 CrossRef.
- T. Ohmura, M. Ichikawa, K.-i. Kamei and Y. T. Maeda, Appl. Phys. Lett., 2015, 107, 074102 CrossRef.
- E. Kadivar, Phys. A, 2016, 443, 486–494 CrossRef CAS.
- E. Kadivar, M. Farrokhbin and F. Ghasemipour, Braz. J. Phys., 2019, 49, 140–150 CrossRef CAS.
- R. Mehrotra, N. Jing and J. Kameoka, Appl. Phys. Lett., 2008, 92, 213109 CrossRef.
- A. C. Hatch, J. S. Fisher, S. L. Pentoney, D. L. Yang and A. P. Lee, Lab Chip, 2011, 11, 2509–2517 RSC.
- C. Priest, S. Herminghaus and R. Seemann, Appl. Phys. Lett., 2006, 88, 024106 CrossRef.
- P. Parthiban, P. S. Doyle and M. Hashimoto, Soft Matter, 2019, 15, 4244–4254 RSC.
- M. Seo, Z. Nie, S. Xu, M. Mok, P. C. Lewis, R. Graham and E. Kumacheva, Langmuir, 2005, 21, 11614–11622 CrossRef CAS PubMed.
- S. Fujiwara, K. Shoji, C. Watanabe, R. Kawano and M. Yanagisawa, Micromachines, 2020, 11, 701 CrossRef PubMed.
- J.-P. Raven and P. Marmottant, Phys. Rev. Lett., 2009, 102, 084501 CrossRef PubMed.
- A. Montessori, M. Lauricella, A. Tiribocchi and S. Succi, Phys. Rev. Fluids, 2019, 4, 072201 CrossRef.
- J. Wang, M. Jin, T. He, G. Zhou and L. Shui, Micromachines, 2015, 6, 1331–1345 CrossRef.
- K. E. Sung, S. A. Vanapalli, D. Mukhija, H. A. McKay, J. Mirecki Millunchick, M. A. Burns and M. J. Solomon, J. Am. Chem. Soc., 2008, 130, 1335–1340 CrossRef CAS PubMed.
- D. Dendukuri and P. S. Doyle, Adv. Mater., 2009, 21, 4071–4086 CrossRef CAS.
- M. Hashimoto, P. Garstecki and G. M. Whitesides, Small, 2007, 3, 1792–1802 CrossRef CAS PubMed.
- M. D. Raj and R. Rengaswamy, Ind. Eng. Chem. Res., 2015, 54, 10835–10842 CrossRef CAS.
- C. M. O'Keefe, A. M. Kaushik and T.-H. Wang, Anal. Chem., 2019, 91, 11275–11282 CrossRef PubMed.
- Y. He, J. Yin, W. Wu, H. Liang, F. Zhu, Y. Mu, H. Fan and T. Zhang, Anal. Chem., 2020, 92, 8530–8535 CrossRef CAS PubMed.
- M. Nie, M. Zheng, C. Li, F. Shen, M. Liu, H. Luo, X. Song, Y. Lan, J.-Z. Pan and W. Du, Anal. Chem., 2019, 91, 1779–1784 CrossRef CAS PubMed.
- W. Postek, P. Gargulinski, O. Scheler, T. S. Kaminski and P. Garstecki, Lab Chip, 2018, 18, 3668–3677 RSC.
- X. Li, D. Zhang, W. Ruan, W. Liu, K. Yin, T. Tian, Y. Bi, Q. Ruan, Y. Zhao and Z. Zhu, et al. , Anal. Chem., 2019, 91, 13611–13619 CrossRef CAS PubMed.
- C. D. Ahrberg, A. Manz and B. G. Chung, Lab Chip, 2016, 16, 3866–3884 RSC.
- K. R. Sreejith, C. H. Ooi, J. Jin, D. V. Dao and N.-T. Nguyen, Lab Chip, 2018, 18, 3717–3732 RSC.
- J. Yin, Y. Suo, Z. Zou, J. Sun, S. Zhang, B. Wang, Y. Xu, D. Darland, J. X. Zhao and Y. Mu, Lab Chip, 2019, 19, 2769–2785 RSC.
- D. Pekin, Y. Skhiri, J.-C. Baret, D. Le Corre, L. Mazutis, C. B. Salem, F. Millot, A. El Harrak, J. B. Hutchison and J. W. Larson, et al. , Lab Chip, 2011, 11, 2156–2166 RSC.
- V. R. Yelleswarapu, H.-H. Jeong, S. Yadavali and D. Issadore, Lab Chip, 2017, 17, 1083–1094 RSC.
- X. Bian, F. Jing, G. Li, X. Fan, C. Jia, H. Zhou, Q. Jin and J. Zhao, Biosens. Bioelectron., 2015, 74, 770–777 CrossRef CAS PubMed.
- S. Tian, Z. Zhang, J. Chen, M. Du, Z. Li, H. Yang, X. Ji and Z. He, Talanta, 2018, 186, 24–28 CrossRef CAS PubMed.
- C.-Y. Ou, T. Vu, J. T. Grunwald, M. Toledano, J. Zimak, M. Toosky, B. Shen, J. A. Zell, E. Gratton and T. J. Abram, et al. , Lab Chip, 2019, 19, 993–1005 RSC.
- X. Xu, H. Yuan, R. Song, M. Yu, H. Y. Chung, Y. Hou, Y. Shang, H. Zhou and S. Yao, Biomicrofluidics, 2018, 12, 014103 CrossRef PubMed.
- W. Postek, T. Kaminski and P. Garstecki, Lab Chip, 2017, 17, 1323–1331 RSC.
- F. Schuler, F. Schwemmer, M. Trotter, S. Wadle, R. Zengerle, F. von Stetten and N. Paust, Lab Chip, 2015, 15, 2759–2766 RSC.
- F. Schuler, M. Trotter, M. Geltman, F. Schwemmer, S. Wadle, E. Domínguez-Garrido, M. López, C. Cervera-Acedo, P. Santibáñez and F. von Stetten, et al. , Lab Chip, 2016, 16, 208–216 RSC.
- H. Peng, M. Zhu, Z. Gao, C. Liao, C. Jia, H. Wang, H. Zhou and J. Zhao, Biomed. Microdevices, 2020, 22, 1–10 CrossRef PubMed.
- Y. Wang, S. Liu, T. Zhang, H. Cong, Y. Wei, J. Xu, Y.-P. Ho, S.-K. Kong and H.-P. Ho, Lab Chip, 2019, 19, 3870–3879 RSC.
- L. Clime, L. Malic, J. Daoud, L. Lukic, M. Geissler and T. Veres, Lab Chip, 2020, 20, 3091–3095 RSC.
- Y.-T. Kao, T. S. Kaminski, W. Postek, J. Guzowski, K. Makuch, A. Ruszczak, F. von Stetten, R. Zengerle and P. Garstecki, Lab Chip, 2020, 20, 54–63 RSC.
- B. Shen, J. Ricouvier, F. Malloggi and P. Tabeling, Adv. Sci., 2016, 3, 1600012 CrossRef PubMed.
- M. D. Raj, A. Gnanasekaran and R. Rengaswamy, Soft Matter, 2019, 15, 7863–7875 RSC.
- F. Bian, L. Sun, L. Cai, Y. Wang, Y. Wang and Y. Zhao, Small, 2020, 16, 1903931 CrossRef CAS PubMed.
- W. Li, H. Palis, R. Mérindol, J. Majimel, S. Ravaine and E. Duguet, Chem. Soc. Rev., 2020, 49, 1955–1976 RSC.
- K. I. Morozov and A. M. Leshansky, Langmuir, 2019, 35, 3987–3991 CrossRef CAS PubMed.
- Z. Ge, O. Tammisola and L. Brandt, Soft Matter, 2019, 15, 3451–3460 RSC.
- J. Zhou and I. Papautsky, Lab Chip, 2013, 13, 1121–1132 RSC.
- H. Amini, W. Lee and D. D. Carlo, Lab Chip, 2014, 14, 2739–2761 RSC.
- D. Stoecklein and D. Di Carlo, Anal. Chem., 2018, 91, 296–314 CrossRef PubMed.
- G. D'Avino, F. Greco and P. L. Maffettone, Annu. Rev. Fluid Mech., 2017, 49, 341–360 CrossRef.
- D. Yuan, Q. Zhao, S. Yan, S.-Y. Tang, G. Alici, J. Zhang and W. Li, Lab Chip, 2018, 18, 551–567 RSC.
- M. K. D. Manshadi, M. Mohammadi, L. K. Monfared and A. Sanati-Nezhad, Biotechnol. Bioeng., 2019, 117, 580–592 CrossRef PubMed.
- J. Zhou and I. Papautsky, Microsyst. Nanoeng., 2020, 6, 113 CrossRef CAS.
- M. Baron, J. Bławzdziewicz and E. Wajnryb, Phys. Rev. Lett., 2008, 100, 174502 CrossRef CAS PubMed.
- P. J. A. Janssen, M. D. Baron, P. D. Anderson, J. Blawzdziewicz, M. Loewenberg and E. Wajnryb, Soft Matter, 2012, 8, 7495 RSC.
- K. J. Humphry, P. M. Kulkarni, D. A. Weitz, J. F. Morris and H. A. Stone, Phys. Fluids, 2010, 22, 081703 CrossRef.
- W. Lee, H. Amini, H. A. Stone and D. Di Carlo, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 22413–22418 CrossRef CAS PubMed.
- Z. Pan, R. Zhang, C. Yuan and H. Wu, Phys. Fluids, 2018, 30, 102005 CrossRef.
- C. Schaaf and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2020, 43, 50 CrossRef CAS PubMed.
- W. Tang, S. Zhu, D. Jiang, L. Zhu, J. Yang and N. Xiang, Lab Chip, 2020, 20, 3485–3502 RSC.
- K. Hood and M. Roper, Phys. Rev. Fluids, 2018, 3, 094201 CrossRef.
- X. Hu, J. Lin, D. Chen and X. Ku, Microfluid. Nanofluid., 2020, 24, 25 CrossRef.
- C. Schaaf, F. Rühle and H. Stark, Soft Matter, 2019, 15, 1988–1998 RSC.
- S. Kahkeshani, H. Haddadi and D. D. Carlo, J. Fluid Mech., 2016, 786, R3 CrossRef.
- C. Dietsche, B. R. Mutlu, J. F. Edd, P. Koumoutsakos and M. Toner, Microfluid. Nanofluid., 2019, 23, 83 CrossRef.
- G. Segré and A. Silberberg, J. Fluid Mech., 1962, 14, 136–157 CrossRef.
- J.-P. Matas, V. Glezer, É. Guazzelli and J. F. Morris, Phys. Fluids, 2004, 16, 4192–4195 CrossRef CAS.
- J. F. Edd, D. Di Carlo, K. J. Humphry, S. Köster, D. Irimia, D. A. Weitz and M. Toner, Lab Chip, 2008, 8, 1262–1264 RSC.
- S. C. Hur, H. T. K. Tse and D. D. Carlo, Lab Chip, 2010, 10, 274–280 RSC.
- Y. Gao, P. Magaud, L. Baldas, C. Lafforgue, M. Abbas and S. Colin, Microfluid. Nanofluid., 2017, 21, 154 CrossRef.
- Y. Gao, P. Magaud, C. Lafforgue, S. Colin and L. Baldas, Microfluid. Nanofluid., 2019, 23, 93 CrossRef.
- X. Hu, J. Lin and X. Ku, Phys. Fluids, 2019, 31, 073306 CrossRef.
- A. Gupta, P. Magaud, C. Lafforgue and M. Abbas, Phys. Rev. Fluids, 2018, 3, 114302 CrossRef.
- G. D'Avino and P. L. Maffettone, Microfluid. Nanofluid., 2019, 23, 82 CrossRef.
- F. Del Giudice, G. D'Avino, F. Greco, P. L. Maffettone and A. Q. Shen, Phys. Rev. Appl., 2018, 10, 064058 CrossRef CAS.
- L. Liu, H. Xu, H. Xiu, N. Xiang and Z. Ni, Analyst, 2020, 145, 5128–5133 RSC.
- A. M. Leshansky, A. Bransky, N. Korin and U. Dinnar, Phys. Rev. Lett., 2007, 98, 234501 CrossRef CAS PubMed.
- X. Lu, C. Liu, G. Hu and X. Xuan, J. Colloid Interface Sci., 2017, 500, 182–201 CrossRef CAS PubMed.
- M. Villone, G. D'avino, M. Hulsen, F. Greco and P. Maffettone, J. Non-Newtonian Fluid Mech., 2013, 195, 1–8 CrossRef CAS.
- F. Del Giudice, S. Sathish, G. D'Avino and A. Q. Shen, Anal. Chem., 2017, 89, 13146–13159 CrossRef CAS PubMed.
- G. D'Avino, M. A. Hulsen and P. L. Maffettone, Comput. Fluids, 2013, 86, 45–55 CrossRef.
- A. Jeyasountharan, K. Shahrivar, G. D’Avino and F. Del Giudice, Anal. Chem., 2021, 93, 5503–5512 CrossRef CAS PubMed.
- G. D'Avino and P. L. Maffettone, Meccanica, 2020, 55, 317–330 CrossRef.
- M. Asghari, X. Cao, B. Mateescu, D. van Leeuwen, M. K. Aslan, S. Stavrakis and A. J. deMello, ACS Nano, 2020, 14, 422–433 CrossRef CAS PubMed.
- E. W. Kemna, R. M. Schoeman, F. Wolbers, I. Vermes, D. A. Weitz and A. Van Den Berg, Lab Chip, 2012, 12, 2881–2887 RSC.
- T. P. Lagus and J. F. Edd, RSC Adv., 2013, 3, 20512–20522 RSC.
- R. Ramji, M. Wang, A. A. S. Bhagat, D. Tan Shao Weng, N. V. Thakor, C. Teck Lim and C.-H. Chen, Biomicrofluidics, 2014, 8, 034104 CrossRef PubMed.
- R. M. Schoeman, E. W. Kemna, F. Wolbers and A. van den Berg, Electrophoresis, 2014, 35, 385–392 CrossRef CAS PubMed.
- X. Xu, F. Tian, X. Liu, R. M. Parker, Y. Lan, Y. Wu, Z. Yu, O. A. Scherman and C. Abell, Chem. – Eur. J., 2015, 21, 15516–15519 CrossRef CAS PubMed.
- S. Sajjadi, M. Alroaithi, A. S. Chaurasia and F. Jahanzad, Langmuir, 2019, 35, 12731–12743 CrossRef CAS PubMed.
- V. A. Turek, Y. Francescato, P. Cadinu, C. R. Crick, L. Elliott, Y. Chen, V. Urland, A. P. Ivanov, L. Velleman and M. Hong, et al. , ACS Photonics, 2016, 3, 35–42 CrossRef CAS.
- Y. Ding, P. D. Howes and A. J. deMello, Anal. Chem., 2019, 92, 132–149 CrossRef PubMed.
- K. Matuła, F. Rivello and W. T. Huck, Adv. Biosyst., 2020, 4, 1900188 CrossRef PubMed.
- A. Sattari, P. Hanafizadeh and M. Hoorfar, Adv. Colloid Interface Sci., 2020, 102208 CrossRef CAS PubMed.
- K. Doufène, C. Tourné-Péteilh, P. Etienne and A. Aubert-Pouëssel, Langmuir, 2019, 35, 12597–12612 CrossRef PubMed.
- Y. Dou, B. Wang, M. Jin, Y. Yu, G. Zhou and L. Shui, J. Micromech. Microeng., 2017, 27, 113002 CrossRef.
- F. Fontana, J. P. Martins, G. Torrieri and H. A. Santos, Adv. Mater. Technol., 2019, 4, 1800611 CrossRef.
- L. Li, P. Wu, Z. Luo, L. Wang, W. Ding, T. Wu, J. Chen, J. He, Y. He and H. Wang, et al. , ACS Sens., 2019, 4, 1299–1305 CrossRef CAS PubMed.
- Y. Wang, T. Cao, J. Ko, Y. Shen, W. Zong, K. Sheng, W. Cao, S. Sun, L. Cai and Y.-L. Zhou, et al. , Adv. Sci., 2020, 7, 1903463 CrossRef CAS PubMed.
- E. Z. Macosko, A. Basu, R. Satija, J. Nemesh, K. Shekhar, M. Goldman, I. Tirosh, A. R. Bialas, N. Kamitaki and E. M. Martersteck, et al. , Cell, 2015, 161, 1202–1214 CrossRef CAS PubMed.
- H.-S. Moon, K. Je, J.-W. Min, D. Park, K.-Y. Han, S.-H. Shin, W.-Y. Park, C. E. Yoo and S.-H. Kim, Lab Chip, 2018, 18, 775–784 RSC.
- Y. Ren, Z. Liu and H. C. Shum, Lab Chip, 2015, 15, 121–134 RSC.
- I. C. Clark and A. R. Abate, Lab Chip, 2018, 18, 3598–3605 RSC.
- A. R. Abate, C.-H. Chen, J. J. Agresti and D. A. Weitz, Lab Chip, 2009, 9, 2628–2631 RSC.
- G.-R. Yi, T. Thorsen, V. N. Manoharan, M.-J. Hwang, S.-J. Jeon, D. J. Pine, S. R. Quake and S.-M. Yang, Adv. Mater., 2003, 15, 1300–1304 CrossRef CAS.
- L. Lei, X. Tang, P. Zhu, Z. Kang, T. Kong and L. Wang, J. Mater. Chem. B, 2017, 5, 6034–6041 RSC.
- V. Gundabala, S. Martinez-Escobar, S. Marquez, M. Marquez and A. Fernandez-Nieves, J. Phys. D: Appl. Phys., 2013, 46, 114006 CrossRef.
- J. Wang, H. Le-The, Z. Wang, H. Li, M. Jin, A. van den Berg, G. Zhou, L. I. Segerink, L. Shui and J. C. Eijkel, ACS Nano, 2019, 13, 3638–3648 CrossRef CAS PubMed.
- S. Okushima, T. Nisisako, T. Torii and T. Higuchi, Langmuir, 2004, 20, 9905–9908 CrossRef CAS PubMed.
- T. Nisisako, S. Okushima and T. Torii, Soft Matter, 2005, 1, 23–27 RSC.
- N. Wang, C. Semprebon, H. Liu, C. Zhang and H. Kusumaatmaja, J. Fluid Mech., 2020, 895, A22 CrossRef CAS.
- A. Tiribocchi, A. Montessori, M. Lauricella, F. Bonaccorso, S. Succi, S. Aime, M. Milani and D. Weitz, Nat. Commun., 2021, 12, 82 CrossRef CAS PubMed.
- A. C. H. Tsang, M. J. Shelley and E. Kanso, Soft Matter, 2018, 14, 945–950 RSC.
- G. Mishler, A. C. H. Tsang and O. S. Pak, J. Nonlinear Sci., 2018, 28, 1379–1396 CrossRef CAS.
- A. Dhar, P. Burada and G. R. Sekhar, Phys. Fluids, 2020, 32, 102005 CrossRef CAS.
- A. Isozaki, J. Harmon, Y. Zhou, S. Li, Y. Nakagawa, M. Hayashi, H. Mikami, C. Lei and K. Goda, Lab Chip, 2020, 20, 3074–3090 RSC.
- N. Nitta, T. Sugimura, A. Isozaki, H. Mikami, K. Hiraki, S. Sakuma, T. Iino, F. Arai, T. Endo and Y. Fujiwaki, et al. , Cell, 2018, 175, 266–276 CrossRef CAS PubMed.
- A. Isozaki, H. Mikami, H. Tezuka, H. Matsumura, K. Huang, M. Akamine, K. Hiramatsu, T. Iino, T. Ito and H. Karakawa, et al. , Lab Chip, 2020, 20, 2263–2273 RSC.
| This journal is © The Royal Society of Chemistry 2021 |