Transition metal oxynitride catalysts for electrochemical reduction of nitrogen to ammonia

Abstract

Electrochemical nitrogen reduction reaction (ENRR) under ambient conditions is beneficial compared to the energy intensive thermochemical Haber–Bosch process for NH₃ production. Here, periodic density functional theory (DFT) calculations are carried out to study the ENRR on transition metal oxynitride (TMNO) catalysts. Our calculations show that the ENRR occurs at thermodynamically more favorable surface nitrogen vacancy (N-vac) sites compared to surface oxygen vacancy (O-vac) sites. The DFT results show that TiNO efficiently catalyzes the ENRR at a low applied potential (U) and its ENRR activity is predicted to be similar to that of VNO, a previously identified excellent ENRR catalyst. We observed a volcano like relationship between the DFT calculated nitrogen binding energy (NBE) and the limiting potential (U_L), which suggests that the NBE can be used as a descriptor of the ENRR activity on TMNO based catalysts.

---

Introduction

Ammonia (NH₃), a key precursor used to produce nitrogen-containing fertilizers, is currently produced by an energy intensive Haber–Bosch process.^1–8 The Haber–Bosch process is typically carried out at high temperatures (400–500 °C) and pressures (200–300 atm) where nitrogen from the atmosphere reacts with the hydrogen produced from non-renewable resources to produce NH₃^9–11 and consumes ∼1–2% of global energy.^12–17 Electrochemical nitrogen reduction reaction (ENRR) to produce NH₃ on a small scale near agricultural fields under ambient conditions using the electricity generated from renewable resources (e.g. solar and wind energy) is a promising alternative to the carbon/energy intensive Haber–Bosch process.^18–26

N₂ is a stable molecule and its activation and transformation under ambient conditions are challenging.^27,28 Different classes of heterogeneous catalysts such as transition metals,²⁹ transition metal carbides and nitrides^30–33 and single atom catalysts anchored on graphene,^34–36 boron nitrides,³⁷ and Mxenes^38,39 have been explored for the ENRR. Among them, transition metal nitride-based materials have emerged as promising catalysts for electrochemical N₂ conversion to NH₃. For example, using density functional theory (DFT) based calculations, Abghoui et al. investigated various transition metal nitrides (TiN, YN, ScN, HfN, ZrN, CrN, VN, TaN, OsN, NbN, MoN, RuN, MnN, IrN, RhN, FeN, CoN, AgN, PdN, NiN, and CuN) and reported that the (100) facets of the rocksalt structures of VN and ZrN are the most promising candidates that catalyze the electrochemical conversion of N₂ to NH₃.^1,18,31 Unlike transition metals, transition metal nitride surfaces are less likely to be covered by hydrogen at the onset potentials needed for the ENRR, and hence the HER is predicted to be less competitive resulting in an enhanced ENRR activity on transition metal nitride based catalysts.^1,18 Furthermore, recent combined experimental and DFT studies have shown that O modified VN (i.e. VNO) is an excellent ENRR catalyst suggesting that transition metal oxynitrides (TMNOs) may serve as a new class of materials that facilitate the ENRR at low potentials.^40,41 The ENRR on VNO was shown to proceed on nitrogen vacancy via the Mars–van Krevelen (MvK) mechanism. Along the MvK mechanism, N₂ adsorption at the N-vacancy is followed by (H⁺ + e⁻) transfer to form *N₂H which further undergoes (H⁺ + e⁻) transfer to form *N₂H₂. Additional (H⁺ + e⁻) transfer to *N₂H₂ facilitates N–N bond scission, a key step of the ENRR. In contrast to the promoting role of the surface nitrogen vacancy, the surface oxygen vacancies on VNO have been shown to bind the ENRR reaction intermediates too strongly and potentially poison the catalyst surface. On VNO(111), the rate-limiting step of the ENRR facilitated by the nitrogen vacancy was predicted to be the reduction of *N₂ to N₂H.⁴¹ Similarly, Kang et al. reported that titanium nitride (TiN) manufactured by plasma-etching as an excellent catalyst for the ENRR.⁴²

In this study, we employed first-principles DFT calculations to study the ENRR on TMNOs. DFT results show that the ENRR follows the MvK mechanism on the surface nitrogen vacancy, whose formation is found to be thermodynamically more favorable compared to the formation of the oxygen vacancy. Our computations predict that TiNO is the best ENRR catalysts with a performance similar to that of VNO which has been experimentally shown to be an excellent ENRR catalyst. Furthermore, the DFT calculations identified the nitrogen binding energy as a potential descriptor of the ENRR activity on TMNO based catalysts.

Computational methods

Density functional theory (DFT)⁴³ calculations were performed using the Vienna Ab Initio Simulation Package (VASP) code.^44,45 All the DFT calculations were spin-polarized and were performed at the GGA level within the PAW-PW91 formalism.^46,47

The bulk structure of transition metal oxynitrides (TMNOs) in the present study was modeled using the rocksalt structure with an oxygen (O) concentration of 25% consistent with the experimental O concentration in VNO, a previously identified efficient catalyst for the ENRR.⁴¹ The TMNO(111) surfaces were modeled using 4 layer 2 × 2 surface slabs. Our modeled TMNO(111) surfaces contain N and O atoms on the topmost surface layer, which allowed us to investigate the ENRR on the surface N and O vacancies. A vacuum of approximately 15 Å was added to the surface in the z-direction to reduce the artificial interplay between the surface and its periodic images.

During calculations, the atoms in the top two layers were allowed to be relaxed, while the atoms in the bottom two layers were fixed until the Hellman–Feynman force on each ion was less than 0.02 eV Å⁻¹. The total energy was calculated using a plane wave basis set at a cut-off energy of 400 eV and a 3 × 3 × 1 Monkhorst–Pack grid was used to carry out the Brillion zone integration.⁴⁸

The binding energy (BE) of the adsorbate was calculated as:

BE(adsorbate) = E(slab + adsorbate) − E(slab) − E(adsorbate)

where E(slab + adsorbate), E(slab), and E(adsorbate) are the total energies of the slab with the adsorbate, the clean slab, and the adsorbate in the gas phase, respectively.

The free energy changes were calculated using the computational hydrogen electrode (CHE) model developed by Norskov and co-workers.⁴⁹ In this model, the chemical potential of a proton–electron pair (H⁺ + e⁻) is equal to half of the chemical potential of the hydrogen gas molecule (1/2μ(H₂)) at zero applied potential (U).

Thus, the total chemical potential of the proton–electron pair as a function of applied potential (U), at all temperatures and pH values, can be calculated as μ(H⁺ + e⁻) = 1/2μ(H₂(g)) – eU.

The CHE model is employed at U = 0 V to construct free energy diagrams (ΔG vs. reaction coordinates) of the ENRR. The Gibbs free energy (G) of a species was calculated as⁴⁹

G = E + ZPE − TS

Here, E is the total energy of a species obtained from DFT calculations, ZPE and S are the zero-point energy and entropy of a species, respectively, and T = 298.15 K.

Results and discussion

Previous DFT studies have shown that the ENRR via associative or dissociative mechanisms is thermodynamically unfavorable on perfect transition metal (TM) nitride surfaces. Along the associative pathway, the formation of *N₂H is found to be thermodynamically unfavorable while the dissociative pathway is predicted to be unfavorable due to the highly activated N₂ dissociation. In contrast, the presence of the surface N-vacancy (N-vac) on TM nitrides is found to facilitate the ENRR via the MvK mechanism by strengthening the binding affinity of the reaction intermediates and significantly reducing the energy barrier for N₂ dissociation.^40,41 Along the MvK mechanism, the first NH₃ molecule is formed by the protonation of a surface N atom creating an N vacancy (N-vac) on the catalyst surface.^1,18,41 The created N-vac then facilitates adsorption of N₂ and its conversion to NH₃. Therefore, firstly, we computed the formation energies of the surface oxygen vacancy (O-vac) and the nitrogen-vacancy (N-vac) on transition metal oxynitride surfaces using the following scheme:

Surface + H₂(g) → O-vac + H₂O(g)

Surface + 3/2H₂(g) → N-vac + NH₃(g)

The DFT calculated formation energies in Table 1 show that except MnNO, the N-vac formation is thermodynamically more favorable compared to the formation of O-vac indicating that the ENRR via the MvK mechanism likely occurs at the N-vac sites. Subsequently, the N-vac promoted ENRR is discussed in detail in the following sections and the results for the O-vac mediated ENRR are summarized at the end of the results and discussion section.

Table 1 DFT calculated formation energies (in eV) of N-vac and O-vac on the (111) surfaces of various TMNOs

TMNO	N-vac	O-vac
CrNO	1.43	3.37
MnNO	−1.00	−1.46
TaNO	0.34	2.41
HfNO	1.92	3.93
ScNO	−3.72	0.81
TiNO	0.31	2.80
YNO	−3.08	1.38
ZrNO	1.21	3.51
VNO	−0.57	2.05

---

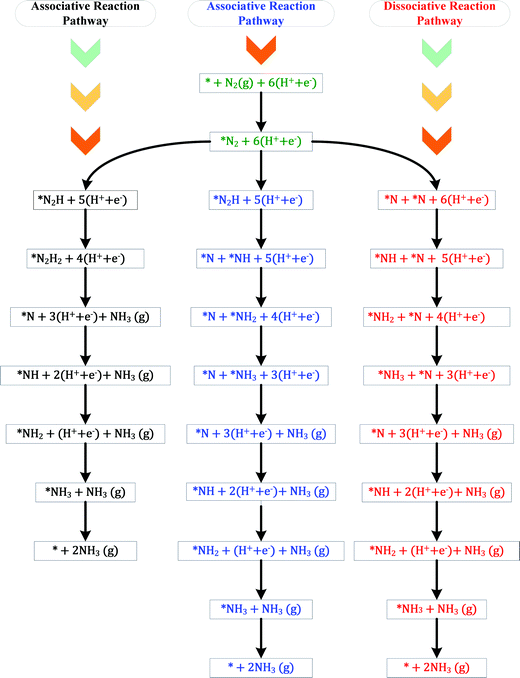
The ENRR can proceed via three main pathways: (i) distal, (ii) alternating, and (iii) enzymatic (Fig. S1 in the ESI†).⁵⁰ Our calculations show that N₂ binds at N/O-vac in an endon configuration which prohibits the ENRR from occurring via the enzymatic pathway. As shown in Fig. S1 (ESI†), the formation of the *N₂H₂ intermediate promotes the distal pathway, while the formation of the *HNNH intermediate promotes the alternating pathway. Our DFT calculated results in Fig. 1 show that the *N₂H₂ formation is energetically more favorable than the formation of *HNNH on all TMNO catalysts considered in the present study. This suggests that the distal pathway is favorable over the alternating pathway. Therefore, the dissociative and the two commonly used associative pathways (along the distal channel) shown in Fig. 2 are discussed in detail in the subsequent sections.

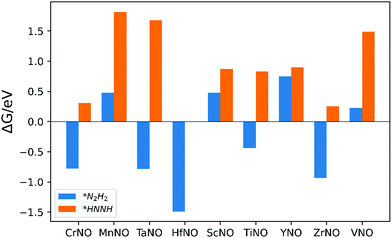Fig. 1 Free energy change for the formation of *N₂H₂ (i.e. step: *N₂H + (H⁺ + e⁻) → *N₂H₂) and *HNNH (i.e. step: *N₂H + (H⁺ + e⁻) → *HNNH) intermediates.

Fig. 2 Three possible reaction pathways of electrochemical N₂ reduction to NH₃. * =active site.

H assisted N–N bond scission prevails in the associative pathways of the ENRR (shown in black and blue in Fig. 2). Along the associative pathway shown in black in Fig. 2 (associative N₂H₂ pathway hereafter) *N₂ (* = active site) is first reduced to *N₂H₂, which subsequently undergoes (H⁺ + e⁻) transfer and dissociation reactions to form *N + NH₃(g). *N then undergoes three sequential (H⁺ + e⁻) transfer reactions to form *NH₃, which desorbs as a product. Along the pathway shown in blue in Fig. 2 (associative N₂H pathway hereafter), N–N bond scission occurs when *N₂H is formed to produce *N + *NH. *N and *NH then undergo (H⁺ + e⁻) transfer reactions to form *NH₃. Along the dissociative pathway (shown in red in Fig. 2), *N₂ adsorbed at N-vac dissociates to 2*N (vacancy dimer). *N then undergoes three subsequent electrochemical (H⁺ + e⁻ transfer) reactions to form *NH₃. *NH₃ finally leaves the active site as NH₃(g), making the site available for the next reaction cycle.

DFT calculations are performed to calculate the binding energies of the reaction intermediates (*H, *N, *N₂, *N₂H, *N₂H₂, *NH, *NH₂, and *NH₃) associated with the reaction channels shown in Fig. 2. The DFT optimized geometries of the reaction intermediates on the N-vac of the TMNO(111) surfaces in Fig. 3 show that *N₂, *N₂H, and *N₂H₂ bind in end on configurations in which only one N forms chemical bonds to the surface sites. The adsorption of *N heals the surface N-vac and the binding of *NH, *NH₂, *NH₃ at N-vac occurs via the N atoms. Similar binding configurations are observed at O-vac on the TMNO(111) surfaces (Fig. S2 in the ESI†).

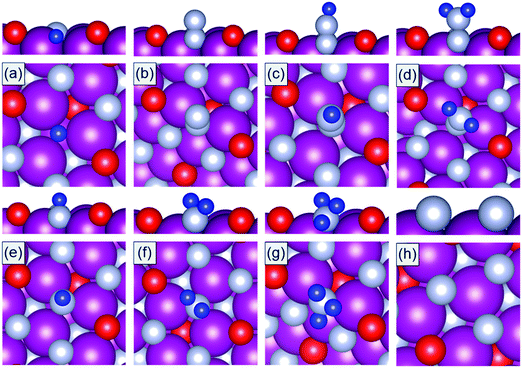Fig. 3 DFT optimized geometries of (a) *H, (b) *N₂, (c) *N₂H, (d) *N₂H₂, (e) *NH, (f) *NH₂, (g) *NH₃, and (h) *N adsorbed on N-vac of the MnNO(111) surface. Mn: purple, N: gray, O: red, H: blue.

The DFT calculated binding energies in Fig. S3(a)–(i) (ESI†) show that most of the reaction intermediates bind more strongly on O-vac compared to N-vac except for MnNO where most of the reaction intermediates bind more strongly on N-vac. The stronger binding of the ENRR intermediates observed on O-vac is most likely due to the more electron density of states available near the Fermi level (for bonding) as shown in the density of state plots in Fig. S4 (ESI†). On MnNO(111), N-vac is predicted to be less favorable compared to O-vac (Table 1) and stronger binding of the ENRR intermediates on N-vac is observed due to the availability of a larger electron density of states near the Fermi level (Fig. S4, ESI†) as expected.

The DFT calculated binding energies are then used to compute the free energy change at an applied potential (U) = 0 V using the CHE model developed by Norskov et al.⁴⁹Fig. 4 and 5 show the DFT computed free energy diagrams of the ENRR along the associative N₂H₂ and N₂H pathways at U = 0 V. It is seen from Fig. 4 and 5 that the overall ENRR activity of ScNO and YNO is limited by the formation of *N from the elementary step: *N₂H₂ + (H⁺ + e⁻) → *N + NH₃(g) with free energy barriers (ΔG) = 2.08 eV and 1.16 eV along the associative N₂H₂ pathway and *N₂H + * → *N + *NH with ΔG = 3.57 eV and 1.34 eV along the associative N₂H pathway, respectively, due to the weaker binding energy of N on N-vac. On the other hand, HfNO, TaNO, CrNO, and ZrNO bind the ENRR intermediates strongly. The most difficult steps on HfNO, TaNO, CrNO, and ZrNO along the associative N₂H₂ pathway are predicted to be *NH₂ + (H⁺ + e⁻) → *NH₃, *NH + (H⁺ + e⁻) → *NH₂, *N + (H⁺ + e⁻) → *NH, and *NH₃ → * + NH₃(g) and have ΔG values of 1.11 eV, 1.27 eV, 1.18 eV, and 1.12 eV, respectively. Similarly, the most difficult steps along the associative N₂H pathway on HfNO, TaNO, CrNO, and ZrNO are *NH₂ + (H⁺ + e⁻) → *NH₃, *NH + (H⁺ + e⁻) → *NH₂, *N + (H⁺ + e⁻) → *NH, and *NH₃ → * + NH₃(g) and have ΔG values of 1.11 eV, 1.27 eV, 2.10 eV, and 1.12 eV, respectively. Interestingly, we find a relatively mild change in the free energy between the steps in both associative pathways for MnNO and TiNO, and the overall features of the free energy diagrams are very similar when compared to VNO. The most difficult steps on MnNO, TiNO, and VNO along the associative N₂H₂ as well as N₂H pathways are *N₂ + (H⁺ + e⁻) → *N₂H, *NH₂ + (H⁺ + e⁻) → *NH₃ and *N₂ + (H⁺ + e⁻) → *N₂H with ΔG values of 0.82 eV, 0.42 eV and 0.68 eV, respectively. The relatively smaller ΔG values of the most difficult steps on MnNO, TiNO, and VNO suggest an efficient ENRR along the associative N₂H₂ and N₂H pathways on these candidates.

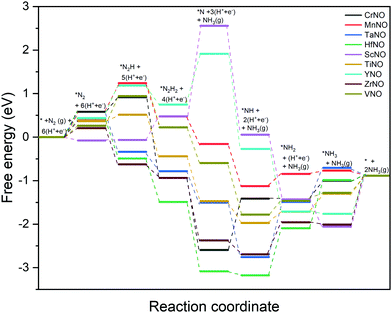Fig. 4 DFT calculated free energy diagrams of the ENRR at U = 0 V along the associative N₂H₂ pathway on N-vac.

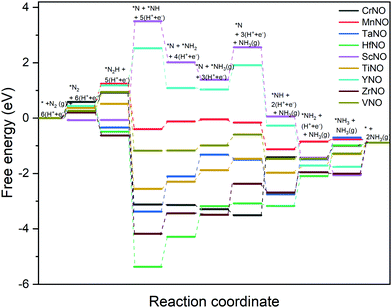Fig. 5 DFT calculated free energy diagrams of the ENRR at U = 0 V along the associative N₂H pathway on N-vac.

Fig. 6 shows the DFT calculated free energy change of the elementary steps of the N-vac mediated ENRR along the dissociative pathway. N₂ dissociation (to 2*N on a vacancy dimer), a non-electrochemical step, is predicted to be the rate-limiting step on ScNO and YNO with an uphill energy barrier of 6.08 eV and 4.27 eV, respectively. Thus, the weaker binding of *N severely limits the ENRR along the dissociative pathway on ScNO and YNO. In contrast, N₂ dissociation is exothermic on all other catalysts (CrNO, MnNO, TaNO, HfNO, TiNO, ZrNO, and VNO). HfNO, CrNO, ZrNO and TaNO bind N/NH_x species too strongly, and their further reduction requires a large energy. The most difficult steps on HfNO, CrNO, ZrNO and TaNO are predicted to be *NH₂ + (H⁺ + e⁻) → *NH₃, *N + (H⁺ + e⁻) → *NH, *NH₃ → * + NH₃(g), and *NH + (H⁺ + e⁻) → *NH₂ with ΔG values of 1.11 eV, 1.18 eV, 1.12 eV and 1.27 eV, respectively. Interestingly, the free energy change between the elementary steps on MnNO, TiNO, and VNO is small and these candidates are predicted to show enhanced performance for the ENRR. On MnNO, TiNO and VNO, the most difficult steps are * + N₂ → *N₂, *NH₂ + (H⁺ + e⁻) → *NH₃, and *NH₃ → * + NH₃(g) and have ΔG values of 0.42 eV, 0.42 eV, and 0.39 eV respectively.

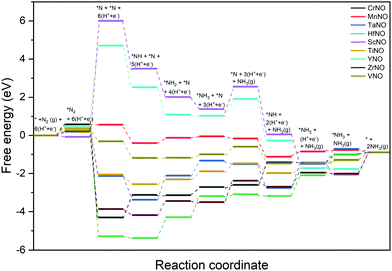Fig. 6 DFT calculated free energy diagrams of the ENRR at U = 0 V along the dissociative pathway on N-vac.

A comparison of the free energy profiles (Fig. 4–6) shows that the ENRR occurs via the associative N₂H₂ pathway on ScNO and YNO and have ΔG values of the rate limiting step as 2.08 eV and 1.16 eV, respectively. In contrast, the dissociative pathway is predicted to be the most favorable pathway on CrNO, MnNO, TaNO, HfNO, TiNO, ZrNO, and VNO. The ΔG values of the rate limiting step are 1.18 eV, 0.42 eV, 1.27 eV, 1.11 eV, 0.42 eV, 1.12 eV and 0.39 eV on CrNO, MnNO, TaNO, HfNO, TiNO, ZrNO and VNO, respectively. The predicted large ΔG values on ScNO, YNO, HfNO, CrNO, ZrNO, and TaNO indicate that the ENRR is sluggish on these candidates. However, we find relatively small and similar ΔG values on MnNO, TiNO, and VNO. As a result, a similar ENRR activity of MnNO and TiNO compared to VNO is expected. Previous experimental and theoretical studies⁴¹ have shown an efficient ENRR catalyzed by the N-vac of VNO at a low potential. Therefore, our DFT calculations predict MnNO and TiNO as potential candidates for N₂ reduction to NH₃ under ambient conditions based on the calculated free energy diagrams of the ENRR.

The overall activity of a catalyst for the ENRR along a reaction pathway is determined by the most difficult step (i.e. a step with the largest uphill energy in free energy diagrams). The limiting potential (U_L), a metric often used in electrochemistry, is defined as a potential at which all the electrochemical steps along the reaction channel are thermodynamically downhill in energy. Thus the most difficult electrochemical step, also called a potential limiting step, would dictate the U_L values along the reaction channel on a catalyst surface. The free energy diagrams shown in Fig. 4–6 are used to compute the U_L values on TMNOs.

Along the most favorable associative N₂H₂ pathway, our calculations predict U_L = −2.08 V and −1.16 V on ScNO and YNO, respectively. The U_L values calculated on CrNO, MnNO, TaNO, HfNO, TiNO, ZrNO, and VNO along the most favorable dissociative pathway are −1.18 V, −0.28 V, −1.27 V, −1.11 V, −0.42 V, −0.74 V, and −0.18 V, respectively. Interestingly we find that the non-electrochemical steps have larger ΔG barriers than the most difficult electrochemical steps on MnNO, ScNO, YNO, ZrNO, and VNO and are predicted to determine the overall ENRR activity on these candidates. In contrast, the electrochemical steps are the overall rate controlling steps on CrNO, TaNO, HfNO, and TiNO. Thus, the ENRR activity of CrNO, TaNO, HfNO, and TiNO can be tuned by applying an external potential.

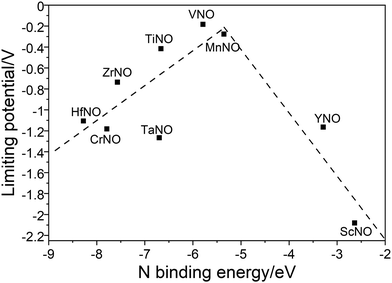
Along the most favorable reaction pathways, the calculated U_L values were plotted against the N binding energies (NBEs). The calculated U_L values show a volcano-like relationship with the NBE as shown in Fig. 7. The U_L calculated on VNO is the lowest and lies close to the top of the volcano. Importantly, the DFT predicted U_L on MnNO and TiNO are smaller than those calculated on some of the previously predicted efficient ENRR catalysts (e.g. VN(100): −0.51 V, ZrN(100): −0.76 V, CrN(100): −0.76 V, NbN(100): −0.65 V, and −0.69 V on the graphene single atom catalyst).^1,34,41 This observation suggests that MnNO and TiNO should show excellent activity for N₂ reduction to NH₃. The volcano-like plots in Fig. 7 also show that YNO and ScNO bind N too weakly and the U_L values of these candidates lie to the right of the volcano. In contrast, HfNO, ZrNO, TaNO, and CrNO bind N too strongly and lie on the left of the volcano. Importantly, our results identified the NBE as a descriptor of the ENRR activity on TMNO based catalysts. Thus, a future catalyst development strategy should focus on finding TM oxynitrides that have an NBE similar to that of VNO.

Fig. 7 Plot between the N binding energy (NBE) and U_L along the most favorable ENRR pathways.

The HER is a competing reaction with the ENRR and most likely competes for the same reaction sites. Thus, the overall ENRR activity of a catalyst is influenced by the HER. DFT calculations are performed to calculate the binding energy of *H (Fig. S3(f), ESI†), a key reaction intermediate of the HER, on all the TMNO(111) surfaces studied in the present study. The calculated *H binding energy is then used to construct free energy diagrams shown in Fig. 8a. Fig. 8a shows that the HER efficiently occurs on MnNO with ΔG close to 0 eV. On CrNO, TaNO, HfNO, ScNO, YNO, TiNO, ZrNO, and VNO, *H + (H⁺ + e⁻) to H₂(g) is predicted to be the rate limiting step. We observed a correlation between the HER limiting potential and the DFT calculated H binding energy (Fig. 8b). The HER activity is predicted to follow the order: MnNO > YNO > CrNO > ScNO > VNO> TaNO > TiNO > HfNO > ZrNO. MnNO lies close to the top of the volcano indicating that it efficiently promotes the HER. We find that the HER activity of TiNO, which has been predicted to be one of the best candidates for the ENRR in our above analysis, is not optimal, and more importantly, the calculated U_L value for the ENRR is smaller than the U_L for the HER. Thus, TiNO is more selective to the ENRR compared to the HER and thus selectively transforms N₂ to NH₃ under electrochemical conditions. Hence, TiNO is a potential candidate for selectively promoting the ENRR among all the TMNO catalysts studied here.

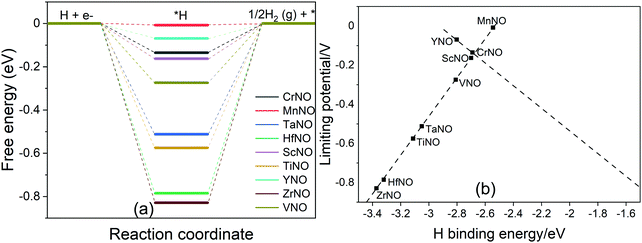Fig. 8 (a) DFT calculated free energy diagram of the HER at U = 0 V on N-vac. (b) Plot between the H binding energy and U_L.

We performed a similar investigation of the ENRR activity on O-vac, whose formation has been predicted to be less favorable compared to N-vac. The calculated free energy diagrams are included in Fig. S5–S7 in the ESI.† On O-vac, the ENRR proceeds along the associative N₂H₂ pathway on MnNO and ScNO. All other candidates (YNO, TaNO, TiNO, ZrNO, HfNO, CrNO, and VNO) promote the ENRR along the dissociative pathway. The most difficult steps along the associative N₂H₂ pathway on MnNO and ScNO are *NH₂ + (H⁺ + e⁻) → *NH₃ and *N₂ + (H⁺ + e⁻) → *N₂H with ΔG values of 1.70 eV and 2.73 eV, respectively. Similarly, the most difficult steps along the most favorable dissociative pathway on CrNO, TaNO, TiNO, YNO, VNO, ZrNO, and HfNO are *NH + (H⁺ + e⁻) → *NH₂, *NH₃ → * + NH₃(g), *NH₂ + (H⁺ + e⁻) → *NH₃, *NH₃ → * + NH₃(g), *NH₃ → * + NH₃(g), *NH₂ + (H⁺ + e⁻), and *NH + (H⁺ + e⁻) → *NH₂ with ΔG values of 1.68 eV, 1.11 eV, 0.63 eV, 1.11 eV, 0.59 eV, 1.09 eV and 1.38 eV, respectively. The calculated U_L values along the most favorable pathways on TiNO and VNO are −0.63 V and −0.56 V, respectively. We find that the ΔG values of the most difficult steps and U_L on TiNO are similar to those on VNO. Thus the DFT calculations predict the ENRR activity of TiNO comparable to VNO, which has been experimentally shown to be an excellent ENRR catalyst.

Conclusions

DFT calculations are performed to study the ENRR on transition metal oxynitrides (TMNOs: TM = Sc, Ti, V, Cr, Mn, Y, Zr, Hf, and Ta). The results show a vacancy mediated ENRR via the MvK mechanism. Our thermodynamic analysis predicted a favorable formation surface N-vac compared to O-vac on all TMNOs except MnNO, and thus N-vacs are the active sites for the adsorption of the reaction intermediates involved in the ENRR. Among all TMNOs in the present study, our DFT calculations identified TiNO as a promising candidate with U_L values similar to those of VNO, which has been shown to be an excellent ENRR catalyst experimentally. Furthermore, a volcano like feature is observed between the calculated U_L values and the NBE suggesting that the NBE is a potential descriptor of the ENRR activity on TMNO based catalysts and the future catalyst development strategy should focus on finding TM oxynitrides that have NBEs similar to those of VNO.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

DFT calculations were performed using computational resources at the Extreme Science and Engineering Discovery Environment, which is supported by the National Science Foundation Grant number ACI-1548562 and at the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231. S. K. acknowledges the faculty start-up fund from Florida A&M University.

References

1. Y. Abghoui, A. L. Garden, V. F. Hlynsson, S. Björgvinsdóttir, H. Ólafsdóttir and E. Skúlason, Phys. Chem. Chem. Phys., 2015, 17, 4909–4918.
2. I. A. Amar, R. Lan, C. T. G. Petit and S. Tao, J. Solid State Electrochem., 2011, 15, 1845–1860.
3. S. Giddey, S. P. S. Badwal and A. Kulkarni, Int. J. Hydrogen Energy, 2013, 38, 14576–14594.
4. J. W. Erisman, M. A. Sutton, J. Galloway, Z. Klimont and W. Winiwarter, Nat. Geosci., 2008, 1, 636–639.
5. R. Zhang, X. Ren, X. Shi, F. Xie, B. Zheng, X. Guo and X. Sun, ACS Appl. Mater. Interfaces, 2018, 10, 28251–28255.
6. I. Garagounis, A. Vourros, D. Stoukides, D. Dasopoulos and M. Stoukides, Membranes, 2019, 9, 112.
7. I. Garagounis, V. Kyriakou, A. Skodra, E. Vasileiou and M. Stoukides, Front. Energy Res., 2014, 2, 1.
8. D. G. H. Ham, C. J. M. Koper and M. T. M. Hetterscheid, Chem. Soc. Rev., 2014, 43, 5183–5191.
9. V. Kyriakou, I. Garagounis, A. Vourros, E. Vasileiou and M. Stoukides, Joule, 2020, 4, 142–158.
10. E. Cussler, A. McCormick, M. Reese and M. Malmali, J. Visualized Exp., 2017, 126, 55691.
11. J. Yu, C. Li, B. Li, X. Zhu, R. Zhang, L. Ji, D. Tang, A. M. Asiri, X. Sun, Q. Li, S. Liu and Y. Luo, Chem. Commun., 2019, 55, 6401–6404.
12. A. Hellman, E. J. Baerends, M. Biczysko, T. Bligaard, C. H. Christensen, D. C. Clary, S. Dahl, R. Van Harrevelt, K. Honkala, H. Jonsson, G. J. Kroes, M. Luppi, U. Manthe, J. K. Nørskov, R. A. Olsen, J. Rossmeisl, E. Skúlason, C. S. Tautermann, A. J. C. Varandas and J. K. Vincent, J. Phys. Chem. B, 2006, 110, 17719–17735.
13. B. H. R. Suryanto, D. Wang, L. M. Azofra, M. Harb, L. Cavallo, R. Jalili, D. R. G. Mitchell, M. Chatti and D. R. MacFarlane, ACS Energy Lett., 2019, 4, 430–435.
14. V. Smil, Sci. Am., 1997, 277, 76–81.
15. Y. Tanabe and Y. Nishibayashi, Coord. Chem. Rev., 2013, 257, 2551–2564.
16. S. Licht, B. Cui, B. Wang, F. F. Li, J. Lau and S. Liu, Science, 2014, 345, 637–640.
17. J. M. Modak, Resonance, 2011, 16, 1159–1167.
18. Y. Abghoui and E. Skúlasson, Proc. Comput. Sci., 2015, 51, 1897–1906.
19. M. Yuan, H. Zhang, D. Gao, H. He, Y. Sun, P. Lu, S. Dipazir, Q. Li, L. Zhou, S. Li, Z. Liu, J. Yang, Y. Xie, H. Zhao and G. Zhang, J. Mater. Chem. A, 2020, 8, 2691–2700.
20. Y. Song, D. Johnson, R. Peng, D. K. Hensley, P. V. Bonnesen, L. Liang, J. Huang, F. Yang, F. Zhang, R. Qiao, A. P. Baddorf, T. J. Tschaplinski, N. L. Engle, M. C. Hatzell, Z. Wu, D. A. Cullen, H. M. Meyer, B. G. Sumpter and A. J. Rondinone, Sci. Adv., 2018, 4, 1700336.
21. L. Hollevoet, M. De Ras, M. Roeffaers, J. Hofkens and J. A. Martens, ACS Energy Lett., 2020, 5, 1124–1127.
22. M. J. Palys, A. McCormick, E. L. Cussler and P. Daoutidis, Processes, 2018, 6, 91.
23. J. M. McEnaney, A. R. Singh, J. A. Schwalbe, J. Kibsgaard, J. C. Lin, M. Cargnello, T. F. Jaramillo and J. K. Nørskov, Energy Environ. Sci., 2017, 10, 1621–1630.
24. A. Klerke, C. H. Christensen, J. K. Nørskov and T. Vegge, J. Mater. Chem., 2008, 18, 2304–2310.
25. J. H. Montoya, C. Tsai, A. Vojvodic and J. K. Nørskov, ChemSusChem, 2015, 8, 2180–2186.
26. Y. Yao, Q. Feng, S. Zhu, J. Li, Y. Yao, Y. Wang, Q. Wang, M. Gu, H. Wang, H. Li, X. Z. Yuan and M. Shao, Small Methods, 2018, 3, 1800324.
27. C. Guo, J. Ran, A. Vasileff and S. Z. Qiao, Energy Environ. Sci., 2018, 11, 45–56.
28. Z. Wang, F. Gong, L. Zhang, R. Wang, L. Ji, Q. Liu, Y. Luo, H. Guo, Y. Li, P. Gao, X. Shi, B. Li, B. Tang and X. Sun, Adv. Sci., 2018, 6, 1801182.
29. M. M. Shi, D. Bao, S. J. Li, B. R. Wulan, J. M. Yan and Q. Jiang, Adv. Energy Mater., 2018, 8, 1800124.
30. Y. Abghoui and E. Skúlason, J. Phys. Chem. C, 2017, 121, 6141–6151.
31. Y. Abghoui, A. L. Garden, J. G. Howalt, T. Vegge and E. Skúlason, ACS Catal., 2016, 6, 635–646.
32. Y. Abghoui and E. Skúlason, Catal. Today, 2017, 286, 78–84.
33. Q. Li, L. He, C. Sun and X. Zhang, J. Phys. Chem. C, 2017, 121, 27563–27568.
34. C. Choi, S. Back, N. Y. Kim, J. Lim, Y. H. Kim and Y. Jung, ACS Catal., 2018, 8, 7517–7525.
35. C. Ling, X. Niu, Q. Li, A. Du and J. Wang, J. Am. Chem. Soc., 2018, 140, 14161–14168.
36. C. Hering-Junghans, Angew. Chem., Int. Ed., 2018, 57, 6738–6740.
37. J. Zhao and Z. Chen, J. Am. Chem. Soc., 2017, 139, 12480–12487.
38. L. M. Azofra, N. Li, D. R. Macfarlane and C. Sun, Energy Environ. Sci., 2016, 9, 2545–2549.
39. S. Zheng, S. Li, Z. Mei, Z. Hu, M. Chu, J. Liu, X. Chen and F. Pan, J. Phys. Chem. Lett., 2019, 10, 6984–6989.
40. X. Yang, J. Nash, J. Anibal, M. Dunwell, S. Kattel, E. Stavitski, K. Attenkofer, J. G. Chen, Y. Yan and B. Xu, J. Am. Chem. Soc., 2018, 140, 13387–13391.
41. X. Yang, S. Kattel, J. Nash, X. Chang, J. H. Lee, Y. Yan, J. G. Chen and B. Xu, Angew. Chem., Int. Ed., 2019, 58, 13768–13772.
42. S. Kang, J. Wang, S. Zhang, C. Zhao, G. Wang, W. Cai and H. Zhang, Electrochem. Commun., 2019, 100, 90–95.
43. W. Kohn and L. J. Sham, Phys. Rev., 1965, 145, 561.
44. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
45. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118.
46. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
47. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 12947–12954.
48. J. D. Pack and H. J. Monkhorst, Phys. Rev. B: Solid State, 1977, 16, 1748–1749.
49. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
50. Z. Wei, Y. Feng and J. Ma, J. Energy Chem., 2020, 48, 322–327.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ma00849d

---