Open Access Article
Open Access ArticleRecent advances in simulating gas permeation through MOF membranes
Hilal
Daglar
 a,
Ilknur
Erucar
a,
Ilknur
Erucar
 b and
Seda
Keskin
b and
Seda
Keskin
 *a
*a
aDepartment of Chemical and Biological Engineering, Koc University, Rumelifeneri Yolu, Sariyer, 34450, Istanbul, Turkey. E-mail: skeskin@ku.edu.tr; Tel: +90-(212)-338-1362
bDepartment of Natural and Mathematical Sciences, Faculty of Engineering, Ozyegin University, Cekmekoy, 34794, Istanbul, Turkey
First published on 22nd July 2021
Abstract
In the last two decades, metal organic frameworks (MOFs) have gained increasing attention in membrane-based gas separations due to their tunable structural properties. Computational methods play a critical role in providing molecular-level information about the membrane properties and identifying the most promising MOF membranes for various gas separations. In this review, we discuss the current state-of-the-art in molecular modeling methods to simulate gas permeation through MOF membranes and review the recent advancements. We finally address current opportunities and challenges of simulating gas permeation through MOF membranes to guide the development of high-performance MOF membranes in the future.
1. Introduction
Membrane-based gas separation has environmental and economic advantages due to its renewable and continuous operation, and low energy consumption.1 Membranes today have several industrially important gas separation applications such as nitrogen separation from air (O2/N2), natural gas purification (CO2/CH4, H2S/CH4, He/CH4), hydrogen recovery (H2/N2, H2/CH4, H2/CO), and recovery of light olefins (C3H6/N2, C2H4/N2, C2H4/Ar, CH4/N2).2 The membrane selectivity and gas permeability (or permeance) are the key parameters to describe the performance of a membrane. Although the commercial market is currently dominated by polymeric membranes due to their scalability and low cost,3 they possess a trade-off between selectivity and gas permeability.4,5 There has been continuous efforts for developing new membrane materials that can offer both high gas permeability and high gas selectivity for different types of gas separation processes.For the last two decades, metal organic frameworks (MOFs), which are composed of inorganic metal nodes linked by organic linkers, have been known as an exciting class of porous materials.6 MOFs are studied in many different fields such as catalysis,7 optics,8 sensing,9 adsorption,10 liquid11 and gas separation12 due to their exceptional chemical and physical properties. Among these fields, MOFs have been widely used in gas adsorption and separation applications since structural features such as high porosities, large surfaces areas, and tunable shape-selective pore sizes make them highly efficient for gas separation. Both thin-film MOF membranes and MOF-based mixed matrix membranes (MMMs) where MOFs are used as fillers in a polymer matrix are studied for gas separations. Since fabricating scalable and defect-free thin-film MOF membranes is challenging, MOF-based MMMs offer the advantages of easy processability of polymers and low-cost manufacturing process for industrial gas separations. Several excellent reviews in the literature summarize experimental fabrication and applications of thin-film MOF membranes and MOF-based MMMs.13–19
Thanks to the existence of various types of organic and inorganic building blocks, the number of synthesized MOFs available in the Cambridge Structural Database (CSD)20 is dramatically increasing in each year and more than 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MOFs have been already reported. Performing experiments for each MOF to assess its desired gas separation performance is highly challenging since fabrication of thin-film MOF membranes, characterizing membrane structures, and further measurements of gas permeation through the pores of new MOF membranes require long times, extensive efforts and sources. Therefore, computational studies, especially high-throughput screening studies, play a significant role in assessing the performance of MOF membranes in a reasonable time in addition to providing molecular-level understanding of gas permeation in MOFs.21 By using molecular simulations, it is possible to quickly and accurately assess the potential of a MOF membrane for many different gas separations and under different operational conditions which may not be easily achieved by experiments.22 Using the key performance metrics, one can computationally screen MOFs and identify the best performing membranes to direct the experimental efforts, time and sources to these potential candidates. Thus, the membrane community significantly benefits from the high-quality computer simulations not only for unlocking the performance of existing MOFs but also for the discovery of new MOF membranes.
000 MOFs have been already reported. Performing experiments for each MOF to assess its desired gas separation performance is highly challenging since fabrication of thin-film MOF membranes, characterizing membrane structures, and further measurements of gas permeation through the pores of new MOF membranes require long times, extensive efforts and sources. Therefore, computational studies, especially high-throughput screening studies, play a significant role in assessing the performance of MOF membranes in a reasonable time in addition to providing molecular-level understanding of gas permeation in MOFs.21 By using molecular simulations, it is possible to quickly and accurately assess the potential of a MOF membrane for many different gas separations and under different operational conditions which may not be easily achieved by experiments.22 Using the key performance metrics, one can computationally screen MOFs and identify the best performing membranes to direct the experimental efforts, time and sources to these potential candidates. Thus, the membrane community significantly benefits from the high-quality computer simulations not only for unlocking the performance of existing MOFs but also for the discovery of new MOF membranes.
In this review, we first introduce the current state-of-the-art for the computational approaches used to simulate gas permeation through MOF membranes. We then discuss the representative examples from the literature to reveal the recent achievements in modeling MOF membranes and finally address both the opportunities and challenges of these computational methods to provide some guidelines for future studies.
2. Computational methods for predicting gas permeation
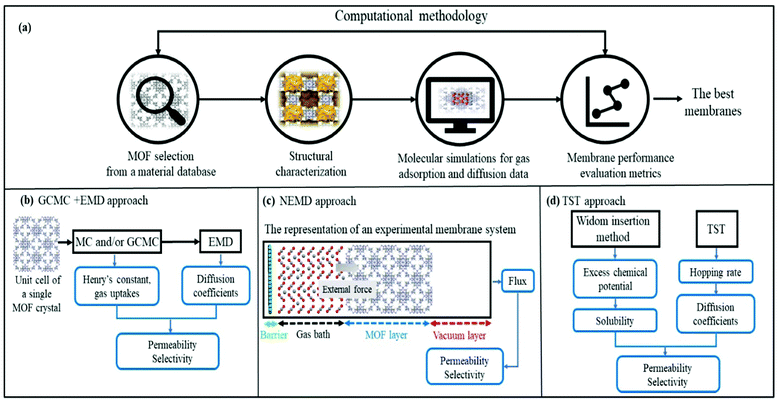
Fig. 1 represents computational methodologies commonly followed to compute gas permeation through MOF membranes. In high-throughput computational screening, MOFs are generally taken from material databases such as CSD MOF subset,23 the computation-ready experimental (CoRE) MOF24 database and hypothetical (computer generated) MOF database.25 As shown in Fig. 1(a), structural properties of MOFs such as surface areas, pore sizes, pore volumes, and densities are first calculated and used to refine the number of MOFs to be studied. For example, if one wants to identify the promising MOF membranes for H2/CO2 separation, discarding MOFs with pore sizes less than 3.3 Å will be useful to narrow down the materials space so that both H2 (2.8 Å) and CO2 (3.3 Å) molecules can pass through the membrane's pores. It is important to note that pore size screening can be done to obtain molecular sieving membranes where one type of gas passes through the pores whereas the others do not.26–28 Although the selectivity of molecular sieving membranes such as zeolite imidazolate framework-7 (ZIF-7) was measured to be very high, gas permeability was generally quite low due to the narrow pores.29 Therefore, MOFs with pore sizes larger than the size of the largest gas molecule can be more preferable to achieve both high selectivity and high permeability. After the selection of appropriate MOFs for a given membrane-based gas separation, molecular simulations can be performed to investigate gas adsorption and diffusion properties of MOFs.In molecular simulations, the intermolecular interactions (between gas-gas and MOF-gas) are described with van der Waals (vdW) and electrostatic interactions. Several potentials in different level of accuracy such as Morse,30 Mie31 and Buckingham32 can be used to compute intermolecular interactions in molecular simulations. Among these, Lennard-Jones 12-6 (LJ)33 and Coulomb34 potentials are the most popular to define repulsion–dispersion forces in vdW interactions and electrostatic interactions, respectively. LJ parameters of MOFs are commonly taken from the generic force fields such as the Universal Force Field (UFF)35 and DREIDING.36 On the other hand, complex interactions such as the ones between gases and open metal sites of MOFs and structural flexibility of MOFs may require highly accurate force fields such as MOF-FF37 and BTW-FF.38 Several studies showed that although generic force fields are not enough to accurately identify some specific interactions between gas and MOFs' atoms, these force fields generally give reasonable results in high-throughput screening studies.39,40 We also previously showed that simulated data of MOFs obtained with generic force fields such as DREIDING and UFF agree well with those of experimentally tested MOFs for several gas separations such as H2/CH4,41 CO2/N2,42,43 H2/CO2,44 CO2/CH4,42 He/CH445 and C2H6/C2H4.46 A variety of gas models can be used to obtain LJ parameters for gases. For example, TraPPE47 is generally used for CH4 which is considered as single-spherical and nonpolar atoms. Five-site model48 is also used for CH4, and it was shown that the single-site model leads to higher gas uptake compared to the results obtained from simulations with the five-site model of CH4.49 Similar to TraPPE model, Buch model50 assumes a single-site and spherical nonpolar atom, and commonly used for H2. However, single-site H2 model can fail to yield accurate gas uptake predictions at low temperature (∼77 K) due to the quantum effects. Yang et al.51 used two-site model for H2 adsorption and showed that H2 uptakes in IRMOF-1 and IRMOF-18 obtained by using two-site model show better agreement with the experimental measurements of H2 uptake at 77 K. Apart from two-site model, a three-site model with diatomic molecule and a dummy atom at the center of mass, is also used for H2 to consider the quadratic Feynman-Hibbs (FH) effective potential.52 EPM2,53 a linear and three-site model, is commonly used for CO2 molecule. Similarly, a three-site model including a dummy atom at the center of mass is used for O254 and N2.55 Adatoz and Keskin56 showed the accuracy of the gas models (single-site model for CH4 and H2, EPM2 for CO2 and three-site model of N2) by comparing the gas permeance predictions with the experimental measurements for eight common MOFs (IRMOF-1, Ni-MOF-74, MIL-53(Al)), and a family of ZIFs (-8, -69, -78, -90, and -95) using GCMC + EMD approach. A good agreement between predicted pure and mixture gas permeances of these MOFs and experimental measurements was reported.
To compute the electrostatic interactions, partial point charges of MOFs are assigned using either a quick charge estimation method such as charge equilibration method (Qeq)57 or a more accurate DFT-based but computationally costly method such as density derived electrostatic and chemical (DDEC),58 charges from electrostatic potentials using a grid (CHELPG)59 and repeating electrostatic potential extracted atomic charge (REPEAT)60 methods. We previously compared DDEC and Qeq methods for CO2/CH4 separation performances of 1500 MOFs and showed that the selection of charge method can quantitatively affect the performances of MOFs but it does not significantly change the ranking of MOFs based on different performance metrics such as regenerability and adsorbent performance score in a high-throughput computational screening study.61
To examine the gas permeation through MOF membranes, the solution-diffusion model62,63 which considers the solubility and mobility of gas molecules in dense membranes is widely used. Since MOFs have permanent pores and the solubility term is based on gas adsorption within these pores, we refer to this model as “sorption-diffusion”. To compute the permeability of gas molecules, two common computational approaches, GCMC + EMD (Fig. 1(b)) and NEMD (Fig. 1(c)) are used. In the first method (GCMC + EMD), the membrane system is mimicked by using the unit cell of single MOF crystals rather than using a real membrane system as shown in Fig. 1(b). Here, MOF crystal is represented by defect-free and continuous single crystallographic unit cell with no grain boundaries. Henry's constants of different gases (K0i and K0j) for adsorption are calculated by performing Monte Carlo (MC) simulations at zero-coverage by the Widom particle insertion method.64 In this method, a ghost particle is inserted to consider only the interactions between gas and framework atoms. It is important to note that since GCMC + EMD approach assumes that the molar volume of the fluid in the membrane phase is the same with the one exists in the bulk phase, this method is more reliable when different gases in the mixture do not have a strong interaction with each other at low pressures.65 Single-component self-diffusivities (D0i, D0j) of gases i and j are then calculated by performing equilibrium molecular dynamics (EMD) simulations at infinite dilution. Gas-gas intermolecular interactions are generally switched-off in EMD simulations to mimic infinite dilution. We note that there is generally an inverse relationship between the adsorption and diffusion properties of gases since strongly adsorbed gas molecules (having high affinity to the framework atoms) generally diffuse slower than the weakly adsorbed ones.43 Gas permeability of MOFs (P0i) at infinite dilution is estimated as the multiplication of adsorption (mol kg−1 Pa−1) and diffusion (m2 s−1) terms which are directly obtained from MC and EMD simulations:
| P0i = K0i × D0i | (1) |
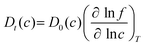 | (2) |
| Ji = −Dt(c)∇c | (3) |
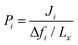 | (4) |
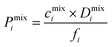 | (5) |
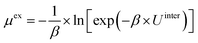 | (6) |
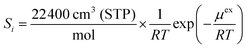 | (7) |
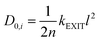 | (8) |
| Pi = D0,i × Si | (9) |
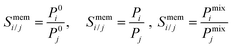 | (10) |
Non-equilibrium molecular dynamics (NEMD) simulations are performed by constructing a more realistic representation of the membrane system. Fig. 1(c) shows a typical computational membrane system, which is constructed by gas bath, MOF and vacuum layers to perform NEMD simulations. An external force is generally applied for introducing a pressure gradient for gas molecules considering permeate and retentate sides of the membrane and feed depletion problem can be tackled using this external force. Due to periodicity of the unit cell, the pressure gradient between gas bath and vacuum layer can cause the gas molecules to escape towards vacuum layer. Therefore, as shown in Fig. 1(c), a physical barrier such as graphene layer before gas bath is required.76 The interaction between gas molecules and the physical barrier should be switched off to eliminate the effect of physical barrier on membrane gas separation. NEMD simulations consider mass transfer resistance, which is a resistance on membrane surface caused by the diffusion of gases through membrane pores.77,78 High mass transfer resistance on the membrane surface can lead to the blockage of the membrane pores and diminishes permeability and membrane selectivity.79 For example, Wenk et al.80 showed that mass transfer coefficient for O2 in a polymeric membrane decreases as the membrane thickness increases. Although the thickness of experimentally tested MOF membranes is higher than the computationally simulated ones, the thickness of MOF membranes is taken as approximately 40–50 Å in computational studies to save computational time.81–83 Therefore, considering mass transfer resistance in simulations is important to mimic the real gas separation unit. Different than the GCMC + EMD approach, membrane properties are directly computed from NEMD simulations. The amount of gas molecules transported through the unit area of MOF membrane per unit simulation time can be calculated as gas flux (Ji). Gas permeability (Pi) is then calculated by using eqn (4) as we mentioned above.
In the literature, although a variety of techniques to consider non-equilibrium conditions in MD simulations has been used to make more accurate representation of a membrane system,84–86 the number of studies on NEMD simulations to estimate gas permeation through MOFs is limited. The most important reason is that performing NEMD simulations takes considerably longer times for getting membrane properties of MOFs compared to performing GCMC + EMD simulations, which promotes GCMC + EMD approach especially in high-throughput computational screening studies as we discuss below.
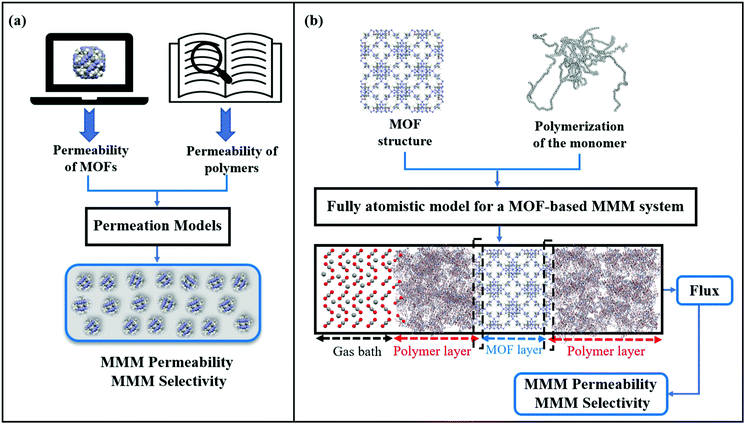
So far, we focused on modelling of pure MOF membranes for gas separation. MOFs can be also used as filler particles incorporated into polymers to improve gas permeability and selectivity of polymers. Fig. 2 shows two different methods used in computational studies to estimate selectivity and gas permeability of MOF-based MMMs. In the first method known as combination of atomistic and continuum modeling, gas permeabilities of MOFs are obtained from atomic simulations and permeability of MOF-based MMMs are estimated by using a theoretical permeation model (Bruggeman,87 Pal,88 Felske,89 and Maxwell90etc.) as shown in Fig. 2(a). When these models are used, gas permeability data of polymer is generally obtained from the single-component gas measurements available in the literature. For example, in Maxwell model, permeability of MMM is dependent on the volume fraction of MOF filler (ϕ) and permeabilities of pure polymer (PP) and pure MOF (PMOF) as follows:
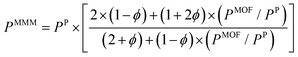 | (11) |
Since defect-free and rigid MOF assumptions are generally used in molecular simulations, representation of MMM morphologies depends on the selection of theoretical permeation models. For example, Maxwell model assumes ideal MMMs where MOF particles are perfectly dispersed in a polymer matrix and no defects in the polymer-particle interface are observed whereas Felske model accounts for non-ideal morphologies which include interface voids and polymer rigidification around particles. We previously showed that using Maxwell model among the theoretical models based on the ideal morphology and the modified Felske model among the ones considering interfacial morphology make accurate predictions for gas permeation through MOF-based MMMs.91
In the second method referred as the fully atomistic approach (Fig. 2(b)), both polymer and MOF are atomically modelled and the effects of interface interactions on properties of MOF-based MMMs are considered in simulation. In this method, three main steps are generally followed: (i) equilibration of the selected monomer chains with various EMD simulation steps at several NVT and NPT ensembles to reach the desired density of a polymer, (ii) combining polymer and MOF surfaces having the lowest surface energy within the same simulation box, (iii) performing several EMD runs for equilibration of the MMM. This method is nontrivial since creating a proper polymer matrix and considering the appropriate model for MOF/polymer interface is computationally costly. After constructing a fully atomistic representation of MOF-based MMMs, either GCMC + EMD or NEMD simulations can be used to predict properties of MMMs.92,93 We note that in fully atomistic simulations, considering the structural flexibility of MOFs and interfacial interactions between MOF surfaces and polymers is important since these interactions play a significant role in identifying MOF/polymer interface compatibility.93,94
3. Simulated membrane properties of MOFs
Achieving high gas purity using polymer membranes is still challenging. For example, polymers only have ∼10% commercial use for the natural gas purification due to their low CO2 permeability and low CO2/CH4 selectivity.2 Since polymers dominate the current market, outperforming the performance of polymers is the primary goal of developing new membranes for industrial use. With the development of efficient MOF membranes and MOF-based MMMs, high separation performance can be achieved for various gas pairs.We compare the performance of MOF membranes and MOF-based MMMs with that of polymers in Fig. 3 by collecting all the experimental and computational data available in the literature for three important gas separations, CO2/CH4, CO2/N2, and H2/CO2. The performance limit of polymer membranes is defined with the Robeson's upper bound4,5 for different gas separations. The upper bound shows the single-component gas permeation data of polymers generally measured at 35 °C and 1–2 bar. Robeson upper bounds provide empirical relationships for membrane-based gas separation.4,5 These upper bounds for several gas separations show the trade-off between membrane selectivity and gas permeability for polymeric membranes. The origin of the trade-off comes from the nature of glassy and rubbery polymers. Glassy polymers have restricted chain motions which yield low gas permeability, but they exhibit high membrane selectivity due to their strong size sieving ability.95 On the other hand, rubbery polymers exhibit high gas permeability due to their high molecular chain mobility, but they provide low selectivity due to the ease of gas penetration through the flexible chains.96 Since polymeric membranes have been commonly used for industrial applications, the performance of new membranes such as MOFs is assessed by considering these upper bounds. Due to a wide range of chemical environments and high porosities of MOFs, gas permeability and membrane selectivity of MOFs have been reported in a very large range.97–99 In addition, when molecular sieving mechanism is used to assess the gas separation performances of MOF, extremely high membrane selectivities (up to 108) are reported in the literature.72 For these reasons, it is difficult to observe a trade-off or define the upper-performance limits of MOF membranes. We used the experimental data of MOF membranes and MOF-based MMMs from a recent study14 and collected the computational data from the corresponding studies listed in Table 1. The conditions for experimental and simulated permeation data that we collected from the literature are different in some cases and we direct the readers to the corresponding studies listed in Table 1.
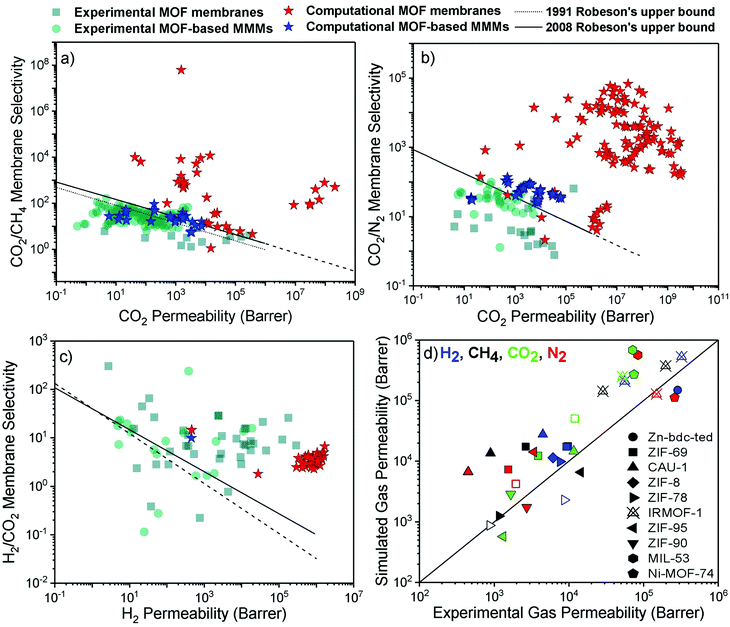 | ||
| Fig. 3 Experimental and computational performance of MOF membranes and MOF-based MMMs for (a) CO2/CH4, (b) CO2/N2, and (c) H2/CO2 separations. The experimental data was redrawn based on the literature.14 (d) Comparison of simulated and experimental gas permeabilities of 10 different MOFs. Filled (unfilled) symbols represent the single-component (mixture) gas permeability. | ||
| MOFs | Gas separation | Computational methodology | Simulation conditions | Performance metrics | Ref. |
|---|---|---|---|---|---|
| SC: single-component, BM: binary mixture, TM: ternary mixture, QM: quaternary mixture, P: permeability, F: flux, D: diffusivity, Prm: permeance. | |||||
| CAU-1 | H2/CH4, CO2/CH4, CO2/H2, CO2/N2, Kr/Xe (SC, BM) | NEMD (dual-control plane (DCP)) | 1 bar, 298–600 K | Prm, Smem | 101 |
| Cu-BTC | CH4, C2H6, C3H8 (SC, BM, TM) | GCMC + EMD | 4–55 bar, 298 K | D, Sdiff, Smem | 117 |
| ZIF-8 | CH4, C2H5, C2H6 (SC), C2H5/C2H6 (BM) | NEMD (Concentration gradient driven (CGD)-MD) | 2–40 bar, 300 K | F, P, Smem | 84 |
| Bio-MOF-11 | CO2/N2 (BM) | GCMC + EMD | 0–20 bar, 298 K | P, Sdiff, Smem | 118 |
| Cu-BDC | CO2/CH4 (BM) | NEMD | 4.5–20 bar, 298 K | F, P, Smem | 119 |
| ZIF-8 | H2/N2/CO2 (TM) | GCMC + EMD, NEMD (CGD-MD) | 35 atm, 300 K | D, F, Smem | 65 |
| ZIF-8, ZIF-67 | C3H8, C3H7 (SC) | Maxwell–Stefan model | NA | D, Sdiff | 120 |
| NH2-MIL-53(Al) | CO2 (SC) | GCMC + EMD | 273 K | D | 121 |
| CAU-10-H MOF | CO2, N2, CH4 (SC) | GCMC + EMD, TST | Infinite dilution, 300 K | Prm, P, Smem | 122 |
| MOF-508a, MOF-508b | C2H2 (SC) | EMD | 300–900 K | D | 123 |
| 4 mixed-ligand MOFs | CH4/H2 (BM) | GCMC + EMD | 0–20 bar, 298 K | P, Sdiff, Smem | 124 |
| MOF-5, CuBTC, ZIF-8, MEFMEQ | H2/CH4 (SC, BM) | GCMC + EMD, NEMD | 1 bar, 2–4.5 bar, 298 K | F, P, Smem | 83 |
| ZIF-8, ZIF-67 | C2H6, C2H5 (SC) | EMD, TST | 308 K | D, Sdiff | 125 |
| ZIF-8, ZIF-7–8 | CO2, CH4, N2 (SC) | EMD, TST | Infinite dilution, 308 K | D, S diff | 71 |
| ZIF-8, ZIF-67, BeIF-1, ZIF-7–8, Co-ZIF-7–8 | He/CH4, H2/CH4, O2/N2, CO2/CH4, CO2/N2 (SC) | TST | Infinite dilution, 308 K | P, Smem | 72 |
| 8 MOFs | CO2, H2, He, N2, CH4 (SC) | GCMC + EMD | ∼1 bar, ∼298 K | Prm | 56 |
| 8 MOFs | Xe/Kr, Xe/Ar (BM) | GCMC + EMD | 0.1–25 bar, 298 K | P, Smem | 126 |
| ZIF-8/PIM-1 MMM | H2/CH4 (SC, BM) | NEMD (CGD-MD) | 5 bar, 300 K | P, Smem | 92 |
| IL-modified ZIF-8/PI MMM | CO2/CH4 (SC) | GCMC + EMD | 1–10 bar, 300 K | D, P, Sdiff, Smem | 127 |
| ZIF-7/PBI MMM | H2/CO2 (SC) | GCMC + EMD | Infinite dilution, 300 °C | D, P, Smem | 93 |
| NUS-8/PIM-1 MMM | CO2/N2, CO2/CH4 (BM) | NEMD (CGD-MD) | 10 bar, 298 K | P, Smem | 128 |
| 102 MOFs | N2/CH4 (BM) | GCMC + EMD | 0.01 bar, 10 bar, 298 K | P, Sdiff, Smem | 129 |
| 115 MOFs | Xe/Kr, Xe/Ar, Rn/Xe (BM) | GCMC + EMD | 1 bar, 298 K | P, Smem | 130 |
| 172 MOFs | H2/CH4 (BM) | GCMC + EMD | 10 bar, 298 K | P, Sdiff, Smem | 102 |
| 175 MOFs | C2H6/C2H4, C2H6/CH4 (BM) | GCMC + EMD | 10 bar, 298 K | P, Sdiff, Smem | 131 |
| 234 MOFs | H2/CH4 (SC) | GCMC + EMD | Infinite dilution, 300 K | D, P, Smem | 132 |
| 278 MOFs | C2H6/C2H4, C2H6/CH4 (BM) | GCMC + EMD | 10 bar, 298 K | D, P, Sdiff, Smem | 46 |
| 288 COFs | H2/CO2 (BM) | GCMC + EMD | 10 bar, 298 K | P, Smem | 133 |
| 298 COFs and 116 MMMs | CO2/CH4 (BM) | GCMC + EMD + MMM model | 10 bar, 298 K | P, Smem | 134 |
| 500 MOFs | He/N2 (SC) | GCMC + EMD | Infinite dilution, 298 K | S diff, Smem | 135 |
| 504 MOFs + 165 Zeolites | H2/CH4 (SC) | GCMC + EMD | Infinite dilution, 298 K | P, Smem | 136 |
| 1163 MOFs | CO2/N2 (SC) | GCMC + EMD | Infinite dilution, 303 K | D, P, Sdiff, Smem | 40 |
| 1525 MOFs | O2/N2 (BM) | GCMC + EMD | 1 bar, 298 K | D, P, Sdiff, Smem | 137 |
| 2932 MOFs | CO2/CH4 (BM) | GCMC + EMD | 1 bar, 298 K | P, Sdiff, Smem | 61 |
| 3080 MOFs | C2H4/C2H6 (SC) | TST | Infinite dilution, 298 K | D | 73 |
| 3432 MOFs | Xe/Rn, Ar/Kr, Kr/Xe (SC) | GCMC + EMD, TST | Infinite dilution, 298 K | D, Sdiff, Smem | 138 |
| 4764 MOFs | Hexane Isomers (SC, BM) | GCMC + EMD | Infinite dilution, 298 K, 10 bar, 433 K | P, Smem | 139 |
| 4764 MOFs | CO2/N2/CH4 (TM) | GCMC + EMD | 10 bar, 298 K | D, P, Sdiff, Smem | 97 |
| 5600 MOFs | Xe/Kr (BM) | GCMC + EMD | 1 bar, 298 K | D, Sdiff, Smem | 140 |
| 6013 MOFs | CO2, CH4, O2, N2, H2, H2S, He (SC) | GCMC + EMD | Infinite dilution, 298 K | P, Smem | 141 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020 MOF and 78 020 MOF and 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 806 MMMs 806 MMMs |
O2/N2 (SC, BM, TM) | GCMC + EMD + MMM model | Infinite dilution, 1 bar, 298 K | P, Sdiff, Smem | 142 |
54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 808 MOFs 808 MOFs |
CO2/H2 (SC) | GCMC + EMD | Infinite dilution, 298 K | P, Sdiff, Smem | 44 |
54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 808 MOFs 808 MOFs |
CO2/N2 (SC, BM), CO2/N2/H2O (TM) | GCMC + EMD | Infinite dilution, 1 bar, 298 K | P, Sdiff, Smem | 43 |
54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 808 MOFs and 64 MMMs 808 MOFs and 64 MMMs |
CO2/CH4 (SC, BM) | GCMC + EMD + MMM model | Infinite dilution, 10 bar, 298 K | D, P, Sdiff, Smem | 143 |
54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 808 MOFs and 78 MMMs 808 MOFs and 78 MMMs |
H2/N2, H2/N2/CO2/CO (SC, BM, QM) | GCMC + EMD + MMM model | Infinite dilution, 1 bar, 298 K | P, Sdiff, Smem | 144 |
67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 675 MOFs 675 MOFs |
CO2/CH4, H2S/CH4 (SC, BM) | GCMC + EMD | Infinite dilution, 10 bar, 298 K | D, P, Smem | 145 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 551 MOFs 551 MOFs |
H2/CO2 (SC) | GCMC + EMD | Infinite dilution, 298 K | P, Sdiff, Smem | 99 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 589 MOFs and 109 589 MOFs and 109![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 508 MMMs 508 MMMs |
CO2/N2 (SC, BM) | GCMC + EMD + MMM model | Infinite dilution, 1 bar, 298 K | P, Smem | 146 |
137![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 953 hMOFs 953 hMOFs |
CO2/N2/CH4 (SC, TM) | GCMC + EMD | Infinite dilution, 10 bar, 298 K | D, P, Sdiff, Smem | 147 |
112![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 888 MOFs and 1 888 MOFs and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 015 015![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 992 MMMs 992 MMMs |
CO2/N2 (SC) | GCMC + EMD + MMM model | Infinite dilution, 298 K | D, P, Sdiff, Smem | 98 |
Fig. 3(a) shows that although many MOF membranes and MOF-based MMMs, investigated either computationally or experimentally, exceed the Robeson's upper bound, there is still a trade-off between gas permeability and membrane selectivity for CO2/CH4 separation. While experimentally reported CO2 permeabilities of MOF membranes are between 4–2.8 × 105 Barrers, selectivities are in the range of 1–13, indicating that experimentally measured MOF membranes are generally close to the upper bound. On the other hand, simulated CO2/CH4 selectivities and CO2 permeabilities of MOF membranes are much higher than the experimental data which may be attributed to the high number and variety of MOFs considered in molecular simulations. Thin-film MOF membranes are frequently fabricated on a substrate and weak adhesion between MOF and the substrate may lead to nonselective openings for gas molecules. Defect formations and structural instability issues can also occur during fabrication of thin-film MOFs.100 Because of these challenges in fabrication of thin-film MOF membranes, the variety of experimentally studied MOF-based MMMs is much more than that of thin-film MOF membranes. CO2/CH4 selectivities of MOF-based MMMs (9–164) are higher compared to those of pure MOF membranes but they still suffer from low permeability (0.5–5677 Barrers) to exceed the upper bound. We note that while the simulated performances of MOF membranes are well above the Robeson's upper bound due to the high gas permeability or high membrane selectivity, the simulated performance of MMMs is close to the upper bound because polymer phase dominates the performance of MMMs.
Fig. 3(b) shows that MOF membranes provide extremely high CO2 permeability and CO2/N2 selectivity based on the results of molecular simulations. Here, we note that experimental gas permeance data for this separation is not currently available for many simulated MOFs; therefore, validation of the simulations is required to assess the actual performance of these membranes. Fig. 3(c) shows that simulated H2/CO2 selectivities are much lower compared to the experiments, although calculated H2 permeabilities are much higher than the experimental H2 permeabilities for many MOF membranes. The lighter and weakly adsorbed H2 molecules diffuse faster through the pores than the strongly adsorbed CO2 molecules, which enhances diffusion selectivity (Sdiff) towards H2. However, adsorption of CO2 is much stronger than that of H2 and CO2 adsorption dominates the separation process. Therefore, calculated CO2 permeabilities for many MOF membranes are much higher than H2 permeabilities, leading to low membrane selectivity towards H2. We note that structural flexibility is generally neglected in molecular simulations which also affects the separation performance of MOF membranes. To understand the accuracy of predicted gas separation performances of MOFs in Fig. 3(a)–(c), we compare simulated and experimental gas permeabilities of 10 different MOFs at the same conditions. We collected computational43,56,101,102 and experimental studies103–112 reporting single-component and mixture gas permeabilities of the same MOFs. Fig. 3(d) includes gas permeability data for 10 different MOF membranes (Zn-bdc-ted, ZIF-69, CAU-1, ZIF-78, ZIF-8, ZIF-90, ZIF-95, IRMOF-1, MIL-53 and Ni-MOF-74). In Fig. 3(d), different computational methodologies were used to simulate gas permeabilities of MOFs. For example, Adatoz and Keskin56 used GCMC + EMD approach to compute H2, N2, CH4 and CO2 permeabilities of ZIF-69 and ZIF-8 and a good agreement was found between the theoretical and the experimental results of ZIF-8113 and ZIF-69.105 Zhai et al.101 performed NEMD simulations to predict H2, N2, CH4 and CO2 permeabilities of CAU-1 and compared their predictions with experimental results reported by Yin et al.112 Similarly to GCMC + EMD approach, NEMD method also agreed with experiments as shown in Fig. 3(d). However, simulated gas permeabilities generally overestimate experimental ones because MOFs are generally modelled as perfect, defect-free membrane materials which may not be true in experiments. Overall, Fig. 3(d) showed that although there can be generally deviations between predicted and experimental data of MOF membranes, the potentials of computational, not experimentally tested MOF-based membranes are shown. In the next section, we review some illustrative computational studies on MOF membranes.
3.1 Thin-film MOF membranes
We provided the information about computational studies on MOF-membranes and MOF-based MMMs in Table 1 by listing computational methodology, simulation conditions, and calculated membrane-based performance metrics. We provided the initial number of MOFs considered in high-throughput screening studies in Table 1. For example, Altintas et al.46 firstly investigated the adsorption-based separation performances of 278 MOFs (we noted this number in Table 1) and then calculated membrane properties of only top 5 MOFs. Although thousands of MOFs have been synthesized and deposited into the CSD, the number of MOFs for which membrane properties are simulated and reported is very limited. Early computational works examined a very small number of MOFs. Table 1 demonstrates that ZIFs, especially ZIF-8, are widely studied due to their high potential in kinetic-driven gas separation, especially for gases having similar sizes with the pore sizes of ZIFs.114 Due to their easy synthesizability and high chemical and thermal stabilities, available experimental data related to gas separation performances of ZIF membranes has rapidly increased.115 This motivated computational researchers to focus on ZIF membranes. For example, GCMC + EMD simulations were performed to estimate the membrane properties of 8 different MOFs, including ZIF-8.56 Predicted H2 permeabilities of ZIF-8 at different conditions agreed well with the experimental measurements, showing that using this computational approach is reasonable and time-efficient to make accurate predictions about the properties of MOF membranes. Krokidas et al.72 computationally investigated ZIF-8 and its tailored analogues based on the metal and/or linker replacement to assess their ideal He/CH4, H2/CH4, O2/N2, CO2/CH4, and CO2/N2 separation performances. Instead of classical EMD simulations, they used TST116 at infinite dilution to compute diffusivity coefficients. This study revealed that the systematic modification based on the replacement of building units of ZIF-8 can alter the performance of membranes by improving gas selectivity.Table 1 shows that molecular simulations of MOF membranes are generally performed at single-component gas conditions. However, separation performance of MOF membranes for gas mixtures can be different at industrial operating conditions due to the competitive adsorption and diffusion between gas molecules. Therefore, mixture simulations which consider industrially relevant gas compositions are needed to unlock the real gas separation performances of MOF membranes. For example, Li et al.118 predicted performance of Bio-MOF-11 membrane using GCMC + EMD approach for CO2/N2:15/85 and CO2/N2:50/50 mixture separations and showed that membrane selectivity of Bio-MOF-11 increases from ∼50 to ∼80 without a significant change in its CO2 permeability (from 3.4 × 104 Barrer to 1.2 × 104 Barrer) when the mixture conditions are used in molecular simulations.
Based on the development in computational algorithms, high-throughput computational screening methodologies have gained a momentum in the MOF research. The advantage of screening studies is to identify the best membrane candidates from a very large number of MOFs. These studies produce a vast amount of data on MOFs which can be further used to establish structure-performance relations for the design and development of high-performance MOF membranes for a target gas separation. For example, 4240 MOFs in CSD MOF subset (over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 in 2021) were screened by using GCMC + EMD approach and MOFs which have generally Cd, Cu, and Zn metals with narrow pores sizes (3.8–6 Å), low surface areas (<1000 m2 g−1), low porosities (<0.75) were found to be promising for H2/CH4 separation.41 This kind of quantitative structure-performance relations are useful to choose the right membrane among the existing ones. In another study, 298 CoRE COFs (covalent organic framework), emerging class of crystalline networks consisted of covalently bonded light elements (H, C, N, O, B) with organic linkers,148 were screened by GCMC + EMD simulations for membrane-based CO2/CH4 separation.134 CO2/CH4 selectivities of COFs were found to be enhanced approximately 100 times by incorporating F− and Cl− groups into the framework compared to the selectivities of unmodified COFs. This result indicated that structural modifications can be a useful strategy to improve the separation performance of MOF and COF membranes to exceed the upper bound of polymers.
000 in 2021) were screened by using GCMC + EMD approach and MOFs which have generally Cd, Cu, and Zn metals with narrow pores sizes (3.8–6 Å), low surface areas (<1000 m2 g−1), low porosities (<0.75) were found to be promising for H2/CH4 separation.41 This kind of quantitative structure-performance relations are useful to choose the right membrane among the existing ones. In another study, 298 CoRE COFs (covalent organic framework), emerging class of crystalline networks consisted of covalently bonded light elements (H, C, N, O, B) with organic linkers,148 were screened by GCMC + EMD simulations for membrane-based CO2/CH4 separation.134 CO2/CH4 selectivities of COFs were found to be enhanced approximately 100 times by incorporating F− and Cl− groups into the framework compared to the selectivities of unmodified COFs. This result indicated that structural modifications can be a useful strategy to improve the separation performance of MOF and COF membranes to exceed the upper bound of polymers.
In addition to synthesized MOFs, computationally generated MOFs which are called hypothetical MOFs (hMOFs) were also screened to explore the structure-performance relationships. For example, Qiao et al.147 used GCMC + EMD approach for 137![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 953 hMOFs25 and showed that MOF membranes having narrow pore sizes (∼3 Å) and large pore size distributions (PSD) in the range of 33–42% are the promising candidates for upgrading natural gas. They first performed simulations at infinite dilution and then for a small number of high-performing MOFs, simulations were repeated at practical operating conditions. This is a common strategy used in a multi-step screening approach to identify the promising MOF membranes. Recently, high-throughput screening approach was combined with the machine learning algorithms to predict performance metrics of 6103 CoRE MOFs with respect to six descriptors (pore limiting diameter (PLD), the largest cavity diameter (LCD), porosity, surface area, density, PSD) for different gas separations.141 PLD was determined as the key parameter for predicting the membrane properties of MOFs especially for mixtures having more than three components. For the separation of binary gas mixtures, LCD and porosity were found to be more important. Using machine learning together with high-throughput computational screening can be effective to analyze the structure–property relations to guide the design of novel MOF membranes for a target gas separation.
953 hMOFs25 and showed that MOF membranes having narrow pore sizes (∼3 Å) and large pore size distributions (PSD) in the range of 33–42% are the promising candidates for upgrading natural gas. They first performed simulations at infinite dilution and then for a small number of high-performing MOFs, simulations were repeated at practical operating conditions. This is a common strategy used in a multi-step screening approach to identify the promising MOF membranes. Recently, high-throughput screening approach was combined with the machine learning algorithms to predict performance metrics of 6103 CoRE MOFs with respect to six descriptors (pore limiting diameter (PLD), the largest cavity diameter (LCD), porosity, surface area, density, PSD) for different gas separations.141 PLD was determined as the key parameter for predicting the membrane properties of MOFs especially for mixtures having more than three components. For the separation of binary gas mixtures, LCD and porosity were found to be more important. Using machine learning together with high-throughput computational screening can be effective to analyze the structure–property relations to guide the design of novel MOF membranes for a target gas separation.
In most of the computational studies, MOFs are assumed to be perfectly crystalline without any defects since accurate representation of the molecular interaction mechanism of gases on a defective surface is challenging. However, synthesized MOFs may have different types of intracrystalline defects which may affect their gas separation performance. To understand the effect of intracrystalline defects on H2/CH4 separation performances of MOF membranes, Kim et al.132 used 234 DFT-minimized MOFs149 and generated their defected structures with a Python script by randomly removing linkers. They used GCMC + EMD approach at infinite dilution to compute membrane properties. With the addition of linker vacancies, although many MOFs remained as promising, selectivities of the top performing MOFs significantly decreased as shown in Fig. 4(a) and (b). Therefore, it can be concluded that considering defects in molecular simulations can change our overall assessment about the top performing membranes. Thus, the selection of MOFs whose performances do not change when the linker vacancies are introduced will be a useful strategy to identify promising MOFs for industrial applications.
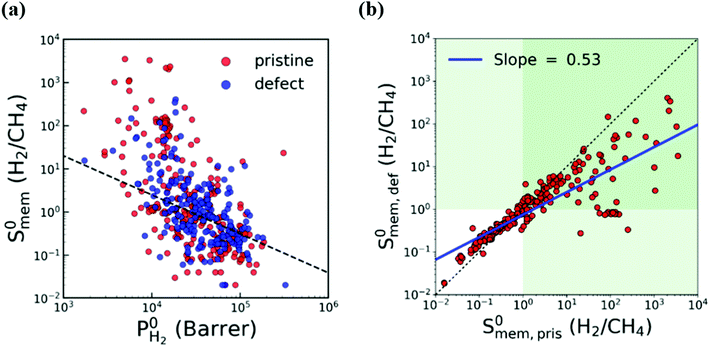 | ||
| Fig. 4 Comparison of H2/CH4 membrane selectivity and H2 permeability of pristine (red) and defective (blue) MOFs. The black dashed line represents the upper bound. The green area indicates H2-selective region. The blue line is the least squares fit for the logarithm of the selectivities of pristine and defective structures. Reprinted from the study of Kim et al.132 | ||
So far, we discussed GCMC + EMD approach which is based on the equilibrium conditions to predict membrane properties of MOF membranes. Velioglu and Keskin83 compared calculated H2 and CH4 permeabilities and selectivities of ZIF-8 obtained from GCMC + EMD and NEMD simulations with the experiments in Fig. 5(a)–(c). Instead of using a fully flexible ZIF-8, they tethered the framework atoms during NEMD simulations and observed a faster gas diffusion compared to EMD.
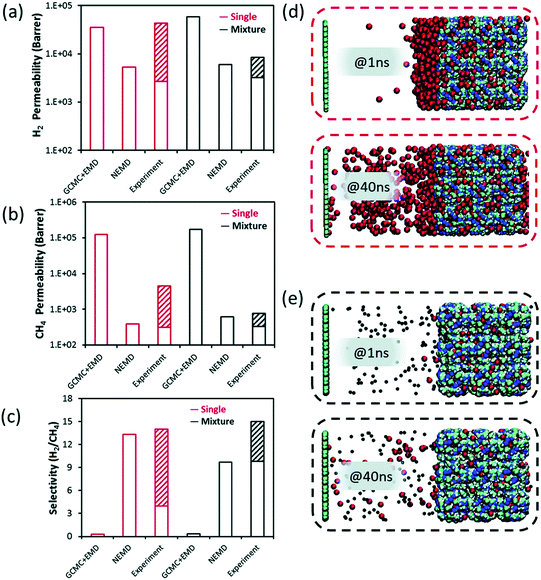 | ||
| Fig. 5 Simulated (a) H2 and (b) CH4 permeabilities, (c) H2/CH4 membrane selectivity obtained from GCMC + EMD, NEMD simulations and their experimental values for ZIF-8. The hashed half-bars represent the range of experimental data reported in different studies. NEMD snapshots for permeation of (d) pure CH4, (e) H2/CH4 mixture at the 1st and 40th ns. The dark blue, white, cyan, and colors represent zinc, hydrogen, and carbon atoms, respectively in (d and e). Black (red) colors also represent H2 (CH4) molecules, respectively in (d and e). Reprinted from the study of Velioglu and Keskin.83 | ||
Velioglu and Keskin83 also provided the NEMD snapshots for pure and mixture gas permeations for H2/CH4 separation. In Fig. 5(d), they showed that CH4 layer in the feed side is thick, referred to as concentration polarization at 1 ns whereas it reduces at 40 ns since at the starting point of the simulation an external force was applied. However, the concentration polarization was not observed for the binary mixture since H2 accelerates the diffusion of slowly diffusing CH4 (Fig. 5(e)). ZIF-8 was reported as a H2 selective membrane in experiments (Fig. 5(c)). However, results obtained from GCMC + EMD simulations gave a higher CH4 permeability, suggesting a CH4 selective ZIF-8 membrane, compared to those obtained from NEMD. For this reason, NEMD simulations gave a better agreement with experiments as the range is represented with pattern-filled columns in Fig. 5(a)–(c) for both the single-component and mixture permeation of H2 and CH4 within ZIF-8 membrane. Thus, GCMC + EMD approach was suggested to quickly identify the most promising materials and then more detailed NEMD simulations which require longer simulation time (at least several days) are suggested to be used for the best membranes candidates to observe the mass transfer resistances on the pore entrance.
Namsani et al.65 developed a new NEMD simulation method, concentration gradient driven molecular dynamics (CGD-MD),84 to investigate H2/N2 and H2/CO2 separation performances of ZIF-8. Both GCMC + EMD and CGD-MD methods were applied by using four different force fields for ZIF-8. Regardless of the force field they used, ZIF-8 was identified as a H2 selective membrane when the CGD-MD method was used whereas the membrane was found to be CO2 selective when GCMC + EMD approach was used. Since the results of CGD-MD simulations agreed well with the experimental one,150 this study reveals that at moderate or high-pressure conditions, a NEMD method such as CGD-MD is better to accurately predict the gas separation performance of MOF membranes.
All these studies show that accurate representation of the system and the operating conditions are important to model gas permeation through MOF membranes. In high-throughput screening studies, performing GCMC + EMD simulations is a practical approach to narrow down the materials space to point out the promising membranes due to the less computational power and time required compared to NEMD simulations. However, it should be kept in mind that GCMC + EMD simulations provide reliable results when gas molecules do not have a strong interaction with each other, especially at low pressures. On the other hand, mass transfer resistance on the membrane surface which affects the gas separation performance is not considered in this approach. For this reason, computationally costly NEMD simulations should be performed for the best performing membranes to ensure their potential for industrial applications. Here, if the MOF structure is flexible, considering the intramolecular forces is also important to figure out the realistic pore properties and performances of materials. We note that structural flexibility can be investigated by using GCMC + EMD or NEMD approaches. However, performing flexible simulations for screening applications is not convenient due to the enormous computational time and the difficulty to define intramolecular forces for each MOF structure. The effect of structural flexibility of MOFs on CO2/CH4 separation was investigated in our previous works.143,151 Results showed that although membrane selectivity and permeability of a MOF having large pores slightly change when structural flexibility is considered, separation performances of MOFs having narrow pores close to the kinetic diameters of gases are dramatically affected. We finally conclude that both GCMC + EMD and NEMD approaches are useful to understand gas transport mechanisms in MOF membranes. However, researchers should be aware of the aforementioned limitations of these two approaches.
3.2 MOF-based MMMs
To overcome the trade-off between gas permeability and selectivity for polymeric membranes, MOFs are used as fillers in a polymeric matrix. Keskin and Sholl152 used two theoretical permeation models, Maxwell90 and Bruggeman,87 to assess the separation performances of MOF-based MMMs. A good agreement between simulated and experimental permeation data of IRMOF-1/Matrimid was found indicating that theoretical models can give meaningful results for the performance prediction of MMM performances. Various gas permeation models such as Maxwell,90 Modified Felske153 were later used to compute the gas permeability of different types of MOF-based MMMs.98,142Since the number of available MOFs and polymers is very high, using permeation models is practical in high-throughput computational screening to evaluate gas separation performances of a large number of MMMs. In some early studies, the best MOF membranes were initially selected via molecular simulations and properties of MMMs made of these MOFs were then predicted using permeation models.143,144 Another way is to compute gas permeability of a large number of MMMs considering many MOF/polymer combinations and then identify the best ones offering the desired MMM properties.146 It is important to note that the properties of MOF and polymer have a synergetic effect on those of MMMs. In our previous studies,142–144,146 we showed that when a MOF filler is incorporated into a low permeable polymer, it generally affects gas permeability without any change in membrane selectivity. On the other hand, when the same MOF is incorporated into a highly permeable polymer, it can probably change both gas permeability and membrane selectivity of the polymer since the identity of MOF filler gains importance for highly permeable (>1000 Barrer) polymers. Therefore, a careful selection of MOF and polymer pairs for high performing MMMs is very important. We note that these approaches assume perfect compatibility between MOF/polymer interface. Gas separation performance of polymer dominates the predicted separation properties of MOF-based MMMs which is called percolation threshold.154 The reason is that rubbery polymers having flexible chains are commonly used to make defect-free and compatible MMMs, but these flexible chains lead to highly permeable regions for gas molecules. This was clearly represented in the literature98 in which properties of CoRE MOF-based MMMs were predicted via atomistic and continuum approach at infinite dilution for CO2/N2 separation. In Fig. 6(a), while square symbol represents the CO2 permeability of pure polymers, the line represents the relationship between CO2 permeability of MMMs and the ratio of permeability of MOF and polymer. This figure gives an important message to understand the effect of the MOF-polymer relation on the separation performances of MMMs. Fig. 6(a) showed that when MOF filler exhibits lower gas permeability than the related polymer, the gas permeability of the MMM consisting of this MOF-polymer pair is lower than pure polymer and vice versa. On the other hand, if gas permeability of MOF is higher than that of polymer, it may enhance the permeability of polymer. Perhaps the most critical result is that if gas permeability of a MOF is at least 10 times higher than that of the polymer, polymer performance cannot be further improved. Therefore, even if gas permeability of a MOF is extremely higher than that of polymer, the maximum achievable gas permeabilities of MMMs is ∼2 times the permeability of related polymers based on Maxwell model.98,143
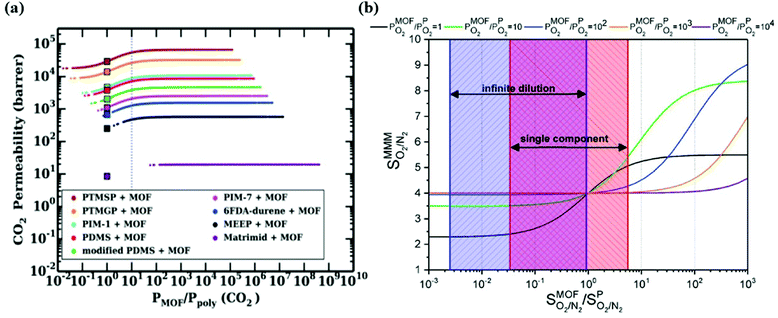 | ||
| Fig. 6 (a) Relations between CO2/N2 selectivity of MMMs, MOFs, and polymers. Square symbols show CO2 permeabilities of pure polymers. Reprinted from the study of Budhathoki et al.98 (b) O2/N2 selectivity of MMMs as a function of the ratio of the selectivity of MOF over the selectivity of polymer (PIM-1 with a selectivity of 4). Reprinted from the study of Daglar et al.142 | ||
Similar results were also observed in our recent work142 where O2 permeability and O2/N2 selectivity of 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 806 MMMs composed of 5629 MOFs and 14 different polymers were estimated by using the Maxwell model. The effect of membrane selectivity of MOFs and polymer (PIM-1 as a reference polymer) on the overall selectivity of MMMs was examined as a function of the ratio of gas permeability of MOFs and polymer. As shown in Fig. 6(b), if selectivity of MOF is lower than selectivity of polymer, it is not possible to obtain a MMM selectivity higher than that of polymer regardless of the gas permeability ratio. In other words, improving the O2/N2 selectivity of polymer is only possible by using MOFs having higher selectivity compared to polymer. In high-throughput screening studies on MMMs, although polymer permeability data used in theoretical models is generally measured at single-component gas conditions, simulations of MOFs are performed at infinite dilution to reduce the computational cost.98,146 We also showed that when molecular simulations of MOFs are performed at infinite dilution (considering only one gas molecule in the framework), the results underestimated O2/N2 membrane selectivities of MMMs calculated at single-component gas conditions (1 bar, 298 K). This result can be explained by the existence of gas-gas interactions at 1 bar and showed that simulation conditions of MOFs affect the predicted performance of MMMs. Therefore, using the same simulation conditions with experimental ones is critical to unlock the potential of MMMs.
806 MMMs composed of 5629 MOFs and 14 different polymers were estimated by using the Maxwell model. The effect of membrane selectivity of MOFs and polymer (PIM-1 as a reference polymer) on the overall selectivity of MMMs was examined as a function of the ratio of gas permeability of MOFs and polymer. As shown in Fig. 6(b), if selectivity of MOF is lower than selectivity of polymer, it is not possible to obtain a MMM selectivity higher than that of polymer regardless of the gas permeability ratio. In other words, improving the O2/N2 selectivity of polymer is only possible by using MOFs having higher selectivity compared to polymer. In high-throughput screening studies on MMMs, although polymer permeability data used in theoretical models is generally measured at single-component gas conditions, simulations of MOFs are performed at infinite dilution to reduce the computational cost.98,146 We also showed that when molecular simulations of MOFs are performed at infinite dilution (considering only one gas molecule in the framework), the results underestimated O2/N2 membrane selectivities of MMMs calculated at single-component gas conditions (1 bar, 298 K). This result can be explained by the existence of gas-gas interactions at 1 bar and showed that simulation conditions of MOFs affect the predicted performance of MMMs. Therefore, using the same simulation conditions with experimental ones is critical to unlock the potential of MMMs.
Although gas permeation models are useful to predict gas permeabilities and selectivities of MOF/polymer MMMs, they do not consider the size and morphology of MOFs and the interfacial compatibility between polymer and MOF phases. We noted that MOF-polymer compatibility can be different based on the selection of MOF-polymer pairs, and it depends on not only the properties of MOF such as crystalline size and shape but also the properties of polymer such as rigidity. Therefore, fully atomistic simulations which consider models for both MOF and polymer phases are necessary. The first example of a fully atomistic simulation for MOF/polymer MMMs was reported for ZIF-7/PBI for H2/CO2 separation.93 ZIF-7/PBI MMM model membranes were constructed considering different ZIF-7 cages and sorption and diffusion properties of H2 and CO2 were predicted using GCMC + EMD approach at 300 °C and infinite dilution. The relationship between gas transport mechanism and gas density distributions in 1-cage ZIF-7/PBI membrane revealed that CO2 cannot diffuse through the small interfacial voids at the interface between ZIF-7 and PBI in contrast to H2 molecules which locate at both ZIF-7 cages and PBI. Therefore, CO2 diffusion decreased with the increase in the number of ZIF-7 cages. Overall, results showed that permeability of H2 and CO2 in ZIF-7/PBI MMM is enhanced with the increase in ZIF-7 loading compared to those in pure PBI whereas H2/CO2 selectivities do not significantly change. Although these results are encouraging, a critical part which is the modelling of the interfacial morphology between MOF and polymer phases was missing.
To fabricate a high-performance MOF-based MMM, the proper selection of MOF and polymer pairs is important because the interfacial compatibility between those is generally poor and agglomeration which diminishes the gas separation performance of membranes may occur.154,155 Recently, Dutta et al.127 examined the interfacial characteristics of ZIF-8/6FDA-durane polyimide MMMs for CO2/CH4 separation using GCMC + EMD approach. To enhance the compatibility of the interface between ZIF-8 and polymer, they used an IL (ionic liquid), which filled the larger voids in the interface between ZIF-8 and 6FDA-durane polyimide polymer. With the incorporation of IL, CO2/CH4 membrane selectivity of MMM increased without a significant change in its permeability and this MMM surpassed the upper bound. Maurin's group94 developed an interface model to understand the compatibility between ZIF-8 and PIM-1 (polymer of intrinsic microporosity-1). The compatibility at ZIF-8/PIM-1 interface was shown with the interactions between CN groups of PIM-1 and NH groups of ZIF-8. This model was also applied to different MOF/polymer systems such as UiO-66/6FDA-DAM156 and HKUST-1/poly(vinyl alcohol).157 In the further study of this group,92 they showed that if atomistic and continuum modelling are used to predict ideal H2/CH4 membrane selectivities of ZIF-8/PIM-1 MMMs, higher selectivities are obtained compared to those obtained from CGD-MD simulations. Ozcan et al.92 showed that H2/CH4 selectivity of ZIF-8/PIM-1 MMM is lower (4.6) than the selectivity of the pure ZIF-8 (5.1) and PIM-1 (6.3) due to non-selective regions occurred at the interface. This result again supports the idea that properties of MOF and polymer have a synergetic effect on the property of MMMs. On the other hand, when CGD-MD were performed for equimolar H2/CH4 mixture for PIM-1/ZIF-8 MMMs, lower H2/CH4 selectivities were found than those computed at single-component gas condition. Overall, simulation conditions affect the gas separation performances of MOF-based MMMs and accurate definition of these conditions in molecular simulations is important. We also noted that there is a common idea in the literature that interfacial porosity has a negative effect on the gas separation performances of MMMs. However, Fan et al.128 very recently showed that the porosity at the interface of NUS-8/PIM-1 MMM leads to an increase in membrane selectivity for MMMs due to the enhanced CO2-MOF interactions.
3.3 Comparison of simulated and experimental performances of MOF membranes
Molecular simulations are highly useful to provide insights into the gas permeation through MOF-based MMMs. To show the validity of computational methodologies for predicting gas permeation through membranes, comparing simulation results with experimental measurements for various gas separations is required. For validation, molecular simulations are computed at the same pressure and temperature with the experiments and then compared with the experiments in several studies.43,144 For example, Wilmer et al.98 calculated CO2 and N2 permeabilities of 11 different MOF-based MMMs using Maxwell Model and compared their predictions with experimental measurements as shown in Fig. 7(a). The good agreement between predicted and experimental gas permeabilities validated their computational methodology. Similarly, our group compared experimental and simulated CO2 and N2 permeabilities of 13 MOF-based MMMs composed of 6 different MOFs and 7 different polymers at the same conditions with experiments.146 We showed that although simulation results agree well with experiments, they generally underestimate experiments as the weight percentage of MOF in polymer increases. In molecular simulations, we generally assume that MOFs are defect-free crystals and MOF/polymer pairs are perfectly compatible to generate MMMs. However, experimentally fabricated MMMs may have defects which can enhance gas diffusion through membranes. In addition, an increase of MOF loading in the polymer may cause agglomeration in MMM, which may play a critical role in creating non-selective regions for gas transport. In computational studies, theoretical permeation models such as Modified Felske and Maxwell are generally used to predict gas permeabilities of MMMs and these models do not consider particle interactions, an important issue especially at high filler loadings. Therefore, these models are noted to be applicable to the MMMs for which low loadings (filler volume fraction range < 0.2) of MOF filler are incorporated into the polymer.158 For these reasons, a much higher gas permeability can be reported by the experiments compared to simulations.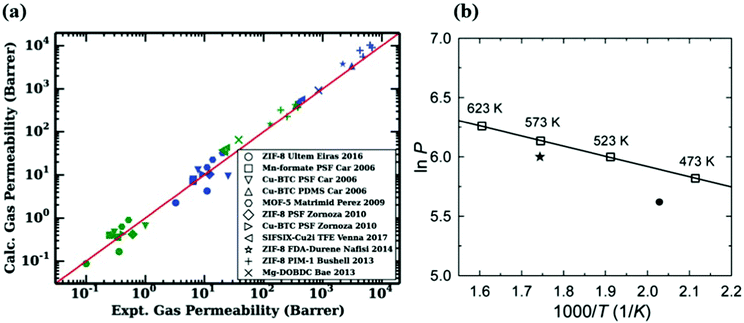 | ||
| Fig. 7 (a) Comparison of experimental and simulated CO2 (blue) and N2 (green) permeabilities of 11 different MMMs. Reprinted from the study of Budhathoki et al.98 (b) The relationship between H2 permeability of ZIF-7 and temperature. The line is the Arrhenius fit based on the simulation data (squares). The circle is the available experimental data at 220 °C and the star is extrapolated at 300 °C. Reprinted from the study of Zhang et al.93 | ||
On the other hand, direct comparisons of simulation results with experiments are not available in some studies due to the lack of available experimental data in the literature. For example, as we discussed before ZIF-7/PBI MMM was constructed to investigate its H2/CO2 separation performance.93 In Fig. 7(b), to validate the accuracy of their predictions, it is required to compare the simulated H2 permeability with experimental data at the same conditions. Since there is no available H2 permeability data of ZIF-7 at 573 K, Zhang et al.93 first fitted simulated data at various temperatures by using Arrhenius equation. Then, they used the Arrhenius fit line to extrapolate available experimental data at 493 K to the data at 573 K. Although predicted H2 and CO2 permeabilities were 461 and 32 Barrers, extrapolated gas permeabilities were reported as 408 and 22 Barrers, respectively, resulting in a fairly good agreement between experimental and simulated permeabilities. We noted that the change in temperature can affect the gas permeability and membrane selectivity. As temperature increases, the amount of adsorbed gas molecules decreases whereas the diffusivity of adsorbed molecules increases. Since gas permeability is the combination of adsorption and diffusion properties of MOFs, it also changes with temperature. The relationship between gas permeability and temperature can be also described by Arrhenius equation, (P ∝ exp(−Ea/RT)) where Ea is the activation energy (J mol−1), R is the ideal gas constant (J K−1 mol−1), and T is the temperature (K). Several studies also showed that, gas permeability generally increases as temperature increases based on Arrhenius equation.93,159–161 In addition, although an inverse relationship between membrane selectivity and temperature can be observed in the literature,160 the effect of temperature on membrane selectivity depends on the type of gas separation applications. Overall, the validation step is critical for assessing the reliability of computational methodologies and molecular simulations should be performed under the same conditions with the experiments to make a direct comparison.
4. Outlook
In this study, we reviewed the current state-of-the-art computational methods to predict gas permeation through MOF membranes and MOF-based MMMs. We finally address the following topics to be considered in future studies:• As we discussed throughout this review, the membrane performances of pristine MOF membranes and MOF-based MMMs can be predicted by different computational methodologies such as GCMC + EMD and NEMD. Perhaps, the most important step to prove the reliability of these methods is to compare simulation results with the experimental data. However, due to the lack of available experimental data on a variety of MOFs, this crucial step is missing in many studies. Therefore, the results obtained from simulations should be compared at least with the available experimental measurements before providing all simulated data of different types of MOF membranes.
• The number of MOFs for which membrane properties are simulated and reported is very limited because EMD and NEMD simulations require higher computational time (up to hundreds of CPU hours per material) compared to GCMC simulations. Since computing diffusion properties of MOFs are computationally demanding, more practical ways for predicting diffusion coefficients are needed to increase the number of studies on MOF membranes. Recently, Wu and Zhou73 developed a massively parallel graphic processing unit (GPU)-accelerated string method by using TST to calculate the diffusivity for MOFs. They showed that by using this method, diffusion calculations can be completed significantly faster (<30 seconds) than conventional MD simulations.
• Currently, all computational studies identify the best MOF membranes or MOF-based MMMs based on the ability of membranes to surpass the Robeson's upper bound. Since Robeson's upper bound is defined for single-component gas permeation, the upper limits of gas separation performances of polymers can be different for mixtures, thus it should be a reference line rather than a standard line for gas mixtures. In addition, separation performance of real MOF membranes can be also significantly different when gas mixtures at industrial conditions are considered. Therefore, performing computational studies considering gas mixtures at different operation conditions is necessary to get a more realistic predictions for the membranes.
• The thickness of the thin-film MOF membrane directly affects the measured gas flux and selectivity. For example, synthesis of one of the thinnest ZIF-8 membranes, 300–400 nm, revealed that this ZIF-8 gives one of the highest propylene/propane selectivity (120) among other reported ZIF-8 membranes in the literature.162 In NEMD simulations, the thickness is defined in the range of 40–50 Å to save computational time and sources.81,163 However, the thickness of fabricated MOF membranes is generally much larger (>25 μm). Membrane thickness considered in simulations can also affect gas separation performances of membranes. For example, Wang et al.164 performed NEMD simulations to understand the effect of carbon membrane thickness on gas flux for O2/N2 separation. Their results showed that as the membrane thickness increases, both O2 and N2 fluxes decrease due to the increase in membrane resistance. Overall, using larger membrane thickness when calculating gas flux in NEMD simulations can be important.
• In molecular simulations, defect-free, purely crystalline and rigid MOF structures are generally assumed. Considering structural stability in molecular simulations is not a trivial task since it requires DFT calculations. However, at least for the promising membrane candidates, DFT calculations can be performed to ensure the structural stability of membrane material. In addition, predictions for mechanical properties of MOF membranes such as Young's modules and mechanical strength will also be highly useful to guide experimental studies. Coudert and coworkers performed molecular simulations to understand the mechanical properties of MIL-53,165 UiO-66,166,167 and ZIF-8.168 Moghadam et al.169 performed a multi-level computational analysis to predict mechanical stability of MOFs and investigated the relationship between structural properties (i.e., topology) and mechanical strength (bulk modulus) of 3385 hypothetical MOFs. Examining experimentally synthesized MOF subsets would be also interesting. In addition, the mechanical strength of MOFs should be also investigated during gas separation process, which is currently missing in the literature.
• In high-throughput computational screening studies on MOF-based MMMs,98,143,146 molecular simulations for MOFs are generally performed at infinite dilution or at 1 bar, 298 K regardless of the measurement conditions of polymers. However, combining the performance data of a polymer tested at a different pressure range (up to 10 bar)170–176 with the performance data of MOFs predicted at infinite dilution may lead to unrealistic gas separation performance for MOF-polymer pairs. Therefore, simulation conditions for MOFs should be the same with the experimental conditions of polymers.
• The ultimate aim of high-throughput computational screening is to identify the top MOF membranes considering their ranking based on gas permeability and/or selectivity. However, the top membranes identified from high-throughput computational screening studies should be experimentally tested. Collaborative studies in which both experimentalists and theoreticians including engineers, chemists, materials scientists work together will be extremely useful for the design, development and testing of new MOF membranes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. K. acknowledges ERC-2017-Starting Grant. This study has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (ERC-2017-Starting Grant, grant agreement No 756489-COSMOS).References
- Y. Ding, Ind. Eng. Chem. Res., 2020, 59, 556–568 CrossRef CAS.
- Q. Qian, P. A. Asinger, M. J. Lee, G. Han, K. Mizrahi Rodriguez, S. Lin, F. M. Benedetti, A. X. Wu, W. S. Chi and Z. P. Smith, Chem. Rev., 2020, 120, 8161–8266 CrossRef CAS PubMed.
- J. Yu, L.-H. Xie, J.-R. Li, Y. Ma, J. M. Seminario and P. B. Balbuena, Chem. Rev., 2017, 117, 9674–9754 CrossRef CAS PubMed.
- L. M. Robeson, J. Membr. Sci., 1991, 62, 165–185 CrossRef CAS.
- L. M. Robeson, J. Membr. Sci., 2008, 320, 390–400 CrossRef CAS.
- O. M. Yaghi, M. O'Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Nature, 2003, 423, 705–714 CrossRef CAS PubMed.
- Q. Yang, Q. Xu and H.-L. Jiang, Chem. Soc. Rev., 2017, 46, 4774–4808 RSC.
- Y. Cui, Y. Yue, G. Qian and B. Chen, Chem. Rev., 2012, 112, 1126–1162 CrossRef CAS PubMed.
- Z. Hu, B. J. Deibert and J. Li, Chem. Soc. Rev., 2014, 43, 5815–5840 RSC.
- M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Science, 2002, 295, 469–472 CrossRef CAS PubMed.
- X. Li, Y. Liu, J. Wang, J. Gascon, J. Li and B. Van der Bruggen, Chem. Soc. Rev., 2017, 46, 7124–7144 RSC.
- K. Adil, Y. Belmabkhout, R. S. Pillai, A. Cadiau, P. M. Bhatt, A. H. Assen, G. Maurin and M. Eddaoudi, Chem. Soc. Rev., 2017, 46, 3402–3430 RSC.
- M. R. A. Hamid and H.-K. Jeong, Korean J. Chem. Eng., 2018, 35, 1577–1600 CrossRef CAS.
- N. Prasetya, N. F. Himma, P. D. Sutrisna, I. G. Wenten and B. P. Ladewig, Chem. Eng. J., 2019, 123575 Search PubMed.
- E. Adatoz, A. K. Avci and S. Keskin, Sep. Purif. Technol., 2015, 152, 207–237 CrossRef CAS.
- J. Yao and H. Wang, Chem. Soc. Rev., 2014, 43, 4470–4493 RSC.
- B. Seoane, J. Coronas, I. Gascon, M. E. Benavides, O. Karvan, J. Caro, F. Kapteijn and J. Gascon, Chem. Soc. Rev., 2015, 44, 2421–2454 RSC.
- M. S. Denny, J. C. Moreton, L. Benz and S. M. Cohen, Nat. Rev. Mater., 2016, 1, 1–17 Search PubMed.
- Y. Zhang, X. Feng, S. Yuan, J. Zhou and B. Wang, Inorg. Chem. Front., 2016, 3, 896–909 RSC.
- F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388 CrossRef PubMed.
- H. Daglar and S. Keskin, Coord. Chem. Rev., 2020, 422, 213470 CrossRef CAS.
- D. Ongari, L. Talirz and B. Smit, ACS Cent. Sci., 2020, 6, 1890–1900 CrossRef CAS PubMed.
- P. Z. Moghadam, A. Li, S. B. Wiggin, A. Tao, A. G. Maloney, P. A. Wood, S. C. Ward and D. Fairen-Jimenez, Chem. Mater., 2017, 29, 2618–2625 CrossRef CAS.
- Y. G. Chung, E. Haldoupis, B. J. Bucior, M. Haranczyk, S. Lee, H. Zhang, K. D. Vogiatzis, M. Milisavljevic, S. Ling and J. S. Camp, J. Chem. Eng. Data, 2019, 64, 5985–5998 CrossRef CAS.
- C. E. Wilmer, M. Leaf, C. Y. Lee, O. K. Farha, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Nat. Chem., 2012, 4, 83 CrossRef CAS PubMed.
- M. J. C. Ordonez, K. J. Balkus Jr, J. P. Ferraris and I. H. Musselman, J. Membr. Sci., 2010, 361, 28–37 CrossRef CAS.
- A. Huang, H. Bux, F. Steinbach and J. Caro, Angew. Chem., Int. Ed., 2010, 49, 4958–4961 CrossRef CAS PubMed.
- F. M. Benedetti, M. G. De Angelis, M. Degli Esposti, P. Fabbri, A. Masili, A. Orsini and A. Pettinau, Membranes, 2020, 10, 56 CrossRef CAS PubMed.
- G. Avci, S. Velioglu and S. Keskin, ACS Appl. Mater. Interfaces, 2018, 10, 33693–33706 CrossRef CAS PubMed.
- P. M. Morse, Phys. Rev., 1929, 34, 57 CrossRef CAS.
- G. Von Mie, Ann. Phys., 1903, 11, 657–697 Search PubMed.
- R. A. Buckingham, The classical equation of state of gaseous helium, neon and argon, 1938, vol. 168, pp. 264–283 Search PubMed.
- J. E. Lennard-Jones, Proc. Phys. Soc., 1931, 43, 461 CrossRef CAS.
- D. Halliday, R. Resnick and J. Walker, Fundamentals of physics, John Wiley & Sons, 2013 Search PubMed.
- A. K. Rappé, C. J. Casewit, K. Colwell, W. Goddard Iii and W. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- S. Bureekaew, S. Amirjalayer, M. Tafipolsky, C. Spickermann, T. K. Roy and R. Schmid, Phys. Status Solidi B, 2013, 250, 1128–1141 CrossRef CAS.
- J. K. Bristow, D. Tiana and A. Walsh, J. Chem. Theory Comput., 2014, 10, 4644–4652 CrossRef CAS PubMed.
- J. G. McDaniel, S. Li, E. Tylianakis, R. Q. Snurr and J. Schmidt, J. Phys. Chem. C, 2015, 119, 3143–3152 CrossRef CAS.
- T. Watanabe and D. S. Sholl, Langmuir, 2012, 28, 14114–14128 CrossRef CAS PubMed.
- C. Altintas, G. Avci, H. Daglar, E. Gulcay, I. Erucar and S. Keskin, J. Mater. Chem. A, 2018, 6, 5836–5847 RSC.
- C. Altintas, G. Avci, H. Daglar, A. Nemati Vesali Azar, S. Velioglu, I. Erucar and S. Keskin, ACS Appl. Mater. Interfaces, 2018, 10, 17257–17268 CrossRef CAS.
- H. Daglar and S. Keskin, J. Phys. Chem. C, 2018, 122, 17347–17357 CrossRef CAS PubMed.
- G. Avci, S. Velioglu and S. Keskin, ACS Appl. Mater. Interfaces, 2018, 10, 33693–33706 CrossRef CAS.
- O. Kadioglu and S. Keskin, Sep. Purif. Technol., 2018, 191, 192–199 CrossRef CAS.
- C. Altintas and S. Keskin, Chem. Eng. Sci., 2016, 139, 49–60 CrossRef CAS.
- J. J. Potoff and J. I. Siepmann, AIChE J., 2001, 47, 1676–1682 CrossRef CAS.
- Y. Sun, D. Spellmeyer, D. A. Pearlman and P. Kollman, J. Am. Chem. Soc., 1992, 114, 6798–6801 CrossRef CAS.
- D. D. Do and H. D. Do, J. Phys. Chem. B, 2005, 109, 19288–19295 CrossRef CAS PubMed.
- V. Buch, J. Chem. Phys., 1994, 100, 7610–7629 CrossRef CAS.
- Q. Yang and C. Zhong, J. Phys. Chem. B, 2005, 109, 11862–11864 CrossRef CAS PubMed.
- Q. Yang and C. Zhong, J. Phys. Chem. B, 2006, 110, 655–658 CrossRef CAS PubMed.
- J. G. Harris and K. H. Yung, J. Phys. Chem., 1995, 99, 12021–12024 CrossRef CAS.
- C. Mellot and J. Lignieres, Mol. Simul., 1997, 18, 349–365 CrossRef CAS.
- K. Makrodimitris, G. K. Papadopoulos and D. N. Theodorou, J. Phys. Chem. B, 2001, 105, 777–788 CrossRef CAS.
- E. Adatoz and S. Keskin, J. Nanomater., 2015, 2015, 1–9 CrossRef.
- C. E. Wilmer and R. Q. Snurr, Chem. Eng. J., 2011, 171, 775–781 CrossRef CAS.
- T. A. Manz and D. S. Sholl, J. Chem. Theory Comput., 2010, 6, 2455–2468 CrossRef CAS PubMed.
- C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373 CrossRef CAS.
- C. Campañá, B. Mussard and T. K. Woo, J. Chem. Theory Comput., 2009, 5, 2866–2878 CrossRef PubMed.
- C. Altintas and S. Keskin, Mol. Syst. Des. Eng., 2020, 5, 532–543 RSC.
- R. W. Baker and B. T. Low, Macromolecules, 2014, 47, 6999–7013 CrossRef CAS.
- J. G. Wijmans and R. W. Baker, J. Membr. Sci., 1995, 107, 1–21 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding molecular simulation: From algorithms to applications, Elsevier (formerly published by Academic Press), 2002, vol. 1, pp. 1–638 Search PubMed.
- S. Namsani, A. Ozcan and A. Ö. Yazaydın, Adv. Theory Simul., 2019, 2, 1900120 CrossRef CAS.
- P. P. Ewald, Ann. Phys., 1921, 369, 253–287 CrossRef.
- A. I. Skoulidas and D. S. Sholl, J. Phys. Chem. B, 2005, 109, 15760–15768 CrossRef CAS PubMed.
- A. H. Farmahini, S. Krishnamurthy, D. Friedrich, S. Brandani and L. Sarkisov, 2020, arXiv preprint arXiv:2009.12289.
- J. Kärger and D. M. Ruthven, New J. Chem., 2016, 40, 4027–4048 RSC.
- R. L. June, A. T. Bell and D. N. Theodorou, J. Phys. Chem., 1991, 95, 8866–8878 CrossRef CAS.
- P. Krokidas, S. Moncho, E. N. Brothers, M. Castier, H.-K. Jeong and I. G. Economou, ACS Appl. Mater. Interfaces, 2018, 10, 39631–39644 CrossRef CAS PubMed.
- P. Krokidas, S. Moncho, E. N. Brothers and I. G. Economou, ACS Appl. Mater. Interfaces, 2020, 12, 20536–20547 CrossRef CAS PubMed.
- M. Zhou and J. Wu, ACS Appl. Nano Mater., 2021, 4, 5394–5403 CrossRef CAS.
- B. Widom, J. Chem. Phys., 1963, 39, 2808–2812 CrossRef CAS.
- D. Dubbeldam, E. Beerdsen, T. Vlugt and B. Smit, J. Chem. Phys., 2005, 122, 224712 CrossRef CAS.
- G. Arya, H.-C. Chang and E. J. Maginn, J. Chem. Phys., 2001, 115, 8112–8124 CrossRef CAS.
- D. A. Newsome and D. S. Sholl, J. Phys. Chem. B, 2005, 109, 7237–7244 CrossRef CAS PubMed.
- H. Babaei, A. J. McGaughey and C. E. Wilmer, ACS Appl. Mater. Interfaces, 2018, 10, 2400–2406 CrossRef CAS PubMed.
- M. Fasano, T. Humplik, A. Bevilacqua, M. Tsapatsis, E. Chiavazzo, E. N. Wang and P. Asinari, Nat. Commun., 2016, 7, 12762 CrossRef CAS PubMed.
- M. J. Berry, C. M. Taylor, W. King, Y.-M. Chew and J. Wenk, Water, 2017, 9, 452 CrossRef.
- K. N. Han, S. Bernardi, L. Wang and D. J. Searles, J. Membr. Sci., 2015, 495, 322–333 CrossRef CAS.
- T. Kovács, S. Papp and T. Kristóf, 2017, arXiv preprint arXiv:1706.07250.
- S. Velioglu and S. Keskin, J. Mater. Chem. A, 2019, 7, 2301–2314 RSC.
- A. Ozcan, C. Perego, M. Salvalaglio, M. Parrinello and O. Yazaydin, Chem. Sci., 2017, 8, 3858–3865 RSC.
- G. S. Heffelfinger and F. v. Swol, J. Chem. Phys., 1994, 100, 7548–7552 CrossRef CAS.
- K. M. Gupta, Z. Qiao, K. Zhang and J. Jiang, ACS Appl. Mater. Interfaces, 2016, 8, 13392–13399 CrossRef CAS.
- G. Banhegyi, Colloid Polym. Sci., 1986, 264, 1030–1050 CrossRef CAS.
- R. Pal, J. Reinf. Plast. Compos., 2007, 26, 643–651 CrossRef CAS.
- J. Felske, Int. J. Heat Mass Transf., 2004, 47, 3453–3461 CrossRef.
- J. Maxwell, Electricity and magnetism, Dover, New York, 1954, vol. 2 Search PubMed.
- I. Erucar and S. Keskin, Ind. Eng. Chem. Res., 2011, 50, 12606–12616 CrossRef CAS.
- A. Ozcan, R. Semino, G. Maurin and A. O. Yazaydin, Chem. Mater., 2020, 32, 1288–1296 CrossRef CAS PubMed.
- L. Zhang, Z. Hu and J. Jiang, J. Phys. Chem. C, 2012, 116, 19268–19277 CrossRef CAS.
- R. Semino, N. A. Ramsahye, A. Ghoufi and G. Maurin, ACS Appl. Mater. Interfaces, 2016, 8, 809–819 CrossRef CAS.
- L. M. Robeson, Z. P. Smith, B. D. Freeman and D. R. Paul, J. Membr. Sci., 2014, 453, 71–83 CrossRef CAS.
- L. M. Robeson, Q. Liu, B. D. Freeman and D. R. Paul, J. Membr. Sci., 2015, 476, 421–431 CrossRef CAS.
- Z. Qiao, Q. Xu and J. Jiang, J. Membr. Sci., 2018, 551, 47–54 CrossRef CAS.
- S. Budhathoki, O. Ajayi, J. A. Steckel and C. E. Wilmer, Energy Environ. Sci., 2019, 12, 1255–1264 RSC.
- G. Avci, I. Erucar and S. Keskin, ACS Appl. Mater. Interfaces, 2020, 12, 41567–41579 CrossRef CAS.
- A. J. Howarth, Y. Liu, P. Li, Z. Li, T. C. Wang, J. T. Hupp and O. K. Farha, Nat. Rev. Mater., 2016, 1, 15018 CrossRef CAS.
- M. Zhai, T. Yoshioka, J. Yang, J. Wang, D. Zhang, J. Lu and Y. Zhang, Chin. J. Chem. Eng., 2021, 33, 104–111 CrossRef.
- I. Erucar and S. Keskin, J. Membr. Sci., 2016, 514, 313–321 CrossRef CAS.
- Y. Yoo, Z. Lai and H.-K. Jeong, Microporous Mesoporous Mater., 2009, 123, 100–106 CrossRef CAS.
- Y. Liu, Z. Ng, E. A. Khan, H.-K. Jeong, C.-b. Ching and Z. Lai, Microporous Mesoporous Mater., 2009, 118, 296–301 CrossRef CAS.
- Y. Liu, E. Hu, E. A. Khan and Z. Lai, J. Membr. Sci., 2010, 353, 36–40 CrossRef CAS.
- X. Dong, K. Huang, S. Liu, R. Ren, W. Jin and Y. S. Lin, J. Mater. Chem., 2012, 22, 19222–19227 RSC.
- A. Huang, Y. Chen, N. Wang, Z. Hu, J. Jiang and J. Caro, Chem. Commun., 2012, 48, 10981–10983 RSC.
- Y. Zhang, Q. Gao, Z. Lin, T. Zhang, J. Xu, Y. Tan, W. Tian and L. Jiang, Sci. Rep., 2014, 4, 1–6 Search PubMed.
- D.-J. Lee, Q. Li, H. Kim and K. Lee, Microporous Mesoporous Mater., 2012, 163, 169–177 CrossRef CAS.
- A. Huang, W. Dou and J. r. Caro, J. Am. Chem. Soc., 2010, 132, 15562–15564 CrossRef CAS.
- Y. Liu, G. Zeng, Y. Pan and Z. Lai, J. Membr. Sci., 2011, 379, 46–51 CrossRef CAS.
- H. Yin, J. Wang, Z. Xie, J. Yang, J. Bai, J. Lu, Y. Zhang, D. Yin and J. Y. Lin, Chem. Commun., 2014, 50, 3699–3701 RSC.
- M. C. McCarthy, V. Varela-Guerrero, G. V. Barnett and H.-K. Jeong, Langmuir, 2010, 26, 14636–14641 CrossRef CAS.
- B. Chen, Z. Yang, Y. Zhu and Y. Xia, J. Mater. Chem. A, 2014, 2, 16811–16831 RSC.
- Y.-R. Lee, M.-S. Jang, H.-Y. Cho, H.-J. Kwon, S. Kim and W.-S. Ahn, Chem. Eng. J., 2015, 271, 276–280 CrossRef CAS.
- R. L. June, A. T. Bell and D. N. Theodorou, J. Phys. Chem., 1991, 95, 8866–8878 CrossRef CAS.
- Y. K. Ponraj and B. Borah, J. Mol. Graphics Modell., 2020, 97, 107574 CrossRef CAS PubMed.
- Z. Li, G. Xu, B. Liu, X. Lv, G. Chen, C. Sun, P. Xiao and Y. Sun, Energies, 2015, 8, 11531–11545 CrossRef CAS.
- M. T. Kallo and M. J. Lennox, Langmuir, 2020, 36, 13591–13600 CrossRef CAS PubMed.
- P. Krokidas, M. Castier, S. Moncho, D. N. Sredojevic, E. N. Brothers, H. T. Kwon, H.-K. Jeong, J. S. Lee and I. G. Economou, J. Phys. Chem. C, 2016, 120, 8116–8124 CrossRef CAS.
- E. Garcia-Perez, P. Serra-Crespo, S. Hamad, F. Kapteijn and J. Gascon, Phys. Chem. Chem. Phys., 2014, 16, 16060–16066 RSC.
- D. S. Chiou, H. J. Yu, T. H. Hung, Q. Lyu, C. K. Chang, J. S. Lee, L. C. Lin and D. Y. Kang, Adv. Funct. Mater., 2020, 2006924 Search PubMed.
- N. Farzi, N. Salehi and A. Mahboubi, Microporous Mesoporous Mater., 2017, 248, 246–255 CrossRef CAS.
- B. Liu, C. Sun and G. Chen, Chem. Eng. Sci., 2011, 66, 3012–3019 CrossRef CAS.
- P. Krokidas, M. Castier and I. G. Economou, J. Phys. Chem. C, 2017, 121, 17999–18011 CrossRef CAS.
- Y. Gurdal and S. Keskin, J. Membr. Sci., 2016, 519, 45–54 CrossRef CAS.
- R. C. Dutta and S. K. Bhatia, J. Phys. Chem. C, 2020, 124, 594–604 CrossRef CAS.
- D. Fan, A. Ozcan, N. A. Ramsahye, D. Zhao, G. Maurin and R. Semino, ACS Mater. Lett., 2021, 3, 344–350 CrossRef CAS.
- Z. Sumer and S. Keskin, Ind. Eng. Chem. Res., 2017, 56, 8713–8722 CrossRef CAS.
- Z. Sumer and S. Keskin, Chem. Eng. Sci., 2017, 164, 108–121 CrossRef CAS.
- C. Altintas and S. Keskin, RSC Adv., 2017, 7, 52283–52295 RSC.
- H. Kim, S. Lee and J. Kim, Langmuir, 2019, 35, 3917–3924 CrossRef CAS PubMed.
- G. O. Aksu, H. Daglar, C. Altintas and S. Keskin, J. Phys. Chem. C, 2020, 124, 22577–22590 CrossRef CAS PubMed.
- T. Yan, Y. Lan, M. Tong and C. Zhong, ACS Sustainable Chem. Eng., 2018, 7, 1220–1227 CrossRef.
- P. Zarabadi-Poor and R. Marek, J. Phys. Chem. C, 2019, 123, 3469–3475 CrossRef CAS.
- E. Haldoupis, S. Nair and D. S. Sholl, J. Am. Chem. Soc., 2010, 132, 7528–7539 CrossRef CAS PubMed.
- E. Gulcay and I. Erucar, Ind. Eng. Chem. Res., 2019, 58, 3225–3237 CrossRef CAS.
- T. Van Heest, S. L. Teich-McGoldrick, J. A. Greathouse, M. D. Allendorf and D. S. Sholl, J. Phys. Chem. C, 2012, 116, 13183–13195 CrossRef CAS.
- V. A. Solanki and B. Borah, J. Phys. Chem. C, 2019, 123, 17808–17822 CrossRef CAS.
- W.-q. Lin, X.-l. Xiong, H. Liang and G.-h. Chen, ACS Appl. Mater. Interfaces, 2021, 13, 17998–18009 CrossRef CAS.
- W. Yang, H. Liang, F. Peng, Z. Liu, J. Liu and Z. Qiao, Nanomaterials, 2019, 9, 467 CrossRef CAS PubMed.
- H. Daglar, I. Erucar and S. Keskin, J. Membr. Sci., 2020, 618, 118555 CrossRef.
- C. Altintas and S. Keskin, ACS Sustainable Chem. Eng., 2019, 7, 2739–2750 CrossRef CAS PubMed.
- A. N. V. Azar, S. Velioglu and S. Keskin, ACS Sustainable Chem. Eng., 2019, 7, 9525–9536 CrossRef CAS.
- E. Besley and J. Glover, Faraday Discuss., 2021 10.1039/D1FD00005E.
- H. Daglar and S. Keskin, Adv. Theory Simul., 2019, 2, 1900109 CrossRef CAS.
- Z. Qiao, C. Peng, J. Zhou and J. Jiang, J. Mater. Chem. A, 2016, 4, 15904–15912 RSC.
- A. P. Cote, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166–1170 CrossRef CAS PubMed.
- D. Nazarian, J. S. Camp, Y. G. Chung, R. Q. Snurr and D. S. Sholl, Chem. Mater., 2017, 29, 2521–2528 CrossRef CAS.
- Y. Pan and Z. Lai, Chem. Commun., 2011, 47, 10275–10277 RSC.
- I. Erucar and S. Keskin, Chem. Eng. Sci., 2015, 130, 120–128 CrossRef CAS.
- S. Keskin and D. S. Sholl, Energy Environ. Sci., 2010, 3, 343–351 RSC.
- B. Shimekit, H. Mukhtar and T. Murugesan, J. Membr. Sci., 2011, 373, 152–159 CrossRef CAS.
- G. Dong, H. Li and V. Chen, J. Mater. Chem. A, 2013, 1, 4610–4630 RSC.
- R. Semino, J. C. Moreton, N. A. Ramsahye, S. M. Cohen and G. Maurin, Chem. Sci., 2018, 9, 315–324 RSC.
- M. Z. Ahmad, M. Navarro, M. Lhotka, B. Zornoza, C. Téllez, W. M. de Vos, N. E. Benes, N. M. Konnertz, T. Visser and R. Semino, J. Membr. Sci., 2018, 558, 64–77 CrossRef CAS.
- R. Semino, J. P. Dürholt, R. Schmid and G. Maurin, J. Phys. Chem. C, 2017, 121, 21491–21496 CrossRef CAS.
- J. Winarta, A. Meshram, F. Zhu, R. Li, H. Jafar, K. Parmar, J. Liu and B. Mu, J. Polym. Sci., 2020, 58, 2518–2546 CrossRef CAS.
- J. Olsson and G. Trägårdh, Sep. Sci. Technol., 1999, 34, 1643–1659 CrossRef CAS.
- E. Lasseuguette, R. Malpass-Evans, M. Carta, N. B. McKeown and M.-C. Ferrari, Membranes, 2018, 8, 132 CrossRef PubMed.
- S. A. Gülmüs and L. Yilmaz, J. Polym. Sci., Part B: Polym. Phys., 2007, 45, 3025–3033 CrossRef.
- H. T. Kwon, H.-K. Jeong, A. S. Lee, H. S. An, T. Lee, E. Jang, J. S. Lee and J. Choi, Chem. Commun., 2016, 52, 11669–11672 RSC.
- T. Kovács, S. Papp and T. Kristóf, Condens. Matter Phys., 2017, 20, 23002 CrossRef.
- S.-M. Wang, Y.-X. Yu and G.-H. Gao, J. Membr. Sci., 2006, 271, 140–150 CrossRef CAS.
- A. U. Ortiz, A. Boutin, A. H. Fuchs and F.-X. Coudert, J. Chem. Phys., 2013, 138, 174703 CrossRef PubMed.
- T. D. Bennett, A. K. Cheetham, A. H. Fuchs and F.-X. Coudert, Nat. Chem., 2017, 9, 11 CrossRef CAS.
- C. L. Hobday, R. J. Marshall, C. F. Murphie, J. Sotelo, T. Richards, D. R. Allan, T. Düren, F. X. Coudert, R. S. Forgan and C. A. Morrison, Angew. Chem., 2016, 128, 2447–2451 CrossRef.
- A. U. Ortiz, A. Boutin, A. H. Fuchs and F.-X. Coudert, J. Phys. Chem. Lett., 2013, 4, 1861–1865 CrossRef CAS PubMed.
- P. Z. Moghadam, S. M. Rogge, A. Li, C.-M. Chow, J. Wieme, N. Moharrami, M. Aragones-Anglada, G. Conduit, D. A. Gomez-Gualdron and V. Van Speybroeck, Matter, 2019, 1, 219–234 CrossRef.
- S. N. Wijenayake, N. P. Panapitiya, S. H. Versteeg, C. N. Nguyen, S. Goel, K. J. Balkus, I. H. Musselman and J. P. Ferraris, Ind. Eng. Chem. Res., 2013, 52, 6991–7001 CrossRef CAS.
- A. Akbari, J. Karimi-Sabet and S. M. Ghoreishi, Chem. Eng. Process., 2020, 148, 107804 CrossRef CAS.
- S. Japip, H. Wang, Y. Xiao and T. S. Chung, J. Membr. Sci., 2014, 467, 162–174 CrossRef CAS.
- H. B. T. Jeazet, C. Staudt and C. Janiak, Chem. Commun., 2012, 48, 2140–2142 RSC.
- M. A. Rodrigues, J. de Souza Ribeiro, E. de Souza Costa, J. L. de Miranda and H. C. Ferraz, Sep. Purif. Technol., 2018, 192, 491–500 CrossRef CAS.
- I. Pinnau and L. G. Toy, J. Membr. Sci., 1996, 109, 125–133 CrossRef CAS.
- S. Basu, A. Cano-Odena and I. F. Vankelecom, Sep. Purif. Technol., 2011, 81, 31–40 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |