Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Rb intercalation enhanced the supercapacitive performance of layer-structured MoS2 as a 2D model material†
Ahmed H.
Biby‡
 ,
Basant A.
Ali‡
,
Basant A.
Ali‡
 and
Nageh K.
Allam
and
Nageh K.
Allam
 *
*
The Energy Materials Laboratory, School of Sciences and Engineering, The American University in Cairo, New Cairo 11835, Egypt. E-mail: Nageh.allam@aucegypt.edu
First published on 25th June 2021
Abstract
Intercalation of alkali metals has proved to be an effective approach for the enhancement of the energy storage performance in layered-2D MoS2. However, the research so far has been limited to the Li and Na ion intercalation with K ions being recently investigated. Herein, we demonstrate, for the first time, the extraordinary capacitance performance of Rb-ion intercalation in the inter-layer of the 1T, 2H, and 3R MoS2 polymorphs. This work elucidates the capacitance performance in terms of quantum capacitance and intercalation strength. Rb-Intercalation into MoS2 layers stabilizes the 1T phase more than Li ions and imparts metallic behavior to the semiconducting 2H and 3R phases. Concurrently, the quantum capacitance of the three phases dramatically increases, surpassing that of graphene and doped graphene. The calculated quantum capacitance can reach as high as 2700, 3250, and 3300 F g−1 for the 1T, 2H, and 3R phases, respectively, rendering the Rb ion a superior choice for boosting the energy storage performance of the MoS2-based supercapacitor electrodes.
Ion intercalation has been one of the leading charge storage mechanisms in energy storage materials, especially alkali metal-ion batteries. However, despite their high energy density, the intercalation in batteries does not meet the present-day demand for high power density. Consequently, recent studies have been targeting supercapacitors as an alternative platform for energy storage.1–5 Li has been the ideal intercalated ion in batteries and supercapacitors due to its low ionic radius and fast kinetics. Yet, Li is not abundant in the Earth's crust, necessitating the search for alkali-metal ion alternatives that are earth-abundant. However, to accommodate alkali-metal ions, the host active material's lattice must have large interlayer spaces to accommodate such ions with relatively larger ionic radii. To this end, layered-2D materials, such as transition metal dichalcogenides (TMDs), have been investigated due to their high interlayer spacing that facilitates the insertion of such larger ions. One of the most leading TMDs in the field of energy storage is MoS2. Li et al. reported the use of bulk MoS2 in Li-ion batteries with a capacity–after 100 cycles– of 1189 mA h g−1 (200 mA g−1).6 Being more abundant than Li, Na-ion batteries have recently emerged as alternatives to Li-ion batteries. Barik et al. investigated the impact of defects on the properties of MoS2 in Li- and Na-ion batteries using first-principles calculations.7 Also, Mortazavi et al. studied the binding sites and stability upon Na-ion intercalation in MoS2, revealing a maximum capacity of 146 mA h g−1 with an average electrode potential of 0.75–1.25 V.8 This was much lower than that obtained experimentally for MoS2-based Na-ion batteries, which exhibited a capacity of 220 mA h g−1 at 2 A g−1.9 As it has the highest transference number among all alkali metals, K ion intercalation has recently been extensively investigated.10 Comparing Na, Li, and K-ion intercalation for MoS2 supercapacitor electrodes, the 1T-MoS2 electrode exhibited 590 F g−1 at a scan rate of 5 mV s−1 in K2SO4 electrolyte, while the symmetric device gave a power density of 225 W kg−1 and an energy density of 4.19 W h kg−1.10 Additionally, K-ion-intercalated MoS2-based batteries have been investigated by Du et al.11 proving their superior performance.
Inspired by the above-mentioned results, Rb-ion intercalation seems to be very promising and worthy of investigation, especially that the diffusion coefficients and motilities of alkali cations increase with increasing atomic number.12 Moreover, the low electronegativity of Rb should enable stronger intercalation with 2D materials such as MoS2.13,14 Further, Rb is more abundant in the Earth's crust than Li. Besides, Rb salts such as the Rb2SO4 are highly soluble in water in comparison to its K counterpart.15 However, to the best of our knowledge, the intercalation of Rb ion in 2D materials is yet to be reported. Herein, we investigated the effect of the intercalation of Rb ion on the three main phases of MoS2 as a model 2D material, demonstrating insights on their quantum capacitance, stability, and binding energy. The results revealed that Rb ion intercalation increased the quantum capacitance of the three phases, stabilized the 1T phase of MoS2, and increased the conductivity of the 2H and 3R phases. It is worthy to note that the ab initio calculations were proven to provide insights on the capacitance performance of a plethora of energy materials,16,17 and electrode materials18–20 and to model alkali metal intercalation.21–25
The density functional theory (DFT) tool was used to perform geometry optimization and the total energy calculations for the three-layered structures of the three pristine MoS2 phases. Although the number of available tetrahedral binding sites is twice that of the octahedral sites,26 it was reported that alkali metals prefer to bind to the octahedral sites in MoS2.8,27 In this study, Rb ions were inserted into the vdW interlayer spacing in the octahedral site with a concentration of Rb0.17MoS2. The structure was then re-relaxed to its minimum energy. The structure of the optimized cells is illustrated in Fig. 1. MoS2 is a layered-2D material, which exists in three main phases according to the arrangement of the S–Mo–S sandwich structure. The metallic 1T phase (AbC) can be identified using only one layered structure, the semiconductor 2H phase (AbA, and BaB) can be identified using two layered structures, and the 3R phase (AbA, CaC, and BcB) should be classified using a three layered structure. For that reason, the study was unified to three layered structures as a minimum number of layers allowed for comparison and for accurate quantum capacitance calculations. The lattice parameters of the relaxed cells are presented in Table 1. For benchmarking, it was found that the bond length, lattice parameters, bandgaps, and total energies for the pristine MoS2 phases perfectly matched those reported in the literature,13,14,28,29 confirming the accuracy of our calculations.
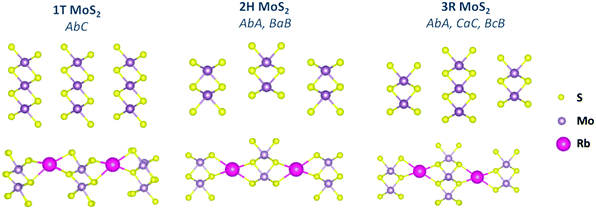 | ||
| Fig. 1 Unit cells of the DFT optimized structures of pristine MoS2 and Rb-intercalated MoS2 phases revealing the layered structure arrangements. | ||
| Phase | Structure | d Mo–Mo (Å) | d′Mo–Mo (Å) | d Mo–S (Å) | d′S–S (Å) | a & b (Å) | α (°) | β (°) | γ (°) | E Tot (eV) | E ad (eV) | E F (eV) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1T | Pristine MoS2 | 3.25 | 6.41 | 2.48 | 6.41 | 6.50 | 90.00 | 90.00 | 120.00 | −162.80 | −3.18 | −0.53 |
| Rb–MoS2 | 3.38 | 8.93 | 2.40 | 7.46 | 6.78 | 90.13 | 89.24 | 120.16 | −169.44 | |||
| 2H | Pristine MoS2 | 3.16 | 6.81 | 2.44 | 4.93 | 6.32 | 90.00 | 90.00 | 120.00 | −170.60 | −0.79 | −0.13 |
| Rb–MoS2 | 3.32 | 10.04 | 2.48 | 6.67 | 6.64 | 90.02 | 89.98 | 119.95 | −172.46 | |||
| 3R | Pristine MoS2 | 3.16 | 6.82 | 2.44 | 3.80 | 6.33 | 90.00 | 90.00 | 120.00 | −170.60 | −0.80 | −0.13 |
| Rb–MoS2 | 3.33 | 9.97 | 2.48 | 7.50 | 6.64 | 90.24 | 89.76 | 120.00 | −172.48 |
Note that Rb intercalation resulted in an expansion of the interlayer spacing as 39.3%, 47.43%, and 46.19% for the 1T, 2H, and 3R phases, respectively. The expansion in the 1T phase is much lower than that of the 2H and 3R phases, indicating an easier insertion of Rb ions. It is noteworthy to mention that this expansion is attributed to the enlargement in the vdW spacing not due to bond breaking, and hence the material can maintain its stability over long charging cycles.8 The calculated total energy of the three pristine phases reflects the metastability of the 1T phase, which has an energy that is ∼8 eV higher than that of the 2H phase. Although Rb intercalation stabilized the energy of the three phases, surprisingly, the stabilization in the 1T phase was very high such that it reached a value equivalent to that of the pristine 2H phase. This may be attributed to the easy insertion of the Rb atom that bonded with 6 bonds in the interlayer spacing and stabilized the structure of the 1T phase. Additionally, Rb intercalation stabilized the MoS2 phases more than that reported for Li and Na intercalation (Table S1, ESI†).25 The stabilization of the 1T phase was greater than that of the 2H and 3R phases as revealed from the calculated total energy listed in Table 1. Moreover, the binding energy per adsorbed Rb atom was calculated, where the more negative binding energy refers to a more thermodynamically stable reaction (exothermic reaction) that favours the formation of the intercalated structure over the decomposition of MoS2 and Rb ions.7,8 It was found that Rb intercalation into the 1T phase possesses a relatively high binding energy compared to that with the 2H and the 3R phases, indicating a stabilization of the metastable metallic phase. This high binding energy in the Rb–1T MoS2 structure can be attributed to the different orbital splitting in the different MoS2 phases.8 The electrons from Rb ions can occupy the low energy partially-filled 4dxy, 4dyz, and 4dxz orbitals of the 1T phase instead of the high energy 4dxy and 4dx2−y2 orbitals of the 2H phase.8 It is also noticed that the binding energy of the Rb-1T is lower than the cohesive energy of the Rb ion,30 revealing a high driving force for Rb to adsorb on the interlayer of the 1T-MoS2 phase and the high electrode stability. Importantly, Rb intercalation exhibited a lower formation energy (per formula cell) than those reported for Li+ and Na+ with the same concentration.8 Furthermore, since the formation energy of the 1T phase is much lower than that of the 2H and 3R phases, it is assumed that the 2H and 3R phases can be thermodynamically transformed into the 1T phase.8
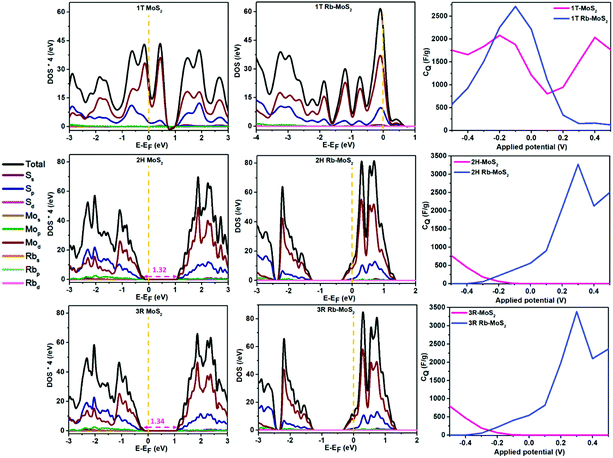
The projected density of states (PDOS) for the pristine and Rb-intercalated structures are depicted in Fig. 2. It can be observed that the d orbital of the Mo atom and the p orbital of the S atoms have the major contribution towards the total density of states (TDOS). Moreover, for the 1T phase, the intercalated Rb ion resulted in an enlargement in the overall intensity of the DOS. However, the arrangement of the intensity of the DOS around the Fermi level (EF) was different. Interestingly, for the 2H and 3R phases, the intercalated Rb ion resulted in a thermodynamic phase shift from semiconducting to metallic behavior. The bandgaps of the pristine 2H and 3R were 1.32 and 1.34 eV, respectively. On the other hand, after Rb intercalation, the DOS intensity increased, and the EF was shifted towards the valence DOS and the phases exhibited metallic nature with no bandgap.
The 2D dichalcogenides can store charges via an intercalation/deintercalation process with adsorbed ions. In addition, the dichalcogenides as 2D materials have quantum characters that affect their overall capacitance. The capacitive behavior of the dichalcogenides can be divided into the classical EDL capacitance represented as the accumulation of charges on the surface of the material and the quantum EDL capacitance (quantum capacitance) represented as the electronic response of the working electrode material upon applying a specific voltage.18,31 To this end, the quantum capacitance (CQ) can provide insights on the enhancement of the overall capacitance of the MoS2 phases. The CQ was calculated as illustrated in eqn (S1) and (S2) (ESI†). We have used a potential window between −0.5 and 0.5 V, which is the usual potential window of MoS2 capacitance in aqueous non-reactive electrolytes.10,32 One of the most important aspects in the performance of a high operating voltage supercapacitor device with high stability is the potential of zero charge (PZC).33 The PZC is identified as the potential at which the working electrode does not accommodate either a positive or negative charge.18 However, in CQ calculations, the EF is considered the PZC of the working electrode and it can identify the positive and negative potential windows at which the electrode can operate when the PZC is identified experimentally. It is noteworthy to mention that the computational calculations of the PZC can explain the presence of capacitance at no applied voltage since working electrodes can accommodate charges if their DOS provided rich occupied states at the Fermi level.34 For Rb intercalation in 1T, the CQ has significantly increased from ∼2000 F g−1 (1T pristine) to ∼2700 F g−1 in the working potential window. This can be attributed to the high contribution of the DOS around the PZC. On the other hand, since the 2H and 3R phases were shifted from semiconductors to metals, their CQ values have changed dramatically. The CQ of the 2H and the 3R phases reached ∼3250 F g−1 and 3400 F g−1, respectively. Nevertheless, this enhancement was in the positive potential window only, while in the negative potential window, the superiority was for their pristine counterparts. It can be observed that the CQ resulting from Rb-intercalated MoS2 is significantly higher (up to 120% increment) than the reported CQ for graphene and doped graphene.19,35,36
To further explore the nature of the adsorption process, the charge density difference was estimated as presented in Fig. 3. The plots were generated according to eqn (S5) (ESI†). It can be clearly observed that the charge is transferred from the Rb atom towards the MoS2 accumulating on the S atoms, where the adsorption is taking place. Moreover, Bader analysis37 was performed to qualitatively identify the amount of charge transferred in the three MoS2 phases. It was found that Rb ions transfer a charge of 0.842 |e|, 0.846 |e|, and 0.844 |e| to the MoS2 system in the 1T, 2H, and 3R phases, respectively, proving the formation of ionic bonding.
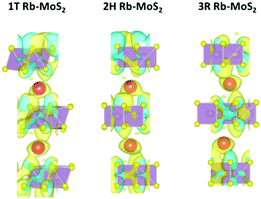 | ||
| Fig. 3 The charge density difference of the Rb-intercalated MoS2 phases. (The cyan color is for the charge accumulation and the yellow color is for the charge depletion.) | ||
Conclusions
In conclusion, Rb is an attractive alkali metal intercalant for enhancing the capacitance performance of 2D layered materials. Rb intercalation stabilizes the metastable 1T phase of MoS2 without altering its metallic character. Also, Rb intercalation results in shifting the 2H and 3R semiconducting phases-thermodynamically- to the metallic 1T phase, while maintaining their stability. Moreover, Rb intercalation improves the quantum capacitance that can enhance the EDL capacitance and increase the overall capacitance of the supercapacitor electrode material. This enhancement in the quantum capacitance renders Rb-intercalated MoS2 a better 2D candidate for supercapacitor devices than graphene and doped graphene. Finally, the charge transferred from Rb ions to the MoS2 stabilizes the adsorption process and is expected to increase the stability of the electrode over a high number of charging cycles.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors acknowledge the financial support of this work by the Arab-German Young Academy of Sciences and Humanities (AGYA).References
- C. Zhan, W. Liu, M. Hu, Q. Liang, X. Yu, Y. Shen, R. Lv, F. Kang and Z. H. Huang, NPG Asia Mater., 2018, 10, 775–787 CrossRef CAS.
- Y. I. Mesbah, N. Ahmed, B. A. Ali and N. K. Allam, ChemElectroChem, 2020, 7, 975–982 CrossRef CAS.
- B. A. Ali, O. I. Metwalli, A. S. G. Khalil and N. K. Allam, ACS Omega, 2018, 3, 16301–16308 CrossRef CAS PubMed.
- N. Ahmed, B. A. Ali, M. Ramadan and N. K. Allam, ACS Appl. Energy Mater., 2019, 2, 3717–3725 CrossRef CAS.
- B. A. Ali and N. K. Allam, Sci. Rep., 2019, 9, 12649 CrossRef PubMed.
- S. Li, P. Liu, X. Huang, Y. Tang and H. Wang, J. Mater. Chem. A, 2019, 7, 10988–10997 RSC.
- G. Barik and S. Pal, J. Phys. Chem. C, 2019, 123, 21852–21865 CrossRef CAS.
- M. Mortazavi, C. Wang, J. Deng, V. B. Shenoy and N. V. Medhekar, J. Power Sources, 2014, 268, 279–286 CrossRef CAS.
- J. Wu, J. Liu, J. Cui, S. Yao, M. Ihsan-Ul-Haq, N. Mubarak, E. Quattrocchi, F. Ciucci and J. K. Kim, J. Mater. Chem. A, 2020, 8, 2114–2122 RSC.
- B. A. Ali, A. M. A. A. Omar, A. S. G. G. Khalil and N. K. Allam, ACS Appl. Mater. Interfaces, 2019, 11, 33955–33965 CrossRef CAS.
- X. Du, J. Huang, X. Guo, X. Lin, J. Q. Huang, H. Tan, Y. Zhu and B. Zhang, Chem. Mater., 2019, 31, 8801–8809 CrossRef CAS.
- S. H. Lee, J. Phys. Chem., 1996, 100, 1420–1425 CrossRef CAS.
- R. B. Somoano, V. Hadek and A. Rembaum, J. Chem. Phys., 1973, 58, 697–701 CrossRef CAS.
- S. Bandow, Y. Maruyama, X.-X. Bi, R. Ochoa, J. M. Holden, W.-T. Lee and P. C. Eklund, Mater. Sci. Eng., A, 1995, 204, 222–226 CrossRef.
- W. M. Haynes, CRC Handbook of Chemistry and Physics, Taylor Fr, Boca Rat. FL, 2017 Search PubMed.
- K. M. Gameel, I. M. Sharafeldin, A. U. Abourayya, A. H. Biby and N. K. Allam, Phys. Chem. Chem. Phys., 2018, 20, 25892–25900 RSC.
- A. H. Biby, S. A. Tolba and N. K. Allam, Int. J. Hydrogen Energy, 2021, 46, 21499–21511 CrossRef CAS.
- B. A. Ali and N. K. Allam, Phys. Chem. Chem. Phys., 2019, 21, 17494–17511 RSC.
- N. Ahmed, A. Amer, B. A. Ali, A. H. Biby, Y. I. Mesbah and N. K. Allam, Sustainable Mater. Technol., 2020, 25, e00206 CrossRef CAS.
- B. A. Ali, A. H. Biby and N. K. Allam, ChemElectroChem, 2020, 7, 1672–1678 CrossRef CAS.
- S. W. Park, A. D. DeYoung, N. R. Dhumal, Y. Shim, H. J. Kim and Y. J. Jung, J. Phys. Chem. Lett., 2016, 7, 1180–1186 CrossRef CAS PubMed.
- S. Loftager, J. M. García-Lastra and T. Vegge, J. Phys. Chem. C, 2016, 120, 18355–18364 CrossRef CAS.
- S. Kretschmer, H. P. Komsa, P. Bøggild and A. V. Krasheninnikov, J. Phys. Chem. Lett., 2017, 8, 3061–3067 CrossRef CAS.
- B. A. Ali, A. H. Biby and N. K. Allam, Chem. Commun., 2021, 57, 3231–3234 RSC.
- A. H. Biby, B. A. Ali and N. K. Allam, Mater. Today Energy, 2021, 20, 100677 CrossRef CAS.
- X. B. Chen, Z. L. Chen and J. Li, Chin. Sci. Bull., 2013, 58, 1632–1641 CrossRef CAS.
- Y. Li, D. Wu, Z. Zhou, C. R. Cabrera and Z. Chen, J. Phys. Chem. Lett., 2012, 3, 2221–2227 CrossRef CAS.
- D. Cao, H. B. Shu, T. Q. Wu, Z. T. Jiang, Z. W. Jiao, M. Q. Cai and W. Y. Hu, Appl. Surf. Sci., 2016, 361, 199–205 CrossRef CAS.
- Y. Shao, P. Gong, H. Pan and X. Shi, Adv. Theory Simul., 2019, 2, 1900045 CrossRef.
- C. Kittel, Introduction to Solid State Physics, Wiley, 2004, p. 704 Search PubMed.
- J. Vatamanu, X. Ni, F. Liu and D. Bedrov, Nanotechnology, 2015, 26, 464001 CrossRef PubMed.
- Q. Mahmood, S. K. Park, K. D. Kwon, S. J. Chang, J. Y. Hong, G. Shen, Y. M. Jung, T. J. Park, S. W. Khang, W. S. Kim, J. Kong and H. S. Park, Adv. Energy Mater., 2016, 6, 1501115 CrossRef.
- D. M. Sayed, M. M. Taha, L. G. Ghanem, M. S. El-Deab and N. K. Allam, J. Power Sources, 2020, 480, 229152 CrossRef CAS.
- D. A. C. da Silva, A. J. Paulista Neto, A. M. Pascon, E. E. Fileti, L. R. C. Fonseca and H. G. Zanin, Phys. Chem. Chem. Phys., 2020, 3906–3913 RSC.
- M. Mousavi-Khoshdel, E. Targholi and M. J. Momeni, J. Phys. Chem. C, 2015, 119, 26290–26295 CrossRef CAS.
- B. C. Wood, T. Ogitsu, M. Otani and J. Biener, J. Phys. Chem. C, 2014, 118, 4–15 CrossRef CAS.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 84204–84211 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Computational details. See DOI: 10.1039/d1ma00145k |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2021 |