Open Access Article
Open Access ArticleStructural evolution, optical gap and thermoelectric properties of CH3NH3SnBr3 hybrid perovskite, prepared by mechanochemistry†
Carlos A.
López
*ab,
Carmen
Abia
ac,
Javier
Gainza
 a,
Paula
Kayser
a,
Paula
Kayser
 a,
N. N.
Nemes
a,
N. N.
Nemes
 ad,
O. J.
Dura
ad,
O. J.
Dura
 e,
J. L.
Martínez
e,
J. L.
Martínez
 a,
María T.
Fernández-Díaz
c,
Consuelo
Álvarez-Galván
f and
José A.
Alonso
a,
María T.
Fernández-Díaz
c,
Consuelo
Álvarez-Galván
f and
José A.
Alonso
 *a
*a
aInstituto de Ciencia de Materiales de Madrid, CSIC, Cantoblanco, 28049 Madrid, Spain. E-mail: ja.alonso@icmm.csic.es
bInstituto de Investigaciones en Tecnología Química (UNSL-CONICET) and Facultad de Química, Bioquímica y Farmacia, Almirante Brown 1455 (5700), San Luis, Argentina. E-mail: calopez@unsl.edu.ar
cInstitut Laue Langevin, BP 156X, F-38042 Grenoble, France
dDepartamento de Física de Materiales, Universidad Complutense de Madrid, E-28040 Madrid, Spain
eDepartamento de Física Aplicada, Universidad de Castilla-La Mancha, Ciudad Real E-13071, Spain
fInstituto de Catálisis y Petroleoquímica, CSIC, Cantoblanco, 28049 Madrid, Spain
First published on 12th April 2021
Abstract
Direct bandgap semiconductors of the hybrid-perovskite family CH3NH3PbX3 (X = I, Br, Cl) exhibit outstanding light absorption properties and are the materials of choice for solar energy applications. As an alternative to poisonous Pb, tin-containing perovskites would show a lower effective mass thus exhibiting a higher charge carrier mobility. An auspicious candidate is CH3NH3SnBr3, with an estimated band gap of 1.902 eV, anticipating applications in photovoltaic devices for the visible to ultra-violet wavelength region. We describe that this perovskite can be prepared by ball milling in a straightforward way, yielding specimens with a superior crystallinity. A structural investigation from synchrotron X-ray powder diffraction (SXRD) data was essential to revisit the successive phase transitions this compound experiences down to 120 K, guided by specific heat capacity and DSC measurements. From the cubic structure identified at RT and 270 K, there is a gradual evolution of the patterns, analysed as a phase admixture between the cubic and the low-symmetry phase present at 160 K. This corresponds to an orthorhombic Pmc21 superstructure; this acentric space group enables polarization along the c-axis where there is a twofold screw axis, evidenced in the distribution of Sn–Br distances. Furthermore, there are two conspicuous changes in the orthorhombic framework, yet keeping the Pmc21 space group, which agree with the main calorimetric events (observed at 224 and 147 K). We interpret these changes as an interplay between the tilting of the SnBr6 octahedra of the inorganic framework and the breaking and reconstruction of H-bond interactions with the organic CH3NH+3 unit. The stereochemical effect of the lone electron pair of the Sn2+ ion is clear in the SnBr6 octahedral distortion. Diffuse reflectance UV/Vis spectroscopy yields an optical gap of ∼2.1 eV, in agreement with ab- initio calculations. A Seebeck coefficient of ∼2000 μV K−1 is determined near RT, which is one order of magnitude higher than those reported for other halide perovskites.
Introduction
Hybrid organic–inorganic halide perovskites have demonstrated applicability in photovoltaic technology,1–6 with a power conversion efficiency (PCE) of about 23%, comparable to the best commercial silicon solar cells. The paradigmatic methylammonium lead iodide CH3NH3PbI3 has thus emerged as a light harvester for hetero-junction solar cells.7–9 Other direct bandgap semiconductors of the MAPbX3 (MA = CH3NH3, X = I, Br, I) family exhibit properties such as outstanding light absorption, excellent ambipolar charge mobility, low exciton binding energy and tolerance to defects.10–18 However, all of them contain poisonous lead, involving toxicity issues with potential public health problems.19 Other divalent elements with a lower toxicity have been evaluated to replace Pb;14,20–24 in particular, many different types of halides containing main group elements such as In(I,III), Sn(II,IV), Sb(III) and Bi(III) have also been studied for solar cell applications;25 however, some of their crystal structures are quite different from the original ABX3 type perovskite. This structural arrangement contains, in its cubic aristotype phase, linear chains –B–X–B– that allow a perfect overlap of the p orbitals of the X and B atoms.26–28Among the different candidates to replace Pb, the most auspicious one is Sn, since its materials possess narrowed optical band gaps and high optical absorption coefficients, given that Sn 5p orbitals are less dispersive than Pb 6p orbitals.29,30 Regarding the effective mass of charge carriers, tin-based perovskites would show a lower magnitude than lead-based ones, and therefore Sn-based perovskites would exhibit a higher charge carrier mobility.31 A particularly interesting material is the CH3NH3SnBr3 perovskite, and closely related CH3NH3SnX3 (X = halogen) derivatives. For an optimized MASnI0.5Br2.5 composition, a power conversion efficiency of 1.51% was demonstrated in liquid-junction PEC solar cells, with an increase of 20.8% with respect to MASnI3 perovskites.32 Recent ab- initio calculations33 enabled the evaluation of a band gap of 1.902 eV for CH3NH3SnBr3, anticipating applications in photovoltaic devices for the visible to ultra-violet wavelength region. Using UV-Vis measurements, the optical bandgap of films prepared by co-evaporation and sequential evaporation methods were determined to be 2.2–2.3 eV.34 The estimated thermoelectric properties at room temperature also predict that CH3NH3SnBr3 may be used in thermoelectric devices.33 Recently, novel applications such as quaternary memories fabricated from CH3NH3SnBr3 memcapacitors have been reported,35 allowing high-density information storage due to their multilevel and adjustable capacitances and long-term retention without a power supply. Despite these interesting precursors, up to now there have been no experimental reports on transport properties such as electronic conductivity, the Seebeck coefficient or thermal transport. By contrast, in halide analogues such as MAPbBr3 or CsSnBr3, these properties have already been studied.36,37
Regarding the structural behavior, CH3NH3SnBr3 has been described as cubic at room temperature (RT), space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (#221), a = 5.903 Å,38 and several phase transitions below RT have been detected by heat capacity measurements, unveiling four anomalies, at 46.0 K (of a displacive type), 188.2 K, 213.0 K, and 229.4 K (of an order–disorder type).39 The transition entropies are consistent with the orientational disorder of the methylammonium ion in a cubic environment. Synchrotron X-ray powder diffraction (SXRD) data indeed reveal the existence of a phase between 230 and 188 K crystallizing in the Pmc21 space group, a = 5.8941(2), b = 8.3862(2), c = 8.2406(2) Å, driven by strong ferroelectric distortions of the octahedra, associated with the stereochemical activity of the Sn 5s2 lone pair.40 The precise nature of a lower-temperature phase remains uncertain, although it appears likely to be triclinic.40
m (#221), a = 5.903 Å,38 and several phase transitions below RT have been detected by heat capacity measurements, unveiling four anomalies, at 46.0 K (of a displacive type), 188.2 K, 213.0 K, and 229.4 K (of an order–disorder type).39 The transition entropies are consistent with the orientational disorder of the methylammonium ion in a cubic environment. Synchrotron X-ray powder diffraction (SXRD) data indeed reveal the existence of a phase between 230 and 188 K crystallizing in the Pmc21 space group, a = 5.8941(2), b = 8.3862(2), c = 8.2406(2) Å, driven by strong ferroelectric distortions of the octahedra, associated with the stereochemical activity of the Sn 5s2 lone pair.40 The precise nature of a lower-temperature phase remains uncertain, although it appears likely to be triclinic.40
In this work, we present results on the structural evolution of CH3NH3SnBr3 from temperature-dependent SXRD data in the 120–295 K interval, from a specimen prepared by ball milling with excellent crystallinity. In the cubic phase at RT, difference Fourier maps show that the methylammonium delocalization obtained differs from that observed in the lead-containing CH3NH3PbBr3 perovskite phase, where the CH3NH3+ unit is oriented along [100]. At 200 K we confirm the existence of a non-centrosymmetric Pmc21 phase that persists down to 120 K. The characterization of this ball-milled specimen is complemented with specific heat measurements, UV-vis spectroscopy and scanning microscopy. Transport measurements reveal a Seebeck coefficient of ∼2000 μV K−1 near RT.
Experimental
CH3NH3SnBr3 was synthesized in polycrystalline form by mechano-chemical synthesis (ball milling) from stoichiometric amounts of SnBr2 and CH3NH3Br. The total mass of reactants was 1.5 g, which were weighed and mixed with 20 zirconia balls (5 mm diameter) in a N2-filled glove-box. The reaction took place in a Retsch PM100 mill for 4 h at 400 rpm, in a sealed zirconia-lined jar under a N2 atmosphere. Laboratory XRPD patterns were collected using a Bruker D5 diffractometer with KαCu (λ = 1.5418 Å) radiation. The thermal evolution of the crystallographic structure was studied by synchrotron X-ray powder diffraction (SXRD) at 120, 140, 160, 200, 221, 240, 270 and 298 K (room temperature). SXRD patterns were collected in high angular resolution mode (so-called MAD set-up) on the MSPD diffractometer in the ALBA synchrotron at Barcelona, Spain, selecting an incident beam with 38 keV energy, λ = 0.3252 Å.41 The sample was contained in a 0.3 mm diameter quartz capillary that was rotating during the data acquisition. XRPD and SXRD patterns were analyzed with the Rietveld method using the FullProf program.42,43 Heat capacity measurements were carried out in the range of 100 K to 300 K at different applied external magnetic fields (up to 9 T) in a PPMS system with a heat pulse method. Scanning Electron Microscopy (SEM) images were obtained using a Hitachi instrument, model TM-1000, coupled to an energy-dispersive X-ray spectrometer (EDX), working with an acceleration voltage of 15 kV and 60 s of acquisition time. The optical diffuse reflectance spectrum of the perovskite powder was measured at room temperature using a Varian Cary 5000 UV-VIS spectrophotometer.The Seebeck coefficient was obtained by measuring simultaneously the drop voltages across the sample and a constantan reference wire with an electrometer (Keithley 6517B) and a nanovoltmeter (Keithley 2182A) under vacuum (10−3 mbar). The electrical resistivity was measured using an Agilent E4980A LCR meter. The total thermal conductivity was calculated from the thermal diffusivity (α) using Linseis LFA 1000 equipment, by the laser-flash technique. The thermal conductivity (κ) was determined using κ = α·Cp·d, where Cp is the specific heat capacity and d is the sample density.
Results and discussion
The sample was obtained as a dark-red microcrystalline powder; the laboratory XRPD pattern at RT exhibits a cubic symmetry, in agreement with previous reports, indexable in the space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.40,44 The crystal structure was confirmed through a Le-Bail fit in this space group, as displayed in Fig. S1 (ESI†), obtaining a unit-cell parameter a = 5.9595(1) Å.
m.40,44 The crystal structure was confirmed through a Le-Bail fit in this space group, as displayed in Fig. S1 (ESI†), obtaining a unit-cell parameter a = 5.9595(1) Å.
Fig. S2 (ESI†) illustrates typical SEM images of the as-prepared CH3NH3SnBr3 perovskite. Large particles with sharp edges and large surfaces are identified, mixed with smaller pieces with less-defined shapes. The growth of large microcrystals, with tenths of microns as the maximal dimensions, is possible after 4 hours of ball milling reaction; this justifies the good crystallinity displayed in the diffraction patterns. The results from EDX analysis (Fig. S2c, ESI†) showed well-defined peaks corresponding to tin and bromine, with the determined weight% of these elements (Sn: 38.4 (33.12), Br: 61.6 (66.88)) in reasonable agreement with the nominal values (in parentheses).
The synchrotron pattern collected at RT confirms the cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group were Sn2+ and Br− ions are located in 1a (0,0,0) and 3d (0.5,0,0) Wyckoff sites. The CH3NH3+ organic cation is centered at the (0.5,0.5,0.5) position. As is well known, in hybrid-perovskite structures, the methylammonium units can be delocalized along the [100], [110] or [111] directions.45,46 In the present case, Difference Fourier Maps (DFM) from the calculated and observed electron density reveal that CH3NH3+ is delocalized along the [100] direction. The final refinement using this model is illustrated in Fig. 1a and the main crystallographic results are listed in Table 1. Two views of the crystal structure and DFM are shown in Fig. 1b and c, respectively. The methylammonium delocalization obtained differs from that observed in the lead-counterpart phase, where it is lying along [110].47 This difference is due to the smaller unit-cell size of the tin phase (a = 5.9038(1) Å) vs. lead perovskite (for CH3NH3PbBr3, a = 5.93076(2) Å), as expected considering the ionic radii of the inorganic cations (r(Sn2+) = 0.93 Å; r(Pb2+) = 1.19 Å).48,49 This correlation between methylammonium alignment and unit-cell size also was observed in the MAPbBr3−xClx series.17
m space group were Sn2+ and Br− ions are located in 1a (0,0,0) and 3d (0.5,0,0) Wyckoff sites. The CH3NH3+ organic cation is centered at the (0.5,0.5,0.5) position. As is well known, in hybrid-perovskite structures, the methylammonium units can be delocalized along the [100], [110] or [111] directions.45,46 In the present case, Difference Fourier Maps (DFM) from the calculated and observed electron density reveal that CH3NH3+ is delocalized along the [100] direction. The final refinement using this model is illustrated in Fig. 1a and the main crystallographic results are listed in Table 1. Two views of the crystal structure and DFM are shown in Fig. 1b and c, respectively. The methylammonium delocalization obtained differs from that observed in the lead-counterpart phase, where it is lying along [110].47 This difference is due to the smaller unit-cell size of the tin phase (a = 5.9038(1) Å) vs. lead perovskite (for CH3NH3PbBr3, a = 5.93076(2) Å), as expected considering the ionic radii of the inorganic cations (r(Sn2+) = 0.93 Å; r(Pb2+) = 1.19 Å).48,49 This correlation between methylammonium alignment and unit-cell size also was observed in the MAPbBr3−xClx series.17
System: cubic, Space group: Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, Z = 1. Unit-cell parameters: a = 5.9038(1) Å, and V = 205.78(1) Å3. m, Z = 1. Unit-cell parameters: a = 5.9038(1) Å, and V = 205.78(1) Å3. |
||||||
|---|---|---|---|---|---|---|
| Atom | x | Y | z | U eq | Occ. | |
| R p: 7.21%; Rwp: 8.98%; Rexp: 7.99%; χ2: 1.26; RBragg: 4.47%. | ||||||
| Sn | 1a | 0 | 0 | 0 | 0.027(1) | 1 |
| Br | 3d | 0.5 | 0 | 0 | 0.099(1) | 1 |
| C | 6f | 0.639(2) | 0.5 | 0.5 | 0.016(9) | 0.166 |
| N | 6f | 0.639(2) | 0.5 | 0.5 | 0.016(9) | 0.166 |
| Anisotropic displacement parameters | ||||||
| U 11 | U 22 | U 33 | U 12 | U 13 | U 23 | |
| Sn | 0.027(1) | 0.027(1) | 0.027(1) | 0 | 0 | 0 |
| Br | 0.044(1) | 0.127(1) | 0.127(1) | 0 | 0 | 0 |
| C/N | 0.028(9) | 0.010(8) | 0.010(8) | 0 | 0 | 0 |
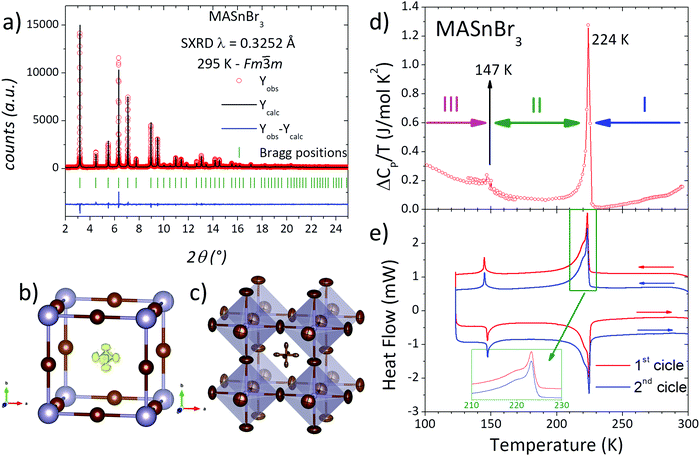
On the other hand, low temperature synchrotron X-ray patterns were used to resolve the crystal structures below room temperature of this sample synthesized mechanochemically, taking into account the calorimetric behaviour analyzed from CP and DSC measurements. The thermal evolution of CP of the present sample is shown in Fig. 1d, showing a sharp peak at 224 K indicating a strong caloric process. Also, there are three additional anomalies at 147 (small peak), 273 (slope change) and 298 K (broad peak). This caloric behaviour is quite different from that reported previously in single-crystal samples growth from solution.28,39 The present anomalies are less intense and the temperatures are shifted with respect to the values mentioned in the introduction. Considering the most defined peaks, it is possible to accept the existence of three crystalline phases or states: T > 224 K, 147 > T > 224 K and T < 147 K, labelled I, II and III, respectively in Fig. 1d. DSC measurements are shown in Fig. 1e. In excellent agreement with Cp data, the DSC curves display two main events at 144 and 223 K, confirming the three states mentioned previously. In addition, the greater resolution of DSC measurements allows observing a shoulder (centred at 220 K) over the main peak. Also, this signal could be deconvoluted into two peaks, where the most intense one is sharp and the shoulder is broad, as illustrated in Fig. 1e (inset). Moreover, DSC data also reveal the complete reversibility of the processes, showing that the second cycle perfectly matches with the first one.
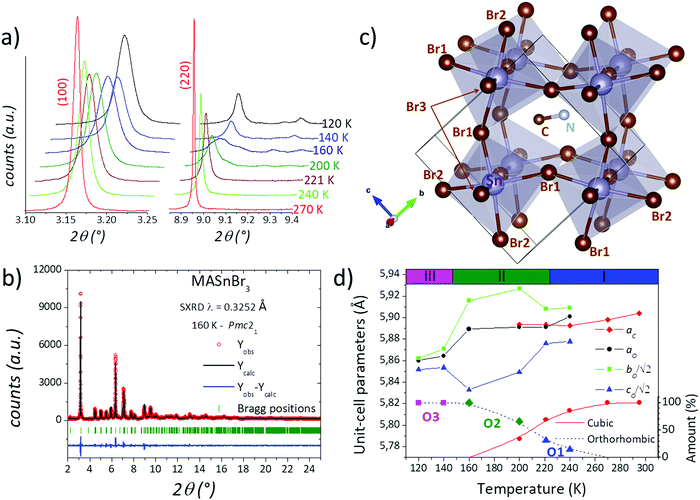
To analyse these structural regions, additional SXRD patterns were collected at 270, 240, 221, 200, 160, 140 and 120 K. Fig. 2(a) plots the evolution of a selection of SXRD reflections, in particular corresponding to the cubic (100) and (220) planes, illustrating the structural changes at different temperatures. While the (100) plane shows no significant changes, the (220) reflection exhibits a conspicuous splitting, which indicates the presence of lower-symmetry phases below 240 K. This is also observed in other reflections, as complementarily shown in Fig. S3 (ESI†). The thermal evolution of the peak shape reveals that, at 270 K, the structure remains cubic, and a gradual change is observed from 240 to 160 K. Besides, the patterns at 140 and 120 K are similar to each other, but they are different from the remaining temperatures. These changes are in agreement with the observed phase regions from calorimetric measurements: above 224 K, between 224 and 147 K and below 147 K, labelled in Fig. 1d as phases I, II and III, respectively.
The low-temperature crystal structure of CH3NH3SnBr3 was first investigated in 1995 by Onoda-Yamamuro et al.44 They reported this deuterated phase from neutron powder diffraction at 195 K as rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c). However, ten years ago, Swainson et al. reported the acentric Pmc21 space group in the 188–230 K temperature range from synchrotron powder diffraction and proposed a monoclinic acentric space group below 188 K.40
c). However, ten years ago, Swainson et al. reported the acentric Pmc21 space group in the 188–230 K temperature range from synchrotron powder diffraction and proposed a monoclinic acentric space group below 188 K.40
As mentioned above, from our SXRPD data we observe that the cubic symmetry remains when the sample is cooled down to 270 K, just showing the expected reduction in the unit-cell volume, while the methylammonium molecule remains aligned along the [100] direction. Fig. S4 and Table S1 (ESI†) show the Rietveld plots and the crystallographic results, respectively.
On the other hand, by analysing the gradual change mentioned above, it is evident that the patterns at 240, 221 and 200 K exhibit a phase mixture between the cubic and the low-symmetry phase present at 160 K. The two previously reported structures (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c and Pmc21) were tested, finding a good agreement only with the orthorhombic Pmc21 space group, as it was previously reported by Swainson et al.40 In this structural model, the unit-cell parameters are related to the cubic unit cell as aO × √2aO × √2aO, with aO being the aristotype cubic edge. Besides, the Sn2+ cation is located at 2a (0,y,z) Wyckoff sites and Br− anions are distributed in two 2a and one 2b (0.5,y,z) sites. The C and N atoms are placed at 2b (0.5,y,z) sites, implying that the methylammonium unit is localized within the (100) plane for x = 0.5. This model yields a good agreement after the Rietveld refinement, as plotted in Fig. 2b. The crystallographic results are listed in Table S2 (ESI†). This acentric space group enables a polarization along the c axis where there is a twofold screw axis. The polarization can be evidenced in the Sn–Br direction, where in the (100) plane there are two Sn–Br distances that are shorter than the other two. In addition, the MA is subtly tilted to the [100] direction in terms of the cubic polytype. These facts can be visualized in Fig. 2c. After resolving this structure in Pmc21 at 160 K, it was possible to refine the patterns at 240, 221 and 200 K, where a mixture of cubic and orthorhombic phases was found. The corresponding Rietveld plots are plotted in Fig. S5–S7 (ESI†), and the crystal data are listed in Tables S3–S5 (ESI†).
c and Pmc21) were tested, finding a good agreement only with the orthorhombic Pmc21 space group, as it was previously reported by Swainson et al.40 In this structural model, the unit-cell parameters are related to the cubic unit cell as aO × √2aO × √2aO, with aO being the aristotype cubic edge. Besides, the Sn2+ cation is located at 2a (0,y,z) Wyckoff sites and Br− anions are distributed in two 2a and one 2b (0.5,y,z) sites. The C and N atoms are placed at 2b (0.5,y,z) sites, implying that the methylammonium unit is localized within the (100) plane for x = 0.5. This model yields a good agreement after the Rietveld refinement, as plotted in Fig. 2b. The crystallographic results are listed in Table S2 (ESI†). This acentric space group enables a polarization along the c axis where there is a twofold screw axis. The polarization can be evidenced in the Sn–Br direction, where in the (100) plane there are two Sn–Br distances that are shorter than the other two. In addition, the MA is subtly tilted to the [100] direction in terms of the cubic polytype. These facts can be visualized in Fig. 2c. After resolving this structure in Pmc21 at 160 K, it was possible to refine the patterns at 240, 221 and 200 K, where a mixture of cubic and orthorhombic phases was found. The corresponding Rietveld plots are plotted in Fig. S5–S7 (ESI†), and the crystal data are listed in Tables S3–S5 (ESI†).
At lower temperatures, two patterns collected at 120 and 140 K are in the temperature range of phase III. Both patterns could also be properly fitted within the Pmc21 space group, but with a noticeably lower distortion with respect to the 160 K phase. This result contrasts with the triclinic models proposed by Swainson et al. for MASnBr3 in this temperature range;38 moreover, attempts to fit the patterns with these triclinic models were unsuccessful. It is remarkable that, despite the fact that the same Pmc21 space group can reliably define the crystal structure at 120 and 140 K, there are conspicuous differences with the 200 K structure; in particular the unit-cell parameters, aO × √2bO × √2cO are more similar to each other than those observed at 160 K. The Rietveld plots at these temperatures are shown in Fig. S8 and S9 (ESI†) and the crystallographic results are listed in Tables S6 and S7 (ESI†).
Therefore, four phases are identified, one cubic and three orthorhombic crystal structures, labelled: C, O1, O2 and O3, in addition to the mentioned mixture between C and O1 (and O2) phases in the 240–200 K range. The thermal evolution of the unit-cell parameters is illustrated in Fig. 2d, where the relative proportion of the four phases and the calorimetric regions are added. The first phase transition occurs in a broad temperature range of at least 50 K (from 250 to 200 K) where both cubic and orthorhombic structures coexist, contrasting with the previous results. Furthermore, there are two changes in the orthorhombic symmetry, which agree with the main calorimetric events (224 and 147 K). In addition, the subtle event at 270 K probably is due to the starting point of the phase transition from cubic to orthorhombic (O1) symmetry. These differences with respect to previous reports can be associated with the single crystal38vs. the polycrystalline state. The mechanochemical procedure generated a well-crystallized powder; however, this method also induces a strained grain surface, which probably modifies the thermal stability of the crystal structures.
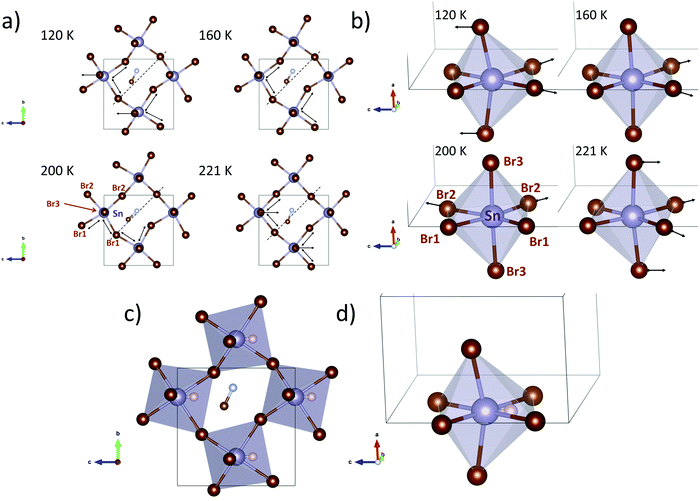
In order to understand the three different structures with orthorhombic symmetry (O1, O2, O3) a careful analysis of selected bonds and angles has been carried out. The analysed parameters are: Sn–Br distances and Br–Sn–Br angles (to observe the SnBr6 octahedral distortion) and the Sn–Br–Sn (to show the octahedral tilting). In addition, the angle between the MA and the ideal [100] direction was calculated, to estimate possible changes in H-bond interactions. These parameters are listed in Table S8, plotted in Fig. S10–S13 (ESI†) and schematized in crystal structure views in Fig. 3. The arrows on the Sn–Br1 and Sn–Br2 bonds indicate the longer (Sn–Br) distances in the equatorial plane of the SnBr6 octahedron. The arrow on Br3 highlights its displacement along the c-axis with respect to the Sn atom. This distortion is sensitive to the Br3–Sn–Br3 angle, as listed in Table S8 (ESI†) and plotted in Fig. S12 (ESI†). In addition, the dashed line indicates the [100] direction (for the cubic polytype) to visualize the MA displacement.
These parameters show that the orthorhombic lattice undergoes gradual changes upon cooling down, as follows. Regarding the inorganic framework, the distortion starts at high temperature (240 and 221 K) with net polarization along the −c-axis, characterized by a low octahedral tilting. At 200 K the distortion in the equatorial plane of the octahedron changes to the b-axis and the tilts become greater. Then, at 160 K, the displacements return to the c direction and the tilt increases. At lower temperatures (120 and 140 K) the octahedral distortion and the tilts are greater, yielding a net polarization along the +c-axis. On the other hand, the organic MA molecules also evolve following the inorganic framework displacements or vice versa. At higher temperatures (240 and 221 K) the linear MA units are far from the [100] directions (see dashed line in Fig. 3a), but they approach the [100] line at 200 K, which is concomitant with the increase of the octahedral tilting (see Sn–Br–Sn angles, Fig. S12 and S13, ESI†). This change probably involves breaking and reconstructing H-bond interactions; these fluctuations involve strong enthalpy changes, in agreement with the intense signal observed in the heat capacity at 224 K (Fig. 1d). As mentioned above, this process in DSC presents a shoulder (Fig. 1e and inset), hence, considering both the organic and inorganic structural evolution in the lattice, the sharp and broad peaks could be assigned to the H-bond and octahedral tilt changes, respectively. Then, at lower temperatures, the organic cation undergoes a gradual displacement towards the c-axis, in order to compensate the polarization of the inorganic lattice along the +c-axis. Finally, the role of the inert pair effect (Sn 5s2) in these changes should not be ignored. The octahedral shape at higher temperatures (>160 K) does not suggest the presence of a localized inert pair. However, at 120 and 140 K the distortion of the SnBr6 octahedron (Fig. 3c and d) shows conclusive stereochemical evidence of the electron density of the 5s2 inert pair in the –c direction. Thus, the calorimetric signal at 147 K can be associated with the localization of the inert electron pair. The expected position of the Sn2+ inert pair is also shown in Fig. 3c and d.
Thermoelectric properties
Fig. 4 shows the three main thermoelectric properties measured near RT: resistivity (Fig. 4a), the Seebeck coefficient (Fig. 4b) and thermal conductivity (Fig. 4c). The resistivity is around 2 × 103 Ω m at 310 K, a high value that is quite far from being competitive with other materials, such as some halide perovskites.37 However, this resistivity is better than that reported for lead-containing MAPbBr3 single-crystals, which is around 106 Ω m, and is about the same as the resistivity of Bi-doped samples.36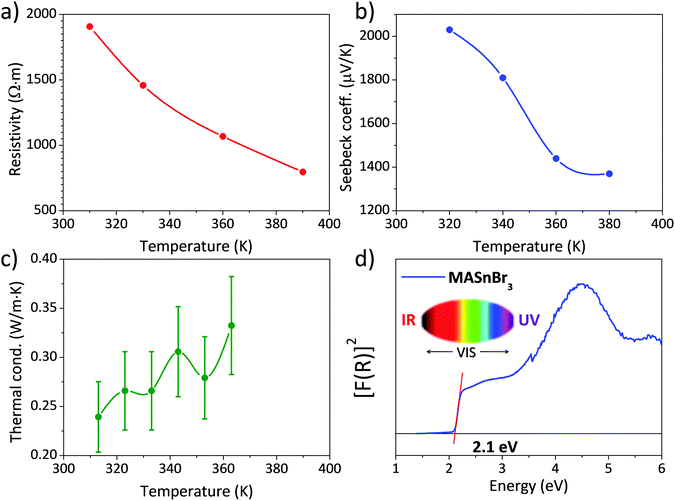 | ||
| Fig. 4 (a) Electrical resistivity, (b) Seebeck coefficient, (c) thermal conductivity and (d) UV–Vis absorption spectrum of MASnBr3. | ||
The Seebeck coefficient shows a value of S = 2030 μV K−1 at 320 K. This value is about one order of magnitude higher than that reported for other halide perovskites like CsSnBr3 and hybrid perovskites like MAPbBr3.36,37 It is also higher than some results obtained from theoretical predictions,33 calculated for a hole concentration of 1 × 1018 cm−3, and projecting a value around S = 300 μV K−1 at 300 K. Both the resistivity and Seebeck coefficient decrease with temperature, which could be the effect of the activation of minority carriers.
The thermal conductivity κ is, on the other hand, lower than that reported for other halide and hybrid perovskites,36,37 and always remains below 0.35 W m·K−1 at all the measured temperatures. Combining these values in a zT figure of merit, defined as zT = S2σT/κ, yields zT = 3 × 16·10−6 at 313 K, which is low compared with state-of-the-art thermoelectric materials, but is superior to other values given for hybrid perovskites, like Bi-doped MAPbBr3, of 1.8 × 10−6.36
Optical gap by UV-Vis spectra
The absorption capacity of MASnBr3 perovskite powder was investigated by diffuse reflectance UV/Vis spectroscopy. Fig. 4d depicts the optical absorption coefficient related to the Kubelka–Munk function (F(R) = a = (1 − R)2/2R, where R is the reflectance versus wavelength in eV).The band gap for this perovskite at RT has been calculated by extrapolating the linear region to the abscissa. The value obtained for MASnBr3 (∼2.1 eV) agrees with data reported in the literature (2.15 eV50 or 2.2–2.3 eV34), being even slightly smaller, which would improve light absorption. This difference could be related, once more, to the preparation procedure of the present specimen, by mechano-synthesis, as opposed to conventional synthesis techniques by co-evaporation34 or solution chemistry.50
Chemical stability
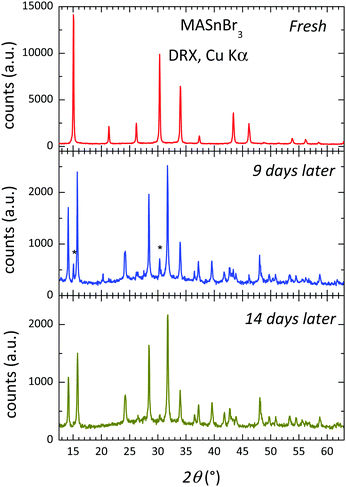
Fig. 5 shows three XRD patterns of MASbBr3, freshly prepared by ball milling, after 9 days and after 14 days of air exposure under laboratory conditions (typically 40% humidity). The pattern of the fresh sample corresponds to the above-described cubic perovskite stable at RT; the patterns after 9 and 14 days are strongly degraded, with just some of the strong perovskite peaks visible (shown as asterisks). Even visually, some days after the sample was synthesized, the characteristic dark red colour became cream and finally white. The products are identified as the hydrates of methylammonium and tin bromides. These results are just included to highlight the great reactivity and instability of the hybrid perovskite under laboratory conditions, which would require adequate protection against the atmosphere in eventual devices.Conclusions
CH3NH3SnBr3 hybrid perovskite has been successfully prepared as a well-crystallized powder by mechano-chemical synthesis under an inert atmosphere. The crystal structure evolution has been revisited from high angular resolution SXRD data. A complex progression is identified, including four phases, including one cubic, C (at, and immediately below RT) and three orthorhombic crystal structures, O1, O2 and O3. The C, O1 and O2 phases coexist in the 240–200 K range, in contrast with the previous results. The three orthorhombic phases are defined in the acentric Pmc21 space group, although they exhibit very different unit-cell parameters. This evolution is the result of an interplay between the octahedral tilting of the inorganic framework and the reconstruction of H–Br hydrogen bonds with the organic moiety, yielding the main calorimetric events (224 and 147 K) detected by Cp and DSC measurements. The shape of the SnBr6 octahedra at higher temperatures (>160 K) does not denote the presence of the localized 5s2 inert pair of the Sn2+ ion. However, at 120 and 140 K its distortion indicates conclusive stereochemical evidence of the electron density of the 5s2 inert pair in the –c direction. Thus, the calorimetric signal at 147 K can be associated with the localization of the inert electron pairs, which can be identified from the structural features. The optical gap of this specimen synthesized by solvent-free mechano-chemistry, of 2.1 eV, is slightly below the values reported for wet-chemistry prepared materials. The thermoelectric properties are appealing, regarding a large Seebeck coefficient and a low thermal conductivity, although the large electrical resistivity leads to negligible figure of merit values. The great reactivity and instability of this hybrid perovskite under laboratory conditions leads to rapid degradation in a humid environment, thus requiring adequate protection against the atmosphere in devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The Spanish Ministry of Science, Innovation and Universities supported this work through grant MAT2017-84496-R. The authors wish to express their gratitude to ALBA technical staff for making the facilities available for the Synchrotron X-ray powder diffraction experiment number 2018092964. J. G. thanks MICINN for granting the contract PRE2018-083398. C. A. thanks financial support from the Institut Laue-Langevin through the DA/SRH/GRI/AS/19-214 contract.References
- M. Grätzel, J. Photochem. Photobiol., C, 2003, 4, 145–153 CrossRef.
- M. A. Green, A. Ho-Baillie and H. J. Snaith, Nat. Photonics, 2014, 8, 506–514 CrossRef CAS.
- J. Burschka, N. Pellet, S.-J. Moon, R. Humphry-Baker, P. Gao, M. K. Nazeeruddin and M. Grätzel, Nature, 2013, 499, 316–319 CrossRef CAS PubMed.
- T. M. Brenner, D. A. Egger, L. Kronik, G. Hodes and D. Cahen, Nat. Rev. Mater., 2016, 1, 15007 CrossRef CAS.
- H. J. Snaith, J. Phys. Chem. Lett., 2013, 4, 3623–3630 CrossRef CAS.
- N.-G. Park, J. Phys. Chem. Lett., 2013, 4, 2423–2429 CrossRef CAS.
- L. Etgar, P. Gao, Z. Xue, Q. Peng, A. K. Chandiran, B. Liu, M. K. Nazeeruddin and M. Grätzel, J. Am. Chem. Soc., 2012, 134, 17396–17399 CrossRef CAS PubMed.
- H.-S. Kim, C.-R. Lee, J.-H. Im, K.-B. Lee, T. Moehl, A. Marchioro, S.-J. Moon, R. Humphry-Baker, J.-H. Yum, J. E. Moser, M. Grätzel and N.-G. Park, Sci. Rep., 2012, 2, 591 CrossRef PubMed.
- H.-Y. Hsu, L. Ji, H. S. Ahn, J. Zhao, E. T. Yu and A. J. Bard, J. Am. Chem. Soc., 2015, 137, 14758–14764 CrossRef CAS PubMed.
- C. R. Kagan, Science, 1999, 286, 945–947 CrossRef CAS PubMed.
- A. Kojima, M. Ikegami, K. Teshima and T. Miyasaka, Chem. Lett., 2012, 41, 397–399 CrossRef CAS.
- P. Gao, M. Grätzel and M. K. Nazeeruddin, Energy Environ. Sci., 2014, 7, 2448–2463 RSC.
- B. Saparov and D. B. Mitzi, Chem. Rev., 2016, 116, 4558–4596 CrossRef CAS PubMed.
- G. Niu, X. Guo and L. Wang, J. Mater. Chem. A, 2015, 3, 8970–8980 RSC.
- M. Zhang, H. Yu, M. Lyu, Q. Wang, J.-H. Yun and L. Wang, Chem. Commun., 2014, 50, 11727–11730 RSC.
- M. C. Alvarez-Galván, J. A. Alonso, C. A. López, E. López-Linares, C. Contreras, M. J. Lázaro, F. Fauth and M. V. Martínez-Huerta, Cryst. Growth Des., 2019, 19, 918–924 CrossRef.
- C. A. López, M. C. Álvarez-Galván, M. V. Martínez-Huerta, M. T. Fernández-Díaz and J. A. Alonso, Chem. – Eur. J., 2019, 25, 4496–4500 CrossRef PubMed.
- C. A. López, M. C. Alvarez-Galván, M. V. Martínez-Huerta, F. Fauth and J. A. Alonso, CrystEngComm, 2020, 22, 767–775 RSC.
- A. Babayigit, A. Ethirajan, M. Muller and B. Conings, Nat. Mater., 2016, 15, 247–251 CrossRef CAS PubMed.
- F. Sani, S. Shafie, H. Lim and A. Musa, Materials, 2018, 11, 1008 CrossRef PubMed.
- F. Giustino and H. J. Snaith, ACS Energy Lett., 2016, 1, 1233–1240 CrossRef CAS.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038 CrossRef CAS PubMed.
- F. Hao, C. C. Stoumpos, D. H. Cao, R. P. H. Chang and M. G. Kanatzidis, Nat. Photonics, 2014, 8, 489–494 CrossRef CAS.
- N. K. Noel, S. D. Stranks, A. Abate, C. Wehrenfennig, S. Guarnera, A.-A. Haghighirad, A. Sadhanala, G. E. Eperon, S. K. Pathak, M. B. Johnston, A. Petrozza, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 3061–3068 RSC.
- S. F. Hoefler, G. Trimmel and T. Rath, Monatshefte für Chemie – Chem. Mon., 2017, 148, 795–826 CrossRef CAS PubMed.
- K. Yamada, K. Nakada, Y. Takeuchi, K. Nawa and Y. Yamane, Bull. Chem. Soc. Jpn., 2011, 84, 926–932 CrossRef CAS.
- K. Yamada, S. Hino, S. Hirose, Y. Yamane, I. Turkevych, T. Urano, H. Tomiyasu, H. Yamagishi and S. Aramaki, Bull. Chem. Soc. Jpn., 2018, 91, 1196–1204 CrossRef CAS.
- K. Yamada, K. Fujise, S. Hino, Y. Yamane and T. Nakagama, Chem. Lett., 2019, 48, 749–752 CrossRef CAS.
- T. Handa, A. Wakamiya and Y. Kanemitsu, APL Mater., 2019, 7, 080903 CrossRef.
- W. Yang, F. Igbari, Y. Lou, Z. Wang and L. Liao, Adv. Energy Mater., 2020, 10, 1902584 CrossRef CAS.
- L. M. Herz, ACS Energy Lett., 2017, 2, 1539–1548 CrossRef CAS.
- H.-Y. Hsu, L. Ji, M. Du, J. Zhao, E. T. Yu and A. J. Bard, Electrochim. Acta, 2016, 220, 205–210 CrossRef CAS.
- A. Shukla, V. K. Sharma, S. K. Gupta and A. S. Verma, Mater. Chem. Phys., 2020, 253, 123389 CrossRef CAS.
- M.-C. Jung, S. R. Raga and Y. Qi, RSC Adv., 2016, 6, 2819–2825 RSC.
- W. Qian, X. Cheng, Y. Zhao, J. Zhou, J. He, H. Li, Q. Xu, N. Li, D. Chen and J. Lu, Adv. Mater., 2019, 31, 1806424 CrossRef PubMed.
- W. Tang, J. Zhang, S. Ratnasingham, F. Liscio, K. Chen, T. Liu, K. Wan, E. S. Galindez, E. Bilotti, M. Reece, M. Baxendale, S. Milita, M. A. McLachlan, L. Su and O. Fenwick, J. Mater. Chem. A, 2020, 8, 13594–13599 RSC.
- H. Xie, S. Hao, J. Bao, T. J. Slade, G. J. Snyder, C. Wolverton and M. G. Kanatzidis, J. Am. Chem. Soc., 2020, 142, 9553–9563 CrossRef CAS PubMed.
- K. Yamada, S. Nose, T. Umehara, T. Okuda and S. Ichiba, Bull. Chem. Soc. Jpn., 1988, 61, 4265–4268 CrossRef CAS.
- N. Onoda-Yamamuro, T. Matsuo and H. Suga, J. Chem. Thermodyn., 1991, 23, 987–999 CrossRef CAS.
- I. Swainson, L. Chi, J.-H. Her, L. Cranswick, P. Stephens, B. Winkler, D. J. Wilson and V. Milman, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 422–429 CrossRef CAS PubMed.
- F. Fauth, R. Boer, F. Gil-Ortiz, C. Popescu, O. Vallcorba, I. Peral, D. Fullà, J. Benach and J. Juanhuix, Eur. Phys. J. Plus, 2015, 130, 160 CrossRef.
- H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71 CrossRef CAS.
- J. Rodríguez-Carvajal, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 192, 55–69 CrossRef.
- N. Onoda-Yamamuro, O. Yamamuro, T. Matsuo, H. Suga, K. Oikawa, N. Tsuchiya, T. Kamiyama and H. Asano, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 213–214, 411–413 CrossRef.
- R. E. Wasylishen, O. Knop and J. B. Macdonald, Solid State Commun., 1985, 56, 581–582 CrossRef CAS.
- N. Onoda-Yamamuro, T. Matsuo and H. Suga, J. Phys. Chem. Solids, 1990, 51, 1383–1395 CrossRef CAS.
- C. A. López, M. V. Martínez-Huerta, M. C. Alvarez-Galván, P. Kayser, P. Gant, A. Castellanos-Gomez, M. T. Fernández-Díaz, F. Fauth and J. A. Alonso, Inorg. Chem., 2017, 56, 14214–14219 CrossRef PubMed.
- L. H. Ahrens, Geochim. Cosmochim. Acta, 1952, 2, 155–169 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr. Sect. A, 1976, 32, 751–767 CrossRef.
- B. Li, R. Long, Y. Xia and Q. Mi, Angew. Chem., Int. Ed., 2018, 57, 13154–13158 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma00196e |
| This journal is © The Royal Society of Chemistry 2021 |