Open Access Article
Open Access ArticleA first-principles study of the relationship between modulus and ideal strength of single-layer, transition metal dichalcogenides
Hao
Sun
a,
Pratyaksh
Agrawal
a and
Chandra Veer
Singh
 *ab
*ab
aDepartment of Mechanical and Industrial Engineering, University of Toronto, Toronto, ON M5S 3G8, Canada. E-mail: chandraveer.singh@utoronto.ca; Tel: +1 416 946-5211
bDepartment of Materials Science and Engineering, University of Toronto, Toronto, ON M5S 3E4, Canada
First published on 30th August 2021
Abstract
Electronic properties of single-layer transition metal dichalcogenides (TMDs), such as bond gap, can be tuned by elastic strain. The regulating range of such strain engineering is determined by ideal strengths, which, according to Griffth's strength limit, is usually estimated as E/10, where E is the elastic modulus. Despite being extensively used, this relationship between ideal strength and moduli has yet to be thoroughly investigated for TMDs. Our extensive density functional theory calculations on six representative, single-layer TMDs (MoS2, MoSe2, NbS2, NbSe2, ReS2, ReSe2) showed that the moduli of TMDs increase as their transition metal elements change from the V to VII group. However, despite having higher moduli, ReS2 and ReSe2 exhibit lower strengths and failure strains than MoS2, MoSe2, and NbSe2. Such strength degeneration is attributed to the multiple bond directions in ReS2 and ReSe2. As strain softening renders stretched bonds easier to deform, deformation gradually concentrates on the bonds most close to the loading direction. Since only a small portion of covalent bonds are stretched, the ideal strength of the whole structure is diminished. Overall, our findings suggest that reducing the variety of bond orientations could increase the apparent ductility of TMDs without decreasing the strength.
1. Introduction
Monolayer transition metal dichalcogenides (TMDs) have attracted intensive attention due to their unique chemical and physical properties. Unlike graphene, whose zero band gap leads to a low intrinsic on–off current ratio,1 the direct band gap (1.1–2.0 eV)2–4 of TMDs significantly enhances the on–off current ratio,5 the luminescence quantum efficiency,6–8 and the intrinsic electronic mobility.9 These outstanding characteristics render TMDs interesting for both fundamental research and applications in field-effect transistors,5 phototransistors,10 optoelectronics,11 and mechanical resonators.12The advantages of TMDs mentioned above have stimulated extensive research on their electronic band structures. Both experiments11 and first-principles calculations13–17 have found that elastic strain can effectively tune the band gap of TMDs. The adjustment range of band gap is determined by the maximum strain a TMD can sustain. Theoretically, a large enough tensile strain can even tune the conduction band minimum to be lower than the Fermi level, resulting in a metal-like TMD.13 The critical strain corresponding to such transition was found to be related to the moduli of TMDs18 and scale roughly with its ideal strength.19 Hence, strain engineering can effectively adjust the electronic band structure of TMDs without varying chemical components and topological atomic arrangements.
As the modulus and ideal strength are two key factors determining the limit of strain engineering, robust literature has investigated the mechanical property of MoS212,20–26 and compared its properties with other TMDs.27–30 The bending stiffness of TMDs was found to increase as the transition metal goes from the IV to VI group.31 The 2D elastic stiffness of TMDs was reported to depend on the bond lengths28 and to soften with increasing lattice parameters.32,33 Despite such a significant expansion of knowledge, prior analysis has only focused on linear mechanical properties.27,28,30,32,33 The nonlinear mechanical properties of TMDs, such as ideal strengths and fracture strains, have yet to be thoroughly investigated.
Without a complete structure-mechanical-property relationship, the ideal strength of TMDs can only be estimated by Griffith's strength limit—a linear correlation between the ideal strength and Young's modulus.29 This relationship, however, is based on a hypothesis that the deformation is mainly undertaken by bond stretching, ignoring the role of bond rotation. Recent research on graphene allotropes has found that bond rotation can significantly lessen bond stretch, enhancing fracture strain.34,35 In one graphene allotrope with a Poisson's ratio as high as 0.8, bond rotation leads to an S-shape stress–strain curve, akin to that of elastomers, with an ultimate tensile strength (UTS) exceeding the Griffth's cohesive strength limit.34 Despite the intense study on graphene allotropes, the bond-rotation effect on the mechanical properties of TMDs remains unexplored. Thus, a complete picture of the structure-mechanical-property relationship for TMDs is still missing.
This paper presents a comprehensive theoretical analysis of the structure-mechanical-property relationship of six representative TMDs (MoS2, MoSe2, NbS2, NbSe2, ReS2, ReSe2) with varying chemical components and topological atomic arrangements. For most of the six TMDs, their nonlinear mechanical properties, such as ideal strengths and fracture strains, have not been reported elsewhere. The relationship between the UTS and modulus was investigated from two perspectives. First, the physical insight of Griffth's strength limit in TMDs was revealed based on the charge-density evolution of their covalent bonds during bond stretching; then we analyzed the effect of bond rotation on the mechanical properties of the TMD. Finally, different fracture mechanisms of TMDs were discussed. The fundamental insights revealed by this research can help experimentalists analyze the fracture mechanism of TMDs.
2. Methodology
The atomic configurations of the six TMDs are shown in Fig. 1. All DFT simulations were performed using the Quantum-ESPRESSO package,36 pseudopotentials with the Perdew-Berke-Ernzerhof (PBE) exchange–correlation functional, generalized gradient approximation,37 and a 13 × 13 × 3 k-point Monkhorst–Pack grid.38 The kinetic energy cut-offs of 60 and 480 Ry were used for the wavefunctions and charge density, respectively. The convergence criterion of the self-consistent field (SCF) procedure was set to 1.0 × 10−6 Ry. A 20-angstrom-thick vacuum in the out-of-plane direction was used to avoid any interlayer interactions. Each system was initially relaxed until the magnitude of the residual Hellmann–Feynman force on each atom was less than 0.001 Ry per bohr.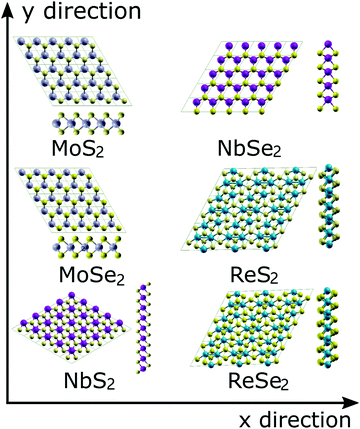 | ||
| Fig. 1 Atomic topologies and the unit cells for the six examined TMDs. The two defomation directions (x and y) are also illustrated by arrows. | ||
To simulate the uniaxial and biaxial tension, the unit cells illustrated in Fig. 1 were subjected to different magnitudes of uniaxial or equal-biaxial strains (see Fig. 1 for cell orientation). Strains were applied by dilating the unit cells along the x or y directions and then applying an equal affine transformation to all atomic positions. The deformed unit cell was then subjected to an energy minimization routine to obtain its ground state configuration under the given boundary conditions. The UTS of the resultant stress–strain curve is the ideal strength of the TMD, and the corresponding strain is the fracture strain. To obtain stress values in 2D terms with units N/m, we multiply the UTS by the thickness of each TMD, which is the thickness of each monolayer TMD structure plus the gap between two TMD layers (∼3 Å39) determined by van der Waals interaction.
3. Results and discussion
3.1 Stress–strain responses
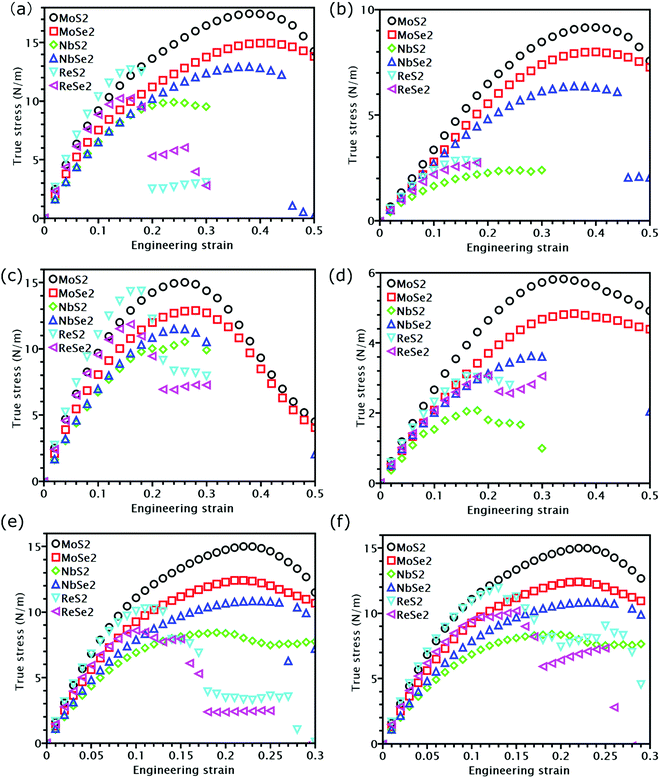
The knowledge of mechanical properties not only provides physical insights into the nature of covalent bond interactions in TMD monolayers, but is also essential for practical applications of TMDs in modern technology. The true stress versus engineering strain responses for the six TMDs are shown in Fig. 2. At strains smaller than approximately 5%, a linear stress–strain relationship is valid for all TMDs. At strains larger than 5%, all stress–strain curves become nonlinear. For TMDs such as MoS2 and MoSe2, strain softening levels off the stress–strain curve gradually until the UTS point, after which mechanical instability occurs. However, ReS2, ReSe2, NbS2, and NbSe2 undergo brittle fracture with a sudden drop in stress magnitudes. MoS2 and MoSe2 exhibit higher UTS and larger failure strain than ReS2 and ReSe2, combining both high strength and high facture strain.Linear mechanical properties, such as elastic constants C11, C22, C12, and C66, are readily calculated from the initial slopes of different stress–strain responses of TMDs. Since C22 is approximately equal to C11, the 2D layer modulus, a quantity that represents the resistance of a nanosheet to stretching, can be calculated as40
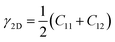 | (1) |
Other linear mechanical properties, such as Young's modulus (E), Poisson's ratio (ν), and shear modulus (G), can be obtained using the following expressions:
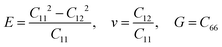 | (2) |
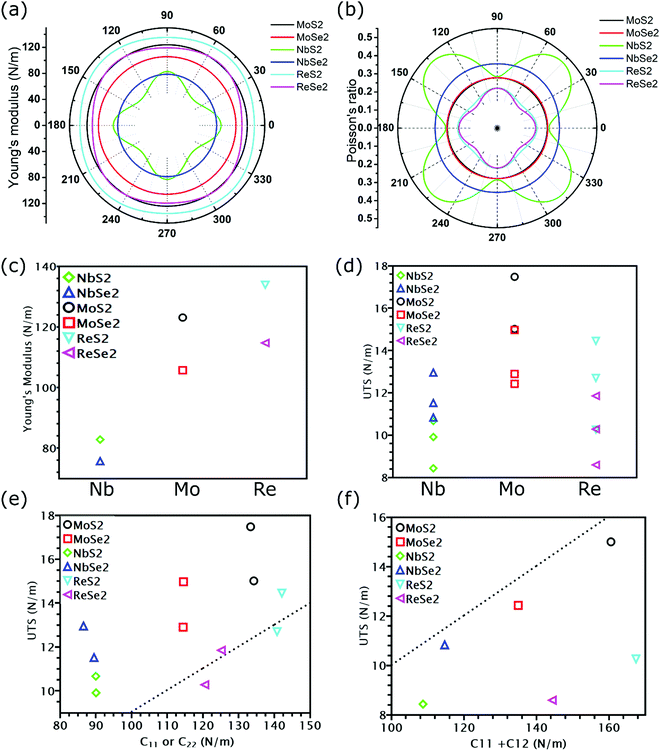
All calculated linear mechanical properties for the six TMDs are listed in Table 1. Our data are in excellent agreement with the reported values in the literature from theoretical and experimental studies.41,42 Compared with graphene,43 all TMDs have smaller elastic constants, Young's modulus, shear modulus, and 2D layer modulus, indicating weaker covalent bonds in TMDs. Although the elements in TMDs have more protons in their nuclei than carbon atoms, the larger atomic radii and stronger shielding effect due to more inner electrons diminish the attraction between the outermost electrons and the nuclei. This weakening effect can be quantified by the first ionization energies of different elements, which have the following order: C(1086 kJ mol−1) > S(999 kJ mol−1) > Se(941 kJ mol−1) > Re(760 kJ mol−1) > Mo(684 kJ mol−1) > Nb(652 kJ mol−1).44 This order explains the dependence of the Young's modulus of TMDs on their chemical components: given the same non-metallic elements, the Young's modulus of TMDs increases as the transition metal goes from the V to VII group (Fig. 3(c)); given the same metallic elements, the TMD containing S atoms has larger Young's modulus than that having Se atoms.
| MoS2 | MoSe2 | NbS2 | NbSe2 | ReS2 | ReSe2 | Graphene41 | |
|---|---|---|---|---|---|---|---|
| C 11 | 133.36 | 114.56 | 90.09 | 86.58 | 140.77 | 120.55 | 359 |
| C 12 | 37.05 | 31.89 | 25.61 | 30.74 | 31.12 | 26.55 | 65.1 |
| UTSx | 17.48 | 14.97 | 9.91 | 12.95 | 12.7 | 10.28 | 31.2 |
| ε x | 0.39 | 0.41 | 0.23 | 0.37 | 0.16 | 0.15 | 0.23 |
| C 22 | 134.26 | 114.5 | 90.03 | 89.53 | 142.11 | 125.17 | 359 |
| C 21 | 36.15 | 30.59 | 22.12 | 28.47 | 31.74 | 25.61 | 65.1 |
| UTSy | 15.01 | 12.89 | 10.67 | 11.52 | 14.45 | 11.85 | 29.3 |
| ε y | 0.26 | 0.27 | 0.23 | 0.25 | 0.17 | 0.16 | 0.18 |
| UTSxbiax | 15.00 | 12.42 | 8.43 | 10.83 | 10.26 | 8.59 | 33.2 |
| E x biax | 160.57 | 135.04 | 108.74 | 114.71 | 167.48 | 144.39 | 418 |
| UTSybiax | 15 | 12.41 | 8.41 | 10.83 | 11.93 | 15.67 | 33.2 |
| E y biax | 160.54 | 134.98 | 111.79 | 116.11 | 170.58 | 151.37 | 418 |
| ε biax | 0.23 | 0.22 | 0.19 | 0.25 | 0.12 | 0.09 | 0.23 |
| G | 48.6 | 41.13 | 18.65 | 28.08 | 59.42 | 53.53 | 147 |
| γ 2D | 85.21 | 73.23 | 57.85 | 58.66 | 85.95 | 73.55 | 212 |
| E | 123.07 | 105.68 | 82.81 | 75.67 | 133.89 | 114.70 | 347 |
| ν | 0.28 | 0.28 | 0.28 | 0.36 | 0.22 | 0.22 | 0.18 |
| D (eV) | 6.8 | 5.84 | 4.59 | 4.41 | 7.17 | 6.14 | 1.2 |
| ε c·L2 | 34.94 | 34.95 | 35.06 | 36.86 | 33.87 | 33.86 | 2.2 |
Except in-plane deformation, we also investigated the bending modulus (D) for a 2D nanosheet45
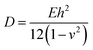 | (3) |
Once knowing D and E, we can study the buckling phenomenon and estimate the critical buckling strain (εc) using Euler's buckling theorem45
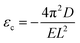 | (4) |
As listed in Table 1, given the same length L, the critical buckling strain for TMDs can be ten times larger than that for graphene due to a larger D and smaller E. Hence, compared to monolayer graphene, TMDs are more robust for in-plane structural deformations and are more resistant to buckling.
Next, we investigated the direction dependent Young modulus E(θ) and Poisson's ratio ν(θ) along an arbitrary in-plane direction θ (θ is the angle relative to the x direction); both can be expressed by elastic constants as follows47
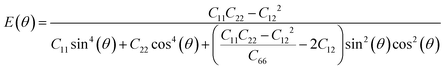 | (5) |
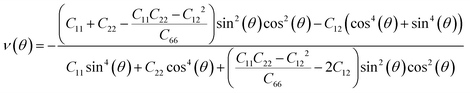 | (6) |
As shown in Fig. 3(a) and (b), TMDs with hexagonal structures, such as MoS2, MoSe2 and NbSe2, are approximately isotropic: their E(θ) and ν(θ) are independent of angular variation. ReS2 and ReSe2 exhibit slight anisotropic behaviors: their E(θ) peaks are at an angle of 45 degrees with respect to the x-uniaxial loading direction. The θ corresponding to the largest modulus also shows the smallest Poisson's ratio. NbS2 shows the strongest anisotropic behavior; its E(θ) reaches the maximum in x and y directions, where its Poisson's ratio reaches minimum.
At last, we studied nonlinear mechanical properties such as UTS and failure strain for the six examined TMDs under different loading methods. Compared with graphene,43 all TMDs have lower UTS, but some TMDs show higher failure strain. Specifically, the failure strain of MoS2 and MoSe2 could even reach 0.4 in uniaxial tension. Nonetheless, previous research found that MoS2 can fracture before reaching the UTS point due to phonon instability.26 The actual fracture strength corresponding to phonon instability, however, is still close to the apparent UTS26 because the slope of the stress–strain curves is close to zero near the UTS point. Thus, the UTS listed in Table 1 can still be utilized as an approximate fracture strength even when phonon instability is considered. Due to their importance in strain engineering, the UTS and its relationship with the modulus of the six examined TMDs will be discussed in detail in the following section.
3.2 The Griffth's strength limit of TMDs
Instead of directly obtaining UTS from stress–strain curves, we can also estimate the ideal strength of TMDs as E/10, where E is the Young's modulus.29 Such an approximation of UTS is known as Griffth's strength limit. Despite being widely used to estimate the ideal strength of brittle materials, this limit is not suitable for all TMDs. For example, for TMDs with the same non-metallic elements, their moduli were found to increase as the transition metal goes from the V to VII group (Fig. 3(c)). However, MoS2 and MoSe2, despite having smaller Young's modulus than ReS2 and ReSe2, exhibit higher UTS (Fig. 3(d)). Thus, E/UTS for ReS2 and ReSe2 is around 11, while that for MoS2 and MoSe2 is approximately 7. These results indicate that it could be possible for TMDs to overcome the Griffth's strength limit.However, our previous research34 has found that Young's modulus equals the slope of the stress–strain curve only in uniaxial tension with a free-boundary condition in the lateral direction, while in our DFT simulations, a fixed boundary condition is applied. Thus, instead of relating UTS with Young's modulus, we plotted the UTS in uniaxial tension with C11 and UTS in biaxial tension with C11 + C12 in Fig. 3(e) and (f), respectively. As shown in Fig. 3(e), except for two uniaxial tensions of ReS2 and ReSe2, the UTS of all TMDs is above the dash line corresponding to C11/UTS = 10, indicating that the UTS of most TMDs is larger than C11/10. However, for biaxial tension, the UTS of all TMDs is below the dash line, with values smaller than (C11 + C12)/10 (Fig. 3(f)). Previous research has found that the reduction of the ratio between modulus and UTS is attributed to less contribution from bond rotation in biaxial tension,34 but these work only focus on graphene allotropes, while the influence of chemical components could also be essential in TMDs. In the next section, we will discuss the mechanical properties of covalent bonds formed by different elements.
3.3 Mechanical properties of covalent bonds in TMDs
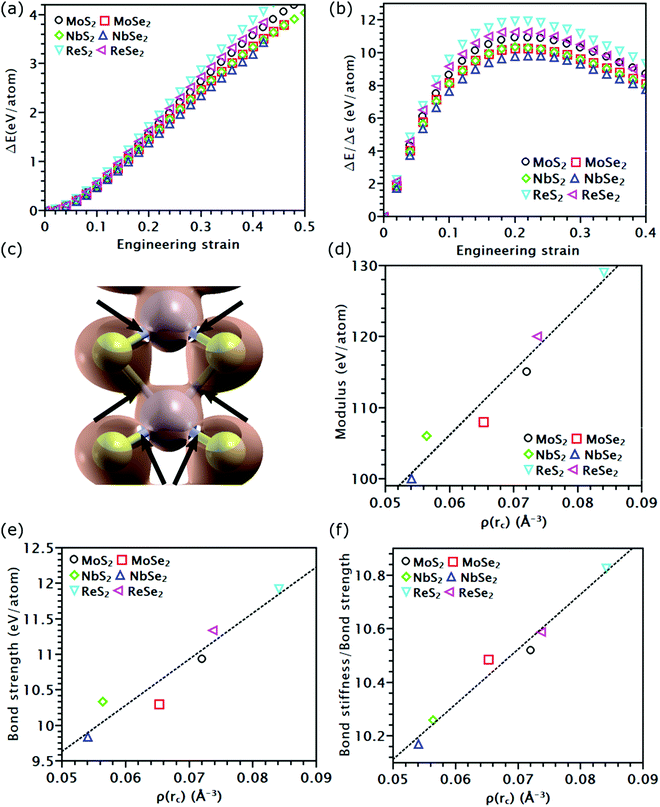
As discussed above, the influence of chemical components on the mechanical properties of different covalent bonds in TMDs remain unexplored. It is possible that some TMDs may be composed of covalent bonds whose strengths S deviates from K/10, where K is the bond stiffness. As a result, the TMD composed of such weaker bonds could have UTS smaller than E/10. To verify this assumption, we applied volumetric expansion to the unit cell of all the six examined TMDs, so only bond stretch is allowed to accommodate the deformation. The distance between all atoms was equally increased while all bond angles remained unchanged. The corresponding energy increase per atom, e(ε), obtained by self-consistent field (SCF) calculations in DFT, was only due to bond stretch (Fig. 4(a)). The force required to stretch all covalent bonds was calculated as the increasing rate of e(ε) with the applied strain, P(ε) = de(ε)/dε.Like the stress–strain responses of TMDs, the bond-force-versus-bond-strain responses are nonlinear (Fig. 4(b)), reaching the maximum strength (S) and then levelling off. Herein, bond stiffness, K, is calculated as 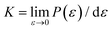 . Despite their difference in K and S, all bonds fracture at approximately the same tensile strain (Table 2). According to our hypothesis, K/S should be lower than 10 for some bonds. However, the values of K/S for all covalent bonds follow the same linear relationship, S ≈ K/10, a result consistent with the Griffth's strength limit.
. Despite their difference in K and S, all bonds fracture at approximately the same tensile strain (Table 2). According to our hypothesis, K/S should be lower than 10 for some bonds. However, the values of K/S for all covalent bonds follow the same linear relationship, S ≈ K/10, a result consistent with the Griffth's strength limit.
| K (eV) | S (eV) | Fracture strain | K/S | ρ(rC) (Å−3) | |
|---|---|---|---|---|---|
| MoS2 | 115 | 10.93 | 0.21 | 10.52 | 0.072 |
| MoSe2 | 108 | 10.3 | 0.21 | 10.48 | 0.065 |
| NbS2 | 106 | 10.33 | 0.2 | 10.26 | 0.056 |
| NbSe2 | 100 | 9.83 | 0.23 | 10.17 | 0.054 |
| ReS2 | 129 | 11.92 | 0.21 | 10.83 | 0.084 |
| ReSe2 | 120 | 11.33 | 0.2 | 10.59 | 0.078 |
To understand the physical insight behind the nearly identical K/S of all the tested covalent bonds, we analyzed the charge density distribution along these bonds. When covalent bonds form,48–50 charge density ρ(r) accumulates along the bond path. The mutual boundary between two atomic volumes intersects this bond path at a saddle point rC (Fig. 4(c)). The charge density at this point, ρ(rC), was found to follow a linear relationship with K (Fig. 4(d)) and S (Fig. 4(e)). This observation is consistent with prior findings that ρ(rC) is proportional to the force exerted on the bonding electrons by the nuclei.51 For covalent bonds with the same non-metallic elements, their ρ(rC), as well as K and S, increases as the metallic element goes from the V to VII group. As the group number increases, the transition metal element has more electrons on the first or second shell; both can contribute to the formation of covalent bonds, thereby increasing ρ(rC). Given the same metallic element, covalent bonds containing Se atoms have lower ρ(rC) than that containing S atoms, reducing their K and S (Fig. 4(e)). This reduction is because compared to Se atoms, sulfur atoms have higher electronegativity, thereby forming a stronger bond with higher ρ(rC). As both K and S follow a linear relationship with ρ(rC), the ratio K/S should also increase linearly with ρ(rC) (Fig. 4(f)). Nonetheless, such increment is negligible, rising only from 10.2 of NbSe2 to 10.8 of ReS2. Thus, K/S of all the tested covalent bonds can still be treated as a constant. However, compared to the other four TMDs, ReS2 and ReSe2 have stronger covalent bonds but inferior UTS. This inconsistency indicates that the UTS of TMD mainly depends on the topological atomic arrangements rather than their chemcial components.
3.4 Bond rotation during the deformation of TMDs
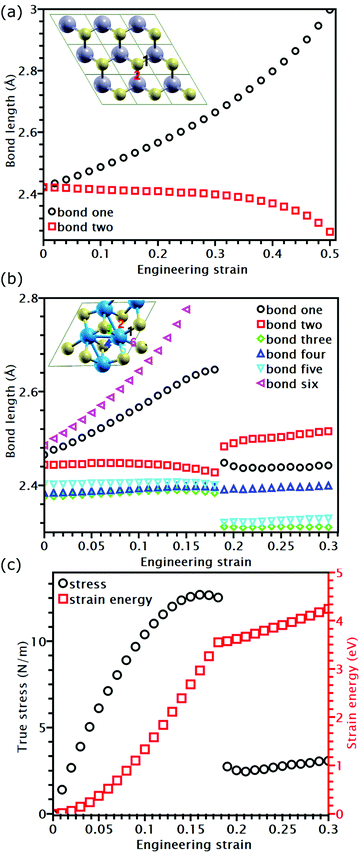
While the covalent bonds in TMDs fracture at a strain of approximately 0.2 (Table 2), the apparent fracture strain of MoSe2 and MoS2 can even reach 0.4 (Table 1). According to previous research, atomic bonds close to the loading direction are more susceptible to fracture.34,35,52 However, this mechanism cannot explain why the fracture strain of most TMDs at the UTS point is larger than the bond breaking strain. Furthermore, the Griffth's strength limit predicts that a structure with a high modulus should also have a high ideal strength. This is not the case for ReS2 and ReSe2, which have larger moduli than MoSe2 and MoS2 but lower strengths. These phenomena indicate that the failure of TMDs cannot be elucidated only based on bond breaking but should also consider their different topological atomic arrangements.As shown in Fig. 5(a), MoS2 has only two bond orientations, so half of their bonds are stretched and rotated in uniaxial tension. Since bond rotation also undertakes part of the external deformation, the failure strain can be much larger than the bond fracture strain. However, for ReS2 and ReSe2, their covalent bonds have multiple lengths and directions; therefore, only the bonds lying close to the loading direction and having largest bond lengths are stretched during deformation. For example, as shown in Fig. 5(b), for all the six bonds connected to a Re atom in the unit cell of ReS2, only two of them are elongated, while other bonds are unstretched. Due to the strain-softening effect, the stretched bonds are easier to be further elongated, so the applied deformation is mainly undertaken by the two stretched bonds. Due to such strain concentration, when the longest bond reaches its failure strain, the engineering strain of the overall structure is smaller than the failure strain of the broken bond. After the longest bond is broken, further elongation stretches the remaining bonds. This transition in deformation mechanism results in a non-differentiable point on the energy-strain relation (Fig. 5(c)) and a sudden stress drop of the stress–strain curve. Our results indicate that reducing the variety of bond orientations can increase the failure strain of TMD structures.
4. Conclusions
In this work, we performed extensive DFT calculations to evaluate the mechanical properties of six TMDs (MoS2, MoSe2, NbS2, NbSe2, ReS2, ReSe2). Our results confirm that the modulus of TMDs increases when the transition metal goes from the V to VII group, or the electronegativity of the non-metallic atoms increases. However, a high modulus does not guarantee a high ideal strength. In particular, ReS2 and ReSe2 have higher modulus but lower strength than MoS2, MoSe2 and NbS2, violating the Griffth's strength limit—a linear relationship between the Young's modulus and ideal strength. This violation is not attributed to different chemical components, as our charge-density analysis found that the bond strength (S) and bond stiffness (K) of all the covalent bonds in the six examined TMDs obey a linear relationship with the charge density at the bond saddle point, resulting in S ≈ K/10 suitable for all covalent bonds regardless of their chemical components. However, for TMDs having multiple bond orientations, such as ReS2 and ReSe2, different bonds are stretched differently during deformation. Due to the strain-softening effect, these bonds undertaken a larger strain are prone to be further elongated at high strain values. Thus, the deformation is concentrated mainly on these stretched bonds, diminishing the failure strain of the whole structure. Thus, our findings suggest that reducing the variety of bond orientations can increase the failure strain of TMD structures without severe degradation of strength.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Financial support for this work was also provided through the Natural Sciences and Engineering Research Council of Canada (NSERC), the Ontario Research Fund (ORF), Ontario Graduate Scholarship (OGS), and the Mitacs Accelerate Scholarships. Chandra Veer Singh is an Erwin Edward Hart Endowed Professor of Materials Science & Engineering–we acknowledge financial support of the Hart fund. The computational resources were provided by the SciNet consortium through the Compute Canada resource allocations.References
- M. S. Jang, H. Kim, Y.-W. Son, H. A. Atwater and W. A. Goddard, Graphene field effect transistor without an energy gap, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 8786–8789 CrossRef CAS PubMed.
- C.-H. Chang, X. Fan, S.-H. Lin and J.-L. Kuo, Orbital analysis of electronic structure and phonon dispersion in MoS2, MoSe2, WS2, and WSe2 monolayers under strain, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 195420 CrossRef.
- H. R. Gutiérrez, N. Perea-López, A. L. Elías, A. Berkdemir, B. Wang, R. Lv, F. López-Urías, V. H. Crespi, H. Terrones and M. Terrones, Extraordinary Room-Temperature Photoluminescence in Triangular WS2 Monolayers, Nano Lett., 2013, 13, 3447–3454 CrossRef PubMed.
- K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Atomically Thin MoS2: A New Direct-Gap Semiconductor, Phys. Rev. Lett., 2010, 105, 136805 CrossRef PubMed.
- B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Single-layer MoS2 transistors, Nat. Nanotechnol., 2011, 6, 147–150 CrossRef CAS PubMed.
- R. Ganatra and Q. Zhang, Few-Layer MoS2: A Promising Layered Semiconductor, ACS Nano, 2014, 8, 4074–4099 CrossRef CAS PubMed.
- A. Ramasubramaniam, Large excitonic effects in monolayers of molybdenum and tungsten dichalcogenides, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 115409 CrossRef.
- K. F. Mak, K. He, C. Lee, G. H. Lee, J. Hone, T. F. Heinz and J. Shan, Tightly bound trions in monolayer MoS2, Nat. Mater., 2013, 12, 207–211 CrossRef CAS PubMed.
- A. Rawat, N. Jena, D. Dimple and A. De, Sarkar, A comprehensive study on carrier mobility and artificial photosynthetic properties in group VI B transition metal dichalcogenide monolayers, J. Mater. Chem. A, 2018, 6, 8693–8704 RSC.
- O. Lopez-Sanchez, D. Lembke, M. Kayci, A. Radenovic and A. Kis, Ultrasensitive photodetectors based on monolayer MoS2, Nat. Nanotechnol., 2013, 8, 497–501 CrossRef CAS PubMed.
- K. He, C. Poole, K. F. Mak and J. Shan, Experimental Demonstration of Continuous Electronic Structure Tuning via Strain in Atomically Thin MoS2, Nano Lett., 2013, 13, 2931–2936 CrossRef CAS PubMed.
- A. Castellanos-Gomez, R. van Leeuwen, M. Buscema, H. S. J. van der Zant, G. A. Steele and W. J. Venstra, Single-Layer MoS2 Mechanical Resonators, Adv. Mater., 2013, 25, 6719–6723 CrossRef CAS PubMed.
- C. V. Nguyen, V. V. Ilyasov, H. V. Nguyen and H. N. Nguyen, Band gap and electronic properties of molybdenum disulphide under strain engineering: density functional theory calculations, Mol. Simul., 2017, 43, 86–91 CrossRef CAS.
- M. G. Sensoy, D. Vinichenko, W. Chen, C. M. Friend and E. Kaxiras, Strain effects on the behavior of isolated and paired sulfur vacancy defects in monolayer MoS2, Phys. Rev. B, 2017, 95, 014106 CrossRef CAS.
- P. Lu, X. Wu, W. Guo and X. C. Zeng, Strain-dependent electronic and magnetic properties of MoS2 monolayer, bilayer, nanoribbons and nanotubes, Phys. Chem. Chem. Phys., 2012, 14, 13035 RSC.
- M. Ghorbani-Asl, S. Borini, A. Kuc and T. Heine, Strain-dependent modulation of conductivity in single-layer transition-metal dichalcogenides, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 235434 CrossRef.
- E. Scalise, M. Houssa, G. Pourtois, V. Afanas’ev and A. Stesmans, Strain-induced semiconductor to metal transition in the two-dimensional honeycomb structure of MoS2, Nano Res., 2012, 5, 43–48 CrossRef CAS.
- S. Deng, L. Li and M. Li, Stability of direct band gap under mechanical strains for monolayer MoS2, MoSe2, WS2 and WSe2, Phys. E, 2018, 101, 44–49 CrossRef CAS.
- T. Zhu and J. Li, Ultra-strength materials, Prog. Mater. Sci., 2010, 55, 710–757 CrossRef.
- S. Bertolazzi, J. Brivio and A. Kis, Stretching and Breaking of Ultrathin MoS2, ACS Nano, 2011, 5, 9703–9709 CrossRef CAS PubMed.
- S. Xiong and G. Cao, Molecular dynamics simulations of mechanical properties of monolayer MoS2, Nanotechnology, 2015, 26, 185705 CrossRef PubMed.
- G. Casillas, U. Santiago, H. Barrón, D. Alducin, A. Ponce and M. José-Yacamán, Elasticity of MoS2 Sheets by Mechanical Deformation Observed by in Situ Electron Microscopy, J. Phys. Chem. C, 2015, 119, 710–715 CrossRef CAS PubMed.
- D.-M. Tang, D. G. Kvashnin, S. Najmaei, Y. Bando, K. Kimoto, P. Koskinen, P. M. Ajayan, B. I. Yakobson, P. B. Sorokin, J. Lou and D. Golberg, Nanomechanical cleavage of molybdenum disulphide atomic layers, Nat. Commun., 2014, 5, 3631 CrossRef PubMed.
- J. Zhao, J.-W. Jiang and T. Rabczuk, Temperature-dependent mechanical properties of single-layer molybdenum disulphide: Molecular dynamics nanoindentation simulations, Appl. Phys. Lett., 2013, 103, 231913 CrossRef.
- J.-W. Jiang, H. S. Park and T. Rabczuk, Molecular dynamics simulations of single-layer molybdenum disulphide (MoS 2): Stillinger-Weber parametrization, mechanical properties, and thermal conductivity, J. Appl. Phys., 2013, 114, 064307 CrossRef.
- T. Li, Ideal strength and phonon instability in single-layer MoS2, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235407 CrossRef.
- P. Hess, Relationships between the elastic and fracture properties of boronitrene and molybdenum disulfide and those of graphene, Nanotechnology, 2017, 28, 064002 CrossRef PubMed.
- J. Kang, H. Sahin and F. M. Peeters, Mechanical properties of monolayer sulphides: a comparative study between MoS2, HfS2 and TiS3, Phys. Chem. Chem. Phys., 2015, 17, 27742–27749 RSC.
- P. Hess, Predictive modeling of intrinsic strengths for several groups of chemically related monolayers by a reference model, Phys. Chem. Chem. Phys., 2018, 20, 7604–7611 RSC.
- Y.-J. Zhang, R.-N. Wang, G.-Y. Dong, S.-F. Wang, G.-S. Fu and J.-L. Wang, Mechanical properties of 1T -, 1T′-, and 1H-MX2 monolayers and their 1H/1T′-MX2 (M = Mo, W and X = S, Se, Te) heterostructures, AIP Adv., 2019, 9, 125208 CrossRef.
- N. K. Nepal, L. Yu, Q. Yan and A. Ruzsinszky, First-principles study of mechanical and electronic properties of bent monolayer transition metal dichalcogenides, Phys. Rev. Mater., 2019, 3, 073601 CrossRef CAS.
- W. Shi and Z. Wang, Mechanical and electronic properties of Janus monolayer transition metal dichalcogenides, J. Phys.: Condens. Matter, 2018, 30, 215301 CrossRef PubMed.
- D. M. Guzman and A. Strachan, Role of strain on electronic and mechanical response of semiconducting transition-metal dichalcogenide monolayers: An ab initio study, J. Appl. Phys., 2014, 115, 243701 CrossRef.
- H. Sun, S. Mukherjee, Z. Shi and C. V. Singh, Elastomer-like deformation in high-Poisson's-ratio graphene allotropes may allow tensile strengths beyond theoretical cohesive strength limits, Carbon, 2019, 143, 752–761 CrossRef CAS.
- H. Sun, S. Mukherjee, M. Daly, A. Krishnan, M. H. Karigerasi and C. V. Singh, New insights into the structure-nonlinear mechanical property relations for graphene allotropes, Carbon, 2016, 110, 443–457 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- J. A. Stewart and D. E. Spearot, Atomistic simulations of nanoindentation on the basal plane of crystalline molybdenum disulfide (MoS2), Modell. Simul. Mater. Sci. Eng., 2013, 21, 045003 CrossRef CAS.
- R. C. Andrew, R. E. Mapasha, A. M. Ukpong and N. Chetty, Mechanical properties of graphene and boronitrene, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125428 CrossRef.
- S. Singh, C. Espejo and A. H. Romero, Structural, electronic, vibrational, and elastic properties of graphene/MoS2 bilayer heterostructures, Phys. Rev. B, 2018, 98, 155309 CrossRef CAS.
- M. K. Mohanta and A. De, Sarkar, Interfacial hybridization of Janus MoSSe and BX (X = P, As) monolayers for ultrathin excitonic solar cells, nanopiezotronics and low-power memory devices, Nanoscale, 2020, 12, 22645–22657 RSC.
- X. Wei, B. Fragneaud, C. A. Marianetti and J. W. Kysar, Nonlinear elastic behavior of graphene: Ab initio calculations to continuum description, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205407 CrossRef.
- P. F. Lang and B. C. Smith, Ionization Energies of Atoms and Atomic Ions, J. Chem. Educ., 2003, 80, 938 CrossRef CAS.
- J.-W. Jiang, Graphene versus MoS2: A short review, Front. Phys., 2015, 10, 287–302 CrossRef.
- Z. Tu and Z. Ou-Yang, Single-walled and multiwalled carbon nanotubes viewed as elastic tubes with the effective Young's moduli dependent on layer number, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 233407 CrossRef.
- E. Cadelano and L. Colombo, Effect of hydrogen coverage on the Young’s modulus of graphene, Phys. Rev. B, 2012, 85, 245434 CrossRef.
- R. F. W. Bader, A quantum theory of molecular structure and its applications, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- R. F. W. Bader, From Schrodinger to atoms in molecules, Pure Appl. Chem., 1988, 60(2), 145–155 CAS.
- R. F. W. Bader and H. Essén, The characterization of atomic interactions, J. Chem. Phys., 1984, 80, 1943–1960 CrossRef CAS.
- D. Cremer and E. Kraka, A description of the chemical bond in terms of local properties of electron density and energy, Croat. Chem. Acta, 1984, 57(6), 1259–1281 Search PubMed.
- H. Sun, S. Mukherjee and C. V. Singh, Mechanical properties of monolayer penta-graphene and phagraphene: a first-principles study, Phys. Chem. Chem. Phys., 2016, 18, 26736–26742 RSC.
| This journal is © The Royal Society of Chemistry 2021 |