Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Metal cation s lone-pairs increase octahedral tilting instabilities in halide perovskites†
Lingyuan
Gao‡
 *a,
Lena
Yadgarov‡
*a,
Lena
Yadgarov‡
 *b,
Rituraj
Sharma
b,
Roman
Korobko
b,
Kyle M.
McCall
*b,
Rituraj
Sharma
b,
Roman
Korobko
b,
Kyle M.
McCall
 c,
Douglas H.
Fabini
c,
Douglas H.
Fabini
 d,
Constantinos C.
Stoumpos
d,
Constantinos C.
Stoumpos
 e,
Mercouri G.
Kanatzidis
e,
Mercouri G.
Kanatzidis
 c,
Andrew M.
Rappe
c,
Andrew M.
Rappe
 a and
Omer
Yaffe
a and
Omer
Yaffe
 b
b
aDepartment of Chemistry, University of Pennsylvania, Philadelphia, Pennsylvania 19104-6323, USA. E-mail: rappe@sas.upenn.edu
bDepartment of Chemical and Biological Physics, Weizmann Institute of Science, Rehovot 76100, Israel. E-mail: omer.yaffe@weizmann.ac.il
cDepartment of Chemistry, Northwestern University, Evanston, Illinois 60208, USA
dMax Planck Institute for Solid State Research, Stuttgart 70569, Germany
eDepartment of Materials Science and Technology, University of Crete, Voutes Campus, Heraklion 70013, Greece
First published on 28th June 2021
Abstract
Halide perovskites exhibit beneficial opto-electronic properties (e.g. long carrier lifetimes and low defect densities), and their dynamic structural instabilities and anharmonic thermal fluctuations are directly implicated in these properties. In this work, we combine in-depth analysis of Raman spectroscopy and ab initio calculations to uncover the critical roles of Group 14 M2+ (M = Pb, Sn, Ge) metal cation s orbital lone pairs in the dynamic instabilities of CsMBr3 and particularly in governing the octahedral tilting. Previous studies concluded that the lone-pair stereochemical activity primarily leads to the off-centering motion of the metal cation, and the tilting is usually ascribed to ionic size effects. Here, we show that the lone-pair stereochemical activity contributes to strong octahedral tilting instabilities that induce liquid-like behavior in all examined crystals, which underlies the robustness of halide perovskites to charged defects. In addition, the lone-pairs induce a local, molecule-like behavior of the Ge2+ with a pyramidal bonding motif in the cubic phase, and they contribute to another phase transition of CsSnBr3 at 60 K. Our findings elucidate the fundamental origin of anharmonicities in halide perovskites and provide the crucial link between chemical composition and optoelectronic properties, opening opportunities for lead-free and solution-processable photovoltaics.
Introduction
Halide perovskites (HPs) are extensively studied as potential replacements for the traditional photovoltaic materials.1 Lead-based HPs have demonstrated solar power conversion efficiencies surpassing 25% in thin films and 29% in tandem cells with Si.2 This motivates recent efforts to develop new photovoltaic cells that are based on nontoxic perovskite halides, where Pb2+ is replaced with Sn2+ and/or Ge2+.3–7From a fundamental standpoint, the fascinating opto-electronic properties of HPs are closely related to their highly anharmonic thermal motions that lead to local, polar fluctuations and thus, localization of charge carriers.8–11,75 The perovskite crystal (with stoichiometry AMX3) consists of a three-dimensional network of corner-sharing MX6 octahedra, with A-site cations occupying the cuboctahedral voids. The high connectivity allows for various lower-symmetry phases, characterized by tilting of the octahedra, making HPs capable of accommodating a wide range of compositions.12,13 This compositional flexibility enables a plethora of phenomena, tuned by competing short- and long–range anharmonic couplings, leading to polar, magnetic, and tilting phase transitions.14–18
Geometric or ionic (hard sphere packing) models, which are based only on the sizes of the constituent ions (rA,M,X), hold great predictive power for whether a perovskite will form.19–23 The tolerance factor, 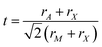 of Goldschmidt19 is the most successful geometric parameter for perovskite prediction: if t > 1, then the A-site cation is too large to fit in the MX6 cuboctahedral cavities, and that disfavors the formation of a perovskite. If t < 1, then the A-site cation is relatively small for the interstitial region between octahedra, and so the corner-sharing octahedra tilt to fill the space. Following different tilting patterns, many low-symmetry structures can be formed due to this tilting instability.21–31 The tilting can also be dynamic, resulting in structural fluctuations.8,9,14,32–36 When t is too low, the corner-sharing octahedra prefer to rearrange into edge-sharing or face-sharing octahedra,37 taking the system away from the perovskite structure. In addition to t, the octahedral factor μ = rM/rX is another important geometric factor. According to Pauling's first rule,20μ should be large enough to guarantee that the M cation makes contact with all surrounding X anions. Recent studies construct structural maps vs. t and μ and correctly categorize oxides and halides as perovskites or non-perovskites at room temperature.38–42
of Goldschmidt19 is the most successful geometric parameter for perovskite prediction: if t > 1, then the A-site cation is too large to fit in the MX6 cuboctahedral cavities, and that disfavors the formation of a perovskite. If t < 1, then the A-site cation is relatively small for the interstitial region between octahedra, and so the corner-sharing octahedra tilt to fill the space. Following different tilting patterns, many low-symmetry structures can be formed due to this tilting instability.21–31 The tilting can also be dynamic, resulting in structural fluctuations.8,9,14,32–36 When t is too low, the corner-sharing octahedra prefer to rearrange into edge-sharing or face-sharing octahedra,37 taking the system away from the perovskite structure. In addition to t, the octahedral factor μ = rM/rX is another important geometric factor. According to Pauling's first rule,20μ should be large enough to guarantee that the M cation makes contact with all surrounding X anions. Recent studies construct structural maps vs. t and μ and correctly categorize oxides and halides as perovskites or non-perovskites at room temperature.38–42
Notably, these geometric models represent an ionic limit and contain no information about covalent bonding. Therefore, they sometimes fail to predict the correct structural phase evolution of compounds with certain electron configurations and bonding preferences.43,44 Heavier halogen ions have lower electronegativity and stronger covalency, reducing the accuracy and applicability of the hard-sphere ionic models.38–41 Furthermore, main-group cations in lower oxidation states (e.g. Pb2+, Sn2+, Ge2+) retain their outermost s electrons as a nonbonded lone pair.45–48 This lone pair occupies space, behaves like an additional ligand, and is said to be stereochemically active. Acentric distortions of the coordination environments induced by such lone-pair cations allow an energetically favorable mixing with the ligand (anion) orbitals which is symmetry-forbidden in the undistorted state.49–53 In oxides such as PbTiO3, Pb(Zr1−xTix)O3, lone-pair cations reside on the A site. The large polar displacements of A cations caused by lone-pair effects give rise to the large polarization and giant piezoelectric responses.54–58 In HPs, they occupy the M site, and significant M off-centering motions are observed experimentally and computationally.9,46,59–66 Importantly, previous studies show in HPs off-centering instabilities induced by lone-pairs and tilting instabilities can coexist and are competing with each other.67,68 The tendency for lone-pair-driven distortion is stronger for lighter cations.50 In PbTiO3-based solid solutions, the overall effects of both instabilities have been used to predict the morphotropic phase boundary (MPB) composition and the transition temperature at the MPB.69
Here, we aim to study the interplay between geometric (ionic size) and lone-pair (covalency) effects on the structural dynamics of halide perovskites. To that end, we combine Raman spectroscopy and ab initio molecular dynamics to compare the structural dynamics of CsMBr3 in their cubic (with M = Pb, Sn, and Ge) and orthorhombic (M = Pb, Sn) phases. This chemical series tunes both the energy scale of the lone-pair-driven distortions and the relative ionic sizes which are the basis for the geometric models. Therefore, changing the central M cation provides an excellent means of establishing the relative importance of concurrent size and covalence effects in the structural dynamics of the HPs. In our analysis, we go beyond the harmonic approximation68,70 as we assign real-space motion from ab initio molecular dynamics to the experimentally observed spectral features.
Our main new finding is that the lone pair contributes significantly to octahedral tilting instabilities that go beyond what is predicted by geometric models. These fluctuations give rise to strong, diffuse inelastic light scattering that increases towards 0 cm−1 (“central peak”) that is similar to that of liquids. In addition to tilting, the strong lone-pair stereochemical activity also induces dynamic Ge2+ off-centering motions as dynamic fluctuations between pyramidal environments in CsGeBr3 that are uncorrelated to neighbors, leading to a molecule-like behavior. At around 60 K, in CsSnBr3 the lone pair contributes to another phase transition to lower symmetry phase. We expect these lone-pair driven structural instabilities discovered in CsMBr3 also prevail in their organic HP counterparts, which are more widely used in photovoltaics.76
Results and discussion
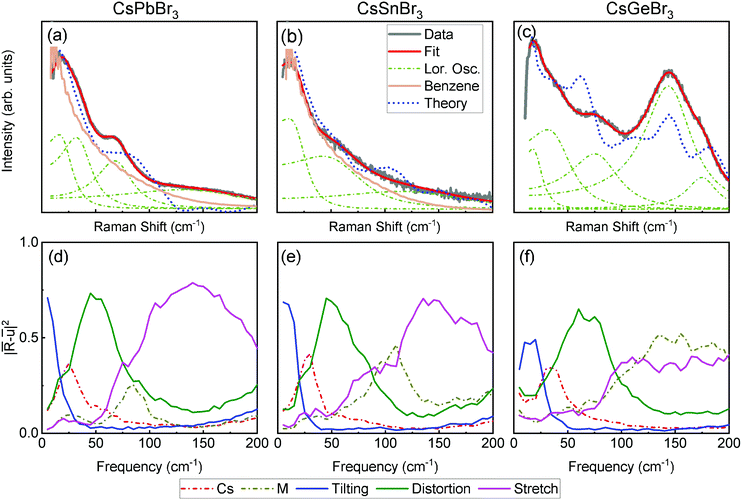
We begin our study by comparing the structural dynamics of CsPbBr3, CsSnBr3, and CsGeBr3 in their cubic phases (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, space group #221). A detailed discussion of the phase sequence, ionic size and lone-pair stereochemical activity of the three crystals is given in the section “Inadequacy of ionic size models” of ESI.† It is important to note that based on the symmetry of average structure, the crystals should be Raman inactive.71 Yet, as shown in Fig. 1(a)–(c) all three crystals show strong, first order Raman scattering. The failure of factor group analysis to predict the Raman spectra is an important indication that the thermal fluctuations of all three crystals are strongly anharmonic. The dash-and-dot lines show the spectral features that are extracted from a fit of each spectrum to the product of the Bose–Einstein distribution and a sum of damped Lorentz oscillators (see ESI† for fitting procedures).
m, space group #221). A detailed discussion of the phase sequence, ionic size and lone-pair stereochemical activity of the three crystals is given in the section “Inadequacy of ionic size models” of ESI.† It is important to note that based on the symmetry of average structure, the crystals should be Raman inactive.71 Yet, as shown in Fig. 1(a)–(c) all three crystals show strong, first order Raman scattering. The failure of factor group analysis to predict the Raman spectra is an important indication that the thermal fluctuations of all three crystals are strongly anharmonic. The dash-and-dot lines show the spectral features that are extracted from a fit of each spectrum to the product of the Bose–Einstein distribution and a sum of damped Lorentz oscillators (see ESI† for fitting procedures).
Next, we performed ab initio molecular dynamics (AIMD) at relevant temperatures (500 K, 330 K and 663 K for CsPbBr3, CsSnBr3, and CsGeBr3, respectively) and calculated dynamic Raman spectra based on AIMD trajectories (calculation details are in the Section “computational methods” of ESI†). As shown in Fig. 1, theoretical spectra well reproduce experimental Raman spectra of all the compounds.
The spectra of all three crystals consist of a broad feature increasing continuously toward 0 cm−1 superimposed by broad shoulders from 50–100 cm−1. The low-frequency broad feature is composed of over-damped Lorentz oscillators (width ≈ 50 cm−1). In that sense, their structural dynamics resemble that of a liquid. To demonstrate this point, the spectrum of benzene at room temperature is overlaid in Fig. 1(a) and (b). Contrary to CsPbBr3 and CsSnBr3, the Raman spectrum of CsGeBr3 (Fig. 1(c)) has a dominant spectral feature centered at ≈ 148 cm−1.
To elucidate the origin of Raman activity for the three perovskites, we frequency-filter the AIMD trajectories and project them onto normal-mode coordinates that are presented in Fig. 1(d)–(f). The frequency-filtering method and projection method are introduced in the Section “computational methods” of ESI.† Below 30 cm−1, for all three crystals, apart from the harmonic Cs motion, Br6 octahedral tiltings are the most dominant motions, expected for CsSnBr3 and CsPbBr3 due to their low tolerance factor (t = 0.92 and 0.86 respectively) but are surprising for CsGeBr3 that has a near ideal t (see ESI† for more details). Therefore, the tilting instabilities cannot be fully reconciled with a geometric model solely from ionic effects. Nevertheless, consistent with its near-ideal tolerance factor, the projection weight of the octahedral tilting in CsGeBr3 is lower than its counterpart in CsSnBr3 and CsPbBr3. It has been shown in CsPbF3 that the Pb lone pair can determine the tilting pattern and ground-state structure by displacing surrounding anions and modifying the A-site environments.67 The clear presence of tilting indicates that apart from ionic effects, the lone pair is another source of such instabilities.
Recent density functional theory (DFT) studies predict that in the cubic phase, tilting instabilities can only emerge in CsSnBr3 and CsPbBr3 but not in CsGeBr3.68,70 This agrees with the geometric analysis but differs from the present results. In DFT, computational analysis of phonons is generally conducted by finding the harmonic vibrations with respect to a reference structure (e.g. the highly symmetric cubic aristotype). AIMD samples the realistic, multi-dimensional potential energy surface and visits various thermally-accessible configurations dynamically. On a time scale of several hundred femtoseconds, the dynamic tilting describes the reorientation of the acentrically-distorted octahedra, and induces various and distinct polar fluctuations in different parts of the solid-which leads to the solid exhibiting spectroscopic signatures like those of a liquid (Fig. 1(a)–(c)).9,10
In the middle frequency range (50–100 cm−1), motions are dominated by Br6 distortion, and its peak is at 50 cm−1. The M motion of CsPbBr3 is also in this middle frequency range, while in CsSnBr3 and CsGeBr3 M motions are at higher frequencies, following a trend inverse to the square root of their masses. As shown in Fig. 1(a)–(c), at 70 cm−1 there are clear shoulders in CsPbBr3 and CsGeBr3, and a broader shoulder in CsSnBr3. By relating the fitted signatures in Fig. 1(a)–(c) with the peak of motions in Fig. 1(d)–(f), we find that these shoulders result from Br6 distortion-driven vibrational modes for all three crystals.
We now turn to discussing the origin of the broad and strong spectral feature that is observed only in CsGeBr3 at ≈ 148 cm−1. At high frequencies (>100 cm−1), the M–Br stretch is similar for all three crystals and is significant in a wide frequency range (magenta lines in Fig. 1(d)–(f)). However, the Raman scattering is very weak in CsPbBr3 and CsSnBr3. Therefore, we ascribe this feature to the Ge off-centering motion. We can expect that Ge will display much stronger off-centering than Pb and Sn for the following reasons related to mass, size, and bonding. First, Br is much closer in mass to Ge2+ than to Sn2+ and Pb2+, so concerted motions will have more weight on the Ge2+ cation. Second, Ge2+ is nominally too small for octahedral coordination with Br, so it can rattle within the octahedral void formed by the anions. Lastly, the Ge2+ lone pair is strongly stereochemically active, favoring a 3+3 coordination (3 short bonds, 3 long bonds; essentially a [GeBr3]− pyramid, Fig. S1, ESI†). This relationship with the pyramidal motif is further reinforced by the shape of the ≈ 148 cm−1 spectral feature in CsGeBr3, which is composed of at least two Lorentz oscillators (Fig. 1(c)). This shape is indicative of the asymmetric stretch ν3 for a pyramidal molecule with C3v symmetry which is split by the inversion doubling effect.72,73 As suggested by Thiele et al.,74 the temperature-driven rhombohedral to cubic phase transition is an order–disorder transition, where the cubic long-range ordering is given by the average of these positions but the local structure remains largely pyramidal due to the outsized stereochemical activity of the Ge2+ lone pair. The noteworthy high-frequency Raman activity in CsGeBr3 suggests dynamic fluctuations between pyramidal environments that are locally similar to the rhombohedral ground state, with significant Ge2+ displacements.
Indeed, from projections of frequency-filtered AIMD, the Ge2+ off-centering motions are markedly different from those of Pb2+ and Sn2+ (yellow trace in Fig. 1(d)–(f)). The latter two show a single-peaked feature within a narrow frequency range, revealing that the M atoms move in a harmonic and collective pattern. As a contrast, CsGeBr3 exhibits a combination of multiple peaks at different frequencies between ≈ 140–200 cm−1, indicating the Ge motion is more disordered and local on individual atom and thus the symmetry of the whole crystal has been lowered. To further demonstrate the weakly correlated Ge motion, we compute the pair-correlation function of neighbor M atoms from the AIMD trajectory as:
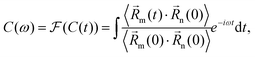 | (1) |
![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) (t) is the atomic displacement. Fig. 2 shows that at their corresponding frequencies, off-centering motions between neighboring M atoms in CsGeBr3 are less correlated than in CsSnBr3 and CsPbBr3. This indicates that the motion of the Ge2+ ion is more local and behaves like a molecule. Combined with above experimental analysis, we ascribe this high-frequency Raman activity to motion of Ge atom in its low-symmetry local environment.
(t) is the atomic displacement. Fig. 2 shows that at their corresponding frequencies, off-centering motions between neighboring M atoms in CsGeBr3 are less correlated than in CsSnBr3 and CsPbBr3. This indicates that the motion of the Ge2+ ion is more local and behaves like a molecule. Combined with above experimental analysis, we ascribe this high-frequency Raman activity to motion of Ge atom in its low-symmetry local environment.
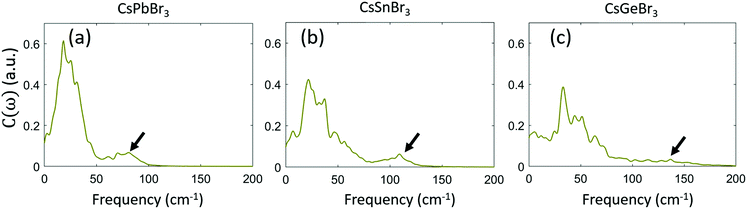 | ||
| Fig. 2 Computed pair-correlation function of neighbor M atoms in CsPbBr3, CsSnBr3, and CsGeBr3. The arrow denotes M off-centering motions according to their frequencies, identified from Fig. 1. M off-centering motion in CsGeBr3 is less correlated than in CsPbBr3 and CsSnBr3. | ||
Summarizing our findings related to the cubic phase of the crystals, we note two different dynamic fluctuations that are related to lone-pair stereochemical activities. The first is the tilting instability that is present in all crystals and results in liquid-like light scattering at low frequencies. The second is the M-cation off-centering instability that only leads to molecular-like light scattering in CsGeBr3 at high frequencies. The tilting is stronger in CsSnBr3 and CsPbBr3, with less active lone pairs and smaller tolerance factors, while the off-centering is stronger in CsGeBr3 with more active lone pair and roughly unity tolerance factor. The prominence of these two instabilities is controlled by the interplay of ionic size and covalency effects. Raman signatures of both type of fluctuations are not predicted by models and computations that are based on either the average static structure or the single ground-state structure of these crystals.
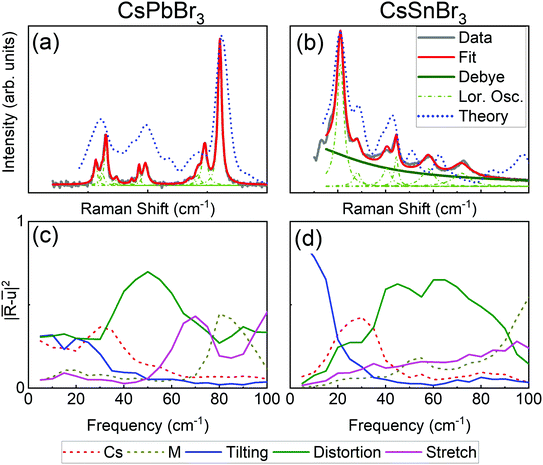
We now compare the structural dynamics of the low-temperature orthorhombic phases (Pnma, space group #62) of CsPbBr3 and CsSnBr3. This comparison has merit because unlike the cubic phase, this phase has well-defined Raman activity based on its space-group symmetry. CsGeBr3 is excluded from this comparison because, as mentioned previously, it acquires a rhombohedral structure at low temperature. Fig. 3(a) and (b) present the Raman spectra of CsPbBr3 and CsSnBr3 at 80 K, where both crystals are in their orthorhombic phase. The Raman spectrum of CsPbBr3 has only sharp and well resolved Raman peaks that are fitted well by a damped Lorentz oscillator model. Three groups of peaks are identified at 20 cm−1, 50 cm−1, and 80 cm−1, respectively. In contrast, the spectral deconvolution of the CsSnBr3 crystal requires a Debye relaxational component (purple solid line in Fig. 3(b)) in addition to the Lorentz oscillators (see ESI†). This relaxational component indicates that the octahedral instabilities are still significant in CsSnBr3 even at 80 K. Four groups of peaks are identified at 20 cm−1, 40 cm−1, and 60 cm−1, 70 cm−1, respectively. We note that for both compounds, theory and experiments agree very well in terms of the magnitudes and frequencies (±10 cm−1) of these well resolved Raman-active peaks.
The above statement is supported by our projected AIMD analysis at 80 K (Fig. 3(c) and (d)). First, at low frequency (<30 cm−1), the tilting motion in CsSnBr3 is dominant (Fig. 3(d)). Its weight continuously decays with increasing frequency, and corresponds to the fitted Debye component in the Raman spectrum (Fig. 3(b)). This is in contrast to what is observed for CsPbBr3 (Fig. 3(c)), where the relaxational behavior of the tilting motion is not as significant as in CsSnBr3, and the low frequency dynamics are also shared by Cs and Br6 distortion motions. The peak at 30 cm−1 in both CsSnBr3 and CsPbBr3 can be ascribed to Cs motion. The peak at 50 cm−1 in CsPbBr3 is also assigned to distortion of the octahedra. In CsSnBr3, distortion motions cover a wider frequency range and likely contribute to the Raman peaks at 40 cm−1–80 cm−1. Finally the features between 70 cm−1–90 cm−1 in CsPbBr3 are connected with stretching and M cation motion.
Similar to the tilting instability of the cubic CsGeBr3 discussed previously, the observed Raman spectra and the results of the projected AIMD analysis for the orthorhombic phases cannot be rationalized by the geometric model that predicts stronger tilting instability for CsPbBr3 (t = 0.86) compared to CsSnBr3 (t = 0.92). This suggests that the stronger tendency for lone-pair driven distortions for Sn2+ contributes to the tilting motion, in concert with intra-octahedral distortions at higher frequencies (green lines in Fig. 3(c) and (d)).
We note that there is additional evidence that supports our suggestion that CsSnBr3 exhibits an instability even at 80 K in the orthorhombic phase. Fig. S4 in the ESI† presents the temperature evolution of the Raman spectrum in the 10 K–80 K range. Around 60 K, we find indication of another phase transition to lower symmetry (possibly monoclinic23) phase. This phase transition is manifested by the appearance of several new peaks and some changes in the existing modes. Furthermore, Fig. S5 in the ESI† presents 0 K, DFT-based phonon dispersion relations that show imaginary modes for orthorhombic CsSnBr3 but not for orthorhombic CsPbBr3.
Conclusions
Our work illustrates the critical role of the metal cation s lone pairs on the nature of the structural dynamics and represents a first step towards tuning the dynamics of perovskite structures. We investigated how the structural dynamics of CsMBr3 (M = Pb, Sn, and Ge) are affected by the stereochemical electron lone pairs on the metal cations. By simultaneously decreasing the energy scale of the tilting instability and increasing the energy scale of the lone-pair polar distortion across the series CsPbBr3 → CsSnBr3 → CsGeBr3, our primary finding is that for all three compounds, the lone-pair stereochemical activity contributes significantly to octahedral tilting instabilities that are unaccounted for in the geometric models or DFT computations at 0 K. This strong instability leads to liquid-like (i.e. central peak) Raman activity in the cubic phase of all three crystals. Since the octahedral tilt angles directly control carrier transport, this study provides the crucial link between chemical composition and optoelectronic properties, opening opportunities for lead-free solution-processable photovoltaics.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
O. Y. acknowledges funding from BSF (grant No. 2016650) and ERC (850041–ANHARMONIC). D. H. F. gratefully acknowledges financial support from the Alexander von Humboldt Foundation. M. G. K. acknowledges support form the Department of Energy, Office of Science, Basic Energy Sciences, under Grant No. SC0012541 (sample synthesis, structure and property characterization). L. G. was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, under Award # DE-FG02-07ER46431. Computational support was provided by the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy, Office of Science User Facility located at Lawrence Berkeley National Laboratory, operated under Contract No. DE-AC02-05CH11231. A.M.R. acknowledges the support of the Office of Naval Research, under grant number N00014-20-1-2701.References
- M. Grätzel, Acc. Chem. Res., 2017, 50, 487 CrossRef PubMed.
- M. A. Green, E. D. Dunlop, J. Hohl-Ebinger, M. Yoshita, N. Kopidakis and X. Hao, Prog. Photovoltaics, 2020, 28, 629 Search PubMed.
- J. Liang, P. Zhao, C. Wang, Y. Wang, Y. Hu, G. Zhu, L. Ma, J. Liu and Z. Jin, J. Am. Chem. Soc., 2017, 139, 14009 CrossRef CAS PubMed.
- F. Liu, C. Ding, Y. Zhang, T. S. Ripolles, T. Kamisaka, T. Toyoda, S. Hayase, T. Minemoto, K. Yoshino and S. Dai, et al. , J. Am. Chem. Soc., 2017, 139, 16708 CrossRef CAS PubMed.
- F. Yang, D. Hirotani, G. Kapil, M. A. Kamarudin, C. H. Ng, Y. Zhang, Q. Shen and S. Hayase, Angew. Chem., 2018, 130, 12927 CrossRef.
- T. Krishnamoorthy, H. Ding, C. Yan, W. L. Leong, T. Baikie, Z. Zhang, M. Sherburne, S. Li, M. Asta and N. Mathews, et al. , J. Mater. Chem. A, 2015, 3, 23829 RSC.
- I. Kopacic, B. Friesenbichler, S. F. Hoefler, B. Kunert, H. Plank, T. Rath and G. Trimmel, ACS Appl. Energy Mater., 2018, 1, 343 CrossRef CAS.
- R. Sharma, Z. Dai, L. Gao, T. M. Brenner, L. Yadgarov, J. Zhang, Y. Rakita, R. Korobko, A. M. Rappe and O. Yaffe, Phys. Rev. Mater., 2020, 4, 092401 CrossRef CAS.
- O. Yaffe, Y. Guo, L. Z. Tan, D. A. Egger, T. Hull, C. C. Stoumpos, F. Zheng, T. F. Heinz, L. Kronik, M. G. Kanatzidis, J. S. Owen, A. M. Rappe, M. A. Pimenta and L. E. Brus, Phys. Rev. Lett., 2017, 118, 136001 CrossRef PubMed.
- M. Z. Mayers, L. Z. Tan, D. A. Egger, A. M. Rappe and D. R. Reichman, Nano Lett., 2018, 18, 8041 CrossRef CAS PubMed.
- A. Lacroix, G. T. de Laissardière, P. Quémerais, J.-P. Julien and D. Mayou, Phys. Rev. Lett., 2020, 124, 196601 CrossRef CAS PubMed.
- A. Poglitsch and D. Weber, J. Chem. Phys., 1987, 87, 6373 CrossRef CAS.
- P. Whitfield, N. Herron, W. Guise, K. Page, Y. Cheng, I. Milas and M. Crawford, Sci. Rep., 2016, 6(35685), 1 Search PubMed.
- M. Keshavarz, M. Ottesen, S. Wiedmann, M. Wharmby, R. Küchler, H. Yuan, E. Debroye, J. A. Steele, J. Martens, N. E. Hussey, M. Bremholm, M. B. J. Roeffaers and J. Hofkens, Adv. Mater., 2019, 31, 1900521 CrossRef PubMed.
- S. Maheshwari, M. B. Fridriksson, S. Seal, J. Meyer and F. C. Grozema, J. Phys. Chem. C, 2019, 123, 14652 CrossRef CAS PubMed.
- A. C. Ferreira, S. Paofai, A. Létoublon, J. Ollivier, S. Raymond, B. Hehlen, B. Rufflé, S. Cordier, C. Katan, J. Even and P. Bourges, Commun. Phys., 2020, 3, 48 CrossRef.
- W. Chu, Q. Zheng, O. V. Prezhdo, J. Zhao and W. A. Saidi, Sci. Adv., 2020, 6, eaaw7453 CrossRef CAS PubMed.
- B. Saparov and D. B. Mitzi, Chem. Rev., 2016, 116, 4558 CrossRef CAS PubMed.
- V. M. Goldschmidt, Naturwissenschaften, 1926, 21, 477 CrossRef.
- L. Pauling, J. Am. Chem. Soc., 1929, 51, 1010 CrossRef CAS.
- A. M. Glazer, Acta Crystallogr., 1972, 28, 3384 CrossRef CAS.
- P. M. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 32 CrossRef.
- C. J. Howard and H. T. Stokes, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 782 CrossRef.
- J. Klarbring and S. I. Simak, Phys. Rev. B, 2018, 97, 024108 CrossRef CAS.
- G. J. Ackland and M. C. Warren, Phase Transitions, 1997, 61, 215 CrossRef CAS.
- J.-J. Zhou, O. Hellman and M. Bernardi, Phys. Rev. Lett., 2018, 121, 226603 CrossRef CAS PubMed.
- W. Zhong, D. Vanderbilt and K. M. Rabe, Phys. Rev. Lett., 1994, 73, 1861 CrossRef CAS PubMed.
- A. Kania, K. Roleder, G. E. Kugel and M. D. Fontana, J. Phys. C: Solid State Phys., 1986, 19, 9 CrossRef CAS.
- J. P. Sokoloff, L. L. Chase and L. A. Boatner, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 2398 CrossRef CAS PubMed.
- J.-H. Ko, S. Kojima, T.-Y. Koo, J. H. Jung, C. J. Won and N. J. Hur, Appl. Phys. Lett., 2008, 93, 102905 CrossRef.
- V. K. Malinovsky, A. M. Pugachev, V. A. Popova, N. V. Surovtsev and S. Kojima, Ferroelectrics, 2013, 443, 124 CrossRef CAS.
- R. X. Yang, J. M. Skelton, E. L. Da Silva, J. M. Frost and A. Walsh, J. Phys. Chem. Lett., 2017, 8, 4720 CrossRef CAS PubMed.
- A. N. Beecher, O. E. Semonin, J. M. Skelton, J. M. Frost, M. W. Terban, H. Zhai, A. Alatas, J. S. Owen, A. Walsh and S. J. Billinge, ACS Energy Lett., 2016, 1, 880 CrossRef CAS.
- T. Baikie, Y. Fang, J. M. Kadro, M. Schreyer, F. Wei, S. G. Mhaisalkar, M. Grätzel and T. J. White, J. Mater. Chem. A, 2013, 1, 5628 RSC.
- M. C. Alvarez-Galván, J. A. Alonso, C. A. López, E. López-Linares, C. Contreras, M. J. Lázaro, F. Fauth and M. V. Martínez-Huerta, Cryst. Growth Des., 2019, 19, 918 CrossRef.
- J. Klarbring, O. Hellman, I. A. Abrikosov and S. I. Simak, Phys. Rev. Lett., 2020, 125, 045701 CrossRef CAS PubMed.
- J. A. Brehm, J. W. Bennett, M. R. Schoenberg, I. Grinberg and A. M. Rappe, J. Chem. Phys., 2014, 140, 224703 CrossRef PubMed.
- C. Li, K. C. K. Soh and P. Wu, J. Alloys Compd., 2004, 372, 40 CrossRef CAS.
- L. Feng, L. Jiang, M. Zhu, H. Liu, X. Zhou and C. Li, J. Phys. Chem. Solids, 2008, 69, 967 CrossRef CAS.
- C. Li, X. Lu, W. Ding, L. Feng, Y. Gao and Z. Guo, Acta Crystallogr., Sect. B: Struct. Sci., 2008, 64, 702 CrossRef CAS PubMed.
- W. Travis, E. Glover, H. Bronstein, D. Scanlon and R. Palgrave, Chem. Sci., 2016, 7, 4548 RSC.
- M. R. Filip and F. Giustino, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5397 CrossRef CAS PubMed.
- F. R. Poulsen and S. E. Rasmussen, Acta Chem. Scand., 1970, 24, 150 CrossRef CAS.
- P. Berastegui, S. Hull and S.-G. Eriksson, J. Phys.: Condens. Matter, 2001, 13, 5077 CrossRef CAS.
- I. Grinberg and A. M. Rappe, Phase Transitions, 2007, 80, 351 CrossRef CAS.
- G. Laurita, D. H. Fabini, C. C. Stoumpos, M. G. Kanatzidis and R. Seshadri, Chem. Sci., 2017, 8, 5628 RSC.
- M. G. Goesten and R. Hoffmann, J. Am. Chem. Soc., 2018, 140, 12996 CrossRef CAS PubMed.
- D. H. Fabini, R. Seshadri and M. G. Kanatzidis, MRS Bull., 2020, 45, 467 CrossRef.
- J. Galy, G. Meunier, S. Andersson and A. Åström, J. Solid State Chem., 1975, 13, 142 CrossRef CAS.
- U. V. Waghmare, N. A. Spaldin, H. C. Kandpal and R. Seshadri, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 125111 CrossRef.
- A. Walsh and G. W. Watson, J. Phys. Chem. B, 2005, 109, 18868 CrossRef CAS PubMed.
- A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Chem. Soc. Rev., 2011, 40, 4455 RSC.
- M. W. Stoltzfus, P. M. Woodward, R. Seshadri, J.-H. Klepeis and B. Bursten, Inorg. Chem., 2007, 46, 3839 CrossRef CAS PubMed.
- S.-E. Park and T. R. Shrout, J. Appl. Phys., 1997, 82, 1804 CrossRef CAS.
- R. Seshadri, Proc. - Indian Acad. Sci., Chem. Sci., 2001, 113, 487 CrossRef CAS.
- B. Noheda, Curr. Opin. Solid State Mater. Sci., 2002, 6, 27 CrossRef CAS.
- I. Grinberg, V. R. Cooper and A. M. Rappe, Nature, 2002, 419, 909 CrossRef CAS.
- Y. Uratani, T. Shishidou and T. Oguchi, Jpn. J. Appl. Phys., 2008, 47, 7735 CrossRef CAS.
- W. M. A. Smit, G. J. Dirksen and D. J. Stufkens, J. Phys. Chem. Solids, 1990, 51, 189 CrossRef CAS.
- H. Ishida, H. Maeda, A. Hirano, Y. Kubozono and Y. Furukawa, Phys. Status Solidi A, 1997, 159, 277 CrossRef CAS.
- R. J. Worhatch, H. Kim, I. P. Swainson, A. L. Yonkeu and S. J. Billinge, Chem. Mater., 2008, 20, 1272 CrossRef CAS.
- S. Liu, F. Zheng, N. Z. Koocher, H. Takenaka, F. Wang and A. M. Rappe, J. Phys. Chem. Lett., 2015, 6, 693, DOI:10.1021/jz502666j.
- D. H. Fabini, G. Laurita, J. S. Bechtel, C. C. Stoumpos, H. A. Evans, A. G. Kontos, Y. S. Raptis, P. Falaras, A. Van der Ven, M. G. Kanatzidis and R. Seshadri, J. Am. Chem. Soc., 2016, 138, 11820 CrossRef CAS.
- J. Liu, A. E. Phillips, D. A. Keen and M. T. Dove, J. Phys. Chem. C, 2019, 123, 14934 CrossRef CAS.
- R. C. Remsing and M. L. Klein, Phys. Rev. Lett., 2020, 124, 066001 CrossRef CAS PubMed.
- R. C. Remsing and M. L. Klein, APL Mater., 2020, 8, 50902 CrossRef CAS.
- E. H. Smith, N. A. Benedek and C. J. Fennie, Inorg. Chem., 2015, 54, 8536 CrossRef CAS PubMed.
- S. K. Radha, C. Bhandari and W. R. Lambrecht, Phys. Rev. Mater., 2018, 2, 063605 CrossRef CAS.
- I. Grinberg, M. R. Suchomel, P. K. Davies and A. M. Rappe, J. Appl. Phys., 2005, 98, 094111 CrossRef.
- R. X. Yang, J. M. Skelton, E. L. Da Silva, J. M. Frost and A. Walsh, J. Chem. Phys., 2020, 152, 024703 CrossRef CAS.
- A. Maalej, Y. Abid, A. Kallel, A. Daoud, A. Lautié and F. Romain, Solid State Commun., 1997, 103, 279 CrossRef CAS.
- K. Nakamoto, Applications in inorganic chemistry, Infrared and Raman Spectra of Inorganic and Coordination Compounds, John Wiley & Sons, Ltd, 2008, ch. 2, pp. 149–354 Search PubMed.
- C. C. Stoumpos, L. Frazer, D. J. Clark, Y. S. Kim, S. H. Rhim, A. J. Freeman, J. B. Ketterson, J. I. Jang and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 6804 CrossRef CAS PubMed.
- G. Thiele, H. W. Rotter and K. D. Schmidt, Z. Anorg. Allg. Chem., 1987, 545, 148 CrossRef CAS.
- T. Lanigan-Atkins, X. He, M. J. Krogstad, D. M. Pajerowski, D. L. Abernathy, G. N. M. N. Xu, Z. Xu, D.-Y. Chung, M. G. Kanatzidis, S. Rosenkranz, R. Osborn and O. Delaire, Nat. Mater., 2021 DOI:10.1038/s41563-021-00947-y.
- X. Lü, C. Stoumpos, Q. Hu, X. Ma, D. Zhang, S. Guo, J. Hoffman, K. Bu, X. Guo, Y. Wang, C. Ji, H. Chen, H. Xu, Q. Jia, W. Yang, M. G Kanatzidis and H.-K. Mao, Natl. Sci. Rev., 2021 Search PubMed , nwaa288.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma00288k |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2021 |