Open Access Article
Open Access ArticleUnderstanding the low voltage losses in high-performance non-fullerene acceptor-based organic solar cells†
Jakob
Hofinger
 *a,
Christoph
Putz
ab,
Felix
Mayr
a,
Katarina
Gugujonovic
a,
Dominik
Wielend
*a,
Christoph
Putz
ab,
Felix
Mayr
a,
Katarina
Gugujonovic
a,
Dominik
Wielend
 a and
Markus C.
Scharber
a and
Markus C.
Scharber
 *a
*a
aLinz Institute of Organic Solar Cells (LIOS), Institute of Physical Chemistry, Johannes Kepler University Linz, Altenbergerstrasse 69, 4040 Linz, Austria. E-mail: jakob.hofinger@jku.at
bDivision of Soft Matter Physics, Institute of Experimental Physics, Johannes Kepler University Linz, Altenbergerstrasse 69, Linz 4040, Austria
First published on 25th May 2021
Abstract
Despite the rapid increase in power conversion efficiency (PCE) of non-fullerene acceptor (NFA) based solar cells in recent years, organic photovoltaic (OPV) devices exhibit considerably larger voltage losses compared to their highly-efficient inorganic counterparts (e.g. Si or GaAs). Further material optimizations and strategies to reduce the voltage losses in OPV systems are required to close the gap to inorganic PV technologies and allow for efficiencies surpassing 20%. The main focus of this study is on understanding the voltage losses in high performance NFA-based solar cells, as furthering the knowledge in this area is critical in promoting their recent success. In this article, the open circuit voltage losses observed in high-performance D18:Y6 organic solar cells with a PCE of 16% are investigated in detail. The voltage losses of D18:Y6 devices are compared to fullerene-devices consisting of D18 and PC71BM in order to highlight the differences between non-fullerene and fullerene acceptors. A low open-circuit voltage loss of 0.51 V has been found for Y6-based devices suggesting a 0.29 V lower voltage loss compared to PC71BM-based devices (0.8 V). The observed differences can be explained by the high-lying charge transfer state energy in Y6-based solar cells and the strong emissivity of the pristine acceptor. Both properties seem to be prerequisites for efficient OPV systems with low voltage losses. Based on the experimental results, we suggest two design strategies to further improve the performance of OPV systems.
Introduction
Over the past 20 years, the efficiencies of photovoltaic devices based on organic semiconductors,1–3 typically consisting of a conjugated polymer (donor) blended with a solution-processable fullerene derivative (acceptor), increased steadily until a plateau of approximately 12% was reached.4,5 The limited performance can be mainly attributed to the weak optical absorption and the wide (indirect) bandgap of fullerenes. The recent development of efficient non-fullerene acceptors (NFAs) featuring strong optical absorption marked the beginning of a new OPV era.6 In 2015 Lin et al. reported the fused-ring (indacenodithieno[3,2-b]thiophene core) acceptor–donor–acceptor (A–D–A) molecule ITIC with strong near-infrared (NIR) absorption and high electron mobility.7 The reported power conversion efficiency (PCE) of 6.8% for the ITIC-based solar cell was still inferior to its fullerene counterparts. Due to the development of new non-fullerene acceptors with improved NIR-light-harvesting properties and readily-tunable electronic energy levels, the PCEs of NFA-based solar cells have increased substantially over the last five years up to efficiencies of 15-18%.8–15 At the beginning of 2020, Liu et al. reported a record-breaking PCE of 18.2% (17.6% certified) for the donor polymer D18 blended with the high-performance NFA Y6.16Despite the great success of NFAs, OPV devices still fall short in some aspects compared to their inorganic counterparts. One of the main factors limiting the efficiencies in OPV is the relatively large total voltage loss (ΔVtotalOC), which is defined as the difference between the bandgap of the absorber (Egap) and the experimentally observed open circuit voltage (VOC). A detailed analysis of the total voltage loss ΔVtotalOC allows to quantify the individual loss contributions and enables a direct comparison between different solar cell devices. According to a paper by Rau et al.,17 it is possible to predict the VOC of a solar cell using
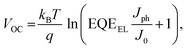 | (1) |
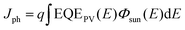 | (2) |
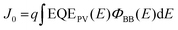 | (3) |
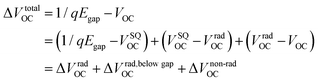 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gapOC) is a consequence of the difference between an ideal step-like EQEPV, as assumed in the calculation of the Shockley Queisser limit (SQ-limit), and the experimentally observed EQEPV. For OPV devices, the measured EQEPV often differs substantially from the steep absorption edges found in inorganic direct semiconductors or perovskite solar cells, due to CT-state absorptions or trap states caused by impurities or molecular aggregates. ΔVrad,below
gapOC) is a consequence of the difference between an ideal step-like EQEPV, as assumed in the calculation of the Shockley Queisser limit (SQ-limit), and the experimentally observed EQEPV. For OPV devices, the measured EQEPV often differs substantially from the steep absorption edges found in inorganic direct semiconductors or perovskite solar cells, due to CT-state absorptions or trap states caused by impurities or molecular aggregates. ΔVrad,below![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gapOC can thus be identified as a combination of the radiative recombination losses below the optical bandgap and the difference between JSQSC and the experimentally observed JSC of the device. The contribution of the latter is rather small and will be neglected in the following.23 The third term (ΔVnon-radOC) takes into account that not every electron–hole pair recombines radiatively (as assumed by VradOC) and accounts for the open-circuit voltage loss due to non-radiative recombination. Experiments on solar cell devices suggest that non-radiative recombination is far more likely than radiative recombination and accounts for the largest part of the observed voltage loss. With eqn (1) the non-radiative voltage loss can be related to the EQEEL and expressed as
gapOC can thus be identified as a combination of the radiative recombination losses below the optical bandgap and the difference between JSQSC and the experimentally observed JSC of the device. The contribution of the latter is rather small and will be neglected in the following.23 The third term (ΔVnon-radOC) takes into account that not every electron–hole pair recombines radiatively (as assumed by VradOC) and accounts for the open-circuit voltage loss due to non-radiative recombination. Experiments on solar cell devices suggest that non-radiative recombination is far more likely than radiative recombination and accounts for the largest part of the observed voltage loss. With eqn (1) the non-radiative voltage loss can be related to the EQEEL and expressed as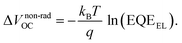 | (5) |
As a consequence of the rapid success of NFA-based solar cells, the fundamental understanding of these new acceptors is lagging behind. For the design of new NFAs, it is crucial to identify the relevant mechanisms and properties, which enable the high performance of current NFA-based solar cells. The described voltage analysis, based on the readily accessible EQEPV spectrum of the solar cell, provides a reliable tool to gain insights into the loss processes, which are an important aspect that separates NFA-based from fullerene-based devices. Herein, we aim to thoroughly investigate the photovoltaic performance and optical properties of the current record-breaking polymer:NFA system D18:Y6 reported by Liu et al.16 The study by Liu et al. is mainly focused on device optimization and gives a detailed analysis of the influence of processing conditions on the photovoltaic parameters of D18:Y6 solar cells. To the best of our knowledge, a thorough analysis of the observed voltage losses for a better understanding of the material combination D18:Y6 has not been reported yet and is the motivation for this work.
In order to investigate the properties that elevate D18:Y6 devices from other systems, high-performance D18:Y6 solar cells were fabricated and compared to their fullerene counterparts based on D18:PC71BM. For both systems, current density–voltage (J–V) curves and the corresponding photovoltaic parameters under AM1.5G illumination and in the dark are shown in this work. Moreover, highly-sensitive EQEPV measurements, as well as photo- and electroluminescence measurements of blend and pristine devices are presented. Based on these results, the described VOC loss analysis was performed to quantify the differences in radiative and non-radiative recombination for D18:Y6 and D18:PC71BM solar cells. The non-radiative losses were validated with EQEEL measurements, and the solar cell performance of both devices was evaluated by comparison to their maximal achievable performance defined by the SQ-limit. Based on the results, two design strategies are formulated to further improve the VOC of NFA-based solar cells, aiming towards efficiencies surpassing the 20% mark.
Results & discussion
Experimental results
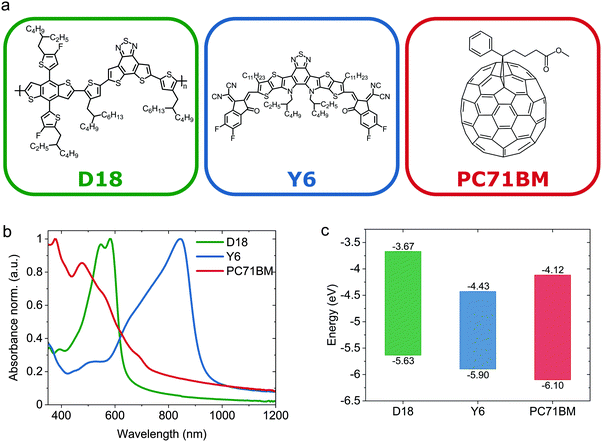
The chemical structures of the investigated OPV materials are presented in Fig. 1a. The D–A copolymer D18 is a wide bandgap donor with strong absorption in the visible light spectrum, whereas the Y6 non-fullerene acceptor has a complementary narrow bandgap, enabling light gathering in the NIR-region as shown in the absorbance spectra in Fig. 1b. In contrast, PC71BM (red curve in Fig. 1b) shows high absorption only in the UV and blue region of the visible light spectrum and exhibits only weak absorption in the range between 600–700 nm, which can be attributed to partly forbidden optical transitions near the band edge observed in fullerene molecules.24,25 In addition to the optical absorbance, HOMO and LUMO levels of the molecules were measured electrochemically using electrochemical voltage spectroscopy (EVS). The slow, stepwise variation of the applied potential in EVS measurements allows the system to be close to thermodynamic equilibrium, which reduces dynamic influences such as the scan speed in standard CV measurements. The EVS measurements of the investigated materials are shown in Fig. S1 (ESI†). HOMO levels of −5.63 eV, −5.90 eV and −6.10 eV and LUMO levels of −3.67 eV, −4.43 eV and −4.12 eV have been found for D18, Y6 and PC71BM respectively and are presented in Fig. 1c. Considering a typical error margin of ±0.1 eV for electrochemical measurements,26 the electrochemical bandgaps are in good agreement with the optical absorption onsets.To evaluate the photovoltaic performance of D18:Y6, solar cell devices with the structure of ITO/PEDOT:PSS/D18:Y6/PDIN/Ag were fabricated. The device geometry and chemical structures of PEDOT:PSS and PDIN are presented in Fig. S2 (ESI†). Different concentrations of the active layer solution and different spin speeds were used to fabricate devices with various thicknesses (see Fig. S3 and S4, ESI†). In Table S1 (ESI†) the photovoltaic parameters of D18:Y6 devices with various thicknesses are presented. PCEs typically varied between 14–16%. Hence, a cell with an efficiency close to 15.2% (see Table 1) was chosen as a typical representative of the fabricated D18:Y6 solar cells, which has been investigated and characterized in detail. Based on earlier results, an optimized D/A ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.6 was used.16 To keep processing as simple as possible, no additives, post-annealing or solvent annealing steps were performed. The best device showed a good photovoltaic efficiency of approximately 16% with a high open-circuit voltage of 0.87 V, a short-circuit current of 25.2 mA cm−2 and an electrical fill factor of 73.6%. Table 1 shows that our results are in good agreement with the National Institute of Metrology (NIM) certified photovoltaic parameters reported earlier.16 The difference in PCE is mainly caused by the reduced FF, which might be related to minor differences in the fabrication process and solar cell geometry. Interestingly, for some devices a, VOC as high as 0.88 V was measured, suggesting that the full PCE potential of the D18:Y6 system might not have been reached yet.
1.6 was used.16 To keep processing as simple as possible, no additives, post-annealing or solvent annealing steps were performed. The best device showed a good photovoltaic efficiency of approximately 16% with a high open-circuit voltage of 0.87 V, a short-circuit current of 25.2 mA cm−2 and an electrical fill factor of 73.6%. Table 1 shows that our results are in good agreement with the National Institute of Metrology (NIM) certified photovoltaic parameters reported earlier.16 The difference in PCE is mainly caused by the reduced FF, which might be related to minor differences in the fabrication process and solar cell geometry. Interestingly, for some devices a, VOC as high as 0.88 V was measured, suggesting that the full PCE potential of the D18:Y6 system might not have been reached yet.
| Material | V OC (V) | J SC (JSC_EQE) (mA cm−2) | FF (%) | PCE (%) | Source |
|---|---|---|---|---|---|
| D18:Y6 | 0.84 | 26.67 | 78.4 | 17.6 | Ref. 16 (NIM) |
| D18:Y6 (best) | 0.87 | 25.24 (24.70) | 73.6 | 16.1 | This work |
| D18:Y6 (average) | 0.87 ± 0.01 | 24.46 ± 0.92 (23.48) | 70.5 ± 0.63 | 15.2 ± 0.51 | This work |
| D18:PC71BM (average) | 0.98 ± 0.01 | 11.26 ± 0.49 (11.15) | 71.4 ± 1.52 | 8.0 ± 0.49 | This work |
Following the successful fabrication of high-performance, state-of-the-art solar cells with PCE >15%, the devices were compared to fullerene-based solar cells with the same device structure (ITO/PEDOT:PSS/D18:PC71BM/PDIN/Ag) and D/A ratio (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
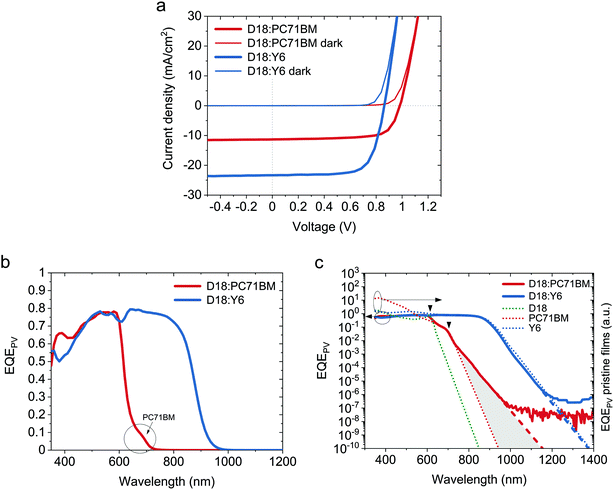
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.6). Throughout this report, the results measured for two representative solar cells, one for the Y6-based and one for the PC71BM-based devices, are presented and compared in detail. J–V-curves were recorded under AM1.5G illumination and in the dark for both devices and are presented in Fig. 2a, while the corresponding photovoltaic parameters are highlighted in Table 1. The fullerene device shows a superior VOC, but at the same time, its JSC is approximately 50% lower compared to the Y6 device. Both solar cells exhibit a high FF of more than 70%, indicating efficient charge transport through the device.
1.6). Throughout this report, the results measured for two representative solar cells, one for the Y6-based and one for the PC71BM-based devices, are presented and compared in detail. J–V-curves were recorded under AM1.5G illumination and in the dark for both devices and are presented in Fig. 2a, while the corresponding photovoltaic parameters are highlighted in Table 1. The fullerene device shows a superior VOC, but at the same time, its JSC is approximately 50% lower compared to the Y6 device. Both solar cells exhibit a high FF of more than 70%, indicating efficient charge transport through the device.
High-sensitivity EQEPV measurements were performed for both solar cells and are shown in Fig. 2b and c on a linear and logarithmic scale, respectively. The EQEPV comparison on the linear scale indicates an almost identical behavior of fullerene and non-fullerene devices in the region of strong light absorption of the donor polymer D18 between 425–600 nm. EQEPV values >75% suggest good charge generation and high collection efficiency for both acceptors. Due to the strong absorption of PC71BM below 425 nm, the EQEPV of the fullerene device is larger in comparison to the NFA device in this region. Similarly, the shoulder in the D18:PC71BM EQEPV spectrum at 675 nm can be attributed to the pristine PC71BM absorption (see Fig. 1b). Furthermore, the EQEPV spectra clearly illustrate the big advantage of the Y6 acceptor, namely its strong absorption in the NIR region, enabling efficient light-harvesting until approximately 920 nm. The semi-logarithmic plot of the high-sensitivity EQEPV measurements reveals the sub-bandgap EQEPV behavior over several orders of magnitude, which plays a critical role in determining the photovoltaic performance of the solar cells. As described in the methods, combining a monochromator, additional long-pass filters, and an external preamplifier with a phase-sensitive lock-in measurement technique allows us to reliably determine the EQEPV of the solar cells over a range of 6–7 orders of magnitude. For both solar cells, the EQEPV values >1000 nm for the fullerene device and >1200 nm for the NFA device are considered as limited by the sensitivity of the measurement. To calculate the dark saturation current J0 using eqn (3), a linear function was fitted to the tail of the EQEPV spectrum (dashed lines in Fig. 2c) to avoid distortion of the determined J0 values by measurement noise. For this method we assume that the main physical behavior of the system is already described by the measured EQEPV, and no physically relevant contributions are hidden below the sensitivity limit of the experimental setup. In addition to the EQEPV spectra of the investigated organic solar cells, Fig. 2c shows the EQEPV of the pristine materials (dotted curves). An active layer of pure D18, PC71BM or Y6 was used for the pristine devices, while the contacts and interlayers were identical to the ones from fullerene and non-fullerene solar cell devices (ITO/PEDOT:PSS and PDIN/Ag). The EQEPV spectra of the neat materials are presented in arbitrary units and scaled to fit the EQEPV spectra of the blend devices. For the sake of visibility, only the linearly extended EQEPV spectra of the pristine devices are depicted in Fig. 2c. A comparison of the measured and linear extended EQEPV of the pristine devices is presented in Fig. S5a (ESI†). The EQEPV spectrum of the D18:PC71BM solar cell exhibits two distinct kinks at approximately 600 and 700 nm highlighted by small black triangles, which correspond to the absorption edges of the pristine materials. Fig. 2c shows a pronounced deviation of the sub-bandgap EQEPV behavior (>800 nm) of D18:PC71BM from the EQEPV of the pristine PC71BM device (red dotted curve). The deviation is highlighted by the grey area under the EQEPV spectrum of D18:PC71BM. This additional absorption below the bandgap of the pristine materials is typical for polymer:fullerene solar cells and can be attributed to CT-state absorption. In contrast, no such additional absorption is found for D18:Y6 solar cells, suggesting a high-lying CT state close to the energy levels of the pure Y6 acceptor.
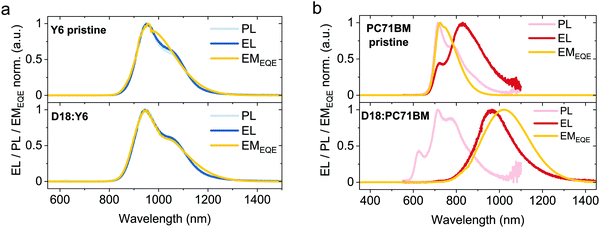
Complementary to the EQEPV measurements, electroluminescence (EL) and photoluminescence (PL) spectra of the pristine and blend devices were recorded and are presented in Fig. 3a and b. For the non-fullerene devices (Fig. 3a), there is no observable difference between EL and PL spectra, suggesting that the recombination process upon charge injection or light stimulation involves the same energetic states. Moreover, the close resemblance of the luminescence spectra of the D18:Y6 device and the pristine Y6 device indicates that in highly-efficient D18:Y6 solar cells, the radiative recombination process is dominated by the energy levels of the pure Y6 acceptor. In addition to EL and PL spectra, the emissivity of the solar cell (EMEQE) is shown (yellow line in Fig. 3a and b). The EMEQE can be calculated as the product of the measured EQEPV spectrum and the black body spectrum at 300 K. Excellent agreement of the calculated EMEQE with the measured EL and PL spectra is found for both Y6-based devices. The PL spectra (light red curves) of both fullerene-containing devices (pristine PC71BM and D18:PC71BM) in Fig. 3b are similar in shape, with the exception of an additional peak at 625 nm for the D18:PC71BM device. During PL measurements the high-energy laser light, which is used to excite the sample (λ = 488 nm), predominantly leads to localized excitons on the pure donor or acceptor molecules. Thus, the PL spectrum of the D18:PC71BM blend device resembles the PL emission peaks of pure D18 (625 nm) and PC71BM (715 and 780 nm). The emission spectra of the pristine D18 device is presented in Fig. S6 (ESI†). In contrast, the EL spectra (red curves) of both fullerene-containing devices vary clearly in position and shape. Direct comparison of the EL maxima of the pure and blend device indicates a significant redshift from 828 nm to 966 nm. In polymer:fullerene solar cells, this behavior can be assigned to the formation of a pronounced CT-state, which is in good agreement with the previously presented EQEPV data. In the top graph in Fig. 3b, the EMEQE of the pristine PC71BM device resembles the observed PL spectrum. The EL spectrum exhibits peaks at the same spectral positions, but with different relative intensities. PL & EL measurements are used to analyze the light emitted due to radiative recombination of either electrically injected (EL) or optically excited (PL) charge carriers. Optically excited charge carriers usually recombine within the typical exciton diffusion length of the organic materials, while electrically injected charge carriers can recombine anywhere within the organic thin film, depending on the injection properties of the electrodes and the hole and electron mobilities of the materials. Thus, the observed differences in intensity of EL and PL measurements could be caused by interference effects, resulting from different recombination positions within the film. In the bottom graph in Fig. 3b, the EMEQE of the D18:PC71BM blend resembles the measured EL spectrum of the CT-state, which can be attributed to light emission from the CT state and suggests that the electrically injected charge carriers recombine predominantly via the CT state.
CT-state and voltage loss analysis
The measured EQEPV and EL spectra of the pure donor and acceptor materials can be used to identify their optical bandgaps.27 The high-energy EL and low-energy EQEPV peaks were normalized, and the intersection point of EQEPV, and EL spectra was used to estimate the optical bandgap. As presented in Fig. S7 (ESI†), the bandgap energies of D18, Y6 and PC71BM are 2.02, 1.38, and 1.78 eV, respectively.As discussed earlier, the presented EL and EQEPV measurement data suggest a strong influence of the CT-state in the fullerene-based device. Thus, a method based on the reduced emission and reduced absorption spectrum suggested by Vandewal et al.27 was performed to determine the CT-state energy. In organic thin films, optical transitions between the vibrationally relaxed ground and excited states (E0–0) are usually broadened by low-frequency vibrations and can be described by mirror image Gaussian absorption A(E) and emission N(E) line shapes:
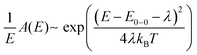 | (6) |
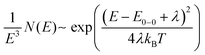 | (7) |
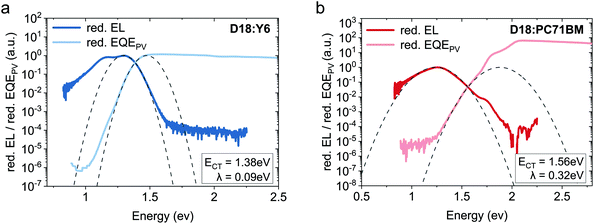 | ||
| Fig. 4 Analysis of the CT-state energy. (a) Reduced EL and reduced EQEPV spectra of the D18:Y6 device. (b) Reduced EL and reduced EQEPV spectra of the D18:PC71BM. Eqn (7) was used to fit the reduced EL spectrum. The fitted parameters for ECT and λ are presented in the small insets. The dashed parabolas were calculated viaeqn (6) and (7) using the derived fit parameters. | ||
A substantial drawback of organic solar cells compared to other photovoltaic technologies is the high voltage loss (ΔVtotalOC), resulting in moderate VOC values. The total voltage loss is defined as the difference between the optical bandgap (Egap/q) and the measured VOC of the photovoltaic device. In this study, the optical bandgap of the small bandgap absorber is defined as the resulting optical gap of the D/A blend. The measured VOC values presented in Table 1 and the obtained optical gaps of pristine Y6 and PC71BM from Fig. S7 (ESI†) allow us to calculate a total voltage loss of 0.51 and 0.80 V for the Y6-based and fullerene-based device, respectively.
In the following, we will perform a detailed analysis (described above) to quantify the contributions of the individual loss terms (as shown in eqn (4)) to the observed total voltage losses and to emphasize the differences between D18:Y6 and D18:PC71BM devices. The highly-sensitive EQEPV measurements presented in Fig. 2c were used to calculate VradOC by substituting eqn (2) and (3) into eqn (1) and assuming EQEEL = 1. The VSQOC was determined using the same set of equations but replacing the measured EQEPV with an ideal step-function EQE, solely defined by the optical gaps of pure Y6 (Egap = 1.38 eV) and PC71BM (Egap = 1.78 eV). The results of the voltage loss analysis based on eqn (4) are summarized in Table 2 and presented graphically in Fig. 5a. The data shows that the increased total voltage loss in the fullerene-based device is results from an increased ΔVrad,below![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gapOC (0.17 V), as well as an increased ΔVnon-radOC (0.33 V) compared to the Y6-based device (0.04 and 0.20 V). The comparatively high voltage loss due to radiative recombination below the bandgap in D18:PC71BM solar cells is a result of the pronounced CT-state absorption below the PC71BM bandgap as highlighted in Fig. 2c (grey area). On the contrary, the absence of a clear CT-state absorption feature in the EQEPV and a steep absorption edge (resembling the one of pure Y6) of the D18:Y6 solar cell translates to a small ΔVrad,below
gapOC (0.17 V), as well as an increased ΔVnon-radOC (0.33 V) compared to the Y6-based device (0.04 and 0.20 V). The comparatively high voltage loss due to radiative recombination below the bandgap in D18:PC71BM solar cells is a result of the pronounced CT-state absorption below the PC71BM bandgap as highlighted in Fig. 2c (grey area). On the contrary, the absence of a clear CT-state absorption feature in the EQEPV and a steep absorption edge (resembling the one of pure Y6) of the D18:Y6 solar cell translates to a small ΔVrad,below![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gapOC of 0.04 V. It should be emphasized that this result is comparable to the values reported for solar cells based on inorganic semiconductors like c-Si (0.01 V)29 or GaAs (0.008 V).30 The enhanced non-radiative recombination loss in the D18:PC71BM device can be related to the formation of a prominent CT-state. As seen from the EL measurements (Fig. 3b), the weak CT-state emission dominates the luminescence spectrum, whereas the emission of the D18:Y6 device is almost identical to the EL of the pure Y6 acceptor device. To the best of our knowledge, a ΔVnon-radOC value of 0.20 V for the D18:Y6 device is one of the lowest ever reported for organic solar cells, closing the gap to c-Si solar cells (ΔVnon-radOC = 0.18 V).29
gapOC of 0.04 V. It should be emphasized that this result is comparable to the values reported for solar cells based on inorganic semiconductors like c-Si (0.01 V)29 or GaAs (0.008 V).30 The enhanced non-radiative recombination loss in the D18:PC71BM device can be related to the formation of a prominent CT-state. As seen from the EL measurements (Fig. 3b), the weak CT-state emission dominates the luminescence spectrum, whereas the emission of the D18:Y6 device is almost identical to the EL of the pure Y6 acceptor device. To the best of our knowledge, a ΔVnon-radOC value of 0.20 V for the D18:Y6 device is one of the lowest ever reported for organic solar cells, closing the gap to c-Si solar cells (ΔVnon-radOC = 0.18 V).29
| Material | E gap/q (V) | ΔVradOC (V) | V SQOC (V) | ΔVrad,below![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gapOC (V) gapOC (V) |
V radOC (V) | ΔVnon-radOC (V) | V OC (V) | ΔVtotalOC (V) |
|---|---|---|---|---|---|---|---|---|
| D18:Y6 | 1.38 | 0.27 | 1.11 | 0.04 | 1.07 | 0.20 | 0.87 | 0.51 |
| D18:PC71BM | 1.78 | 0.30 | 1.48 | 0.17 | 1.31 | 0.33 | 0.98 | 0.80 |
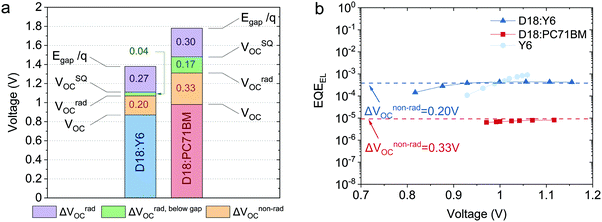 | ||
| Fig. 5 Voltage loss diagram and EQEEL measurements: (a) Illustration of the voltage losses derived for D18:Y6 and D18:PC71BM solar cells. The data is presented in Table 2. (b) EQEEL measurements of D18:PC71BM, D18:Y6 and pristine Y6 devices. The dashed lines represent the EQEEL values calculated viaeqn (5), assuming a non-radiative voltage loss of 0.20 V and 0.33 V, respectively. | ||
In order to validate the voltage loss analysis, EQEEL measurements of D18:Y6, D18:PC71BM and pristine Y6 were performed. The EQEEL values measured at different applied voltages are presented in Fig. 5b. The non-radiative voltage losses for D18:Y6 and D18:PC71BM were used to calculate the respective EQEEL values using eqn (5). The calculated EQEEL values are indicated by the dashed lines in Fig. 5b. The good agreement of measured and calculated EQEEL data indicates the validity of the performed analysis.
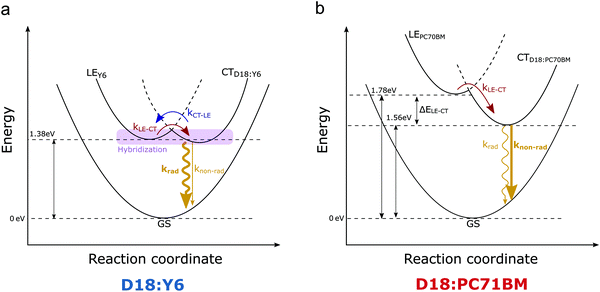
In addition, the presented results are in excellent agreement with the findings reported by Qian et al.,31 which highlight the importance of a high-lying CT state for low non-radiative voltage losses. As a consequence of the high-lying CT state, the widely used two-state Mulliken–Hush model has to be adapted to a three-state model, including the influence of the strongly absorbing local-exciton (LE) state.32 A sketch of the three-state model for D18:Y6 and D18:PC71BM solar cells is presented in Fig. 6. According to the three-state model, small energy offsets between the lowest energy LE and CT states (ΔELE-CT) can result in hybridization between LE and CT states. For small ΔELE-CT systems, transitions from the CT state back to the LE state are allowed and provide an additional radiative recombination pathway. Due to the typically high-emissive nature of the LE state an increased radiative, and a decreased non-radiative recombination rate are expected, resulting in a relatively large EQEEL (reduced ΔVnon-radOC). In the fullerene-based device the hybridization is reduced due to an increased ΔELE-CT offset of 0.22 eV. The lowest energy LE state in the D18:PC71BM device is defined by the LE state of the fullerene. The resulting CT-state shows very moderate emissivity due to the low oscillator strength of the partly forbidden optical transitions in fullerene molecules. Therefore, the EQEEL is expected to be severely reduced in comparison to the Y6-based solar cell, which is confirmed by the increased non-radiative voltage loss shown in Table 2 and the significantly lower EQEEL values presented in Fig. 5.
Efficiency limit and optimization potential of D18:Y6 solar cells
In the following, we try to estimate upper-efficiency limits for D18:Y6 solar cells and discuss potential optimization strategies to further improve the performance of this material combination. The fundamental limit for any solar cell with a defined bandgap is the Shockley Queisser limit.19 Knowledge of the optical bandgaps of D18:Y6 and D18:PC71BM blends allows the determination of power conversion efficiencies in the SQ-limit PCESQ of 33.1% and 27.2%, respectively. To compare the performance of the solar cells regarding their fundamental limit, the measured photovoltaic parameters were normalized by the respective photovoltaic parameters in the SQ-limit (see Table S2, ESI†). Fig. 7 presents the measured photovoltaic parameters (VOC, JSC, FF, PCE) in % of the SQ-limit. The reduced voltage loss in Y6-based devices leads to an impressive value of 80% of its VSQOC, while the fullerene-based device barely reaches 65%. Moreover, Fig. 7 shows that the JSC is comparatively higher for D18:Y6. The low JSC for D18:PC71BM is a result of the limited optical absorption of the fullerene, which severely limits the EQEPV beyond the absorption of D18. Both devices reach approximately 80% of their FFSQ. For D18:Y6 solar cells, this leads to a relative PCE of almost 50% of its SQ-limit. The fullerene-containing device is limited to approximately 30% of its PCESQ.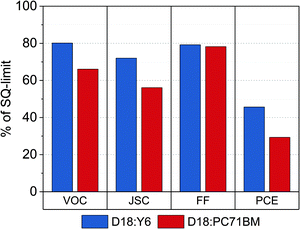 | ||
| Fig. 7 Relative photovoltaic performance with respect to the SQ limit. The relative photovoltaic parameters of D18:Y6 and D18:PC71BM in % of their respective values in the SQ-limit. | ||
While JSC and FF of D18:Y6 solar cells can be improved by optimizing the fabrication process to improve parameters such as film thickness, morphology, domain sizes, light management, etc., the VOC is mainly limited by the previously discussed voltage losses, which are a result of fundamental properties of the investigated materials. Reducing the total voltage loss in OPV will be critical to push organic solar cell efficiencies beyond 20%. To achieve higher VOC's, further improvements in the synthesis of high-performance donor and acceptor materials are needed. Based on the presented results, two strategies to improve the VOC of D18:Y6 solar cells are suggested in the following.
Several reports have shown high-efficiency OPV material combinations where the measured HOMOD − HOMOA offset (ΔHOMO) between donor and acceptor is almost zero.33–36 Considering the presented HOMO levels for D18 and Y6 suggests a ΔHOMO offset of 0.27 eV. Carefully reducing the ΔHOMO offset (without affecting the bandgaps) results in a larger HOMOD − LUMOA difference, which could potentially result in a higher VOC. Minor chemical modifications to either reduce the HOMO level of D18 or to increase the LUMO level of Y6 (without changing Egap) could help to increase the VOC of solar cells based on D18 and Y6 derivatives. An optimum balance has to be found since the ΔHOMO offset is considered as the driving force for charge separation. A too low offset could result in a reduced IQEPV. A recent study by Karuthedath et al.37 on several OPV materials showed a strong correlation between the ΔHOMO offset and the observed IQEPV. Their results suggest high IQEPV's of almost 100% for D/A blends with a ΔHOMO offset >0.5 eV. Below this value, the IQEPV is reduced rapidly to values lower than 50%. A minimal ΔHOMO offset of 0.5 eV is contradicting the high-performance systems reported earlier with a ΔHOMO offset close to 0 eV.33–36 It should be noted that the HOMO levels reported by Karuthedath et al. were measured with ultraviolet photoelectron spectroscopy (UPS), while for the reports with ΔHOMO ≈ 0 eV, the energy levels were determined using cyclic voltammetry (CV). Various reports point out large discrepancies between HOMO levels derived by UPS and CV,37,38 while others claim excellent conformity.33,35,36 The correct determination of HOMO and LUMO levels remains controversial but the contradicting reports suggest that both methods are prone to measurement, and most notably, evaluation errors of several tenths of eV. Despite the difficulties accompanied when comparing different methods, the statement that the IQEPV is reduced significantly below a critical ΔHOMO offset holds true. Minor chemical modifications, such as incorporating different heteroatoms or blending of similar components with slightly different energy levels, to gradually shift the energy levels of the acceptor (or donor) would be necessary to find the lowest ΔHOMO offset without reducing the IQEPV of the solar cell.
A second possible strategy to improve the VOC of D18:Y6 solar cells is to further reduce the non-radiative voltage losses. The high-lying CT state in D18:Y6 solar cells and the associated hybridization of the LE and CT state, as discussed above,31 underlines the importance of the LE state of the small bandgap component. As seen from Fig. 5, the measured EQEEL of D18:Y6 is almost identical to the one of Y6. This result raises the question if the observed EQEEL in the blend is limited by the EQEEL of the pure Y6. Thus, modifying the chemical structure of Y6 to increase its EQEEL might lead to a higher VOC of D18:Y6 solar cells. Based on the NIM-certified JSC and FF values from Table 1, a tenfold increase of the EQEEL would boost the PCE of D18:Y6 to 19.3% (VOC = 0.93 V), while a hundredfold increase would break the 20% efficiency mark by delivering a PCE of 20.5% (VOC = 0.99 V).
Conclusion
In summary, optical and electrochemical measurements on the high-performance OPV materials D18, Y6 and PC71BM have been shown. Furthermore, we report the fabrication of high-performance D18:Y6 solar cells with a PCE of 16% and fullerene-based solar cells (D18:PC71BM) with a PCE of 8%. Two representative devices of the fabricated fullerene- and non-fullerene-based solar cells were analyzed and compared in detail. High-sensitivity EQEPV and luminescence (EL, PL) measurements strongly suggest the formation of a pronounced charge transfer (CT) state in the fullerene-based device. In contrast to this observation, the EQEPV and luminescence spectra of the D18:Y6 device essentially coincide with the spectra of pristine Y6, suggesting a high-lying CT state, which cannot be distinguished from the local exciton (LE) state of pristine Y6. CT-state energy levels of 1.38 eV and 1.56 eV have been found for D18:Y6 and D18:PC71BM devices, respectively. The results from EQEPV and electroluminescence measurements were used to quantify the observed VOC losses of D18:Y6 and D18:PC71BM solar cell devices. The non-fullerene device exhibits a decreased radiative and decreased non-radiative voltage loss compared to the fullerene device. A ΔVrad,below![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gapOC of 0.04 V and a ΔVnon-radOC of 0.20 V for the D18:Y6 device are among the lowest values ever reported for OPV devices. The CT-absorption below the PC71BM bandgap of the D18:PC71BM device leads to a substantially higher ΔVrad,below
gapOC of 0.04 V and a ΔVnon-radOC of 0.20 V for the D18:Y6 device are among the lowest values ever reported for OPV devices. The CT-absorption below the PC71BM bandgap of the D18:PC71BM device leads to a substantially higher ΔVrad,below![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gapOC of 0.17 V. The weak PC71BM oscillator strength leads to a low emissivity of the formed CT-state, which can be attributed to the high ΔVnon-radOC of 0.33 V. For both devices, the measured non-radiative voltage losses are in good agreement with the calculated ΔVnon-radOC values from EQEEL measurements. The three-state model was used to describe the observed experimental results successfully.
gapOC of 0.17 V. The weak PC71BM oscillator strength leads to a low emissivity of the formed CT-state, which can be attributed to the high ΔVnon-radOC of 0.33 V. For both devices, the measured non-radiative voltage losses are in good agreement with the calculated ΔVnon-radOC values from EQEEL measurements. The three-state model was used to describe the observed experimental results successfully.
To conclude, a high-lying CT-state appears to be a prerequisite to achieve low voltage losses. Furthermore, the three-state model and the experimental results highlight the importance of a strongly emissive LE-state of the small bandgap component, which seems to significantly reduce the non-radiative voltage loss in low ΔELE-CT systems. Based on the experimental results two possible strategies to improve the VOC of D18:Y6 solar cells are proposed. The EVS measurements of D18 and Y6 (ΔHOMO = 0.27 eV) supports the idea to reduce the ΔHOMO offset between donor and acceptor without affecting the IQEPV of the solar cell. As a result, the increased energetic difference between HOMOD and LUMOA could potentially lead to a higher VOC. Another approach to improve the VOC is to reduce the non-radiative voltage losses of D18:Y6 solar cells by enhancing the EQEEL. As suggested by the experimental results, this may be achieved by improving the luminescence properties of Y6. The proposed optimization strategies might be of paramount importance to further reduce the observed voltage losses and allow for OPV efficiencies to exceed the 20% mark.
Methods
Materials & device preparation
The materials used for D18:Y6 solar cell preparation (D18, Y6, and PDIN) were purchased from 1-materials, while the PC71BM was purchased from Solenne BV. Pre-patterned ITO glass was thoroughly cleaned by wiping it with toluene followed by subsequent ultrasonication in Hellmanex (2% v/v solution in deionized water, approx. 50 °C), 2× Milli-Q water, acetone and isopropanol for 15 min each. After blow-drying with N2, the cleaned substrates were plasma treated for 5 min (O2, 100 W). Next, 0.45 μm filtered PEDOT:PSS (Clevios Al4083) was spin-coated onto the substrates for 45 s with 3000 rps in ambient conditions resulting in films with a thickness of 30–40 nm. The thickness was determined with a DekTak profilometer. The active layer solutions D18:Y6 and D18:PC71BM were prepared in chloroform with a D/A ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.6. The concentration of D18:Y6 was 7–11 mg ml−1 while the concentration of D18:PC71BM was 9 mg ml−1. The active layer was spin-coated in a glovebox under a dry nitrogen atmosphere using various spin speeds ranging from 1000–5000 rps resulting in active layer film thicknesses from 55 nm to 190 nm. As a next step, a thin (<10 nm) PDIN layer was spin-coated on top of the active layer with 5000 rps for 30 s. The PDIN solution was dissolved in a mix of methanol and acetic acid (100%) with a volume ratio of 1000
1.6. The concentration of D18:Y6 was 7–11 mg ml−1 while the concentration of D18:PC71BM was 9 mg ml−1. The active layer was spin-coated in a glovebox under a dry nitrogen atmosphere using various spin speeds ranging from 1000–5000 rps resulting in active layer film thicknesses from 55 nm to 190 nm. As a next step, a thin (<10 nm) PDIN layer was spin-coated on top of the active layer with 5000 rps for 30 s. The PDIN solution was dissolved in a mix of methanol and acetic acid (100%) with a volume ratio of 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and a concentration of 2 mg ml−1. As the last step, 100 nm Ag electrodes were thermally evaporated at a pressure <10−6 mbar. A home-made shadow mask was used to define the evaporated electrodes resulting in an active device area of 0.173 cm2. All cells were encapsulated in the glovebox using a UV-curable epoxy sealant. The UV-exposure time was approximately 5 minutes.
3 and a concentration of 2 mg ml−1. As the last step, 100 nm Ag electrodes were thermally evaporated at a pressure <10−6 mbar. A home-made shadow mask was used to define the evaporated electrodes resulting in an active device area of 0.173 cm2. All cells were encapsulated in the glovebox using a UV-curable epoxy sealant. The UV-exposure time was approximately 5 minutes.
Sun-simulator
J–V-measurements of the solar cell devices were performed with a LOT-QD solar simulator (LS0821) and a Keithley 2401 SourceMeter unit. The intensity was calibrated using a reference Si-diode and set to 100 mW cm−2 (= AM1.5G). The current response of the solar cell upon external bias voltages under AM1.5G illumination and in the dark was recorded using a custom built LabVIEW software.EQEPV
All the EQEPV spectra presented in this study are the superposition of several EQEPV measurements from two different setups. The first setup is optimized for EQEPV measurements at wavelengths <1000 nm (EQEs1) while the second setup allows for highly-sensitive EQEPV measurements up to wavelengths of 1600 nm (EQEs2). The first EQEPV setup (EQEs1) consists of a xenon lamp, a monochromator (Oriel Cornerstone), a Jaissle 1002 potentiostat and a lock-in amplifier (SR830, Stanford Research Systems). The light from the xenon lamp was modulated by a mechanical chopper and coupled into the monochromator. A mechanical filter wheel equipped with long pass (LP) filters was used to avoid higher-order contributions and guarantees monochromatic illumination of the device. The potentiostat was used in a two-electrode configuration and serves as a current to voltage converter and as a high-performance preamplifier with variable gain ranging from 10 to 108 V A−1. The preamplifier, in combination with a phase-sensitive lock-in measurement technique (chopping frequency 173 Hz) enables highly-sensitive EQEPV measurements over several orders of magnitude. A calibrated silicon diode (Hamamatsu S2281) was used as a reference to correct for the xenon lamp spectrum. To extend the measurement range up to 1600 nm, a similar setup but equipped with a different light source was used (Tungsten-Halogen light source TS-428S, Princeton Instruments). The monochromator in this setup was a SpectraPro-300i from ARC. Furthermore, a DLPCA-200 Variable Gain Low Noise Current Amplifier from Femto was used as a preamplifier instead of the potentiostat. The rest of the setup is similar to the previously described EQEs1 setup featuring an optical chopper, mechanical filter wheel, and an SR830 lock-in amplifier. In addition to the calibrated silicon diode (Hamamatsu S2281), a calibrated InGaAs diode (Hamamatsu G12180) was used as a reference in the spectral region above 1100 nm. For any given device, typically 4 measurements were performed (with different amplification factors) form 350–1000 nm (×104), 600–1000 nm (×104), 900–1200 nm (×106) and 1010–1400 nm (×109). During measurements with high amplification (106–109) either a 800 nm LP or a combination of 800 nm LP and 1000 nm LP-filter were used to reduce stray light and improve the signal/noise ratio of the setup. As shown in Fig. S5b (ESI†) the individual EQEPV measurements coincide well and their large spectral overlaps allow to reliably combine the individual measurements.Optical absorbance
Optical transmission (T) measurements were performed with a double-beam UV-vis-NIR spectrometer from PerkinElmer (Lambda 1050). The optical absorbance (A) was calculated using the negative decadic logarithm of the transmission (A = −log10(T)).Electrochemistry
Electrochemical voltage spectroscopy (EVS) measurements of D18, Y6 and PC71BM were performed to determine their respective HOMO–LUMO energy levels using a Jaissle Potentiostat–Galvanostat IMP 88 PC-100. A three-electrode setup was used where an Ag/AgCl wire served as a quasi-reference electrode and two Pt-plates served as working and counter electrodes, respectively. The investigated organic materials were deposited onto the working electrode via drop-casting from chloroform solution in an N2 atmosphere. All EVS measurements were performed in a nitrogen filled glovebox using 0.1 M tetrabutylammonium hexafluorophosphate (TBAPF6) in acetonitrile (MeCN) as the electrolyte solution. All EVS measurements were started at a potential of 0 V followed by a stepwise increase/decrease of the applied potential by 10 mV. At each potential step, the resulting current was measured for 20 s and integrated to obtain the amount of charge (ΔQ) passing through the system for each voltage step. In the absence of an electrochemical reaction, no net current is observed leading to a constant baseline of ΔQ. The oxidation and reduction onsets of the materials were determined at the position where ΔQ starts to deviate from the baseline. Two separate measurements on freshly drop-casted materials were carried out to determine the oxidation and reduction onset respectively. Every measurement was externally calibrated by measuring the half-wave potential of a ferrocene/ferrocenium (Fc/Fc+)redox couple. The measured Fc/Fc+ half-wave potential was used to correct the RE and plot the measured data referring to the normal hydrogen electrode (NHE). An oxidation potential for Fc/Fc+ vs normal hydrogen electrode (NHE) of 400 mV39 was used. To convert the onset potentials vs. NHE into HOMO/LUMO levels in electron volt vs vacuum, the Fermi level of NHE vs. vacuum was taken as −4.75 eV.40Photoluminescence and electroluminescence
Photoluminescence and electroluminescence measurements of all the devices were acquired using a Shamrock SR-303i monochromator and an Andor Peltier-cooled iDus Si-CCD (420-OE) and InGaAs detector array (DU420A). A calibrated tungsten halogen source (Ocean Optics HL-2000) was used to determine the overall spectral response of the monochromator/detector systems. A 550 nm LP-filter was used for luminescence spectra recorded with the Si-CCD and a 795 nm LP-filter was used for measurements with the InGaAs detector array.For PL measurements the devices were excited with a solid-state laser (OBIS 488 nm LX 150 mW) with a wavelength of 488 nm and optical output power of 1 mW. The LP-filters in front of the monochromator successfully suppressed the 488 nm laser light and allowed the acquisition of a PL spectrum without the influence of the excitation light.
For EL measurements different potentials were applied to the solar cell using a Keithley 2401SourceMeter unit. The injection currents were kept low and typically did not, or just barely exceed the observed photocurrents under AM1.5G illumination.
EQEEL
Measurements to estimate the EQEEL were performed using a calibrated, large area Si-photodiode (Hamamatsu S2281). The organic solar cell (0.173 cm2) was positioned in the center and directly in front of the large area Si photodiode (1 cm2). A Keithley 2401SourceMeter was used to operate the solar cell as a LED, while another Keithley 2401SourceMeter unit was used to measure the photocurrent of the Si-photodiode. When operated in the dark, photocurrent measured on the Si-diode results from the absorption of photons which were emitted by the organic solar cell. The photocurrent can be transformed into the equivalent light power using the spectral responsivity (A W−1) of the calibrated Si-diode. From EL measurements of the organic solar cell as described above, the relative spectral distribution of the photons is known. Under the assumption that all light emitted from the solar cell is collected by the large area Si-diode, integration of the EL-spectrum has to match the total absorbed light power at the photodiode. Thus, the absorbed light power at the photodiode can be used to appropriately scale the measured relative EL-spectrum. The resulting absolute EL-spectrum represents the amount of emitted photons per second at each wavelength. The EQEEL (#photons/#electrons) can be estimated by comparing the injection current (∝ #electrons per s) with the integral of the absolute EL-spectrum over all wavelengths (#photons per s). This procedure only considers photons that can escape the device. Due to the device geometry of organic solar cells consisting of layers of materials with different refractive indices this is not the case and outcoupling losses due to total reflection and light-guiding must be considered. The main outcoupling loss is caused by total reflection at the glass–air interface where the change of the refractive index is most significant. Calculating the escape cone based on the refractive indices of air(n = 1.00) and glass (n = 1.51) and assuming a fully reflective back surface (Ag-electrode) leads to a correction factor of 4.00, which was multiplied to the experimentally derived EQEEL values. Y6-based devices had to be corrected additionally due to their extended NIR emission. Typically, a minor part of the EL-spectrum was extending beyond 1100 nm. In this spectral region, the radiation does not contribute to the photocurrent measured on the Si-photodiode and had to be considered in the calculation of the EQEEL.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support by the Austrian ‘‘Climate and Energy Fund’’ within the program Energy Emission Austria (Project: ALTAFOS, FFG No. 865 072) is gratefully acknowledged.References
- V. R. Bommisetty, N. S. Sariciftci, K. Narayan, G. Rumbles, P. Peumans, J. van de Lagemaat, G. Dennler and S. E. Shaheen, Organic Photovoltaics and Related Electronics - From Excitons to Devices, Materials Research Society Symposium Proceedings vol. 1270, 2010.
- A. J. Heeger, N. S. Sariciftci and E. B. Namdas, Semiconducting and Metallic Polymers, Oxford University Press, 2010 Search PubMed.
- M. C. Scharber and N. S. Sariciftci, Low Band Gap Conjugated Semiconducting Polymers, Adv. Mater. Technol., 2021, 2000857 Search PubMed.
- J. Zhao, Y. Li, G. Yang, K. Jiang, H. Lin, H. Ade, W. Ma and H. Yan, Efficient organic solar cells processed from hydrocarbon solvents, Nat. Energy, 2016, 1, 15027 Search PubMed.
- M. C. Scharber, On the Efficiency Limit of Conjugated Polymer:Fullerene-Based Bulk Heterojunction Solar Cells, Adv. Mater., 2016, 28, 1994–2001 Search PubMed.
- S. Holliday, R. S. Ashraf, C. B. Nielsen, M. Kirkus, J. A. Röhr, C.-H. Tan, E. Collado-Fregoso, A.-C. Knall, J. R. Durrant, J. Nelson and I. McCulloch, A Rhodanine Flanked Nonfullerene Acceptor for Solution-Processed Organic Photovoltaics, J. Am. Chem. Soc., 2015, 137, 898–904 Search PubMed.
- Y. Lin, J. Wang, Z.-G. Zhang, H. Bai, Y. Li, D. Zhu and X. Zhan, An electron acceptor challenging fullerenes for efficient polymer solar cells, Adv. Mater., 2015, 27, 1170–1174 Search PubMed.
- K. Jin, Z. Xiao and L. Ding, D18, an eximious solar polymer!, J. Semicond., 2021, 42, 10502 Search PubMed.
- Y. Cui, H. Yao, L. Hong, T. Zhang, Y. Tang, B. Lin, K. Xian, B. Gao, C. An, P. Bi, W. Ma and J. Hou, 17% efficiency organic photovoltaic cell with superior processability, Nat. Sci. Rev., 2020, 7, 1239–1246 Search PubMed.
- S. Liu, J. Yuan, W. Deng, M. Luo, Y. Xie, Q. Liang, Y. Zou, Z. He, H. Wu and Y. Cao, High-efficiency organic solar cells with low non-radiative recombination loss and low energetic disorder, Nat. Photonics, 2020, 14, 300–305 Search PubMed.
- B. Fan, D. Zhang, M. Li, W. Zhong, Z. Zeng, L. Ying, F. Huang and Y. Cao, Achieving over 16% efficiency for single-junction organic solar cells, Sci. China: Chem., 2019, 62, 746–752 Search PubMed.
- T. Wang, J. Qin, Z. Xiao, X. Meng, C. Zuo, B. Yang, H. Tan, J. Yang, S. Yang, K. Sun, S. Xie and L. Ding, A 2.16 eV bandgap polymer donor gives 16% power conversion efficiency, Sci. Bull., 2020, 65, 179–181 Search PubMed.
- Y. Wu, Y. Zheng, H. Yang, C. Sun, Y. Dong, C. Cui, H. Yan and Y. Li, Rationally pairing photoactive materials for high-performance polymer solar cells with efficiency of 16.53%, Sci. China: Chem., 2020, 63, 265–271 Search PubMed.
- J. Xiong, K. Jin, Y. Jiang, J. Qin, T. Wang, J. Liu, Q. Liu, H. Peng, X. Li, A. Sun, X. Meng, L. Zhang, L. Liu, W. Li, Z. Fang, X. Jia, Z. Xiao, Y. Feng, X. Zhang, K. Sun, S. Yang, S. Shi and L. Ding, Thiolactone copolymer donor gifts organic solar cells a 16.72% efficiency, Sci. Bull., 2019, 64, 1573–1576 Search PubMed.
- J. Yuan, Y. Zhang, L. Zhou, G. Zhang, H.-L. Yip, T.-K. Lau, X. Lu, C. Zhu, H. Peng, P. A. Johnson, M. Leclerc, Y. Cao, J. Ulanski, Y. Li and Y. Zou, Single-Junction Organic Solar Cell with over 15% Efficiency Using Fused-Ring Acceptor with Electron-Deficient Core, Joule, 2019, 3, 1140–1151 Search PubMed.
- Q. Liu, Y. Jiang, K. Jin, J. Qin, J. Xu, W. Li, J. Xiong, J. Liu, Z. Xiao, K. Sun, S. Yang, X. Zhang and L. Ding, 18% Efficiency organic solar cells, Sci. Bull., 2020, 65, 272–275 Search PubMed.
- U. Rau, Reciprocity relation between photovoltaic quantum efficiency and electroluminescent emission of solar cells, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76(8), 085303 Search PubMed.
- T. Kirchartz and U. Rau, Detailed balance and reciprocity in solar cells, Phys. Status Solidi A, 2008, 205, 2737–2751 Search PubMed.
- W. Shockley and H. J. Queisser, Detailed Balance Limit of Efficiency of p-n Junction Solar Cells, J. Appl. Phys., 1961, 32, 510–519 Search PubMed.
- J. Yao, T. Kirchartz, M. S. Vezie, M. A. Faist, W. Gong, Z. He, H. Wu, J. Troughton, T. Watson, D. Bryant and J. Nelson, Quantifying Losses in Open-Circuit Voltage in Solution-Processable Solar Cells, Phys. Rev. Appl., 2015, 4(1), 014020 Search PubMed.
- J. Wang, H. Yao, Y. Xu, L. Ma and J. Hou, Recent progress in reducing voltage loss in organic photovoltaic cells, Mater. Chem. Front., 2021, 5, 709–722 Search PubMed.
- L. C. Hirst and N. J. Ekins-Daukes, Fundamental losses in solar cells, Prog. Photovoltaics, 2011, 19, 286–293 Search PubMed.
- U. Rau, B. Blank, T. C. M. Müller and T. Kirchartz, Efficiency Potential of Photovoltaic Materials and Devices Unveiled by Detailed-Balance Analysis, Phys. Rev. Appl., 2017, 7(4), 044016 Search PubMed.
- W. Zhou, S. Xie, S. Qian, G. Wang and L. Qian, Photothermal deflection spectra of solid C60, J. Phys.: Condens. Matter, 1996, 8, 5793–5800 Search PubMed.
- T. E. Saraswati, U. H. Setiawan, M. R. Ihsan, I. Isnaeni and Y. Herbani, The Study of the Optical Properties of C60 Fullerene in Different Organic Solvents, Open Chem., 2019, 17, 1198–1212 Search PubMed.
- C. M. Cardona, W. Li, A. E. Kaifer, D. Stockdale and G. C. Bazan, Electrochemical considerations for determining absolute frontier orbital energy levels of conjugated polymers for solar cell applications, Adv. Mater., 2011, 23, 2367–2371 Search PubMed.
- K. Vandewal, J. Benduhn and V. C. Nikolis, How to determine optical gaps and voltage losses in organic photovoltaic materials, Sustainable Energy Fuels, 2018, 2, 538–544 Search PubMed.
- K. Vandewal, S. Albrecht, E. T. Hoke, K. R. Graham, J. Widmer, J. D. Douglas, M. Schubert, W. R. Mateker, J. T. Bloking, G. F. Burkhard, A. Sellinger, J. M. J. Fréchet, A. Amassian, M. K. Riede, M. D. McGehee, D. Neher and A. Salleo, Efficient charge generation by relaxed charge-transfer states at organic interfaces, Nat. Mater., 2014, 13, 63–68 Search PubMed.
- T. Kirchartz, U. Rau, M. Kurth, J. Mattheis and J. H. Werner, Comparative study of electroluminescence from Cu(In,Ga)Se2 and Si solar cells, Thin Solid Films, 2007, 515, 6238–6242 Search PubMed.
- M. A. Green, Radiative efficiency of state-of-the-art photovoltaic cells, Prog. Photovoltaics, 2012, 20, 472–476 Search PubMed.
- D. Qian, Z. Zheng, H. Yao, W. Tress, T. R. Hopper, S. Chen, S. Li, J. Liu, S. Chen, J. Zhang, X.-K. Liu, B. Gao, L. Ouyang, Y. Jin, G. Pozina, I. A. Buyanova, W. M. Chen, O. Inganäs, V. Coropceanu, J.-L. Bredas, H. Yan, J. Hou, F. Zhang, A. A. Bakulin and F. Gao, Design rules for minimizing voltage losses in high-efficiency organic solar cells, Nat. Mater., 2018, 17, 703–709 Search PubMed.
- X.-K. Chen, V. Coropceanu and J.-L. Brédas, Assessing the nature of the charge-transfer electronic states in organic solar cells, Nat. Commun., 2018, 9, 5295 Search PubMed.
- S. Li, L. Zhan, C. Sun, H. Zhu, G. Zhou, W. Yang, M. Shi, C.-Z. Li, J. Hou, Y. Li and H. Chen, Highly Efficient Fullerene-Free Organic Solar Cells Operate at Near Zero Highest Occupied Molecular Orbital Offsets, J. Am. Chem. Soc., 2019, 141, 3073–3082 Search PubMed.
- Y. Zou, Y. Dong, C. Sun, Y. Wu, H. Yang, C. Cui and Y. Li, High-Performance Polymer Solar Cells with Minimal Energy Loss Enabled by a Main-Chain-Twisted Nonfullerene Acceptor, Chem. Mater., 2019, 31, 4222–4227 Search PubMed.
- J. Zhang, W. Liu, G. Zhou, Y. Yi, S. Xu, F. Liu, H. Zhu and X. Zhu, Accurate Determination of the Minimum HOMO Offset for Efficient Charge Generation using Organic Semiconducting Alloys, Adv. Energy Mater., 2020, 10, 1903298 Search PubMed.
- C. Sun, S. Qin, R. Wang, S. Chen, F. Pan, B. Qiu, Z. Shang, L. Meng, C. Zhang, M. Xiao, C. Yang and Y. Li, High Efficiency Polymer Solar Cells with Efficient Hole Transfer at Zero Highest Occupied Molecular Orbital Offset between Methylated Polymer Donor and Brominated Acceptor, J. Am. Chem. Soc., 2020, 142, 1465–1474 Search PubMed.
- S. Karuthedath, J. Gorenflot, Y. Firdaus, N. Chaturvedi, C. S. P. de Castro, G. T. Harrison, J. I. Khan, A. Markina, A. H. Balawi, T. A. D. Peña, W. Liu, R.-Z. Liang, A. Sharma, S. H. K. Paleti, W. Zhang, Y. Lin, E. Alarousu, D. H. Anjum, P. M. Beaujuge, S. de Wolf, I. McCulloch, T. D. Anthopoulos, D. Baran, D. Andrienko and F. Laquai, Intrinsic efficiency limits in low-bandgap non-fullerene acceptor organic solar cells, Nat. Mater., 2021, 20, 378–384 Search PubMed.
- J. Sworakowski, How accurate are energies of HOMO and LUMO levels in small-molecule organic semiconductors determined from cyclic voltammetry or optical spectroscopy?, Synth. Met., 2018, 235, 125–130 Search PubMed.
- T. Nishinaga, Organic Redox Systems. Synthesis, Properties, and Applications, John Wiley & Sons, Inc., Hoboken, New Jersey, 2016 Search PubMed.
- D. Baran, A. Balan, S. Celebi, B. Meana Esteban, H. Neugebauer, N. S. Sariciftci and L. Toppare, Processable Multipurpose Conjugated Polymer for Electrochromic and Photovoltaic Applications, Chem. Mater., 2010, 22, 2978–2987 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma00293g |
| This journal is © The Royal Society of Chemistry 2021 |