Open Access Article
Open Access ArticleAnharmonicity and ultralow thermal conductivity in layered oxychalcogenides BiAgOCh (Ch = S, Se, and Te)†
Jingyu
Li‡
 a,
Wenya
Zhai‡
a,
Wenya
Zhai‡
 a,
Chi
Zhang
b,
Yuli
Yan
*a,
Peng-Fei
Liu
a,
Chi
Zhang
b,
Yuli
Yan
*a,
Peng-Fei
Liu
 *cd and
Gui
Yang
e
*cd and
Gui
Yang
e
aInstitute for Computational Materials Science, School of Physics and Electronics, International Joint Research Laboratory of New Energy Materials and Devices of Henan Province, Henan University, Kaifeng 475004, China. E-mail: yanyl@henu.edu.cn
bCollege of Electrical Engineering, Henan University of Technology, Zhengzhou 450001, China
cInstitute of High Energy Physics, Chinese Academy of Sciences (CAS), Beijing 100049, China. E-mail: pfliu@ihep.ac.cn
dSpallation Neutron Source Science Center, Dongguan 523803, China
eSchool of Physics and Electrical Engineering, Anyang Normal University, Anyang 455000, China
First published on 14th June 2021
Abstract
Understanding the lattice dynamics and low thermal conductivities of oxychalcogenide materials is critical to the development of a new generation of better thermoelectric oxide materials. Here we systematically investigate the lattice vibrational modes as well as phonon thermal conductivity of experimentally synthesized layered oxychalcogenides BiAgOCh (Ch = S, Se, and Te). First-principles calculations indicate that BiAgOSe and BiAgOTe are dynamically stable and low-thermal-conductivity materials. The room-temperature lattice thermal conductivity for BiAgOTe is calculated to be 0.53 W m−1 K−1, which is smaller than that (0.88 W m−1 K−1) of the promising thermoelectric material BiCuOSe. The strong anharmonicity in BiAgOTe causes short lifetime and low group velocity, which accordingly gives rise to ultralow thermal conductivity in BiAgOTe compounds. Our work of the insights into the lattice dynamics and low thermal conductivity will help the development of high-performance thermoelectric oxide materials.
1. Introduction
Thermoelectric (TE) materials have long been considered as an alternative tool for power generation and refrigeration due to the capability of direct conversion between thermal and electrical energy without any mechanical moving parts.1 The conversion efficiency of TE materials is determined by a dimensionless figure of merit ZT = S2σT/κ, where S, σ, κ, and T are the Seebeck coefficient, electrical conductivity, thermal conductivity, and absolute temperature, respectively.2 Extensive efforts have been devoted to enhancing ZT with strategies of optimizing S2σ by band engineering3 and reducing κ through alloying/nanostructuring. However, the complex coupling in the thermoelectric performance parameters usually hampers the enhancement of ZT. The discovery of thermoelectric material SnSe (2.6 ± 0.3 at T = 935 K)4 demonstrates that screening materials with intrinsically low thermal conductivity is an effective strategy for achieving a high ZT.5,6 This simple method helps people to focus on the optimization of electrical transport properties alone without considering complex thermoelectric parameters.Recently, BiCuOSe oxyselenides have acquired ever-increasing attention as very promising thermoelectric materials due to their high value of ZT (1.5 at 900 K).7–12 The outstanding TE properties could be mainly ascribed to the intrinsically low thermal conductivity of BiCuOSe and its alloys.13–18 In previous studies, much attention has been paid to the lattice dynamics of BiCuOSe with first-principles calculations. The data on Ag-based compounds are still scarce in the literature. As the isomorphic crystals of BiCuOSe, Ag atoms have larger atomic radius and heavier atomic mass than Cu atoms, which enable BiAgOCh to exhibit large unit cell volumes and low thermal conductivity. The dual effects of lone pairs in Bi atoms and rattling vibrations in Ag atoms give BiAgOCh compounds weakly bonded [Bi2O2] and [Ag2Ch2] layers, which could lead to distinct interlayer interactions and further decrease the lattice thermal conductivity. To discriminate differences and understand the origin of the intrinsically low thermal conductivity for both BiAgOCh and BiCuOCh compounds, the study of the lattice dynamics in BiAgOCh compounds is of fundamental interest.
In this work, we investigate the phonon transport of BiAgOCh through solving the linearized phonon Boltzmann transport equation. The lattice thermal conductivity for BiAgOTe is calculated to be 0.53 W m−1 K−1 at room temperature, which is smaller than that for BiCuOSe (0.88 W m−1 K−1). The large Grüneisen parameters in the wide frequency range indicate strong anharmonicity in BiAgOTe. Besides, the compounds have low group velocities and short phonon lifetimes. The low-frequency optical modes contribute observably to the total thermal conductivity, while high-frequency optical phonons cannot be neglected. These features synergistically dominate the ultralow thermal conductivity of BiAgOTe.
2. Computational details
First-principles calculations are performed by the projector augmented-wave (PAW) method within the framework of density functional theory (DFT) as implemented in Vienna Ab initio Simulation Package (VASP).19,20 The structure is relaxed with the generalized gradient approximation (GGA) with Perdew Burke–Ernzerhof (PBE) exchange–correlation potential.21 The convergence threshold and Hellmann–Feynman forces are set at 10−6 eV and 0.01 eV Å−1, respectively. The O: 2s22p4, Ag: 4s14d10, S: 3s23p4, Bi: 6s26p3, Se: 4s24p4, and Te: 5s25p4 are treated as basis set of valence electronic orbits, respectively. The plane wave basis set with kinetic energy cutoff is chosen to be 500 eV, and the 13 × 13 × 8 Monkhorst–Pack special k-point meshes are used to sample the Brillouin Zone. The van der Waals D3 (vdW-D3) corrections are taken into account for the interlayer van der Waals interactions.The phonon dispersions and density of states (DOS) are calculated using density functional perturbation theory (DFPT) implemented in Phonopy code.22,23 In this process, the 3 × 3 × 2 supercell containing 144 atoms with a 3 × 3 × 2 k-mesh for the Brillouin zone sampling is used for second- and third-order force constant calculations. The lattice thermal conductivity using a single-mode relaxation-time (SMRT) method is obtained from the following formulae:24
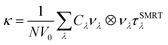 | (1) |
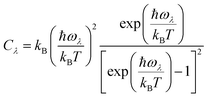 | (2) |
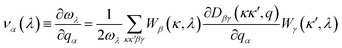 | (3) |
In this study, the phonon relaxation time is given by
τλSMRT ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) τλ τλ | (4) |
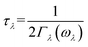 | (5) |
In addition, the phonon mode contributions to the anisotropic κ are discussed using cumulative lattice thermal conductivity defined by
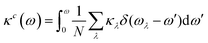 | (6) |
This method above with the simulation package Phono3py code23 has been successfully applied to predicting the thermal conductivities of many other materials, such as ZrNiPb,25 BiTeBr,26 and TaCoSn27et al.
3. Results and discussion
As shown in Fig. 1(a), similar to the geometry of BiCuOSe, isostructural BiAgOCh crystals can be described as a stacking of two layers consisting of a positively charged oxide (Bi2O22+) layer and a negatively charged chalcogenide (Ag2Ch22−) layer in the sequence. The optimized lattice constants are a = 3.99, 4.04, 4.14 Å and c = 9.26, 9.65, 10.21 Å for BiAgOS, BiAgOSe, and BiAgOTe, respectively, which are close to the experimentally measured values.8 These smallish differences are mainly due to the fact that GGA often overestimates the lattice constants of solids.28Fig. 1(b) shows the calculated electron localization function for BiAgOCh with a cut by the (100) plane. In BiAgOCh compounds, Ag and Ch atoms show a weaker bonding than that of Bi and O atoms, which is similar to BiCuOSe materials. This reveals anisotropy in bonding character occurring due to the existence of a distinct oxide (Bi2O22+) layer and chalcogenide (Ag2Ch22−) layer. As discussed in our prior work,29 the Ag–Ch bonding is substantially stronger than the Bi–Ch, Bi–Ag and Bi–O bonding. The coexistence of global and local chemical bonds with hierarchical strengths7 may lead to strong anisotropic lattice thermal conductivity. Distinctly, Ag and Ch atoms show a relatively weaker bonding than Cu and Ch atoms, and this is consistent with the fact that Ag–Ch distances are always longer than the values of Cu–Ch bonds. The weak bonding of the Cu atoms in BiCuOSe compounds and superionic conductor Cu2−xSe30 has been confirmed to play a key role in decreasing lattice thermal conductivity. Hence the weak Ag bonding may also reduce the κ in BiAgOCh.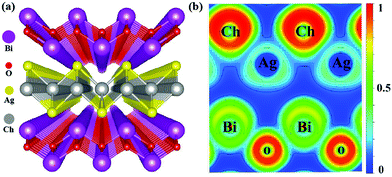 | ||
| Fig. 1 (a) Schematic illustration of the layered BiAgOCh (Ch = S, Se, and Te) crystal structures. (b) Electron localization function of BiAgOCh projected on the (100) plane. | ||
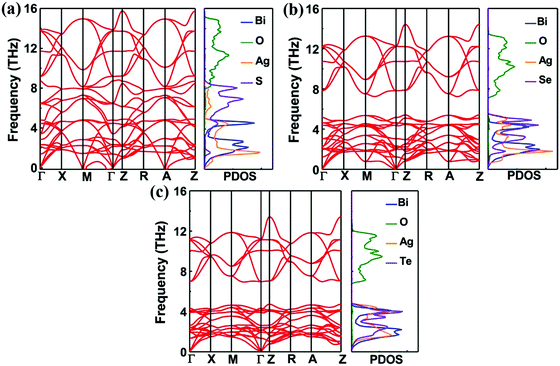
Fig. 2 shows the phonon dispersion and vibrational DOS for BiAgOCh materials. All of the phonon frequencies of BiAgOSe and BiAgOTe are positive in the Brillouin zone, which indicates that the structures of the two materials are dynamically stable. For BiAgOS, these are a few negative modes around Γ, M, and A points. The highest cutoff frequencies are 15.74, 14.41, and 13.42 THz for BiAgOS, BiAgOSe and BiAgOTe, respectively, with the chalcogen atomic number increasing. In all compounds, the vibrations of O decoupled from other atoms and occupy the high-frequency optical region above about 6.73 THz, while the acoustic vibrations and the low-frequency optical branches are mainly from the Bi, Ag, and Ch atoms. Such distributions are primarily ascribed to the large mass difference between O and Bi/Ag/Ch atoms. In BiAgOS, there is no phonon gap in the range from 4 and 8 THz with weak coupling vibrations between O and S atoms. Meanwhile, a complete decoupling optic phonon gap appears in BiAgOSe and BiAgOTe and gradually increases when going from S to Se, and Te with the increasing mass. The mass homology relation can be employed to explain the above mode frequency difference.16 In particular, the mass of the unit cell Muc changes from 729.826 amu for BiOAgS to 920.896 amu for BiOAgTe, by a factor of 1.26. Therefore, the mode frequencies can be decreased by the factor if replacing the mass of S by that of Te. The change in the middle low-frequency region of the phonon dispersion is the reason for the formation of the optical–optical gap.
In order to analyze the origin of low lattice thermal conductivity in BiAgOCh, the phonon lifetime τ and Grüneisen parameters γ are calculated in Fig. 3. The three lowest phonon Grüneisen parameters and lifetime are shown in Fig. S2 (ESI†). The γ is a dimensionless quantity measuring the anharmonic interaction of a crystal, which can be obtained by31,32
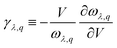 | (7) |
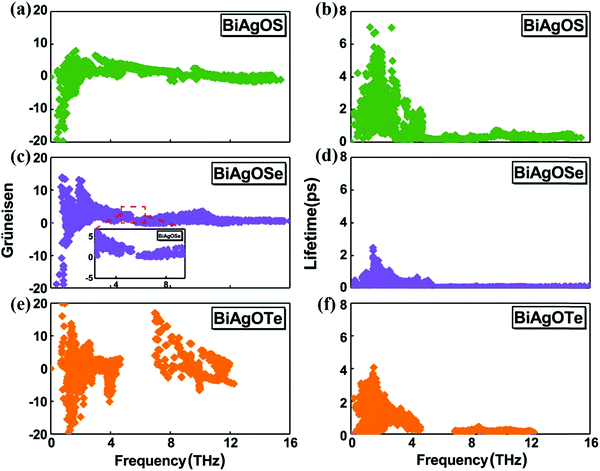 | ||
| Fig. 3 Calculated Grüneisen parameters for (a) BiAgOS, (c) BiAgOSe, and (e) BiAgOTe. Phonon lifetime for (b) BiAgOS, (d) BiAgOSe, and (f) BiAgOTe. | ||
Generally, a system with large |γ| implies that it possesses strong anharmonicity and phonon–phonon scattering, resulting in short phonon relaxation time τ and low κ. Obviously, the BiAgOCh possess obviously large |γ| at low-frequency acoustic phonon modes (Fig. 3). This will generate strong phonon–phonon interaction, and thus lead to the low lattice thermal conductivity in BiAgOCh. Generally speaking, acoustic phonon modes dominate the lattice thermal conductivity. The tiny unstable acoustic phonon modes for BiAgOS and softened phonon modes for BiAgOSe along the Γ–M direction can be seen as the reason for strong anharmonicity in the low-frequency region. From Fig. 3(b), (d) and (f), the phonon lifetime of acoustic branches is higher than their optical modes for all materials. The τ of BiAgOSe at low frequency acoustic branches is apparently smaller than that of BiAgOTe and BiAgOS. In high-frequency optical branches, the phonon lifetime for BiAgOTe in a wide frequency range remains unaffected, which indicates that optical branches do not enhance the scattering channels for BiAgOTe.
The phonon velocities (υ) are closely relevant to the phonon transportation of BiAgOCh. In general, the reduced υ will lower κ. Herein we calculate the υ in Fig. 4. For all compounds, it is clearly seen that the group velocities of optical phonon modes are higher than those of acoustic modes. In BiAgOS and BiAgOTe, the group velocities along the x-direction are different from those along the z-direction, which leads to a strong anisotropy of lattice thermal conductivity. Among the three compounds, BiAgOTe possesses the lowest group velocities along both the x and z-direction. Combined with the above analysis, the slow speed of phonon, large phonon lifetime τ, and strong phonon anharmonicity will give an ultralow κ in BiAgOTe according to Slack's theory.33
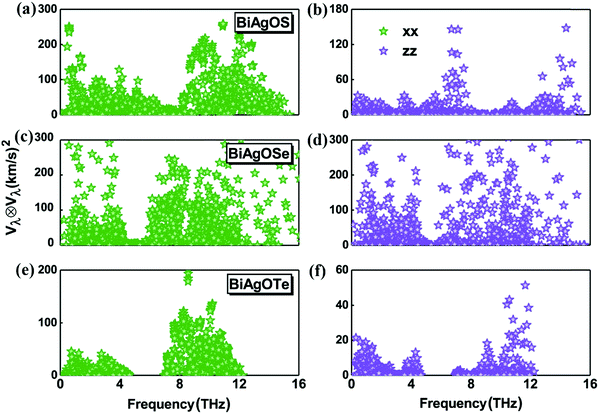 | ||
| Fig. 4 Phonon group velocities as a function of frequency for (a and b) BiAgOS, (c and d) BiAgOSe, and (e and f) BiAgOTe along x (left column) or z-direction (right column). | ||
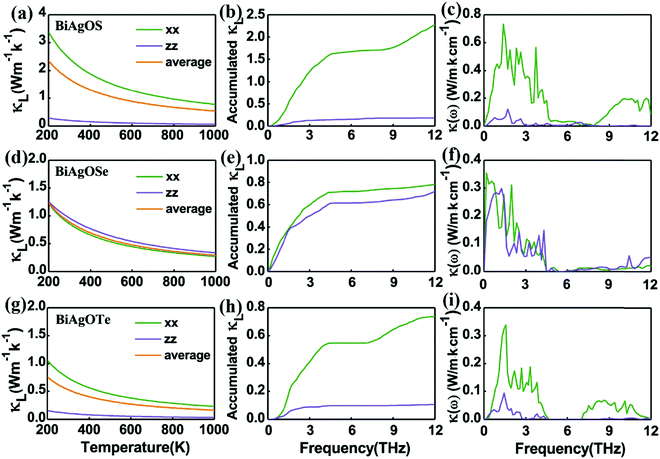
The calculated lattice thermal conductivity of BiAgOCh as a function of temperature is shown in Fig. 5. BiAgOTe shows the lowest lattice thermal conductivity among the three compounds. The average lattice thermal conductivity is calculated to be 0.53 W m−1 K−1 at room temperature for BiAgOTe, which is lower than those of 2.35 W m−1 K−1 for PbTe,34 0.62 W m−1 K−1 for SnSe,35 0.88 W m−1 K−1 for BiCuSeO,36 and 0.82 W m−1 K−1 for MgAgSb.37 Meanwhile, its κ exhibits strong anisotropy. There are two reasons for this: (1) the acoustic branches and some optical branches present different dispersions along the Γ–Z and Γ–X directions, which causes an enormous difference in low group velocities along two different directions; (2) the atomic interactions along the z (weak electrostatic interactions) and x directions (strong covalent and ionic bonding interactions) are different. The weak electrostatic interactions along the z direction impede the phonon transport and result in low κ. For BiAgOS and BiAgOTe, the room temperature lattice thermal conductivities along z-directions are 0.20 and 0.11 Wm−1 K−1, which are much lower than the x-direction (2.43 and 0.74 Wm−1 K−1). In the case of BiAgOSe, the in-plane thermal conductivity is initially larger than the cross-plane value, decreases with raising the temperature, and becomes slightly lower than the cross-plane value after 200 K. In order to probe into its origin, we have calculated the band structures and density of states of BiAgOSe. As shown in Fig. S3 (ESI†), BiAgOS, BiAgOSe, and BiAgOTe are all indirect band gap semiconductors since the valence-band maximum (VBM) and conduction band minimum (CBM) locate at different points. The band edges changes and exhibit multi-valley features when going from S, Se, to Te. As for BiAgOSe, the VBM is along the Γ to M direction and the CBM is at the Z point. Although it shows a similar band structure as BiAgOS, the electronic transitions at the points along the Γ to Z direction easily occur with the smaller energy difference in BiAgOSe. From the density of states in Fig. S4 (ESI†), the Se p and Bi p electrons in BiAgOSe are highly delocalized in the VB and CB zones with sharp peaks. Such delocalized p electrons contribute to more orbital overlap along the out-of-plane direction for BiAgOSe, which endow BiAgOSe with 3D charge and accordingly quasi-3D phonon transports. Thus, BiAgOSe has quite different phonon transport among the three compounds.
The cumulative thermal conductivities along different directions first keep increasing quickly as frequency increases, and then gradually approach a plateau. In Fig. 5(b), (e) and (h), the peak of the derivatives drops rapidly at the high-frequency region because the acoustic phonon branches and the low-frequency optical phonon branches strongly coupled with acoustic modes dominate the lattice thermal conductivity of BiAgOCh. In the high-frequency region, it can be seen that the cumulative thermal conductivities of BiAgOS and BiAgOTe along the x-direction still increase further than that of BiAgOSe. This indicates phonons with a high-frequency region for BiCuOS and BiCuOTe along the x-direction have non-negligible contribution to the lattice thermal conductivity, which is different from most semiconductor materials.38–41
4. Conclusions
In summary, based on first-principles and phonon Boltzmann transport theory, we study in detail the intrinsic lattice thermal conductivity of BiAgOCh. The room-temperature lattice thermal conductivity of BiAgOTe is found to be 0.53 W m−1 K−1. Its low lattice thermal conductivity is mainly from relatively strong anharmonicity, short relaxation time, and low group velocities. In addition, we find that the anisotropy of lattice thermal conductivity stems from the presence of a distinct charged oxide (Bi2O22+) layer and a negatively charged chalcogenide (Ag2Ch22−) layer. Different from most semiconductors, the optical branches for BiAgOTe also contribute to total lattice thermal conductivity. These results imply that BiAgOTe may be a potential low thermal conductivity material, which will stimulate further experimental work to investigate the thermoelectric performance of BiAgOTe.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We acknowledge grants from the National Natural Science Foundation of China (U20041103 and 11805214).References
- L. E. Bell, Cooling, heating, generating power, and recovering waste heat with thermoelectric systems, Science, 2008, 321(5895), 1457–1461 CrossRef CAS PubMed.
- G. J. Snyder and E. S. Toberer, Complex thermoelectric materials. Materials for Sustainable Energy, 2011, pp. 101–110 Search PubMed.
- J. R. Sootsman, D. Y. Chung and M. G. Kanatzidis, New and old concepts in thermoelectric materials, Angew. Chem., Int. Ed., 2009, 48(46), 8616–8639 CrossRef CAS PubMed.
- L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals, Nature, 2014, 508(7496), 373–377 CrossRef CAS PubMed.
- X. Li, P.-F. Liu, E. Zhao, Z. Zhang, T. Guidi, M. D. Le, M. Avdeev, K. Ikeda, T. Otomo and M. Kofu, Ultralow thermal conductivity from transverse acoustic phonon suppression in distorted crystalline α-MgAgSb, Nat. Commun., 2020, 11(1), 1–9 CrossRef PubMed.
- P.-F. Liu, T. Bo, J. Xu, W. Yin, J. Zhang, F. Wang, O. Eriksson and B.-T. Wang, First-principles calculations of the ultralow thermal conductivity in two-dimensional group-IV selenides, Phys. Rev. B, 2018, 98(23), 235426 CrossRef CAS.
- M. Mukherjee and A. K. Singh, Strong Chemical Bond Hierarchy Leading to Exceptionally High Thermoelectric Figure of Merit in Oxychalcogenide AgBiTeO, ACS Appl. Mater. Interfaces, 2020, 12(7), 8280–8287 CrossRef CAS PubMed.
- J. Gamon, D. Giaume, G. Wallez, J.-B. Labégorre, O. Lebedev, R. Al Rahal Al Orabi, S. Haller, T. Le Mercier, E. Guilmeau and A. Maignan, Substituting copper with silver in the BiMOCh layered compounds (M = Cu or Ag; Ch = S, Se, or Te): crystal, electronic structure, and optoelectronic properties, Chem. Mater., 2018, 30(2), 549–558 CrossRef CAS.
- J. Li, C. Zhang, Y. Yan, J. Yang, B. Shi, Y. Wang and Z. Cheng, Predicting excellent anisotropic thermoelectric performance of the layered oxychalcogenides BiAgOCh (Ch = S, Se, and Te), Comput. Mater. Sci., 2020, 171, 109273 CrossRef CAS.
- M. M. Alsalama, H. Hamoudi, A. Abdala, Z. K. Ghouri and K. M. Youssef, Enhancement of Thermoelectric Properties of Layered Chalcogenide Materials, Rev. Adv. Mater. Sci., 2020, 59(1), 371–378 Search PubMed.
- S. Tippireddy, D. S. Prem Kumar, S. Das and R. C. Mallik, Oxychalcogenides as Thermoelectric Materials: an Overview, ACS Appl. Energy Mater., 2021, 4(3), 2022–2040 CrossRef CAS.
- Y. Liu, L. D. Zhao, Y. Zhu, Y. Liu, F. Li, M. Yu, D. B. Liu, W. Xu, Y. H. Lin and C. W. Nan, Synergistically optimizing electrical and thermal transport properties of BiCuSeO via a dual-doping approach, Adv. Energy Mater., 2016, 6(9), 1502423 CrossRef.
- J. Ding, B. Xu, Y. Lin, C. Nan and W. Liu, Lattice vibration modes of the layered material BiCuSeO and first principles study of its thermoelectric properties, New J. Phys., 2015, 17(8), 083012 CrossRef.
- D. Lin, S.-T. Dong, Y.-Y. Zhang, Y.-Y. Lv, J. Zhou, Y. Chen, R. Mole, S.-H. Yao and D. Yu, The physical mechanism of extremely low thermal conductivity of BiCuTeO and BiCuSeO revealed by inelastic neutron and Raman spectroscopy, J. Alloys Compd., 2020, 826, 154161 CrossRef CAS.
- D. Fan, H. Liu, L. Cheng, J. Zhang, P. Jiang, J. Wei, J. Liang and J. Shi, Understanding the electronic and phonon transport properties of a thermoelectric material BiCuSeO: a first-principles study, Phys. Chem. Chem. Phys., 2017, 19(20), 12913–12920 RSC.
- S. Saha, Exploring the origin of ultralow thermal conductivity in layered BiOCuSe, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92(4), 041202 CrossRef.
- S. Saha and G. Dutta, Elastic and thermal properties of the layered thermoelectrics BiOCuSe and LaOCuSe, Phys. Rev. B, 2016, 94(12), 12520 CrossRef.
- H. Shao, X. Tan, G.-Q. Liu, J. Jiang and H. Jiang, A first-principles study on the phonon transport in layered BiCuOSe, Sci. Rep., 2016, 6(1), 1–9 CrossRef PubMed.
- J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Real-space grid implementation of the projector augmented wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71(3), 035109 CrossRef.
- J. Hafner, Ab initio simulations of materials using VASP: density-functional theory and beyond, J. Comput. Chem., 2008, 29(13), 2044–2078 Search PubMed.
- M. Ernzerhof and J. P. Perdew, Generalized gradient approximation to the angle-and system-averaged exchange hole, J. Chem. Phys., 1998, 109(9), 3313–3320 CrossRef CAS.
- L. Chaput, A. Togo, I. Tanaka and G. Hug, Phonon–phonon interactions in transition metals, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84(9), 094302 CrossRef.
- L. Chaput, Direct solution to the linearized phonon Boltzmann equation, Phys. Rev. Lett., 2013, 110(26), 265506 CrossRef PubMed.
- A. Togo, L. Chaput and I. Tanaka, Distributions of phonon lifetimes in Brillouin zones, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91(9), 094306 CrossRef.
- D. Wang and G. Wang, First-principles study the elastic constant, electronic structure and thermoelectric properties of Zr1−xHfxNiPb (x = 0, 0.25, 0.5, 0.75, 1), Phys. Lett. A, 2017, 381(8), 801–807 CrossRef CAS.
- S.-D. Guo and H.-C. Li, Monolayer enhanced thermoelectric properties compared with bulk for BiTeBr, Comput. Mater. Sci., 2017, 139, 361–367 CrossRef CAS.
- E. Haque and M. A. Hossain, First-principles study of elastic, electronic, thermodynamic, and thermoelectric transport properties of TaCoSn, Results Phys., 2018, 10, 458–465 CrossRef.
- Z. Wu and R. E. Cohen, More accurate generalized gradient approximation for solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(23), 235116 CrossRef.
- J. Li, C. Zhang, Y. Yan, J. Yang and Z. Cheng, Predicting excellent anisotropic thermoelectric performance of the layered oxychalcogenides BiAgOCh (Ch = S, Se, and Te), Comput. Mater. Sci., 2020, 171, 109273 CrossRef CAS.
- H. Liu, X. Shi, F. Xu, L. Zhang, W. Zhang, L. Chen, Q. Li, C. Uher, T. Day and G. J. Snyder, Copper ion liquid-like thermoelectrics, Nat. Mater., 2012, 11(5), 422–425 CrossRef CAS PubMed.
- T. Barron, Grüneisen parameters for the equation of state of solids, Ann. Phys., 1957, 1(1), 77–90 CAS.
- J. Tan, Q.-D. Hao, Z.-Y. Zeng, X.-R. Chen and H.-Y. Geng, First-principles study of structural, electronic, and thermal conductivity properties of monolayer SrFBr, J. Phys. Chem. Solids, 2021, 109956 CrossRef CAS.
- G. A. Slack, The thermal conductivity of nonmetallic crystals, Solid State Phys., 1979, 34, 1–71 CAS.
- T. Parashchuk, I. Horichok, A. Kosonowski, O. Cherniushok, P. Wyzga, G. Cempura, A. Kruk and K. T. Wojciechowski, Insight into the transport properties and enhanced thermoelectric performance of n-type Pb1−xSbxTe, J. Alloys Compd., 2021, 860, 158355 CrossRef CAS.
- Y. Xiao, C. Chang, Y. Pei, D. Wu, K. Peng, X. Zhou, S. Gong, J. He, Y. Zhang and Z. Zeng, Origin of low thermal conductivity in SnSe, Phys. Rev. B, 2016, 94(12), 125203 CrossRef.
- Y.-L. Pei, J. He, J.-F. Li, F. Li, Q. Liu, W. Pan, C. Barreteau, D. Berardan, N. Dragoe and L.-D. Zhao, High thermoelectric performance of oxyselenides: intrinsically low thermal conductivity of Ca-doped BiCuSeO, NPG Asia Mater., 2013, 5(5), e47 CrossRef CAS.
- Y. Zheng, C. Liu, L. Miao, C. Li, R. Huang, J. Gao, X. Wang, J. Chen, Y. Zhou and E. Nishibori, Extraordinary thermoelectric performance in MgAgSb alloy with ultralow thermal conductivity, Nano Energy, 2019, 59, 311–320 CrossRef CAS.
- R. Guo, X. Wang and B. Huang, Thermal conductivity of skutterudite CoSb3 from first principles: substitution and nanoengineering effects, Sci. Rep., 2015, 5(1), 1–9 Search PubMed.
- K. Biswas, J. He, Q. Zhang, G. Wang, C. Uher, V. P. Dravid and M. G. Kanatzidis, Strained endotaxial nanostructures with high thermoelectric figure of merit, Nat. Chem., 2011, 3(2), 160–166 CrossRef CAS.
- C.-J. Yao, H.-L. Zhang and Q. Zhang, Recent progress in thermoelectric materials based on conjugated polymers, Polymers, 2019, 11(1), 107 CrossRef PubMed.
- J. Wu, Y. Sun, W.-B. Pei, L. Huang, W. Xu and Q. Zhang, Polypyrrole nanotube film for flexible thermoelectric application, Synth. Met., 2014, 196, 173–177 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma00375e |
| ‡ These two authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2021 |