Open Access Article
Open Access ArticleRapid production of bicontinuous macroporous materials using intrinsically polymerizable bijels†
Herman
Ching
,
Todd J.
Thorson
 ,
Brian
Paul‡
,
Brian
Paul‡
 and
Ali
Mohraz
and
Ali
Mohraz
 *
*
Department of Chemical and Biomolecular Engineering, University of California, Irvine, CA 92697-2580, USA. E-mail: mohraz@uci.edu
First published on 5th July 2021
Abstract
The discovery of bicontinuous interfacially jammed emulsion gels (bijels) in 2007 motivated the development of processing techniques to harness their unique morphological attributes in applications such as electrochemical energy storage and conversion, catalysis, and regenerative biomaterials. These techniques are primarily based on selective polymerization of one phase, and subsequent chemical processing of the resultant scaffold into porous, micro-architectured materials. A significant limitation of these protocols is the need to transport polymer precursors into one of the fluid phases after bijel formation, a time-consuming step that can also impose disruptive gravitational and interfacial stresses, sometimes causing a complete breakdown of the bijel backbone. Here, we introduce a class of intrinsically polymerizable bijels (IPBs) comprising partially miscible mixtures of solvent and poly(ethylene glycol) precursor, which can be directly transformed into bijel-templated materials (BTMs), completely bypassing the precursor transport step and relaxing the associated limitations of previous protocols. To achieve selective polymerization, we incorporated into the mixture a common fluorescent dye, sodium fluorescein, which had strong affinity for the monomer-poor phase. Spectrophotometry experiments demonstrated a local photon quenching effect due to the fluorescent dye, which in turn curtailed activation of the photoinitiator and thus prevented polymerization in the monomer-poor phase. We establish the generality of our approach by using different monomers and monomer blends, and demonstrate how this modularity enables tuning of the mechanical properties of BTMs, measured by flexural testing. Our protocol establishes a scalable and efficient platform for producing BTMs, paving the way for their protential applications in emerging technologies.
1. Introduction
Bicontinuous interfacially jammed emulsion gels, or bijels, are an emerging class of soft materials conceptualized in 2005 by Stratford et al.,1 and later experimentally realized in 2007 by Herzig et al.2 Bijels are typically formed by rapidly quenching a critical mixture of two partially miscible fluids into their miscibility gap, in the presence of near-neutrally wetting colloidal particles.3 The rapid quench initiates de-mixing of the fluids by spinodal decomposition, while the near-neutrally wetting particles irreversibly adsorb to the fluid–fluid interface.4 Eventually, the particles become jammed as a result of a reduction in fluid interfacial area, and de-mixing comes to a kinetic halt.5 The resulting material, a bijel, is a solid-stabilized emulsion with bicontinuous morphology and weak gel-like mechanical properties.6,7 Since their discovery, bijels have attracted considerable attention as templates for advanced materials synthesis, with applications ranging from cell delivery8 and regenerative biomaterials9 to electrochemical energy storage10–12 and catalysis.13 The main driver for this rapid surge in interest is twofold. First, inherent to the mechanism by which they are formed, bijels have a unique microstructure with desirable attributes at length scales relevant to the applications mentioned above.14 Particularly, they comprise a bicontinuous, tubular arrangement of two fluid phases with a uniform and tunable characteristic domain size, and a continuous interface with predominantly negative Gaussian curvatures (akin to saddle points) separating the two phases.15 These morphological characteristics are particularly attractive in applications that require transport of different species, reactants, ions, redox agents, cells, nutrients, drugs, or other materials throughout the structure, to drive their desired function.16,17 Second, because bijels are formed by a thermodynamically-driven de-mixing process, materials synthesis techniques based on bijel templating are inherently amenable to scaleup.10,18 In pursuit of utilizing the unique morphology of bijels for technological applications, Lee and Mohraz developed a robust method to chemically solidify and lock in their three-dimensional (3D) microstructure, transforming them into near-uniform macroporous functional materials bearing the beneficial morphological attributes of their parent bijels.19 This invention paved the way for the utility of bijels in the applications mentioned above to be demonstrated. However, a significant shortcoming of Lee's method is that polymer precursors, such as liquid monomers or oligomers, must be introduced into one of the continuous fluid domains by selective mass transfer, after the bijel is formed. This key intermediate step presents the following issues and challenges. First, it makes the process quite time-consuming: while a bijel typically takes a few seconds to form, replacing one of the fluid phases with a monomer solution can take several hours. Further, relying on mass transfer kinetics for this step puts limits on the dimensions and geometries of bijel-templated materials (BTMs) that can be synthesized. Finally, introduction of a third component (monomer solution) can impose interfacial or gravitational stresses within the system, which in turn can alter the bijel microstructure or result in its complete breakdown during the solvent–monomer exchange process.6,20To overcome these issues, here we introduce an alternative bijel processing route, using intrinsically polymerizable bijels (IPBs) comprising partially miscible mixtures of a solvent and a monomer. Upon quenching such a mixture into its miscibility gap, the fluids separate into monomer-rich and monomer-poor phases.21 The use of a reactive monomer in the mixture's original chemical makeup preconditions the bijel with crosslinking compounds and avoids the need for monomer infiltration. Bijels made from solvent and monomer mixtures are readily transformable into BTMs via selective photo-polymerization of their monomer-rich phase in the presence of a photoinitiator with strong affinity for this phase. To achieve full selectivity in polymerizing the monomer-rich phase, we implement local photon quenching by a fluorescent dye with preferential solubility into the monomer-poor phase. Our method relaxes all the constraints of Lee's method for bijel-based materials synthesis, provides a means for their large-scale production, and thereby opens the door for bringing the applications of these emerging materials to fruition.
Three IPB systems are presented to demonstrate the generality of our approach, and the ability to tune the mechanical properties of the resultant porous materials via their chemical makeup. The first system is a mixture of 1,4-butanediol (BD) and a difunctional monomer, poly(ethylene glycol) diacrylate (PEGDA, Mn: 250 g mol−1). The second system is a mixture of propylene glycol (PG) and a trifunctional monomer, trimethylolpropane ethoxylate triacrylate (TMPETA, Mn: 692 g mol−1). A third system comprising a blend of two different monomers will be discussed in the context of mechanical property modulation. For this, a monofunctional monomer, methoxy poly(ethylene glycol) monoacrylate (MPGA, Mw: 350 g mol−1), is added to replace a fraction of the PEGDA in the BD/PEGDA mixture. Three-point flexural testing demonstrates similar trends between the mechanical properties of BTMs and those of bulk solid samples prepared with their respective monomers. These results show how the mechanical properties of BTMs can be systematically modulated by using a mixture of two different monomers and changing their relative amounts.
Before we proceed, a note to compare our method to relevant existing technologies is warranted. Inclusion of a monomer in the bijel's precursor formulation has been demonstrated in other systems, particularly in bijels formed by direct mixing,22 solvent transfer,23 and solvent evaporation.24 However, our method offers important advantages over these existing protocols. First, bicontinuous structures formed through spinodal decomposition enjoy a number of morphological features unique to this mode of de-mixing, namely dynamic self similarity, uniform domain sizes, and negative Gaussian interfacial curvatures, as well as tunability of these parameters, which cannot be guaranteed through direct mixing routes. These particular attributes have been shown to offer critical utility and benefits to bijel-derived materials in health care and energy applications.8–10 Second, our pathway to spinodal decomposition is based on a temperature change mediated by heat transfer, rather than a compositional change controlled by mass transfer invoked in solvent transfer and solvent evaporation methods. The competition between these two modes of transport is enumerated by the Lewis number, Le = α/D, where α is the thermal diffusivity and D is the mass diffusivity. With D ∼ 10−10 m2 s−1 and α ∼ 10−4 m2 s−1 typical for the liquids used in our study,25 we get Le ∼ 106. The dramatically faster transport kinetics of our temperature-based process, quantified by Le, enables more consistent de-mixing rates throughout the volume, in turn providing access to bijel-derived materials with larger overall dimensions, more diverse geometries, and more uniform microstructure with our method.
2. Results and discussion
2.1. Phase behavior
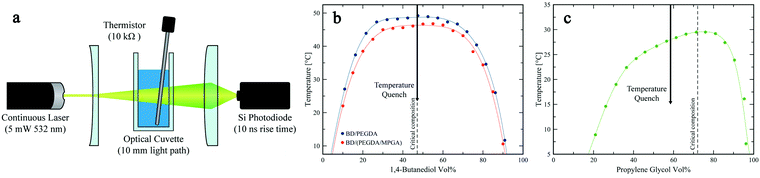
Development of bijels with new chemistries requires complete mapping of the phase diagram and miscibility limits of their candidate fluids.2 This information is important for the following reasons. First, to ensure bicontinuity, the pathway to phase separation should minimize the likelihood of droplet nucleation during de-mixing.26 This is typically achieved by instigating a rapid change in the mixture's thermodynamic state (either temperature or composition), from miscible conditions to deep within its miscibility gap. Knowledge of the mixture's critical point is key to ensuring that this pathway can bypass the nucleation and growth region of the phase diagram. Second, the shape, and particularly symmetry, of the phase diagram dictates the volumetric ratio of the fluid phases upon de-mixing. This parameter plays an important role in the formation of bijels: volumetric ratios significantly deviating from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 will influence the interfacial curvatures, which can in turn complicate particle packing, induce additional stresses at the fluid–fluid interface, and pinch off the bicontinuous domains or even break them up into discrete droplets.27–29 To this end, we assembled a simple thermometer-coupled turbidity meter and experimentally determined the phase boundaries of our three IPB systems.30Fig. 1a depicts a schematic of the turbidity meter setup, which is based on measuring light transmission through the mixture at different temperatures, as detailed in Section 4.2. We defined the cloud point, or phase transition temperature, as the temperature at which light transmission dropped below 95% of its maximum value at zero turbidity (i.e., when the formation of fluid–fluid interfaces resulted in at least 5% scattering of the incident beam).31 It must be noted that the locus of the phase boundary identified by this method is not very sensitive to the chosen scattering threshold. This was ascertained by observing that the transmitted light intensity drops dramatically over a narrow temperature range (see Fig. S1, ESI†). For each mixture, the cloud points were measured at various compositions to construct a binary phase diagram (plotted in Fig. 1b and c), and the mixture's upper critical solution temperature (UCST) and its corresponding composition were identified as the highest point on the concave down phase boundary, by fitting a third order Fourier series to the cloud point experimental data and numerically solving for its global maximum to within an accuracy of 0.1 °C.32 Notably, all three fluid systems have a UCST below 50 °C, easily accessible in simple laboratory settings. The critical compositions for the BD/PEGDA and BD/(PEGDA/MPGA) systems are both 47.5 vol% BD, with UCSTs of 48.7 °C and 46.3 °C, respectively. Because the phase boundaries represent equilibrium conditions governed by the chemical potential of the different constituents,26 deliberately choosing chemically alike monomers and replacing only a small amount of PEGDA with MPGA (PEGDA
1 will influence the interfacial curvatures, which can in turn complicate particle packing, induce additional stresses at the fluid–fluid interface, and pinch off the bicontinuous domains or even break them up into discrete droplets.27–29 To this end, we assembled a simple thermometer-coupled turbidity meter and experimentally determined the phase boundaries of our three IPB systems.30Fig. 1a depicts a schematic of the turbidity meter setup, which is based on measuring light transmission through the mixture at different temperatures, as detailed in Section 4.2. We defined the cloud point, or phase transition temperature, as the temperature at which light transmission dropped below 95% of its maximum value at zero turbidity (i.e., when the formation of fluid–fluid interfaces resulted in at least 5% scattering of the incident beam).31 It must be noted that the locus of the phase boundary identified by this method is not very sensitive to the chosen scattering threshold. This was ascertained by observing that the transmitted light intensity drops dramatically over a narrow temperature range (see Fig. S1, ESI†). For each mixture, the cloud points were measured at various compositions to construct a binary phase diagram (plotted in Fig. 1b and c), and the mixture's upper critical solution temperature (UCST) and its corresponding composition were identified as the highest point on the concave down phase boundary, by fitting a third order Fourier series to the cloud point experimental data and numerically solving for its global maximum to within an accuracy of 0.1 °C.32 Notably, all three fluid systems have a UCST below 50 °C, easily accessible in simple laboratory settings. The critical compositions for the BD/PEGDA and BD/(PEGDA/MPGA) systems are both 47.5 vol% BD, with UCSTs of 48.7 °C and 46.3 °C, respectively. Because the phase boundaries represent equilibrium conditions governed by the chemical potential of the different constituents,26 deliberately choosing chemically alike monomers and replacing only a small amount of PEGDA with MPGA (PEGDA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MPGA, volume ratio = 90
MPGA, volume ratio = 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10) would not significantly alter the phase behavior. This is further corroborated by the similarly-shaped binodal curves and the same critical composition between the two systems. Importantly, this enables blending a third, chemically similar, component into a binary IPB system, as a facile route for fine-tuning the mechanical properties of BTMs (detailed in Section 2.5) without the need to re-map the phase diagram for every new composition. The symmetric phase diagrams observed in Fig. 1b are advantageous to bijel formation, because the mixtures de-mix into near-equal volume domains.2,32 For the PG/TMPETA system (Fig. 1c), the critical composition is 72.2 vol% PG with a UCST of 29.5 °C. Because of its asymmetric binodal curve, spinodal decomposition at the critical composition will result in fluid domains of considerable disparate volumes in this system, which is not ideal for bijel formation.32 Nonetheless, Bai et al. have demonstrated a method to induce spinodal decomposition in an off-critical mixture by applying a deep quench that bypasses droplet nucleation.33 Similarly, we formed PG/TMPETA IPBs using an off-critical quench (at 58.5 vol% PG) that de-mixed into near-equal volume domains. The color coding used for the symbols in Fig. 1b and c will be utilized throughout the text to differentiate the three different systems.
10) would not significantly alter the phase behavior. This is further corroborated by the similarly-shaped binodal curves and the same critical composition between the two systems. Importantly, this enables blending a third, chemically similar, component into a binary IPB system, as a facile route for fine-tuning the mechanical properties of BTMs (detailed in Section 2.5) without the need to re-map the phase diagram for every new composition. The symmetric phase diagrams observed in Fig. 1b are advantageous to bijel formation, because the mixtures de-mix into near-equal volume domains.2,32 For the PG/TMPETA system (Fig. 1c), the critical composition is 72.2 vol% PG with a UCST of 29.5 °C. Because of its asymmetric binodal curve, spinodal decomposition at the critical composition will result in fluid domains of considerable disparate volumes in this system, which is not ideal for bijel formation.32 Nonetheless, Bai et al. have demonstrated a method to induce spinodal decomposition in an off-critical mixture by applying a deep quench that bypasses droplet nucleation.33 Similarly, we formed PG/TMPETA IPBs using an off-critical quench (at 58.5 vol% PG) that de-mixed into near-equal volume domains. The color coding used for the symbols in Fig. 1b and c will be utilized throughout the text to differentiate the three different systems.
2.2. Formation of IPBs
Previous bijel studies have shown that near-neutrally wetting particles can be fabricated by surface modification of silica nanoparticles (SNPs).32–34 We employed a similar process to synthesize fluorescently tagged SNPs with an average diameter of 200 nm and a coefficient of variance of 8.7%, as measured by scanning electron microscopy (SEM).35 To render the SNPs near-neutrally wetting, they were treated with hexamethyldisilazane (HMDS) to decorate their surfaces with hydrophobic trimethylsilyl groups (i.e., adding methyl groups to the surface),36 thereby resulting in a change of particle wettability with respect to the solvent and monomer fluids.37 For any tested IPB mixture, SNPs treated with too much or too little HMDS became too hydrophobic or too hydrophilic, respectively, to sustain a net-zero curvature at the fluid–fluid interface (see Fig. S2, ESI† for examples).28 These non-optimal SNPs preferentially wetted one phase and imparted curvature on the interface to produce discrete droplets.4,38 For each IPB system, the appropriate HMDS/particle ratio (detailed in Section 4.3) was determined experimentally through systematic variations until near-neutrally wetting conditions were met, marked by successful bijel formation.32To form BD/PEGDA and BD/(PEGDA/MPGA) bijels, near-neutrally wetting SNPs were dispersed in their respective critical mixtures at 70.0 °C and quenched by placing samples in direct contact with an aluminum heat sink at 22.5 °C. We note that the choice of our starting temperature was simply due to an existing oven in the laboratory that was maintained at 70.0 °C. In principle, other starting temperatures above the UCST should also yield the same results. Fig. 2a and b display confocal laser scanning microscopy (CLSM) images of these IPBs stabilized with 1 vol% SNPs. The bright regions in these images correspond to the fluid–fluid interfaces laden with fluorescently tagged SNPs. The bicontinuous and near-uniform fluid domains in these images confirm successful bijel formation. Interestingly, although PEGDA and MPGA are chemically similar, SNPs that formed bijels in the BD/PEGDA system failed to stabilize a BD/(PEGDA/MPGA) IPB, and vice versa. This outcome suggests that a small substitution of PEGDA with MPGA alters the overall liquid–particle interactions and the three-phase contact angle, and the surface treatment of the SNPs must be adjusted to compensate for this variation.39 As mentioned earlier, PG/TMPETA IPBs were made by quenching off-critical mixtures, which we found was necessary for successful bijel formation. If, instead, a critical mixture of PG/TMPETA was used, CLSM recordings of the de-mixing process revealed phase separation by droplet nucleation (CLSM frames shown in Fig. S3 (ESI†), where a fluorescein dye, which selectively partitions into the PG-rich phase, was added to the mixture to help visualize the de-mixing process). This result concurs with previous simulations of critical quenching in a fluid mixture with an asymmetric phase diagram, which predicted a transition to discrete droplet formation, and loss of bicontinuity.27,29 We tested various combinations of fluid composition and quenching temperatures, and observed bicontinuous phase separation when a mixture containing 58.5 vol% PG was quenched from 35.0 to 15.0 °C. This pathway enabled the formation of PG/TMPETA IPBs, as shown in Fig. 2c, and represents an atypical instance of bijel formation by quenching an off-critical mixture to a relatively shallow depth within its miscibility gap.33
The coarsening process of spinodal decomposition in simple liquid mixtures is governed by the interplay between surface tension and fluid viscosities.26 Asymmetry in molecular dynamics between the fluids, if present, can result in viscoelastic effects and unusual phenomena such as phase inversion or formation of a sponge-like network.40,41 Such disparity in physical and molecular properties is often linked to the appearance of an asymmetrical binodal phase diagram, akin to the PG/TMPETA mixture presented in Fig. 1c.42 Recently, Zhang et al. simulated thermally induced phase separation of a mixture with a highly asymmetric phase diagram that resulted in asynchronous growth between the two phases, giving rise to a morphological evolution pattern of droplets coalescing to form a bicontinuous network.43 We acknowledge that our off-critical quenches in the PG/TMPETA mixture may have initiated nucleation of droplets in the early stage of separation, which subsequently evolved into a percolating network with bicontinuous properties, similar to the mechanism proposed by Zhang et al. Determining the exact phase separation pathway in this case is beyond the scope of the current study. Nonetheless, our results demonstrate successful formation of bijels in the three tested mixtures, enabled by careful tuning of particle wettability and pathway to phase separation in each system. Note that similar unusual kinetics have been predicted in fluid mixtures exhibiting significant differences in domain volumes or shear viscosities between the two phases.44–47 Therefore, solvent/monomer mixtures that inherently involve ingredients of drastically different molecular weight or interactions may invoke unusual phase separation phenomena, and alternative pathways to bicontinuous phase separation, such as the off-critical quenching implemented here, should be considered in developing new IPB systems.
2.3. Photo-polymerization of IPBs
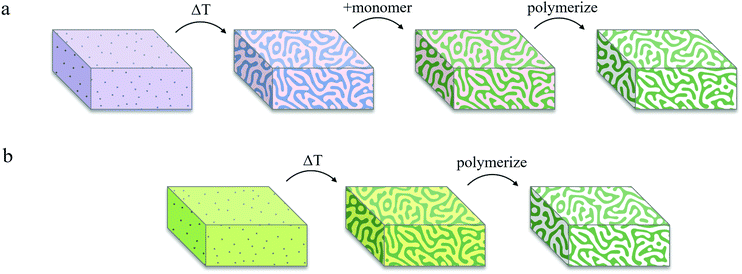
Fig. 3 represents a schematic comparison between Lee's bijel processing technique and our new IPB approach. To achieve selective templating, Lee exposed a bijel to a liquid mixture of monomer and photoinitiator that would selectively partition into one of the bijel fluid phases, typically requiring several hours (∼4 h) to complete, by far the longest step in the whole process, with the rest of the steps taking only a few minutes combined (Fig. 3a).19 This procedure also puts practical limits on the geometries in which BTMs can be formed. Our IPBs are preconditioned with reactive monomers within one of the fluid phases, which are immediately polymerizable using a photoinitiator (Fig. 3b). By eliminating the monomer infiltration step, the geometry and dimensions of the BTMs are restricted only by the heat transfer rate for IPB formation (a rapid temperature change is required to initiate spinodal decomposition, as discussed previously).3 However, an unwelcome consequence of bijel formation using a monomer/solvent mixture is that the monomer-poor phase still contains a finite concentration of monomer, which can negate selective polymerization of the monomer-rich phase. For example, the BD/PEGDA phase diagram (Fig. 1b) indicates that the monomer-poor phase of a critical mixture at 22.5 °C contains 12.4 vol% PEGDA. Our initial attempts to create a BTM from such a sample by incorporating 2,2-dimethoxy-2-phenylacetophenone (DMPA) as photoinitiator and exposing the IPB to ultraviolet (UV) light (wavelength, λ = 320–390 nm) resulted in a polymerized monomer-rich phase and a partially-polymerized monomer-poor phase (see Fig. S4, ESI†). A potential resolution could be to widen the mixture's miscibility gap via a deeper temperature quench, further reducing the monomer concentration within the monomer-poor phase.21 To emulate this process, we extrapolated the BD/PEGDA binodal curve to −22.0 °C, well below the freezing point of BD, and determined the monomer concentration to be approximately 3 vol% PEGDA. A mixture of BD/PEGDA at 3 vol% PEGDA was then prepared and exposed to UV in the presence of photoinitiator, which still resulted in the formation of a loose polymer network. Therefore, we deemed this deep quenching strategy not viable for achieving selective polymerization in our systems.To prevent polymerization within the monomer-poor phase, we implemented the following procedure. Sodium fluorescein, a hydrophilic fluorescent dye, and DMPA, a hydrophobic UV-activated photoinitiator, were chosen for their respective preferential solubilities in the monomer-poor and monomer-rich phases of the three tested IPBs. For each IPB system, sodium fluorescein (0.1 mM) was dissolved in the pure solvent liquid, and DMPA (1.0 mM) was dissolved in the pure monomer liquid, before combining the two solutions. Upon de-mixing, fluorescein and DMPA selectively partitioned into the monomer-poor and monomer-rich phases, respectively. The IPBs were subsequently exposed to UV light to initiate polymerization. Within the monomer-poor phase, fluorescein molecules absorbed the incident UV light and emitted visible light (λ = 460–670 nm), in effect locally quenching the UV photons and suppressing partial polymerization in this phase by limiting UV-activation of the photoinitiator. Meanwhile, the monomer-rich domains were polymerized to produce BTMs. Fig. 2d–f display SEM images of BTM cross-sections, showing macroporous and spinodal-like structures across all three samples.3,12 Utilization of IPBs with local photon quenching circumvents the time-consuming monomer infiltration process and enables rapid selective polymerization to produce macroporous BTMs within a total of two minutes, as opposed to ∼4 h via the original Lee method. In our experience, selective solubility of the photoinitiator alone could not be exploited for exclusive polymerization of the monomer-rich phase, and local photon quenching in the monomer-poor phase was necessary for successful formation of a mechanically robust macroporous polymer scaffold. However, we note that the inclusion of fluorescent dyes may result in a gradient in UV intensity across larger samples, ultimately limiting the maximum size of polymerized samples that can be synthesized by this method. This limit was not explored in our work.
2.4. Characterization of photon quenching
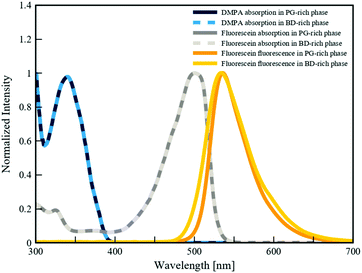
To quantitatively demonstrate the preferential partitioning of fluorescein and DMPA, and their competitive absorption of UV light, we performed a series of spectrophotometry experiments (detailed in Section 4.5) to determine the partition coefficients and the UV-absorbances of each additive within the two phases of the BD/PEGDA and PG/TMPETA IPBs. The partition coefficient is determined by the relative solubilities of additives between the two bijel phases (Csolvent/Cmonomer), which varies primarily with temperature and the compositions of the two fluid phases.48 For the following discussion, spectrophotometry analyses (summarized in Table 1) were conducted to illustrate the behavior of the chemical additives at concentrations corresponding to the polymerization process described in the previous section. The partition coefficient of fluorescein within the BD/PEGDA mixture is 2.55, indicating that fluorescein expresses affinity toward the monomer-poor phase in this system. This affinity is much greater in the PG/TMPETA mixture, where the partition coefficient is 94.72. Conversely, the partition coefficients for DMPA within both IPB systems are of order 10−3, indicating strong affinities for their respective monomer-rich phases. We then calculated the UV-absorbances (λ = 350 nm) of the partitioned fluorescein and DMPA. In each IPB system, the concentrations of the additives within the monomer-poor phase were calculated based on the partition coefficients and then multiplied by the experimentally measured molar extinction coefficients (detailed in Section 4.5) and the bijel characteristic domain size (34 μm, determined from confocal microscopy images) to obtain the reported UV-absorbance values. Although these values correspond to different concentrations, they are reflective of the photoactivity within the two phases of the IPBs during the polymerization process. In both IPBs, the UV-absorbance values for fluorescein within the monomer-rich phases are two orders of magnitude larger than those of DMPA, showing that fluorescein competitively interacts with, and absorbs, the incident UV light. The fluorescence and absorption spectra of fluorescein and DMPA, respectively, dissolved in the monomer-poor phases of the three different systems are plotted in Fig. 4. The mismatches between the emission ranges (λ = 460–670 nm) of fluorescein and the absorption ranges of DMPA (λ < 390 nm) establish a quenching effect where the activation of DMPA is curtailed by lowering the local UV intensity. Based on our findings, we attribute the effectiveness of our selective polymerization strategy to the partitioning and relative concentrations of additives, fluorescein's competitive absorption of UV light, and its fluorescence effect.| IPB system | Partition coefficient (Csolvent/Cmonomer) | UV-absorbancea (λ = 350 nm) | ||
|---|---|---|---|---|
| Fluorescein | DMPA (× 10−3) | Fluorescein (× 10−4) | DMPA (× 10−6) | |
| a Absorbance values were calculated using the concentrations of the partitioned additives: 0.14 mM fluorescein in BD-rich phase, 0.25 mM fluorescein in PG-rich phase, 1.87 mM DMPA in PEGDA-rich phase, and 1.63 mM DMPA in TMPETA-rich phase. | ||||
| BD/PEGDA | 2.55 | 3.92 | 8.44 | 3.57 |
| PG/TMPETA | 94.72 | 5.74 | 4.96 | 3.42 |
2.5. Modulating the mechanical properties of BTMs
In this section we demonstrate the ability to modulate the chemical makeup and thereby the properties of BTMs, using different monomer fluids that have comparable miscibility gaps with a given solvent, such as those shown in Fig. 1b. While we demonstrate this in the context of mechanical properties, our intent is to establish a general approach for expanding the chemical library of IPBs and the desired characteristics of BTMs derived from them, using monomer or oligomer blends. Three-point bending tests were conducted to measure the flexural moduli of the BTMs and bulk control polymers. BTMs were prepared with 1 vol% SNPs to produce macroporous materials with similar characteristic domain sizes (25–28 μm, as determined from SEM images).2 Control bulk polymer samples were prepared by UV-polymerization of the monomer-rich fluids, prepared as a single phase. The BTMs and bulk polymer samples were cut into rectangular coupons and bent using a custom three-point bending test fixture attached to a mechanical tester (see Section 4.6 for details). The average flexural moduli of BTMs and bulk polymer samples are presented in Fig. 5. As expected, the macroporous BTMs exhibited lower flexural moduli than their bulk polymer counterparts, which can be attributed to their porosity.49 Materials derived from the BD/PEGDA mixture exhibited the highest flexural moduli among the three different chemistries tested, while those derived from the PG/TMPETA mixture exhibited the lowest. For crosslinked poly(ethylene glycol), the stiffness of the polymer increases as crosslinking density increases.50 PEGDA is a short-chain difunctional monomer that polymerizes to form a dense network of highly crosslinked poly(ethylene glycol).51 In contrast, TMPETA is a larger trifunctional monomer, resulting in a sparser polymer network with a lower degree of crosslinking, hence a more flexible material. As discussed earlier, we take advantage of the relatively similar phase diagrams shown in Fig. 1b to create IPBs with a blend of functional monomers, thereby adjusting the crosslink density of the resultant polymer. For this, 10 vol% of the PEGDA in the BD/PEGDA IPB was replaced by a higher molecular weight mono-functional monomer MPGA, which reduced the number of crosslinkable groups and introduced pendent poly(ethylene glycol) chains within the polymer network, resulting in a lower degree of crosslinking.52 This effect is evidenced by the decreased flexural moduli of the materials derived from the BD/(PEGDA/MPGA) mixture relative to those derived from BD/PEGDA. Overall, flexural testing shows a similar trend between the moduli of the bulk polymers and BTMs, affirming that our approach enables facile tuning of the crosslink density in BTMs by using monomer blends in the original IPB formulations.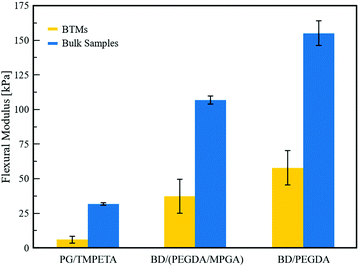 | ||
| Fig. 5 Three-point flexural testing results for BTMs and bulk polymer samples. Error bars represent standard deviation (n = 4, 4, 6). | ||
3. Conclusions
We established a general two-step approach to produce BTMs that circumvents a number of limitations in existing protocols. IPBs were formed via the kinetic arrest of thermally induced spinodal decomposition in partially miscible mixtures of solvent and monomer fluids. The use of a reactive monomer within the bijel formulation preconditions one fluid phase with a polymerizable compound, averting the time-consuming process of monomer infiltration, as well as relaxing the geometric restrictions associated with this step. Selective polymerization of the monomer-rich phase was made possible by premixing a photoinitiator and a photon quencher with disparate affinities for the two fluid phases, and exposing to UV light to initiate localized polymerization. The resulting BTMs exhibited a morphological resemblance to their IPB templates. By changing the formulation of the monomer-rich phase, we demonstrated a technique to modulate the mechanical properties of BTMs. Our IPB and photon quenching methods are amenable to scalable manufacturing processes. Furthermore, application of our IPB approach to different monomers yields BTMs with tunable mechanical and chemical properties, important design parameters for future research and development of advanced biomedical devices, metallic scaffoldings, or mechanical support materials for electrodes.4. Materials and methods
4.1. Materials
The following materials were used as received. 1,4-Butanediol (BD, 99%), propylene glycol (PG, ≥99.5%), poly(ethylene glycol) diacrylate (PEGDA, Mn: 250 g mol−1), trimethylolpropane ethoxylate triacrylate (TMPETA, Mn: 692 g mol−1), 2,2-dimethoxy-2-phenylacetophenone (DMPA, 99%), fluorescein isothiocyanate isomer I (FITC, ≥90%), and tetraethyl orthosilicate (TEOS, ≥99.0%) were purchased from Sigma-Aldrich. Hexamethyldisilazane (HMDS, 98+%) was purchased from Alfa Aesar. Methoxy polyethylene glycol monoacrylate (MPGA, Mw: 350 g mol−1) was provided by Sartomer USA. (3-Aminopropyl) triethoxysilane (APTES, ≥98%) were purchased from TCI America. Sodium fluorescein salt was purchased from HiMedia. Anhydrous ethanol (200 proof) was purchased from Rossville Gold Shield. Strong ammonia (27–30%) was purchased from VWR. Deionized water was purified with a Milli-Q Advantage A10 water purification system (Millipore Sigma, 18.2 MΩ cm at 25 °C).4.2. Turbidity meter and cloud point measurement
Fig. 1a depicts a schematic of our turbidity meter set up. A generic continuous 5 mW 532 nm laser powered by a constant voltage (2.6 V) power supply emitted a constant power laser beam. A negative lens expanded the laser beam to increase the sampling area (∼1 cm dia.), and a positive lens focused the transmitted light onto a silicon photodiode (ThorLabs, 400 ns rise time). The voltage across a load resistor within the photodiode circuit was measured and correlated to the intensity of the transmitted laser beam. The mixture temperature was measured using an immersion thermistor (Omega, 10 kΩ). For each cloud point measurement, a 7 mL mixture of solvent and monomer of known composition was added to a glass optical cuvette (Macro Cell, 10 mm light path), and subsequently heated while being stirred. The intensity of the light transmitted through the single-phase mixture was calibrated as the baseline transmittance. To determine the cloud point, a slow temperature ramp (−0.5 °C min−1) was applied to the sample holder using a fluid bath heated cuvette holder; meanwhile, the temperature and voltage were recorded simultaneously using a myDAQ (National Instruments) acquisition device. Cloud points were determined when transmission intensity dropped below the 95% threshold. Binodal curves were generated by fitting the cloud point data with a Fourier series (number of harmonics = 3).4.3. SNP synthesis
A silane-coupled fluorescein solution was prepared by mixing 8.0 mg of FITC, 33.8 μL of APTES, and 6.4 mL of anhydrous ethanol for 15 min. SNPs were synthesized using a modified Stöber method by mixing 1.0 mL of the FITC-APTES solution, 8.0 g of ethanol, 1.0 mL of deionized water, 680 μL of TEOS, and 295 μL of strong ammonia solution, and stirring at room temperature for 4.5 h.53 After this, HMDS (250 μL for BD/PEGDA IPBs, 160 μL for BD/(PEGDA/MPGA) IPBs, or 80 μL for PG/TMPETA IPBs) was added directly to the reaction vial and stirred for another 18 h at room temperature. Particles were washed by repeated centrifugation and resuspension in ethanol, then subsequently dried in a 75 °C vacuum oven for 1 h.4.4. BTM preparation and imaging
IPBs were prepared by combining SNPs, solvent solution (0.1 mM sodium fluorescein), and monomer solution (1.0 mM DMPA) in 1.5 mL centrifuge tubes. An ultrasonic horn (Branson Ultrasonics) was used to disperse the SNPs, also heating and mixing the fluids. The dispersions were transferred to a custom disk-shaped sample holder made of two glass coverslips and a 3 mm spacer. IPBs were formed by placing the sample holders onto an aluminum heat sink conditioned to the quench temperature (22.5 °C for BD/PEGDA and BD/(PEGDA/MPGA), 15.0 °C for PG/TMPETA). An inverted microscope coupled to a VT-Eye confocal scanner (VisiTech International) was used to examine the phase separation of the PG/TMPETA mixture. A FluoView 1200 CLSM system (Olympus) was used to examine the internal microstructure of the stabilized IPBs. An EXFO UV lamp (Lumen Dynamics) with a 320–390 nm bandpass filter was used to supply UV light to initiate polymerization. Samples were exposed to UV light for 30 s. The remaining fluids were subsequently removed with repeated ethanol washes and dried in a 70 °C oven. BTMs were cut using a surgical blade to expose a cross-sectional view of the internal microstructure. Before SEM imaging, the BTMs were dried in a 75 °C vacuum oven for 1 h. An EM ACE600 sputter coater (Leica) was used to deposit an 8 nm iridium coating on the BTMs to minimize the degradation of polymer caused by the electron beam. A Magellan 400 XHR SEM (FEI) was used to obtain images of the BTMs.4.5. Spectroscopy
A series of calibration experiments were conducted to determine the molar extinction coefficients of the fluorescein and DMPA within the monomer-poor phase of each IPB system. Stock solutions of the monomer-poor phase for each system were prepared by mixing IPB solvent/monomer pairs without adding SNPs, fluorescein, or DMPA, and quenching to the bijel formation temperatures to de-mix the fluids. The two resultant phases were separately extracted and loaded into different containers. Fluorescein (0.050–2.4 mM) and DMPA (0.0050–10.0 mM) calibration solutions were prepared by dissolving either sodium fluorescein or DMPA in the monomer-poor stock solutions. The prepared solutions were loaded into a 96-well plate and their UV-absorptions (λ = 320–390 nm, 10 nm increments) were measured using a SpectraMax M3 plate reader (Molecular Devices). For samples containing fluorescein, a UV-blue bandpass filter (Newport, 210–500 nm) was placed on top of the 96-well plate to filter out fluorescent light. The molar extinction coefficients for fluorescein and DMPA in the monomer-poor fluids were determined using the Beer–Lambert Law, A = εlCi, where A is the absorbance, ε is the molar extinction coefficient, l is the optical path length, and C is the concentration of the additive in fluid phase i. For each wavelength, the molar extinction coefficient (plotted in Fig. S5, ESI†) was calculated by multiplying the optical path length by the slope of the absorbance vs. concentration graph.54To determine the partition coefficients, fluorescein (0.050–2.4 mM) or DMPA (0.0050–10.0 mM) solutions were prepared by dissolving sodium fluorescein or DMPA in the pure solvent or monomer liquids, respectively. IPB mixtures without SNPs were prepared using either fluorescein or DMPA solutions and subsequently quenched to the IPB formation temperature to mirror the fluid phase separation and additive partitioning within the IPBs. The monomer-poor phases were extracted and loaded into a 96-well plate. UV-absorption tests were performed (λ = 320–390 nm, 10 nm increments) to measure the absorbances of the partitioned additives. The concentrations of fluorescein or DMPA in the monomer-poor fluids (shown in Fig. S6, ESI†) were calculated using the measured extinction coefficients and the Beer–Lambert Law. The concentrations of additives within the monomer-rich phases were calculated through conservation of mass, CmixtureVmixture = CsolventVsolvent + CmonomerVmonomer, where C is the concentration, V is the volume, and the subscripts denote the fluid phases.55 The relative volumes of the fluid domains within the IPBs were calculated using the Lever rule and the measured phase diagrams.32
The absorption and fluorescence spectra of fluorescein and DMPA were measured using 1.0 mM fluorescein solutions and 10.0 mM DMPA solutions prepared with the stock monomer-poor fluids described above. Absorption tests (λ = 300–750 nm, 1 nm increments) were conducted on the DMPA solutions. Fluorescence tests were conducted by exciting the fluorescein solutions with 350 nm UV light and recording the emitted light intensity for each wavelength (λ = 300–750 nm, 1 nm increments). Each spectrum was normalized by the maximum recorded value for each respective test.
4.6. Mechanical testing
Three-point bending tests were performed using an MTS Synergie 100 mechanical tester (MTS Systems) fitted with a custom bending fixture (support span of 10 mm). BTMs and bulk samples were prepared in a parallel plate sample holder made of two glass coverslips and a 1 mm spacer to produce sheets. The polymerized samples were cut into 8 × 15 mm rectangular coupons and bent to 10% strain. The flexural modulus was calculated as the slope of the initial linear portion of the stress–strain curve.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by the NASA Research Opportunities in Complex Fluids and Macromolecular Biophysics Program (80NSSC18K1554). We thank Professor Han Li for providing access to the plate reader, and Professor Elliot Botvinick for providing access to the FluoView CLSM system. SEM and sputter coating were performed at the UC Irvine Materials Research Institute (IMRI). T. J. T. recognizes the National Science Foundation Interdisciplinary Graduate Education and Research Traineeship (IGERT) Biophotonics across Energy, Space, and Time (BEST) program for financial support and training (NSF-DGE-1144901). B. P. recognizes the UC Irvine Summer Undergraduate Research Program (SURP) for financial support and training.Notes and references
- K. Stratford, R. Adhikari, I. Pagonabarraga, J.-C. Desplat and M. E. Cates, Science, 2005, 309, 2198–2201 CrossRef CAS PubMed.
- E. M. Herzig, K. A. White, A. B. Schofield, W. C. K. Poon and P. S. Clegg, Nat. Mater., 2007, 6, 966–971 CrossRef CAS PubMed.
- P. S. Clegg and J. H. J. Thijssen, in Bijels: Bicontinuous Particle-stabilized Emulsions, ed. P. S. Clegg, Royal Society of Chemistry, Cambridge, 2020, ch. 1, pp. 1–33.39 Search PubMed.
- M. Reeves, A. T. Brown, A. B. Schofield, M. E. Cates and J. H. J. Thijssen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 032308 CrossRef CAS PubMed.
- J. H. J. Thijissen and J. Vermant, J. Phys.: Condens. Matter, 2018, 30, 023002 CrossRef.
- M. N. Lee, J. H. J. Thijssen, J. A. Witt, P. S. Clegg and A. Mohraz, Adv. Funct. Mater., 2013, 23, 417–423 CrossRef CAS.
- L. Imperiali, C. Clasen, J. Fransaer, C. W. Macosko and J. Vermant, Mater. Horiz., 2014, 1, 139–145 RSC.
- T. J. Thorson, E. L. Botvinick and A. Mohraz, ACS Biomater. Sci. Eng., 2018, 4, 587–594 CrossRef CAS PubMed.
- T. J. Thorson, R. E. Gurlin, E. L. Botvinick and A. Mohraz, Acta Biomater., 2019, 94, 173–182 CrossRef CAS.
- J. A. Witt, D. R. Mumm and A. Mohraz, J. Mater. Chem. A, 2016, 4, 1000–1007 RSC.
- D. Cai, F. H. Richter, J. H. J. Thijssen, P. G. Bruce and P. S. Clegg, Mater. Horiz., 2018, 5, 499–505 RSC.
- M. N. Lee, M. A. Santiago-Cordoba, C. E. Hamilton, N. K. Subbaiyan, J. G. Duque and K. A. D. Obrey, J. Phys. Chem. Lett., 2014, 5, 809–812 CrossRef CAS.
- S. Cha, H. G. Lim, M. F. Haase, K. J. Stebe, G. Y. Jung and D. Lee, Sci. Rep., 2019, 9, 6363 CrossRef.
- M. E. Cates and P. S. Clegg, Soft Matter, 2008, 4, 2132–2138 RSC.
- M. Reeves, K. Stratford and J. H. J. Thijssen, Soft Matter, 2016, 12, 4082–4092 RSC.
- H.-Y. Chen, Y. Kwon and K. Thornton, Scr. Mater., 2009, 61, 52–55 CrossRef CAS.
- K. M. McDevitt, T. J. Thorson, E. L. Botvinick, D. R. Mumm and A. Mohraz, Materialia, 2019, 7, 100393 CrossRef.
- M. F. Haase, H. Jeon, N. Hough, J. H. Kim, K. J. Stebe and D. Lee, Nat. Commun., 2017, 8, 1234 CrossRef PubMed.
- M. N. Lee and A. Mohraz, Adv. Mater., 2010, 22, 4836–4841 CrossRef CAS PubMed.
- J. W. Tavacoli, J. H. J. Thijssen and P. S. Clegg, in Particle-Stabilized Emulsions and Colloids: Formation and Applications, ed. T. Ngai and S. Bon, Royal Society of Chemistry, Cambridge, 2014, ch. 6, pp. 129–168 Search PubMed.
- A. Mohraz and T. J. Thorson, in Bijels: Bicontinuous Particle-stabilized Emulsions, ed. P. S. Clegg, Royal Society of Chemistry, Cambridge, 2020, ch. 2, pp. 34–60 Search PubMed.
- C. Huang, J. Forth, W. Wang, K. Hong, G. S. Smith, B. A. Helms and T. P. Russell, Nat. Nanotechnol., 2017, 12, 1060–1064 CrossRef CAS.
- M. F. Haase, K. J. Stebe and D. Lee, Adv. Mater., 2015, 27, 7065–7071 CrossRef CAS.
- T. Wang, G. D. Vitantonio, K. J. Stebe and D. Lee, ACS Mater. Lett., 2020, 2, 524–530 CrossRef CAS.
- C. R. Wilke and P. Chang, AIChE J., 1955, 1, 264–270 CrossRef CAS.
- J. W. Cahn, J. Chem. Phys., 1965, 42, 93–99 CrossRef CAS.
- A. L. Genau and P. W. Voorhees, Acta Mater., 2009, 57, 6226–6233 CrossRef CAS.
- R. Aveyard, B. P. Binks and J. H. Clint, Adv. Colloid Interface Sci., 2003, 100–102, 503–546 CrossRef CAS.
- E. Kim, K. Stratford, R. Adhikari and M. E. Cates, Langmuir, 2008, 24, 6549–6556 CrossRef CAS PubMed.
- N.-C. Wong and C. M. Knobler, J. Chem. Phys., 1978, 69, 725–735 CrossRef CAS.
- R. V. D. Haegen and B. W. Ready, in Comprehensive Polymer Science and Supplements, ed. G. Allen and J. C. Bevington, Pergamon, Oxford, 1989, ch. 2, pp. 34–60 Search PubMed.
- J. W. Tavacoli, J. H. J. Thijssen, A. B. Schofield and P. S. Clegg, Adv. Funct. Mater., 2011, 21, 2020–2027 CrossRef CAS.
- L. Bai, J. W. Fruehwirth, X. Cheng and C. W. Macosko, Soft Matter, 2015, 11, 5282–5293 RSC.
- D. Cai and P. S. Clegg, Chem. Commun., 2015, 51, 16984 RSC.
- X.-D. Wang, Z.-X. Shen, T. Sang, X.-B. Cheng, M.-F. Li, L.-Y. Chen and Z.-S. Wang, J. Colloid Interface Sci., 2010, 341, 23–29 CrossRef CAS.
- V. M. Gun’ko, M. S. Vedamuthu, G. L. Henderson and J. P. Blitz, J. Colloid Interface Sci., 2000, 228, 157–170 CrossRef.
- S. A. Kulkarni, S. B. Ogale and K. P. Vijayamohanan, J. Colloid Interface Sci., 2008, 318, 372–379 CrossRef CAS PubMed.
- P. A. Kralchevsky, I. B. Ivanov, K. P. Ananthapadmanabhan and A. Lips, Langmuir, 2005, 21, 50–63 CrossRef CAS PubMed.
- B. P. Binks and J. H. Clint, Langmuir, 2002, 18, 1270–1273 CrossRef CAS.
- H. Tanaka, Phys. Rev. Lett., 1993, 71, 3158–3161 CrossRef CAS PubMed.
- H. Tanaka, J. Chem. Phys., 1994, 100, 5323–5337 CrossRef CAS.
- J. K. Yeganeh, F. Goharpey and R. Foudazi, RSC Adv., 2014, 4, 12809 RSC.
- G. Zhang, T. Yang, S. Yang and Y. Wang, Phys. Rev. E, 2017, 96, 032501 CrossRef.
- H. Tanaka, Prog. Theor. Phys., 1999, 101, 863–873 CrossRef CAS.
- D. Sappelt and J. Jäckle, Polymer, 1998, 39, 5253–5256 CrossRef CAS.
- F. Jansen and J. Harting, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 046707 CrossRef.
- K. E. Novik and P. V. Coveney, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 435–448 CrossRef CAS PubMed.
- W. M. Deen, Analysis of Transport Phenomena, Oxford University Press, New York, 2012 Search PubMed.
- M.-T. Hsieh, B. Endo, Y. Zhang, J. Bauer and L. Valdevit, J. Mech. Phys. Solids, 2019, 125, 401–419 CrossRef.
- A. Priola, G. Gozzelino, F. Ferrero and G. Malucelli, Polymer, 1993, 34, 3653–3657 CrossRef CAS.
- S. Kalakkunnath, D. S. Kalika, H. Lin and B. Freeman, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 2058–2070 CrossRef CAS.
- M. Kim and C. Cha, Sci. Rep., 2018, 8, 4315 CrossRef.
- A. V. Blaaderen and A. Vrij, Langmuir, 1992, 8, 2921–2931 CrossRef.
- J. Georges, Spectrochim. Acta, Part A, 1995, 51, 985–994 CrossRef.
- H. S. Fogler, Elements of Chemical Reaction Engineering, Prentice Hall, Upper Saddle River, 2006 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Results of a cloud point measurement, CLSM images of failed BD/PEGDA bijel and SEM images of failed BD/PEGDA BTM, CLSM frames of PG/TMPETA phase separation, SEM image of polymerized BD/PEGDA BTM, and additional spectroscopy experiments and analysis. See DOI: 10.1039/d1ma00404b |
| ‡ Present address: Department of Chemical and Biomolecular Engineering, University of Delaware, Newark, DE 19716-3196, USA. |
| This journal is © The Royal Society of Chemistry 2021 |