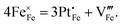Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Iron cation vacancies in Pt(IV)-doped hematite†
Michael
Anenburg
 *a,
Jeremy L.
Wykes
*a,
Jeremy L.
Wykes
 ab,
Ulrike
Troitzsch
ab,
Ulrike
Troitzsch
 a,
Charles
Le Losq
a,
Charles
Le Losq
 c and
Jeff
Chen
d
c and
Jeff
Chen
d
aResearch School of Earth Sciences, Australian National University, Canberra, ACT 2600, Australia. E-mail: michael.anenburg@anu.edu.au
bANSTO Australian Synchrotron, Clayton, VIC 3168, Australia
cInstitut de Physique du Globe de Paris, Université de Paris, CNRS, F-75005 Paris, France
dCentre for Advanced Microscopy, Australian National University, Canberra, ACT 2600, Australia
First published on 9th July 2021
Abstract
Platinum-doping of hematite (α-Fe2O3) is a popular method to increase the performance of hematite in photoelectrochemical applications. The precise mode of Pt incorporation is however unclear, as it can occur as Pt0, Pt2+ or Pt4+, either on the surface, as dispersed inclusions, or as part of the hematite crystal lattice. These different Pt-doping varieties can have major effects on the hematite performance. Here, we employ a high-pressure synthesis method assisted by silicate liquid flux to grow Pt-doped hematite crystals large enough for elemental analysis by wavelength dispersive spectroscopy (WDS). We find that the total cations are lower than the expected 2 atoms per formula unit, and together with Fe, they are inversely correlated with Pt contents. Linear regressions in compositional space reveal that the slopes are consistent with 4Fe3+ = 3Pt4+ + VFe as the charge-balanced substitution mechanism. Therefore, Pt4+-doping of hematite at high oxygen fugacities, which does not allow Fe2+ to form, will lead to removal of Fe and formation of cation vacancies. Our hematite also contains significant Al3+, Ti4+ and Mg2+, raising the possibility of fine tuning the hematite properties by co-doping with other elements. Photoelectrochemical performance of cation vacancy bearing hematite is experimentally understudied and is a potentially promising future field of study.
Introduction
Hematite (α-Fe2O3) is commonly used in water-splitting and solar photoelectrical applications due to its abundance, low price, and capacity for fine-tuning of morphological and chemical varieties that improve its performance. A common way of modifying hematite properties is doping by various elements that substitute for Fe. These dopants affect the crystallographic structure of hematite, and when manifested on the surface, allow the splitting of H2O into hydrogen and oxygen on solar irradiation with the eventual goal of harvesting solar energy and converting it to chemical energy.1–5Platinum-doped hematite has proven useful in various applications due to enhanced charge-transfer, conductivity, and ability to catalyse redox reactions.6–20 However, the thermodynamically stable oxidation state of Pt at high temperatures and atmospheric pressures is Pt0, which does not partition into hematite. Thus, the presence of cationic Pt in hematite is likely to be metastable, an idea supported by Pt exsolution as Pt0 during high temperature annealing.14,21 Knowledge of any coupled substitutions that can stabilise Pt in hematite—either as Pt2+ or Pt4+—can lead to controlled Pt incorporation, and possibly enhanced thermal stability and longer lifetime of the material.
Understanding the reasons for the effectiveness of Pt and other dopants in improving the electrochemical properties of hematite relies on knowing their mode of incorporation into the hematite crystal structure, but this can be challenging for nanomaterials. Chemical analysis using EDS is often hampered by incorporation of the substrate signal and the lack of appropriate reference materials. Likewise, the XRD signal is often dominated by the substrate,18 possible preferred orientation effects, and the unsuitability of nanomaterials for single crystal diffraction experiments. Information gained by routine XPS (itself not without problems22) also has limitations as it is only sensitive to the outermost several nanometres of a material, which may not be representative of the bulk composition. Furthermore, it is not suitable for composite materials where hematite is coated by other oxide or metal layers or nanoparticles.14,23
Given the above challenges, synthesis of micrometre-scale hematite crystals doped with the same elements used in its various applications allows further characterisation. The chemical composition of larger crystals can be easily analysed by WDS, which provides—when compared to EDS—superior precision, energy resolution, detection limits, and the common use of reference materials for improved accuracy.24 It is conducted on a polished section of the crystal and the fluorescence photons are emitted from a region extending 1–2 μm below the surface, thus it is not disturbed by any surface effects. The accurate chemical data can then be translated into the substitution vectors that describe the thermodynamically stable incorporation of dopants into the hematite structure.
Crystallisation of micrometre-scale hematite crystals is challenging but can be assisted by flux-melting or hydrothermal methods. Growth of Pt-bearing hematite is particularly challenging, as oxidised Pt will tend to reduce to Pt0. Indeed, Pt crucibles are often used in flux-growth of crystals due to their stability and resistance to chemical reactions, reflecting the minimal solubility of Pt in commonly employed fluxes. In order to circumvent this limitation, we synthesised Pt-bearing hematite using a high-pressure piston-cylinder apparatus using a natural-like aluminosilicate flux composition. The high pressure allows oxygen fugacity to be maintained at values sufficiently high to stabilise cationic Pt in hematite. We then characterise the resulting glass, hematite and by-product Mg–Fe-platinate with XRD, Raman spectroscopy, EDS and WDS chemical analyses. We investigate the charge-balanced substitution vectors that allow incorporation of Pt4+ in the crystalline structure, and propose methods to stabilise these cations during conventional synthesis of hematite.
Methods
Materials and experimental procedure
The composition for the silicate flux is based on natural glass YB#2 (SiO2: 42.74%, Al2O3: 8.09%, TiO2: 3.607%, FeO: 22.22%, MnO: 0.307%, CaO: 8.26%, MgO: 13.63%, Na2O: 0.263%, K2O: 0.080%, with the rest being trace amounts of Cl, Cd, Ag, Te, Sb, and Se).25 The silica flux was prepared by mixing analytical and reagent grade oxides and carbonates in an agate mortar and pestle under acetone, following by pelletising and calcining at 1100 °C in air for 16 hours. This mix was reground and placed, together with two layers of PtO2 at the top and bottom, into a doubly-crimped Pt tube (5.0 mm internal diameter) which was arc-welded on both sides to form a sealed capsule. Platinum oxide had two roles – imposing an exceptionally high oxygen fugacity (by the coexistence of Pt metal and PtO2), and providing a source for Pt doping of hematite.Hematite synthesis was conducted utilising an end-loaded piston-cylinder apparatus using a 12.7 mm NaCl–Pyrex–MgO assembly with a graphite heater. Teflon foil formed a low-friction interface between the NaCl pressure medium and the pressure vessel wall. Temperature was controlled using a Eurotherm PID controller that monitored temperature via a Type B (Pt70Rh30–Pt94Rh6) thermocouple insulated in 2-bore mullite tubing with a 10 mm tip of high purity Al2O3 tubing in the hottest portion of the assembly. No correction for the effect of pressure on EMF was applied. A 0.5 mm thick disc of MgO separated the thermocouple bead from the Pt capsule. Temperatures reported here are thermocouple temperatures; actual temperature experienced by the sample is likely to be 10–25 °C higher because of the temperature gradients inherent in solid media assemblies.
The resulting experimental capsule was mounted in epoxy resin and sanded with SiC paper to expose the interior of the capsule. The surface was then polished with progressively finer SiC paper and diamond paste up to a grade of 0.25 μm.
X-ray diffraction
X-ray diffraction analysis was carried out with a Malvern Panalytical Empyrean 3 which is equipped with a Bragg–Brentanno High Definition (BBHD) divergent beam optic and a PIXcel 3D detector (1D scanning mode, 3.347° active length), using CoKα radiation. The sample was placed on a programmable xy-platform with z-adjustment and brought into diffraction position with an automatic height sensor and alignment camera. The incoming X-ray beam diameter was optimised to irradiate the area of interest by using a 2 mm fixed mask, a 1/4° anti-scatter slit, and a 1/16° divergence slit. The scan range was 5–85° 2θ, with a step width of 0.0131303° 2θ and a total counting time of 797 s per step.The phases were identified using the software DiffracPlus Eva version 10.0 (2004) and database PDF-2 (ICDD, 2004). Unit-cell parameters of the phases were determined with Rietveld refinement using the software HighScore (Plus) version 4.8 (2018).26 The background, including a pronounced ‘amorphous hump’ was subtracted before the refinement. Refined phases were platinum, hematite and MgPt3O6 using starting parameters and space groups from previously published studies.27–29 The profile was fitted with Pseudo-Voigt functions. Refined parameters included specimen displacement, scale parameters, up to five peak-shape parameters, unit cell dimensions and preferred orientation parameters of all phases. Preferred orientation was pronounced in all three phases probably due to insufficient number of crystallites (hematite and MgPt3O6) and possibly uniaxial stress (Pt capsule). The numerical criteria of fit were Rwp = 2.9864, Rexp = 1.94, Rp = 1.732, S = 1.537 (Table 1).
Chemical composition
The polished sample was coated with a conductive carbon of 15 nm thickness. The quantitative elemental analysis was carried out on a JEOL 8530F Plus field emission electron probe microanalyser (FE-EPMA) equipped with five WDS spectrometers. Full spectrometer wavelength scans were performed on glass and hematite prior to quantitative analysis for element identification, selection of appropriate X-ray emission lines and determination of background positions for each element. Quantitative analysis was performed using acceleration voltage of 15 keV and probe current of 20 nA. Probe diameter was set at 30 μm for glass and 2 μm for hematite. Reference materials from Astimex mineral (MINM25-53) and metal (METM25-44) blocks were used for quantitative calibration. They include hematite for Fe-Kα, sanidine for Al-Kα and K-Kα, albite for Na-Kα, diopside for Ca-Kα and Mg-Kα, rhodonite for Mn-Kα, rutile for Ti-Kα, Sb2Te3 for Sb-Lβ and Te-Lα, Ag metal for Ag-Lα, Bi2Se3 for Se-Lα, Cd metal for Cd-Lα, and Pt metal for Pt-Mα. Simplified matrix correction (XPP) based on Pouchou and Pichoir (PAP) method was applied in the quantification process.30 The analysis error was estimated to be within 1% for elements greater than 10 wt%, within 3% for elements between 1 to 10 wt% and within 15% for elements between 0.1 to 1 wt%.| a [Å] | b [Å] | c [Å] | V [Å]3 | |
|---|---|---|---|---|
| Hematite (this study) | 5.0627(8) | 13.7614(9) | 305.46 | |
| Hematite (ideal)27 | 5.0355(5) | 13.7471(7) | 301.88 | |
| Difference (%) | 0.54 | 0.10 | 1.19 | |
| (Mg,Fe)Pt3O6 (this study) | 7.1632(7) | 9.9445(9) | 3.1245(8) | 222.57 |
| MgPt3O6 (ideal)28 | 7.112(1) | 9.940(1) | 3.141(1) | 222.36 |
| Difference (%) | 0.58 | 0.05 | −0.53 | 0.09 |
Raman spectroscopy
Raman spectroscopy was conducted using a Peltier-cooled detector on a Renishaw InVia spectrometer, exciting the sample using a 532 nm laser focused on an analysis spot of 1 μm via a ×100 objective. A 2400 l mm−1 grating was used for Raman signal diffraction. Several measurements were obtained from hematite and Mg–Fe-platinate crystals to check for consistency.Results
Fig. 1a shows an overview of the experimental run product. The capsule is filled with quenched glass containing several horizontal decompression cracks. The top PtO2 layer partly decomposed to metallic Pt, and partly reacted with the silicate liquid to form hematite. In contrast, the bottom PtO2 layer reacted to form hematite and a Mg–Fe-platinate. Hematite forms slightly rounded crystals in which individual crystal faces can still be discerned, commonly 10 to 20 μm across (Fig. 1b). The platinate forms elongated crystals up to ∼10 μm long and ∼2 μm wide. “Whiskers” of an unknown composition appear on the platinate and formed during quench. Rounded grains of hematite also occur as a coating on the capsule interior throughout the capsule, where no PtO2 was placed (Fig. 1c). They were most likely formed by oxidation of the Pt capsule, enhanced by the catalytic properties of the metal.31 Platinum nanoparticles are known to nucleate on crystallising oxides in similar systems,32,33 but none were observed in the present study. This may be explained by the high oxygen fugacity imposed by the PtO2 used in the starting materials.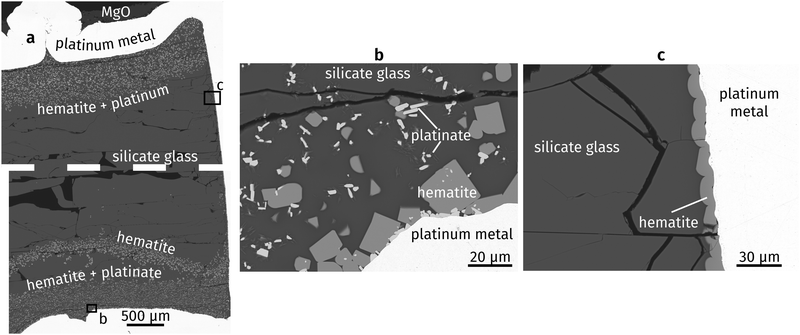 | ||
| Fig. 1 Backscattered electron images of run products: (a) experimental capsule (dashed line represents a small horizontal imaging gap), (b) bottom of capsule, (c) side wall of capsule. | ||
The X-ray diffraction pattern collected from the surface of the polished sample displays a large ‘amorphous hump’ in agreement with the significant amount of glass (i.e., quenched melt) present. All diffraction peaks were identified and assigned to three crystalline phases (Fig. 2): hematite, a compound with MgPt3O6 structure, and platinum (capsule material). The unit-cell dimensions of this study's hematite and MgPt3O6 differ slightly from those of the pure compounds (Table 1).27,28 This is expected as those compounds form solid solutions (see below).
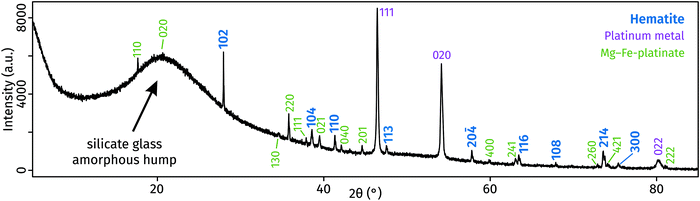 | ||
| Fig. 2 X-ray diffraction patterns of run products, obtained from the polished surface of the glass-containing experimental capsule. | ||
Compared to ideal hematite, our Pt-hematite has expanded a and c unit cell lengths, leading to an overall increase in unit-cell volume of 1.2% due to exchange of Fe3+ with large amount of Mg2+ and Pt4+, both of which are larger cations than Fe3+.34 The incorporation of predominantly Fe and possible vacancies into MgPt3O6 leads to an increase in the a dimension and a decrease in the c dimension. These effects cancel each other, causing the unit cell volume to remain mostly unchanged.
Raman spectra of the glass, Pt-hematite and Mg–Fe-platinate confirm the XRD determinations (Fig. 3). Raman spectra of the glass is marked by a noisy signal between 100 and 700 cm−1, and a broad peak centred around 900 cm−1 that originates from T–O stretching (T = Si4+, Al3+, Fe3+) in the tetrahedral network of the glass. The noisy 100–700 cm−1 signal may arise from the presence of nanoparticles in the glass which can result in destructive interferences of the signals characteristic of medium-range order vibrations. The lack of any peak at ∼3500 cm−1 indicates no H2O in the glass. Raman spectra present peaks at 230, 291, 411 and 1340 cm−1. It is comparable to previously-measured spectra, with possible differences originating from the non-pure character of the Pt-bearing hematite grown in this study and various orientation effects.8,9,11 The Mg–Fe-platinate spectra present three main peaks at 567, 730 and 758 cm−1, and three minor peaks at 106, 308 and 485 cm−1.
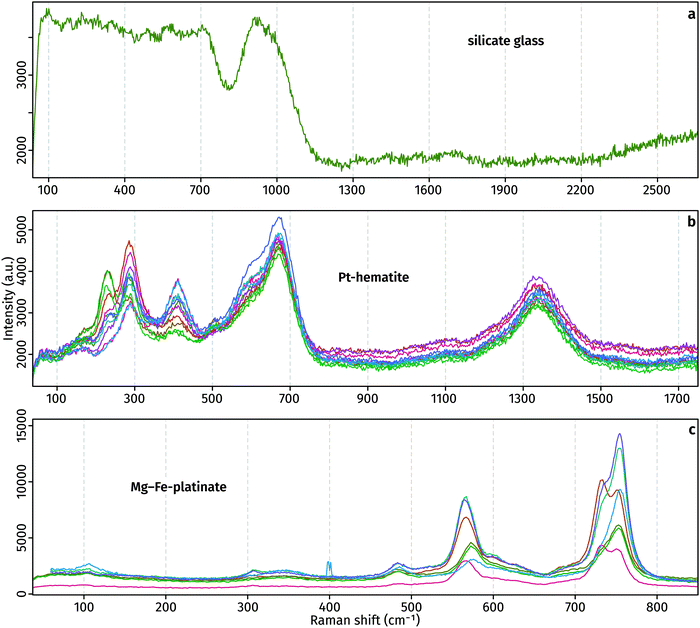 | ||
| Fig. 3 Raman spectra of run products. The different colours distinguish between individual analyses of the same material type. | ||
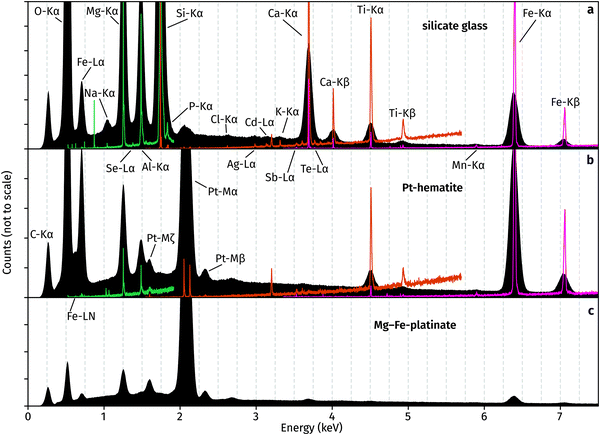
The superior detection limits and energy resolution of WDS relative to EDS are evident from Fig. 4. In the glass, P, Sb and Te are not detectable in EDS but obvious in WDS. The elements Cl, Ag, Cd, K are hard to distinguish from the background noise and prior knowledge of their presence assists in their determination from EDS. Likewise, hematite contains Sb, Ca, and Mn which prove challenging to detect and quantify using EDS, but their X-ray emission peaks are clearly observed in WDS. Interestingly, EDS spectra of both hematite and platinate contain a Cl peak, which is not observed in the WDS scans. The source of this peak is unknown, and it demonstrates the importance of using WDS for accurate element identification and quantification. Results of WDS chemical measurements are available in Table S1 (ESI†).
Oxygen was calculated from cations during our WDS analysis, and all Pt was assumed tetravalent. In the case of a mixed Pt2+–Pt4+ compound, this assumption would lead to analytical totals greater than 100% as they represent O2− which does not exist in the material. Thus, the presence of Pt2+ in the platinate is confirmed by analytical totals of 104.5 ± 0.9%. On the other hand, analytical totals for hematite are 100.6 ± 1.5%, demonstrating the accuracy of the method and providing evidence for the lack of Pt2+.
Discussion
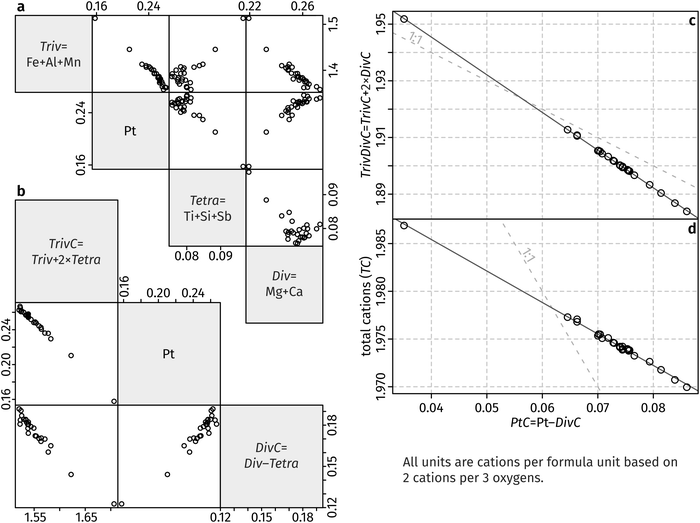
The chemical data shown in Table S1 (ESI†) reveals that the major elements in the synthesised hematite other than Fe are Al, Ti, Mg and Pt, with trace amounts of Si, Ca, Sb and Mn. A charge balance has to be conducted in order to identify the chemical components incorporated into the hematite. The redox-insensitive elements can be assigned as Si4+, Ti4+, Al3+, Ca2+ and Mg2+. At our extremely oxidising conditions, ferrous Fe is most likely impossible, and thus Fe is inferred to be present entirely as ferric Fe.35 Manganese can be either trivalent or quadrivalent in high-temperature oxidising conditions. Our run does not contain a calibrated oxygen fugacity buffer, but the lack of pure PtO2 indicates that oxygen fugacity is lower than a hypothetical Pt–PtO2 buffer.36 Moving on to the next most oxidising buffer known in the literature, Pd–PdO (used as an analogue for our fO2 conditions), oxygen fugacity at our run conditions equals 103.73 bar.37 Using calibrated Mn2O3 and MnO2 equilibria, it is possible to infer than the stable oxidation state of Mn at our experimental conditions is Mn3+.38 The presence of Fe3+ and Mn3+ also indicates Sb is pentavalent, but it will be grouped with the other tetravalent elements for simplicity.39 Finally, Pt occurs either as Pt2+ or Pt4+ in the silicate glass,40,41 and both as Pt2+ and Pt4+ in the platinate. Analytical totals for hematite are consistent with no Pt2+, but the relatively large uncertainty (1.5%) leads to low sensitivity using this “by-difference” method. Therefore, both oxidation states are potentially possible in the hematite crystals grown in this study.We now identify the oxidation state of Pt in hematite by eliminating all other possible substitution pairs. First, we use the compositional data from Table S1 (ESI†) to derive cation contents based on full O occupancy at 3 anions per formula unit. We then assume that all trivalent elements substitute for Fe3+ on a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 basis, and define:
1 basis, and define:
| Triv = Fe3+ + Al3+ + Mn3+ |
Likewise, we group all divalent and quadrivalent elements together:
| Div = Mg2+ + Ca2+ |
| Tetra = Ti4+ + Si4+ + Sb5+ |
| DivC = Div − Tetra |
And compensate Fe:
| TrivC = Triv + 2 × Tetra. |
At this stage we have a simplified hematite composition, containing only Fe (as TrivC), Mg (as DivC), and Pt. The improved correlation is evident in Fig. 5b. Platinum contents are greater than DivC, so we assume that equal amounts of divalent DivC are charge-balanced by Pt4+ by a hypothetical “Pt-geikielite” component:
MgPtO3:2Fe3+ = Mg2+ + Pt4+, and define the following:
| PtC = Pt4+ − DivC |
| TrivDivC = TrivC + 2 × DivC. |
| TC = 1.9986 − 0.3298 × PtC (r2 = 0.9973) |
| TrivDivC = 1.999 − 1.330 × PtC (r2 = 0.9998) |
Standard errors for both intercepts are about 0.01%, about 1% for the first slope, and about 0.25% for the second slope. The regressions indicates that removal of four Fe cations requires introduction of three Pt cations and an additional cation vacancy. Therefore, Pt must be quadrivalent by charge-balance considerations. Writing in Kröger–Ving notation, the substitution of Fe3+ by Pt4+ is:
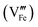 is present.
is present.
Our data show that a maximum of ∼0.085 atoms per formula unit (apfu) of Pt4+ introduced via the cation vacancy substitution, whereas ∼0.18 Pt4+ apfu were charge balanced by Mg2+, for a total of ∼0.265 apfu Pt4+ (out of 2 apfu cations, equivalent to ∼7.5% Pt/[Pt + Fe] on a pure-hematite basis). The overall linear relationships shown in Fig. 5c and d show that the two substitution components increase together. This raises the question of whether the substitution mechanism of Pt has been correctly identified in previous studies. Our experiment was conducted at extreme oxygen fugacity, ensuring that all Fe is trivalent and the only significant cation to charge balance Pt4+ is Mg2+ (i.e., a “Pt-geikielite”). However, such conditions are not generally achieved in routine synthesis of Pt-hematite. The presence of Fe2+ in Pt-hematite has been indicated by some studies,8,11,12 leading to incorporation of Pt4+ as a “Pt-ilmenite” component (Fe2+Pt4+O3). A recent study successfully incorporated Pt2+ alone into hematite, but the charge-balancing mechanism is unclear.17 Elsewhere, either or both Pt2+ and Pt4+ were reported in hematite without any supporting evidence, other than presumably the oxidation state of Pt that was present in the starting materials.6,12 This is problematic due to the poor thermal stability of oxidised Pt. As shown previously, the Pt oxidation state at the hematite surface can be altered by atmospheric interaction or annealing.14 Furthermore, Pt contents of the hematite surface may not be necessarily indicative of the bulk composition.14 DFT calculations show that Pt can be viewed either as Pt2+ or Pt4+, depending on whether the Pt atom is considered by itself or together with its environment, but Pt is overall quadrivalent and charge balanced by reduction of Fe3+ to Fe2+.46 We found no evidence of Pt2+ incorporation into the hematite synthesised in our experimental run.
Iron vacancies in hematite surfaces have been given some attention in computational studies.47–50 However, Fe cation vacancies in bulk hematite were never demonstrated in experimental studies. To the best of our knowledge, the present study is the first to report Fe vacancies in hematite doped with a quadrivalent transition metal. As most M4+-doped hematites are assumed to be charge balanced by Fe2+,51 this raises the possibility that Fe-vacancies formed in previous studies were not properly identified. Alternatively, the substitution process outlined here raises the possibility of a new substitution type of quadrivalent metal doping with a potentially different influence on the properties of hematite. This essentially doubles the exploration space for hematite composition with optimised properties.
Al3+-Doping of hematite is often used for fine-tuning various parameters such as unit cell size or crystallinity during nanocrystal synthesis.52 Aluminium contents are constant across our analysed compositions (0.078 ± 0.002 apfu), suggesting that Al-doping levels can be precisely controlled while varying Pt contents. Mg2+-Doped hematite is known to alter its mechanical properties and make it softer.53 Like Al, Mg contents in our hematite are constant at 0.25 ± 0.01 apfu. Ti4+-Doping is likewise occasionally employed to improve water oxidation efficiency.54,55 Our results demonstrate that a thermodynamically equilibrated hematite containing several charge-balanced substitutions is feasible, opening the possibility for Pt-doped hematite with improved photoelectrochemical properties.
Conclusions
We synthesised Pt-doped hematite at high pressure and temperature. Quantitative chemical data obtained by WDS show that all Pt is quadrivalent, with some Pt4+ charge balanced by Mg2+ while the rest is charge balanced by the formation of a cation vacancy following the removal of Fe from the hematite lattice. Additionally, the hematite was doped with Al3+ and Ti4+. The multiple element doping demonstrates the thermodynamically stable miscibility of the end-member components: Fe3+2O3, Mg2+Ti4+O3, Al3+2O3, Mg2+Pt4+O3, and Fe3+(Pt4+0.75□0.25)O3.Conflicts of interest
There are no conflicts to declare.References
- K. Sivula, F. Le Formal and M. Gratzel, ChemSusChem, 2011, 4, 432–449 CrossRef CAS PubMed.
- D. A. Wheeler, G. Wang, Y. Ling, Y. Li and J. Z. Zhang, Energy Environ. Sci., 2012, 5, 6682–6702 RSC.
- A. J. R. Hensley, Y. Wang and J.-S. McEwen, Appl. Catal., A, 2019, 582, 116989 CrossRef CAS.
- A. G. Tamirat, J. Rick, A. A. Dubale, W.-N. Su and B.-J. Hwang, Nanoscale Horiz., 2016, 1, 243–267 RSC.
- X. Zhang, P. Klaver, R. van Santen, M. C. M. van de Sanden and A. Bieberle-Hütter, J. Phys. Chem. C, 2016, 120, 18201–18208 CrossRef CAS.
- C. Jorand Sartoretti, B. D. Alexander, R. Solarska, I. A. Rutkowska, J. Augustynski and R. Cerny, J. Phys. Chem. B, 2005, 109, 13685–13692 CrossRef.
- G. K. Pradhan and K. M. Parida, ACS Appl. Mater. Interfaces, 2011, 3, 317–323 CrossRef CAS PubMed.
- Y.-S. Hu, A. Kleiman-Shwarsctein, A. J. Forman, D. Hazen, J.-N. Park and E. W. McFarland, Chem. Mater., 2008, 20, 3803–3805 CrossRef CAS.
- K. Kamada, A. Moriyasu and N. Soh, J. Phys. Chem. C, 2012, 116, 20694–20699 CrossRef CAS.
- J. Y. Kim, G. Magesh, D. H. Youn, J. W. Jang, J. Kubota, K. Domen and J. S. Lee, Sci. Rep., 2013, 3, 2681 CrossRef PubMed.
- G. Rahman and O.-S. Joo, Mater. Chem. Phys., 2013, 140, 316–322 CrossRef CAS.
- A. Bak, S. K. Choi and H. Park, Bull. Korean Chem. Soc., 2015, 36, 1487–1494 CrossRef CAS.
- A. Mao, N. G. Park, G. Y. Han and J. H. Park, Nanotechnology, 2011, 22, 175703 CrossRef PubMed.
- M. E. Warwick, D. Barreca, E. Bontempi, G. Carraro, A. Gasparotto, C. Maccato, K. Kaunisto, T. P. Ruoko, H. Lemmetyinen, C. Sada, Y. Gonullu and S. Mathur, Phys. Chem. Chem. Phys., 2015, 17, 12899–12907 RSC.
- H. G. Cha, J. Song, H. S. Kim, W. Shin, K. B. Yoon and Y. S. Kang, Chem. Commun., 2011, 47, 2441–2443 RSC.
- J. Deng, X. Lv, H. Zhang, B. Zhao, X. Sun and J. Zhong, Phys. Chem. Chem. Phys., 2016, 18, 10453–10458 RSC.
- H. Liu, K. Tian, J. Ning, Y. Zhong, Z. Zhang and Y. Hu, ACS Catal., 2019, 9, 1211–1219 CrossRef CAS.
- Y.-P. Hsu, S.-W. Lee, J.-K. Chang, C.-J. Tseng, K.-R. Lee and C.-H. Wang, Int. J. Electrochem. Sci., 2013, 8, 11615–11623 CAS.
- L. Guo, N. Xie, C. Wang, X. Kou, M. Ding, H. Zhang, Y. Sun, H. Song, Y. Wang and G. Lu, Sens. Actuators, B, 2018, 255, 1015–1023 CrossRef CAS.
- Y. W. Phuan, M. N. Chong, K. Egamparan, B. K. Lee, T. Zhu and E. S. Chan, J. Taiwan Inst. Chem. Eng., 2016, 66, 249–257 CrossRef CAS.
- M. E. A. Warwick, K. Kaunisto, G. Carraro, A. Gasparotto, C. Maccato and D. Barreca, Surf. Sci. Spectra, 2015, 22, 47–57 CrossRef CAS.
- M. R. Linford, V. S. Smentkowski, J. T. Grant, C. R. Brundle, P. M. A. Sherwood, M. C. Biesinger, J. Terry, K. Artyushkova, A. Herrera-Gomez, S. Tougaard, W. Skinner, J. J. Pireaux, C. F. McConville, C. D. Easton, T. R. Gengenbach, G. H. Major, P. Dietrich, A. Thissen, M. Engelhard, C. J. Powell, K. J. Gaskell and D. R. Baer, Microsc. Microanal., 2020, 26, 1–2 CrossRef CAS PubMed.
- H. Liang, X. Jiang, W. Chen, S. Wang, B. Xu and Z. Wang, Ceram. Int., 2014, 40, 5653–5658 CrossRef CAS.
- H. E. Çubukçu, O. Ersoy, E. Aydar and U. Çakir, Micron, 2008, 39, 88–94 CrossRef PubMed.
- A. E. Saal, E. H. Hauri, M. L. Cascio, J. A. Van Orman, M. C. Rutherford and R. F. Cooper, Nature, 2008, 454, 192–195 CrossRef CAS PubMed.
- T. Degen, M. Sadki, E. Bron, U. König and G. Nénert, Powder Diffr., 2014, 29, S13–S18 CrossRef CAS.
- E. N. Maslen, V. A. Streltsov, N. R. Streltsova and N. Ishizawa, Acta Crystallogr., Sect. B: Struct. Sci., 1994, 50, 435–441 CrossRef.
- K. B. Schwartz, J. B. Parise, C. T. Prewitt and R. D. Shannon, Acta Crystallogr., Sect. B: Struct. Sci., 1983, 39, 217–226 CrossRef.
- R. W. Wyckoff, Crystal structures, 1963, vol. 1, p. 33 Search PubMed.
- J.-L. Pouchou and F. Pichoir, in Electron Probe Quantitation, ed. K. F. J. Heinrich and D. E. Newbury, Springer, 1991, ch. 4, pp. 31–75 DOI:10.1007/978-1-4899-2617-3_4.
- M. Anenburg and C. Le Losq, SN Appl. Sci., 2019, 1, 372 CrossRef CAS.
- C. S. Finnigan, J. M. Brenan, J. E. Mungall and W. F. McDonough, J. Petrol., 2008, 49, 1647–1665 CrossRef CAS.
- M. Anenburg and J. A. Mavrogenes, Geochim. Cosmochim. Acta, 2016, 192, 258–278 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- H. S. C. O’Neill, Am. Mineral., 1988, 73, 470–486 Search PubMed.
- M. Anenburg and H. S. C. O’Neill, J. Petrol., 2019, 60, 1825–1832 CAS.
- J. Nell and H. S. C. O’Neill, Geochim. Cosmochim. Acta, 1996, 60, 2487–2493 CrossRef CAS.
- A. N. Grundy, B. Hallstedt and L. J. Gauckler, J. Phase Equilib., 2003, 24, 21–39 CAS.
- N. Belzile, Y.-W. Chen and Z. Wang, Chem. Geol., 2001, 174, 379–387 CrossRef CAS.
- A. Borisov and H. Palme, Geochim. Cosmochim. Acta, 1997, 61, 4349–4357 CrossRef CAS.
- F. Farges, D. R. Neuville and G. E. Brown, Am. Mineral., 1999, 84, 1562–1568 CrossRef CAS.
- M. S. Ghiorso, Contrib. Mineral. Petrol., 1990, 104, 645–667 CrossRef CAS.
- B. Reynard and F. Guyot, Phys. Chem. Miner., 1994, 21, 441–450 CrossRef CAS.
- B. A. Wechsler and R. B. Von Dreele, Acta Crystallogr., Sect. B: Struct. Sci., 1989, 45, 542–549 CrossRef.
- M. S. Ghiorso and B. W. Evans, Am. J. Sci., 2008, 308, 957–1039 CrossRef CAS.
- O. Neufeld and M. C. Toroker, J. Phys. Chem. C, 2015, 119, 5836–5847 CrossRef CAS.
- M.-T. Nguyen, S. Piccinin, N. Seriani and R. Gebauer, ACS Catal., 2015, 5, 715–721 CrossRef CAS.
- S. Yin and D. E. Ellis, Surf. Sci., 2008, 602, 2047–2054 CrossRef CAS.
- M. E. McBriarty, S. Kerisit, E. J. Bylaska, S. Shaw, K. Morris and E. S. Ilton, Environ. Sci. Technol., 2018, 52, 6282–6290 CrossRef CAS.
- P. Liao, M. C. Toroker and E. A. Carter, Nano Lett., 2011, 11, 1775–1781 CrossRef CAS PubMed.
- J. Velev, A. Bandyopadhyay, W. H. Butler and S. Sarker, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 205208 CrossRef.
- C. Jorand Sartoretti, M. Ulmann, B. D. Alexander, J. Augustynski and A. Weidenkaff, Chem. Phys. Lett., 2003, 376, 194–200 CrossRef CAS.
- M. Kosa, H. N. Barad, V. Singh, D. A. Keller, K. Shimanovich, S. Ruhle, A. Y. Anderson, A. Zaban and D. T. Major, Phys. Chem. Chem. Phys., 2016, 18, 781–791 RSC.
- D. Cao, W. Luo, J. Feng, X. Zhao, Z. Li and Z. Zou, Energy Environ. Sci., 2014, 7, 752–759 RSC.
- A. Pu, J. Deng, M. Li, J. Gao, H. Zhang, Y. Hao, J. Zhong and X. Sun, J. Mater. Chem. A, 2014, 2, 2491–2497 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma00458a |
| This journal is © The Royal Society of Chemistry 2021 |