Strain-controlled single Cr-embedded nitrogen-doped graphene achieves efficient nitrogen reduction

Abstract

Single atom catalysts (SACs) have received much attention in the nitrogen reduction reaction (NRR) field due to their high atomic utilization and controllable electronic state regulation. It is attractive to explore the mechanism for regulating the electronic state of the active center of single-atom catalysts. Herein, we propose a new regulation mechanism by applying a strain that can change the coordination bond length of Cr–N and quantitatively regulate the electronic state of the active center in Cr-SACs. Based on this mechanism, we achieve an ultra-low 0.174 V over-potential for the NRR in the single Cr-embedded nitrogen-doped graphene (CrN₃@graphene) by applying lattice stretch of 2.5% compared to the pristine CrN₃@graphene. Computational results show that the d band center, the Cr–N anti-bonding orbital and the spin-polarization state of the single Cr atom can be adjusted by tuning the coordination length of Cr–3N. The applied lattice stretch of 2.5% can transform the spin-polarization state of the single Cr atom from a high-spin-polarization state to low-spin-polarization. This conversion weakened the adsorption capacity of N₂ for CrN₃@graphene and finally achieved an ultra-low over-potential. Our findings open up a new path of NH₃ production by exploiting strained SACs under ambient conditions.

---

1. Introduction

The production of ammonia for fertilizers is of significant importance for agricultural development.¹ The current mainstream method of industrial production of ammonia is the Haber–Bosch process. However, this process requires high pressure (about 150–300 bar) and high temperature (500 °C), which is responsible for about 2% of the world's energy consumption and 3% of global CO₂ emissions.^2–5 Therefore, it is necessary to find a more sustainable, highly efficient synthetic ammonia production method. In nature, nitrogen is usually fixed by nitrogenase through an associative mechanism under mild conditions.^6,7 As biomimetic catalysts, the electro-catalysts in nitrogenase can reduce nitrogen to ammonia through a six-proton–electron process when it is energized.⁸ Thus, it is very attractive to use electro-catalysts to reduce nitrogen to ammonia under ambient conditions.

However, the electro-catalysts that have been used for the NRR in the literature still face a series of challenges, such as instability, low selectivity, low NH₃ yield and low Faradaic efficiency (FE).^9–12 As the two major types of electro-catalysts, both molecular catalysts and metal catalysts have their own strengths and weaknesses.^13,14 For example, molecular catalysts and enzymes exhibit high catalytic activity for the NRR, but it is difficult to maintain their stability at room temperature. Metal catalysts and nanoparticles show excellent room temperature stability, but their low selectivities for the NRR limit their application.^15,16 Fortunately, single atom catalysts (SACs), which can be dispersed on different substrates perfectly, combine the advantages of molecular catalysts and homogeneous catalysts.¹⁷ Benefiting from the ultra-high atom utilization rate and single active center, SACs show better catalytic activity and selectivity for many electrochemical reactions.^18–21 Many SACs, such as B–graphene,²² Fe–graphene,²³ Ru-g-C₃N₄,²⁴ and Mo–BN,²⁵ were predicted to be excellent catalysts for the NRR. SACs for the NRR that can restrain the hydrogen evolution reaction (HER) have also been prepared experimentally.²⁶ In these theoretical and experimental works, the electron occupation state of the single atom was recognized as the most critical factor for the catalytic performance. Because the electron occupation state of a single atom determines its ability to adsorb and activate nitrogen, the adsorption and activation of nitrogen was considered to be the most critical step in nitrogen reduction.^27,28 The mainstream method currently used to regulate the coordination environment of SACs is the introduction of different vacancies to adjust the type and number of coordination bonds, such as oxygen²⁹ and nitrogen vacancies.^30,31 Recently researchers have recognized that the catalytic activity can be different even with the same type and number of coordination bonds. For instance, the N-doped carbon framework substrate of a single Fe atom can effectively reduce nitrogen to ammonia, while the porphyrin substrate of a single Fe atom cannot even adsorb nitrogen,^32,33 even though they belong to the same Fe–4N–C coordination and only have different bond lengths of Fe–N. Therefore, it is critical to understand how the bond length regulates the coordination environment of single atoms.

At present, there are few research works on the mechanism of bond length affecting the coordination environment. This is mainly due to the difficulty of accurately controlling and characterizing the bond length experimentally. In this respect, first principles calculations can overcome this difficulty easily by applying lattice strain. As a member of non-precious metals, the Cr metal atom possesses a half-full and easily regulated outermost electronic shell.³⁴ As for the substrate for single atom, nitrogen-doped graphene, which has high conductivity, is able to obtain high current density.³⁵ Many experimental works have confirmed the possibility of stretching graphene.³⁶ Pristine single Cr-embedded nitrogen-doped graphene (CrN₃@graphene) has been predicted to induce a low over-potential of 0.59 V and high selectivity.³⁷

In our present work, we propose a new regulation method to adjust the coordination conditions of single atoms by applying lattice strains to change the bond lengths of single atoms with substrates. Our work shows that CrN₃@graphene with lattice stretch of 2.5% can induce an ultra-low over-potential of 0.17 V. The electron occupation state of a single Cr atom will change with the application of lattice strain. When the lattice strain exceeds 2%, the spin-polarization state of a single Cr atom changes from a high-spin-polarization state to a low-spin-polarization state. These transformations result in changes in the adsorption capacity of the single Cr atom for nitrogen and ultimately improve the catalytic performance. Computational results show that the subtle lattice strain can change the catalytic performance of the single atom catalysts towards the NRR, and also shed new light for designing high catalytic performance SACs in other fields.

2. Results and discussion

2.1 Strain influence on the structural stability of CrN₃@graphene

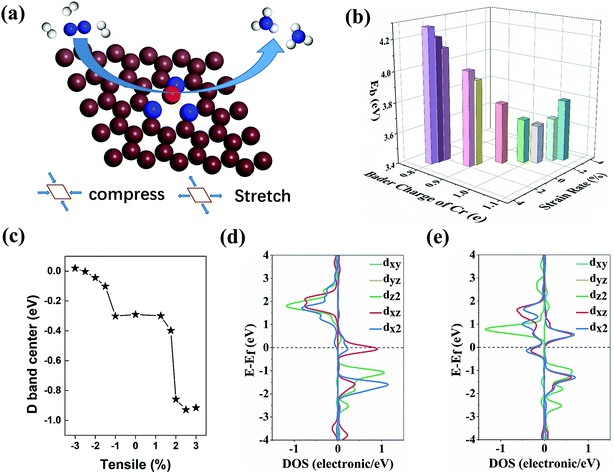
The structural stability of a single-atom catalyst is related to its intrinsic bonding strength between the metal atom and its nearby coordination atoms of N. Only when the bonding strength of Cr–N is greater than the polymerization energy between Cr metallic atoms, the single Cr atom state can stay separately without agglomerating after multiple catalytic cycles. Thus, we first applied the binding energy of the single Cr atom to evaluate the stability of CrN₃@graphene. The binding energy E_b is defined as:

E_b = E_Cr + E_N3@graphene − E_tot

Herein, E_Cr, E_N3@graphene and E_tot represent the metallic state energy of the single Cr atom, the energy of the nitrogen-doped graphene and the total energy of the complex of the single Cr atom and the nitrogen-doped graphene. Hence, a more positive E_b means stronger bonding strength between the Cr–N atoms than that between the Cr–Cr in the Cr metal. The optimized structure of CrN₃@graphene is shown in Fig. 1a. The binding energies of a single Cr atom in strained CrN₃@graphene range from 3.636 eV to 4.276 eV (Fig. 1b) when the Cr–N bond length changed from 1.832 Å to 1.971 Å. Further computational results suggest that the bond length does not linearly increase/decrease as the lattice stretches/compresses since the single Cr atom is not coplanar with nitrogen-doped graphene. The Cr–N bond length hardly changes (1.954 Å to 1.971 Å) in the interval when the lattice tensile/compression rate (−3% to 1.75%) is relatively small. Only when the stretch rate is higher than 2% does the Cr–N bond length drop sharply to 1.832 Å.

Fig. 1 (a) The schematic diagram of the NRR in the CrN₃@graphene. Brown, blue, red and white spheres represent carbon atoms, nitrogen atoms, chromium atoms and hydrogen atoms, respectively. The stretch/compression method is a biaxial strain method. The two axes selected are written in vector form as (1.000, 0.000, 0.000) and (−0.500, 0.732, 0.000). (b) The binding energy and the Bader charge of CrN₃@graphene with different lattice strains. The Bader charge is the change in the amount of charge of a single Cr atom when compared with an intrinsic single Cr atom (6e). (c) The d-band center of the Cr atom of CrN₃@graphene with different lattice strains. The density of states of the single Cr atom for CrN₃@graphene with lattice strains of 1.75% (d) and 2% (e).

We further analyze the Bader charge of a single Cr atom to clarify the effect induced by the change of bond length and binding energy. Because the outer electron arrangement of a single Cr atom is 3d⁵4s¹, the first electron lost by a single Cr atom is the electron filled in the 4s orbital. When the charge transfer of a single Cr atom is less than 1e, the extra electrons will fill the s orbital of the Cr atom and the p orbital of the N atom. As a result, s–p orbital hybridization occurs between the Cr–N atom pair. On the contrary, when the charge transfer of a single Cr atom is more than 1e, the extra electrons will fill the d orbital of the Cr atom and the p orbital of the N atom, resulting in d–p orbital hybridization between Cr–N atoms. Both hybridizations can lead to enhanced binding strength between the Cr atom and the coordinated N atom. With the lattice strain of −2%, the Bader charge of the Cr atom is very close to 1e. Thus, the charge transfer between the 3d orbital of the Cr atom and N₃@graphene is very small and causes the weakest pristine binding energy for the Cr atom. The weakest pristine binding energy is still strong enough to maintain structural stability. In the stretching region where the lattice strain is −3% to 1.75%, the absolute value of charge transfer is not very high (−0.11e to 0.05e). Correspondingly, the binding energy for Cr of these systems is not large. When the lattice strain is higher than 2%, the Bader charge of Cr decreases to −0.20e. Benefitting from the steep charge transfer, these systems possess stronger binding ability to single Cr. Due to the difference in charge transfer between Cr and N₃@graphene, we can further infer that the electronic state filled on the Cr will also be different, which further affects the adsorption process of the intermediate products in the NRR.

To verify this conjecture, we calculated the d band center of the Cr atom. As shown in the illustration of Fig. 1c and Fig. S3 (ESI†), the d-band center of the Cr atom moves to the deeper energy level as the stretching increases. This can be mainly attributed to the change of the amounts of electrons transferred from the Cr atom to the substrate during the stretching process. The electrons filled in the high energy level are gradually lost, and then the d band of the Cr atom moves to the deep energy level as a whole, which explains the shift of the d band center of the Cr atom. When the lattice strain reaches 2%, the number of electrons flowing from the Cr atom to the substrate dramatically increases, resulting in a sharp drop of the d band center of the Cr atom. To further understand the electronic energy state changes of the Cr atom near the mutation point, we calculated the density of states (DOS) of the Cr atom near the dip. Fig. 1d and e show that the spin state of the Cr atom near the Fermi level changes greatly, and this significant change is caused by the hybridization between the d orbital of the Cr atom and p orbital of coordinated N atoms.

2.2 Catalytic performance of Cr-embedded nitrogen-doped graphene

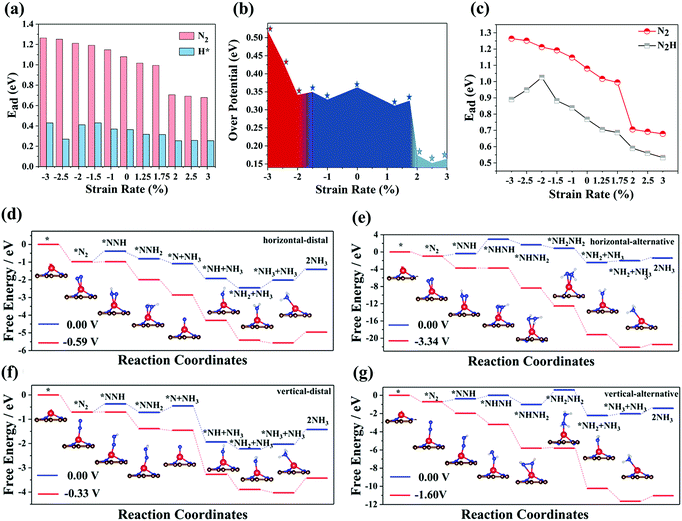
Next, we investigate the catalytic performance of Cr-embedded nitrogen-doped graphene. Fig. S2a and b (ESI†) reveal that the electrons always flow from the Cr atom to small molecules regardless of the adsorption of a H* atom or N₂ molecule. For the adsorption of N₂, the electrons shared between two nitrogen atoms from nitrogen decreased after N₂ adsorbed on the substrate, which plays the critical role in activating nitrogen. Herein, we calculated the different catalytic pathways of the substrate, where four possible mechanisms via various intermediates are considered. According to the difference between the way of adsorbing nitrogen and the way of forming and desorbing ammonia, we refer to the four mechanisms as horizontal–distal, horizontal–alternative, vertical–distal, and vertical–alternative. For substrates with different stretching rates, the maximum value of the positive free energy difference in each path at 0 V applied potential was considered as the potential-determining step (PDS) of the path, while the minimum value of the PDS of four paths can be considered as the PDS for the whole NRR process. In fact, for all the NRR processes we studied, the PDS of CrN₃@graphene with different lattice strains was *N₂ to *N₂H of the vertical–distal mechanism, indicating that the introduction of lattice strain does not change the PDS of SACs. The over-potentials of different lattice strains calculated are summarized in Fig. 2b, while the free energy evolution for the NRR and the optimized structures of the intermediates for CrN₃@graphene with a lattice strain of 2.5% are shown as insets in Fig. 2d–g. The reaction coordinates for CrN₃@graphene with lattice strains of other values are shown in Fig. S3–S12 (ESI†).

Fig. 2 (a) The adsorption energies of H* and N₂, which adsorbed on the CrN₃@graphene with different lattice strains. (b) The over-potentials of CrN₃@graphene with different lattice strains. (c) The adsorption energies of N₂ and N₂H, which adsorbed on the CrN₃@graphene with different lattice strains. The specific calculation formula of adsorption energy is: E_ad = E_molecular + E_{crN3@graphene} − E_tot. Here, E_molecular, E_{crN3@graphene} and E_tot represent the energy of molecule (N₂ or N₂H), the energy of the single Cr-embedded nitrogen-doped graphene and the total energy of molecules adsorbed on single Cr-embedded nitrogen-doped graphene. Free energy process of the (d) horizontal–distal, (e) horizontal–alternative, (f) vertical–distal and (g) vertical–alternative reaction mechanism for CrN₃@graphene with a lattice strain of 2.5%. Structural evolution is shown in the upper right corner of each panel. Brown, blue, red and gray spheres represent carbon atoms, nitrogen atoms, chromium atoms and hydrogen atoms, respectively. The last step indicates the recovery of the catalysts and this process does not involve electronic gains and losses. It is not an electrochemical step and does not change with the applied potential.

As the lattice strain changed from −3% to −2%, the over-potential of CrN₃@graphene decreased with the increase in the lattice strain. As the lattice strain varied from −2% to 1.75%, the over-potential of CrN₃@graphene did not change much. It is very surprising that when the lattice strain exceeds 2%, there exists a dip in the over-potential. The over-potential of CrN₃@graphene with a lattice strain of 2% is 0.17 V. As the lattice strain interval ranges from 2% to 3%, the over-potential of CrN₃@graphene is incredibly low, which clearly suggests that CrN₃@graphene with lattice stretching can be an excellent catalyst for the NRR.

2.3 Competitive reactions between hydrogen evolution and nitrogen reduction

The hydrogen evolution reaction (HER) is the most common competitive reaction for the NRR. Protons and electrons will be consumed in the HER and this results in low FE of the NRR. The ideal electro-catalysts for the NRR should have strong adsorption capacity for N₂ and weak adsorption capacity for H*. Thus, we calculated the adsorption energy of N₂ and H* for CrN₃@graphene with different lattice strains. As depicted in Fig. 2a, the adsorption energy of N₂ slowly decreases with the increase of lattice strain. It is worth noting that there is a dip for the adsorption of N₂ at the lattice strain of 2%. CrN₃@graphene with 3% applied strain possesses the lowest adsorption energy (0.70 eV) for N₂. However, with the application of the lattice strain, the adsorption energy of H atoms in CrN₃@graphene does not change much. The biggest adsorption energy of H atoms in CrN₃@graphene is 0.45 eV. Hence, the adsorption energy of H atoms is always lower than the adsorption energy of N₂. Thus, CrN₃@graphene has superior ability in adsorbing nitrogen, leading to better catalytic performance for the NRR.

2.4 Mechanism of lattice strain affecting over-potential

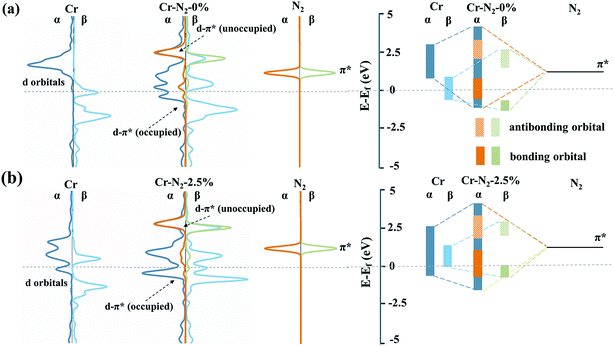
The PDS of CrN₃@graphene with different lattice strains is always *N₂ to *N₂H, indicating that an additional electrochemical potential to drive *N₂ to *N₂H is required. Weaker adsorption energy of *N₂ and stronger adsorption energy of *N₂H can reduce the potential difference of this process. Thus, we calculated the adsorption energy of *N₂ and *N₂H, as shown in Fig. 2c. The evolution of adsorption energies can be divided into three stages. In the first region where the lattice strain changed from −3% to −2%, the adsorption energy of *N₂ decreased, while the adsorption energy of *N₂H increased, which reduced the over-potential of NRR. In the second region where the lattice strain changed from −1.5% to 1.5%, the adsorption energy of *N₂ and *N₂H exhibits a similar declining trend, which induces slight fluctuation of the over-potential. In the third region where the lattice strain changed from 2% to 3%, the adsorption energies of *N₂ and *N₂H still have a similar downward trend, which makes the over-potential change a little. However, there is a 0.3 eV decrease in the adsorption energy of *N₂ and 0.1 eV decrease in the adsorption energy of *N₂H when the lattice strain changed from 1.5% to 2%. As a result, the over-potential of single CrN₃@graphene with a lattice strain of 2% is lower by 0.2 eV than the over-potential of CrN₃@graphene with a lattice strain of 1.5%.

Since the biggest change comes from the adsorption of *N₂, we focused on the electronic energy state transition and bonding strength of Cr–N in the adsorption of *N₂. Fig. 3 shows the orbital interaction between N₂ and a single Cr atom. As shown in Fig. 3a and b, the π* orbital of N₂ and 3d orbital of a single Cr atom are located near the Fermi level. After nitrogen adsorption, the orbitals of the single Cr atom and N₂ hybridize, resulting in occupied bonding orbitals with lower energy and unoccupied anti-bonding orbitals with higher energy. Compared with the pristine CrN₃@graphene, the 3d up-spin orbital of CrN₃@graphene with a lattice strain of 2.5% had a small orbital peak located above the Fermi level. This makes the position of the bonding orbital coupled through this orbital move greatly towards the shallow energy level. Since the DOS of Cr near the Fermi level for the up-spin orbital decreased after stretching by 2.5%, we have reasons to believe that the strength of this bonding orbital will also decrease. At the same time, the 3d down-spin orbital of CrN₃@graphene with a lattice strain of 2.5% has a small orbital peak that moved below the Fermi level. This makes the position of the anti-bonding orbital coupled through this orbital move below the Fermi level, and the anti-bonding states appear below the Fermi level.

Fig. 3 (a) Projected electronic densities of states (pDOS) and partial description of 3d orbitals of Cr, anchored in nitrogen-doped graphene with a lattice strain of 0%, 2p orbitals of N₂, and their interaction. (b) Projected electronic densities of states (pDOS) and partial description of 3d orbitals of Cr, anchored in nitrogen-doped graphene with a lattice strain of 2.5%, 2p orbitals of N₂, and their interaction; α and β mean down-spin and up-spin, respectively. The orange and brownish-green solid boxes on the right side of this figure represent the energy range of the bonding orbitals of the 3d orbital for Cr.

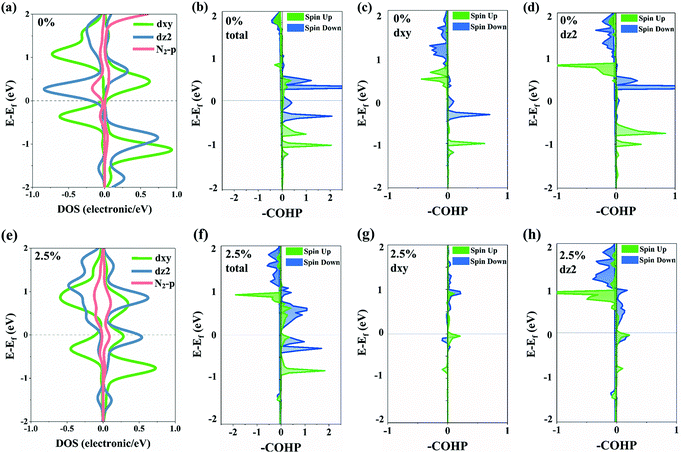
We further analyze the partial density of states that is divided by orbital components of a single Cr atom (Fig. 4a and e). The PDOS of single Cr experiences very big changes. Overall, the PDOS of Cr moves toward the shallow energy level when applying the stretch, and such a shift of hybridization states of the Cr–N bond induces weakness of the Cr–N bond. In terms of each orbital, the spin state of the occupied d_xy orbital near the Fermi level inverts from down-spin to up-spin. Meanwhile, the up-spin state of the d_z² orbital moves from −1 eV to the Fermi level. The simulation of crystal orbital Hamilton populations (Fig. 4b–d and f–h) further confirms this result. Both the bond strength of d_xy–p and d_z²–p states weakens after stretching. The integral crystal orbital Hamilton population (-ICOHP) of the d_xy–p state decreased from 0.1179 eV to 0.0072 eV, while that of the d_z²–p state decreased from 0.1247 eV to 0.0093 eV. The down-spin state of the d_xy–p state changed from bonding orbital to anti-bonding orbital, which weakens the bond strength of d_xy–p. The decrease in the amount of filled electrons on the d_z² orbital and the energy level shift may be the main two reasons for the weakness of the bond strength of d_z²–p.

Fig. 4 The partial densities of states that are divided by orbital components of N₂ and Cr for CrN₃@graphene with strain rates of 0% (a) and 2.5% (e), the spin state of the electron filled in the right/left orbit is up/down-spin. The crystal orbital Hamilton populations of Cr–N divided by orbital composition for CrN₃@graphene with a lattice strain of 0% (b–d). The crystal orbital Hamilton populations of Cr–N divided by orbital composition for CrN₃@graphene with a lattice strain of 0% (f–h).

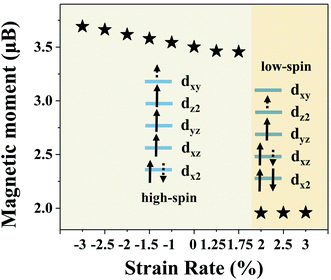
The COHP results show the influence of the change of the single Cr atom's spin state on its ability to adsorb intermediate products. Therefore, it is necessary to reveal the role of spin polarization in the adsorption process of intermediate products. To this aim, we apply the crystal field theory to reveal the role of spin polarization in the adsorption process of N₂. Since the bond length of Cr–N for the single Cr atom and the three coordinated nitrogen atoms has little difference, we consider that the single Cr atom maintains a tetrahedron-like field even after the application of stretching. In view of this, the energy levels of the 3d orbital of a single Cr atom arrange from high to low in the order: d_xy, d_z², d_yz, d_xz, d_x². Fig. 5 lists the magnetic moments of a single Cr atom for CrN₃@graphene with different lattice strains. When the lattice strain is less than 2%, the calculated magnetic moment of a single Cr atom is ∼3.6 μB, indicating that the single Cr atom is in a high-spin-polarization state. A single Cr atom in a high-spin-polarization state owns more electrons to pair with N₂, resulting in strong adsorption ability for N₂. It is worth mentioning that since the number of electrons filled in the d_xy orbital decreases with stretching, the magnetic moment of a single Cr atom in the first step region will also decrease (Fig. S17, ESI†). When the lattice strain is greater than 2%, the calculated magnetic moment of a single Cr atom is ∼1.9 μB, indicating that the single Cr atom is in a low-spin-polarization state. The single Cr atom in the low-spin-polarization state has fewer electrons to pair with N₂, and thus the adsorption ability for N₂ decreased, leading to a lower over-potential for the single Cr atom in the low-spin-polarization state. These results indicate that the single Cr atom in the low-spin-polarization state has a weak nitrogen adsorption capacity, and this promotes the protonation from N₂ to N₂H. Our calculation results show that the spin polarization state of the single atom plays a decisive role in the adsorption of small molecules in the electrocatalytic process. Lattice strain can effectively affect the spin-polarization state of a single atom by changing the bond lengths of the single atom and coordination atom, and finally changing the over-potential significantly.

Fig. 5 The magnetic moment of a single Cr atom for CrN₃@graphene with different lattice strains when N₂ is not adsorbed on. The illustration shows the electron occupation states of the 3d orbital of a single Cr atom in different areas. The number of black squares under the arrow indicates the number of electrons.

3. Conclusion

In summary, we systematically investigated the NRR performance of CrN₃@graphene with different lattice strains. Comprehensive DFT computational results show that in the CrN₃@graphene with different lattice strains, the binding energy of a single Cr is large enough to make the single Cr atom tightly bonded to the substrate. The introduction of lattice strain cannot change the PDS of CrN₃@graphene with different lattice strains, and the PDS is *N₂ to *N₂H of vertical–distal mechanism. Since the adsorption energy of *N₂ is always higher than the adsorption energy of *H, CrN₃@graphene with a different lattice strain has good to excellent selectivity for the NRR. CrN₃@graphene with lattice strain of 2.5% has weaker adsorption of N₂ and finally achieved an ultra-low over-potential of 0.17 V for the NRR. The calculated partial density of states and integral crystal orbital Hamilton population indicate that the weakness of d_xy–p and d_z²–p is the main reason for the weak adsorption of N₂. Crystal field analysis reveals that the change of spin-polarization state of a single Cr atom plays a vital role in the adsorption of N₂. Our calculation results predict that CrN₃@graphene with a lattice strain of 2.5% is a promising single-atom catalyst for the NRR. We hope that our study is able to promote experimental and theoretical research efforts in adjusting the coordination environment of single atoms by changing the bond length.

4. Computational methods

All of the simulation results were done through the Vienna ab initio simulation package (VASP) built on density functional theory (DFT) based on first-principles simulations.^38–40 The projector augmented wave (PAW) method⁴¹ and the Perdew–Burke–Ernzerhof (PBE)^42,43 pseudopotential based on the generalized gradient approximation (GGA)⁴⁴ were carried out. The cut off energy was set as 420 eV for structure optimization and total energy calculation. The force convergence condition was 0.02 eV Å⁻¹. The Brillouin zone was tested using a Monkhorst–Pack method k-point mesh of 3 × 3 × 1. In our work, a 5 × 5 × 1 supercell of graphene (a = b = 12.436 Å, and c = 19.957 Å) was adopted for the investigations. The structure of CrN₃@graphene is shown in Fig. 1a. The coordination number of Cr is three. A slight lattice strain did not change the coordination number of Cr. It only changed the bond length of Cr–N and thus changed the electron occupation state of Cr. We calculated the potential-determining step (PDS), applied potential (U_L) and over-potential (η) to compare the catalytic performance of different reaction pathways for the electrochemical NRR. The reaction step with the largest positive free energy change is the PDS. Applied potential is added to make this step occur spontaneously. Thus, the applied potential is calculated by U_L = ΔG_max/e⁻. The ΔG_max means the maximum free energy change in the reaction. Over-potential is calculated by η = U_equilibrium − U_L; U_equilibrium is the equilibrium potential for the reaction. For the NRR, this value is set as −0.16 V. The smaller the over-potential, the higher the catalytic efficiency for the catalysts. The reaction free energy change is defined as ΔG = ΔE + ΔZPE − TΔS, where ΔE is the energy calculated by DFT, ΔZPE is the zero-point energy (ZPE) correction, and ΔS is the entropy change. ZPE is calculated by the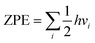 , and v_i is the vibration frequency of a small molecule with the unit of cm⁻¹. The entropy values of small molecules such as N₂, H₂, and NH₃ are obtained from the NIST database. In this work, only vibration entropy was considered in the calculation. The nitrogen reduction reaction is a six-proton and a six-electron process. Usually, four paths are suggested to be possible reaction paths, including horizontal–distal, horizontal–alternative, vertical–distal and vertical–alternative. The reaction pathways are explained as follows. (a) Horizontal–distal ways: the adsorbed N₂ molecule is nearly parallel to the catalyst surface. The first three H⁺ pairs appear on the N atom furthest from the catalyst, caused a release of NH₃ molecule and left an N atom to form the second NH₃ molecule. (b) Horizontal–alternative ways: the adsorbed N₂ molecule is nearly parallel to the catalyst surface. The H⁺ pairs appear alternately on different sides of the N₂ molecule. Once the hydrogenation by the fifth H⁺, the first NH₃ molecule is released. The formation of the second NH₃ molecule is accompanied by the hydrogenation of the sixth H⁺. (c) Vertical–distal ways: the adsorbed N₂ molecule is nearly perpendicular to the catalyst surface. The first three H⁺ pairs appear on the N atom furthest from the catalyst, causing a release of an NH₃ molecule and leaving a N atom to form the second NH₃ molecule. (d) Vertical–alternative ways: the adsorbed N₂ molecule is nearly perpendicular to the catalyst surface. The H⁺ pairs appear alternately on different sides of the N₂ molecule. Upon the hydrogenation of the fifth H⁺, the first NH₃ molecule is released. The formation of the second NH₃ molecule is accompanied by the hydrogenation of the sixth H⁺.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

Q. Z. was supported by the Beijing Natural Science Foundation (2192029), the National Key Research and Development Program of China (2017YFB0702100), the National Natural Science Foundation of China (11404017), the Technology Foundation for Selected Overseas Chinese Scholars, and the Ministry of Human Resources and Social Security of China. Z. W. S. acknowledges the support of the Singapore National Research Foundation (NRF-NRFF2017-04).

References

1. R. Schlögl, Angew. Chem., Int. Ed., 2003, 42, 2004–2008.
2. J. W. Erisman, M. A. Sutton, J. Galloway, Z. Klimont and W. Winiwarter, Nat. Geosci., 2008, 1, 636–639.
3. J. N. Galloway, A. R. Townsend, J. W. Erisman, M. Bekunda, Z. Cai, J. R. Freney, L. A. Martinelli, S. P. Seitzinger and M. A. Sutton, Science, 2008, 320, 889–892.
4. J. G. Chen, R. M. Crooks, L. C. Seefeldt, K. L. Bren, R. M. Bullock, M. Y. Darensbourg, P. L. Holland, B. Hoffman, M. J. Janik, A. K. Jones, M. G. Kanatzidis, P. King, K. M. Lancaster, S. V. Lymar, P. Pfromm, W. F. Schneider and R. R. Schrock, Science, 2018, 360, eaar6611.
5. P. Chen, N. Zhang, S. Wang, T. Zhou, Y. Tong, C. Ao, W. Yan, L. Zhang, W. Chu, C. Wu and Y. Xie, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 6635–6640.
6. K. A. Brown, D. F. Harris, M. B. Wilker, A. Rasmussen, N. Khadka, H. Hamby, S. Keable, G. Dukovic, J. W. Peters, L. C. Seefeldt and P. W. King, Science, 2016, 352, 448–450.
7. B. M. Hoffman, D. Lukoyanov, Z. Yang, D. R. Dean and L. C. Seefeldt, Chem. Rev., 2014, 114, 4041–4062.
8. S. L. Foster, S. I. P. Bakovic, R. D. Duda, S. Maheshwari, R. D. Milton, S. D. Minteer, M. J. Janik, J. N. Renner and L. F. Greenlee, Nat. Catal., 2018, 1, 490–500.
9. S. Giddey, S. P. S. Badwal and A. Kulkarni, Int. J. Hydrogen Energy, 2013, 38, 14576–14594.
10. C. Guo, J. Ran, A. Vasileff and S. Qiao, Energy Environ. Sci., 2018, 11, 45–56.
11. X. Cui, C. Tang and Q. Zhang, Adv. Energy Mater., 2018, 8, 1800369.
12. A. R. Singh, B. A. Rohr, J. A. Schwalbe, M. Cargnello, K. Chan, T. F. Jaramillo, I. Chorkendorff and J. K. Nørskov, ACS Catal., 2016, 7, 706–709.
13. L. Zhang, X. Ji, X. Ren, Y. Ma, X. Shi, Z. Tian, A. M. Asiri, L. Chen, B. Tang and X. Sun, Adv. Mater., 2018, 30, 1800191.
14. D. Bao, Q. Zhang, F. Meng, H. Zhong, M. Shi, Y. Zhang, J. Yan, Q. Jiang and X. Zhang, Adv. Mater., 2017, 29, 1604799.
15. Z. Xue, S. Zhang, Y. Lin, H. Su, G. Zhai, J. Han, Q. Yu, X. Li, M. Antonietti and J. Chen, J. Am. Chem. Soc., 2019, 141, 14976–14980.
16. B. Hinnemann and J. K. Nørskov, J. Am. Chem. Soc., 2003, 125, 1466–1467.
17. H. Zhang, G. Liu, L. Shi and J. Ye, Adv. Energy Mater., 2018, 8, 1701343.
18. H. Yan, H. Cheng, H. Yi, Y. Lin, T. Yao, C. Wang, J. Li, S. Wei and J. Lu, J. Am. Chem. Soc., 2015, 137, 10484–10487.
19. B. Chen, T. Wang, S. Zhao, J. Tan, N. Zhao, S. Jiang, Q. Zhang, G. Zhou and H. Cheng, Adv. Mater., 2021, 33, 2007090.
20. G. Zhou, S. Zhao, T. Wang, S. Z. Yang, B. Johannessen, H. Chen, C. Liu, Y. Ye, Y. Wu, Y. Peng, C. Liu, S. Jiang, Q. Zhang and Y. Cui, Nano Lett., 2020, 20, 1252–1261.
21. L. M. Azofra, C. Sun, L. Cavallo and D. R. MacFarlane, Chem. – Eur. J., 2017, 23, 8275–8279.
22. C. Liu, Q. Li, C. Wu, J. Zhang, Y. Jin, D. R. MacFarlane and C. Sun, J. Am. Chem. Soc., 2019, 141, 2884–2888.
23. X. Guo and S. Huang, Electrochim. Acta, 2018, 284, 392–399.
24. X. Liu, Y. Jiao, Y. Zheng, M. Jaroniec and S. Qiao, J. Am. Chem. Soc., 2019, 141, 9664–9672.
25. J. Zhao and Z. Chen, J. Am. Chem. Soc., 2017, 139, 12480–12487.
26. L. Hui, Y. Xue, H. Yu, Y. Liu, Y. Fang, C. Xing, B. Huang and Y. Li, J. Am. Chem. Soc., 2019, 141, 10677–10683.
27. Y. Guo, T. Wang, Q. Yang, X. Li, H. Li, Y. Wang, T. Jiao, Z. Huang, B. Dong, W. Zhang, J. Fan and C. Zhi, ACS Nano, 2020, 14, 9089–9097.
28. S. Liu, M. Wang, H. Ji, X. Shen, C. Yan and T. Qian, Natl. Sci. Rev., 2020, 8, nwaa136.
29. J. Kong, A. Lim, C. Yoon, J. H. Jang, H. C. Ham, J. Han, S. Nam, D. Kim, Y. Sung, J. Choi and H. S. Park, ACS Sustainable Chem. Eng., 2017, 5, 10986–10995.
30. S. Chen, S. Perathoner, C. Ampelli, C. Mebrahtu, D. Su and G. Centi, ACS Sustainable Chem. Eng., 2017, 5, 7393–7400.
31. S. Zhao, G. Chen, G. Zhou, L. Yin, J. P. Veder, B. Johannessen, M. Sauuders, S. Z. Yang, R. D. Marco, C. Liu and S. Jiang, Adv. Funct. Mater., 2020, 20, 1906157.
32. F. Lü, S. Zhao, R. Guo, H. Jia and X. Peng, Nano Energy, 2019, 61, 420–427.
33. X. Yao, Z. Chen, Y. Wang, X. Lang, Y. Zhu, W. Gao and Q. Jiang, Appl. Surf. Sci., 2020, 529, 147183.
34. A. Griesmaier, J. Werner, S. Hensler, J. Stuhler and T. Pfau, Phys. Rev. Lett., 2005, 94, 160401.
35. L. Wang, Q. Luo, W. Zhang and J. Yang, Int. J. Hydrogen Energy, 2014, 39, 20190–20196.
36. Z. H. Ni, T. Yu, Y. H. Lu, Y. Y. Wang, Y. P. Feng and Z. X. Shen, ACS Nano, 2008, 2, 2301–2305.
37. W. Zhao, L. Zhang, Q. Luo, Z. Hu, W. Zhang, S. Smith and J. Yang, ACS Catal., 2019, 9, 3419–3425.
38. J. Hafner and G. Kresse, Prop. Complex Inorg. Solids, 1997, 1, 69–82.
39. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
40. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
41. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
42. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
43. J. P. Perdew, J. A. Chevary, J. S. H. Vosko, K. A. Jackson and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
44. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma00476j

---