Open Access Article
Open Access ArticleExplosive molecule sensing at lattice defect sites in metallic carbon nanotubes†
Manasi
Doshi
 and
Eric P.
Fahrenthold
and
Eric P.
Fahrenthold
 *
*
Department of Mechanical Engineering, University of Texas, Austin, TX 78712, USA. E-mail: epfahren@mail.utexas.edu
First published on 19th August 2021
Abstract
Explosives and hazardous gas sensing using carbon nanotube (CNT) based sensors has been a focus of considerable experimental research. The simplest sensors have employed a chemiresistive sensing mechanism, and rely on substitutional doping or structural flaws (vacancy, divacancy, or Stone–Wales defects) to increase sensitivity. However since chemiresistive sensors often show poor selectivity, further improvements are needed. Ab initio analysis of the chemiresistive response of five metallic CNT sensors incorporating substitutional doping or structural flaws suggests that arrays of these devices may be effectively employed to improve selectivity. In particular, arrays composed of doped or flawed CNTs can distinguish nitroaromatic and nitramine explosive molecules from each other and from four common background gases. Array selectivity is improved by capitalizing upon the nonlinear current–voltage characteristics of the substitutionally doped or structurally flawed CNTs.
1. Introduction
Trace detection of explosive materials1 presents a wide range of challenges.2 In the gas phase, high sensitivity is often needed to address low vapor pressures,3 while good selectivity4 is required to distinguish target analytes from background gases and other explosive molecules. There is considerable demand for mobile, low power sensing systems to replace mass spectrometers5 or other traditional explosive detection devices which can be bulky, complex, and expensive. Hence recent research on hazardous gas sensing has placed considerable emphasis on the development of nanosensors,6,7 including one and two dimensional nanocarbons.8–10Published experimental studies have tested carbon nanotube (CNT) based devices in gas sensing applications,11–16 and reported considerable success in detecting a wide range of molecules, from hydrogen15 to complex nerve agents.16 All of the papers just cited employed ‘as produced’ carbon nanotubes (CNTs). By contrast, studies employing ‘pristine’ nanotubes have generally measured weak interactions with analyte gases,9,17,18 suggesting that CNT defects play an important role in determining sensor performance.19 Similarly, recent work20 evaluated the effects of defects on the chemiresistive sensing properties of Field Effect Transistors (FETs) made from semiconducting CNTs. Plasma irradiation was used to intentionally add defects to the CNTs, and the presence of defects (primarily vacancies) was confirmed through Raman spectroscopy. The chemiresistive response to NO2 of the CNT-FETs with added defects was much greater than those with the baseline level of defects, again showing that defects improve chemiresistive response.
A large body of CNT research has investigated lattice defects, which here refers to both structural flaws and substitutional deviations from a perfect network of sp2 bonded carbon atoms. During the growth of CNTs substitutional ‘doping’ may occur when one or more of the carbon atoms are replaced by atoms of other elements. Nitrogen21,22 and boron23,24 are the most commonly studied substitutional dopants. Since CNTs doped by both these elements have shown good energy storage performance in batteries, controlled processes have been developed to apply such dopants on demand. The dopant elements produce local changes in the CNT structure25 which enhance the surface reactivity of the nanotube26 and may therefore also improve gas sensing performance. In published experiments, boron and nitrogen doped double-wall and multi-wall CNTs have shown an improved chemiresistive sensitivity for NH3 and NO2 detection.26–28 Structural lattice defects (e.g. vacancies, divacancies, and and Stone–Wales defects) are also likely to occur during CNT production29–31 and are known to change the electronic properties of the nanotubes.32,33 Their sensitivity and selectivity effects on chemiresistive gas sensing have been investigated19,34 and been found to improve CNT performance in NH3, NO2 and H2 detection.
It is important to note, given the extensive literature on CNT defects, that much published computational work infers improvements in sensing performance from property changes generated by the introduction of defects. Zhang et al.35 studied the interaction of CNTs, substitutionally doped by palladium (Pd), with the decomposition products of SF6. Based on calculations for adsorption energy, changes in the density of states (DOS) and HOMO–LUMO energy gaps, they concluded that the nature of the interaction of such CNTs with SO2, H2S, SOF2, SO2F2, and CF4 will be very species dependent. Similarly Kuganathan et al.36 computed the adsorption energy, charge transfer, magnetic moment, charge density, and DOS for SO2 and H2 interaction with CNTs substitutionally doped by ruthenium (Ru). Based on large adsorption energy values, they inferred that Ru-doped CNTs may be good candidates for SO2 and H2 sensing. Demir et al.37 studied a variety of properties (adsorption energy, HOMO–LUMO structures, charge density, DOS) for carbon monoxide interaction with CNTs substitutionally doped by platinum (Pt). Based on charge density difference plots and HOMO–LUMO energy gap data, they concluded that Pt doped CNTs could be used to detect carbon monoxide. With respect to structural defects, Andzelm et al.38 studied adsorption energy, HOMO–LUMO structures, DOS, and Fourier-transform infrared spectroscopy (FTIR) spectra for CNTs with Stone–Wales, vacancy, and interstitial defects, concluding that such nanotubes would perform well as ammonia sensors.
This paper extends previous computational research on gas sensing using carbon nanotubes with defects, with the following focus:
• The target molecules are one nitroaromatic (TNT) and two nitramine (RDX and HMX) explosives; the response to four background gases (N2, CO2, H2O, and O2) is also computed, to determine the relative sensitivity of the CNTs to explosives and the selectivity of the modeled sensors in identifying various analytes;
• The modeled CNTs incorporate one of five different defects, two substitutional dopants (boron and nitrogen) and three structural defect types (vacancy, divacancy, and Stone–Wales);
• The five sensor types are evaluated for their performance as a sensor array, using Principal Component Analysis (PCA) to estimate the array's effectiveness in explosive molecule sensing.
Unlike previous work, since the introduction of defects renders the modeled metallic CNT sensing performance highly nonlinear, ab initio current transmission calculations are performed over a range of bias voltages (0.2–0.9 volts), at an increment of 0.1 volts. This provides an eight-fold increase in the sensor array degrees of freedom considered in the PCA, and is aimed at improving the selectivity of the modeled sensing device, a central concern in chemiresistive sensing.
Initial computations for each combination of analyte and sensor type include: (1) adsorption energy, (2) zero-bias conductance, and (3) charge density difference distribution. Next, changes in the CNT current as a function of the applied bias voltage are computed and used to evaluate the chemiresistive sensing properties of the CNT-based array. Principal Component Analysis of the current data indicates that the defect based sensor array will show good sensitivity and selectivity, for all three explosives and for all four background gases included in the analysis, in particular distinguishing all three explosives from each other and from all four background gases.
The subsequent sections of the paper are arranged as follows. The next section describes the computational methods used in the analysis. The section which follows presents: (1) the ab initio modeling results for the five CNT sensor configurations and seven analytes of interest, in all combinations, followed by (2) a principal component analysis which evaluates the performance of the proposed sensor array. Finally the conclusions section summarizes the results presented in the paper and offers suggestions for future research.
2. Computational methods
The ab initio analyses described in this paper were performed using the open source code suite SIESTA,39 which employs Kohn–Sham self-consistent density functional theory to compute equilibrium configurations for the nuclear-electronic structure. A Generalized Gradient Approximation (GGA) exchange correlation functional with Perdew–Burke–Ernzerhof (PBE) parameterization was used in all of the calculations. A double-zeta polarized (DZP) basis set was assumed for all of the elements. Brillouin zone k-point sampling employed a Monkhorst–Pack mesh with an energy cutoff of 300 Ry. The analysis assumed zero temperature and a maximum force convergence criterion of 0.04 eV Å−1. The electrical transport properties of the modeled systems were computed using a non-equilibrium Green's function (NEGF) method implemented in the TranSIESTA40 module, and conductance was computed using the Landauer–Buttiker formula.41The substitutional dopants and structural defects modeled in this paper were applied to a metallic, single walled carbon nanotube of chirality (5,5), with a unit cell length of 2.46 Å. Starting geometries for the background gases and explosives molecules are taken from published work.42–44 The starting analyte molecule orientations assumed in this paper were obtained from a preliminary analysis which identified the minimum energy orientations for analyte adsorption on a pristine CNT(5,5). A typical atom count for the models is 330. In the non-transport directions, the scattering zone boundaries were separated from the nearest nuclei by at least 20 Å, to avoid any neighboring supercell interactions. In the transport direction, the scattering zone was bounded by electrodes composed of pristine (5,5) nanotubes, modeling a conductor of infinite length.
The results and discussions section applies three metrics to quantify the performance of the sensor array and evaluate its effectiveness. The first two metrics describe the equilibrium states of the modeled systems at zero bias voltage. The first metric is the adsorption energy, defined by
| ΔE = Etotal − Esensor − Eanalyte | (1) |
| ΔG = Gsensor+analyte − Gsensor | (2) |
| ΔI = I(V, sensor, analyte) − Iref(V, sensor) | (3) |
Published work indicates that electronic transport through pristine CNTs occurs without spin polarization for hundreds of nanometers.45 A computational study46 on CNTs with Stone–Wales defects showed that the presence of a Stone–Wales defect does not induce spin polarization as long as the defect density is lower than one defect per nine unit cells. Our computations consider one defect per sixteen unit cells of CNT, much lower than the cited threshold. Computational studies20,47 also indicate that isolated vacancies do not cause spin polarization, since they undergo a ‘reconstruction’ of the type described later in the paper. Hence the sensing models described in this paper do not consider the effects of spin polarization. Finally note that recently published work48 investigating surface adsorption processes for the same exchange correlation function, nanotube type, background mesh, and convergence criteria applied here found that van der Waals interaction effects were negligible.
3. Results and discussion
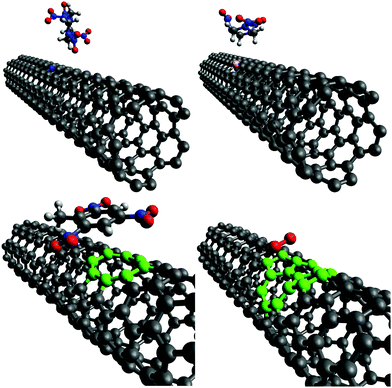
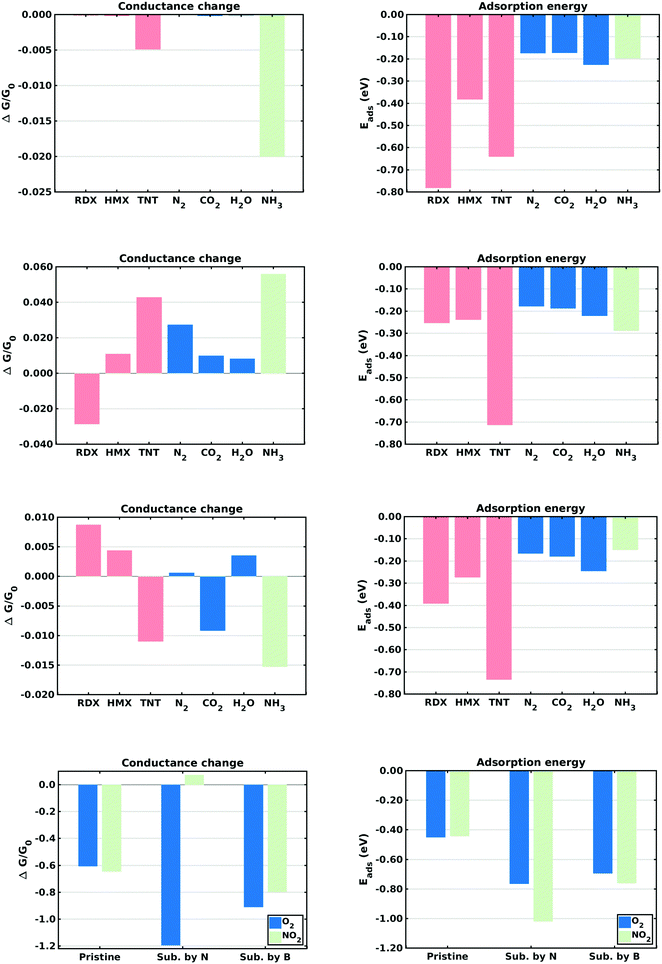
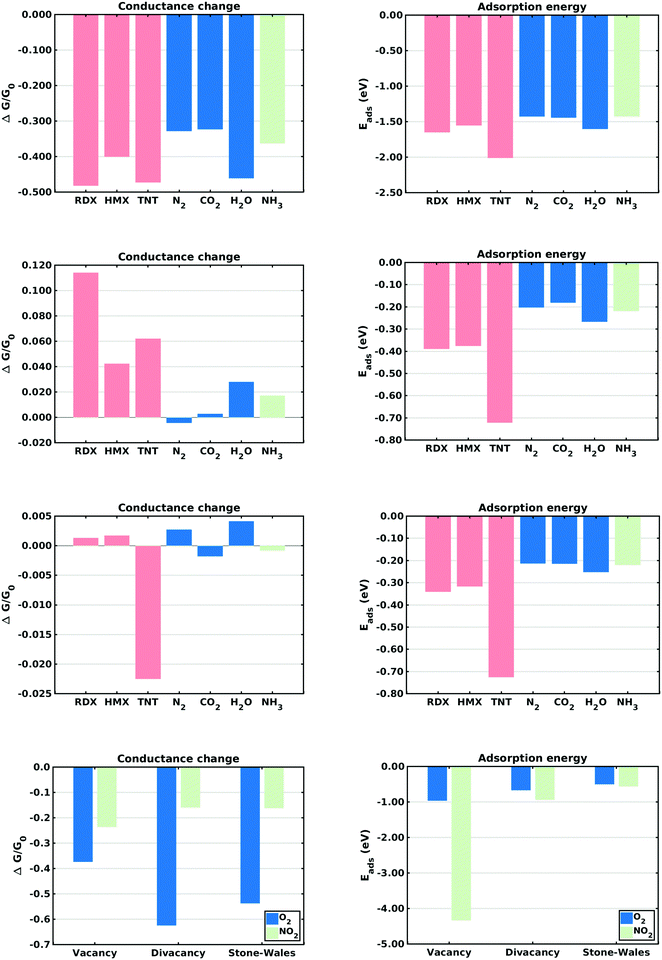
This section describes the ab initio modeling results for the response of the five CNT sensors to the seven analytes (three explosives and four background gases) considered in this paper. The ab initio modeling results for the sensor current response are then used, in a Principal Component Analysis, to evaluate the performance of the sensor array for its sensitivity and selectivity in the detection of explosive molecules.Fig. 1 depicts four of the total of 35 modeled sensor-analyte combinations, showing equilibrium configurations for HMX, RDX, TNT, and O2 adsorbed on nitrogen-doped, boron-doped, divacancy flawed, and Stone–Wales defect flawed nanotubes respectively. Note that color distinguishes the dopant atoms and the CNT sidewall flaws, at which the analytes are adsorbed. To clarify the nature of the vacancy, divacancy, and Stone–Wales defects, Fig. 2 provides schematic descriptions of all three defects on a lattice segment with the same connectivities as the full lattice which makes up the sidewall. Fig. 3 and 4 plot adsorption energy (eqn (1)) and the change in zero bias voltage conductance (due to adsorption, eqn (2)) for all five sensors and all seven analytes considered in this paper. Modeling results for a pristine CNT sensor and for two widely studied hazardous gas analytes (NO2 and NH3) are also included in these two figures, for reference in discussions of previous work. Note that Fig. 3 and 4 break out the O2 and NO2 adsorption results in separate plots, since the chemiresistive sensitivity to those analytes is, in comparison to the other species, rather high.
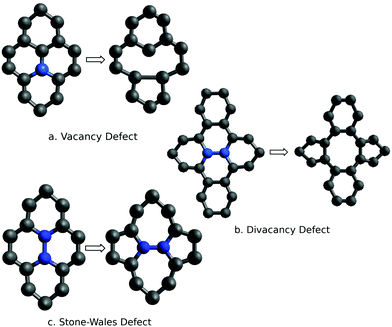 | ||
| Fig. 2 Schematics descriptions of three defects in a metallic CNT; the atoms highlighted in blue are either missing (vacancy and divacancy defects) or realigned (Stone–Wales defect). | ||
Pristine CNT response
In the pristine CNT sensor case, all of the analyte molecules reduce the CNT conductance, however the change is significant only for O2 and NO2 (see Fig. 3). The relatively high computed sensitivities to O2 and NO2 are consistent with experiment49,50 and reflect the strong electron-withdrawing properties of O2 and NO2. With respect to the explosives, TNT produces a slightly larger change in conductance than the nitramines, and all three explosives show higher adsorption energies than the background gases. Consistent with the modeling results, experiments on pristine CNTs have generally shown low sensitivity and low selectivity;9,51 pristine CNTs have however been been shown to detect O211,52,53 and NH3;54 the conductance change results presented here are sign consistent with the cited experiments. Experimental work sensing ammonia55 has shown a relatively small drop in conductance, also consistent with the modeling results.Doped CNT response
As nearest neighbors with carbon in the periodic table, nitrogen and boron are known to sometimes replace carbon atoms in CNTs; this effect has been studied in battery applications.56–58 Consistent with experiment,26 the equilibrium analyses conducted here show that both nitrogen and boron can replace carbon without distorting the CNT lattice. The ESI† provides charge density difference plots which depict equilibrium configurations for all three modeled explosives, and for an oxygen molecule, adsorbed on both nitrogen (Fig. S1, ESI†) and Boron (Fig. S2, ESI†) substitutional dopant sites.In the case of nitrogen, both in situ doping21,22 and post treatment methods59,60 have been used to produce substitutionally doped CNTs, which have been evaluated in NH3, NO2 and H2O detection experiments.27 As indicated in Fig. 3, O2 sensing shows the largest change in conductance and NO2 shows the largest adsorption energy. The computed change in conductance for NO2 sensing is sign consistent with experimental studies on single-wall13,27 and and double-wall28 CNTs. With regard to the explosives, TNT shows the largest adsorption energy while RDX shows a change in conductance which differs in sign from those of the other explosives. Note that such distinctions can be very important in determining the selectivity properties of sensor arrays. In the case of boron, substitutional doping has been accomplished using laser ablation,23 arc discharge,24 chemical vapor deposition,61 and post-manufacturing reactions.62 As indicated in Fig. 3, the modeling results indicate that O2 and NO2 show the largest sensitivity. With regard to the explosives, TNT shows the largest adsorption energy as well as a change in conductance which differs in sign from those of the nitramines.
Comparing the sensing results for the two substitutional doping cases, the conductance change results frequently differ in sign, perhaps since nitrogen n-dopes carbon while boron p-dopes carbon. The response to oxygen is consistently a large negative change in conductance. These results would generally support array selectivity, in the case of oxygen by isolating this analyte in the sensor response space.
Defective CNT response
The removal of atoms from a CNT can produce vacancy defects of several types, which can significantly change the electrical, chemical, and mechanical properties of CNTs.63–65 Of specific interest here are the changes in electrical conductance due to the adsorption of analytes at these sites. The ESI† provides charge density difference plots which depict equilibrium configurations for all three modeled explosives, and for an oxygen molecule, adsorbed on monovacancy (Fig. S3, ESI†), divacancy (Fig. S4, ESI†), and Stone–Wales (Fig. S5, ESI†) defect sites.If only one carbon atom is missing from the sidewall, the defect is called a monovacancy or simply a vacancy defect. The mechanical effects of such defects on CNTs have been widely studied.63,64,66 Recombination of the two-atom coordinated carbons at the defect forms a pentagonal structure (a Jahn–Teller distortion20), which has been observed in experiments and previous computational studies.29,67 Here the conductance modeling results (Fig. 4) indicate that all three of the explosives and H2O show a large response to the vacancy defect, and that TNT and NO2 show the largest adsorption energies. The closest reported experimental work has been on semiconducting CNTs, which showed a reduction in the conductance of defective CNTs upon exposure to ammonia.34,68 The present computational work, which considers metallic nanotubes, also shows a reduced conductance.
If two neighboring carbon atoms are removed from the sidewall, a divacancy defect is produced. Recombination of the neighboring carbon atoms creates two pentagonal rings and one 8 membered ring. Divacancy defects are common at room temperature in CNTs and affect their electrical and mechanical properties.64,69 The modeling results for sensing at these defects are shown in Fig. 4. Note that O2 and NO2 show negative changes in conductance, while the other analytes show positive changes in conductance. The explosives show relatively large conductance changes, as compared to most of the analytes, however as in the case of substitutional doping oxygen sensitivity is high. Comparing the vacancy and divacancy defects, there are significant differences in the computed response. The magnitudes of the adsorption energies and the magnitudes of the conductance changes are much higher in the monovacancy case than in the divacancy case, apparently since monovacancy defects result in a carbon atom bonded to only two neighbors, instead of three. This creates a highly reactive site20 which attracts any analyte.
The third defect modeled here is a Stone–Wales defect, which takes a pentagon-heptagon shape. Two π-bonded C atoms rotate by 90° along the mid point of their common bond, converting four adjacent 6 atom rings to two 5 atom rings and two 7 atom rings.65,70,71 The modeling results shown in Fig. 4 indicate that the response is strongest to O2, NO2 and TNT. Among the explosives, TNT shows a change in conductance which is opposite in sign to those for the nitramines, and TNT also shows a larger adsorption energy. The present modeling work on NH3 and NO2 shows adsorption energies which are consistent with a previous computational study of Stone–Wales defects in graphene.72 Note that the overall analyte response to the Stone–Wales defect is qualitatively similar to that for a pristine CNT. In both cases all of the carbon atoms in the sidewall remain bonded to three other carbon atoms.
Current–voltage characteristics
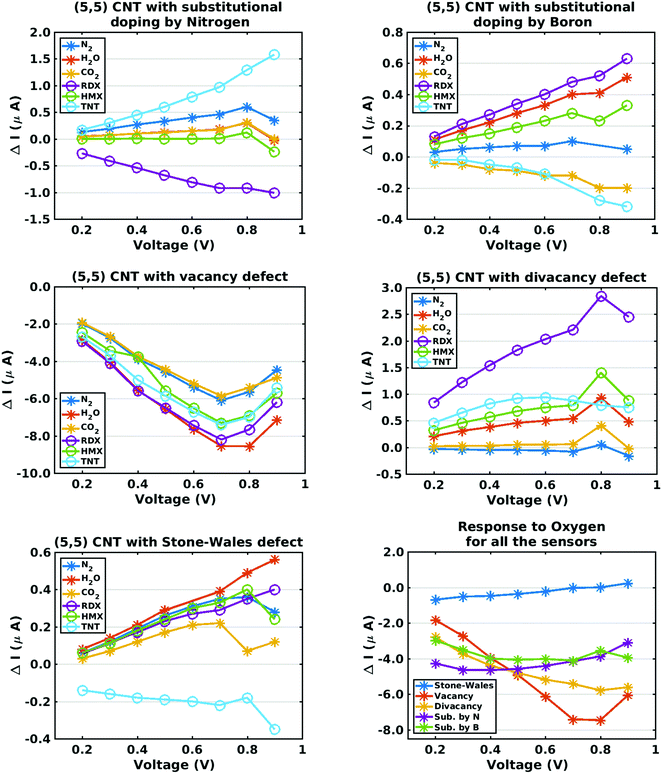
The preceding discussion has emphasized the somewhat disparate zero-bias conductance characteristics of five chemiresitive sensors defined by introducing lattice defects, of either the substitutional or vacancy type, to a pristine metallic CNT. Since such defects would be expected to produce a nonlinear current response under bias voltage loads, I–V characteristic curves for each sensor-analyte combination were computed, covering the bias voltage range 0.2–0.9 volts. Assuming a bias voltage interval of 0.1 volts, this creates a (non-degenerate) eight-fold larger discrete description of a sensor array response which can be employed in a ‘pattern matching’ algorithm (such as Principal Component Analysis) to add sensitivity to a chemiresistive sensing device. Fig. 5 plots the current–voltage characteristics of all five sensors, where the plotted response is the current increment defined by eqn (3). As expected from the zero-bias conductance results, the current changes for oxygen adsorption are relatively high, hence they are presented separately on a sixth plot which includes results for all five sensor types. Although I–V curves for the nitrogen dioxide and ammonia analytes were not computed, they could be generated in order to perform a hazardous gas analysis similar to one presented in this paper for explosives.As in the case of the zero-bias conductance calculations, the current response results show disparate trends. In the case of the nitrogen-doped sensor, the RDX and TNT curves show opposite signs while the current curve for HMX is near zero. Comparing the nitrogen-doped and boron-doped sensors, the current responses for RDX and TNT differ in sign. In the case of the vacancy and divacancy defect sensors, the response trends are non-monotonic. In the case of the Stone–Wales defect, the current response for TNT differs sharply from that of all the other analytes, including oxygen. Overall the results support the suggested selectivity analysis approach.
Principal component analysis
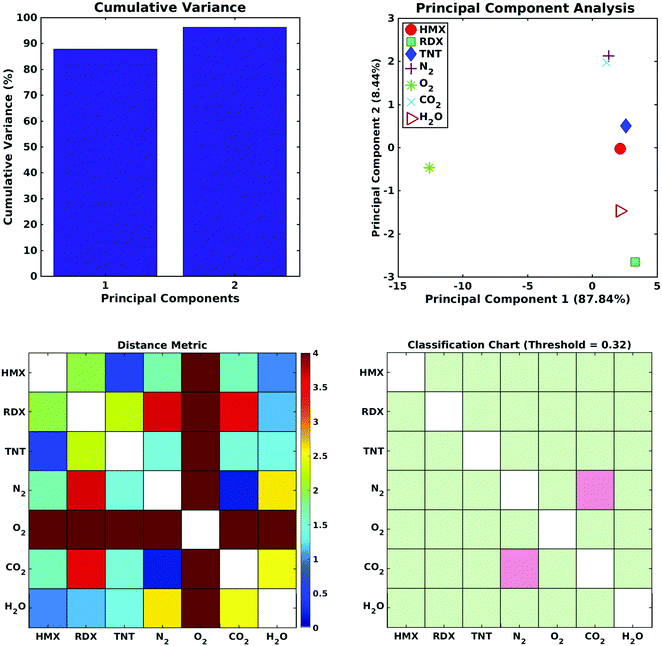
An evaluation of the sensor array performance was made by performing a principal component analysis (PCA) of the data plotted in Fig. 5. PCA is commonly used73–78 to process output data from gas sensor arrays or other systems with olfactory structures. PCA constructs a linear transformation of the original sensor output variable space, defining a new system of ordered orthogonal coordinates, called principal components. The principal components are ranked according to their ability to account for the variance in the sensor data, and are (typically) used to reduce the order of the basis set describing the sensor output variable space. The reduced order model is composed of ‘n‘ principal components, where ‘n‘ is the minimum number of principal components required to account for (typically) 95% of the variance in the sensor output data set.79–81 The ability of the output data set to distinguish between the various analytes is measured by their ‘separation distance’ in the reduced order principal component space; if the separation distance between any two analytes exceeds a specified classification threshold, the analytes are considered to be distinguishable. This process estimates the selectivity of the sensor array.The computational data set developed here was analyzed as follows: (1) a principal component analysis was performed using commercial software, (2) the cumulative variance of the data set was plotted, as a function of the number of principal components, (3) a reduced order model was defined by determining (from the cumulative variance plot) the number of principal components needed to account for at least 95% of the variance in the data, (4) the separation distance for all analyte pairs was computed, and displayed on a Distance Metric plot, and (5) a classification criterion was selected to identify the distinguishable analytes, and the results displayed on a Classification Chart. The Distance metric (Djk) used here to describe the separation of the jth and kth analytes in an n-dimensional, reduced order principal component space is
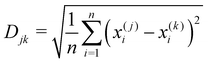 | (4) |
Fig. 6 (top left) shows the cumulative variance plot for the CNT sensor data set; only two principal components are needed to account for 95% of the variance in the sensor output data set. Fig. 6 (top right) shows the separation of the seven analytes (three explosives and four background gases) in the reduced order principal component space. Note in the Distance Metrics (Fig. 6, lower left) the clear separation of oxygen from all the remaining analytes, the close proximity of the N2 and CO2 coordinates in principal component space, and the distances separating the three explosive molecules from all of the other analytes. As indicated in Fig. 6 (lower right), where green squares denote distinguishable analyte pairs, if a classification threshold of 0.322 is chosen for this data set the sensor array shows excellent selectivity. All the explosives can be distinguished from all of the background gases, and from each other. The only indistinguishable analytes are N2 and CO2. A review of published data on measured sensor currents in hazardous gas detection experiments11,82,83 suggests that the classification threshold chosen here is reasonable, perhaps conservative, and that selective detection of explosive molecules using defect modulated metallic CNTs is feasible.
4. Conclusions
Trace detection of explosives using carbon nanotube based sensors has attracted much research attention, since it might produce a light weight, low power, low cost solution to a hazardous materials detection problem of very wide military, government, and commercial interest. Chemiresistive sensing solutions often provide simplicity and robustness, but lack selectivity. The present paper employs a sensor array to address the need for selectivity, and applies Principal Component Analysis to quantify the array's performance. Recognizing the importance of a large data set to any pattern recognition based sensing algorithm, the present work capitalizes upon the nonlinear current–voltage characteristics of the defect-based sensors by analysis of the sensor response over a range of bias voltages. In the linear sensor case, data collected at more than one bias voltage would be redundant; in the nonlinear case, data collected over a range of bias voltages expands the sensor data set and will in general improve the selectivity of the array.Building on previous experimental and computational work on the study of defects in carbon nanotubes, and their effects on chemiresistive sensing performance, the present paper suggests that sensor arrays which capitalize on the nonlinear response of substitutionally doped and structurally flawed metallic CNTs may offer opportunities for sensitive and selective detection of explosive molecules. Although this paper considers only basic sensing mechanisms, it does motivate further research exploring the sensing scheme developed here and extension of the approach to address other hazardous gas sensing applications. Important opportunities for immediate extension of the present work include the analysis of nanotube sensors of other chiralities and the application of machine learning, as an alternative to PCA, in the interpretation of sensor data. The present work considered single wall (5,5) CNTs in order to minimize the modeled atom count and thereby reduce computational cost. Other chiralities might offer surface curvature or other properties with sensing advantages. With regards to data analysis, machine learning methods84–86 merit close attention as a possible means to make more effective use of sensor array measurements.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Office of Naval Research (Grant number N00014-16-2357). Computer time support was provided by the Department of Defense High Performance Computing Modernization Program (Project number ONRDC40983493) and the Texas Advanced Computing Center (Project number G-815029) at the University of Texas at Austin.References
- K. C. To, S. Ben-Jaber and I. P. Parkin, ACS Nano, 2020, 14, 10804–10833 CrossRef CAS.
- Council, N. R. Existing and Potential Standoff Explosives Detection Techniques; 2004.
- K. A. Morrison, E. H. Denis, M. K. Nims, A. M. Broderick, R. C. Fausey, H. J. Rose, P. E. Gongwer and R. G. Ewing, J. Phys. Chem. A, 2021, 125, 1279–1288 CrossRef CAS PubMed.
- C. Tancharoen, W. Sukjee, P.-T. Yenchitsomanus, A. Panya, P. A. Lieberzeit and C. Sangma, Mater. Lett., 2021, 285, 129201 CrossRef CAS.
- Y. Hashimoto, Mass Spectrom., 2017, 6, A0054 CrossRef PubMed.
- L. Senesac and T. G. Thundat, Materials Today, 2008, 11, 28–36 CrossRef CAS.
- P.-C. Chen, S. Sukcharoenchoke, K. Ryu, L. Gomez de Arco, A. Badmaev, C. Wang and C. Zhou, Adv. Mater., 2010, 22, 1900–1904 CrossRef CAS.
- M. Meyyappan, Small, 2016, 12, 2118–2129 CrossRef CAS PubMed.
- R. Tang, Y. Shi, Z. Hou and L. Wei, Sensors, 2017, 17, 882 CrossRef PubMed.
- J. Zhang and E. P. Fahrenthold, Nanoscale, 2020, 12, 10730–10736 RSC.
- P. G. Collins, K. Bradley, M. Ishigami and D. A. Zettl, Science, 2000, 287, 1801–1804 CrossRef CAS PubMed.
- C. Huang, B. Huang, Y. Jang, M. Tsai and C. Yeh, Diamond Relat. Mater., 2005, 14, 1872–1875 CrossRef CAS.
- L. Valentini, F. Mercuri, I. Armentano, C. Cantalini, S. Picozzi, L. Lozzi, S. Santucci, A. Sgamellotti and J. Kenny, Chem. Phys. Lett., 2004, 387, 356–361 CrossRef CAS.
- D. Ding, Z. Chen, S. Rajaputra and V. Singh, Sens. Actuators, B, 2007, 124, 12–17 CrossRef CAS.
- J. Suehiro, S. Yamane and K. Imasaka, Carbon nanotube-based hydrogen gas sensor electrochemically functionalized with palladium. Sensors, IEEE. 2007, pp. 554–557 Search PubMed.
- J. Novak, E. Snow, E. Houser, D. Park, J. Stepnowski and R. McGill, Appl. Phys. Lett., 2003, 83, 4026–4028 CrossRef CAS.
- J. Zhao, A. Buldum, J. Han and J. P. Lu, Nanotechnology, 2002, 13, 195 CrossRef CAS.
- N. Chakrapani, Y. M. Zhang, S. K. Nayak, J. A. Moore, D. L. Carroll, Y. Y. Choi and P. M. Ajayan, J. Phys. Chem. B, 2003, 107, 9308–9311 CrossRef CAS.
- J. A. Robinson, E. S. Snow, S. C. Bǎdescu, T. L. Reinecke and F. K. Perkins, Nano Lett., 2006, 6, 1747–1751 CrossRef CAS.
- A. Hankins, T. C. Willard, A. Y. Liu and M. Paranjape, J. Appl. Phys., 2020, 128, 084501 CrossRef.
- P. Ayala, A. Grüneis, T. Gemming, D. Grimm, C. Kramberger, M. H. Rümmeli, F. L. Freire Jr., H. Kuzmany, R. Pfeiffer and A. Barreiro, et al., Tailoring N-doped single and double wall carbon nanotubes from a nondiluted carbon/nitrogen feedstock, J. Phys. Chem. C, 2007, 111, 2879–2884 CrossRef CAS.
- Y. Wang, X. Cui, Y. Li, L. Chen, H. Chen, L. Zhang and J. Shi, Carbon, 2014, 68, 232–239 CrossRef CAS.
- K. McGuire, N. Gothard, P. Gai, M. Dresselhaus, G. Sumanasekera and A. Rao, Carbon, 2005, 43, 219–227 CrossRef CAS.
- O. Stephan, P. Ajayan, C. Colliex, P. Redlich, J. Lambert, P. Bernier and P. Lefin, Science, 1994, 266, 1683–1685 CrossRef CAS PubMed.
- A. A. Koos, F. Dillon, E. A. Obraztsova, A. Crossley and N. Grobert, Carbon, 2010, 48, 3033–3041 CrossRef CAS.
- J.-J. Adjizian, R. Leghrib, A. A. Koos, I. Suarez-Martinez, A. Crossley, P. Wagner, N. Grobert, E. Llobet and C. P. Ewels, Carbon, 2014, 66, 662–673 CrossRef CAS.
- Y. Battie, O. Ducloux, P. Thobois, T. Susi, E. I. Kauppinen and A. Loiseau, Phys. Status Solidi B, 2011, 248, 2462–2466 CrossRef CAS.
- W. Muangrat, W. Wongwiriyapan, V. Yordsri, T. Chobsilp, S. Inpaeng, C. Issro, O. Domanov, P. Ayala, T. Pichler and L. Shi, Phys. Status Solidi A, 2018, 215, 1800004 CrossRef.
- P. Ajayan, V. Ravikumar and J.-C. Charlier, Phys. Rev. Lett., 1998, 81, 1437 CrossRef CAS.
- A. Hashimoto, K. Suenaga, A. Gloter, K. Urita and S. Iijima, Nature, 2004, 430, 870–873 CrossRef CAS.
- K. Suenaga, H. Wakabayashi, M. Koshino, Y. Sato, K. Urita and S. Iijima, Nat. Nanotechnol., 2007, 2, 358–360 CrossRef CAS PubMed.
- M. Bockrath, W. Liang, D. Bozovic, J. H. Hafner, C. M. Lieber, M. Tinkham and H. Park, Science, 2001, 291, 283–285 CrossRef CAS PubMed.
- N. Neophytou, D. Kienle, E. Polizzi and M. Anantram, Appl. Phys. Lett., 2006, 88, 242106 CrossRef.
- J. Kim, S.-W. Choi, J.-H. Lee, Y. Chung and Y. T. Byun, Sens. Actuators, B, 2016, 228, 688–692 CrossRef CAS.
- X. Zhang, Y. Gui and Z. Dai, Appl. Surf. Sci., 2014, 315, 196–202 CrossRef CAS.
- N. Kuganathan and A. Chroneos, Chemosensors, 2021, 9, 120 CrossRef.
- S. Demir and M. F. Fellah, Appl. Surf. Sci., 2020, 504, 144141 CrossRef CAS.
- J. Andzelm, N. Govind and A. Maiti, Chem. Phys. Lett., 2006, 421, 58–62 CrossRef CAS.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745 CrossRef CAS.
- K. Stokbro, J. Taylor, M. Brandbyge and P. Ordejon, Ann. N. Y. Acad. Sci., 2003, 1006, 212–226 CrossRef CAS PubMed.
- S. Datta, Electronic transport in mesoscopic systems, Cambridge university press, 1997 Search PubMed.
- C. S. Choi and H. P. Boutin, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1970, 26, 1235–1240 CrossRef CAS.
- C. S. Choi and E. Prince, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 2857–2862 CrossRef CAS.
- R. M. Vrcelj, J. N. Sherwood, A. R. Kennedy, H. G. Gallagher and T. Gelbrich, Cryst. Growth Des., 2003, 3, 1027–1032 CrossRef CAS.
- S. Krompiewski, Phys. Status Solidi B, 2005, 242, 226–233 CrossRef CAS.
- H. Santos, L. Chico, J. Alvarellos and A. Latge, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 165401 CrossRef.
- Y.-W. Son, M. L. Cohen and S. G. Louie, Nano Lett., 2007, 7, 3518–3522 CrossRef CAS PubMed.
- K. Y. Chin and E. P. Fahrenthold, Comput. Mater. Sci., 2021, 197, 110573 CrossRef CAS.
- Q. Vermesh, O. Grecu, M. Javey, A. Wang, Q. Dai, H. Peng and S. Cho, Nanotechnol. Lett., 2003, 3(3), 347–351 Search PubMed.
- A. D. Rushi, K. P. Datta, P. S. Ghosh, A. Mulchandani and M. D. Shirsat, Perspective of Carbon Nanotubes, IntechOpen, Rijeka, 2019, ch. 6 Search PubMed.
- M. D. Shirsat, T. Sarkar, J. Kakoullis Jr., N. V. Myung, B. Konnanath, A. Spanias and A. Mulchandani, J. Phys. Chem. C, 2012, 116, 3845–3850 CrossRef CAS PubMed.
- G. Sumanasekera, C. Adu, S. Fang and P. Eklund, Phys. Rev. Lett., 2000, 85, 1096 CrossRef CAS PubMed.
- E. S. Muckley, A. J. Nelson, C. B. Jacobs and I. N. Ivanov, J. Photonics Energy, 2016, 6, 025506 CrossRef.
- F. Rigoni, S. Tognolini, P. Borghetti, G. Drera, S. Pagliara, A. Goldoni and L. Sangaletti, Analyst, 2013, 138, 7392–7399 RSC.
- G. Chen, T. M. Paronyan, E. M. Pigos and A. R. Harutyunyan, Sci. Rep., 2012, 2, 1–7 Search PubMed.
- W. H. Shin, H. M. Jeong, B. G. Kim, J. K. Kang and J. W. Choi, Nano Lett., 2012, 12, 2283–2288 CrossRef CAS.
- B. Liu, X. Sun, Z. Liao, X. Lu, L. Zhang and G.-P. Hao, Sci. Rep., 2021, 11, 1–11 CrossRef PubMed.
- L. Bulusheva, A. Okotrub, A. Kurenya, H. Zhang, H. Zhang, X. Chen and H. Song, Carbon, 2011, 49, 4013–4023 CrossRef CAS.
- T. C. Nagaiah, S. Kundu, M. Bron, M. Muhler and W. Schuhmann, Electrochem. Commun., 2010, 12, 338–341 CrossRef CAS.
- L. Chan, K. Hong, D. Xiao, T. Lin, S. Lai, W. Hsieh and H. Shih, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 125408 CrossRef.
- P. Ayala, W. Plank, A. Grüneis, E. I. Kauppinen, M. H. Rümmeli, H. Kuzmany and T. Pichler, J. Mater. Chem., 2008, 18, 5676–5681 RSC.
- E. Borowiak-Palen, T. Pichler, A. Graff, R. Kalenczuk, M. Knupfer and J. Fink, Carbon, 2004, 42, 1123–1126 CrossRef CAS.
- K. Ang, D. Kulathunga and J. Reddy, Buckling of defective carbon nanotube, Proceedings of the International Conference on Computing in Civil and Building Engineering, 2010 Search PubMed.
- M. Sammalkorpi, A. Krasheninnikov, A. Kuronen, K. Nordlund and K. Kaski, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 245416 CrossRef.
- L. Zhou and S.-Q. Shi, Appl. Phys. Lett., 2003, 83, 1222–1224 CrossRef CAS.
- Q. Wang, W. Duan, N. Richards and K. Liew, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 201405 CrossRef.
- Z. Zanolli and J.-C. Charlier, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155447 CrossRef.
- N. D. Hoa, N. Van Quy, Y. Cho and D. Kim, Sens. Actuators, B, 2007, 127, 447–454 CrossRef CAS.
- C. Gómez-Navarro, P. J. De Pablo, J. Gómez-Herrero, B. Biel, F. Garcia-Vidal, A. Rubio and F. Flores, Nat. Mater., 2005, 4, 534–539 CrossRef PubMed.
- D. B. Mawhinney, V. Naumenko, A. Kuznetsova, J. T. Yates Jr., J. Liu and R. Smalley, Chem. Phys. Lett., 2000, 324, 213–216 CrossRef CAS.
- G.-D. Lee, C. Wang, E. Yoon, N.-M. Hwang and K. Ho, Appl. Phys. Lett., 2008, 92, 043104 CrossRef.
- Y.-H. Zhang, K.-G. Zhou, K.-F. Xie, X.-C. Gou, J. Zeng, H.-L. Zhang and Y. Peng, J. Nanosci. Nanotechnol., 2010, 10, 7347–7350 CrossRef CAS PubMed.
- J. M. Schnorr, D. van der Zwaag, J. J. Walish, Y. Weizmann and T. M. Swager, Adv. Funct. Mater., 2013, 23, 5285–5291 CrossRef CAS.
- M. Kermit and O. Tomic, IEEE Sens. J., 2003, 3, 218–228 CrossRef.
- Z. Xiaobo, Z. Jiewen, W. Shouyi and H. Xingyi, Sensors, 2003, 3, 101–109 CrossRef.
- A. S. R. Murthy, D. Pathak, G. Sharma, K. Gnanasekar, V. Jayaraman, A. Umarji and T. Gnanasekaran, Anal. Chim. Acta, 2015, 892, 175–182 CrossRef.
- A. Hannon, Y. Lu, J. Li and M. Meyyappan, Sensors, 2016, 16, 1163 CrossRef.
- J. Chen, K. Wang and W. Zhou, IEEE Trans. Nanotechnol., 2010, 10, 968–974 Search PubMed.
- I. T. Jolliffe and J. Cadima, Philos. Trans. R. Soc., A, 2016, 374, 20150202 CrossRef.
- J. E. Jackson, A user's guide to principal components, John Wiley & Sons, 2005, vol. 587 Search PubMed.
- Z. Li, J. R. Askim and K. S. Suslick, Chem. Rev., 2019, 119, 231–292 CrossRef CAS PubMed.
- J. Kong, N. R. Franklin, C. Zhou, M. G. Chapline, S. Peng, K. Cho and H. Dai, Science, 2000, 287, 622–625 CrossRef CAS PubMed.
- P. Qi, O. Vermesh, M. Grecu, A. Javey, Q. Wang, H. Dai, S. Peng and K. Cho, Nano Lett., 2003, 3, 347–351 CrossRef CAS.
- S. I. Hwang, N. G. Franconi, M. A. Rothfuss, K. N. Bocan, L. Bian, D. L. White, S. C. Burkert, R. W. Euler, B. J. Sopher and M. L. Vinay, et al., Tetrahydrocannabinol detection using semiconductor-enriched single-walled carbon nanotube chemiresistors, ACS Sensors, 2019, 4, 2084–2093 CrossRef CAS PubMed.
- B. Kim, T. J. Norman, R. S. Jones, D.-I. Moon, J.-W. Han and M. Meyyappan, ACS Appl. Nano Mater., 2019, 2, 6445–6451 CrossRef CAS.
- T. Hayasaka, A. Lin, V. C. Copa, L. P. Lopez, R. A. Loberternos, L. I. M. Ballesteros, Y. Kubota, Y. Liu, A. A. Salvador and L. Lin, Microsyst. Nanoeng., 2020, 6, 1–13 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: The supporting information file includes charge density difference plots which describe the adsorption of the three modeled explosives and one background gas (oxygen) on substitutional dopant sites for nitrogen and boron, as well as the adsorption of the same four analytes on vacancy, divacancy, and Stone–Wales defect sites. See DOI: 10.1039/d1ma00571e |
| This journal is © The Royal Society of Chemistry 2021 |