Linking optical spectra to free charges in donor/acceptor heterojunctions: cross-correlation of transient microwave and optical spectroscopy†
Hyun Suk
Kang
 a,
Samuel
Peurifoy
b,
Boyuan
Zhang
b,
Andrew J.
Ferguson
a,
Samuel
Peurifoy
b,
Boyuan
Zhang
b,
Andrew J.
Ferguson
 a,
Obadiah G.
Reid
a,
Obadiah G.
Reid
 ac,
Colin
Nuckolls
ac,
Colin
Nuckolls
 b and
Jeffrey L.
Blackburn
b and
Jeffrey L.
Blackburn
 *a
*a
aNational Renewable Energy Laboratory, Golden, CO 80401, USA. E-mail: jeffrey.blackburn@nrel.gov
bColumbia University, New York, NY 10027, USA
cUniversity of Colorado, Boulder, CO 80303, USA
First published on 5th March 2021
Abstract
The primary photoexcited species in excitonic semiconductors is a bound electron–hole pair, or exciton. An important strategy for producing separated electrons and holes in photoexcited excitonic semiconductors is the use of donor/acceptor heterojunctions, but the degree to which the carriers can escape their mutual Coulomb attraction is still debated for many systems. Here, we employ a combined pump–probe ultrafast transient absorption (TA) spectroscopy and time-resolved microwave conductivity (TRMC) study on a suite of model excitonic heterojunctions consisting of mono-chiral semiconducting single-walled carbon nanotube (s-SWCNT) electron donors and small-molecule electron acceptors. Comparison of the charge-separated state dynamics between TA and TRMC photoconductance reveals a quantitative match over the 0.5 microsecond time scale. Charge separation yields derived from TA allow extraction of s-SWCNT hole mobilities of ca. 1.5 cm2 V−1 s−1 (at 9 GHz) by TRMC. The correlation between the techniques conclusively demonstrates that photoinduced charge carriers separated across these heterojunctions do not form bound charge transfer states, but instead form free/mobile charge carriers.
New conceptsThe cornerstone of excitonic solar cells is the efficient conversion of bound electron–hole pairs, or excitons, into free carriers across an interface between electron donor and acceptor components, where a thermodynamic driving force leads to photoinduced charge separation. Time-resolved spectroscopic studies are critical for probing this charge separation process. Such studies provide crucial mechanistic insights related to overcoming or bypassing deleterious bound interfacial charge transfer (CT) states, enabling device efficiency improvements. Our study uses transient absorption (TA) and time-resolved microwave conductivity (TRMC) – commonly employed independently but seldom combined – to provide a deeper understanding of photoinduced charge separation for model donor/acceptor heterojunctions. Out study demonstrates that the rigid bonds, low reorganization energy, and highly delocalized charge carriers in s-SWCNTs appear to limit the formation of CT states. This suggests that (i) chemical structure offers a means to control interfacial charge separation processes and (ii) the spectroscopic approach employed here can be applied to a broad array of heterojunctions formed between excitonic semiconductors. |
Introduction
In organic semiconductors and/or materials with reduced dimensionality (e.g. semiconducting polymers, single-walled carbon nanotubes, and monolayer transition metal dichalcogenides), the primary excited state produced by absorption of a photon is often an exciton, a Coulomb-bound electron–hole pair.1–3 To produce electricity or fuels with such ‘excitonic’ semiconductors, it is essential to dissociate excitons into uncorrelated charge carriers, electrons and holes, that have appreciable mobility. Donor/acceptor heterojunctions are thus crucial interfaces where a thermodynamic driving force facilitates photoinduced electron transfer from a donor semiconductor to the acceptor semiconductor (or hole transfer in the opposite direction) to dissociate photogenerated excitons.4–6 Despite the ubiquity of donor/acceptor interfaces in devices like organic photovoltaic (OPV) solar cells, the mechanisms underlying charge separation across these interfaces are still actively investigated. Low dielectric screening of the electron–hole Coulomb potential in many excitonic semiconductors and interfaces can lead to bound interfacial charge-transfer (CT) states that can impede efficient charge separation.7 The precise role of CT states in the progression from excitons to uncorrelated carriers is heavily debated,4,8–11 and many studies have suggested mechanisms (e.g. hot CT states, carrier delocalization, etc.) by which CT states may be bypassed.7Semiconducting single-walled carbon nanotubes (s-SWCNTs) are excitonic semiconductors with a number of promising properties for various opto-electronic applications such as OPVs,12 photodetectors (PDs),13 sensors,14 and quantum information processing.15,16 In heterojunctions with a number of organic electron acceptors, s-SWCNT films show high charge generation yields in the visible and near-infrared that depend sensitively on the thermodynamic driving force available for charge separation.6,17–20 In OPV devices, s-SWCNT films have shown high values for both internal and external quantum efficiency (IQE and EQE),21–23 and it has also been suggested that CT states are absent, leading to low nonradiative open-circuit voltage (Voc,nonrad) loss.24 The photodynamics of exciton dissociation and charge recombination processes at heterojunctions between s-SWCNTs and various electron acceptors such as fullerenes,6,17,25,26 perylene diimides (PDIs),19 and two-dimensional (2D) molybdenum disulfide (MoS2) monolayers20 have been explored, and the charge separation processes therein occur rapidly, in the range of 120 fs–1.6 ps, with charge recombination times often exceeding 1 μs. The ultrafast charge separation and long-lived charge separated states from s-SWCNT-based heterojunctions are often attributed to a high degree of charge carrier delocalization in the s-SWCNTs phase, resulting in the fast extraction of charge carriers from the donor–acceptor interface after exciton dissociation.6,17,19,20,25,26 However, the fundamental nature of charges in s-SWCNTs is still debated, with some studies suggesting that poor dielectric screening yields localized charges that are not truly free carriers.27,28
Here we demonstrate that quantitative comparison of charge dynamics with different time-resolved spectroscopy techniques can provide crucial insight into how truly ‘free’ charge carriers are once they have been separated across an excitonic semiconductor donor/acceptor heterojunction. In particular, transient absorption (TA) is a common technique whereby charge carriers can be spectrally identified and tracked over time scales ranging from femtoseconds to milliseconds. While TA can spectrally identify charge carriers (e.g. via polaron signatures in semiconducting polymers29 and anion/cation signatures in small molecules),30 this technique typically cannot differentiate between free and localized charges.31 Previous analyses have specifically noted for semiconducting polymers that charge signatures in the visible region of the spectrum cannot distinguish between free and trapped charge carriers.31 Thus, to identify the contribution of free charges to TA spectral signatures requires careful correlation between TA spectra/dynamics and other measurements which conclusively identify mobile carriers. Time-resolved microwave conductivity (TRMC) probes the time-dependent conductance of photoinduced free charge carriers which can absorb microwave radiation. However, TRMC measures the optical conductivity over a narrow microwave spectral range (e.g. ca. 8–10 GHz for X-band), and thus cannot provide spectral information of free charge carriers.
While the quantitative comparison of TA and TRMC dynamics should clearly provide important insights into the nature of charge generation in donor/acceptor heterojunctions, such comparisons are surprisingly rare in the literature. Of a handful of existing studies,32–36 only one is performed on an organic donor/acceptor heterojunction,36 with the rest applied to a single organic semiconductor. In this study, we rigorously compare TA and TRMC charge carrier dynamics to investigate a series of model donor/acceptor heterojunctions consisting of s-SWCNTs and organic electron acceptors. While the exceptionally long charge separation lifetimes and high carrier mobilities of s-SWCNTs make these heterojunctions a promising model system for spectroscopically probing charge carriers, a quantitative comparison of TA and TRMC techniques has never been performed for such systems. In heterojunctions formed between (6,5) s-SWCNTs and PDI electron acceptors, we find a near-perfect match of the TRMC photoconductance dynamics to the dynamics of photoinduced charges measured by TA. This result suggests that the charges generated in such heterojunctions are truly ‘free’ and not localized in CT states, despite the low dielectric screening expected at the donor/acceptor interface. The results also provide clarity to the debate over the contribution of free versus localized charges to the TA spectral signatures observed for charges in s-SWCNTs. Finally, the correlation between TA and TRMC allows us to estimate the hole mobility in the s-SWCNT films for a number of different heterojunctions, which we find to be in the range of ca. 0.7–2.7 cm2 V−1 s−1 at 9 GHz (average value of 1.5 ± 0.6 cm2 V−1 s−1).
Results
Ground-state and transient absorption spectra
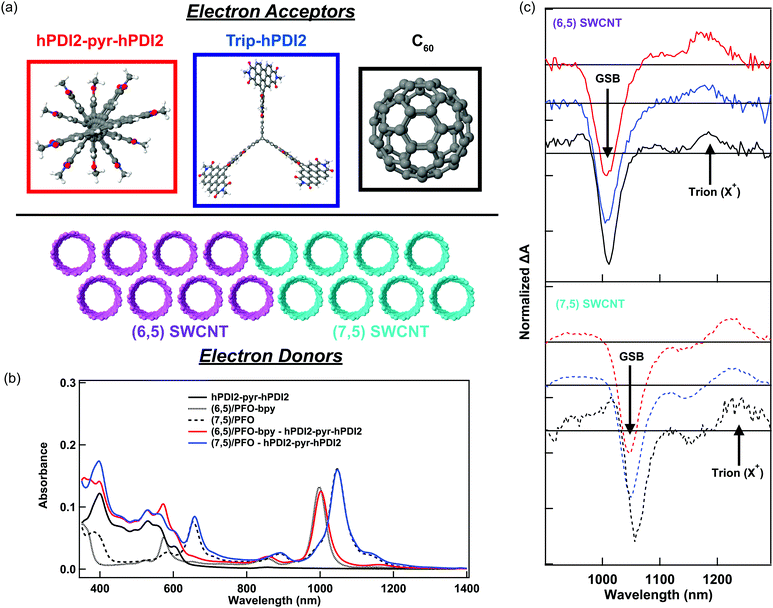
In this study, we probe charge generation across bilayer heterojunctions formed between two different near-monochiral s-SWCNT thin films (dominated by either the (6,5) or (7,5) species) and three different electron acceptors (Fig. 1a). One electron acceptor is the C60 fullerene17,21,24–26,37,38 and the other two are perylene diimide based electron acceptors18,19 that we abbreviate hPDI2-pyr-hPDI2 and Trip-hPDI2. Exemplary ground-state absorption spectra of neat films and bilayers of s-SWCNTs and hPDI2-pyr-hPDI2 are displayed in Fig. 1b, and those for s-SWCNTs with Trip-hPDI2 or C60 are shown in ESI,† (Fig. S1). All three of these electron acceptors form Type-II heterojunctions in which there is a thermodynamic driving force for photoinduced electron transfer from the s-SWCNT donor to the acceptor, as well as photoinduced hole transfer from the acceptor to the s-SWCNT donor.18,19,25,26The absorption spectra of the neat films exhibit the primary characteristics shown in previous studies.6,19,25,26 Neat films of s-SWCNTs have excitonic absorption bands at 998/1047 nm (S11) and 574/654 nm (S22) for (6,5)/(7,5) SWCNTs, respectively. The K-momentum phonon sidebands (X1)39 are also located at 855/891 nm for (6,5)/(7,5) SWCNTs. Absorption in the ultraviolet region corresponds to the polyfluorene wrapping polymer and s-SWCNT S33 absorption. The neat films of PDI-based electron acceptors show monomeric and aggregate S1 absorption bands of hPDI2-pyr-hPDI2 at 555 and 602 nm (Fig. 1b), respectively, and vibronic progressions of Trip-hPDI2 starting from 401 and 555 nm (Fig. S1, ESI†).19 Neat films of C60 have weak S1 and strong S2 bands at 612 and 436 nm (Fig. S1, ESI†), respectively.
Fig. 1c shows the TA spectra of s-SWCNT/electron acceptor bilayers, in which the pump photon wavelength was chosen to primarily excite the electron acceptors to induce hole transfer. The pump–probe delay of 300 ps was used for s-SWCNT/C60 bilayers instead of 100 ps for s-SWCNTs/PDI-based acceptors bilayers due to significant exciton diffusion effect for the thick C60 layer (90 nm).26 The two representative TA features of charge carriers within s-SWCNTs are S11 ground state bleaching (GSB) and trion induced absorption (X+) at 170-180 meV lower than S11 energy level.19,25,26 Note that the X+ designation is based on the original assignment by Matsunaga et al.,40 where this absorption represents the creation event of a charged exciton (trion). Most importantly for the current study, this peak indicates that photoinduced charge transfer has generated holes in the s-SWCNT network. All s-SWCNT/PDI-based acceptor bilayers show GSB at 1008/1050 nm and X+ at 1178/1223 nm for (6,5)/(7,5) SWCNTs, respectively. At similar pump photon fluences, neat (6,5) or (7,5) s-SWCNT films do not exhibit the X+ induced absorption, but only show a relatively short-lived GSB. The direct comparison of TA features of s-SWCNT neat film and bilayer is shown for the (6,5) SWCNT – hPDI2-pyr-hPDI2 bilayer in ESI,† (Fig. S2(a)).
The absence of the X+ peak in neat films indicates that, when pumped at low photon fluence (≲3 × 1012 photons cm−2 pulse−1), charge generation in neat films is below the limit of detection for the TA experiment. As shown previously,19,20,25,26 the concomitant observation of the GSB and X+ peak (Fig. 1c), along with the long GSB and X+ lifetimes (Fig. S2 and Table S1, ESI†), indicate that all of the bilayers studied here produce charges via photoinduced interfacial charge transfer, producing a charge-separated state that consists of holes in the s-SWCNTs and electrons in the acceptor phase.
Comparison of TA and TRMC kinetics
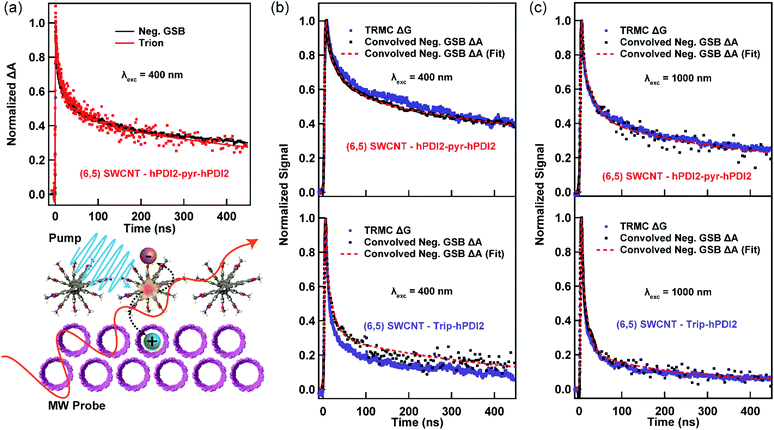
We now turn to a comparison of TA and TRMC dynamics for charges separated across s-SWCNT/acceptor bilayers. For this comparison, we primarily discuss (6,5) s-SWCNT bilayers with PDI-based acceptors, and (7,5) s-SWCNT bilayers are discussed in the SI (Fig. S3 and S4, ESI†). All TA dynamics discussed here track charge carrier (hole) spectral features arising from s-SWCNTs, since the large oscillator strengths and narrow peak widths of these transitions allow us to follow charge dynamics while keeping the absorbed photon fluence as low as possible.As demonstrated by Fig. 1c, all of the heterojunctions exhibit the S11 GSB and X+ induced absorption peaks following exciton dissociation across the heterojunction interface. Since both peaks correspond to holes produced by exciton dissociation, their kinetics should be identical, as can be seen in Fig. 2a for the (6,5) SWCNT/hPDI2-pyr-hPDI2 bilayer. This equivalence also holds for other bilayers (Fig. S2, ESI†) and allows us to use the S11 GSB kinetics (with higher signal-to-noise than X+ kinetics) to compare to TRMC-measured hole dynamics. Since all exciton-related processes such as exciton diffusion/dissociation and exciton–exciton annihilation are complete for all bilayers within the instrument response function (IRF) time of the nanosecond pump–probe laser spectroscopy setup, ≈300 ps, the GSB decay dynamics in this comparison solely track the recombination of holes in s-SWCNTs with electrons in the acceptor phase. What we cannot discern from the TA measurement is the degree to which the TA spectral features arise from free/mobile holes, trapped holes, or some combination of both.
In contrast to the white light probe laser of the TA measurement, TRMC measures time-dependent absorption of a microwave probe. The microwave probe is absorbed only by charge carriers with appreciable mobilities (free charge carriers), resulting in measurement of high-frequency (≈9.9 GHz) photoconductance (ΔG). ΔG is proportional to the photoinduced free carrier generation yield (φ) and the sum of the high-frequency free carrier mobilities (Σμ):
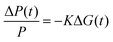 | (1) |
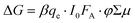 | (2) |
Fig. 2b and c demonstrates a near-quantitative match for the TA and TRMC dynamics for (6,5) SWCNT bilayers measured for conditions probing both hole and electron transfer. These matching dynamics strongly suggest that the photoinduced charge carriers created by exciton dissociation in these (6,5) SWCNT bilayers are predominantly free charge carriers that are not bound in a charge transfer state. These results demonstrate that, in this prototypical Type-II s-SWCNT heterojunction, the GSB and X+ peaks observed in TA following interfacial exciton dissociation are characteristic spectral features of free/mobile excited-state holes. While trapped charges may also have similar spectral features (see Discussion below), it is clear that free charges produce strong GSB and X+ peaks. These are important conclusions that add clarity to the debate over the fundamental nature of charges (and charge-related spectroscopic signatures) in s-SWCNT-based heterojunctions, and we further discuss the implications for these conclusions in the Discussion section below.
Charge separation yield and s-SWCNT hole mobility
The combination of TA and TRMC measurements can provide not only qualitative information regarding the relative contribution of free charge carriers to that of the total photoinduced charge carrier population, but can also give quantitative information on the interfacial charge separation (CS) yield (φ) and s-SWCNT hole mobility (μh). TRMC provides the product of the CS yield and the sum of the carrier mobilities (φΣμ):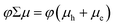 | (3) |
We first describe the extraction of the yield–mobility product from TRMC measurements of charges produced by exciton dissociation in six distinct s-SWCNT donor/acceptor heterojunctions. Fig. 3a and b shows the fluence dependence of φΣμ for these heterojunctions, studied under selective excitation conditions that either induce photoinduced hole transfer (PHT) or photoinduced electron transfer (PET), respectively. The φΣμ value is plotted as the CS yield–mobility product at t = 0 ((φΣμ)t=0) that is extracted by a global multi-exponential analysis of the fluence-dependent TRMC decays. As demonstrated in our previous studies, extrapolating φΣμ values to t = 0 accounts for carrier loss processes that may occur within the 4 ns pump pulse, since the yield–mobility product decreases with increasing fluence.17,37,41 While this reduction of φΣμ at high fluence could potentially result from a decrease in charge carrier yield and/or mobility, comparison to fluence-dependent TA measurements of the peak GSB magnitude (Fig. 3c and d) demonstrate that increasing fluence primarily contributes to a decrease in carrier yield. The GSB magnitude is proportional to the total population of excitons and/or charges and does not depend on charge carrier mobility. Thus, the strong correlation between the fluence-dependent GSB and φΣμ magnitudes is consistent with the expectation that second-order loss processes (e.g. exciton–exciton annihilation)37,41,42 limit the initial exciton population and ultimate exciton dissociation yield as the fluence increases. This correlation also suggests that exciton-charge annihilation43 does not play a substantial role in limiting the free carrier yield in the TRMC measurement.
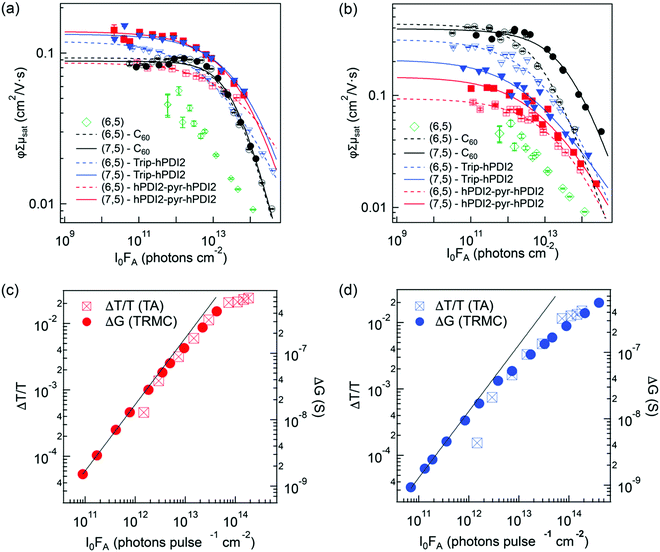 | ||
| Fig. 3 (a) and (b) show the CS yield – carrier mobility product (φΣμ) vs. absorbed photon fluence (I0FA) for all s-SWCNTs – electron acceptor bilayers in (a) hole transfer and (b) electron transfer. The solid lines are empirical fits to eqn (4), used to estimate the low-fluence limit to φΣμ and to interpolate φΣμ values appropriately for TA/TRMC comparisons. A fit is not shown for the neat (6,5) film, due to the low signal-to-noise ratio and the uncertainty associated with the low-fluence saturation behavior. (c) and (d) compare S11 ΔT/T and TRMC ΔG vs. I0FA for hole transfer at (6,5) SWCNT heterojunctions paring with (c) hPDI2-pyr-hPDI2 and (d) Trip-PDI2. | ||
The fluence-dependent yield–mobility products are fitted by an empirically demonstrated dependence of photoconductance on absorbed fluence due to second-order loss processes:37
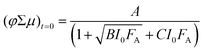 | (4) |
| hPDI2-pyr-hPDI2 | Trip-hPDI2 | C60 | |
|---|---|---|---|
| Yield-mobility product (φΣμ) | |||
| (6,5) SWCNT | 0.077 | 0.099 | 0.093 |
| (7,5) SWCNT | 0.130 | 0.136 | 0.096 |
| Charge separation yield (φPHT) | |||
| (6,5) SWCNT | 0.066 (0.059) | 0.056 (0.055) | 0.039 (0.033) |
| (7,5) SWCNT | 0.131 (0.137) | 0.18 (0.211) | 0.050 (0.044) |
| s-SWCNT hole mobility (μh) | |||
| (6,5) SWCNT | 1.17 | 1.77 | 2.38 |
| (7,5) SWCNT | 0.99 | 0.76 | 1.92 |
| hPDI2-pyr-hPDI2 | Trip-hPDI2 | C60 | |
|---|---|---|---|
| Yield-mobility product (φΣμ) | |||
| (6,5) SWCNT | 0.104 | 0.269 | 0.384 |
| (7,5) SWCNT | 0.116 | 0.189 | 0.388 |
| Charge separation yield (φPET) | |||
| (6,5) SWCNT | 0.153 | 0.18 | 0.21 |
| (7,5) SWCNT | 0.133 | 0.070 | 0.263 |
| SWCNT hole mobility (μh) | |||
| (6,5) SWCNT | 0.68 | 1.49 | 1.82 |
| (7,5) SWCNT | 0.87 | 2.70 | 1.48 |
As discussed in our prior studies, the extended pi network and rigidity of s-SWCNTs lead us to the conclusion that the s-SWCNT hole mobility significantly exceeds the electron mobilities in the organic electron acceptors studied here (μh ≫ μe).17,37 As an example, the 9 GHz hole mobility was estimated to be in the range of ca. 0.2 cm2 V−1 s−1 for (7,5) s-SWCNTs (originating from CoMoCAT SWCNT source)37 and ca. 1.1 cm2 V−1 s−1 for HiPCO thin films containing five primary s-SWCNT species.17 These values are much larger than the electron mobility of ca. 0.01 cm2 V−1 s−1 estimated for evaporated C60 films.37 While measurements or estimates of the 9 GHz electron mobilities do not exist for these PDI-based acceptors, space-charge limited current (SCLC) measurements44 suggest electron mobilities that are about two orders of magnitude smaller than found in evaporated C60 films.45 As such, the sum of the mobilities in our current measurements should be dominated by the s-SWCNT hole mobility (Σμ = μh + μe ≈ μh) and the φΣμ values in Tables 1 and 2 reduce to φΣμ = φμh.
To deconstruct the s-SWCNT hole yield–mobility product (φμh) and estimate the hole mobility, we use TA to estimate the charge carrier yield (φ) generated by photoinduced charge separation. The interfacial CS yields (φ) for s-SWCNT – electron acceptor heterojunctions is calculated as φ = Nh/Nex = Nh/I0FA, where Nh is the hole density created by exciton dissociation, Nex is the initial photogenerated exciton density, I0 is the incident photon density, and FA is the fraction of absorbed photons (absorptance). The determination of Nh is based on a previously developed method that considers the dependence of the S11 GSB and X+ intensities on carrier density.20,25 To obtain the maximum X+ intensity from TA spectra, the spectral contributions of charges were separated from those of excitons by global analysis based on singular value decomposition (SVD).20,46
The interfacial CS yields from both PHT and PET are listed in Tables 1 and 2, respectively. The CS yields are then used to calculate s-SWCNT hole mobilities following exciton dissociation by PHT and PET (Tables 1 and 2, respectively). Parenthetical PHT yields in Table 1 are corrected for the small amount of photon absorption by the s-SWCNT layers,20 but μh is calculated from uncorrected (total) CS yield. The s-SWCNT hole mobility values obtained from this analysis cover a range of 0.68–2.7 cm2 V−1 s−1, with an average value of 1.5 ± 0.6 cm2 V−1 s−1. Notably, the magnitude of this range is consistent with the results of our recent study cross-correlating dark microwave conductivity and DC conductivity to estimate the 9 GHz hole mobility in doped (6,5) s-SWCNT networks.47
Discussion
The matched TA and TRMC dynamics and reasonable charge carrier mobilities extracted from the analyses described above suggest that (1) the excited-state charges produced by exciton dissociation across prototypical Type-II s-SWCNT heterojunctions are primarily free charge carriers, and (2) by extension, free/mobile excited-state holes produced in such a heterojunction give rise to strong GSB and X+ peaks in the TA spectra. Here, we discuss the implications of these results, both from the standpoint of s-SWCNT photophysics and from the broader standpoint of carrier generation in heterojunctions of excitonic semiconductors.It is important to note that some or all charge carriers separated across many heterojunctions formed between low-dielectric semiconductors cannot escape the Coulomb attraction of the opposite charge carrier, even when that carrier resides in another material. Charge transfer excitons (CTEs), consisting of a Coulomb-bound electron in the acceptor and hole in the donor, are ubiquitous features in many such heterojunctions.7 For example, strongly bound CTEs (binding energy ≈ 90 to 200 meV) called interlayer excitons (ILEs) are the typical result of interfacial exciton dissociation in numerous heterojunctions formed between two transition metal dichalcogenides (TMDCs).48–51 CTEs have also been identified in numerous TMDC heterojunctions with small molecules.52–54 In organic donor/acceptor heterojunctions, CTEs have been observed in sensitive sub-bandgap absorption and photoluminescence measurements, along with some evidence of very small photocurrents in quantum efficiency measurements of photovoltaic devices.55 While some CTEs may dissociate into free carriers, a number of analyses suggest that such CTEs can inhibit free charge generation and reduce the voltage of OPVs.7–9,55 Importantly, s-SWCNTs possess many of the properties that have been suggested for overcoming this interfacial Coulomb attraction – e.g. rigid bonds, low reorganization energy, and highly delocalized charge carriers.7,8,10,56
The results of the current study demonstrate that photogenerated charges in model s-SWCNT donor/acceptor heterojunctions do not ultimately produce Coulomb-bound CTEs, since such interfacial excitons would not be probed by TRMC. Classen et al. recently noted that the large open-circuit voltage of s-SWCNT/fullerene solar cells was consistent with the lack of an observable charge-transfer state absorption feature in external quantum efficiency (EQE) measurements.24 While such EQE studies can identify the contribution (or lack thereof) of charge-transfer states to photocurrent generation via sub-bandgap absorption, they cannot rule out the possibility that some fraction of separated charges form CTEs following absorption at or above the s-SWCNT or fullerene optical bandgaps. Our study conclusively demonstrates that such a mechanism does not occur in these prototypical s-SWCNT heterojunctions. The quantitative match of TA and TRMC dynamics observed here contrasts markedly with the only other study we are aware of comparing TA and TRMC dynamics following exciton dissociation across an organic heterojunction.36 In that study, the TRMC dynamics of charges separated across a polymer/fullerene heterojunction were dominated by a population of long-lived mobile carriers while the relatively short-lived TA dynamics were dominated by the fast recombination of the majority of photogenerated carriers.36
Our results also provide clarity regarding the spectral signatures of excited-state mobile charge carriers in TA measurements of s-SWCNTs – namely whether or not such features reflect the presence of free or localized carriers (or both). This question has been debated for the ground-state charges in doped (6,5) s-SWCNTs, where the primary spectral changes to the UV-Vis absorption spectra are GSB and trion induced absorption features that are nominally identical to the features observed in our TA measurements for excited-state charges.28,47 It is sometimes proposed that the charge carriers in doped s-SWCNTs are predominantly localized near the dopant site as a Coulomb-bound “mirror charge” or “charge puddle”,28 analogous to the excited-state CTEs discussed above. However, Ferguson et al. paired 9 GHz and direct current (DC) conductivity measurements to conclude that a significant portion of charge carriers in doped (6,5) s-SWCNT films are “mobile” or free charge carriers.47 Consistently, a recent study employing charge modulation spectroscopy also observed GSB and X+ spectral features for mobile free charge carriers in electrostatically doped (6,5) s-SWCNT thin films.57 The current study conclusively demonstrates that concomitant GSB and X+ peaks are ubiquitous spectroscopic signatures of free/mobile excited-state charges in photoexcited s-SWCNTs-based donor/acceptor heterojunctions. While localized charge carriers may also contribute to these spectral features in some doped s-SWCNT samples or photoexcited heterojunctions, using these peaks to discriminate between localized and delocalized carriers may hinge upon deducing a more nuanced appreciation of the effect of localization on the relative oscillator strengths, peak widths, and energies of such transitions. Alternatively, spectral characteristics of charges at much lower energies (e.g. mid-infrared) may prove more promising for making this distinction, as has recently been demonstrated for some semiconducting polymers.58,59
Finally, we note that our combined TA/TRMC analysis is also useful for determining the excited-state carrier mobility for systems where estimates are available for charge carrier absorption coefficients.25,41 It is encouraging that the s-SWCNT hole mobilities extracted by our analysis only vary by a factor of ca. 6 across all of the twelve unique experimental combinations. We also conclude that the average mobility value is in a sensible range when contextualized with other recent analyses.37 For example, the hole mobility in (7,5) SWCNT/C60 heterojunctions was recently estimated to be 0.2 cm2 V−1 s−1 by utilizing solar cell quantum efficiency measurements to estimate carrier yield for similarly prepared heterojunctions.37 While the average (7,5) hole mobility extracted here (1.5 ± 0.6 cm2 V−1 s−1) is appreciably larger than that estimate, there is significant difference in s-SWCNT tip-sonication time in the current (15 min) and previous (60 min)37 studies. Studies from our own group and others have found that shorter sonication time yields longer tube lengths and lower defect densities,60–62 which in turn translate to higher luminescence quantum yields,62 film conductivities,60 and higher solar cell quantum efficiencies.61 Since these improvements all result from a reduced probability for carrier scattering or trapping events, the charge carrier mobility (and by extension the yield–mobility products) of (7,5) SWCNTs in this study should be larger than that in our previous study.37
While the similarity between TA and TRMC kinetics suggests that the charge carriers produced by exciton dissociation are predominantly free charge carriers, the charge separation yields for these heterojunctions are still relatively low. Low charge separation yields in s-SWCNT heterojunctions can be traced, in part, to the relatively fast exciton decay and inefficient transverse exciton diffusion.23 As shown in Fig. S2(b) (ESI†), nearly 80% of the initially excited exciton population decays within 10 ps. Bindl et al. also demonstrated a relatively short cross-plane inter-tube exciton diffusion length of ca. 5 nm,22 similar to the ca. 5 nm exciton diffusion length found by Dowgiallo et al. in C60 thin films.63 The thermodynamic driving force also plays an important role in the charge separation yield.6,64 Even in SWCNT heterojunctions of <5 nm SWCNT layer thickness, Wang et al. found low overall device IQEs with PDI acceptors, due to relatively low charge transfer driving force.64 We are currently investigating the impacts of thermodynamic driving force and molecular structure on charge separation in a systematic series of SWCNT-PDI heterojunctions.
Conclusions
In this study, we performed a correlated spectroscopic analysis on heterojunctions of s-SWCNTs and organic electron acceptors by transient absorption and time-resolved microwave conductivity. Combined analysis from two different spectroscopic techniques provides insights into the charge carrier separation process and charge carrier spectroscopic signatures that cannot be gleaned from either technique alone. The close correlation between TA and TRMC dynamics for (6,5) SWCNTs heterojunctions points to free charge carriers, and not interfacial charge-transfer states, as the primary outcome of exciton dissociation in these model systems. Quantitative analysis also demonstrates that excited-state carriers in s-SWCNTs have appreciable mobilities, with an average value of 1.5 ± 0.6 cm2 V−1 s−1. The cross-analysis approach demonstrated here provides a roadmap for better understanding exciton dissociation and charge separation in a wide variety of donor/acceptor heterojunctions containing excitonic semiconductors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was authored in part by the National Renewable Energy Laboratory, operated by Alliance for Sustainable Energy, LLC, for the U.S. Department of Energy (DOE) under Contract No. DE-AC36-08GO28308. Funding provided by the Solar Photochemistry Program, Division of Chemical Sciences, Geosciences, and Biosciences, Office of Basic Energy Sciences, U.S. Department of Energy (DOE). The syntheses of PDI acceptors from C. N. were supported by the U.S. Department of Energy (DOE) under Award No. DE-SC0014563 and the Office of Naval Research (ONR) under Award No. N00014-17-1-2205.Notes and references
- K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 136805 CrossRef PubMed.
- F. Wang, G. Dukovic, L. E. Brus and T. F. Heinz, Science, 2005, 308, 838–841 CrossRef CAS PubMed.
- G. D. Scholes and G. Rumbles, Nat. Mater., 2006, 5, 683–696 CrossRef CAS PubMed.
- D. C. Coffey, B. W. Larson, A. W. Hains, J. B. Whitaker, N. Kopidakis, O. V. Boltalina, S. H. Strauss and G. Rumbles, J. Phys. Chem. C, 2012, 116, 8916–8923 CrossRef CAS.
- X. Hong, J. Kim, S.-F. Shi, Y. Zhang, C. Jin, Y. Sun, S. Tongay, J. Wu, Y. Zhang and F. Wang, Nat. Nanotechnol., 2014, 9, 682 CrossRef CAS PubMed.
- R. Ihly, K. S. Mistry, A. J. Ferguson, T. T. Clikeman, B. W. Larson, O. Reid, O. V. Boltalina, S. H. Strauss, G. Rumbles and J. L. Blackburn, Nat. Chem., 2016, 8, 603 CrossRef CAS PubMed.
- X. Zhu, N. R. Monahan, Z. Gong, H. Zhu, K. W. Williams and C. A. Nelson, J. Am. Chem. Soc., 2015, 137, 8313–8320 CrossRef CAS PubMed.
- A. A. Bakulin, A. Rao, V. G. Pavelyev, P. H. M. van Loosdrecht, M. S. Pshenichnikov, D. Niedzialek, J. Cornil, D. Beljonne and R. H. Friend, Science, 2012, 335, 1340–1344 CrossRef CAS PubMed.
- T. M. Burke, S. Sweetnam, K. Vandewal and M. D. McGehee, Adv. Energy Mater., 2015, 5, 1500123 CrossRef.
- N. A. Pace, O. G. Reid and G. Rumbles, ACS Energy Lett., 2018, 3, 735–741 CrossRef CAS.
- J. Zhang, A. C. Jakowetz, G. Li, D. Di, S. M. Menke, A. Rao, R. H. Friend and A. A. Bakulin, J. Mater. Chem. A, 2017, 5, 11949–11959 RSC.
- J. L. Blackburn, ACS Energy Lett., 2017, 2, 1598–1613 CrossRef CAS.
- X. He, F. Léonard and J. Kono, Adv. Opt. Mater., 2015, 3, 989–1011 CrossRef CAS.
- V. Schroeder, S. Savagatrup, M. He, S. Lin and T. M. Swager, Chem. Rev., 2019, 119, 599–663 CrossRef CAS PubMed.
- X. He, H. Htoon, S. K. Doorn, W. H. P. Pernice, F. Pyatkov, R. Krupke, A. Jeantet, Y. Chassagneux and C. Voisin, Nat. Mater., 2018, 17, 663–670 CrossRef CAS PubMed.
- A. H. Brozena, M. Kim, L. R. Powell and Y. Wang, Nat. Rev. Chem., 2019, 3, 375–392 CrossRef CAS PubMed.
- D. J. Bindl, A. J. Ferguson, M.-Y. Wu, N. Kopidakis, J. L. Blackburn and M. S. Arnold, J. Phys. Chem. Lett., 2013, 4, 3550–3559 CrossRef CAS.
- J. Wang, S. R. Peurifoy, M. T. Bender, F. Ng, K.-S. Choi, C. Nuckolls and M. S. Arnold, J. Phys. Chem. C, 2019, 123, 21395–21402 CrossRef CAS.
- H. S. Kang, T. J. Sisto, S. Peurifoy, D. H. Arias, B. Zhang, C. Nuckolls and J. L. Blackburn, J. Phys. Chem. C, 2018, 122, 14150–14161 CrossRef CAS.
- D. B. Sulas-Kern, H. Zhang, Z. Li and J. L. Blackburn, Mater. Horiz., 2019, 6, 2103–2111 RSC.
- D. J. Bindl and M. S. Arnold, J. Phys. Chem. C, 2013, 117, 2390–2395 CrossRef CAS.
- D. J. Bindl, M.-Y. Wu, F. C. Prehn and M. S. Arnold, Nano Lett., 2011, 11, 455–460 CrossRef CAS PubMed.
- M. J. Shea and M. S. Arnold, Appl. Phys. Lett., 2013, 102, 243101 CrossRef.
- A. Classen, L. Einsiedler, T. Heumueller, A. Graf, M. Brohmann, F. Berger, S. Kahmann, M. Richter, G. J. Matt, K. Forberich, J. Zaumseil and C. J. Brabec, Adv. Energy Mater., 2019, 9, 1801913 CrossRef.
- A.-M. Dowgiallo, K. S. Mistry, J. C. Johnson and J. L. Blackburn, ACS Nano, 2014, 8, 8573–8581 CrossRef CAS PubMed.
- A.-M. Dowgiallo, K. S. Mistry, J. C. Johnson, O. G. Reid and J. L. Blackburn, J. Phys. Chem. Lett., 2016, 7, 1794–1799 CrossRef CAS PubMed.
- K. H. Eckstein, H. Hartleb, M. M. Achsnich, F. Schöppler and T. Hertel, ACS Nano, 2017, 11, 10401–10408 CrossRef CAS PubMed.
- K. H. Eckstein, F. Oberndorfer, M. M. Achsnich, F. Schöppler and T. Hertel, J. Phys. Chem. C, 2019, 123, 30001–30006 CrossRef CAS.
- T. Clarke, A. Ballantyne, F. Jamieson, C. Brabec, J. Nelson and J. Durrant, Chem. Commun., 2009, 89–91, 10.1039/B813815J.
- H. Ohkita and S. Ito, Polymer, 2011, 52, 4397–4417 CrossRef CAS.
- O. G. Reid, R. D. Pensack, Y. Song, G. D. Scholes and G. Rumbles, Chem. Mater., 2014, 26, 561–575 CrossRef CAS.
- A. Saeki, S. Seki, T. Sunagawa, K. Ushida and S. Tagawa, Philos. Mag., 2006, 86, 1261–1276 CrossRef CAS.
- R. Yamagami, K. Kobayashi, A. Saeki, S. Seki and S. Tagawa, J. Am. Chem. Soc., 2006, 128, 2212–2213 CrossRef CAS PubMed.
- A. Saeki, S. Seki, Y. Koizumi and S. Tagawa, J. Photochem. Photobiol., A, 2007, 186, 158–165 CrossRef CAS.
- J. Park, O. G. Reid and G. Rumbles, Proc. SPIE 9549, Physical Chemistry of Interfaces and Nanomaterials XIV, San Diego, CA, 2015.
- R. Katoh, H. Matsuzaki, A. Furube, P. Sonar, E. L. Williams, C. Vijila, G. S. Subramanian, S. Gorelik and J. Hobley, J. Phys. Chem. C, 2016, 120, 28398–28406 CrossRef CAS.
- A. J. Ferguson, A.-M. Dowgiallo, D. J. Bindl, K. S. Mistry, O. G. Reid, N. Kopidakis, M. S. Arnold and J. L. Blackburn, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 245311 CrossRef.
- S. L. Guillot, K. S. Mistry, A. D. Avery, J. Richard, A.-M. Dowgiallo, P. F. Ndione, J. van de Lagemaat, M. O. Reese and J. L. Blackburn, Nanoscale, 2015, 7, 6556–6566 RSC.
- J. L. Blackburn, J. M. Holt, V. M. Irurzun, D. E. Resasco and G. Rumbles, Nano Lett., 2012, 12, 1398–1403 CrossRef CAS PubMed.
- R. Matsunaga, K. Matsuda and Y. Kanemitsu, Phys. Rev. Lett., 2011, 106, 037404 CrossRef.
- O. G. Reid and G. Rumbles, J. Phys. Chem. Lett., 2013, 4, 2348–2355 CrossRef CAS.
- B. Yuma, S. Berciaud, J. Besbas, J. Shaver, S. Santos, S. Ghosh, R. B. Weisman, L. Cognet, M. Gallart, M. Ziegler, B. Hnerlage, B. Lounis and P. Gilliot, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 205412 CrossRef.
- J. M. Hodgkiss, S. Albert-Seifried, A. Rao, A. J. Barker, A. R. Campbell, R. A. Marsh and R. H. Friend, Adv. Funct. Mater., 2012, 22, 1567–1577 CrossRef CAS.
- S. R. Peurifoy, E. Castro, F. Liu, X. Y. Zhu, F. Ng, S. Jockusch, M. L. Steigerwald, L. Echegoyen, C. Nuckolls and T. J. Sisto, J. Am. Chem. Soc., 2018, 140, 9341–9345 CrossRef CAS PubMed.
- R. C. Haddon, A. S. Perel, R. C. Morris, T. T. M. Palstra, A. F. Hebard and R. M. Fleming, Appl. Phys. Lett., 1995, 67, 121–123 CrossRef CAS.
- J. J. Snellenburg, S. Laptenok, R. Seger, K. M. Mullen and I. H. M. van Stokkum, J. Stat. Soft., 2012, 49, 1–22 Search PubMed.
- A. J. Ferguson, O. G. Reid, S. U. Nanayakkara, R. Ihly and J. L. Blackburn, J. Phys. Chem. Lett., 2018, 9, 6864–6870 CrossRef CAS PubMed.
- P. Rivera, J. R. Schaibley, A. M. Jones, J. S. Ross, S. Wu, G. Aivazian, P. Klement, K. Seyler, G. Clark, N. J. Ghimire, J. Yan, D. G. Mandrus, W. Yao and X. Xu, Nat. Commun., 2015, 6, 6242 CrossRef CAS PubMed.
- B. Miller, A. Steinhoff, B. Pano, J. Klein, F. Jahnke, A. Holleitner and U. Wurstbauer, Nano Lett., 2017, 17, 5229–5237 CrossRef CAS PubMed.
- P. Rivera, H. Yu, K. L. Seyler, N. P. Wilson, W. Yao and X. Xu, Nat. Nanotechnol., 2018, 13, 1004–1015 CrossRef CAS PubMed.
- J. Blackburn, D. B. Sulas-Kern and E. M. Miller, Energy Environ. Sci., 2020, 13, 2684–2740 RSC.
- T. Zhu, L. Yuan, Y. Zhao, M. Zhou, Y. Wan, J. Mei and L. Huang, Sci. Adv., 2018, 4, eaao3104 CrossRef PubMed.
- S. H. Amsterdam, T. K. Stanev, Q. Zhou, A. J. T. Lou, H. Bergeron, P. Darancet, M. C. Hersam, N. P. Stern and T. J. Marks, ACS Nano, 2019, 13, 4183–4190 CrossRef CAS PubMed.
- Arramel, X. Yin, Q. Wang, Y. J. Zheng, Z. Song, M. H. B. Hassan, D. Qi, J. Wu, A. Rusydi and A. T. S. Wee, ACS Appl. Mater. Interfaces, 2017, 9, 5566–5573 CrossRef CAS PubMed.
- J. Benduhn, K. Tvingstedt, F. Piersimoni, S. Ullbrich, Y. Fan, M. Tropiano, K. A. McGarry, O. Zeika, M. K. Riede, C. J. Douglas, S. Barlow, S. R. Marder, D. Neher, D. Spoltore and K. Vandewal, Nat. Energy, 2017, 2, 17053 CrossRef CAS.
- A. Y. Sosorev, D. Y. Godovsky and D. Y. Paraschuk, Phys. Chem. Chem. Phys., 2018, 20, 3658–3671 RSC.
- N. F. Zorn, F. Scuratti, F. J. Berger, A. Perinot, D. Heimfarth, M. Caironi and J. Zaumseil, ACS Nano, 2020, 14, 2412–2423 CrossRef CAS PubMed.
- R. Ghosh, A. R. Chew, J. Onorato, V. Pakhnyuk, C. K. Luscombe, A. Salleo and F. C. Spano, J. Phys. Chem. C, 2018, 122, 18048–18060 CrossRef CAS.
- T. J. Aubry, J. C. Axtell, V. M. Basile, K. J. Winchell, J. R. Lindemuth, T. M. Porter, J.-Y. Liu, A. N. Alexandrova, C. P. Kubiak, S. H. Tolbert, A. M. Spokoyny and B. J. Schwartz, Adv. Mater., 2019, 31, 1805647 CrossRef PubMed.
- R. C. Tenent, T. M. Barnes, J. D. Bergeson, A. J. Ferguson, B. To, L. M. Gedvilas, M. J. Heben and J. L. Blackburn, Adv. Mater., 2009, 21, 3210–3216 CrossRef CAS.
- J. Wang, M. J. Shea, J. T. Flach, T. J. McDonough, A. J. Way, M. T. Zanni and M. S. Arnold, J. Phys. Chem. C, 2017, 121, 8310–8318 CrossRef CAS.
- A. Graf, Y. Zakharko, S. P. Schießl, C. Backes, M. Pfohl, B. S. Flavel and J. Zaumseil, Carbon, 2016, 105, 593–599 CrossRef CAS.
- A.-M. Dowgiallo, K. S. Mistry, J. C. Johnson, O. G. Reid and J. L. Blackburn, J. Phys. Chem. Lett., 2016, 7, 1794–1799 CrossRef CAS PubMed.
- J. Wang, S. R. Peurifoy, M. T. Bender, F. Ng, K.-S. Choi, C. Nuckolls and M. S. Arnold, J. Phys. Chem. C, 2019, 123, 21395–21402 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Methods, additional absorption spectra, TA/TRMC dynamics and analysis. See DOI: 10.1039/d0mh01810d |
| This journal is © The Royal Society of Chemistry 2021 |