Open Access Article
Open Access ArticleWater droplet bouncing on a non-superhydrophobic Si nanospring array†
Samir
Kumar
 ab,
Kyoko
Namura
a,
Motofumi
Suzuki
a and
Jitendra P.
Singh
ab,
Kyoko
Namura
a,
Motofumi
Suzuki
a and
Jitendra P.
Singh
 *b
*b
aDepartment of Micro Engineering, Graduate School of Engineering, Kyoto University, Nishikyo, Kyoto 615-8540, Japan
bDepartment of Physics, Indian Institute of Technology Delhi, Hauz Khas, New Delhi 110016, India. E-mail: jpsingh@physics.iitd.ac.in
First published on 11th December 2020
Abstract
Self-cleaning surfaces often make use of superhydrophobic coatings that repel water. Here, we report a hydrophobic Si nanospring surface that effectively suppresses wetting by repelling water droplets. The dynamic response of Si nanospring arrays fabricated by glancing-angle deposition is investigated. These hydrophobic arrays of vertically standing nanosprings (about 250 nm high and 60 nm apart) allow the droplets to rebound within a few milliseconds after contact. Amazingly, the morphology of the nanostructures influences the impact dynamics. The rebound time and coefficient of restitution are higher for Si nanosprings than for vertical Si columns. By considering the droplet/nanospring surface as a coupled-spring system, we argue that the restoring force of the nanosprings may be responsible for the water-droplet rebound. The bouncing phenomena studied here are essential in the design of self-cleaning surfaces and are also of fundamental importance for the study of wetting behavior on nanostructures.
1. Introduction
Self-cleaning surfaces are of increasing technological importance. The discovery of a new class of films that could render ordinary surfaces self-cleaning is of evident technological importance, and, if it proves economical, of great practical importance. Micro- and nanostructured surfaces with special wetting behaviors have received considerable attention in recent years.1–6 Non-wettability is a crucial surface property that plays an important role in daily life, industry, and agriculture. The lotus effect is an example of self-cleaning in nature: superhydrophobic leaves protect the lotus plant against pathogens or fungi.7Depending on the surface energy and ruggedness of its microstructures, a surface can be hydrophilic, hydrophobic, or superhydrophobic.8 Superhydrophobic surfaces can be fabricated by chemically modifying a surface with a low surface energy coating or by creating a surface from a hydrophobic material that exhibits roughness at the micro- or nanoscale.9 For any practical applications, the superhydrophobicity and non-wetting behavior must be maintained under dynamic conditions when the droplet impacts the surface with a given velocity. On superhydrophobic surfaces, water will form almost spherical droplets with very high contact angles. When landing on such a surface, the water droplet may rebound; this is critical in situations where the impact of the water droplets on the surface is important, for example, in deicing applications.10,11
The necessary conditions for droplet-bouncing have been considered in the literature. For example, bouncing can be easily achieved on superhydrophobic surfaces, as the interactions between the droplet and surface that might prevent the drop from bouncing are minimal.12 When a droplet falls on such a surface, the rough structures of the surface and the air trapped in them can produce a significant capillary pressure that helps the droplet rebound from the surface.13–16 Several studies have elucidated the dynamics of a bouncing droplet16–22 as a function of the surface micro-and nanostructure18,23,24 or of the impact velocity.25 The shape-change in the droplet has also been shown to be a direct indicator of the contact angle and hydrophobicity. The bouncing of water droplets has been studied to determine the hydrophobicity of surfaces, and a relationship has been established between the contact angle of the water and the number of bounces.26 It has also been reported that the surface must have a contact angle of at least 150° for a droplet to bounce (i.e., for the kinetic energy of the impinging droplet to be transformed into surface energy).12,26,27 Other studies suggest that the hysteresis of the contact angle plays a crucial role in the bouncing behavior of impacting droplets.28 Moreover, in addition to depending on the wetting properties of the surface, the rebound depends on such parameters as the surface tension, viscosity, and velocity of the droplet at impact.12,18,20,22,25
There are many reports of the bouncing of a water droplet on high contact-angle (superhydrophobic) static surfaces,22,29–31 but bouncing on a hydrophobic nanosprings structure, to the best of our knowledge, has not been reported. Here, we show that an ultrathin film of nanospring arrays can cause water droplets to rebound. We demonstrate that nanostructured surfaces that have comparable static contact angles exhibit remarkably different droplet-rebound dynamics. Even though millions of nanostructures interact simultaneously with a single water droplet, the underlying shape of the nanostructures can determine whether the droplet flies off the surface.
2. Materials and methods
2.1. Samples: fabrication of nanostructures
We used the glancing angle deposition (GLAD) technique to fabricate nanostructured surfaces with different morphologies.32,33 GLAD can be used to grow porous and hydrophobic surfaces from a variety of materials.34–40 Depositions were performed in a vacuum chamber having pressures in the range 10−7 to 10−6 torr. The angle between the substrate normal and the incident vapor flux was 85° during the entire deposition. The substrate was rotated continuously and slowly for the fabrication of Si nanosprings arrays.41,42 Si samples with different morphologies, such as slanted column (SC), vertical column (VC), nanospring arrays (NS), and thin-film (TF), were grown using the GLAD method. These samples were coated with trichlorooctadecylsilane (>99.0%, Tokyo Chemical Industry Co., Ltd.) to modify the sticking behavior of the surface.2.2. SEM analysis
The as-grown Si nanostructures were imaged using a scanning electron microscope (SEM; Hitachi High Tech. SU3800) with a LaB6 detector in the secondary electron mode operating at an acceleration voltage of 10 kV. The cross-sectional SEM images were acquired by cleaving the wafer to expose a pristine edge.2.3. Drop impact experiments
For the measurement of the static apparent contact angle (APCA), 10 μL droplets of ultrapure water (18.2 MΩ cm from Millipore Direct Q UV3, Merck) of about 1.3 mm radius were gently dropped onto the substrate. The contact angle measurements were repeatedly performed at ten different positions on the sample surfaces. The impact and rebound dynamics of the water droplet were followed using a high-speed camera (FASTCAM Mini AX100, Photron) operating at 3000 frames per s.43 In the dynamic measurements, water droplets of volume 10 μL were allowed to fall under gravity onto the nanostructured sample surfaces. The impact velocity (v0) was changed by varying the droplet release height (h). Water droplets were positioned at 10, 15, and 20 mm above the surface with corresponding impact velocities of 44, 54, and 63 cm s−1 and Weber number (We) of 7.2, 10.8, and 14.3, respectively. The impact velocities of the water droplets were calculated using the relation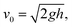 where g is the acceleration due to gravity. All measurements were performed at room temperature and 37% relative humidity (RH) value.
where g is the acceleration due to gravity. All measurements were performed at room temperature and 37% relative humidity (RH) value.
3. Results and discussion
Fig. 1 shows the top and cross-sectional SEM micrographs of the different Si nanostructures used in this study. The inset shows optical images of 10 μL water droplets on the corresponding surfaces. The average thickness, average diameter, and solid fraction of each sample are given in Table 1.| Sample | Average thickness (nm) | Average diameter (nm) | Solid fraction (%) | |
|---|---|---|---|---|
| From contact angle | From SEM image | |||
| TF | 553 ± 2 | NA | NA | NA |
| SC | 265 ± 8 | 53 ± 15 | 35 | 43 |
| VC | 240 ± 2 | 48 ± 15 | 20 | 27 |
| NS | 256 ± 4 | 45 ± 10 | 35 | 45 |
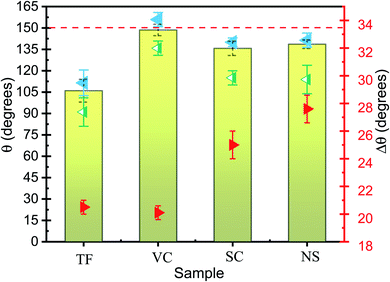
Each nanostructured sample had a thickness of approximately 250 nm and an average diameter of approximately 50 nm. Generally, when a droplet is placed statically on a periodic nanostructured surface, the droplet shape is symmetric and is determined by the minimization of the total surface energy. The static apparent contact angle (APCA) values of water droplets on TF, SC, VC, and NS were observed to be 106.0°, 135.7°, 148.6°, and 138.6°, respectively (Fig. 2). The contact angle was minimum for the TF and maximum for the VC. The contact angles of the SC and NS were approximately equal, although the water-droplet impact dynamics were found to be very different.
The chemical composition and morphology of a surface define its wetting properties. All the samples were made of Si and were coated with the same chemical (which resulted in a slightly higher contact angle). Given this compositional uniformity, the difference in contact angle must be due to the surface morphology of the samples. The nanocolumnar structure made the sample surface very rough and porous, resulting in an increase in contact angle as compared to the conventional thin film. The contact angle was found to increase from 106° for the conventional film to 148° for the vertical nanocolumnar sample. The increase in contact angle on the nanocolumnar samples can be attributed to the decrease in the solid fraction of the nanostructures, as per the Cassie–Baxter model.8 In this model, the surface is a composite of air and Si, and the water droplet sits on the air trapped between the rough surfaces with apparent contact angle θA. The solid fraction f is given by
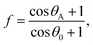 | (1) |
The droplet size, liquid viscosity μ, and impact velocity v0 all influence the impact dynamics. A dimensionless variable—the Weber number We (the ratio of the kinetic energy to the surface energy)—can be used to characterize the impact dynamics:48
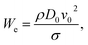 | (2) |
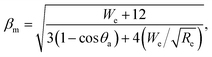 | (3) |
 | ||
| Fig. 3 Time evolution of 10 μL water droplets dropped from a height of 10 mm on different nanostructures (ESI).† Water droplet bouncing was observed on vertical columns and nanospring samples. The water droplet rebounded on VC and NS and left the surface in approximately 16 ms. | ||
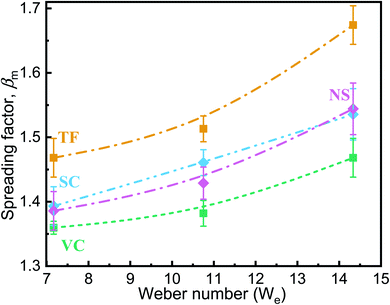
The spreading mechanism of a drop onto a solid surface has been studied in detail in the past.52 The evolution of the spreading factor is divided into four phases: the kinematic, spreading, relaxation, and wetting phases, respectively. Most of the spreading occurs during the second of these, which is dominated by inertia.53 The increase in inertia can explain the increase in the maximum spreading diameter with increasing We.
The time to reach maximum deformation was also found to depend on the impacting surface: it was maximum for TF and minimum for NS (Table 2). Sample NS took around 3.67 ms, on average, for maximum deformation when We ≈ 7. For the VC sample, the droplet reached its maximum deformation at approximately t = 4.11 ms; after that, surface tension and viscous forces overcame inertia so that fluid accumulated at the leading edge of the splash and started pulling back. Droplets with higher velocity will have higher inertia and will take less time for maximum deformation. Hence, the time for maximum deformation decreased with an increase in impact velocity.
| Sample | Velocity (cm s−1) | Weber no. We | maximum spreading diameter (dmax) (mm) | Time for max. deformation (ms) | Rebound Time (ms) | Time of flight (ms) | Coefficient of restitution (COR) |
|---|---|---|---|---|---|---|---|
| TF | 44.3 | 7.2 | 3.92 | 4.67 | — | ||
| 54.2 | 10.8 | 4.04 | 4.11 | — | |||
| 62.6 | 14.3s | 4.47 | 3.56 | — | |||
| SC | 44.3 | 7.2 | 3.72 | 4.89 | — | ||
| 54.2 | 10.8 | 3.90 | 3.56 | — | |||
| 62.6 | 14.3 | 4.10 | 3.33 | — | |||
| VC | 44.3 | 7.2 | 3.63 | 4.11 | 16.11 | 22.67 | 0.25 |
| 54.2 | 10.8 | 3.69 | 3.56 | 15.67 | 27.22 | 0.25 | |
| 62.6 | 14.3 | 3.92 | 3.33 | 16.33 | 29 | 0.23 | |
| NS | 44.3 | 7.2 | 3.70 | 3.87 | 15.33 | 14.68 | 0.16 |
| 54.2 | 10.8 | 3.82 | 3.67 | 17.42 | 19.33 | 0.18 | |
| 62.6 | 14.3 | 4.12 | 3.44 | 18.58 | 26.33 | 0.21 |
The rebound time at which the droplet bounces off the surface is crucial because it determines the degree of energy transfer. When the droplet fell on vertically aligned nanorods from a height of 10 mm, it rebounded and left the surface in about 16.11 ms. However, when a droplet of the same volume fell with the same impact velocity of 44 cm s−1 on the Si nanosprings (APCA < 150°), instead of wetting the surface, the droplet bounced, leaving the surface in about 15.33 ms. The NS structure not only showed the bouncing of the droplet on the hydrophobic surface but also reduced the contact time (≈15.33 ms) and the time for maximum spreading (≈3.67 ms) relative to that of VC samples.31 It is interesting to note that the rebound time for the VC sample was almost constant (≈16 ms) with increasing We, but the rebound time for the NS sample increased from 15.3 to 18.5 ms. The spreading dynamics, in the case of VC, is consistent with the previous report by Fan et al.47
The bouncing behavior on the VC was not unexpected, as it had a contact angle of ≈ 148.6° ± 4.0 and thus satisfied the first necessary condition for bouncing behavior. The contact angle for the NS was around 138.6° ± 3.0, but surprisingly this sample also showed the bouncing behavior. Some prior works have concluded that contact angle hysteresis (CAH) plays a significant role in bouncing from the surface.28 The droplet impact process involves an interplay between the kinetic energy, surface energy, and viscous dissipation of the water droplet. The elastic force is due to the surface tension of the water droplet, whereas viscous dissipation is the cause of energy dissipation. Before the impact with the surface, the droplet possesses only kinetic energy. A drop impacting a solid is deformed, and a shock wave spreads radially outward towards the surface up to the point when the viscosity dissipates the kinetic energy (the dissipation due to heat can be neglected for water.) When the droplet reaches its maximum deformation, the restitution force due to surface tension comes into play, causing the droplet to recoil. Now the droplet shrinks and moves radially inward, gaining kinetic energy; a jet rises in the center (the Worthington jet), which may lead to the lift of the droplet (Fig. 3). The droplet must do work to overcome the resistance force produced by CAH. The total work W done in the spreading and receding process of a droplet is given by28
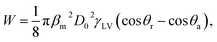 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θr and cos
θr and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θa are the cosines of the receding and advancing contact angles (cos
θa are the cosines of the receding and advancing contact angles (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θr − cos
θr − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θa) is the CAH, and D0 is the initial diameter of the droplet. Lower CAH values result in less work against the resistive force, and very little energy is required to overcome the work done, resulting in a rebound. The lower CAH value for the VC sample may be the other reason that it exhibits a rebound despite the longer contact time. SC and NS had mutually similar CAH values (25 and 27.6, respectively), but only NS showed the rebounding property.
θa) is the CAH, and D0 is the initial diameter of the droplet. Lower CAH values result in less work against the resistive force, and very little energy is required to overcome the work done, resulting in a rebound. The lower CAH value for the VC sample may be the other reason that it exhibits a rebound despite the longer contact time. SC and NS had mutually similar CAH values (25 and 27.6, respectively), but only NS showed the rebounding property.
On superhydrophobic surfaces, the dynamics of a droplet impinging on a surface depending on the competition between the three wetting pressures: water-hammer pressure, Pwh = ρCwv0, dynamic pressure, 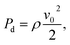 and anti-wetting capillary pressure,
and anti-wetting capillary pressure, 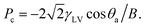 Here, ρ is the water density, Cw is the speed of sound in water, Vi is the droplet velocity, γLV is the surface energy of the water at the water and vapor interface, θa is the advancing contact angle, and B is the spacing between the nanostructures.54,55 Capillary pressure is caused by the air trapped by the surface roughness. The air cushion trapped between the nanorods and the water droplet acts as an effective spring. For a droplet to rebound from the surface, the non-wetting condition Pc > Pwh > Pd must be satisfied. In this study, for the three experimental heights in increasing order and considering ρ = 1000 kg m−3 and Cw = 1482 m s−1, Pwh and Pd were found to vary from 0.66–0.93 MPa and 0.1–0.2 kPa, respectively. Pc was calculated as 2.44 MPa, 2.76 MPa, and 4.33 MPa for the SC, NS, and VC, respectively. The maximum capillary pressure was generated by the VC. For NS and SC nanostructured surfaces, the Pc values were comparable to each other; however, the bouncing phenomenon was observed only on the nanosprings surface. Thus, capillary pressure alone cannot be the reason for the observed bouncing behavior of the droplet on the nanospring surface.
Here, ρ is the water density, Cw is the speed of sound in water, Vi is the droplet velocity, γLV is the surface energy of the water at the water and vapor interface, θa is the advancing contact angle, and B is the spacing between the nanostructures.54,55 Capillary pressure is caused by the air trapped by the surface roughness. The air cushion trapped between the nanorods and the water droplet acts as an effective spring. For a droplet to rebound from the surface, the non-wetting condition Pc > Pwh > Pd must be satisfied. In this study, for the three experimental heights in increasing order and considering ρ = 1000 kg m−3 and Cw = 1482 m s−1, Pwh and Pd were found to vary from 0.66–0.93 MPa and 0.1–0.2 kPa, respectively. Pc was calculated as 2.44 MPa, 2.76 MPa, and 4.33 MPa for the SC, NS, and VC, respectively. The maximum capillary pressure was generated by the VC. For NS and SC nanostructured surfaces, the Pc values were comparable to each other; however, the bouncing phenomenon was observed only on the nanosprings surface. Thus, capillary pressure alone cannot be the reason for the observed bouncing behavior of the droplet on the nanospring surface.
The rebound of the droplet on the surface of the nanosprings is surprising: it is generally assumed that only superhydrophobic surfaces support bouncing, as only on them do the capillary forces allow the drop to leave the surface. A detailed model for the rebound of a water droplet on vertically aligned nanorods can be found in the ESI.† We propose the hypothesis that the elastic property of the nanosprings has a significant role in the bouncing of the water droplet. The rebound of an impinging droplet is only possible if its kinetic energy is larger than the surface energy dissipated during the retraction stage. Bouncing water droplets are vertically deformable, and, upon impact, some of the kinetic energy can be stored by the deformation of the droplet itself.27 Thus, the droplet itself behaves like a spring, the stiffness of which is the surface tension.27,56 The nanosprings can store sufficient energy to facilitate a rebound that causes the droplet to detach from the surface completely.
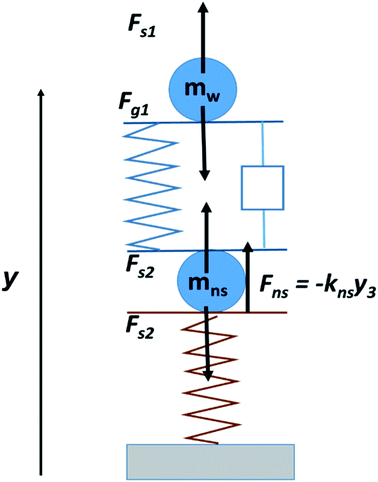
We have modeled the elasticity of the droplet in contact with the elastic nanosprings as an effective mechanically coupled double-spring system. More specifically, we model the droplet by two identical masses m linked by a spring of stiffness kw and rest length L. The viscous effects are modeled by a mechanical damper with a dissipation parameter β. The coordinate y is taken vertically upward; the vertical positions of the upper and lower mass are y1 and y2, respectively. A schematic representation of the spring system is given in Fig. 5. The force of gravity acting on the two masses is Fg1 = −mg = Fg2. The spring also exerts forces on each mass given by Fs1 = −kw(y1 − y2 − L) and Fs2 = kw(y1 − y2 − L). When the lower mass is in contact with the nanospring, it experiences a normal force Fns = −knsy3, where kns is the stiffness constant of the nanospring. Fns depends on the compression of the nanospring, which varies during contact; it is zero when the droplet is not in contact with the surface. The constant kw determines the undamped frequency of the spring, given by f0 = √(kw/m).
The loss of energy of two objects after a collision can be described in terms of the coefficient of restitution (COR), which itself depends on the elastic properties of the colliding objects. Since, in this study, one of the colliding objects is always a water droplet, the COR will change only with the elastic properties of the nanostructured surfaces. For an increase in We, the COR was found to be almost constant for VC but to increase for NS (the decrease in the COR value of VC when We = 14 may be due to the fact that the air trapped under the water droplet was forced out because of the higher impact velocity).
We can explain the increase in the rebound time and COR for the NS sample if we consider the compression of the nanospring structure by droplet impact. The relation between the initial velocity v0, maximum compression ym of the nanospring, and spring constant k is given by57
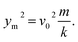 | (5) |
A higher velocity will lead to a higher compression, which may increase the rebound time on the nanospring sample. The potential energy of the nanosprings is also directly proportional to the square of the maximum compression and spring constant. The nanospring will absorb more energy for higher We and return a higher fraction of energy on recoil. Kaneko et al. have already shown that a Si nanospring fabricated using the GLAD technique exhibits nonlinear elastic mechanical behavior.58 They reported the load–displacement (F–δ) relationships obtained during the loading and unloading processes. The nanospring showed nonlinear reversible behavior; the relationship between load, F [nN], and displacement, δ [nm], was determined to be F = 4.1δ + 0.0041δ2. They also confirmed that this nonlinearity originated from the large deformation permitted by the spring shape. Therefore, if we consider the droplet/nanospring surface as a coupled-spring device, we can understand the bouncing behavior on the NS sample along with the increase in the rebound time and COR.
4. Conclusion
The dynamics of water droplets falling on vertical nanorods, tilted nanorods, and nanosprings of silicon were studied. After impact with the surface, the water droplet initially spreads and flattens. It then recoils in a way that is greatly influenced by the underlying morphology of the nanostructured surface. On slanted Si nanorods, no recoil was observed, whereas, on vertical nanorods and on nano-helices, the recoil was completed in approximately 16 ms. Interestingly, water droplets were observed to bounce on hydrophobic nanosprings with higher rebound time and COR than on vertical nanostructures. The elastic force arising from the difference between the equilibrium droplet shape and the deformed droplet shape drives the recoiling flow. The restoring force of the nanosprings may be responsible for the rebound of the water droplet; this may be seen by considering the droplet/nanospring surface as a coupled-spring system. As dust particles can be removed easily by the bouncing and rolling of droplets, there is enormous scope for multifunctional applications involving such nanospring arrays: self-cleaning windows, liquid-repellent exteriors, glass panels of solar cells, and antifouling agents for roof tiling.Funding
Author JPS acknowledges DST Nanomission, India project number DST/NM/NS/2019/289 for support. This work was supported by JST COI under Grant Number JPMJCE1307.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors thank Dr Kosuke Ishikawa of Kyoto University for helping us with the SEM observations.References
- X. Zhang, F. Shi, J. Niu, Y. Jiang and Z. Wang, J. Mater. Chem., 2008, 18, 621–633 RSC.
- X.-T. Zhang, O. Sato, M. Taguchi, Y. Einaga, T. Murakami and A. Fujishima, Chem. Mater., 2005, 17, 696–700 CrossRef CAS.
- I. P. Parkin and R. G. Palgrave, J. Mater. Chem., 2005, 15, 1689 RSC.
- R. Blossey, Nat. Mater., 2003, 2, 301–306 CrossRef CAS.
- T. Sun, L. Feng, X. Gao and L. Jiang, Acc. Chem. Res., 2005, 38(8), 644–652 CrossRef CAS.
- P. Roach, N. J. Shirtcliffe and M. I. Newton, Soft Matter, 2008, 4, 224 RSC.
- W. Barthlott, C. Neinhuis, H. Verlot and C. L. Schott, Planta, 1997, 202, 1–8 CrossRef CAS.
- A. B. D. Cassie and S. Baxter, Trans. Faraday Soc., 1944, 40, 546–551 RSC.
- D. Quéré, Rep. Prog. Phys., 2005, 68, 2495–2532 CrossRef.
- G. Dupeux, P. Bourrianne, Q. Magdelaine, C. Clanet and D. Quéré, Sci. Rep., 2014, 4, 5280 CrossRef CAS.
- C. Journet, S. Moulinet, C. Ybert, S. T. Purcell and L. Bocquet, Europhys. Lett. EPL, 2005, 71, 104–109 CrossRef CAS.
- C. R. Crick and I. P. Parkin, Chem. Commun., 2011, 47, 12059–12061 RSC.
- T. Deng, K. K. Varanasi, M. Hsu, N. Bhate, C. Keimel, J. Stein and M. Blohm, Appl. Phys. Lett., 2009, 94, 18–20 Search PubMed.
- A. Tuteja, W. Choi, J. M. Mabry, G. H. McKinley and R. E. Cohen, Proc. Natl. Acad. Sci. U.S.A., 2008, 105, 18200–18205 CrossRef CAS.
- Y. C. Hong and H. S. Uhm, Appl. Phys. Lett., 2006, 88, 244101 CrossRef.
- Y. C. Jung and B. Bhushan, Langmuir, 2008, 24, 6262–6269 CrossRef CAS.
- M. Callies, Y. Chen, F. Marty, A. Pépin and D. Quéré, Microelectron. Eng., 2005, 78–79, 100–105 CrossRef CAS.
- M. Reyssat, A. Pépin, F. Marty, Y. Chen and D. Quéré, Europhys. Lett. EPL, 2007, 74, 306–312 CrossRef.
- K. R. Khedir, G. K. Kannarpady, H. Ishihara, J. Woo, M. P. Asar, C. Ryerson and A. S. Biris, Appl. Surf. Sci., 2013, 279, 76–84 CrossRef CAS.
- Y. Lu, S. Sathasivam, J. Song, W. Xu, C. J. Carmalt and I. P. Parkin, J. Mater. Chem. A, 2014, 2, 12177 RSC.
- P. Tsai, S. Pacheco, C. Pirat, L. Lefferts and D. Lohse, Langmuir, 2009, 25, 12293–12298 CrossRef CAS.
- D. J. Lee, H. M. Kim, Y. S. Song and J. R. Youn, ACS Nano, 2012, 6, 7656–7664 CrossRef CAS.
- L. Chen, Z. Xiao, P. C. H. Chan and Y.-K. Lee, J. Micromech. Microeng., 2010, 20, 105001 CrossRef.
- L. Chen, Z. Xiao, P. C. H. Chan, Y. K. Lee and Z. Li, Appl. Surf. Sci., 2011, 257, 8857–8863 CrossRef CAS.
- D. Bartolo, F. Bouamrirene, É. Verneuil, A. Buguin, P. Silberzan and S. Moulinet, Europhys. Lett. EPL, 2006, 74, 299–305 CrossRef CAS.
- C. R. Crick and I. P. Parkin, J. Mater. Chem. A, 2013, 1, 799 RSC.
- D. Richard and D. Quéré, Europhys. Lett. EPL, 2000, 50, 769–775 CrossRef CAS.
- Y. Shen, J. Tao, H. Tao, S. Chen, L. Pan and T. Wang, ACS Appl. Mater. Interfaces, 2015, 7, 20972–20978 CrossRef CAS.
- Y. Liu, L. Moevius, X. Xu, T. Qian, J. M. Yeomans and Z. Wang, Nat. Phys., 2014, 10, 515–519 Search PubMed.
- T. M. Schutzius, S. Jung, T. Maitra, G. Graeber, M. Köhme and D. Poulikakos, Nature, 2015, 527, 82–85 CrossRef CAS.
- Y. Shen, J. Tao, H. Tao, S. Chen, L. Pan and T. Wang, Appl. Phys. Lett., 2015, 107, 111604 CrossRef.
- S. Kumar, P. Goel and J. P. Singh, Sens. Actuators, B, 2017, 241, 577–583 CrossRef CAS.
- M. Suzuki, W. Maekita, Y. Wada, K. Nagai, K. Nakajima, K. Kimura, T. Fukuoka and Y. Mori, Nanotechnology, 2008, 19, 265304 CrossRef.
- K. R. Khedir, G. K. Kannarpady, H. Ishihara, J. Woo, C. Ryerson and A. S. Biris, Langmuir, 2011, 27, 4661–4668 CrossRef CAS.
- D. P. Singh and J. P. Singh, Appl. Phys. Lett., 2013, 102, 243112 CrossRef.
- S. Kumar, P. Goel, D. P. Singh and J. P. Singh, Appl. Phys. Lett., 2014, 104, 023107 CrossRef.
- Y.-P. Zhao, D.-X. Ye, G.-C. Wang and T.-M. Lu, Nano Lett., 2002, 2, 351–354 CrossRef CAS.
- M. Malac, R. F. Egerton, M. J. Brett and B. Dick, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.--Process., Meas., Phenom., 1999, 17, 2671 CrossRef CAS.
- T. Karabacak, J. P. Singh, Y.-P. Zhao, G.-C. Wang and T.-M. Lu, Phys. Rev. B, 2003, 68, 125408 CrossRef.
- J. G. Gibbs, A. G. Mark, T.-C. Lee, S. Eslami, D. Schamel and P. Fischer, Nanoscale, 2014, 6, 9457–9466 RSC.
- M. Suzuki, K. Nakajima, K. Kimura, T. Fukuoka and Y. Mori, Anal. Sci., 2007, 23, 829–833 CrossRef CAS.
- S. Kumar, Y. Doi, K. Namura and M. Suzuki, ACS Appl. Bio Mater., 2020, 3, 3226–3235 CrossRef CAS.
- K. Namura, S. Imafuku, S. Kumar, K. Nakajima, M. Sakakura and M. Suzuki, Sci. Rep., 2019, 9, 1–9 CrossRef CAS.
- W. J. Khudhayer, R. Sharma and T. Karabacak, Nanotechnology, 2009, 20, 275302 CrossRef.
- J.-G. Fan, X.-J. Tang and Y.-P. Zhao, Nanotechnology, 2004, 15, 501–504 CrossRef CAS.
- D. P. Singh and J. P. Singh, J. Phys. Chem. C, 2011, 115, 11914–11919 CrossRef CAS.
- J.-G. Fan and Y.-P. Zhao, Appl. Phys. Lett., 2007, 90, 013102 CrossRef.
- C. Clanet, C. Béguin, D. Richard and D. Quéré, J. Fluid Mech., 2004, 517, 199–208 CrossRef.
- Y. Wang and S. Chen, Appl. Surf. Sci., 2015, 327, 159–167 CrossRef CAS.
- Y. Yonemoto and T. Kunugi, Sci. Rep., 2017, 7, 2362 CrossRef.
- M. Pasandideh-Fard, Y. M. Qiao, S. Chandra and J. Mostaghimi, Phys. Fluids, 1996, 8, 650–659 CrossRef CAS.
- R. Rioboo, M. Marengo and C. Tropea, Exp. Fluids, 2002, 33, 112–124 CrossRef.
- I. V. Roisman, R. Rioboo and C. Tropea, Proc. R. Soc. London, Ser. A, 2002, 458, 1411–1430 CrossRef CAS.
- K. K. Haller, D. Poulikakos, Y. Ventikos and P. Monkewitz, J. Fluid Mech., 2003, 490, 1–14 CrossRef.
- J. E. Field, Phys. Med. Biol., 1991, 36, 1475–1484 CrossRef CAS.
- K. Okumura, F. Chevy, D. Richard, D. Quéré and C. Clanet, EPL Europhys. Lett., 2003, 62, 237 CrossRef CAS.
- R. Cross, Am. J. Phys., 2000, 68, 1025–1031 CrossRef.
- R. Kaneko, T. Yukishita, T. Sumigawa and T. Kitamura, Thin Solid Films, 2020, 695, 137749 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Movies showing the water droplet dynamics on the samples, model for the rebound of the water droplet on vertically aligned nanorods, and spreading factor, as a function of We for VC, and NS up to We = 70. See DOI: 10.1039/d0na00544d |
| This journal is © The Royal Society of Chemistry 2021 |