Open Access Article
Open Access ArticleTheoretical insights into C–H bond activation of methane by transition metal clusters: the role of anharmonic effects†
Preeti
Bhumla
 *,
Manish
Kumar
*,
Manish
Kumar
 and
Saswata
Bhattacharya
and
Saswata
Bhattacharya
 *
*
Department of Physics, Indian Institute of Technology Delhi, New Delhi, India. E-mail: Preeti.Bhumla@physics.iitd.ac.in; saswata@physics.iitd.ac.in; Fax: +91 11 2658 2037; Tel: +91 11 2659 1359
First published on 16th November 2020
Abstract
In heterogeneous catalysis, the determination of active phases has been a long-standing challenge, as materials' properties change under operational conditions (i.e. temperature (T) and pressure (p) in an atmosphere of reactive molecules). As a first step towards materials design for methane activation, we study the T and p dependence of the composition, structure, and stability of metal oxide clusters in a reactive atmosphere at thermodynamic equilibrium using a prototypical model catalyst having wide practical applications: free transition metal (Ni) clusters in a combined oxygen and methane atmosphere. A robust methodological approach is employed, where the starting point is systematic scanning of the potential energy surface (PES) to obtain the global minimum structures using a massively parallel cascade genetic algorithm (cGA) at the hybrid density functional level. The low energy clusters are further analyzed to estimate their thermodynamic stability at realistic T, pO2 and pCH4 using ab initio atomistic thermodynamics (aiAT). To incorporate the anharmonicity in the vibrational free energy contribution to the configurational entropy, we evaluate the excess free energy of the clusters numerically by a thermodynamic integration method with ab initio molecular dynamics (aiMD) simulation inputs. By analyzing a large dataset, we show that the conventional harmonic approximation miserably fails for this class of materials, and capturing the anharmonic effects on the vibration free energy contribution is indispensable. The latter has a significant impact on detecting the activation of the C–H bond, while the harmonic infrared spectrum fails to capture this, due to the wrong prediction of the vibrational modes.
1 Introduction
Methane is the primary component of natural gas, which is one of the simplest, nearly ubiquitous, low-cost, clean and easily extractable energy sources found in nature.1–6 Additionally, methane is also a prominent greenhouse gas. Therefore, it is highly desirable to convert methane into valuable products.7 Synthesis gas (syngas, a mixture of CO and H2) production from methane is an important route for the effective utilization of abundant natural gas in producing methanol, liquid hydrocarbons, ammonia and dimethyl ether.8–10 The efficient activation of methane has been a major challenge as C–H bonds in methane possess high bond strength (4.5 eV), low polarizability and negligible electron affinity making it a least reactive hydrocarbon.11–13 Since methane is extremely inert, its conversion to chemical products is difficult. To circumvent this problem, a suitable catalyst must be developed. Hence, the catalytic conversion of methane is one of the most appealing fields of study in both academia and industry.14–26Numerous experimental and theoretical studies have established that the reactivity of small metal clusters (as catalysts) in the gas phase varies with the number of atoms.20,27–30 It has been found that reducing particle size in the cluster reveals the possibility of several interesting size effects.31–34 Particularly, transition metal (TM) clusters are well known for their efficient homogeneous and heterogeneous catalytic activity.35–40 This is primarily ascribed to the presence of partially occupied d-shells, which assist in exhibiting multiple oxidation states in their complexes.32,41–43 Note that the properties of a material change substantially in the operational environment, particularly in an atmosphere of reactive molecules. Under reaction conditions, the catalyst consists of a wide range of structures including different numbers of atoms with various oxidation states, all of which could be active to some extent in the catalytic reaction. As a result, some inevitable questions arise naturally, e.g., “what are the species present in the real catalyst and what are their structures?”, and “how do those catalysts change their structure and catalytic properties upon adsorption of different ligand molecules?”.
In order to address the above questions in the context of heterogeneous catalysis, one of the most important aspects is to identify the active species and to determine the structure of the catalyst.44 In light of this, there is a justified need to provide theoretical guidance to experiments on the stoichiometry and stability of the clusters under realistic conditions, i.e. at a finite temperature (T) and pressure (p). To better understand the situation theoretically, we consider a prototypical model system of nickel (Ni4, which has already been experimentally synthesized and has high selectivity45–47) in a reactive atmosphere of O2 and CH4 gas molecules under realistic conditions. Note that Ni-based catalysts, owing to their low cost, high selectivity and high activity, have been extensively employed experimentally in catalysis in the past.48–53 Typically, in the presence of a reactive atmosphere, clusters adsorb surrounding gas molecules and form intermediate phases [Ni4Ox(CH4)y] at thermodynamic equilibrium. The latter generally proves to be an active material for various applications in the field of heterogeneous catalysis. However, determining such stable phases (stoichiometries) theoretically has never been an easy task. This requires a comprehensive understanding of all the possible structures of [Ni4Ox(CH4)y] and their thermodynamic stability at a given T and p. This demands a robust methodological approach that integrates various levels of theory combined into one multi-scale simulation.54 Moreover, at a finite temperature, anharmonicity may play a role in molecular vibrations and quantum oscillations. The atoms in a molecule or a solid vibrate around their equilibrium positions. At low temperature, when these vibrations have smaller amplitudes, they can be described by harmonic oscillators. However, when the vibrational amplitudes are large, for example at high temperatures, anharmonicity becomes important. Studying vibrating anharmonic systems using quantum mechanics is a computationally demanding task because anharmonicity not only makes the potential experienced by each atom (oscillator) complicated, but also introduces coupling between the oscillators. It is, therefore, more feasible to use first-principles methods such as those within the framework of density functional theory (DFT)55,56 to map the anharmonic potential experienced by the atoms. Accurate anharmonic vibrational energies can then be obtained numerically from first-principles calculations. This helps in determining the correct thermodynamic stability of the active species (i.e. catalysts) responsible for driving a favourable reaction kinetics.
In this article, we have investigated the role of environment [i.e., temperature (T), partial pressure of oxygen (pO2) and partial pressure of methane (pCH4)] to understand the thermodynamic stability of different configurations of Ni4Ox(CH4)y (0 ≤ x ≤ 8, 0 ≤ y ≤ 3) clusters in a reactive atmosphere of O2 and CH4 molecules. As a first step, a systematic scanning of the potential energy surface (PES) is done via a cascade genetic algorithm (cGA)57–59 approach to obtain the global minimum (GM) configurations of Ni4Ox(CH4)y clusters. Subsequently, we employ ab initio atomistic thermodynamics (aiAT)57,60,61 in the framework of DFT to determine the thermodynamic stability of those configurations under operational conditions. To incorporate the anharmonicity in the vibrational free energy contribution to the configurational entropy, we evaluate the excess free energy of the clusters numerically by a thermodynamic integration method62 with ab initio molecular dynamics (aiMD) simulation inputs. By analyzing a large dataset, we try to establish the important contribution of vibrational free energy to predict potential catalysts for C–H bond activation. We have thoroughly addressed the contribution of vibrational free energy using harmonic approximation and compared the same after inclusion of anharmonic effects at a moderately high temperature (relevant for the catalysis). We further validate our findings through infrared (IR) spectrum analysis.
2 Methodology
We proceed very systematically to solve this problem – (i) the first step is an extensive and efficient scanning of the potential energy surface (PES) by an efficient well-established global structure optimization procedure; (ii) subsequently, the influence of the experimental conditions (here, temperature and pressure of a reactive atmosphere) is included. For the latter, we have shown three suites of three different approaches to establish the importance of accurate estimation of the contribution of free energy of vibration in determining the thermodynamic stability of the concerned material.2.1 Efficient scanning of the potential energy surface
As a first step, we have generated a large data set of Ni4Ox(CH4)y (0 ≤ x ≤ 8, 0 ≤ y ≤ 3) clusters. Here, we have varied the value of x and y (x = no. of oxygen atoms, y = no. of CH4 molecules) from zero to the saturation value, which means that x and y values are increased with all possible combinations until no more O atoms/CH4 molecules can be adsorbed by the cluster. To do this, we used a massively parallel cascade genetic algorithm (cGA) to thoroughly scan the PES in determining all possible low-energy structures including the global minimum (GM).57–59 GA is a global optimization technique based on the principles of natural evolution. In general, this algorithm includes the following steps – an initial population is formed with a group of individuals, created as absolutely random. The individuals in the running population are then evaluated via a fitness function, i.e. lower energy structures have a higher fitness function and vice versa. This algorithm aims to optimize this (scalar) fitness function. Two individuals (i.e. structures) are then selected at random, with their respective weights based on their fitness – i.e. the higher the fitness, the higher the chance of being selected. These individuals then ‘mate’, i.e., they are combined to create one candidate offspring that can in turn be ‘mutated’ randomly. In the next selection for ‘mating’, this new individual is included in the pool of candidates and can be selected on the basis of its fitness. This algorithm continues until a convergence criterion is met.‡The term “cascade” means a multi-stepped algorithm, where successive steps employ a higher level of theory and each succeeding level takes information obtained at its immediate lower level. Typically, a cGA algorithm starts with a classical force field and goes up to density functional theory (DFT) with hybrid exchange and correlation (εxc) functionals. Note that the prototypical model system that we have chosen here is a representative of a class of systems for which very accurate evaluation of the PES is mandatory for meaningful experimental predictions. Incidentally, we have already explained that hybrid εxc functionals are required58 since, as we have reported, the PBE εxc functional63 highly overestimates the stability of clusters containing larger concentrations of O atoms.30,44,58,64 This results in a qualitatively wrong prediction of O2 adsorption for O-rich cases. Such behavior is not confirmed by more advanced hybrid εxc functionals [e.g. HSE06,65 PBE066]. Moreover, the spin states of the clusters are also different as found by PBE and PBE0/HSE06 εxc functionals. However, doing everything at the level of high-accuracy hybrid εxc functionals is computationally very expensive. This is why a hierarchical scheme for an efficient scanning of the PES (starting from a classical force field and going up to DFT with hybrid εxc) is thoroughly benchmarked and proposed in order to avoid wasting time and computational resources with high-accuracy calculations in uninteresting regions of the configurational phase space [see details in ref. 57–59].
In view of this, in this cascade GA algorithm, after preparing a crude database of structures using GA at the level of classical force field (ReaxFF), we start our DFT-GA. In DFT-GA, we optimize the structures with PBE but the energetics are computed with an advanced hybrid εxc functional to evaluate the fitness function of the cluster correctly. This is due to the reason that in optimization of the structures, we basically compute the forces amongst atoms, which are determined by the gradient of energy i.e. precisely the differences of energies in order to compute the derivatives. As a result, the electron's self-interaction error present in the PBE εxc functional gets canceled out. Therefore, there is not much difference in the structures that we get from PBE and/or HSE06 εxc functionals. In addition, the HSE06 εxc functional is computationally much more expensive than the PBE εxc functional making the PBE εxc functional an efficient choice for structural optimization in our system. However, to evaluate the fitness function PBE energetics cannot be used. Thus we need to perform additional single point energy calculations at the level of hybrid εxc on top of the PBE optimized structure. We have incorporated all these settings in cGA implementation. For details of this cGA implementation, accuracy and validation, we recommend our previous studies as given in ref. 57–59.
All DFT calculations are performed using the FHI-aims code, employing an all-electron code with numerical atom centered basis sets.67 Considering the fact that first-principles based calculations are computationally demanding, lighter (viz. light settings with a tier 2 basis set67) DFT settings are implemented in the cGA to find the global minimum structures. The atomic zero-order regular approximation (ZORA) is used for the scalar relativistic correction.68 The vdW correction is calculated according to the Tkatchenko–Scheffler scheme.69 The low energy structures obtained from the cGA are further optimized with PBE at higher level settings (viz. tight settings with a tier 2 basis set67). The atomic forces are converged up to 10−5 eV Å−1. Finally, the total single point energy is calculated on top of this optimized structure using the HSE06 hybrid εxc functional (see further details for validation of εxc functionals in Section I in the ESI†).
2.2 Accurate estimation of free energy of formation
After the cGA search is completed, with each of these selected structures (within an energy window of 1 eV from the GM), we have performed calculations of the harmonic vibrations using finite differences of the analytic forces. This step is necessary to achieve the following two objectives. The immediate purpose is to identify the unstable structures, i.e., those having imaginary vibrational frequencies. The other objective is to note down the frequencies to determine the vibrational free energy (Fvib)57,60 within harmonic approximations. Next, to capture the anharmonic effects using a thermodynamic integration method,62 we have carried out ab initio molecular dynamics (aiMD) simulations for 8 ps each at different temperatures viz. T = 50 K, 100 K, 300 K, 600 K and 800 K in a canonical ensemble (i.e., one with constant temperature and volume). We have employed the velocity Verlet scheme70 for the integration of Newtonian equations with a time-step of 1 fs and the temperature of the system is controlled using the Nose–Hoover thermostat71 (for details see Section II in the ESI†). In the following section this whole procedure is explained in steps to determine the thermodynamically stable components at different levels of accuracy to estimate the free energy of formation of the candidate structures under realistic conditions.2.3 Determination of stable phases of the [Ni4Ox(CH4)y] clusters
After obtaining all low energy isomers corresponding to different configurations of Ni4Ox(CH4)y clusters from cGA, we study their thermodynamic stability under realistic conditions using the aiAT approach. Here, we assume that there is an exchange of atoms between the system (Ni4 cluster) and the surroundings (consisting of O2 and CH4 gas molecules) at finite temperatures and pressures, via the following reaction: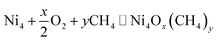 | (1) |
Note that adsorption and desorption of O2, H2, H2O and CO2 moieties are also taken into account by cGA, where all sorts of mutation and crossover operations take place giving rise to all possible structural moieties. Therefore even if the configuration stoichiometrically reads as Ni4Ox(CH4)y, it does include all possible moieties.
The Gibbs free energy of formation (ΔG) of all the Ni4Ox(CH4)y structures is then evaluated as a function of T, pO2 and pCH4 by applying aiAT. The composition (for a particular value of x and y) having the minimum Gibbs free energy of formation is most likely to be found in the experiments at a specific T, pO2 and pCH4. ΔG(T,p) is therefore calculated as per the following equation:
| ΔG(T,pO2,pCH4) = FNi4Ox(CH4)y(T) − FNi4(T) − x × μO(T,pO2) − y × μCH4(T,pCH4) | (2) |
The Helmholtz free energies FNi4Ox(CH4)y(T) and FNi4(T) consist of the respective total DFT energy along with their free energy contributions from translational, rotational, vibrational, symmetry and spin-degeneracy terms.57,60 The contributions of different terms in the expression of Helmholtz free energies F are given as follows:57
| F = Ftrans + Frot + Fvib + Fsymm + Fspin + EDFT | (3) |
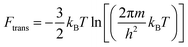 | (4) |
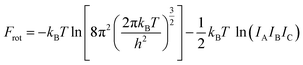 | (5) |
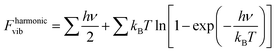 | (6) |
Fsymmetry = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ σ | (7) |
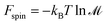 | (8) |
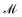 is the spin multiplicity. kB, h, and EDFT are respectively the Boltzmann constant, Planck constant, and total DFT energy.
is the spin multiplicity. kB, h, and EDFT are respectively the Boltzmann constant, Planck constant, and total DFT energy.
It has been noticed that the total DFT energy is the dominant term, which is evaluated in its ground state configuration with respect to both geometry and spin state. The rest of the terms, except the contribution from the vibrational degrees of freedom (Fvib), are usually considered as invariant since they do not change much (and even if they change, the order is insignificant) due to the dependence on most of the constant terms viz. mass, moment of inertia, universal constants, etc. However, the vibrational contribution is dependent on the frequencies of vibration, which are unique for a given structure. Thus, the Helmholtz free energy can be written as follows:
| F(T) = EDFT + Fvib + Δ | (9) |
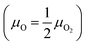 and a methane molecule, respectively. The relation of μO(T,pO2) with T and pO2 is governed by the ideal (diatomic) gas approximation. The expression is as follows:57
and a methane molecule, respectively. The relation of μO(T,pO2) with T and pO2 is governed by the ideal (diatomic) gas approximation. The expression is as follows:57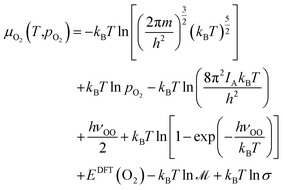 | (10) |
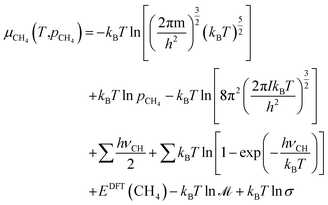 | (11) |
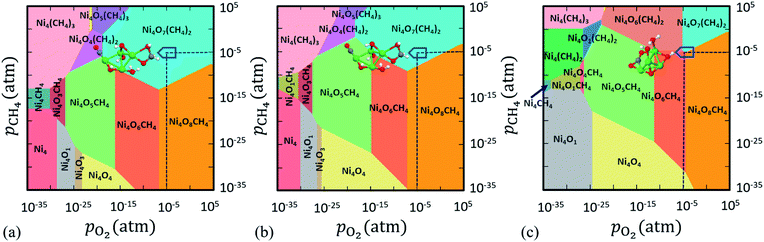 | ||
| Fig. 1 2D projection of the 3D phase diagram obtained for Ni4Ox(CH4)y clusters in the reactive atmosphere of O2 and CH4. In this plot ΔG(T,p) is computed when (a) only DFT total energies are included, (b) DFT + Fharmonicvib are included and (c) DFT + Fanharmonicvib are included to compute F(T) of the respective configurations as shown in eqn (2). Colored regions show the most stable compositions in a wide range of pressure at T = 800 K. | ||
3 Results
3.1 Comparing the role of Fvib in ΔG(T,p): importance of capturing anharmonic effects
Herein, we have implemented a suite of three state-of-the-art techniques to compute ΔG(T,p). The first one is without any explicit contribution of Fvib (as in eqn (9)), i.e. only the total DFT energy (EDFT) of the cluster with and without ligands is considered (see Fig. 1a). In the second case, we duly consider Fvib but up to harmonic approximation to calculate ΔG(T,p). Fharmonicvib is computed using eqn (6). Note that after adding Fharmonicvib with EDFT (as in eqn (9)), a new phase is introduced along with slight rearrangement of the existing phases, especially near the boundary region of competing configurations (see Fig. 1b). However, despite some small changes in Fig. 1a and b, we do not see any significant difference to identify the most stable phases in the experimentally realistic pressure range. In this region, Ni4O6CH4, Ni4O7(CH4)2 and Ni4O8CH4 are the stable phases and if we look at the region where pO2 = pCH4 = 10−5 atm (T = 800 K), Ni4O7(CH4)2 turns out to be the most stable phase (see Fig. 1a and b), irrespective of whether Fharmonicvib is taken into consideration or not.Now here, it is assumed that at T = 800 K, the oscillations are constrained to vibrate at a harmonic potential. However, the real system does not necessarily follow this assumption. And if so, the real anharmonic potential can be very different from the harmonic potential. In such case, the expression for Fvib can vary from one configuration to the other.
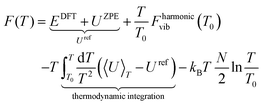
Therefore, in an attempt to refine the expression of ΔG(T,p) at finite T,p, we include anharmonic effects in the PES (see Fig. 1c). In order to quantitatively account for the anharmonic effects, we perform the thermodynamic integration62 taking input from aiMD simulations to evaluate the excess free energy of clusters. Here, we have assumed that at low T (e.g. 10 K), neither harmonic nor anharmonic potentials diverge much. Taking such low T as our reference state, the Helmholtz free energy F(T) is calculated according to the following equation (for a detailed derivation, see Section IV in the ESI†):
 | (12) |
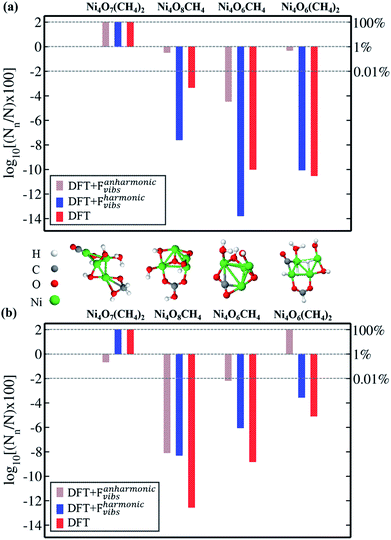
To clearly examine the relative probability of all the competing isomers simultaneously, we have estimated the probability of occurrence of all (meta)stable phases using all three methods (viz. DFT, DFT + Fharmonicvib and DFT + Fanharmonicvib) under different reaction conditions. It is calculated using the following equation (see the detailed derivation in Section V of the ESI†):
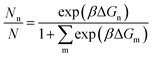 | (13) |
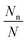 is the probability of occurrence of the type-n configuration.73 ΔGn is the Gibbs free energy of formation of the type-n configuration. As the range of
is the probability of occurrence of the type-n configuration.73 ΔGn is the Gibbs free energy of formation of the type-n configuration. As the range of 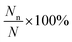 is significantly large, we have taken the logarithm of the above equation in the plots (see Fig. 2). Therefore, the maximum possible value on the y-axis is ∼2 when Nn ≈ N; i.e. type-n is the most dominant configuration. In Fig. 2a, we can clearly see by all three methods that the first structure [viz. Ni4O7(CH4)2] is most likely to be stable. But after that, for the next three structures (viz. Ni4O8CH4, Ni4O6CH4 and Ni4O6(CH4)2), DFT + Fharmonicvib and DFT + Fanharmonicvib work counter to each other. Moreover, if we see Fig. 2b, the situation is even worse and inclusion of DFT + Fanharmonicvib is absolutely essential as both DFT and DFT + Fharmonicvib find different structures to be thermodynamically more stable and vice versa.
is significantly large, we have taken the logarithm of the above equation in the plots (see Fig. 2). Therefore, the maximum possible value on the y-axis is ∼2 when Nn ≈ N; i.e. type-n is the most dominant configuration. In Fig. 2a, we can clearly see by all three methods that the first structure [viz. Ni4O7(CH4)2] is most likely to be stable. But after that, for the next three structures (viz. Ni4O8CH4, Ni4O6CH4 and Ni4O6(CH4)2), DFT + Fharmonicvib and DFT + Fanharmonicvib work counter to each other. Moreover, if we see Fig. 2b, the situation is even worse and inclusion of DFT + Fanharmonicvib is absolutely essential as both DFT and DFT + Fharmonicvib find different structures to be thermodynamically more stable and vice versa.
Next, we show two important applications of these findings by computing the IR spectra of two test cases: (i) Ni4O6(CH4)2 and (ii) Ni4O7(CH4)2.
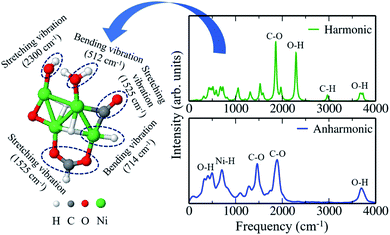
3.2 Ni4O6(CH4)2 cluster: harmonic IR vs. anharmonic IR
IR spectroscopy covers the infrared region of the electromagnetic spectrum with frequencies ranging from 4000 cm−1 to 40 cm−1.74–78 In IR spectroscopy, specific frequencies are absorbed by the molecules which are characteristic of their structure. Here, we have simulated the IR spectra of one of the clusters, viz. Ni4O6(CH4)2, that are explicitly stable on including the anharmonic contribution to the free energy, to determine its characteristic vibrational normal modes. For this, we have run 8 ps aiMD simulation in the canonical ensemble with the Bussi–Donadio–Parrinello (BDP)79 thermostat. From Fig. 3, we notice significant dissimilarities between the harmonic and anharmonic IR spectra of Ni4O6(CH4)2. Aside from the usual difference in peak intensities, the O–H stretching mode as per harmonic IR analysis near 2300 cm−1 (see Fig. 3 upper panel) is just a negligible hump in the anharmonic IR spectrum (see Fig. 3 lower panel). Similarly, the C–H stretching mode at around 3000 cm−1 also does not contribute to the anharmonic IR spectrum. Hence, it is evident that there is a fundamental difference in the characteristic frequencies of vibration of this structure when computed with harmonic approximation and after capturing the anharmonic effects. As a result, they contribute differently to the free energy of vibration. This makes Ni4O6(CH4)2 stable in the anharmonic case, but unstable under the harmonic approximation. Note that we have taken just a prototypical model system here viz. Ni4 cluster to study its stable phases under the reactive atmosphere of O2 and CH4. Nevertheless, this model system is relevant and sufficient for conveying the underlying message that there is a high chance of leaving important stable phases of the catalyst while ignoring the anharmonic effects under reaction conditions.3.3 Ni4O7(CH4)2 cluster and C–H bond activation
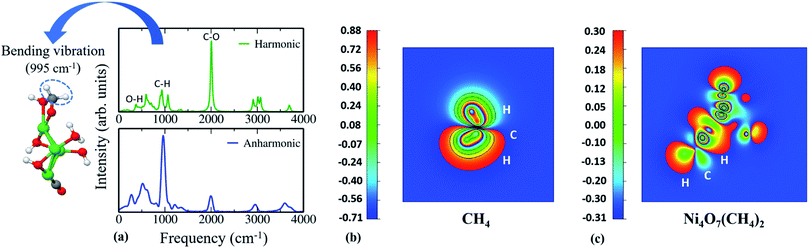
Apart from the above important facts, we note that incorporation of anharmonic effects helps in predicting the potential catalyst for C–H bond activation. For this, we have considered a test case, viz. Ni4O7(CH4)2 cluster, which is stable in all three cases as shown in Fig. 1a–c. We plotted its IR spectra (harmonic vs. anharmonic) and compared them in Fig. 4a. From Fig. 4a, we notice that O–H stretching presents significant anharmonic red-shifts in comparison to that of the harmonic case at around 273 cm−1. These red-shift corrections lead to a change in the IR spectrum shape due to a reorganization of the vibrational modes. Primarily, we observe some remarkable dissimilarities between harmonic and anharmonic IR spectra, e.g., the intensity of the C–O stretching peak has reduced significantly after the inclusion of anharmonic effects. Moreover, in the anharmonic IR spectrum, we find an intense peak at around 995 cm−1 corresponding to the C–H bending vibration. This type of highly intense IR absorption is due to the change in dipole moment that occurs during a vibration, especially when the bond is highly polar in nature so that its dipole moment changes considerably as the bond stretches. However, the harmonic IR spectrum completely fails to capture this information. To validate this enhanced dipolar interaction in this structure, we have plotted the charge density of the Ni4O7(CH4)2 cluster and compared it with that of CH4 (see Fig. 4b and c). To perform the charge density contour analysis, we have plotted the electron charge density for CH4 and the Ni4O7(CH4)2 cluster for the electronic levels near the respective Highest Occupied Molecular Orbital (HOMO). The constant slicing plane is chosen such that both the C and H atoms of the C–H bond are covered. The value of electron charge density varies from a maximum (red color) to a minimum (blue color). Now, if we pay attention to the nature of the C–H bond in either case, we can clearly see the difference in charge localization. In conventional CH4, the C–H bond is purely covalent, which makes it rather inert to be functionalized easily. However, in the Ni4O7(CH4)2 cluster, the C–H bond is very polar with the localized charge on C and H, respectively. This unusual localization of charge in the C–H bond gives rise to enhanced dipolar interactions (see Fig. 4c), and as a consequence of this, Ni4 is expected to be a reliable catalyst in activating the C–H bonds in methane. It should be noted that there are indeed various other factors that also play an important part to confirm whether the catalyst is good for C–H bond activation or not and finding them needs further in-depth study through performing Nudged Elastic Band (NEB) calculations followed by kinetic Monte Carlo (kMC) simulations. But prior to that, this type of sharp peak of C–H stretching mode helps to identify possible structures for further analysis. However, if this entire analysis is done using only harmonic approximation, this stable configuration would not even be considered for C–H bond activation as its peak in the IR spectrum is pretty small and delocalized. This further confirms the importance of capturing the anharmonic contribution to this class of materials.4 Conclusions
In summary, we have carried out state-of-the-art hybrid density functional theory (DFT) calculations combined with ab initio atomistic thermodynamics (aiAT) and ab initio molecular dynamics (aiMD) simulations to see how the thermodynamic stability of TM oxide clusters changes as a function of temperature and pressure (T, pO2 and pCH4). While finding the accurate thermodynamic stability, we have seen that the inclusion of anharmonicity introduces new stable phases that are entirely ignored by DFT and DFT + Fharmonicvib. This has a significant impact on detecting the activation of the C–H bond, where the harmonic IR is unable to capture the correct vibrational modes. The key point that emerges out of these studies is that to understand the activation of the stable C–H bonds in methane using a metal oxide cluster as a catalyst, capturing the anharmonic effects is essential for this class of materials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. B. acknowledges UGC, India, for the junior research fellowship [1392/(CSIR-UGC NET JUNE 2018)]. M. K. acknowledges CSIR, India, for the senior research fellowship [grant no. 09/086(1292)/2017-EMR-I]. S. B. acknowledges the financial support from SERB under a core research grant (grant no. CRG/2019/000647). P. B. acknowledges Shikha Saini for helpful discussions. We acknowledge the High Performance Computing (HPC) facility at IIT Delhi for computational resources.Notes and references
- H. Prats, R. A. Gutierrez, J. J. Pinero, F. Vines, S. T. Bromley, P. J. Ramirez, J. A. Rodriguez and F. Illas, J. Am. Chem. Soc., 2019, 141, 5303–5313 CrossRef CAS PubMed.
- E. D. Goodman, A. A. Latimer, A.-C. Yang, L. Wu, N. Tahsini, F. Abild-Pedersen and M. Cargnello, ACS Appl. Nano Mater., 2018, 1, 5258–5267 CrossRef CAS.
- P. Pal, R. K. Singha, A. Saha, R. Bal and A. B. Panda, J. Phys. Chem. C, 2015, 119, 13610–13618 CrossRef CAS.
- J. Su, L. Cao, L. Li, J. Wei, G. Li and Y. Yuan, Nanoscale, 2013, 5, 9720–9725 RSC.
- B. C. Enger, R. Lodeng and A. Holmen, Appl. Catal., A, 2008, 346, 1–27 CrossRef CAS.
- S. H. Leenders, R. Gramage-Doria, B. de Bruin and J. N. Reek, Chem. Soc. Rev., 2015, 44, 433–448 RSC.
- K. Aasberg-Petersen, J.-H. B. Hansen, T. Christensen, I. Dybkjaer, P. S. Christensen, C. S. Nielsen, S. W. Madsen and J. Rostrup-Nielsen, Appl. Catal., A, 2001, 221, 379–387 CrossRef CAS.
- S. Das, M. Sengupta, A. Bag, M. Shah and A. Bordoloi, Nanoscale, 2018, 10, 6409–6425 RSC.
- P. Tang, Q. Zhu, Z. Wu and D. Ma, Energy Environ. Sci., 2014, 7, 2580–2591 RSC.
- H. T. Luk, C. Mondelli, D. C. Ferre, J. A. Stewart and J. Perez-Ramrez, Chem. Soc. Rev., 2017, 46, 1358–1426 RSC.
- Y.-X. Zhao, Z.-Y. Li, Y. Yang and S.-G. He, Acc. Chem. Res., 2018, 51, 2603–2610 CrossRef CAS PubMed.
- H.-F. Li, Y.-X. Zhao, Z. Yuan, Q.-Y. Liu, Z.-Y. Li, X.-N. Li, C.-G. Ning and S.-G. He, J. Phys. Chem. Lett., 2017, 8, 605–610 CrossRef CAS PubMed.
- H.-F. Li, Z.-Y. Li, Q.-Y. Liu, X.-N. Li, Y.-X. Zhao and S.-G. He, J. Phys. Chem. Lett., 2015, 6, 2287–2291 CrossRef CAS PubMed.
- M. Fleys, Y. Simon, D. Swierczynski, A. Kiennemann and P.-M. Marquaire, Energy Fuels, 2006, 20, 2321–2329 CrossRef CAS.
- M. Gil-Calvo, C. Jimenez-Gonzalez, B. de Rivas, J. I. Gutierrez-Ortiz and R. Lopez-Fonseca, Ind. Eng. Chem. Res., 2017, 56, 6186–6197 CrossRef CAS.
- S. Bhavsar and G. Veser, RSC Adv., 2014, 4, 47254–47267 RSC.
- D. A. Hickman and L. D. Schmidt, Science, 1993, 259, 343–346 CrossRef CAS PubMed.
- D. Neumann, M. Kirchhoff and G. Veser, Catal. Today, 2004, 98, 565–574 CrossRef CAS.
- A. Ashcroft, A. Cheetham, J. a. Foord, M. Green, C. Grey, A. Murrell and P. Vernon, Nature, 1990, 344, 319–321 CrossRef CAS.
- S. Bhattacharya, G. Wu, C. Ping, Y. P. Feng and G. P. Das, J. Phys. Chem. B, 2008, 112, 11381–11384 CrossRef CAS PubMed.
- P. D. Vernon, M. L. Green, A. K. Cheetham and A. T. Ashcroft, Catal. Lett., 1990, 6, 181–186 CrossRef CAS.
- R. C. Ramaswamy, P. A. Ramachandran and M. P. Dudukovic, Ind. Eng. Chem. Res., 2007, 46, 8638–8651 CrossRef CAS.
- Y. H. Hu and E. Ruckenstein, Ind. Eng. Chem. Res., 1998, 37, 2333–2335 CrossRef CAS.
- S. Bharadwaj and L. Schmidt, Fuel Process. Technol., 1995, 42, 109–127 CrossRef CAS.
- A. Hellman, A. Resta, N. M. Martin, J. Gustafson, A. Trinchero, P.-A. Carlsson, O. Balmes, R. Felici, R. van Rijn, J. W. M. Frenken, J. N. Andersen, E. Lundgren and H. Gronbeck, J. Phys. Chem. Lett., 2012, 3, 678–682 CrossRef CAS PubMed.
- P. M. Hundt, M. E. van Reijzen, H. Ueta and R. D. Beck, J. Phys. Chem. Lett., 2014, 5, 1963–1967 CrossRef CAS PubMed.
- A. Bhattacharya and S. Bhattacharya, J. Phys. Chem. Lett., 2015, 6, 3726–3730 CrossRef CAS PubMed.
- M. T. Reetz and W. Helbig, J. Am. Chem. Soc., 1994, 116, 7401–7402 CrossRef CAS.
- V. Sudheeshkumar, K. O. Sulaiman and R. W. Scott, Nanoscale Adv., 2020, 2, 55 RSC.
- S. Bhattacharya, B. H. Sonin, C. J. Jumonville, L. M. Ghiringhelli and N. Marom, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 241115 CrossRef.
- T. M. Soini and N. Rausch, Phys. Chem. Chem. Phys., 2015, 17, 28463–28483 RSC.
- J. Kauhler, J.-H. Chang and M.-H. Whangbo, J. Am. Chem. Soc., 2005, 127, 2277–2284 CrossRef PubMed.
- E. Roduner, Chem. Soc. Rev., 2006, 35, 583–592 RSC.
- L. Li, A. H. Larsen, N. A. Romero, V. A. Morozov, C. Glinsvad, F. Abild-Pedersen, J. Greeley, K. W. Jacobsen and J. K. Nørskov, J. Phys. Chem. Lett., 2013, 4, 222–226 CrossRef CAS PubMed.
- J. D. Aiken III and R. G. Finke, J. Mol. Catal. A: Chem., 1999, 145, 1–44 CrossRef.
- C. L. Hill and C. M. Prosser-McCartha, Coord. Chem. Rev., 1995, 143, 407–455 CrossRef CAS.
- H. Guo, P. Sautet and A. N. Alexandrova, J. Phys. Chem. Lett., 2020, 11, 3089–3094 CrossRef CAS PubMed.
- H. Lee, X. Wu and L. Sun, Nanoscale, 2020, 12, 4187 RSC.
- S. Zhu, X. Lian, T. Fan, Z. Chen, Y. Dong, W. Weng, X. Yi and W. Fang, Nanoscale, 2018, 10, 14031–14038 RSC.
- D. Wang and D. Astruc, Chem. Soc. Rev., 2017, 46, 816–854 RSC.
- A. Ruiz Puigdollers, P. Schlexer, S. Tosoni and G. Pacchioni, ACS Catal., 2017, 7, 6493–6513 CrossRef CAS.
- M. T. Greiner, L. Chai, M. G. Helander, W.-M. Tang and Z.-H. Lu, Adv. Funct. Mater., 2012, 22, 4557–4568 CrossRef CAS.
- S. Bhattacharya and G. P. Das, in First-Principles Design of Complex Chemical Hydrides as Hydrogen Storage Materials, Taylor and Francis Group, 2013, ch. 20, pp. 424–439 Search PubMed.
- S. Saini, P. Basera, E. Arora and S. Bhattacharya, J. Phys. Chem. C, 2019, 123, 15495–15502 CrossRef CAS.
- P. L. Rodriguez Kessler and A. R. Rodriguez Dominguez, J. Phys. Chem. C, 2015, 119, 12378–12384 CrossRef CAS.
- A. Sieber, C. Boskovic, R. Bircher, O. Waldmann, S. T. Ochsenbein, G. Chaboussant, H. U. Güdel, N. Kirchner, J. van Slageren, W. Wernsdorfer, A. Neels, H. Stoeckli-Evans, S. Janssen, F. Juranyi and H. Mutka, Inorg. Chem., 2005, 44, 4315–4325 CrossRef CAS PubMed.
- J. Ye, L. Gagliardi, C. J. Cramer and D. G. Truhlar, J. Catal., 2017, 354, 278–286 CrossRef CAS.
- S. Z. Tasker, E. A. Standley and T. F. Jamison, Nature, 2014, 509, 299–309 CrossRef CAS PubMed.
- W. Keim, Angew. Chem., Int. Ed. Engl., 1990, 29, 235–244 CrossRef.
- E. Monachino, M. Greiner, A. Knop-Gericke, R. Schlogl, C. Dri, E. Vesselli and G. Comelli, J. Phys. Chem. Lett., 2014, 5, 1929–1934 CrossRef CAS PubMed.
- S. De, J. Zhang, R. Luque and N. Yan, Energy Environ. Sci., 2016, 9, 3314–3347 RSC.
- F. Li, D. R. MacFarlane and J. Zhang, Nanoscale, 2018, 10, 6235–6260 RSC.
- P. Bothra and S. K. Pati, Nanoscale, 2014, 6, 6738–6744 RSC.
- M. Andersen, C. Panosetti and K. Reuter, Front. Chem., 2019, 7, 202 CrossRef CAS PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- S. Bhattacharya, S. V. Levchenko, L. M. Ghiringhelli and M. Scheffler, New J. Phys., 2014, 16, 123016 CrossRef.
- S. Bhattacharya, S. V. Levchenko, L. M. Ghiringhelli and M. Scheffler, Phys. Rev. Lett., 2013, 111, 135501 CrossRef PubMed.
- S. Bhattacharya, B. H. Sonin, C. J. Jumonville, L. M. Ghiringhelli and N. Marom, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 241115 CrossRef.
- K. Reuter, C. Stampf and M. Scheffler, in AB Initio Atomistic Thermodynamics and Statistical Mechanics of Surface Properties and Functions, ed. S. Yip, Springer Netherlands, Dordrecht, 2005, pp. 149–194 Search PubMed.
- A. Bhattacharya and S. Bhattacharya, Phys. Rev. B, 2016, 94, 094305 CrossRef.
- D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic Press, San Diego, 2nd edn, 2002, pp. 167–200 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Saini, D. Sarker, P. Basera, S. V. Levchenko, L. M. Ghiringhelli and S. Bhattacharya, J. Phys. Chem. C, 2018, 122, 16788–16794 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS.
- E. v. Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- N. S. Martys and R. D. Mountain, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 3733–3736 CrossRef CAS.
- D. J. Evans and B. L. Holian, J. Chem. Phys., 1985, 83, 4069–4074 CrossRef CAS.
- E. Arora, S. Saini, P. Basera, M. Kumar, A. Singh and S. Bhattacharya, J. Phys. Chem. C, 2019, 123, 62–69 CrossRef CAS.
- S. Bhattacharya, D. Berger, K. Reuter, L. M. Ghiringhelli and S. V. Levchenko, Phys. Rev. Mater., 2017, 1, 071601 CrossRef.
- B. Stuart, in Infrared Spectroscopy, American Cancer Society, 2015, pp. 1–18 Search PubMed.
- W. Z. Weng, M. S. Chen, Q. G. Yan, T. H. Wu, Z. S. Chao, Y. Y. Liao and H. L. Wan, Catal. Today, 2000, 63, 317–326 CrossRef CAS.
- V. L. Sushkevich, R. Verel and J. A. van Bokhoven, Angew. Chem., Int. Ed., 2020, 59, 910–918 CrossRef CAS PubMed.
- S. Fouladvand, M. Skoglundh and P.-A. Carlsson, Catal. Sci. Technol., 2014, 4, 3463–3473 RSC.
- X. Wang, N. M. Martin, J. Nilsson, S. Carlson, J. Gustafson, M. Skoglundh and P.-A. Carlsson, Catalysts, 2018, 8, 545 CrossRef.
- J. Ruiz-Franco, L. Rovigatti and E. Zaccarelli, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 80 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Details of choice of functionals, temperature control using Nose–Hoover thermostat, contribution of Fvib at different temperatures, thermodynamic integration and probability of occurence of different configurations. See DOI: 10.1039/d0na00669f |
| ‡ First, we have provided typically about 50–100 random structures in the initial pool of cGA to start the scanning. Clusters with more atoms were scanned for more isomers owing to their more complex PES to determine the GM structure. Typically, for a PES with 15+ atoms, we have scanned about 800–1000 structures. However for a system with less than 10 atoms, we could figure out the minimum after scanning ∼500 structures. For even smaller clusters (less than 5 atoms), this number is even smaller. We have taken the best 20–30 structures having low energies from the total pool of structures within a 1 eV energy window for further post processing to confirm the stable conformers separately. |
| This journal is © The Royal Society of Chemistry 2021 |