Open Access Article
Open Access ArticleKinetics of nanoparticle uptake into and distribution in human cells
Christoffer
Åberg
 *
*
Groningen Research Institute of Pharmacy, University of Groningen, Antonius Deusinglaan 1, 9713AV Groningen, The Netherlands. E-mail: christoffer.aberg@rug.nl
First published on 18th March 2021
Abstract
Whether one wishes to optimise drug delivery using nano-sized carriers or avoid hazard posed by engineered nanomaterials, the kinetics of nanoparticle uptake into human cells and their subsequent intracellular distribution is key. Unique properties of the nanoscale implies that such nanoparticles are taken up and trafficked in a different fashion compared to molecular species. In this review, we discuss in detail how to describe the kinetics of nanoparticle uptake and intracellular distribution, using previous studies for illustration. We also cover the extracellular kinetics, particle degradation, endosomal escape and cell division, ending with an outlook on the future of kinetic studies.
Introduction
Nanoparticles are increasingly being employed for a range of applications, including as drug carriers to treat a range of diseases such as cancers,1–3 neurodegenerative disorders4,5 and AIDS.6 In such applications it is often paramount to know how many carriers enter the (target) cells, in order to understand how much drug is actually delivered. For some applications it is, furthermore, of interest to know the subsequent intracellular distribution; for example, for genetic medicines a key barrier is thought to be escape from endolysosomal trafficking7,8 in order to access the cytosol (RNA-based therapeutics) or nucleus (DNA). Similar questions arise when one is interested in understanding the risks posed by nanomaterials to human health,9–11 where the possible effects are dictated by the location of action of the material. These processes, while still not completely understood, are heavily researched worldwide. Nevertheless, one aspect to these processes which has received much less attention is their kinetics, that is, how rapidly they occur. This is somewhat surprising given that, regardless of whether one is trying to optimise a nano-sized drug delivery vector or mitigate the hazard posed by an engineered nanomaterial, it would seem crucial to know, say, how many nanoparticles enter a cell per time. A number of reviews have discussed the pharmacokinetics at organism level,12–16 but the cell level has scarcely been reviewed.17 Our aim with this text is to take the first step towards addressing this shortcoming.For small molecule drugs the subject of pharmacokinetics is well-established18 (though the cell level is less developed), so what differs for nanoparticles? The answer lies in the different cellular processes activated by nanoparticles: typically, nanoparticles are taken up by cells by endocytosis,19–22 whereby the cell membrane invaginates to form an intracellular vesicle that ultimately pinches off from the cell membrane inside the cell.23,24 Subsequently, the nanoparticle remains enclosed in vesicles as it is transported along the cell membrane trafficking system through various organelles.19,20,22 In contrast, small molecules typically enter passively through the cell membrane; passively through a channel or via a transporter; or actively via a transporter.18 Regardless, the end result is that once the molecule has passed the (outer) cell membrane, it is free in the cytosol and the cell plays little further role, the subsequent distribution taking place via diffusion (at least until the molecule encounters another membrane). This is in stark contrast to nanoparticles, whose distribution is slaved to the cell transport system (at least until they can break out of it).
The fundamentally different uptake and distribution processes naturally have consequences also for how to describe these processes. We stress that we specifically consider particles taken up by endocytosis, while the rules governing the kinetics of particles that have been reported to enter by direct membrane penetration25,26 are likely more akin to those of small molecule drugs. The biological mechanisms underlying the uptake and distribution of such particles are well-studied and the topic of several previous reviews.17,19,27–31 However, the kinetic aspects, that is, a mathematical description that allows predicting how quickly they occur, have been much less covered. Indeed, there is, as yet, no well-established general kinetic framework. However, even in the absence of a well-established framework, there are some aspects that must be considered in order to take into account the different manner with which nanoparticles engage with the cell. We may therefore frame our discussion using “precursory” kinetic models that, while as yet preliminary, at least take into account these aspects. We focus our discussion on the cell uptake process and the subsequent intracellular distribution, but for completeness also briefly discuss degradation, endosomal escape and cell division, as well as transport in the extracellular environment. As for our general approach, given that kinetic studies are highly underrepresented in the field, we felt a survey of the literature in itself would not suffice. We have therefore opted for a more narrative approach, describing the (precursory) kinetic models and using previous studies to illustrate the ideas. We have also explicitly included both the kinetic equations themselves as well as their solutions. We thus hope to satisfy both the reader looking for a literature survey, as well as those interested in performing such studies or in helping erect a more well-established kinetic framework. Indeed, one purpose of this text is to stimulate the pursuit of more studies on nanoparticle kinetics, and hence we end with a rather extended outlook detailing how kinetics modelling can usefully play a larger role in future.
Overview
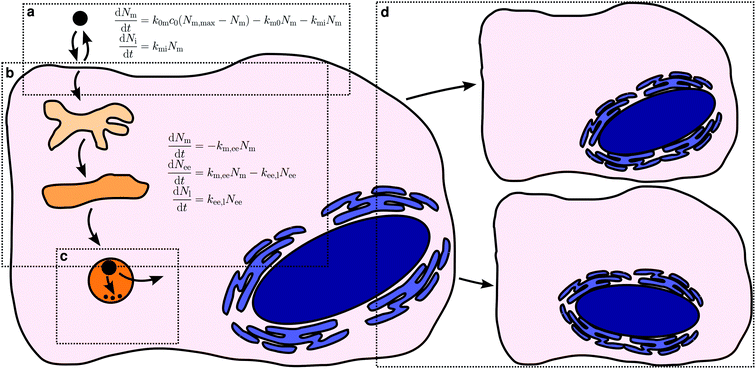
The various processes we will cover are illustrated in Fig. 1, together with the precursory kinetic models that we will use to describe them. Before describing these different processes in more detail we should stress some general points. First, the kinetic models illustrated by Fig. 1 should be viewed as illustrating the aspects that need to be considered, rather than validated models that can be applied to any system in future. It is certainly the case that each of these models has been usefully applied to an experimental dataset. Nevertheless, that does not mean that they, as yet, describe all details. Indeed, we will explicitly mention examples where more development is needed below. We also do not expect details to be the same for all nanoparticles, cells or nanoparticle/cell combinations. However, we do expect some general features of the models to be the same.Related to this, we note that the kinetic model to use for a given application is in no way fixed, but rather may be adapted to either take advantage of all experimental data that is available or, conversely, to account for a more limited dataset. For example, the model for intracellular distribution kinetics exemplified by Fig. 1b includes two organelles, early endosomes and late endosomes/lysosomes. If data is also available for, say, late endosomes specifically, then the model can be extended to also include such transport steps. Conversely, if data is only available for, say, late endosomes/lysosomes then we could write down a more limited model that includes only these organelles. Naturally, the simpler model may not be sufficient to describe the data, but the extent (or lack) of agreement between model and experiments will show whether this is the case or not. If the simpler model describes the data well, one should be able to derive it as an approximation to the more complete model and relate the parameters of the two models to each other.
We will now continue discussing the various processes, and precursory models that illustrate how to describe them mathematically, in more detail.
Cellular adsorption/desorption and internalisation kinetics
We will start by discussing the uptake process, but before delving into the kinetic modelling aspects, we first note that a prerequisite is, of course, that the number of nanoparticles taken up by a cell is measurable. For this purpose, many different techniques have been developed or adapted, as reviewed previously.30,32–36 Some of these techniques are specific to a given class of nanoparticles, while others can be adapted more broadly. As an example of the former, metal-based particles are often assessed using inductively coupled plasma mass spectrometry.37,38 While this was originally used to quantify the amount of nanoparticles internalised by all cells in total, it is now possible to do the same also at individual cell level.39,40 Similarly, the association of magnetic nanoparticles with cells can be measured using magnetophoresis, on a cell-by-cell basis, and also using magnetic particle imaging.41 For nanoparticles that can be distinguished from the cell background, electron microscopy is also a useful technique for particle uptake quantification,42 with unbiased stereological methods already available.43–45The broadest category of particles is possibly those that can be investigated based on fluorescence, whether intrinsic to the particle (e.g., quantum dots) or from a fluorescent label. Flow cytometry is very useful to investigate the uptake of such particles,36 though it can also be used for non-fluorescent particles, if they scatter light strongly enough.36,46 Either way, flow cytometry is high-throughput, but still allows a single-cell level assessment, though without intracellular detail.36 In contrast, fluorescence microscopy can also give subcellular localisation. While traditionally applied only to measure nanoparticle uptake in one or a few handfuls of cells,25,47–49 fluorescence microscopy is now increasingly used in a high-throughput manner,50 both in imaging cytometers51 and by automated imaging using more conventional microscopes.52 The uptake of strongly scattering nanoparticles, such as gold, can also be measured using microscopy in dark-field mode,53 even without fluorescent labelling. A disadvantage with optical microscopy of nanoparticles in cells is naturally that, due to the diffraction limit, individual nanoparticles cannot be resolved individually if too close together.54 Super-resolution microscopy approaches, such as stimulated emission depletion microscopy55,56 and photoactivation localization microscopy,57 can remedy this issue and allow quantification of individual nanoparticles, even without the superior resolution provided by electron microscopy.
Other techniques to measure nanoparticle association with cells include particle-induced X-ray emission,58–60 Raman (including confocal61), electron spin resonance62 and synchrotron X-ray fluorescence microscopy.63,64
An important aspect of the technique used to assess cellular nanoparticle accumulation is whether the measurement gives the actual number of nanoparticles or something related to this number. Electron microscopy is perhaps the gold standard in that regard, especially when coupled to stereological methods,45 because one can explicitly quantify numbers; however, it is not high-throughput and not applicable to all particles. Inductively coupled plasma mass spectrometry also gives a fairly direct measurement of the number of particles, though in actuality it measures the number of metal atoms, and needs an estimate of the number of such metal atoms per particle in order to arrive at a quantification of the number of particles.37 In addition, it does not distinguish between particles and dissolved ions (which could also be present or produced), though this state of affairs has been remedied with the advent of single-particle inductively coupled plasma mass spectrometry.65,66 If uptake is assessed using nanoparticle fluorescence, then the relation between the measured fluorescence and the number of nanoparticles is typically indirect.34 An exception is, of course, if the number of nanoparticles is assessed using super-resolution microscopy, in which case assessment of actual numbers can be done.67 When assessed using flow cytometry or diffraction-limited fluorescence microscopy, however, either one has to measure the fluorescence of single particles to convert the signal to numbers,68,69 or one resorts to measuring something that is related to the number of particles.
It is certainly preferred to have actual numbers to continue with a kinetic analysis. Still, it is not strictly necessary and under fortuitous circumstances the analysis will still give information, albeit less (examples will be mentioned below). However, some control of the relation between the signal measured and the number of particles is key. In the case of fluorescence, for instance, one must consider quenching and/or Förster resonance energy transfer to other wavelengths, which will both lower the measured signal and hamper an estimation of the number of particles from their fluorescence. Particle (or dye) degradation is another important process but this, we feel, is better dealt with as a scientific problem, rather than a technical one. Hence, it should probably be included in the kinetic analysis as discussed in a later section. In general, for a kinetic analysis it would seem wise to ensure, if possible, that the experimental settings allow a proportionality between the signal measured and the number of particles (a linear relationship can, of course, be put into a proportionality by subtracting the background). We will assume this to be the case in the following to allow us to more clearly focus on the kinetic aspects.
Let us now turn to how to actually describe the uptake process in kinetic terms. It seems a priori reasonable to describe the overall uptake process of a nanoparticle by a cell in terms of the nanoparticle first adsorbing to the (outer) cell membrane and subsequently being internalised by the cell.38,62,70 Of course, the nanoparticle also has to remain at the membrane long enough in order that it be internalised, that is, it should not desorb. In this description, there are thus three processes that contribute to the overall uptake kinetics: cell membrane adsorption and desorption, as well as internalisation (Fig. 1a).
We will start with discussing the adsorption/desorption kinetics in the absence of internalisation. Various approaches have been used to measure the adsorption/desorption kinetics separately from the overall uptake process, including cooling down the cells or exposing them to sodium azide (NaN3) to inhibit internalisation,46,62,70 chemical removal of nanoparticles from the outer cell membrane38 and fluorescence microscopy and subsequent image analysis to separate nanoparticles inside from outside.25,47,49,71,72 The various approaches give slightly different outcomes, in the sense that some measure the adsorption/desorption kinetics in the absence of internalisation, while others measure the adsorption/desorption kinetics in the presence of internalisation, but nevertheless separately from internalisation. Both options give useful information on the processes, though all of these approaches, of course, have their limits. Fig. 2 shows an example, reproduced from literature,49 of the number of nanoparticles adsorbed to the cell membrane as a function of time during continuous exposure and in the presence of internalisation. In relation to our earlier discussion, we note that this data is in fluorescence, meaning that the number of particles was not directly measured. However, the authors suggest that the signal is proportional to the number of particles,49 so with them we will assume so in the following. The data suggest that the nanoparticles rapidly, within 10–20 min, adsorb to the cell, and this appears to be a general observation.25,46,62,70
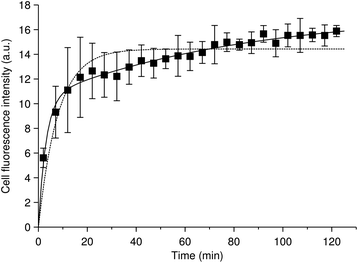 | ||
| Fig. 2 Nanoparticle cellular membrane adsorption kinetics. (Datapoints) HeLa cells exposed to quantum dots pre-coated with succinylated human serum albumin and observed during the exposure by fluorescence microscopy. The quantum dot fluorescence at the membrane was quantified and averaged over cells as a measure of the number of nanoparticles adsorbed to the membrane. Data reproduced from literature.49 (Dotted line) Fit of a model including a single adsorption process [eqn (2) or (6a)] to the data. (Solid line) Fit of a model including two adsorption processes [eqn (4)] to the data. Note that the data is for an experiment where the cells also internalised particles. However, this is irrelevant for the fits, since the mathematical form of the equation describing the number of nanoparticles adsorbed to the cell membrane is the same regardless of whether internalisation is occurring or not [cf.eqn (2) and (6a)]. | ||
To describe the kinetics of adsorption to/desorption from the cell membrane a first attack on the problem is provided by the following kinetic model62,70,73
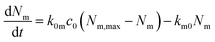 | (1) |
The rate of desorption (second term) we assume is proportional to the number of nanoparticles that are currently adsorbed to the cell membrane – the more there are, the higher probability of desorption – with the proportionality constant being a desorption rate constant, km0. This assumption is typical for modelling of cell membrane receptor binding75 or, indeed, binding in general. It is also analogous to the assumption of linear kinetics in classical (organism level) pharmacokinetics.18,76,77 It is the simplest assumption one may make (the only simpler assumption would be a constant desorption rate, but that assumption could lead to a negative number of particles at the membrane and hence is not feasible from a physical point of view). Thus we may view it as the most parsimonious assumption one may make in the absence of other knowledge. A different way of viewing this assumption is based on the fact that, in the absence of further adsorption, it leads to an exponentially decaying number of particles at the membrane. An exponential decay is characteristic of a process where, loosely speaking, the occurrence of events is completely random.78–80 In other words, we assume that nanoparticle desorption occurs at random times.
The rate of adsorption (first term) is a bit more complicated. Here we assume that there is a maximum number of sites to which the nanoparticles can adsorb, Nm,max, and that once these are all occupied, no more nanoparticles may adsorb. Note that this does not imply that the adsorption sites by necessity become saturated; in the presence of internalisation (see below), they will remain at low occupation if internalisation is rapid. We assume that the number of nanoparticles impinging on the cell membrane is proportional to the extracellular nanoparticle concentration, c0; how many of these actually adsorb we then assume is given by the product of an adsorption rate constant, k0m, and the currently available number of adsorption sites, Nm,max − Nm. The term Nm,max − Nm is guaranteed to be positive [as can, e.g., be shown from the solution, eqn (2), below] so the second term always gives rise to an increase in the number of particles, as it should. Aside from the effect of a finite number of sites, the reason for the proportionality is the same as for the desorption process (previous paragraph).
It is perhaps worthwhile to note that the two rate constants have different dimensions, that is, the desorption rate constant, km0, has dimension of inverse time, while the adsorption rate constant, k0m, has dimension of inverse time times concentration (the latter depending upon how the concentration, c0, is measured). Indeed, this is consistent with how rate constants are used in chemistry.
The solution to this model (under the condition that there initially are no nanoparticles adsorbed to the membrane) is that the number of nanoparticles at the membrane varies as a function of time according to
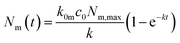 | (2) |
| k = k0mc0 + km0. | (3) |
Despite a moderate success in describing the data, it is clear that there is a systematic deviation between model and experiment, starting from the end of the initial rapid adsorption (after the first 20 min). The experimental data here shows a slow, roughly linear, increase of the number of nanoparticles adsorbed to the membrane as a function of time, whereas the model reaches a plateau. It is perhaps worthwhile to briefly note that this slow increase is unlikely to be due to quenching or Förster resonance energy transfer, because these processes would give a lower signal at higher membrane coverage. This argument illustrates the general point that even if the measured signal is not strictly proportional to particle numbers (as we have assumed), a kinetic analysis can still give useful information with auxiliary arguments.
The model [eqn (1)] can never capture the experimental behaviour, because if the initial adsorption is rapid, then also the time to saturate the membrane will be quick; it is not possible to have both an initial rapid adsorption and slow subsequent increase within this model. The observation of a slow increase at longer time-scales appears to be fairly general,25,46,49,62,70 though it is not completely established. We have previously listed a number of possible processes70 – and there are more – that could explain this slower increase, but at present fear that its mechanistic origin remains unresolved.
Without a mechanistic explanation it is impossible to write down a model for the slow increase with any confidence. However, there may be situations where it is nevertheless useful to have a good description of the data, despite it not being based on mechanistic understanding. For example, for actual applications (e.g., drug delivery) the nanoparticle concentrations are likely far smaller than those typically used in fundamental studies (e.g., Fig. 2). This implies that the first process will be the dominant one and extracting the kinetic parameters that describes that process will be useful. Thus, say we only want to describe the data, rather than use the fitted model as an interpretative framework. Then we may use a model composed of two Langmuir adsorption processes, viz.
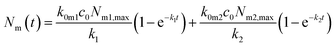 | (4) |
Let us now continue with discussing the internalisation process. The same approaches25,38,46,47,49,62,70–72 that have been used to measure the number of nanoparticles at the cell membrane separately from those inside can naturally also be used to measure the number of nanoparticles within the cell. In order to describe such experiments, we must thus include also an internalisation rate into the model. We assume the rate to be proportional to the number of nanoparticles already adsorbed – the more there are, the higher probability of internalisation – with the corresponding rate constant, kmi. Again this assumption is completely analogous to the assumption of linear kinetics in classical (organism level) pharmacokinetics,18,76,77 where it would be akin to the absorption rate constant that describes absorption into the systemic circulation. It has also been used for modelling endocytosis.75 As we have already discussed, it is also equivalent to, loosely speaking, assuming that nanoparticle uptake is a random process (see above).78–80
A useful first attempt at describing the kinetics is thus the differential equation system48,70,73
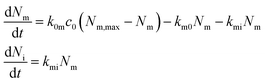 | (5) |
Under the condition that there are no nanoparticles on the membrane or inside the cell initially, the solution to this equation system is given by
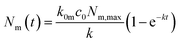 | (6a) |
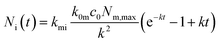 | (6b) |
| k = k0mc0 + km0 + kmi. | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70 (human adenocarcinomic alveolar basal epithelial) cells, as well as the uptake kinetics of 200 nm aminated and carboxylated polystyrene nanoparticles in HUVECs48 (Human Umbilical Vein Endothelial Cells).
70 (human adenocarcinomic alveolar basal epithelial) cells, as well as the uptake kinetics of 200 nm aminated and carboxylated polystyrene nanoparticles in HUVECs48 (Human Umbilical Vein Endothelial Cells).
The number of nanoparticles inside the cell within the model [eqn (6b)], of course, depends on the various parameters. We note that the majority of these parameters set the overall scale (i.e., exactly how many nanoparticles) and that the general behaviour is again given by a single parameter, namely the parameter k defined by eqn (7). Thus, we show in Fig. 3 the general behaviour at typical experimental time-scales for two exemplar values of the parameter k, illustrating two different behaviours. In Fig. 3a we have used a relatively large parameter k and we then observe that the number of nanoparticles inside the cell grows linearly with time. Indeed, for t ≫ k−1 we may approximate eqn (6b) with the expression
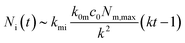 | (8) |
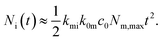 | (9) |
 | ||
| Fig. 3 The two different uptake kinetics that may be observed. The two graphs show the number of nanoparticles inside a cell (in arbitrary units) as a function of time predicted from the model [eqn (6b)]. Which of the two types of behaviour occurs is determined by the parameter k defined by eqn (7). (a) Relatively large k (k = 1 min−1) where linear behaviour is observed. (b) Relatively small k (k = 0.01 min−1) where a quadratic behaviour is observed. The lower axes measure actual time, while the upper axes represent a dimensionless version. | ||
These conclusions are trivial from a mathematical point of view, but that should not distract from their physical consequence. Thus an uptake process described in terms of adsorption to/desorption from the cell membrane and subsequent internalisation is sufficient to describe two different behaviours, with no need for the introduction of more esoteric hypotheses. The first behaviour, a largely linear uptake process, appears to be fairly common. For example, for uptake of polystyrene nanoparticles we have previously noted that, after an initial transient, the uptake process is essentially linear.22,70 This would be indicative of a relatively large parameter k under these conditions, such that experimentally accessible time-scales are always larger than k−1. In contrast, Zerial and colleagues observed a clearly non-linear uptake process for lipid nanoparticles,8 something which has also been observed with transferrin-targeted nanoparticles.82 A non-linear behaviour is expected for a relatively small parameter k. At least in the former case, it would appear that the model discussed here [eqn (5)] is anyway not sufficient to describe the data (the data8 appears to grow as t4 rather than t2). Nevertheless, the point that a non-linear behaviour is not necessarily a sign of more complex kinetics is generally true.
In this context, we should note that the parameter k actually holds contributions from three different processes: adsorption to the cell membrane, desorption from the cell membrane and internalisation [eqn (7)]. In particular, it is linear in the extracellular concentration, c0, which implies that the magnitude of k can be varied by changing the concentration. Under furtious circumstances it may thus be possible to observe the two different behaviours illustrated by Fig. 3 experimentally for the same nanoparticle-cell system, simply by changing the concentration.
We have already mentioned that there exists experimental approaches to exclude the contribution from membrane-adsorbed nanoparticles (at least approximately). Still, it is far easier, and more common, to perform kinetic experiments8,21,22,25,37,47,68,70–72,83–91 that do not differentiate between the nanoparticles on the membrane and those within the cell. This may be done using a wide variety of different experimental approaches, including flow cytometry, inductively coupled plasma mass spectrometry (ICP-MS), surface plasmon resonance and magnetic resonance.36 If it may be assumed that the measured signal is independent of whether the nanoparticles are at the membrane or within the cell, it will thus be advantageous to consider not Nm(t) and Ni(t) themselves, but their sum, Nm(t) + Ni(t). This assumption is essentially the same we made above when discussing the relationship between signal and number of particles. Only having access to the sum will not provide as much information, and some parts of the behaviour may be obscured, but it may be all that it is feasible to do.
We will next discuss how to determine the various parameters of a model. These obviously depend upon (at least) the particular nanoparticle and cell system. The procedure to extract these parameters will depend upon which model is being used, but also upon what data is available, the quality of the data etc. Some ideas, however, appear to be general, so we use our preliminary model to briefly illustrate one possible procedure here.
In the simplest case, there are in total four parameters, the kinetic rate constants k0m, km0 and kmi, as well as Nm,max. These can be evaluated by fitting eqn (6a) and (b) to data, or possibly eqn (2) and the corresponding expression for Nm(t) + Ni(t) if only the total number of nanoparticles associated with cells has been measured. A general observation, though, is that one needs data for several concentrations in order to evaluate all rate constants. For example, if one has data of the number of particles adsorbed to the cell membrane in the absence of internalisation, then a fit of eqn (2) to the data yields only k and not k0m and km0 separately. However, if one has evaluated k for several different concentrations, then one can find k0m and km0 separately [cf.eqn (3)]. In the presence of internalisation, the equivalent procedure gives k0m and km0 + kmi [cf.eqn (7)]; if k0m and km0 are already known separately from adsorption experiments, then this allows determination of kmi. A second general observation is that Nm,max can only be found if the data is in terms of number of nanoparticles (as opposed to, e.g., fluorescence). If not, then fitting gives a quantity related to Nm,max, but with an unknown relation, something without physical significance.
There appears to be not very many instances where the kinetic rate constants have been measured. The first that we are aware of is Wilhelm et al. who measured iron oxide particles in HeLa (human cervical cancer) and RAW264.7 (mouse macrophage) cells.62 They found an adsorption rate constant of k0m = 761 M−1 s−1 and a desorption rate constant of km0 = 4.4 × 10−5 s−1, for both cell types. [They also present internalisation rate constants, but for a different model than that described by eqn (5).] Goodman et al. measured all three rate constants for the model described by eqn (5) for 40 nm carboxylated polystyrene nanoparticles interacting with SiHa (human cervical cancer) cells, resulting in k0m = 1.71 × 109 M−1 s−1, km0 = 4.55 × 10−4 s−1 and kmi = 0.69 × 10−4 s−1.73 Finally, Yaehne et al. measured the adsorption rate constants for the adsorption of 200 nm aminated and carboxylated polystyrene nanoparticles in HUVEC (Human Umbilical Vein Endothelial Cells) to be k0m = 1.3 × 107 M−1 s−1 and 1.8 × 106 M−1 s−1 for the aminated and carboxylated particles, respectively.48
Thus far in our discussion we have not considered the detailed mechanism(s) underlying the adsorption/desorption and internalisation processes. Here is where biology meets (nano)materials science. Thus we would ideally like to identify the adsorption/desorption process [eqn (1)] in terms of the nanoparticle interacting with a specific site. With site we mean in this context a receptor in the cell membrane or a distinct part of the membrane itself. From our reading of the literature, it seems safe to conclude that in the majority of cases, nanoparticles do not interact with one site specifically, but with a range of different types of sites.
The situation is particularly complex for nanoparticles (presumably most) which carry a “biomolecular corona”, that is, nanoparticles which have a layer of (strongly) adsorbed proteins and other biomolecules on their surface.92–96 The interaction between such a nanoparticle and the cell membrane is widely thought to be driven by the biomolecules in the adsorbed corona. From one point of view, this simplifies the situation, because we may not need to consider all the detailed physicochemical properties of the nanoparticles. Rather we can focus on the adsorbed biomolecules, and possibly a few other parameters such as size and shape which certainly affects internalisation.37,85,97 On the other hand, each biomolecule present in the corona and its corresponding receptor(s) in the cell membrane are potential interaction partners and may constitute a type of adsorption/desorption site. For each such site we could then write down an adsorption/desorption process in analogy with eqn (1) and then we would have a clear identification between the kinetic parameters and biology: Nm,max would be the number of sites and k0m and km0 the binding and unbinding rate constants, respectively, for the nanoparticle to that site. This picture would be highly complex in terms of the number of sites it would have to include (one for each interaction partner) but would at least conceptually be straightforward.
The interaction with a specific site (as represented by the adsorption/internalisation processes just discussed) may of course also lead to actual internalisation. Thus, the internalisation rate constant, kmi, is connected to the biology of the subsequent internalisation, being driven by an endocytic process (we consider only particles entering via endocytosis in this work). Endocytosis encompasses a range of mechanisms,23,24 including phagocytosis, macropinocytosis and clathrin-mediated endocytosis.98–100 There also exist a variety of less well-defined, potentially overlapping and sometimes controversial clathrin-independent mechanisms,101–104 such as caveolin-mediated endocytosis,24,101,105 flotillin-1-dependent endocytosis,106 the CLIC/GEEC pathway,101,107,108 and the ARF6-regulated pathway,24,101 though their importance for endocytic flux has been questioned.109 It is not our purpose here to discuss in detail how nanoparticles engage with these mechanisms, for there already exist a variety of reviews on this topic.17,19,27–31 However, a clear outcome of the many reports that have studied this aspect appears to be that most, if not all, nanoparticles engage with more than one of these mechanisms. This is not to say that a given nanoparticle engages with all of the mechanisms, of course. For example, the biological literature has suggested size ranges for some of the mechanisms, such as clathrin-mediated endocytosis operating at a scale of around 120 nm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23 (though this depends on the species) with an upper limit of around 200 nm.24 Such limits have commonly been believed to be respected also by the internalisation of nanoparticles, but results challenging this view are now emerging.31 One possible explanation for the fact that nanoparticles engage with several processes is that their internalisation is ultimately due to them interacting (via their biomolecular corona) with several different receptors, their internalisation being driven by the internalisation of the corresponding receptor. Alternatively, the internalisation of nanoparticles could be driven by membrane turn-over or, in general, by the nanoparticle adsorbing to the cell membrane and simply entering once an endocytic event occurs at that location, leading to a utilisation of several different mechanisms. Regardless of scenario, we may then identify the internalisation rate constant, kmi, with the rate of the corresponding endocytic process(es).
23 (though this depends on the species) with an upper limit of around 200 nm.24 Such limits have commonly been believed to be respected also by the internalisation of nanoparticles, but results challenging this view are now emerging.31 One possible explanation for the fact that nanoparticles engage with several processes is that their internalisation is ultimately due to them interacting (via their biomolecular corona) with several different receptors, their internalisation being driven by the internalisation of the corresponding receptor. Alternatively, the internalisation of nanoparticles could be driven by membrane turn-over or, in general, by the nanoparticle adsorbing to the cell membrane and simply entering once an endocytic event occurs at that location, leading to a utilisation of several different mechanisms. Regardless of scenario, we may then identify the internalisation rate constant, kmi, with the rate of the corresponding endocytic process(es).
We are currently far from making such an identification, however – even for an isolated example. Indeed, the multitude of potential interaction partners makes such an identification highly complex experimentally. This is the case even when data necessitates a description in terms of two processes [as in eqn (4)]. Such a description may appear to point towards (only) two interaction sites, but may equally well represent two sets of interaction sites, each comprising a number of different interaction sites with roughly the same kinetics and where the kinetics is widely different between the two sets.
In addition, it is not known whether the picture of adsorption/desorption and internalisation from fixed sites, extravagant in numbers but otherwise simple, is even appropriate. One could, for example, imagine that nanoparticles adsorb to the membrane and subsequently diffuse on the cell membrane before being internalised by a receptor it subsequently finds.110 The link between binding/unbinding and internalisation would then be even more complex. Overall, at present it appears wiser to view the kinetic equations [eqn (1) or (5)] as phenomenological.
Kinetics of organellar distribution
The literature is scarce when it comes to the intracellular distribution kinetics of nanoparticles, no doubt a reflection of the experimental effort required. The few reports8,72,111–114 that we are aware of have mainly followed the trafficking along the endolysosomal pathway (Fig. 1b) so we will focus our discussion on these processes. The endolysosomal pathway115 starts with the formation of an endocytic vesicle that envelopes the internalised cargo;23,116 the endocytic vesicle subsequently fuses with an early endosome98,116–118 which later matures into a late endosome.116,118–120 There used to be a competing model for the arrival of cargo in late endosomes, namely vesicular transport between early and late endosomes, but the question now appears to be settled in favour of the maturation model.120,121 Late endosomes ultimately fuse with lysosomes to form endolysosomes, a hybrid organelle where the remaining cargo is degraded (if it can be degraded).116,121,122 Endolysosomes eventually mature back into a lysosomes.121,122 Concomitant with transport along the different organelles, a change in pH occurs along the pathway, from a pH of around 6.8–6.1 in early endosomes, to 6.0–4.8 in late endosomes and eventually 4.5 in lysosomes.116Proteins belonging to the Rab GTPases family are involved throughout the endolysosomal pathway.118,119 For example, Rab5 is found at the (cytoplasmic side of the) cell membrane123 and is subsequently associated with early endosomes, while both Rab7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 118,124,125 and Rab9
118,124,125 and Rab9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 118,126 are associated with late endosomes. Specifically, the maturation of early endosomes into late endosomes is associated with the replacement of Rab5 with Rab7.120 While Rab7 is thus typically associated with late endosomes, some reports have suggested that Rab7 is (also) associated with terminal vesicles in the endolysosomal pathway,127 which would typically be considered to be lysosomes.
118,126 are associated with late endosomes. Specifically, the maturation of early endosomes into late endosomes is associated with the replacement of Rab5 with Rab7.120 While Rab7 is thus typically associated with late endosomes, some reports have suggested that Rab7 is (also) associated with terminal vesicles in the endolysosomal pathway,127 which would typically be considered to be lysosomes.
Experiments that follow the distribution of nanoparticles within cells are typically performed by observing the association of fluorescently labelled nanoparticles with likewise labelled organelles using fluorescence microscopy. The organelles may be labelled using specific stains or by transfecting cells to (transiently or permanently) express fluorescent variants of various proteins known to be associated with the organelle in question. Commonly used markers include Early Endosome Antigen 1 (EEA1) for early endosomes8,22 and Lysosomal-Associated Membrane Protein 1 (LAMP1) for lysosomes,8,72,111–113 both endogenous proteins, as well as LysoTracker for lysosomes,114,128 a dye. In addition, fluorescently labelled Rabs are also useful markers, including Rab5 for early endosomes,72,111–114 as well as Rab7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 111–114 and Rab9
111–114 and Rab9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 112,113 for late endosomes.
112,113 for late endosomes.
Having acquired fluorescence microscopy images (or time-lapses; “movies”) of fluorescently labelled nanoparticles and organelles, the association of nanoparticles with the organelle of interest must then be quantified, taking into account the limited resolution of light microscopy. There are a range of different measures in use for measuring such a co-localisation.128 Some are based directly on the fluorescence signal, such as Pearson's correlation coefficient129 and Manders' overlap coefficients;130 others are based on identifying the location of the nanoparticles and the organelles, and only subsequently evaluating whether the two objects are in the same position.111,112,128 The latter procedure has also been performed on time-lapses,111,112 to avoid false positives due to a nanoparticle and organelle being intermittently close together before separating again, without the nanoparticle actually remaining within the organelle.128
Aside from fluorescence microscopy studies, the intracellular distribution of nanoparticles has also been quantified using quantitative electron microscopy, where the location of nanoparticles in early endosomes, late endosomes and lysosomes was deduced directly from the appearance of the vesicles.8 In this case one avoids having to use a co-localisation measure and, in general, the issues related to the limited resolution of light microscopy.
An example of the kind of data available is given by Fig. 4 which shows data reproduced from literature of the association of nanoparticles with Rab5-positive vesicles and Rab7-positive vesicles as a function of time. For simplicity, we will refer to the Rab5-positive vesicles as early endosomes and the Rab7-positive vesicles as late endosomes/lysosomes. In the latter case, we note that the particles do not subsequently exit the Rab7-positive vesicles (Fig. 4b and c), consistent with the notion that Rab7 is associated with terminal vesicles of the endolysosomal pathway,127 as discussed above. Obviously, the kinetics and mathematics are the same regardless of the name and this will remain our focus.
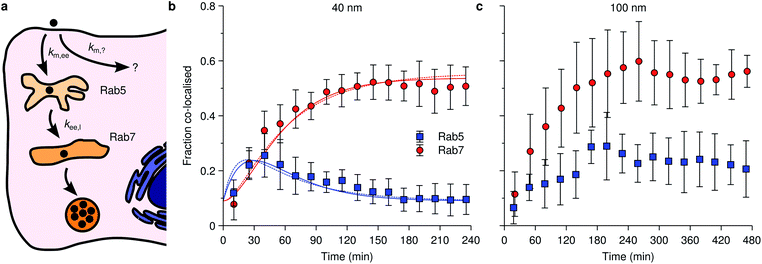 | ||
| Fig. 4 Nanoparticle distribution along the endolysosomal pathway. (a) Illustration of the endolysosomal pathway showing early/sorting endosomes, late endosomes and lysosomes. Rab5 is associated with early endosomes, while Rab7 is associated with both late endosomes and lysosomes. The corresponding rate constants for a kinetic model [eqn (10)] are also indicated, including one representing non-endolysosomal processing. (b) Fraction of 40 nm carboxylated nanoparticles associated with Rab5 and Rab7 as a function of time in HeLa cells. (Datapoints) Experimental data, averaged over 5 cells. (Solid lines) Fit of eqn (11) to the experimental data. In performing the fit, 0.09 was subtracted from all datapoints, assuming this constitutes a background signal. (Dotted lines) Fit of a modified model where the “diversion” from lysosomal processing takes place after early endosomes instead of before. (c) The same type of data as shown in panel (b) but for 100 nm nanoparticles instead. Datapoints in panels (b) and (c) reproduced from literature.112 | ||
Fig. 4b shows specifically the association of 40 nm polystyrene nanoparticles with these proteins, from which we may observe how the nanoparticles transiently associate with early endosomes (blue data points), with a maximum number of particles within them at around 40 min, before all particles eventually leave the early endosomes (we assume the remaining value of around 0.09 is background). As for the late endosomes/lysosomes (red data points), the nanoparticles are steadily transported to them until a plateau is reached after around 100 min, after which no more nanoparticles arrive there. Importantly, it appears that not all nanoparticles eventually end up in the lysosomes, the maximum value being around 45% (again, assuming a background value of around 0.09), something which appears to be a fairly general observation.8,72,111,112
An attempt at describing this data kinetically would be to write the change in the number of nanoparticles at the membrane, Nm, in early endosomes, Nee, and late endosomes/lysosomes, Nl as
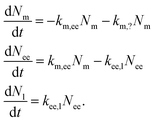 | (10) |
For the reader versed in classical (organism level) pharmacokinetics,18,76,77eqn (10) has the appearance of a multi-compartment model and this may be a useful way of viewing it. This analogy again points to the fact that the underlying assumptions are the same as for linear pharmacokinetics, that is, the simplest assumption one may make in the absence of other guiding principles. As above, though, a different way of viewing this assumption is that it, loosely speaking, is equivalent to the various transfer processes occurring at random times.78–80
An important part of this model – and one that sets it out from typical multicompartment pharmacokinetics models18,76,77 – is that the flow is unidirectional. That is, the particles go from the membrane to early endosomes and subsequently to late endosomes/lysosomes – but not in the opposite direction. This reflects the biology of the endolysosomal pathway and distinguishes the active distribution of nanoparticles from distribution by passive processes.
We are here, in a sense, viewing all endosomes as one compartment, not taking into account that they are individual vesicles, and likewise for late endosomes/lysosomes. This would not seem to be a serious limitation, at least at the current state of experimental knowledge. The reason is that we expect that, say, the number of nanoparticles that transfer into a late endosome/lysosome is proportional to the number of particles in early endosomes, regardless of which particular endosome they are in. For the same reason we do not expect the fact that several nanoparticles may be located in one organelle to play a major role.
In eqn (10) we have also introduced the two rate constants, km,ee and kee,l, that describe the transfer from cell membrane to early endosomes and from early endosomes to lysosomes, respectively. Furthermore, km,? describes nanoparticles that do not end up following the endolysosomal pathway, something which we will get back to below. All of these rate constants have dimension of inverse time.
We should also note that, compared to eqn (1), we have simplified the description of the processes occurring at the membrane slightly: first, we have excluded the adsorption process, in line with a pulse-loading of the cells to the nanoparticles, the common experimental condition for this type of studies. Second, we have disregarded the desorption processes; this has no further consequences, since desorbing nanoparticles will anyway not continue along the endolysosomal pathway.
The solution to eqn (10), assuming that all particles are initially at the membrane, is given by
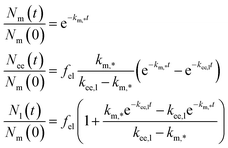 | (11) |
We should note that the experimental data shown in Fig. 4b is averaged over a handful of cells so in practice the model, and its rate constants, is some sort of averaged model. We should differentiate this approach from evaluating rate constants from kinetic curves of individual cells which, of course, may also be subsequently averaged. These two approaches do not necessarily give the same results, though likely they will tend to the same value if the number of cells included is very large.
An observation worth mentioning with regard to this example is the inclusion of non-endolysosomal pathways into the model [the rate constant km,? in Fig. 4a or eqn (10)]. We are forced to include this to account for the experimental observation that not all particles accumulate in the lysosomes. The data does not uniquely determine where the “diversion” from endolysosomal processing takes place, however. In the model presented thus far [Fig. 4a and eqn (10)] we assumed this took place before the early endosomes. However, a similar model where this instead takes place after the early endosomes, fits the data equally well (Fig. 4b; dotted lines). The resulting rate constants are different though, so if there is complementary information on how long one of the steps takes, then this may be useful to fix the model.
The successful description of the kinetic data in Fig. 4b by the simple model given by eqn (10) is challenged when we consider the same type of data for a larger nanoparticle (100 nm instead of 40 nm) as shown in Fig. 4c. Partly the kinetics looks similar as for the smaller nanoparticle (Fig. 4b): the association with early endosomes grows during 2 h or so, while the association with late endosomes/lysosomes increases for 3 h until it reaches a plateau and remains constant. The crucial difference is that the association with early endosomes does not decay, but rather remains largely constant between 3–8 h. It thus appears as if there is a substantial fraction of nanoparticles “stuck” in early endosomes. Assuming this association to be correctly quantified, it is difficult, if not impossible, to reconcile this behaviour with a kinetic model of the form exhibited by eqn (10).
Other observations also challenge the simple approach. Thus, Braeckmans and colleagues developed a trajectory-based co-localisation measure and appear to thereby have completely obliviated the incidence of false positives.111 This is important, because with a reduction in false positives it is possible to observe the details of how the nanoparticles enter the various organelles. Interestingly, one discovers a lag time before the particles enter late endosomes/lysosomes,111 something which may also be discerned in other examples from literature.8,72 Indeed, the observation of lag times is natural, because it will necessarily take some time for a nanoparticle to go from the cell membrane to early endosomes and so on for the following transport steps; nevertheless, lag times are not included in the simple approach exemplified by eqn (10) and, indeed, are often not justified by the data.
Overall, it thus appears that there is a need for more sophisticated kinetic models. Possibly a useful point of departure is a description in terms of how long a particle remains in each compartment – how long it has to wait – before arriving in the next compartment. It is possible to generalise the approach represented by eqn (10) for this purpose, by letting the rate “constants” become functions of time.131 Such a description could, at least in principle, incorporate both the observation of long waiting times (Fig. 4c), as well as that of a lag-time. However, it needs experimental input to suggest what kind of waiting times may be suitable.
Kinetics of other cellular processes: degradation, endosomal escape and cell division
For completeness, we should briefly comment also on other processes that may occur once the nanoparticles are within the cell. Before doing so, however, we note that from a modelling point of view, it is of course useful to consider the case that a particle does not degrade and exit organelles, because the corresponding model is much easier. Fortunately, such systems also appear to exist in reality (e.g., carboxylated polystyrene84) which thus allows, also experimentally, decoupling the kinetics of uptake and intracellular transport from all other processes. Other possibilities of “blocking” various intracellular processes to isolate certain parts of the kinetics include tuning particle properties (e.g., having particles with and without membranolytic compounds that facilitate endosomal escape). Naturally, we cannot always assume that the “blocked” particle behaves otherwise the same as the original particle. Nevertheless, having access to a “negative” control for the kinetics is useful and worth considering.As for the processes that particles may undergo inside the cell, it is clear that non-endolysosomal pathways play a role in the intracellular processing of nanoparticles (see above). Unfortunately, in the absence of detailed experimental data, it is impossible to discuss this kinetics. A bit more can, however, be said about the subsequent fate of nanoparticles that follow the endolysosomal pathway. Exit processes appear to be absent for these particles,84,132 shifting attention towards the stability of the particle and vesicle in themselves (Fig. 1c). We miss the experimental data to discuss these processes in detail, but will attempt to discuss some aspects that we believe will become important for describing their kinetics in future. It is certainly the case that some nanoparticles may degrade or otherwise transform and that their contents may thereby be released into the cytosol. Such processes would be more within the realm of chemical kinetics, which is better understood than the intracellular transport kinetics. Nevertheless, it would be prudent to keep in mind that the degradation will take place in a biological milieu and thus that the detailed conditions will likely depend upon where the nanoparticle is. For instance, the pH changes between early endosomes and lysosomes, so if pH is a major determinant of the degradation kinetics, then a coupling between intracellular transport and degradation will arise. Various active transport processes are also present within the intracellular organelles – as are passive – and they may possibly export the degradation products and thereby lead to an increased degradation rate, again in an organelle-dependent manner. On the other hand, for nanoparticles that carry with them a biomolecular corona into the cell,133–135 the corona must likely degrade before the particle itself is exposed. First measurements of corona degradation suggest that the corona is shed at lysosomal level.134 If this is a general observation, then this would imply that particle degradation will only take place in lysosomes and hence simplify the conditions that need to be examined.
Escape of the nanoparticle from the intracellular organelles also has to be considered. This is of prime importance for genetic medicines, where endosomal escape is believed to be a key obstacle,7,8 but is also important for engineered nanomaterials, where the existence or not of cytosolic access may dictate the hazard they pose. Different mechanisms and approaches have been suggested to facilitate endosomal escape, including the putative “proton sponge” effect,136,137 lipid mixing7,138 and inclusion of membranolytic compounds with/on the particle. The detailed mechanism of endosomal escape will dictate the kinetics, so it is not possible to discuss it in detail. Generally speaking, though, it would appear that one must consider similar issues as for particle degradation. In particular, a coupling between the particle location (and hence intracellular transport) may arise if the escape depends on the biological environment.
Finally, we should briefly discuss also cell division (Fig. 1d), a process that will affect the kinetics at a bit longer time-scale. Thus, experiments on cell lines are typically performed on proliferating cells and hence cell division is omnipresent. The same is true also for other more complex in vitro and ex vivo cell models, to various extents depending upon the system in question. Upon cell division, the nanoparticles within and on the original cell are necessarily shared between the resulting two cells; the division may be completely symmetric, completely asymmetric or something in between,51,139,140 but regardless, the average number of nanoparticles per cell is in this way halved. Halving of the number of nanoparticles per cell will necessarily affect the (average) cellular accumulation kinetics and it does so at a time-scale corresponding to the cell proliferation time. Unless the process of cell division is of prime concern, for detailed measurements of adsorption and internalisation kinetics, it is thus easier to simply limit experiments to shorter time-scales and avoid having to disentangle the various processes.
Still, if cell division kinetics is of interest, then it is most readily interpretable for exponentially growing cell populations. Under these conditions, cell division can be incorporated into models of the uptake kinetics, at various levels of detail as we have discussed in a number of previous works.22,84,132,141,142 An outcome is that cell division will affect the number of nanoparticles per cell at times of the order of the cell population doubling time. For example, for a cell population doubling time of about a day, the effect starts being visible around, say, 8 h. A range of other outcomes can be analysed in detail, but to keep this text short we refer the reader to the original works for details.22,84,132,141,142
Cell division can, of course, also modulate the intracellular distribution kinetics. We can differentiate between two effects: first, cell division is expected to double the number of organelles. If nanoparticle distribution is quantified in terms of co-localisation measures (such as Pearson's)128 which do not make a distinction between object A being co-localised with object B and vice versa, then an increased number of organelles is expected to lead to a decreased co-localisation. If the distribution kinetics is instead quantified directly in terms of number (or fraction) of particles in a given organelle (cf.Fig. 4b and c), then we expect this measure to be unaffected by cell division. These issues are, naturally, only relevant if the intracellular distribution kinetics is quantified in different cells at different times (rather than following individual cells) so that whether a cell has divided or not is unknown.
The second, and more interesting, effect would be if nanoparticles distribute intracellularly during cell division. For example, we may imagine that the organelles they reside within fuse with other organelles, mature or otherwise change identity. To our knowledge, the presence and importance of such processes are currently not well understood.
Kinetics of extracellular transport
The discussion above of the kinetics of cellular uptake (implicitly) assumed a constant extracellular nanoparticle concentration. This assumption is often justified. However, in some systems one may also have to consider the kinetics of extracellular transport. If so, then the uptake kinetics [eqn (5) or equivalent] will be coupled to the extracellular transport and the two problems cannot be solved independently. In the most complicated cases, a rate equation approach will not even be able to describe the system, because diffusional processes in general cannot be phrased as rate equations (fundamentally due to the diffusion equation admitting solutions that are square root in time143). It is consequently important to know whether extracellular transport is important for a given system or not.The transport of nanoparticles in the extracellular medium can be divided into three different mechanisms: diffusion, sedimentation and bulk fluid flow. Diffusion is the movement of the nanoparticles due to collisions with molecules of the extracellular medium (notably, water molecules) and has the appearance of a completely random erratic motion, with no preferred direction. Sedimentation, instead, is the biased downwards-movement due to gravity of dense objects, that is, denser than the surrounding medium. Of course, if the nanoparticles are lighter than the surrounding medium, the particles will move upwards instead (creaming rather than sedimentation). Whether an object will sediment/cream depends only on the densities of the object and fluid, but the actual sedimentation rate also depends on nanoparticle size (among other parameters), making these processes more important for larger particles. There is a fairly large body of literature on how these two transport mechanisms affect extracellular transport,144–147 including reviews,148,149 so we will not repeat that discussion here.
However, what appears to be missing from this literature is a discussion of the third transport mechanism, namely nanoparticle transport via bulk fluid flow. What this means is the transport of nanoparticles that occurs simply because the fluid as a whole is moving and carries the nanoparticles with it (in fact, diffusion is defined relative to the nett overall movement of the fluid). This transport mechanism is important, because it is notoriously difficult to prevent bulk fluid flow in any container of a reasonable size. For example, if the container is moved or shaken, this will create flows of the fluid that take a significant time before dissipating. Indeed, we suspect that even small vibrations due to people working in a lab will cause some such transport, and continuously so. Furthermore, if the medium is, however slowly, evaporating from the container then this creates convection currents within the fluid. Since humidity is often not matched, such evaporation is likely present in many experiments.
All in all, we suspect that bulk fluid flow, unless painstakingly avoided, is a dominant mechanism of extracellular transport of nanoparticles in a range of experiments. This will cause a significant amount of mixing throughout the fluid and, broadly speaking, we expect this to completely eradicate any effects due to at least diffusional transport. The conclusion is less obvious for systems where sedimentation plays a role. Certainly for particles with a very high propensity to sediment, we expect sedimentation to still be important in the presence of bulk fluid flows, though we do not expect it to be easily modelled, as bulk fluid flows will modulate it. For particles with a moderate propensity to sediment we suspect that bulk fluid flows will eliminate the effects of sedimentation, at least to some extent. In conclusion, for dense particles further consideration is needed as to the relative importance of sedimentation and bulk fluid flow, a point which would be a useful addition to the literature. For light and moderately dense particles, we expect that the final outcome is a fairly uniform extracellular nanoparticle concentration and hence there is no need to consider the kinetics of extracellular transport.
To complete the discussion we should add a few points. First, we have considered the situation where the number of nanoparticles is in excess with respect to the number taken up by the cells. Modelling of a decreasing extracellular concentration can be done, but then needs to be disentangled from other potential processes that would slow down uptake. Consequently, we feel that conditions of excess (if practically possible) are by far preferred, as it makes interpretation of the kinetics simpler. For the same reason, we have not considered changes to the (extracellular) dispersion characteristics, such as agglomeration or nanoparticle degradation. We accept that not all nanomaterials may be readily dispersed nor are stable against degradation, but from a scientific point of view it is, again, far preferable to work with stable dispersions and particles where possible.
Outlook
We can foresee several directions in which this arena could usefully develop in future; others may obviously also materialize in due course. First, already now, isolated studies on kinetics of uptake or distribution could support more mechanistically oriented studies, because when a kinetic model describes the data well, it can be used to “disentangle” the various processes. For example, the overall nanoparticle uptake rate by cells is a combination of adsorption to/desorption from the cell membrane and internalisation. The relative importance of these three processes cannot be assessed from measuring only a nanoparticle uptake rate; however, by performing a kinetic analysis one can evaluate all three processes and thereby assess each in isolation. This type of separation of the relative importance of the various processes may be difficult or sometimes even impossible with more molecular biologically-oriented methods.A bit more into the future, another direction kinetic studies may take is the analysis of how the kinetic rate constants connect to nanomaterial properties. For example, one may consider how an internalisation rate constant (kmi in Fig. 1a) varies as a function, say, nanoparticle radius. Such information would have huge implications, both from a fundamental, as well as a very practical, point of view. From a practical point of view, such an analysis would suggest the appropriate design criteria to use for a given application. For instance, if a high uptake is desired it would suggest which nanoparticle radius to use, or vice versa.
From a more fundamental point of view, it could, again, inform or support mechanistic hypotheses. To take a different example, say an endosomal escape rate constant has been studied as a function of the number of protonatable groups on the surface of a set of nanoparticles and no correlation has been found. This result may then suggest that the mechanism of escape of those nanoparticles is not consistent with a proton sponge hypothesis. We should reiterate that such a hypothesis could be visible already from measuring the “end point”, that is, the number of escaped particles in this case. However, if the particles also show different distribution kinetics prior to escape, then the number of escaped particles is an overall measure of both the distribution and escape kinetics and this can obscure the fundamental mechanisms. Again, kinetic analysis is a way of disentangling the different processes.
In this context, it is worthwhile to connect the discussion to nanomaterial quantitative structure–activity relationships (nano-QSAR).150,151 These models are, loosely speaking, based on finding empirical mathematical relationships between an experimental outcome (e.g., cytotoxicity) and various nanomaterial properties (e.g., ζ potential). Once such mathematical relationships have been established, they can subsequently be used to predict the experimental outcome also for other nanomaterials (not included in the set used to create the model) based on their respective properties. Typically, such nano-QSAR models are applied directly to “end point” data, such as cytotoxicity. Particularly for the cytotoxicity of metal oxide nanoparticles this appears to work well. This may be due to these particles all accumulating in lysosomes to a largely similar extent, and oxidative stress, for which the band-gap hypothesis152 may be applied, being the dominant mechanism of cytotoxicity; if there were, in addition, differences in uptake and distribution kinetics between the particles or a more subtle mixture of response, then focussing on only the end-point may not allow setting up a useful model. We envisage that instead applying nano-QSAR models to rate constants would give a more fundamental and broadly applicable description.
We should note that investigating how rate constants depend upon nanomaterial properties demands a significant amount of (kinetic) data. That is, the initial data is, for instance, number of nanoparticles per cell as a function of time, but from such data obviously only the rate constants for the given nanoparticle can be deduced; in order to study how rate constants depend upon nanoparticle properties thus demands kinetic data for a multitude of different particles. Currently this is not available, so this type of analysis cannot yet be done. It may be possible to perform such an analysis in future, if sufficient kinetically-oriented studies are published. However, most likely it will demand a concerted effort to acquire enough data, rather than separate studies from which the data can be pieced together post-publication. It will probably also require development of technologies that can assess cell uptake and intracellular distribution kinetics with high-throughput, and so we expect progress here to only come once such technologies are widely available and in use.
Another aspect where significant technical development will need to take place is in the assessment, and understanding, of cell-to-cell variability in nanomaterial distribution kinetics. Currently, we only have “snapshots” (i.e., one or two handful of cells) of how the kinetics differ within cells of the same population.111,112 It is nevertheless clear that the variability is large enough that advances in quantifying it must come from more high-throughput techniques than semi-manual live-cell imaging of cells over time. It would also seem clear that the variability will matter, in the sense that if endolysosomal accumulation can vary between 35–60%,112 then subsequent endosomal escape and drug release will likely vary even wider. Attention from a more theoretical point of view is thus also needed in order to provide the appropriate framework to consider the aspect of variability. The drivers of the variability are, naturally, also unknown at present, but progress will only come once we are able to quantify it.
Finally, an initially almost independent strand within kinetic studies could be a more sophisticated description than that allowed by linear rate equations (such as those shown in Fig. 1 and used as examples throughout). As discussed above, we expect on theoretical grounds that rate equations, while useful as approximations, are fundamentally not the right approach to describe the kinetics of cellular processes. It may seem extravagant to pursue more complex mathematical models, but, again as mentioned above, there are already hints in the experimental data (see Fig. 4c above) that delays and/or broadly distributed waiting times play a role. We expect such observations to become more common as experimental efforts, including from usage of tools and methodologies developed within molecular biophysics and contingent fields, uncover more details about the processes and this will necessitate developing appropriate models that describe the data aptly. We suggest that the theoretical basis for these models can usefully be adapted from similar models developed within the statistical physics of complex systems (we have previously suggested one such idea69), possibly with some further development. Ultimately, such models will both allow a more fundamental description, as well as a quantification of the limits of the simpler rate equation approach. Upon such a basis, we will (when the approximation is acceptable) have confidence in the simpler rate equation approach.
Overall, we envisage that coupling of kinetic thinking to experimental exploration and nanomaterials development will provide fruitful outcomes and hope that the notes supplied here may further that potential.
Conflicts of interest
There are no conflicts to declare.Notes and references
- J. Wolfram and M. Ferrari, Nano Today, 2019, 25, 85–98 CrossRef CAS PubMed.
- D. Peer, J. M. Karp, S. Hong, O. C. Farokhzad, R. Margalit and R. Langer, Nat. Nanotechnol., 2007, 2, 751–760 CrossRef CAS PubMed.
- E. Ruoslahti, S. N. Bhatia and M. J. Sailor, J. Cell Biol., 2010, 188, 759–768 CrossRef CAS.
- J. Kreuter, Adv. Drug Delivery Rev., 2012, 64, 213–222 CrossRef.
- D. Brambilla, B. Le Droumaguet, J. Nicolas, S. H. Hashemi, L.-P. Wu, S. M. Moghimi, P. Couvreur and K. Andrieux, Nanomedicine, 2011, 7, 521–540 CrossRef CAS.
- I. Brasnjevic, H. W. M. Steinbusch, C. Schmitz and P. Martinez-Martinez, Prog. Neurobiol., 2009, 87, 212–251 CrossRef CAS PubMed.
- T. F. Martens, K. Remaut, J. Demeester, S. C. De Smedt and K. Braeckmans, Nano Today, 2014, 9, 344–364 CrossRef CAS.
- J. Gilleron, W. Querbes, A. Zeigerer, A. Borodovsky, G. Marsico, U. Schubert, K. Manygoats, S. Seifert, C. Andree, M. Stöter, H. Epstein-Barash, L. Zhang, V. Koteliansky, K. Fitzgerald, E. Fava, M. Bickle, Y. Kalaidzidis, A. Akinc, M. Maier and M. Zerial, Nat. Biotechnol., 2013, 31, 638–646 CrossRef CAS PubMed.
- G. Oberdörster, E. Oberdörster and J. Oberdörster, Environ. Health Perspect., 2005, 113, 823–839 CrossRef PubMed.
- A. Nel, T. Xia, L. Mädler and N. Li, Science, 2006, 311, 622–627 CrossRef CAS PubMed.
- E. Valsami-Jones and I. Lynch, Science, 2015, 350, 388–389 CrossRef CAS PubMed.
- D. E. Owens and N. A. Peppas, Int. J. Pharm., 2006, 307, 93–102 CrossRef CAS PubMed.
- M. Li, K. T. Al-Jamal, K. Kostarelos and J. Reineke, ACS Nano, 2010, 4, 6303–6317 CrossRef CAS PubMed.
- S. M. Moghimi, A. C. Hunter and T. L. Andresen, Annu. Rev. Pharmacol. Toxicol., 2012, 52, 481–503 CrossRef CAS PubMed.
- Z. Lin, N. A. Monteiro-Riviere and J. E. Riviere, WIREs Nanomedicine and Nanobiotechnology, 2015, 7, 189–217 CrossRef CAS PubMed.
- H. Kang, S. Mintri, A. V. Menon, H. Y. Lee, H. S. Choi and J. Kim, Nanoscale, 2015, 7, 18848–18862 RSC.
- N. D. Donahue, H. Acar and S. Wilhelm, Adv. Drug Delivery Rev., 2019, 143, 68–96 CrossRef CAS PubMed.
- M. Rowland and T. N. Tozer, Clinical Pharmacokinetics and Pharmacodynamics: Concepts and Applications, Wolters Kluwer Health/Lippincott William & Wilkins, Baltimore, MD, 4th edn, 2011 Search PubMed.
- T.-G. Iversen, T. Skotland and K. Sandvig, Nano Today, 2011, 6, 176–185 CrossRef CAS.
- J. Rejman, V. Oberle, I. S. Zuhorn and D. Hoekstra, Biochem. J., 2004, 377, 159–169 CrossRef CAS PubMed.
- B. D. Chithrani and W. C. W. Chan, Nano Lett., 2007, 7, 1542–1550 CrossRef CAS PubMed.
- A. Salvati, C. Åberg, T. dos Santos, J. Varela, P. Pinto, I. Lynch and K. A. Dawson, Nanomedicine, 2011, 7, 818–826 CrossRef CAS PubMed.
- S. D. Conner and S. L. Schmid, Nature, 2003, 422, 37–44 CrossRef CAS PubMed.
- G. J. Doherty and H. T. McMahon, Annu. Rev. Biochem., 2009, 78, 857–902 CrossRef CAS PubMed.
- X. Jiang, C. Röcker, M. Hafner, S. Brandholt, R. M. Dörlich and G. U. Nienhaus, ACS Nano, 2010, 4, 6787–6797 CrossRef CAS PubMed.
- T. Wang, J. Bai, X. Jiang and G. U. Nienhaus, ACS Nano, 2012, 6, 1251–1259 CrossRef CAS PubMed.
- D. Vercauteren, J. Rejman, T. F. Martens, J. Demeester, S. C. De Smedt and K. Braeckmans, J. Controlled Release, 2012, 161, 566–581 CrossRef CAS PubMed.
- L. Shang, K. Nienhaus and G. U. Nienhaus, J. Nanobiotechnol., 2014, 12, 5 CrossRef PubMed.
- S. Behzadi, V. Serpooshan, W. Tao, M. A. Hamaly, M. Y. Alkawareek, E. C. Dreaden, D. Brown, A. M. Alkilany, O. C. Farokhzad and M. Mahmoudi, Chem. Soc. Rev., 2017, 46, 4218–4244 RSC.
- K. Fytianos, F. Blank and L. Müller, in Biological Responses to Nanoscale Particles: Molecular and Cellular Aspects and Methodological Approaches, ed. P. Gehr and R. Zellner, Springer International Publishing, Cham, 2019, pp. 191–211 Search PubMed.
- V. Francia, D. Montizaan and A. Salvati, Beilstein J. Nanotechnol., 2020, 11, 338–353 CrossRef CAS PubMed.
- A. Elsaesser, A. Taylor, G. S. de Yanés, G. McKerr, E.-M. Kim, E. O'Hare and C. V. Howard, Nanomedicine, 2010, 5, 1447–1457 CrossRef CAS PubMed.
- D. Vanhecke, L. Rodriguez-Lorenzo, M. J. D. Clift, F. Blank, A. Petri-Fink and B. Rothen-Rutishauser, Nanomedicine, 2014, 9, 1885–1900 CrossRef CAS PubMed.
- B. Drasler, D. Vanhecke, L. Rodriguez-Lorenzo, A. Petri-Fink and B. Rothen-Rutishauser, Nanomedicine, 2017, 12, 1095–1099 CrossRef CAS PubMed.
- A. Ivask, A. J. Mitchell, A. Malysheva, N. H. Voelcker and E. Lombi, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2018, 10, e1486 Search PubMed.
- A. Salvati, I. Nelissen, A. Haase, C. Åberg, S. Moya, A. Jacobs, F. Alnasser, T. Bewersdorff, S. Deville, A. Luch and K. A. Dawson, NanoImpact, 2018, 9, 42–50 CrossRef.
- B. D. Chithrani, A. A. Ghazani and W. C. W. Chan, Nano Lett., 2006, 6, 662–668 CrossRef CAS.
- E. C. Cho, J. Xie, P. A. Wurm and Y. Xia, Nano Lett., 2009, 9, 1080–1084 CrossRef CAS.
- K.-S. Ho and W.-T. Chan, J. Anal. At. Spectrom., 2010, 25, 1114–1122 RSC.
- D. Drescher, C. Giesen, H. Traub, U. Panne, J. Kneipp and N. Jakubowski, Anal. Chem., 2012, 84, 9684–9688 CrossRef CAS PubMed.
- H. Paysen, N. Loewa, A. Stach, J. Wells, O. Kosch, S. Twamley, M. R. Makowski, T. Schaeffter, A. Ludwig and F. Wiekhorst, Sci. Rep., 2020, 10, 1922 CrossRef CAS PubMed.
- M. J. Ware, B. Godin, N. Singh, R. Majithia, S. Shamsudeen, R. E. Serda, K. E. Meissner, P. Rees and H. D. Summers, ACS Nano, 2014, 8, 6693–6700 CrossRef CAS PubMed.
- C. Mühlfeld, B. Rothen-Rutishauser, D. Vanhecke, F. Blank, P. Gehr and M. Ochs, Part. Fibre Toxicol., 2007, 4, 11 CrossRef PubMed.
- C. Brandenberger, C. Mühlfeld, Z. Ali, A.-G. Lenz, O. Schmid, W. J. Parak, P. Gehr and B. Rothen-Rutishauser, Small, 2010, 6, 1669–1678 CrossRef CAS PubMed.
- A. Elsaesser, C. A. Barnes, G. McKerr, A. Salvati, I. Lynch, K. A. Dawson and C. V. Howard, Nanomedicine, 2011, 6, 1189–1198 CrossRef CAS PubMed.
- M. Safi, J. Courtois, M. Seigneuret, H. Conjeaud and J.-F. Berret, Biomaterials, 2011, 32, 9353–9363 CrossRef CAS PubMed.
- X. Jiang, J. Dausend, M. Hafner, A. Musyanovych, C. Röcker, K. Landfester, V. Mailänder and G. U. Nienhaus, Biomacromolecules, 2010, 11, 748–753 CrossRef CAS PubMed.
- K. Yaehne, A. Tekrony, A. Clancy, Y. Gregoriou, J. Walker, K. Dean, T. Nguyen, A. Doiron, K. Rinker, X. Y. Jiang, S. Childs and D. Cramb, Small, 2013, 9, 3118–3127 CrossRef CAS PubMed.
- L. Treuel, S. Brandholt, P. Maffre, S. Wiegele, L. Shang and G. U. Nienhaus, ACS Nano, 2014, 8, 503–513 CrossRef CAS PubMed.
- A. R. Collins, B. Annangi, L. Rubio, R. Marcos, M. Dorn, C. Merker, I. Estrela-Lopis, M. R. Cimpan, M. Ibrahim, E. Cimpan, M. Ostermann, A. Sauter, N. E. Yamani, S. Shaposhnikov, S. Chevillard, V. Paget, R. Grall, J. Delic, F. G. de-Cerio, B. Suarez-Merino, V. Fessard, K. N. Hogeveen, L. M. Fjellsbø, E. R. Pran, T. Brzicova, J. Topinka, M. J. Silva, P. E. Leite, A. R. Ribeiro, J. M. Granjeiro, R. Grafström, A. Prina-Mello and M. Dusinska, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2017, 9, e1413 Search PubMed.
- H. D. Summers, P. Rees, M. D. Holton, M. R. Brown, S. C. Chappell, P. J. Smith and R. J. Errington, Nat. Nanotechnol., 2011, 6, 170–174 CrossRef CAS PubMed.
- P. Rees, J. W. Wills, M. R. Brown, C. M. Barnes and H. D. Summers, Nat. Commun., 2019, 10, 2341 CrossRef PubMed.
- B. Kang, M. A. Mackey and M. A. El-Sayed, J. Am. Chem. Soc., 2010, 132, 1517–1519 CrossRef CAS PubMed.
- L. Schermelleh, A. Ferrand, T. Huser, C. Eggeling, M. Sauer, O. Biehlmaier and G. P. C. Drummen, Nat. Cell Biol., 2019, 21, 72–84 CrossRef CAS PubMed.
- S. Schübbe, C. Cavelius, C. Schumann, M. Koch and A. Kraegeloh, Adv. Eng. Mater., 2010, 12, 417–422 CrossRef.
- T. Müller, C. Schumann and A. Kraegeloh, ChemPhysChem, 2012, 13, 1986–2000 CrossRef PubMed.
- Y. Li, L. Shang and G. U. Nienhaus, Nanoscale, 2016, 8, 7423–7429 RSC.
- O. Lozano, J. Mejia, B. Masereel, O. Toussaint, D. Lison and S. Lucas, Nanotoxicology, 2012, 6, 263–271 CrossRef CAS PubMed.
- N. Ogrinc, P. Pelicon, P. Vavpetič, M. Kelemen, N. Grlj, L. Jeromel, S. Tomić, M. Čolić and A. Beran, Nucl. Instrum. Methods Phys. Res., Sect. B, 2013, 306, 121–124 CrossRef CAS.
- J. C. G. Jeynes, C. Jeynes, M. J. Merchant and K. J. Kirkby, Analyst, 2013, 138, 7070–7074 RSC.
- N. B. Shah, J. Dong and J. C. Bischof, Mol. Pharm., 2011, 8, 176–184 CrossRef CAS PubMed.
- C. Wilhelm, F. Gazeau, J. Roger, J. N. Pons and J.-C. Bacri, Langmuir, 2002, 18, 8148–8155 CrossRef CAS.
- C. Bussy, J. Cambedouzou, S. Lanone, E. Leccia, V. Heresanu, M. Pinault, M. Mayne-l'Hermite, N. Brun, C. Mory, M. Cotte, J. Doucet, J. Boczkowski and P. Launois, Nano Lett., 2008, 8, 2659–2663 CrossRef CAS PubMed.
- J. T. Rashkow, S. C. Patel, R. Tappero and B. Sitharaman, J. R. Soc., Interface, 2014, 11, 20131152 CrossRef PubMed.
- H. E. Pace, N. J. Rogers, C. Jarolimek, V. A. Coleman, C. P. Higgins and J. F. Ranville, Anal. Chem., 2011, 83, 9361–9369 CrossRef CAS PubMed.
- R. J. B. Peters, Z. H. Rivera, G. van Bemmel, H. J. P. Marvin, S. Weigel and H. Bouwmeester, Anal. Bioanal. Chem., 2014, 406, 3875–3885 CAS.
- H. Peuschel, T. Ruckelshausen, C. Cavelius and A. Kraegeloh, BioMed Res. Int., 2015, 2015, 961208 Search PubMed.
- K. Shapero, F. Fenaroli, I. Lynch, D. C. Cottell, A. Salvati and K. A. Dawson, Mol. BioSyst., 2011, 7, 371–378 RSC.
- C. Åberg, J. A. Varela, L. W. Fitzpatrick and K. A. Dawson, Sci. Rep., 2016, 6, 34457 CrossRef PubMed.
- A. Lesniak, A. Salvati, M. J. Santos-Martinez, M. W. Radomski, K. A. Dawson and C. Åberg, J. Am. Chem. Soc., 2013, 135, 1438–1444 CrossRef CAS PubMed.
- X. Jiang, A. Musyanovych, C. Röcker, K. Landfester, V. Mailänder and G. U. Nienhaus, Nanoscale, 2011, 3, 2028 RSC.
- L. Yang, L. Shang and G. U. Nienhaus, Nanoscale, 2013, 5, 1537–1543 RSC.
- T. T. Goodman, J. Chen, K. Matveev and S. H. Pun, Biotechnol. Bioeng., 2008, 101, 388–399 CrossRef CAS PubMed.
- I. Langmuir, J. Am. Chem. Soc., 1918, 40, 1361–1403 CrossRef CAS.
- A. Ciechanover, A. L. Schwartz, A. Dautry-Varsat and H. F. Lodish, J. Biol. Chem., 1983, 258, 9681–9689 CrossRef CAS.
- S. S. Jambhekar and P. J. Breen, Basic Pharmacokinetics, Pharmaceutical Press, London, UK, 2nd edn, 2012 Search PubMed.
- W. J. Spruill, J. T. DiPiro, D. W. W. Fashp Pharmd, R. A. Blouin and J. M. P. Bcop Pharmd, Concepts in Clinical Pharmacokinetics, American Society of Health-System Pharmacists, Bethesda, MD, 6th edn, 2014 Search PubMed.
- W. Feller, An introduction to probability theory and its applications, Wiley, London, UK, 3rd edn, 1968, vol. 1 Search PubMed.
- N. G. van Kampen, Stochastic Processes in Physics and Chemistry, Elsevier, Amsterdam, 3rd edn, 2007 Search PubMed.
- S. M. Ross, Introduction to probability and statistics for engineers and scientists, Academic Press, London, UK, 5th edn, 2014 Search PubMed.
- S. Deville, W. W. Hadiwikarta, N. Smisdom, B. Wathiong, M. Ameloot, I. Nelissen and J. Hooyberghs, Int. J. Nanomed., 2017, 2017, 459–472 CrossRef PubMed.
- A. Salvati, A. S. Pitek, M. P. Monopoli, K. Prapainop, F. Baldelli Bombelli, D. R. Hristov, P. M. Kelly, C. Åberg, E. Mahon and K. A. Dawson, Nat. Nanotechnol., 2013, 8, 137–143 CrossRef CAS PubMed.
- O. Lunov, V. Zablotskii, T. Syrovets, C. Röcker, K. Tron, G. U. Nienhaus and T. Simmet, Biomaterials, 2011, 32, 547–555 CrossRef CAS PubMed.
- J. A. Kim, C. Åberg, A. Salvati and K. A. Dawson, Nat. Nanotechnol., 2012, 7, 62–68 CrossRef CAS PubMed.
- J. A. Varela, M. Bexiga, C. Åberg, J. C. Simpson and K. A. Dawson, J. Nanobiotechnol., 2012, 10, 39 CrossRef CAS PubMed.
- J. Blechinger, A. T. Bauer, A. A. Torrano, C. Gorzelanny, C. Bräuchle and S. W. Schneider, Small, 2013, 9, 3970–3980 CrossRef CAS PubMed.
- K. Li and M. Schneider, J. Biomed. Opt., 2014, 19, 101505 CrossRef PubMed.
- C. Loos, T. Syrovets, A. Musyanovych, V. Mailänder, K. Landfester, G. U. Nienhaus and T. Simmet, Beilstein J. Nanotechnol., 2014, 5, 2403–2412 CrossRef PubMed.
- W.-L. L. Suen and Y. Chau, J. Pharm. Pharmacol., 2014, 66, 564–573 CrossRef CAS PubMed.
- K. Kettler, C. Giannakou, W. H. de Jong, A. J. Hendriks and P. Krystek, J. Nanopart. Res., 2016, 18, 286 CrossRef PubMed.
- P. Jurney, R. Agarwal, V. Singh, D. Choi, K. Roy, S. V. Sreenivasan and L. Shi, J. Controlled Release, 2017, 245, 170–176 CrossRef CAS PubMed.
- M. P. Monopoli, C. Åberg, A. Salvati and K. A. Dawson, Nat. Nanotechnol., 2012, 7, 779–786 CrossRef CAS PubMed.
- M. Mahmoudi, I. Lynch, M. R. Ejtehadi, M. P. Monopoli, F. B. Bombelli and S. Laurent, Chem. Rev., 2011, 111, 5610–5637 CrossRef CAS PubMed.
- C. D. Walkey and W. C. W. Chan, Chem. Soc. Rev., 2012, 41, 2780–2799 RSC.
- L. Treuel and G. Nienhaus, Biophys. Rev., 2012, 4, 137–147 CrossRef CAS PubMed.
- P. del Pino, B. Pelaz, Q. Zhang, P. Maffre, G. U. Nienhaus and W. J. Parak, Mater. Horiz., 2014, 1, 301–313 RSC.
- W. Jiang, B. Y. S. Kim, J. T. Rutka and W. C. W. Chan, Nat. Nanotechnol., 2008, 3, 145–150 CrossRef CAS PubMed.
- H. T. McMahon and E. Boucrot, Nat. Rev. Mol. Cell Biol., 2011, 12, 517–533 CrossRef CAS PubMed.
- T. Kirchhausen, Annu. Rev. Biochem., 2000, 69, 699–727 CrossRef CAS PubMed.
- M. Ehrlich, W. Boll, A. van Oijen, R. Hariharan, K. Chandran, M. L. Nibert and T. Kirchhausen, Cell, 2004, 118, 591–605 CrossRef CAS PubMed.
- S. Mayor and R. E. Pagano, Nat. Rev. Mol. Cell Biol., 2007, 8, 603–612 CrossRef CAS PubMed.
- L. Johannes, R. G. Parton, P. Bassereau and S. Mayor, Nat. Rev. Mol. Cell Biol., 2015, 16, 311–321 CrossRef CAS PubMed.
- K. Sandvig, S. Kavaliauskiene and T. Skotland, Histochem. Cell Biol., 2018, 150, 107–118 CrossRef CAS PubMed.
- A. P. A. Ferreira and E. Boucrot, Trends Cell Biol., 2018, 28, 188–200 CrossRef CAS PubMed.
- M. Stoeber, P. Schellenberger, C. A. Siebert, C. Leyrat, A. Helenius and K. Grünewald, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E8069–E8078 CrossRef CAS PubMed.
- O. O. Glebov, N. A. Bright and B. J. Nichols, Nat. Cell Biol., 2006, 8, 46–54 CrossRef CAS PubMed.
- R. Lundmark, G. J. Doherty, M. T. Howes, K. Cortese, Y. Vallis, R. G. Parton and H. T. McMahon, Curr. Biol., 2008, 18, 1802–1808 CrossRef CAS PubMed.
- G. J. Doherty and R. Lundmark, Biochem. Soc. Trans., 2009, 37, 1061–1065 CrossRef CAS PubMed.
- V. Bitsikas, I. R. Corrêa Jr and B. J. Nichols, eLife, 2014, 3, e03970 CrossRef PubMed.
- A. V. Weigel, M. M. Tamkun and D. Krapf, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E4591–E4600 CrossRef CAS PubMed.
- D. Vercauteren, H. Deschout, K. Remaut, J. F. J. Engbersen, A. T. Jones, J. Demeester, S. C. De Smedt and K. Braeckmans, ACS Nano, 2011, 5, 7874–7884 CrossRef CAS PubMed.
- P. Sandin, L. W. Fitzpatrick, J. C. Simpson and K. A. Dawson, ACS Nano, 2012, 6, 1513–1521 CrossRef CAS PubMed.
- J. Reinholz, C. Diesler, S. Schöttler, M. Kokkinopoulou, S. Ritz, K. Landfester and V. Mailänder, Acta Biomater., 2018, 71, 432–443 CrossRef CAS PubMed.
- M. Liu, Q. Li, L. Liang, J. Li, K. Wang, J. Li, M. Lv, N. Chen, H. Song, J. Lee, J. Shi, L. Wang, R. Lal and C. Fan, Nat. Commun., 2017, 8, 1–10 CrossRef PubMed.
- B. Alberts, A. Johnson, J. Lewis, M. Raff, K. Roberts and P. Walter, in Molecular Biology of the Cell, Garland Science, New York, 5th edn, 2008 Search PubMed.
- J. Huotari and A. Helenius, EMBO J., 2011, 30, 3481–3500 CrossRef CAS PubMed.
- M. Jovic, M. Sharma, J. Rahajeng and S. Caplan, Histol. Histopathol., 2010, 25, 99–112 CAS.
- A. H. Hutagalung and P. J. Novick, Physiol. Rev., 2011, 91, 119–149 CrossRef CAS PubMed.
- H. Stenmark, Nat. Rev. Mol. Cell Biol., 2009, 10, 513–525 CrossRef CAS PubMed.
- J. Rink, E. Ghigo, Y. Kalaidzidis and M. Zerial, Cell, 2005, 122, 735–749 CrossRef CAS PubMed.
- J. P. Luzio, P. R. Pryor and N. A. Bright, Nat. Rev. Mol. Cell Biol., 2007, 8, 622–632 CrossRef CAS PubMed.
- N. A. Bright, L. J. Davis and J. P. Luzio, Curr. Biol., 2016, 26, 2233–2245 CrossRef CAS PubMed.
- P. Chavrier, R. G. Parton, H. P. Hauri, K. Simons and M. Zerial, Cell, 1990, 62, 317–329 CrossRef CAS PubMed.
- Y. Feng, B. Press and A. Wandinger-Ness, J. Cell Biol., 1995, 131, 1435–1452 CrossRef CAS PubMed.
- P. A. Vanlandingham and B. P. Ceresa, J. Biol. Chem., 2009, 284, 12110–12124 CrossRef CAS PubMed.
- A. Kucera, O. Bakke and C. Progida, Commun. Integr. Biol., 2016, 9, e1204498 CrossRef PubMed.
- W. H. I. Humphries, C. J. Szymanski and C. K. Payne, PLoS One, 2011, 6, e26626 CrossRef CAS PubMed.
- J. A. Varela, C. Åberg, J. C. Simpson and K. A. Dawson, Small, 2015, 11, 2026–2031 CrossRef CAS PubMed.
- E. M. Manders, J. Stap, G. J. Brakenhoff, R. van Driel and J. A. Aten, J. Cell Sci., 1992, 103, 857–862 CrossRef CAS PubMed.
- E. M. M. Manders, F. J. Verbeek and J. A. Aten, J. Microsc., 1993, 169, 375–382 CrossRef CAS PubMed.
- M. Gex-Fabry and C. DeLisi, Am. J. Physiol., 1984, 247, R768–R779 CAS.
- C. Åberg, J. A. Kim, A. Salvati and K. A. Dawson, Nat. Nanotechnol., 2017, 12, 600–603 CrossRef PubMed.
- G. W. Doorley and C. K. Payne, Chem. Commun., 2012, 48, 2961–2963 RSC.
- F. Wang, L. Yu, M. P. Monopoli, P. Sandin, E. Mahon, A. Salvati and K. A. Dawson, Nanomedicine, 2013, 9, 1159–1168 CrossRef CAS PubMed.
- F. Bertoli, D. Garry, M. P. Monopoli, A. Salvati and K. A. Dawson, ACS Nano, 2016, 10, 10471–10479 CrossRef CAS PubMed.
- J.-P. Behr, Chim. Int. J. Chem., 1997, 51, 34–36 CAS.
- L. M. P. Vermeulen, S. C. De Smedt, K. Remaut and K. Braeckmans, Eur. J. Pharm. Biopharm., 2018, 129, 184–190 CrossRef CAS PubMed.
- Z. ur Rehman, D. Hoekstra and I. S. Zuhorn, ACS Nano, 2013, 7, 3767–3777 CrossRef CAS PubMed.
- Y. Yan, Z. W. Lai, R. J. A. Goode, J. Cui, T. Bacic, M. M. J. Kamphuis, E. C. Nice and F. Caruso, ACS Nano, 2013, 7, 5558–5567 CrossRef CAS PubMed.
- R. Xiong, F. Joris, S. Liang, R. De Rycke, S. Lippens, J. Demeester, A. Skirtach, K. Raemdonck, U. Himmelreich, S. C. De Smedt and K. Braeckmans, Nano Lett., 2016, 16, 5975–5986 CrossRef CAS PubMed.
- C. Åberg, J. A. Kim, A. Salvati and K. A. Dawson, EPL, 2013, 101, 38007 CrossRef.
- J. A. Kim, C. Åberg, G. de Cárcer, M. Malumbres, A. Salvati and K. A. Dawson, ACS Nano, 2013, 7, 7483–7494 CrossRef CAS PubMed.
- J. Crank, The mathematics of diffusion, Oxford University Press, Oxford, 2nd edn, 1975 Search PubMed.
- L. K. Limbach, Y. Li, R. N. Grass, T. J. Brunner, M. A. Hintermann, M. Muller, D. Gunther and W. J. Stark, Environ. Sci. Technol., 2005, 39, 9370–9376 CrossRef CAS PubMed.
- P. M. Hinderliter, K. R. Minard, G. Orr, W. B. Chrisler, B. D. Thrall, J. G. Pounds and J. G. Teeguarden, Part. Fibre Toxicol., 2010, 7, 36 CrossRef CAS PubMed.
- J. M. Cohen, J. G. Teeguarden and P. Demokritou, Part. Fibre Toxicol., 2014, 11, 20 CrossRef PubMed.
- G. M. DeLoid, J. M. Cohen, G. Pyrgiotakis and P. Demokritou, Nat. Protoc., 2017, 12, 355–371 CrossRef CAS PubMed.
- J. M. Cohen, G. M. DeLoid and P. Demokritou, Nanomedicine, 2015, 10, 3015–3032 CrossRef CAS PubMed.
- J. G. Teeguarden, P. M. Hinderliter, G. Orr, B. D. Thrall and J. G. Pounds, Toxicol. Sci., 2007, 95, 300–312 CrossRef CAS PubMed.
- T. Puzyn, B. Rasulev, A. Gajewicz, X. Hu, T. P. Dasari, A. Michalkova, H.-M. Hwang, A. Toropov, D. Leszczynska and J. Leszczynski, Nat. Nanotechnol., 2011, 6, 175–178 CrossRef CAS PubMed.
- R. Liu, R. Rallo, S. George, Z. Ji, S. Nair, A. E. Nel and Y. Cohen, Small, 2011, 7, 1118–1126 CrossRef CAS PubMed.
- E. Burello and A. P. Worth, Nanotoxicology, 2011, 5, 228–235 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2021 |