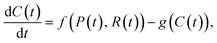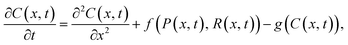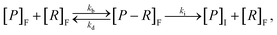Open Access Article
Open Access ArticleUnderstanding nano-engineered particle–cell interactions: biological insights from mathematical models
Stuart T.
Johnston
 *abc,
Matthew
Faria
bcd and
Edmund J.
Crampin
*abc,
Matthew
Faria
bcd and
Edmund J.
Crampin
 bce
bce
aSchool of Mathematics and Statistics, University of Melbourne, Parkville, Victoria 3010, Australia. E-mail: stuart.johnston@unimelb.edu.au
bARC Centre of Excellence in Convergent Bio-Nano Science and Technology, Melbourne School of Engineering, University of Melbourne, Parkville, Victoria 3010, Australia
cSystems Biology Laboratory, School of Mathematics and Statistics, Department of Biomedical Engineering, University of Melbourne, Parkville, Victoria 3010, Australia
dDepartment of Biomedical Engineering, University of Melbourne, Parkville, Victoria 3010, Australia
eSchool of Medicine, Faculty of Medicine Dentistry and Health Sciences, University of Melbourne, Parkville, Victoria 3010, Australia
First published on 9th March 2021
Abstract
Understanding the interactions between nano-engineered particles and cells is necessary for the rational design of particles for therapeutic, diagnostic and imaging purposes. In particular, the informed design of particles relies on the quantification of the relationship between the physicochemical properties of the particles and the rate at which cells interact with, and subsequently internalise, particles. Quantitative models, both mathematical and computational, provide a powerful tool for elucidating this relationship, as well as for understanding the mechanisms governing the intertwined processes of interaction and internalisation. Here we review the different types of mathematical and computational models that have been used to examine particle–cell interactions and particle internalisation. We detail the mathematical methodology for each type of model, the benefits and limitations associated with the different types of models, and highlight the advances in understanding gleaned from the application of these models to experimental observations of particle internalisation. We discuss the recent proposal and ongoing community adoption of standardised experimental reporting, and how this adoption is an important step toward unlocking the full potential of modelling approaches. Finally, we consider future directions in quantitative models of particle–cell interactions and highlight the need for hybrid experimental and theoretical investigations to address hitherto unanswered questions.
1 Introduction
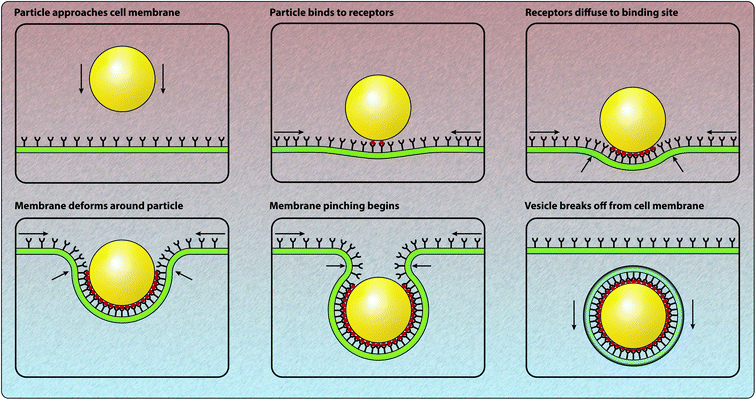
Understanding the mechanisms involved with the cellular association and internalisation of nano-engineered particles remains a key research challenge.1,2 There is significant potential for targeted drug and gene delivery, as well as the delivery of labelling and imaging agents, through the use of nano-engineered particles.3–6 However, the interactions between particles and cells are exceedingly complex and are not yet fully understood.7–10 This is not for a lack of effort: in the last ten years, the number of papers published per year relating to particle endocytosis or internalisation has increased threefold.† Increasingly, there is a realisation that mathematical and computational approaches can provide insight into the complicated physical, chemical and biological processes involved in the association and internalisation of particles.11–13 Here we focus on the various mathematical and computational techniques that have been used to provide quantitative insight into particle–cell interactions and the subsequent internalisation of particles by cells. Note that throughout this review we refer to nano-engineered particles to be consistent with the Food and Drug Administration's terminology for nanotechnology: “products that contain or are manufactured using materials in the nanoscale range.”14 This is a more broad definition than the use of the word “nanoparticles”, which implies that the particles have a diameter less than 100 nm, as particles created with nano-engineering techniques may have diameters in the hundreds of nanometres.The process of nano-engineered particle–cell interaction and internalisation first involves a particle arriving at the cell membrane.9 To arrive at the cell membrane, particles must travel through a fluid such as human blood or cell culture media. During this journey, particles will interact with free proteins present in the fluid.15,16 A layer of proteins, known as a protein corona, is formed via the adsorption of proteins to the particle surface.15,16 As such, the identity of the particle at the moment of particle–cell contact depends both on the protein content of the corona, as well as the physicochemical properties of the particle.15,16 Reviews of this process can be found elsewhere.15,16 Upon arrival at the cell membrane, particles can bind to receptors present on the membrane through either specific or non-specific interactions.17,18 Subsequently, at the beginning of the endocytosis process, the process by which the cell internalises external substances, the cell membrane begins to develop a budding structure (Fig. 1). The specific type of budding structure, such as clathrin-coated pits, caveolae or phagocytic invaginations, depends on the type of cell and the properties of the particle.8,9,17,19,20 In general, the budding structure ultimately fully envelops the particle and forms a vesicle, which can contain receptors and various extracellular material as well as the particle.18 Once inside the cytoplasm, in many endocytic pathways, the vesicle fuses with an early endosome. As the endosome matures, the acidity increases and hence the material contained within the endosome may be subject to degradation.18 The material within the endosome can also be recycled to the cell membrane, a process referred to as exocytosis. There are a range of endocytic pathways that are involved in the internalisation of nano-engineered particles, such as phagocytosis, macropinocytosis, clathrin-mediated endocytosis and clathrin-independent endocytosis, which includes caveolae-mediated endocytosis.7,19,21,22 Certain endocytosis mechanisms are restricted to specialised cell types.19 In particular, phagocytosis, which is the primary mechanism of internalisation for larger particles with a diameter around 1 μm, only occurs in phagocytes, such as neutrophils, macrophages and monocytes.7,20 In general, there is a size-dependent relationship between the size of the particle and the dominant endocytic pathway.21–26 Previous research by Rejman et al.21 suggests that clathrin-mediated endocytosis is the preferred pathway for particles up to 200 nm in diameter. However, this observation is in conflict with the observation that clathrin-coated vesicles are typically 60–120 nm in diameter,27 as 200 nm diameter particles cannot be fully enclosed by 60–120 nm diameter vesicles. This highlights the uncertainty about which specific internalisation pathway is employed to internalise particles of a particular size. Suen and Chau22 report that only caveolae-mediated endocytosis occurs for 250 nm particles, caveolae-mediated endocytosis dominates clathrin-mediated endocytosis for 50 nm particles, and that there is no preference for either endocytosis pathway for 120 nm particles. Suen and Chau22 also find that the uptake rate of the particles depends on the particle size, with 50 nm particles internalised most rapidly and 250 nm particles internalised slowest. Shape, charge and surface chemistry have also been demonstrated to influence the rate of endocytosis, as well as influence cell fate.28–39 In this review we predominantly focus on receptor-mediated endocytosis as a pathway for particle interaction and internalisation, rather than phagocytosis or macropinocytosis. In particular, we focus on the role of mathematical and computational models to provide insight into how the physicochemical properties of nano-engineered particles influence interaction and internalisation.
 | ||
| Fig. 1 Schematic of particle–cell interactions and the various modelling approaches applied to different components of the interaction and internalisation process. | ||
In general, the use of mathematical and computational models provides a range of valuable benefits, particularly when employed in concert with experimental data. Mathematical models can be utilised to provide insight into specific mechanisms that may not be obtainable from experimental data. Further, models can be employed to integrate sets of experimental data, which may not have originated from within the same laboratory, to generate additional information compared to the individual datasets. Once sufficient data has been integrated, synthesised and analysed, predictions obtained from mathematical models can be used to inform future experimental designs via prediction of de novo interactions or behaviour.
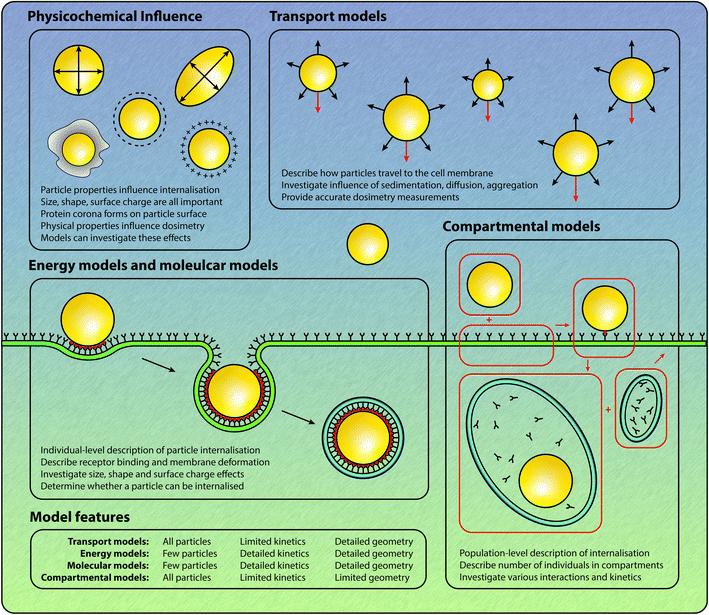
Quantitative predictions about the strength of interaction and the rate of internalisation based on particle characteristics would be invaluable for the rational design of particles in the context of drug delivery and imaging. As such, mathematical models have been employed in an attempt to understand and quantify the effect of size, shape, charge and surface chemistry on particle–cell interactions and internalisation.40–44 Broadly, mathematical models of the internalisation process can be classified into four types of models, as shown in Fig. 1:
• Compartmental models, which describe the temporal evolution of the number of various entities, including particles, receptors and vesicles. In these models interactions between particles and cellular entities are assumed to occur in a spatially-independent manner, which gives rise to systems of ordinary differential equations.
• Energy models, which describe the wrapping of particles by the cell membrane, and give insight into the balance between the energy gained from particle–receptor binding and the energy required for membrane deformation.
• Molecular models, which model the interaction and internalisation process by evaluating Newton's laws of motion for each atom. Such models provide great insight but are prohibitively computationally expensive for simulations on all but the smallest temporal and spatial scales; and,
• Transport models, which describe the transport process of particles in fluid, and the removal of particles from the fluid by cellular interaction and internalisation. In both in vitro and in vivo experiments, the particles are transported to the cell membrane via fluid. Hence, to fully understand the internalisation of particles by cells, the processes by which the particles arrive at the cells must be considered.
In this review we provide information regarding the assumptions and techniques involved in each type of model, as well as the benefits and limitations of a particular type of model. We discuss the collective insight obtained from analysing and simulating the models in the context of particle internalisation, as well as the potential for each model to interface with experimental data. We highlight the ongoing community adoption of recently-proposed experimental reporting standards as a welcome step towards a future where experimental data and mathematical models can be readily combined to generate further insight. Finally, we discuss future opportunities for interdisciplinary work involving experimental and theoretical approaches to answer questions about particle–cell interactions and particle internalisation that cannot currently be resolved.
2 A brief introduction to mathematical modelling
Mathematical modelling is a flexible tool that can be employed to extract additional insight from experimental observations. Once a mathematical model has been formulated and parameterised (fitted to data), the model can be used to extrapolate beyond the range of the data used in model fitting, to investigate different potential mechanisms and to formulate new hypotheses. The flexibility in mathematical modelling means that there are a multitude of choices that must be made when selecting the class of model for a particular application. However, it is rarely immediately obvious which choices will best represent the system of interest. In this section we introduce the modelling choices that must be considered along with the benefits, drawbacks and assumptions associated with each class of model. We briefly discuss the methods of obtaining solutions to different classes of models, and present examples of each class of model in the context of particle–cell interaction and internalisation in Table 1. Detailed discussion about the insight obtained about particle–cell interaction and internalisation from the application of these models can be found in the following sections. In this section we subdivide models according to the type of mathematical formalism that is used to describe the particle–cell interaction and internalisation, showing that these fall into several distinct mathematical categories according to the model features. In contrast, in subsequent sections, we focus on different aspects of particle–cell interaction and internalisation, and in each case provide a review of the different mathematical models that have been developed, and the insights that have been gained from these models.| Model class | Model features | Interaction/internalisation model | Select references |
|---|---|---|---|
| Ordinary differential equation | Continuous variables, deterministic, analytic and numerical solutions | Compartmental models | 22, 42 and 45–51 |
| Energy and force models | 25 | ||
| Molecular models | 52 | ||
| Partial differential equation | Continuous variables, spatial effects, deterministic, numerical solutions | Compartmental models | 53 |
| Energy and force models | 41 and 44 | ||
| Transport models | 54–56 | ||
| Stochastic differential equation | Continuous variables, stochastic effects, numerical solutions | Compartmental models | 57 |
| Deterministic discrete model | Discrete variables, deterministic, numerical solutions | Energy and force models | 58 |
| Transport models | 59 and 60 | ||
| Stochastic discrete model | Discrete variables, stochastic effects, numerical solutions | Compartmental models | 61 and 62 |
| Transport models | 63 and 64 |
Differential equations
A common class of mathematical models are differential equation models.65,66 In differential equation models, a key assumption is that the quantity of interest, such as the number of particles or receptors, can be represented as a continuous variable (i.e. not restricted to integers).65 This assumption is appropriate provided that the quantity of interest is not limited to small numbers.65 Additionally, outside of specific classes of differential equations, these models do not include stochastic effects such as environmental or demographic stochasticity.66 One implication of this is that all entities represented by a single quantity of interest are identical.63 Further, given an initial state for the quantities of interest and a set of parameter values, the solution trajectory will always be the same.65 Stochastic effects are most important at small values of the quantity of interest.67 Differential equation models can be separated into three main categories: ordinary differential equations (ODEs), partial differential equations (PDEs) and stochastic differential equations (SDEs).66ODE models are the simplest type of differential equation model, and describe the evolution of the quantities(s) of interest in time based on the interactions between entities. An example ODE model of particle–receptor binding is68
The assumption that spatial effects are unimportant can be relaxed through the use of PDE models, where the role of space is explicitly considered.66 An example PDE model of particle–receptor binding is
SDE models allow for stochastic effects to be incorporated within a differential equation framework.66 An example SDE model of particle–receptor binding is
| dC(t) = f(P(t), R(t))dt − g(C(t))dt + dW(t), |
Force-based models such as molecular dynamics models can be considered as another type of differential equation model.52 Here, the change in location of individuals (typically molecules) occurs due to the velocity of individuals which, in turn, changes due to the force experienced by each individual according to Newton's laws of motion. The interaction forces between individuals relies on a specified potential function (or force field).52 Due to the large number of individuals, analytic solutions to the system of equations cannot typically be obtained. Numerical solutions are possible via integration through time, though the structure of the interactions between individuals means that these solutions are limited in terms of the time and space that can be represented.72 Further detail can be found in the section on molecular dynamics models.
Discrete models
Another class of mathematical models are discrete models. Instead of treating the quantity of interest as a continuous variable, the variable is restricted to integer states.73 As such, discrete models are well-suited for describing processes that occur with small numbers of entities.67 The model evolves by considering how single events can change the integer state of the system. For example, consider the above model where we describe the evolution of the number of particle–receptor complexes over time. In a discrete framework, we can describe this through| Ck = f(i, j)Ck−1 + g(k + 1)Ck+1 − f(i, j)Ck − g(k)Ck, |
| Ct = Ct−1 + X(Pt−1, Rt−1, Ct−1), |
3 Compartmental models
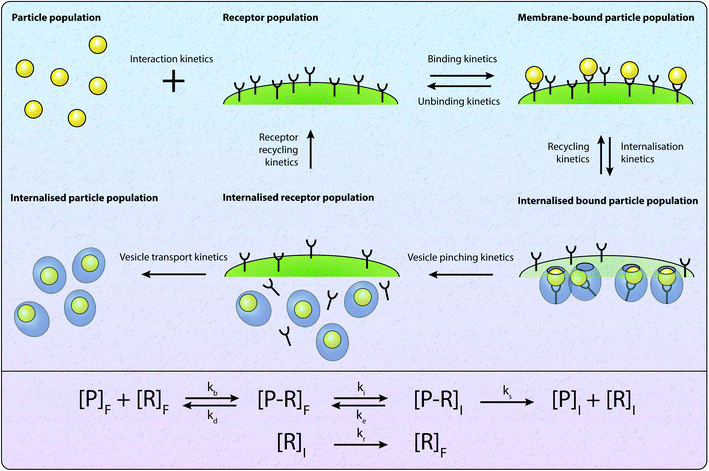
To investigate the insight obtained about particle–cell interaction and internalisation via mathematical approaches, we first consider compartmental models of particle–cell interactions and particle internalisation. Compartmental models are relatively commonly employed to describe the internalisation process,22,42,45–47,49–51,74 and have been widely used to describe the related process of the binding and internalisation of molecules.68 A schematic of the processes considered in compartmental models is presented in Fig. 2, where compartments represent “species” such as particles, receptors and particle–receptor complexes. The simplest type of compartmental model involves only receptors and particles, and describes the evolution of the number of particle–receptor complexes.68Receptor binding
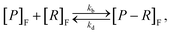
Given a number of receptors, [R]F, and a number density of particles, [P]F, the evolution of the density of particle–receptor complexes, [P − R]F, can be represented aswhere kb is a constant that represents the binding rate between the receptors and particles, and kd is a constant that represents the disassociation of the particle–receptor complex.68 The subscript F highlights that these species are present in the fluid, rather than inside the cell. This model is relatively simple, but provides a platform for more detailed compartmental models, which have been employed to obtain insight into particle internalisation.22,42,47,49,74,75 In particular, this model relies on the assumption that the number of receptors is essentially unchanged, implying that there are significantly more receptors on the cell membrane than particles arriving at the cell membrane. To evaluate whether this assumption is valid, the transport of the particles through fluid to the cell membrane must be well understood.54 The model further assumes that there is no local spatial variation in the receptors or particles, the particles are roughly the same size as the receptors, and that the particles can only be bound to a single receptor at a time. Given the influence of size effects on particle internalisation21,22 and the number of experiments performed with particles of different sizes, it is reasonable to assume that incorporating size dependence is important. Additionally, this type of model does not describe the internalisation of the particle–receptor complex. The influence of each of these assumptions has been investigated via extensions to the basic model.42,47,53 For example, Kolhar et al.74 extend this simple model of particle binding to incorporate an shape-dependent binding rate that relies on an energy balance approach, and demonstrate that under shear flow, elongated particles are more likely to bind to the cell membrane due to the increase in surface area in contact with the membrane.
Internalisation
To incorporate the endocytosis of receptor–bound particles, an additional step can be introduced where the particle–receptor complex is internalised. Specifically, the complex is internalised and separates into the individual particle and receptor. The receptor is immediately exocytosed (recycled) and the particle remains within the cell, and is now denoted [P]I.22,47,51 Mathematically, this is representedwhere ki is the rate of internalisation. Again, this model is relatively simplistic and does not explicitly account for size effects, and relies on the assumption that all internalised particles remain within the cell rather than being exoctyosed. Belli et al.47 introduce an additional conservation equation to reflect the change in density of available particles at the cell surface. To account for inhibition of particle endocytosis, Suen et al.22 introduce an additional step where the particle–receptor complex can bind with an inhibitor. The resulting inhibited complex can still be internalised, albeit at a significantly reduced rate, and both the inhibitor and receptor are immediately exocytosed upon separation after internalisation. The authors acknowledge that inhibitors do not actually bind to the particle–receptor complex, and instead present the above model as a potential method for incorporating endocytic inhibition.22 The model is used to investigate two types of inhibitor to elucidate which endocytosis pathway is employed to uptake folate-decorated particles in retinal pigment epithelium cells.22 Hauert et al.53 implement the kinetic internalisation model as a reaction term in a reaction-diffusion framework. This allows for the evaluation of the particle and receptor concentration across a spatial domain that represents tumour tissue.53 The authors find that incorporating a delay before particle binding occurs allows for the particles to diffuse throughout the tissue, thereby interacting with more cells compared to instantaneous binding.53 Byun and Jung57 consider a stochastic differential equation approach, with an age-structured model to account for endosomal trafficking. Importantly, the stochastic nature of the model allows for the ever-present variability in experimental data to be described, as well as the extinction time for the delivery of particles to be calculated.57 Slabu et al.75 consider a three-stage model, where particles are either bound to the membrane, endocytosed or exocytosed. By calibrating their model to a suite of experimental data, the authors demonstrate that differences in the number of internalised particles between cell lines can be attributed to differences in the rate of endocytosis, rather than the rate of exocytosis or adsorption to the membrane.75
Multivalent binding
Ohta et al.49 present an extended model that incorporates additional detail in terms of allowing multiple receptors to bind to a particle, includes particle exocytosis, and includes an explicit description of the number of receptors within the cell. Particles can bind to a receptor to form a complex, and the complex can either be internalised or disassociate. The complex can bind to additional receptors during the internalisation processes, corresponding to receptors on the cell membrane that are within the invaginated area. As the complex is internalised into an endosome, the pH level decreases and a portion of complexes will disassociate. If a complex disassociates, the receptors are exocytosed back to the cell membrane while the particle remains within the cell. Alternatively, if a complex does not disassociate, the entire complex is recycled back to the cell membrane. To simplify the corresponding system of equations, an assumption is made that the total number of receptors is conserved. Ohta et al.49 employ this model to investigate the uptake and recycling of quantum dots, and find that the parameter governing the dissociation rate of the internalised complex significantly influences the ultimate accumulation of the quantum dots.To account for the formation of particle clusters on the cell membrane, Jin et al.42 propose a model that allows a particle–receptor complex to bind to other complexes. If a particle binds to a receptor, it forms a single complex. These complexes diffuse on the cell membrane,41,42 which allows for the complex to interact with other particle–receptor complexes. The complexes can bind together to form complexes with two particles and two receptors which, in turn, can bind to other single complexes to form complexes with three particles and three receptors. Hence the model describes the evolution of the number of complexes with i particles and i receptors.42 Each of these clusters can be internalised with a rate that depends on the radius of the cluster.42 The internalisation rate arises from the work of Gao et al.,41 who consider receptor diffusion on the cell membrane in response to a particle binding to receptors at a point, and the corresponding energy required to internalise the particle. This work is discussed in detail in the following section.
Aires et al.45 consider a similar compartmental model where multiple binding events can occur. In contrast with the model presented by Jin et al.,42 particles are functionalised with multiple ligands, each of which can bind to a receptor on the cell surface. This model is consistent with the observation that arises from the analysis of Lunov et al.,76 who find that between two and twenty receptors are involved in the endocytosis of a nano-engineered particle. The initial receptor–ligand binding can arise from either specific or non-specific interactions. After the initial binding, the number of receptor–ligand connections can either increase or decrease, with the rate of increase depending on the number of free receptors remaining in the system. Aires et al.45 use the model to investigate different particle targeting strengths and the subsequent relative impact on tumorigenic cells and non-tumorigenic cells for particle capsules containing the chemotherapeutic drug gemcitabine. The authors find that an increase in the strength of specific interactions due to functionalisation results in the preferential killing of tumorigenic cells compared to both non-functionalised particles and free drug molecules.45
Bai et al.46,77 also consider a model where particles can bind to multiple receptors. However, in contrast with previous models where the particles are assumed to be in a static fluid, the model presented by Bai et al.46,77 considers particles that are immersed in a flowing fluid. The authors find that the shear rate is less important in determining the number of particles internalised than the rate of ligand-receptor bond formation and rupture, as the formation and rupture rates are not significantly influenced by the rate of shear flow. In fact, the rate of bond rupture in shear flow did not change significantly compared to static culture. As washing cells after incubation to dislodge particles that are not fully endocytosed is a common component of experimental protocols,78 the observation that shear flow does not induce additional bond rupture may inform experimental protocols in the future.
The major strength of compartmental models is that it is relatively straightforward to compare the model predictions with experimental data. For example, a standard experimental measurement is the number of internalised or associated particles. The majority of compartmental models directly predict the number of internalised particles, and hence comparison between the model and experimental data is not complicated. Further, compartmental models are typically a system of ordinary differential equations, which can be numerically solved using standard differential equation software packages. As such, there is not a high barrier to obtaining predictions from compartmental models. However, the ease in obtaining model predictions and comparisons with data comes at a cost; complicated mechanisms are replaced by abstract parameters, which may not provide insight into the underlying mechanisms. Compartmental models also typically ignore information about spatial processes, such as particles arriving at the fluid–cell interface, which makes comparisons between experiments problematic. As such, there is a trade-off to be considered; between the ease of solution and the need to incorporate more complicated biological and physical processes in the model.
Pharmacokinetic approaches
Other types of compartmental models that have been employed to examine particle internalisation include physiologically-based pharmacokinetic (PBPK) models.48,79–86 PBPK models incorporate physiological and anatomical detail regarding the interconnection of the organs and tissue throughout the body to analyse and predict the biodistribution of a substance of interest. One benefit of PBPK models is that it is relatively straightforward to compare predictions about biodistribution with in vivo experimental data. Typically, each organ or tissue component is represented by a compartment with anatomical knowledge informing the transition between compartments.48 Li et al.83 present a model containing seven compartments: blood, body, gastrointestinal tract, kidneys, liver, lungs and spleen. The blood consisted of two sub-regions for arterial and venous blood, and a lumen and urine sub-region for the gastrointestinal tract and kidney, respectively, provides a route for excretion.83 The authors find that a model where the transport across cell membranes is the limiting factor rather than the blood flow describes the biodistribution for PEG-ylated particles more accurately.83 However, the model does not explicitly include internalisation. Subsequently, a number of models have been proposed that include the influence of particle internalisation,48,79,80,84–86 which is critical for understanding how particles remain within the circulatory system. The model presented by Bachler79,80 allows for particles to undergo phagocytosis in a size-dependent manner in the lung, liver and spleen components whereas the model presented by Li et al.84 involves the assumption that phagocytosis can occur in each component. Carlander et al.48 employ a modified version of the model presented by Li et al.83 for a suite of particles and three different sets of membrane permeability coefficients. Carlander et al.48 are able to describe the biodistribution of all four types of particles considered and note that the difference in particle properties significantly alter the biokinetic parameters. This result is consistent with prior expectations, as the type of circulation pathway for particles is strongly size-dependent.87,88 For example, particles with a diameter of less than 10 nm are cleared by the renal system whereas particles with a diameter greater than 200 nm leave the blood stream and build up in both the liver and spleen.87 Lin et al.86 develop a PBPK model that is capable of describing the biodistribution of gold particles for mice, rats and pigs. A major benefit of PBPK models is that they can be readily calibrated to available experimental data, as highlighted by the recent meta-analysis of Cheng et al.89 In this meta-analysis, the authors sought to explain the consistently low delivery efficiency of particles to solid tumours, and as a result of the modelling analysis, attribute the delivery efficiency to low permeability at the tumour site.89 Additional detail regarding PBPK models for particle biodistribution can be found in the reviews by Moss and Siccardi90 and by Li et al.124 Energy and force models
Another approach for the theoretical analysis of certain pathways for particle internalisation is to consider how the cell membrane can elastically envelop a particle that is bound to the receptors on the cell surface, as presented in Fig. 3.40,41,44,91–93 As the ligands on the surface of the particle bind to the receptors on the cell membrane, the membrane deforms at the location of the bound ligand-receptor complex due to the specific or non-specific interaction between the ligand and the receptor.9,25,93 Hence the energy associated with this interaction needs to be sufficiently strong to overcome the energy required to bend and/or stretch the cell membrane.9,93 As the receptors bind to the particles, the distribution of the receptors on the cell surface becomes clustered at the locations of the particles.40,41,44,91,92 This induces a concentration gradient in the receptor density and, consequently, the unbound receptors are driven towards the particles via diffusive motion.Rigid nano-engineered particles
Gao et al.41 were among the first to propose and analyse such a model, and considered receptors that could rapidly diffuse towards the location of a cylindrical or spherical particle bound to a cell membrane. Gao et al.41 demonstrate that the evolution of the receptor density is analogous to a Stefan problem that describes the moving interface between ice and water. By combining the solution to the Stefan problem with a balance between the energy obtained from receptor–ligand binding and the energy required for receptor transport, Gao et al.41 obtain the time required for the particle to be wrapped by the cell membrane. These results highlight the effect of size on particle internalisation, with particles under a critical radius of approximately 24 nm unable to enter the cell through membrane deformation. Additionally, the presence of an optimal particle radius at 27–30 nm, with respect to wrapping time, is consistent with certain experimental observations.41 Decuzzi and Ferrari40 extend the model presented by Gao et al.41 to include non-specific interactions between particles and cell receptors, which can either be attractive or repulsive. Intuitively, if these interactions are repulsive, both the wrapping time and the minimum particle size that can undergo internalisation increase. Conversely, if the interactions are attractive, smaller particles can undergo internalisation and the wrapping time decreases. In the case of non-specific interaction, Di Michele et al.94 demonstrate that allowing ligands to diffuse freely on the surface of a particle inhibits the internalisation of the particle. Tseng and Huang95 combine an energy balance model with a model of fluid flow and examine the ability of a particle to undergo internalisation in different flow regimes. The authors find that the fluid motion can inhibit internalisation due to energy dissipation in the fluid.95 Banerjee et al.58 develop a model that combines stochastic binding events with a free energy description of pit formation and predict that particles with a diameter of approximately 60 nm are internalised most efficiently. Deng et al.96 implement a stochastic energy-based model of clathrin-mediated endocytosis, where the presence of clathrin affects the intrinsic curvature and bending rigidity of the cell membrane. The authors demonstrate that particle size is a key mediator of internalisation, as particles below a threshold size are unable to be internalised in the model,96 consistent with the results obtained in previous modelling studies.Elastic nano-engineered particles
Thus far, all of the analysis of energy-based particle internalisation has been performed in the context of rigid particles that are unable to change orientation during the internalisation process. Yi et al.97 investigate particles that can undergo elastic deformation. Intuitively, elastic particles are less able to undergo complete wrapping than comparable rigid particles. The binding of rigid particles to the cell membrane allows only the membrane to deform, whereas for elastic particles both the membrane and the particle deform.97–100 This approach has also been applied to the problem of exocytosis of elastic particles.101 The result of inhibited wrapping for elastic particles is also observed for a similar model that contains stochastic receptor–ligand binding, rather than instantaneous deterministic binding.100 Elastic particles can undergo asymmetric wrapping, in contrast to stiff particles which undergo reorientation in the same parameter regimes.99 Rotation during the internalisation process appears in both molecular and particle dynamics simulations,43 and allows for the maximisation of the contact area between the particle and the cell membrane. The optimal particle radius and corresponding wrapping time decrease with the density of receptors on the cell membrane100 and do not appear to be significantly influenced by nonlinear spacing of ligands on the particle surface.102Non-spherical nano-engineered particles
While the work by Decuzzi and Ferrari only considered spherical particles, extensions to non-spherical shapes have been presented.44,92 Richards and Endres44 extend the model to consider shapes that are not symmetrical around the vertical axis. Richards and Endres44 show that non-spherical shapes are engulfed at a rate proportional to the local curvature at the interface between the bound particle and the free receptors. This is in contrast with spherical shapes, which are engulfed proportional to the square root of time.41 If the shape is sufficiently prolate with respect to the axis perpendicular to the membrane, the initially high curvature in contact with the cell membrane prevents the particle being engulfed. Alternatively, if the shape is sufficiently oblate, the particle becomes partially engulfed, as the curvature is initially small enough for engulfment but the particle eventually becomes stuck due to the increase in curvature towards the middle of the particle. In between these two extremes, the particle becomes engulfed, and Richards and Endres44 demonstrate that prolate spheroids are engulfed faster than both spheres and oblate spheroids. For nanomaterials that approach one-dimensionality, the membrane tension of the cell determines whether the dominant direction of the particle is perpendicular or parallel to cell membrane during internalisation.103Multiple nano-engineered particles
As surface receptors must move across the cell membrane toward a particle, the presence of multiple particles on the cell membrane may influence the wrapping time. Raatz et al.104 examine whether membrane wrapping of multiple particles within a single invagination is energetically favourable compared to individual wrapping of particles. The authors find that, provided the repulsive interaction between the particles only occurs over a limited range, it is favourable for particles to undergo co-operative wrapping, up to a threshold particle radius.104 Zhang et al.25 consider a thermodynamic approach where many particles are able to be internalised simultaneously, provided that the cell is at thermodynamic equilibrium. The authors find an optimal particle diameter of approximately 25 nm, which is consistent with the results obtained from the single particle internalisation model of Gao et al.41 The thermodynamic model of Zhang et al.25 also predicts an upper limit of approximately 60 nm, above which internalisation can stall due to a lack of receptors. It is important to note that other, non-receptor mediated, forms of endocytosis can occur above this limit. Richards and Endres13 review similar energy-based models in the context of phagocytosis, which, while a distinct form of internalisation, shares certain similarities with receptor-mediated endocytosis. Yuan and Zhang105 also consider a thermodynamic approach and investigate the interplay between receptor density and particle size with respect to the time taken for internalisation to occur. Yuan and Zhang105 find that a minimum time exists in terms of these two parameters, and corresponds to a particle with a diameter of approximately 28 nm.Energy balance models provide an elegant approach for analysing the internalisation of particles. In particular, these models are well-suited for the investigation of the influence of the physicochemical parameters of the particles on the rate of endocytosis, as well as whether the internalisation process is successful or whether the process stalls. While these models examine the energetic process of the wrapping process in considerable detail, the models do not consider the energy that must be expended by the cell in the membrane fission process, which may alter the overall fate of the particle.106,107 While extensions to multiple particles have been presented,25,104 energy balance models are less appropriate for population-level analysis of particle internalisation, compared to compartmental models. Population-level measures, such as the number of internalised or membrane-bound particles, are standard experimental measurements. It is difficult to extrapolate analysis of the wrapping time of a single particle to the internalisation of a specific particle dose, and hence it is not straightforward to interface energy balance models with standard experimental data. Additionally, it is difficult to incorporate information about the time course of dosage in the models. Therefore, there is potential for the development of multiscale approaches that embed realistic particle–membrane interactions within a population-level framework. These multiscale approaches would incorporate high fidelity descriptions of particle–cell interactions while still being able to provide insight into the evolution of the number of internalised particles in a cell.
5 Molecular models
Molecular dynamics provides a method for accurately modelling the movement of individual atoms via Newton's laws of motion.23,52,93,108,109 Such an approach provides unparalleled spatial and temporal resolution of particle internalisation. However, the computational power required to simulate each atom restricts both the spatial and temporal domains of the process of interest that can be simulated.72 As such, molecular dynamics simulations are not a panacea for all unresolved questions regarding the mechanisms governing particle internalisation. The simulations are typically limited to, at most, microseconds,110 compared to the seconds required for a typical endocytic event.111 Coarse-grain approximations, where the motion of clusters of atoms are modelled instead of individual atoms, allow for the simulation of processes on larger domains for longer times due to the decrease in the number of agents simulated.93,108,109 The reduction in the number of atoms comes at a price, as certain structural details that may be important are neglected, such as hydrogen bonds.72 However, coarse-grained models have been successfully employed to describe the internalisation of various individual particles.108,109 Huang et al.108 examine the internalisation of spherocylindrical particles for a range of aspect ratios. Similar to results obtained from the energy balance models, Huang et al.108 find that there exists an optimal size for the internalisation of spherical particles, with respect to the time required for the particle to be enveloped by the membrane. Additionally, the authors find that particles with a sufficiently high aspect ratio that approach narrow-end first undergo a rotation such that the particles “lay down” on the membrane before being internalised.108 As the particles are internalised, they again undergo rotation, which ultimately results in the particle being in a “standing up” position. Shen et al.112 investigate the membrane wrapping efficiency for a range of particle shapes, sizes and surface stiffnesses, and find that surface stiffness has a greater influence on wrapping efficiency for particles with larger diameters. Yue and Zhang113 implement a dissipative particle dynamics model to examine whether particle internalisation is enhanced in the presence of multiple particles. The authors find that the process is co-operative provided that the particle diameter is below a threshold value.113 Hence sufficiently small particles will cluster together on the cell membrane and are internalised together, whereas larger particles will be internalised individually.113 Similar results are observed by Xiong et al.,114 albeit in a coarse-grained framework. Several reviews of molecular dynamics in the context of particle internalisation have been published in recent years and hence we refer the interested reader to these reviews for detailed information.17,23,52,115–117 Similar to the energy balance models, molecular models provide great insight into the internalisation of individual particles but have difficulty informing population-level measures, such as the overall number of internalised particles.6 Transport models
While mathematical models of particle transport through fluid do not solely describe the internalisation process, such models provide important insight into the time course of particles that arrive at the fluid–cell interface. Accurate quantification of the number of particles that interact with cells is critical for consistent dosimetry estimates, which is of key importance for nanotoxicology and nanomedicine.118–130 The dose metric corresponding to the particle mass initially immersed in the fluid, referred to the administered dose, does not contain this information. As particle transport is both diameter- and material-dependent,118,128,131 it is not straightforward to robustly compare experiments that use different particles via the administered dose. Metrics that involve the particle surface area have been proposed, but again do not incorporate the amount of particles that interact with the cells.124,125,132 As such, an alternative metric that describes the number of particles that arrive at the fluid–cell interface, referred to as the delivered dose, has been proposed.54,118,127,128,131,133,134 The delivered dose is typically obtained from a mathematical model of particle transport. Notable dosimetry models that have been widely employed and validated135 in nanotoxicology and bionanoscience include the “In vitro Sedimentation Diffusion Dosimetry (ISDD)” model118 (and its extension, the ISD3 model136), the “Distorted Grid” model120 and the “Bionano Interaction Kinetics Estimator” (BIKE) model.55 Importantly, the code for all of these models can be freely obtained and can be implemented in a straightforward manner. Here we provide a relatively brief review of particle transport models; additional information can be found in the review of in vitro dosimetry by Cohen et al.54Partial differential equations
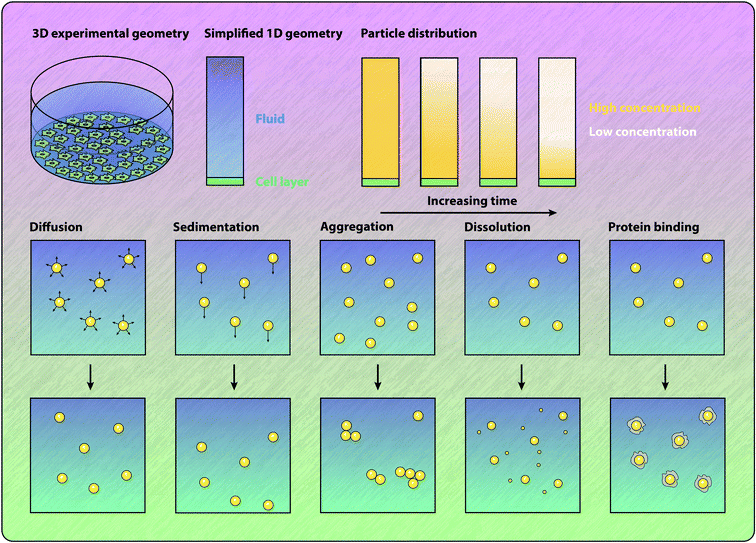
The standard approach for calculating the delivered dose is to numerically solve a partial differential equation model. This approach provides the time course of the mass or number of particles that arrive at the cell surface, as well as the distribution of the particles throughout the fluid, as shown in Fig. 4. Typically, these models will describe particles undergoing both diffusion and sedimentation.11,56,118,120,121,136–141 The relative contributions of diffusion and sedimentation to the overall rate of transport depends on the size and density of the particles. In particular, the sedimentation velocity of a particle increases linearly with the difference between the particle density and the fluid density, and increases quadratically with the particle diameter.118,133 In contrast, the rate of diffusion is inversely proportional to the particle diameter.118,133 Corrections to the rate of diffusion for high-aspect ratio particles have been introduced.142 Dosimetry models have been successfully employed to investigate the influence of sedimentation on particle–cell association and internalisation in various experimental geometries,137,138,141,143,144 and to investigate the mechanisms of internalisation.120 Johnston and Crampin56 present a method for analytically determining the influence of particle polydispersity on the delivered dose, and find that representative amounts of polydispersity can influence the delivered dose by a factor of two. The importance of accurately estimating polydispersity is highlighted by the study of Petersen et al.,145 who show that employing different techniques for measuring the particle size distribution can result in different estimates of the delivered dose. Schneider et al.146 demonstrate that the sonication of particles to disrupt aggregate formation has a significant impact on the ratio of administered dose to delivered dose. Cohen et al.147 approximate the output from a sedimentation–diffusion model with a sigmoidal function with a single free parameter that represents the rate of deposition for a particular particle and media combination. Calculating this parameter value for a library of particle–media pairs allows for rapid quantification and comparison of the ability for particles to interact with the cells. The standard sedimentation–diffusion models make the assumption that particles are non-interacting and hence do not dynamically form aggregates during the transport process. Aggregation influences both the effective density and diameter of the particles and can be included in the model.133,148 However, formation of particle aggregates is typically assumed to occur before the transport process and hence particle aggregation is static in the model.148 The review by Moore et al.149 highlights the importance of understanding particle aggregation in cell culture media, and notes that current theoretical approaches for describing the formation of aggregates cannot fully explain all colloidal systems. Significantly, Moore et al.150 note that even the method by which particles are introduced to cell culture experiments can influence the association and internalisation of the particles. The authors show that an initially concentrated dose of particles results in more particle–cell interactions compared to a well-mixed particle solution.150Extensions to the ISDD model to incorporate the change in particle size due to dissolution in the media have recently been presented.136 Thomas et al.136 use the extended ISD3 model to investigate the internalisation of silver particles, as well as the uptake of silver ions, which are present in the system as a result of dissolution. Grabinski et al.151 consider transport in an in vitro experiment containing dynamic flow and find that the influence of sedimentation is significantly reduced in the presence of shear flow. Another extension considered is a three-dimensional model of sedimentation and diffusion.152 The standard one dimensional nature of the model is no longer sufficient to calculate the delivered dose for cell populations that grow on both the sides and bottom of a culture dish, which occurs for cell lines that must be incubated over multiple cell doubling times to differentiate sufficiently to realise their full function.152 The wide range of experimental factors that have been demonstrated to significantly impact the delivered dose, and hence impact the rate of particle–cell interaction and particle internalisation, highlights the need for experimental protocols to be robustly described such that dosimetry calculations can be performed. Without dosimetry calculations it is exceedingly difficult to draw conclusions between experiments due to potential disparities in the number of particles interacting with cells.
Stochastic models
An alternative approach for describing particle transport is to employ stochastic methods, where the transport of individual particles is described explicitly with Monte Carlo simulations.61,62,64 While it is more straightforward to incorporate particle interactions in such models, the inherent stochasticity typically increases the computational effort required to obtain population-level behaviour. Rodriguez-Lorenzo et al.64 implement a random walk process of sedimentation and diffusion for a polydisperse particle population and demonstrate that the delivered dose depends on the degree of polydispersity. Mukherjee et al.62 extend the dynamic agglomeration model presented by Liu et al.61 to describe the agglomeration, diffusion, sedimentation and dissolution of particles in a direct simulation Monte Carlo framework. Mukherjee et al.62 employ their model to examine the influence of each type of mechanism on the particle population characteristics, as well as the delivered dose. By accounting for the delivered dose, calculated from a stochastic model of aggregation, sedimentation and diffusion, Liu et al.122 are able to compare the toxicity for a range of metal oxide particles.Internalisation in transport models
In models of particle transport the influence of particle internalisation manifests itself through a condition on the boundary of the experimental domain. As these models are primarily focused on describing the transport processes, this condition is typically not as sophisticated as the models described in the previous sections. Historically, in much of the literature, a strong distinction has not been made between the processes of cell membrane binding and particle internalisation. Instead, the number of “associated” particles is typically reported, which is a catch-all term for particles that are either bound strongly to the cell membrane or have been internalised.55 For example, a common assumption is that particles bind to the cell membrane and are instantly internalised,118,136,138,140 thereby avoiding the build-up of particles on the cell surface. This assumption results in a dosage estimate that is the upper bound on the delivered dose, as there is no inhibition of particle association. However, it is possible that the particles are deposited on the cell surface sufficiently rapidly such that is not possible for all of the particles to associate with the cell.120,134 Hence a gradient in the particle density will form towards the location of the cell, inhibiting the transport of particles to the cell. This can be described in several ways. The simplest approach is to employ a flux-limited condition, where only a fixed proportion of the particles that arrive at the cell surface associate, and the remainder of the particles remain in the fluid.56 DeLoid et al.120 account for this phenomenon by describing the particle association as a Langmuir isotherm adsorption process. This approach imposes a maximum particle density on the cell surface, and inhibits association as the density increases.120 Faria et al.55 conducted a thorough investigation into boundary conditions that represent particle–cell association by calibrating a transport model with a range of boundary conditions to a library of particle–cell association data. These boundary conditions represent particle–cell association as either: (i) instantaneous; (ii) proportional to the particle density; (iii) proportional to the particle density but limited by cell surface area; (iv) proportional to the particle density but limited by the finite particle capacity of a cell; or (v) a combination of (iii) and (iv).55 The authors demonstrate conclusively that the finite particle capacity of a cell is a key factor in particle internalisation. Further, the authors provide a freely-available methodology for extracting quantitative estimates from data to allow for comparison between experiments.153Models that incorporate particle transport, stochastic particle behaviour, and internalisation kinetics have been successfully employed to understand the phenomenon of heterogeneity in particle dosage at an individual cell level.59,60,63,154,155 Heterogeneity in particle dosage has potentially severe consequences for particle-based therapeutics, as successful treatment may rely on each cell internalising a threshold number of drug-loaded particles. Particle internalisation, on a particle-by-particle case, can be considered as a random event.60 As such, heterogeneity in particle dosage on a cell population level can be described via appropriate statistical distributions and has been attributed to the cell cycle due to changes in cell surface area.59 By extending the particle internalisation and transport model of Faria et al.55 to account for stochastic particle behaviour, Johnston et al.63 demonstrate that the heterogeneity in particle dosage can be explained by accounting for three factors: (i) stochastic particle motion; (ii) heterogeneity in the rate of particle–cell association, and; (iii) heterogeneity in the finite particle capacity of cells. Further, the authors show that all three factors are needed to explain experimental observations.63 This systematic unpacking of complex phenomena to reveal the key governing mechanisms highlights the insight that can be gained by combining mathematical models and particle–cell experiments. As described in the previous sections, there are many sophisticated approaches to explicitly model particle internalisation, and hence there remains significant potential for developing techniques that interface particle transport models with models of particle internalisation to obtain hitherto unknown information regarding particle–cell interactions and particle internalisation.
7 Mathematical models and standardisation of experimental reporting
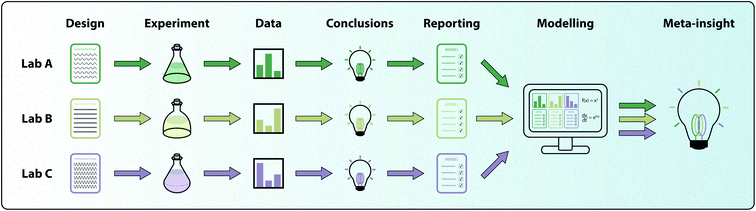
Throughout this review, we have highlighted the role that mathematical modelling plays in obtaining insight into particle–cell interactions and particle internalisation. Mathematical models have additional benefit in that they can be retroactively calibrated to previously-published experimental data to gain new insight.89 However, for the full value of this benefit to be realised, the details of the experiments need to be reported in a consistent and accessible way. We present an example of how a combination of standardised reporting and mathematical modelling can result in additional insight in Fig. 5. In 2018, the minimum information reporting in bio-nano experimental literature (MIRIBEL) standard was proposed.156 This standard provides a reporting checklist for details regarding materials characterisation, biological characterisation and experimental protocol. Crucially, the information that is provided in this checklist allows for the relevant parameters in mathematical models of particle–cell interactions and particle internalisation to be established, and for the models' full predictive and analytic power to be realised. Models provide a method for the unbiased and robust comparison of experiments performed with different particles, different cell lines and in different laboratory conditions.156,157 This robust comparison would allow for collective insight to be gathered by combining data from experiments performed all over the world. However, for this insight to be realised, experimental data must be made available and standards in experimental reporting must be followed. For example, it is now well accepted that particle density strongly influences particle–cell interactions via sedimentation.137,138,141,143,144 If standardised experimental reporting had been adhered to, then previous experimental data could be revisited via models that now account for sedimentation effects to determine whether the original conclusions drawn regarding particle–cell interactions are appropriate. As it stands now, it is impossible to effectively compare conclusions from recent investigations into particle–cell interactions, where the aforementioned range of confounding variables are reported and accounted for via mathematical modelling, with investigations conducted before the advent of standardised experimental reporting, where information about confounding variables is scarce. However, the future is bright, as the bionanoscience community has begun to embrace the MIRIBEL standards. This suggests that both meta- and retrospective-analyses via mathematical modelling will become significantly easier to conduct, thereby value-adding to published experimental studies.8 Outlook and conclusions
Understanding nano-engineered particle–cell interactions and particle internalisation remains a key area of research in bionanoscience. Due to the complex intertwining of a variety of biological, physical and chemical processes, the critical mechanisms governing the internalisation of the particles and the interactions between particles and cells are yet to be completely elucidated. Mathematical and computational models provide a method for obtaining insight into a simplified view of particle–cell interactions. Energy balance and molecular models have been utilised to examine how particle shape, particle size and the strength of specific interactions of particles with cell receptors can influence how rapidly, or indeed whether, an individual particle will undergo internalisation. Promisingly, the results from these models are consistent with experimental observations. Compartmental models are able provide information about the time course of the number of particles that have been internalised by an individual cell and, again, have been successfully calibrated to experimental internalisation data. These past successes highlight the need for future investigations to driven through a marriage of experimental and theoretical approaches. Models are able to generate predictions that can inform experimental direction, thereby providing a rational basis for future experimental design choices. In turn, the experimental data, reported according to established community guidelines,156 provides insight into the features of the models that may be inappropriate, or highlight the need for the inclusion of more sophisticated mechanisms in the model. However, the number of experimental investigations of particle–cell interactions still dwarfs the number of theoretical, or hybrid experimental-theoretical investigations. Hence there is significant opportunity for high impact interdisciplinary work involving both experimentalists and theoreticians.Current mathematical and computational models have made important developments toward understanding various aspects of particle–cell interactions and particle internalisation. However, other aspects are yet to be explored comprehensively. In particular, the signalling processes initialised by the binding of particles to the receptors on the cell membrane and the subsequent downstream cellular effects remain an open problem from a modelling perspective. Additionally, spatiotemporal population-level descriptions of the prevalence of internalised particles are relatively sparse in the literature. While these models are perhaps more complicated than current models, there is significant potential for the systematic development of such models in concert with experimental data. It is critical for newly-developed models to be designed with experimental limitations in mind, as otherwise models run the risk of being overly complicated and may contain parameters or variables that cannot be reliably estimated or investigated, respectively, with current experimental techniques. For example, it is not common in experimental protocols to distinguish between internalised particles and particles that are merely bound to the cell membrane.55,158,159 To robustly calibrate the model, either the mathematical model must calculate the number of associated particles,55,63 rather than internalised particles, or more complex experimental protocols must be implemented.158,159 Another likely fruitful avenue for future research is the combination of existing models of particle internalisation in a multiscale framework. In such a framework, conclusions about population-level behaviour can be drawn without the model being both computationally and analytically intractable, while still incorporating detailed information about individual particle–cell interactions.
Mathematical and computational approaches provide a powerful tool for understanding particle–cell interactions and particle internalisation. However, there is still significant room for both the development of novel models of particle internalisation and for interdisciplinary investigations incorporating both experimental data and existing models. Significant strides have been made in recent years with respect to understanding how the physicochemical properties of particles influence the rate of internalisation but many open questions remain. We believe that hybrid theoretical and experimental investigations represent a fruitful opportunity for answering questions that appear intractable currently.
Author contributions
Conceptualisation (STJ, MF, EJC); data curation (STJ, MF, EJC); investigation (STJ); visualisation (STJ); writing – original draft (STJ); writing – review and editing (STJ, MF, EJC); funding acquisition (EJC).Conflicts of interest
The authors declare that there are no conflicts of interest.Acknowledgements
This research was in part conducted and funded by the Australian Research Council Centre of Excellence in Convergent Bio-Nano Science and Technology (project no. CE140100036). S. T. J. is supported by the Australian Research Council (project no. DE200100988).Notes and references
- A. H. Faraji and P. Wipf, Bioorg. Med. Chem., 2009, 17, 2950–2962 CrossRef CAS PubMed.
- E. A. Sykes, J. Chen, G. Zheng and W. C. Chan, ACS Nano, 2014, 8, 5696–5706 CrossRef CAS PubMed.
- D. Bobo, K. J. Robinson, J. Islam, K. J. Thurecht and S. R. Corrie, Pharm. Res., 2016, 33, 2373–2387 CrossRef CAS PubMed.
- Y. Gao, Y. Chen, X. Ji, X. He, Q. Yin, Z. Zhang, J. Shi and Y. Li, ACS Nano, 2011, 5, 9788–9798 CrossRef CAS PubMed.
- J.-H. Lee, Y.-M. Huh, Y.-W. Jun, J.-W. Seo, J.-T. Jang, H.-T. Song, S. Kim, E.-J. Cho, H.-G. Yoon, J.-S. Suh and J. Cheon, Nat. Med., 2007, 13, 95–99 CrossRef CAS PubMed.
- Y. Yan, A. P. Johnston, S. J. Dodds, M. M. Kamphuis, C. Ferguson, R. G. Parton, E. C. Nice, J. K. Heath and F. Caruso, ACS Nano, 2010, 4, 2928–2936 CrossRef CAS PubMed.
- I. Canton and G. Battaglia, Chem. Soc. Rev., 2012, 41, 2718–2739 RSC.
- N. D. Donahue, H. Acar and S. Wilhelm, Adv. Drug Delivery Rev., 2019, 143, 68–96 CrossRef CAS PubMed.
- A. E. Nel, L. Mädler, D. Velegol, T. Xia, E. M. Hoek, P. Somasundaran, F. Klaessig, V. Castranova and M. Thompson, Nat. Mater., 2009, 8, 543 CrossRef CAS PubMed.
- L. Treuel, X. Jiang and G. U. Nienhaus, J. R. Soc., Interface, 2013, 10, 20120939 CrossRef PubMed.
- G. M. DeLoid, J. M. Cohen, G. Pyrgiotakis and P. Demokritou, Nat. Protoc., 2017, 12, 355 CrossRef CAS PubMed.
- M. Li, P. Zou, K. Tyner and S. Lee, AAPS J., 2017, 19, 26–42 CrossRef CAS PubMed.
- D. M. Richards and R. G. Endres, Rep. Prog. Phys., 2017, 80, 126601 CrossRef PubMed.
- Food and Drug Administration, 2014, FDA-2010-D-0530.
- P. Del Pino, B. Pelaz, Q. Zhang, P. Maffre, G. U. Nienhaus and W. J. Parak, Mater. Horiz., 2014, 1, 301–313 RSC.
- C. Ge, J. Tian, Y. Zhao, C. Chen, R. Zhou and Z. Chai, Arch. Toxicol., 2015, 89, 519–539 CrossRef CAS PubMed.
- X. C. He, M. Lin, F. Li, B. Y. Sha, F. Xu, Z. G. Qu and L. Wang, Nanomedicine, 2015, 10, 121–141 CrossRef CAS PubMed.
- P. V. Rewatkar, R. G. Parton, H. S. Parekh and M.-O. Parat, Adv. Drug Delivery Rev., 2015, 91, 92–108 CrossRef CAS PubMed.
- G. J. Doherty and H. T. McMahon, Annu. Rev. Biochem., 2009, 78, 857–902 CrossRef CAS PubMed.
- L. Shang, K. Nienhaus and G. U. Nienhaus, J. Nanobiotechnol., 2014, 12, 5 CrossRef PubMed.
- J. Rejman, V. Oberle, I. S. Zuhorn and D. Hoekstra, Biochem. J., 2004, 377, 159–169 CrossRef CAS PubMed.
- W.-L. L. Suen and Y. Chau, J. Pharm. Pharmacol., 2014, 66, 564–573 CrossRef CAS PubMed.
- H.-M. Ding and Y.-Q. Ma, Nanoscale Horiz., 2018, 3, 6–27 RSC.
- Y. Shan, S. Ma, L. Nie, X. Shang, X. Hao, Z. Tang and H. Wang, Chem. Commun., 2011, 47, 8091–8093 RSC.
- S. Zhang, J. Li, G. Lykotrafitis, G. Bao and S. Suresh, Adv. Mater., 2009, 21, 419–424 CrossRef CAS PubMed.
- J. Zhao and M. H. Stenzel, Polym. Chem., 2018, 9, 259–272 RSC.
- M. Kaksonen and A. Roux, Nat. Rev. Mol. Cell Biol., 2018, 19, 313 CrossRef CAS PubMed.
- A. Albanese, P. S. Tang and W. C. Chan, Annu. Rev. Biomed. Eng., 2012, 14, 1–16 CrossRef CAS PubMed.
- M. S. Boyles, L. Young, D. M. Brown, L. MacCalman, H. Cowie, A. Moisala, F. Smail, P. J. Smith, L. Proudfoot, A. H. Windle and V. Stone, Toxicol. in Vitro, 2015, 29, 1513–1528 CrossRef CAS PubMed.
- M. Björnmalm, M. Faria, X. Chen, J. Cui and F. Caruso, Langmuir, 2016, 32, 10995–11001 CrossRef PubMed.
- B. D. Chithrani and W. C. Chan, Nano Lett., 2007, 7, 1542–1550 CrossRef CAS PubMed.
- C. Kinnear, T. L. Moore, L. Rodriguez-Lorenzo, B. Rothen-Rutishauser and A. Petri-Fink, Chem. Rev., 2017, 117, 11476–11521 CrossRef CAS PubMed.
- R. Pan, G. Liu, Y. Li, Y. Wei, S. Li and L. Tao, Nanoscale, 2018, 10, 8269–8274 RSC.
- R. Podila and J. M. Brown, J. Biochem. Mol. Toxicol., 2013, 27, 50–55 CrossRef CAS PubMed.
- S. Sharifi, S. Behzadi, S. Laurent, M. L. Forrest, P. Stroeve and M. Mahmoudi, Chem. Soc. Rev., 2012, 41, 2323–2343 RSC.
- N. P. Truong, M. R. Whittaker, C. W. Mak and T. P. Davis, Expert Opin. Drug Delivery, 2015, 12, 129–142 CrossRef CAS PubMed.
- E. A. Untener, K. K. Comfort, E. I. Maurer, C. M. Grabinski, D. A. Comfort and S. M. Hussain, ACS Appl. Mater. Interfaces, 2013, 5, 8366–8373 CrossRef CAS PubMed.
- X. Wang, X. Hu, J. Li, A. C. M. Russe, N. Kawazoe, Y. Yang and G. Chen, Biomater. Sci., 2016, 4, 970–978 RSC.
- W. Wang, K. Gaus, R. D. Tilley and J. J. Gooding, Mater. Horiz., 2019, 6, 1538–1547 RSC.
- P. Decuzzi and M. Ferrari, Biomaterials, 2007, 28, 2915–2922 CrossRef CAS PubMed.
- H. Gao, W. Shi and L. B. Freund, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 9469–9474 CrossRef CAS PubMed.
- H. Jin, D. A. Heller, R. Sharma and M. S. Strano, ACS Nano, 2009, 3, 149–158 CrossRef CAS.
- Y. Li, T. Yue, K. Yang and X. Zhang, Biomaterials, 2012, 33, 4965–4973 CrossRef CAS PubMed.
- D. M. Richards and R. G. Endres, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 6113–6118 CrossRef CAS PubMed.
- A. Aires, J. Cadenas, R. Guantes and A. Cortajarena, Nanoscale, 2017, 9, 13760–13771 RSC.
- F. Bai, J. Wu and R. Sun, Math. Biosci., 2018, 295, 55–61 CrossRef CAS.
- V. Belli, D. Guarnieri, M. Biondi, F. della Sala and P. A. Netti, Colloids Surf., B, 2017, 149, 7–15 CrossRef CAS.
- U. Carlander, D. Li, O. Jolliet, C. Emond and G. Johanson, Int. J. Nanomed., 2016, 11, 625 CrossRef CAS PubMed.
- S. Ohta, S. Inasawa and Y. Yamaguchi, Biomaterials, 2012, 33, 4639–4645 CrossRef CAS PubMed.
- M.-S. Martina, V. Nicolas, C. Wilhelm, C. Ménager, G. Barratt and S. Lesieur, Biomaterials, 2007, 28, 4143–4153 CrossRef CAS PubMed.
- C. Wilhelm, F. Gazeau, J. Roger, J. Pons and J.-C. Bacri, Langmuir, 2002, 18, 8148–8155 CrossRef CAS.
- H.-M. Ding and Y.-Q. Ma, Small, 2015, 11, 1055–1071 CrossRef CAS PubMed.
- S. Hauert, S. Berman, R. Nagpal and S. N. Bhatia, Nano Today, 2013, 8, 566–576 CrossRef CAS PubMed.
- J. M. Cohen, G. M. DeLoid and P. Demokritou, Nanomedicine, 2015, 10, 3015–3032 CrossRef CAS PubMed.
- M. Faria, K. F. Noi, Q. Dai, M. Björnmalm, S. T. Johnston, K. Kempe, F. Caruso and E. J. Crampin, J. Controlled Release, 2019, 307, 355–367 CrossRef CAS PubMed.
- S. T. Johnston, M. Faria and E. J. Crampin, J. R. Soc., Interface, 2018, 15, 20180364 CrossRef PubMed.
- J. H. Byun and I. H. Jung, Applied Mathematical Modelling, 2020, 79, 300–313 CrossRef.
- A. Banerjee, A. Berezhkovskii and R. Nossal, Phys. Biol., 2016, 13, 016005 CrossRef PubMed.
- P. Rees, J. W. Wills, M. R. Brown, C. M. Barnes and H. D. Summers, Nat. Commun., 2019, 10, 1–8 CrossRef CAS PubMed.
- H. D. Summers, P. Rees, M. D. Holton, M. R. Brown, S. C. Chappell, P. J. Smith and R. J. Errington, Nat. Nanotechnol., 2011, 6, 170–174 CrossRef CAS PubMed.
- H. H. Liu, S. Surawanvijit, R. Rallo, G. Orkoulas and Y. Cohen, Environ. Sci. Technol., 2011, 45, 9284–9292 CrossRef CAS PubMed.
- D. Mukherjee, B. F. Leo, S. G. Royce, A. E. Porter, M. P. Ryan, S. Schwander, K. F. Chung, T. D. Tetley, J. Zhang and P. G. Georgopoulos, J. Nanopart. Res., 2014, 16, 2616 CrossRef PubMed.
- S. T. Johnston, M. Faria and E. J. Crampin, J. R. Soc., Interface, 2020, 17, 20200221 CrossRef PubMed.
- L. Rodriguez-Lorenzo, B. Rothen-Rutishauser, A. Petri-Fink and S. Balog, Part. Part. Syst. Charact., 2015, 32, 321–333 CrossRef CAS.
- M. Braun, C. S. Coleman, D. A. Drew and W. F. Lucas, Differential equation models, Springer, 1983, vol. 1 Search PubMed.
- D. Zwillinger, Handbook of differential equations, Gulf Professional Publishing, 1998, vol. 1 Search PubMed.
- S. T. Johnston, M. J. Simpson and E. J. Crampin, Proc. R. Soc. A, 2020, 476, 20200089 CrossRef PubMed.
- D. A. Lauffenburger and J. Linderman, Receptors: models for binding, trafficking, and signaling, Oxford University Press, 1993 Search PubMed.
- L. F. Shampine and M. W. Reichelt, SIAM Journal on Scientific Computing, 1997, 18, 1–22 CrossRef.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser and J. Bright, et al. , Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- W. H. Press, H. William, S. A. Teukolsky, A. Saul, W. T. Vetterling and B. P. Flannery, Numerical recipes 3rd edition: the art of scientific computing, Cambridge University Press, 2007 Search PubMed.
- J. A. Nash, A. L. Kwansa, J. S. Peerless, H. S. Kim and Y. G. Yingling, Bioconjugate Chem., 2017, 28, 3–10 CrossRef CAS PubMed.
- D. G. Kendall, Ann. Math. Stat., 1948, 19, 1–15 CrossRef.
- P. Kolhar, A. C. Anselmo, V. Gupta, K. Pant, B. Prabhakarpandian, E. Ruoslahti and S. Mitragotri, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 10753–10758 CrossRef CAS PubMed.
- I. Slabu, A. A. Roeth, U. M. Engelmann, F. Wiekhorst, E. M. Buhl, U. P. Neumann and T. Schmitz-Rode, Nanotechnology, 2019, 30, 184004 CrossRef CAS PubMed.
- O. Lunov, V. Zablotskii, T. Syrovets, C. Röcker, K. Tron, G. U. Nienhaus and T. Simmet, Biomaterials, 2011, 32, 547–555 CrossRef CAS PubMed.
- F. Bai and R. Sun, Biophys. Rev. Lett., 2019, 14, 75–99 CrossRef CAS.
- J. M. Chan, P. M. Valencia, L. Zhang, R. Langer and O. C. Farokhzad, Cancer Nanotechnology, Springer, 2010, pp. 163–175 Search PubMed.
- G. Bachler, N. von Goetz and K. Hungerbühler, Int. J. Nanomed., 2013, 8, 3365 Search PubMed.
- G. Bachler, N. von Goetz and K. Hungerbuhler, Nanotoxicology, 2015, 9, 373–380 CrossRef CAS PubMed.
- R. Chen and J. E. Riviere, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2017, 9, 1–31 Search PubMed.
- M. Li, K. T. Al-Jamal, K. Kostarelos and J. Reineke, ACS Nano, 2010, 4, 6303–6317 CrossRef CAS PubMed.
- M. Li, Z. Panagi, K. Avgoustakis and J. Reineke, Int. J. Nanomed., 2012, 7, 1345 CrossRef CAS PubMed.
- D. Li, G. Johanson, C. Emond, U. Carlander, M. Philbert and O. Jolliet, Nanotoxicology, 2014, 8, 128–137 CrossRef CAS.
- Z. Lin, N. A. Monteiro-Riviere and J. E. Riviere, Nanotoxicology, 2016, 10, 162–172 CAS.
- Z. Lin, N. A. Monteiro-Riviere, R. Kannan and J. E. Riviere, Nanomedicine, 2016, 11, 107–119 CrossRef CAS PubMed.
- N. Hoshyar, S. Gray, H. Han and G. Bao, Nanomedicine, 2016, 11, 673–692 CrossRef CAS PubMed.
- J. Tan, S. Shah, A. Thomas, H. D. Ou-Yang and Y. Liu, Microfluid. Nanofluid., 2013, 14, 77–87 CrossRef CAS PubMed.
- Y.-H. Cheng, C. He, J. E. Riviere, N. A. Monteiro-Riviere and Z. Lin, ACS Nano, 2020, 14, 3075–3095 CrossRef CAS PubMed.
- D. M. Moss and M. Siccardi, Br. J. Pharmacol., 2014, 171, 3963–3979 CrossRef CAS PubMed.
- G. Bao and X. R. Bao, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 9997–9998 CrossRef CAS PubMed.
- P. Decuzzi and M. Ferrari, Biophys. J., 2008, 94, 3790–3797 CrossRef CAS PubMed.
- S. Zhang, H. Gao and G. Bao, ACS Nano, 2015, 9, 8655–8671 CrossRef CAS PubMed.
- L. Di Michele, P. K. Jana and B. M. Mognetti, Phys. Rev. E, 2018, 98, 032406 CrossRef CAS.
- Y.-H. Tseng and H. Huang, J. Comput. Phys., 2014, 273, 143–159 CrossRef.
- H. Deng, P. Dutta and J. Liu, Biochim. Biophys. Acta, 2018, 1862, 2104–2111 CrossRef CAS PubMed.
- X. Yi, X. Shi and H. Gao, Phys. Rev. Lett., 2011, 107, 098101 CrossRef PubMed.
- H. Tang, H. Zhang, H. Ye and Y. Zheng, J. Appl. Phys., 2016, 120, 114701 CrossRef.
- X. Yi and H. Gao, Phys. Rev. E, 2014, 89, 062712 CrossRef PubMed.
- X. Yi and H. Gao, Nanoscale, 2017, 9, 454–463 RSC.
- X. Yi and H. Gao, ACS Biomater. Sci. Eng., 2017, 3, 2954–2961 CrossRef CAS PubMed.
- L. Li, Y. Zhang and J. Wang, Open Sci., 2017, 4, 170063 Search PubMed.
- X. Yi, X. Shi and H. Gao, Nano Lett., 2014, 14, 1049–1055 CrossRef CAS PubMed.
- M. Raatz, R. Lipowsky and T. R. Weikl, Soft Matter, 2014, 10, 3570–3577 RSC.
- H. Yuan and S. Zhang, Appl. Phys. Lett., 2010, 96, 033704 CrossRef.
- O. Daumke, A. Roux and V. Haucke, Cell, 2014, 156, 882–892 CrossRef CAS PubMed.
- S. Morlot, V. Galli, M. Klein, N. Chiaruttini, J. Manzi, F. Humbert, L. Dinis, M. Lenz, G. Cappello and A. Roux, Cell, 2012, 151, 619–629 CrossRef CAS PubMed.
- C. Huang, Y. Zhang, H. Yuan, H. Gao and S. Zhang, Nano Lett., 2013, 13, 4546–4550 CrossRef CAS PubMed.
- R. Vácha, F. J. Martinez-Veracoechea and D. Frenkel, Nano Lett., 2011, 11, 5391–5395 CrossRef PubMed.
- J. R. Perilla, B. C. Goh, C. K. Cassidy, B. Liu, R. C. Bernardi, T. Rudack, H. Yu, Z. Wu and K. Schulten, Curr. Opin. Struct. Biol., 2015, 31, 64–74 CrossRef CAS PubMed.
- M. Shamir, Y. Bar-On, R. Phillips and R. Milo, Cell, 2016, 164, 1302 CrossRef CAS.
- Z. Shen, H. Ye, X. Yi and Y. Li, ACS Nano, 2018, 13, 215–228 CrossRef PubMed.
- T. Yue and X. Zhang, ACS Nano, 2012, 6, 3196–3205 CrossRef CAS PubMed.
- K. Xiong, J. Zhao, D. Yang, Q. Cheng, J. Wang and H. Ji, Soft Matter, 2017, 13, 4644–4652 RSC.
- M. Ramezanpour, S. Leung, K. Delgado-Magnero, B. Bashe, J. Thewalt and D. Tieleman, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 1688–1709 CrossRef CAS PubMed.
- G. Rossi and L. Monticelli, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 2380–2389 CrossRef CAS PubMed.
- M. Shamsi, A. Mohammadi, M. K. Manshadi and A. Sanati-Nezhad, J. Controlled Release, 2019, 307, 150–165 CrossRef CAS PubMed.
- P. M. Hinderliter, K. R. Minard, G. Orr, W. B. Chrisler, B. D. Thrall, J. G. Pounds and J. G. Teeguarden, Part. Fibre Toxicol., 2010, 7, 36 CrossRef CAS PubMed.
- S. M. Hussain, D. B. Warheit, S. P. Ng, K. K. Comfort, C. M. Grabinski and L. K. Braydich-Stolle, Toxicol. Sci., 2015, 147, 5–16 CrossRef CAS PubMed.
- G. M. DeLoid, J. M. Cohen, G. Pyrgiotakis, S. V. Pirela, A. Pal, J. Liu, J. Srebric and P. Demokritou, Part. Fibre Toxicol., 2015, 12, 32 CrossRef PubMed.
- N. Feliu, X. Sun, R. A. Alvarez Puebla and W. J. Parak, Langmuir, 2017, 33, 6639–6646 CrossRef CAS.
- R. Liu, H. H. Liu, Z. Ji, C. H. Chang, T. Xia, A. E. Nel and Y. Cohen, ACS Nano, 2015, 9, 9303–9313 CrossRef CAS PubMed.
- D. Lichtenstein, T. Meyer, L. Böhmert, S. Juling, C. Fahrenson, S. Selve, A. Thünemann, J. Meijer, I. Estrela-Lopis, A. Braeuning and A. Lampen, Langmuir, 2017, 33, 13087–13097 CrossRef CAS PubMed.
- G. Oberdörster, E. Oberdörster and J. Oberdörster, Environ. Health Perspect., 2005, 113, 823 CrossRef PubMed.
- G. Oberdörster, E. Oberdörster and J. Oberdörster, Environ. Health Perspect., 2007, 115, 290 CrossRef.
- A. K. Pal, D. Bello, J. Cohen and P. Demokritou, Nanotoxicology, 2015, 9, 871–885 CrossRef PubMed.
- U. Taylor, C. Rehbock, C. Streich, D. Rath and S. Barcikowski, Nanomedicine, 2014, 9, 1971–1989 CrossRef CAS.
- J. G. Teeguarden, P. M. Hinderliter, G. Orr, B. D. Thrall and J. G. Pounds, Toxicol. Sci., 2006, 95, 300–312 CrossRef PubMed.
- J. W. Wills, H. D. Summers, N. Hondow, A. Sooresh, K. E. Meissner, P. A. White, P. Rees, A. Brown and S. H. Doak, ACS Nano, 2017, 11(12), 11986–12000 CrossRef CAS PubMed.
- K. Wittmaack, Environ. Health Perspect., 2007, 115, 187 CrossRef CAS PubMed.
- R. A. Khanbeigi, A. Kumar, F. Sadouki, C. Lorenz, B. Forbes, L. A. Dailey and H. Collins, J. Controlled Release, 2012, 162, 259–266 CrossRef PubMed.
- R. Duffin, L. Tran, D. Brown, V. Stone and K. Donaldson, Inhalation Toxicol., 2007, 19, 849–856 CrossRef CAS PubMed.
- L. K. Limbach, Y. Li, R. N. Grass, T. J. Brunner, M. A. Hintermann, M. Muller, D. Gunther and W. J. Stark, Environ. Sci. Technol., 2005, 39, 9370–9376 CrossRef CAS PubMed.
- G. Rischitor, M. Parracino, R. La Spina, P. Urbán, I. Ojea-Jiménez, E. Bellido, A. Valsesia, S. Gioria, R. Capomaccio, A. Kinsner-Ovaskainen, D. Gilliland, F. Rossi and P. Colpo, Part. Fibre Toxicol., 2016, 13, 47 CrossRef PubMed.
- T. Kowoll, S. Fritsch-Decker, S. Diabaté, G. U. Nienhaus, D. Gerthsen and C. Weiss, J. Nanobiotechnol., 2018, 16, 100 CrossRef CAS PubMed.
- D. G. Thomas, J. N. Smith, B. D. Thrall, D. R. Baer, H. Jolley, P. Munusamy, V. Kodali, P. Demokritou, J. Cohen and J. G. Teeguarden, Part. Fibre Toxicol., 2018, 15, 6 CrossRef.
- E. C. Cho, Q. Zhang and Y. Xia, Nat. Nanotechnol., 2011, 6, 385 CrossRef CAS.
- J. Cui, M. Faria, M. Björnmalm, Y. Ju, T. Suma, S. T. Gunawan, J. J. Richardson, H. Heidari, S. Bals, E. J. Crampin and F. Caruso, Langmuir, 2016, 32, 12394–12402 CrossRef CAS PubMed.
- G. DeLoid, J. M. Cohen, T. Darrah, R. Derk, L. Rojanasakul, G. Pyrgiotakis, W. Wohlleben and P. Demokritou, Nat. Commun., 2014, 5, 3514 CrossRef PubMed.
- V. Hirsch, C. Kinnear, L. Rodriguez-Lorenzo, C. A. Monnier, B. Rothen-Rutishauser, S. Balog and A. Petri-Fink, Nanoscale, 2014, 6, 7325–7331 RSC.
- A. Spyrogianni, I. K. Herrmann, M. S. Lucas, J.-C. Leroux and G. A. Sotiriou, Nanomedicine, 2016, 11, 2483–2496 CrossRef CAS PubMed.
- S. R. Price, C. Kinnear and S. Balog, Nanoscale, 2019, 11, 5209–5214 RSC.
- A. Spyrogianni, G. A. Sotiriou, D. Brambilla, J.-C. Leroux and S. E. Pratsinis, J. Aerosol Sci., 2017, 108, 56–66 CrossRef CAS.
- C. Y. Watson, G. M. DeLoid, A. K. Pal and P. Demokritou, Small, 2016, 12, 3172–3180 CrossRef CAS PubMed.
- E. J. Petersen, A. R. M. Bustos, B. Toman, M. E. Johnson, M. Ellefson, G. C. Caceres, A. L. Neuer, Q. Chan, J. W. Kemling, B. Mader, K. Murphy and M. Roesslein, Environ. Sci.: Nano, 2019, 6, 2876–2896 RSC.
- T. Schneider, M. Westermann and M. Glei, Colloids Surf., A, 2020, 601, 125026 CrossRef CAS.
- J. Cohen, G. DeLoid, G. Pyrgiotakis and P. Demokritou, Nanotoxicology, 2013, 7, 417–431 CrossRef CAS PubMed.
- G. Sharma, V. Kodali, M. Gaffrey, W. Wang, K. R. Minard, N. J. Karin, J. G. Teeguarden and B. D. Thrall, Nanotoxicology, 2014, 8, 663–675 CrossRef CAS.
- T. L. Moore, L. Rodriguez-Lorenzo, V. Hirsch, S. Balog, D. Urban, C. Jud, B. Rothen-Rutishauser, M. Lattuada and A. Petri-Fink, Chem. Soc. Rev., 2015, 44, 6287–6305 RSC.
- T. L. Moore, D. A. Urban, L. Rodriguez-Lorenzo, A. Milosevic, F. Crippa, M. Spuch-Calvar, S. Balog, B. Rothen-Rutishauser, M. Lattuada and A. Petri-Fink, Sci. Rep., 2019, 9, 1–9 CAS.
- C. Grabinski, M. Sharma, E. Maurer, C. Sulentic, R. Mohan Sankaran and S. Hussain, Nanotoxicology, 2016, 10, 74–83 CAS.
- L. Böhmert, L. König, H. Sieg, D. Lichtenstein, N. Paul, A. Braeuning, A. Voigt and A. Lampen, Part. Fibre Toxicol., 2018, 15, 42 CrossRef PubMed.
- Bionano Interaction Kinetics Estimator, accessed: 2020-09-04, http://bionano.xyz/estimator.
- J. C. G. Jeynes, C. Jeynes, M. J. Merchant and K. J. Kirkby, Analyst, 2013, 138, 7070–7074 RSC.
- T. Turnbull, M. Douglass, N. H. Williamson, D. Howard, R. Bhardwaj, M. Lawrence, D. J. Paterson, E. Bezak, B. Thierry and I. M. Kempson, ACS Nano, 2019, 13, 5077–5090 CrossRef CAS.
- M. Faria, M. Björnmalm, K. J. Thurecht, S. J. Kent, R. G. Parton, M. Kavallaris, A. P. Johnston, J. J. Gooding, S. R. Corrie and B. J. Boyd, et al. , Nat. Nanotechnol., 2018, 13, 777–785 CrossRef CAS.
- S. Ashraf, A. Hassan Said, R. Hartmann, M.-A. Assmann, N. Feliu, P. Lenz and W. J. Parak, Angew. Chem., Int. Ed., 2020, 59, 5438–5453 CrossRef CAS PubMed.
- S. K. Mann, E. Czuba, L. I. Selby, G. K. Such and A. P. Johnston, Pharm. Res., 2016, 33, 2421–2432 CrossRef CAS.
- L. I. Selby, L. Aurelio, D. Yuen, B. Graham and A. P. Johnston, ACS Sens., 2018, 3, 1182–1189 CrossRef CAS PubMed.
Footnote |
| † Number of Scopus search results for (“nanoparticle” OR “particle”) AND (“endocytosis” OR “internalisation”) in 2019 and 2009. |
| This journal is © The Royal Society of Chemistry 2021 |