Reply to the ‘Comment on “Design and circuit simulation of nanoscale vacuum channel transistors”’ by R. Forbes, Nanoscale Adv., 2020, 2, DOI: 10.1039/D0NA00687D

Abstract

Prof. Forbes takes a critical view of our paper on nanoscale vacuum channel transistors (NVCTs), arguing mainly about the weaknesses in the theory of field electron emission. On the one hand, we agree with the theoretical derivation details given by Prof. Forbes, and we would correct the “simplified formula” accordingly (eqn (2)–(5)). On the other hand, the main part of our work focuses on the simulation results of structural parameters and circuit behavior, which is not involved with eqn (2)–(5). Thus, the reported results and conclusions remain reliable.

---

Prof. Forbes has raised several questions about our investigation on NVCTs, for which we would give point-to-point responses here. Overall, we appreciate the comments and helpful theory derivation from Prof. Forbes, while we would also clarify some points in our initial work.

First, the main concern in the comment is that whether eqn (2)–(5) were used to derive the simulation results (including structural parameters and circuit simulations). To clarify, we utilized the zero-temperature form of the F–E equation developed by Murphy and Good¹ in the numerical simulations of the TCAD program, which performs as eqn (1) in this circumstance. In other words, only eqn (1) was introduced in the programming codes and determines the electrical properties of the simulated device, and eqn (2)–(5) (including the wrong relation between F and V) cannot influence the calculations. As a result, the reported simulations and conclusions of circuit behaviors in the original manuscript still remain reliable, which is the main innovative point of this manuscript.

Second, Prof. Forbes states that the Fowler–Nordheim (F–N) constants (A and B) are physical constants with units that should not be written as pure numbers. We agree that our simplification of A and B as constants can lead to dimensional inconsistency and discrepancies. Therefore, we would correct the F–N constants below eqn (2) in our paper as: A ≡ e³/8πh ≅ 1.541434 × 10⁻⁶ A eV V⁻² and B ≡ 8π(2m)^1/2/3eh ≅ 6.830890 × 10⁹ eV^−3/2 V m⁻¹.

Third, we agree that using the same symbol “F” for both the local emitter surface field and the average field may cause confusion. We would correct the symbol “F” in our eqn (2) as F_av, with the relationship between the two types of field given by F = βF_av, where β is a field enhancement factor. Meanwhile, this “definition” will not lead to theoretical problems, just as the comment suggested. Besides, we would also correct the wrongly written relation “F = V × d” into “F_av = V/d”, and our eqn (5) would be written as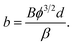

Fourth, Prof. Forbes states that the simplification of eqn (4) by setting t(y) and v(y) equal to unity can also introduce numerical error, namely under-prediction of current density by a large factor,^2,3 which is related to the work function Φ. Indeed, we should point out that an under-prediction of the performance of the NVCTs can arise from this “simplification”. However, our intention is to ensure that the proposed devices behave in an ideal manner, so that the simulation results can qualitatively reveal the electrical properties of NVCTs. From our perspective, this “simplification” may not be theoretically appropriate while it does not influence the main content. Still, we would additionally remark in the paper that simplifying t(y) and v(y) to unity could lead to under-prediction of current density in practical situations.

Lastly, we agree that the theory in our work is suitable for a diode configuration, while the discussed devices present are a transistor including the emitter, the collector, and the back-gate. The modulation effect of the gate electric field cannot be neglected. Just as Prof. Forbes suggested, the distribution of local surface field F may need to be determined by numerical methods. As a matter of fact, our simulation results show that the increasing gate voltage in the forward direction would suppress the output current of NVCTs. This phenomenon is consistent with the experimental results reported by Nirantar et al.,⁴ which demonstrates that Silvaco TCAD does consider the influence of the electric field from different directions.

To conclude, the authors wish to amend the sections of the manuscript detailed below: (1) the F–N constants below eqn (2) should be present as: A ≡ e³/8πh ≅ 1.541434 × 10⁻⁶ A eV V⁻² and B ≡ 8π(2m)^1/2/3eh ≅ 6.830890 × 10⁹ eV^−3/2 V m⁻¹; (2) the symbol “F” in our eqn (2) should be present as F_av, with the relationship between the two types of field given by F = βF_av; (3) the relation “F = V × d” should be corrected into “F_av = V/d”, and our eqn (5) would be written as 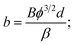(4) simplifying t(y) and v(y) to unity could lead to under-prediction of current density in a practical situation, which should be cautiously considered. However, these corrections are due to inaccuracies of formula derivation (eqn (2)–(5)), while the Murphy–Good FE equation (eqn (1)) was utilized in the numerical simulations. As a result, the reported simulations of circuit behavior still remain reliable.

Putting aside the “simplified” formula and F–N theory, the main purpose of our work is to optimize the structural parameters of NVCTs by using the conventional semiconductor design software. Therefore, we successfully demonstrate the possibility of implementing logic circuits with NVCTs. The vacuum-state inverter can provide an important theoretical basis for the future development of on-chip vacuum devices so the above flaws cannot obscure the main innovative points.

We would like to thank Prof. Forbes again for the helpful comments. We appreciate the theoretical derivations and suggestions, which would certainly improve the quality of the theoretical discussion in our work.

Conflicts of interest

There are no conflicts to declare.

References

1. E. L. Murphy and R. H. Good, Phys. Rev., 1956, 102, 1464.
2. R. G. Forbes, J. Appl. Phys., 2019, 126, 210901.
3. R. G. Forbes, Proc. R. Soc. London, Ser. A, 2013, 469, 20130271.
4. S. Nirantar, T. Ahmed, G. Ren, P. Gutruf, C. Xu, M. Bhaskaran, S. Walia and S. Sriram, Nano Lett., 2018, 18, 7478–7484.

---