Incommensurate transition-metal dichalcogenides via mechanochemical reshuffling of binary precursors

Abstract

A new family of heterostructured transition-metal dichalcogenides (TMDCs) with incommensurate (“misfit”) spatial arrangements of well-defined layers was prepared from structurally dissimilar single-phase 2H-MoS₂ and 1T-HfS₂ materials. The experimentally observed heterostructuring is energetically favorable over the formation of homogeneous multi-principle element dichalcogenides observed in related dichalcogenide systems of Mo, W, and Ta. The resulting three-dimensional (3D) heterostructures show semiconducting behavior with an indirect band gap around 1 eV, agreeing with values predicted from density functional theory. Results of this joint experimental and theoretical study open new avenues for generating unexplored metal-dichalcogenide heteroassemblies with incommensurate structures and tunable physical properties.

---

1 Introduction

Layered transition-metal dichalcogenides (TMDCs) with a chemical formula of MX₂, where M is a group 4–6 refractory metal and X is a chalcogen (S, Se, or Te), continue to receive much attention as easily accessible sources of single-layer 2D-nanomaterials and building blocks for 3D-heterostructures that demonstrate a broad variety of physical properties suitable for diverse applications.^1–7 Generally, heterostructured materials are formed as a result of elaborate syntheses and in minuscule quantities. A versatile synthetic approach enabling simple and reliable preparation of 3D-heterostructured TMDCs in bulk will make those materials broadly available for both fundamental and applied research, potentially revealing new physics and new areas for applications.

Bulk TMDCs are built from layers of covalently bonded metal and chalcogen atoms held together via weak van der Waals (vdW) forces (see ESI, Fig. S1†). As a result, they can be easily exfoliated into 2D-nanosheets, even down to single layers.⁸ Both bulk and 2D-TMDCs demonstrate a broad range of electronic transport properties that span from indirect and direct gap semiconductivity, semimetallic and metallic behavior, to low-temperature superconductivity, depending on the chemical composition and the spatial configurations of the material as well as external stimuli applied.^1,9

While binary TMDCs are well known,¹⁰ the preparation of layered multi-principal element metal chalcogenides, where different metals (M) and chalcogens (X) share a common crystal lattice, remained challenging until our recent report.¹¹ One of the intriguing outcomes of this earlier study was the observed heterostructuring of different group 5 and 6 binary TMDCs upon mechanical milling at room temperature. Thus-produced 3D-heterostructures are metastable and, when subjected to high-temperature annealing, they transform into uniform single-phase materials. However, if the starting metal chalcogenides possess different crystal structures and stoichiometries, e.g. TaS₂ and SmS, or NbSe₂ and LaSe, under similar processing conditions they form well-defined and thermodynamically stable heterostructures with incommensurate (misfit) spatial arrangements, where slabs of the mono-chalcogenide (SmS or LaSe) with cubic crystal structures alternate with hexagonal 2D layers of the TMDC (TaS₂ or NbSe₂).¹²

The latter discovery raised questions about possibility to design layered misfit materials from chemically related yet structurally dissimilar building blocks, such as hexagonal 2H-MoS₂ ¹³ and trigonal 1T-HfS₂,¹⁴ by their simultaneous mechanochemical exfoliation and re-assembly into TMDCs heterostructures. If feasible, this would open a new avenue to an unexplored family of incommensurate 3D-heterostructures with tunable physical properties. Below we report on the successful implementation of this idea.

2 Experimental

2.1 Synthesis of 3D-heterostructures

In a standard experiment, 3 g of a mixture of MoS₂ and HfS₂ (see ESI, and Fig. S2†) weighed in a desired stoichiometric ratio was loaded in a zirconia vial together with five 12.7 mm zirconia balls. To prevent oxidation. All operations were conducted under the inert atmosphere of an argon-filled glovebox. The sample was milled for 30 hours in a planetary mill (Fritsch, Pulverisette 7) and transferred back to the argon-filled glovebox for loading into a quartz ampule. The ampule was sealed under ultra-high purity helium and the sample was annealed for 3 days at 1000 °C. Thereafter it was cooled down to room temperature and transferred back to the glovebox for further handling.

2.2 Powder X-ray diffraction (PXRD)

Phase analyses and structural characterizations of all reactions products were carried out by powder X-ray diffraction (XRD) at room temperature on a PANalytical powder diffractometer using Cu-Kα radiation in the range of Bragg angles 10° ≤ 2θ ≤ 80° with a 0.02° step. Considering lack of periodicity along the stacking direction of a few nanometer thick slabs of the constituent phases, unavoidable and strong texturing, and highly anisotropic peak broadening, Rietveld refinement was impossible. Hence, Le Bail refinements (see ESI and Fig. S3† as an example) of the lattice parameters of the individual phases were performed using FullProf sofware.¹⁵ The backgrounds were fitted by linear interpolations between selected data points in the regions with no Bragg peaks present. The pseudo-Voigt function was used to approximate peak shapes, with peak shape parameters refined separately for each of the two phases present.

2.3 Scanning transmission electron microscopy (STEM)

High-angle annular dark-field (HAADF) scanning transmission electron microscopy (STEM) and energy dispersive X-ray spectrometry (EDS) experiments were performed on a Titan Themis (FEI) probe Cs-corrected TEM. The high-resolution HAADF-STEM imaging was carried out using a convergence semi-angle of 18 mrad and a collection semi-angle of 99–200 mrad at 200 kV. STEM-EDS analysis was performed using a Super-X EDS detector attached to the Titan Themis.

2.4 Band gap measurements

Optical measurements were performed using a custom-built experimental setup (ESI, and Fig. S4† for further details) based on a diffractive monochromator (focal length of the lens 600 mm). A quartz halogen lamp was utilized as a light source and a photomultiplier tube (PMT) was used to detect the radiation. Samples were placed inside the integrating sphere and their diffuse reflectance spectra (DRS) were recorded. Barium sulphate served as a standard. The acquired DRS were converted to Kubelka–Munk function (absorption-to-scattering ratio α/S).

2.5 Density functional theory calculations

Density Functional Theory (DFT) calculations were employed as implemented in the Vienna ab initio simulations package (VASP)^16–18 with Projector Augmented Wave (PAW) method.^19,20 The plane-wave basis cut-off was set at 500 eV, and the k-mesh to sample the first Brillouin zone for geometry optimization and band structure were, respectively, 5 × 5 × 1 and 7 × 7 × 2. Unit-cell translation vectors, cell volumes, and atomic positions were fully optimized in the heterostructures and single-phase solid solution (SS) materials. The convergence criteria for the residual force and energy were set to 10⁻³ eV Å⁻¹ and 10⁻⁵ eV per atom, respectively. The parameter-free van der Waals density functional (optB88-vdW)²¹ was employed to account for dispersive interactions,²² whereas the hybrid Heyd–Scuseria–Ernzerhof²³ functional was employed for band-gap calculations as the van der Waals functionals have a minor effect on the band structure.²⁴ Two main structural configurations that are common for transition-metal dichalcogenides, namely 2H-MX₂ and 1T-MX₂ polytypes,¹ are used to assess the formation energies of different heterostructured and single-phase materials.

For DFT calculations of (Mo_0.5W_0.5)S₂ and (Mo_0.5W_0.5)(S_0.5Se_0.5)₂, we used (I) 24-atom supercell (2 × 2 × 1 unit cells of 2H-MoS₂) to mimic disorder, whereas 2H-MoS₂ was used to model 1 × 1 × 4 heterostructure supercell. For disorder cases: we use 5 × 5 × 1 and 11 × 11 × 5 k-mesh for structural relaxation and energy. For heterostructures: we use 3 × 3 × 1 and 11 × 11 × 1 k-mesh for structural relaxation and energy. For (Mo₄₀W₄₀Ta₂₀)S₂, (II) a 96-atom supercell (4 × 4 × 1 unit cells of 2H-MoS₂) was used to mimic disorder, whereas 1 × 1 × 10 supercell of 2H-MoS₂ was used to model an ordered 4(TaS₂):8(MoS₂):8(WS₂) heterostructure. For disorder case: we use 5 × 5 × 3 and 8 × 8 × 6 k-mesh for structural relaxation and energy. For heterostructures: we use 3 × 3 × 1 and 9 × 9 × 1 k-mesh for structural relaxation and energy. A manual stacking approach was used to create vertical vdW heterostructures of 2H-MoS₂ and 1T-HfS₂ in the present study.

3 Results and discussion

3.1 Synthesis and characterization

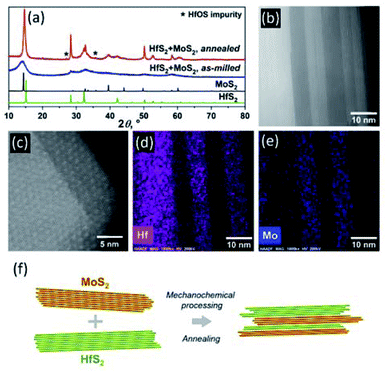
In contrast to the mixtures of binary MX₂, where M = Mo, W, Ta, Nb, and X = S or Se, that yield single-phase TMDCs upon mechanical milling and subsequent annealing,¹¹ ball milling of an equimolar mixture of HfS₂ and MoS₂ in a planetary mill (Fritsch, Pulverisette 7) for 30 hours, followed by a high-temperature annealing at 1000 °C for 72 hours, does not produce a single-phase (Mo_0.5Hf_0.5)S₂. While the X-ray diffraction (XRD) pattern of the as-milled powder consists of several broad peaks characteristic of a highly disordered solid (Fig. 1a), the material obtained after the subsequent annealing is composed of the distinguishable HfS₂ and MoS₂ phases (Table 1, Fig. 1a).

Fig. 1 (a) Powder XRD patterns of an equimolar mixture of HfS₂ and MoS₂ after ball-milling in a planetary mill for 30 hours and subsequent annealing at 1000 °C for 72 hours. XRD patterns of pure HfS₂ and MoS₂ are shown as references. Bragg peaks corresponding to an oxysulfide impurity {HfOS} are indicated by asterisks. (b) HAADF-STEM and (d, e) STEM-EDS images of the same material. Due to higher Z-contrast, HfS₂ fragments produce brighter shades, while MoS₂ layers appear as dark slabs. (c) The Moiré pattern on the surface of another, differently oriented particle of the same material. (f) Schematic diagram illustrating the formation of 3D-heterostructured TMDCs.

Table 1 Lattice parameters of the 3D-heterostructured TMDCs derived from the Rietveld refinements of the corresponding powder XRD patterns^a

MoS2 : HfS2 molar ratio	MoS2 (2H) lattice parameters^b (Å)	HfS2 (1T) lattice parameters^c (Å)	R p, %
a The Rp values correspond to the profile residuals. b Space group symmetry P63/mmc (#194). c Space group symmetry P3̄m1 (#164). d Processed twice using the same synthesis protocol as the previous material.
1 : 0	a = 3.160(1) Å	—	6.07
	c = 12.298(2) Å
0.75 : 0.25	a = 3.157(1) Å	a = 3.626(1) Å	7.83
	c = 12.286(1) Å	c = 5.852(1) Å
0.5 : 0.5	a = 3.162(1) Å	a = 3.634(1) Å	7.68
	c = 12.124(1) Å	c = 5.880(1) Å
0.5 : 0.5^d	a = 3.159(1) Å	a = 3.629(1) Å	6.01
	c = 12.074(1) Å	c = 5.881(1) Å
0.25 : 0.75	a = 3.163(1) Å	a = 3.634(1) Å	6.52
	c = 12.255(1) Å	c = 5.951(1) Å
0 : 1	—	a = 3.628(1) Å	9.88
		c = 5.854(1) Å

---

Lattice parameters of both TMDC phases in the annealed sample reveal a slight reduction (∼1.4%) of the parameter c in the MoS₂ phase and a smaller but noticeable expansion (∼0.5%) of the parameter c in the HfS₂ constituent. Considering that r_Mo = 1.400 Å < r_Hf = 1.580 Å (metallic radii for coordination number 12), these anomalies cannot be attributed to minor substitutions on the metal sites. The changes that occur in opposite direction are not likely to be related to various concentrations of defects in two different structural motifs and, therefore, we ascribe them to large errors that arise from a number of factors. These are: strong diffuse scattering due to a few-nanometer thick slabs stacked along the c direction (see Fig. 1b–e); heavy overlap of the majority of the strongest Bragg peaks; and highly anisotropic broadening due to epitaxial strains that are unavoidable and cannot be removed by annealing. All of them combined, Le-Bail-refined unit-cell dimensions, and in particular those parallel to the stacking direction, become susceptible to random errors, even though the formal least squares standard deviations listed in Table 1 are low.

A minor impurity detected in the annealed sample almost certainly belongs to an off-stoichiometric hafnium oxysulfide that has formed in the sample even though all operations were carried out under high-purity argon or helium. The annealed material was further studied using High-Angle Annular Dark Field Scanning Transmission Electron Microscopy (HAADF-STEM) and Energy Dispersive Spectroscopy (STEM-EDS), which reveal a well-defined sandwich-like arrangement of the separate phases in the material as shown in Fig. 1b. The alternating phases have different Z-contrast, whereby the MoS₂ slabs appear dark and HfS₂ produces much brighter segments. The thickness of specific slabs varies, indicating stochastic nature of the mechanical exfoliation and self-assembly processes. Furthermore, the HAADF-STEM images reveal the presence of the Moiré pattern on the surface of the material (Fig. 1c), which is characteristic for TMDCs with lattice mismatch layers positioned on the top of each other,²⁵i.e. incommensurate structural arrangements. STEM-EDS (Fig. 1d, e) confirms the 3D-heterostructured arrangement of the layers in the sample. The schematic diagram illustrating the formation of 3D-heterostructured TMDCs is shown in Fig. 1f.

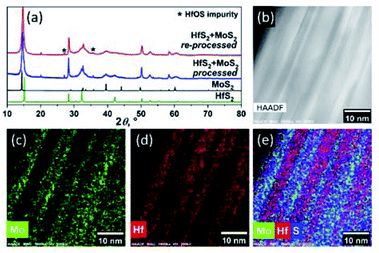
Reprocessing of the annealed material by its milling for additional 30 hours, followed by annealing at 1000 °C for 72 hours, does not eliminate the phase separation in the sample. Its XRD, HAADF-STEM and STEM-EDS analyses clearly indicate that the sandwich-like arrangement of the MoS₂ and HfS₂ slabs is retained in the reprocessed material (Fig. 2, Table 1), although the slabs become markedly thinner.

Fig. 2 (a) XRD powder patterns, (b) HAADF-STEM and (c–e) STEM-EDS images of the ball-milled sample of an equimolar mixture of HfS₂ and MoS₂ in a planetary mill for 30 hours and subsequent annealing at 1000 °C for 72 hours, followed by reworking of the material formed using the same processing protocol. XRD patterns of HfS₂ and MoS₂ are shown as references. Bragg peaks of {HfOS} impurity are indicated by asterisks.

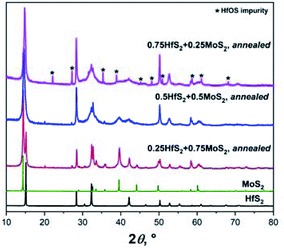
Two other MoS₂-HfS₂ compositions that are rich in one or another component were prepared and investigated as well.

The XRD patterns and the structural parameters of the obtained samples are shown in Fig. 3 and Table 1. Also, in these cases, a distinctive formation of solid solutions could not be detected. The increased fraction of the HfOS impurity seen in the XRD pattern of Hf_0.75Mo_0.25S₂ correlates with increased concentration of Hf in the material and indicates higher sensitivity of the Hf-rich material to oxygen. As discussed above, minor non-systematic changes in the c lattice parameters are related to contributions from diffuse scattering and varying anisotropic peak broadening.

Fig. 3 The XRD patterns of different mixtures of HfS₂ and MoS₂ ball milled in a planetary mill for 30 hours and subsequent annealing at 1000 °C for 72 hours. XRD patterns of starting materials HfS₂ and MoS₂ are shown as references. The Bragg peaks of an oxysulfide impurity {HfOS} are indicated by asterisks.

3.2 Density functional theory calculations

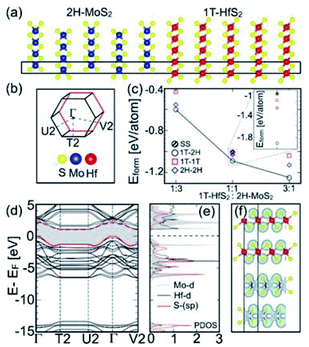
To gain initial insight into different chemical behaviours of structurally similar group 4, 5 and 6 TMDCs, we analysed phase stability, nature of band gap, and electronic structure calculated from DFT.

Phase stability and electronic-structure of the 2H-MoS₂:1T-HfS₂ heterostructure. An evaluation of the stable ground-state structures was carried out for two possible atomic arrangements – the heterostructure (I), where Mo and Hf are confined to separate parts of the supercell, see Fig. 4, and the solid solution (II) with statistical distribution of Hf and Mo throughout the supercell. Additional assemblies, like m(1T-HfS₂)/n(1T-MoS₂) and m(2H-HfS₂)/n(1T-MoS₂), were also considered. The number of layers in HfS₂ and MoS₂ fragments were consistently kept at m/n = 5/5 ratio for the equimolar chemical compositions, or m/n = 5x/5y for other xHfS₂/yMoS₂ materials.

Fig. 4 (a) Atomic arrangements in 5(1T-HfS₂)/5(2H-MoS₂) heterostructure. (b) The first Brillouin zone is shown in (d). Sulphur atoms (S) are represented by yellow circles, Mo atoms are coloured blue, and Hf atoms are red. (c) Formation energies (eV per atom) of 5(1T-HfS₂)/5(2H-MoS₂) [denoted 1T/2H], 5(1T-HfS₂)/5(1T-MoS₂) [denoted 1T/1T] and 5(2H-HfS₂)/5(2H-MoS₂) [denoted 2H/2H] heterostructure, along with the (Mo_0.5Hf_0.5)S₂ solid-solution [denoted SS] arrangements. (d) Electronic band-structure, (e) partial density of states (states/eV-atom), and (f) charge-density distribution in the 5(1T-HfS₂)/5(2H-MoS₂) heterostructure Calculated indirect band gap is 1.01 eV and the charge-density iso-surfaces (set to 0.08 eV Å⁻¹) are plotted.

The formation energies (E_form) calculated for equimolar. (5 : 5) HfS₂/MoS₂ heterostructures and the solid-solution (SS) compound are shown in Fig. 4c. Their comparison indicates that the 5(1T-HfS₂)/5(2H-MoS₂) arrangement is the most stable among evaluated structures, as its E_form is as low as −1.0902 eV per atom [which is 59.92, 73.45, and 84.32 meV below the E_form calculated, respectively, for 5(1T-HfS₂)/5(1T-MoS₂), 5(2H-HfS₂)/5(2H-MoS₂), and SS-(Mo_0.5Hf_0.5)S₂].

In addition, two other families of x5HfS₂/y5MoS₂ materials were investigated. Their unit cells were built from five-layer HfS₂ and MoS₂ slabs taken in 1 : 3 (x = 1, y = 3) and 3 : 1 (x = 3, y = 1) stoichiometric proportions or SS, (Mo_yHf_x)S₂, layers. The calculated E_form values are plotted in Fig. 4c. Here, we also find that the x5(1T-HfS₂)/y5(2H-MoS₂) heterostructural arrangements are the most energy favorable among other evaluated cases. We also investigated several other possibilities, for example, solubility of Hf in 2H-MoS₂ or Mo in 1T-HfS₂ or anti-site defects (Mo and Hf at the interface were interchanged to see the effects on energetics), vacancies (Mo or Hf or S). However, none of these possibilities are thermodynamically stable compared to pure 2H-MoS₂-1T-HfS₂ interface.

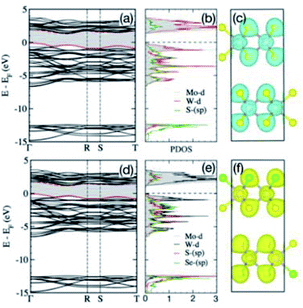
The calculated partial density of states (DOS) and the charge-density for 5(1T-HfS₂)/5(2H-MoS₂) heterostructures, and the Mo-d, Hf-d, and S-sp bands are shown in Fig. 4d–f. The bands near the Fermi energy (E_F in Fig. 4d-e) mainly consist of the S-p states that are hybridized with the Mo-d and Hf-d states, whereas the S-s orbitals emerge way below E_F, and are separated from the other valence states by 8.0 eV, i.e., are chemically inactive. The strong intralayer hybridization between the d-orbitals of Mo and Hf, and the p-orbitals of S is also evident from the overlapping charge densities shown in Fig. 4f, which stabilizes the 5(1T-HfS₂)/5(2H-MoS₂) heterostructure. The charge density in both 1T-HfS₂ and 2H-MoS₂ layers is localized on the S atoms with the directional intralayer bonding toward Mo and Hf and the band gap of 1.01 eV.

Phase stability and electronic structure of other group 5 and 6 mixed TMDCs. We have also evaluated the phase stability and electronic structures of some other group 6 TMDCs prepared and described elsewhere.¹¹ Further details of our calculations are shown in the ESI,† file. The calculated E_form of the material with overall (Mo_0.5W_0.5)S₂ chemical composition in the SS or heterostructure states differ by more than 0.01 eV per atom in the favour of SS (−0.845 eV per atom vs. −0.833 eV per atom). Replacement of S by Se in (Mo_0.5W_0.5)SSe further destabilizes the hypothetical heterostructured arrangement and makes the formation of SS inevitable, in line with earlier experimental data.¹¹ The electronic band-structure, partial density of states, and charge density for (Mo_0.5W_0.5)S₂ and (Mo_0.5W_0.5)SSe materials are displayed in Fig. 5.

Fig. 5 Electronic band-structure, partial densities of states (states/eV-atom), and charge-density iso-surfaces (set to 0.08 eV Å⁻¹) of (Mo_0.5W_0.5)S₂, (a–c) and (Mo_0.5W_0.5)SSe₂ (d, e), respectively. The indirect band gaps were calculated at 1.02 eV for (Mo_0.5W_0.5)S₂ and 1.17 eV for (Mo_0.5W_0.5)SSe. A 2 × 2 × 2 supercell was used to model W-disorder on Mo site with 24 atom cell (Mo = 4, W = 4, S = 16; and Mo = 4, W = 4, S = 8, Se = 8) atom per cell.

The calculated band gaps for (Mo_0.5W_0.5)S₂ and (Mo_0.5W_0.5)SSe are 1.02 eV and 1.17 eV, respectively. They are indirect in nature and follow the Γ–R high-symmetry direction. Surprisingly, the effect of Se-substitution is quite moderate in this case.

Finally, we also evaluated the formation energies and electronic structures of the single-phase material with the nominal composition of (Mo_0.4W_0.4Ta_0.2)S₂. Partial replacement of Mo and W by Ta in (Mo_0.5W_0.5)S₂ can be seen as an injection of 0.2 holes per molecule into the system. Once again, the calculated E_form of the “hole-doped” (Mo_0.4W_0.4Ta_0.2)S₂ is substantially lower than that of the heterostructure material (−0.875 vs. −0.835 eV per atom), which explains the experimentally observed formation of the solid-solution phase in this case.¹¹

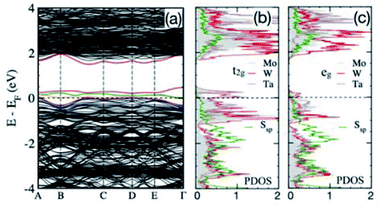
The band structure and partial DOS for (Mo_0.4W_0.4Ta_0.2)S₂ are shown in Fig. 6. The presence of Ta is responsible for only a partial filling of bonding Mo/W d-states, while they are completely filled in (Mo_0.5W_0.5)S₂ (Fig. 5a and b). This moves the bonding t_2g and e_g states (Fig. 6b and c) to E_F, where the majority of states belong to Mo/W/Ta t_2g-bands. Here, t_2g is a combination of d_xy, d_yz, and d_xz orbitals and e_g represents d_x²y² and d_z² orbitals. The S p-bands near E_F are situated in the same energy range as the Mo/W d-bands in (Mo_0.5W_0.5)S₂ (Fig. 5b), and Ta causes reduced filling of S p-bands that also move closer to E_F. Thus, the crossover of partially-filled Mo/W-d and S-p bands at E_F caused by Ta predicts metallic behaviour of (Mo_0.4W_0.4Ta_0.2)S₂.

Fig. 6 Electronic band-structure (a), and Mo/W/Ta(t_2g, e_g)/S-sp partial density of states (states/eV-atom) (b, c) calculated for single-phase (Mo_0.4W_0.4Ta_0.2)S₂. Presence of Ta at the metal site changes the semiconducting behavior of (Mo_0.5W_0.5)S₂ to metallic in (Mo_0.4W_0.4Ta_0.2)S₂. A 4 × 4 × 2 supercell was used to model the 0.4 (Mo):0.4 (W):0.2 (Ta) disorder with 96 atom per cell (Mo = 13, W = 13, Ta = 6, S = 64).

In summary, our DFT results reveal that combining structurally different 1T-HfS₂ and 2H-MoS₂ phases stabilizes the heterostructured arrangement over solid-solution-like single-phase (1T or 2H) states. At the same time, blending isostructural TMDCs, such as 2H-MoX₂ and 2H-WX₂ (X = S, Se), produces single-phase materials; even so, the metastable heterostructured intermediates are observed after the low-temperature stages of the previous experiments.¹¹ Doping group 6 TMDCs with a group 5 metal (Ta) is not expected to affect the phase stability of the resulting compounds, but it changes transport behaviour from semiconducting to metallic.

3.3 Electronic transport measurements

Electronic transport of the equimolar HfS₂/MoS₂ heterostructure and some previously prepared multi-principal element, single-phase TMDCs,¹¹ have been studied using photoconductivity, optical band gap, and electrical resistivity measurements. The experimental band gap values along with those predicted by the DFT calculations are summarized in Table 2, together with those reported in the literature.

Table 2 Indirect band gaps determined by photoconductivity and optical measurements

Sample	E g, eV photoconductivity	E g, eV optical (Tauc plot)	E g, eV (DFT)
MoS2	1.26	1.23 (lit.^26)	1.32
HfS2	—	1.80 (lit.^27)	1.82
HfS2/MoS2	0.96	1.09	1.01
WS2	—	1.35 (lit.^26)	1.15
WSe2	1.20	1.20 (lit.^28,29)	1.36
MoSe2	—	1.10 (lit.^27)	1.28
Mo0.5W0.5S2	0.92	0.81	1.02
Mo0.5W0.5SSe	—	1.10	1.17

---

The additional experimental details on measurements performed can be found in the ESI.† Several observations are worth noting. First, in the majority of the cases, the experimental values are in a good agreement with those predicted by DFT or published in the literature. The band gap values experimentally determined for both the HfS₂/MoS₂ and the multi-principal elements TMDCs shown in Table 2 are below those observed in the pure binary precursors, and obviously can be fine-tuned by altering the material's chemical and phase compositions.

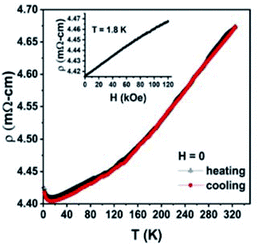
The electronic transport behaviour of multi-principal element TMDCs can be further manipulated by doping with group 5 transition metals, such as Ta, that converts them from semiconductors into metallic-type conductors.³⁰ To illustrate this, we measured temperature dependence of the electrical resistivity, ρ(T), of W_0.4Mo_0.4Ta_0.2S₂ using a Physical Property Measurements System (PPMS, Quantum Design, Inc.) employing a standard four-probe technique in magnetic field up to 120 kOe. The ρ vs. (T) measured during cooling and heating between 320 K and 1.8 K in the absence of magnetic field (H = 0) is shown in Fig. 7. Both the heating and cooling curves are practically identical. Consistent with the theoretical prediction, W_0.4Mo_0.4Ta_0.2S₂ demonstrates a weakly temperature-dependent metallic conductivity between 300 and 14 K. A minor increase in the resistivity observed at T ≤ 14 K can be attributed to the presence of electron transport barriers between crystallites in the sample that reduce its overall conductivity at cryogenic temperatures. The electrical resistivity measured as a function of the magnetic field up to 120 kOe (Fig. 7, inset) indicates very weak but positive magnetoresistance of ∼1.2% at T = 1.8 K without any sign of saturation.

Fig. 7 Electrical resistivity of W_0.4Mo_0.4Ta_0.2S₂ as a function of temperature, measured at heating (black triangle), and cooling (red solid circle) in the absence of magnetic field. Inset shows resistivity as a function of the magnetic field up to 120 kOe at T = 1.8 K.

4 Conclusions

In contrast to the group 5 and 6 TMDCs, HfS₂ does not form a solid solution with MoS₂ after prolonged mechanical milling and annealing, even if they are performed in a cyclic manner. The misfit 3D-heterostructures formed from 1T-HfS₂ and 2H-MoS₂ building blocks show semiconducting behaviour with indirect band gap around 1 eV, which agrees well with the value predicted by DFT calculations and is lower than the values reported for the pure binary precursor materials. Our results also demonstrate that electronic transport in bulk TMDCs can be successfully manipulated using doping with appropriate refractory metals, which opens new avenues for engineering of vdW materials with tuneable physical properties.

Author contributions

I. Z. H., O. D. contributed to design of experiments, performed materials synthesis, materials characterization and contributed to interpretation of results; O. D. performed Rietveld refinements; S. Z. M., R. V. G and A. K. P. performed electronic transport experiments and data interpretation; V. K. P. contributed to structural data interpretation; P. S. and D. D. J. performed DFT calculations and analysis; V. P. B. conceived the idea, supervised and guided the study, contributed to design of experiments and data interpretation. All authors provided comments and edits during the preparation of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The materials development was supported by the Ames Laboratory's Laboratory Directed Research and Development (LDRD) program. Theoretical design & analysis, structural and physical property characterization efforts were supported by the U.S. Department of Energy (DOE) Office of Science, Basic Energy Sciences, Materials Science & Engineering Division. Ames Laboratory is operated for the U.S. DOE by Iowa State University of Science and Technology under Contract No. DE-AC02-07CH11358. Theoretical calculations were conducted using the advanced computing resources provided by Texas A&M High-Performance Research Computing.

Notes and references

1. A. V. Kolobov and J. Tominaga, Two-Dimensional Transition-Metal Dichalcogenides, Springer International Publishing, Switzerland, 2016.
2. A. K. Geim and I. V. Grigorieva, Nature, 2013, 499, 419–425.
3. K. S. Novoselov, A. Mishchenko, A. Carvalho and A. H. Castro Neto, Science, 2016, 353, aac9439.
4. V. S. Pervov and E. V. Makhonina, Russ. Chem. Rev., 2000, 69, 481–489.
5. M. Serra and R. Tenne, J. Coord. Chem., 2018, 71, 1669–1678.
6. H. Taghinejad, M. Taghinejad, A. A. Eftekhar, Z. Li, M. P. West, M. H. Javani, S. Abdollahramezani, X. Zhang, M. Tian, T. Johnson-Averette, P. M. Ajayan, E. M. Vogel, S.-F. Shi, W. Cai and A. Adibi, ACS Nano, 2020, 14, 6323–6330.
7. J. Joshi, T. Zhou, S. Krylyuk, A. V. Davydov, I. Žutić and P. M. Vora, ACS Nano, 2020, 14, 8528–8538.
8. J. R. Brent, N. Savjani and P. O'Brien, Prog. Mater. Sci., 2017, 89, 411–478.
9. F. Lacopi, J. J. Boeckl and C. Jagadish, Semiconductors and Semimetals. v. 95, 2D Materials, Academic Press, Cambridge, San Diego, Oxford, London, 2016.
10. F. A. Cotton, G. Wilkinson, C. A. Murillo, M. Bochmann and R. Grimes, Advanced Inorganic Chemistry, Wiley, New York, 5th edn, 1988.
11. I. Z. Hlova, O. Dolotko, B. W. Boote, A. K. Pathak, E. A. Smith, V. K. Pecharsky and V. P. Balema, Chem. Commun., 2018, 54, 12574–12577.
12. O. Dolotko, I. Z. Hlova, A. K. Pathak, Y. Mudryk, V. K. Pecharsky, P. Singh, D. D. Johnson, B. W. Boote, J. Li, E. A. Smith, S. L. Carnahan, A. J. Rossini, L. Zhou, E. M. Eastman and V. P. Balema, Nat. Commun., 2020, 11, 1–10.
13. I. Song, C. Park and H. C. Choi, RSC Adv., 2015, 5, 7495–7514.
14. L. F. Mattheiss, Phys. Rev. B: Condens. Matter Mater. Phys., 1973, 8, 3719.
15. T. Roisnel and J. Rodriguez-Carvajal, Mater. Sci. Forum, 2001, 378, 118–123.
16. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
17. G. Kresse and J. Furthmüller, Comp. Mater. Sci, 1996, 6, 15.
18. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
19. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
20. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
21. G. Roman-Perez and J. M. Soler, Phys. Rev. Lett., 2009, 103, 096102.
22. J. Klimes, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131.
23. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906.
24. Z.-X. Hu, H. P. Lan and W. Ji, Sci. Rep., 2014, 4, 5036.
25. A. B. Naden, K. J. O'Shea and D. A. MacLaren, Nanotechnology, 2018, 29, 165704.
26. K. Kobayashi and J. Yamauchi, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 17085.
27. K. Terashima and I. Imai, Solid State Commun., 1987, 63, 315–318.
28. R. Coehoorn, C. Haas and R. de Groot R, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 6203–6206.
29. A. Prakash and J. Appenzeller, ACS Nano, 2017, 11, 1626–1632.
30. V. P. Balema, S. Padalkar, I. Z. Hlova, T. Lan, O. Dolotko, V. K. Pecharsky, D. D. Johnson, A. Pathak and P. Singh, U.S. Pat. Appl. Publ., 2020, US 20200109479 A1 20200409.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional experimental details on precursor synthesis, Rietveld refinement, photoconductivity and magnetoresistance measurements, and density functional theory calculations. See DOI: 10.1039/d1na00064k

‡ These authors contributed equally.

---