Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The effect of mechanical strain on the Dirac surface states in the (0001) surface and the cohesive energy of the topological insulator Bi2Se3†
Soumendra Kumar
Das
and
Prahallad
Padhan
 *
*
Department of Physics, Indian Institute of Technology Madras, Chennai 600036, Tamil Nadu, India. E-mail: Padhan@iitm.ac.in
First published on 8th July 2021
Abstract
The band gap (Eg) engineering and Dirac point tuning of the (0001) surface of 8 QLs (quintuple layers) thick Bi2Se3 slab are explored using the first-principles density functional theory calculations by varying the strain. The strain on the Bi2Se3 slab primarily varies the bandwidth, modifies the pz – orbital population of Bi and moves the Dirac point of the (0001) surface of Bi2Se3. The Dirac cone feature of the (0001) surface of Bi2Se3 is preserved for the entire range of the biaxial strain. However, around 5% tensile uniaxial strain and even lower value of volume conservation strain annihilate the Dirac cone, which causes the loss of topological (0001) surface states of Bi2Se3. The biaxial strain provides ease in achieving the Dirac cone at the Fermi energy (EF) than the uniaxial and volume conservation strains. Interestingly, the transition from direct Eg to indirect Eg state of the (0001) surface of Bi2Se3 is observed in the volume conservation strain-dependent Eg. The strain on Bi2Se3, significantly modifies the conduction band of Se2 atoms near EF compared to Bi and Se1, and plays a vital role in the conduction of the (0001) surface of Bi2Se3. The atomic cohesive energy of the Bi2Se3 slab is very close to that of (0001) oriented nanocrystals extracted from the Raman spectra. The strain-dependent cohesive energy indicates that at a higher value of strain, the uniaxial and volume conservation strain provides better stability than that of the biaxial strain (0001) oriented growth of the Bi2Se3 nanocrystals. Our study establishes the relationship between the strained lattice and electronic structures of Bi2Se3, and more generally demonstrates the tuning of the Dirac point with the mechanical strain.
1. Introduction
The concept of topological insulators (TIs) has changed the conventional way of classifying solids based on symmetry breaking since it possesses symmetry protected topologically active surface states. TIs have created considerable attention among the condensed matter physics community, which behave as an insulator in its bulk but possess topologically active metallic surface states. TIs are characterized by a number known as the Z2 topological invariant, which can be calculated from the parity of the occupied bands for systems having inversion symmetry.1 Among the different compounds showing topological properties, Bi2Se3 is considered as the prototype of three-dimensional (3D) TIs and has been extensively studied over the last few years due to some of its unique features such as a simple band structure with a direct band gap (Eg) of 0.3 eV, single Dirac cone at the Γ point2 and the helical spin texture of opposite spin helicity for the upper and lower Dirac cones.3 The tailoring of the topological surface states has been investigated using different external and internal agents to make the exotic topological phenomena viable for potential applications.4,5 Some of the widely studied agents are stress, electromagnetic field, chemical substitutions, stacking defects,6etc. In particular, strain plays a significant role in tuning the physical properties of TIs. For example, the first-principles density functional theory (DFT) calculations show the shift of the Dirac point of the helical surface states,7 enhancement or destruction of surface states,8 improvement in thermoelectric properties,9 decrease in the bulk carrier density,10 decrease in the coulombic gap, and increase in the strength of the spin–orbit interaction11 in Bi2Se3. Using van der Waals DFT and semi-classical Boltzmann theory, the thermoelectric figure of merit of a single quintuple layer (QL) of Bi2Se3 is found to be 0.27, which is more than the bulk value 0.10, and can be further increased to 0.30 by introducing 2.5% compressive strain.12 DFT calculations have also established that strain plays a crucial role to tune the ground state of the monolayer (ML) In2Se3. The strain fully suppresses the polarization in ML-In2Se3 and causes out-of-plane polarization in 2D non-polar materials, i.e., ML-Bi2Se3, ML-Bi2Te3, ML-Sb2Te3 and ML-Sb2Se3.13 Strain engineering also predicts the occurrence of new 3D TI compounds with anti-perovskite structures in ternary cubic centrosymmetric compounds (M3N)Bi where M = Ca, Sr, Ba.14 Strain engineering plays a unique role in controlling the band structure and influences the Dirac point energy, Fermi velocity, metallic character, and the topology of the Bi based chalcogenide compounds. Ab initio calculations suggest the modification in the band structures, the absence of bulk-free carrier states, enhancement in the Eg opening in highly strained Bi2Se3 films that create the possibilities for a TI-based field-effect transistor.15Inspired from the theoretical prediction of the possible tuning of bulk band gap and surface states of Bi2Se3 by the elastic strain, the strain has been applied on Bi2Se3 using different configurations, such as substrate-induced strain, stretching of the flexible substrate, doping, and the intercalation. Chae et al. have grown Bi2Se3 films on graphene/SiO2 and SiO2 surface.16 The 3 QLs thick film of Bi2Se3 grown on graphene/SiO2 exhibits strain values of 5.4%, while the film on SiO2 surface shows 7.6%. Interestingly, the strain on 2 QLs Bi2Se3 films is much lower than that of the 3 QLs film, implying that the interfacial strain from the graphene substrate is much more dominant as the thickness decreases within 3 QLs.16 However, the strain induced by the GaN substrate on Bi2Se3 is relatively low between 3% to 2.7%, although the lattice mismatch is 30%.17 The substrate-induced stress increases with thickness in the case of In2Se3 and decreases in the case of Bi2Se3 grown on sapphire because of the opposite lattice mismatch and different thermal expansion coefficients between the sample and the substrate.18 Flötotto et al. have grown ultrathin epitaxial Bi2Se3 films bonded onto conductive polyimide foils (Kapton).19 By using the strain holder, the strain has been applied to Kapton. This technique allows inducing around 2.1% in-plane strain on Bi2Se3. In addition, elemental doping in Bi2Se3 is a fundamental approach to introduce a mismatch in the effective ionic radii, i.e., strain. Though there are several studies on elemental doping in Bi2Se3, the measurement of the induced strain is very scarce. Qi et al. have measured the strain induced by Mn in Bi2Se3 after doping. The doping of Mn introduces 6% strain in Bi2Se3.20 The other technique to introduce strain in Bi2Se3 is through intercalation of various species. The predominantly ionic nature of an intercalant requires either a change in the host lattice oxidation states or the presence of atomic vacancies to maintain charge neutrality, thus limiting the intercalant concentration.21 A zero-valent intercalant does not require a change in the oxidation state of the host lattice, thus allowing a high intercalation concentration.22 Using Rietveld refinement of the Bi2Se3 host lattice structure, Koski et al. have measured lattice parameters of Bi2Se3 and Cu-intercalated Bi2Se3.21 A 10% Cu intercalation in Bi2Se3 introduced strain of 9.66% in the plane and 0.35% along out-of-plane directions. Through an alternative measurement, electron diffraction confirmed, the introduction of 8.69% in-plane and 19.64% out-of-plane strain due to the 60% intercalation of Cu in Bi2Se3.21
Through low-temperature magneto-transport measurement, it is shown that the TI surface under the compressive strain of ±0.1% experiences a significant Dirac point shift (∓30 meV) as compared to the relaxed surface. The carrier mobility of TI is also increased for the surface under tensile strain.23 Although numerous reports available in the literature, a systematic study of strain engineering on surface states of Bi2Se3 is still lacking. In the present work, we have performed first-principles DFT calculations to study the electronic structure evolution of (0001) surface states of Bi2Se3 under the influence of in-plane and out-of-plane strain. The (0001) surface band structures show a substantial variation in the topological properties with the direction of strain (anisotropic behaviour).
2. Computational details
Band structure calculations were performed for (0001) Bi2Se3 surface using the Projector Augmented Wave (PAW) pseudopotential and plane-wave basis set as implemented in the Quantum Espresso (QE) package.24 Exchange-correlation potential was approximated through the Perdew–Burke–Ernzerhof general gradient approximation (PBE-GGA) functional. Further, the dispersion corrections were included through the semi-empirical Grimme-D2 van der Waals correction.25 The kinetic energy cut-off to fix the number of plane waves was taken as 50 Ry with the charge density cut-off 200 Ry. The Brillouin zone integration was carried out using a 6 × 6 × 1 Monkhorst pack k-point grid for structural relaxation, and a denser k-mesh 8 × 8 × 1 was used for electronic structure calculations. The convergence criterion for self-consistent energy was taken to be 10−8 Ry and the atomic positions were optimized until the force on each atom was lower than 10−3 eV Å−1. The surface calculations were performed using a slab model. An eight QLs slab of hexagonal Bi2Se3 with 40 atoms in the unit cell was generated using VESTA26 and XCrySDen software. A vacuum of 15 Å was added to the top QL to avoid the interaction among the surfaces of neighbouring slabs.3. Experimental methods
Bi2Se3 nanostructures were prepared at 250 °C by the chemical hot injection method. Commercial grade Bi2O3 (99.999%) and elemental Se (99.99%) powders were chosen as precursors, while 1-octadecane and oleic acid were used as solvent and reducing agent, respectively. To prepare the Bi precursor, 1 mmol of Bi2O3 was mixed with 5 ml of oleic acid and 20 ml of octadecane in a round bottom flask, mixed vigorously using a magnetic stirrer for 60 min, then heated to 100 °C and were kept at that temperature for 30 min for degassing. Then, the Bi precursor was prepared at 250 °C for 360 min under a nitrogen flow. In a typical synthesis, the elemental Se powder was mixed in 15 ml of octadecane in another round bottom flask, heated to 250 °C, after degassing at 100 °C, then the Bi-precursor solution was injected into the flask. Finally, the solution was cooled to room temperature, washed with ethanol and hexane (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio) several times, centrifuged, and finally, the product was dried at 60 °C.
3 ratio) several times, centrifuged, and finally, the product was dried at 60 °C.
The phase of these nanoplates was confirmed using a Rigaku Smart lab X-ray diffractometer with Cu-Kα radiation (λ = 1.5405 Å) (see Fig. S2†). The morphological studies were carried out by using a high-resolution transmission electron microscope (HRTEM) (FEI Tecnai-G2 T20) with an operating voltage of 200 kV (see Fig. S3†). The Raman spectra were recorded on a Jobin-Yvon LabRAM HR800UV spectrometer instrument equipped with a highly efficient thermo-electrically cooled charge-coupled device (CCD). The spectra were taken at different temperatures in the backscattering configuration using a 632 nm emission line of a He–Ne laser with laser power of 65 μW on the sample surface.
4. Result and discussion
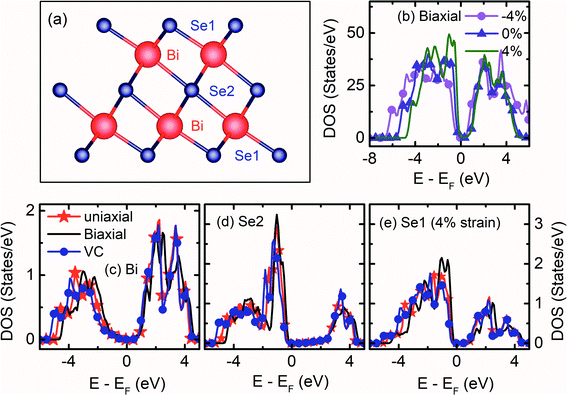
Bulk Bi2Se3 belongs to the tetradymite type crystal with a hexagonal structure of the space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (D53d). Bi2Se3 possess a layered structure along the hexagonal c-axis [Fig. S1a†]. The conventional unit cell of the hexagonal Bi2Se3 contains 15 atoms, with five atomic layers arranged in a particular order called ‘Quintuple Layer’ (QL) along the c-direction. There are three quintuple layers in a conventional hexagonal unit cell. Each QL consists of five atomic layers in the order Se1–Bi–Se2–Bi–Se1 [Fig. 1a]. The top and bottom Se1 atoms have the same Wyckoff positions and are in a similar interaction environment. The Se2 layer acts as the inversion center with two equivalent Bi and Se1 atoms [Fig. S1b†]. Due to the presence of inversion symmetry, the topological invariant can be calculated through the parity of occupied bands at ‘Γ’ point.2 Within a QL, the atomic interaction forms stronger covalent bonds, whereas the inter-quintuple layer interaction is weak van der Waals type. The thickness of each QL is about 0.96 nm.27
m (D53d). Bi2Se3 possess a layered structure along the hexagonal c-axis [Fig. S1a†]. The conventional unit cell of the hexagonal Bi2Se3 contains 15 atoms, with five atomic layers arranged in a particular order called ‘Quintuple Layer’ (QL) along the c-direction. There are three quintuple layers in a conventional hexagonal unit cell. Each QL consists of five atomic layers in the order Se1–Bi–Se2–Bi–Se1 [Fig. 1a]. The top and bottom Se1 atoms have the same Wyckoff positions and are in a similar interaction environment. The Se2 layer acts as the inversion center with two equivalent Bi and Se1 atoms [Fig. S1b†]. Due to the presence of inversion symmetry, the topological invariant can be calculated through the parity of occupied bands at ‘Γ’ point.2 Within a QL, the atomic interaction forms stronger covalent bonds, whereas the inter-quintuple layer interaction is weak van der Waals type. The thickness of each QL is about 0.96 nm.27
The Slab model has been used for the surface states calculations of (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1) Bi2Se3.28 The calculations show that the energy gap at the Dirac point is closed for slab thickness larger than 6 QLs of Bi2Se3. However, the (0001) surface Eg of the Bi2Se3 is vanishingly small but finite for 6 QLs thick slab and becomes ideally zero with slab thickness above 6 QLs.29 Therefore, we have chosen an 8 QLs thick slab with 40 atoms to minimize the computational error and acquire reliable results. The unstrained 8 QLs slab constructed using the lattice parameters of the hexagonal-shaped nanocrystals of Bi2Se3 prepared by adopting a chemical hot-injection method is used.29 The crystal structures of these nanocrystals are established from the Rietveld refinement analysis, which confirmed the R
1) Bi2Se3.28 The calculations show that the energy gap at the Dirac point is closed for slab thickness larger than 6 QLs of Bi2Se3. However, the (0001) surface Eg of the Bi2Se3 is vanishingly small but finite for 6 QLs thick slab and becomes ideally zero with slab thickness above 6 QLs.29 Therefore, we have chosen an 8 QLs thick slab with 40 atoms to minimize the computational error and acquire reliable results. The unstrained 8 QLs slab constructed using the lattice parameters of the hexagonal-shaped nanocrystals of Bi2Se3 prepared by adopting a chemical hot-injection method is used.29 The crystal structures of these nanocrystals are established from the Rietveld refinement analysis, which confirmed the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (D53d) crystallographic group of Bi2Se3. The refinement of the X-ray diffraction profile with a high degree of precision reveals the cell parameters; a = 4.136 Å and c = 28.59 Å of Bi2Se3 [Fig. S2†].29 The hexagonal shape morphology and the (0001) orientation of nanocrystals are further confirmed by the transmission electron microscopy measurement [Fig. S3†]. Thus, the reference lattice parameters of 8 QLs hexagonal Bi2Se3 slab with 15 Å vacuum layer are aref = 4.136 Å and cref = 100.9 Å. These lattice parameters are varied individually or simultaneously to apply strain on the slab and study the band structure of the strained Bi2Se3 (0001) surface. The out-of-plane lattice parameter ‘c’ is varied to apply uniaxial strain, which can be defined as
m (D53d) crystallographic group of Bi2Se3. The refinement of the X-ray diffraction profile with a high degree of precision reveals the cell parameters; a = 4.136 Å and c = 28.59 Å of Bi2Se3 [Fig. S2†].29 The hexagonal shape morphology and the (0001) orientation of nanocrystals are further confirmed by the transmission electron microscopy measurement [Fig. S3†]. Thus, the reference lattice parameters of 8 QLs hexagonal Bi2Se3 slab with 15 Å vacuum layer are aref = 4.136 Å and cref = 100.9 Å. These lattice parameters are varied individually or simultaneously to apply strain on the slab and study the band structure of the strained Bi2Se3 (0001) surface. The out-of-plane lattice parameter ‘c’ is varied to apply uniaxial strain, which can be defined as 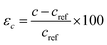 . The in-plane lattice parameter ‘a’ is changed for the application of biaxial strain
. The in-plane lattice parameter ‘a’ is changed for the application of biaxial strain 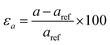 . While the εa = −εc strain with the conservation of volume
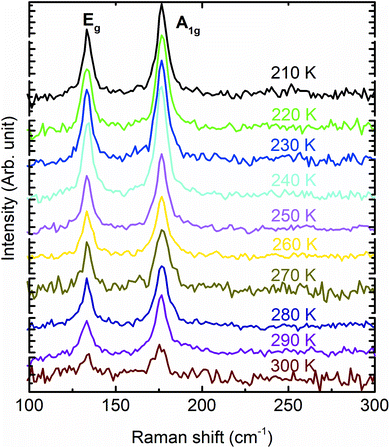
. While the εa = −εc strain with the conservation of volume 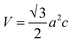 is generated by varying both ‘a’ and ‘c’, simultaneously. The strain on the Bi2Se3 slab primarily varies the band width, which is reflected in the density of states (DOS).
is generated by varying both ‘a’ and ‘c’, simultaneously. The strain on the Bi2Se3 slab primarily varies the band width, which is reflected in the density of states (DOS).
Before the studies of the (0001) surface band structure of Bi2Se3, the bulk band structure calculations are carried out after relaxing the atomic coordinates to the minimum energy. The bulk band structure shows a direct Eg ≈ 0.19 eV [Fig. S4a†], which is very close to the reported experimental30–32 and theoretical33,34 values. The kinetic energy in the Hamiltonian without spin–orbit coupling term does not depend on the spin degrees of freedom. However, in real crystals, the spin and orbital motions of the electrons couple together. The incorporation of SOC in the band structure calculation of Bi2Se3 removes the spin degeneracy with the metallic edge or surface states are consistent with the high-momentum-resolution angle-resolved photoemission spectroscopy experiment.35 Interestingly, after including the SOC, the band structure shows an expansion of the Eg = 0.38 eV [Fig. S4b†], the bulk Eg consistent with previous reports.2,11,34,36 The representative total DOS of the (0001) surface of Bi2Se3 with εa strain are shown in Fig. 1b. The compressive εa strain expands the band width, while tensile εa strain compresses the band width. The band width of Bi and Se represents the orbital occupancy, and the modification in the band width indicates the change in the electron density, orbital overlap and Eg. The band width of the surface QL atoms due to the tensile εa = −εc strain expands, while that of the tensile εa compresses, as compared to the tensile εc strain [Fig. 1c–e]. The Bi atoms in the surface QL remain insulating irrespective of the nature or direction of the strain applied to the slab. However, Se atoms are very sensitive to the nature or directions of the strain applied to the slab. The Se atoms in the surface QL present away from the EF for tensile εc and εa = −εc strain as compared to that of the tensile εa strain [Fig. 1c–e]. The conduction band (CB) band width of Se2 shrinks as well as shifts away from the EF as compared to that of Bi and Se1, irrespective of the nature or direction of the applied strain. Thus, Se2 atoms play an essential role in the Bi2Se3 (0001) surface conduction.36
The Bi atoms in Bi2Se3 contribute to the CB, while Se atoms contribute to the valence band (VB) near the EF. The px and py orbitals of both Bi and Se atoms are degenerate. The px and py orbitals of Bi atoms do not contribute at the Γ point and spread over the Γ–M–K path, while pz orbital of Bi atoms disperse at and around the Γ point for the compressive εc strain on the Bi2Se3 slab [Fig. 2a and b]. As the compressive εc strain on the (0001) surface of Bi2Se3 decreases the px and py orbitals of Bi atoms move toward the EF along the Γ–M path and the pz orbital of Bi atoms move away from EF [Fig. 2g and h]. Similar to Bi atoms, the px and py orbitals of Se atoms do not contribute at the Γ point, but populate over the Γ–K and Γ–M–K paths and pz orbital populates around the Γ point due to compressive εc strain on the Bi2Se3 slab [Fig. 2c–f]. On decreasing the εc compression on the (0001) surface of Bi2Se3, the population near the Γ point due to the px, py and pz orbitals of Se atoms increase, and interestingly the pz orbitals of Se1 atoms spread over the Γ–M–K path [Fig. 2i–l]. It is interesting to note that the orbital population of Bi and Se after the compressive εa strain on the Bi2Se3 slab is qualitatively similar to that of the tensile εc and the orbitals dispersion of Bi and Se due to the tensile εa strain is analogous to that of the compressive εc strain. The orbital population because of εa = −εc strain on the Bi2Se3 slab is similar to that of the εc strain.
 | ||
| Fig. 2 Projected band structures of the px and pz orbitals of the Bi, Se2 and Se1 atoms on the (0001) surface of Bi2Se3 under uniaxial strain with −6% (a–f) and 6% (g–l). | ||
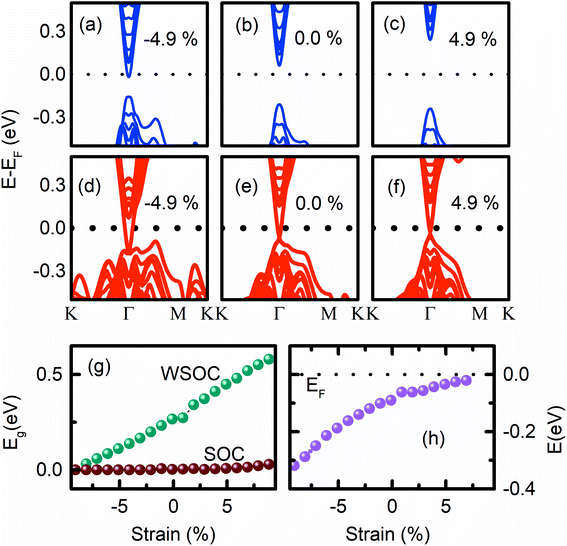
The calculated Eg of the (0001) surface of unstrained Bi2Se3 slab without SOC (WSOC), i.e., a = 4.136 Å, and c = 100.9 Å is ∼0.3 eV [Fig. 3b], which is closed to the reported value 0.26 eV for six QLs slabs.12,37 The corresponding band structures show an insulating direct Eg with the position of the conduction band minimum (CBM) near the Fermi energy (EF), but after including SOC, the surface shows metallic behaviour with the single Dirac cone at the Γ point [Fig. 3e], which is the hallmark for TIs.2,38,39 The occurrence of the Dirac point (DP) below EF is consistent with previous reports of Bi2Se3.40,35
As the 8 QLs of the Bi2Se3 slab are compressed uniaxially by decreasing the ‘c’ value keeping ‘a’ and ‘b’ fixed, the direct Eg decreases gradually and becomes indirect at 4.9% compressive strain due to the formation of “M” shape at the VB maximum [Fig. 3a]. The Eg vanishes at a very large 10% compression [Fig. 3g]. This metallic state formation in the (0001) surface of the Bi2Se3 slab has been explained by the increase in the band width of pz orbitals of Bi and Se in the valence band region.36 The indirect Eg in the (0001) surface of the Bi2Se3 has been observed previously for different combinations of lattice parameters under uniaxial strain.41 The compressive uniaxial strain has been imposed on the Sb2Se3 for the realization of its metallic state.28 On the other hand, as the tensile stress increases, i.e., the value of ‘c’ increases above 100.9 Å, the Eg monotonically increases and moves the pz orbital of Bi and Se atoms away from the EF, preserving the direct Eg [Fig. 3c and g]. Although achieving such a large value of strain is practically challenging, a recent experimental study demonstrates the occurrence of 9.6% strain along ‘a’ and 19.6% along ‘c’ through the intercalation of 60% zero-valent Cu into Bi2Se3 nanoribbons without disrupting the host lattice. The ‘a’ and ‘c’ lattice constants of Bi2Se3 increase from 4.14 ± 0.01 Å and 28.5 ± 0.01 Å to 4.54 ± 0.74 Å and 34.1 ± 0.76 Å, after the intercalation of Cu, respectively.21
The SOC makes the (0001) surface of Bi2Se3 conducting for an ample range of ‘c’ values. The Dirac cone appears deep inside the VB region at −0.16 eV due to the −4.9% εc strain, and px and py orbitals of Bi and the pz orbital of Se1 atoms disperse along the Γ–M–K direction [Fig. 3d]. As the εc strain decreases, DP moves up towards EF and appear very close to EF (at −0.02 eV) for 4.9% εc strain [Fig. 3f], and the flat band feature in the VB is suppressed. The observed shift of DP energy in the band structure of the (0001) surface of Bi2Se3 by the variation of strain is consistent with previous studies on the strain-dependent DP energy of the (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1) surface of Bi2Se3.8 On further increasing the tensile εc strain, i.e., increasing the ‘c’ value, the band structure opens a finite energy gap (0.05 eV) with the annihilation of the Dirac point [Fig. 3g]. The reports on the strain-induced annihilation of DP of the (0001) surface of the Bi2Se3 and the transition to a topologically trivial insulating phase is consistent with previous reports.8,28
1) surface of Bi2Se3.8 On further increasing the tensile εc strain, i.e., increasing the ‘c’ value, the band structure opens a finite energy gap (0.05 eV) with the annihilation of the Dirac point [Fig. 3g]. The reports on the strain-induced annihilation of DP of the (0001) surface of the Bi2Se3 and the transition to a topologically trivial insulating phase is consistent with previous reports.8,28
The non-degenerate helical surface states of topological insulators provide many interesting topological phenomena and are the starting point for the Majorana excitations.42 The Dirac point should be at the EF so that the conventionally confined states within the vertex are well separated from the Majorana-type excitations. The observed (0001) surface band structures of Bi2Se3 with the variation of εc strain confirmed that the uniaxial strain could be an effective tool to tune DP to be present at EF. The surface band structures show that the compressive strain moves DP away from EF, whereas the tensile strain moves the DP towards EF [Fig. 3h]. In addition, the variation of εc strain provides the change of (0001) surface of Bi2Se3 from metallic-to-topological-to-normal insulator.28,36 The normal-to-topological insulator transition has been observed in β-As2Te3 by the application εc strain.43
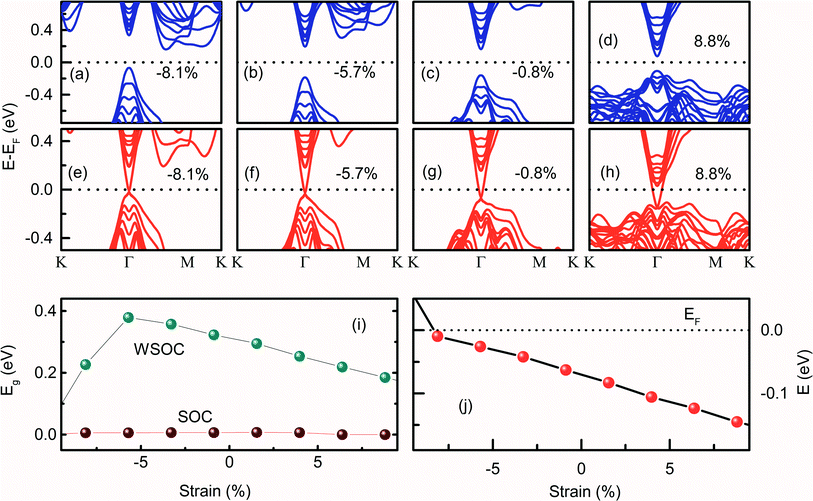
The (0001) surface band structure of Bi2Se3 is investigated by applying the biaxial strain in the range of ±10%. The (0001) surface band structure of Bi2Se3 with −8.1% of εa strain exhibits the indirect Eg and the px and py orbitals of Bi atoms and pz orbitals of Se atoms are dispersed near EF [Fig. 4a]. As the compressive εa strain decreases, px and py orbitals of the Bi atoms disperse away from EF, while pz orbitals of Bi atoms disperse towards EF, thus, the Eg becomes direct at −5.7% of εa strain [Fig. 4b]. In addition to the re-dispersion of orbitals, Eg increases from 0.28 eV to 0.38 eV, and the indirect-to-direct Eg transition occurs by the decrease of εa from −8.1% to −5.7%. On further decreasing the εa strain, i.e., increasing the ‘a’ value, pz orbitals of Bi and Se approaches towards EF, thus, the direct Eg decreases monotonically [Fig. 4c, d and i]. Interestingly, the biaxial strain is very sensitive to tune Eg, the change of in-plane lattice parameter by 0.1 Å corresponds to approximately 2% variation in strain, which changes Eg by 0.02 eV. The change in Eg with εa is consistent with the variation of Eg in N-doped Sb2Te3, where an appropriate in-plane strain can enlarge the bulk Eg.44 It is to be noted that the Bi2Se3 slab shows the direct Eg from −5.7% to 8.8% biaxial strain. The observation of direct Eg in a similar range of strain (−6% to +6% along the x-direction and −6% to 10% along the y-direction) is reported previously in Bi2Se3.45 On incorporating the SOC effect, the Dirac like dispersion is observed for the entire range of εa strain [Fig. 4e–h]. Interestingly, the DP is exactly at the Γ point at −8.1% of εa strain. As the εa strain decreases from −8.1%, the DP energy moves away from EF [Fig. 4j]. It is interesting to note that both compressive and tensile εa strain could not open the Eg at the DP. The Dirac cone is preserved for the entire range of εa strain, which indicates that the topological properties remain preserved. A similar variation of tensile biaxial strain on the band structure of the (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1) Bi2Se3 slab was observed for one to six QLs thickness with the SOC effect.36 However, the result is limited to the tensile εa strain study and the effect of εa strain without SOC on the Eg of Bi2Se3 is very scarce.36
1) Bi2Se3 slab was observed for one to six QLs thickness with the SOC effect.36 However, the result is limited to the tensile εa strain study and the effect of εa strain without SOC on the Eg of Bi2Se3 is very scarce.36
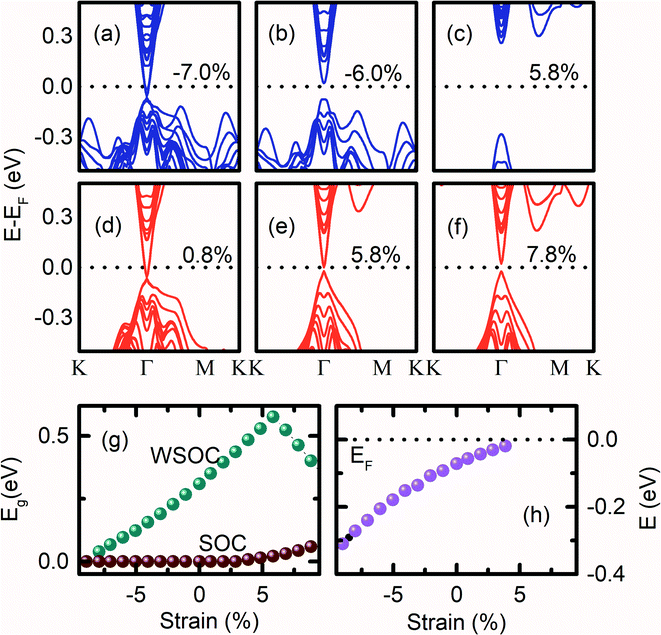
The influence of strength of strain while keeping the volume of the Bi2Se3 slab constant, on the (0001) surface band structure of Bi2Se3 is also investigated. At −7.0% of compressive volume conservation strain, the (0001) surface of Bi2Se3 behaves like a degenerate semiconductor as pz orbitals of Bi atoms cross the EF [Fig. 5a]. However, the (0001) surface of Bi2Se3 behaves like a direct Eg semiconductor by reducing the compressive volume conservation strain to −6.0%, which moves pz orbitals of Bi atoms away from EF [Fig. 5b]. On further reducing the volume conservation strain from the compressive state to the tensile state, the (0001) surface gap increases up to 5.8% [Fig. 5c]. In addition, px and py orbital dispersions of Bi atoms spread towards EF along the Γ–M direction. The (0001) surface of Bi2Se3 shows that the Dirac surface state feature with the Dirac point below the Fermi level for a smaller value of tensile strain [Fig. 5d]. Above 5.8% volume conservation strain, the (0001) surface gap decreases and becomes indirect as the pz orbital of the Se atoms come closer to the px and py orbitals of the Bi atoms [Fig. 5g]. The decrease in the (0001) surface Eg at higher tensile strain could be due to the compressive εa, which increases the band width. Note that the study of the band structure of Bi2Se3 with the variation of εc = −εa strain is very rare to compare our results. In the presence of SOC, the (0001) surface of Bi2Se3 is conducting if the strength of the applied strain with the conservation of the volume of the slab is between −7.9% to 4.9% [Fig. 5g]. The (0001) surface of Bi2Se3 is a normal semiconductor if the strain on the slab is larger than 4.9%. For εc = −εa > 4.9%, the band structures of the (0001) surface show an opening of the energy gap, which increases slowly with the increase in the strain [Fig. 5e and f]. For εc = −εa = −9.9%, DP is deep inside VB at −0.345 eV below EF [Fig. 5h]. As the volume conservation strain decreases from −9.9%, DP moves towards EF and appear at EF for εc = −εa = 5.9%. On further increasing volume conservation strain, the Dirac cone feature of Bi2Se3 gets annihilated, and a finite Eg emerges at the Γ point. The position of the DP energy with the variation of εc = −εa strain is plotted in Fig. 5h, which is qualitatively very similar to the case of εc strain variation.
There are several DFT studies on the DP energy of Bi2Se3 surface,7,8,28,40 which interestingly indicates that the position of the DP energy depends on the orientation of the Bi2Se3 surface. For example, the DP exactly appears at EF in the unstrained condition of (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1) oriented rhombohedral Bi2Se3.2 In contrast, the DP energy is located below and above EF in (0001) and (1
1) oriented rhombohedral Bi2Se3.2 In contrast, the DP energy is located below and above EF in (0001) and (1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00) surfaces of the unstrained hexagonal Bi2Se3, respectively.40,46 The electrons are naturally accumulated on the surface of the real Bi2Se3 single crystals because of Se deficiency, EF appears in the conduction band, which makes the detection of topological surface states difficult. Thus, the tuning of EF position in the band gap is necessary for the realization of the topological surface states of Bi2Se3.47 Interestingly, our band structure calculations of the (0001) surface of Bi2Se3 show the tuning of the energy position of DP by the application of strain on Bi2Se3 slab. The DP energy can be tuned from −0.318 eV to −0.02 eV by changing uniaxial/volume conservation strain from −9.1% to 6.9%. As the uniaxial/volume conservation strain switches from compressive to the tensile state, the DP energy in CB moves towards EF. However, DP energy shifts from −0.009 eV to −0.145 eV by changing biaxial strain on the Bi2Se3 slab from −8.12% to 8.8%, the opposite effect of uniaxial/volume conservation strain. Moreover, the (0001) surface of Bi2Se3 becomes insulating, even in the presence of SOC for large tensile volume conservation strain, which indicates the reduction in the SOC strength. However, it is reported that the volume conservation strain on Bi2Se3 with the (1
00) surfaces of the unstrained hexagonal Bi2Se3, respectively.40,46 The electrons are naturally accumulated on the surface of the real Bi2Se3 single crystals because of Se deficiency, EF appears in the conduction band, which makes the detection of topological surface states difficult. Thus, the tuning of EF position in the band gap is necessary for the realization of the topological surface states of Bi2Se3.47 Interestingly, our band structure calculations of the (0001) surface of Bi2Se3 show the tuning of the energy position of DP by the application of strain on Bi2Se3 slab. The DP energy can be tuned from −0.318 eV to −0.02 eV by changing uniaxial/volume conservation strain from −9.1% to 6.9%. As the uniaxial/volume conservation strain switches from compressive to the tensile state, the DP energy in CB moves towards EF. However, DP energy shifts from −0.009 eV to −0.145 eV by changing biaxial strain on the Bi2Se3 slab from −8.12% to 8.8%, the opposite effect of uniaxial/volume conservation strain. Moreover, the (0001) surface of Bi2Se3 becomes insulating, even in the presence of SOC for large tensile volume conservation strain, which indicates the reduction in the SOC strength. However, it is reported that the volume conservation strain on Bi2Se3 with the (1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00) oriented surface lifts the spin degeneracy and shifts the DP energy away from the Γ point.46 For (11
00) oriented surface lifts the spin degeneracy and shifts the DP energy away from the Γ point.46 For (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) surface Bi2Se3, the DP energy appears above and below EF for the tensile and compressive strain on the Bi2Se3 slab, respectively.46
0) surface Bi2Se3, the DP energy appears above and below EF for the tensile and compressive strain on the Bi2Se3 slab, respectively.46
Fig. 3–5 show that the occurrence of the redistribution of the orbital population of the (0001) surface due to the variable strain on Bi2Se3. The compressive εa strain increases the px and py orbitals overlap, which moves the orbital population towards the EF along the Γ–M–K in the CB. Thus, the band gap becomes indirect and shows a peak in the band gap vs. strain graph [Fig. 4i]. A similar situation arises while applying tensile volume conservation strain, and a peak appears in the band gap vs. strain graph [Fig. 5g]. However, under compressive εc strain, the dispersion of pz orbitals is dominated at the Γ point, and a direct band gap is observed in the +4.9% to +10% εc strain region. The band gap linearly varies with the εc strain without the application of SOC.
The result indicates that the (0001) surface of hexagonal Bi2Se3 is very sensitive to uniaxial strain, which can drive the (0001) surface state from metallic-to-topological-to-semiconducting nature with a maximum surface gap of 0.6 eV. The topological phase is observed in the range of ±6% variation of ‘c’. In contrast, the biaxial strain controls the dispersion of px and py bands, which toggles the (0001) surface of Bi2Se3 between the metallic and topological states. The topological state is observed for the variation of ‘a’ from −8% to 8%. Thus, the probability of achieving the topological surface states in the (0001) oriented hexagonal Bi2Se3 is higher for biaxial strain than the case of the uniaxial and volume conservation strain. Interestingly, biaxial strain could not create a finite energy gap at the Dirac point; hence, it does not play a significant role in destroying topological surface states. Therefore, the annihilation of the Dirac point largely depends on the out-of-plane interaction among the atomic orbitals of Bi and Se. The variation of px, py and pz orbitals with εc = −εa alleviate the (0001) surface of Bi2Se3 similar to the case of uniaxial strain. However, the tensile volume conservation strain distinguishes a transition from a direct Eg state to an indirect Eg state from the strain-dependent Eg plot without SOC. Overall, the Dirac cone can be tuned to EF by the application of tensile uniaxial, compressive biaxial, and tensile volume conservation strain.
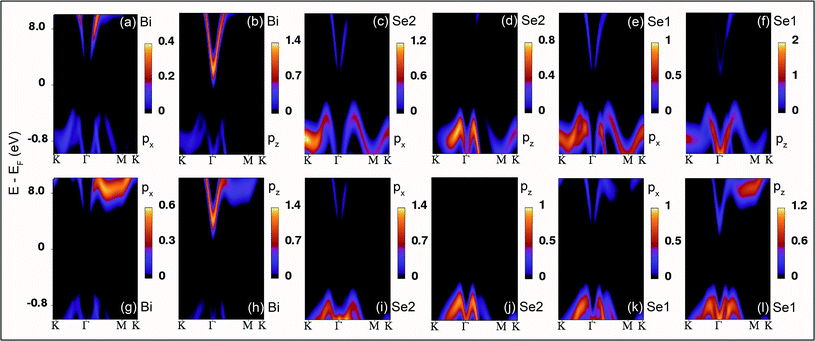
Further, the atomic cohesive energy of the (0001) Bi2Se3 slab is calculated for different values of uniaxial, biaxial, and volume conservation strain. Fig. 6 shows the variation of cohesive energy per atom in the Bi2Se3 slab with the strain. The cohesive energy (Ecoh) is calculated using the expression;
 | ||
| Fig. 6 Atomic cohesive energy of the 8 QLs Bi2Se3 slab under the uniaxial, biaxial, and volume conservation strain. | ||
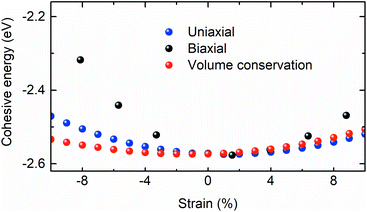
To compare the theoretically calculated cohesive energy with that of Bi2Se3 nanocrystals, Raman spectra of Bi2Se3 nanocrystals were recorded at various temperatures above the Debye temperature (∼185 K)49 of the Bi2Se3 [Fig. 7]. The Raman spectra of these nanocrystals in the assessable Raman shift range of the Raman spectrometer exhibits a Raman line appearing at ∼131.2 and ∼173.4 cm−1, which correspond to the Eg and A1g modes, respectively. The Eg mode appears because of the in-plane vibrations of Se and Bi atoms and A1g mode appears from the out-of-plane vibrations of Se and Bi atoms.50 The peak position of different modes in Raman spectra of Bi2Se3 are extracted using the Lorentz fit and plotted in Fig. 8. The Raman shift (ω(zb,T)) of both modes varies linearly with temperature consistent with the following expression;49
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4% the variation of strain, which could be the foundation of the (0001) oriented growth of Bi2Se3 nanocrystals. Note that, the variation of cohesive energy is higher in biaxial strain as compared to the uniaxial and volume conservation strain state for the strain larger than ±
4% the variation of strain, which could be the foundation of the (0001) oriented growth of Bi2Se3 nanocrystals. Note that, the variation of cohesive energy is higher in biaxial strain as compared to the uniaxial and volume conservation strain state for the strain larger than ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4%. The strain-dependent cohesive energy indicates that at a higher value of strain, uniaxial and volume conservation strain provides better stability than that of the biaxial strain (0001) oriented growth of Bi2Se3 nanocrystals. The strain (±4%) independent cohesive energy and the tuning of the Dirac point position with strain will shed light on achieving the dissipationless (0001) surface transport in Bi2Se3, which is the essential requirement for the application of topological insulators in topological quantum computation and low-power spintronic devices.
4%. The strain-dependent cohesive energy indicates that at a higher value of strain, uniaxial and volume conservation strain provides better stability than that of the biaxial strain (0001) oriented growth of Bi2Se3 nanocrystals. The strain (±4%) independent cohesive energy and the tuning of the Dirac point position with strain will shed light on achieving the dissipationless (0001) surface transport in Bi2Se3, which is the essential requirement for the application of topological insulators in topological quantum computation and low-power spintronic devices.
 | ||
| Fig. 7 Raman spectra of the Bi2Se3 hexagon plates synthesized at 250 °C, recorded at various temperatures. | ||
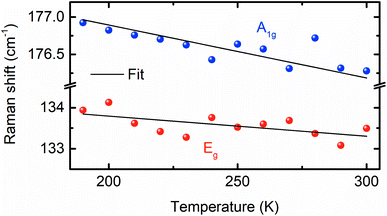 | ||
| Fig. 8 Temperature-dependent Raman shift of the Eg and A1g modes of the Bi2Se3 hexagon plates synthesized at 250 °C. The solid line is the fit to the data. | ||
5. Conclusion
In conclusion, the (0001) oriented Bi2Se3 nanocrystals were prepared by a hot injection method using a nontoxic solvent. The atomic cohesive energy of these nanocrystals extracted from the temperature-dependent Raman spectra is 2.58 eV. By utilizing the lattice parameters of these nanocrystals, an 8 QLs thick Bi2Se3 slab is constructed to explore the effects of strain on the (0001) surface states and the cohesive energy calculated using the first-principles DFT calculations without and with the presence of SOC effects. The CB band width of the Se2 shrinks as well as shifts away from EF compared to that of Bi and Se1 irrespective of the nature or directions of the applied strain. The band structures of the (0001) surface of Bi2Se3 show that Se2 is very sensitive to mechanical strain, and strain can tune the Dirac point energy. The Dirac cone feature of the (0001) surface of Bi2Se3 is preserved for the entire range of the biaxial strain. However, around 5% tensile uniaxial strain and even lower value of volume conservation strains annihilate the Dirac cone, which causes the loss of topological (0001) surface states of Bi2Se3. The biaxial strain provide ease in achieving the Dirac cone at EF than uniaxial and volume conservation strains. The volume conservation strain distinguishes a transition from a direct Eg state to an indirect Eg state in the strain-dependent Eg plot without the SOC. The strain-dependent cohesive energy indicates that at a higher value of strain, uniaxial and volume conservation strain provides better stability compared to that of the biaxial strain (0001) oriented growth of Bi2Se3 nanocrystals. The application of mechanical strain on Bi2Se3 slab has a significant influence on the band width of ‘p’ orbitals of Bi and Se, Eg and Dirac point energy, which may provide a new pathway to control many physical properties of Bi2Se3 with strain and shade light on designing artificial topological materials for technological applications.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We acknowledge the use of the computing resources at HPCE, IIT Madras.References
- M. Z. Hasan and C. L. Kane, Rev. Mod. Phys., 2010, 82, 3045 CrossRef CAS.
- H. Zhang, C.-X. Liu, X. L. Qi, X. Dai, Z. Fang and S. C. Zhang, Nat. Phys., 2009, 5, 438 Search PubMed.
- Y. Zhao, Y. Hu, L. Liu, Y. Zhu and H. Guo, Nano Lett., 2011, 11, 2088 CrossRef CAS PubMed.
- J.-M. Zhang, W. Zhu, Y. Zhang, D. Xiao and Y. Yao, Phys. Rev. Lett., 2012, 109, 266405 CrossRef PubMed.
- D. Pesin and A. H. MacDonald, Nat. Mater., 2012, 11, 409 CrossRef CAS PubMed.
- H. Aramberri, J. I. Cerdá and M. C. Muñoz, Nano Lett., 2015, 15, 3840 CrossRef CAS PubMed.
- L. Zhao, J. Liu, P. Tang and W. Duan, Appl. Phys. Lett., 2012, 100, 131602 CrossRef.
- Y. Liu, Y. Y. Li, S. Rajput, D. Gilks, L. Lari, P. L. Galindo, M. Weinert, V. K. Lazarov and L. Li, Nat. Phys., 2014, 10, 294 Search PubMed.
- Y. Saeed, N. Singh and U. Schwingenschlogl, Appl. Phys. Lett., 2014, 105, 031915 CrossRef.
- S. H. Park, J. Chae, K. S. Jeong, T.-H. Kim, H. Choi, M.-H. Cho, I. Hwang, M.-H. Bae and C. Kang, Nano Lett., 2015, 15, 3820 CrossRef CAS PubMed.
- S. M. Young, S. Chowdhury, E. J. Walter, E. J. Mele, C. L. Kane and A. M. Rappe, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 085106 CrossRef.
- Y. Saeed, N. Singh and U. Schwingenschlogl, Appl. Phys. Lett., 2014, 104, 033105 CrossRef.
- J. Z. Zhao, L. C. Chen, B. Xu, B. B. Zheng, J. Fan and H. Xu, Phys. Rev. B, 2020, 101, 121407(R) CrossRef.
- Y. Sun, X.-Q. Chen, S. Yunoki, D. Li and Y. Li, Phys. Rev. Lett., 2010, 105, 216406 CrossRef PubMed.
- T.-H. Kim, K. S. Jeong, B. C. Park, H. Choi, S. H. Park, S. Jung, J. Park, K.-H. Jeong, J. W. Kim, J. H. Kim and M.-H. Cho, Nanoscale, 2016, 8, 741 RSC.
- J. Chae, S.-H. Kang, S. H. Park, H. Park, K. Keong, T. H. Kim, S.-B. Hong, K. S. Kim, Y. K. Kwon, J. W. Kim and M.-H. Cho, ACS Nano, 2019, 13, 3931 CrossRef CAS PubMed.
- G.-C. Wang and T.-M. Lu, J. Appl. Phys., 2019, 125, 082401 CrossRef.
- Q. Li, Y. Wang, T. Li, W. Li, F. Wang, A. Janotti, S. Law and T. Gu, ACS Omega, 2020, 5, 8090 CrossRef CAS PubMed.
- D. Flötotto, Y. Bai, Y.-H. Chan, P. Chen, X. Wang, P. Rossi, C.-Z. Xu, C. Zhang, J. A. Hlevyack, J. D. Denlinger, H. Hong, M.-Y. Chou, E. J. Mittemeijer, J. N. Eckstein and T.-C. Chiang, Nano Lett., 2018, 18, 5628 CrossRef PubMed.
- S. Qi, H. Yang, J. Chen, X. Zhang, Y. Yang and X. Xu, Sci. Rep., 2016, 6, 29161 CrossRef CAS PubMed.
- K. J. Koski, J. J. Cha, B. W. Reed, C. D. Wessells, D. Kong and Y. Cui, J. Am. Chem. Soc., 2012, 134, 7584 CrossRef CAS PubMed.
- M. V. Sidorov, M. J. McKelvy, J. M. Cowley and W. S. Glaunsinger, Chem. Mater., 1998, 10, 3290 CrossRef CAS.
- C. Schindler, C. Wiegand, J. Sichau, L. Tiemann, K. Nielsch, R. Zierold and R. H. Blick, Appl. Phys. Lett., 2017, 111, 171601 CrossRef.
- P. Giannozzi, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272 CrossRef CAS.
- Y. Sun, H. Cheng, S. Gao, Q. Liu, Z. Sun, C. Xiao, C. Wu, S. Wei and Y. Xie, J. Am. Chem. Soc., 2012, 134, 20294 CrossRef CAS PubMed.
- W. Liu, X. Peng, C. Tang, L. Sun, K. Zhang and J. Zhong, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 245105 CrossRef.
- S. K. Das and P. Padhan, ACS Appl. Nano Mater., 2020, 3, 274–282 CrossRef CAS.
- G. Martinez, B. A. Piot, M. Hakl, M. Potemski, Y. S. Hor, A. Materna, S. G. Strzelecka, A. Hruban, O. Caha, J. Novák, A. Dubroka, Č. Drašar and M. Orlita, Sci. Rep., 2017, 7, 6891 CrossRef CAS PubMed.
- M. Orlita, B. A. Piot, G. Martinez, N. K. Sampath Kumar, C. Faugeras, M. Potemski, C. Michel, E. M. Hankiewicz, T. Brauner, Č. Drašar, S. Schreyeck, S. Grauer, K. Brunner, C. Gould, C. Brüne and L. W. Molenkamp, Phys. Rev. Lett., 2015, 114, 186401 CrossRef CAS.
- A. Dubroka, O. Caha, M. Hroncek, P. Friš, M. Orlita, V. Holý, H. Steiner, G. Bauer, G. Springholz and J. Humlícek, Phys. Rev. B, 2017, 96, 235202 CrossRef.
- S. K. Mishra, S. Satpathy and O. Jepsen, J. Phys.: Condens. Matter, 1997, 9, 461 CrossRef CAS.
- M. Jurczyszyn, M. Sikora, M. Chrobak and L. Jurczyszyn, Appl. Surf. Sci., 2020, 528, 146978 CrossRef CAS.
- Y. Xia, D. Qian, D. Hsieh, L. Wray, A. Pal, H. Lin, A. Bansil, D. Grauer, Y. S. Hor, R. J. Cava and M. Z. Hasan, Nat. Phys., 2009, 5, 398 Search PubMed.
- H. Aramberri and M. C. Muñoz, Phys. Rev. B, 2017, 95, 205422 CrossRef.
- S. Chege, P. Ning'I, J. Sifuna and G. O. Amolo, AIP Adv., 2020, 10, 095018 CrossRef CAS.
- O. V. Yazyev, J. E. Moore and S. G. Louie, Phys. Rev. Lett., 2010, 105, 266806 CrossRef PubMed.
- W. Zhang, R. Yu, H.-J. Zhang, X. Dai and Z. Fang, New J. Phys., 2010, 12, 065013 CrossRef.
- A. Bera, K. Pal, D. V. S. Muthu, U. V. Waghmare and A. K. Sood, J. Phys.: Condens. Matter, 2016, 28, 105401 CrossRef.
- H. Aramberri and M. C. Muñoz, J. Phys.: Condens. Matter, 2018, 1, 015009 CAS.
- J. Kellner, M. Eschbach, J. Kampmeier, M. Lanius, E. Mły'nczak, G. Mussler, B. Holländer, L. Plucinski, M. Liebmann, D. Grützmacher, C. M. Schneider and M. Morgenstern, Appl. Phys. Lett., 2015, 107, 251603 CrossRef.
- K. Pal and U. V. Waghmare, Appl. Phys. Lett., 2014, 105, 062105 CrossRef.
- S. Qi, R. Gao, M. Chang, T. Hou, Y. Han and Z. Qiao, Phys. Rev. B, 2020, 102, 085419 CrossRef CAS.
- Z. Lu, Y. Wu, Y. Xu, C. Ma, Y. Chen, K. Xu, H. Zhang, H. Zhub and Z. Fang, Nanoscale, 2019, 11, 20620 RSC.
- Y. Takagaki, B. Jenichen and J. Tominaga, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 245302 CrossRef.
- E. Uesugi, T. Uchiyama, H. Goto, H. Ota, T. Ueno, H. Fujiwara, K. Terashima, T. Yokoya, F. Matsui, J. Akimitsu, K. Kobayashi and Y. Kubozono, Sci. Rep., 2019, 9, 5376 CrossRef PubMed.
- Y. Liu, Y. Xu, Y. Jia and H. Zhang, Phys. Chem. Chem. Phys., 2020, 22, 9685 RSC.
- X. X. Yang, Z. F. Zhou, Y. Wang, R. Jiang, W. T. Zheng and C. Q. Sun, J. Appl. Phys., 2012, 112, 083508 CrossRef.
- J. Zhang, Z. Peng, A. Soni, Y. Zhao, Y. Xiong, B. Peng, J. Wang, M. S. Dresselhaus and Q. Xiong, Nano Lett., 2011, 11, 2407 CrossRef CAS PubMed.
- L. B. Abdalla, L. Seixas, T. M. Schmidt, R. H. Miwa and A. Fazzio, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 045312 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: The schematic of crystal symmetry, X-ray diffraction spectra, high-resolution transmission electron microscopy image, and bulk band structure of Bi2Se3 nanocrystals. See DOI: 10.1039/d1na00139f |
| This journal is © The Royal Society of Chemistry 2021 |