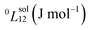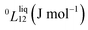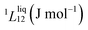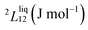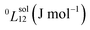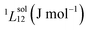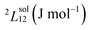Open Access Article
Open Access ArticleSubstitutional–interstitial structural transition in Cu–Pt nano-alloys
Luke D.
Geoffrion
 a,
Miguel
José-Yacaman
b,
Alexander
Lehr
b,
Shi-ze
Yang
c,
John
Sanchez
b,
J. Jesus
Velazquez-Salazar
b and
Grégory
Guisbiers
a,
Miguel
José-Yacaman
b,
Alexander
Lehr
b,
Shi-ze
Yang
c,
John
Sanchez
b,
J. Jesus
Velazquez-Salazar
b and
Grégory
Guisbiers
 *a
*a
aDepartment of Physics & Astronomy, University of Arkansas at Little Rock, 2801 South University Avenue, Little Rock, AR 72204, USA. E-mail: gxguisbiers@ualr.edu
bDepartment of Applied Physics & Materials Science, Northern Arizona University, 624 S. Knowles Drive, Flagstaff, AZ 86011, USA
cEyring Materials Center, Arizona State University, 300 E University Drive, Tempe, AZ 85287, USA
First published on 27th May 2021
Abstract
Copper–platinum alloys are important binary alloys in catalysis. In this communication, we demonstrate that it is possible to preserve the thermal properties of platinum with a copper–platinum alloy by converting the substitutional alloy into an interstitial one. This conversion occurs when the size of the copper–platinum system is reduced down to the nanoscale. The size-dependent phase diagram of Cu–Pt for a spherical nanoparticle is calculated at various sizes (50, 10 and 5 nm) demonstrating that Cu–Pt alloyed nanoparticles can be formed all over the composition range. Experimentally, the electron microscopy characterization of copper–platinum alloyed nanoparticles synthesized by wet chemistry supports the predicted structural transition.
Platinum is an outstanding catalyst used to produce nitric acid, silicone, and benzene and it is also used to improve the efficiency of fuel cells.1 Platinum is classified as an energy critical element by the American Physical Society and the Materials Research Society2,3 due to its low abundance in the Earth's crust which makes its price high and accessibility at risk. Therefore, any strategy to reduce the amount of platinum in applications is highly welcomed. The strategy followed in this paper is first alloying platinum with an abundant metal such as copper because the copper–platinum system displays total miscibility all over its composition range; second reducing the size of the system. In order to achieve this goal experimentally, theoretical guidance is necessary to determine how platinum and copper are going to mix at the nanoscale. Compared to the wealth of research performed on other binary alloys at the nanoscale, Cu–Pt has not been fully explored.4–8
To answer this fundamental question, the knowledge of the binary phase diagram at the nanoscale is required. Indeed, the binary phase diagram is the fingerprint of any binary alloy, displaying a temperature–composition map which indicates the equilibrium phases present at a given temperature and composition.9–11 Several models (ideal, regular and sub-regular) have been developed to predict theoretically any phase diagram. All those models rely on minimizing the Gibbs free energy of the system. The ideal solution model assumes that the solid solution is completely miscible i.e., not having a miscibility gap, resulting in the classical lens-shape phase diagram. This model is too simple to simulate a binary alloy with ordered phases such as Cu–Pt. By considering explicitly the chemical interaction between Cu and Pt within the solid solution, a composition-dependent mixing term is added to the Gibbs free energy, resulting in the so-called regular solution model. However, this addition is not sufficient to accurately describe the Cu–Pt phase diagram.12 In order to describe the Cu–Pt system, the mixing enthalpy needs to be temperature–composition-dependent which falls under the sub-regular solution model.12 In the sub-regular model, the Gibbs free energy of a non-ideal binary system such as Cu–Pt is represented by:13,14
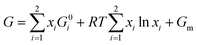 | (1) |
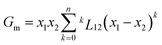 | (2) |
Experimentally, the bulk binary phase diagram of Cu–Pt does not display any miscibility gap; consequently, both 0th order Redlich–Kister parameters 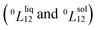 need to be negative for both phases (Table 1). Indeed, for miscibility gaps to arise in a phase diagram, both 0th order Redlich–Kister parameters
need to be negative for both phases (Table 1). Indeed, for miscibility gaps to arise in a phase diagram, both 0th order Redlich–Kister parameters 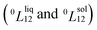 need to be positive for both phases, liquid and solid.9 This is apparent in other binary systems such as Si–Ge,17 Cu–Ni18 and Bi–Sb.19 Cu–Pt is not known to have any regions of immiscibility, i.e. displaying miscibility gaps as shown in ref. 8. So, it is curious how the authors of ref. 8 determined that this system would have a miscibility gap since they provided a negative Gibbs free energy of mixing for this alloy. In addition to the analysis concerning the Redlich–Kister parameters, it is also noted that binary systems displaying miscibility gaps typically break at least one of the Hume-Rothery rules.20 But, Cu–Pt does not break any Hume-Rothery rules as mentioned in ref. 8. Therefore, it makes perfect sense that Cu–Pt does not display any miscibility gap in its binary phase diagram. Moreover, the Cu–Pt system has several ordered structures appearing at low temperature and low platinum concentration namely the L11 and L12 ordered structures.12 As a note, the Hume-Rothery rules are used to determine whether a binary system would form a miscible solid solution (negative mixing enthalpy). But, those rules do not inform which model (regular or sub-regular) is the best to calculate the binary phase diagram.
need to be positive for both phases, liquid and solid.9 This is apparent in other binary systems such as Si–Ge,17 Cu–Ni18 and Bi–Sb.19 Cu–Pt is not known to have any regions of immiscibility, i.e. displaying miscibility gaps as shown in ref. 8. So, it is curious how the authors of ref. 8 determined that this system would have a miscibility gap since they provided a negative Gibbs free energy of mixing for this alloy. In addition to the analysis concerning the Redlich–Kister parameters, it is also noted that binary systems displaying miscibility gaps typically break at least one of the Hume-Rothery rules.20 But, Cu–Pt does not break any Hume-Rothery rules as mentioned in ref. 8. Therefore, it makes perfect sense that Cu–Pt does not display any miscibility gap in its binary phase diagram. Moreover, the Cu–Pt system has several ordered structures appearing at low temperature and low platinum concentration namely the L11 and L12 ordered structures.12 As a note, the Hume-Rothery rules are used to determine whether a binary system would form a miscible solid solution (negative mixing enthalpy). But, those rules do not inform which model (regular or sub-regular) is the best to calculate the binary phase diagram.
According to Fig. 1, the bulk Cu–Pt system is best modeled by using the sub-regular solution model. Indeed, the sub-regular solution model is in good agreement with all the available experimental data, while the regular solution model from ref. 8 does not fit all the available experimental data very well, except below 20% platinum weight composition. Above 20% platinum weight composition, the solidus–liquidus curves predicted by the regular solution model vastly underestimate the experimental data points provided by ref. 12, 21 and 22. Furthermore, the choice of a sub-regular solution model over a regular solution model is clearly justified by inspecting the mixing enthalpy of the alloy at various temperatures.12 Indeed, with respect to chemical composition, a sub-regular model is more adequate when the mixing enthalpy of the alloy is non-symmetrical with respect to the chemical composition at 50%, while the regular solution model is preferred when the mixing enthalpy is symmetrical with respect to the chemical composition at 50%.16
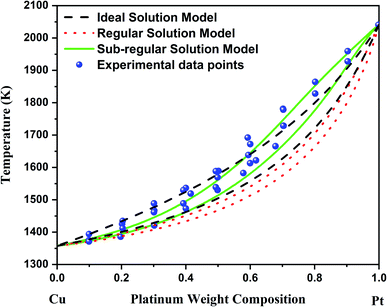 | ||
| Fig. 1 Bulk phase diagram of Cu–Pt. The black solidus–liquidus curves are obtained by using an ideal solution model. The red solidus–liquidus curves are obtained by using a regular solution model as performed by Che et al.8 The green solidus–liquidus curves are obtained by using a sub-regular solution model as shown by Abe et al.12 The experimental data points come from ref. 12, 21 and 22. | ||
At the nanoscale, Cu–Pt alloys experience size effects just as any other material.23 Therefore, the nanophase diagram for a Cu–Pt spherical nanoparticle was predicted by using nano-thermodynamic concepts; see Fig. 2. The size-dependent parameters used in the sub-regular solution model were varied by using the following relationship:24–26
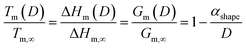 | (3) |
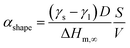 | (4) |
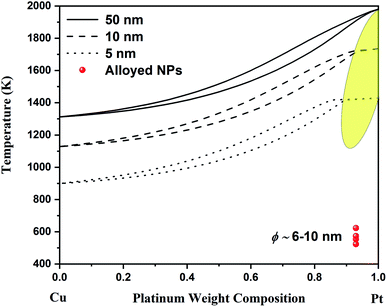 | ||
| Fig. 2 Nano-phase diagram for spherical Cu–Pt nanoparticles having a diameter of 50, 10 and 5 nm. The solidus–liquidus curves are obtained by using a sub-regular model. The experimental data come from Belenov et al.30,35 The experimental data points symbolize alloyed Cu–Pt nanoparticles after undergoing a thermal treatment. The diameter of the nanoparticles ranged between ∼6 and ∼10 nm. The yellow region indicates the region where the interstitial Cu–Pt alloy is expected. | ||
Since, the Gibbs free energy of mixing for Cu–Pt is negative at the bulk scale, the Gibbs free energy of mixing at the nanoscale will also be negative as per eqn (3); see ref. 13 and 24. This is supported by Monte Carlo simulations completed in ref. 27. Consequently, the binary phase diagram of Cu–Pt will not display any miscibility gap at the nanoscale, meaning that the formation of alloyed Cu–Pt nanoparticles is possible for any chemical composition. Experimentally, the synthesis of alloyed Cu–Pt nanoparticles with sizes around 3 nm and around 4–15 nm was successfully achieved by Khanal et al.28 and Peng et al.,29 respectively. Furthermore, Belenov et al.30 demonstrated that Cu–Pt nanoparticles with sizes between ∼6 and ∼10 nm formed a solid solution (i.e. an alloy) at ∼523–623 K. Those results are well in agreement with our predicted nano-phase diagram displayed in Fig. 2 as the experimental data points are within the solid region of the phase diagram.
In order to further support the theoretical investigation, Cu–Pt alloyed nanoparticles were synthesized by wet chemistry, which is a common method to synthesize Cu–Pt nanoparticles.28–31 The chemicals used were purchased from Sigma Aldrich and include platinum(IV) chloride, copper(II) chloride, oleylamine (C18H35NH2), 1-dodecanethiol (C12H26S), and hydrochloric acid. Both platinum chloride and copper chloride were prepared as aqueous solutions at a concentration of 0.1 M. Platinum chloride was prepared in 1 M hydrochloric acid, while copper chloride was in ethanol. 100 μl of the platinum solution was poured in a 15 ml glass vial and heated to 100 °C to evaporate any water. Once dried, 5 ml of oleylamine was added, the solution was stirred and 100 μl of copper chloride was added. The solution was heated to 250 °C for 2 hours. There was a color change from golden yellow to deep red. 10 μl of 1-dodecanethiol was then added to the solution. The reaction was finished once the color of the solution changed to a dark brown color, which was achieved after ∼1 hour.
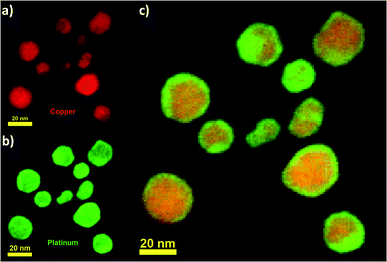
The nanoparticles were then observed with a NION Scanning Transmission Electron Microscope (STEM) operating at 80 kV with atomic resolution. For STEM observations, samples were prepared by drop-casting one or two droplets of the colloidal solution onto a holey carbon coated TEM grid, which was then let to dry in air at room temperature. A careful observation of the synthesized nanoparticles through Electron Energy Loss Spectroscopy (EELS) confirmed the alloyed structure of the Cu–Pt nanoparticles (Fig. 3). Fig. 3a–c show EELS chemical mapping for Cu and Pt elements as well as the overlay between Cu and Pt, respectively. From the observation of Fig. 3, it is clear that Cu and Pt are well-mixed throughout the nanoparticle. Additionally, it is observed that Pt segregates preferentially to the surface compared to Cu. This is well in agreement with the segregation rules established by Guisbiers et al. in ref. 32.
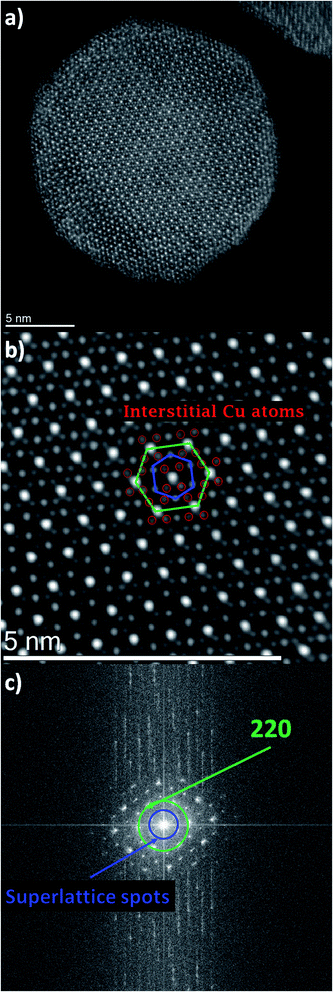
Let's look in detail at one Cu–Pt nanoparticle in particular through the high angle annular dark field image mode (HAADF). Fig. 4a shows a nanoparticle of Cu–Pt. The whole structure of the particle was a superlattice made of intercalated layers of Pt and Cu, with a FCC structure, occupying regular lattice sites. However, it is clearly seen that Cu atoms were also occupying interstitial positions (Fig. 4b). In Fig. 4b, a closer look at the distance between two bright spots is 0.675 nm, corresponding to the separation distance between two Pt atoms. However, this distance needs to be divided by 2 (0.338 nm), to get the distance between two Pt planes in the superlattice structure. To better characterize the crystallinity of the nanoparticle, Fast Fourier Transform (FFT) was applied on Fig. 4a and is shown in Fig. 4c. The inner most spots denote a superlattice structure in the particle. The brighter spots of the second ring indicate growth along the (220) direction.
The interstitial presence of Cu atoms was also observed with other particles on the same grid with sizes ranging between ∼2 and ∼20 nm. Due to the small size, high resolution was not possible; however, FFT information was still gathered from those nanoparticles. Fig. 5 shows the TEM images of two small particles with their corresponding FFT pattern. In Fig. 5a, the particle size is measured to be around ∼7.6 nm and its FFT pattern showed the same superlattice structure as that observed in larger particles. Fig. 5b shows a smaller particle on the order of ∼3.8 nm and its FFT also indicates a structure similar to the other nanoparticles as confirmed by the two diffraction rings.
Although theory predicts this transition to occur in a small composition range above 90%, experimentally, it is observed in a much larger composition range. By looking at Fig. 2, it is noticeable that the theoretical region where the transition occurs occupies a larger compositional range as the size of the particle decreases. It is important to remember that nanothermodynamics describes a system (i.e. a nanoparticle in this case) at equilibrium, while the synthesis of nanoparticles may not actually be an equilibrium process during the entire synthesis time and consequently depend on kinetic effects. These effects are the source of the difference between theoretical predictions and experimental observations with respect to the chemical composition range. Theory and experiment agree on Cu–Pt nano-alloys having substitutional–interstitial structural transition below ∼20 nm. Finally, this study points out that nanothermodynamics may be used as a fast theoretical framework to identify phase transitions in nano-alloys. Indeed, molecular dynamics and density functional theory studies typically take a very long time and are limited to very small sizes due their complexity and the iterative nature of those techniques.
In conclusion, the bulk phase diagram for the Cu–Pt system has been calculated in this work by using a sub-regular solution model which is found to be in excellent agreement with all the available experimental data. Furthermore, the nanophase diagram for spherical Cu–Pt nanoparticles was provided at various sizes (50, 10 and 5 nm), where solidus–liquidus curves were also obtained by using a sub-regular solution model. From the theoretical calculations, copper and platinum continue to mix fairly well all over the composition range whatever the scale of the system is. Finally, a transition between a substitutional solid solution and an interstitial solid solution is predicted theoretically above 90% platinum weight composition at sizes around 5 nm. This structural transition has been observed experimentally on Cu–Pt nanoparticles having sizes less than ∼20 nm in a composition range up to ∼50%. Therefore, the theoretical framework used in this paper may be used as a predictive tool to identify structural phase transitions in binary nano-alloys. This discovery is particularly interesting for potential future applications, as the amount of platinum is reduced while preserving the thermal properties of pure platinum.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the financial support from the NSF Rapid Grant # 2030488. We also acknowledge the NSF-NCI-SW center for financial support in using ASU cores and the MIRA-NAU institute for a grant on metallic nanoparticles.References
- https://www.rsc.org/periodic-table/element/78/platinum .
- R. Jaffe, et al., Energy Critical Elements: Securing Materials for Emerging Technologies, POPA Reports, February 2011, pp. 1–28 Search PubMed.
- A. J. Hurd, et al., Energy-critical elements for sustainable development, MRS Bull., 2012, 37, 405–410 CrossRef.
- R. Ferrando, J. Jellinek and R. L. Johnston, Nanoalloys: From Theory to Applications of Alloy Clusters and Nanoparticles, Chem. Rev., 2008, 108, 845–910 CrossRef CAS PubMed.
- J. Jellinek, Nanoalloys: tuning properties and characteristics through size and composition, Faraday Discuss., 2008, 138, 11–35 RSC.
- K. Rossi, et al., Thermodynamics of CuPt nanoalloys, Sci. Rep., 2018, 8, 9150 CrossRef CAS PubMed.
- J. Tang, et al., Chemical Ordering and Surface Segregation in Cu–Pt Nanoalloys: The Synergetic Roles in the Formation of Multishell Structures, J. Phys. Chem. C, 2015, 119, 21515–21527 CrossRef CAS.
- C. Che, et al., Theoretical Study on the Structural, Thermal and Phase Stability of Pt–Cu Alloy Clusters, J. Cluster Sci., 2019, 31(3), 615–626 CrossRef.
- A. D. Pelton and W. T. Thompson, Phase diagrams, Prog. Solid State Chem., 1975, 10, 119–155 CrossRef.
- H. Okamoto, Phase Diagrams for Binary Alloys, ASM International, United States of America, 2nd edn, 2010 Search PubMed.
- Y. A. Chang, et al., Phase diagram calculation: past, present and future, Prog. Mater. Sci., 2004, 49, 313–345 CrossRef CAS.
- T. Abe, B. Sundman and H. Onodera, Thermodynamic assessment of the Cu–Pt system, J. Phase Equilib. Diffus., 2006, 27(1), 5–13 CrossRef CAS.
- G. Guisbiers, Advances in thermodynamic modelling of nanoparticles, Adv. Phys.: X, 2019, 4, 1668299 CAS.
- G. Kaptay, Nano-Calphad: extension of the Calphad method to systems with nano-phases and complexions, J. Mater. Sci., 2012, 47, 8320–8335 CrossRef CAS.
- M. Hillert, Partial Gibbs energies from Redlich Kister polynomials, Thermochim. Acta, 1988, 129, 71–75 CrossRef CAS.
- T. Abe, K. Ogawa and K. Hashimoto, Analysis of miscibility gaps based on the Redlich–Kister polynomial for binary solutions, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2012, 38, 161–167 CrossRef CAS.
- B. Bonham and G. Guisbiers, Thermal stability and optical properties of Si–Ge nanoparticles, Nanotechnology, 2017, 28, 245702 CrossRef PubMed.
- G. Guisbiers, et al., Cu–Ni nano-alloy: mixed, core–shell or Janus nano-particle?, Nanoscale, 2014, 6, 14630–14635 RSC.
- L. D. Geoffrion and G. Guisbiers, Chemical Ordering in Bi1–xSbx Nanostructures: Alloy, Janus, or Core–Shell, J. Phys. Chem. C, 2020, 124(25), 14061–14068 CrossRef CAS.
- W. Hume-Rothery, G. W. Mabbott and K. M. C. Evans, The freezing points, melting points, and solid solubility limits of the alloys of sliver and copper with the elements of the b sub-groups, Philos. Trans. R. Soc., A, 1997, 233(721–730), 1–97 Search PubMed.
- M. Hansen, R. P. Elliot, and F. A. Shunk, Metallurgy and metallurgical engineering series, Constitution of Binary Alloys, McGraw-Hill, 1958 Search PubMed.
- T. B. Massalski, Binary Alloy Phase Diagrams, ASM International, Materials Park, Ohio, 1993, vol. 2 Search PubMed.
- E. Roduner, Size matters: why nanomaterials are different, Chem. Soc. Rev., 2006, 35, 583–592 RSC.
- G. Guisbiers, Size-dependent materials properties toward a universal equation, Nanoscale Res. Lett., 2010, 5(7), 1132–1136 CrossRef CAS PubMed.
- G. Guisbiers and G. Abudukelimu, Influence of nanomorphology on the melting and catalytic properties of convex polyhedral nanoparticles, J. Nanopart. Res., 2013, 15(2), 1431 CrossRef.
- G. Guisbiers and L. Buchaillot, Universal size/shape-dependent law for characteristic temperatures, Phys. Lett. A, 2009, 374, 305–308 CrossRef CAS.
- K. Yun, et al., Monte Carlo simulations of the structure of Pt-based bimetallic nanoparticles, Acta Mater., 2012, 60, 4908–4916 CrossRef CAS.
- S. Khanal, et al., Synthesis, characterization, and growth simulations of Cu–Pt bimetallic nanoclusters, Beilstein J. Nanotechnol., 2014, 5, 1371–1379 CrossRef PubMed.
- H. Peng, et al., Structural stability of alloyed and core–shell Cu–Pt bimetallic nanoparticles, Int. J. Mod. Phys. B, 2017, 31, 1741012 CrossRef CAS.
- S. V. Belenov, et al., Phase Behavior of Pt–Cu Nanoparticles with Different Architecture upon Their Thermal Treatment, Nanotechnol. Russ., 2017, 12, 147–155 CrossRef CAS.
- M. Zhang, et al., Ultrafast and surfactant-free synthesis of Sub-3 nm nanoalloys by shear-assisted liquid–metal reduction, Nanoscale Adv., 2020, 2, 4873–4880 RSC.
- G. Guisbiers, et al., Electrum, the Gold–Silver Alloy, from the Bulk Scale to the Nanoscale: Synthesis, Properties, and Segregation Rules, ACS Nano, 2016, 10, 188–198 CrossRef CAS PubMed.
- W. Martienssen and H. Warlimont, Springer Handbook of Condensed Matter and Materials Data, Springer Berlin Heidelberg, Germany. 2005 Search PubMed.
- G. Guisbiers and M. José-Yacaman, Use of Chemical Functionalities to Control Stability of Nanoparticles, in Encyclopedia of Interfacial Chemistry: Surface Science and Electrochemistry, 2018, pp. 875–885 Search PubMed.
- V. E. Guterman, et al., PtM/C (M = Ni, Cu, or Ag) electrocatalysts: effects of alloying components on morphology and electrochemically active surface areas, J. Solid State Electrochem., 2014, 18, 1307–1317 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |

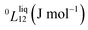
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 932
932