Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Predicting hydration layers on surfaces using deep learning†
Yashasvi S.
Ranawat
 a,
Ygor M.
Jaques
a,
Ygor M.
Jaques
 a and
Adam S.
Foster
a and
Adam S.
Foster
 ab
ab
aDepartment of Applied Physics, Aalto University, Finland. E-mail: yashasvi.ranawat@aalto.fi; ymjaques@gmail.com; adam.foster@aalto.fi
bWPI Nano Life Science Institute (WPI-NanoLSI), Kanazawa University, Kakuma-machi, Kanazawa 920-1192, Japan
First published on 6th May 2021
Abstract
Characterisation of the nanoscale interface formed between minerals and water is essential to the understanding of natural processes, such as biomineralization, and to develop new technologies where function is dominated by the mineral–water interface. Atomic force microscopy offers the potential to characterize solid–liquid interfaces in high-resolution, with several experimental and theoretical studies offering molecular scale resolution by linking measurements directly to water density on the surface. However, the theoretical techniques used to interpret such results are computationally intensive and development of the approach has been limited by interpretation challenges. In this work, we develop a deep learning architecture to learn the solid–liquid interface of polymorphs of calcium carbonate, allowing for the rapid predictions of density profiles with reasonable accuracy.
Solid–liquid interfaces are ubiquitous in nanoscale materials' science.1 At the atomic scale, liquid molecules are differently adsorbed on the surface, forming complex hydration structures. These atomic scale interactions largely influence macroscopic surface phenomena,2 which in turn drive various natural and technological processes.3 Atomic force microscopy (AFM)4 is being developed to image these critical atomic interactions at high speed—commensurate to the molecular-diffusion time-scales—and atomic-scale resolution.5–14 However, the interpretation of the AFM images at such resolutions still remains a massive challenge. The measured force between an AFM tip and the surface hydration layers in the solution comprises tip–surface–solvent interactions and entropic effects, and linking this to the image-contrast mechanism requires an intensive modelling approach for reliable understanding.15–18
The demonstration of a direct relationship between experimental AFM force data and water densities opened an easier route to interpret the images through simulations,19,20 which were further advanced by inclusion of the influence of the tip's hydration structure in the forces21 and an analysis of the role of tip radius.17 However, these studies still require detailed molecular dynamics (MD) simulation of water over various estimates of surface structures to describe the hydration structure formed at the mineral–liquid interface – this is computationally expensive and requires complex parameterisation of classical force fields. These technical challenges encumber nanoscale characterisation of solid–liquid interfaces through AFM and is in stark contrast to the breakthroughs in molecular characterization offered by low-temperature functional-tip AFM in ultra-high vacuum.22,23 In an effort to provide a rapid and reliable interpretation tool, in this work we develop a machine learning approach that can predict water densities, and hence AFM images, directly from the atomic structure.
In order to benchmark our approach, we focus on ideal and defected surfaces of calcium carbonate (CaCO3) polymorphs25 (see Fig. 1). The calcite (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface has become a benchmark surface for AFM studies in liquids.12 Alongside this, a wealth of computational studies of the calcite–water interface have been undertaken, providing a critical background of structural understanding and reliable forces fields necessary for our approach. These studies extensively delineate the calcite (10
4) surface has become a benchmark surface for AFM studies in liquids.12 Alongside this, a wealth of computational studies of the calcite–water interface have been undertaken, providing a critical background of structural understanding and reliable forces fields necessary for our approach. These studies extensively delineate the calcite (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface and water interactions,26,27 AFM imaging,16,28–31 surface ion dissolution,32,33 and effects of point defects and step edges on the hydration layer densities.14,34–37 Alongside calcite, we further consider the other most common polymorphs of CaCO3, aragonite and vaterite. Aragonite is the second most stable polymorph of CaCO3, and plays a vital role in biomineralization.38 Surfaces of aragonite show predominantly the (001), (010) and (110) planes.39 In these surfaces, the carbonate groups are aligned differently from those in (10
4) surface and water interactions,26,27 AFM imaging,16,28–31 surface ion dissolution,32,33 and effects of point defects and step edges on the hydration layer densities.14,34–37 Alongside calcite, we further consider the other most common polymorphs of CaCO3, aragonite and vaterite. Aragonite is the second most stable polymorph of CaCO3, and plays a vital role in biomineralization.38 Surfaces of aragonite show predominantly the (001), (010) and (110) planes.39 In these surfaces, the carbonate groups are aligned differently from those in (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) calcite, cif.Fig. 1. Experimental works40,41 have found clearly distinct patterns in the hydration layer of aragonite (001) surface in comparison to calcite (10
4) calcite, cif.Fig. 1. Experimental works40,41 have found clearly distinct patterns in the hydration layer of aragonite (001) surface in comparison to calcite (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4). Secondly, of those commonly considered, vaterite is the least thermodynamically stable polymorph of CaCO3, and is possibly related to calcite nucleation and dissolution processes.42 The vaterite surface structure has been elusive, as only micro and nano-sized crystals are obtained42 and large enough areas for reliable experimental characterization are rare – as yet, there are no experimental results on the interface of water with vaterite. Current studies indicate two competing/interspersed structures with space groups P3221 and C121.42,43 We use the P3221 structure with the (010) cleavage plane, since this was found to have one of the lowest surface energies.44,45 The different morphologies of these polymorphs, as compared to calcite, and their significant applications make them suitable test cases.
4). Secondly, of those commonly considered, vaterite is the least thermodynamically stable polymorph of CaCO3, and is possibly related to calcite nucleation and dissolution processes.42 The vaterite surface structure has been elusive, as only micro and nano-sized crystals are obtained42 and large enough areas for reliable experimental characterization are rare – as yet, there are no experimental results on the interface of water with vaterite. Current studies indicate two competing/interspersed structures with space groups P3221 and C121.42,43 We use the P3221 structure with the (010) cleavage plane, since this was found to have one of the lowest surface energies.44,45 The different morphologies of these polymorphs, as compared to calcite, and their significant applications make them suitable test cases.
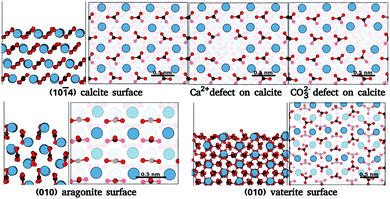 | ||
Fig. 1 Surface atomic structures of the different polymorphs of calcium carbonate: calcite (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface, aragonite (010) surfaces, and vaterite (010) surface. For each case, the slab and the top view of the surface are shown. Each surface figure has two translucent layers added to ease the surface visualisation, the first translucent layer demarcates the top layer of a slab, while the second translucent layer demarcates the depths of atoms in the top layer. The atoms of calcium, oxygen, and carbon are represented by blue, red, and brown spheres. (The atomic structure is imaged using VESTA24). 4) surface, aragonite (010) surfaces, and vaterite (010) surface. For each case, the slab and the top view of the surface are shown. Each surface figure has two translucent layers added to ease the surface visualisation, the first translucent layer demarcates the top layer of a slab, while the second translucent layer demarcates the depths of atoms in the top layer. The atoms of calcium, oxygen, and carbon are represented by blue, red, and brown spheres. (The atomic structure is imaged using VESTA24). | ||
Our methodological approach builds upon the general philosophy of using machine learning to handle data analysis challenges in Scanning Probe Microscopy (SPM)46–49 and the specific use of deep learning Convolutional Neural Networks (CNN)50 to recognize features in high-resolution SPM images. Recent examples include conditioning of SPM tips,51 identification of defects with STM52,53 and nanostructures with AFM,54 and making molecular structure predictions from AFM images.55 However, to the best of our knowledge, no earlier studies have applied machine learning to SPM at solid–liquid interfaces. We also note that despite sharing some common machine learning algorithms, in each case mentioned, the training data and machine learning architecture are designed for the system being studied, so that they can be effectively considered entirely different computational models from the present applications in SPM.
In this work, we aim to derive a robust computational tool that could predict the hydration layers over surfaces (see Fig. 2), and ease the rapid discovery of possible surface structure from candidate surfaces. This can provide experiments with unprecedented on-the-fly AFM analysis in liquids over CaCO3 surfaces. Further, we progressively include data from molecular dynamics (MD) simulations of water with calcium carbonate polymorphs into the machine learning training to determine the general applicability of these deep-learning techniques to hydration structure prediction. This opens the door to a method for rapid and reliable interpretation of any system imaged by AFM in liquids in the future.
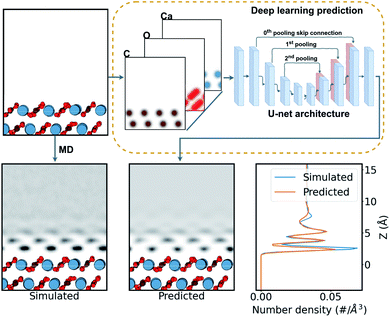 | ||
| Fig. 2 Schematic of the prediction process of water density over a calcite surface. The surface structure is firstly expressed as a three-channel density of Gaussian-smeared carbon, oxygen, and calcium atoms. Then this density is fed into the neural network, shown as a schematic of the U-net network (see ESI† for more details). The network predicts a single-channel density of water over the surface. This is compared with the MD-simulated water density as a target. | ||
To generate a neural network training set for each surface considered, we calculated the water density over the surfaces using the LAMMPS MD code56 (for a more detail discussion see the ESI†). We utilized the inter-atomic potentials from Raiteri et al.,33 a well established potential for carbonate minerals in the context of AFM imaging in liquids14,16,34 that implements the SPC/Fw flexible model for water.57
We trained our models on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) calcite dataset, and the combined (10
4) calcite dataset, and the combined (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) calcite and (010) aragonite dataset, to gauge the generality of the models trained. To create the large database, which includes a wide variety of local chemical environments—crucial for an effective learning—we generated a wide variety of the (10
4) calcite and (010) aragonite dataset, to gauge the generality of the models trained. To create the large database, which includes a wide variety of local chemical environments—crucial for an effective learning—we generated a wide variety of the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) calcite and the (010) aragonite surfaces by removing permutations of Ca2+ and CO32− pairs from the surface of each mineral, always retaining net charge zero in the system. We generated 26
4) calcite and the (010) aragonite surfaces by removing permutations of Ca2+ and CO32− pairs from the surface of each mineral, always retaining net charge zero in the system. We generated 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 784 cases of the calcite dataset and 51
784 cases of the calcite dataset and 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 336 cases of the calcite + aragonite dataset. Each data pair, of input and target, comprises three-channels of the atomic-density of carbon, oxygen, and calcium from the surface as input, and water over the surface as the target, as seen in Fig. 2. These densities are given in a 10 × 10 × 20 Å3 volume (see ESI† for data extraction method). For training, the dataset was split into 70% training, 20% validation, and 10% testing cases, approximately.
336 cases of the calcite + aragonite dataset. Each data pair, of input and target, comprises three-channels of the atomic-density of carbon, oxygen, and calcium from the surface as input, and water over the surface as the target, as seen in Fig. 2. These densities are given in a 10 × 10 × 20 Å3 volume (see ESI† for data extraction method). For training, the dataset was split into 70% training, 20% validation, and 10% testing cases, approximately.
The task of simulating the hydration structures over a given surface can be categorised as an image-to-image problem58 in computer vision (see Fig. 2), specifically in three dimensions. Machine learning models tackling such image-to-image problems have originated from the introduction of encoder–decoder models in machine translation.59 These models distill the input into a condensed latent-space feature-vector using an encoder, that retains only the higher-level semantic information. This information is then translated by the decoder into the output. The U-net CNN architecture60 further enhances such encoder–decoder models with their introduction of skip connections, connecting layers in the encoder to the decoder. This mitigates any loss of spacial information during the encoding in image-to-image applications. Recently, many such image-to-image deep learning methods have found their applications in image segmentation,58,60,61 high resolution image synthesis,62 image synthesis from semantic labels,62,63 and style transfer,64,65 among others. Further, the introduction of the attention mechanism66 in ML models has seen improvements in machine translation. The success is attributed to their ability to draw the global spacial dependencies in the inputs.66 A transformer architecture,67 an attention mechanism variant, has also been successfully extended to image-to-image problems.61,68,69
Here we trained the data with the U-net architecture, with three pooling scales and their corresponding skip connections,60 as seen in Fig. 2. We also applied a soft self-attention mechanism61 to the skip connections to derive an attention variant of the U-net in order to provide more detail on what the network is actually focusing on (attention U-net – for a more detailed discussion see ESI†).
The surfaces of calcite with CO32− and Ca2+ defects and pristine surfaces of (010) aragonite, (001) aragonite, and (010) vaterite are used to test the neural network predictions. These surfaces are unseen by the networks during training, and thus they represent reasonable test cases. We use mean absolute error (MAE)—L1 loss function—to derive a figure-of-merit to compare the predictions in various cases. We also plot and qualitatively compare the simulated and predicted densities in three ways: the 1D mean density along the z direction, the 2D mean density from in the xz plane, and finally, xy slices corresponding to the peaks in water density along the z direction. Moreover, we analyse the attention with respect to atom positions in the (010) aragonite surface case to gain an insight into the evaluations exercised by the network during the predictions.
The MAE of prediction of the U-net and the attention U-net is shown in Table 1. In general, these predictions took less than a second on a standard desktop computer. It is seen from the table that both the simple and attention U-net networks show low errors on their respective test sets. The prediction errors for simple U-net are lower than the attention variant, albeit with minor differences. Naturally, the absolute errors by networks are higher on subsequent test surfaces than that in their test datasets, including for defected systems (where the errors are calculated within 3 Å of the defect site). In general, the overall prediction errors are low, giving us confidence in the reliability of the method. To further generalise the networks, they are also trained with the calcite + (010) aragonite dataset. With the new morphologies incorporated in the network training, the errors of the network are lower on the test dataset. The predictions over the unseen defects and surfaces are similar to that of the networks trained with just the calcite dataset, albeit with slightly higher errors. Only a small change in prediction error with the additional inclusion of distinct surfaces implies generality of the trained networks to materials beyond calcium carbonate in the future. Since there are no significant benefits to the expanded training set for the examples we consider in detail, we focus on the network trained on the calcite dataset alone (using U-net unless otherwise mentioned).
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) calcite surfaces with CO32− and Ca2+ defect is presented
4) calcite surfaces with CO32− and Ca2+ defect is presented
| U-net (c) | Att U-net (c) | U-net (c + a) | Att U-net (c + a) | |
|---|---|---|---|---|
| Respective test set | 1.1015 × 10−3 | 1.1433 × 10−3 | 8.8640 × 10 −4 | 1.0575 × 10−3 |
| CO32− point defect | 2.7288 × 10 −3 | 3.0565 × 10−3 | 2.8357 × 10 −3 | 3.1721 × 10−3 |
| Ca2+ point defect | 2.6579 × 10−3 | 2.6496 × 10−3 | 2.9125 × 10−3 | 2.8362 × 10 −3 |
| (010) aragonite | 9.4199 × 10−3 | 1.0148 × 10−2 | In training data | In training data |
| (010) CO32− vaterite | 6.4501 × 10 −3 | 7.4893 × 10−3 | 6.6732 × 10 −3 | 7.9105 × 10−3 |
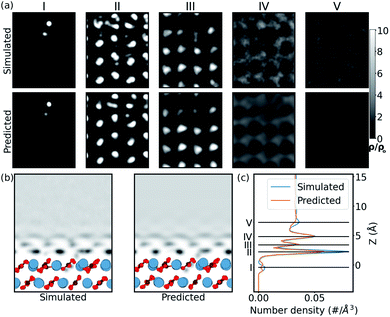
In order to confirm that this quantitative accuracy translates into a meaningful qualitative description of the water density, we now consider each system in detail. Firstly, we look at the case of the CO32− vacancy defect in the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) calcite surface (Ca2+ vacancy is discussed in the ESI†). From Fig. 3, we see that in the 1D plot the position of the peaks are very well predicted, with slight differences in the peak magnitudes. The differences in magnitude can be attributed to the choice of loss function – a network trained with a L1 loss function has been shown to predict blurry images in image-to-image models.58 From the 2D slice, it is seen that the network is able to predict the water density in the defect region, below the surface. The network is also able to predict the perturbation in slices further from the surface. The extent is visible up to ≈5 Å from the surface. This corroborates with the previous experimental defect study by Söngen et al.14 Notwithstanding the stability of the (10
4) calcite surface (Ca2+ vacancy is discussed in the ESI†). From Fig. 3, we see that in the 1D plot the position of the peaks are very well predicted, with slight differences in the peak magnitudes. The differences in magnitude can be attributed to the choice of loss function – a network trained with a L1 loss function has been shown to predict blurry images in image-to-image models.58 From the 2D slice, it is seen that the network is able to predict the water density in the defect region, below the surface. The network is also able to predict the perturbation in slices further from the surface. The extent is visible up to ≈5 Å from the surface. This corroborates with the previous experimental defect study by Söngen et al.14 Notwithstanding the stability of the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) cleavage plane, some extreme neutral defects created in the training process lead to the Ca2+ and the CO32− ions to diffuse into the second or the third hydration layers. We suspect these unexpected solvated ions improve the generality of the learning process and play a role in the high accuracy of prediction over ionic defects.
4) cleavage plane, some extreme neutral defects created in the training process lead to the Ca2+ and the CO32− ions to diffuse into the second or the third hydration layers. We suspect these unexpected solvated ions improve the generality of the learning process and play a role in the high accuracy of prediction over ionic defects.
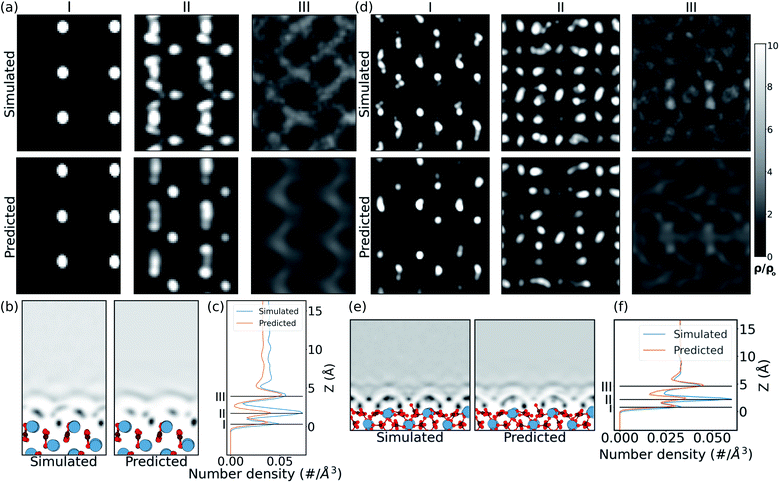
In the case of the prediction over the pristine (010) aragonite surface (the (001) aragonite surface is discussed in ESI†) the errors are larger. We attribute this to the very different morphology of aragonite as compared to the calcite surfaces in the training cases. The resulting hydration density prediction, with simple U-net, over the aragonite surface is compared with the simulated density in Fig. 4. There we can see that the 2D predicted slices at the first and third peak positions, are similar to the simulated data. The predicted slice at second peak is unable to capture detailed features in that position, albeit following the same trends from the simulated data. This is further visible in the mean density along the z direction, in the xz plane. In the comparison of 1D mean density along the z direction, the network predicts all the peak positions remarkably well, but with lower magnitudes, just like the prediction in CO32− defect.
The approach is also tested on the vaterite surface (see Fig. 4). The prediction errors are found to be lower than in the aragonite case. The hydration density peaks, like the aragonite and CO32− cases, are predicted with lower magnitudes, although at correct heights, cif.Fig. 4. The 2D slices in predicted density are visibly similar to that in the simulated case, although some features are somewhat fainter in comparison. We note that should molecularly resolved AFM images of water on vaterite surface be available, our approach could be used to easily compare possible surface structures without any of the associated complexity of modelling thermodynamic stability and/or deriving new force fields.
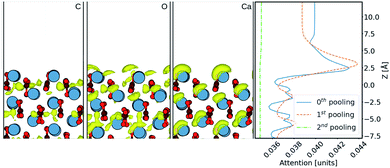
Finally, in order to try and understand in more detail how the machine learning makes predictions of the density, we now consider results using the Att U-net. The attention values coming from the network prediction over the aragonite surface are shown in Fig. 5. The 1D attention values are plotted along z direction at different scales. In the network, these attention values are extracted from the skip connections at three pooling scales: 0th (with no scaling), 1st, and 2nd, cif.Fig. 2. It is seen that the perturbations in the attention values align with the atoms from the surface, especially with the Ca2+ ions. It is clear that more attention is given to the ≈5 Å region above the surface, where most water density peaks reside. While this applies to the 0th and 1st pooling scales, the attention at the 2nd scale, with the widest reaching kernel, demarcates the surface with the bulk water density. This reveals that the layers at each scale play different roles during prediction. Additionally, the attention at the 0th pooling scale is weighted with the carbon, oxygen, and calcium densities and visualised at the same isosurface value in Fig. 5. The atom-density-weighted attention shows higher affinity of the network in regions with higher probability of water around the atom. This apparent correlation of these attention values with the elements in the space implies some learning of real-space physics in the network at the layers at every scale. However, in the weighted-attention isovalues of Ca2+ the attention is positioned on top regardless of the layer-depth of the atom. This highlights a bias in the network towards predicting water on top of atomic structures, i.e. surfaces with surface normal towards z direction. We attribute this to all the cases in the training data being surfaces and should be noted when considering generalizing the method to other structures. In particular, nanoclusters are commonly used to depict an AFM tip in simulations and would require further development to be incorporated reliably.
The simple and the attention variant of the U-net CNN are used to predict the water densities over polymorphs of calcite. The network is shown to learn the water densities, with reasonable peak locations, albeit lower magnitudes near the surface. The generality of the network is established by comparing the loss over surfaces not seen by the network, when trained with calcite data and calcite + aragonite data. The attention mechanism is shown to indicate parallels of the inner layer mechanism with the physical nature of the interactions.
The network makes it possible to predict hydration densities over any surface of calcite, and will help expedite surface characterisation during experiments. Further inclusion of other surface orientations can extend the network to predict water densities around, for example, nanoclusters. It also paves the way for networks that can predict water densities over systems with wider elemental composition than carbon, oxygen, and calcium. This will likely require development of the descriptor used in the training process, taking into account a more detailed description of the local chemical character than offered by the elemental name alone.70,71
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by World Premier International Research Center Initiative (WPI), MEXT, Japan and by the Academy of Finland (project no. 314862). We are grateful to Ondřej Krejčí for careful reading of the manuscript. We also acknowledge the computational resources provided by the Aalto Science-IT project.Notes and references
- Solid-Liquid Interfaces: Macroscopic Phenomena—Microscopic Understanding, ed. K. Wandelt and S. Thurgate, Springer-Verlag, 2003 Search PubMed.
- F. Zaera, Chem. Rev., 2012, 112, 2920–2986 CrossRef CAS PubMed.
- G. E. Brown, V. E. Henrich, W. H. Casey, D. L. Clark, C. Eggleston, A. Felmy, D. W. Goodman, M. Grätzel, G. Maciel and M. I. McCarthy, et al. , Chem. Rev., 1999, 99, 77–174 CrossRef CAS PubMed.
- G. Binnig, C. Gerber, E. Stoll, T. Albrecht and C. Quate, Europhys. Lett., 1987, 3, 1281 CrossRef CAS.
- T. Fukuma, T. Ichii, K. Kobayashi, H. Yamada and K. Matsushige, Appl. Phys. Lett., 2005, 86, 034103 CrossRef.
- T. Fukuma, Y. Ueda, S. Yoshioka and H. Asakawa, Phys. Rev. Lett., 2010, 104, 016101 CrossRef PubMed.
- K. Voïtchovsky, K. Vo Iuml Tchovsky, J. J. Kuna, J. J. Kuna, S. A. Contera, S. A. Contera, E. Tosatti, E. Tosatti and F. Stellacci, Nat. Nanotechnol., 2010, 5, 401 CrossRef PubMed.
- S. Rode, N. Oyabu, K. Kobayashi, H. Yamada and A. Kuehnle, Langmuir, 2009, 25, 2850–2853 CrossRef CAS PubMed.
- I. Siretanu, D. van den Ende and F. Mugele, Nanoscale, 2016, 8, 8220–8227 RSC.
- K. Umeda, L. Zivanovic, K. Kobayashi, J. Ritala, H. Kominami, P. Spijker, A. S. Foster and H. Yamada, Nat. Commun., 2017, 8, 2111 CrossRef PubMed.
- Y. F. Dufrene, T. Ando, R. Garcia, D. Alsteens, D. Martínez-Martín, A. Engel, C. Gerber and D. J. Müller, Nat. Nanotechnol., 2017, 12, 295–307 CrossRef CAS PubMed.
- T. Fukuma and R. Garcia, ACS Nano, 2018, 12, 11785–11797 CrossRef CAS PubMed.
- Y. Teduka, A. Sasahara and H. Onishi, ACS Omega, 2020, 5, 2569–2574 CrossRef CAS PubMed.
- H. Söngen, B. Reischl, K. Miyata, R. Bechstein, P. Raiteri, A. L. Rohl, J. D. Gale, T. Fukuma and A. Kühnle, Phys. Rev. Lett., 2018, 120, 116101 CrossRef PubMed.
- M. Watkins and A. L. Shluger, Phys. Rev. Lett., 2010, 105, 196101 CrossRef PubMed.
- T. Fukuma, B. Reischl, N. Kobayashi, P. Spijker, F. F. Canova, K. Miyazawa and A. S. Foster, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 155412 CrossRef.
- E. Nakouzi, A. G. Stack, S. Kerisit, B. A. Legg, C. J. Mundy, G. K. Schenter, J. Chun and J. J. De Yoreo, J. Phys. Chem. C, 2021, 125, 1282–1291 CrossRef CAS.
- M. R. Uhlig, S. Benaglia, R. Thakkar, J. Comer and R. Garcia, Nanoscale, 2021, 13, 5275–5283 RSC.
- M. Watkins and B. Reischl, J. Chem. Phys., 2013, 138, 154703 CrossRef PubMed.
- K.-i. Amano, K. Suzuki, T. Fukuma, O. Takahashi and H. Onishi, J. Chem. Phys., 2013, 139, 224710 CrossRef PubMed.
- K. Miyazawa, J. Tracey, B. Reischl, P. Spijker, A. S. Foster, A. L. Rohl and T. Fukuma, Nanoscale, 2020, 12, 12856–12868 RSC.
- L. Gross, F. Mohn, N. Moll, P. Liljeroth and G. Meyer, Science, 2009, 325, 1110–1114 CrossRef CAS PubMed.
- N. Pavliček and L. Gross, Nat. Rev. Chem., 2017, 1, 1–11 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- F. Heberling, D. Bosbach, J.-D. Eckhardt, U. Fischer, J. Glowacky, M. Haist, U. Kramar, S. Loos, H. S. Müller, T. Neumann, C. Pust, T. Schäfer, J. Stelling, M. Ukrainczyk, V. Vinograd, M. Vučak and B. Winkler, Appl. Geochem., 2014, 45, 158–190 CrossRef CAS.
- M. Wolthers, D. Di Tommaso, Z. Du and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2012, 14, 15145 RSC.
- A. Silvestri, A. Budi, E. Ataman, M. H. M. Olsson, M. P. Andersson, S. L. S. Stipp, J. D. Gale and P. Raiteri, J. Phys. Chem. C, 2017, 121, 24025–24035 CrossRef CAS.
- B. Reischl, M. Watkins and A. S. Foster, J. Chem. Theory Comput., 2013, 9, 600–608 CrossRef CAS PubMed.
- J. Tracey, K. Miyazawa, P. Spijker, K. Miyata, B. Reischl, F. F. Canova, A. L. Rohl, T. Fukuma and A. S. Foster, Nanotechnology, 2016, 27, 415709 CrossRef PubMed.
- H. Söngen, C. Marutschke, P. Spijker, E. Holmgren, I. Hermes, R. Bechstein, S. Klassen, J. Tracey, A. S. Foster and A. Kühnle, Langmuir, 2017, 33, 125–129 CrossRef PubMed.
- B. Reischl, P. Raiteri, J. D. Gale and A. L. Rohl, J. Phys. Chem. C, 2019, 123, 14985–14992 CrossRef CAS.
- D. Spagnoli, S. Kerisit and S. C. Parker, J. Cryst. Growth, 2006, 294, 103–110 CrossRef CAS.
- P. Raiteri, R. Demichelis and J. D. Gale, J. Phys. Chem. C, 2015, 119, 24447–24458 CrossRef CAS.
- B. Reischl, P. Raiteri, J. D. Gale and A. L. Rohl, Phys. Rev. Lett., 2016, 117, 226101 CrossRef PubMed.
- M. De La Pierre, P. Raiteri and J. D. Gale, Cryst. Growth Des., 2016, 16, 5907–5914 CrossRef CAS.
- H. Chen, S. L. Eichmann and N. A. Burnham, J. Phys. Chem. C, 2020, 124, 17648–17654 CrossRef CAS.
- J. Zhao, J. Wang, X. Qin and Y. Cao, Solid State Commun., 2020, 313, 113892 CrossRef CAS.
- S. Mann, Biomineralization: principles and concepts in bioinorganic materials chemistry, Oxford University Press on Demand, 2001, vol. 5 Search PubMed.
- T. Akiyama, K. Nakamura and T. Ito, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 085428 CrossRef.
- R. Giles, S. Manne, S. Mann, D. E. Morse, G. D. Stucky and P. K. Hansma, Biol. Bull., 1995, 188, 8–15 CrossRef CAS PubMed.
- Y. Araki, K. Tsukamoto, N. Oyabu, K. Kobayashi and H. Yamada, Jpn. J. Appl. Phys., 2012, 51, 08KB09 CrossRef.
- A. G. Christy, Cryst. Growth Des., 2017, 17, 3567–3578 CrossRef CAS.
- K. M. N. Burgess and D. L. Bryce, Solid State Nucl. Magn. Reson., 2015, 65, 75–83 CrossRef CAS PubMed.
- W. Sekkal and A. Zaoui, Sci. Rep., 2013, 3, 1587 CrossRef CAS PubMed.
- N. H. de Leeuw and S. C. Parker, J. Phys. Chem. B, 1998, 102, 2914–2922 CrossRef CAS.
- S. V. Kalinin, B. G. Sumpter and R. K. Archibald, Nat. Mater., 2015, 14, 973–980 CrossRef CAS PubMed.
- S. V. Kalinin, E. Strelcov, A. Belianinov, S. Somnath, R. K. Vasudevan, E. J. Lingerfelt, R. K. Archibald, C. Chen, R. Proksch, N. Laanait and S. Jesse, ACS Nano, 2016, 10, 9068–9086 CrossRef CAS PubMed.
- M. Ziatdinov, A. Maksov and S. V. Kalinin, npj Comput. Mater., 2017, 3, 31 CrossRef.
- O. M. Gordon and P. J. Moriarty, Mach. Learn.: Sci. Technol., 2020, 1, 023001 CrossRef.
- Y. LeCun, Y. Bengio and G. Hinton, Nature, 2015, 521, 436–444 CrossRef CAS PubMed.
- M. Rashidi and R. A. Wolkow, ACS Nano, 2018, 12, 5185–5189 CrossRef CAS PubMed.
- J. Croshaw, T. Dienel, T. Huff and R. Wolkow, Beilstein J. Nanotechnol., 2020, 11, 1346–1360 CrossRef CAS PubMed.
- M. Rashidi, J. Croshaw, K. Mastel, M. Tamura, H. Hosseinzadeh and R. A. Wolkow, Mach. Learn.: Sci. Technol., 2020, 1, 025001 CrossRef.
- O. M. Gordon, J. E. A. Hodgkinson, S. M. Farley, E. L. Hunsicker and P. J. Moriarty, Nano Lett., 2020, 20, 7688–7693 CrossRef CAS PubMed.
- B. Alldritt, P. Hapala, N. Oinonen, F. Urtev, O. Krejci, F. F. Canova, J. Kannala, F. Schulz, P. Liljeroth and A. S. Foster, Sci. Adv., 2020, 6, eaay6913 CrossRef CAS PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- Y. Wu, H. L. Tepper and G. A. Voth, J. Chem. Phys., 2006, 124, 024503 CrossRef PubMed.
- P. Isola, J.-Y. Zhu, T. Zhou and A. A. Efros, 2016, 1125–1134, arXiv:1611.07004 [cs].
- K. Cho, B. van Merrienboer, D. Bahdanau and Y. Bengio, 2014, arXiv:1409.1259 [cs, stat].
- O. Ronneberger, P. Fischer and T. Brox, International Conference on Medical image computing and computer-assisted intervention, 2015, pp. 234–241 Search PubMed.
- O. Oktay, J. Schlemper, L. L. Folgoc, M. Lee, M. Heinrich, K. Misawa, K. Mori, S. McDonagh, N. Y. Hammerla, B. Kainz, B. Glocker and D. Rueckert, 2018, arXiv:1804.03999 [cs].
- T.-C. Wang, M.-Y. Liu, J.-Y. Zhu, A. Tao, J. Kautz and B. Catanzaro, 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018, pp. 8798–8807 Search PubMed.
- T. Park, M.-Y. Liu, T.-C. Wang and J.-Y. Zhu, 2019, arXiv:1903.07291 [cs].
- B. Kim, V. C. Azevedo, M. Gross and B. Solenthaler, 2020, arXiv:2005.00803 [cs].
- L. Zhang, Y. Ji, X. Lin and C. Liu, 2017 4th IAPR Asian Conference on Pattern Recognition (ACPR), 2017, pp. 506–511 Search PubMed.
- D. Bahdanau, K. Cho and Y. Bengio, 2014, arXiv:1409.0473 [cs, stat].
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. Kaiser and I. Polosukhin, 2017, arXiv:1706.03762 [cs].
- N. Abraham and N. M. Khan, 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), 2019, pp. 683–687 Search PubMed.
- F. Altaf, S. M. S. Islam, N. Akhtar and N. K. Janjua, IEEE Access, 2019, 7, 99540–99572 Search PubMed.
- L. Himanen, M. O. J. Jäger, E. V. Morooka, F. Federici Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, Comput. Phys. Commun., 2020, 247, 106949 CrossRef CAS.
- M. O. J. Jäger, Y. S. Ranawat, F. F. Canova, E. V. Morooka and A. S. Foster, ACS Comb. Sci., 2020, 22, 768–781 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed description of MD, data preparation for training, and deep learning models. Comparison of prediction over calcite surface with Ca2+ vacancy and (001) aragonite surface. See DOI: 10.1039/d1na00253h |
| This journal is © The Royal Society of Chemistry 2021 |