Open Access Article
Open Access ArticleDetermination of the valence band edge of Fe oxide nanoparticles dispersed in aqueous solution through resonant photoelectron spectroscopy from a liquid microjet†
Giorgia
Olivieri‡§
 *a,
Gregor
Kladnik‡
bc,
Dean
Cvetko
bcd and
Matthew A.
Brown
ae
*a,
Gregor
Kladnik‡
bc,
Dean
Cvetko
bcd and
Matthew A.
Brown
ae
aLaboratory for Surface Science and Technology, Department of Materials, ETH Zürich, Vladimir-Prelog-Weg 5, CH-8093, Zürich, Switzerland. E-mail: olivieri.giorgia85@gmail.com
bFaculty for Mathematics and Physics, University of Ljubljana, Jadranska 19, Ljubljana, SI-1000, Slovenia
cIOM-CNR, Laboratorio TASC, Basovizza SS-14, km 163.5, Trieste 34149, Italy
dJožef Stefan Institute, Jamova 39, Ljubljana, SI-1000, Slovenia
eMetrology Research Centre, National Research Council of Canada, Ottawa, Ontario, Canada
First published on 5th July 2021
Abstract
We use X-ray photoemission and a near ambient pressure with a liquid microjet setup to investigate the electronic structure of FeOOH nanoparticles dispersed in aqueous solution. In particular, we show that by using X-ray resonant photoemission in dilute solutions, we can overcome the limits of conventional photoemission such as low nanoparticle-to-solvent signal ratio, and local nanoparticle charging and measure the valence band structure of FeOOH nanoparticles in aqueous solution with chemical specificity. The resonant photoemission signal across the Fe 2p3/2 absorption edge is measured for 2 wt% aqueous solutions of FeOOH nanoparticles (NPs) and the valence band maximum (VBM) of the hydrated FeOOH nanoparticles is determined. We compare the obtained VBM value in aqueous solution to that of FeOOH NPs in the dry phase. We show that the valence band edge position of NPs in the liquid phase can be accurately predicted from the values obtained in the dry phase provided that a simple potential shift due to solution chemistry is applied. Our results demonstrate the suitability of resonant photoemission in measuring the electronic structure of strongly diluted nanosystems where the conventional non-resonant photoemission technique fails.
Introduction
Since the work of Fujishima and Honda on the production of hydrogen from the photoelectrochemical splitting of water,1 metal oxide based materials have been used as the photoactive element in (photo)electrochemical cells for the production and storage of clean energy. In addition to energy storage in water splitting devices and energy conversion in dye-sensitized solar cells,2,3 heterogeneous photocatalysis involving metal oxides immersed in electrolyte solutions has been employed for a number of other applications including the removal of pollutants from water, photocatalytic organic synthesis and antitumoral medical applications.Exploiting the unique properties of nanoscale objects, such as increased surface area, decreased charge carrier path or variations of band gap due to quantum size effects, is one of the strategies employed to enhance the efficiency of existing semiconductors and metal oxides in (photo)electrochemical devices.4 The determination of the band edges of nanosized materials used in such systems, where the nanoparticle (NP) semiconductor operates in aqueous electrolyte solutions, is of fundamental importance to understand the device operation since the position of the band edges gives information on the reductive and oxidative power of the generated electrons and holes.5,6 Experimental determination of the relative energies of the band edges is critical to assess whether charge transfer can take place, since charge transfer occurs when an electron in the semiconductor conduction band reduces an electron acceptor species in the electrolyte and/or a hole in the semiconductor valence band oxidizes an electron donor species in solution.
The position of the band edges of a semiconductor cannot be easily predicted or taken from the literature due to the dependence on its surface charge and, for a semiconductor in contact with an electrolyte solution, the influence of the ionic conditions of the electrolyte. Additionally, the structural arrangement and composition of the semiconductor surface, which depends on the synthetic strategy used, also directly affects the band edge position. Here, in situ experimental methods can give a direct insight into the NP band edge position.
Most of the (photo)electrochemical methods available to measure band edges under in operando conditions are based on the determination of the so-called flat-band potential, i.e. the potential at which the bending of semiconductor bands at the semiconductor/electrolyte interface is zero.7 The determination of the flat-band potential gives directly the position of the conduction band edge with respect to the normal hydrogen electrode (NHE). However, it is well known that the various techniques for determining the flat-band potential can yield different results and could mislead the analysis of photoelectrode performance.8 Furthermore, the valence band edge is determined only indirectly by adding the optical band gap of the material as no known experiment can directly interrogate its position.
The magnitude of the band bending is directly related to the space-charge layer that arises in the semiconductor during the thermodynamic equilibration process via electron transfer through the interface. For nanosized objects, the space-charge layer thickness cannot exceed the size of the nano-object (i.e. the radius in case of spherical nanoparticles), restraining the possible barrier height at the interface. This means that in the absence of a strong applied field, the bands in a nanoparticle are essentially flat and most electrochemical methods cannot be applied to measure the band edge position. To the best of our knowledge, the only method available to measure the conduction band edge in the case of nanoparticles in aqueous solution is the one developed by Roy9 which exploits the pH dependence of band edges. This method requires the nanoparticle solution to be stable over a broad range of pH and therefore can be used only with a limited number of nanoparticles in aqueous solution.
Spectroscopic methods such as ultraviolet or X-ray photoemission spectroscopy (XPS) give the possibility to directly probe the position of the valence band maximum relative to the vacuum level (VL) of the system through the measurement of the ionization energy (IE). Although traditionally limited to (ultra)high vacuum conditions, and therefore applicable to the dry state measurements only, XPS can nowadays be coupled with a liquid microjet in order to measure aqueous samples such as nanoparticle solutions.10 Limitations in this approach have to date prevented the direct measurement of valence band edges from nanoparticle solutions because strong signals from the solvent dominate the region of the spectra in question.
Here we show that X-ray resonant photoemission spectroscopy (RPES), an extension of XPS, can be used to selectively enhance and identify the valence band features of nanoparticles dispersed in aqueous solution and ultimately to determine the valence band edge of such objects with chemical resolution. RPES in thin films has been extensively used in studies of ultrafast electron delocalization11–16 and also for spectral recognition with chemical and oxidation state selectivity in the valence electronic structure in complex systems.17–21 In particular, in RPES, the photon energy is tuned to the atom-specific absorption edge, whereupon the process of core hole creation and decay with autoionization resonantly enhances the VB electron emission. The strength of resonances reflects the spatial overlap among the core and the excited and the VB wavefunctions involved in the RPES, allowing chemical and orbital recognition of the VB spectral features. Notably, recent work by Ali et al. has demonstrated the power of RPES in enhancing the photoemission signal in liquid dispersed systems.17
In this work we use RPES for FeOOH NPs dispersed in aqueous solutions to evidence the Fe related photoemission signal in the upper valence band of the NP and determine the energy position of the valence band edge in the FeOOH NPs.
Experimental
We use the near ambient pressure XPS endstation of the Swiss Light Source22 in conjunction with a liquid microjet23 to investigate the electronic structure of iron oxide nanoparticles dispersed in aqueous solution. The photon energy resolution was better than 150 meV and the overall photoemission spectra resolution was better than 300 meV.24 The NP aqueous solution, purchased from PlasmaChem, has a certified nanoparticle concentration of 2 wt% and contains spherical iron oxide NPs with a mean size of 6 nm. The pH of the solution, measured before injecting the solution into the microjet with a four point calibrated pH meter, is 1.7(±0.1). Through powder X-ray diffraction measurements of an evaporated aliquot of the nanoparticle solution (ESI Fig. S1†), we are able to identify the crystalline structure of the NPs as goethite (FeOOH). Moreover, the NPs are declared by the producing company to be ligand-free, and the XPS survey of the solution (ESI Fig. S2†) does not show any detectable element characteristic of a ligand, such as carbon or nitrogen.Results and discussion
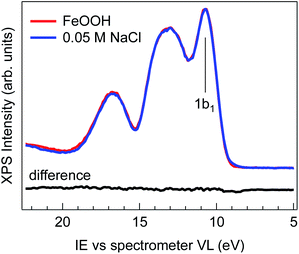
Fig. 1 shows the comparison of the valence band spectra of 2 wt% FeOOH nanoparticles in water (red trace) and of 0.05 M NaCl electrolyte solution (blue trace), both taken with a photon energy of 706.47(±0.14) eV. The high photon energy used for the VB measurement provides higher kinetic energies and therefore larger escape depths of emitted electrons, allowing probing of a larger sample volume. During the measurement, the liquid jet was biased with −25 V in order to separate the gas phase from the liquid phase VB contributions and eliminate the former from the valence band region.25 No shifting or broadening of spectral features due to sample charging is observed, as demonstrated by comparing the spectra measured with different photon fluxes (ESI Fig. S3†). The overall shape of the 0.05 M NaCl spectrum is virtually indistinguishable from that of FeOOH NPs, as evidenced by the absence of any features in the difference spectrum (Fig. 1, black trace).The evidently featureless difference spectrum indicates that the solvent (water) spectral features completely dominate the valence band signal of the NP aqueous solution in this energy range. This may be expected especially for diluted solutions and in cases where the valence band orbitals of NPs and of the solvent are energetically degenerate. However, for iron oxides, the valence band edge is expected to lie between 6 and 8 eV below the vacuum level,26 which is considerably higher than the highest lying orbital (1b1) of water (i.e. closer to the vacuum level).27–30 The lack of any detectable signal above the 1b1 peak of water can be rationalized when considering the NP spatial distribution at the liquid/gas interface. In fact, depending on their hydrophilicity, the NP spatial distribution is not exclusively concentrated at the liquid/gas interface but may also extend into the liquid phase.31,32 The water layer then strongly attenuates the photoelectrons generated from the more hydrophilic NPs farther from the interface, resulting in a valence band spectrum where only the features of the solvent are evident. This makes XPS measurements of the NP VB edge in dilute solutions practically unfeasible.
In order to increase the NP signal relative to that of the solvent, a straightforward strategy would be to increase the concentration of NPs in the solution. However, the concentration range is limited by the stability of the solution and typically low concentrations are required in order to avoid NP precipitation. Moreover, charging effects can be observed in the XP spectra when using higher NP concentrations or too high photon fluxes, both of which prevent quantitative determination of the band edge position. Finally, low concentrated solutions are easier to synthesize and, particularly for expensive materials, reduce the overall cost of liquid jet experiments since several hundred milliliters of solution are consumed.
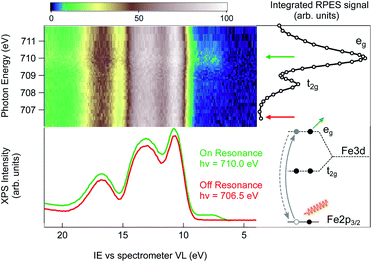
An alternative strategy to selectively enhance the photoelectron signal coming from the NPs is to tune the photon energy to an absorption edge characteristic of the NP constituents and to perform a resonant photoemission spectroscopy (RPES) measurement. Here, the photon energy is swept across an element specific absorption edge and the VB photoemission spectra are collected at each photon energy. The whole set of RPE spectra can be represented in a 2D color map of photoemission intensity (see Fig. 2) as a function of photon energy (vertical scale) and electron ionization energy (abscissa). Across the absorption resonance, the direct photoemission from the valence band is rivaled by indirect, Auger mediated processes of core-hole creation and subsequent de-excitation through autoionization termed participant Auger decay (see the inset of Fig. 2 and ESI† for details). Although energetically degenerate with direct photoemission, the intensity of the participant Auger decay usually dominates the spectrum due to the resonant increase of the photon absorption cross-section when the photon energy is tuned to the absorption edge. The chemical specificity of RPES is a direct consequence of the resonant nature of the process in which the initial, atomically localized core orbital, the intermediate empty orbital and the final valence orbital need to overlap.11 Observation of VB resonances therefore evidences the specific element involvement in the VB features.
The Fe L3 near-edge X-ray absorption fine structure (NEXAFS) spectrum of the 2 wt% FeOOH aqueous solution is shown on the right hand side of the RPES map (Fig. 2, open circles). It is obtained by integrating the total signal measured in the Fe LMV Auger energy window (from 560 eV to 640 eV kinetic energy), in order to compare the absorption peak position with the VB resonances in the RPES map. In this photon energy range, the NEXAFS spectrum shows two peaks that, according to previous results on iron oxide systems, can be attributed to the crystal-field splitting of the Fe 3d orbitals due to the octahedral symmetry around the iron site.33 The position of both the main (eg) and the minor peak (t2g) at 710.0 eV and 708.5 eV, respectively, yield a crystal field splitting of 1.5(±0.1) eV, and the relative peak intensities are consistent with the NEXAFS absorption spectra reported for goethite nano-objects in a non-aqueous environment.34 From this close resemblance of our Fe NEXAFS with that of goethite NPs in the dry phase, we conclude that the contribution from other iron species, such as dispersed Fe+ ions, is negligible. In fact, the NEXAFS spectrum of Fe+ ions is significantly different from our spectrum,35 with the main absorption peak of Fe+ ions occurring at 708.4 eV, whereas it has a minimum at 710.0 eV, where the FeOOH 2p → eg resonance lies. We can therefore safely assign the observed resonances to the dispersed FeOOH NPs.
Next, we turn to the Fe L3-edge RPES map of the 2 wt% FeOOH aqueous solution shown in Fig. 2. Under off-resonance conditions, i.e. with the photon energy set just below the absorption edge (hν = 706.5 eV), the valence band spectrum of the NP aqueous solution closely resembles that of a low electrolyte concentration water solution (red trace, below the RPES map, compare to Fig. 1). However, when the photon energy is swept across the Fe-L3 edge, the appearance of additional features on the lower IE side of the valence band region is observed (green trace, below the RPES map). The two photoemission spectra have been collected over several repeated scans in order to obtain a better signal/noise ratio (36 scans for the on-resonance and 40 scans for the off-resonance spectrum). The additional features in the valence band photoemission resonate in correspondence to the two NEXAFS peaks with the highest intensity enhancement at the eg absorption peak at a photon energy of 710.0 eV. Since the matrix element for the resonant photoemission process requires spatial overlap between the wavefunctions of the three orbitals involved in the process, i.e. the empty orbitals (t2g, eg), the occupied valence band orbitals and the core–shell wavefunction (Fe 2p),11 we conclude that the observed VB spectral resonances are related to NPs and must have to a certain degree iron character. In other words, the resonating VB orbitals at an IE of about 7.5 eV in Fig. 2 are at least partially spread over the Fe sites of the NPs. Moreover, the fact that the observed photoemission resonances occur exactly in correspondence with the Fe 2p → t2g/eg NEXAFS transition ensures that the resonating features are characteristic of iron belonging to a FeOOH crystalline phase.
We obtain the Fe 2p → eg resonant photoemission spectrum of the 2 wt% FeOOH NP solution as the difference between the on-resonance and off-resonance spectra, shown in Fig. 3a. A Shirley type inelastic background has been subtracted for both the on- and off-resonance spectra before subtraction. The ionization energy (IE) scale has been corrected by 0.63(±0.08) eV in order to account for the vacuum level offset between the solution and the photoelectron analyzer (see ESI Fig. S4†).25 A tentative fit of the spectral features, following the one reported in the work by Ali et al.,17 is shown. Such resonant photoemission spectra are in general composed of both participant decay and spectator/normal Auger decay channels;11 however, only the participant channel is energetically degenerate with direct VB photoemission and gives the projection of the VB on the Fe sites of the FeOOH NPs (see ESI Fig. S5† for the RPES energy level diagram). Both the spectator and normal Auger channels are found at a significantly lower KE (higher IE) due to their energy loss decay process and therefore do not play any role in the valence band maximum position. We also note that the resonant spectra, for the Fe 2p → eg and the 2p → t2g excitations, exhibit an identical VBM edge, proving that this resonant feature comes from the Fe NPs (see ESI Fig. S6†). It is commonplace to extrapolate the valence band maximum (VBM) by separately fitting the linear part of the valence band leading edge and the constant background in the low IE part of the spectrum to determine the intersection of the two straight line segments, Fig. 3b. This linear extrapolation method is often used to determine the VBM, and it has been shown to give accurate results for oxides provided that the magnitude of the experimental resolution (FWHM = 0.3 eV) is lower than the width of the rising VB edge (1 eV, Fig. 3a).36 Extrapolating the leading edge to the level of background intensity removes the resolution-induced tail and gives a VBM equal to EV = 6.97(±0.16) eV (relative to the vacuum level of the solution).
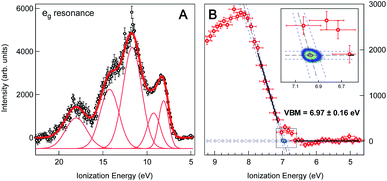 | ||
| Fig. 3 (A) Valence band region of 2 wt% FeOOH NP aqueous solution taken at the resonant Fe L3-edge (∼710.0 eV) after subtraction of the pre-edge (non-resonant) signal and Shirley type background. The ionization energy scale has been corrected by the work function offset (ϕsol − ϕana = 0.63(±0.08) eV) determined from the secondary electron energy distribution curve (SEEDC). The fits of the spectral features in Fig. 3a follow the ones reported by H. Ali et al. for aqueous solution of Fe2O3 NPs.17 (B) Close-up view of the VB leading edge. Thick black lines show the linear fits of the background and the leading edge used to determine the fit line intersection, i.e. the onset of the valence band maximum (VBM), which is found to be at 6.97(±0.16) eV below the vacuum level. Blue dashed lines show the 95% confidence bands of the fits with additional Monte Carlo error analysis represented by the 2D probability density of the fit line intersection position (2D color map, see also the inset), resulting in a ±0.03 eV statistical error. The overall error of 0.16 eV additionally accounts for the experimental resolution (FWHM = 0.3 eV) and energy calibration error (±0.08 eV). | ||
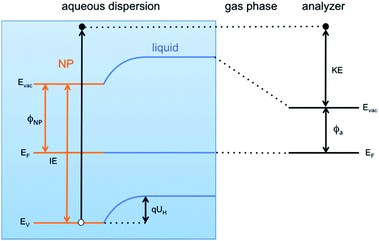
This result is the first experimentally obtained value of the VBM for FeOOH nanoparticles measured in aqueous solution. However, it is worth noting that this value depends on the specific pH of the solution, and a change of the latter would result in a different measured position of the VBM. This is a consequence of the formation of the so-called Helmholtz double layer,7 a potential drop at the liquid side of the NP surface caused by an accumulation of charges on the surface of the NP compensated by a layer of mobile hydrated ions close to the NP surface. The Helmholtz double layer at semiconductors immersed in aqueous solutions typically forms by adsorption and desorption of hydronium (H+) and hydroxyl (OH−) ions present in solution which charge the surface either positively or negatively depending on the pH of the aqueous solution. The schematic energy level diagram of a liquid microjet setup, with NPs dispersed in aqueous solution, is shown in Fig. 4.
The VBM position of FeOOH NPs immersed in solution can be related to that of NPs dispersed in vacuum, and therefore without any kind of environment (referred hereafter as “pristine”), by a simple energy shift as
| EV = E0V − qUH. | (1) |
Here EV is the position of the valence band edge at the NP surface in the solution, qUH is the potential energy shift of the band edge due to the Helmholtz layer and E0V is the band edge at the pristine NP surface with no Helmholtz layer (UH = 0). Expressing the Helmholtz potential energy as a function of the pH of the solution, eqn (1) becomes
| EV = E0V + 2.3kT(pH − pHPZC) | (2) |
Conclusions
In conclusion, we have used X-ray resonant photoemission from a liquid microjet source to measure the electronic structure of (goethite) FeOOH nanoparticles in aqueous solution, where conventional non-resonant photoemission signal is below the detection limit. We show that RPES tuned to an absorption edge of nanoparticle constituents is a suitable technique for the determination of the VB edge energies of dispersed nanoparticles in solution, owing to its chemical specificity and resonant enhancement of the NP VB signal. In particular, due to resonant nature of the electron emission, the VB spectral features at the eg and t2g resonances across the Fe L3 absorption edge are directly related to the Fe constituents of the FeOOH NPs used in this study. This enables us to identify and successfully disentangle the NP related spectral features from the dominant spectral features of the solution. We determine the VBM of the FeOOH NPs in aqueous solution at the point of zero charge pH to lie E0V = 7.31(±0.17) eV below the vacuum level. We show that in solutions with different pH, a general Nernst relation for the potential correction may be applied to relate the electronic levels of nanoparticles in chemically different environments.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr Alok Goel for his contribution to the synchrotron experiments and to the XRD measurements. DC and GK acknowledge partial financial support from the Slovenian Research Agency (research programs P1-0112 and P1-0044). Part of this work was performed at the SIM beamline of the Swiss Light Source. MAB performed the experiments while at ETH Zurich. The analysis and interpretation of the results and writing the paper were done while MAB was at NRC.Notes and references
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS PubMed
.
- M. Grätzel, Nature, 2001, 414, 338–344 CrossRef PubMed
.
- B. C. O'Regan and J. R. Durrant, Acc. Chem. Res., 2009, 42, 1799–1808 CrossRef PubMed
.
- F. E. Osterloh, Chem. Soc. Rev., 2013, 42, 2294–2320 RSC
.
- S. Chu, Y. Wang, Y. Guo, J. Feng, C. Wang, W. Luo, X. Fan and Z. Zou, ACS Catal., 2013, 3, 912–919 CrossRef CAS
.
- S. E. Koops, B. C. O'Regan, P. R. F. Barnes and J. R. Durrant, J. Am. Chem. Soc., 2009, 131, 4808–4818 CrossRef CAS PubMed
.
- R. Beranek, Adv. Phys. Chem., 2011, 2011, 1–20 CrossRef
.
- A. Hankin, F. E. Bedoya-Lora, J. C. Alexander, A. Regoutz and G. H. Kelsall, J. Mater. Chem. A, 2019, 7, 26162–26176 RSC
.
- A. Roy, Int. J. Hydrogen Energy, 1995, 20, 627–630 CrossRef CAS
.
- M. A. Brown, I. Jordan, A. Beloqui Redondo, A. Kleibert, H. J. Wörner and J. A. van Bokhoven, Surf. Sci., 2013, 610, 1–6 CrossRef CAS
.
- P. A. Brühwiler, O. Karis and N. Mårtensson, Rev. Mod. Phys., 2002, 74, 703–740 CrossRef
.
- J. Schnadt, P. A. Brühwiler, L. Patthey, J. N. O'Shea, S. Södergren, M. Odelius, R. Ahuja, O. Karis, M. Bässler, P. Persson, H. Siegbahn, S. Lunell and N. Mårtensson, Nature, 2002, 418, 620–623 CrossRef CAS PubMed
.
- A. Batra, G. Kladnik, H. Vázquez, J. S. Meisner, L. Floreano, C. Nuckolls, D. Cvetko, A. Morgante and L. Venkataraman, Nat. Commun., 2012, 3, 1086 CrossRef
.
- G. Kladnik, D. Cvetko, A. Batra, M. Dell'Angela, A. Cossaro, M. Kamenetska, L. Venkataraman and A. Morgante, J. Phys. Chem. C, 2013, 117, 16477–16482 CrossRef CAS
.
- O. Adak, G. Kladnik, G. Bavdek, A. Cossaro, A. Morgante, D. Cvetko and L. Venkataraman, Nano Lett., 2015, 15, 8316–8321 CrossRef CAS
.
- G. Kladnik, M. Puppin, M. Coreno, M. de Simone, L. Floreano, A. Verdini, A. Morgante, D. Cvetko and A. Cossaro, Nano Lett., 2016, 16, 1955–1959 CrossRef CAS PubMed
.
- H. Ali, R. Seidel, M. N. Pohl and B. Winter, Chem. Sci., 2018, 9, 4511–4523 RSC
.
- M. Dell'Angela, G. Kladnik, A. Cossaro, A. Verdini, M. Kamenetska, I. Tamblyn, S. Y. Quek, J. B. Neaton, D. Cvetko, A. Morgante, L. Venkataraman, M. Dell'Angela, G. Kladnik, A. Cossaro, A. Verdini, M. Kamenetska, I. Tamblyn, S. Y. Quek, J. B. Neaton, D. Cvetko, A. Morgante and L. Venkataraman, Nano Lett., 2010, 10, 2470–2474 CrossRef PubMed
.
-
A. Verdini, P. Krüger and L. Floreano, in Surface Science Techniques, ed. G. Bracco and B. Holst, Springer Berlin Heidelberg, 2013 Search PubMed
.
- H. Magnan, P. Le Fèvre, D. Chandesris, P. Krüger, S. Bourgeois, B. Domenichini, A. Verdini, L. Floreano and A. Morgante, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085121 CrossRef
.
- J. Kubacki, D. Kajewski, J. Goraus, K. Szot, A. Koehl, C. Lenser, R. Dittmann and J. Szade, J. Chem. Phys., 2018, 148, 154702 CrossRef CAS PubMed
.
- M. A. Brown, A. B. Redondo, I. Jordan, N. Duyckaerts, M.-T. Lee, M. Ammann, F. Nolting, A. Kleibert, T. Huthwelker, J.-P. Mächler, M. Birrer, J. Honegger, R. Wetter, H. J. Wörner and J. A. van Bokhoven, Rev. Sci. Instrum., 2013, 84, 073904 CrossRef
.
- G. Olivieri, J. B. Giorgi, R. G. Green and M. A. Brown, J. Electron Spectrosc. Relat. Phenom., 2017, 216, 1–16 CrossRef CAS
.
- U. Flechsig, F. Nolting, A. Fraile Rodríguez, J. Krempaský, C. Quitmann, T. Schmidt, S. Spielmann, D. Zimoch, R. Garrett, I. Gentle, K. Nugent and S. Wilkins, AIP Conf. Proc., 2010, 1234, 319–322 CrossRef
.
- G. Olivieri, A. Goel, A. Kleibert, D. Cvetko and M. A. Brown, Phys. Chem. Chem. Phys., 2016, 18, 29506–29515 RSC
.
- Y. Xu and M. A. A. Schoonen, Am. Mineral., 2000, 85, 543–556 CrossRef CAS
.
- M. S. Banna, B. H. McQuaide, R. Malutzki and V. Schmidt, J. Chem. Phys., 1986, 84, 4739–4744 CrossRef CAS
.
- S. Y. Truong, A. J. Yencha, A. M. Juarez, S. J. Cavanagh, P. Bolognesi and G. C. King, Chem. Phys., 2009, 355, 183–193 CrossRef CAS
.
- S. Barth, M. Ončák, V. Ulrich, M. Mucke, T. Lischke, P. Slavíček and U. Hergenhahn, J. Phys. Chem. A, 2009, 113, 13519–13527 CrossRef CAS PubMed
.
- D. Hollas, E. Muchová and P. Slavíček, J. Chem. Theory Comput., 2016, 12, 5009–5017 CrossRef CAS PubMed
.
- J. van Rijssel, M. van der Linden, J. D. Meeldijk, R. J. A. van Dijk-Moes, A. P. Philipse and B. H. Erné, Phys. Rev. Lett., 2013, 111, 108302 CrossRef
.
- I. Jordan, A. Beloqui Redondo, M. A. Brown, D. Fodor, M. Staniuk, A. Kleibert, H. J. Wörner, J. B. Giorgi and J. A. van Bokhoven, Chem. Commun., 2014, 50, 4242–4244 RSC
.
- D. M. Sherman, Geochim. Cosmochim. Acta, 2005, 69, 3249–3255 CrossRef CAS
.
- S.-Y. Chen, A. Gloter, A. Zobelli, L. Wang, C.-H. Chen and C. Colliex, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 104103 CrossRef
.
- R. Golnak, S. I. Bokarev, R. Seidel, J. Xiao, G. Grell, K. Atak, I. Unger, S. Thürmer, S. G. Aziz, O. Kühn, B. Winter and E. F. Aziz, Sci. Rep., 2016, 6, 24659 CrossRef CAS
.
- S. A. Chambers, T. Droubay, T. C. Kaspar and M. Gutowski, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct., 2004, 22, 2205 CrossRef CAS
.
- M. Kosmulski, J. Colloid Interface Sci., 2002, 253, 77–87 CrossRef CAS PubMed
.
- M. Kosmulski, J. Colloid Interface Sci., 2004, 275, 214–224 CrossRef CAS PubMed
.
- M. Kosmulski, J. Colloid Interface Sci., 2006, 298, 730–741 CrossRef CAS PubMed
.
- K. R. Wilson, B. S. Rude, J. Smith, C. Cappa, D. T. Co, R. D. Schaller, M. Larsson, T. Catalano and R. J. Saykally, Rev. Sci. Instrum., 2004, 75, 725–736 CrossRef CAS
.
- Y. Wang and N. Herron, J. Phys. Chem., 1991, 95, 525–532 CrossRef CAS
.
-
S. R. Morrison, Electrochemistry at Semiconductor and Oxidized Metal Electrodes, Plenum Press, New York, NY, USA, 1980 Search PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: X-ray diffraction patterns, XPS survey, photon flux effect and secondary electron energy distribution curves. See DOI: 10.1039/d1na00275a |
| ‡ These authors contributed equally to this work. |
| § Current address: European Research Council Executive Agency, Place Rogier 16, 1210, Brussels, Belgium. The views expressed are purely those of the writer and may not in any circumstances be regarded as stating an official position of the European Commission. |
| This journal is © The Royal Society of Chemistry 2021 |