Open Access Article
Open Access ArticleElectron transport properties of PAl12-based cluster complexes†
John
Shen
a,
Haiying
He
 *a,
Turbasu
Sengupta
*a,
Turbasu
Sengupta
 b,
Dinesh
Bista
b,
Dinesh
Bista
 b,
Arthur C.
Reber
b,
Arthur C.
Reber
 b,
Ravindra
Pandey
b,
Ravindra
Pandey
 c and
Shiv N.
Khanna
c and
Shiv N.
Khanna
 *b
*b
aDepartment of Physics and Astronomy, Valparaiso University, Valparaiso, Indiana 46383, USA. E-mail: haiying.he@valpo.edu
bDepartment of Physics, Virginia Commonwealth University, Richmond, Virginia 23284, USA. E-mail: Snkhanna@vcu.edu
cDepartment of Physics, Michigan Technological University, Houghton, Michigan 49931, USA
First published on 13th September 2021
Abstract
The electronic transport properties of PAl12-based cluster complexes are investigated by density functional theory (DFT) in combination with the non-equilibrium Green's function (NEGF) method. Joining two PAl12 clusters via a germanium linker creates a stable semiconducting complex with a large HOMO–LUMO gap. Sequential attachment of an electron-donating ligand, N-ethyl-2-pyrrolidone, to one of the two linked clusters results in the shifting of the electronic spectrum of the ligated cluster while the energy levels of the unligated cluster are mostly unchanged. Using this approach, one can eventually align the HOMO of the ligated cluster to the LUMO of the non-ligated cluster, thereby significantly reducing the HOMO–LUMO gap of the complex. As a result, the transport properties of the complex are highly dependent on the number of attached ligands. Although a single ligand is observed to generally decrease the current, the inclusion of two or more ligands shows a significant increase in the amount of current at most voltages. The resulting increase of the current can be attributed to two factors, first the reduction in the HOMO–LUMO gap due to ligand attachment which has moved the transmission orbitals into the bias window. Secondly, when two or more ligands are attached to the complex, the HOMOs become delocalized across the scattering region, and this significantly enhances the currents.
1. Introduction
In the current era of information technology, fabrication and modification of nanoscale devices have taken center stage. Modern electronic devices are composed of multiple complex components like diodes, transistors, sensors, and switches.1 Reducing their sizes to the microscopic level unfolds the possibility of creating compact nanoscopic devices with enhanced functionalities.1,2 Thus, in the past few decades, scientists have searched for a way to rationally design molecules that can be utilized as the crucial components in electronic devices.3,4 The possible existence of such systems was originally predicted by Aviram and Ratner,5 who have shown that a unimolecular rectifier can be constructed by combining donor and acceptor moiety via an insulating linker. This theoretical prediction eventually paved the way for the intriguing field of molecular electronics.3,4,6 To construct such devices, it is important to understand how a particular molecule behaves when it is placed in an electric field.2 In other words, one needs to rationalize the quantum transport properties of the respective molecule by placing it between two electrodes in a break junction experiment. The response of a molecule in an electric field depends on various factors. For example, a molecule can have multiple contact points and can orient itself in many different ways. The transport properties are also dependent on the length of the molecule and how far they are placed from the electrodes. Exploring all such possibilities by experimental means is often difficult. Thus, computational modeling of quantum transport has become an essential tool for determining the applicability of a single molecular junction. Moreover, conventional single molecular junction also suffers from some significant limitations such as low-temperature dependence and coherent tunneling.7 As Moore's law is faltering,8 scientists are now trying to use different components to increase the computer's computing power, like using carbon nanotubes, nanoclusters, or quantum transistors. Recent researches have shown promising transport results for metal9,10 and metal chalcogenide7,11 clusters. It was also noticed that by using such nanoclusters for charge transport, one could circumvent the limitations of common organic or organometallic molecules.7 In the spirit of this, semiconducting cluster complexes constituted of atomic clusters and choices of ligands are proposed to mimic the functions of transistors to achieve the goal of increasing computing power.In our recent work,12 we have shown that such a semiconducting cluster complex can be composed by joining two open-shell PAl12 clusters utilizing an organometallic linker. It is well known that the electronic structure of metallic clusters can be modeled as a confined nearly free electron gas against a uniform positively charged background.13,14 Solving the Schrödinger equation15,16 based on such approximation yields superatomic shells for the whole system similar to the atomic orbitals. Considering the model, the valence electron count of the PAl12 cluster is 41, which results in a superatomic configuration17–19 of 1S2, 1P6, 1D10, 2S2, 1F14, 2P6, 1G1. Joining two such clusters via an organometallic linker, e.g., –CH2CH3GeCH3CH2–, generates a semiconducting cluster complex in which both the PAl12 clusters are closed-shell (40 e) due to the sharing of the unpaired electron with the linker. As a result, the resulting cluster complex (PAl12–CH2CH3GeCH3CH2–PAl12) is marked by a significantly large HOMO–LUMO gap.12 It is also shown that by attaching a donor ligand like N-ethyl-2-pyrrolidone (C6H11NO, abbreviated as EP) on one of the PAl12 clusters, one can alter the position of the frontier orbitals of one side without perturbing the electronic shell structure of the monomers. Upon addition of multiple ligands, the HOMO of the ligated cluster can eventually be aligned to the LUMO of the non-ligated cluster, mimicking a broken gap energy alignment.12 The direction of the dipole moment is also observed to be dependent on the location of the attached EP ligand. In addition, such asymmetrically ligated superatomic dimers show prominent indications of electron–hole separation, which can have useful applications in photovoltaics.12,20 Therefore, the quantum transport properties of such a system will be interesting. In this paper, we focus on the recently proposed PAl12-based cluster complexes and investigating their electron transport properties in a two-terminal device configuration. Moreover, the role of ligands in determining the electron transport properties of such cluster-based devices is investigated employing density functional theory (DFT) together with the non-equilibrium Green's function21–23 (NEGF) method.
2. Methods
The DFT calculations of the PAl12 and the bridged clusters are performed using the Amsterdam Density Functional (ADF) suite of codes.24 The generalized gradient approximation (GGA) based exchange–correlation functional of Perdew, Burke, and Ernzerhof's25 (PBE) were used for the optimizations and single point calculations. The Slater type TZ2P basis set26 (triple-ζ basis set with two polarization functions) with a large frozen core is used for all the elements. Calculation of basis set superposition error (BSSE) for a few selected systems (see Fig. S1 in the ESI†) was observed to be quite small and hence not considered for the present study. The optimizations were carried out by using the hessian-based quasi-Newton method27 without any symmetry restrictions as implemented in ADF.24 During optimizations, a wide range of spin multiplicities was investigated for each structure, and the lowest energy conformer was selected in all cases. The electronic convergence threshold was set to 10−8 Hartree, whereas the default optimization criteria24 was used for all systems. The scalar relativistic correction was incorporated by using the zeroth-order regular approximation (ZORA).28For the transport calculations, the central scattering region was described in the DFT framework with the PBE exchange–correlation functional25 and the double-zeta with polarization (DZP) basis sets.29,30 For Au atoms, the core electrons were described by the norm-conserving pseudopotential,31,32 and the 5d106s1 valence electrons were described by a DZP basis set. Structures of the cluster complexes with and without ligands are fully optimized, with all atoms being allowed to relax. Calculations were considered to be converged when the force on each ion is less than 0.01 eV Å−1 with convergence in the RMS density matrix to 10−8 and the total energy to 10−5 eV.
The bias-dependent electron transmission and current were calculated using the NEGF method as implemented in the TranSIESTA module21,22 of the SIESTA program.23 The PAl12–Ge–PAl12 cluster complex was oriented parallel to the electrode Au nanowire (see Fig. S2 for Au structure in the ESI†), and the distance between the electrodes (the two upmost Au atoms) was kept fixed at 24.1 Å to simulate a fixed break junction setup. As the number of ligands changes, the connecting Al–Au distance varies a bit due to the actual change in the length of the cluster complex (see Fig. S3 in the ESI†). The direction of a finite bias potential V was set up to have a lower potential (−V/2) at the left electrode and a higher potential (V/2) at the right electrode. We considered Γ-point for the scattering region and a mesh of (1 × 1 × 100) k-points for the contacts. The charge density was obtained by integrating Green's function over 200 imaginary and 1000 real energy points, giving rise to less than 0.03% deviation in the total charge of the system.
The total tunneling current of the system under a bias of V can be written as
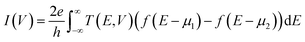 | (1) |
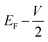 and
and 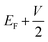 , respectively; f(E) is the Fermi–Dirac distribution function, and EF is the Fermi level for such an open and non-equilibrium system, which is treated self-consistently. T(E, V) is the electron transmission function, which varies with both the energy E and the bias V. We have set the temperature to 300 K for transmission and current calculations.
, respectively; f(E) is the Fermi–Dirac distribution function, and EF is the Fermi level for such an open and non-equilibrium system, which is treated self-consistently. T(E, V) is the electron transmission function, which varies with both the energy E and the bias V. We have set the temperature to 300 K for transmission and current calculations.
3. Results and discussion
3.1. The electronic structure of the PAl12 cluster complexes
To construct the cluster-based semiconducting complex, we have chosen the PAl12 cluster as the primary component. Since aluminum is trivalent, the valence electron count of the icosahedral Al13 cluster is 39. This results in a superatomic electronic configuration of 1S2, 1P6, 1D10, 2S2, 1F14, 2P5, which is similar to a halogen atom. Replacing the core Al atom with pentavalent phosphorus alters the configuration to 1S2, 1P6, 1D10, 2S2, 1F14, 2P6, 1G1 (41 e). Consequently, the PAl12 cluster behaves like an alkali superatom. Such an open-shell system with a single electron in the outer shell act as an effective donor with very low ionization energy. As an insulator linker, we have chosen –CH2CH3GeCH3CH2– (denoted as GeB), a derivative of tetramethylgermanium (TMG, (CH3)4Ge), in which one hydrogen atom is removed from two of the methyl groups to allow bonding with both clusters. Attaching two PAl12 clusters via GeB allowed us to create a stable semiconducting cluster complex (PAl12[GeB]PAl12, denoted hereby as EP0) with a large HOMO–LUMO gap of 1.53 eV. Our investigation showed that during the formation of the polar covalent C–Al σ-bond, each of the PAl12 clusters shares its outer shell electron with the linker. Thus, in the cluster complex, each of the component clusters has a 40 electronic closed-shell configuration, which is the reasoning behind the observed high HOMO–LUMO gap. Important to note that the icosahedral shape of each PAl12 cluster has also remained intact during the formation of the cluster complex. The optimized structure of PAl12[GeB]PAl12 is shown in Fig. 1a with a few important bond distances (in Å). The adiabatic ionization energy (AIE) and adiabatic electron affinity (AEA) of PAl12[GeB]PAl12 are calculated as 5.66 and 2.16 eV, respectively. Due to the sharing of electrons with the linker, each PAl12 cluster is observed to be positively charged (Hirshfeld33 Charge: +0.18), whereas the GeB holds a negative Hirshfeld33 charge of −0.36 to maintain the overall charge neutrality.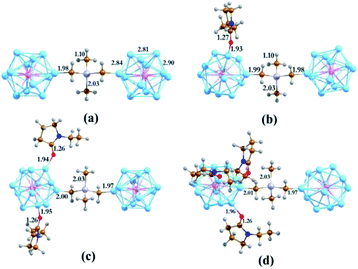 | ||
| Fig. 1 The optimized ground state structures of (EP)nPAl12[GeB]PAl12 (n = 0–3 for (a–d) respectively). Bond distances are in Å. | ||
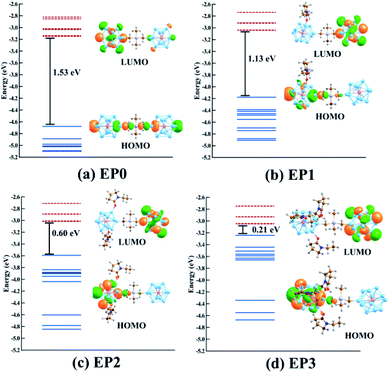
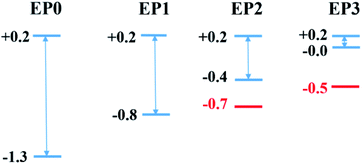
As shown in our earlier work,12,20,34,35 the inclusion of an electron donor or acceptor ligands to a cluster creates a coulomb well surrounding the metallic core, which shifts the whole electronic spectrum of the cluster upward or downward depending on the nature of the attached ligands. Using this strategy, one can create superatoms with very low ionization energy or high electron affinity, as desired, just by altering the nature and number of ligands attached to the cluster. In this work, we have investigated how the transport property of the superatomic cluster complex can be controlled by the addition of such ligands. To achieve this, we have chosen the N-ethyl-2-pyrrolidone (EP) ligand, which acts as an effective donor when attached to a metallic cluster by the O atom. To investigate the effect of the EP ligand on the electronic structure of the PAl12 cluster complex, we have modeled the ligated complexes in which one to three EP ligands (denoted as EP1, EP2, and EP3, respectively) are sequentially attached to one of the PAl12 clusters, keeping the second cluster on the other side non-ligated. During the optimizations, we have explored all the possible Al sites for the EP ligand attachment, and only the global minima are considered herewith (see Fig. S4 in the ESI†). The ground state spin multiplicities (singlet) are also ascertained similarly. The optimized structures of (EP)nPAl12[GeB]PAl12 (n = 1–3) are shown in Fig. 2b–d. The binding energies of the EP ligand are observed to decrease as additional ligands are added. Thus, the binding energy values of 0.91, 0.79, 0.56 eV are calculated for first, second, and third EP ligands, respectively. The binding energy decreases because adding charge donating ligands means that additional ligands will bind more weakly. As the number of EP ligands is increased, the net Hirshfeld charge33 on the ligated cluster shows a monotonic increase starting from +0.18 for the non-ligated to +0.23, +0.26, and +0.29 for the single, double, and triply ligated (EP)nPAl12[GeB]PAl12 complexes, respectively.
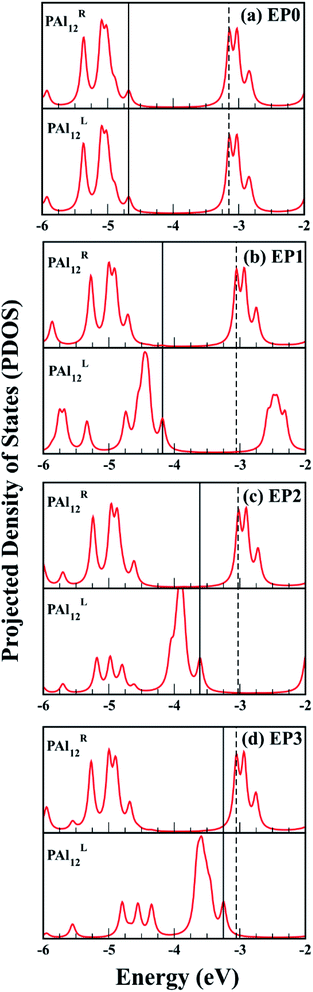
The major effect of attaching EP ligands to the cluster complex is observed in the molecular orbital (MO) diagram, as shown in Fig. 2. As the number of ligands is increased, the HOMO of the complex is observed to shift to higher energy keeping the LUMO nearly at the same position. This results in a decrease in the overall HOMO–LUMO gap of the complex as more numbers of ligands are attached. The HOMO–LUMO gap for the EP1, EP2, and EP3 are calculated as 1.14, 0.60, and 0.21, respectively. To investigate the reason for this decrease in the gap, we have plotted the projected density of states (PDOS) of both clusters separately (Fig. 3). It is evident from the PDOS plot that the EP ligands are shifting the whole electronic spectrum, including the frontier orbitals of the ligated PAl12 cluster (marked as left or ‘L’ in Fig. 3). In contrast, the electronic spectrum of the non-ligated (marked as right or ‘R’ in Fig. 3) site remain mostly unperturbed. As a result, in the (EP)nPAl12[GeB]PAl12 cluster complexes, the HOMO of the structure is originating from the ligated site, whereas the LUMO of the non-ligated site is acting as the effective LUMO of the wire. The representative isosurfaces of HOMO and LUMO (Fig. 2) also show the same. Thus, as the EP ligands are successively introduced, the HOMO–LUMO gap is observed to decrease. Important to note that the individual cluster on each side maintains a high HOMO–LUMO gap irrespective of the number of the ligands attached. The increase of the HOMO energy also led to a monotonic change in the AIE values, which decreases from 5.21 eV to 4.19 eV upon altering the numbers of the attached ligand from one to three.
3.2. Calculation of the transport properties of PAl12-based cluster complexes
In calculations of the quantum transport of electrons, the (EP)nPAl12[GeB]PAl12 cluster complex is sandwiched between two Au electrodes. The central scattering region of such a device is shown in Fig. 4, which includes the (EP)nPAl12[GeB]PAl12 complex and a sufficient number of Au sublayers to ensure electrostatic screening at the boundary. The Au electrode was modeled by a semi-infinite Au nanowire with alternating planes of three and seven gold atoms (Fig. S2 in the ESI†) which were previously considered as viable Au contacts in a device configuration.36,37 The Au–Au distance in the sublayers was taken to be that in bulk. At the interface, a protruding Au atom as part of an Au pyramid belonging to the electrode connects with a cluster Al atom with the Al–Au distance ≥3.5 Å. This simulation setup represents a weak-coupling regime in which the complex and the electrode are sufficiently apart such that the interfacial states arising from the direct contact and hybridization of the complex and electrode orbitals are eliminated.38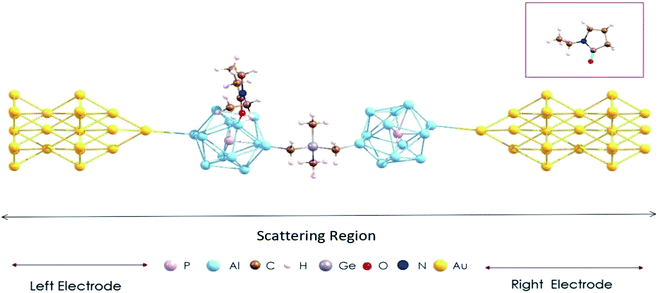 | ||
| Fig. 4 The device configuration consisting of the Au contact and PAl12[GeB]PAl12 cluster complex with one ligand. A ball and stick structure of the ligand, C6H11NO is given in the inset. | ||
The calculated current–voltage (I–V) characteristics of the (EP)nPAl12[GeB]PAl12 cluster complexes with (n = 1–3) and without (n = 0) ligands are shown in Fig. 5. In the ligand-free complex (EP0), the tunneling current appears to increase linearly from the onset voltage for the current rise of 0.3 V to 0.6 V. It decreases slightly up to 0.8 V and then shows a non-linear increase up to 1.0 V. We note that the applied voltage of about 1 V corresponds to the electric field strength of about 108 V m−1.
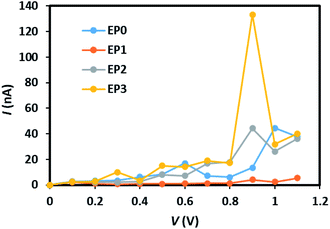 | ||
| Fig. 5 Current–voltage characteristics of the (EP)nPAl12[GeB]PAl12 (n = 0–3) cluster complexes, labeled as EP0, EP1, EP2, and EP3. | ||
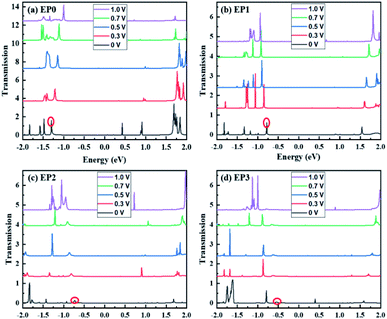
An attachment of a ligand to the complex (EP1) leads to quenching of the tunneling current within the bias region of 0–1 V. Interestingly, the subsequent addition of ligands to the complex (Fig. S3 in the ESI†) leads to an increase in the tunneling current with the reduced value of the onset voltage for the current rise. The peak tunneling current appears to be associated with the bias voltage of 0.9 V, and the peak current associated with the complex with three ligands (EP3) is significantly higher than that associated with the complex with two ligands (EP2). The predicted variation in current with the number of ligands attached to the complex can be understood from an analysis of the transmission function, which, in general, reflects the intrinsic transport characteristics of the system.
The calculated transmission functions are shown in Fig. 6. Since the current is obtained by integrating the transmission function within the bias voltage window, we find distinct differences in transmission functions in going from zero to three ligands attached to the cluster complexes. For all cases, we find that the transmission peaks above the Fermi level barely contribute to the tunneling current passing through the complex. Below the Fermi level (E < EF), the peaks show the different shapes and shift to higher or lower energies, depending upon the number of ligands attached to the complex. For example, the first transmission peak (red-circled) associated with the cases of EP0 and EP1 is narrow in shape and large in magnitude, while those associated with EP2 and EP3 cases are diffuse in shape and small in peak magnitude. Furthermore, with the increase in the bias, the first transmission peak for EP0 shifts towards EF, while that for EP1, EP2, or EP3 shifts away from EF. The energy shifting direction depends on the nature of the transmission orbitals in response to an external electric field due to the applied bias.39,40 This is further explored below.
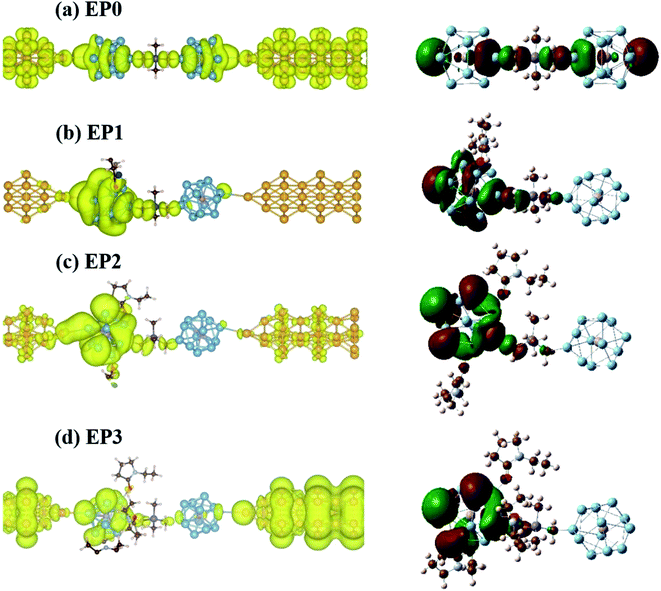
Next, we find a general correspondence between the transmission function and the projected density of states (PDOS) of the complex shown in Fig. S5 (ESI†), in which the first significant transmission peak/orbital below EF corresponds to a state at or close to the top edge of the valence band of the extended system with significant contribution from Al and some contribution from C. We, therefore, expect that a close examination of the nature of these states can provide an understanding of ligand effects on the I–V characteristics of the (EP)nPAl12[GeB]PAl12 complex. Fig. 7 displays the charge density plots of the PDOS peak at or close to the top edge of the valence band in comparison to the associated HOMO plots of the isolated cluster complexes with zero, one, two, and three ligands. They have good correspondence for all the cases. The HOMOs associated with the first transmission peaks below the Fermi level for the cases with ligands (EP1, EP2, and EP3) are on the side of the ligated clusters. An intrinsic dipole moment is produced with a non-zero component parallel to the direction of the external bias of such an asymmetric molecular complex. Under the forward bias, the HOMO shifts to lower energy and so does the transmission peak. In contrast, for the symmetric molecular complex EP0, the HOMO symmetrically expands to both clusters and its shift under bias is the same for both forward and backward biases.
We find that resonant tunneling through the scattering region occurs in the case of the complex without ligands (EP0). Interestingly, the addition of a ligand (EP1) greatly localizes the charge density onto the ligated PAl12 cluster, thereby narrowing the transmission peak and reducing the transmission, and hence the current at a given bias. The increase in the Al (cluster)-to-Au (electrode) distance due to the shrinkage of the complex upon interacting with one EP ligand (highly asymmetrically positioned) has also contributed to this current reduction. This, however, is to less extent compared to the effect of the attached ligand (see Fig. S6 in the ESI† for a comparison of currents at the same Al–Au distance). The addition of another ligand (EP2) to the complex results in a more delocalized distribution of charge density which broadens the transmission peak. Finally, the complex with three ligands (EP3) yields a larger degree of delocalization in the charge density giving rise to a higher current at a given bias.
To decouple the effects of the HOMO–LUMO gap of the complex and the electrode-cluster distance, we have done a series of transport calculations for EP1 with the Al–Au nearest distance ranging from 3.1 to 4.1 Å (see Fig. S7a and b in the ESI† for transmission functions). It is shown that there are no additional transmission peaks until the distance is reduced to 3.3 Å when the interface hybrid states start to form. In addition, the shape of the first transmission peak below EF remains the same, while only its position shifts. This suggests that the nature of this transmission orbital does not change. Since this transmission peak is well beyond the integration voltage window for the current calculation at low biases as considered here (V ≤1.0 V), the probability of electron transmission is governed by quantum tunnelling, which is evidenced by the exponential decay as a function of the electrode-cluster distance as shown in Fig. S7c.†
Finally, we relate the transmission peaks and HOMOs to show that the substantial reduction in the HOMO–LUMO gap (see also Fig. 2) for the case of the cluster complex with three ligands primarily contributes to the enhanced current at a given bias. Fig. 8 displays the energy levels obtained from the cluster calculations correlating the location of DOS or transmission peaks. We find that the HOMO–LUMO gap depends on the number of ligands and reduces to a small value (∼0.2 eV) for the case of the complex with three ligands. It is interesting to note that the LUMO level remains the same as we increase the number of ligands, and the HOMO–LUMO gap reduces due to upward shifts in the HOMO level. This is because the LUMO contribution comes from the PAl12 metal cluster on the side with no ligand, while the HOMO is ascribed to the PAl12 metal cluster on the side with added ligands. These ligands effectively shift the eigenvalue of the HOMO upward, narrowing down the HOMO–LUMO gap.
The location of the first transmission orbital below EF is at the location of HOMO for 0-ligand (EP0) and 1-ligand (EP1) cases. The presence of contact Au atoms barely changes the relative energies of these states. However, the first transmission orbital location shifts down by 0.3 eV and 0.5 eV for the 2-ligand (EP2) and 3-ligand (EP3) cases, respectively, as shown in Fig. 8. As previously shown in Fig. 7, extended electronic states are formed in these cases. These states largely mimic those of the HOMOs of the complexes with ligands with a small extension of wavefunctions onto the Au atoms, resulting in lower eigenvalue energies. This shift makes the corresponding transmission peak further away from the Fermi level, thereby reduces its contribution to the current at low voltages. Therefore, overall speaking, the closing HOMO–LUMO gap in the complex due to the addition of ligands does not bring a directly proportional increase in the current. Nevertheless, EP2 and EP3 still show a peaking of current at a lower bias than EP0 and EP1, with EP3 has a significantly higher current (Fig. 5).
4. Conclusions
In molecular electronics, the flexibility of tuning electronic energy levels via molecular engineering opens a new horizon in designing controllable electronic devices. In this study, we have shown that the addition of EP ligands onto a PAl12[GeB]PAl12 complex can consistently lower the HOMO–LUMO gap of the system. Also, adding EP ligands on one side breaks the symmetry of the (EP)nPAl12[GeB]PAl12 complex causing the frontier molecular orbitals to be localized. These changes in the electronic structure have profound effects on the electron transport properties of the cluster complexes. The ligand is shown to be a useful handle to vary the current through the complex. By and large, the addition of EP ligands shifts the HOMOs up while leaving the location of LUMOs almost intact. The more EP ligands are added onto the complex, the closer the HOMO is to the Fermi level closing up the energy gap. The addition of one EP ligand is, however, not sufficient to have an impact on the current in the range of 0 to 1.1 V. The current turns out to be even smaller than the current for the ligand-free case because the HOMO of the complex is far below the Fermi level and it is strongly localized on the PAl12 cluster accepting the ligand. When the number of added ligands increases to 2 and 3, the currents are shown to be higher than the case without ligand at most voltages and peak at ∼0.9 V. This means that the reduction in the HOMO–LUMO gap has moved the transmission orbitals into the bias window and contributed to the surge in current at 0.9 V, especially for EP3. It is notable that when the complexes with two and three ligands are sandwiched between two Au electrodes, the HOMOs become extended states across the scattering region and contribute significantly to the transmission functions, thereby the currents. These energy levels are, however, greatly pushed down (farther away from EF) compared to the location of HOMOs in the isolated cluster complexes.In general, such principles can be applied to the purpose-driven design of devices in molecular electronics and nanoelectronics. Our proof-of-concept study has demonstrated that one can effectively alter the HOMO–LUMO gap and related transport properties of the bridged PAl12 dimer via sequential attachment of a donor ligand (e.g., EP) to one cluster. It is notable that when the system size gets to the nanometer and subnanometer scale, the behavior deviates from a monotonic variation. This is because electron transport properties in the quantum regime depend on several factors: the nature and location of molecular orbitals, the coupling to the electrodes, and the delocalization of the resultant transmission orbital. The interplay of all these factors may change the magnitude of current in a non-monotonic way. This type of complicated behavior is predictable using electronic structure and quantum transport computational tools.
Conflicts of interest
The authors declare no competing interests.Acknowledgements
This research was supported by the US Air Force Office of Scientific Research (AFOSR), Grant No. FA 9550-18-1-0511. JS acknowledges financial support from Michigan Technological University (MTU). JS, HH, and RP acknowledge the use of Superior, a high-performance computing cluster at MTU.References
- P. Gehring, J. M. Thijssen and H. S. van der Zant, Single-Molecule Quantum-Transport Phenomena in Break Junctions, Nat. Rev. Phys., 2019, 1(6), 381–396 CrossRef.
- Y. Komoto, S. Fujii, M. Iwane and M. Kiguchi, Single-Molecule Junctions for Molecular Electronics, J. Mater. Chem. C, 2016, 4(38), 8842–8858 RSC.
- M. Ratner, A Brief History of Molecular Electronics, Nat. Nanotechnol., 2013, 8(6), 378–381 CrossRef CAS PubMed.
- E. Scheer and J. C. Cuevas, Molecular Electronics: an Introduction to Theory and Experiment, World Scientific, 2017, vol. 15 Search PubMed.
- A. Aviram and M. A. Ratner, Molecular Rectifiers, Chem. Phys. Lett., 1974, 29(2), 277–283 CrossRef CAS.
- G. Cuniberti, G. Fagas and K. Richter, Introducing Molecular Electronics: A Brief Overview, Introd. Mol. Electron., 2006, 1–10 Search PubMed.
- S. Gunasekaran, D. A. Reed, D. W. Paley, A. K. Bartholomew, L. Venkataraman, M. L. Steigerwald, X. Roy and C. Nuckolls, Single-Electron Currents in Designer Single-Cluster Devices, J. Am. Chem. Soc., 2020, 142(35), 14924–14932 CrossRef CAS PubMed.
- M. M. Waldrop, The Chips Are down for Moore's Law, Nature, 2016, 530(7589), 144 CrossRef CAS PubMed.
- L. A. Zotti, E. Leary, M. Soriano, J. C. Cuevas and J. J. Palacios, A Molecular Platinum Cluster Junction: A Single-Molecule Switch, J. Am. Chem. Soc., 2013, 135(6), 2052–2055 CrossRef CAS PubMed.
- D. I. Gittins, D. Bethell, D. J. Schiffrin and R. J. Nichols, A Nanometre-Scale Electronic Switch Consisting of a Metal Cluster and Redox-Addressable Groups, Nature, 2000, 408(6808), 67–69 CrossRef CAS PubMed.
- B. M. Boardman, J. R. Widawsky, Y. S. Park, C. L. Schenck, L. Venkataraman, M. L. Steigerwald and C. Nuckolls, Conductance of Single Cobalt Chalcogenide Cluster Junctions, J. Am. Chem. Soc., 2011, 133(22), 8455–8457 CrossRef CAS PubMed.
- D. Bista, V. Chauhan, T. Sengupta, A. C. Reber and S. N. Khanna, A Ligand-Induced Homojunction between Aluminum-Based Superatomic Clusters, Nanoscale, 2020, 12, 12046–12056 RSC.
- W. D. Knight, K. Clemenger, W. A. de Heer, W. A. Saunders, M. Y. Chou and M. L. Cohen, Electronic Shell Structure and Abundances of Sodium Clusters, Phys. Rev. Lett., 1984, 52(24), 2141 CrossRef CAS.
- W. D. Knight, W. A. de Heer, K. Clemenger and W. A. Saunders, Electronic Shell Structure in Potassium Clusters, Solid State Commun., 1985, 53(5), 445–446 CrossRef CAS.
- E. Schrödinger, An Undulatory Theory of the Mechanics of Atoms and Molecules, Phys. Rev., 1926, 28(6), 1049 CrossRef.
- D. J. Griffiths and D. F. Schroeter, Introduction to Quantum Mechanics, Cambridge University Press, 2018 Search PubMed.
- S. N. Khanna and P. Jena, Atomic Clusters: Building Blocks for a Class of Solids, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51(19), 13705 CrossRef CAS PubMed.
- A. C. Reber and S. N. Khanna, Superatoms: Electronic and Geometric Effects on Reactivity, Acc. Chem. Res., 2017, 50(2), 255–263 CrossRef CAS PubMed.
- D. E. Bergeron, A. W. Castleman, T. Morisato and S. N. Khanna, Formation of Al13I-: Evidence for the Superhalogen Character of Al13, Science, 2004, 304(5667), 84–87 CrossRef CAS PubMed.
- A. C. Reber, V. Chauhan, D. Bista and S. N. Khanna, Superatomic Molecules with Internal Electric Fields for Light Harvesting, Nanoscale, 2020, 12(7), 4736–4742 RSC.
- M. Brandbyge, J.-L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Density-Functional Method for Nonequilibrium Electron Transport, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65(16), 165401 CrossRef.
- K. Stokbro, J. Taylor, M. Brandbyge and P. Ordejon, TranSIESTA: A Spice for Molecular Electronics, Ann. N. Y. Acad. Sci., 2003, 1006(1), 212–226 CrossRef CAS PubMed.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, The SIESTA Method for Ab Initio Order-N Materials Simulation, J. Phys.: Condens. Matter, 2002, 14(11), 2745 CrossRef CAS.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22(9), 931–967, DOI:10.1002/jcc.1056.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- E. Van Lenthe and E. J. Baerends, Optimized Slater-Type Basis Sets for the Elements 1–118, J. Comput. Chem., 2003, 24(9), 1142–1156 CrossRef CAS PubMed.
- L. Fan and T. Ziegler, Optimization of Molecular Structures by Self-Consistent and Nonlocal Density-Functional Theory, J. Chem. Phys., 1991, 95(10), 7401–7408 CrossRef CAS.
- E. van Lenthe, J. G. Snijders and E. J. Baerends, The Zero-order Regular Approximation for Relativistic Effects: The Effect of Spin–Orbit Coupling in Closed Shell Molecules, J. Chem. Phys., 1996, 105(15), 6505–6516, DOI:10.1063/1.472460.
- J. Junquera, Ó. Paz, D. Sánchez-Portal and E. Artacho, Numerical Atomic Orbitals for Linear-Scaling Calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64(23), 235111 CrossRef.
- E. Anglada, J. M. Soler, J. Junquera and E. Artacho, Systematic Generation of Finite-Range Atomic Basis Sets for Linear-Scaling Calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(20), 205101 CrossRef.
- P. Rivero, V. M. García-Suárez, D. Pereñiguez, K. Utt, Y. Yang, L. Bellaiche, K. Park, J. Ferrer and S. Barraza-Lopez, Systematic Pseudopotentials from Reference Eigenvalue Sets for DFT Calculations, Comput. Mater. Sci., 2015, 98, 372–389 CrossRef CAS.
- P. Rivero, V. M. García-Suárez, D. Pereñiguez, K. Utt, Y. Yang, L. Bellaiche, K. Park, J. Ferrer and S. Barraza-Lopez, Systematic Pseudopotentials from Reference Eigenvalue Sets for DFT Calculations: Pseudopotential Files, Data Brief, 2015, 3, 21–23 CrossRef PubMed.
- F. L. Hirshfeld, Bonded-Atom Fragments for Describing Molecular Charge Densities, Theor. Chim. Acta, 1977, 44(2), 129–138 CrossRef CAS.
- V. Chauhan, A. C. Reber and S. N. Khanna, Metal Chalcogenide Clusters with Closed Electronic Shells and the Electronic Properties of Alkalis and Halogens, J. Am. Chem. Soc., 2017, 139(5), 1871–1877 CrossRef CAS PubMed.
- V. Chauhan, A. C. Reber and S. N. Khanna, Strong Lowering of Ionization Energy of Metallic Clusters by Organic Ligands without Changing Shell Filling, Nat. Commun., 2018, 9(1), 1–7 CrossRef CAS PubMed.
- P. S. Krstić, X.-G. Zhang and W. H. Butler, Generalized Conductance Formula for the Multiband Tight-Binding Model, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(20), 205319 CrossRef.
- S. Hedström, A. J. Matula and V. S. Batista, Charge Transport and Rectification in Donor–Acceptor Dyads, J. Phys. Chem. C, 2017, 121(35), 19053–19062 CrossRef.
- X. Zhong, R. G. Amorim, A. R. Rocha and R. Pandey, Hybridization Effects on the Out-of-Plane Electron Tunneling Properties of Monolayers: Is h-BN More Conductive than Graphene?, Nanotechnology, 2014, 25(34), 345703 CrossRef PubMed.
- H. He, R. Pandey, G. Mallick and S. P. Karna, Asymmetric Currents in a Donor-Bridge-Acceptor Single Molecule: Revisit of the Aviram-Ratner Diode, J. Phys. Chem. C, 2009, 113, 1575–1579 CrossRef CAS.
- H. He, R. Pandey, G. Mallick and S. P. Karna, Electronic Conduction in a Model Three-Terminal Molecular Transistor, Nanotechnology, 2008, 19, 505203 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1na00355k |
| This journal is © The Royal Society of Chemistry 2021 |