Electrical response of organic molecule supported preformed and in situ formed antimony sulfide nanoparticles under frequency conditions

Abstract

A complexation route mediated synthesis of orthorhombic antimony sulfide nanoparticles is described in this report where uniformly distributed particles within the size range of 2–12 nm are stabilized within the aniline matrix. The organic–inorganic hybrid system was investigated for dielectric capacitance and electric field-induced polarization performances under varying temperature and frequency conditions. The AC-conductivity revealed a correlated barrier hopping conduction mechanism in the hybrid system. A fatigue free polarization was achieved under the electric field of 9 kV mm⁻¹ for the preformed antimony sulfide system with a stable value of 0.18 μC cm⁻². The in situ dielectric capacitance and field dependent polarization measurements were also performed for the in situ synthesized antimony sulfide using the antimony–aniline complex as the precursor.

---

1. Introduction

The organic–inorganic hybrid system has received extensive attention for a wide range of applications, such as energy storage, chemical sensors and catalysis.^1–3 The hybrid material represents the interface between two separate types of material that can demonstrate better properties compared with their individual components. The system acquires good stability and different physical properties from the inorganic counterpart and easy processing and flexibility from the organic counterpart.⁴

Among the various inorganic systems, metal oxides and sulfides are often reported for diverse applications. Several metal oxide nanomaterials exhibited outstanding physical, chemical and biological properties and play an important role in gas sensors, fuel cells, advanced ceramics, chemical sensors, biosensors, batteries, solar cells, pyroelectrics, supercapacitors, catalysts, and anticorrosion coating applications.⁵ In a similar way, nanostructured metal sulfides have been extensively studied and their potential applications have been reported in a variety of fields, such as solar cells, light-emitting diodes, sensors, thermoelectric devices, lithium-ion batteries, fuel cells and nonvolatile memory devices.^6–8 Some of the metallic sulfides, such as one dimensional zinc and cadmium sulfides have been reported for various optoelectronic applications, such as optical waveguides, field-effect transistors, lasers, solar cells, photodetectors, and light emitting diodes.^9,10 The magnetic susceptibility measurement of various phases of cobalt sulfides exhibited temperature-independent paramagnetism.¹¹ Gallium doped zinc sulfide nanomaterials have the potential to serve as photocatalysts for the degradation of organic pollutants in water.¹² It has been reported that nickel sulfide and copper sulfide nanowire arrays grown on a metal current collector substrate can function as a working cathode for lithium-ion batteries.^13,14 A copper sulfide embedded carbon nitride thin film based device exhibited nonvolatile resistive switching behaviour and the transport mechanism of the device was followed by Poole–Frenkel and ohmic behaviour for the OFF-state and ON-state, respectively, with an ON to OFF ratio of 10⁴.¹⁵

The sulfides of other non-transition elements, such as tin, lead and bismuth sulfides are well explored and exhibited good photocatalytic, photovoltaic and energy storage performances.^16–21 Apart from those, antimony sulfide has also received attention as a potential candidate for the anode material in sodium and lithium ion battery applications due to its high specific capacity value.^22–25 Antimony sulfide was reported as a Janus catalyst for the selective nitrogen reduction reaction²⁶ and also as a photovoltaic absorber material.²⁷ There are some reports also available in the literature where antimony based hybrid systems are employed for electronic applications. The antimony–phosphorus based field effect transistor has been reported for light detecting sensor application.²⁸ The effectiveness of solar cells has been improved for light induced electrical signals by using an antimony doped perovskite halide system.^29,30 Our recent studies also demonstrated the light sensitive resistive switching behaviour of antimony-sulfide based materials where the device exhibited unipolar and bipolar switching behaviour under two different optical conditions with a moderately high ON to OFF ratio.³¹

The dielectric capacitance and field induced polarization behaviour of antimony based materials either in the bulk or nano-form has been neglected in the literature. In this study, we report a complexation mediated synthesis of aniline stabilized antimony sulfide nanoparticles by applying a one pot, two step preparation protocol. The synthesis method involved the formation of the antimony(III)–aniline complex followed by the addition of sodium sulfide (sulphur source). The aniline molecule stabilized antimony sulfide, preformed antimony sulfide, was investigated for dielectric capacitance and field induced polarization performances under varying temperature and frequency conditions. The dielectric capacitance and polarization performances of the antimony–aniline complex during the addition of sodium sulfide (in situ formation of antimony sulfide) were also investigated.

2. Experimental

2.1 Materials

In this study, all chemical chemicals (SbCl₃, Na₂S and aniline) were purchased from Sigma-Aldrich and applied without further purification.

2.2 Synthesis of aniline stabilized antimony sulfide nanoparticles

For the synthesis of aniline stabilized antimony sulfide nanoparticles, 1.0 mL of aniline was diluted in 10 mL of methanol. To this methanolic solution, 0.456 g of SbCl₃ (dissolved in methanol with a concentration of 0.2 mol dm⁻³) was added and a white precipitate, antimony–aniline complex, was formed, immediately. A solution of sodium sulfide (0.047 g in 3.0 mL of distilled water) was added dropwise to the above precipitate and the colour of the precipitate turned orange. The orange coloured precipitate was filtered, and the solid mass was dried at 80 °C for 2 h under vacuum. The dried powder material (aniline stabilized antimony sulfide) was used for microscopy, surface and electrical characterization.

2.3 Device fabrication

Initially, a slurry, made with aniline stabilized antimony sulfide and chloroform (as a solvent), was deposited using a drop and dry method in the form of a film (∼100 μm) on a copper plate. The copper plate was dried on a hot plate for 30 minutes and then a gold electrode was printed on the top of the film using the physical vapour deposition technique (EMSCOPE SC 500).

2.4 Material characterization

Microscopy study was performed using a JEOL (JEM-2100) transmission electron microscope (TEM). The X-ray diffraction (XRD) pattern of the synthesized material was obtained using a Philips PANalytical X'pert diffractometer using Cu-Kα radiation. The dielectric constant, AC-conductivity and impedance spectra were measured with an HP 4284A LCR meter under varying temperature (from 30 to 70 °C) and frequency (from 100 Hz to 1 MHz) conditions. Polarization hysteresis studies were performed using a modified Sawyer–Tower circuit (PolyK Technologies), where the sample was subjected to a triangular wave with a varying frequency from 1–10 Hz.

3. Results and discussion

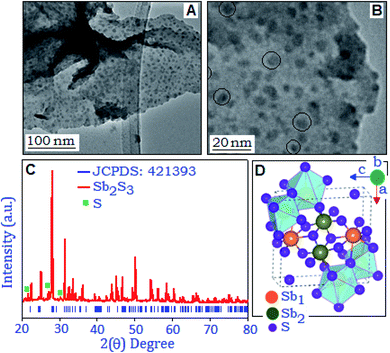
Fig. 1(A and B) show the transmission electron microscopy images of the synthesized product with different magnifications. The dark spots in the TEM images are antimony sulfide nanoparticles stabilized by the organic matrix. The uniformly distributed particles are within the size range of 2–12 nm and some of the individual nanoparticles are displayed within the circles (Fig. 1B). The X-ray diffraction pattern of the aniline stabilized antimony sulfide was recorded within the range (2θ) from 20° to 80°, Fig. 1C. From the figure it is evident that the major diffraction peaks are matched with the orthorhombic phase of Sb₂S₃, (JCPDS: 421393, space group: Pbnm) with lattice constant values of 11.23, 11.31 and 3.84 Å for a, b and c, respectively. Some low intensity diffraction peaks, positioned at 21.6°, 27.1° and 30.1°, correspond to the orthorhombic phase of sulphur (JCPDS: 740791), formed during the synthesis process. For the current system, the evidence of any secondary peak was not observed within the detection limit of the XRD spectra, suggesting that the final composition belongs to the Sb₂S₃. The sharp and well defined diffraction peaks revealed the crystalline nature of the synthesized material. Fig. 1D illustrates the unit cell representation of the layered structure of Sb₂S₃ which is projected perpendicular along the b-axis.³² In the structure, the cations Sb³⁺ are present at two different Wyckoff sites (Sb₁ and Sb₂) and coordinated with the sulfide (S²⁻) ion in a distorted seven fold SbS₇ network.

Fig. 1 (A and B) TEM images of antimony sulfide nanoparticles under different magnifications. (C) X-ray diffraction pattern of antimony sulfide (red line) with the JCPDS number: 421393 (blue bar). The sulphur peaks (green symbol) are also identified in the spectra. (D) Unit cell representation of the antimony sulfide nanocrystal.

3.1Field induced polarization and electrical studies of the preformed antimony sulfide system

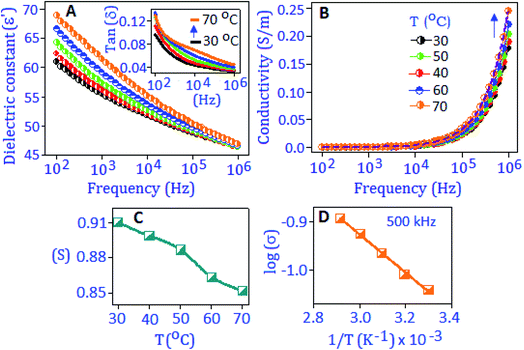
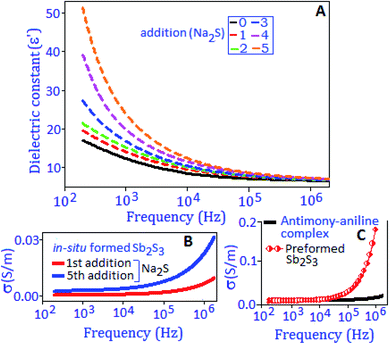
The broadband dielectric spectroscopic technique was applied to measure the dielectric constant (ε′), dielectric loss factor (tan δ), and conductivity (σ_ac) performance of the synthesized material. The dielectric constant, ε′ = Cd/ε₀A was extracted from the capacitance (C) value, where ε₀ is the dielectric constant of free space, ‘d’ is the thickness of the material and ‘A’ is the area of the working electrode. Fig. 2A exhibits the dielectric constant of the preformed Sb₂S₃ nanomaterial, measured under different temperature conditions (from 30 °C to 70 °C) within the frequency range from 100 Hz to 1 MHz. It was observed that at low frequency the dielectric constant value was enhanced with temperature and attained a maximum value of ∼68 at 70 °C. The high value of dielectric constant at lower frequencies is due to the different types of polarization contributions (interfacial, dipolar, ionic and electronic) in the material.³³ At high temperature, the space charge between the grain and grain boundary region is thermally activated and has switched the response along the direction of applied frequency.³⁴ With increasing frequency, the dielectric constant value decreased, and this behavior indicates that the charge species were unable to follow the variation of high frequency. A similar behavior was observed for the dielectric loss factor with rising temperature and frequency conditions, as illustrated in Fig. 2A, inset. A hump like feature is observed at 70 °C in tan (δ) curves at around 10 kHz, attributed to the thermally activated relaxation process in the material.

Fig. 2 (A) Temperature and frequency dependence dielectric constant (ε′) and the inset represent the dielectric loss tangent, tan (δ). (B) AC-conductivity versus frequency curve with rising temperature (indicated by an arrow). (C) Variation of the parameter ‘S’ with temperature and (D) Arrhenius fitting curves (log σ vs. 1/T) extracted at 500 kHz.

To realize the relaxation process of the nanoparticles, the AC-conductivity of the material was calculated from the dielectric constant data, σ_ac = 2πf × ε′ × tan (δ), under different temperature conditions, Fig. 2B. Frequency independent behaviour is related to the DC-part of the conductivity process and associated with the boundary of the nanoparticle.³⁵ On the higher frequency side, the frequency dependent behavior was observed that followed the Jonscher's power law, σ_ac = σ_dc + A(T)ω^S, where σ_dc is the frequency independent DC-part of the conductivity, A is the temperature dependent factor that determines the strength of the polarizability and ‘S’ is the frequency and temperature dependent parameter (0 < S < 1), which determines the conduction mechanism. It was reported that the polaronic type of charge carriers are responsible for the conduction process in sulfide based nanomaterials.^36,37 The structural distortion and defect centers in the sulfide nanoparticles enhance the polaronic contribution, which is subject to temperature and change in dopant concentration.^38–40 The variation of the ‘S’ parameter is shown in Fig. 2C and values of ‘S’ decrease with rising temperature, which revealed the correlated barrier hopping (CBH) conduction mechanism within the material. The thermal activation energy (E_a) of the material was calculated at 500 kHz using the Arrhenius relation; σ(T) = σ₀ exp (−E_a/K_BT), and is graphically presented in Fig. 2D. A linear fit to the equation (log σ vs. 1/T) delivers the value of E_a (activation energy) ∼34 meV.

The impedance property of the synthesized nanoparticle is presented in Fig. 3 for the selected temperatures (30 °C and 70 °C). The figure shows that the real part (Z′) of the impedance decreases with rising temperature and the values are merged towards the higher frequency region. The phase as a function of frequency diagram (Bode-plot), with rising temperature (from 30 to 70 °C), confirms the existence of low frequency dispersion, usually obtained from the grain (nanoparticle) boundary,³⁵Fig. 3, inset. The overall impedance performances revealed the negative temperature coefficient resistive behaviour.³⁸

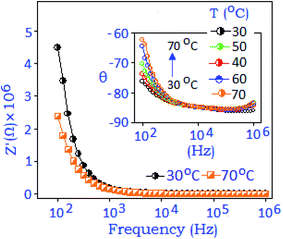Fig. 3 Real part of the impedance spectra (Z′) recorded at 30 °C and 70 °C and the inset represents the phase (θ) angle variation with respect to frequency with rising temperature (arrow).

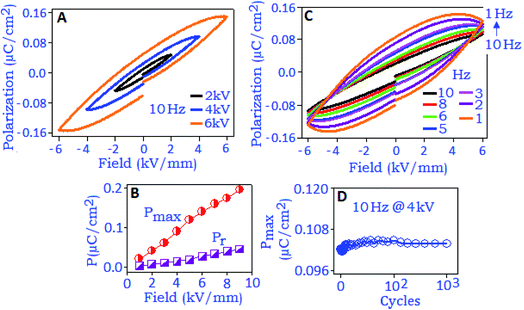
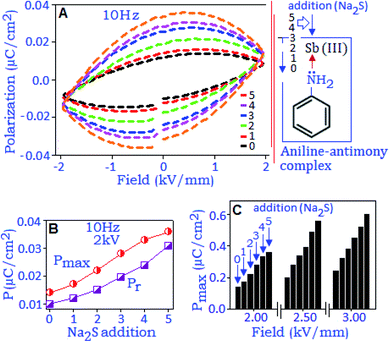
Fig. 4A exhibits the variation of polarization hysteresis loops measured under different field conditions (2, 4 and 6 kV mm⁻¹) at the frequency of 10 Hz. The maximum polarization (P_max) and remanent polarization (P_r) values increase with increasing electric field (from 1 to 10 kV mm⁻¹), Fig. 4B. At 10 kV mm⁻¹, the maximum polarization (P_max) value was ∼0.22 μC cm⁻² and the unsaturated polarization at the maximum applied field indicates the absence of polarization switching. The hysteresis loop also showed strong frequency dependence when measured under different frequency conditions (from 10 Hz to 1 Hz), Fig. 4C. An increasing trend of the values of P_max, P_r and the area under the loop was noticed with decreasing frequency and this behavior can be related to the space charge polarization within the material.⁴¹ With the increase of electric field (E) the space charge accumulation will also increase along the field direction⁴² and the charge carrier species buildup at the nanoparticle surface and surrounding.⁴³ When the applied frequency is low and the operational field is high, the amount of space charges will be high, which brings the polarization to a maximum value and consequently P_max, P_r and area under the loop increased with decreasing frequency. The stability study of the device was performed at 4 kV mm⁻¹ (field conditions) for 10³ cycles, and the result revealed a fatigue free polarization performance with the value of ∼0.10 μC cm⁻², Fig. 4D.

Fig. 4 (A) Polarization as a function of the electric field (P–E) hysteresis loop of preformed antimony sulfide recorded at 10 Hz. (B) Variation of P_max and P_r with respect to the applied electric field. (C) P–E loop, frequency dependent (from 1 Hz to 10 Hz), at 6 kV. (D) Polarization fatigue behaviour for 10³ cycles under the electric field of 4 kV mm⁻¹.

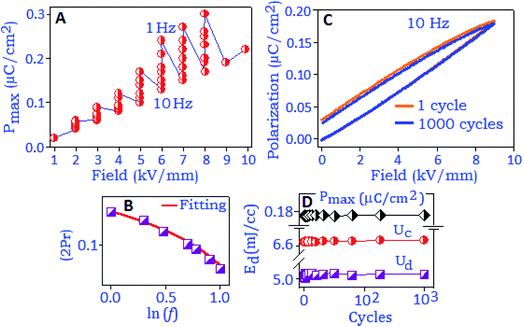
The variation of maximum polarization (P_max) under different frequencies (from 1 Hz to 10 Hz) as a function of field (2–8 kV mm⁻¹) is plotted in Fig. 5A. The polarization value increases with increasing electric field and reached the maximum value under the lowest frequency conditions, which are associated with a long response time for space charge carriers to align along the field direction. The remanent polarization (P_r and 2P_r) values are extracted from different frequency conditions during the depolarization process for the reverse field condition. The values decrease with increasing frequency and satisfied the power relation, (2P_r ∼ f^β), where ‘β’ is the frequency coefficient, Fig. 5B. The frequency dependent power relation for double remanent polarization (2P_r) has been applied to optimize the ferroelectric effect in thin film devices.⁴⁴ With rising the frequency condition, the space charge polarization are not able to follow the direction of the electric field as a result the polarization value decreases.⁴⁵ Such a reduction in P_r values is also associated with defects or vacancies of the particles that trapped the charge carriers, also reported for oxide based ferroelectric nanomaterials.^46,47 The charge storage properties of the synthesized material were investigated with the unipolar hysteresis loop, Fig. 5C. The endurance performance of the material was tested for 10³ cycles and the loop maintained the original pattern at the end of the cycling process. The polarization performance exhibited a fatigue-free behaviour with the P_max value of ∼0.18 μC cm⁻² at 9 kV mm⁻¹, Fig. 5D. Room temperature charge–discharge performances of the material were calculated from the unipolar loop. The extracted energy densities for charging (U_c) and discharging (U_d) values are ∼6.6 mJ cc⁻¹ and ∼5.0 mJ cc⁻¹, respectively, at 9 kV mm⁻¹, and maintained for 10³ cycles, Fig. 5D.

Fig. 5 (A) Frequency response of P_max under varying field conditions (2–8 kV mm⁻¹) and (B) 2P_r as a function of frequency. (C) A fatigue free unipolar hysteresis pattern for 1 and 1000 cycles. (D) The durability study for the charging, discharging and polarization performance at the 9 kV mm⁻¹ field for 1000 cycles.

3.2Field induced polarization and electrical studies of in situ formed antimony sulfide

All the above-mentioned studies involved the preformed antimony sulfide nanoparticles. In the current section, we will discuss the field induced polarization and dielectric properties of the in situ formed antimony sulfide within the organic matrix. For this, the antimony–aniline complex was deposited in the form of a film on a copper disk using a drop and dry method. A gold electrode was deposited, using a sputter coating technique, on the top of the complex material. A methanolic solution of sodium sulfide (1.0 μL) with the concentration of 0.5 × 10⁻¹ mol dm⁻³ was added to the complex material (at the peripheral sites of the electrode) five consecutive times and in situ dielectric capacitance and field dependent polarization measurements were performed after each addition. The formation of antimony sulfide nanoparticles has been confirmed through the TEM analysis (Fig. S1, ESI†).

Fig. 6A shows the change in the polarization loop pattern of the antimony–aniline complex for five successive additions of sodium sulfide. The black dashed-line represents the polarization hysteresis response of the antimony–aniline complex at 10 Hz, which was generated due to a weak dipolar type of interaction between the Sb³⁺ cation and the lone-pair of nitrogen (from aniline ligand). The gradual increment of the hysteresis loop after each addition of sodium sulfide indicates the enhancement of the dipole-induced charge trapping process due to the formation of more antimony sulfide atoms, with a stable dipole. An elliptical shape of the hysteresis loop revealed that the major contribution in the polarization process is due to the space charge formation and the presence of free Na⁺ ions induced the conductive nature under the applied electric field.⁴⁸ The variation of P_max and P_r with increasing concentration of sodium sulfide is presented in Fig. 6B. The polarization response was further analyzed under the electric fields of 2.0, 2.5 and 3.0 kV. Fig. 6C exhibits the variation of P_max (extracted from each hysteresis loop, not shown in the figure), as a function of the electric field, due to the successive addition of sodium sulfide to the antimony–aniline complex and the formation of antimony sulfide.

Fig. 6 (A) The effect of the polarization hysteresis loop of the antimony–aniline complex in the presence of sodium sulfide (with varying concentration), measured at 10 Hz, the inset shows the schematic diagram. (B) Variation of P_max and P_r with varying concentration of sodium sulfide, extracted from the polarization hysteresis loop and (C) field dependent response of the antimony–aniline complex under different Na₂S concentrations.

The comparative polarization hysteresis loop of the preformed antimony sulfide nanoparticles and antimony–aniline complex is displayed in Fig. S2(A), ESI.† Higher values of polarization and coercive fields originated from the nanoparticle component, which are nearly 10-orders of magnitude higher than those of the antimony–aniline complex. The polarization behavior of the antimony–aniline complex was also investigated in the presence of methanol, as a control experiment. Fig. S2(B), ESI,† exhibits no significant change in the polarization hysteresis loop of the antimony–aniline complex in the presence of methanol.

The charge storage ability and the charge migration mechanism of the in situ synthesized antimony sulfide nanoparticles were investigated by dielectric capacitance and AC-conductivity measurements. An identical protocol, as mentioned earlier, was applied for the addition of sodium sulfide to the antimony–aniline complex. Fig. 7A, black line, exhibits the graphical representation of the dielectric constant (ε′) as a function of the frequency of the antimony–aniline complex. After each addition of sodium sulfide to the complex the ε′ value increased and finally reached ∼50 @ 200 Hz, at the end of the fifth addition. Towards the low frequency range the high value of dielectric constant can be explained on the basis of interfacial polarization created by the trapped charges at the boundaries of aniline stabilized in situ formed antimony sulfide. The AC-conductivity behaviour (30 °C) of in situ formed Sb₂S₃ after the 1^st and 5^th addition of Na₂S is presented in Fig. 7B. The conductivity behaviour of the preformed Sb₂S₃ and antimony–aniline complex is exhibited in Fig. 7C. The conductivity pattern shows dispersion behavior for all cases towards the higher frequency side and the frequency where the slope of the conductivity starts to change is recognized as hopping phenomena.^35,38 Conductivity increases with the sequential addition of Na₂S and followed a similar trend like the preformed antimony sulfide nanoparticles. The following two phenomena are responsible for the charge conduction process at high frequency: (i) the charge carrier species transfer through localized states, and (ii) freedom of the charge carrier species from different trapping sites.⁴⁹

Fig. 7 (A) Dielectric constant of the antimony–aniline complex under different sodium sulfide concentrations. The variation of AC-conductivity of (B) in situ formed antimony sulfide after the 1^st and 5^th addition of sodium sulfide and (C) the preformed antimony sulfide and antimony–aniline complex.

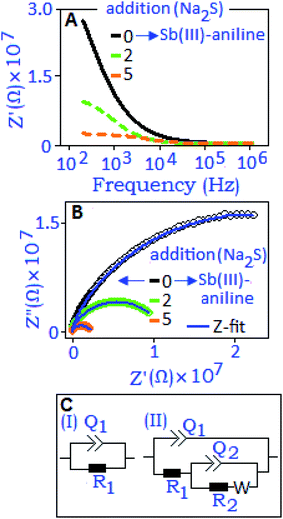
Impedance performance of the antimony–aniline complex, indexed as ‘0’ addition, and in situ formed Sb₂S₃ (for the 2^nd and 5^th addition of Na₂S) has been illustrated in Fig. 8A. The magnitude of impedance (Z′) decreases with the increase of Na₂S concentration which indicates the formation of space charge at the interfaces of the in situ formed antimony sulfide. In the Nyquist plots (Fig. 8B), semi-circular arcs were developed and shifted towards the high frequency region with increasing concentration of Na₂S, due to the contribution of in situ formed antimony sulfide. Two different electrical circuits were used to model the Nyquist plots. Fig. 8C(I) presents the R₁Q₁ component connected in parallel combination that describes the antimony–aniline complex (‘0’ addition) system where we assumed a non-deal capacitance (Q) behavior for the antimony–aniline complex. With the addition of Na₂S in the complex, the nascent antimony-sulfide nanoparticles introduced an additional contribution in the material which is assigned as the R₂Q₂ component in the electrical circuit, Fig. 8C(II). The Warburg diffusive component (W) was also introduced in the circuit to correlate the diffuse behavior of the untreated Na⁺ ions during the in situ process. The extracted parameters for the various additions of Na₂S to the antimony–aniline complex and antimony–aniline complex (‘0’ addition) are listed in Table S1, ESI.† From the extracted parameters, it was evident that with decreasing the resistance values (R₁ and R₂) the capacitive values (Q₁ and Q₂) were increasing with increasing the concentration of Na₂S, as graphically illustrated in Fig. S3, ESI.† The increment of capacitance (Q) values with increasing concentration of Na₂S revealed the formation of space charge polarization. The increment is more distinct for Q₂ which was due to the accumulation of more trapped charges at the material interfaces.

Fig. 8 (A) Impedance and (B) Nyquist plots of the antimony–aniline complex and in situ formed antimony sulfide after the 2^nd and 5^th addition of sodium sulfide, respectively. (C-I) and (C-II) The equivalent circuit model for the antimony–aniline complex and in situ formed antimony sulfide after the 2^nd and 5^th addition of sodium sulfide, respectively.

4. Conclusion

The electrical response of preformed and in situ formed antimony sulfide nanoparticles was investigated using dielectric capacitance and field induced polarization techniques. In preformed nanoparticles, the capacitance and polarization hysteresis performances were enhanced with rising temperature and followed a correlated barrier hopping mechanism in the conductivity process. Polarization stability was achieved for 10³ switching cycles for the preformed nanoparticles under 9 kV mm⁻¹ field conditions. The in situ formation of antimony sulfide nanoparticles during the reaction between the antimony–aniline complex and sodium sulfide was also detected via polarization and capacitance measurements. The change of impedance of the system during the in situ process was correlated with trapping and de-trapping of charge carriers across the localized states and that modelled to a single equivalent electrical circuit. The current study involved sulfide ion recognition using in situ capacitance and field induced polarization measurement techniques and has the potential for chemical sensor application.

Conflicts of interest

No conflicts of interest to declare.

Acknowledgements

This study was supported by the Faculty of Science, University of Johannesburg.

References

1. S. K. Ghosh, V. K. Perla and K. Mallick, Phys. Chem. Chem. Phys., 2020, 22, 3345–3351.
2. M. Choudhary, S. Shukla, A. Taher, S. Siwal and K. Mallick, ACS Sustainable Chem. Eng., 2014, 2, 2852–2858.
3. D. Nandi, V. K. Perla, S. K. Ghosh, C. Arderne and K. Mallick, Sci. Rep., 2020, 10, 16720.
4. S. H. Mir, L. A. Nagahara, T. Thundat, P. M. Tabari, H. Furukawa and A. Khosla, J. Electrochem. Soc., 2018, 165, B3137–B3156.
5. S. S. Prasanna, K. Balaji, S. Pandey and S. Rana, in Nanomaterials and polymer nanocomposites, ed. N. Karak, Elsevier, 2019, vol. 1, pp. 123–144.
6. Y. Wu, C. Wadia, W. L. Ma, B. Sadtler and A. P. Alivisatos, Nano Lett., 2008, 8, 2551–2555.
7. T. L. Li, Y. L. Lee and H. S. Teng, J. Mater. Chem., 2011, 21, 5089–5098.
8. M. J. Bierman and S. Jin, Energy Environ. Sci., 2009, 2, 1050–1059.
9. L. Li, P. Wu, X. Fang, T. Zhai, L. Dai, M. Liao, Y. Koide, H. Wang, Y. Bando and D. Golberg, Adv. Mater., 2010, 22, 3161–3165.
10. J. F. Hall, J. Opt. Soc. Am., 1956, 46, 1013–1015.
11. R. F. Heidelberg, A. H. Luxem, S. Talhouk and J. J. Banewicz, Inorg. Chem., 1996, 5, 194–197.
12. M. Y. Lu, M. P. Lu, Y. A. Chung, M. J. Chen, Z. L. Wang and L. J. Chen, J. Phys. Chem. C, 2009, 113, 12878–12882.
13. C. H. Lai, K. W. Huang, J. H. Cheng, C. Y. Lee, B. J. Hwang and L. J. Chen, J. Mater. Chem., 2010, 20, 6638–6645.
14. C. H. Lai, K. W. Huang, J. H. Cheng, C. Y. Lee, W. F. Lee, C. T. Huang, B. J. Hwang and L. J. Chen, J. Mater. Chem., 2009, 19, 7277–7283.
15. V. K. Perla, S. K. Ghosh and K. Mallick, Mater. Adv., 2020, 1, 228–234.
16. M. Cheraghizade, F. J. Sheini, R. Yousefi, F. Niknia, M. R. Mahmoudian and M. Sookhakian, Mater. Chem. Phys., 2017, 195, 187–194.
17. K. Liang, L. Ju, S. Koul, A. Kushima and Y. Yang, Adv. Energy Mater., 2019, 9, 1802543.
18. H. Jahromi and M. Moaddeli, Mater. Res. Express, 2019, 6, 116220.
19. A. Lemsi, D. C. Morcoso, M. Haro, C. G. Barrachina, C. Aranda, H. M. Meherzi, M. G. Tecedor, S. Giménez and B. J. López, Energy Technol., 2020, 8, 2000301.
20. H. Demir, Ö. Şahin, O. Baytar and S. Horoz, J. Mater. Sci.: Mater. Electron., 2020, 31, 10347–10354.
21. A. Moyseowicz, J. Solid State Electrochem., 2019, 23, 1191–1199.
22. M. Deng, S. Li, W. Hong, Y. Jiang, W. Xu, H. Shuai, H. Li, W. Wang, H. Hou and X. Ji, RSC Adv., 2019, 9, 15210–15216.
23. J. Li, D. Yan, X. Zhang, S. Hou, D. Li, T. Lu, Y. Yao and L. Pan, Electrochim. Acta, 2017, 228, 436–446.
24. X. Zhou, L. Bai, J. Yan, S. He and Z. Lei, Electrochim. Acta, 2013, 108, 17–21.
25. P. V. Prikhodchenko, J. Gun, S. Sladkevich, A. A. Mikhaylov, O. Lev, Y. Y. Tay, S. K. Batabyal and D. Y. W. Yu, Chem. Mater., 2012, 24, 4750–4757.
26. H. Nan, Y. Liu, Q. Li, P. Shena and K. Chu, Chem. Commun., 2020, 56, 10345–10348.
27. Y. Zeng, K. Sun, J. Huang, M. P. Nielsen, J. F. Ji, C. Sha, S. Yuan, X. Zhang, C. Yan, X. Liu, H. Deng, Y. Lai, J. Seidel, N. E. Daukes, F. Liu, H. Song, M. Green and X. Hao, ACS Appl. Mater. Interfaces, 2020, 12, 22825–22834.
28. F. Baumer, Y. Ma, C. Shen, A. Zhang, L. Chen, Y. Liu, D. Pfister, T. Nilges and C. Zhou, ACS Nano, 2017, 11, 4105–4113.
29. Y. C. Choi and K. W. Jung, Nanomaterials, 2020, 10, 2284.
30. C. E. A. Grigorescu and R. A. Stradling, Thin Films, 2001, 28, 147–191.
31. V. K. Perla, S. K. Ghosh and K. Mallick, J. Mater. Chem. C, 2021, 9, 6904–6910.
32. I. Efthimiopoulos, C. Buchan and Y. Wang, Sci. Rep., 2016, 6, 24246.
33. J. N. Wilson, J. M. Frost, S. K. Wallace and A. Walsh, APL Mater., 2019, 7, 010901.
34. B. Wang, W. Huang, L. Chi, M. Hashimi, T. J. Marks and A. Facchetti, Chem. Rev., 2018, 118, 5690–5754.
35. F. Rehman, J. Li, J. Zhang, M. Rizwan, C. Niu and H. Jin, J. Appl. Phys., 2015, 118, 214101.
36. A. Chandran, S. Samuel, J. Koshy and K. George, J. Appl. Phys., 2011, 109, 084314.
37. H. Ali, S. Karim, M. Rafiq, K. Maaz, A. Rahman, A. Nisar and M. Ahmad, J. Alloys Compd., 2014, 612, 64–68.
38. A. Jamil, S. S. Batool, F. Sher and M. A. Rafiq, AIP Adv., 2016, 6, 055120.
39. K. Shimakawa, Philos. Mag. B, 1982, 46, 123–135.
40. W. S. Choi, H. K. Yoo and H. Ohta, Adv. Funct. Mater., 2015, 25, 799–804.
41. X. Chen, X. Dong, F. Cao, J. Wang and G. Wang, J. Am. Ceram. Soc., 2014, 97, 213–219.
42. M. Vollman and R. Waser, J. Am. Ceram. Soc., 1994, 77, 235–243.
43. D. Fu, K. Suzuki and K. Kato, Integr. Ferroelectr., 2004, 61, 19–23.
44. A. Tagantsev, C. Pawlaczyk, K. Brooks, M. Landivar, E. Colla and N. Setter, Integr. Ferroelectr., 1995, 6, 309–320.
45. Y. Ishibashi and H. Orihara, Integr. Ferroelectr., 1995, 9, 57–61.
46. J. F. Scott, Integr. Ferroelectr., 2016, 12, 71–81.
47. D. Guo, C. Wang, Q. Shen, L. Zhang, M. Li and J. Liu, Appl. Phys. A: Mater. Sci. Process., 2009, 97, 877–881.
48. L. Jin, F. Li and S. Zhang, J. Am. Ceram. Soc., 2014, 97, 1–27.
49. V. I. Arkhipov, P. Heremans, E. V. Emelianova and H. Bässler, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 045214.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1na00361e

---