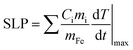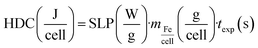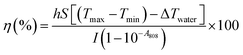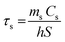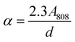DOI:
10.1039/D1NA00601K
(Paper)
Nanoscale Adv., 2021,
3, 6490-6502
Assessing the parameters modulating optical losses of iron oxide nanoparticles under near infrared irradiation†
Received
4th August 2021
, Accepted 26th September 2021
First published on 28th September 2021
Abstract
Heating mediated by iron oxide nanoparticles subjected to near infrared irradiation has recently gained lots of interest. The high optical loss values reported in combination with the optical technologies already existing in current clinical practices, have made optical heating mediated by iron oxide nanoparticles an attractive choice for treating internal or skin tumors. However, the identification of the relevant parameters and the influence of methodologies for quantifying the optical losses released by iron oxide nanoparticles are not fully clear. Here, we report on a systematic study of different intrinsic (size, shape, crystallinity, and iron oxidation state) and extrinsic (aggregation, concentration, intracellular environment and irradiation conditions) parameters involved in the photothermal conversion of iron oxide nanoparticles under near infrared irradiation. We have probed the temperature increments to determine the specific loss power of iron oxide nanoparticles with different sizes and shapes dispersed in colloidal suspensions or inside live breast cancer cells. Our results underline the relevance of crystal surface defects, aggregation, concentration, magnetite abundance, excitation wavelength and density power on the modulation of the photothermal conversion. Contrary to plasmonic or magnetic losses, no significant influence of nanoparticle size nor shape was observed on the optical losses released by the studied iron oxide nanoparticles. Interestingly, no significant differences of measured temperature increments and specific loss power values were either observed when nanoparticles were inside live cells or in colloidal dispersion. Our findings highlight the advantages of optical heat losses released by iron oxide nanoparticles for therapeutic applications.
Introduction
Light-matter interactions1–3 have been widely explored due to the vast and assorted amount of related physical phenomena ranging from plasmonic charge excitations4 to black holes.5 When light reaches matter, the interaction of photons with atoms depends on the electronic properties of matter, photon energy and polarization.6 Photon absorption generally results in photocarriers promoted to excited states defined by quantum mechanics, and the return to their ground state is ruled by radiative (i.e. photon emission) or non-radiative processes.7,8 The latter is related-among others-to phonon, charge or spin excitations, or photo-carrier tunnelling processes between defect/impurity electronic states when the transition energy is very low. At the nanoscale, non-radiative processes result in highly efficient photothermal conversion processes, for which the absorbed optical energy dissipates into heat.9,10 One example is given by metallic nanoparticles that have been widely studied due to their outstanding photothermal conversion efficiencies when irradiated by photons whose energy is at/or near their plasmon resonance. The resulting heat released from the photothermal conversion renders metallic nanoparticles, such as gold nanoparticles, in extremely attractive candidates for photothermal therapies.11 These therapies employ nanoparticles as heating mediators to induce cell death by generating thermal stress inside cells or tissues.12,13 However, little is known about the parameters ruling the photothermal conversion in other nanomaterials such as organic nanoparticles (e.g. cyanine14 and polyaniline15 derivates, or melanin16 nanoparticles) or non-metallic inorganic nanoparticles (e.g. carbon nanostructures,17,18 metallic oxides,19,20 or semiconductors21). In fact, the photothermal conversion capabilities of these nanoparticle families have shown more moderate efficiencies and broader optical absorption than the metallic counterparts.15,22–24 Non-metallic inorganic nanoparticles provide new possibilities for combining optically activated heating capabilities with other external stimuli such as alternating magnetic fields (HAC) in biomedical applications.25 This is the case of iron oxide nanoparticles (IONPs), the most widely employed nanomaterial in biomedical applications. IONPs can be precisely synthesized with tailored structural, colloidal, and magnetic properties, and they are highly biocompatible26 and fully biodegradated in few days.27 Recent studies have shown that the photoconversion capabilities of IONPs under near infrared irradiation (NIR)20 and the subsequent heat release becomes a simultaneous strategy to enhance the thermal stress supplied by HAC,28,29 which benefits solid tumour removal.25 Moreover, the use of NIR to activate IONP optical losses is gaining interest because in this wavelength range: (i) tissue absorption is low;30 (ii) no significant phototoxic effects are reported;31 (iii) NIR technologies are already present in clinical practices;32–34 (iv) IONPs are reported to maintain highly stable during photothermal performance, with no change in size or crystallinity.35 However, the physical mechanisms driving the photothermal conversion of IONPs are not yet fully understood. Consequently, the parameters involved on modulating the IONP optical losses are not totally identified. Several studies performed in different laboratories using distinct IONPs assess the influence of IONPs shape,20 size,36 clustering,37–39 crystal defects,40 iron oxidation states,41,42 irradiation power and wavelength20,41,43,44 on the optically activated heating efficiency. More research is needed to unambiguously define the parameters influencing optical losses of IONPs when subjected to NIR.
Here, we report on a systematic study of the influence of different intrinsic (size, shape, crystallinity and Fe2+/Fe3+ oxidation state) and extrinsic (aggregation, concentration, intracellular environment, irradiation power density and excitation wavelength) parameters on the photothermal conversion of a wide set of IONPs. Our results supply new evidences on the relevance of nanoparticle crystallite size, aggregation, and excitation wavelength (between 700 and 1300 nm) on the benefit of photothermal conversion of IONPs. Interestingly, diffuse and direct optical transmission and reflectance components play an important role on the fate of photon absorption/scattering by colloids, especially when IONPs aggregate. The latest highlights the relevance of the experimental methodologies for stressing the correlation between optical absorption and heat losses. Contrary to plasmonic or magnetic losses, no significant influence of IONP size or shape was observed under the experimental conditions explored in this study. We have confirmed that temperature increments and optical SLP of IONPs dispersed in aqueous suspensions or inside live breast cancer cells are maintained. Thus, we propose a novel method to quantify the intracellular heat dose (HDC) released by IONP under NIR. We also assessed the limitation of the employed methodology to determine SLP values of IONP under NIR.
Experimental section
Iron oxide nanoparticles
Table 1 lists the IONPs employed in this study, whose structural and colloidal properties show typical values of high quality IONPs, with the exception of 18-IONP and P-IONP. The two latest display magnetic properties strongly influenced by spin disorder. These disordered IONPs were intentionally selected to provide experimental results that contribute to unambiguously reflect the distinct origin of magnetic and optical losses in IONPs. On one hand, a set of IONPs with different sizes ranging from 8 to 19 nm (8-IONP, 14-IONP, 15-IONP, 18-IONP, 19-IONP) was synthesized at iMdea Nanociencia (iMdea) by a thermal decomposition method.45 Then, IONPs were transferred to aqueous media through ligand substitution with meso-2,3-dimercaptosuccinic acid (DMSA), as previously described.45,46 On the other hand, a set of IONPs with comparable size (between 15 and 18 nm) and different shapes: spheres (S-IONP), cubes (C-IONP), platelets (P-IONP) and octopods (O-IONP) were synthesized at Institut de Physique et Chimie des Matériaux de Strasbourg (IPCMS) by a thermal decomposition method described elsewhere.47–50 IONPs were transferred to aqueous media following a well-established protocol.49,51,52 The resulting IONPs were coated with dendrons bearing phosphonic acid tweezers and three PEG chains for biocompatibility to ensure a strong coupling to the IONP surface. Finally, two commercial IONPs were used: (i) FluidMag-CT (FM-CT; product number: 4122-1) are manufactured by Chemicell GmbH (Berlin, Germany); (ii) HyperMAG® C (LRL) are manufactured by Liquids Research Limited (Bangor, United Kingdom).
Table 1 Summary of structural, and colloidal parameters from the studied IONPs at RT. L = length; W = width
| Name |
IONP shape |
Coating |
TEM size (nm) |
Hydrodynamic size (nm) |
Number of IONPs per gram of Fe (number of IONP/gFe) |
| 8-IONP |
Spherical |
DMSA |
8 ± 1 |
109 (PDI = 0.26) |
26.8 ± 4.5 × 10 14 |
| 14-IONP |
Spherical |
DMSA |
14 ± 3 |
57 (PDI = 0.24) |
12.1 ± 0.8 × 10 14 |
| 15-IONP |
Polyhedron |
DMSA |
15 ± 2 |
69 (PDI = 0.25) |
18.0 ± 0.7 × 10 14 |
| 18-IONP |
Polyhedron |
DMSA |
18 ± 2 |
102 (PDI = 0.24) |
26.2 ± 1.5 × 10 14 |
| 19-IONP |
Polyhedron |
DMSA |
19 ± 3 |
79 (PDI = 0.36) |
26.2 ± 2.1 × 10 14 |
| FM-CT |
Polyhedron |
Citric acid |
11 ± 2 |
50 (PDI = 0.12) |
4.6 ± 0.1 × 10 14 |
| LRL |
Polyhedron |
DMSA |
16 ± 4 |
93 (PDI = 0.19) |
23.3 ± 0.7 × 10 14 |
| P-IONP |
Platelet |
Dendron |
L: 17 ± 5 |
51 (PDI = 0.18) |
41.2 ± 5.6 × 10 14 |
|
W: 6 ± 2 |
| S-IONP |
Spherical |
Dendron |
18 ± 1 |
49 (PDI = 0.25) |
20.4 ± 0.5 × 10 14 |
| C-IONP |
Cubic |
Dendron |
15 ± 2 |
80 (PDI = 0.42) |
22.8 ± 1.7 × 10 14 |
| O-IONP |
Octopods |
Dendron |
17 ± 2 |
39 (PDI = 0.16) |
23.8 ± 2.6 × 10 14 |
Structural characterization
The size and shape of the studied IONPs were evaluated by transmission electron microscopy (TEM) (see Fig. S1† at ESI): JEOL 2100 microscope operating at 200 kV (point resolution 0.18 nm) was employed at IPCMS; and JEOL JEM 1010 microscope operating at 100 kV was employed at Servicio Interdepartamental de Investigación, Universidad Autónoma de Madrid. TEM images were examined through manual analysis of more than 150 particles randomly selected in different areas of TEM micrographs using Image-J software to obtain the mean size and size distribution listed in Table 1. The crystal structure of IONPs with different sizes synthesized at iMdea was identified by X-ray powder diffraction (XRD) performed at room temperature (RT) with a Bruker D8 Advance powder diffractometer (Bruker, Billerica, MA, USA) using Cu Kα radiation (λ = 0.154056 nm) with an energy-discriminator (Sol-X) detector. The patterns were collected in the range 2θ = 20°–80°. The XRD spectra were indexed to an inverse spinel structure (as magnetite and maghemite). The average crystallite size was calculated by Scherrer's equation using the half width of the (311) peak. The crystal structure of IONPs with different shapes synthesized at IPCMS were examined by XRD at RT with Bruker D8 Advance powder diffractometer equipped with a monochromatic Cu Kα radiation source and a Lynx-Eye detector in the range 2θ = 27°–65°. High purity silicon powder (a = 0.543082 nm) was systematically used as an internal standard. Profile matching refinements were performed through the Fullprof program using Le Bail's method53 with the modified Thompson–Cox–Hasting pseudo-Voigt profile function. The iron oxidation states (Fe3+ and Fe2+) present in the studied IONPs were examined by Raman spectroscopy, whose vibrational spectra were acquired using a confocal Raman microscope (CRM) integrated with an atomic force microscope into an Alpha300RA Microscope (WITec, Ulm, Germany). The employed Nd:YAG laser 532 nm line was linearly p-polarized and focused by an objective with numerical aperture of 0.95. A few IONP dispersion drops were placed onto a silica buffer and dried for 10 minutes prior to the measurements. The incident laser power was fixed at 0.01–0.02 mW to prevent oxidation changes resulting on IONP compositional modifications. Average Raman spectra consisted of 30 single spectra with an integration time of 10 seconds. The collected spectra were then analyzed with WiTec Project Plus software, and Raman mode positions were fitted using Lorentzian functions.
Colloidal characterization: hydrodynamic diameter
The hydrodynamic size (DH) of IONPs was determined by dynamic light scattering (DLS) with a Zetasizer Nano ZS equipment (Malvern Instruments, USA). IONP suspensions were diluted in double distilled water (DDW) to a final concentration of 0.05 gFe L−1 in a commercial cuvette. The energy source was a laser emitting at 633 nm, and the angle between sample and detector was 173°.
Quantification of IONP concentration
IONP concentration is based in the iron (Fe) content in the magnetic colloids. The Fe concentration was determined by measuring the Fe content by inductively coupled plasma mass spectrometry in ICP-OES (PerkinElmer Optima 2100 DV).
Variation of hydrodynamic size
In order to study IONP aggregation effects, we have used LRL IONPs. The original DH of LRL (80 nm and PDI = 0.18) in DDW was intentionally altered to obtain stable colloids of up to 246 nm (see Table 2). For this purpose, aqueous IONP suspensions were diluted with phosphate buffered saline (PBS) 1X to achieve different salt concentration ratios ranging from 0.2X to 0.45X at a final iron concentration of 1 gFe L−1. Then, the dispersions were sonicated for 20 minutes and incubated at RT for 45 minutes.
Table 2 Hydrodynamic size and polydispersity index (PDI) for aggregated LRL nanoparticles employed to test the influence of DH on magnetic and optical SLP values shown in Fig. 7a and S3 at ESI
|
D
H (nm) |
PDI |
| 81 |
0.18 |
| 88 |
0.17 |
| 103 |
0.24 |
| 133 |
0.29 |
| 154 |
0.28 |
| 246 |
0.49 |
Nanoparticle tracking analyse (NTA)
For the determination of number of IONPs per unit volume in magnetic suspensions with iron contents of 0.5 and 1 gFe L−1, we employed Nanosight NS300 (Malvern Instruments, USA). The 0.5 and 1 gFe L−1 samples were diluted 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5000 in DDW and injected into the instrument chamber using a 1 mL syringe. Camera settings were adjusted in order to focus the objective. The video data was collected for 60 seconds and repeated 3 times per sample.
5000 in DDW and injected into the instrument chamber using a 1 mL syringe. Camera settings were adjusted in order to focus the objective. The video data was collected for 60 seconds and repeated 3 times per sample.
Magnetic characterization
Quasi-static conditions.
Magnetic characterization of IONP (iron mass of 200 μg) under quasi-static conditions was carried out in a vibrating sample magnetometer (VSM, Oxford Instrument MLVSM9 MagLab 2T) shown in Fig. S2a† at ESI. The variation of sample magnetization as a function of the applied external magnetic field was acquired at RT by first saturating the sample under a field of 1600 kA m−1. Saturation magnetization (MS) values were calculated by extrapolating to infinite field the experimental results obtained in the high field range where the magnetization linearly increases with 1/H. Magnetization units are expressed in Am2 per kilogram of magnetic mass (i.e. iron mass).
Dynamical conditions.
AC magnetometry measurements of the magnetic colloids with an iron mass of 40 μgFe (Advance AC Hyster) and 200 μgFe (LF AC Hyster) were carried out by commercial inductive magnetometers (AC Hyster Series; Nanotech Solutions, Spain). The LF AC Hyster Series magnetometer works at a single field frequency (1.2 kHz) and amplitudes are automatically tuned up to 120 kA m−1 (see Fig. S2b and c,† at ESI). The Advance AC Hyster Series magnetometer offers a wider field frequency range from 10 kHz up to 300 kHz and field intensities up to 24 kA m−1 that are automatically selected. Each magnetization cycle is obtained out of three repetitions, resulting in the averaged magnetization cycle and the related magnetic parameters (HC, MR, area). In order to accurately quantify the magnetic losses of LRL suspensions with intentionally increased hydrodynamic size, the specific absorption rate (SAR) values were calculated according to SAR = A·f,54 where A is the magnetic area and f is AC magnetic field frequency. These magnetic SAR measurements take less than 1 minute, contrary to the calorimetry ones (∼20 minutes). Thus, colloidal stability (i.e. DH) is maintained during measurements of optical and magnetic losses. Magnetization units were normalised by the magnetic mass (i.e. iron mass).
Optical characterization
Optical transmission measurements were carried out by UV-VIS-NIR Spectroscopy (Varian Cary spectrometer) in the 600–1300 nm spectral range (see Fig. S2d–f at ESI†). For the measurements, iron concentration of IONP suspensions was 1 gFe L−1 in a reduced volume quartz cuvette (200 μL) placed in different configurations into the spectrometer. The optical path of the cuvette has 2 mm length. Direct transmittance (TD) of different size and shape IONPs was extrapolated from the absorbance values obtained using the following expression: A = −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TD. The total (TT), diffuse (Td), and direct transmittance and reflectance (RT, and Rd) measurements for LRL with distinct DH were carried out by UV-VIS-NIR spectroscopy (LAMBDA 650/850/950 spectrometer, PerkinElmer) in the spectral range from 600 to 1300 nm using the integrating sphere and universal reflectance accessories (see Fig. S4 at ESI†). The quartz cuvette was rotated 6° with respect to the incident light beam in the case of Rd measurements, in accordance with previous procedures.55,56 The TD configuration is the one supplied by spectrophotometers not having integrating sphere for transmission measurements. Control samples were the quartz cuvette filled with DDW or PBS.
TD. The total (TT), diffuse (Td), and direct transmittance and reflectance (RT, and Rd) measurements for LRL with distinct DH were carried out by UV-VIS-NIR spectroscopy (LAMBDA 650/850/950 spectrometer, PerkinElmer) in the spectral range from 600 to 1300 nm using the integrating sphere and universal reflectance accessories (see Fig. S4 at ESI†). The quartz cuvette was rotated 6° with respect to the incident light beam in the case of Rd measurements, in accordance with previous procedures.55,56 The TD configuration is the one supplied by spectrophotometers not having integrating sphere for transmission measurements. Control samples were the quartz cuvette filled with DDW or PBS.
Calorimetry measurements in magnetic colloidal dispersions
In order to quantify the optical and magnetic losses of IONP suspensions, non-adiabatic calorimetric measurements were performed by recording the changes in temperature of IONP suspensions while subjected to NIR or HAC. This experimental methodology directly probes the heat losses released by IONPs into colloidal suspensions by measuring the increment of the colloid temperature (ΔT). For this purpose, IONPs dispersed in DDW at a concentration of 1 gFe L−1 of 40 μl were placed in a quartz Dewar under reduced thermal exchange losses conditions.57 For calorimetry measurements of magnetic losses, IONP colloids were subjected to a single field condition (100 kHz and 32 kA m−1) generated by a home-made frequency and intensity adjustable field generator. The interest of the employed HAC frequency (100 kHz) relies on its availability in HAC generators employed in human magnetic hyperthermia clinics.58,59 For calorimetry measurements of optical losses, IONPs colloids were irradiated from upper part (see Fig. S5† at ESI) using an 808 nm-laser coupled with an optical fibre at different power densities ranging from 0.01 up to 1.0 W cm−2. The spot diameter size was adjusted to achieve the desired power density. Temperature variations during the application of HAC or NIR were recorded using a commercial optical fibre thermal probe (TS2/2) located at the bottom of the Dewar and connected to a FOTEMP2-16 two-channel signal conditioner from Optocon AG with an experimental error of ± 0.2 °C. SLP values under non-adiabatic conditions were determined57 by dT/dt|max according to the following expression:| | 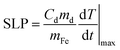 | (1) |
where Cd is the mass specific heat of the dispersion media, md is the mass dispersion, mFe is the iron mass related to the IONP diluted in the dispersion and dT/dt|max is the maximal temperature slope immediately after switching HAC or laser on. The value of Cd considered in this study was 4.18 J g−1 K−1 for water dispersion. SLP and net ΔT values were obtained from subtracting the initial slope (dT/dt|max) of water/cell suspensions (i.e. in absence of IONPs) to the ones recorded in IONP suspensions under NIR. Fig. S6† at ESI plots typical heating curves comparing the colloidal temperature raise in absence/presence of IONPs (0.5 gFe L−1) in water suspension. The observed temperature increments due to experimental artifacts tightly depend on irradiation conditions, being ≤1 °C for all power densities ≤0.5 W cm−2 at 808 nm.
Calorimetry measurements in cells
MCF-7 breast cancer cells (purchased from American Type Culture Collection) were seeded in T75 flasks and cultured in Dulbecco's modified Eagle's medium (DMEM) supplemented with 10% fetal bovine serum (FBS), 1% penicillin/streptomycin (VWR) and 2 mM L-glutamine in air atmosphere with 5% CO2 at 37 °C. After 48 hours, the culture media was exchanged with fresh media containing IONPs at 0.1 gFe L−1. Cells were returned to the incubator for 24 hours. At this point, cells were washed with PBS 1X five times to remove all non-internalized IONPs and detached with trypsin (Biowest). 2 million cells were centrifuged, pelletised, and resuspended in 25 μL of supplemented media. The quantification of optical heat losses was performed by calorimetry measurements as described in the previous section. The experiment was repeated three times, and untreated cells were used as controls. Once calorimetry measurements were finished, cell suspensions were treated with a solution of hydrochloric acid and nitric acid (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to lysate cells and dissolve the particles, in order to quantify the iron content. To compare the IONPs heating behaviour in aqueous solution and inside cells, IONP colloidal dispersions were prepared at the same iron concentration than cell pellets (2 gFe L−1) and subjected to the same NIR and HAC conditions previously described. SLP values were determined by employing an extension of eqn (1):
1) to lysate cells and dissolve the particles, in order to quantify the iron content. To compare the IONPs heating behaviour in aqueous solution and inside cells, IONP colloidal dispersions were prepared at the same iron concentration than cell pellets (2 gFe L−1) and subjected to the same NIR and HAC conditions previously described. SLP values were determined by employing an extension of eqn (1):| | 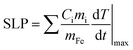 | (2) |
where i = dispersion medium, cell pellet and IONPs; the total sample volume (cells plus cell media) was 25 μL: mmedia = 25 mg for 25 μL of cell media, and Cmedia = 3.91 ± 0.03 J g−1 K−1; Ccell = 3.71 ± 0.03 J g−1 K−1 and mcell = 2 mg (for 2 × 106 cells); CFe = 0.47 J g−1 K−1 and mFe = [Fe/cell] × 2 × 106 cells = 51 μgFe. The product CFemFe is so small with respect to other Cimi values that was neglected in SLP calculations. The mass specific heat values of cell media, and cells were obtained at 25 °C with a calorimeter Discovery DSC (TA Instruments) at Servicio Interdepartamental de Investigación, Universidad Autónoma de Madrid. The HDC was determined according to recent report:60| | 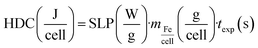 | (3) |
where SLP (W gFe−1) is the optical SLP value obtained when IONPs are in cells, mFe/cell (g/cell) is the iron mass related to IONPs per cell, and texp (s) is the time under NIR exposure.
Calculation of the photothermal conversion efficiency
The photothermal conversion efficiency (η) of the studied IONPs was calculated61 from the cooling rate, according to the following expression:| | 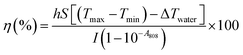 | (4) |
where h is the heat transfer coefficient, S is the sample surface area, Tmax is the maximum temperature of the IONP suspension after NIR, Tmin is the ambient temperature, ΔTwater is the temperature increment of the same volume of solvent (DDW) under the studied irradiation conditions, I is the incident laser power and A808 is the optical absorbance of the IONP suspensions at 808 nm. The value of hS was obtained from the fitting of the decay time in the temperature decay (see Fig. S7†) by using the following equation:| | 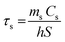 | (5) |
where ms and Cs are the mass and the heat capacity of the solvent (DDW) respectively, and τs is the sample system time constant, which is calculated through the exponential fit of water decay (see Fig. S7†). The value of τs was 80 ms in the Dewar container employed for calorimetry measurements. The value of A808 in our irradiation set up was calculated from the attenuation coefficient (α), according to the following expression:| | 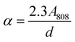 | (6) |
where d is the optical path length. In order to calculate α constant, A808 and d were substituted by the optical absorbance and the light path length measured in the UV-VIS-NIR spectrophotometer. Once we determined the value of α constant, A808 was calculated using the value of d in our SLP experimental set up (d = 8 mm).
Results and discussion
IONP concentration effects on the photo-thermal conversion
In order to unveil the influence of nanoparticle concentration on the photothermal conversion of IONPs, optical SLP values were determined under non-adiabatic calorimetry measurements (see Experimental section). For this purpose, we studied spherical shape IONP (S-IONP) to determine optical losses when Fe content ranges from 0.25 to 2 gFe L−1. SLP is a well-established physical parameter related to the heat power released per mass of iron (W gFe−1). Since the influence of the studied parameters (such as IONP aggregation, concentration, size, crystal defects, or shape) on the magnetic SLP have been widely studied,28 magnetic SLP values were also obtained for the same IONP suspension in order to guide how the studied parameters modulates optical losses. It is worth noting that magnetic SAR shows slight increase from 210 to 260 W gFe−1 in the studied IONP concentration range (see Fig. S8†). As mentioned above, photon absorption by IONPs results in photothermal conversion processes in which optical energy dissipates into heat. When photon energy couples with the energy transitions of Fe2+/3+ into IONP crystal,62,63 light extinction becomes more and more pronounced when crossing colloidal suspensions. At the same time, the number of IONPs in colloidal suspensions (i.e. IONP concentration) plays also a relevant role on increasing light extinction (i.e. absorbing light for heat release) across colloidal suspensions. As shown in Fig. 1a, optical absorbance increases linearly with S-IONP concentration from 0.25 gFe L−1 to 2 gFe L−1, in agreement with recent studies.25,40,41 However, the observed optical SLP values progressive decrease from 211 W gFe−1 to 46 W gFe−1 when increasing IONP concentration, in spite photothermal efficiency (η) values remain invariable (≈12%). These results confirm that IONP photothermal conversion is highly efficient at low iron concentrations resulting in measurable optical losses. However, the progressive increase of absorbance (see Fig. S9†) in the studied IONP concentration range is not reflected in temperature increments (ΔT). The latest rises with concentration up to 1 gFe L−1, and beyond this value, ΔT remains constant. This behaviour can be understood in terms of the Lambert–Beer's law for the distinct experimental set-ups employed for optical absorbance (2 mm optical path) and optical SLP (8 mm optical path) measurements (see Experimental section): our experimental SLP calorimetry set-up exclusively irradiates the colloidal suspension from its top part while reading temperature from the bottom (Fig. S5†). Under this condition, photons are mainly absorbed and/or scattered in the top of IONP suspension. The saturation of ΔT values beyond 1 gFe L−1 (i.e. when Abs808 nm > 0.2) indicates that the IONP suspension is homogenously shined. Consequently, when light absorption is not homogenous along the IONP suspension, the release of heat will be inhomogenous, resulting in temperature gradients along the irradiation direction (see Fig. S10†), in contrast to magnetic activation (i.e. IONPS subjected to HAC). Under NIR irradiation, larger temperatures are observed at the upper part of colloidal suspension (i.e., where more photons are absorbed) than at the bottom of colloid (where less photons are available to be absorbed). When the overall absorbance of IONP suspension is low, the temperature gradient diminishes (see Fig. S10†). Therefore, our experimental configuration is limited to observe direct correlation between optical absorbance and SLP when IONP absorbance is higher than 0.2.
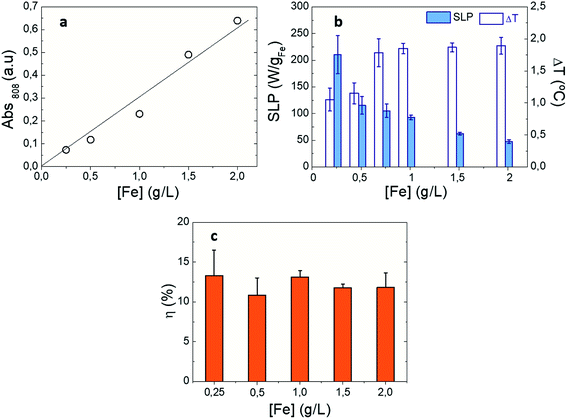 |
| | Fig. 1 Photothermal response of S-IONPs at different iron concentrations: (a) optical absorbance values at λ = 808 nm. Solid line is a guide to the eye; (b) optical SLP (colour columns) and temperature increment (DT) values (white columns) at λ = 808 nm, 0.3 W cm−2; (c) photothermal conversion values at λ = 808 nm, 0.3 W cm−2. IONPs were dispersed in DDW at [Fe] = 1 g L−1. | |
Morphology, surface defects, iron oxidation state and size effects on the photo-thermal conversion of IONPs
In order to unveil the influence of IONP morphology, crystal defects, size, and iron oxidation state on their photothermal efficiency, optical SLP values of different-size and shape IONPs were determined. The studied IONPs (see Table 1) were dispersed in DDW at 1 gFe L−1. Fig. 2a and b show the optical SLP values obtained in suspensions for IONPs of different sizes between 8 and 19 nm subjected to NIR (808 nm and 0.3 W cm−2). The observed optical SLP values vary from 68 W gFe−1 (at 8-IONP) up to 93 W gFe−1 (at 14-IONP). As expected,64 magnetic SLP values (see Fig. S11†) are more sensitive to IONP size than the optical ones. Nevertheless, there is not a clear correlation between optic SLP values and TEM size. However, this changes when representing SLP values versus XRD size, i.e. crystallite size (see Table 3): both absorbance and optical SLP values at 808 nm rise when increasing crystal size. The role of crystallite size is also reflected on the magnetic SLP (see Fig. S11b†). The latest linearly increases (from 0 to 325 W gFe−1) with crystallite size from 8 to 15 nm. Recent reports correlate the influence of IONP size and surface defects on the magnetic properties (including magnetic losses) due to spin canting and the modulation of magnetic anisotropy barrier.45,65 Interestingly, the optical SLP and absorbance values at 808 nm also benefit when IONP crystallinity is high.
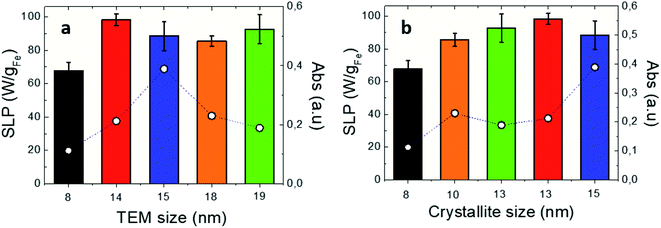 |
| | Fig. 2 Optical SLP (bars) and absorbance (empty dots) values for IONPs of different (a) TEM sizes; (b) crystallite sizes (see Table 3). Irradiation conditions: 808 nm, 0.3 W cm−2. IONPs were dispersed in DDW at [Fe] = 1 g L−1. Absorbance values obtained at 808 nm from Fig. S2d.† | |
Table 3 Optical transmission values at 808 nm for studied IONPs, and averaged nanoparticle sizes obtained by TEM and XRD
| IONP name |
TEM size (nm) |
Crystallite size (nm) |
| 8-IONP |
8 |
8 |
| 14-IONP |
14 |
13 |
| 15-IONP |
15 |
15 |
| 18-IONP |
18 |
10 |
| 19-IONP |
19 |
13 |
| P-IONP |
17 |
9 |
| S-IONP |
18 |
12 |
| C-IONP |
15 |
— |
| O-IONP |
17 |
13 |
Fig. S2† shows the absorption spectra of the studied IONP colloidal suspensions. Those spectra are characterized by the same asymmetrical V shape with a more pronounced absorption increase at wavelengths shorter than 700 nm, and a weaker absorption beyond 750 nm. However, absorption values vary depending on IONPs. Indeed, optical absorbance is tightly sensitive to crystallite size, more than optical SLP values. Indeed, when IONP crystallinity increases, absorbance raises but the optical SLP values increase or remain constant as a general observation (see Fig. 1b–d). Such different behaviour of optical absorption and SLP can be understood again in terms of the Lambert–Beer law for the aforementioned optical transmission and SLP set-ups employed in this work. In overall, our findings underline that optical and magnetic losses are both sensitive to IONP surface disorder in agreement with previous reports40,64,65 but to a different extent. This is clearly observed for 18-IONPs, whose reduced Ms value (see Table S1†) reflects a strong spin disorder onto the nanoparticle surface, resulting in very low magnetic SLP values (18 W gFe−1). However, the SLP value (83 W gFe−1) obtained in the same sample under NIR is comparable to other IONP crystallite sizes.
Fig. 3 shows the SLP values obtained for IONPs of different morphologies subjected to the same NIR (and HAC) conditions than in Fig. 1. At a first sight, optical SLP values of this set of IONP are larger than the magnetic ones (with the exception of C-IONP, see Fig. S12†), and the optical ones observed in Fig. 1. Similar to IONPs of different size, the optical SLP values vary in a narrow range between 111 and 147 W gFe−1. Moreover, crystal defects modulate the optical SLP, absorption, and magnetic SLP as observed for P-IONPs. The latest show the lowest MS (see Fig. S2b†), magnetic and optical SLP values. However, it is worth noting that the optical SLP value for P-IONP is almost 10-fold higher than the magnetic one. Suspensions of IONPs with different shapes showed distinct optical transmission: S-IONP and C-IONP have the largest absorbances (see Fig. S2e, and S13†). However, such different absorbance values are not fully reflected on the optical losses due to the aforementioned experimental limitation related to Lambert–Beer law. Our results underline that IONP shapes are not a clear variable for photothermal conversion, contrary to plasmonic66,67 or the magnetic losses68–71 (see Fig. S12†).
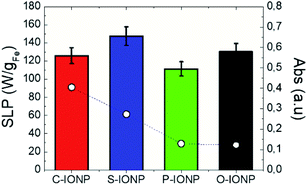 |
| | Fig. 3 Optical SLP (bars) and absorbance (empty dots) values at 808 nm for different shape IONPs. Irradiation conditions: 808 nm, 0.3 W cm−2. IONPs were dispersed in DDW at [Fe] = 1 g L−1. Absorbance values were obtained from absorption spectra from Fig. S2e.† | |
Besides, the pronounced differences of IONP absorbance values can be also attributed to their intrinsic optical properties of iron oxide phases. Thus, magnetite (Fe2+ and Fe3+) displays a charge transfer band in the NIR range, while in case of maghemite with oxidized Fe cations (Fe3+), there is a reduction of its optical performance at this NIR range due to its spinel structure.42,72 Raman spectra of the studied IONPs provide valuable information to confirm such electronic and optical properties as shown in Fig. 4. All studied IONPs with different sizes and shapes display typical active vibrational phonon modes around 670 cm−1, 720 cm−1 (associated with the A1g mode), 365 cm−1 (T2g) and 511 cm−1 (Eg) for maghemite structure.72–74 The presence of a magnetite phase that would mainly contribute to the intensity of the 670–675 cm−1 mode (A1g) cannot be excluded.75 Specifically, S-IONP show the largest intensity of the 670 cm−1 vibrational band with respect to that at 720 cm−1 in addition to an emerging band around 550 cm−1, which could be indicative of a greater presence of the magnetite phase. Other iron oxide phases have not been identified in the studied IONPs. Modifications in the position, full width high maximum (FWHM) and relative intensity of the Raman bands are found. The differences in the relative intensity (mainly at 670 and 720 cm−1) could be attributed to different morphologies of IONPs and their orientation or arrangement during the measurement, in addition to possible contributions of magnetite phase.76 Indeed, the magnetite abundance seems to be correlated to optical absorption and SLP values, showing the maximum expression for 15-IONPs and S-IONPs. The variations in the Raman shift and the FWHM may be associated with changes in the particle size, phonon confinement agglomeration state or strain in the structure. Thus, as previously seen64 the magnetite band (670 cm−1) gains intensity when IONP size increases from 8 to 15 nm.
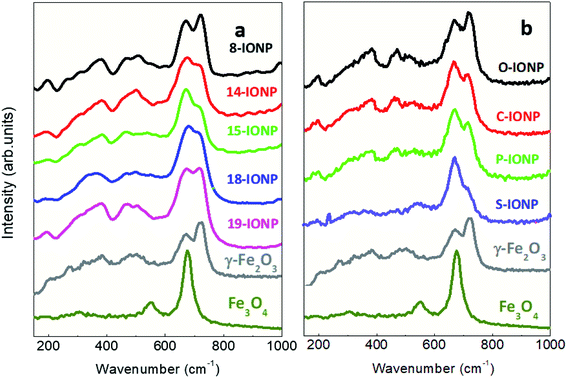 |
| | Fig. 4 Raman spectra from 150 to 1000 cm−1 for IONPs of different (a) sizes; (b) shapes. | |
Altogether, our findings indicate that IONP size and shape are not a determinant factor for photothermal performance, while crystallinity is extremely sensitive to enhance optical absorption. Iron oxidation state is also an important parameter modulating optical and magnetic losses.77 IONPs with magnetite phase abundance show higher optical absorption than maghemite.
Irradiation effects on the photo-thermal conversion of IONPs
According to optical absorption spectra (see Fig. S2d–f†), the excitation wavelength (λexc) are extremely relevant to the photothermal conversion in the NIR range. Depending on photon energy (i.e. λexc), light is differently absorbed, transmitted and/or reflected.78 Furthermore, power density delimits the use of optically activated IONPs in vitro or in vivo, as not all λexc and power densities are suitable for tissue penetration and safety. On one hand, the maximum permissible exposure of NIR light on the skin ranges from 0.2 W cm−2 at 630 nm to 0.4 W cm−2 at 850 nm. These limits vary depending on many factors such as wavelength, coherence, duration and area of exposure, according to Strangman et al.31 Thus, we have studied the effects of power densities ranging from 0.01 to 1 W cm−2 on the SLP values. Fig. 5a shows that optical SLP values increase linearly when raising power density, independently of IONP size or shape (see Fig. S14†). It is important to highlight that IONPs exhibit high SLP values (up to 150 W gFe−1) in the safe power range31 (<0.33 W cm−2). Higher power densities (up to 1 W cm−2) result in higher SLP values up to 323 W gFe−1. Fig. 5b shows the evolution of optical losses of 8-IONPs when varying λexc from 700 to 1300 nm under safe optical intensity values (i.e. 0.33 W cm−2), which comprises the so-called first and second biological window where optical radiation is minimally absorbed by blood, skin or fat,79–81 allowing light to penetrate deeper into tissues.82 As shown in Fig. 5b, optical SLP values linearly increases from 40 to 110 W gFe−1 when λexc increases up to 1300 nm. Such SLP enhancement is related to the linear increase of the optical absorption. Interestingly, photothermal efficiency increase with the wavelength in the studied range. To date, the majority of photothermal studies using NPs have been focused in first biological window (690–900 nm) due to the peak of transmission for tissues at approximately 800 nm.82 However, based on our results, future research should consider second biological window (1000–1350 nm) as an efficient option for IONP photoconversion.
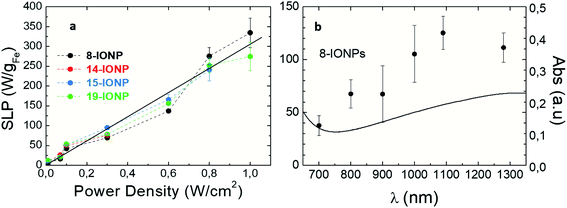 |
| | Fig. 5 Optical SLP values (a) as a function of irradiation power densities at λexc = 808 nm for IONPs of different sizes. Solid line is a guide to the eye; (b) comparison of optical absorption spectrum (solid line) and optical SLP values (solid dots) obtained at different lexc and power density: 0.3 W cm−2 for 8-IONPs. IONPs were dispersed in DDW at [Fe] = 1 g L−1. | |
Besides, it is worth noting that NIR does not influence magnetic losses, as shown in Fig. S15.† The absence or presence of NIR at different power densities up to 0.8 W cm−2 does not seem to influence the shape nor the magnetic area of the AC hysteresis loops recorded for 19-IONPs under HAC. Hence, this result unveils that IONP optical losses have a totally different nature than the magnetic ones.
Photothermal conversion efficiencies of IONPs
Photothermal conversion efficiency (η) is a parameter that reflects the percentage of optical energy (i.e. absorbed photons) that is transformed into heat.61 This particular parameter reflects the capability of nanomaterials to dissipate heat under NIR.83Fig. 6 shows the values of η obtained from IONPs with different size, and shape and under different λexc (only for 8-IONPs). While the set of IONPs with different sizes shows an averaged photothermal efficiency of 13%, IONPs with different shapes almost double the average η value (21%). Such differences of η values between the sets of size and shape IONPs can be related to distinct compositions and/or optical absorbance. The obtained η values are lower than others reported for iron-based nanomaterials which used to be around 30%.39 Finally, Fig. 6c reflects the spectral dependence of η for the 8-IONP sample. η values show a progressive 2-fold increase favoured by the optical absorption enhancement in the studied spectral range (see Fig. 5b). This underlines the tight correlation between optical absorption and photothermal conversion in the studied excitation wavelength range.
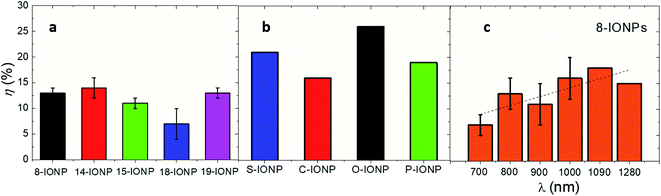 |
| | Fig. 6 Photothermal conversion efficiencies for (a) IONPs of different size (b) IONPs of different shape; (c) 8-IONPs subjected to different λexc at constant power density (0.3 W cm−2). The studied IONPs were dispersed in DDW at [Fe] = 1 g L−1. Irradiation conditions: λexc = 808 nm; 0.3 W cm−2. Solid line is a guide to the eye. | |
IONP aggregation effects on their photo-thermal conversion
In order to unveil the role of aggregation on IONP photothermal performance, LRL nanoparticles were intentionally aggregated to vary their hydrodynamic size (DH) from 80 to 236 nm while maintaining colloidal stability during measurements (see Table 2). Fig. 7a shows the net temperature increments (white columns) and the optical SLP (colour columns) values of IONPs suspensions on increasing DH at two different iron contents (0.5 and 1 gFe L−1, black and blue columns, respectively). Optical SLP and ΔT differently decrease depending on iron content (32% reduction at 0.5 gFe L−1 and 19% at 1 gFe L−1) when their DH increases 2-fold. Interestingly, the number of LRL aggregates is reduced to half when doubling DH (see Fig. S16†) indicating that the absorbance per LRL aggregate increases more than twice. The latest observation is in agreement with recent reports that show that IONP clustering leads to an significant increase of their photothermal capacity.37,84 Hence, the significant enhancement of the optical absorption induced by IONP agglomeration may explain why SLP and ΔT decrease in terms of the aforementioned Lambert–Beer's law. It is also worth noting that, the effect of IONP aggregation on magnetic losses is more pronounced than on optical SLP (Fig. S3†).85
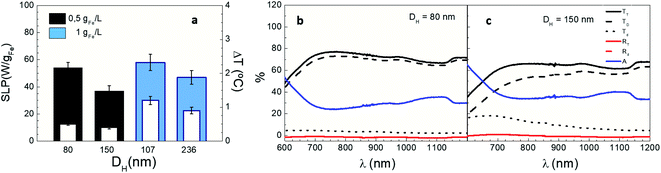 |
| | Fig. 7 Photothermal response of LRL IONPs at different DH. (a) Optical SLP values (colour columns) and temperature increments (white columns) at [Fe] = 1 gFe L−1 and 0.5 gFe L−1 (black and cyan colour); (b and c) total (TT), diffuse (Td) and direct (TD) transmission, total (RT) and diffuse (Rd) reflectance and absorbance (A) of LRL nanoparticles for DH = 80 and 150 nm at 1 gFe L−1. Irradiation conditions: 808 nm, 0.3 W cm−2. | |
Finally, Fig. 7b and c show how aggregation influences optical transmission across IONP suspensions. Direct transmission (TD) drops, and diffuse transmission (Td) decrease when increasing DH from 80 to 150 nm as a result of scattering between light and IONP clusters, in agreement with previous studies.38Fig. 7b and c also reveals that optical absorbance (A) at 808 nm slightly increase from 25% (for DH = 80 nm) to 35% (for DH = 150 nm). The same trend is found at lower iron concentrations (0.5 gFe L−1); indeed, the variations of TD, Td and A when increasing DH are more pronounced at 0.5 gFe L−1 than at 1 gFe L−1 (see Fig. 7b, c and S17†). On this basis, for the sake of an accurate determination of the optical absorbance in IONP suspensions, it is important to track the evolution of both TD, and Td when DH > 100 nm.
Cell internalization effects on the IONP photo-thermal conversion
The assessment of cell internalization effects on the optical thermal losses is key for in vitro and in vivo application purposes. Magnetic losses have been recently shown to be reduced87 due to immobilization and agglomeration of IONPs86 when located into intracellular environment (i.e. subcellular vesicles). In our case, Fig. 8 shows the net temperature increments and optical SLP values of FM-CT IONPs in colloidal dispersion or inside cells at similar iron content, irradiation (and HAC) conditions. On one hand, our results show that FM-CT exhibits better heating efficiency under optical activation than upon HAC (see Fig. S18†). Indeed, the optical SLP and ΔT values are twice higher than the magnetic ones. At the same time, optical SLP values inside cells are comparable to those obtained in colloidal dispersions. In agreement with recent reports,41 the average ΔT or SLP values are slightly larger for IONPS under NIR into cells than in suspensions. However, the variability of the values does not result in significant differences. Therefore, optical losses are not significantly influenced by the biological environment. This trend was also observed for magnetic SLP values. The small FM-CT size (11 nm) minimizes interacting phenomena, resulting in no variation of magnetic SLP, in agreement with recent reports.86 The related values of ΔT under NIR (and HAC) reflect a similar behaviour than SLP ones (see Fig. S19† in ESI). Indeed, the values of ΔT are twice higher under NIR than under HAC, while they are independent on IONP location (i.e. in suspensions or inside live cells). The invariability of the IONP optically losses inside biological matrices simplifies the procedure to determine the heat dose released by IONP into intracellular environments.60,86–90 Recent works60 have shown how to determine the average heat dose per cell (HDC) out of procedures based on calorimetry measurements in cell pellets. According to this methodology (see Experimental section), we determined that the intracellular HDC released by FM-CT IONPs was 1 μJ per cell. The quantification of HDC provides valuable information to perform in vitro and in vivo dose ranging studies for treating cancer by exposure to thermal stress mediated by IONPs.73,80,81
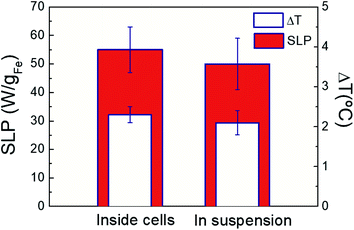 |
| | Fig. 8 Optical SLP values (colour columns) and temperature increments (white columns) of FM-CT IONPs ([Fe] = 2 g L−1) inside MCF7 breast cancer cells and dispersed in DDW suspension under NIR irradiation. Measurements the averaged of three repetitions on three independent samples. Irradiation conditions: 808 nm, 0.3 W cm−2. | |
Conclusions
We systematically investigated the influence of different intrinsic (size, shape, surface defects, and iron oxidation state) and extrinsic (aggregation, concentration, cell internalization, and irradiation conditions) parameters on the heat losses of IONPs activated under NIR. Our results provide unambiguos evidences of the distinct origin of magnetic and optical losses. Moreover, our results reflect the need of probing the direct and diffuse transmission and reflectance components for an accurate determination of IONP optical absorption. In addition to irradiation conditions, IONP concentration, and magnetite abundance, our results probe that IONP crystallinity, and aggregation benefit optical absorption and SLP values. At the same time, our experimental evidences show that cell internalization, IONP shape, and size do not significantly influence optical losses. Thus, we propose a methodology to quantify the intracellular HDC released by IONPs under NIR. Our experimental results provides better understanding on the relevant parameters that play a role on the modulation of optical losses. The identification of these parameter will allow to develop theoretical models for simulating sustained heating profile mediated by IONPs under NIR into biological matrices.
Author contributions
FJT designed the research. GS, CBA, GC, DF, and SBC prepared the different sets of studied IONP. CLP, and EPM performed the optical transmission and SLP experiments, and BS participated in the in vitro hyperthermia studies. AE and AS performed and analysed Raman experiments. CLP, EPM, AE, AS and FJT analysed and discussed the results. CLP and FJT wrote the first draft and the rest of authors contributed to tail the submitted and revised manuscript.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Authors are deeply acknowledged to the funding by Spanish Ministry of Science, Innovation and Universities (MAT2017-85617-R, MAT2017-86540-C4-1-R, RTI2018-095303-A-C52, SEV-2016-0686, PEJ2018-005496-A and PID2019-106301RB-I00) and Comunidad de Madrid (NANOMAGCOST, S2018/NMT-4321, and PEJ-2017-AI/IND-6283). Spanish Scientific Network (Hipernano, RED2018-102626-T), European COST Actions CA17115 (MyWave), and CA17140 (Nano2Clinic) are also acknowledged. Authors thanks David Sigüenza and Rebeca Amaro (IMDEA Nanociencia) for their support in nanoparticle preparation and characterization. A. E. and A.S. acknowledges the financial support from the Comunidad de Madrid for an “Atracción de Talento Investigador” (2018-T1/IND10058 and 2017-t2/IND5395). A. E. is also grateful to AECC Ideas Semilla 2019 Grant.
References
-
Photobiology: the Science of Life and Light, ed. L. O. Björn, Springer, New York, NY, 2nd edn, 2008 Search PubMed.
-
B. McParland, Photon Interactions with Matter, in Nuclear Medicine Radiation Dosimetry, Springer, London, 2010 Search PubMed.
-
J. Weiner and F. Nunes, Light-Matter Interaction: Physics and Engineering at the Nanoscale, Oxford University Press, Oxford, 2012 Search PubMed.
- N. S. Mueller, Y. Okamura, B. G. M. Vieira, S. Juergensen, H. Lange, E. B. Barros, F. Schulz and S. Reich, Nature, 2020, 583, 780–784 CrossRef CAS PubMed.
- R. M. T. Connors, J. A. García, T. Dauser, V. Grinberg, J. F. Steiner, N. Sridhar, J. Wilms, J. Tomsick, F. Harrison and S. Licklederer, Astrophys. J., 2020, 892, 47 CrossRef CAS.
-
R. H. Pratt, Indo-US Workshop Radiat. Phys. Synchrotrons New Sources, 2004, vol. 70, pp. 595–603 Search PubMed.
- W. A. Noyes, Rev. Mod. Phys., 1933, 5, 280–287 CrossRef CAS.
- A. Jablonski, Nature, 1933, 131, 839–840 CrossRef CAS.
- N. D. Thorat, S. A. M. Tofail, B. von Rechenberg, H. Townley, G. Brennan, C. Silien, H. M. Yadav, T. Steffen and J. Bauer, Appl. Phys. Rev., 2019, 6, 041306 CAS.
- A. C. V. Doughty, A. R. Hoover, E. Layton, C. K. Murray, E. W. Howard and W. R. Chen, Mater, 2019, 12, 779 CrossRef CAS PubMed.
- S. Nomura, Y. Morimoto, H. Tsujimoto, M. Arake, M. Harada, D. Saitoh, I. Hara, E. Ozeki, A. Satoh, E. Takayama, K. Hase, Y. Kishi and H. Ueno, Sci. Rep., 2020, 10, 9765 CrossRef CAS PubMed.
- M. Kim, J.-H. Lee and J.-M. Nam, Adv. Sci., 2019, 6, 1900471 CrossRef PubMed.
- J. B. Vines, J.-H. Yoon, N.-E. Ryu, D.-J. Lim and H. Park, Front Chem., 2019, 7, 167 CrossRef CAS PubMed.
- X. Zheng, F. Zhou, B. Wu, W. R. Chen and D. Xing, Mol. Pharm., 2012, 9, 514–522 CrossRef CAS PubMed.
- J. Zhou, Z. Lu, X. Zhu, X. Wang, Y. Liao, Z. Ma and F. Li, Biomaterials, 2013, 34, 9584–9592 CrossRef CAS PubMed.
- Y. Liu, K. Ai, J. Liu, M. Deng, Y. He and L. Lu, Adv. Mater., 2013, 25, 1353–1359 CrossRef CAS PubMed.
- Y. Shen, A. G. Skirtach, T. Seki, S. Yagai, H. Li, H. Möhwald and T. Nakanishi, J. Am. Chem. Soc., 2010, 132, 8566–8568 CrossRef CAS PubMed.
- Q. Zhang, W. Xu and X. Wang, Sci. China Mater., 2018, 61, 905–914 CrossRef CAS.
- Z. Meng, F. Wei, W. Ma, N. Yu, P. Wei, Z. Wang, Y. Tang, Z. Chen, H. Wang and M. Zhu, Adv. Funct. Mater., 2016, 26, 8231–8242 CrossRef CAS.
- M. Chu, Y. Shao, J. Peng, X. Dai, H. Li, Q. Wu and D. Shi, Biomaterials, 2013, 34, 4078–4088 CrossRef CAS PubMed.
- J. Wang, Y. Li, L. Deng, N. Wei, Y. Weng, S. Dong, D. Qi, J. Qiu, X. Chen and T. Wu, Adv. Mater., 2017, 29, 1603730 CrossRef PubMed.
- X. Yao, X. Niu, K. Ma, P. Huang, J. Grothe, S. Kaskel and Y. Zhu, Small, 2017, 13, 1602225 CrossRef PubMed.
- P. Yang, S. Zhang, N. Zhang, Y. Wang, J. Zhong, X. Sun, Y. Qi, X. Chen, Z. Li and Y. Li, ACS Appl. Mater. Interfaces, 2019, 11, 42671–42679 CrossRef CAS PubMed.
- D. Jaque, L. Martínez Maestro, B. del Rosal, P. Haro-Gonzalez, A. Benayas, J. L. Plaza, E. Martín Rodríguez and J. García Solé, Nanoscale, 2014, 6, 9494–9530 RSC.
- A. Espinosa, R. Di Corato, J. Kolosnjaj-Tabi, P. Flaud, T. Pellegrino and C. Wilhelm, ACS Nano, 2016, 10, 2436–2446 CrossRef CAS PubMed.
- H. Markides, M. Rotherham and A. J. El Haj, J. Nanomater., 2012, 2012, 614094 Search PubMed.
- A. Van de Walle, J. Kolosnjaj-Tabi, Y. Lalatonne and C. Wilhelm, Acc. Chem. Res., 2020, 53, 2212–2224 CrossRef CAS PubMed.
- E. A. Périgo, G. Hemery, O. Sandre, D. Ortega, E. Garaio, F. Plazaola and F. J. Teran, Appl. Phys. Rev., 2015, 2, 041302 Search PubMed.
- I. Rubia-Rodríguez, A. Santana-Otero, S. Spassov, E. Tombácz, C. Johansson, P. De La Presa, F. J. Teran, M. D. Morales, S. Veintemillas-Verdaguer, N. T. K. Thanh, M. O. Besenhard, C. Wilhelm, F. Gazeau, Q. Harmer, E. Mayes, B. B. Manshian, S. J. Soenen, Y. Gu, Á. Millán, E. K. Efthimiadou, J. Gaudet, P. Goodwill, J. Mansfield, U. Steinhoff, J. Wells, F. Wiekhorst and D. Ortega, Materials, 2021, 14(4), 706 CrossRef PubMed.
- E. Hemmer, A. Benayas, F. Légaré and F. Vetrone, Nanoscale Horiz., 2016, 1, 168–184 RSC.
- G. Strangman, J. P. Culver, J. H. Thompson and D. A. Boas, Neuroimage, 2002, 17, 719–731 CrossRef PubMed.
-
Fluorescent Imaging in Medicinal Chemistry, ed. Z. Cheng, Springer International Publishing, Cham, 2020, vol. 34 Search PubMed.
-
P. Castella, N. J. Kemp, T. E. Milner and D. G. Rosenbaum, US Pat. US20090043191, Volcano Corporation, 2009 Search PubMed.
-
Z. Gourgouliatos and D. Chang, US Pat., US20080172112, Lerner Medical Devices Inc, 2012 Search PubMed.
- R. J. G. Johnson, K. M. Haas and B. J. Lear, Chem. Commun., 2015, 51, 417–420 RSC.
- R. J. G. Johnson, J. D. Schultz and B. J. Lear, Molecules, 2018, 23(5), 1234 CrossRef PubMed.
- S. Shen, S. Wang, R. Zheng, X. Zhu, X. Jiang, D. Fu and W. Yang, Biomaterials, 2015, 39, 67–74 CrossRef CAS PubMed.
- S. Nemec, S. Kralj, C. Wilhelm, A. Abou-Hassan, M.-P. Rols and J. Kolosnjaj-Tabi, Appl. Sci., 2020, 10, 7322 CrossRef CAS.
- A. Kolokithas-Ntoukas, A. Bakandritsos, J. Belza, P. Kesa, V. Herynek, J. Pankrac, A. Angelopoulou, O. Malina, K. Avgoustakis, V. Georgakilas, K. Polakova and R. Zboril, ACS Appl. Mater. Interfaces, 2021, 13, 29247–29256 CrossRef CAS PubMed.
- H. Chen, J. Burnett, F. Zhang, J. Zhang, H. Paholak and D. Sun, J. Mater. Chem. B, 2014, 2, 757–765 RSC.
- A. Espinosa, J. Kolosnjaj-Tabi, A. Abou-Hassan, A. P. Sangnier, A. Curcio, A. K. A. Silva, R. Di Corato, S. Neveu, T. Pellegrino, L. M. Liz-Marzán and C. Wilhelm, Adv. Funct. Mater., 2018, 28, 1803660 CrossRef.
- S. Cabana, A. Curcio, A. Michel, C. Wilhelm and A. Abou-Hassan, Nanomaterials, 2020, 10(8), 1548 CrossRef CAS PubMed.
- K. Bilici, A. Muti, F. Demir Duman, A. Sennaroğlu and H. Yağcı Acar, Photochem. Photobiol. Sci., 2018, 17, 1787–1793 CrossRef CAS PubMed.
- H. Rodríguez-Rodríguez, G. Salas and J. R. Arias-Gonzalez, J. Phys. Chem. Lett., 2020, 11, 2182–2187 CrossRef PubMed.
- G. Salas, C. Casado, F. J. Teran, R. Miranda, C. J. Serna and M. P. Morales, J. Mater. Chem., 2012, 22, 21065–21075 RSC.
- B. Pacakova, S. Kubickova, G. Salas, A. R. Mantlikova, M. Marciello, M. P. Morales, D. Niznansky and J. Vejpravova, Nanoscale, 2017, 9, 5129–5140 RSC.
- G. Cotin, C. Kiefer, F. Perton, D. Ihiawakrim, C. Blanco-Andujar, S. Moldovan, C. Lefevre, O. Ersen, B. Pichon, D. Mertz and S. Bégin-Colin, Nanomaterials, 2018, 8, 881 CrossRef PubMed.
- G. Cotin, F. Perton, C. Petit, S. Sall, C. Kiefer, V. Begin, B. Pichon, C. Lefevre, D. Mertz, J.-M. Greneche and S. Begin-Colin, Chem. Mater., 2020, 32, 9245–9259 CrossRef CAS.
- G. Cotin, C. Blanco-Andujar, D.-V. Nguyen, C. Affolter, S. Boutry, A. Boos, P. Ronot, B. Uring-Lambert, P. Choquet, P. E. Zorn, D. Mertz, S. Laurent, R. N. Muller, F. Meyer, D. Felder Flesch and S. Begin-Colin, Nanotechnology, 2019, 30, 374002 CrossRef CAS PubMed.
- A. Walter, C. Billotey, A. Garofalo, C. Ulhaq-Bouillet, C. Lefèvre, J. Taleb, S. Laurent, L. Vander Elst, R. N. Muller, L. Lartigue, F. Gazeau, D. Felder-Flesch and S. Begin-Colin, Chem. Mater., 2014, 26, 5252–5264 CrossRef CAS.
- A. Walter, A. Garofalo, A. Parat, H. Martinez, D. Felder-Flesch and S. Begin-Colin, Nanotechnol. Rev., 2015, 4, 581–593 CAS.
- A. Walter, A. Garofalo, P. Bonazza, F. Meyer, H. Martinez, S. Fleutot, C. Billotey, J. Taleb, D. Felder-Flesch and S. Begin-Colin, ChemPlusChem, 2017, 82, 647–659 CrossRef CAS PubMed.
- A. Le Bail, Powder Diffr., 2005, 20, 316–326 CrossRef CAS.
- B. Mehdaoui, J. Carrey, M. Stadler, A. Cornejo, C. Nayral, F. Delpech, B. Chaudret and M. Respaud, Appl. Phys. Lett., 2012, 100, 052403 CrossRef.
- J. M. Miranda-Muñoz, D. Geng, M. E. Calvo, G. Lozano and H. Míguez, J. Mater. Chem. C, 2019, 7, 267–274 RSC.
- J. M. Miranda-Muñoz, V. Esteso, A. Jiménez-Solano, G. Lozano and H. Míguez, Adv. Opt. Mater., 2020, 8, 1901196 CrossRef.
- F. J. Teran, C. Casado, N. Mikuszeit, G. Salas, A. Bollero, M. P. Morales, J. Camarero and R. Miranda, Appl. Phys. Lett., 2012, 101, 062413 CrossRef.
- M. Johannsen, U. Gneveckow, L. Eckelt, A. Feussner, N. WaldÖFner, R. Scholz, S. Deger, P. Wust, S. A. Loening and A. Jordan, Int. J. Hyperthermia, 2005, 21, 637–647 CrossRef CAS PubMed.
- K. Maier-Hauff, F. Ulrich, D. Nestler, H. Niehoff, P. Wust, B. Thiesen, H. Orawa, V. Budach and A. Jordan, J. Neuro-Oncol., 2011, 103, 317–324 CrossRef PubMed.
- A. I. Martínez-Banderas, A. Aires, M. Quintanilla, J. A. Holguín-Lerma, C. Lozano-Pedraza, F. J. Teran, J. A. Moreno, J. E. Perez, B. S. Ooi, T. Ravasi, J. S. Merzaban, A. L. Cortajarena and J. Kosel, ACS Appl. Mater. Interfaces, 2019, 11, 43976–43988 CrossRef PubMed.
- O. A. Savchuk, J. J. Carvajal, J. Massons, M. Aguiló and F. Díaz, Carbon, 2016, 103, 134–141 CrossRef CAS.
- Y. P. He, Y. M. Miao, C. R. Li, S. Q. Wang, L. Cao, S. S. Xie, G. Z. Yang, B. S. Zou and C. Burda, Phys. Rev. B, 2005, 71, 125411 CrossRef.
-
R. M. Cornell and U. Schwertmann, The Iron Oxides: Structure, Properties, Reactions, Occurrences, and Uses: Wiley-VCH, Weinheim, 2nd, completely rev. and extended ed. edn, 2003 Search PubMed.
- G. Salas, J. Camarero, D. Cabrera, H. Takacs, M. Varela, R. Ludwig, H. Dähring, I. Hilger, R. Miranda, M. del P. Morales and F. J. Teran, J. Phys. Chem. C, 2014, 118, 19985–19994 CrossRef CAS.
- S. Kubickova, D. Niznansky, M. P. Morales Herrero, G. Salas and J. Vejpravova, Appl. Phys. Lett., 2014, 104, 223105 CrossRef.
- G. Baffou, I. Bordacchini, A. Baldi and R. Quidant, Light Sci. Appl., 2020, 9, 108 CrossRef PubMed.
- L. León Félix, B. Sanz, V. Sebastián, T. E. Torres, M. H. Sousa, J. A. H. Coaquira, M. R. Ibarra and G. F. Goya, Sci. Rep., 2019, 9, 4185 CrossRef PubMed.
- C. S. B. Dias, T. D. M. Hanchuk, H. Wender, W. T. Shigeyosi, J. Kobarg, A. L. Rossi, M. N. Tanaka, M. B. Cardoso and F. Garcia, Sci. Rep., 2017, 7, 14843 CrossRef PubMed.
- P. Hugounenq, M. Levy, D. Alloyeau, L. Lartigue, E. Dubois, V. Cabuil, C. Ricolleau, S. Roux, C. Wilhelm, F. Gazeau and R. Bazzi, J. Phys. Chem. C, 2012, 116, 15702–15712 CrossRef CAS.
- D. Lisjak and A. Mertelj, Prog. Mater. Sci., 2018, 95, 286–328 CrossRef CAS.
- D. Cheng, X. Li, G. Zhang and H. Shi, Nanoscale Res. Lett., 2014, 9, 195 CrossRef PubMed.
- Á. Gallo-Cordova, A. Espinosa, A. Serrano, L. Gutiérrez, N. Menéndez, M. del Puerto Morales and E. Mazarío, Mater. Chem. Front., 2020, 4, 3063–3073 RSC.
- A. Serrano, O. Rodríguez de la Fuente, M. García-Hernández, G. Campo, C. de Julián Fernández, J. F. Fernández and M. A. García, Appl. Phys. Lett., 2018, 113, 101908 CrossRef.
- S. P. Schwaminger, D. Bauer, P. Fraga-García, F. E. Wagner and S. Berensmeier, CrystEngComm, 2017, 19, 246–255 RSC.
- M. Testa-Anta, M. A. Ramos-Docampo, M. Comesaña-Hermo, B. Rivas-Murias and V. Salgueiriño, Nanoscale Adv., 2019, 1, 2086–2103 RSC.
- I. Chamritski and G. Burns, J. Phys. Chem. B, 2005, 109, 4965–4968 CrossRef CAS PubMed.
- A. Lak, M. Cassani, B. T. Mai, N. Winckelmans, D. Cabrera, E. Sadrollahi, S. Marras, H. Remmer, S. Fiorito, L. Cremades-Jimeno, F. J. Litterst, F. Ludwig, L. Manna, F. J. Teran, S. Bals and T. Pellegrino, Nano Lett., 2018, 18, 6856–6866 CrossRef CAS PubMed.
-
D. J. David
J. Griffiths, 1942-, Introduction to Electrodynamics, Fourth edition, Pearson, Boston, 2013, ©2013, p. 2013 Search PubMed.
- J. R. Melamed, R. S. Edelstein and E. S. Day, ACS Nano, 2015, 9, 6–11 CrossRef CAS PubMed.
- A. N. Bashkatov, E. A. Genina, V. I. Kochubey and V. V. Tuchin, J. Phys. D: Appl. Phys., 2005, 38, 2543–2555 CrossRef CAS.
- M. Friebel, J. . Helfmann, U. J. Netz and M. C. Meinke, J. Biomed. Opt., 2009, 14, 1–6 Search PubMed.
- J. Estelrich and M. A. Busquets, Molecule, 2018, 23(8), 1567 CrossRef PubMed.
- Z. Bao, X. Liu, Y. Liu, H. Liu and K. Zhao, Asian J. Pharm. Sci., 2016, 11, 349–364 CrossRef.
- X. Wang, Z. Li, Y. Ding, K. Wang, Z. Xing, X. Sun, W. Guo, X. Hong, X. Zhu and Y. Liu, Chem. Eng. J., 2020, 381, 122693 CrossRef CAS.
- J. G. Ovejero, D. Cabrera, J. Carrey, T. Valdivielso, G. Salas and F. J. Teran, Phys. Chem. Chem. Phys., 2016, 18, 10954–10963 RSC.
- D. Cabrera, A. Coene, J. Leliaert, E. J. Artés-Ibáñez, L. Dupré, N. D. Telling and F. J. Teran, ACS Nano, 2018, 12, 2741–2752 CrossRef CAS PubMed.
- R. Di Corato, A. Espinosa, L. Lartigue, M. Tharaud, S. Chat, T. Pellegrino, C. Ménager, F. Gazeau and C. Wilhelm, Biomaterials, 2014, 35, 6400–6411 CrossRef CAS PubMed.
- U. M. Engelmann, A. A. Roeth, D. Eberbeck, E. M. Buhl, U. P. Neumann, T. Schmitz-Rode and I. Slabu, Sci. Rep., 2018, 8, 13210 CrossRef PubMed.
- C. Blanco-Andujar, D. Ortega, P. Southern, S. A. Nesbitt, N. T. K. Thanh and Q. A. Pankhurst, Nanomed, 2016, 11, 121–136 CrossRef CAS PubMed.
- M. V. Zyuzin, M. Cassani, M. J. Barthel, H. Gavilan, N. Silvestri, A. Escudero, A. Scarpellini, F. Lucchesi, F. J. Teran, W. J. Parak and T. Pellegrino, ACS Appl. Mater. Interfaces, 2019, 11, 41957–41971 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1na00601k |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Ana
Espinosa
ab,
Begoña
Sot
ab,
Aida
Serrano
a,
Ana
Espinosa
ab,
Begoña
Sot
ab,
Aida
Serrano
 c,
Gorka
Salas
c,
Gorka
Salas
 ab,
Cristina
Blanco-Andujar
d,
Geoffrey
Cotin
d,
Delphine
Felder-Flesch
ab,
Cristina
Blanco-Andujar
d,
Geoffrey
Cotin
d,
Delphine
Felder-Flesch
 d,
Sylvie
Begin-Colin
d,
Sylvie
Begin-Colin
 d and
Francisco J.
Teran
d and
Francisco J.
Teran
 *ab
*ab
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5000 in DDW and injected into the instrument chamber using a 1 mL syringe. Camera settings were adjusted in order to focus the objective. The video data was collected for 60 seconds and repeated 3 times per sample.
5000 in DDW and injected into the instrument chamber using a 1 mL syringe. Camera settings were adjusted in order to focus the objective. The video data was collected for 60 seconds and repeated 3 times per sample.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TD. The total (TT), diffuse (Td), and direct transmittance and reflectance (RT, and Rd) measurements for LRL with distinct DH were carried out by UV-VIS-NIR spectroscopy (LAMBDA 650/850/950 spectrometer, PerkinElmer) in the spectral range from 600 to 1300 nm using the integrating sphere and universal reflectance accessories (see Fig. S4 at ESI†). The quartz cuvette was rotated 6° with respect to the incident light beam in the case of Rd measurements, in accordance with previous procedures.55,56 The TD configuration is the one supplied by spectrophotometers not having integrating sphere for transmission measurements. Control samples were the quartz cuvette filled with DDW or PBS.
TD. The total (TT), diffuse (Td), and direct transmittance and reflectance (RT, and Rd) measurements for LRL with distinct DH were carried out by UV-VIS-NIR spectroscopy (LAMBDA 650/850/950 spectrometer, PerkinElmer) in the spectral range from 600 to 1300 nm using the integrating sphere and universal reflectance accessories (see Fig. S4 at ESI†). The quartz cuvette was rotated 6° with respect to the incident light beam in the case of Rd measurements, in accordance with previous procedures.55,56 The TD configuration is the one supplied by spectrophotometers not having integrating sphere for transmission measurements. Control samples were the quartz cuvette filled with DDW or PBS.
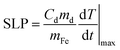
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to lysate cells and dissolve the particles, in order to quantify the iron content. To compare the IONPs heating behaviour in aqueous solution and inside cells, IONP colloidal dispersions were prepared at the same iron concentration than cell pellets (2 gFe L−1) and subjected to the same NIR and HAC conditions previously described. SLP values were determined by employing an extension of eqn (1):
1) to lysate cells and dissolve the particles, in order to quantify the iron content. To compare the IONPs heating behaviour in aqueous solution and inside cells, IONP colloidal dispersions were prepared at the same iron concentration than cell pellets (2 gFe L−1) and subjected to the same NIR and HAC conditions previously described. SLP values were determined by employing an extension of eqn (1):