Self-passivation leads to semiconducting edges of black phosphorene†
Li Ping
Ding
 ab and
Feng
Ding
ab and
Feng
Ding
 *ac
*ac
aCenter for Multidimensional Carbon Materials, Institute for Basic Science (IBS), Ulsan 44919, Republic of Korea. E-mail: f.ding@unist.ac.kr
bDepartment of Optoelectronic Science & Technology, School of Electronic Information and Artificial Intelligence, Shaanxi University of Science & Technology, Xi’an 710021, China
cDepartment of Materials Science and Engineering, Ulsan National Institute of Science and Technology (UNIST), Ulsan 44919, Republic of Korea
First published on 14th December 2020
Abstract
The edges of black phosphorene (BP) have been extensively explored. The previous experimental observations that all the BP edges are semiconducting implies that the as-cut edges of BP tend to be reconstructed. Here we present a global structural search of three typical BP edges, namely armchair, zigzag and zigzag-1 edges. It is found that all the three pristine edges are metastable, and all of them can be quickly self-passivated by (i) forming P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P double bonds (one σ and one π bond), (ii) reconstructing new polygonal rings will all P atoms bonded with three sp3 bonds or (iii) forming a special P(2)–P(4) configuration with a two-coordinated P atom accommodating two lone pair electrons and one four-coordinated P atom without lone pair electrons. Highly different from the pristine edges, all these highly stable reconstructed edges are semiconducting. This study showed that the reconstruction of the edges of a 2D material, just like the surfaces of a 3D crystal, must be considered for both fundamental studies and practical applications. Besides BP, this study also sheds light on the structures and properties of the edges of many other 2D materials.
P double bonds (one σ and one π bond), (ii) reconstructing new polygonal rings will all P atoms bonded with three sp3 bonds or (iii) forming a special P(2)–P(4) configuration with a two-coordinated P atom accommodating two lone pair electrons and one four-coordinated P atom without lone pair electrons. Highly different from the pristine edges, all these highly stable reconstructed edges are semiconducting. This study showed that the reconstruction of the edges of a 2D material, just like the surfaces of a 3D crystal, must be considered for both fundamental studies and practical applications. Besides BP, this study also sheds light on the structures and properties of the edges of many other 2D materials.
New conceptsSimilar to the surface of three-dimensional (3D) materials, the edge of a two-dimensional (2D) material has a great impact on its fundamental properties and applications. In this study, using black phosphorene as an example, we showed that the complete understanding of the edge reconstruction of a 2D material is possible because of the reduced dimensionality. Three typical edges of black phosphorene (BP), namely armchair, zigzag and zigzag-1 edges, have been studied based on a global structural search method, which is different from the previous manual studies. It is found that all the three pristine edges are metastable, and they can be quickly self-passivated by three types of configurations. Highly different from the previous pristine edges, all these highly stable reconstructed edges are found to be semiconducting, which explains the puzzling experimental observations. This study implies that the highly stable reconstructed edges of BP are expected to pave a way for stabilizing BP for real applications. Furthermore, it also demonstrates the importance of considering the edge reconstruction in understanding the fundamental properties of various 2D materials and, therefore, carefully re-exploring the electronic properties of the edges of various 2D materials, such as those of various 2D nanoribbons, is necessary. |
Introduction
On the tenth anniversary of the birth of graphene, another single element two-dimensional (2D) material, black phosphorene (BP), was successfully exfoliated from the black phosphorus bulk and immediately received considerable attention because of its exotic properties, such as very high carrier mobility, tunable bandgap and high anisotropy.1–3 Unlike graphene, 2D black phosphorus is a promising semiconductor possessing a direct band gap which can be tuned from 0.59 eV (five-layers) to 1.51 eV (mono-layer) by thickness control.4 In addition, its peculiar orthorhombic structure resembling corrugated cardboard results in high anisotropy with respect to the in-plane direction. Together with the high carrier mobility of over 1000 cm2 V−1 s−1 at room temperature, the layer-dependent direct band gap and anisotropic property promise its applications in high performance optoelectronics,5,6 transistors7,8 and other novel devices.9–14 For example, BP based field-effect transistors2,7,8 have exhibited a high on/off ratio of 105. Meanwhile, in sharp contrast with graphene, BP is known to be highly unstable and to stabilize BP is the primary goal towards its applications.As is well known, the surface is a key part of a three-dimensional (3D) material, and it may affect the mechanical, electronic and chemical properties of the material greatly, but finding the exact surface structure of a 3D material is a great challenge until now. Just like the surface of a 3D material, the edges of a 2D material also have a great impact on its properties,15–19 and it is lucky that the reduced dimensionality allows us to explore the exact atomic structure of the one dimensional (1D) edges of 2D materials relatively easily.20,21 In this study, we explore the edge reconstruction of BP and the electronic properties of the reconstructed edges. Generally, a freshly cleaved edge of a 2D material has some unsaturated orbitals or dangling bonds, which results in a high formation energy of the edge and possible rearrangement of electrons or atoms in the vicinity of the edge to form more stable bonding configurations or reconstructed edges. A reconstructed edge generally has very different electronic, optical and magnetic properties from the pristine one and is more practical for real applications.19,22–26
Because of the excellent properties of BP, BPNRs have drawn great attention and have been explored extensively. Although some previous studies have mentioned the possibility of edge reconstruction, most of them consider freshly cleaved pristine BP edges and have found that BPNRs with pristine armchair (AC) edges are semiconducting,27,28 while those with pristine zigzag (ZZ) and zigzag-1 (ZZ1) edges are metallic.29–32 In 2014, Meunier et al.33 determined a model for phosphorene edge reconstruction through a combination of high-resolution scanning tunnelling spectroscopy (STS) and first-principles calculations. Their results showed that most of the dangling bonds of the edge are self-passivated by switching the coordination number of edge atoms. In 2016, Gao et al.34 identified a highly stable zigzag edge with nanotube-like reconstruction theoretically. In 2017, Kim and co-workers35 showed two reconstructed models of the ZZ edge of few-layer phosphorene based on transmission electron microscopy (TEM) and density functional theory (DFT) calculations. These pioneering studies emphasized the fact that the as-cut edges of BP are generally unstable and may undergo reconstructions. However, all the structures in previous studies were made manually based on the experiences of the researchers and a systematic search for all possible edge configurations and the exploration of their electronic stabilities are still absent.
In this study, we present a systematic study on the edge reconstruction of BP based on an unbiased global search method with the software package of Crystal structure AnaLYsis by Particle Swarm Optimization (CALYPSO),36,37 combined with first-principles calculations. Three series of reconstructed phosphorene edges along the AC, ZZ and ZZ1 directions, respectively (Fig. 1b), are revealed and their relative stabilities are calculated. It was found that all highly stable edges are self-passivated and are semiconducting, which proves that edge self-passivation is highly important for determining the electronic properties of BPNRs and their applications.
Results and discussion
The structures of the reconstructed edges of BP
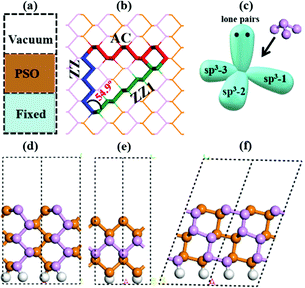
To explicitly explore the edge reconstruction of BP, we have performed a systematic structural search. As shown in Fig. 1a, there are three parts in the search model: fixed, relaxed and the vacuum region. Three types of highly symmetric edges (Fig. 1b), AC (Fig. 1d), ZZ (Fig. 1e) and ZZ1 (Fig. 1f), are considered. The purpose of frozen nanoribbons with hydrogen-passivated armchair (zigzag) edges is to simplify the edge prediction calculations. The edge formation energies of the final structures are calculated by: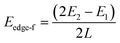 | (1) |
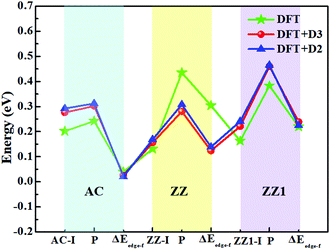
The top five most stable structures and their formation energies of the AC, ZZ and ZZ1 edges are presented in Fig. 2. For comparison, the broadly explored pristine edge structures in previous studies27–31 are also shown. More low-lying energy structures are displayed in Fig. S1 of the ESI.† It is found that some of the optimized structures have been reported in previous experimental33,35 and theoretical studies,34 indicating the reliability of our global structural search. To verify the effect of van der Waals force correction in the calculations, we re-optimized the lowest energy reconstructed-edge structures (AC-I, ZZ-I and ZZ1-I) and pristine edge structures using the DFT-D3 and DFT-D2 methods.38,39 The results are shown in Fig. 3 and Table S1 (ESI†). It is found that the stability orders of the structures based on the three methods are identical, and the structures with edge reconstruction are still more stable than the pristine ones.
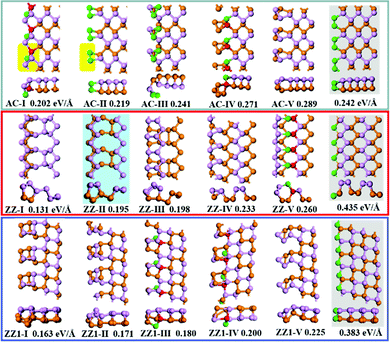 | ||
| Fig. 2 The highly stable structures of AC, ZZ and ZZ1 edges together with their edge formation energies (units of eV Å−1) shown below each configuration. The pristine edge structures without considering edge reconstruction are shown with a gray background. The structure ZZ-II with a light blue background has been reported in the literature.34 The orange, pink, red and green spheres represent the lower level phosphorus atoms, the upper level phosphorus atoms, and the phosphorus atoms which have four sp3 bonds and two sp3 bonds, respectively. | ||
In all stable isomers of bulk phosphorus, an sp3-hybridized P atom bonds with three neighboring P atoms and one of its sp3 orbitals is occupied by a lone pair (Fig. 1c). A pristine phosphorene edge generally has unpaired electrons known as dangling bonds, leading to a high formation energy and lower stability. As will be seen in our analysis, the dangling bonds in most low-lying reconstructed edges are properly passivated and the stabilities of these edges are greatly enhanced. From their edge formation energies shown below each configuration of Fig. 2, we can see that most of these reconstructed edges are much more stable than the pristine ones.
The most stable AC edge, AC-I, has a quadrangle and a pentagon in a unit cell (shown with the region with a yellow background). This leads to a unique edge reconstruction with one P atom being two coordinated and one of its neighboring P atoms being four coordinated; we name it the P(2)–P(4) reconstruction hereafter. The edge formation energy of this structure is 0.202 eV Å−1, which is lower than the pristine AC edge (0.242 eV Å−1). The P(2)–P(4) reconstruction is also shown in other low-lying structures, such as AC-IV, AC-VII, AC-IX and AC-XII (some of these structures are shown in Fig. S1, ESI†). In the reconstructed edge of the second low-lying structure (AC-II), the two P edge atoms are connected by a double bond P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P (one σ and one π bond). The P
P (one σ and one π bond). The P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P reconstruction is highly different from the sp3 hybridized P atoms in bulk black phosphorus isomers.41,42 In edge structure AC-V, four edge atoms were reconstructed into a P4 cluster and the P4 cluster connects with the bulk part of BP with two σ bonds. In such a configuration, all atoms have three sp3 bonds. However, the angles between neighboring sp3 bonds in structure AC-V are very different from those in bulk BP, resulting in a relative higher energy of the AC-V edge.
P reconstruction is highly different from the sp3 hybridized P atoms in bulk black phosphorus isomers.41,42 In edge structure AC-V, four edge atoms were reconstructed into a P4 cluster and the P4 cluster connects with the bulk part of BP with two σ bonds. In such a configuration, all atoms have three sp3 bonds. However, the angles between neighboring sp3 bonds in structure AC-V are very different from those in bulk BP, resulting in a relative higher energy of the AC-V edge.
The most stable reconstructed ZZ-I edge exhibits a greatly reconstructed nanotube-like structure, which is very different from those shown in previous studies.27–31,33–35 In comparison with the pristine AC edge, the pristine ZZ edge possesses a much larger formation energy, 0.435 eV Å−1, but the ZZ-I edge has a much lower formation energy of 0.131 eV Å−1 only. It is worth mentioning that the tube-like zigzag edge reconstruction that was proposed by Gao and coauthors in a previous study (structure z5 in ref. 34) is the second low-lying reconstructed ZZ edge (ZZ-II) in this work. In the ZZ-I structure and the most low-lying reconstructed edges, all phosphorus atoms are bonded with three neighboring atoms and the bonding configuration of P(2)–P(4) is also seen in some low-lying structures (e.g., ZZ-V, ZZ-VII, ZZ-VIII, ZZ-IX and ZZ-XI), which further validated the preferred bonding configuration analysis.
The pristine ZZ1 edge has a similar bonding configuration to the pristine ZZ one and is also highly unstable and the formation energy of the most stable reconstructed edge (ZZ1-I) is just 0.032 eV Å−1 higher than that of the ZZ-I edge. Similar to the ZZ edge, many low-lying reconstructed ZZ1 edges have the bonding configuration of three neighboring σ bonds (ZZ1-II, ZZ1-VI, ZZ1-VIII, ZZ1-IX and ZZ1-XI) and some have the P(2)–P(4) bonding configuration (ZZ1-III, ZZ1-IV).
To explore the effect of edge stress, which has been confirmed to have a significant effect on pristine BP nanoribbons,40 we have optimized the unit cell length of BP ribbons with the three most stable edges (AC-I, ZZ-I and ZZ1-I) and two types of pristine edges (AC and ZZ). The residual stress versus the inverse width of the BP nanoribbons is shown in Fig. S2 of the ESI.† From Fig. S2 (ESI†), a linear relationship is observed between the residual strain and 1/W. The effect of the edge stress on the structures with AC and AC-I edges is minor, and the ZZ, ZZ-I and ZZ1-I edges have much larger residual strain, which is in good agreement with the previous results (AC and ZZ edges).40 Obviously, the residual strains of various edges of BP ribbons are less than 2%, indicating that the the effect of edge stress on the morphology of BP ribbons is negligible.
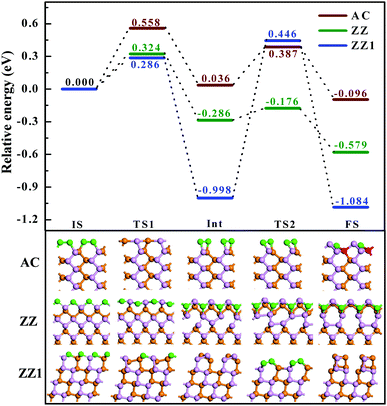
Next, let's consider how difficult it is to reconstruct a pristine edge of BP. By searching the transition path and the corresponding energy barriers, we analyze the kinetic processes of the three pristine edge reconstructions. The optimized route of a pristine AC edge reconstruction is presented using the wine line in Fig. 4. The pristine AC edge can be easily transformed into the most stable edge via AC-II as an intermediate state by overcoming two small barriers of 0.558 and 0.387 eV, respectively. This means such an edge reconstruction may occur quickly at room temperature and thus the experimental observation of pristine AC edges in BP is impossible. As shown by the green line in Fig. 4, the barrier of the ZZ edge reconstruction, 0.324 eV, is even lower than that of the AC edge and, therefore, the experimental observation of the pristine ZZ edge at room temperature is also impossible. In comparison with the ZZ edge, there is a low energy intermediate for the ZZ1 edge reconstruction and the barrier between the intermediate and the final structure is ∼1.4 eV, which is significantly larger than those of the AC and ZZ edge reconstructions. Although such a barrier is a little higher, overcoming such a barrier is quite easy at an elevated temperature, such as 500 K.
The types and stabilities of BP edge reconstruction
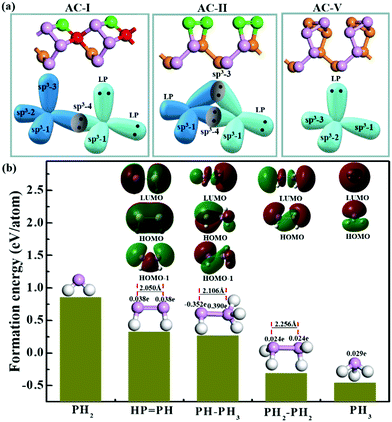
As mentioned above, all the low-lying AC, ZZ and ZZ1 reconstructed edges are dominated by the three primary types of specific edge configurations shown in Fig. 5a, P(2)–P(4) (e.g., AC-I), P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P (e.g., AC-II) and a reconstructed edge with all P atoms having three sp3 bonds (e.g., AC-V). The high stabilities of these three types of bonding configurations can be quantified based on the formation energy of PxHy stoichiometries, which is defined as:
P (e.g., AC-II) and a reconstructed edge with all P atoms having three sp3 bonds (e.g., AC-V). The high stabilities of these three types of bonding configurations can be quantified based on the formation energy of PxHy stoichiometries, which is defined as: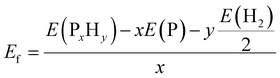 | (2) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PH > PH2. This result clearly indicates that (i) each P atom connected by three sp3 bonds (PH3 and PH2–PH2), which is similar to the bonding configuration of bulk phosphorus, is the most preferred bonding configuration; (ii) the bonding configuration of one P atom possessing two sp3 bonds connecting with a neighboring P atom possessing four sp3 bonds (PH–PH3) or two neighboring P atoms forming a double bond (HP
PH > PH2. This result clearly indicates that (i) each P atom connected by three sp3 bonds (PH3 and PH2–PH2), which is similar to the bonding configuration of bulk phosphorus, is the most preferred bonding configuration; (ii) the bonding configuration of one P atom possessing two sp3 bonds connecting with a neighboring P atom possessing four sp3 bonds (PH–PH3) or two neighboring P atoms forming a double bond (HP![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PH) is the secondary option of edge reconstruction; and (iii) the bonding configuration in which the P atom has dangling bonds (PH2) is highly unfavorable. This further explains why the freshly cleaved edges of phosphorene, which always have some dangling bonds, tend to be reconstructed.
PH) is the secondary option of edge reconstruction; and (iii) the bonding configuration in which the P atom has dangling bonds (PH2) is highly unfavorable. This further explains why the freshly cleaved edges of phosphorene, which always have some dangling bonds, tend to be reconstructed.
The stability of the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P configuration (AC-II) can be easily understood based on the similarity of graphene AC edge reconstruction, where two unpaired electrons of a pair of neighboring atoms form an additional C–C π bond.21 In a BP edge, the two neighboring dangling σ bonds and the two unpaired electrons tend to be reconstructed into a π bond between the two neighboring edge P atoms, which leads to the transformation from P*–P* (where * represents a dangling bond or radical) to a P
P configuration (AC-II) can be easily understood based on the similarity of graphene AC edge reconstruction, where two unpaired electrons of a pair of neighboring atoms form an additional C–C π bond.21 In a BP edge, the two neighboring dangling σ bonds and the two unpaired electrons tend to be reconstructed into a π bond between the two neighboring edge P atoms, which leads to the transformation from P*–P* (where * represents a dangling bond or radical) to a P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P double bond with the P atoms sp2 hybridized. This existence of a π bond can be clearly seen in the highest occupied orbital (HOMO) of the HP
P double bond with the P atoms sp2 hybridized. This existence of a π bond can be clearly seen in the highest occupied orbital (HOMO) of the HP![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PH cluster (as shown in Fig. 5b) and the two lone pairs (green regions) and a σ bond (red region) are shown in the HOMO−1 orbital. Besides, the length of the P
PH cluster (as shown in Fig. 5b) and the two lone pairs (green regions) and a σ bond (red region) are shown in the HOMO−1 orbital. Besides, the length of the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P double bond (2.050 Å) is about 10% shorter than that of the single bond, shown in the PH2–PH2 (2.256 Å) configuration. In the most preferred bonding configurations (PH3 and PH2–PH2), the lone pairs (red regions) are shown in their HOMOs. The HOMOs, the LUMOs (lowest unoccupied orbitals) and the natural population analysis (NPA) were obtained by using the Gaussian 09 program package.43
P double bond (2.050 Å) is about 10% shorter than that of the single bond, shown in the PH2–PH2 (2.256 Å) configuration. In the most preferred bonding configurations (PH3 and PH2–PH2), the lone pairs (red regions) are shown in their HOMOs. The HOMOs, the LUMOs (lowest unoccupied orbitals) and the natural population analysis (NPA) were obtained by using the Gaussian 09 program package.43
The stability of the P(2)–P(4) configuration can be understood based on the octet rule. In the P(2)–P(4) configuration, each P atom is sp3 hybridized and has four σ orbitals. The four orbitals of the P atom which is four coordinated are occupied by sharing electrons with its neighbors. Two σ orbitals of the P atom which is two coordinated are occupied by sharing electrons with neighboring P atoms to form σ bonds, while the other two σ orbitals are occupied by two lone pairs, which can be clearly seen in the HOMO of the PH–PH3 molecule (Fig. 5b). With two lone pairs, the P atom which is two coordinated must be electron rich and the P atom without lone pairs must be electron deficient. The computational results clearly showed that the P atom with two lone pairs is heavily negatively charged (−0.35 e) and its neighboring P atom, which is four coordinated, is positively charged (+0.39 e). Such a bonding configuration ensures that each atom satisfies the octet rule and thus is a stable configuration as shown in many low-lying edge structures.
In order to further verify the thermal stability of these reconstructed edges, we have performed molecular dynamics (MD) simulations of the three lowest-energy BP nanoribbons (with AC-I, ZZ-I and ZZ1-I edges) at a temperature of 900 K. The energy profiles and some structures observed in the MD simulations are shown in Fig. S3 of the ESI.† It is found that all these edges only undergo slight changes in the MD trajectories of ∼9 ps (see the videos in the ESI†) and all the final structures of the simulations can be easily optimized to be the initial ones exactly (AC-I, ZZ-I and ZZ1-I), indicating the high stability of these edges.
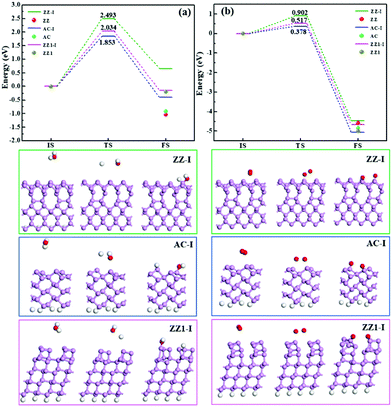
Besides the thermal stability of these edges in a vacuum, it is important to explore their chemical stability in an ambient environment. We have studied the reactions between the edge reconstructed BP nanoribbons and O2 and H2O molecules, respectively. As can be seen in Fig. 6, the dissociation of an H2O molecule on the ZZ-I edge is endothermic with a high reaction barrier of 2.493 eV (Fig. 6a). The dissociation of an H2O molecule on the AC-I and ZZ1-I edges is slightly exothermic and the reactions are as high as 1.853 eV and 2.034 eV, respectively, suggesting that all these three types of reconstructed edges are chemically stable to H2O. For the dissociation of an O2 molecule on the three reconstructed edges (AC-I, ZZ-I and ZZ1-I), all the processes are exothermic, and the energy barriers (Fig. 6b) are relative lower, implying that the O2 molecule can react with BP at room temperature. For comparison, the reaction energies of H2O or O2 dissociation on the pristine AC, ZZ and ZZ1 edges are also shown in Fig. 6. The exothermic reaction energy (−0.918 eV) of H2O dissociation on the pristine AC edge agrees well with the previous theoretical value (∼0.8 eV).44 It can be clearly seen that all the reconstructed edges are more stable than the pristine ones.
In a brief summary, we have systematically explored the most stable configurations of three typical edges of BP and significant reconstruction to self-passivate the dangling bonds formed during the cleavage of phosphorene was found for all edges. Three typical self-passivation configurations, the formation of P(2)–P(4), P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P double bonds and all atoms forming three σ sp3 bonds, have been found to dominate most of the low-lying edge configurations. Besides, the kinetic analysis proves that the energy barriers of edge passivation are all very small, which means that the pristine edges of BP are hardly observed experimentally.
P double bonds and all atoms forming three σ sp3 bonds, have been found to dominate most of the low-lying edge configurations. Besides, the kinetic analysis proves that the energy barriers of edge passivation are all very small, which means that the pristine edges of BP are hardly observed experimentally.
Electronic properties of the reconstructed edges of BP
With very high carrier mobility and a mild band gap, the electronic properties of BP are highly distinct from those of other 2D materials. The electronic properties of the edge of BP have been extensively explored based on the BP nanoribbon (BPNR) model. The results of edge reconstruction shown above proved that pristine edges in BP or BPNRs with pristine edges are hardly observed in real experiments, so understanding the electronic properties of the reconstructed edges is important for both fundamental studies and applications. To explore the electronic properties with high accuracy, all the electronic band structures, band decomposed charge densities and densities of states (DOSs) are calculated based on the HSE06 exchange–correlation functional, which is known to be highly reliable for electronic property calculations.4,45,46The calculated band structures of some edge-reconstructed BPNRs are displayed in Fig. 7. In all the plots of the band structures, the conduction band minimum (CBM) and valence band maximum (VBM) of 2D phosphorene are labeled as 2D-CBM and 2D-VBM, respectively. In comparison, the band structures calculated by the PBE method are presented in Fig. S4 (ESI†) and we can see clearly that the band gaps are greatly underestimated.
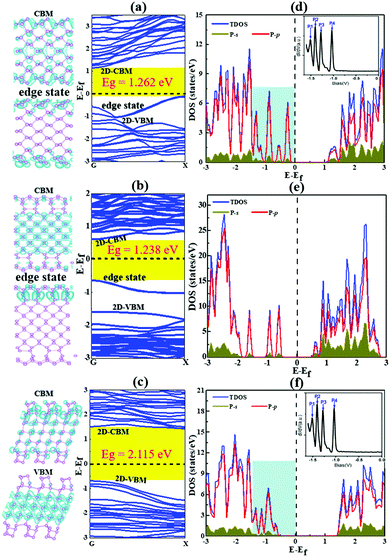 | ||
| Fig. 7 The band structures and band decomposed charge density of BP nanoribbons with the most stable reconstructed edges, AC-I (a), ZZ-I (b) and ZZ1-I (c). The valence band maximum (VBM) and conduction band minimum (CBM) are labeled as 2D-VBM and 2D-CBM, respectively, and the edge states around the Fermi level are also labeled in all plots. (d–f) The corresponding density of states of these BPNRs. The Fermi level is set at 0 eV. The DOSs of both the AC-I and ZZ1-I edges within the light blue background are similar to the experimental dI/dV spectra33 (Copyright 2014, American Chemical Society) as shown in the inserted figure. | ||
As presented in Fig. 7, our calculation shows that all the reconstructed edges are semiconducting and the bandgaps of them are 1.26, 1.23 and 2.11 eV for AC-I, ZZ-I and ZZ1-I, respectively. The band gap opening at the reconstructed edges of BP can be easily understood by the self-passivation of dangling bonds or the unpaired electrons of the pristine edges. Both the AC-I and ZZ-I edges have occupied edge states between the VBM and CPM of bulk BP, and thus the band gaps of both AC-BPNR and ZZ-BPNR are greatly reduced in comparison with the band gap of bulk BP (∼2.0 eV). An important feature of all these BPNRs is the edge states above the bulk VBM. In a previous experimental study,33 the electronic properties of BP edges have been explored and the key features, that there are four peaks above the VBM of the bulk (inset of Fig. 7 and Fig. S5a, ESI†), are in excellent agreement with our study. As shown in Fig. 7, we can see that the DOSs of BPNRs with reconstructed AC-I or ZZ1-I edges show the exact same feature as that shown in the experimental dI/dV curve, which confirms that the edges of BP observed in the previous experiment must be reconstructed. Furthermore, the band gaps of the three edge reconstructed BPNRs as a function of the width of the BPNR have been explored (Fig. S6, ESI†). It is found that all the edge reconstructed AC-I BPNRs have indirect band gaps and most BPNRs with reconstructed ZZ-I and ZZ1-I edges have direct band gaps at the G point. When the width of the ribbon is small, the band gap of AC-I increases with the ribbon width (<∼1.35 nm), while the band gap of ZZ-I decreases very slightly and that of ZZ1-I undergoes odd–even oscillation (<∼2.25 nm). It may be due to the fact that the direct interaction between the two edges becomes dominant when the two edges are very close to each other, which results in the irregular variation of the band gaps. Once the width of a BPNR is greater than ∼2.25 nm, the band gap will not vary much with the further increase of the width. This implies that tuning the band gap of a BPNR by varying its width is not as efficient as that by increasing the thickness of BP, which allows the band gap to be reduced from ∼2.0 to 0.3 eV.4,33,47
In comparison, the band structures of the pristine BPNRs are shown in Fig. S7. We can see that only BPNRs with pristine AC edges are semiconducting with a band gap of 1.02 eV. In a unit cell of a pristine AC edge, the two dangling bonds are located at two neighboring AC atoms and the two unpaired electrons and the two half-filled orbitals will rehybridize into a new chemical bond and make the two edge atoms bonded with a double bond. The double bonds formed at the pristine AC edge greatly enhance its stability and the paired electrons lead to its semiconducting properties. With the dangling bonds distributed along the pristine ZZ and ZZ1 edges, it is not surprising that both edges are significantly less stable and are conducting. Their edge states are located between the VBM and CBM of bulk BP and both are half-occupied, which contributes to the conductivity of the pristine edges.
Conclusions
In summary, our global search has shown that all the pristine edges of black phosphorene, including AC, ZZ and ZZI, are energetically not stable and they can be quickly reconstructed into more stable ones under ambient conditions. Three series of reconstructed edges are revealed and those highly stable ones are self-passivated by three primary configurations: (i) forming out-of-plane polygons with all P atoms bonded with three sp3 bonds; (ii) forming a special P(2)–P(4) configuration with one P atom accommodating two lone pair orbitals and another P atom having four sp3 bonds; and (iii) forming a double bond between the two neighboring P atoms. Further analysis showed that all the reconstructed edges are semiconducting and the band gaps are drastically different from those of the pristine edges. This study implies that most previously predicated electronic properties of BPNRs are hardly observed experimentally. In real applications, the highly stable reconstructed edges of BP are expected to pave a way for stabilizing BP. This study clearly demonstrates the importance of considering the edge reconstruction in understanding the fundamental properties of various 2D materials and, therefore, carefully re-exploring the electronic properties of the edges of various 2D materials, such as 2D nanoribbons, is necessary.Computational details
We have explored the reconstructions of AC, ZZ and ZZ1 edges of black phosphorene by using the CALYPSO package.36,37 CALYPSO is an unbiased global structure search package which has the capability of predicting the surface reconstruction of bulk materials.48,49 During the structural search, we considered two supercells with one and two unit cell sizes, respectively, and the atoms far from the edge were fixed during the structural optimization to mimic the bulk of black phosphorene. During the structure search, 60% of the 50 candidates in each generation are generated by the Particle Swarm Optimization (PSO) algorithm and another 40% are generated randomly and all the structures are optimized by the density functional theory (DFT) method implemented in the Vienna Ab initio Simulation Package (VASP)50,51 with a relatively low cutoff energy of 300 eV. After the search terminated at 30 generations, the most stable 100 structures were further optimized by using a cutoff energy of 450 eV. The generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) functional and projector augmented wave (PAW) potentials are adopted in all calculations.52,53 The energy and force convergence criteria of structure optimization are 10−5 eV and 0.01 eV Å−1, respectively. A vacuum space larger than 15 Å was used to avoid interactions between neighboring images along the non-periodic directions. The calculations of the electronic properties are carried out using the Heyd–Scuseria–Ernzerhof (HSE06)54,55 hybrid exchange–correlation functional. The energy barriers are calculated by using the climbing image nudged elastic band (CI-NEB) method56 with a force threshold of 0.02 eV Å−1.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Institute for Basic Science (IBS-R019-D1) of South Korea and the computational resources from CMCM, IBS, National Natural Science Foundation of China (No. 11804212), Natural Science Foundations of Shaanxi Province (No. 2019JM-053), and Youth Talent Invitation Scheme of Shaanxi Association for science and technology (No. 20190506). We acknowledge Dr Bo Gao, who is a group member of Prof. Yan-Ming Ma, for his help during the structure search.Notes and references
- A. S. Rodin, A. Carvalho and A. H. Castro Neto, Phys. Rev. Lett., 2014, 112, 176801 CrossRef CAS.
- L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2014, 9, 041411 Search PubMed.
- X. Ling, H. Wang, S. X. Huang, F. N. Xia and M. S. Dresselhaus, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4523–4530 CrossRef CAS.
- J. S. Qiao, X. H. Kong, Z. X. Hu, F. Yang and W. Ji, Nat. Commun., 2014, 5, 4475 CrossRef CAS.
- J. Bullock, M. Amani, J. Cho, Y. Z. Chen, G. H. Ahn, V. Adinolfi, V. R. Shrestha, Y. Gao, K. B. Crozier, Y. L. Chueh and A. Javey, Nat. Photonics, 2018, 12, 601–607 CrossRef CAS.
- J. Liu, Y. Chen, Y. Li, H. Zhang, S. Zheng and S. Xu, Photonics Res., 2018, 6, 198–203 CrossRef CAS.
- R. A. Doganov, S. P. Koenig, Y. Yeo, K. Watanabe, T. Taniguchi and B. Özyil-maz, Appl. Phys. Lett., 2015, 106, 083505 CrossRef.
- F. Ahmed, Y. D. Kim, Z. Yang, P. He, E. H. Hwang, H. S. Yang, J. Hone and W. J. Yoo, Nat. Commun., 2018, 9, 3414–3421 CrossRef.
- L. Chen, G. Zhou, Z. Liu, X. Ma, J. Chen, Z. Zhang, X. Ma, F. Li, H. M. Cheng and W. Ren, Adv. Mater., 2016, 28, 510–517 CrossRef CAS.
- Q. Li, H. Liu, Z. Yao, J. Cheng, T. Li, Y. Li, C. Wolverton, J. Wu and V. P. Dravid, ACS Nano, 2016, 10, 8788–8795 CrossRef CAS.
- G. Zhao, T. L. Wang, Y. L. Shao, Y. Z. Wu, B. B. Huang and X. P. Hao, Small, 2017, 13, 1602243 CrossRef.
- J. Hu, Z. Guo, P. E. McWilliams, J. E. Darges, D. L. Druffel, A. M. Moran and S. C. Warren, Nano Lett., 2016, 16, 74–79 CrossRef CAS.
- L. Kou, T. Frauenheim and C. Chen, J. Phys. Chem. Lett., 2014, 5, 2675–2681 CrossRef CAS.
- Y. Yao, H. Zhang, J. Sun, W. Ma, L. Li, W. Li and J. Du, Sens. Actuators, B, 2017, 244, 259–264 CrossRef CAS.
- P. Koskinen, S. Malola and H. Häkkinen, Phys. Rev. Lett., 2008, 101, 115502 CrossRef.
- T. Wassmann, A. P. Seitsonen, A. M. Saitta, M. Lazzeri and F. Mauri, Phys. Rev. Lett., 2008, 101, 096402 CrossRef.
- B. Huang, M. Liu, N. Su, J. Wu, W. Duan, B. L. Gu and F. Liu, Phys. Rev. Lett., 2009, 102, 166404 CrossRef.
- J. Gao, J. Zhao and F. Ding, J. Am. Chem. Soc., 2012, 134, 6204–6209 CrossRef CAS.
- X. Yin, Z. L. Ye, D. A. Chenet, Y. Ye, K. O’Brien, J. C. Hone and X. Zhang, Science, 2014, 344, 488–490 CrossRef CAS.
- X. T. Jia, M. Hofmann, V. Meunier, B. G. Sunpter, J. Campos-Delgado, J. M. Romo-Herrera, H. Son, Y. P. Hsieh, A. Reina, J. Kong, M. Terrones and M. S. Dresselhaus, Science, 2009, 323, 1701–1705 CrossRef CAS.
- P. Koskinen, S. Malola and H. Häkkinen, Phys. Rev. Lett., 2008, 101, 115502 CrossRef.
- A. H. Castro Neto, F. Guinea and N. M. R. Peres, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205408 CrossRef.
- Y. W. Son, M. L. Cohen and S. G. Louie, Nature, 2006, 444, 347–349 CrossRef CAS.
- Y. Li, Z. Zhou, S. Zhang and Z. Chen, J. Am. Chem. Soc., 2008, 130(167), 39–16744 Search PubMed.
- E. V. Castro, N. M. R. Peres, J. M. B. Lopes dos Santos, A. H. C. Neto and F. Guinea, Phys. Rev. Lett., 2008, 100, 026802 CrossRef.
- X. H. Deng, Z. Y. Li and J. L. Yang, J. Phys. Chem. Lett., 2020, 11, 7531–7535 CrossRef CAS.
- M. U. Farooq, A. Hashmi and J. Hong, ACS Appl. Mater. Interfaces, 2015, 7, 14423–14430 CrossRef CAS.
- X. Peng, A. Copple and Q. Wei, J. Appl. Phys., 2014, 116, 144301 CrossRef.
- W. Li, G. Zhang and Y. W. Zhang, J. Phys. Chem. C, 2014, 118, 22368–22372 CrossRef CAS.
- H. Guo, N. Lu, J. Dai, X. Wu and X. C. Zeng, J. Phys. Chem. C, 2014, 118, 14051–14059 CrossRef CAS.
- A. Carvalho, A. S. Rodin and A. H. C. Neto, Europhys. Lett., 2014, 108, 47005–47011 CrossRef.
- J. H. Huang, X. F. Wang, Y. S. Liu and L. P. Zhou, Nanoscale Res. Lett., 2019, 14, 145–156 CrossRef.
- L. B. Liang, J. Wang, W. Z. Lin, B. G. Sumpter, V. Meunier and M. H. Pan, Nano Lett., 2014, 14, 6400–6406 CrossRef CAS.
- J. F. Gao, X. J. Liu, G. Zhang and Y. W. Zhang, Nanoscale, 2016, 8, 17940–17949 RSC.
- Y. J. Lee, J. Y. Yoon, D. Scullion, J. S. Jang, E. J. G. Santos, H. Y. Jeong and K. Kim, J. Phys. D: Appl. Phys., 2017, 50, 084003 CrossRef.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116 CrossRef.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- V. Sorkin and Y. W. Zhang, Nanotechnology, 2015, 26, 235707 CrossRef CAS.
- M. Hart, E. E. White, J. Chen, C. M. McGilvery, C. J. Pickard, A. Michaelides, A. Sella, M. S. P. Shaffer and C. G. Salzmann, Angew. Chem., Int. Ed., 2017, 56, 8144–8148 CrossRef CAS.
- M. Ruck, D. Hoppe, B. Wahl, P. Simon, Y. K. Wang and G. Seifert, Angew. Chem., Int. Ed., 2005, 44, 7616–7619 CrossRef CAS.
- M. J. Frisch, et al., Gaussian 09 (Revision C.0), Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- T. M. Zhang, Y. Y. Wan, H. Y. Xie, Y. Mu, P. W. Du, D. Wang, X. J. Wu, H. X. Ji and L. J. Wan, J. Am. Chem. Soc., 2018, 140, 7561–7567 CrossRef CAS.
- S. Khalid, A. Sharan and A. Janotti, Phys. Rev. B, 2020, 101, 125105 CrossRef CAS.
- L. Qiu, J. C. Dong and F. Ding, Nanoscale, 2019, 11, 7135–7139 RSC.
- H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. F. Xu, D. Tománek and P. D. Ye, ACS Nano, 2014, 8, 4033–4041 CrossRef CAS.
- S. H. Lu, D. Fan, C. K. Chen, Y. S. Mei, Y. M. Ma and X. J. Hu, Carbon, 2020, 159, 9–15 CrossRef CAS.
- Q. Wang, R. Pang and X. Q. Shi, J. Phys. Chem. C, 2015, 119, 22534–22541 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11189 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Paier, M. Marsman, K. Hummer, G. Kress, I. C. Gerber and J. G. Angyan, J. Chem. Phys., 2006, 125, 249901 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The metastable edge structures of black phosphorene, the band structures based on the PBE method, the experimental results from Meunier's group, the band structures and density of states of pristine edges, and the band gaps of edge reconstructed BPNRs as a function of their width. See DOI: 10.1039/d0nh00506a |
| This journal is © The Royal Society of Chemistry 2021 |